We consider the connected-sum method of constructing compact Riemannian 7-manifolds with holonomy G2 developed by the first named author. The method requires pairs of projective complex threefolds endowed with anticanonical K3 divisors and the latter K3 surfaces should satisfy a certain ‘matching condition’ intertwining on their periods and Kähler classes. Suitable examples of threefolds were previously obtained by blowing up curves in Fano threefolds.

In this paper, we give a large new class of suitable algebraic threefolds using theory of K3 surfaces with non-symplectic involution due to Nikulin. These threefolds are not obtainable from Fano threefolds as above, and admit matching pairs leading to topologically new examples of compact irreducible G2-manifolds. ‘Geography’ of the values of Betti numbers b2, b3 for the new (and previously known) examples of irreducible G2 manifolds is also discussed.

Let m ≥ 2 be an integer, and π an irreducible unitary cuspidal representation for GLm(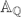), whose attached automorphic L-function is denoted by L(s, π). Let {λπ(n)}n=1∞ be the sequence of coefficients in the Dirichlet series expression of L(s, π) in the half-plane ℜs > 1. It is proved in this paper that, if π is such that the sequence {λπ(n)}n=1∞ is real, then the first sign change in the sequence {λπ(n)}n=1∞ occurs at some n ≪ Qπ1 + ϵ, where Qπ is the conductor of π, and the implied constant depends only on m and ϵ. This improves the previous bound with the above exponent 1 + ϵ replaced by m/2 + ϵ. A result of the same quality is also established for {Λ(n)aπ(n)}n=1∞, the sequence of coefficients in the Dirichlet series expression of −(L′/L)(s, π) in the half-plane ℜs > 1.

We study the Selmer group of an elliptic curve over an admissible p-adic Lie extension of a number field F. We give a formula for the Akashi series attached to this module, in terms of the corresponding objects for the cyclotomic ℤp-extension and certain correction terms. This extends our earlier work [16], in particular since it applies to elliptic curves having split multiplicative reduction at some primes above p, in which case the Akashi series can have additional zeros.

Let A1 = K〈X, Y|[Y, X]=1〉 be the (first) Weyl algebra over a field K of characteristic zero. It is known that the set of eigenvalues of the inner derivation ad(YX) of A1 is ℤ. Let A1 → A1, X ↦ x, Y ↦ y, be a K-algebra homomorphism, i.e. [y, x] = 1. It is proved that the set of eigenvalues of the inner derivation ad(yx) of the Weyl algebra A1 is ℤ and the eigenvector algebra of ad(yx) is K〈x, y〉 (this would be an easy corollary of the Problem/Conjecture of Dixmier of 1968 [still open]: is an algebra endomorphism of A1 an automorphism?).

We present a method to construct examples of K3 surfaces of geometric Picard rank 1. Our approach is a refinement of that of R. van Luijk. It is based on an analysis of the Galois module structure on étale cohomology. This allows us to abandon the original limitation to cases of Picard rank 2 after reduction modulo p. Furthermore, the use of Galois data enables us to construct examples that require significantly less computation time.

In this paper, as a suitable application of the well-known generalized maximum principle of Omori–Yau, we obtain uniqueness results concerning to complete spacelike hypersurfaces with constant mean curvature immersed in a Robertson–Walker (RW) spacetime. As an application of such uniqueness results for the case of vertical graphs in a RW spacetime, we also get non-parametric rigidity results.

A chain is a configuration in ℝd of segments of length ℓ1, . . ., ℓn−1 consecutively joined to each other such that the resulting broken line connects two given points at a distance ℓn. For a fixed generic set of length parameters the space of all chains in ℝd is a closed smooth manifold of dimension (n − 2)(d − 1) − 1. In this paper we study cohomology algebras of spaces of chains. We give a complete classification of these spaces (up to equivariant diffeomorphism) in terms of linear inequalities of a special kind which are satisfied by the length parameters ℓ1, . . ., ℓn. This result is analogous to the conjecture of K. Walker which concerns the special case d=2.

Following an example discovered by John Berge [2], we show that there is a 4-component link L ⊂ (S1 × S2)#(S1 × S2) so that, generically, the result of Dehn surgery on L is a 3-manifold with two inequivalent genus 2 Heegaard splittings, and each of these Heegaard splittings is of Hempel distance 3.

We show that any nonminimal bridge decomposition of a torus knot is stabilized and that n-bridge decompositions of a torus knot are unique for any integer n. This implies that a knot in a bridge position is a torus knot if and only if there exists a torus containing the knot such that it intersects the bridge sphere in two essential loops.

We generalize the notion of totally peripheral 3-manifolds to define homologically peripheral 3-manifolds. The homologically peripheral property survives canonical decompositions of 3-manifolds as well as it defines a sufficiently large class of 3-manifolds containing link exteriors. The aim of this paper is to study finite group actions on a homologically peripheral 3-manifold, which agree on the boundary, up to equivalence relative to the boundary. As an application, we generalize Sakuma's theorems on the uniqueness of symmetries of knots to the case of symmetries of links.

It is shown that the well-known connection between the second order linear differential equation h″ + B(z)h = 0, with a solution base {h1, h2}, and the Schwarzian derivativeof f = h1/h2, can be extended to the equation h(k) + B(z) h = 0 where k ≥ 2. This generalization depends upon an appropriate definition of the generalized Schwarzian derivative Sk(f) of a function f which is induced by k−1 ratios of linearly independent solutions of h(k) + B(z) h = 0. The class k(Ω) of meromorphic functions f such that Sk(f) is analytic in a given domain Ω is also completely described. It is shown that if Ω is the unit disc or the complex plane , then the order of growth of f ∈ k(Ω) is precisely determined by the growth of Sk(f), and vice versa. Also the oscillation of solutions of h(k) + B(z) h = 0, with the analytic coefficient B in or , in terms of the exponent of convergence of solutions is briefly discussed.

We investigate the box dimensions of the horizon of a fractal surface defined by a function f ∈ C[0,1]2. In particular we show that a prevalent surface satisfies the ‘horizon property’, namely that the box dimension of the horizon is one less than that of the surface. Since a prevalent surface has box dimension 3, this does not give us any information about the horizon of surfaces of dimension strictly less than 3. To examine this situation we introduce spaces of functions with surfaces of upper box dimension at most α, for α ∈ [2,3). In this setting the behaviour of the horizon is more subtle. We construct a prevalent subset of these spaces where the lower box dimension of the horizon lies between the dimension of the surface minus one and 2. We show that in the sense of prevalence these bounds are as tight as possible if the spaces are defined purely in terms of dimension. However, if we work in Lipschitz spaces, the horizon property does indeed hold for prevalent functions. Along the way, we obtain a range of properties of box dimensions of sums of functions.

Let n be the collection of all (Littlewood) polynomials of degree n with coefficients in {−1, 1}. In this paper we prove that if (P2ν) is a sequence of cyclotomic polynomials P2ν ∈ 2ν, thenfor every q > 2 with some a = a(q) > 1/2 depending only on q, whereThe case q = 4 of the above result is due to P. Borwein, Choi and Ferguson. We also prove that if (P2ν) is a sequence of cyclotomic polynomials P2ν ∈ 2ν, thenfor every 0 < q < 2 with some 0 < b = b(q) < 1/2 depending only on q. Similar results are conjectured for Littlewood polynomials of odd degree. Our main tool here is the Borwein–Choi Factorization Theorem.