Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-14T08:27:47.705Z Has data issue: false hasContentIssue false
  • English
  • Français

The Product of Exponents in the Factorization of Consecutive Integers

Part of: Multiplicative number theory

Published online by Cambridge University Press:  21 December 2009

Jean-Marie de Koninck  and
Florian Luca
Jean-Marie de Koninck
Affiliation:
Département de mathématiques, Université Laval, Québec G1K 7P4, Canada, E-mail: jmdk@mat.ulaval.ca
Florian Luca
Affiliation:
Mathematical Institute, UNAM, Ap. Postal 61-3 (Xangari), CP 58 089, Morelia, Michoacán, Mexico, E-mail: fluca@matmor.unam.mx
Get access

Abstract

For each integer n ≥ 2, let β(n) stand for the product of the exponents in the prime factorization of n. Given an arbitrary integer k ≥ 2, let nk be the smallest positive integer n such that β(n + 1) = β(n + 2) = … = β(n + k). We prove that there exist positive constants c1 and c2 such that, for all integers k ≥ 2,

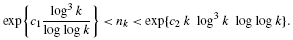
MSC classification

Secondary: 11N37: Asymptotic results on arithmetic functions
Type
Research Article
Information
Mathematika , Volume 55 , Issue 1-2 , December 2009 , pp. 59 - 65
Copyright
Copyright © University College London 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Heath-Brown, D. R., The divisor function at consecutive integers. Mathematika 31 (1984), 141–149.CrossRefGoogle Scholar