Contents
Research Article
Exponential Squared Integrability of the Discrepancy Function in Two Dimensions
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 1-27
-
- Article
- Export citation
Spectral Convergence for High-Contrast Elliptic Periodic Problems with a Defect Via Homogenization
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 29-57
-
- Article
- Export citation
The Product of Exponents in the Factorization of Consecutive Integers
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 59-65
-
- Article
- Export citation
A Step Beyond Kemperman's Structure Theorem
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 67-114
-
- Article
- Export citation
Multiplicative Invariants and the Finite Co-Hopfian Property
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 115-127
-
- Article
- Export citation
Approximate Kernel Clustering
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 129-165
-
- Article
- Export citation
The Artin–Carmichael Primitive Root Problem on Average
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 167-176
-
- Article
- Export citation
Markov Type of Alexandrov Spaces of Non-Negative Curvature Shin-Ichi Ohta
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 177-189
-
- Article
- Export citation
On Extensions of Valuations with given Residue Field and Value Group
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2009, pp. 191-197
-
- Article
- Export citation
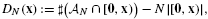
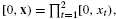 and |[
and |[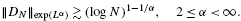
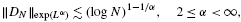
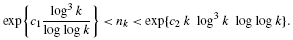
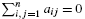 and a small
and a small