Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T21:41:32.939Z Has data issue: false hasContentIssue false
  • English
  • Français

A Large Deviations Approach to the Geometry of Random Polytopes

Part of: General convexity Geometric probability and stochastic geometry

Published online by Cambridge University Press:  21 December 2009

D. Gatzouras  and
A. Giannopoulos
D. Gatzouras
Affiliation:
Department of Mathematics, Secondary, Agricultural University of Athens, Iera Odos 75, 118 55 Athens, Greece. E-mail: gatzoura@aua.gr
A. Giannopoulos
Affiliation:
Department of Mathematics, University of Athens, Panepistimiopolis, 157 84, Athens, Greece. E-mail: apgiannop@math.uoa.gr
Get access

Extract

The aim of this article is to present a general “large deviations approach” to the geometry of polytopes spanned by random points with independent coordinates. The origin of our work is in the study of the structure of ±1-polytopes, the convex hulls of subsets of the combinatorial cube 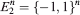. Understanding the complexity of this class of polytopes is important for the “polyhedral combinatorics” approach to combinatorial optimization, and was put forward by Ziegler in [20]. Many natural questions regarding the behaviour of ±1-polytopes in high dimensions are open, since, for many important geometric parameters, low-dimensional intuition does not help to identify the extremal ±1-polytopes. The study of random ±1-polytopes sheds light to some of these questions, the main reason being that random behaviour is often the extremal one.

MSC classification

Secondary: 52A22: Random convex sets and integral geometry 60D05: Geometric probability and stochastic geometry
Type
Research Article
Information
Mathematika , Volume 53 , Issue 2 , December 2006 , pp. 173 - 210
Copyright
Copyright © University College London 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bahadur, R. R. and Rao, R. Ranga, On deviations of the sample mean. Ann. Math. Statist. 31 (1960), 1015–1027.CrossRefGoogle Scholar
2Bárány, I. and Pór, A., On 0–1 polytopes with many facets. Advances Math. 161 (2001), 209–228.CrossRefGoogle Scholar
3Dembo, A. and Zeitouni, O., Large Deviations Techniques and Applications (2nd ed.). Springer (New York, 1998).CrossRefGoogle Scholar
4Dyer, M. E., Füredi, Z. and McDiarmid, C., Volumes spanned by random points in the hypercube. Random Structures Algorithms 3 (1992), 91–106.CrossRefGoogle Scholar
5Feller, W., An Introduction to Probability and its Applications Vol. I (3rd ed.). Wiley (New York, 1968).Google Scholar
6Feller, W., An Introduction to Probability and its Applications Vol. II (2nd ed.). Wiley (New York, 1971).Google Scholar
7Gatzouras, D. and Giannopoulos, A., Threshold for the volume spanned by random points with independent coordinates (preprint).Google Scholar
8Gatzouras, D., Giannopoulos, A. and Markoulakis, N., Lower bound for the maximal number of facets of a 0/1 polytope. Discrete Comput. Geom. 34 (2005), 331–349.CrossRefGoogle Scholar
9Gatzouras, D., Giannopoulos, A. and Markoulakis, N., On the maximal number of facets of 0/1 polytopes. GAFA Seminar Volume (to appear).Google Scholar
10Giannopoulos, A. and Hartzoulaki, M., Random spaces generated by vertices of the cube. Discrete Comput. Geom. 28 (2002), 255–273.CrossRefGoogle Scholar
11Ito, K. and McKean, H. P., Diffusion Processes and their Sample Paths. Springer-Verlag (1965).Google Scholar
12Klartag, B. and Vershynin, R., Small ball probability and Dvoretzky theorem. Israel J. Math. (to appear).Google Scholar
13Latala, R., Private communication.Google Scholar
14Litvak, A. E., Pajor, A., Rudelson, M. and Tomczak-Jaegermann, N., Smallest singular value of random matrices and geometry of random polytopes. Advances Math. 195 (2005), 491–523.CrossRefGoogle Scholar
15Mendelson, S., Pajor, A. and Rudelson, M., On the geometry of random {−1, 1}-polytopes. Discrete Comput. Geom. 34 (2005), 365–379.CrossRefGoogle Scholar
16Montgomery-Smith, S. J., The distribution of Rademacher Sums. Proc. Amer. Math. Soc. 109 (1990), 517–522.CrossRefGoogle Scholar
17Schneider, R., Convex Bodies: the Brunn-Minkowski Theory (Encyclopedia of Mathematics and its Applications 44). Cambridge University Press (Cambridge, 1993).CrossRefGoogle Scholar
18Stroock, D., Probability Theory: an Analytic View. Cambridge University Press (Cambridge, 1993).Google Scholar
19Szarek, S. J. and Werner, E., A nonsymmetric correlation inequality for Gaussian measure. J. Multivariate Anal. 68 (1999), No. 2, 193–211.CrossRefGoogle Scholar
20Ziegler, G. M., Lectures on 0/1 polytopes. In Polytopes – Combinatorics and Computation (Kalai, G. and Ziegler, G. M., eds.), DMV Seminars, Birkhäuser (Basel, 2000), 1–44.Google Scholar