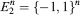The aim of this article is to present a general “large deviations approach” to the geometry of polytopes spanned by random points with independent coordinates. The origin of our work is in the study of the structure of ±1-polytopes, the convex hulls of subsets of the combinatorial cube . Understanding the complexity of this class of polytopes is important for the “polyhedral combinatorics” approach to combinatorial optimization, and was put forward by Ziegler in [20]. Many natural questions regarding the behaviour of ±1-polytopes in high dimensions are open, since, for many important geometric parameters, low-dimensional intuition does not help to identify the extremal ±1-polytopes. The study of random ±1-polytopes sheds light to some of these questions, the main reason being that random behaviour is often the extremal one.

Analogues of the classical inequalities from the Brunn-Minkowski theory for rotation intertwining additive maps of convex bodies are developed. Analogues are also proved of inequalities from the dual Brunn-Minkowski theory for intertwining additive maps of star bodies. These inequalities provide generalizations of results for projection and intersection bodies. As a corollary, a new Brunn-Minkowski inequality is obtained for the volume of polar projection bodies.

The lower dimensional Busemann-Petty problem asks whether origin-symmetric convex bodies in ℝ n with smaller i-dimensional central sections necessarily have smaller volume. A generalization of this problem is studied, when the volumes are measured with weights satisfying certain conditions. The case of hyperplane sections (i = n − 1) has been studied by A. Zvavitch.

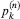Assume that n points P1,…,Pn are distributed independently and uniformly in the triangle with vertices (0, 1), (0, 0), and (1, 0). Consider the convex hull of (0, 1), P1,…,Pn, and (1, 0). The vertices of the convex hull form a convex chain. Let be the probability that the convex chain consists – apart from the points (0, 1) and (1, 0) – of exactly 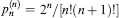k of the points P1,…,Pn. Bárány, Rote, Steiger, and Zhang [3] proved that . The values of are determined for k = 1,…,n − 1, and thus the distribution of the number of vertices of a random convex chain is obtained. Knowing this distribution provides the key to the answer of some long-standing questions in geometrical probability.

For a stationary random closed set Ξ in ℝd it is well known that the first-order characteristics volume fraction VV, surface intensity SV and spherical contact distribution function Hs(t) are related by

(1 – VV) Hs′(0) = SV.

It is shown that every Banach space with a norming Markushevich basis has a strong Markushevich basis. It is also shown that the converse is false.