Article contents
Neighbourliness of centrally symmetric polytopes in high dimensions
Published online by Cambridge University Press: 26 February 2010
Extract
A centrally symmetric d-polytope (d-dimensional convex polytope) P in Euclidean space Ed is called k-neighbourly provided every subset of k vertices of P, which does not contain two opposite vertices of P, is the set of vertices of a (k − 1)-simplex which is a face of P. Contrasting the situation of neighbourly polytopes without the symmetry assumption (see, e.g., Griinbaum [1; chap. 7]), it appears that the possible neighbourliness properties of centrally symmetric polytopes are rather restricted. For d ≥ 2 and n ≥ 1, let k(d, n) denote the greatest integer k, such that there exists a k-neighbourly, centrally symmetric d-polytope with 2(d + n) vertices. McMullen and Shephard [4] have shown that 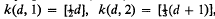 , and
, and 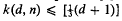 for n ≥ 3. They conjectured that
for n ≥ 3. They conjectured that
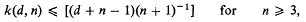
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1975
References
- 8
- Cited by

