Contents
Research Article
One-class genera of positive ternary quadratic forms—II
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-11
-
- Article
- Export citation
On the periods of Abelian functions in two variables
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 97-107
-
- Article
- Export citation
An Ω-result for the coefficients of cusp forms
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 12-19
-
- Article
- Export citation
On norms of integers in a full module of an algebraic number field and the distribution of values of binary integral quadratic forms
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 108-111
-
- Article
- Export citation
Spira's theorems on complete linear proofs of systems of linear inequalities
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 112-121
-
- Article
- Export citation
On a theorem of Heilbronn
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 20-28
-
- Article
- Export citation
On a metrical theorem of Weyl
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 29-33
-
- Article
- Export citation
Short surface waves due to a heaving torus
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 122-134
-
- Article
- Export citation
On the two-dimensional inviscid flow from symmetric slowly varying nozzles
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 135-140
-
- Article
- Export citation
On the theory of stress concentration for shear-strained prismatical bodies with a non-linear stress-strain law
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 34-42
-
- Article
- Export citation
A note on universal sets for classes of countable Gδ'S
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 43-45
-
- Article
- Export citation
Discrete parabolic representations of link groups
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-150
-
- Article
- Export citation
On waves in a thin rotating spherical shell of slightly viscous fluid
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 46-59
-
- Article
- Export citation
A property of polynomials over a finite field
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-153
-
- Article
- Export citation
On the first end invariant of an exact sequence
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 60-70
-
- Article
- Export citation
On the fractional parts of the sum of powers of rational numbers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 154-155
-
- Article
- Export citation
Galois module structure of classgroups and units
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 156-160
-
- Article
- Export citation
On the norms of algebraic integers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 71-80
-
- Article
- Export citation
A lattice-point problem in hyperbolic space
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 81-88
-
- Article
- Export citation
Absolutely non-measurable and singular co-analytic set
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 161-163
-
- Article
- Export citation
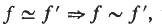 , where
, where 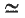 denote equivalence and semi-equivalence respectively. Trivially, it suffices to find the primitive
denote equivalence and semi-equivalence respectively. Trivially, it suffices to find the primitive 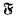 of Abelian functions on the quotient space C
of Abelian functions on the quotient space C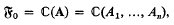
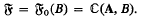
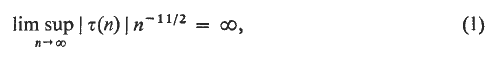
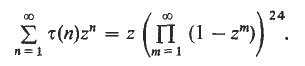
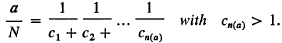
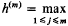 h
h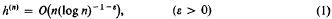
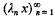
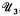 , and that each discrete subgroup of PSL(ℂ) acts discontinuously on
, and that each discrete subgroup of PSL(ℂ) acts discontinuously on 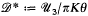 . The present paper is a study of the general relations between the algebraic properties of a discrete image
. The present paper is a study of the general relations between the algebraic properties of a discrete image 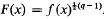 . Consider the continued fraction expansions
. Consider the continued fraction expansions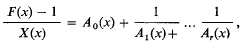
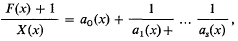
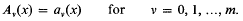
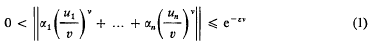
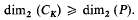
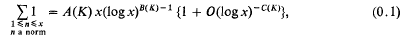
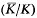 and Gal
and Gal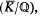 , where
, where 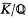 is the normal hull of
is the normal hull of 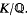 .
.