Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T21:51:12.894Z Has data issue: false hasContentIssue false
  • English
  • Français

Unions of products of independent sets

Part of: Classical measure theory

Published online by Cambridge University Press:  26 February 2010

Zoltán Buczolich
Zoltán Buczolich
Affiliation:
Department of Analysis, Eötvös Loránd University, Múzeum krt. 6-8, Budapest, Hungary, H-1088.
Get access

Abstract

We show that there exists an open set H⊆[0, 1] × [0, 1] with λ2(H) = 1 such that for any ε > 0 there exists a set E satisfying 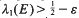and H contains the product set E × E but there is no set S with 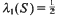and S × S ⊆ H. Especially this property is verified for sets of the form H = 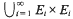where the sets Ei are independent and 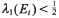. The results of this paper answer questions of M. Laczkovich and are related to a paper of D. H. Fremlin.

MSC classification

Secondary: 28A35: Measures and integrals in product spaces
Type
Research Article
Information
Mathematika , Volume 42 , Issue 1 , June 1995 , pp. 25 - 29
Copyright
Copyright © University College London 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Freralin, D. H.. Covering squares with independent squares. Mathematika, 38 (1991), 329–333.Google Scholar
1.Sazonov, V. V.. On perfect measures. Amer. Math. Soc. Translations (2), 48 (1965), 229–254. (Original version: Izv. Akad. Nauk. USSR, 26 (1962), 391-414.)CrossRefGoogle Scholar