Contents
Research Article
Order-two density of sets and measures with non-integral dimension
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-14
-
- Article
- Export citation
On the existence of subsets of finite positive packing measure
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 15-24
-
- Article
- Export citation
Unions of products of independent sets
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-29
-
- Article
- Export citation
Baire trees, bad norms and the Namioka property
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 30-42
-
- Article
- Export citation
Recovering Baire 1 functions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 43-48
-
- Article
- Export citation
On metrizable E with Cp(E) ≇ Cp(E) × Cp(E)
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-55
-
- Article
- Export citation
A generic factorization theorem
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 56-66
-
- Article
- Export citation
Infima of hyperspace topologies
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 67-86
-
- Article
- Export citation
On Cesaro summable sequences of continuous functions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 87-104
-
- Article
- Export citation
The rotation of two circular cylinders in a viscous fluid
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 105-126
-
- Article
- Export citation
A note on Stokes flow due to a line rotlet
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-132
-
- Article
- Export citation
Mean values of character sums III
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 133-136
-
- Article
- Export citation
A special triple exponential sum
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 137-143
-
- Article
- Export citation
A sharp inequality of Halász type for the mean value of a multiplicative arithmetic function
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 144-157
-
- Article
- Export citation
Mean-values of the Riemann zeta-function
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 158-174
-
- Article
- Export citation
A lattice without a basis of minimal vectors
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 175-177
-
- Article
- Export citation
How do convex bodies sit?
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 178-181
-
- Article
- Export citation
Symbolic powers and local cohomology
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 182-187
-
- Article
- Export citation
Ascendant subgroups of factorized FC-groups
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 188-189
-
- Article
- Export citation
The value set of polynomials over ℤm and the combinatorics of sequences
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 190-198
-
- Article
- Export citation
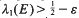 and
and 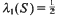 and
and 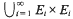 where the sets
where the sets 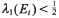 . The results of this paper answer questions of M. Laczkovich and are related to a paper of D. H. Fremlin.
. The results of this paper answer questions of M. Laczkovich and are related to a paper of D. H. Fremlin.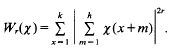
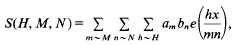
 ,
, 
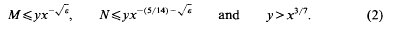
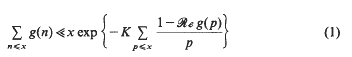
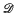 for all primes
for all primes 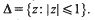 Thus our point of view is similar to that of Halász [Hz 2] in that we seek a general inequality in terms of simple quantities, albeit
Thus our point of view is similar to that of Halász [Hz 2] in that we seek a general inequality in terms of simple quantities, albeit 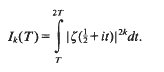
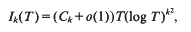
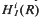 , and the comparison of the topologies defined by the
, and the comparison of the topologies defined by the