No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 20 January 2009
§ 1. It is well known that, if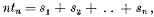 
, the convergence of sn to a limit implies the convergence of tn to the same limit. The converse theorem, that the convergence of tn implies the convergence of sn, is false. Mercer1 proved, however, that if 
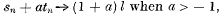, then both sn and tn tend to l. This theorem has recently been extended in various directions.2 In the present note the case of Abel limits is considered.
page 108 note 1 Proc. London Math. Soc., (2), 5, (1907), 206–224.Google Scholar
page 108 note 2 Cf. Vijayaraghavan, Journal London Math. Soc., 3, (1928), 130–134, (who gives references to previous work on the subject); Copson and Ferrar, ibid., 4, (1929), 258–264 ; 5 (1930), 21–27.
page 108 note 3 See, for example, Knopp, Infinite Series, (1928), 498et seq.Google Scholar
page 110 note 1 Journal London Math. Soc., 4 (1929), 258–264; Theorem IV .Google Scholar
You have
Access