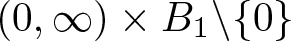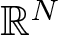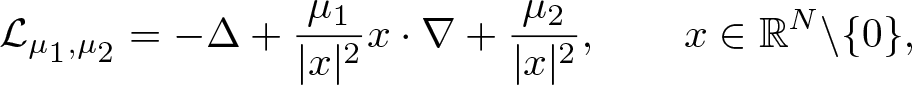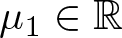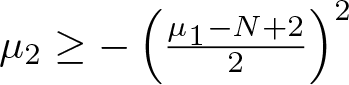1. Introduction
For a natural number ![]() $N\geq 2$ and
$N\geq 2$ and ![]() $\mu_1,\mu_2\in \mathbb{R}$, we consider differential operators of the form
$\mu_1,\mu_2\in \mathbb{R}$, we consider differential operators of the form
 \begin{equation*}
\mathcal{L}_{\mu_1,\mu_2}=-\Delta +\frac{\mu_1}{|x|^2}x\cdot \nabla +\frac{\mu_2}{|x|^2},\qquad x\in \mathbb{R}^N\backslash\{0\},
\end{equation*}
\begin{equation*}
\mathcal{L}_{\mu_1,\mu_2}=-\Delta +\frac{\mu_1}{|x|^2}x\cdot \nabla +\frac{\mu_2}{|x|^2},\qquad x\in \mathbb{R}^N\backslash\{0\},
\end{equation*}where · denotes the inner product in ![]() $\mathbb{R}^N$. The considered operators arise from the critical Caffarelli–Kohn–Nirenberg inequality, see [Reference Caffarelli, Kohn and Nirenberg5, Reference Chen and Zheng9, Reference Wang and Willem35] for more details. Notice that for
$\mathbb{R}^N$. The considered operators arise from the critical Caffarelli–Kohn–Nirenberg inequality, see [Reference Caffarelli, Kohn and Nirenberg5, Reference Chen and Zheng9, Reference Wang and Willem35] for more details. Notice that for ![]() $\mu_i\neq 0$,
$\mu_i\neq 0$, ![]() $i=1,2$,
$i=1,2$, ![]() $\mathcal{L}_{\mu_1,\mu_2}$ is degenerate at the origin both for the gradient term and the critical Hardy term.
$\mathcal{L}_{\mu_1,\mu_2}$ is degenerate at the origin both for the gradient term and the critical Hardy term.
In this paper, we are concerned with the study of existence and non-existence of weak solutions to evolution inequalities of the form
 \begin{eqnarray}
\left\{\begin{array}{llll}
\partial_t^k u+\mathcal{L}_{\mu_1,\mu_2}(|u|^{q-1}u)\geq |x|^{-a} |u|^p \quad &\mbox{in }\ (0,\infty)\times B_1\backslash\{0\}, \\[3.5mm]
|u|^{q-1}u(t,x)\geq f(x)\quad &\mbox{for }\ (t,x)\in (0,\infty)\times \partial B_1,
\end{array}
\right.
\end{eqnarray}
\begin{eqnarray}
\left\{\begin{array}{llll}
\partial_t^k u+\mathcal{L}_{\mu_1,\mu_2}(|u|^{q-1}u)\geq |x|^{-a} |u|^p \quad &\mbox{in }\ (0,\infty)\times B_1\backslash\{0\}, \\[3.5mm]
|u|^{q-1}u(t,x)\geq f(x)\quad &\mbox{for }\ (t,x)\in (0,\infty)\times \partial B_1,
\end{array}
\right.
\end{eqnarray}where ![]() $k\geq 1$ is a natural number,
$k\geq 1$ is a natural number,  $\partial_t^k:=\frac{\partial^k}{\partial t^k}$,
$\partial_t^k:=\frac{\partial^k}{\partial t^k}$, ![]() $\mu_1\in \mathbb{R}$,
$\mu_1\in \mathbb{R}$,  $\mu_2\geq -\left(\frac{\mu_1-N+2}{2}\right)^2$,
$\mu_2\geq -\left(\frac{\mu_1-N+2}{2}\right)^2$, ![]() $p \gt q\geq 1$,
$p \gt q\geq 1$, ![]() $a\in \mathbb{R}$,
$a\in \mathbb{R}$, ![]() $B_1=\{x\in \mathbb{R}^N: |x|\leq 1\}$ and
$B_1=\{x\in \mathbb{R}^N: |x|\leq 1\}$ and ![]() $f\in L^1(\partial B_1)$ is a non-trivial function.
$f\in L^1(\partial B_1)$ is a non-trivial function.
In the special case ![]() $\mu_2=0$, the operator
$\mu_2=0$, the operator  $\mathcal{L}_{\mu_1,0}=-\Delta +\frac{\mu_1}{|x|^2}x\cdot \nabla$ is a type of degenerate elliptic operator, which together with its divergence form plays an important role in the harmonic analysis, see for example [Reference Muckenhoupt29]. Some studies related to regularities and qualitative properties for elliptic equations with more general degenerate operators in divergence form can be found in [Reference Fabes, Kenig and Serapioni13, Reference Sire, Terracini and Vita31]. The study of existence and non-existence of solutions to evolution equations and inequalities involving operators of the form
$\mathcal{L}_{\mu_1,0}=-\Delta +\frac{\mu_1}{|x|^2}x\cdot \nabla$ is a type of degenerate elliptic operator, which together with its divergence form plays an important role in the harmonic analysis, see for example [Reference Muckenhoupt29]. Some studies related to regularities and qualitative properties for elliptic equations with more general degenerate operators in divergence form can be found in [Reference Fabes, Kenig and Serapioni13, Reference Sire, Terracini and Vita31]. The study of existence and non-existence of solutions to evolution equations and inequalities involving operators of the form ![]() $\mathcal{L}_{\mu,_10}$ has been considered in infinite domains of
$\mathcal{L}_{\mu,_10}$ has been considered in infinite domains of ![]() $\mathbb{R}^N$, see for example [Reference Guo, Wang, Du and Wen18, Reference Jleli, Samet and Sun19, Reference Na, Zhou, Zhou and Gai30, Reference Zheng and Wang37, Reference Zhou, Nie and Han38] and the references therein. For instance, in [Reference Zheng and Wang37], the authors investigated parabolic equations of the form
$\mathbb{R}^N$, see for example [Reference Guo, Wang, Du and Wen18, Reference Jleli, Samet and Sun19, Reference Na, Zhou, Zhou and Gai30, Reference Zheng and Wang37, Reference Zhou, Nie and Han38] and the references therein. For instance, in [Reference Zheng and Wang37], the authors investigated parabolic equations of the form
 \begin{eqnarray}
\left\{\begin{array}{llll}
|x|^{\lambda_1}\partial_tu+\mathcal{L}_{\mu_1,0}u^m =|x|^{\lambda_2}u^p,\ \ u\geq 0 \quad &\mbox{in }\ (0,\infty)\times \mathbb{R}^N\backslash\overline{\Omega}, \\[2mm]
u(t,\cdot)=0\quad &\mbox{on }\ (0,\infty)\times \partial \Omega,\\[2mm]
u(0,\cdot)=u_0\quad &\mbox{in } \ \mathbb{R}^N\backslash\overline{\Omega},
\end{array}
\right.
\end{eqnarray}
\begin{eqnarray}
\left\{\begin{array}{llll}
|x|^{\lambda_1}\partial_tu+\mathcal{L}_{\mu_1,0}u^m =|x|^{\lambda_2}u^p,\ \ u\geq 0 \quad &\mbox{in }\ (0,\infty)\times \mathbb{R}^N\backslash\overline{\Omega}, \\[2mm]
u(t,\cdot)=0\quad &\mbox{on }\ (0,\infty)\times \partial \Omega,\\[2mm]
u(0,\cdot)=u_0\quad &\mbox{in } \ \mathbb{R}^N\backslash\overline{\Omega},
\end{array}
\right.
\end{eqnarray}where Ω is a regular bounded domain in ![]() $\mathbb{R}^N$ containing the origin,
$\mathbb{R}^N$ containing the origin, ![]() $m\geq 1$, p > m,
$m\geq 1$, p > m, ![]() $-2 \lt \lambda_1\leq \lambda_2$ and
$-2 \lt \lambda_1\leq \lambda_2$ and ![]() $\mu_1 \lt N-2$. It was shown that Equation (1.2) admits as Fujita critical exponent the real number
$\mu_1 \lt N-2$. It was shown that Equation (1.2) admits as Fujita critical exponent the real number
 \begin{equation*}
p_c=m+\frac{\lambda_2+2}{\lambda_1+N-\mu_1}.
\end{equation*}
\begin{equation*}
p_c=m+\frac{\lambda_2+2}{\lambda_1+N-\mu_1}.
\end{equation*}More precisely, it was proven that
(i) if
 $0\leq u_0 \in C_0\left(\mathbb{R}^N\backslash\Omega\right)$,
$0\leq u_0 \in C_0\left(\mathbb{R}^N\backslash\Omega\right)$,  $u_0|_{\partial \Omega}=0$,
$u_0|_{\partial \Omega}=0$,  $u_0\not\equiv 0$ and
$u_0\not\equiv 0$ and  $m \lt p \lt p_c$, then any solution to Equation (1.2) blows up in a finite time;
$m \lt p \lt p_c$, then any solution to Equation (1.2) blows up in a finite time;(ii) if
 $p=p_c$, then any nontrivial solution to Equation (1.2) blows up in a finite time;
$p=p_c$, then any nontrivial solution to Equation (1.2) blows up in a finite time;(iii) if
 $p \gt p_c$, then Equation (1.2) admits non-trivial global solutions for some small initial value u 0.
$p \gt p_c$, then Equation (1.2) admits non-trivial global solutions for some small initial value u 0.
Observe that in the special case ![]() $\lambda_1=\lambda_2=\mu_1=0$, m = 1 and
$\lambda_1=\lambda_2=\mu_1=0$, m = 1 and ![]() $N\geq 3$, one has
$N\geq 3$, one has  $p_c=1+\frac{2}{N}$, which is the Fujita critical exponent for the semilinear heat equation
$p_c=1+\frac{2}{N}$, which is the Fujita critical exponent for the semilinear heat equation
For more references related to the study of evolution equations and inequalities in exterior domains, see for example [Reference Jleli, Samet and Vetro20, Reference Jleli, Samet and Ye21, Reference Levine and Zhang23, Reference Sun32, Reference Zhang36].
When ![]() $\mu_1=0$,
$\mu_1=0$,  $\mathcal{L}_{0,\mu_2}=-\Delta +\frac{\mu_2}{|x|^2}$ is the Hardy–Leray operator. Elliptic equations involving such operators have been investigated extensively in the last decades, for instance, the analysis of isolated singular solutions [Reference Chaudhuri and Cirstea6–Reference Chen and Véron8, Reference Cirstea11, Reference Guerch and Véron17], existence and non-existence of solutions [Reference Fall14, Reference Filippucci, Pucci and Robert15, Reference Li24, Reference Merchán and Montoro25, Reference Wang, Wei and Kang34] and qualitative properties of solutions [Reference Chen, Quaas and Zhou10, Reference Lei22, Reference Merchán, Montoro, Peral and Sciunzi26, Reference Montoro and Sciunzi28]. The study of existence and non-existence of solutions to evolution equations and inequalities involving Hardy–Leray potential in infinite domains has been considered in several papers. In [Reference El Hamidi and Laptev12], Hamidi and Laptev investigated the nonexistence of weak solutions to higher-order evolution inequalities of the form
$\mathcal{L}_{0,\mu_2}=-\Delta +\frac{\mu_2}{|x|^2}$ is the Hardy–Leray operator. Elliptic equations involving such operators have been investigated extensively in the last decades, for instance, the analysis of isolated singular solutions [Reference Chaudhuri and Cirstea6–Reference Chen and Véron8, Reference Cirstea11, Reference Guerch and Véron17], existence and non-existence of solutions [Reference Fall14, Reference Filippucci, Pucci and Robert15, Reference Li24, Reference Merchán and Montoro25, Reference Wang, Wei and Kang34] and qualitative properties of solutions [Reference Chen, Quaas and Zhou10, Reference Lei22, Reference Merchán, Montoro, Peral and Sciunzi26, Reference Montoro and Sciunzi28]. The study of existence and non-existence of solutions to evolution equations and inequalities involving Hardy–Leray potential in infinite domains has been considered in several papers. In [Reference El Hamidi and Laptev12], Hamidi and Laptev investigated the nonexistence of weak solutions to higher-order evolution inequalities of the form
 \begin{eqnarray}
\left\{\begin{array}{llll}
\partial_t^k u +\mathcal{L}_{0,\mu_2} u\geq |u|^p\quad \mbox{in }\ (0,\infty)\times \mathbb{R}^N,\\[3mm]
\partial_t^{k-1} u(0,\cdot)\geq 0\quad \mbox{in } \ \mathbb{R}^N,
\end{array}
\right.
\end{eqnarray}
\begin{eqnarray}
\left\{\begin{array}{llll}
\partial_t^k u +\mathcal{L}_{0,\mu_2} u\geq |u|^p\quad \mbox{in }\ (0,\infty)\times \mathbb{R}^N,\\[3mm]
\partial_t^{k-1} u(0,\cdot)\geq 0\quad \mbox{in } \ \mathbb{R}^N,
\end{array}
\right.
\end{eqnarray}where ![]() $N\geq 3$,
$N\geq 3$,  $\mu_2\geq -\left(\frac{N-2}{2}\right)^2$ and p > 1. Namely, it was shown that, if either
$\mu_2\geq -\left(\frac{N-2}{2}\right)^2$ and p > 1. Namely, it was shown that, if either
 \begin{equation*}
\mu_2\geq 0,\qquad 1 \lt p\leq 1+\frac{2}{\frac{2}{k}+s^*};
\end{equation*}
\begin{equation*}
\mu_2\geq 0,\qquad 1 \lt p\leq 1+\frac{2}{\frac{2}{k}+s^*};
\end{equation*}or
 \begin{equation*}
-\left(\frac{N-2}{2}\right)^2\leq \mu_2 \lt 0,\qquad 1 \lt p\leq 1+\frac{2}{\frac{2}{k}-s_*},
\end{equation*}
\begin{equation*}
-\left(\frac{N-2}{2}\right)^2\leq \mu_2 \lt 0,\qquad 1 \lt p\leq 1+\frac{2}{\frac{2}{k}-s_*},
\end{equation*}where
 \begin{equation*}
s^*=\frac{N-2}{2}+\sqrt{\mu_2+\left(\frac{N-2}{2}\right)^2}, \qquad \ s_*=s^*+2-N,
\end{equation*}
\begin{equation*}
s^*=\frac{N-2}{2}+\sqrt{\mu_2+\left(\frac{N-2}{2}\right)^2}, \qquad \ s_*=s^*+2-N,
\end{equation*}then Equation (1.3) admits no non-trivial weak solution. In [Reference Jleli, Samet and Vetro20], the authors considered hyperbolic inequalities of the form
 \begin{eqnarray}
\left\{\begin{array}{llll}
\partial_t^2 u+\mathcal{L}_{0,\mu_2} u\geq |u|^p\quad &\mbox{in }\ (0,\infty)\times \mathbb{R}^N\backslash B_1,\\[2mm]
\alpha\, \displaystyle\frac{\partial u}{\partial \nu} (t,x)+\beta u(t,x)\geq f(x) \quad &\mbox{for }\ (t,x) \in (0,\infty)\times \partial B_1,
\end{array}
\right.
\end{eqnarray}
\begin{eqnarray}
\left\{\begin{array}{llll}
\partial_t^2 u+\mathcal{L}_{0,\mu_2} u\geq |u|^p\quad &\mbox{in }\ (0,\infty)\times \mathbb{R}^N\backslash B_1,\\[2mm]
\alpha\, \displaystyle\frac{\partial u}{\partial \nu} (t,x)+\beta u(t,x)\geq f(x) \quad &\mbox{for }\ (t,x) \in (0,\infty)\times \partial B_1,
\end{array}
\right.
\end{eqnarray}where ![]() $N\geq 2$,
$N\geq 2$,  $\mu_2\geq -\left(({N-2})/{2}\right)^2$,
$\mu_2\geq -\left(({N-2})/{2}\right)^2$, ![]() $\alpha,\beta\geq 0$,
$\alpha,\beta\geq 0$, ![]() $(\alpha,\beta)\neq (0,0)$ and ν is the outward unit normal vector on
$(\alpha,\beta)\neq (0,0)$ and ν is the outward unit normal vector on ![]() $\partial B_1$, relative to
$\partial B_1$, relative to ![]() $\Omega= \mathbb{R}^N\backslash B_1$. It was shown that Equation (1.4) admits a Fujita critical exponent
$\Omega= \mathbb{R}^N\backslash B_1$. It was shown that Equation (1.4) admits a Fujita critical exponent
 \begin{equation*}
p_c(\mu_2,N)=\left\{\begin{array}{llll}
\infty &\mbox{if}\ \ N-2+2\mu_N=0,\\[2mm]
1+\displaystyle\frac{4}{N-2+2\mu_N} &\mbox{if}\ \ N-2+2\mu_N \gt 0,
\end{array}
\right.
\end{equation*}
\begin{equation*}
p_c(\mu_2,N)=\left\{\begin{array}{llll}
\infty &\mbox{if}\ \ N-2+2\mu_N=0,\\[2mm]
1+\displaystyle\frac{4}{N-2+2\mu_N} &\mbox{if}\ \ N-2+2\mu_N \gt 0,
\end{array}
\right.
\end{equation*}where
 \begin{equation*}
\mu_N=\sqrt{\mu_2+\left(\frac{N-2}{2}\right)^2}.
\end{equation*}
\begin{equation*}
\mu_N=\sqrt{\mu_2+\left(\frac{N-2}{2}\right)^2}.
\end{equation*}More precisely, it was proven that
(i) if
 $1 \lt p \lt p_c(\mu_2,N)$ and
$1 \lt p \lt p_c(\mu_2,N)$ and  $\displaystyle\int_{\partial B_1}f(x)\,{\rm d}\sigma \gt 0$, then Equation (1.4) admits no global weak solution;
$\displaystyle\int_{\partial B_1}f(x)\,{\rm d}\sigma \gt 0$, then Equation (1.4) admits no global weak solution;(ii) if
 $p \gt p_c(\mu_2,N)$, then Equation (1.4) admits global solutions for some f > 0.
$p \gt p_c(\mu_2,N)$, then Equation (1.4) admits global solutions for some f > 0.
In the case of bounded domains, some results related to parabolic equations have been obtained. For instance, Abdellaoui et al. [Reference Abdellaoui, Peral and Primo1] considered parabolic equations of the form
 \begin{equation}
\left\{\begin{array}{llll}
\partial_t u+\mathcal{L}_{0,\mu_2} u= u^p+f, \quad u\geq 0 & \mbox{in }\ (0,\infty)\times \Omega, \\[2mm]
u(t,\cdot)=0 &\mbox{on }\ (0,\infty)\times \partial \Omega,\\[2mm]
u(0,\cdot)=u_0 &\mbox{in }\ \ \Omega,
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{\begin{array}{llll}
\partial_t u+\mathcal{L}_{0,\mu_2} u= u^p+f, \quad u\geq 0 & \mbox{in }\ (0,\infty)\times \Omega, \\[2mm]
u(t,\cdot)=0 &\mbox{on }\ (0,\infty)\times \partial \Omega,\\[2mm]
u(0,\cdot)=u_0 &\mbox{in }\ \ \Omega,
\end{array}
\right.
\end{equation}where ![]() $\Omega \subset \mathbb{R}^N$ (
$\Omega \subset \mathbb{R}^N$ (![]() $N\geq 3$) is a bounded regular domain containing the origin, p > 1,
$N\geq 3$) is a bounded regular domain containing the origin, p > 1, ![]() $\mu_2 \lt 0$, and
$\mu_2 \lt 0$, and ![]() $u_0,f\geq 0$ belong to a suitable class of functions. Namely, the existence of a critical exponent
$u_0,f\geq 0$ belong to a suitable class of functions. Namely, the existence of a critical exponent ![]() $p_+(\mu_2)$ was shown such that for
$p_+(\mu_2)$ was shown such that for ![]() $p\geq p_+(\mu_2)$, there is no distributional solution to Equation (1.5), while for
$p\geq p_+(\mu_2)$, there is no distributional solution to Equation (1.5), while for ![]() $p \lt p_+(\mu_2)$ and under some additional conditions on the data, Equation (1.5) admits solutions. Notice that in [Reference Abdellaoui, Peral and Primo1], the positivity of u is essential in the proof of the obtained results. Moreover, in this reference, the authors used the comparison principle for the heat equation, which cannot be applied for our problem (1.1) in the case
$p \lt p_+(\mu_2)$ and under some additional conditions on the data, Equation (1.5) admits solutions. Notice that in [Reference Abdellaoui, Peral and Primo1], the positivity of u is essential in the proof of the obtained results. Moreover, in this reference, the authors used the comparison principle for the heat equation, which cannot be applied for our problem (1.1) in the case ![]() $k\geq 2$. For other contributions related to the study of parabolic equations with Hardy–Leray potential in bounded domains, see for example [Reference Attar, Merchan and Peral2–Reference Cabré and Martel4, Reference Goldstein, Goldstein, Kömbe and Tellioglu16, Reference Vazquez and Zuazua33] and the references therein. To the best of our knowledge, the study of sign-changing solutions to evolution equations or inequalities involving Hardy–Leray potential in bounded domains has not been previously considered in the literature.
$k\geq 2$. For other contributions related to the study of parabolic equations with Hardy–Leray potential in bounded domains, see for example [Reference Attar, Merchan and Peral2–Reference Cabré and Martel4, Reference Goldstein, Goldstein, Kömbe and Tellioglu16, Reference Vazquez and Zuazua33] and the references therein. To the best of our knowledge, the study of sign-changing solutions to evolution equations or inequalities involving Hardy–Leray potential in bounded domains has not been previously considered in the literature.
Very recently, the authors [Reference Chen and Zheng9] studied some basic properties of the operator ![]() $\mathcal{L}_{\mu_1,\mu_2}$. Namely, they analyzed the fundamental solutions in a weighted distributional identity and derived a Liouville-type result for positive solutions to the elliptic inequality
$\mathcal{L}_{\mu_1,\mu_2}$. Namely, they analyzed the fundamental solutions in a weighted distributional identity and derived a Liouville-type result for positive solutions to the elliptic inequality
 \begin{eqnarray}
\left\{\begin{array}{llll}
\mathcal{L}_{\mu_1,\mu_2} u\geq V u^p\quad &\mbox{in }\ \Omega\backslash\{0\},\\[2mm]
u\geq 0\quad &\mbox{on }\ \partial \Omega,
\end{array}
\right.
\end{eqnarray}
\begin{eqnarray}
\left\{\begin{array}{llll}
\mathcal{L}_{\mu_1,\mu_2} u\geq V u^p\quad &\mbox{in }\ \Omega\backslash\{0\},\\[2mm]
u\geq 0\quad &\mbox{on }\ \partial \Omega,
\end{array}
\right.
\end{eqnarray}where p > 1, Ω is a bounded domain in ![]() $\mathbb{R}^N$ (
$\mathbb{R}^N$ (![]() $N\geq 3$) containing the origin, V > 0,
$N\geq 3$) containing the origin, V > 0,  $V\in C_{\operatorname{loc}}^\beta(\mathbb{R}^N\backslash\{0\})$,
$V\in C_{\operatorname{loc}}^\beta(\mathbb{R}^N\backslash\{0\})$, ![]() $0 \lt \beta \lt 1$ and
$0 \lt \beta \lt 1$ and
 \begin{equation*}
\liminf_{|x|\to 0^+} V(x)|x|^{-\rho} \gt 0
\end{equation*}
\begin{equation*}
\liminf_{|x|\to 0^+} V(x)|x|^{-\rho} \gt 0
\end{equation*}for some ![]() $\rho \gt -2$. It was proven that if
$\rho \gt -2$. It was proven that if
 \begin{equation*}
\mu_1 \lt N-2,\qquad -\left(\frac{2-N+\mu_1}{2}\right)^2\leq \mu_2 \lt 0,
\end{equation*}
\begin{equation*}
\mu_1 \lt N-2,\qquad -\left(\frac{2-N+\mu_1}{2}\right)^2\leq \mu_2 \lt 0,
\end{equation*}then for all ![]() $p\geq p^*(\mu_1,\mu_2,\rho)$, Equation (1.3) admits no positive solution, where
$p\geq p^*(\mu_1,\mu_2,\rho)$, Equation (1.3) admits no positive solution, where
 \begin{equation}
p^*(\mu_1,\mu_2,\rho)=1+\frac{2+\rho}{\tau_+(\mu_1,\mu_2)}
\end{equation}
\begin{equation}
p^*(\mu_1,\mu_2,\rho)=1+\frac{2+\rho}{\tau_+(\mu_1,\mu_2)}
\end{equation}and
 \begin{equation*}
\tau_+(\mu_1,\mu_2)=\frac{N-2-\mu_1}{2}-\sqrt{\mu_2+\left(\frac{2-N+\mu_1}{2}\right)^2}.
\end{equation*}
\begin{equation*}
\tau_+(\mu_1,\mu_2)=\frac{N-2-\mu_1}{2}-\sqrt{\mu_2+\left(\frac{2-N+\mu_1}{2}\right)^2}.
\end{equation*}The used approach in [Reference Chen and Zheng9] is based on the classification of isolated singular solutions to the related Poisson problem.
Motivated by the above-mentioned contributions, problem (1.1) is investigated in this paper. Notice that no restriction on the sign of solutions is imposed. Moreover, our obtained results yield naturally existence and non-existence results for the corresponding stationary problem.
It is interesting to observe that in the special case q = 1, making use of the change of variable
 \begin{equation*}
u(t,x)=v(t,x) |x|^{\frac{\mu_1}{2}},\quad t \gt 0,\ x\in B_1\backslash\{0\},
\end{equation*}
\begin{equation*}
u(t,x)=v(t,x) |x|^{\frac{\mu_1}{2}},\quad t \gt 0,\ x\in B_1\backslash\{0\},
\end{equation*}problem (1.1) reduces to
 \begin{eqnarray*}
\left\{\begin{array}{llll}
\partial_t^k v+\mathcal{L}_{0,\mu} v \geq |x|^{\frac{\mu_1(p-1)-2a}{2}} |v|^p \quad &\mbox{in }\ (0,\infty)\times B_1\backslash\{0\}, \\[3mm]
v(t,x)\geq f(x)\quad &\mbox{for }\ (t,x)\in(0,\infty)\times \partial B_1,
\end{array}
\right.
\end{eqnarray*}
\begin{eqnarray*}
\left\{\begin{array}{llll}
\partial_t^k v+\mathcal{L}_{0,\mu} v \geq |x|^{\frac{\mu_1(p-1)-2a}{2}} |v|^p \quad &\mbox{in }\ (0,\infty)\times B_1\backslash\{0\}, \\[3mm]
v(t,x)\geq f(x)\quad &\mbox{for }\ (t,x)\in(0,\infty)\times \partial B_1,
\end{array}
\right.
\end{eqnarray*}where
 \begin{equation*}
\mu=\frac{1}{4}\mu_1^2-\frac{N-2}{2}\mu_1+\mu_2.
\end{equation*}
\begin{equation*}
\mu=\frac{1}{4}\mu_1^2-\frac{N-2}{2}\mu_1+\mu_2.
\end{equation*}Before stating our obtained results, we need to define weak solutions to the considered problem. Let
Notice that ![]() $\Gamma\subset \partial Q$. We introduce the functional space Φ defined as follows.
$\Gamma\subset \partial Q$. We introduce the functional space Φ defined as follows.
Definition 1.1. We say that ![]() $\varphi=\varphi(t,x)$ belongs to Φ if the following conditions are satisfied:
$\varphi=\varphi(t,x)$ belongs to Φ if the following conditions are satisfied:
(i)
 $\varphi\in C_{t,x}^{k,2}(Q)$,
$\varphi\in C_{t,x}^{k,2}(Q)$,  $\varphi\geq 0$;
$\varphi\geq 0$;(ii)
 $\operatorname{supp}(\varphi)\subset\subset Q$;
$\operatorname{supp}(\varphi)\subset\subset Q$;(iii)
 $\varphi|_{\Gamma}=0$,
$\varphi|_{\Gamma}=0$,  $\displaystyle\frac{\partial \varphi}{\partial \nu}\Big|_{\Gamma}\leq 0$, where ν denotes the outward unit normal vector on
$\displaystyle\frac{\partial \varphi}{\partial \nu}\Big|_{\Gamma}\leq 0$, where ν denotes the outward unit normal vector on  $\partial B_1$.
$\partial B_1$.
Using standard integration by parts, we define weak solutions to Equation (1.1) as follows.
Definition 1.2. Weak solutions
We say that ![]() $u\in L^p_{\rm loc}(Q)$ is a weak solution to Equation (1.1), if for all
$u\in L^p_{\rm loc}(Q)$ is a weak solution to Equation (1.1), if for all ![]() $\varphi\in \Phi$, there holds
$\varphi\in \Phi$, there holds
 \begin{equation}
\int_Q |x|^{-a} |u|^p\varphi\,{\rm d}x\,{\rm d}t -\int_{\Gamma} \frac{\partial \varphi}{\partial \nu}f\,{\rm d}\sigma\,{\rm d}t\leq (-1)^k\int_Q u \partial_t^k\varphi\,{\rm d}x\,{\rm d}t + \int_Q |u|^{q-1}u\,\mathcal{L}_{\mu_1,\mu_2}^*\varphi\,{\rm d}x\,{\rm d}t,
\end{equation}
\begin{equation}
\int_Q |x|^{-a} |u|^p\varphi\,{\rm d}x\,{\rm d}t -\int_{\Gamma} \frac{\partial \varphi}{\partial \nu}f\,{\rm d}\sigma\,{\rm d}t\leq (-1)^k\int_Q u \partial_t^k\varphi\,{\rm d}x\,{\rm d}t + \int_Q |u|^{q-1}u\,\mathcal{L}_{\mu_1,\mu_2}^*\varphi\,{\rm d}x\,{\rm d}t,
\end{equation}where ![]() $\mathcal{L}_{\mu_1,\mu_2}^*$ is the adjoint operator of
$\mathcal{L}_{\mu_1,\mu_2}^*$ is the adjoint operator of ![]() $\mathcal{L}_{\mu_1,\mu_2}$, given by
$\mathcal{L}_{\mu_1,\mu_2}$, given by
 \begin{equation}
\mathcal{L}_{\mu_1,\mu_2}^*\varphi =-\Delta \varphi-\mu_1\operatorname{div}\left(\frac{\varphi x}{|x|^2}\right)+\frac{\mu_2}{|x|^2}\varphi.
\end{equation}
\begin{equation}
\mathcal{L}_{\mu_1,\mu_2}^*\varphi =-\Delta \varphi-\mu_1\operatorname{div}\left(\frac{\varphi x}{|x|^2}\right)+\frac{\mu_2}{|x|^2}\varphi.
\end{equation} For ![]() $\mu_1\in \mathbb{R}$ and
$\mu_1\in \mathbb{R}$ and  $\mu_2\geq -\left(\frac{\mu_1-N+2}{2}\right)^2$, we introduce the parameter α given by
$\mu_2\geq -\left(\frac{\mu_1-N+2}{2}\right)^2$, we introduce the parameter α given by
 \begin{equation}
\alpha=\frac{2-N-\mu_1}{2}+\sqrt{\mu_2+\left(\frac{\mu_1-N+2}{2}\right)^2}.
\end{equation}
\begin{equation}
\alpha=\frac{2-N-\mu_1}{2}+\sqrt{\mu_2+\left(\frac{\mu_1-N+2}{2}\right)^2}.
\end{equation} For ![]() $f\in L^1(\partial B_1)$, let
$f\in L^1(\partial B_1)$, let
 \begin{equation*}
I_f=\int_{\partial B_1} f(x)\,{\rm d}\sigma.
\end{equation*}
\begin{equation*}
I_f=\int_{\partial B_1} f(x)\,{\rm d}\sigma.
\end{equation*} We denote by ![]() $L^{1,+}(\partial B_1)$ the functional space defined by
$L^{1,+}(\partial B_1)$ the functional space defined by
 \begin{equation*}
L^{1,+}(\partial B_1)=\left\{f\in L^1(\partial B_1): I_f \gt 0\right\}.
\end{equation*}
\begin{equation*}
L^{1,+}(\partial B_1)=\left\{f\in L^1(\partial B_1): I_f \gt 0\right\}.
\end{equation*}Our main result is stated in the following theorem.
Theorem 1.3. Let ![]() $k\geq 1$,
$k\geq 1$, ![]() $N\geq 2$,
$N\geq 2$, ![]() $p \gt q\geq 1$,
$p \gt q\geq 1$, ![]() $\mu_1\in \mathbb{R}$ and
$\mu_1\in \mathbb{R}$ and  $\mu_2\geq -\left(\frac{\mu_1-N+2}{2}\right)^2$.
$\mu_2\geq -\left(\frac{\mu_1-N+2}{2}\right)^2$.
(I) If
 $f\in L^{1,+}(\partial B_1)$ and
(1.11)then Equation (1.1) admits no weak solution.
$f\in L^{1,+}(\partial B_1)$ and
(1.11)then Equation (1.1) admits no weak solution. \begin{equation}
(\mu_1+\alpha)p \lt (a-2+\mu_1+\alpha)q ,
\end{equation}
\begin{equation}
(\mu_1+\alpha)p \lt (a-2+\mu_1+\alpha)q ,
\end{equation}(II) If
(1.12)then Equation (1.1) admits positive solutions (stationary solutions) for some \begin{equation}
(\mu_1+\alpha)p \gt (a-2+\mu_1+\alpha)q ,
\end{equation}
\begin{equation}
(\mu_1+\alpha)p \gt (a-2+\mu_1+\alpha)q ,
\end{equation} $f\in L^{1,+}(\partial B_1)$.
$f\in L^{1,+}(\partial B_1)$.
The proof of part (I) of Theorem 1.3 relies on nonlinear capacity estimates specifically adapted to the operator ![]() $\mathcal{L}_{\mu_1,\mu_2}$, the boundedness of the domain and the considered boundary condition. Namely, we use the nonlinear capacity method (see, e.g., [Reference Mitidieri and Pokhozhaev27] for more details about this approach) with a judicious choice of a family of test functions belonging to Φ and involving a function
$\mathcal{L}_{\mu_1,\mu_2}$, the boundedness of the domain and the considered boundary condition. Namely, we use the nonlinear capacity method (see, e.g., [Reference Mitidieri and Pokhozhaev27] for more details about this approach) with a judicious choice of a family of test functions belonging to Φ and involving a function ![]() $H\geq 0$, solution to
$H\geq 0$, solution to
 \begin{equation*}
-\Delta H-\mu_1\operatorname{div}\left(\frac{H x}{|x|^2}\right)+\frac{\mu_2}{|x|^2}H=0\ \mbox{in }B_1\backslash\{0\},\quad H=0\ \mbox{on }\partial B_1.
\end{equation*}
\begin{equation*}
-\Delta H-\mu_1\operatorname{div}\left(\frac{H x}{|x|^2}\right)+\frac{\mu_2}{|x|^2}H=0\ \mbox{in }B_1\backslash\{0\},\quad H=0\ \mbox{on }\partial B_1.
\end{equation*}The existence result given by part (II) of Theorem 1.3 is established by the construction of explicit solutions.
Remark 1.4. Theorem 1.3 leaves open the issue of existence and non-existence in the critical case:
Remark 1.5. Consider the case  $\mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2$.
$\mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2$.
(i) Let
 $\mu_1\geq N-2$. In this case, one has
$\mu_1\geq N-2$. In this case, one has  $\mu_1+\alpha \gt 0$. Hence, Equation (1.11) reduces to
(1.13)
$\mu_1+\alpha \gt 0$. Hence, Equation (1.11) reduces to
(1.13) \begin{equation}
a \gt 2,\qquad1\leq q \lt p \lt q\left(1+\frac{a-2}{\mu_1+\alpha}\right).
\end{equation}
\begin{equation}
a \gt 2,\qquad1\leq q \lt p \lt q\left(1+\frac{a-2}{\mu_1+\alpha}\right).
\end{equation}(ii) Let
 $\mu_1 \lt N-2$.
$\mu_1 \lt N-2$.• If
 $\mu_2=0$, then
$\mu_2=0$, then  $\mu_1+\alpha=0$ and Equation (1.11) reduces to a > 2.
$\mu_1+\alpha=0$ and Equation (1.11) reduces to a > 2.• If
 $\mu_2 \gt 0$, then
$\mu_2 \gt 0$, then  $\mu_1+\alpha \gt 0$ and Equation (1.11) reduces to Equation (1.13).
$\mu_1+\alpha \gt 0$ and Equation (1.11) reduces to Equation (1.13).• If
 $-\left(\frac{\mu_1-N+2}{2}\right)^2 \lt \mu_2 \lt 0$, then
$-\left(\frac{\mu_1-N+2}{2}\right)^2 \lt \mu_2 \lt 0$, then  $\mu_1+\alpha \lt 0$ and Equation (1.11) reduces to
(1.14)
$\mu_1+\alpha \lt 0$ and Equation (1.11) reduces to
(1.14) \begin{equation}
a\geq 2;\quad\mbox{or}\quad a \lt 2,\ \ p \gt q\left(1+\frac{a-2}{\mu_1+\alpha}\right).
\end{equation}
\begin{equation}
a\geq 2;\quad\mbox{or}\quad a \lt 2,\ \ p \gt q\left(1+\frac{a-2}{\mu_1+\alpha}\right).
\end{equation}
Remark 1.6. Consider now the case  $\mu_2=-\left(\frac{\mu_1-N+2}{2}\right)^2$.
$\mu_2=-\left(\frac{\mu_1-N+2}{2}\right)^2$.
(i) Let
 $\mu_1=N-2$. In this case, one has
$\mu_1=N-2$. In this case, one has  $\mu_1+\alpha=0$. Hence, Equation (1.11) reduces to a > 2.
$\mu_1+\alpha=0$. Hence, Equation (1.11) reduces to a > 2.(ii) Let
 $\mu_1 \gt N-2$. In this case, we have
$\mu_1 \gt N-2$. In this case, we have  $\mu_1+\alpha \gt 0$ and Equation (1.11) reduces to Equation (1.13).
$\mu_1+\alpha \gt 0$ and Equation (1.11) reduces to Equation (1.13).(iii) Let
 $\mu_1 \lt N-2$. In this case, we get
$\mu_1 \lt N-2$. In this case, we get  $\mu_1+\alpha \lt 0$ and Equation (1.11) reduces to Equation (1.14).
$\mu_1+\alpha \lt 0$ and Equation (1.11) reduces to Equation (1.14).
Clearly, Theorem 1.3 yields naturally existence and non-existence results for the corresponding stationary problem
 \begin{eqnarray}
\left\{\begin{array}{llll}
\mathcal{L}_{\mu_1,\mu_2}\left(|u|^{q-1}u\right)(x)\geq |x|^{-a} |u(x)|^p \quad &\mbox{in }B_1\backslash\{0\},\\[3mm]
|u|^{q-1}u \geq f \quad &\mbox{on }\partial B_1.
\end{array}
\right.
\end{eqnarray}
\begin{eqnarray}
\left\{\begin{array}{llll}
\mathcal{L}_{\mu_1,\mu_2}\left(|u|^{q-1}u\right)(x)\geq |x|^{-a} |u(x)|^p \quad &\mbox{in }B_1\backslash\{0\},\\[3mm]
|u|^{q-1}u \geq f \quad &\mbox{on }\partial B_1.
\end{array}
\right.
\end{eqnarray}Corollary 1.7. Let ![]() $N\geq 2$,
$N\geq 2$, ![]() $p \gt q\geq 1$,
$p \gt q\geq 1$, ![]() $\mu_1\in \mathbb{R}$ and
$\mu_1\in \mathbb{R}$ and  $\mu_2\geq -\left(\frac{\mu_1-N+2}{2}\right)^2$.
$\mu_2\geq -\left(\frac{\mu_1-N+2}{2}\right)^2$.
(I) If
 $f\in L^{1,+}(\partial B_1)$ and Equation (1.11) holds, then Equation (1.15) admits no weak solution.
$f\in L^{1,+}(\partial B_1)$ and Equation (1.11) holds, then Equation (1.15) admits no weak solution.(II) If Equation (1.12) holds, then Equation (1.15) admits positive solutions for some
 $f\in L^{1,+}(\partial B_1)$.
$f\in L^{1,+}(\partial B_1)$.
Remark 1.8. Notice that in the special case
 \begin{equation*}
a \lt 2,\quad q=1,\quad \mu_1 \lt N-2,\quad -\left(\frac{\mu_1-N+2}{2}\right)^2\leq \mu_2 \lt 0,
\end{equation*}
\begin{equation*}
a \lt 2,\quad q=1,\quad \mu_1 \lt N-2,\quad -\left(\frac{\mu_1-N+2}{2}\right)^2\leq \mu_2 \lt 0,
\end{equation*}condition (1.11) reduces to (see Remark 1.5) that obtained in [Reference Chen and Zheng9] (for the non-existence of positive solutions to Equation (1.6))
 \begin{equation*}
p \gt 1+\frac{a-2}{\mu_1+\alpha}=p^*(\mu_1,\mu_2,\rho),
\end{equation*}
\begin{equation*}
p \gt 1+\frac{a-2}{\mu_1+\alpha}=p^*(\mu_1,\mu_2,\rho),
\end{equation*}where ![]() $\rho=-a$ and
$\rho=-a$ and ![]() $p^*(\mu_1,\mu_2,\rho)$ is given by Equation (1.7).
$p^*(\mu_1,\mu_2,\rho)$ is given by Equation (1.7).
The rest of the paper is organized as follows. In ![]() $\S$ 2, we establish some preliminary results that will be useful in the proof of Theorem 1.3. Namely, we first establish an a priori estimate for problem (1.1). Next, we introduce a certain class of test functions belonging to Φ and specifically adapted to our problem and prove some useful estimates involving such functions. Finally, the proof of Theorem 1.3 is given in
$\S$ 2, we establish some preliminary results that will be useful in the proof of Theorem 1.3. Namely, we first establish an a priori estimate for problem (1.1). Next, we introduce a certain class of test functions belonging to Φ and specifically adapted to our problem and prove some useful estimates involving such functions. Finally, the proof of Theorem 1.3 is given in ![]() $\S$ 3.
$\S$ 3.
Throughout this paper, the symbol C denotes always a generic positive constant, which is independent of the scaling parameters T, R and the solution u. Its value could be changed from one line to another.
2. Preliminary estimates
Let ![]() $k\geq 1$,
$k\geq 1$, ![]() $N\geq 2$,
$N\geq 2$, ![]() $a\in \mathbb{R}$,
$a\in \mathbb{R}$, ![]() $p \gt q\geq 1$,
$p \gt q\geq 1$, ![]() $\mu_1\in \mathbb{R}$ and
$\mu_1\in \mathbb{R}$ and  $\mu_2\geq -\left(\frac{\mu_1-N+2}{2}\right)^2$. For
$\mu_2\geq -\left(\frac{\mu_1-N+2}{2}\right)^2$. For ![]() $\varphi\in \Phi$, let
$\varphi\in \Phi$, let
 \begin{eqnarray} J_1(\varphi)&=& \int_{\operatorname{supp}(\varphi)} \varphi^{\frac{-1}{p-1}} \left|\partial_t^k\varphi\right|^{\frac{p}{p-1}}|x|^{\frac{a}{p-1}}\,{\rm d}x\,{\rm d}t,
\end{eqnarray}
\begin{eqnarray} J_1(\varphi)&=& \int_{\operatorname{supp}(\varphi)} \varphi^{\frac{-1}{p-1}} \left|\partial_t^k\varphi\right|^{\frac{p}{p-1}}|x|^{\frac{a}{p-1}}\,{\rm d}x\,{\rm d}t,
\end{eqnarray} \begin{eqnarray} J_2(\varphi)&=& \int_{\operatorname{supp}(\varphi)} \varphi^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\varphi\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\,{\rm d}x\,{\rm d}t,
\end{eqnarray}
\begin{eqnarray} J_2(\varphi)&=& \int_{\operatorname{supp}(\varphi)} \varphi^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\varphi\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\,{\rm d}x\,{\rm d}t,
\end{eqnarray}2.1. (A priori estimate)
We have the following a priori estimate.
Lemma 2.1. A priori estimate
Let ![]() $u\in L^p_{\rm loc}(Q)$ be a weak solution to Equation (1.1). Then, there holds
$u\in L^p_{\rm loc}(Q)$ be a weak solution to Equation (1.1). Then, there holds
 \begin{equation}
-\int_{\Gamma} f(x)\,\frac{\partial \varphi}{\partial \nu}\,{\rm d}\sigma\,{\rm d}t\leq C \sum_{i=1}^2 J_i(\varphi)
\end{equation}
\begin{equation}
-\int_{\Gamma} f(x)\,\frac{\partial \varphi}{\partial \nu}\,{\rm d}\sigma\,{\rm d}t\leq C \sum_{i=1}^2 J_i(\varphi)
\end{equation}for all ![]() $\varphi\in \Phi$, provided that
$\varphi\in \Phi$, provided that ![]() $J_i(\varphi) \lt \infty$,
$J_i(\varphi) \lt \infty$, ![]() $i=1,2$.
$i=1,2$.
Proof. Let ![]() $u\in L^p_{\rm loc}(Q)$ be a weak solution to Equation (1.1). By Equation (1.8), there holds
$u\in L^p_{\rm loc}(Q)$ be a weak solution to Equation (1.1). By Equation (1.8), there holds
 \begin{equation}
\int_Q |x|^{-a} |u|^p\varphi\,{\rm d}x\,{\rm d}t -\int_{\Gamma} f(x)\,\frac{\partial \varphi}{\partial \nu}\,{\rm d}\sigma\,{\rm d}t\leq \int_Q |u| \left|\partial_t^k\varphi\right|\,{\rm d}x\,{\rm d}t + \int_Q |u|^q\left|\mathcal{L}_{\mu_1,\mu_2}^*\varphi\right|\,{\rm d}x\,{\rm d}t
\end{equation}
\begin{equation}
\int_Q |x|^{-a} |u|^p\varphi\,{\rm d}x\,{\rm d}t -\int_{\Gamma} f(x)\,\frac{\partial \varphi}{\partial \nu}\,{\rm d}\sigma\,{\rm d}t\leq \int_Q |u| \left|\partial_t^k\varphi\right|\,{\rm d}x\,{\rm d}t + \int_Q |u|^q\left|\mathcal{L}_{\mu_1,\mu_2}^*\varphi\right|\,{\rm d}x\,{\rm d}t
\end{equation}for all ![]() $\varphi\in \Phi$. On the other hand, by means of Young’s inequality, we obtain
$\varphi\in \Phi$. On the other hand, by means of Young’s inequality, we obtain
 \begin{eqnarray}
\nonumber \int_Q |u| \left|\partial_t^k\varphi\right|\,{\rm d}x\,{\rm d}t &=& \int_{\operatorname{supp}(\varphi)}\left(|x|^{\frac{-a}{p}} |u|\varphi^{\frac{1}{p}}\right) \left(\varphi^{\frac{-1}{p}}\left|\partial_t^k\varphi\right||x|^{\frac{a}{p}}\right)\,{\rm d}x\,{\rm d}t
\end{eqnarray}
\begin{eqnarray}
\nonumber \int_Q |u| \left|\partial_t^k\varphi\right|\,{\rm d}x\,{\rm d}t &=& \int_{\operatorname{supp}(\varphi)}\left(|x|^{\frac{-a}{p}} |u|\varphi^{\frac{1}{p}}\right) \left(\varphi^{\frac{-1}{p}}\left|\partial_t^k\varphi\right||x|^{\frac{a}{p}}\right)\,{\rm d}x\,{\rm d}t
\end{eqnarray} \begin{eqnarray}
&\leq & \frac{1}{2}\int_Q |x|^{-a} |u|^p\varphi\,{\rm d}x\,{\rm d}t+C J_1(\varphi).
\end{eqnarray}
\begin{eqnarray}
&\leq & \frac{1}{2}\int_Q |x|^{-a} |u|^p\varphi\,{\rm d}x\,{\rm d}t+C J_1(\varphi).
\end{eqnarray}Similarly, we get
 \begin{eqnarray}
\nonumber \int_Q |u|^q\left|\mathcal{L}_{\mu_1,\mu_2}^*\varphi\right|\,{\rm d}x\,{\rm d}t&=&\int_Q \left(|x|^{\frac{-aq}{p}}|u|^q \varphi^{\frac{q}{p}}\right)\left(|x|^{\frac{aq}{p}}\varphi^{\frac{-q}{p}}\left|\mathcal{L}_{\mu_1,\mu_2}^*\varphi\right|\right)\,{\rm d}x\,{\rm d}t
\end{eqnarray}
\begin{eqnarray}
\nonumber \int_Q |u|^q\left|\mathcal{L}_{\mu_1,\mu_2}^*\varphi\right|\,{\rm d}x\,{\rm d}t&=&\int_Q \left(|x|^{\frac{-aq}{p}}|u|^q \varphi^{\frac{q}{p}}\right)\left(|x|^{\frac{aq}{p}}\varphi^{\frac{-q}{p}}\left|\mathcal{L}_{\mu_1,\mu_2}^*\varphi\right|\right)\,{\rm d}x\,{\rm d}t
\end{eqnarray} \begin{eqnarray}
&\leq& \frac{1}{2}\int_Q |x|^{-a} |u|^p\varphi\,{\rm d}x\,{\rm d}t+C J_2(\varphi).
\end{eqnarray}
\begin{eqnarray}
&\leq& \frac{1}{2}\int_Q |x|^{-a} |u|^p\varphi\,{\rm d}x\,{\rm d}t+C J_2(\varphi).
\end{eqnarray}Thus, Equation (2.3) follows from Equations (2.4), (2.5) and (2.6).
2.2. Test functions
Let us introduce the function H defined in ![]() $B_1\backslash\{0\}$ by
$B_1\backslash\{0\}$ by
 \begin{equation}
H(x)=\left\{\begin{array}{llll}
|x|^{2-N-\mu_1-\alpha}\left(1-|x|^{2\alpha-2+N+\mu_1}\right) &\mbox{if}\ \ \mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2,\\[2mm]
-|x|^{\alpha}\,\ln |x| &\mbox{if}\ \ \mu_2= -\left(\frac{\mu_1-N+2}{2}\right)^2,
\end{array}
\right.
\end{equation}
\begin{equation}
H(x)=\left\{\begin{array}{llll}
|x|^{2-N-\mu_1-\alpha}\left(1-|x|^{2\alpha-2+N+\mu_1}\right) &\mbox{if}\ \ \mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2,\\[2mm]
-|x|^{\alpha}\,\ln |x| &\mbox{if}\ \ \mu_2= -\left(\frac{\mu_1-N+2}{2}\right)^2,
\end{array}
\right.
\end{equation}where the parameter α is given by Equation (1.10). It can be easily seen that ![]() $H\geq 0$ in
$H\geq 0$ in ![]() $B_1\backslash\{0\}$. Moreover, elementary calculations show that
$B_1\backslash\{0\}$. Moreover, elementary calculations show that
 \begin{eqnarray}
\left\{\begin{array}{llll}
\mathcal{L}_{\mu_1,\mu_2}^* H(x)=0 &\mbox{in}\ \ B_1\backslash\{0\},\\[2mm]
H(x)=0&\mbox{on}\ \ \partial B_1.
\end{array}
\right.
\end{eqnarray}
\begin{eqnarray}
\left\{\begin{array}{llll}
\mathcal{L}_{\mu_1,\mu_2}^* H(x)=0 &\mbox{in}\ \ B_1\backslash\{0\},\\[2mm]
H(x)=0&\mbox{on}\ \ \partial B_1.
\end{array}
\right.
\end{eqnarray} Let ![]() $\eta,\xi\in C^\infty([0,\infty))$ be two cutoff functions satisfying, respectively,
$\eta,\xi\in C^\infty([0,\infty))$ be two cutoff functions satisfying, respectively,
and
 \begin{equation}
0\leq \xi\leq 1,\quad \xi(s)=0\quad \mbox{if } 0\leq s\leq \frac{1}{2},\quad \xi(s)=1\quad \mbox{if } s\geq 1.
\end{equation}
\begin{equation}
0\leq \xi\leq 1,\quad \xi(s)=0\quad \mbox{if } 0\leq s\leq \frac{1}{2},\quad \xi(s)=1\quad \mbox{if } s\geq 1.
\end{equation} For sufficiently large T, R and ![]() $\ell$, let
$\ell$, let
 \begin{equation}
\eta_T(t)=\eta\left(\frac{t}{T}\right)^\ell,\quad t\geq 0
\end{equation}
\begin{equation}
\eta_T(t)=\eta\left(\frac{t}{T}\right)^\ell,\quad t\geq 0
\end{equation}and
that is,
 \begin{equation}
\xi_R(x)=\left\{\begin{array}{llll}
0 &\mbox{if}\ \ 0 \lt |x|\leq (2R)^{-1},\\[2mm]
H(x)\xi(R|x|)^\ell &\mbox{if}\ \ (2R)^{-1}\leq |x|\leq R^{-1},\\[2mm]
H(x) &\mbox{if}\ \ R^{-1}\leq |x|\leq 1.
\end{array}
\right.
\end{equation}
\begin{equation}
\xi_R(x)=\left\{\begin{array}{llll}
0 &\mbox{if}\ \ 0 \lt |x|\leq (2R)^{-1},\\[2mm]
H(x)\xi(R|x|)^\ell &\mbox{if}\ \ (2R)^{-1}\leq |x|\leq R^{-1},\\[2mm]
H(x) &\mbox{if}\ \ R^{-1}\leq |x|\leq 1.
\end{array}
\right.
\end{equation}We introduce test functions of the form
Lemma 2.2. For sufficiently large T, R and ![]() $\ell$, the function φ defined by Equation (2.14) belongs to Φ.
$\ell$, the function φ defined by Equation (2.14) belongs to Φ.
Proof. By Equations (2.7), (2.9), (2.10), (2.11) and (2.12), it can be easily seen that for sufficiently large T, R and ![]() $\ell$, the function φ defined by Equation (2.14) satisfies properties (i) and (ii) of Definition 1.1. Moreover,
$\ell$, the function φ defined by Equation (2.14) satisfies properties (i) and (ii) of Definition 1.1. Moreover, ![]() $H|_{\partial B_1}=0$ implies that
$H|_{\partial B_1}=0$ implies that ![]() $\varphi|_{\Gamma}=0$. So, we have just to show that
$\varphi|_{\Gamma}=0$. So, we have just to show that
 \begin{equation}
\frac{\partial \varphi}{\partial \nu}(t,x)\leq 0,\quad (t,x)\in \Gamma.
\end{equation}
\begin{equation}
\frac{\partial \varphi}{\partial \nu}(t,x)\leq 0,\quad (t,x)\in \Gamma.
\end{equation}In view of Equations (2.13) and (2.14) , we obtain
 \begin{equation}
\frac{\partial \varphi}{\partial \nu}(t,x)=\eta_T(t)\, \frac{\partial \xi_R}{\partial \nu}(x)=\eta_T(t)\, \frac{\partial H}{\partial \nu}(x),\quad (t,x)\in \Gamma.
\end{equation}
\begin{equation}
\frac{\partial \varphi}{\partial \nu}(t,x)=\eta_T(t)\, \frac{\partial \xi_R}{\partial \nu}(x)=\eta_T(t)\, \frac{\partial H}{\partial \nu}(x),\quad (t,x)\in \Gamma.
\end{equation} On the other hand, by Equation (2.7), for all ![]() $x\in B_1\backslash\{0\}$, if
$x\in B_1\backslash\{0\}$, if  $\mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2$, we have
$\mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2$, we have
 \begin{equation*}
\nabla H(x)=\left((2-N-\mu_1-\alpha) |x|^{1-N-\mu_1-\alpha}-\alpha |x|^{\alpha-1}\right) \frac{x}{|x|};
\end{equation*}
\begin{equation*}
\nabla H(x)=\left((2-N-\mu_1-\alpha) |x|^{1-N-\mu_1-\alpha}-\alpha |x|^{\alpha-1}\right) \frac{x}{|x|};
\end{equation*}if  $\mu_2= -\left(\frac{\mu_1-N+2}{2}\right)^2$, we have
$\mu_2= -\left(\frac{\mu_1-N+2}{2}\right)^2$, we have
 \begin{equation*}
\nabla H(x)=\left(-\alpha |x|^{\alpha-1}\,\ln |x|-|x|^{\alpha-1}\right)\frac{x}{|x|}.
\end{equation*}
\begin{equation*}
\nabla H(x)=\left(-\alpha |x|^{\alpha-1}\,\ln |x|-|x|^{\alpha-1}\right)\frac{x}{|x|}.
\end{equation*}Hence, by Equation (1.10), we get
 \begin{equation}
\frac{\partial H}{\partial \nu}(x)=\left\{\begin{array}{llll}
-\left(2\alpha-2+N+\mu_1\right) \lt 0 &\mbox{if}\ \ \mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2,\\[2mm]
-1 &\mbox{if}\ \ \mu_2= -\left(\frac{\mu_1-N+2}{2}\right)^2.
\end{array}
\right.
\end{equation}
\begin{equation}
\frac{\partial H}{\partial \nu}(x)=\left\{\begin{array}{llll}
-\left(2\alpha-2+N+\mu_1\right) \lt 0 &\mbox{if}\ \ \mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2,\\[2mm]
-1 &\mbox{if}\ \ \mu_2= -\left(\frac{\mu_1-N+2}{2}\right)^2.
\end{array}
\right.
\end{equation} Using Equations (2.9), (2.11), (2.16) and (2.17), for all ![]() $(t,x)\in \Gamma$, we obtain
$(t,x)\in \Gamma$, we obtain
 \begin{equation}
\frac{\partial \varphi}{\partial \nu}(t,x)=\left\{\begin{array}{llll}
-\left(2\alpha-2+N+\mu_1\right) \eta_T(t) \leq 0 &\mbox{if}\ \ \mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2,\\[2mm]
-\eta_T(t)\leq 0 &\mbox{if}\ \ \mu_2= -\left(\frac{\mu_1-N+2}{2}\right)^2,
\end{array}
\right.
\end{equation}
\begin{equation}
\frac{\partial \varphi}{\partial \nu}(t,x)=\left\{\begin{array}{llll}
-\left(2\alpha-2+N+\mu_1\right) \eta_T(t) \leq 0 &\mbox{if}\ \ \mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2,\\[2mm]
-\eta_T(t)\leq 0 &\mbox{if}\ \ \mu_2= -\left(\frac{\mu_1-N+2}{2}\right)^2,
\end{array}
\right.
\end{equation}which proves Equation (2.15).
2.3. Estimates of  $J_i(\varphi)$
$J_i(\varphi)$
The aim of this subsection is to estimate the terms ![]() $J_1(\varphi)$ and
$J_1(\varphi)$ and ![]() $J_2(\varphi)$ defined, respectively, by Equations (2.1) and (2.2), where φ is the function defined by Equation (2.14). Such estimates will play a crucial role in the proof of our non-existence results.
$J_2(\varphi)$ defined, respectively, by Equations (2.1) and (2.2), where φ is the function defined by Equation (2.14). Such estimates will play a crucial role in the proof of our non-existence results.
Lemma 2.3. For sufficiently large T and ![]() $\ell$, there holds
$\ell$, there holds
 \begin{equation}
\int_{\operatorname{supp}(\eta_T)} \eta_T(t)^{\frac{-1}{p-1}}\left|\eta_T^{(k)}(t)\right|^{\frac{p}{p-1}}\,{\rm d}t\leq CT^{1-\frac{kp}{p-1}},
\end{equation}
\begin{equation}
\int_{\operatorname{supp}(\eta_T)} \eta_T(t)^{\frac{-1}{p-1}}\left|\eta_T^{(k)}(t)\right|^{\frac{p}{p-1}}\,{\rm d}t\leq CT^{1-\frac{kp}{p-1}},
\end{equation}where  $\eta_T^{(k)}=\displaystyle\frac{{\rm d}^k\eta}{{\rm d}t^k}$.
$\eta_T^{(k)}=\displaystyle\frac{{\rm d}^k\eta}{{\rm d}t^k}$.
Proof. In view of Equations (2.9) and (2.11), we obtain
 \begin{equation*}
\int_{\operatorname{supp}(\eta_T)} \eta_T(t)^{\frac{-1}{p-1}}\left|\eta_T^{(k)}(t)\right|^{\frac{p}{p-1}}\,{\rm d}t=\int_0^T \eta\left(\frac{t}{T}\right)^{\frac{-\ell}{p-1}}\left|\left[ \eta\left(\frac{t}{T}\right)^\ell\right]^{(k)}\right|^{\frac{p}{p-1}} \,{\rm d}t
\end{equation*}
\begin{equation*}
\int_{\operatorname{supp}(\eta_T)} \eta_T(t)^{\frac{-1}{p-1}}\left|\eta_T^{(k)}(t)\right|^{\frac{p}{p-1}}\,{\rm d}t=\int_0^T \eta\left(\frac{t}{T}\right)^{\frac{-\ell}{p-1}}\left|\left[ \eta\left(\frac{t}{T}\right)^\ell\right]^{(k)}\right|^{\frac{p}{p-1}} \,{\rm d}t
\end{equation*}and
 \begin{equation*}
\left|\left[\eta\left(\frac{t}{T}\right)^\ell\right]^{(k)}\right|\leq C T^{-k} \eta\left(\frac{t}{T}\right)^{\ell-k},\quad 0 \lt t \lt T.
\end{equation*}
\begin{equation*}
\left|\left[\eta\left(\frac{t}{T}\right)^\ell\right]^{(k)}\right|\leq C T^{-k} \eta\left(\frac{t}{T}\right)^{\ell-k},\quad 0 \lt t \lt T.
\end{equation*}Hence, there holds
 \begin{eqnarray*}
\int_{\operatorname{supp}(\eta_T)} \eta_T(t)^{\frac{-1}{p-1}}\left|\eta_T^{(k)}(t)\right|^{\frac{p}{p-1}}\,{\rm d}t&\leq & C T^{\frac{-kp}{p-1}} \int_0^T \eta\left(\frac{t}{T}\right)^{\ell-\frac{kp}{p-1}}\,{\rm d}t\\
&=& C T^{1-\frac{kp}{p-1}} \int_0^1 \eta(s)^{\ell-\frac{k}{p-1}}\,{\rm d}s ,
\end{eqnarray*}
\begin{eqnarray*}
\int_{\operatorname{supp}(\eta_T)} \eta_T(t)^{\frac{-1}{p-1}}\left|\eta_T^{(k)}(t)\right|^{\frac{p}{p-1}}\,{\rm d}t&\leq & C T^{\frac{-kp}{p-1}} \int_0^T \eta\left(\frac{t}{T}\right)^{\ell-\frac{kp}{p-1}}\,{\rm d}t\\
&=& C T^{1-\frac{kp}{p-1}} \int_0^1 \eta(s)^{\ell-\frac{k}{p-1}}\,{\rm d}s ,
\end{eqnarray*}which proves Equation (2.19).
(i) Let
 $\mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2$. For sufficiently large R, there holds
(2.20)
$\mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2$. For sufficiently large R, there holds
(2.20) \begin{equation}
\int_{\operatorname{supp}(\xi_R)}\xi_R(x)|x|^{\frac{a}{p-1}}\,{\rm d}x\leq C\left(\ln R+ R^{\alpha+\mu_1-2-\frac{a}{p-1}}\right).
\end{equation}
\begin{equation}
\int_{\operatorname{supp}(\xi_R)}\xi_R(x)|x|^{\frac{a}{p-1}}\,{\rm d}x\leq C\left(\ln R+ R^{\alpha+\mu_1-2-\frac{a}{p-1}}\right).
\end{equation}(ii) Let
 $\mu_2=-\left(\frac{\mu_1-N+2}{2}\right)^2$. For sufficiently large R, there holds
(2.21)
$\mu_2=-\left(\frac{\mu_1-N+2}{2}\right)^2$. For sufficiently large R, there holds
(2.21) \begin{equation}
\int_{\operatorname{supp}(\xi_R)}\xi_R(x)|x|^{\frac{a}{p-1}}\,{\rm d}x\leq C\,\ln R\left(\ln R+R^{-\left(\frac{a}{p-1}+\alpha+N\right)}\right).
\end{equation}
\begin{equation}
\int_{\operatorname{supp}(\xi_R)}\xi_R(x)|x|^{\frac{a}{p-1}}\,{\rm d}x\leq C\,\ln R\left(\ln R+R^{-\left(\frac{a}{p-1}+\alpha+N\right)}\right).
\end{equation}
(i) In view of Equations (2.7), (2.10) and (2.12), for sufficiently large R, we obtain
which proves Equation (2.20). \begin{eqnarray*}
\int_{\operatorname{supp}(\xi_R)}\xi_R(x)|x|^{\frac{a}{p-1}}\,{\rm d}x&=&\int_{\frac{1}{2R} \lt |x| \lt 1} |x|^{\frac{a}{p-1}}H(x) \xi(R|x|)^\ell\,{\rm d}x\\
&\leq & \int_{\frac{1}{2R} \lt |x| \lt 1} |x|^{\frac{a}{p-1}} H(x)\,{\rm d}x \\
&\leq & \int_{\frac{1}{2R} \lt |x| \lt 1} |x|^{2-N-\mu_1-\alpha+\frac{a}{p-1}}\,{\rm d}x \\
&=& C \int_{r=\frac{1}{2R}}^{1} r^{1-\mu_1-\alpha+\frac{a}{p-1}}\,{\rm d}r\\
&\leq & \left\{\begin{array}{llll}
C\, \ln R &\mbox{if}\ \ (2-\mu_1-\alpha)(p-1)+a=0,\\[1mm]
C &\mbox{if}\ \ (2-\mu_1-\alpha)(p-1)+a \gt 0,\\[1mm]
C R^{\mu_1+\alpha-2-\frac{a}{p-1}} &\mbox{if}\ \ (2-\mu_1-\alpha)(p-1)+a \lt 0,
\end{array}
\right.
\end{eqnarray*}
\begin{eqnarray*}
\int_{\operatorname{supp}(\xi_R)}\xi_R(x)|x|^{\frac{a}{p-1}}\,{\rm d}x&=&\int_{\frac{1}{2R} \lt |x| \lt 1} |x|^{\frac{a}{p-1}}H(x) \xi(R|x|)^\ell\,{\rm d}x\\
&\leq & \int_{\frac{1}{2R} \lt |x| \lt 1} |x|^{\frac{a}{p-1}} H(x)\,{\rm d}x \\
&\leq & \int_{\frac{1}{2R} \lt |x| \lt 1} |x|^{2-N-\mu_1-\alpha+\frac{a}{p-1}}\,{\rm d}x \\
&=& C \int_{r=\frac{1}{2R}}^{1} r^{1-\mu_1-\alpha+\frac{a}{p-1}}\,{\rm d}r\\
&\leq & \left\{\begin{array}{llll}
C\, \ln R &\mbox{if}\ \ (2-\mu_1-\alpha)(p-1)+a=0,\\[1mm]
C &\mbox{if}\ \ (2-\mu_1-\alpha)(p-1)+a \gt 0,\\[1mm]
C R^{\mu_1+\alpha-2-\frac{a}{p-1}} &\mbox{if}\ \ (2-\mu_1-\alpha)(p-1)+a \lt 0,
\end{array}
\right.
\end{eqnarray*}(ii) Similarly, using Equations (2.7), (2.10) and (2.12), for sufficiently large R, we obtain
which proves Equation (2.21). \begin{eqnarray*}
\int_{\operatorname{supp}(\xi_R)}\xi_R(x)|x|^{\frac{a}{p-1}}\,{\rm d}x&=&\int_{\frac{1}{2R} \lt |x| \lt 1} |x|^{\frac{a}{p-1}}H(x) \xi(R|x|)^\ell\,{\rm d}x\\
&\leq & \int_{\frac{1}{2R} \lt |x| \lt 1} |x|^{\frac{a}{p-1}} H(x)\,{\rm d}x \\
&= & \int_{\frac{1}{2R} \lt |x| \lt 1} |x|^{\frac{a}{p-1}+\alpha}\,\ln \left(\frac{1}{|x|}\right)\,{\rm d}x \\
&\leq & C\, \ln R\int_{r=\frac{1}{2R}}^{1} r^{\frac{a}{p-1}+\alpha+N-1}\,{\rm d}r\\
&\leq & \ln R\left\{\begin{array}{llll}
C\, \ln R &\mbox{if}\ \ (\alpha+N)(p-1)+a=0,\\[1mm]
C &\mbox{if}\ \ (\alpha+N)(p-1)+a \gt 0,\\[1mm]
C R^{-\left(\frac{a}{p-1}+\alpha+N\right)} &\mbox{if}\ \ (\alpha+N)(p-1)+a \lt 0,
\end{array}
\right.
\end{eqnarray*}
\begin{eqnarray*}
\int_{\operatorname{supp}(\xi_R)}\xi_R(x)|x|^{\frac{a}{p-1}}\,{\rm d}x&=&\int_{\frac{1}{2R} \lt |x| \lt 1} |x|^{\frac{a}{p-1}}H(x) \xi(R|x|)^\ell\,{\rm d}x\\
&\leq & \int_{\frac{1}{2R} \lt |x| \lt 1} |x|^{\frac{a}{p-1}} H(x)\,{\rm d}x \\
&= & \int_{\frac{1}{2R} \lt |x| \lt 1} |x|^{\frac{a}{p-1}+\alpha}\,\ln \left(\frac{1}{|x|}\right)\,{\rm d}x \\
&\leq & C\, \ln R\int_{r=\frac{1}{2R}}^{1} r^{\frac{a}{p-1}+\alpha+N-1}\,{\rm d}r\\
&\leq & \ln R\left\{\begin{array}{llll}
C\, \ln R &\mbox{if}\ \ (\alpha+N)(p-1)+a=0,\\[1mm]
C &\mbox{if}\ \ (\alpha+N)(p-1)+a \gt 0,\\[1mm]
C R^{-\left(\frac{a}{p-1}+\alpha+N\right)} &\mbox{if}\ \ (\alpha+N)(p-1)+a \lt 0,
\end{array}
\right.
\end{eqnarray*}
(i) Let
 $\mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2$. For sufficiently large T, R and
$\mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2$. For sufficiently large T, R and  $\ell$, there holds
(2.22)where φ is the function defined by Equation (2.14).
$\ell$, there holds
(2.22)where φ is the function defined by Equation (2.14). \begin{equation}
J_1(\varphi)\leq C T^{1-\frac{kp}{p-1}} \left(\ln R+ R^{\alpha+\mu_1-2-\frac{a}{p-1}}\right),
\end{equation}
\begin{equation}
J_1(\varphi)\leq C T^{1-\frac{kp}{p-1}} \left(\ln R+ R^{\alpha+\mu_1-2-\frac{a}{p-1}}\right),
\end{equation}(ii) Let
 $\mu_2=-\left(\frac{\mu_1-N+2}{2}\right)^2$. For sufficiently large T, R and
$\mu_2=-\left(\frac{\mu_1-N+2}{2}\right)^2$. For sufficiently large T, R and  $\ell$, there holds
(2.23)
$\ell$, there holds
(2.23) \begin{equation}
J_1(\varphi)\leq C T^{1-\frac{kp}{p-1}}\, \ln R\left(\ln R+R^{-\left(\frac{a}{p-1}+\alpha+N\right)}\right).
\end{equation}
\begin{equation}
J_1(\varphi)\leq C T^{1-\frac{kp}{p-1}}\, \ln R\left(\ln R+R^{-\left(\frac{a}{p-1}+\alpha+N\right)}\right).
\end{equation}
Proof. By Equations (2.1) and (2.14), we obtain
 \begin{equation}
J_1(\varphi)=\left(\int_{\operatorname{supp}(\eta_T)} \eta_T(t)^{\frac{-1}{p-1}}\left|\eta_T^{(k)}(t)\right|^{\frac{p}{p-1}}\,{\rm d}t\right) \left(\int_{\operatorname{supp}(\xi_R)}\xi_R(x)|x|^{\frac{a}{p-1}}\,{\rm d}x\right).
\end{equation}
\begin{equation}
J_1(\varphi)=\left(\int_{\operatorname{supp}(\eta_T)} \eta_T(t)^{\frac{-1}{p-1}}\left|\eta_T^{(k)}(t)\right|^{\frac{p}{p-1}}\,{\rm d}t\right) \left(\int_{\operatorname{supp}(\xi_R)}\xi_R(x)|x|^{\frac{a}{p-1}}\,{\rm d}x\right).
\end{equation}Using Lemma 2.3, Lemma 2.4 and Equation (2.24), we obtain Equations (2.22) and (2.23).
(i) Let
 $\mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2$. For sufficiently large R and
$\mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2$. For sufficiently large R and  $\ell$, there holds
(2.25)
$\ell$, there holds
(2.25) \begin{equation}
\int_{\operatorname{supp}(\xi_R)} \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\,{\rm d}x \leq CR^{\frac{(\mu_1+\alpha)p-(a-2+\mu_1+\alpha)q}{p-q}}.
\end{equation}
\begin{equation}
\int_{\operatorname{supp}(\xi_R)} \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\,{\rm d}x \leq CR^{\frac{(\mu_1+\alpha)p-(a-2+\mu_1+\alpha)q}{p-q}}.
\end{equation}(ii) Let
 $\mu_2=-\left(\frac{\mu_1-N+2}{2}\right)^2$. For sufficiently large R and
$\mu_2=-\left(\frac{\mu_1-N+2}{2}\right)^2$. For sufficiently large R and  $\ell$, there holds
(2.26)
$\ell$, there holds
(2.26) \begin{equation}
\int_{\operatorname{supp}(\xi_R)} \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\,{\rm d}x \leq C R^{\frac{(2-\alpha-N)p+(\alpha-a+N)q}{p-q}}\,\ln R.
\end{equation}
\begin{equation}
\int_{\operatorname{supp}(\xi_R)} \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\,{\rm d}x \leq C R^{\frac{(2-\alpha-N)p+(\alpha-a+N)q}{p-q}}\,\ln R.
\end{equation}
(i) By Equations (1.9) and (2.12), for
 $x\in B_1\backslash\{0\}$, we obtain
$x\in B_1\backslash\{0\}$, we obtain
 \begin{eqnarray*}
\mathcal{L}_{\mu_1,\mu_2}^*\xi_R(x)&=&\mathcal{L}_{\mu_1,\mu_2}^* (H(x)\xi(R|x|)^\ell)\\
&=&-\Delta(H(x)\xi(R|x|)^\ell)-\mu_1\operatorname{div}\left(\frac{H(x)\xi(R|x|)^\ell x}{|x|^2}\right)\\
&& + \frac{\mu_2}{|x|^2}H(x)\xi(R|x|)^\ell \\
&=& -\xi(R|x|)^\ell\Delta H(x)-H(x)\Delta (\xi(R|x|)^\ell)\\
&&-2\nabla H(x)\cdot\nabla(\xi(R|x|)^\ell)-\mu_1\left(\xi(R|x|)^\ell\operatorname{div}\left( \frac{H(x) x}{|x|^2}\right)\right. \\ && + \left. \frac{H(x) x}{|x|^2}\cdot \nabla (\xi(R|x|)^\ell)\right) +\frac{\mu_2}{|x|^2}H(x)\xi(R|x|)^\ell\\
&=& \xi(R|x|)^\ell \left(-\Delta H(x)-\mu_1\operatorname{div}\left( \frac{H(x) x}{|x|^2}\right)+\frac{\mu_2}{|x|^2}H(x)\right)\\
&&-H(x)\Delta \left(\xi(R|x|)^\ell\right)-2\nabla H(x)\cdot\nabla(\xi(R|x|)^\ell)\\
&& -\mu_1 \frac{H(x) x}{|x|^2}\cdot \nabla \left(\xi(R|x|)^\ell\right)\\
&=& \xi(R|x|)^\ell \mathcal{L}_{\mu_1,\mu_2}^* H(x) -H(x)\Delta \left(\xi(R|x|)^\ell\right)\\ && - 2\nabla H(x)\cdot\nabla\left(\xi(R|x|)^\ell\right) - \mu_1 \frac{H(x) x}{|x|^2}\cdot \nabla \left(\xi(R|x|)^\ell\right).
\end{eqnarray*}
\begin{eqnarray*}
\mathcal{L}_{\mu_1,\mu_2}^*\xi_R(x)&=&\mathcal{L}_{\mu_1,\mu_2}^* (H(x)\xi(R|x|)^\ell)\\
&=&-\Delta(H(x)\xi(R|x|)^\ell)-\mu_1\operatorname{div}\left(\frac{H(x)\xi(R|x|)^\ell x}{|x|^2}\right)\\
&& + \frac{\mu_2}{|x|^2}H(x)\xi(R|x|)^\ell \\
&=& -\xi(R|x|)^\ell\Delta H(x)-H(x)\Delta (\xi(R|x|)^\ell)\\
&&-2\nabla H(x)\cdot\nabla(\xi(R|x|)^\ell)-\mu_1\left(\xi(R|x|)^\ell\operatorname{div}\left( \frac{H(x) x}{|x|^2}\right)\right. \\ && + \left. \frac{H(x) x}{|x|^2}\cdot \nabla (\xi(R|x|)^\ell)\right) +\frac{\mu_2}{|x|^2}H(x)\xi(R|x|)^\ell\\
&=& \xi(R|x|)^\ell \left(-\Delta H(x)-\mu_1\operatorname{div}\left( \frac{H(x) x}{|x|^2}\right)+\frac{\mu_2}{|x|^2}H(x)\right)\\
&&-H(x)\Delta \left(\xi(R|x|)^\ell\right)-2\nabla H(x)\cdot\nabla(\xi(R|x|)^\ell)\\
&& -\mu_1 \frac{H(x) x}{|x|^2}\cdot \nabla \left(\xi(R|x|)^\ell\right)\\
&=& \xi(R|x|)^\ell \mathcal{L}_{\mu_1,\mu_2}^* H(x) -H(x)\Delta \left(\xi(R|x|)^\ell\right)\\ && - 2\nabla H(x)\cdot\nabla\left(\xi(R|x|)^\ell\right) - \mu_1 \frac{H(x) x}{|x|^2}\cdot \nabla \left(\xi(R|x|)^\ell\right).
\end{eqnarray*}In view of Equation (2.8), we get
 \begin{equation*}
\mathcal{L}_{\mu_1,\mu_2}^*\xi_R(x)= -H(x)\Delta (\xi(R|x|)^\ell)-2\nabla H(x)\cdot\nabla\left(\xi(R|x|)^\ell\right)-\mu_1 \frac{H(x) x}{|x|^2}\cdot \nabla \left(\xi(R|x|)^\ell\right),
\end{equation*}
\begin{equation*}
\mathcal{L}_{\mu_1,\mu_2}^*\xi_R(x)= -H(x)\Delta (\xi(R|x|)^\ell)-2\nabla H(x)\cdot\nabla\left(\xi(R|x|)^\ell\right)-\mu_1 \frac{H(x) x}{|x|^2}\cdot \nabla \left(\xi(R|x|)^\ell\right),
\end{equation*}which implies by Equation (2.10) and Cauchy–Schwarz inequality that
(2.27)and \begin{equation}
\int_{\operatorname{supp}(\xi_R)} \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\,{\rm d}x=\int_{\frac{1}{2R} \lt |x| \lt \frac{1}{R}} \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\,{\rm d}x
\end{equation}(2.28)
\begin{equation}
\int_{\operatorname{supp}(\xi_R)} \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\,{\rm d}x=\int_{\frac{1}{2R} \lt |x| \lt \frac{1}{R}} \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\,{\rm d}x
\end{equation}(2.28) \begin{equation}
\left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|\leq H(x)\left|\Delta \left(\xi(R|x|)^\ell\right)\right|+C \left|\nabla \left(\xi(R|x|)^\ell\right)\right|\left(|\nabla H(x)|+\frac{H(x)}{|x|}\right).
\end{equation}
\begin{equation}
\left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|\leq H(x)\left|\Delta \left(\xi(R|x|)^\ell\right)\right|+C \left|\nabla \left(\xi(R|x|)^\ell\right)\right|\left(|\nabla H(x)|+\frac{H(x)}{|x|}\right).
\end{equation}On the other hand, using Equations (2.7) and (2.10), for
 $\frac{1}{2R} \lt |x| \lt \frac{1}{R}$, we obtain
(2.29)
$\frac{1}{2R} \lt |x| \lt \frac{1}{R}$, we obtain
(2.29) \begin{equation}
\left|\Delta \left(\xi(R|x|)^\ell\right)\right|\leq C R^2 \xi(R|x|)^{\ell-2},\qquad \left|\nabla \left(\xi(R|x|)^\ell\right)\right|\leq C R \xi(R|x|)^{\ell-1}.
\end{equation}
\begin{equation}
\left|\Delta \left(\xi(R|x|)^\ell\right)\right|\leq C R^2 \xi(R|x|)^{\ell-2},\qquad \left|\nabla \left(\xi(R|x|)^\ell\right)\right|\leq C R \xi(R|x|)^{\ell-1}.
\end{equation}In view of Equations (2.7) and (2.29), for
 $\frac{1}{2R} \lt |x| \lt \frac{1}{R}$, we get
and(2.30)
$\frac{1}{2R} \lt |x| \lt \frac{1}{R}$, we get
and(2.30) \begin{eqnarray}
\nonumber H(x)\left|\Delta \left(\xi(R|x|)^\ell\right)\right| &\leq & C R^2 |x|^{2-N-\mu_1-\alpha}\left(1-|x|^{2\alpha-2+N+\mu_1}\right)\xi(R|x|)^{\ell-2}
\end{eqnarray}
\begin{eqnarray}
\nonumber H(x)\left|\Delta \left(\xi(R|x|)^\ell\right)\right| &\leq & C R^2 |x|^{2-N-\mu_1-\alpha}\left(1-|x|^{2\alpha-2+N+\mu_1}\right)\xi(R|x|)^{\ell-2}
\end{eqnarray} \begin{eqnarray}
[1mm]
&\leq & C R^{N+\mu_1+\alpha} \xi(R|x|)^{\ell-2}
\end{eqnarray}
\begin{eqnarray}
[1mm]
&\leq & C R^{N+\mu_1+\alpha} \xi(R|x|)^{\ell-2}
\end{eqnarray} \begin{eqnarray*}
&&\left|\nabla \left(\xi(R|x|)^\ell\right)\right|\left(\left|\nabla H(x)\right|+\frac{H(x)}{|x|}\right)\\[1mm]
&\leq& CR\left(|x|^{1-N-\mu_1-\alpha}+|x|^{\alpha-1}+|x|^{1-N-\mu_1-\alpha}\left(1-|x|^{2\alpha-2+N+\mu_1}\right)\right) \xi(R|x|)^{\ell-1}\\[1mm]
&\leq& C R \left(|x|^{1-N-\mu_1-\alpha}+|x|^{\alpha-1}\right)\xi(R|x|)^{\ell-1}\\[1mm]
&\leq& C R|x|^{1-N-\mu_1-\alpha}\left(1+|x|^{2\alpha+N+\mu_1-2}\right)\xi(R|x|)^{\ell-1}\\[1mm]
&\leq& C R^{N+\mu_1+\alpha}\left(1+R^{-2\alpha-N-\mu_1+2}\right)\xi(R|x|)^{\ell-1}.
\end{eqnarray*}
\begin{eqnarray*}
&&\left|\nabla \left(\xi(R|x|)^\ell\right)\right|\left(\left|\nabla H(x)\right|+\frac{H(x)}{|x|}\right)\\[1mm]
&\leq& CR\left(|x|^{1-N-\mu_1-\alpha}+|x|^{\alpha-1}+|x|^{1-N-\mu_1-\alpha}\left(1-|x|^{2\alpha-2+N+\mu_1}\right)\right) \xi(R|x|)^{\ell-1}\\[1mm]
&\leq& C R \left(|x|^{1-N-\mu_1-\alpha}+|x|^{\alpha-1}\right)\xi(R|x|)^{\ell-1}\\[1mm]
&\leq& C R|x|^{1-N-\mu_1-\alpha}\left(1+|x|^{2\alpha+N+\mu_1-2}\right)\xi(R|x|)^{\ell-1}\\[1mm]
&\leq& C R^{N+\mu_1+\alpha}\left(1+R^{-2\alpha-N-\mu_1+2}\right)\xi(R|x|)^{\ell-1}.
\end{eqnarray*}Notice that
 $-2\alpha-N-\mu_1+2 \lt 0$, which implies that for sufficiently large R,
(2.31)
$-2\alpha-N-\mu_1+2 \lt 0$, which implies that for sufficiently large R,
(2.31) \begin{equation}
\left|\nabla \left(\xi(R|x|)^\ell\right)\right|\left(|\nabla H(x)|+\frac{H(x)}{|x|}\right)\leq C R^{N+\mu_1+\alpha}\xi(R|x|)^{\ell-1}.
\end{equation}
\begin{equation}
\left|\nabla \left(\xi(R|x|)^\ell\right)\right|\left(|\nabla H(x)|+\frac{H(x)}{|x|}\right)\leq C R^{N+\mu_1+\alpha}\xi(R|x|)^{\ell-1}.
\end{equation}Thus, in view of Equations (2.10), (2.28), (2.30) and (2.31), we obtain
(2.32) \begin{equation}
\left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}\leq C R^{\frac{(N+\mu_1+\alpha)p}{p-q}} \xi(R|x|)^{\frac{(\ell-2)p}{p-q}},\quad \frac{1}{2R} \lt |x| \lt \frac{1}{R}.
\end{equation}
\begin{equation}
\left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}\leq C R^{\frac{(N+\mu_1+\alpha)p}{p-q}} \xi(R|x|)^{\frac{(\ell-2)p}{p-q}},\quad \frac{1}{2R} \lt |x| \lt \frac{1}{R}.
\end{equation}Moreover, we have (for
 $\frac{1}{2R} \lt |x| \lt \frac{1}{R}$),
(2.33)
$\frac{1}{2R} \lt |x| \lt \frac{1}{R}$),
(2.33) \begin{eqnarray}
\nonumber \xi_R(x)^{\frac{-q}{p-q}} |x|^{\frac{aq}{p-q}}&=& |x|^{\frac{aq}{p-q}} H(x)^{\frac{-q}{p-q}} \xi(R|x|)^{\frac{-\ell q}{p-q}}
\end{eqnarray}
\begin{eqnarray}
\nonumber \xi_R(x)^{\frac{-q}{p-q}} |x|^{\frac{aq}{p-q}}&=& |x|^{\frac{aq}{p-q}} H(x)^{\frac{-q}{p-q}} \xi(R|x|)^{\frac{-\ell q}{p-q}}
\end{eqnarray} \begin{eqnarray}
\nonumber &=& |x|^{\frac{aq}{p-q}} |x|^{\frac{(-2+N+\mu_1+\alpha)q}{p-q}}\left(1-|x|^{2\alpha-2+N+\mu_1}\right)^{\frac{-q}{p-q}}\xi(R|x|)^{\frac{-\ell q}{p-q}}
\end{eqnarray}
\begin{eqnarray}
\nonumber &=& |x|^{\frac{aq}{p-q}} |x|^{\frac{(-2+N+\mu_1+\alpha)q}{p-q}}\left(1-|x|^{2\alpha-2+N+\mu_1}\right)^{\frac{-q}{p-q}}\xi(R|x|)^{\frac{-\ell q}{p-q}}
\end{eqnarray} \begin{eqnarray}
\nonumber &\leq & C |x|^{\frac{aq+q(-2+N+\mu_1+\alpha)}{p-q}}\xi(R|x|)^{\frac{-\ell q}{p-q}}
\end{eqnarray}
\begin{eqnarray}
\nonumber &\leq & C |x|^{\frac{aq+q(-2+N+\mu_1+\alpha)}{p-q}}\xi(R|x|)^{\frac{-\ell q}{p-q}}
\end{eqnarray} \begin{eqnarray}
&\leq & C R^{\frac{q(-a+2-N-\mu_1-\alpha)}{p-q}}\xi(R|x|)^{\frac{-\ell q}{p-q}}.
\end{eqnarray}
\begin{eqnarray}
&\leq & C R^{\frac{q(-a+2-N-\mu_1-\alpha)}{p-q}}\xi(R|x|)^{\frac{-\ell q}{p-q}}.
\end{eqnarray}Combining Equation (2.32) with Equation (2.33), we get
(2.34) \begin{align}
& \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\leq C R^{\frac{(N+\mu_1+\alpha)p+q(-a+2-N-\mu_1-\alpha)}{p-q}} \xi(R|x|)^{\ell-\frac{2p}{p-q}},\nonumber \\ & \quad \frac{1}{2R} \lt |x| \lt \frac{1}{R}.
\end{align}
\begin{align}
& \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\leq C R^{\frac{(N+\mu_1+\alpha)p+q(-a+2-N-\mu_1-\alpha)}{p-q}} \xi(R|x|)^{\ell-\frac{2p}{p-q}},\nonumber \\ & \quad \frac{1}{2R} \lt |x| \lt \frac{1}{R}.
\end{align}Thus, using Equations (2.10), (2.27) and (2.34), we obtain
which proves Equation (2.25). \begin{eqnarray*}
&&\int_{\operatorname{supp}(\xi_R)} \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\,{\rm d}x\\
&\leq& C R^{\frac{(N+\mu_1+\alpha)p+q(-a+2-N-\mu_1-\alpha)}{p-q}}\int_{\frac{1}{2R} \lt |x| \lt \frac{1}{R}} \xi(R|x|)^{\ell-\frac{2p}{p-q}}\,{\rm d}x\\
&\leq& C R^{\frac{(N+\mu_1+\alpha)p+q(-a+2-N-\mu_1-\alpha)}{p-q}}R^{-N},
\end{eqnarray*}
\begin{eqnarray*}
&&\int_{\operatorname{supp}(\xi_R)} \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\,{\rm d}x\\
&\leq& C R^{\frac{(N+\mu_1+\alpha)p+q(-a+2-N-\mu_1-\alpha)}{p-q}}\int_{\frac{1}{2R} \lt |x| \lt \frac{1}{R}} \xi(R|x|)^{\ell-\frac{2p}{p-q}}\,{\rm d}x\\
&\leq& C R^{\frac{(N+\mu_1+\alpha)p+q(-a+2-N-\mu_1-\alpha)}{p-q}}R^{-N},
\end{eqnarray*}(ii) In view of Equations (2.7) and (2.29), for
 $\frac{1}{2R} \lt |x| \lt \frac{1}{R}$, we get
and(2.35)
$\frac{1}{2R} \lt |x| \lt \frac{1}{R}$, we get
and(2.35) \begin{eqnarray}
\nonumber H(x)\left|\Delta \left(\xi(R|x|)^\ell\right)\right| &\leq & C R^2 |x|^\alpha\, \ln\left(\frac{1}{|x|}\right)\xi(R|x|)^{\ell-2}
\end{eqnarray}
\begin{eqnarray}
\nonumber H(x)\left|\Delta \left(\xi(R|x|)^\ell\right)\right| &\leq & C R^2 |x|^\alpha\, \ln\left(\frac{1}{|x|}\right)\xi(R|x|)^{\ell-2}
\end{eqnarray} \begin{eqnarray}
&\leq & C R^{2-\alpha}\,\ln R\, \xi(R|x|)^{\ell-2}
\end{eqnarray}(2.36)
\begin{eqnarray}
&\leq & C R^{2-\alpha}\,\ln R\, \xi(R|x|)^{\ell-2}
\end{eqnarray}(2.36) \begin{eqnarray}
\nonumber \left|\nabla \left(\xi(R|x|)^\ell\right)\right|\left(|\nabla H(x)|+\frac{H(x)}{|x|}\right)
&\leq & CR\left(|x|^{\alpha-1}-|x|^{\alpha-1}\,\ln|x|\right) \xi(R|x|)^{\ell-1}
\end{eqnarray}
\begin{eqnarray}
\nonumber \left|\nabla \left(\xi(R|x|)^\ell\right)\right|\left(|\nabla H(x)|+\frac{H(x)}{|x|}\right)
&\leq & CR\left(|x|^{\alpha-1}-|x|^{\alpha-1}\,\ln|x|\right) \xi(R|x|)^{\ell-1}
\end{eqnarray} \begin{eqnarray}
\nonumber &\leq & CR^{2-\alpha}\left(1+\ln R\right)\xi(R|x|)^{\ell-1}
\end{eqnarray}
\begin{eqnarray}
\nonumber &\leq & CR^{2-\alpha}\left(1+\ln R\right)\xi(R|x|)^{\ell-1}
\end{eqnarray} \begin{eqnarray}
&\leq & CR^{2-\alpha}\,\ln R \xi(R|x|)^{\ell-1}.
\end{eqnarray}
\begin{eqnarray}
&\leq & CR^{2-\alpha}\,\ln R \xi(R|x|)^{\ell-1}.
\end{eqnarray}Thus, in view of Equations (2.10), (2.28), (2.35) and (2.36), we obtain
(2.37) \begin{equation}
\left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}\leq C R^{\frac{(2-\alpha)p}{p-q}}(\ln R)^{\frac{p}{p-q}} \xi(R|x|)^{\frac{(\ell-2)p}{p-q}},\quad \frac{1}{2R} \lt |x| \lt \frac{1}{R}.
\end{equation}
\begin{equation}
\left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}\leq C R^{\frac{(2-\alpha)p}{p-q}}(\ln R)^{\frac{p}{p-q}} \xi(R|x|)^{\frac{(\ell-2)p}{p-q}},\quad \frac{1}{2R} \lt |x| \lt \frac{1}{R}.
\end{equation}Moreover, we have (for
 $\frac{1}{2R} \lt |x| \lt \frac{1}{R}$)
(2.38)
$\frac{1}{2R} \lt |x| \lt \frac{1}{R}$)
(2.38) \begin{eqnarray}
\nonumber \xi_R(x)^{\frac{-q}{p-q}} |x|^{\frac{aq}{p-q}}&=& |x|^{\frac{aq}{p-q}} H(x)^{\frac{-q}{p-q}} \xi(R|x|)^{\frac{-\ell q}{p-q}}
\end{eqnarray}
\begin{eqnarray}
\nonumber \xi_R(x)^{\frac{-q}{p-q}} |x|^{\frac{aq}{p-q}}&=& |x|^{\frac{aq}{p-q}} H(x)^{\frac{-q}{p-q}} \xi(R|x|)^{\frac{-\ell q}{p-q}}
\end{eqnarray} \begin{eqnarray}
\nonumber &=& |x|^{\frac{aq}{p-q}}|x|^{\frac{-\alpha q}{p-q}}\left(\ln \left(\frac{1}{|x|}\right)\right)^{\frac{-q}{p-q}} \xi(R|x|)^{\frac{-\ell q}{p-q}}
\end{eqnarray}
\begin{eqnarray}
\nonumber &=& |x|^{\frac{aq}{p-q}}|x|^{\frac{-\alpha q}{p-q}}\left(\ln \left(\frac{1}{|x|}\right)\right)^{\frac{-q}{p-q}} \xi(R|x|)^{\frac{-\ell q}{p-q}}
\end{eqnarray} \begin{eqnarray}
&\leq & C R^{\frac{q(\alpha-a)}{p-q}}(\ln R)^{\frac{-q}{p-q}}\xi(R|x|)^{\frac{-\ell q}{p-q}}.
\end{eqnarray}
\begin{eqnarray}
&\leq & C R^{\frac{q(\alpha-a)}{p-q}}(\ln R)^{\frac{-q}{p-q}}\xi(R|x|)^{\frac{-\ell q}{p-q}}.
\end{eqnarray}Combining Equation (2.37) with Equation (2.38), we get
(2.39) \begin{align}
& \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\leq C R^{\frac{(2-\alpha)p+q(\alpha-a)}{p-q}}\,\ln R \xi(R|x|)^{\ell-\frac{2p}{p-q}},\nonumber \\& \quad \frac{1}{2R} \lt |x| \lt \frac{1}{R}.
\end{align}
\begin{align}
& \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\leq C R^{\frac{(2-\alpha)p+q(\alpha-a)}{p-q}}\,\ln R \xi(R|x|)^{\ell-\frac{2p}{p-q}},\nonumber \\& \quad \frac{1}{2R} \lt |x| \lt \frac{1}{R}.
\end{align}Thus, using Equations (2.10), (2.27) and (2.39), we obtain
which proves Equation (2.26). \begin{eqnarray*}
&&\int_{\operatorname{supp}(\xi_R)} \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\,{\rm d}x\\
&\leq& C R^{\frac{(2-\alpha)p+q(\alpha-a)}{p-q}}\,\ln R \int_{\frac{1}{2R} \lt |x| \lt \frac{1}{R}} \xi(R|x|)^{\ell-\frac{2p}{p-q}}\,{\rm d}x\\
&\leq& C R^{\frac{(2-\alpha)p+q(\alpha-a)}{p-q}}R^{-N}\, \ln R,
\end{eqnarray*}
\begin{eqnarray*}
&&\int_{\operatorname{supp}(\xi_R)} \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\,{\rm d}x\\
&\leq& C R^{\frac{(2-\alpha)p+q(\alpha-a)}{p-q}}\,\ln R \int_{\frac{1}{2R} \lt |x| \lt \frac{1}{R}} \xi(R|x|)^{\ell-\frac{2p}{p-q}}\,{\rm d}x\\
&\leq& C R^{\frac{(2-\alpha)p+q(\alpha-a)}{p-q}}R^{-N}\, \ln R,
\end{eqnarray*}
(i) Let
 $\mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2$. For sufficiently large T, R and
$\mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2$. For sufficiently large T, R and  $\ell$, there holds
(2.40)where φ is the function defined by Equation (2.14).
$\ell$, there holds
(2.40)where φ is the function defined by Equation (2.14). \begin{equation}
J_2(\varphi)\leq CT R^{\frac{(\mu_1+\alpha)p-(a-2+\mu_1+\alpha)q}{p-q}},
\end{equation}
\begin{equation}
J_2(\varphi)\leq CT R^{\frac{(\mu_1+\alpha)p-(a-2+\mu_1+\alpha)q}{p-q}},
\end{equation}(ii) Let
 $\mu_2=-\left(\frac{\mu_1-N+2}{2}\right)^2$. For sufficiently large T, R and
$\mu_2=-\left(\frac{\mu_1-N+2}{2}\right)^2$. For sufficiently large T, R and  $\ell$, there holds
(2.41)
$\ell$, there holds
(2.41) \begin{equation}
J_2(\varphi)\leq CT R^{\frac{(2-\alpha-N)p+(\alpha-a+N)q}{p-q}}\,\ln R.
\end{equation}
\begin{equation}
J_2(\varphi)\leq CT R^{\frac{(2-\alpha-N)p+(\alpha-a+N)q}{p-q}}\,\ln R.
\end{equation}
Proof. By Equation (2.2) and (2.14), we have
 \begin{equation}
J_2(\varphi)=\left(\int_{\operatorname{supp}(\eta_T)} \eta_T(t)\,{\rm d}t\right) \left(\int_{\operatorname{supp}(\xi_R)} \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\,{\rm d}x \right).
\end{equation}
\begin{equation}
J_2(\varphi)=\left(\int_{\operatorname{supp}(\eta_T)} \eta_T(t)\,{\rm d}t\right) \left(\int_{\operatorname{supp}(\xi_R)} \xi_R^{\frac{-q}{p-q}} \left|\mathcal{L}_{\mu_1,\mu_2}^*\xi_R\right|^{\frac{p}{p-q}}|x|^{\frac{aq}{p-q}}\,{\rm d}x \right).
\end{equation}On the other hand, using Equations (2.9) and (2.11), we obtain
 \begin{eqnarray}
\int_{\operatorname{supp}(\eta_T)} \eta_T(t)\,{\rm d}t &=& \int_0^T \eta\left(\frac{t}{T}\right)^\ell\,{\rm d}t
= T \int_0^1\eta(s)^\ell\,{\rm d}s.
\end{eqnarray}
\begin{eqnarray}
\int_{\operatorname{supp}(\eta_T)} \eta_T(t)\,{\rm d}t &=& \int_0^T \eta\left(\frac{t}{T}\right)^\ell\,{\rm d}t
= T \int_0^1\eta(s)^\ell\,{\rm d}s.
\end{eqnarray}Hence, using Lemma 2.6 and Equations (2.42) and (2.43), we obtain Equation (2.40) and (2.41).
3. Proof of Theorem 1.3
3.1. Proof of part (I)
We use the contradiction argument by supposing that ![]() $u\in L^p_{\rm loc}(Q)$ is a weak solution to Equation (1.1). By Lemma 2.1, Equation (2.3) holds for all
$u\in L^p_{\rm loc}(Q)$ is a weak solution to Equation (1.1). By Lemma 2.1, Equation (2.3) holds for all ![]() $\varphi\in \Phi$ (with
$\varphi\in \Phi$ (with ![]() $J_i(\varphi) \lt \infty$,
$J_i(\varphi) \lt \infty$, ![]() $i=1,2$). Hence, by Lemma 2.2, we deduce that for sufficiently large T, R and
$i=1,2$). Hence, by Lemma 2.2, we deduce that for sufficiently large T, R and ![]() $\ell$,
$\ell$,
 \begin{equation}
-\int_{\Gamma} f(x)\,\frac{\partial \varphi}{\partial \nu}\,{\rm d}\sigma\,{\rm d}t\leq C \sum_{i=1}^2 J_i(\varphi),
\end{equation}
\begin{equation}
-\int_{\Gamma} f(x)\,\frac{\partial \varphi}{\partial \nu}\,{\rm d}\sigma\,{\rm d}t\leq C \sum_{i=1}^2 J_i(\varphi),
\end{equation}where φ is the function defined by Equation (2.14). We first consider the following:
![]() $\bullet$ The case:
$\bullet$ The case:  $\mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2$. In view of Equations (2.18) and (2.43), we obtain
$\mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2$. In view of Equations (2.18) and (2.43), we obtain
 \begin{eqnarray*}
-\int_{\Gamma} f(x)\,\frac{\partial \varphi}{\partial \nu}\,{\rm d}\sigma\,{\rm d}t &=& (2\alpha-2+N+\mu_1) \int_{\operatorname{supp}(\eta_T)} \int_{\partial B_1} f(x)\eta_T(t)\,{\rm d}\sigma\,{\rm d}t\\
&=& (2\alpha-2+N+\mu_1) \left(\int_0^1\eta(s)^\ell\,{\rm d}s\right)T \int_{\partial B_1} f(x)\,{\rm d}\sigma.
\end{eqnarray*}
\begin{eqnarray*}
-\int_{\Gamma} f(x)\,\frac{\partial \varphi}{\partial \nu}\,{\rm d}\sigma\,{\rm d}t &=& (2\alpha-2+N+\mu_1) \int_{\operatorname{supp}(\eta_T)} \int_{\partial B_1} f(x)\eta_T(t)\,{\rm d}\sigma\,{\rm d}t\\
&=& (2\alpha-2+N+\mu_1) \left(\int_0^1\eta(s)^\ell\,{\rm d}s\right)T \int_{\partial B_1} f(x)\,{\rm d}\sigma.
\end{eqnarray*}Notice that
Hence, there holds
 \begin{equation}
-\int_{\Gamma} f(x)\,\frac{\partial \varphi}{\partial \nu}\,{\rm d}\sigma\,{\rm d}t=CTI_f.
\end{equation}
\begin{equation}
-\int_{\Gamma} f(x)\,\frac{\partial \varphi}{\partial \nu}\,{\rm d}\sigma\,{\rm d}t=CTI_f.
\end{equation}Using Equations (2.22), (2.40), (3.1) and (3.2), we obtain
 \begin{equation*}
TI_f \leq C \left(T^{1-\frac{kp}{p-1}} \left(\ln R+ R^{\alpha+\mu_1-2-\frac{a}{p-1}}\right)+TR^{\frac{(\mu_1+\alpha)p-(a-2+\mu_1+\alpha)q}{p-q}}\right),
\end{equation*}
\begin{equation*}
TI_f \leq C \left(T^{1-\frac{kp}{p-1}} \left(\ln R+ R^{\alpha+\mu_1-2-\frac{a}{p-1}}\right)+TR^{\frac{(\mu_1+\alpha)p-(a-2+\mu_1+\alpha)q}{p-q}}\right),
\end{equation*}that is,
 \begin{equation}
I_f\leq C\left(T^{\frac{-kp}{p-1}} \left(\ln R+ R^{\alpha+\mu_1-2-\frac{a}{p-1}}\right)+R^{\frac{(\mu_1+\alpha)p-(a-2+\mu_1+\alpha)q}{p-q}}\right).
\end{equation}
\begin{equation}
I_f\leq C\left(T^{\frac{-kp}{p-1}} \left(\ln R+ R^{\alpha+\mu_1-2-\frac{a}{p-1}}\right)+R^{\frac{(\mu_1+\alpha)p-(a-2+\mu_1+\alpha)q}{p-q}}\right).
\end{equation} Next, taking ![]() $T=R^\theta$, where
$T=R^\theta$, where
 \begin{equation}
\theta \gt \max\left\{\frac{(\alpha+\mu_1-2-\frac{a}{p-1})(p-1)}{kp},0\right\},
\end{equation}
\begin{equation}
\theta \gt \max\left\{\frac{(\alpha+\mu_1-2-\frac{a}{p-1})(p-1)}{kp},0\right\},
\end{equation}Equation (3.3) reduces to
 \begin{equation}
I_f\leq C\left(R^{\frac{-kp\theta}{p-1}}\,\ln R+ R^{\lambda_1}+R^{\lambda_2}\right),
\end{equation}
\begin{equation}
I_f\leq C\left(R^{\frac{-kp\theta}{p-1}}\,\ln R+ R^{\lambda_1}+R^{\lambda_2}\right),
\end{equation}where
 \begin{equation}
\lambda_1=\alpha+\mu_1-2-\frac{a}{p-1}-\frac{kp\theta}{p-1}
\end{equation}
\begin{equation}
\lambda_1=\alpha+\mu_1-2-\frac{a}{p-1}-\frac{kp\theta}{p-1}
\end{equation}and
 \begin{equation}
\lambda_2=\frac{(\mu_1+\alpha)p-(a-2+\mu_1+\alpha)q}{p-q}.
\end{equation}
\begin{equation}
\lambda_2=\frac{(\mu_1+\alpha)p-(a-2+\mu_1+\alpha)q}{p-q}.
\end{equation} Observe that by the choice (3.4) of the parameter θ, one has ![]() $\lambda_1 \lt 0$. Moreover, by Equation (1.11), there holds
$\lambda_1 \lt 0$. Moreover, by Equation (1.11), there holds ![]() $\lambda_2 \lt 0$. Thus, passing to the limit as
$\lambda_2 \lt 0$. Thus, passing to the limit as ![]() $R\to \infty$ in Equation (3.5), we get
$R\to \infty$ in Equation (3.5), we get ![]() $I_f\leq 0$, which contradicts the positivity of I f. Next, we consider the following:
$I_f\leq 0$, which contradicts the positivity of I f. Next, we consider the following:
![]() $\bullet$ The case:
$\bullet$ The case:  $\mu_2=-\left(\frac{\mu_1-N+2}{2}\right)^2$. In view of Equations (2.18) and (2.43), we obtain
$\mu_2=-\left(\frac{\mu_1-N+2}{2}\right)^2$. In view of Equations (2.18) and (2.43), we obtain
 \begin{eqnarray*}
-\int_{\Gamma} f(x)\,\frac{\partial \varphi}{\partial \nu}\,{\rm d}\sigma\,{\rm d}t &=& \int_{\operatorname{supp}(\eta_T)} \int_{\partial B_1} f(x)\eta_T(t)\,{\rm d}\sigma\,{\rm d}t\\
&=& \left(\int_0^1\eta(s)^\ell\,{\rm d}s\right)T \int_{\partial B_1} f(x)\,{\rm d}\sigma,
\end{eqnarray*}
\begin{eqnarray*}
-\int_{\Gamma} f(x)\,\frac{\partial \varphi}{\partial \nu}\,{\rm d}\sigma\,{\rm d}t &=& \int_{\operatorname{supp}(\eta_T)} \int_{\partial B_1} f(x)\eta_T(t)\,{\rm d}\sigma\,{\rm d}t\\
&=& \left(\int_0^1\eta(s)^\ell\,{\rm d}s\right)T \int_{\partial B_1} f(x)\,{\rm d}\sigma,
\end{eqnarray*}which yields Equation (3.2). Using Equations (2.23), (2.41), (3.1) and (3.2), we obtain
 \begin{equation*}
TI_f \leq C \left(T^{1-\frac{kp}{p-1}}\, \ln R\left(\ln R+R^{-\left(\frac{a}{p-1}+\alpha+N\right)}\right)+T R^{\frac{(2-\alpha-N)p+(\alpha-a+N)q}{p-q}}\,\ln R\right).
\end{equation*}
\begin{equation*}
TI_f \leq C \left(T^{1-\frac{kp}{p-1}}\, \ln R\left(\ln R+R^{-\left(\frac{a}{p-1}+\alpha+N\right)}\right)+T R^{\frac{(2-\alpha-N)p+(\alpha-a+N)q}{p-q}}\,\ln R\right).
\end{equation*}Notice that
Hence, the above estimate is equivalent to
 \begin{equation}
I_f \leq C \left(T^{-\frac{kp}{p-1}}\, \ln R\left(\ln R+R^{\alpha+\mu_1-2-\frac{a}{p-1}}\right)+R^{\frac{(\mu_1+\alpha)p-(a-2+\mu_1+\alpha)q}{p-q}}\,\ln R\right).
\end{equation}
\begin{equation}
I_f \leq C \left(T^{-\frac{kp}{p-1}}\, \ln R\left(\ln R+R^{\alpha+\mu_1-2-\frac{a}{p-1}}\right)+R^{\frac{(\mu_1+\alpha)p-(a-2+\mu_1+\alpha)q}{p-q}}\,\ln R\right).
\end{equation} Taking ![]() $T=R^\theta$, where the parameter θ satisfies Equation (3.4), Equation (3.8) reduces to
$T=R^\theta$, where the parameter θ satisfies Equation (3.4), Equation (3.8) reduces to
 \begin{equation}
I_f\leq C\left(R^{\frac{-kp\theta}{p-1}}(\ln R)^2+ R^{\lambda_1}\,\ln R+R^{\lambda_2}\,\ln R\right),
\end{equation}
\begin{equation}
I_f\leq C\left(R^{\frac{-kp\theta}{p-1}}(\ln R)^2+ R^{\lambda_1}\,\ln R+R^{\lambda_2}\,\ln R\right),
\end{equation}where λ 1 and λ 2 are given, respectively, by Equations (3.6) and (3.7). As in the previous case, due to Equations (3.4) and (1.11), one has ![]() $\lambda_i \lt 0$,
$\lambda_i \lt 0$, ![]() $i=1,2$. Thus, passing to the limit as
$i=1,2$. Thus, passing to the limit as ![]() $R\to \infty$ in Equation (3.9), we get a contradiction with
$R\to \infty$ in Equation (3.9), we get a contradiction with ![]() $I_f \gt 0$.
$I_f \gt 0$.
Consequently, Equation (1.1) admits no weak solution. This completes the proof of part (I) of Theorem 1.3. ![]() $\square$
$\square$
3.2. Proof of part (II)
We first consider the following:
• Case 1:
 $\mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2$. Let δ and ϵ be two real numbers satisfying, respectively,
(3.10)and
$\mu_2 \gt -\left(\frac{\mu_1-N+2}{2}\right)^2$. Let δ and ϵ be two real numbers satisfying, respectively,
(3.10)and \begin{equation}
\delta_1 \lt \delta \lt \min\left\{\delta_2,\frac{2-a}{p-q}\right\}
\end{equation}(3.11)where
\begin{equation}
\delta_1 \lt \delta \lt \min\left\{\delta_2,\frac{2-a}{p-q}\right\}
\end{equation}(3.11)where \begin{equation}
0 \lt \epsilon \lt \left[P_{q,\mu_1,\mu_2,N}(\delta)\right]^{\frac{1}{p-q}},
\end{equation}and δ i,
\begin{equation}
0 \lt \epsilon \lt \left[P_{q,\mu_1,\mu_2,N}(\delta)\right]^{\frac{1}{p-q}},
\end{equation}and δ i, \begin{equation*}
P_{q,\mu_1,\mu_2,N}(\delta)= -q^2\delta^2+q(N-\mu_1-2)\delta+\mu_2
\end{equation*}
\begin{equation*}
P_{q,\mu_1,\mu_2,N}(\delta)= -q^2\delta^2+q(N-\mu_1-2)\delta+\mu_2
\end{equation*} $i=1,2$, are the roots of
$i=1,2$, are the roots of  $P_{q,\mu_1,\mu_2,N}(\delta)$, given by
$P_{q,\mu_1,\mu_2,N}(\delta)$, given by
 \begin{equation*}
\delta_1=-\frac{\mu_1+\alpha}{q} \lt \delta_2=\frac{N-2+\alpha}{q}.
\end{equation*}
\begin{equation*}
\delta_1=-\frac{\mu_1+\alpha}{q} \lt \delta_2=\frac{N-2+\alpha}{q}.
\end{equation*}Notice that by Equation (1.12), one has
 \begin{equation*}
\delta_1 \lt \frac{2-a}{p-q}.
\end{equation*}
\begin{equation*}
\delta_1 \lt \frac{2-a}{p-q}.
\end{equation*}Hence, the set of δ satisfying Equation (3.10) is non-empty. Moreover, for
 $\delta_1 \lt \delta \lt \delta_2$, one has
$\delta_1 \lt \delta \lt \delta_2$, one has  $P_{q,\mu_1,\mu_2,N}(\delta) \gt 0$. Hence,
$P_{q,\mu_1,\mu_2,N}(\delta) \gt 0$. Hence,  $\left[P_{q,\mu_1,\mu_2,N}(\delta)\right]^{\frac{1}{p-q}}$ is well-defined, and the set of ϵ satisfying Equation (3.11) is non-empty. Let us consider functions of the form
(3.12)
$\left[P_{q,\mu_1,\mu_2,N}(\delta)\right]^{\frac{1}{p-q}}$ is well-defined, and the set of ϵ satisfying Equation (3.11) is non-empty. Let us consider functions of the form
(3.12) \begin{equation}
u_{\delta,\epsilon}(x)=\epsilon |x|^{-\delta},\quad x\in B_1\backslash\{0\}.
\end{equation}
\begin{equation}
u_{\delta,\epsilon}(x)=\epsilon |x|^{-\delta},\quad x\in B_1\backslash\{0\}.
\end{equation}Elementary calculations show that
(3.13) \begin{equation}
\mathcal{L}_{\mu_1,\mu_2}u_{\delta,\epsilon}^q(x)=\epsilon^q P_{q,\mu_1,\mu_2,N}(\delta)|x|^{-q\delta-2},\quad x\in B_1\backslash\{0\}.
\end{equation}
\begin{equation}
\mathcal{L}_{\mu_1,\mu_2}u_{\delta,\epsilon}^q(x)=\epsilon^q P_{q,\mu_1,\mu_2,N}(\delta)|x|^{-q\delta-2},\quad x\in B_1\backslash\{0\}.
\end{equation}In view of Equations (3.10), (3.11), (3.12) and (3.13), for all
 $x\in B_1\backslash\{0\}$, we obtain
$x\in B_1\backslash\{0\}$, we obtain
 \begin{eqnarray*}
\mathcal{L}_{\mu_1,\mu_2}u_{\delta,\epsilon}^q(x)&\geq & \epsilon^q \epsilon^{p-q} |x|^{-q\delta-2}\\
&\geq & \epsilon^p|x|^{-\delta p-a}\\
&=& |x|^{-a} u_{\delta,\epsilon}^p(x).
\end{eqnarray*}
\begin{eqnarray*}
\mathcal{L}_{\mu_1,\mu_2}u_{\delta,\epsilon}^q(x)&\geq & \epsilon^q \epsilon^{p-q} |x|^{-q\delta-2}\\
&\geq & \epsilon^p|x|^{-\delta p-a}\\
&=& |x|^{-a} u_{\delta,\epsilon}^p(x).
\end{eqnarray*}Hence, for any δ and ϵ satisfying, respectively, Equations (3.10) and (3.11), functions of the form (3.12) are stationary positive solutions to Equation (1.1) with
 $f\equiv \epsilon^q$. Next, we consider the following:
$f\equiv \epsilon^q$. Next, we consider the following:• Case 2:
 $\mu_2=-\left(\frac{\mu_1-N+2}{2}\right)^2$. For
(3.14)and
$\mu_2=-\left(\frac{\mu_1-N+2}{2}\right)^2$. For
(3.14)and \begin{equation}
0 \lt \delta \lt \frac{1}{q}
\end{equation}(3.15)let
\begin{equation}
0 \lt \delta \lt \frac{1}{q}
\end{equation}(3.15)let \begin{equation}
0 \lt \epsilon \lt \left[\delta q(1-\delta q)\right]^{\frac{1}{p-q}},
\end{equation}(3.16)
\begin{equation}
0 \lt \epsilon \lt \left[\delta q(1-\delta q)\right]^{\frac{1}{p-q}},
\end{equation}(3.16) \begin{equation}
u_{\delta,\epsilon}(x)=\left\{\begin{array}{llll}
0 &\mbox{if}\ \ 0 \lt |x|\leq {\rm e}^{-1},\\[1.5mm]
\epsilon |x|^{\frac{\mu_1+\alpha}{q}}\left[\ln(e|x|)\right]^\delta &\mbox{if}\ \ e^{-1} \lt |x|\leq 1.
\end{array}
\right.
\end{equation}
\begin{equation}
u_{\delta,\epsilon}(x)=\left\{\begin{array}{llll}
0 &\mbox{if}\ \ 0 \lt |x|\leq {\rm e}^{-1},\\[1.5mm]
\epsilon |x|^{\frac{\mu_1+\alpha}{q}}\left[\ln(e|x|)\right]^\delta &\mbox{if}\ \ e^{-1} \lt |x|\leq 1.
\end{array}
\right.
\end{equation}Elementary calculations show that
(3.17) \begin{equation}
\mathcal{L}_{\mu_1,\mu_2}u_{\delta,\epsilon}^q(x)=\left\{\begin{array}{llll}
0=|x|^{-a}u_{\delta,\epsilon}^p(x) &\mbox{if}\ \ 0 \lt |x|\leq {\rm e}^{-1},\\[2mm]
\epsilon^q \delta q (1-\delta q)|x|^{\mu_1+\alpha-2} \left[\ln(e|x|)\right]^{\delta q-2} &\mbox{if}\ \ {\rm e}^{-1} \lt |x|\leq 1.
\end{array}
\right.
\end{equation}
\begin{equation}
\mathcal{L}_{\mu_1,\mu_2}u_{\delta,\epsilon}^q(x)=\left\{\begin{array}{llll}
0=|x|^{-a}u_{\delta,\epsilon}^p(x) &\mbox{if}\ \ 0 \lt |x|\leq {\rm e}^{-1},\\[2mm]
\epsilon^q \delta q (1-\delta q)|x|^{\mu_1+\alpha-2} \left[\ln(e|x|)\right]^{\delta q-2} &\mbox{if}\ \ {\rm e}^{-1} \lt |x|\leq 1.
\end{array}
\right.
\end{equation}Using Equations (3.15) and (3.16), for
 ${\rm e}^{-1} \lt |x|\leq 1$, we obtain
(3.18)
${\rm e}^{-1} \lt |x|\leq 1$, we obtain
(3.18) \begin{equation}
\begin{aligned}
&\epsilon^q \delta q (1-\delta q)|x|^{\mu_1+\alpha-2} \left[\ln(e|x|)\right]^{\delta q-2}\\[1mm]
&\geq \epsilon^q\epsilon^{p-q} |x|^{\mu_1+\alpha-2} \left[\ln(e|x|)\right]^{\delta q-2}\\[1mm]
&= |x|^{-a}u_{\delta,\epsilon}^p(x) |x|^{a+\mu_1+\alpha-2-\frac{(\mu_1+\alpha)p}{q}} \left[\ln(e|x|)\right]^{\delta(q-p)-2}.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
&\epsilon^q \delta q (1-\delta q)|x|^{\mu_1+\alpha-2} \left[\ln(e|x|)\right]^{\delta q-2}\\[1mm]
&\geq \epsilon^q\epsilon^{p-q} |x|^{\mu_1+\alpha-2} \left[\ln(e|x|)\right]^{\delta q-2}\\[1mm]
&= |x|^{-a}u_{\delta,\epsilon}^p(x) |x|^{a+\mu_1+\alpha-2-\frac{(\mu_1+\alpha)p}{q}} \left[\ln(e|x|)\right]^{\delta(q-p)-2}.
\end{aligned}
\end{equation}Notice that, in view of Equation (1.12), one has
(3.19) \begin{equation}
a+\mu_1+\alpha-2-\frac{(\mu_1+\alpha)p}{q} \lt 0.
\end{equation}
\begin{equation}
a+\mu_1+\alpha-2-\frac{(\mu_1+\alpha)p}{q} \lt 0.
\end{equation}Moreover, since δ > 0 and p > q, there holds
(3.20) \begin{equation}
\delta(q-p)-2 \lt 0.
\end{equation}
\begin{equation}
\delta(q-p)-2 \lt 0.
\end{equation}Hence, it follows from Equations (3.19) and (3.20) that
(3.21) \begin{equation}
|x|^{a+\mu_1+\alpha-2-\frac{(\mu_1+\alpha)p}{q}} \left[\ln(e|x|)\right]^{\delta(q-p)-2} \geq 1,\quad e^{-1} \lt |x|\leq 1.
\end{equation}
\begin{equation}
|x|^{a+\mu_1+\alpha-2-\frac{(\mu_1+\alpha)p}{q}} \left[\ln(e|x|)\right]^{\delta(q-p)-2} \geq 1,\quad e^{-1} \lt |x|\leq 1.
\end{equation}Then, Equations (3.18) and (3.21) yield
(3.22) \begin{equation}
\epsilon^q \delta q (1-\delta q)|x|^{\mu_1+\alpha-2} \left[\ln(e|x|)\right]^{\delta q-2}\geq |x|^{-a}u_{\delta,\epsilon}^p(x),\quad e^{-1} \lt |x|\leq 1.
\end{equation}
\begin{equation}
\epsilon^q \delta q (1-\delta q)|x|^{\mu_1+\alpha-2} \left[\ln(e|x|)\right]^{\delta q-2}\geq |x|^{-a}u_{\delta,\epsilon}^p(x),\quad e^{-1} \lt |x|\leq 1.
\end{equation}Thus, in view of Equations (3.17) and (3.22), we obtain
 \begin{equation*}
\mathcal{L}_{\mu_1,\mu_2}u_{\delta,\epsilon}^q(x)\geq |x|^{-a}u_{\delta,\epsilon}^p(x),\quad x\in B_1\backslash\{0\}.
\end{equation*}
\begin{equation*}
\mathcal{L}_{\mu_1,\mu_2}u_{\delta,\epsilon}^q(x)\geq |x|^{-a}u_{\delta,\epsilon}^p(x),\quad x\in B_1\backslash\{0\}.
\end{equation*}Consequently, for any δ and ϵ satisfying, respectively, Equations (3.14) and (3.15), functions of the form (3.16) are stationary positive solutions to Equation (1.1) with
 $f\equiv \epsilon^q$. This completes the proof of part (II) of Theorem 1.3.
$f\equiv \epsilon^q$. This completes the proof of part (II) of Theorem 1.3.  $\square$
$\square$
Funding Statement
H. Chen is supported by NSFC (No. 12071189) by Jiangxi Province Science Fund No. 20212ACB211005. M. Jleli is supported by Researchers Supporting Project number (RSP2023R57), King Saud University, Riyadh, Saudi Arabia.