Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T08:46:31.825Z Has data issue: false hasContentIssue false
  • English
  • Français

On a result in Young's quantitative substitutional analysis

Published online by Cambridge University Press:  20 January 2009

D. B. Hunter
D. B. Hunter
Affiliation:
School of MathematicsUniversity of Bradford, Bradford, 7, Yorkshire
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

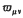In (4) Young investigates the representation in terms of his exact seminormal units of substitutional expressions which are unchanged on premultiplication by any permutation of a given set of consecutive letters, or which are changed in sign on premultiplication by an odd permutation of those letters. He illustrates his results by deducing the forms of the matrices representing the positive and negative symmetric groups on a set of consecutive letters.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 15 , Issue 4 , December 1967 , pp. 257 - 262
Copyright
Copyright © Edinburgh Mathematical Society 1967

References

REFERENCES

(1) Aitken, A. C., The monomial expansion of determinantal symmetric functions, Proc. Royal Soc. Edinburgh, A, 61 (1943), 300–310.Google Scholar
(2) Rutherford, D. E., Substitutional Analysis (Edinburgh, 1948).Google Scholar
(3)Young, A., On quantitative substitutional analysis (sixth paper), Proc. London Math. Soc. (2), 34 (1931), 196–230.Google Scholar
(4) Young, A., On quantitative substitutional analysis (eighth paper), Proc. London Math. Soc. (2), 37 (1934), 441–495.Google Scholar