Research Article
B# Modular Annihilator Algebras†
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 89-102
-
- Article
-
- You have access
- Export citation
An estimate for trigonometrical sums over square-free integers with a constant number of prime factors
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 249-255
-
- Article
-
- You have access
- Export citation
Genetic Algebras Associated with Polyploidy
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-9
-
- Article
-
- You have access
- Export citation
Some Integral Equations Involving Hypergeometric Functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 169-198
-
- Article
-
- You have access
- Export citation
On Extending Semigroup Characters
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 199-202
-
- Article
-
- You have access
- Export citation
On a result in Young's quantitative substitutional analysis
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 257-262
-
- Article
-
- You have access
- Export citation
Operators with a Single Spectrum
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 11-18
-
- Article
-
- You have access
- Export citation
On a Theorem of Korous
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 103-106
-
- Article
-
- You have access
- Export citation
Generation of an acoustic pulse by a baffled circular piston
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 263-277
-
- Article
-
- You have access
- Export citation
Useful Theorems on Commutative Non-associative Algebras
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 203-208
-
- Article
-
- You have access
- Export citation
Theorems on Strong Riesz Summability Factors
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 19-27
-
- Article
-
- You have access
- Export citation
Ancestral Rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 107-109
-
- Article
-
- You have access
- Export citation
On the Cauchy Problem for the n-Dimensional Wave Equation
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 29-32
-
- Article
-
- You have access
- Export citation
On Certain Integral Equations of Convolution Type with Bessel-Function Kernels
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 111-116
-
- Article
-
- You have access
- Export citation
The Asymptotic Value of the Volume of a Certain Set of Matrices
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 209-213
-
- Article
-
- You have access
- Export citation
On the absolute summability by Borel's integral method of the derived Fourier series and its conjugate series
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 279-284
-
- Article
-
- You have access
- Export citation
Total Graphs and Traversability
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 117-120
-
- Article
-
- You have access
- Export citation
A Class of Integral Equations Involving Laguerre Polynomials as Kernel
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 33-36
-
- Article
-
- You have access
- Export citation
The number of partitions of a set of N points in k dimensions induced by hyperplanes
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 285-289
-
- Article
-
- You have access
- Export citation
On the Sum
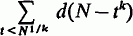
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 215-219
-
- Article
-
- You have access
- Export citation

 with the properties
with the properties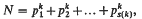


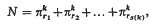
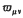 of substitutional expressions which are unchanged on premultiplication by any permutation of a given set of consecutive letters, or which are changed in sign on premultiplication by an odd permutation of those letters. He illustrates his results by deducing the forms of the matrices representing the positive and negative symmetric groups on a set of consecutive letters.
of substitutional expressions which are unchanged on premultiplication by any permutation of a given set of consecutive letters, or which are changed in sign on premultiplication by an odd permutation of those letters. He illustrates his results by deducing the forms of the matrices representing the positive and negative symmetric groups on a set of consecutive letters.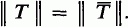 and
and 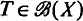 . The resolvent set of
. The resolvent set of 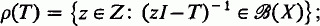




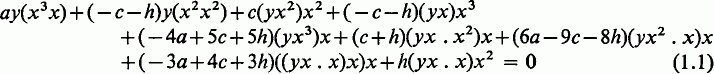



 multiplying both sides of the equations by α
multiplying both sides of the equations by α