Article contents
Strong morita equivalence for conditional expectations
Published online by Cambridge University Press: 08 February 2022
Abstract
We consider two inclusions of $C^{*}$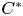 -algebras whose small $C^{*}$
-algebras whose small $C^{*}$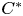 -algebras have approximate units of the large $C^{*}$
-algebras have approximate units of the large $C^{*}$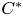 -algebras and their two spaces of all bounded bimodule linear maps. We suppose that the two inclusions of $C^{*}$
-algebras and their two spaces of all bounded bimodule linear maps. We suppose that the two inclusions of $C^{*}$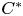 -algebras are strongly Morita equivalent. In this paper, we shall show that there exists an isometric isomorphism from one of the spaces of all bounded bimodule linear maps to the other space and we shall study the basic properties about the isometric isomorphism. And, using this isometric isomorphism, we define the Picard group for a bimodule linear map and discuss the Picard group for a bimodule linear map.
-algebras are strongly Morita equivalent. In this paper, we shall show that there exists an isometric isomorphism from one of the spaces of all bounded bimodule linear maps to the other space and we shall study the basic properties about the isometric isomorphism. And, using this isometric isomorphism, we define the Picard group for a bimodule linear map and discuss the Picard group for a bimodule linear map.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 1 , February 2022 , pp. 182 - 213
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society
References
- 1
- Cited by



