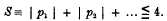1. In obtaining a solution of the differential equations corresponding to the motion of a particle about a position of equilibrium, it is usual to express the displacements in terms of a series of periodic terms, each sine or cosine having for its coefficient a series of powers of small quantities. Korteweg has discussed the general form of such solutions, and, from the developments in series which he has obtained, has deduced certain features of interest. In particular, he has shown that, under certain circumstances, it is possible that certain vibrations of higher order, which are normally of small intensity compared with the principal vibrations, may acquire an abnormally large intensity. Considering the oscillations of a dynamical system having a number of degrees of freedom, and supposing 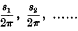 to be the frequencies corresponding to infinitesimal oscillations in the different normal coordinates, Korteweg has shown that these cases of interest arise only when
to be the frequencies corresponding to infinitesimal oscillations in the different normal coordinates, Korteweg has shown that these cases of interest arise only when
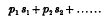
is zero or very small, where p1, p2,… are small integers, positive or negative; the most important cases occur when