1. Introduction
In this paper, we consider the following chemotaxis system with anisotropic porous medium-type diffusion:
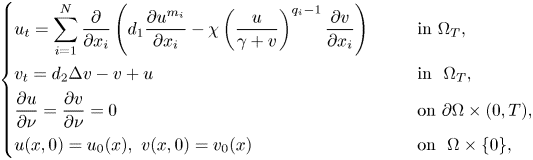
where $\Omega _{T}=\Omega \times (0,T)$![]() , $T>0$
, $T>0$![]() is a fixed time, $\Omega$
is a fixed time, $\Omega$![]() is a bounded domain in $\mathbb {R}^{N}$
is a bounded domain in $\mathbb {R}^{N}$![]() , $N\geq 3$
, $N\geq 3$![]() with smooth boundary $\partial \Omega$
with smooth boundary $\partial \Omega$![]() , $q_{i}\geq 2$
, $q_{i}\geq 2$![]() and $m^{-}>q_{i}-\frac {2}{N}$
and $m^{-}>q_{i}-\frac {2}{N}$![]() for all $i=1,..,N$
for all $i=1,..,N$![]() , such that
, such that
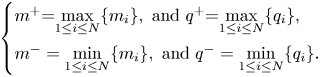
The positive constant $\chi$![]() is called the chemotaxis coefficient, $d_{1},d_{2}>0$
is called the chemotaxis coefficient, $d_{1},d_{2}>0$![]() are the diffusion coefficients and $\gamma \geq 1$
are the diffusion coefficients and $\gamma \geq 1$![]() .
.
In general, organism or cell moves from a lower concentration towards a higher concentration of the chemo attractant, which is known as positive chemotaxis. In the same way, the opposite movement of the organisms is known as negative chemotaxis. In particular, microorganisms use chemotaxis to position themselves within the optimal portion of their habitats by monitoring the environmental concentration gradients of specific chemical attractant (positive chemotaxis) and repellent ligands (negative chemotaxis). Famous examples of biological species experiencing chemotaxis are the flagellated bacteria Salmonella typhimurium and Escherichia coli, the slime mould amoebae Dictyostelium discoideum and the human endothelial cells (see [Reference Adler1, Reference Bonner4, Reference Eisenbach6]). Theoretical and mathematical modelling of chemotaxis phenomena dates back to the pioneering works of Patlak in 1950s [Reference Patlak20] and Keller–Segel in 1970s [Reference Keller and Segel18]. A general form of Patlak–Keller–Segel model for chemotaxis is given by
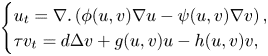
where $u$![]() denotes the density of cell population and $v$
denotes the density of cell population and $v$![]() is the chemical attractant concentration. The mobility function $\phi (u,v)$
is the chemical attractant concentration. The mobility function $\phi (u,v)$![]() describes the diffusivity of the cells and $\psi (u,v)$
describes the diffusivity of the cells and $\psi (u,v)$![]() represents the chemotaxis sensibility, while the functions $g(u,v)$
represents the chemotaxis sensibility, while the functions $g(u,v)$![]() and $h(u,v)$
and $h(u,v)$![]() are kinetic functions that describe production and degradation of the chemical signal, respectively. When $\phi (u,v)=1$
are kinetic functions that describe production and degradation of the chemical signal, respectively. When $\phi (u,v)=1$![]() and $\tau >0$
and $\tau >0$![]() , system (1.2) becomes the classical parabolic–parabolic Keller–Segel system, such system has been extensively studied, see for example [Reference Tao27, Reference Tao and Winkler28, Reference Yan and Li32] and references therein. For the study of the parabolic-elliptic Keller–Segel system of quasilinear type, namely $\tau =0$
, system (1.2) becomes the classical parabolic–parabolic Keller–Segel system, such system has been extensively studied, see for example [Reference Tao27, Reference Tao and Winkler28, Reference Yan and Li32] and references therein. For the study of the parabolic-elliptic Keller–Segel system of quasilinear type, namely $\tau =0$![]() , with general $\phi (u,v)$
, with general $\phi (u,v)$![]() in (1.2), we refer to [Reference Sugiyama23–Reference Sugiyama and Kunii25] and references therein.
in (1.2), we refer to [Reference Sugiyama23–Reference Sugiyama and Kunii25] and references therein.
Equation (1.1) with $m_i=m$![]() and $q_i=q$
and $q_i=q$![]() is sometimes called the equation of isotropic diffusion. In the case of degenerate diffusion, the model $\phi (u,v)=mu^{m-1}$
is sometimes called the equation of isotropic diffusion. In the case of degenerate diffusion, the model $\phi (u,v)=mu^{m-1}$![]() and $\psi (u,v)=u^{q-1}$
and $\psi (u,v)=u^{q-1}$![]() in $\mathbb {R}^{N}$
in $\mathbb {R}^{N}$![]() was studied by several authors. The existence of the weak solutions was shown when $q-m<0$
was studied by several authors. The existence of the weak solutions was shown when $q-m<0$![]() in [Reference Sugiyama and Kunii25] and when $q-m<\frac {2}{N}$
in [Reference Sugiyama and Kunii25] and when $q-m<\frac {2}{N}$![]() in [Reference Ishida and Yokota13]. When $q-m\geq \frac {2}{N}$
in [Reference Ishida and Yokota13]. When $q-m\geq \frac {2}{N}$![]() and the initial data $(u_{0},v_{0})$
and the initial data $(u_{0},v_{0})$![]() is small in some sense, the existence of the weak solutions was proved in [14], whereas, if $q-m>\frac {2}{N}$
is small in some sense, the existence of the weak solutions was proved in [14], whereas, if $q-m>\frac {2}{N}$![]() then blow-up of solutions as in [Reference Winkler30] was studied in [Reference Ishida, Ono and Yokota15, Reference Ishida and Yokota16].
then blow-up of solutions as in [Reference Winkler30] was studied in [Reference Ishida, Ono and Yokota15, Reference Ishida and Yokota16].
In the present work, we are interested in the anisotropic case where the diffusion rates differ according to the direction $x_i$![]() . Despite the resemblance with the isotropic cases presented in the previous mentioned works, the properties of the solutions to anisotropic equations are in striking contrast with the properties of the classical isotropic equations. The difficulties brought in by the anisotropy and the inhomogeneity of the diffusion operator are illustrated by the analysis of the self-similar solutions of anisotropic porous medium and $\vec {p}$
. Despite the resemblance with the isotropic cases presented in the previous mentioned works, the properties of the solutions to anisotropic equations are in striking contrast with the properties of the classical isotropic equations. The difficulties brought in by the anisotropy and the inhomogeneity of the diffusion operator are illustrated by the analysis of the self-similar solutions of anisotropic porous medium and $\vec {p}$![]() -Laplacian types [Reference Antontsev and Shmarev2, Reference Antontsev and Shmarev3, Reference Düzgün, Mosconi and Vespri5]. Unlike the isotropic case where the typical geometry is defined in terms of balls in $\mathbb {R}^{N}$
-Laplacian types [Reference Antontsev and Shmarev2, Reference Antontsev and Shmarev3, Reference Düzgün, Mosconi and Vespri5]. Unlike the isotropic case where the typical geometry is defined in terms of balls in $\mathbb {R}^{N}$![]() , in the anisotropic case it is defined by parallelepipeds with the edge lengths related to the exponents $m_i$
, in the anisotropic case it is defined by parallelepipeds with the edge lengths related to the exponents $m_i$![]() and $q_i$
and $q_i$![]() .
.
The chemotaxis model with anisotropic porous medium diffusion type is motivated from a biological point of view [Reference Szymanska, Morales-Rodrigo, Lachowicz and Chaplain26]. It is worthy of mentioning that the porous medium type diffusion can represent population pressure in cell invasion models [Reference Rosen21], which initially arises from the ecology literature [Reference Gurney and Nisbet12, Reference Xu, Ji, Jin, Mei and Yin31]. In fact, experimental investigation has shown that the diffusion coefficient depends on the bacterial density [Reference Wakita, Komatsu, Nakahara, Matsuyama and Matsushita29]. In the bacterial experiments done by Ohgiwari, Matsushita and Matsuyama [Reference Ohgiwari, Matsushita and Matsuyama19], they recognized that cells located inside the bacterial colonies move actively, but cells became sluggish at the outermost front with apparently low cell density. This phenomenon indicates that bacteria become active as the cell density $u$![]() increases. Thus, a natural choice of the bacterial diffusion coefficient is $\phi (u,v)=m_{i}u^{m_{i}-1}$
increases. Thus, a natural choice of the bacterial diffusion coefficient is $\phi (u,v)=m_{i}u^{m_{i}-1}$![]() with $m_{i}>1$
with $m_{i}>1$![]() for all $i=1,..,N$
for all $i=1,..,N$![]() , and this porous medium type bacterial diffusivity is based on the degenerate diffusion model proposed by Kawasaki et al. [Reference Kawasaki, Mochizuki, Matsushita, Umeda and Shigesada17]. To our knowledge, Keller–Segel system with anisotropic porous medium diffusion models has not been studied specially and systematically.
, and this porous medium type bacterial diffusivity is based on the degenerate diffusion model proposed by Kawasaki et al. [Reference Kawasaki, Mochizuki, Matsushita, Umeda and Shigesada17]. To our knowledge, Keller–Segel system with anisotropic porous medium diffusion models has not been studied specially and systematically.
2. Preliminary and main result
2.1 Imbedding and technical lemmas
To derive our existence and regularity results, we will need the following
Theorem 2.1 [Reference Esfahani9], Theorem 1.1. Let $N\geq 2$![]() , $\alpha _{j}\in (0,1)$
, $\alpha _{j}\in (0,1)$![]() , $1\leq p< q$
, $1\leq p< q$![]() and $p_{j}\geq 1$
and $p_{j}\geq 1$![]() , $j=1,..,N$
, $j=1,..,N$![]() , be such that $\displaystyle \sum _{j=1}^{N}\frac {1}{\alpha _{j}p_{j}}>1$
, be such that $\displaystyle \sum _{j=1}^{N}\frac {1}{\alpha _{j}p_{j}}>1$ . Then, for $u\in W^{(\alpha ),(p,\vec {p})}(\mathbb {R}^{N})$
. Then, for $u\in W^{(\alpha ),(p,\vec {p})}(\mathbb {R}^{N})$![]() (The fractional Sobolev–Liouville space) the inequality
(The fractional Sobolev–Liouville space) the inequality
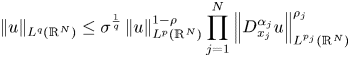
hold provided $M_{N}>0$![]() and
and
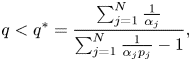
where
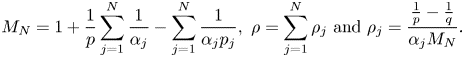
The following lemma will show that theorem 2.1 holds true even for the case where $0< p<1$![]() and $p_{j}=2,~\forall j=1,..,N$
and $p_{j}=2,~\forall j=1,..,N$![]() .
.
Lemma 2.2 Let $\Omega \subset \mathbb {R}^{N}$![]() with $N\geq 3$
with $N\geq 3$![]() be a bounded domain with smooth boundary, and $0< p<1\leq q<\frac {2N}{N-2}$
be a bounded domain with smooth boundary, and $0< p<1\leq q<\frac {2N}{N-2}$![]() . Then, for all $u\in H^{1}(\Omega )$
. Then, for all $u\in H^{1}(\Omega )$![]() we have
we have
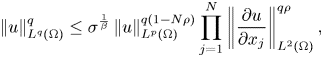
where $\rho =\frac {2(q-p)}{q(p(2-N)+2N)}$![]() , and $\frac {1}{\beta }=\frac {(q-p)(2+N)}{(q-1)(p(2-N)+2N)}$
, and $\frac {1}{\beta }=\frac {(q-p)(2+N)}{(q-1)(p(2-N)+2N)}$![]() .
.
Proof. By Hölder's inequality , we get that

Then, by using theorem 1 of section 5.4 in [Reference Evans10] and applying theorem 2.1 for $p=1$![]() and $p_{j}=2,~\forall j=1,..,N$
and $p_{j}=2,~\forall j=1,..,N$![]() , we obtain
, we obtain
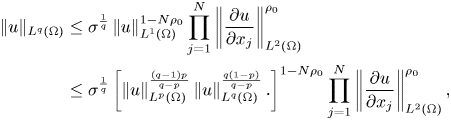
where $\rho _{0}=\frac {1-\frac {1}{q}}{N(\frac {1}{N}+\frac {1}{2})}$![]() . Then from (2.3) we get (2.2) with
. Then from (2.3) we get (2.2) with
□
Possible references on the theory of anisotropic Sobolev spaces are in [Reference El Bahja7, Reference El Bahja8] and references therein. Next, we give some fundamental estimates of solutions to the following Cauchy problem for inhomogeneous linear heat equations:
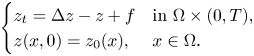
The following lemma can be found in [14].
Lemma 2.3 Let $\Omega \subset \mathbb {R}^{N}$![]() with $N\in \mathbb {N}$
with $N\in \mathbb {N}$![]() be a bounded domain with smooth boundary, $T>0$
be a bounded domain with smooth boundary, $T>0$![]() , $1\leq p\leq \infty$
, $1\leq p\leq \infty$![]() and $z_{0}\in L^{p}(\Omega )$
and $z_{0}\in L^{p}(\Omega )$![]() . If $f\in L^{1}(0,T; L^{p}(\Omega ))$
. If $f\in L^{1}(0,T; L^{p}(\Omega ))$![]() , then (2.4) has a unique mild solution $z\in C([0,T]; L^{p}(\Omega ))$
, then (2.4) has a unique mild solution $z\in C([0,T]; L^{p}(\Omega ))$![]() given by
given by
where $(e^{t\Delta }f)(x,t)=(4\pi t)^{-\frac {N}{2}}\int _{\Omega }e^{-\frac {|x-y|^{2}}{4t}}f(y,t)~dy$![]() . Moreover, the following estimates hold.
. Moreover, the following estimates hold.
• Let $1\leq q\leq p\leq \infty$
 and $\frac {1}{q}-\frac {1}{p}<\frac {1}{N}$
and $\frac {1}{q}-\frac {1}{p}<\frac {1}{N}$ . Assume further that $z_{0}\in W^{2,p}(\Omega )$
. Assume further that $z_{0}\in W^{2,p}(\Omega )$ and $f\in L^{\infty }(0,T; W^{1,q}(\Omega ))$
and $f\in L^{\infty }(0,T; W^{1,q}(\Omega ))$ . Then for every $t\in [0,T]$
. Then for every $t\in [0,T]$ ,
(2.6)\begin{align} & \|z(t)\|_{L^{p}(\Omega)}\leq\|z_{0}\|_{L^{p}(\Omega)}+C_{0}\|f\|_{L^{\infty}(0,T;L^{q}(\Omega))}, \end{align}
,
(2.6)\begin{align} & \|z(t)\|_{L^{p}(\Omega)}\leq\|z_{0}\|_{L^{p}(\Omega)}+C_{0}\|f\|_{L^{\infty}(0,T;L^{q}(\Omega))}, \end{align} (2.7)\begin{align} & \|\nabla z(t)\|_{L^{p}(\Omega)}\leq\|\nabla z_{0}\|_{L^{p}(\Omega)}+C_{0}\|f\|_{L^{\infty}(0,T;L^{q}(\Omega))}, \end{align}
(2.7)\begin{align} & \|\nabla z(t)\|_{L^{p}(\Omega)}\leq\|\nabla z_{0}\|_{L^{p}(\Omega)}+C_{0}\|f\|_{L^{\infty}(0,T;L^{q}(\Omega))}, \end{align} (2.8)\begin{align} & \|\Delta z(t)\|_{L^{p}(\Omega)}\leq\|\Delta z_{0}\|_{L^{p}(\Omega)}+C_{0}\|\nabla f\|_{L^{\infty}(0,T;L^{q}(\Omega))}, \end{align}where $C_{0}$
(2.8)\begin{align} & \|\Delta z(t)\|_{L^{p}(\Omega)}\leq\|\Delta z_{0}\|_{L^{p}(\Omega)}+C_{0}\|\nabla f\|_{L^{\infty}(0,T;L^{q}(\Omega))}, \end{align}where $C_{0}$
 is a positive constant depending on $p,q$
is a positive constant depending on $p,q$ and $N$
and $N$ .
.• Let $1< p<\infty$
 and $f\in L^{p}(0,T;L^{p}(\Omega ))$
and $f\in L^{p}(0,T;L^{p}(\Omega ))$ . Then for every $t\in [0,T]$
. Then for every $t\in [0,T]$ ,
(2.9)\begin{equation} \|\Delta z(t)\|_{L^{p}(0,t;L^{p}(\Omega))}\leq\|\Delta z_{0}\|_{L^{p}(\Omega)}\left(1-e^{{-}pt}\right)^{\frac{1}{p}}+C_{ }\|f\|_{L^{p}(0,T;L^{p}(\Omega))}, \end{equation}where $C_{0}$
,
(2.9)\begin{equation} \|\Delta z(t)\|_{L^{p}(0,t;L^{p}(\Omega))}\leq\|\Delta z_{0}\|_{L^{p}(\Omega)}\left(1-e^{{-}pt}\right)^{\frac{1}{p}}+C_{ }\|f\|_{L^{p}(0,T;L^{p}(\Omega))}, \end{equation}where $C_{0}$
 is a positive constant depending on $N$
is a positive constant depending on $N$ and $p$
and $p$ .
.
2.2 Formulation of the problem and main result
Throughout this paper, we deal with weak solutions of (1.1). Our definition of the weak solutions now reads
Definition 2.4 A pair of nonnegative functions $(u,v)$![]() is said to be a weak solution of (1.1) if and only if for all $i=1,..,N$
is said to be a weak solution of (1.1) if and only if for all $i=1,..,N$![]() we have
we have
such that $(u,v)$![]() satisfies the equations in the sense of distribution, i.e., that
satisfies the equations in the sense of distribution, i.e., that
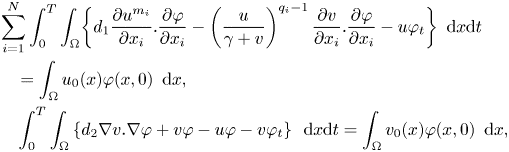
for any continuously differentiable function $\varphi$![]() with compact support in $\Omega \times [0,T)$
with compact support in $\Omega \times [0,T)$![]() .
.
Motivated by the works mentioned in the previous section, our paper extends the results in [14, Reference Sugiyama and Kunii25] to the system (1.1) with anisotropic nonlinear diffusion. Now we state the main result of this paper. To be precise, we will assume the initial data $(u_{0},v_{0})$![]() to satisfy
to satisfy

Theorem 2.5 Let $q_{i}\geq 2$![]() and $m^{-}>q_{i}-\frac {2}{N}$
and $m^{-}>q_{i}-\frac {2}{N}$![]() for every $i=1,..N$
for every $i=1,..N$![]() , $\Omega \subset \mathbb {R}^{N}$
, $\Omega \subset \mathbb {R}^{N}$![]() for $N\geq 3$
for $N\geq 3$![]() be a bounded domain with smooth boundary. Then for all $(u_{0},v_{0})$
be a bounded domain with smooth boundary. Then for all $(u_{0},v_{0})$![]() satisfying (2.10), the system (1.1) possesses at last one weak solution in the sense of definition 2.4.
satisfying (2.10), the system (1.1) possesses at last one weak solution in the sense of definition 2.4.
3. Approximated equations
The first equation of (1.1) is a quasilinear parabolic equation of degenerate type. Therefore, we cannot expect the system (1.1) to have a classical solution at the point where $u$![]() vanishes. In order to prove theorem 2.5, we use a compactness method and introduce the following approximated equation of (1.1):
vanishes. In order to prove theorem 2.5, we use a compactness method and introduce the following approximated equation of (1.1):

where $\varepsilon \in (0,1)$![]() .
.
3.1 Existence of weak solutions of (3.1)
We are going to give an existence result of (3.1) under the condition that there exists a positive constant $k$![]() such that
such that
Theorem 3.1 Assume that (3.2) holds. If $u_{0},v_{0}\in L^{2}(\Omega )$![]() , then (3.1) possesses a nonnegative weak solution $(u_{\varepsilon },v_{\varepsilon })$
, then (3.1) possesses a nonnegative weak solution $(u_{\varepsilon },v_{\varepsilon })$![]() such that
such that
such that $u_{\varepsilon }$![]() has the conservation law
has the conservation law
Proof. The existence of the weak solution to (3.1) can be obtained by using Schauder's fixed point theorem, a priori estimates and using the compactness results. We start by introducing for a small number $\delta >0$![]() the following
the following

such that we have $0\leq f_{\delta }(s)\leq \min \{s^+,\frac {1}{\delta }\}$![]() for any $s\in \mathbb {R}$
for any $s\in \mathbb {R}$![]() and $f_{\delta }(s)\longrightarrow s$
and $f_{\delta }(s)\longrightarrow s$![]() pointwise in $\mathbb {R}$
pointwise in $\mathbb {R}$![]() as $\delta \longrightarrow 0$
as $\delta \longrightarrow 0$![]() . Therefore, we can conclude that there exists a positive constant $K$
. Therefore, we can conclude that there exists a positive constant $K$![]() such that
such that
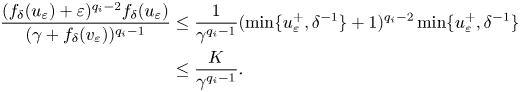
Let $\overline {u}_{\varepsilon },\overline {v}_{\varepsilon }\in L^{2}(\Omega _{T})$![]() be given and consider the linear problem
be given and consider the linear problem
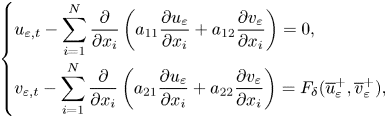
where the diffusion matrix $A _{i}=(a_{jk})_{i}$![]() is given by
is given by

Moreover, the matrix $A _{i}$![]() is uniformly positive definite, since for any $X=(x,y)\in \mathbb {R}^{2}$
is uniformly positive definite, since for any $X=(x,y)\in \mathbb {R}^{2}$![]() we have
we have
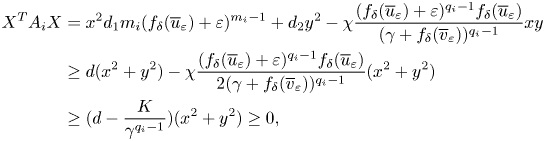
where we used (3.2) and the fact that $xy=\frac {1}{2}(x+y)^{2}-\frac {1}{2}(x^{2}+y^{2})\geq -\frac {1}{2}(x^{2}+y^{2})$![]() and $-xy=\frac {1}{2}(x-y)^{2}-\frac {1}{2}(x^{2}+y^{2})\geq -\frac {1}{2}(x^{2}+y^{2})$
and $-xy=\frac {1}{2}(x-y)^{2}-\frac {1}{2}(x^{2}+y^{2})\geq -\frac {1}{2}(x^{2}+y^{2})$![]() . Hence, the desired existence result is guaranteed by theorem 1 in [Reference Galiano, Garzón and Jüngel11].
. Hence, the desired existence result is guaranteed by theorem 1 in [Reference Galiano, Garzón and Jüngel11].
3.2 A priori estimates
In order to prove theorem 2.5, we state and prove two key propositions which control $L^{r}-$![]() and $L^{\infty }-$
and $L^{\infty }-$![]() estimates of the solution $(u_{\varepsilon },v_{\varepsilon })$
estimates of the solution $(u_{\varepsilon },v_{\varepsilon })$![]() of (3.1).
of (3.1).
Proposition 3.2 Assume that (2.10), and (3.2) hold. Let $N\geq 3$![]() , $q_{i}\geq 2$
, $q_{i}\geq 2$![]() and $m^{-}>q_{i}-\frac {2}{3}$
and $m^{-}>q_{i}-\frac {2}{3}$![]() for all $i=1,..,N$
for all $i=1,..,N$![]() . Then $(u_{\varepsilon },v_{\varepsilon })$
. Then $(u_{\varepsilon },v_{\varepsilon })$![]() satisfies the following estimates
satisfies the following estimates
where $C$![]() is a positive constant independent of $\varepsilon$
is a positive constant independent of $\varepsilon$![]() .
.
Proof. By taking $r\in (1,\infty )$![]() , multiplying the first equation in (3.1) by $u_{\varepsilon }^{r-1}$
, multiplying the first equation in (3.1) by $u_{\varepsilon }^{r-1}$![]() and integrating by parts, we get
and integrating by parts, we get
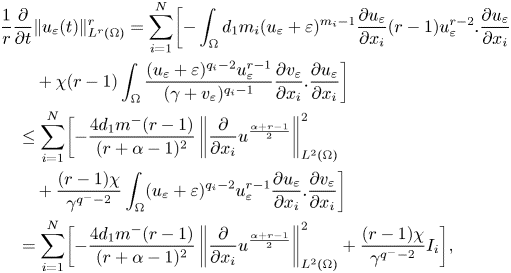
where
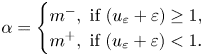
Next, we set
such that
Therefore, $I_{i}$![]() becomes
becomes
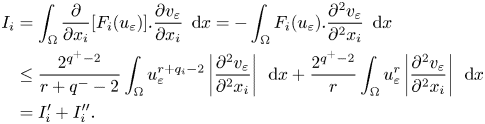
Next, we are going to integrate $I_{i}'$![]() over $(0,t)$
over $(0,t)$![]() for $t\in (0,T)$
for $t\in (0,T)$![]() such that
such that
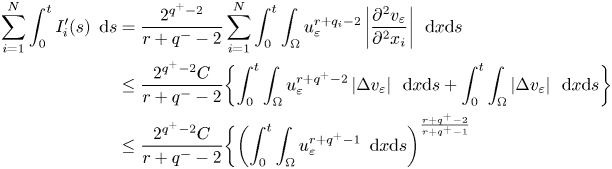
where we used Hölder's inequality, (2.9) and Young's inequality.
Next, we are going to simplify the last integral in the right-hand side of (3.9) by using lemma 2.2. As a consequence, by letting $r>r_{0}\!=\!\max \{\alpha -2q^+\!+\!1,\frac {N}{2}(q^+-\alpha ) -q^++1,\frac {2(N-1)}{N}-\alpha \}$ , we have the following
, we have the following
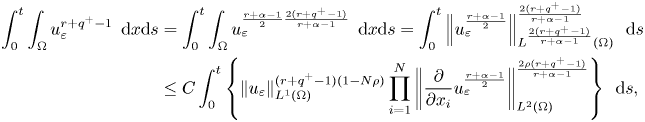
where
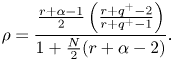
We can replace the geometric mean on the right-hand side of (3.10) by an arithmetic mean. Indeed, by the inequality between geometric and arithmetic means we get
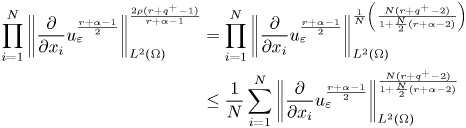
Since, we took $q_{i}<\frac {2}{N}+m^{-}\leq \frac {2}{N}+\alpha$![]() for all $i=1,..,N$
for all $i=1,..,N$![]() . Then we get
. Then we get
Therefore, by using (3.11), (3.12), Young's inequality and the mass conservation law (3.3), we obtain
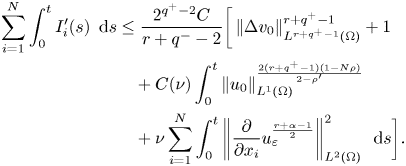
The integral $I''_{i}$![]() can be controlled by the same way as $I'_{i}$
can be controlled by the same way as $I'_{i}$![]() for all $i=1,..,N$
for all $i=1,..,N$![]() . Consequently, we omit that $\sum _{i}^{N}\int _{0}^{t}I''_{i}~\,{\rm d}s$
. Consequently, we omit that $\sum _{i}^{N}\int _{0}^{t}I''_{i}~\,{\rm d}s$![]() satisfy the same estimation as in (3.13). Therefore, by integrating (3.6) over $(0,t)$
satisfy the same estimation as in (3.13). Therefore, by integrating (3.6) over $(0,t)$![]() and using the previous estimates, we arrive at
and using the previous estimates, we arrive at
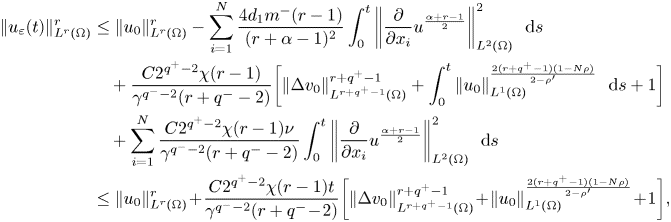
where we took $\nu =\frac {4d_{1}m^{-}\gamma ^{q^{-}-2}(r+q^{-}-2)}{2^{q^+-2}C\chi (r+\alpha -1)^{2}}$![]() . Moreover, by letting $r>r_{1}=\{r_{0},\beta -q^++1\}$
. Moreover, by letting $r>r_{1}=\{r_{0},\beta -q^++1\}$![]() for $\beta > > 1$
for $\beta > > 1$![]() , we obtain that
, we obtain that
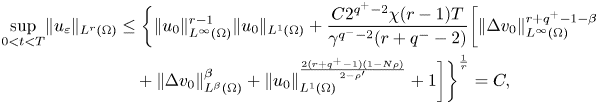
where $C$![]() is a positive constant independent of $\varepsilon$
is a positive constant independent of $\varepsilon$![]() .
.
Now, for the case $1\leq r\leq r_{1}$![]() we have the following
we have the following
where we used Hölder's inequality, the mass conservation law (3.3) and Young's inequality. Hence, (3.15) and (3.16) give us the desired estimation for every $r\in [1,\infty )$![]() .
.
Finally estimation (3.5) is a direct consequence of (2.6), (2.7) and (3.4) with $r=N+1$![]() .
.
We conclude this section with the proof of $L^{\infty }$![]() -estimates of the approximated solutions.
-estimates of the approximated solutions.
Proposition 3.3 Let the same assumptions as those in proposition 3.2 hold. Then, there exists a positive constant $C$![]() independent of $\varepsilon$
independent of $\varepsilon$![]() such that
such that
Proof. We begin by multiplying the first equation in (3.1) by $u_{\varepsilon }^{r-1}$![]() such that
such that
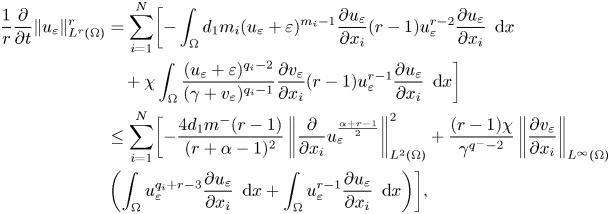
where $\alpha$![]() is defined in (3.7). Next, we are going to simplify the last two integrals in the right-hand side of (3.18). Then, for all $i=1,..,N$
is defined in (3.7). Next, we are going to simplify the last two integrals in the right-hand side of (3.18). Then, for all $i=1,..,N$![]() we have
we have

where we used Young's inequality and choose $\nu$![]() accordingly.
accordingly.
We will deal only with the norm $\left \| u_{\varepsilon } \right \|_{L^{r+2q_{i}-\alpha -3}(\Omega )}^{r+2q_{i}-\alpha -3}$![]() in the right-hand side of (3.19), because the last norm can be controlled by the same way. Furthermore, we are going to study the following two possible cases.
in the right-hand side of (3.19), because the last norm can be controlled by the same way. Furthermore, we are going to study the following two possible cases.
Case 1: $q_{i}>3-\frac {2}{N},~\forall i=1,..,N.$![]()
Let $l$![]() be a natural number which is chosen later. Therefore, by applying lemma 2.2, we obtain
be a natural number which is chosen later. Therefore, by applying lemma 2.2, we obtain
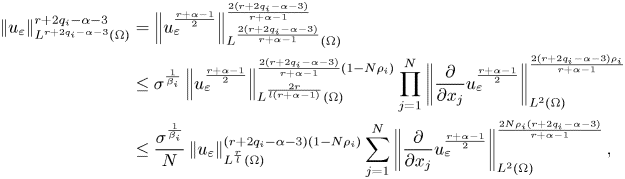
for $r\!>\!r_{0}=\max \{3\alpha -4q_{i}+5, -\frac {N}{2}(\alpha -1)+\frac {(N-2)}{2}(2q_{i}-\alpha -3),\alpha -2q_{i}+3\}, l\!>\!1$![]() ,
,
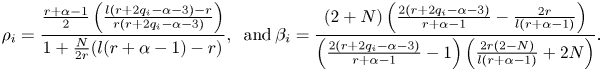
By simple computation, we find that $\frac {2N\rho _{i}(r+2q_{i}-\alpha -3)}{r+\alpha -1}<2$![]() and $\frac {1}{\beta _{i}}\leq 6$
and $\frac {1}{\beta _{i}}\leq 6$![]() for every $r>r_{0}$
for every $r>r_{0}$![]() and $i=1,..,N$
and $i=1,..,N$![]() . Therefore, by Young's inequality we get
. Therefore, by Young's inequality we get

where
Next, by taking $\nu =\frac {d_{1}m^{-}}{(r+\alpha -1)^{2}}$![]() , then $\displaystyle C(\nu )=\frac {1}{q_{i}(\nu p_{i})^{\frac {q_{i}}{p_{i}}}}$
, then $\displaystyle C(\nu )=\frac {1}{q_{i}(\nu p_{i})^{\frac {q_{i}}{p_{i}}}}$![]() , where
, where
Then, (3.21) becomes
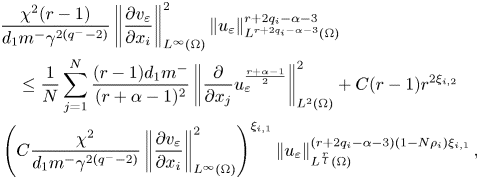
where
Next, for $l>1$![]() , $r>r_{0}$
, $r>r_{0}$![]() and for every $i=1,..N$
and for every $i=1,..N$![]() , we have
, we have
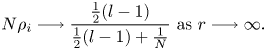
Consequently, we obtain that
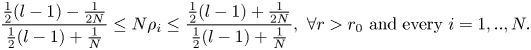
Then, by (3.24) we get the following estimations
Therefore, (3.22) becomes
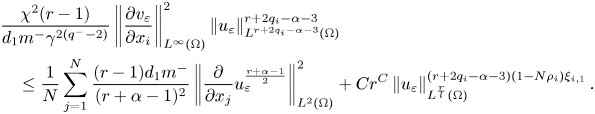
Next, we are going to simplify the last term in the right-hand side of (3.25). For this reason, we choose $l$![]() to verify
to verify
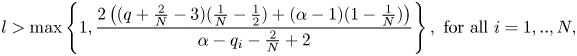
such that
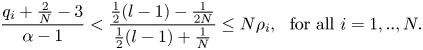
Therefore, by taking
we get that
By simple computation, we get also $\xi _{i,3}\leq Nl+2$![]() for all $i=1,..,N$
for all $i=1,..,N$![]() . To this end, we apply Young's inequality on the last term in the right-hand side of (3.25) such that
. To this end, we apply Young's inequality on the last term in the right-hand side of (3.25) such that
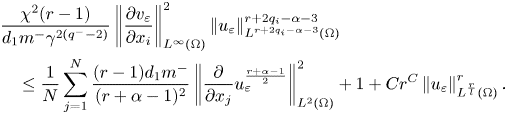
By the same method, we get also that
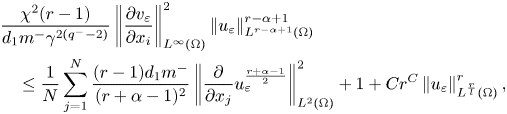
for every $r>r_{1}$![]() . Then, by putting (3.26) and (3.27) into (3.18) we obtain
. Then, by putting (3.26) and (3.27) into (3.18) we obtain
Integrating (3.28) from 0 to $t$![]() , we obtain
, we obtain
Since
Then,
We are now in a position to derive the claimed $L^{\infty }-$![]() estimate. Therefore, we set
estimate. Therefore, we set
Thereafter, we take $r=l^{p}$![]() in (3.31) which leads to
in (3.31) which leads to
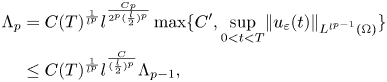
since $p\leq 2^{p}$![]() for $p\geq 1$
for $p\geq 1$![]() . By induction, we get
. By induction, we get
Then, by using the mass conservation law (3.3), taking $l>2$![]() and letting $p\longrightarrow \infty$
and letting $p\longrightarrow \infty$![]() , we arrive at
, we arrive at
where $C''$![]() is a positive constant independent of $\varepsilon$
is a positive constant independent of $\varepsilon$![]() .
.
Case 2: $2\leq q_{i}\leq 3-\frac {2}{N},~\forall i=1,..,N.$![]()
Knowing that $q_{i}<\alpha +\frac {2}{N}$![]() , then $2q_{i}<\alpha +3$
, then $2q_{i}<\alpha +3$![]() for every $i=1,..,N$
for every $i=1,..,N$![]() . Therefore,
. Therefore,
Then, (3.18) becomes
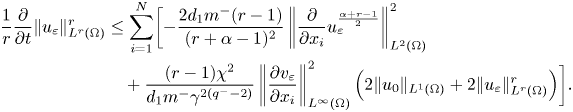
Thereafter, by applying lemma 2.2 once again we obtain
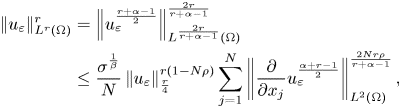
where

It is easy to verify that $\frac {2Nr\rho }{r+\alpha -1}<2$![]() and $\frac {1}{\beta }\leq 6$
and $\frac {1}{\beta }\leq 6$![]() for suitable $r>0$
for suitable $r>0$![]() . Then, by using the same method we used to get (3.27), we obtain
. Then, by using the same method we used to get (3.27), we obtain
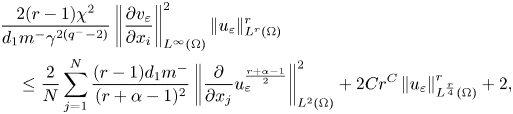
for suitable $r>0$![]() . Hence, by putting (3.37) into (3.35) and applying similar arguments of the case $q>3-\frac {2}{N}$
. Hence, by putting (3.37) into (3.35) and applying similar arguments of the case $q>3-\frac {2}{N}$![]() we get the desired $L^{\infty }-$
we get the desired $L^{\infty }-$![]() estimate.
estimate.
We complete this section by discussing some uniform estimates (with respect to $\varepsilon$![]() ) of $u_{\varepsilon }$
) of $u_{\varepsilon }$![]() and $v_{\varepsilon }$
and $v_{\varepsilon }$![]() .
.
Lemma 3.4 For $q_{i}\geq 2$![]() and $m^{-}>q_{i}-\frac {2}{N}$
and $m^{-}>q_{i}-\frac {2}{N}$![]() for all $i\!=\!1,..N$
for all $i\!=\!1,..N$![]() , there exists a constant $C$
, there exists a constant $C$![]() such that
such that
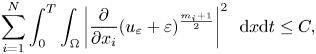
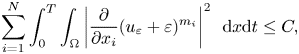
and,
for each $\varepsilon \in (0,1)$![]() and $\beta$
and $\beta$![]() a big enough positive constant.
a big enough positive constant.
Proof. We multiply the first equation of (3.1) by $u_{\varepsilon }$![]() and integrate over $\Omega \times (0,T)$
and integrate over $\Omega \times (0,T)$![]() such that
such that
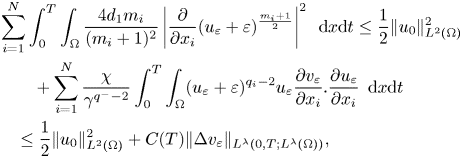
where we used the same method we introduced to get (3.8), applying proposition 3.17 and for $\lambda > > 1$![]() . Therefore, by (2.9) we get (3.8). Moreover, we note that
. Therefore, by (2.9) we get (3.8). Moreover, we note that
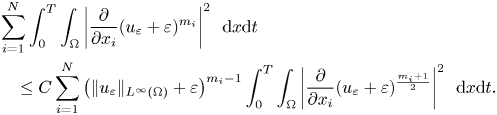
Then, (3.39) follows from (3.38).
Next, taking $\varphi \in C^{\infty }(\Omega _{T})$![]() , multiplying the first equation of (3.1) by $\beta u_{\varepsilon }^{\beta -1}\varphi$
, multiplying the first equation of (3.1) by $\beta u_{\varepsilon }^{\beta -1}\varphi$![]() , and integrating by parts, we obtain
, and integrating by parts, we obtain

where we used proposition 3.3, the embedding of $W^{1,N+1}(\Omega )$![]() into $L^{\infty }(\Omega )$
into $L^{\infty }(\Omega )$![]() , and (3.38). Thus, we get (3.40). Also, by the same method and using (3.5) and (3.17) we get (3.41).
, and (3.38). Thus, we get (3.40). Also, by the same method and using (3.5) and (3.17) we get (3.41).
4. Proof of theorem 2.5
The goal of this section is to prove theorem 2.5. In the proof, we need the strong convergence of $u_{\varepsilon }$![]() and $v_{\varepsilon }$
and $v_{\varepsilon }$![]() . Then, from (3.18), (3.19), proposition 3.3 and integrating over $(0,T)$
. Then, from (3.18), (3.19), proposition 3.3 and integrating over $(0,T)$![]() , we get
, we get
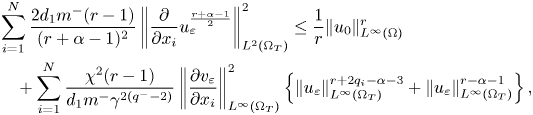
for suitable $r$![]() . Therefore, by taking $r=2\beta -\alpha +1$
. Therefore, by taking $r=2\beta -\alpha +1$![]() in (4.1) and using (3.5) and proposition 3.3 we get that $u_{\varepsilon }^{\beta }\in L^{2}(0,T;H^{1}(\Omega ))$
in (4.1) and using (3.5) and proposition 3.3 we get that $u_{\varepsilon }^{\beta }\in L^{2}(0,T;H^{1}(\Omega ))$![]() while $\partial _{t}u_{\varepsilon }^{\beta }$
while $\partial _{t}u_{\varepsilon }^{\beta }$![]() is bounded in $L^{1}(0,T;(W^{1,N+1}(\Omega ))')$
is bounded in $L^{1}(0,T;(W^{1,N+1}(\Omega ))')$![]() by lemma 3.4. Since $H^{1}(\Omega )$
by lemma 3.4. Since $H^{1}(\Omega )$![]() is compactly embedded in $L^{2}(\Omega )$
is compactly embedded in $L^{2}(\Omega )$![]() and $L^{2}(\Omega )$
and $L^{2}(\Omega )$![]() is continuously embedded in $(W^{1,N+1}(\Omega ))'$
is continuously embedded in $(W^{1,N+1}(\Omega ))'$![]() , it follows from corollary 4 in [Reference Simon22] that $u_{\varepsilon }^{\beta }$
, it follows from corollary 4 in [Reference Simon22] that $u_{\varepsilon }^{\beta }$![]() is compact in $L^{2}(0,T;L^{2}(\Omega ))$
is compact in $L^{2}(0,T;L^{2}(\Omega ))$![]() . Since $u_{\varepsilon }\longmapsto u_{\varepsilon }^{\frac {1}{\beta }}$
. Since $u_{\varepsilon }\longmapsto u_{\varepsilon }^{\frac {1}{\beta }}$![]() is Hölder continuous with exponent $\frac {1}{\beta }$
is Hölder continuous with exponent $\frac {1}{\beta }$![]() , we get that $u_{\varepsilon }$
, we get that $u_{\varepsilon }$![]() is compact in $L^{2\beta }(0,T;L^{2\beta }(\Omega ))$
is compact in $L^{2\beta }(0,T;L^{2\beta }(\Omega ))$![]() . Thus, there exist a function $u\in L^{2\beta }(0,T;L^{2\beta }(\Omega ))$
. Thus, there exist a function $u\in L^{2\beta }(0,T;L^{2\beta }(\Omega ))$![]() and a subsequence $(\varepsilon _{n})_{n\geq 1}$
and a subsequence $(\varepsilon _{n})_{n\geq 1}$![]() such that
such that
This gives
On the other hand, by proposition 3.3 we get that
As a consequence, we get that
Therefore, by using Lebesgue dominated convergence theorem, (4.3) and (4.5), we obtain
By using the following inequality
we get
where we used (4.6) for $p=2$![]() . Then, we get that
. Then, we get that
Since $\frac {\partial u^{m_{i}}}{\partial x_{i}}$![]() is bounded in $L^{2}(0,T;L^{2}(\Omega ))$
is bounded in $L^{2}(0,T;L^{2}(\Omega ))$![]() by (3.39), and using (4.9) we arrive at
by (3.39), and using (4.9) we arrive at
for any $i=1,..,N$![]() . Thereafter, by using (3.5), (3.41) and the same method we used to get (4.6), we obtain
. Thereafter, by using (3.5), (3.41) and the same method we used to get (4.6), we obtain
and
Using (4.6), (4.11), (4.7) for $q_{i}-1$![]() instead of $m_{i}$
instead of $m_{i}$![]() , and since $q_i\geq 2$
, and since $q_i\geq 2$![]() and $\gamma \geq 1$
and $\gamma \geq 1$![]() we get that
we get that
Integrating (3.1) with respect to $x$![]() and $t$
and $t$![]() , we see that $(u_{\varepsilon _{n}},v_{\varepsilon _{n}})$
, we see that $(u_{\varepsilon _{n}},v_{\varepsilon _{n}})$![]() satisfies
satisfies

for any continuously differentiable function $\varphi$![]() with compact support in $\Omega \times [0,T)$
with compact support in $\Omega \times [0,T)$![]() . Wherefore, by using (4.6), (4.9), (4.10), (4.11), (4.12), (4.13) and by the standard convergence argument we obtain
. Wherefore, by using (4.6), (4.9), (4.10), (4.11), (4.12), (4.13) and by the standard convergence argument we obtain
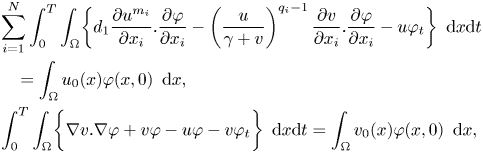
where $q_{i}\geq 2$![]() and $m^{-}>q_{i}-\frac {2}{N}$
and $m^{-}>q_{i}-\frac {2}{N}$![]() for any $i=1,..,N$
for any $i=1,..,N$![]() . Hence, we conclude the proof of theorem 2.5.
. Hence, we conclude the proof of theorem 2.5.



