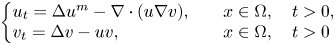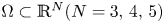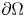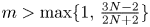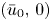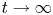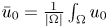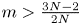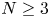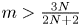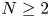1. Introduction
Chemotaxis is one of the most important components in the process of reproduction and migration, it describes the biased movement of biological species or cells towards chemotaxis substances. In this paper, we study the following quasilinear chemotaxis system with consumption of chemoattractant

in a bounded domain $\Omega \subset \mathbb {R}^N$![]() with smooth boundary $\partial \Omega,$
with smooth boundary $\partial \Omega,$![]() where $m>1$
where $m>1$![]() is a constant, $\nu$
is a constant, $\nu$![]() denotes the outer normal derivative on $\partial \Omega$
denotes the outer normal derivative on $\partial \Omega$![]() , $u(x,\,t)$
, $u(x,\,t)$![]() and $v(x,\,t)$
and $v(x,\,t)$![]() denote the density of cells population and the concentration of oxygen, respectively. And the initial data $(u_0,\,v_0)$
denote the density of cells population and the concentration of oxygen, respectively. And the initial data $(u_0,\,v_0)$![]() satisfies
satisfies
To better understand the chemotaxis model (1.1), we recall several previous works. Firstly, we recall the following system that has been studied for more than ten years,
where the function $D(u)$![]() denotes the diffusive function of cells, and the effect of $D(u)$
denotes the diffusive function of cells, and the effect of $D(u)$![]() on the global solvability of solutions has attracted widespread attention. Note that for the corresponding no-flux type initial-boundary value problem (1.3), for the case of $D(u)=1$
on the global solvability of solutions has attracted widespread attention. Note that for the corresponding no-flux type initial-boundary value problem (1.3), for the case of $D(u)=1$![]() and $N\geq 2$
and $N\geq 2$![]() , Tao [Reference Tao12] proved that system (1.3) possesses a unique global bounded classical solution under the assumption that $\|v_0\|_{L^\infty (\Omega )}$
, Tao [Reference Tao12] proved that system (1.3) possesses a unique global bounded classical solution under the assumption that $\|v_0\|_{L^\infty (\Omega )}$![]() is small. Especially, the domain is convex when $N=3$
is small. Especially, the domain is convex when $N=3$![]() , Tao and Winkler [Reference Tao and Winkler14] removed the smallness condition of initial data and proved that the system admits at least one global weak solution for arbitrarily large initial data; moreover, they showed that this solution is eventually smooth and converges to the constant equilibria in the large time limit.
, Tao and Winkler [Reference Tao and Winkler14] removed the smallness condition of initial data and proved that the system admits at least one global weak solution for arbitrarily large initial data; moreover, they showed that this solution is eventually smooth and converges to the constant equilibria in the large time limit.
Considering the quasilinear diffusion function $D(u)\geq D_0(u+1)^{m-1}$![]() with some constant $D_0>0$
with some constant $D_0>0$![]() , if $N\geq 2$
, if $N\geq 2$![]() and the domain is convex, Wang et al. [Reference Wang, Mu and Zhou20] established the globally bounded classical solution when $m>2-\frac 2N$
and the domain is convex, Wang et al. [Reference Wang, Mu and Zhou20] established the globally bounded classical solution when $m>2-\frac 2N$![]() . Subsequently, Wang et al. [Reference Wang, Mu, Lin and Zhao19] removed the convexity assumption and showed that the global solution is locally bounded if $m>2-\frac {6}{N+4}$
. Subsequently, Wang et al. [Reference Wang, Mu, Lin and Zhao19] removed the convexity assumption and showed that the global solution is locally bounded if $m>2-\frac {6}{N+4}$![]() with $N\geq 3$
with $N\geq 3$![]() . In addition, Zheng and Wang [Reference Zheng and Wang41] improved the global existence result for the case $m>\frac {3N}{2N+2}$
. In addition, Zheng and Wang [Reference Zheng and Wang41] improved the global existence result for the case $m>\frac {3N}{2N+2}$![]() .
.
Furthermore, taking account of the degenerate diffusion function $D(u)\geq D_0u^{m-1}$![]() with some constant $D_0>0$
with some constant $D_0>0$![]() , under the assumption $m>\frac {3N-2}{2N}$
, under the assumption $m>\frac {3N-2}{2N}$![]() , $N\geq 3$
, $N\geq 3$![]() , the globally bounded weak solution was obtained in [Reference Fan and Jin5, Reference Wang and Xiang24], and the asymptotic behaviour of solution was obtained in [Reference Fan and Jin5]. And for the convex domain case, the global existence result of the weak solution was further raised to the case $m>\frac {3N}{2N+2}(N\geq 2)$
, the globally bounded weak solution was obtained in [Reference Fan and Jin5, Reference Wang and Xiang24], and the asymptotic behaviour of solution was obtained in [Reference Fan and Jin5]. And for the convex domain case, the global existence result of the weak solution was further raised to the case $m>\frac {3N}{2N+2}(N\geq 2)$![]() in [Reference Zheng and Wang41]. Since then, no further research was conducted.
in [Reference Zheng and Wang41]. Since then, no further research was conducted.
Besides, chemotaxis processes with signal absorption coupling to the fluid motion are often considered, such as the following chemotaxis system which describes the movement of bacterial cells to oxygen in incompressible fluids [Reference Tuval, Cisneros, Dombrowski, Wolgemuth, Kessler and Goldstein18]

where $S$![]() is a given chemotactic sensitivity function, $\kappa \in \mathbb {R}$
is a given chemotactic sensitivity function, $\kappa \in \mathbb {R}$![]() is a constant, $P$
is a constant, $P$![]() is the pressure, $\phi$
is the pressure, $\phi$![]() is the gravitational force, and $\mathcal {V}$
is the gravitational force, and $\mathcal {V}$![]() is the velocity of the fluid. Note that if the effect of fluids is absent (i.e. $\mathcal {V}=0$
is the velocity of the fluid. Note that if the effect of fluids is absent (i.e. $\mathcal {V}=0$![]() ), system (1.4) is reduced to system (1.3). Readers who are interested in the study of (1.4) could refer to [Reference Cao1–Reference Di Francesco, Lorz and Markowich3, Reference Jin6, Reference Lorz10, Reference Tao and Winkler15, Reference Tao and Winkler16, Reference Wang21–Reference Wang and Xie23, Reference Winkler26–Reference Winkler33, Reference Zhang and Li36–Reference Zheng and Qi40]. Particularly, we point out that when $D(u)=mu^{m-1}$
), system (1.4) is reduced to system (1.3). Readers who are interested in the study of (1.4) could refer to [Reference Cao1–Reference Di Francesco, Lorz and Markowich3, Reference Jin6, Reference Lorz10, Reference Tao and Winkler15, Reference Tao and Winkler16, Reference Wang21–Reference Wang and Xie23, Reference Winkler26–Reference Winkler33, Reference Zhang and Li36–Reference Zheng and Qi40]. Particularly, we point out that when $D(u)=mu^{m-1}$![]() , there is a long process of how far $m$
, there is a long process of how far $m$![]() can ensure the solvability of system (1.4) with $\kappa =0$
can ensure the solvability of system (1.4) with $\kappa =0$![]() in $\Omega \subset \mathbb {R}^3$
in $\Omega \subset \mathbb {R}^3$![]() . When $S$
. When $S$![]() is a scalar function, Francesco et al. [Reference Di Francesco, Lorz and Markowich3] proved global bounded weak solutions for $m\in (\tfrac {7+\sqrt {217}}{12},\,2]$
is a scalar function, Francesco et al. [Reference Di Francesco, Lorz and Markowich3] proved global bounded weak solutions for $m\in (\tfrac {7+\sqrt {217}}{12},\,2]$![]() , Tao and Winkler [Reference Tao and Winkler16] established the existence of global weak solutions for $m>\frac {8}{7}$
, Tao and Winkler [Reference Tao and Winkler16] established the existence of global weak solutions for $m>\frac {8}{7}$![]() , Winkler [Reference Winkler31] and Jin [Reference Jin6] enhanced the boundedness result to $m>\frac {9}{8}$
, Winkler [Reference Winkler31] and Jin [Reference Jin6] enhanced the boundedness result to $m>\frac {9}{8}$![]() and $m>1$
and $m>1$![]() , respectively. When $S$
, respectively. When $S$![]() is a given parameter matrix, Winkler [Reference Winkler28] presented the boundedness of solutions in convex domains for $m>\frac {7}{6}$
is a given parameter matrix, Winkler [Reference Winkler28] presented the boundedness of solutions in convex domains for $m>\frac {7}{6}$![]() . Additionally, this result was extended to the case $m>\frac {10}{9}$
. Additionally, this result was extended to the case $m>\frac {10}{9}$![]() [Reference Zheng37], $m>\frac {65}{63}$
[Reference Zheng37], $m>\frac {65}{63}$![]() [Reference Tian and Xiang17], and $m>\frac {11}{4}-\sqrt {3}$
[Reference Tian and Xiang17], and $m>\frac {11}{4}-\sqrt {3}$![]() [Reference Zheng and Ke39]. Recently, Winkler [Reference Winkler34, corollary 1.4] has shown that the system admits a globally bounded weak solution for $m>1$
[Reference Zheng and Ke39]. Recently, Winkler [Reference Winkler34, corollary 1.4] has shown that the system admits a globally bounded weak solution for $m>1$![]() in the convex domain.
in the convex domain.
Comparing the results of systems (1.3) and (1.4) in three dimensions, we see that the conditions of parameter $m>\frac {7}{6}$![]() [Reference Fan and Jin5, Reference Wang and Xiang24] and $m>\frac {9}{8}$
[Reference Fan and Jin5, Reference Wang and Xiang24] and $m>\frac {9}{8}$![]() [Reference Zheng and Wang41] are worse than $m>1$
[Reference Zheng and Wang41] are worse than $m>1$![]() [Reference Jin6, Reference Winkler34] from the point of ensuring the solvability of the solution. Therefore, it is a natural question whether the range of $m$
[Reference Jin6, Reference Winkler34] from the point of ensuring the solvability of the solution. Therefore, it is a natural question whether the range of $m$![]() of system (1.1) in higher dimensions is wider than that in [Reference Fan and Jin5, Reference Wang and Xiang24, Reference Zheng and Wang41]. If the range of $m$
of system (1.1) in higher dimensions is wider than that in [Reference Fan and Jin5, Reference Wang and Xiang24, Reference Zheng and Wang41]. If the range of $m$![]() can be extended, what is the large time behaviour of the corresponding solution? Indeed, those questions are partially answered by the main results of this paper.
can be extended, what is the large time behaviour of the corresponding solution? Indeed, those questions are partially answered by the main results of this paper.
Main idea: As aforementioned, under the assumption $m>\frac {3N-2}{2N}$![]() , the global boundedness weak solution of system (1.1) has been obtained in [Reference Fan and Jin5, Reference Wang and Xiang24], thus we focus on the case $m\leq \frac {3N-2}{2N}$
, the global boundedness weak solution of system (1.1) has been obtained in [Reference Fan and Jin5, Reference Wang and Xiang24], thus we focus on the case $m\leq \frac {3N-2}{2N}$![]() . Without loss of generality, we shall assume that $2>m>1$
. Without loss of generality, we shall assume that $2>m>1$![]() in the sequel. Note that the term $\int _\Omega (u_\varepsilon +\varepsilon )^{p-m+1}|\nabla v_\varepsilon |^2$
in the sequel. Note that the term $\int _\Omega (u_\varepsilon +\varepsilon )^{p-m+1}|\nabla v_\varepsilon |^2$![]() was decoupled into two parts in [Reference Fan and Jin5, Reference Wang and Xiang24], namely the integrals containing only $u_\varepsilon$
was decoupled into two parts in [Reference Fan and Jin5, Reference Wang and Xiang24], namely the integrals containing only $u_\varepsilon$![]() and $\nabla v_\varepsilon$
and $\nabla v_\varepsilon$![]() separately. In this paper, inspired by [Reference Winkler34], we choose $p=m+1$
separately. In this paper, inspired by [Reference Winkler34], we choose $p=m+1$![]() to be the dissipative part of the inequality describing the evolution of $\int _\Omega (u_\varepsilon +\varepsilon )|\nabla v_\varepsilon |^2$
to be the dissipative part of the inequality describing the evolution of $\int _\Omega (u_\varepsilon +\varepsilon )|\nabla v_\varepsilon |^2$![]() . Unfortunately, there are additional bad terms that must be addressed. Therefore, we construct a new functional
. Unfortunately, there are additional bad terms that must be addressed. Therefore, we construct a new functional
to obtain the boundedness of $\|u_\varepsilon +\varepsilon \|_{L^{m+1}(\Omega )}$![]() for $2>m>1$
for $2>m>1$![]() , which is the most critical step. Next, under the assumption of $2>m>\max \{1,\,\frac {3N-2}{2N+2}\}$
, which is the most critical step. Next, under the assumption of $2>m>\max \{1,\,\frac {3N-2}{2N+2}\}$![]() (where $N=3,\,4,\,5$
(where $N=3,\,4,\,5$![]() ), the boundedness of functional $\int _\Omega (u_\varepsilon +\varepsilon )^p+\int _\Omega |\nabla v_\varepsilon |^{2q}$
), the boundedness of functional $\int _\Omega (u_\varepsilon +\varepsilon )^p+\int _\Omega |\nabla v_\varepsilon |^{2q}$![]() for large $p$
for large $p$![]() and large $q$
and large $q$![]() can be obtained. And then by the iteration procedure in [Reference Tao and Winkler13, theorem A.1], we get the uniform bounds for $\|u_\varepsilon \|_{L^\infty (\Omega )}$
can be obtained. And then by the iteration procedure in [Reference Tao and Winkler13, theorem A.1], we get the uniform bounds for $\|u_\varepsilon \|_{L^\infty (\Omega )}$![]() and $\|\nabla v_\varepsilon \|_{L^\infty (\Omega )}$
and $\|\nabla v_\varepsilon \|_{L^\infty (\Omega )}$![]() .
.
At first, we introduce the following definition of weak solutions.
Definition 1.1 For a global weak solution of (1.1), we mean a pair of nonnegative functions $(u,\,v)$![]() satisfying
satisfying
and for any $\varphi \in C_0^{\infty } (\bar {\Omega }\times [0,\, \infty ))$![]() ,
,

The main results are stated as follows.
Theorem 1.2 Let $\Omega \subset \mathbb {R}^N~(N=3,\,4,\,5)$![]() be a bounded domain with smooth boundary, assume that
be a bounded domain with smooth boundary, assume that

then system (1.1) with (1.2) at least has one globally bounded weak solution.
Remark 1.3 For the case $3\leq N\leq 5$![]() , our theorem 1.2 extends the previous results in [Reference Fan and Jin5, Reference Wang and Xiang24, Reference Zheng and Wang41]. In addition, our result is consistent with the associated fluid-free system [Reference Jin6, Reference Winkler34] for $N=3$
, our theorem 1.2 extends the previous results in [Reference Fan and Jin5, Reference Wang and Xiang24, Reference Zheng and Wang41]. In addition, our result is consistent with the associated fluid-free system [Reference Jin6, Reference Winkler34] for $N=3$![]() .
.
Remark 1.4 In this paper, our method is motivated by Winkler [Reference Winkler34], but we can only solve the case for $N=3,\,4,\,5$![]() , whether it can be further solved for the case $N>5$
, whether it can be further solved for the case $N>5$![]() is uncertain. Fortunately, we have removed the convexity assumption on the domain in [Reference Winkler34].
is uncertain. Fortunately, we have removed the convexity assumption on the domain in [Reference Winkler34].
Remark 1.5 In the case $N=3,\,4$![]() , we can find that if $m=1$
, we can find that if $m=1$![]() the system must be imposed on the smallness condition of the initial data [Reference Tao12]. As we all know, the condition $m>1$
the system must be imposed on the smallness condition of the initial data [Reference Tao12]. As we all know, the condition $m>1$![]() means that the diffusion is stronger than $m=1$
means that the diffusion is stronger than $m=1$![]() . From these points of view, our result is optimal. But in the case $N=5$
. From these points of view, our result is optimal. But in the case $N=5$![]() , it is not clear whether the assumptions of $m>\frac {13}{12}$
, it is not clear whether the assumptions of $m>\frac {13}{12}$![]() is optimal to ensure global boundedness of the solution.
is optimal to ensure global boundedness of the solution.
As a byproduct of theorem 1.2, large time behaviour of the solution to system (1.1) can be achieved.
Theorem 1.6 Under the assumptions of theorem 1.2, the global weak solution constructed in theorem 1.2 satisfies
as $t\rightarrow \infty$![]() , where $\bar {u}_0:=\frac {1}{|\Omega |}\int _\Omega u_0$
, where $\bar {u}_0:=\frac {1}{|\Omega |}\int _\Omega u_0$![]() .
.
The rest of this paper is organized as follows. In § 2, we introduce the approximated system (2.1) and provide the local existence of the approximated solution and some crucial properties. In § 3, we present some important estimates, and obtain the global bounded classical solution to the approximate system (2.1). In § 4, we deduce some convergence properties and complete the proof of theorem 1.2 by an approximation procedure. Finally, in § 5, we establish the convergence of the solution.
2. Approximate problems and crucial properties
In this section, in order to construct a weak solution of (1.1), we consider the following approximate problems

for $\varepsilon \in (0,\,1)$![]() .
.
For each $\varepsilon \in (0,\,1)$![]() , the regularized problem (2.1) is locally solvable in the classical sense.
, the regularized problem (2.1) is locally solvable in the classical sense.
Lemma 2.1 Suppose that $\Omega \subset \mathbb {R}^N (N\geq 3)$![]() is a bounded domain with smooth boundary. Assume that the initial data $(u_0,\,v_0)$
is a bounded domain with smooth boundary. Assume that the initial data $(u_0,\,v_0)$![]() fulfils (1.2). Then problem (2.1) has a unique classical solution
fulfils (1.2). Then problem (2.1) has a unique classical solution
where $T_{\max,\varepsilon }$![]() denotes the maximal existence time. Moreover, if $T_{\max,\varepsilon }<\infty$
denotes the maximal existence time. Moreover, if $T_{\max,\varepsilon }<\infty$![]() , then
, then
Proof. The local existence, extensibility criterion, and regularity of (2.1) are well-established (see [Reference Wang, Mu and Zhou20]), the uniqueness can be achieved by the same procedure as in [Reference Horstmann and Winkler7, Reference Winkler25], so we omit the details of the proof for the sake of brevity.
Lemma 2.2 The solution $(u_\varepsilon,\, v_\varepsilon )$![]() of (2.1) satisfies
of (2.1) satisfies
Proof. A direct integration in the first equation in (2.1) yields (2.4). Equation (2.5) follows from an application of the maximum principle to the second equation in (2.1).
In order to prove the main result, we state two basic lemmas which will be used later. The first is Gagliardo–Nirenberg inequality.
Lemma 2.3 Let $\Omega \subset \mathbb {R}^N(N\geq 3)$![]() be a bounded smooth domain
be a bounded smooth domain
then there exists $C>0$![]() such that
such that

for all $\varphi \in C^1(\Omega )\cap L^r(\Omega )$![]() .
.
Particularly, if $q=p+m-1+\frac {2r}{N}$![]() , then there exists $C>0$
, then there exists $C>0$![]() such that
such that

for all $\varphi \in C^1(\Omega )\cap L^r(\Omega )$![]() .
.
Proof. Condition (2.6) entails that

and hence the Gagliardo–Nirenberg inequality provides $C_1>0$![]() satisfying
satisfying

for all $\varphi \in C^1({\Omega })\cap L^r (\Omega )$![]() with $C_2=C_1\max \{1,\,\frac {(p+m-1)^2}{4}\}$
with $C_2=C_1\max \{1,\,\frac {(p+m-1)^2}{4}\}$![]() . Note that
. Note that

Thus, (2.7) is proved. Moreover, since $\frac {qa}{p+m-1}=\frac {\frac {q}{2r}-\frac {1}{2}}{\frac {p+m-1}{2r}+\frac {1}{N}-\frac {1}{2}}=1$![]() with the additional assumption $q=p+m-1+\frac {2r}{N}$
with the additional assumption $q=p+m-1+\frac {2r}{N}$![]() , (2.8) results from (2.7).
, (2.8) results from (2.7).
The next is interpolation inequality.
Lemma 2.4 (Lemma 3.3 of [Reference Wang and Xiang24])
Suppose that $q>\max \{1,\,\frac {N-2}{2}\}$![]() and ${\Omega \subset \mathbb {R}^N(N\geq 3)}$
and ${\Omega \subset \mathbb {R}^N(N\geq 3)}$![]() is a bounded domain with smooth boundary. Moreover, assume that
is a bounded domain with smooth boundary. Moreover, assume that

then there exists $C > 0$![]() such that for all $\varphi \in C^2(\bar {\Omega })$
such that for all $\varphi \in C^2(\bar {\Omega })$![]() fulfilling $\varphi \cdot \frac {\partial \varphi }{\partial \nu }= 0$
fulfilling $\varphi \cdot \frac {\partial \varphi }{\partial \nu }= 0$![]() on $\partial \Omega$
on $\partial \Omega$![]() , we have
, we have
3. Uniform estimates for ($u_\varepsilon,\,v_\varepsilon$ ) and global boundedness of approximate solutions
) and global boundedness of approximate solutions
In this section, we establish some priori estimates for solutions and get the global boundedness of approximate solutions (2.1). Firstly, we apply standard testing procedures to establish a differential inequality for the first equation in (2.1).
Lemma 3.1 Let $p>1$![]() and $\Omega \subset \mathbb {R}^N$
and $\Omega \subset \mathbb {R}^N$![]() be a bounded domain with smooth boundary. Assume $(u_\varepsilon,\,v_\varepsilon )$
be a bounded domain with smooth boundary. Assume $(u_\varepsilon,\,v_\varepsilon )$![]() is a classical solution to system (2.1) on $[0,\,T_{\max,\varepsilon })$
is a classical solution to system (2.1) on $[0,\,T_{\max,\varepsilon })$![]() . Then for all $t\in (0,\,T_{\max,\varepsilon })$
. Then for all $t\in (0,\,T_{\max,\varepsilon })$![]() and $\varepsilon \in (0,\,1)$
and $\varepsilon \in (0,\,1)$![]() , we can see that
, we can see that

Proof. We multiply the first equation of (2.1) by $(u_\varepsilon +\varepsilon )^{p-1}$![]() integrating by parts and together with Young's inequality to obtain
integrating by parts and together with Young's inequality to obtain

for all $t\in (0,\, T_{\max,\varepsilon })$![]() , which results in (3.1).
, which results in (3.1).
Lemma 3.2 Let $\Omega \subset \mathbb {R}^N(N=3,\,4,\,5)$![]() be a bounded domain with smooth boundary. Assume $2>m>1$
be a bounded domain with smooth boundary. Assume $2>m>1$![]() , then for all $\varepsilon \in (0,\,1)$
, then for all $\varepsilon \in (0,\,1)$![]() , there exists $C>0$
, there exists $C>0$![]() independent of $\varepsilon$
independent of $\varepsilon$![]() such that the solution of (2.1) satisfies
such that the solution of (2.1) satisfies
with $\tau :=\min \{1,\,\frac {T_{\max,\varepsilon }}{2}\}$![]() .
.
Proof. The proof is divided into five steps.
Step 1. Using (3.1) to $u_\varepsilon$![]() with $p:=m+1$
with $p:=m+1$![]() , for all $t\in (0,\,T_{\max,\varepsilon })$
, for all $t\in (0,\,T_{\max,\varepsilon })$![]() we get
we get
Step 2. For any $\eta _1>0$![]() , one can find four positive constants $C_1,\,C_2(\eta _1),\,C_3$
, one can find four positive constants $C_1,\,C_2(\eta _1),\,C_3$![]() , and $\widetilde {C}$
, and $\widetilde {C}$![]() such that
such that

Indeed, on the basis of (2.5) and the identities $\nabla v_\varepsilon \cdot \nabla \Delta v_\varepsilon =\frac {1}{2}\Delta |\nabla v_\varepsilon |^2-|D^2 v_\varepsilon |^2$![]() and $\nabla |\nabla v_\varepsilon |^2=2D^2v_\varepsilon \cdot \nabla v_\varepsilon$
and $\nabla |\nabla v_\varepsilon |^2=2D^2v_\varepsilon \cdot \nabla v_\varepsilon$![]() , upon integrating by parts, for all $t\in (0,\,T_{\max,\varepsilon })$
, upon integrating by parts, for all $t\in (0,\,T_{\max,\varepsilon })$![]() , we compute
, we compute

Now, we will estimate the right-hand side of (3.8). To this end, given any $\eta _1>0$![]() , utilize Young's inequality to see that for all $t\in (0,\,T_{\max,\varepsilon })$
, utilize Young's inequality to see that for all $t\in (0,\,T_{\max,\varepsilon })$![]() satisfies
satisfies


and
Next, we will estimate the boundary integral in (3.8). According to [Reference Nagai, Senba and Yoshida11], there exists $c_2>0$![]() such that $\partial _\nu |\nabla \varphi |^2 \leq c_2|\nabla \varphi |^2$
such that $\partial _\nu |\nabla \varphi |^2 \leq c_2|\nabla \varphi |^2$![]() on $\partial \Omega$
on $\partial \Omega$![]() for all $\varphi \in C^2(\bar {\Omega })$
for all $\varphi \in C^2(\bar {\Omega })$![]() with $\partial _\nu \varphi |_{\partial \Omega }=0$
with $\partial _\nu \varphi |_{\partial \Omega }=0$![]() . And notice the equivalent trace inequality [Reference Xiang35, P.1186]: for all $\epsilon >0$
. And notice the equivalent trace inequality [Reference Xiang35, P.1186]: for all $\epsilon >0$![]() , one has
, one has
Now, for any $\epsilon >0$![]() , it follows that for all $t\in(0,T_{\max,\varepsilon})$
, it follows that for all $t\in(0,T_{\max,\varepsilon})$![]() ,
,

Moreover, let $c_3$![]() denote the embedding constant for trace embedding $W^{1,1}(\Omega )\hookrightarrow L^1(\partial \Omega )$
denote the embedding constant for trace embedding $W^{1,1}(\Omega )\hookrightarrow L^1(\partial \Omega )$![]() [Reference Evans4]. Using lemma 2.4 for $v_\varepsilon$
[Reference Evans4]. Using lemma 2.4 for $v_\varepsilon$![]() with $q:=2$
with $q:=2$![]() , $\lambda :=6$
, $\lambda :=6$![]() , $3\leq N\leq 5$
, $3\leq N\leq 5$![]() , and (2.5), one has
, and (2.5), one has
This combined with Young's inequality yields

Therefore, combining (3.12), (3.14) and (2.4) by letting $\epsilon =1$![]() , the boundary integral in (3.8) can be simplified to
, the boundary integral in (3.8) can be simplified to
Next, using (2.5) and Young's inequality, it is obvious that for all $t\in (0,\,T_{\max,\varepsilon })$![]() ,
,

Since $\varepsilon \in (0,\,1)$![]() , and using Young's inequality, it follows that for all $t\in (0,\,T_{\max,\varepsilon })$
, and using Young's inequality, it follows that for all $t\in (0,\,T_{\max,\varepsilon })$![]() ,
,

From (3.9)–(3.16), we obtain (3.7) upon letting $C_1:=2+4\|v_0\|_{L^\infty (\Omega )}$![]() , $C_2 (\eta _1):=\frac {m^2}{\eta _1}+\frac {13}{4}$
, $C_2 (\eta _1):=\frac {m^2}{\eta _1}+\frac {13}{4}$![]() and $C_3=4$
and $C_3=4$![]() .
.
Step 3. In order to absorb the third term on the right-hand side of (3.7), our goal is to show that the integral $\int _\Omega |\nabla v_\varepsilon |^4$![]() satisfies
satisfies
In fact, using the second equation in (2.1) along with the pointwise identities $\nabla v_\varepsilon \cdot \nabla \Delta v_\varepsilon =\frac {1}{2}\Delta |\nabla v_\varepsilon |^2-|D^2 v_\varepsilon |^2$![]() and $\nabla |\nabla v_\varepsilon |^2=2D^2v_\varepsilon \cdot \nabla v_\varepsilon$
and $\nabla |\nabla v_\varepsilon |^2=2D^2v_\varepsilon \cdot \nabla v_\varepsilon$![]() , we differentiate $\int _\Omega |\nabla {v_\varepsilon }|^4$
, we differentiate $\int _\Omega |\nabla {v_\varepsilon }|^4$![]() directly and integrate by parts to yield
directly and integrate by parts to yield

Applying Young's inequality, for all $\delta >0$![]() , we obtain
, we obtain
In light of (3.13), we can choose a suitable $\delta$![]() such that exists a constant $c_1>0$
such that exists a constant $c_1>0$![]() satisfying
satisfying
Similar to (3.14), the boundary integral in (3.18) fulfils

From (3.18)–(3.21), we obtain (3.17) upon an obvious choice of $C_4:=\frac {\|v_0\|_{L^\infty (\Omega )}^2}{\delta }$![]() and $C_5:=4c_1+4c_4$
and $C_5:=4c_1+4c_4$![]() .
.
Step 4. Let the term $\int _\Omega |\nabla u_\varepsilon |^2$![]() of both (3.7) and (3.17) appears on the left-hand side of an inequality. Namely, for all $t\in (0,\,T_{\max,\varepsilon })$
of both (3.7) and (3.17) appears on the left-hand side of an inequality. Namely, for all $t\in (0,\,T_{\max,\varepsilon })$![]() and for any $\eta _2>0$
and for any $\eta _2>0$![]() , there exists $C_6(\eta _2):=\eta _2^{\frac {m-1}{m-2}}\cdot (\frac {2-m}{2m})^{\frac {1}{2-m}}$
, there exists $C_6(\eta _2):=\eta _2^{\frac {m-1}{m-2}}\cdot (\frac {2-m}{2m})^{\frac {1}{2-m}}$![]() such that
such that

Actually, due to $2>m>1$![]() , using (3.1) to $u_\varepsilon$
, using (3.1) to $u_\varepsilon$![]() with $p:=3-m$
with $p:=3-m$![]() , and upon Young's inequality the result is obtained.
, and upon Young's inequality the result is obtained.
Step 5. Subtly combining (3.6), (3.7), (3.17) and (3.22), let

Due to $2>m>1$![]() , we can see that
, we can see that

Choose suitable $\eta _1$![]() and $\eta _2$
and $\eta _2$![]() such that $\eta _1=\frac {1}{16}$
such that $\eta _1=\frac {1}{16}$![]() and $\eta _2\frac {4C_1+8{C_2(\eta _1)}C_4}{2-m}=\frac {1}{2}$
and $\eta _2\frac {4C_1+8{C_2(\eta _1)}C_4}{2-m}=\frac {1}{2}$![]() . In view of lemma 2.3, Young's inequality, and (2.4), there exists $c_1>0$
. In view of lemma 2.3, Young's inequality, and (2.4), there exists $c_1>0$![]() such that
such that

Using Young's inequality, we have
Upon Young's inequality and (3.20), there exist $c_2 ~\mbox {and} ~c_3>0$![]() such that
such that

It follows from (3.24)–(3.27) that
where $h(t):=\frac {1}{16}\int _\Omega (u_\varepsilon +\varepsilon )^{2m-2}|\nabla u_\varepsilon |^2 +(C_1+2{C_2(\eta _1)}C_4)\int _\Omega |\nabla u_\varepsilon |^2$![]() and $\widehat {C}:=2{C_2(\eta _1)}C_5+c_1+c_3+\widetilde {C}$
and $\widehat {C}:=2{C_2(\eta _1)}C_5+c_1+c_3+\widetilde {C}$![]() . By an ordinary differential equations (ODE) comparison argument, it yields
. By an ordinary differential equations (ODE) comparison argument, it yields
which implies (3.3). Finally, integration of (3.28) shows that (3.4)–(3.5) hold.
According to lemma 3.2, the boundedness of $\|u_\varepsilon +\varepsilon \|_{L^{m+1}(\Omega )}$![]() can be obtained without any restriction on $m$
can be obtained without any restriction on $m$![]() except for the condition $2>m>1$
except for the condition $2>m>1$![]() . Next, we use the boundedness of $\|u_\varepsilon +\varepsilon \|_{L^{m+1}(\Omega )}$
. Next, we use the boundedness of $\|u_\varepsilon +\varepsilon \|_{L^{m+1}(\Omega )}$![]() to establish a further estimate for solutions to the approximated system (2.1). As in [Reference Tao and Winkler13], we provide an estimate on $\nabla v_\varepsilon$
to establish a further estimate for solutions to the approximated system (2.1). As in [Reference Tao and Winkler13], we provide an estimate on $\nabla v_\varepsilon$![]() . The proof of the following lemma is the same as that in lemma 3.2 of [Reference Wang and Xiang24], so we omit it.
. The proof of the following lemma is the same as that in lemma 3.2 of [Reference Wang and Xiang24], so we omit it.
Lemma 3.3 Let $q>1$![]() , then for all $\varepsilon \in (0,\,1),$
, then for all $\varepsilon \in (0,\,1),$![]() we have
we have

for all $t\in (0,\,T_{\max,\varepsilon })$![]() with a positive constant $C_7.$
with a positive constant $C_7.$![]()
Next, we will estimate the combination of $\int _\Omega (u_\varepsilon +\varepsilon )^p+\int _\Omega |\nabla v_\varepsilon |^{2q}$![]() .
.
Lemma 3.4 Assume that $2>m>1$![]() , then for all $p>2$
, then for all $p>2$![]() and any $q>1$
and any $q>1$![]() , one can find three constants $C_8,\,C_9,\,C_{10}>0$
, one can find three constants $C_8,\,C_9,\,C_{10}>0$![]() such that
such that

where the function $F_\varepsilon (t)$![]() is defined as
is defined as
Proof. Combining lemma 3.1 with lemma 3.3 and using $m>1$![]() , we obtain
, we obtain

Next, by Young's inequality for any $\eta _3>0$![]() , we have
, we have
and
Using interpolation inequality (2.10) and Young's inequality, we can choose a suitably $\eta _3$![]() such that
such that
Therefore, we obtain the boundedness of $\int _\Omega (u_\varepsilon +\varepsilon )^p+\int _\Omega |\nabla v_\varepsilon |^{2q}$![]() with $p>2$
with $p>2$![]() and $q>1$
and $q>1$![]() .
.
Lemma 3.5 Let $\Omega \subset \mathbb {R}^N(N=3,\,4,\,5)$![]() be a bounded domain with smooth boundary. Assume $2>m>\max \{1,\,\frac {3N-2}{2N+2}\}$
be a bounded domain with smooth boundary. Assume $2>m>\max \{1,\,\frac {3N-2}{2N+2}\}$![]() , whenever $p>2$
, whenever $p>2$![]() and $q>1$
and $q>1$![]() are such that
are such that
then for all $\varepsilon \in (0,\,1)$![]() , we can find a constant $C=C(p,\,q)>0$
, we can find a constant $C=C(p,\,q)>0$![]() satisfying
satisfying
Proof. Using the boundedness of $\|u_\varepsilon +\varepsilon \|_{L^{m+1}(\Omega )}$![]() to (2.8) with $r:=m+1$
to (2.8) with $r:=m+1$![]() , there exists $C_{11}>0$
, there exists $C_{11}>0$![]() such that for all $\varepsilon \in (0,\,1)$
such that for all $\varepsilon \in (0,\,1)$![]() satisfies
satisfies
Moreover, $m>\max \{1,\,\frac {3N-2}{2N+2}\}$![]() ensures that hypothesis (3.33) holds. (3.33) asserts that $q+1< p+m-1+\frac {2(m+1)}{N}$
ensures that hypothesis (3.33) holds. (3.33) asserts that $q+1< p+m-1+\frac {2(m+1)}{N}$![]() and
and

Consequently, utilizing Young's inequality, we obtain
and
Since $p< p+m-1+\frac {2(m+1)}{N}$![]() , it is similar to deduce
, it is similar to deduce
Collecting (3.35)–(3.38) and (3.30), it follows that
with $c_4>0$![]() . It is obvious to obtain (3.34) by a comparison argument.
. It is obvious to obtain (3.34) by a comparison argument.
By means of Moser–Alikakos iteration procedure, an application of the above to suitably large but fixed $p$![]() and $q$
and $q$![]() yields bounds in $L^\infty (\Omega )\times W^{1,\infty }(\Omega )$
yields bounds in $L^\infty (\Omega )\times W^{1,\infty }(\Omega )$![]() .
.
Lemma 3.6 Let $\Omega \subset \mathbb {R}^N(N=3,\,4,\,5)$![]() be a bounded domain with smooth boundary. Assume that $2>m>\max \{1,\,\frac {3N-2}{2N+2}\}$
be a bounded domain with smooth boundary. Assume that $2>m>\max \{1,\,\frac {3N-2}{2N+2}\}$![]() . Then there exists $C>0$
. Then there exists $C>0$![]() such that for all $\varepsilon \in (0,\,1)$
such that for all $\varepsilon \in (0,\,1)$![]() the solution of (2.1) satisfies
the solution of (2.1) satisfies
and
Proof. In light of using the result of lemma 3.5, lemma A.1 in [Reference Tao and Winkler13], and (2.5), we derive
where $C > 0$![]() is independent of $\varepsilon \in (0,\, 1)$
is independent of $\varepsilon \in (0,\, 1)$![]() . From this and the extensibility criterion (2.3), it is evident that $T_{\max,\varepsilon }=\infty$
. From this and the extensibility criterion (2.3), it is evident that $T_{\max,\varepsilon }=\infty$![]() , which finishes the proof.
, which finishes the proof.
4. Global bounded weak solutions to system (1.1)
In order to finish the proof of theorem 1.2, we will give some regularity properties with $(u_\varepsilon,\,v_\varepsilon )$![]() in this section.
in this section.
Lemma 4.1 Let $\Omega \subset \mathbb {R}^N(N=3,\,4,\,5)$![]() be a bounded domain with smooth boundary. Assume that $m>\max \{1,\,\frac {3N-2}{2N+2}\}$
be a bounded domain with smooth boundary. Assume that $m>\max \{1,\,\frac {3N-2}{2N+2}\}$![]() , then we get
, then we get
and
Proof. Multiplying the second equation of (2.1) by 1 and $v_\varepsilon$![]() separately, upon integrating by parts, and integrating with respect to $t$
separately, upon integrating by parts, and integrating with respect to $t$![]() , we obtain
, we obtain
and
for all $\varepsilon \in (0,\,1)$![]() . As a result, we immediately obtain (4.1) and (4.2).
. As a result, we immediately obtain (4.1) and (4.2).
Lemma 4.2 Let $\Omega \subset \mathbb {R}^N(N=3,\,4,\,5)$![]() be a bounded domain with smooth boundary. Assume that $2>m>\max \{1,\,\frac {3N-2}{2N+2}\}$
be a bounded domain with smooth boundary. Assume that $2>m>\max \{1,\,\frac {3N-2}{2N+2}\}$![]() , then for any $T>0$
, then for any $T>0$![]() there exists $C(T)>0$
there exists $C(T)>0$![]() such that
such that
and
Proof. Due to lemma 3.2, for any $T>0$![]() , we have
, we have
and
which indicates (4.4) is valid. Due to lemma 3.6, there exists a positive constant $c_1>0$![]() such that $0< u_\varepsilon < c_1$
such that $0< u_\varepsilon < c_1$![]() in $\Omega \times (0,\,\infty )$
in $\Omega \times (0,\,\infty )$![]() for all $\varepsilon \in (0,\,1)$
for all $\varepsilon \in (0,\,1)$![]() . Multiplying the first equation of (2.1) by $(u_\varepsilon +\varepsilon )^{m-1}$
. Multiplying the first equation of (2.1) by $(u_\varepsilon +\varepsilon )^{m-1}$![]() , one has
, one has
integrating with respect to $t$![]() and using (4.2), which indicates
and using (4.2), which indicates
Next, multiplying the first equation of (2.1) by $(u_\varepsilon +\varepsilon )^{m}\psi$![]() with $\psi \in C^\infty _0(\Omega )$
with $\psi \in C^\infty _0(\Omega )$![]() , and integrating over $\Omega$
, and integrating over $\Omega$![]() , for all $\varepsilon \in (0,\,1)$
, for all $\varepsilon \in (0,\,1)$![]() , we obtain
, we obtain

Using the boundedness of $\|u_\varepsilon \|_{L^\infty (\Omega )}$![]() and Young's inequality, it yields
and Young's inequality, it yields

and

Moreover, by the boundedness of $\|u_\varepsilon \|_{L^\infty (\Omega )}$![]() and $\|\nabla v_\varepsilon \|_{L^\infty (\Omega )}$
and $\|\nabla v_\varepsilon \|_{L^\infty (\Omega )}$![]() , we get
, we get
and

According to (4.6)–(4.12) and the continuity of the embedding $W_0^{N,2}(\Omega )\hookrightarrow W^{1,\infty }(\Omega )$![]() , there exists $C(T)>0$
, there exists $C(T)>0$![]() such that
such that
The proof of this lemma is completed.
Lemma 4.3 Let $2>m>\max \{1,\,\frac {3N-2}{2N+2}\}$![]() , then for any $T>0$
, then for any $T>0$![]() there exists $C(T)>0$
there exists $C(T)>0$![]() such that
such that
Proof. Multiplying $\psi (x)$![]() on both sides of the second equation with $\psi (x)\in W^{1,2}(\Omega )$
on both sides of the second equation with $\psi (x)\in W^{1,2}(\Omega )$![]() , and integrating over $\Omega$
, and integrating over $\Omega$![]() and using the Hölder inequality, we have
and using the Hölder inequality, we have
By the boundedness of $\|u_\varepsilon \|_{L^\infty (\Omega )}$![]() and $\|v_\varepsilon \|_{L^\infty (\Omega )}$
and $\|v_\varepsilon \|_{L^\infty (\Omega )}$![]() , it shows that
, it shows that
Combining (4.2) and (4.14), it follows that
The proof of throrem 1.2. Lemma 3.6 shows that there exists $(\varepsilon _j)_{j\in \mathbb {N}}\subset (0,\,1)$![]() such that $\varepsilon _j\rightarrow 0$
such that $\varepsilon _j\rightarrow 0$![]() as $j\rightarrow \infty$
as $j\rightarrow \infty$![]() and that $u_{\varepsilon _j}\stackrel {\ast }\rightharpoonup u$
and that $u_{\varepsilon _j}\stackrel {\ast }\rightharpoonup u$![]() in $L^\infty (\Omega \times (0,\,\infty ))$
in $L^\infty (\Omega \times (0,\,\infty ))$![]() and $\nabla v_{\varepsilon _j}\stackrel {\ast }\rightharpoonup \nabla v$
and $\nabla v_{\varepsilon _j}\stackrel {\ast }\rightharpoonup \nabla v$![]() in $L^\infty (\Omega \times (0,\,\infty ))$
in $L^\infty (\Omega \times (0,\,\infty ))$![]() hold. Lemma 4.2 implies that $(u_\varepsilon ^{m})_{\varepsilon \in (0,1)}$
hold. Lemma 4.2 implies that $(u_\varepsilon ^{m})_{\varepsilon \in (0,1)}$![]() is bounded in $L^2([0,T];W^{1,2}(\Omega ))$
is bounded in $L^2([0,T];W^{1,2}(\Omega ))$![]() . Hence, $\nabla u_{\varepsilon _j}^{m} \rightharpoonup \nabla u^{m}$
. Hence, $\nabla u_{\varepsilon _j}^{m} \rightharpoonup \nabla u^{m}$![]() in $L^2_{loc}([0,\,\infty );L^2(\Omega ))$
in $L^2_{loc}([0,\,\infty );L^2(\Omega ))$![]() . Furthermore, using the Aubin–Lions lemma and $(\partial _tu_\varepsilon ^{m})_{\varepsilon \in (0,1)}$
. Furthermore, using the Aubin–Lions lemma and $(\partial _tu_\varepsilon ^{m})_{\varepsilon \in (0,1)}$![]() is bounded in $L^1([0,T];(W_0^{N,2}(\Omega ))^\ast )$
is bounded in $L^1([0,T];(W_0^{N,2}(\Omega ))^\ast )$![]() , it yields $u^{m}_{\varepsilon _j}\rightarrow u^{m}$
, it yields $u^{m}_{\varepsilon _j}\rightarrow u^{m}$![]() in $L^2([0,T];L^2(\Omega ))$
in $L^2([0,T];L^2(\Omega ))$![]() . By the Riesz lemma and $m>1$
. By the Riesz lemma and $m>1$![]() , we have $u_{\varepsilon _j}\rightarrow u$
, we have $u_{\varepsilon _j}\rightarrow u$![]() a.e. in $\Omega \times (0,\,\infty )$
a.e. in $\Omega \times (0,\,\infty )$![]() . Likewise, by lemmas 3.6 and 4.3, it follows that $v_{\varepsilon _j}\rightarrow v$
. Likewise, by lemmas 3.6 and 4.3, it follows that $v_{\varepsilon _j}\rightarrow v$![]() in $L^2([0,T];L^2(\Omega ))$
in $L^2([0,T];L^2(\Omega ))$![]() and a.e. in $\Omega \times (0,\,\infty )$
and a.e. in $\Omega \times (0,\,\infty )$![]() . Because of these convergence properties, one may readily prove that $(u,\,v)$
. Because of these convergence properties, one may readily prove that $(u,\,v)$![]() is a global weak solution of (1.1) in the sense of definition 1.1. Consequently, $(u,\,v)$
is a global weak solution of (1.1) in the sense of definition 1.1. Consequently, $(u,\,v)$![]() is a global bounded weak solution of (1.1) by lemma 3.6. The proof is completed. $\square$
is a global bounded weak solution of (1.1) by lemma 3.6. The proof is completed. $\square$![]()
5. Large time behaviour
This section discusses the asymptotic behaviour of the system for large time. Motivated by [Reference Fan and Jin5, Reference Winkler28], the required properties of the solutions are first presented.
Lemma 5.1 Let $m>\max \{1,\,\frac {3N-2}{2N+2}\}$![]() , then there exists $\theta \in (0,\,1)$
, then there exists $\theta \in (0,\,1)$![]() such that for some $C>0$
such that for some $C>0$![]() , we obtain
, we obtain
and for all $\tau >0$![]() , we can find $C(\tau )>0$
, we can find $C(\tau )>0$![]() such that
such that
Proof. In view of lemma 3.6, $-u_\varepsilon v_\varepsilon$![]() is bounded in $L^\infty (\Omega \times (0,\,\infty ))$
is bounded in $L^\infty (\Omega \times (0,\,\infty ))$![]() for all $\varepsilon \in (0,\,1)$
for all $\varepsilon \in (0,\,1)$![]() . Therefore, applying the standard parabolic regularity theory [Reference Ladyzhenskaia, Solonnikov and Ural'tseva8, Chapter III], both estimates (5.1) and (5.2) are obtained.
. Therefore, applying the standard parabolic regularity theory [Reference Ladyzhenskaia, Solonnikov and Ural'tseva8, Chapter III], both estimates (5.1) and (5.2) are obtained.
Lemma 5.2 Let $\Omega \subset \mathbb {R}^N(N=3,\,4,\,5)$![]() be a bounded domain with smooth boundary. Assume that $m>\max \{1,\,\frac {3N-2}{2N+2}\}$
be a bounded domain with smooth boundary. Assume that $m>\max \{1,\,\frac {3N-2}{2N+2}\}$![]() and $p>\max \{1,\,m-1\}$
and $p>\max \{1,\,m-1\}$![]() , then there exists $C>0$
, then there exists $C>0$![]() such that
such that
Proof. By virtue of lemma 3.6, there exists a positive constant $c_1>0$![]() such that $0< u_\varepsilon < c_1$
such that $0< u_\varepsilon < c_1$![]() in $\Omega \times (0,\,\infty )$
in $\Omega \times (0,\,\infty )$![]() for all $\varepsilon \in (0,\,1)$
for all $\varepsilon \in (0,\,1)$![]() . From lemma 3.1 and $p>\max \{1,\,m-1\}$
. From lemma 3.1 and $p>\max \{1,\,m-1\}$![]() , it follows that
, it follows that
Therefore, an integration of (3.1) shows that

for all $\varepsilon \in (0,\,1)$![]() , which together with (4.2) indicate that (5.3) is valid.
, which together with (4.2) indicate that (5.3) is valid.
Lemma 5.3 Let $\Omega \subset \mathbb {R}^N(N=3,\,4,\,5)$![]() be a bounded domain with smooth boundary. Assume that $m>\max \{1,\,\frac {3N-2}{2N+2}\}$
be a bounded domain with smooth boundary. Assume that $m>\max \{1,\,\frac {3N-2}{2N+2}\}$![]() , then there exist $C>0$
, then there exist $C>0$![]() such that
such that
Particularly,
Proof. Multiplying the first equation of (2.1) by $\psi$![]() with $\psi \in C^\infty _0(\Omega )$
with $\psi \in C^\infty _0(\Omega )$![]() , and integrating over $\Omega$
, and integrating over $\Omega$![]() , one has
, one has

According to lemma 3.6, there exist two positive constants $c_1,\,c_2>0$![]() such that $0< u_\varepsilon < c_1$
such that $0< u_\varepsilon < c_1$![]() and $|\nabla v_\varepsilon |\leq c_2$
and $|\nabla v_\varepsilon |\leq c_2$![]() in $\Omega \times (0,\,\infty )$
in $\Omega \times (0,\,\infty )$![]() for all $\varepsilon \in (0,\,1)$
for all $\varepsilon \in (0,\,1)$![]() . Then (5.6) implies
. Then (5.6) implies

and

With the above information on solutions, the convergence of $u$![]() is shown as follows.
is shown as follows.
Lemma 5.4 Let $m>\max \{1,\,\frac {3N-2}{2N+2}\}~(\mbox {where}~ N=3,\,4,\,5)$![]() and $(u,\,v)$
and $(u,\,v)$![]() as given by theorem 1.2, we can see that
as given by theorem 1.2, we can see that
Proof. Similar to lemma 5.1 of [Reference Winkler28] and lemma 3.16 of [Reference Fan and Jin5], the proof of this lemma can be completed. In fact, assuming the lemma is false, then there exists a sequence $(t_j)_{j\subset \mathbb {N}}\subset (0,\,\infty )$![]() such that $t_j\rightarrow \infty$
such that $t_j\rightarrow \infty$![]() as $j\rightarrow \infty$
as $j\rightarrow \infty$![]() , and such that for some $\tilde {\psi }\in L^1(\Omega )$
, and such that for some $\tilde {\psi }\in L^1(\Omega )$![]() one has
one has
with $c_1>0$![]() . Note that theorem 1.2 implies that there exists a positive constant $c_2>0$
. Note that theorem 1.2 implies that there exists a positive constant $c_2>0$![]() such that $0< u< c_2$
such that $0< u< c_2$![]() for a.e. $(x,\,t)\in \Omega \times (0,\,\infty )$
for a.e. $(x,\,t)\in \Omega \times (0,\,\infty )$![]() . And then using the density of $C_0^\infty (\Omega )$
. And then using the density of $C_0^\infty (\Omega )$![]() in $L^1(\Omega )$
in $L^1(\Omega )$![]() in choosing $\psi \in C_0^\infty (\Omega )$
in choosing $\psi \in C_0^\infty (\Omega )$![]() such that $\|\psi -\tilde {\psi }\|_{L^1(\Omega )}\leq \frac {c_1}{4c_2}$
such that $\|\psi -\tilde {\psi }\|_{L^1(\Omega )}\leq \frac {c_1}{4c_2}$![]() , (5.8) yields
, (5.8) yields

Due to $L^\infty (\Omega )\hookrightarrow (W_0^{2,2}(\Omega ))^\ast$![]() is compact, using Arzelà–Ascoli theorem, the equicontinuity properties (5.5) and the boundedness of $(u_\varepsilon )_{\varepsilon \in (0,1)}$
is compact, using Arzelà–Ascoli theorem, the equicontinuity properties (5.5) and the boundedness of $(u_\varepsilon )_{\varepsilon \in (0,1)}$![]() in $C^0([0,\infty );L^\infty (\Omega ))$
in $C^0([0,\infty );L^\infty (\Omega ))$![]() ensure that $u_\varepsilon \rightarrow u$
ensure that $u_\varepsilon \rightarrow u$![]() in $C_{loc}^0([0,\,\infty );(W_0^{2,2}(\Omega ))^\ast )$
in $C_{loc}^0([0,\,\infty );(W_0^{2,2}(\Omega ))^\ast )$![]() holds. According to (5.5), there exists a positive constant $c_3>0$
holds. According to (5.5), there exists a positive constant $c_3>0$![]() such that
such that
Then, taking limits to get
If let $\tau \in (0,\,1)$![]() such that $\tau \leq \frac {c_1}{4c_3\|\psi \|_{W_0^{2,2}(\Omega )}}$
such that $\tau \leq \frac {c_1}{4c_3\|\psi \|_{W_0^{2,2}(\Omega )}}$![]() , then for all $j\subset \mathbb {N}$
, then for all $j\subset \mathbb {N}$![]() and each $t\in (t_j,\,t_j+\tau )$
and each $t\in (t_j,\,t_j+\tau )$![]() one has
one has

which together with (5.9) implies that
Next, we will prove (5.10) contradicts lemma 5.2. Taking the Poincaré constant $c_4>0$![]() such that
such that
Fix any $p>1$![]() such that $p\geq \max \{1,\,m-1,\,3-m\}$
such that $p\geq \max \{1,\,m-1,\,3-m\}$![]() , and using lemma 5.2, it is obvious that
, and using lemma 5.2, it is obvious that

for all $\varepsilon \in (0,\,1)$![]() , where $a_\varepsilon (t):=(\frac {1}{|\Omega |}\int _\Omega u_\varepsilon ^{\frac {p+m-1}{2}})^{\frac {2}{p+m-1}}$
, where $a_\varepsilon (t):=(\frac {1}{|\Omega |}\int _\Omega u_\varepsilon ^{\frac {p+m-1}{2}})^{\frac {2}{p+m-1}}$![]() and $c_5>0$
and $c_5>0$![]() . Using the convergence property $u_\varepsilon \rightarrow u$
. Using the convergence property $u_\varepsilon \rightarrow u$![]() a.e. in $\Omega \times (0,\,\infty )$
a.e. in $\Omega \times (0,\,\infty )$![]() as $\varepsilon \rightarrow 0$
as $\varepsilon \rightarrow 0$![]() , the boundedness of $(u_\varepsilon )_{\varepsilon \in (0,1)}$
, the boundedness of $(u_\varepsilon )_{\varepsilon \in (0,1)}$![]() in $L^\infty (\Omega \times (0,\,\infty ))$
in $L^\infty (\Omega \times (0,\,\infty ))$![]() and the dominated convergence theorem, one obtains
and the dominated convergence theorem, one obtains
where $a(t):=(\frac {1}{|\Omega |}\int _\Omega u^{\frac {p+m-1}{2}})^{\frac {2}{p+m-1}}$![]() . Again using $u_\varepsilon \rightarrow u$
. Again using $u_\varepsilon \rightarrow u$![]() a.e. in $\Omega \times (0,\,\infty )$
a.e. in $\Omega \times (0,\,\infty )$![]() as $\varepsilon \rightarrow 0$
as $\varepsilon \rightarrow 0$![]() and Fatou's lemma, (5.11) and (5.12) imply that
and Fatou's lemma, (5.11) and (5.12) imply that
Review the following inequality: If $\mu >1$![]() , then $\frac {\xi ^\mu -\eta ^\mu }{\xi -\eta }\geq \eta ^{\mu -1}$
, then $\frac {\xi ^\mu -\eta ^\mu }{\xi -\eta }\geq \eta ^{\mu -1}$![]() for all $\xi,\,\eta \leq 0$
for all $\xi,\,\eta \leq 0$![]() with $\xi \neq \eta$
with $\xi \neq \eta$![]() . And since by the Hölder inequality, and the $L^1(\Omega )$
. And since by the Hölder inequality, and the $L^1(\Omega )$![]() conservation of $u$
conservation of $u$![]() means that
means that

Thus, on the left-hand side of (5.13) indicates

and
Now, we introduce
and
Therefore, (5.14) implies that

which means
By the definition of $a(t)$![]() and the boundedness of $u(x,\,t)$
and the boundedness of $u(x,\,t)$![]() , $(a_j)_{j\subset \mathbb {N}}$
, $(a_j)_{j\subset \mathbb {N}}$![]() is bounded in $L^2((0,\,\tau ))$
is bounded in $L^2((0,\,\tau ))$![]() . Then, for some nonnegative $a_\infty \in L^2((0,\,\tau ))$
. Then, for some nonnegative $a_\infty \in L^2((0,\,\tau ))$![]() satisfying
satisfying
By utilizing the $L^1(\Omega )$![]() conservation of $u$
conservation of $u$![]() , we have
, we have

which combined with (5.15), one has
On the other hand, (5.10) and (5.17) show that

This is a contradiction and then the proof of this lemma is completed.
Finally, the convergence of $v$![]() can be obtained.
can be obtained.
Lemma 5.5 Let $m>\max \{1,\frac {3N-2}{2N+2}\}~(\mbox {where}~ N=3,\,4,\,5)$![]() and $(u,\,v)$
and $(u,\,v)$![]() as given by theorem 1.2, we obtain
as given by theorem 1.2, we obtain
Proof. Similar to lemma 5.2 of [Reference Winkler28] and lemma 3.17 of [Reference Fan and Jin5], the proof of this lemma can be completed. Similarly, assume the lemma is false, then there exist two sequences $(x_j)_{j\subset \mathbb {N}}\subset \Omega$![]() and $(t_j)_{j\subset \mathbb {N}}\subset (0,\,\infty )$
and $(t_j)_{j\subset \mathbb {N}}\subset (0,\,\infty )$![]() such that $t_j\rightarrow \infty$
such that $t_j\rightarrow \infty$![]() as $j\rightarrow \infty$
as $j\rightarrow \infty$![]() satisfies
satisfies
with $c_1>0$![]() , where passing to subsequences we may assume that there exists $x_0\in \bar {\Omega }$
, where passing to subsequences we may assume that there exists $x_0\in \bar {\Omega }$![]() such that $x_j\rightarrow x_0$
such that $x_j\rightarrow x_0$![]() as $j\rightarrow \infty$
as $j\rightarrow \infty$![]() . Due to lemma 5.1, $v$
. Due to lemma 5.1, $v$![]() is uniformly continuous in $\cup _{j\in \mathbb {N}}(\bar {\Omega }\times [t_j,\,t_j+1])$
is uniformly continuous in $\cup _{j\in \mathbb {N}}(\bar {\Omega }\times [t_j,\,t_j+1])$![]() , which entails that there exist $\delta >0$
, which entails that there exist $\delta >0$![]() , $\tau \in (0,\,1)$
, $\tau \in (0,\,1)$![]() and $B:=B_\delta (x_0)\cap \Omega$
and $B:=B_\delta (x_0)\cap \Omega$![]() such that
such that
Now, let $u_j(x,\,s):=u(x,\,t_j+s)\mbox { and } v_j(x,\,s):=v(x,\,t_j+s)~\mbox {for } x\in \Omega,\, s\in (0,\,\tau ) \mbox{ and }j\in \mathbb {N}$![]() , then from (4.1), we noticed that
, then from (4.1), we noticed that

On the other hand, let $\psi (x):=\chi _B(x)$![]() for $x\in \Omega$
for $x\in \Omega$![]() , then in light of lemma 5.4, it follows that
, then in light of lemma 5.4, it follows that

and that hence
In summary, the combination of (5.20) and (5.21) indicates that

which contradicts (5.21), then the proof of this lemma is completed.
The proof of theorem 1.6. The claimed convergence properties are precisely asserted by lemmas 5.4 and 5.5. $\square$![]()
Acknowledgements
The second author is partially supported by the NSFC (Grant No. 12271064), the Chongqing Talent Support program (Grant No. cstc2022ycjh-bgzxm0169), Natural Science Foundation of Chongqing (Grant No. CSTB2023NSCQ-LZX0089), the Fundamental Research Funds for the Central Universities (Grant Nos. 2022CDJJCLK002, 2020CDJQY-Z001, 2019CDJCYJ001), Chongqing Key Laboratory of Analytic Mathematics and Applications, and Key Laboratory of Nonlinear Analysis and its Applications (Chongqing University), Ministry of Education. The third author is partially supported by the Interdisciplinary Research Program of Shihezi University (Grant No. JCYJ202316), Corps Science and Technology Plan Project (Grant No. 2023CB008-13), and Launch Project of High-Level Talent Scientific Research of Shihezi University (Grant No. 2022ZK008).