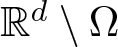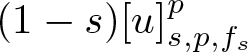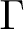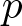FirstView articles
Contents
Research Article
Quantitative bounds in a popular polynomial Szemerédi theorem
- Part of:
-
- Published online by Cambridge University Press:
- 05 December 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform bounds for polynomial Carleson operators and oscillatory integrals of Radon type
- Part of:
-
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-23
-
- Article
- Export citation
Genus g Cantor sets and germane Julia sets
- Part of:
-
- Published online by Cambridge University Press:
- 02 December 2025, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Γ-limit of weighted fractional energies
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the string topology of symmetric spaces of higher rank
- Part of:
-
- Published online by Cambridge University Press:
- 30 November 2025, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Liouville-type theorems for the quasilinear elliptic equation and inequality with logarithmic nonlinearity
- Part of:
-
- Published online by Cambridge University Press:
- 26 November 2025, pp. 1-15
-
- Article
- Export citation
Wreath products and the non-coprime k(GV) problem
- Part of:
-
- Published online by Cambridge University Press:
- 26 November 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniqueness of solution for logarithm Choquard equation
- Part of:
-
- Published online by Cambridge University Press:
- 25 November 2025, pp. 1-29
-
- Article
- Export citation
Quantitative stability in fractional Hardy–Sobolev inequalities: the role of Euler–Lagrange equations
- Part of:
-
- Published online by Cambridge University Press:
- 24 November 2025, pp. 1-39
-
- Article
- Export citation
Large Salem sets avoiding nonlinear configurations
- Part of:
-
- Published online by Cambridge University Press:
- 21 November 2025, pp. 1-46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The boundary value problem for triholomorphic maps
- Part of:
-
- Published online by Cambridge University Press:
- 20 November 2025, pp. 1-29
-
- Article
- Export citation
On approximation of convex functionals with a convexity constraint and general Lagrangians
- Part of:
-
- Published online by Cambridge University Press:
- 19 November 2025, pp. 1-17
-
- Article
- Export citation
Thin Gordian unlinks
- Part of:
-
- Published online by Cambridge University Press:
- 19 November 2025, pp. 1-15
-
- Article
- Export citation
The Born approximation for the fixed energy Calderón problem
-
- Published online by Cambridge University Press:
- 17 November 2025, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reflexive homology and involutive Hochschild homology as equivariant Loday constructions
- Part of:
-
- Published online by Cambridge University Press:
- 17 November 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak porosity on metric measure spaces
- Part of:
-
- Published online by Cambridge University Press:
- 17 November 2025, pp. 1-48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ideal structure of uniform Roe algebras: beyond Property A
- Part of:
-
- Published online by Cambridge University Press:
- 14 November 2025, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the dimension theory of Okamoto’s function
- Part of:
-
- Published online by Cambridge University Press:
- 14 November 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlocal carrier’s double phase problem
- Part of:
-
- Published online by Cambridge University Press:
- 13 November 2025, pp. 1-24
-
- Article
- Export citation
Normalized solutions for p-Laplacian equation with general nonlinearities on bounded domain
- Part of:
-
- Published online by Cambridge University Press:
- 13 November 2025, pp. 1-31
-
- Article
- Export citation