Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T20:51:49.140Z Has data issue: false hasContentIssue false
  • English
  • Français

A branch and bound algorithm for the two-machine flowshopproblem with unit-time operations and time delays

Published online by Cambridge University Press:  07 March 2014

Aziz Moukrim ,
Djamal Rebaine  and
Mehdi Serairi
Aziz Moukrim
Affiliation:
Universitéde Technologie de Compiègne, Heudiasyc, CNRS UMR 7253 Rue Roger Couttolenc CS 60319 60203 Compiègne Cedex, France.. aziz.moukrim@hds.utc.fr; mehdi.serairi@hds.utc.fr
Djamal Rebaine
Affiliation:
Département d’Informatique et Mathématique, Université du Québec à Chicoutimi, Saguenay, Canada G7H 2B1.; DjamalRebaine@uqac.ca
Mehdi Serairi
Affiliation:
Universitéde Technologie de Compiègne, Heudiasyc, CNRS UMR 7253 Rue Roger Couttolenc CS 60319 60203 Compiègne Cedex, France.. aziz.moukrim@hds.utc.fr; mehdi.serairi@hds.utc.fr
Get access

Abstract

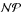In this paper we consider the problem of scheduling, on a two-machine flowshop, a set ofunit-time operations subject to time delays with respect to the makespan. This problem isknown to be \hbox{${\cal NP}$}𝒩𝒫-hard in the strong sense. We propose an algorithm basedon a branch and bound enumeration scheme. This algorithm includes the implementation ofnew lower and upper bound procedures, and dominance rules. A computer simulation tomeasure the performance of the algorithm is provided for a wide range of testproblems.

Keywords

Branch and bounddominance ruleflowshoplower and upper boundstime delays
Type
Research Article
Information
RAIRO - Operations Research , Volume 48 , Issue 2: Isco 2012, guest editors Nelson Maculan, A. Ridha Mahjoub, Eduardo Uchoa , April 2014 , pp. 235 - 254
Copyright
© EDP Sciences, ROADEF, SMAI, 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

E. Balas and P. Toth, Branch and bound methods, chapter 10, in The traveling salesman problems: a guided tour of Combinatorial Opt., edited by E.L. Lawler. John Wiley (1985).
T.H. Cormen, C.E. Leiserson and R.L. Rivest, Introduction to Algorithms. McGraw-Hill (1990).
S. French, Sequencing and scheduling: an introduction to the mathematics of the job-shop. Series: Math. and its Appl. Ellis Horwood Ltd. (1982).
Gonzalez, T. and Sahni, S., Flow shop and job shop schedules: complexity and approximations. Oper. Res. 26 (1978) 36–52. Google Scholar
Johnson, S., Optimal two- and three-stage production with set-up times included. Nav. Res. Log. Quart. 1 (1954) 61–68. Google Scholar
Munier-Kordon, A. and Rebaine, D., Polynomial time algorithms for the UET permutation flowshop problem with time delays. Comput. Oper. Res. 35 (2008) 525–537. Google Scholar
Rayward-Smith, V.J. and Rebaine, D., Analysis of heuristics for the UET two-machine flow shop. Comput. Oper. Res. 35 (2008) 3298-3310. Google Scholar
Rebaine, D., Permutation shop vs. non permutation flow shop with delays. J. Comput. Industrial Engrg. 48 (2005) 357–362. Google Scholar
Yu, W., Hoogeveen, H. and Lenstra, J.K., Minimizing makespan in a two-machine flow with delays and unit-time operations is NP-hard. J. Schedul. 7 (2004) 333–348. Google Scholar
W. Yu, The two-machine flow shop problem and the one-machine total tardiness problem. Ph.D. thesis, Eindhoven University of Technology, The Netherlands (1996).