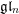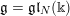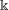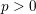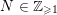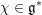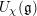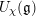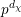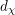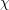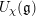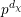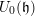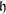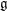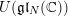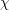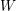1 Introduction
Let
![]() $\Bbbk$
be an algebraically closed field of characteristic
$\Bbbk$
be an algebraically closed field of characteristic
![]() $p>0$
, and
$p>0$
, and
![]() $N\in \mathbb{Z}_{{\geqslant}1}$
. Let
$N\in \mathbb{Z}_{{\geqslant}1}$
. Let
![]() $G:=\text{GL}_{N}(\Bbbk )$
and
$G:=\text{GL}_{N}(\Bbbk )$
and
![]() $\mathfrak{g}:=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )=\operatorname{Lie}G$
. For
$\mathfrak{g}:=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )=\operatorname{Lie}G$
. For
![]() $x\in \mathfrak{g}$
, we write
$x\in \mathfrak{g}$
, we write
![]() $x^{[p]}$
for the
$x^{[p]}$
for the
![]() $p$
th power of
$p$
th power of
![]() $x$
as a matrix, and recall that
$x$
as a matrix, and recall that
![]() $x\mapsto x^{[p]}$
is the
$x\mapsto x^{[p]}$
is the
![]() $p$
-power map for the restricted Lie algebra structure on
$p$
-power map for the restricted Lie algebra structure on
![]() $\mathfrak{g}$
. Also we write
$\mathfrak{g}$
. Also we write
![]() $x^{p}$
for the
$x^{p}$
for the
![]() $p$
th power of
$p$
th power of
![]() $x$
in the universal enveloping algebra
$x$
in the universal enveloping algebra
![]() $U(\mathfrak{g})$
of
$U(\mathfrak{g})$
of
![]() $\mathfrak{g}$
. Then the elements
$\mathfrak{g}$
. Then the elements
![]() $x^{p}-x^{[p]}$
are central elements in
$x^{p}-x^{[p]}$
are central elements in
![]() $U(\mathfrak{g})$
, and the
$U(\mathfrak{g})$
, and the
![]() $p$
-centre
$p$
-centre
![]() $Z_{p}(\mathfrak{g})$
of
$Z_{p}(\mathfrak{g})$
of
![]() $U(\mathfrak{g})$
is defined to be the subalgebra generated by
$U(\mathfrak{g})$
is defined to be the subalgebra generated by
![]() $\{x^{p}-x^{[p]}\mid x\in \mathfrak{g}\}$
. It is well known that
$\{x^{p}-x^{[p]}\mid x\in \mathfrak{g}\}$
. It is well known that
![]() $Z_{p}(\mathfrak{g})$
is
$Z_{p}(\mathfrak{g})$
is
![]() $G$
-isomorphic to the Frobenius twist
$G$
-isomorphic to the Frobenius twist
![]() $S(\mathfrak{g})^{(1)}$
of the symmetric algebra on
$S(\mathfrak{g})^{(1)}$
of the symmetric algebra on
![]() $\mathfrak{g}$
and that
$\mathfrak{g}$
and that
![]() $U(\mathfrak{g})$
is free of rank
$U(\mathfrak{g})$
is free of rank
![]() $p^{\dim \mathfrak{g}}$
over
$p^{\dim \mathfrak{g}}$
over
![]() $Z_{p}(\mathfrak{g})$
.
$Z_{p}(\mathfrak{g})$
.
For an irreducible
![]() $U(\mathfrak{g})$
-module
$U(\mathfrak{g})$
-module
![]() $M$
, the central elements
$M$
, the central elements
![]() $x^{p}-x^{[p]}$
act on
$x^{p}-x^{[p]}$
act on
![]() $M$
as
$M$
as
![]() $\unicode[STIX]{x1D712}(x)^{p}$
for some
$\unicode[STIX]{x1D712}(x)^{p}$
for some
![]() $\unicode[STIX]{x1D712}\in \mathfrak{g}^{\ast }$
, thanks to Quillen’s lemma. We define the ideal
$\unicode[STIX]{x1D712}\in \mathfrak{g}^{\ast }$
, thanks to Quillen’s lemma. We define the ideal
![]() $J_{\unicode[STIX]{x1D712}}$
of
$J_{\unicode[STIX]{x1D712}}$
of
![]() $U(\mathfrak{g})$
to be generated by
$U(\mathfrak{g})$
to be generated by
![]() $\{x^{p}-x^{[p]}-\unicode[STIX]{x1D712}(x)^{p}\mid x\in \mathfrak{g}\}$
, and the reduced enveloping algebra associated to
$\{x^{p}-x^{[p]}-\unicode[STIX]{x1D712}(x)^{p}\mid x\in \mathfrak{g}\}$
, and the reduced enveloping algebra associated to
![]() $\unicode[STIX]{x1D712}$
to be
$\unicode[STIX]{x1D712}$
to be
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g}):=U(\mathfrak{g})/J_{\unicode[STIX]{x1D712}}$
. Then we have seen that any irreducible
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g}):=U(\mathfrak{g})/J_{\unicode[STIX]{x1D712}}$
. Then we have seen that any irreducible
![]() $U(\mathfrak{g})$
-module factors through
$U(\mathfrak{g})$
-module factors through
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
for some
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
for some
![]() $\unicode[STIX]{x1D712}\in \mathfrak{g}^{\ast }$
, and that
$\unicode[STIX]{x1D712}\in \mathfrak{g}^{\ast }$
, and that
![]() $\dim U_{\unicode[STIX]{x1D712}}(\mathfrak{g})=p^{\dim \mathfrak{g}}$
.
$\dim U_{\unicode[STIX]{x1D712}}(\mathfrak{g})=p^{\dim \mathfrak{g}}$
.
Reduced enveloping algebras
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
, are defined more generally for the Lie algebra
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
, are defined more generally for the Lie algebra
![]() $\mathfrak{g}$
of a reductive algebraic group
$\mathfrak{g}$
of a reductive algebraic group
![]() $G$
over
$G$
over
![]() $\Bbbk$
, and their representation theory attracted a great deal of research interest from leading mathematicians including Friedlander and Parshall, Humphreys, Jantzen, Kac and Premet in the late twentieth century; we refer to the survey articles [Reference Jantzen and BroerJan98] and [Reference HumphreysHum98] for an overview. There has been continued interest and progress in the representation theory of reduced enveloping algebra, a notable advance being the proof by Bezrukavnikov and Mirkovic in [Reference Bezrukavnikov and MirkovicBM13] of a conjecture of Lusztig regarding irreducible modules, for
$\Bbbk$
, and their representation theory attracted a great deal of research interest from leading mathematicians including Friedlander and Parshall, Humphreys, Jantzen, Kac and Premet in the late twentieth century; we refer to the survey articles [Reference Jantzen and BroerJan98] and [Reference HumphreysHum98] for an overview. There has been continued interest and progress in the representation theory of reduced enveloping algebra, a notable advance being the proof by Bezrukavnikov and Mirkovic in [Reference Bezrukavnikov and MirkovicBM13] of a conjecture of Lusztig regarding irreducible modules, for
![]() $p$
sufficiently large. An important conjecture of Kac and Weisfeiler stated in [Reference Veisfeiler and KatsVK71] asserts that, for
$p$
sufficiently large. An important conjecture of Kac and Weisfeiler stated in [Reference Veisfeiler and KatsVK71] asserts that, for
![]() $G$
simple, a
$G$
simple, a
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module has dimension divisible by
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module has dimension divisible by
![]() $p^{d_{\unicode[STIX]{x1D712}}}$
, where
$p^{d_{\unicode[STIX]{x1D712}}}$
, where
![]() $d_{\unicode[STIX]{x1D712}}$
is half the dimension of the coadjoint orbit of
$d_{\unicode[STIX]{x1D712}}$
is half the dimension of the coadjoint orbit of
![]() $\unicode[STIX]{x1D712}$
, and was proved by Premet in [Reference PremetPre95, Theorem I] (under some mild restrictions on
$\unicode[STIX]{x1D712}$
, and was proved by Premet in [Reference PremetPre95, Theorem I] (under some mild restrictions on
![]() $G$
and
$G$
and
![]() $p$
). The case
$p$
). The case
![]() $\mathfrak{g}=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$
can be deduced directly if
$\mathfrak{g}=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$
can be deduced directly if
![]() $p\nmid N$
; also the case
$p\nmid N$
; also the case
![]() $p\mid N$
can now be obtained from an alternative proof by Premet in [Reference PremetPre02, §2.6]. We also mention that Friedlander and Parshall previously proved the conjecture for
$p\mid N$
can now be obtained from an alternative proof by Premet in [Reference PremetPre02, §2.6]. We also mention that Friedlander and Parshall previously proved the conjecture for
![]() $\mathfrak{g}=\mathfrak{s}\mathfrak{l}_{N}(\Bbbk )$
and
$\mathfrak{g}=\mathfrak{s}\mathfrak{l}_{N}(\Bbbk )$
and
![]() $p\nmid N$
in [Reference Friedlander and ParshallFP91, Theorem 5.1]. Consequently,
$p\nmid N$
in [Reference Friedlander and ParshallFP91, Theorem 5.1]. Consequently,
![]() $p^{d_{\unicode[STIX]{x1D712}}}$
is the smallest dimension of a
$p^{d_{\unicode[STIX]{x1D712}}}$
is the smallest dimension of a
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module, so we refer to
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module, so we refer to
![]() $p^{d_{\unicode[STIX]{x1D712}}}$
-dimensional modules for
$p^{d_{\unicode[STIX]{x1D712}}}$
-dimensional modules for
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
as minimal-dimensional modules. We note that there is a relatively straightforward way, via parabolic induction, to construct minimal-dimensional
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
as minimal-dimensional modules. We note that there is a relatively straightforward way, via parabolic induction, to construct minimal-dimensional
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-modules for
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-modules for
![]() $\mathfrak{g}=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$
, as was first observed by Friedlander and Parshall in [Reference Friedlander and ParshallFP91, Corollary 5.2].
$\mathfrak{g}=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$
, as was first observed by Friedlander and Parshall in [Reference Friedlander and ParshallFP91, Corollary 5.2].
In this paper we classify the minimal-dimensional
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-modules (for
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-modules (for
![]() $\mathfrak{g}=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$
), as stated in Theorem 1.1. As a consequence we show that they all can be obtained by parabolically inducing a one-dimensional
$\mathfrak{g}=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$
), as stated in Theorem 1.1. As a consequence we show that they all can be obtained by parabolically inducing a one-dimensional
![]() $U_{0}(\mathfrak{h})$
-module for a certain Levi subalgebra
$U_{0}(\mathfrak{h})$
-module for a certain Levi subalgebra
![]() $\mathfrak{h}$
of
$\mathfrak{h}$
of
![]() $\mathfrak{g}$
, as stated in Corollary 1.2. Both of these results are formulated for
$\mathfrak{g}$
, as stated in Corollary 1.2. Both of these results are formulated for
![]() $\unicode[STIX]{x1D712}\in \mathfrak{g}^{\ast }$
nilpotent, but as explained in § 2.1 there is a reduction to this case. We note that Corollary 1.2 can be viewed as a modular analogue of Mœglin’s theorem, from [Reference MœglinMœ87] on completely prime ideals of
$\unicode[STIX]{x1D712}\in \mathfrak{g}^{\ast }$
nilpotent, but as explained in § 2.1 there is a reduction to this case. We note that Corollary 1.2 can be viewed as a modular analogue of Mœglin’s theorem, from [Reference MœglinMœ87] on completely prime ideals of
![]() $U(\mathfrak{g}\mathfrak{l}_{N}(\mathbb{C}))$
. Further, we remark some of our methods adapt those of Brundan in [Reference BrundanBru11], in which he gives an alternative proof of Mœglin’s theorem.
$U(\mathfrak{g}\mathfrak{l}_{N}(\mathbb{C}))$
. Further, we remark some of our methods adapt those of Brundan in [Reference BrundanBru11], in which he gives an alternative proof of Mœglin’s theorem.
We require some notation to state our main results. This is all set out in detail in § 2, and here we only point out the necessary parts for the statements of Theorem 1.1 and Corollary 1.2.
The trace form on
![]() $\mathfrak{g}:=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$
is denoted by
$\mathfrak{g}:=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$
is denoted by
![]() $(\cdot \,,\cdot )$
and allows us to identify
$(\cdot \,,\cdot )$
and allows us to identify
![]() $\mathfrak{g}\cong \mathfrak{g}^{\ast }$
. Consequently, we can talk about Jordan decomposition of elements of
$\mathfrak{g}\cong \mathfrak{g}^{\ast }$
. Consequently, we can talk about Jordan decomposition of elements of
![]() $\mathfrak{g}^{\ast }$
and nilpotent elements of
$\mathfrak{g}^{\ast }$
and nilpotent elements of
![]() $\mathfrak{g}^{\ast }$
. We let
$\mathfrak{g}^{\ast }$
. We let
![]() $\mathfrak{b}$
be the Borel subalgebra of upper triangular matrices and
$\mathfrak{b}$
be the Borel subalgebra of upper triangular matrices and
![]() $\mathfrak{t}$
the maximal toral subalgebra of diagonal matrices.
$\mathfrak{t}$
the maximal toral subalgebra of diagonal matrices.
Let
![]() $\boldsymbol{p}=(p_{1}\leqslant p_{2}\leqslant \cdots \leqslant p_{n})$
be a partition of
$\boldsymbol{p}=(p_{1}\leqslant p_{2}\leqslant \cdots \leqslant p_{n})$
be a partition of
![]() $N$
, and let
$N$
, and let
![]() $\unicode[STIX]{x1D70B}$
be a pyramid associated to
$\unicode[STIX]{x1D70B}$
be a pyramid associated to
![]() $\boldsymbol{p}$
. This means that
$\boldsymbol{p}$
. This means that
![]() $\unicode[STIX]{x1D70B}$
is a diagram with
$\unicode[STIX]{x1D70B}$
is a diagram with
![]() $N$
boxes organized in rows, with row lengths given by
$N$
boxes organized in rows, with row lengths given by
![]() $\boldsymbol{p}$
as defined in § 2.2. Further, the boxes in
$\boldsymbol{p}$
as defined in § 2.2. Further, the boxes in
![]() $\unicode[STIX]{x1D70B}$
are labelled from 1 to
$\unicode[STIX]{x1D70B}$
are labelled from 1 to
![]() $N$
along rows starting from the top row. There is some choice of the pyramid
$N$
along rows starting from the top row. There is some choice of the pyramid
![]() $\unicode[STIX]{x1D70B}$
, and much of the notation below is dependent on this choice; as the results are all valid for any choice of
$\unicode[STIX]{x1D70B}$
, and much of the notation below is dependent on this choice; as the results are all valid for any choice of
![]() $\unicode[STIX]{x1D70B}$
, we choose to work in this generality, and just note that the left justified pyramid is one choice that can be made.
$\unicode[STIX]{x1D70B}$
, we choose to work in this generality, and just note that the left justified pyramid is one choice that can be made.
From
![]() $\unicode[STIX]{x1D70B}$
we define the nilpotent element
$\unicode[STIX]{x1D70B}$
we define the nilpotent element
![]() $e\in \mathfrak{g}$
as in (3), and let
$e\in \mathfrak{g}$
as in (3), and let
![]() $\unicode[STIX]{x1D712}:=(e,\cdot )\in \mathfrak{g}^{\ast }$
. Then
$\unicode[STIX]{x1D712}:=(e,\cdot )\in \mathfrak{g}^{\ast }$
. Then
![]() $\unicode[STIX]{x1D712}\in \mathfrak{g}^{\ast }$
is nilpotent, and as we range over all partitions
$\unicode[STIX]{x1D712}\in \mathfrak{g}^{\ast }$
is nilpotent, and as we range over all partitions
![]() $\boldsymbol{p}$
of
$\boldsymbol{p}$
of
![]() $N$
, we get representatives of all coadjoint
$N$
, we get representatives of all coadjoint
![]() $G$
-orbits of nilpotent elements of
$G$
-orbits of nilpotent elements of
![]() $\mathfrak{g}^{\ast }$
. As explained in § 2.2, we have that
$\mathfrak{g}^{\ast }$
. As explained in § 2.2, we have that
![]() $\unicode[STIX]{x1D712}$
is in standard Levi form with respect to
$\unicode[STIX]{x1D712}$
is in standard Levi form with respect to
![]() $\mathfrak{b}$
. A good grading of
$\mathfrak{b}$
. A good grading of
![]() $\mathfrak{g}$
for
$\mathfrak{g}$
for
![]() $e$
is defined in (4), and from this we can define the parabolic subalgebra
$e$
is defined in (4), and from this we can define the parabolic subalgebra
![]() $\mathfrak{p}$
with Levi factor
$\mathfrak{p}$
with Levi factor
![]() $\mathfrak{h}$
as in (5). We note that
$\mathfrak{h}$
as in (5). We note that
![]() $\mathfrak{t}$
is contained in
$\mathfrak{t}$
is contained in
![]() $\mathfrak{p}$
and
$\mathfrak{p}$
and
![]() $\mathfrak{h}$
, but that
$\mathfrak{h}$
, but that
![]() $\mathfrak{b}\nsubseteq \mathfrak{p}$
.
$\mathfrak{b}\nsubseteq \mathfrak{p}$
.
Let
![]() $\mathbb{F}_{p}\subseteq \Bbbk$
denote the field of
$\mathbb{F}_{p}\subseteq \Bbbk$
denote the field of
![]() $p$
elements. We define
$p$
elements. We define
![]() $\operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
to be fillings of the boxes of
$\operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
to be fillings of the boxes of
![]() $\unicode[STIX]{x1D70B}$
with elements from
$\unicode[STIX]{x1D70B}$
with elements from
![]() $\Bbbk$
; and we define
$\Bbbk$
; and we define
![]() $\operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})\subseteq \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
to be the filling with elements from
$\operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})\subseteq \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
to be the filling with elements from
![]() $\mathbb{F}_{p}$
. We refer to elements of
$\mathbb{F}_{p}$
. We refer to elements of
![]() $\operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
as
$\operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
as
![]() $\unicode[STIX]{x1D70B}$
-tableaux. Given
$\unicode[STIX]{x1D70B}$
-tableaux. Given
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
, we denote the entry in the box labelled
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
, we denote the entry in the box labelled
![]() $i$
in
$i$
in
![]() $\unicode[STIX]{x1D70B}$
by
$\unicode[STIX]{x1D70B}$
by
![]() $a_{i}$
. Let
$a_{i}$
. Let
![]() $\unicode[STIX]{x1D700}_{1},\ldots ,\unicode[STIX]{x1D700}_{N}$
be the standard basis of
$\unicode[STIX]{x1D700}_{1},\ldots ,\unicode[STIX]{x1D700}_{N}$
be the standard basis of
![]() $\mathfrak{t}^{\ast }$
and define
$\mathfrak{t}^{\ast }$
and define
![]() $\unicode[STIX]{x1D706}_{A}=\sum _{i=1}^{N}a_{i}\unicode[STIX]{x1D700}_{i}\in \mathfrak{t}^{\ast }$
for
$\unicode[STIX]{x1D706}_{A}=\sum _{i=1}^{N}a_{i}\unicode[STIX]{x1D700}_{i}\in \mathfrak{t}^{\ast }$
for
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
. We say that
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
. We say that
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
is column connected if
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
is column connected if
![]() $a_{i}=a_{j}+1$
whenever box
$a_{i}=a_{j}+1$
whenever box
![]() $i$
is directly above box
$i$
is directly above box
![]() $j$
in
$j$
in
![]() $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.
The weight
![]() $\unicode[STIX]{x1D70C}\in \mathfrak{t}^{\ast }$
is defined in (6): it is a convenient renormalization of the half sum of positive roots corresponding to
$\unicode[STIX]{x1D70C}\in \mathfrak{t}^{\ast }$
is defined in (6): it is a convenient renormalization of the half sum of positive roots corresponding to
![]() $\mathfrak{b}$
. Also we define
$\mathfrak{b}$
. Also we define
![]() $\overline{\unicode[STIX]{x1D70C}}\in \mathfrak{t}^{\ast }$
in (7), which is the half sum of positive roots for a Borel subalgebra of
$\overline{\unicode[STIX]{x1D70C}}\in \mathfrak{t}^{\ast }$
in (7), which is the half sum of positive roots for a Borel subalgebra of
![]() $\mathfrak{p}$
, with a convenient renormalization.
$\mathfrak{p}$
, with a convenient renormalization.
We recap some established representation theory of
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
and interpret it in our notation; see, for example, [Reference Jantzen and BroerJan98, §10], and more detail is given in § 2.5. Since
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
and interpret it in our notation; see, for example, [Reference Jantzen and BroerJan98, §10], and more detail is given in § 2.5. Since
![]() $e\in \mathfrak{b}$
, we have that
$e\in \mathfrak{b}$
, we have that
![]() $\unicode[STIX]{x1D712}(\mathfrak{b})=0$
. Given
$\unicode[STIX]{x1D712}(\mathfrak{b})=0$
. Given
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
we define
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
we define
![]() $\Bbbk _{A}$
to be the one-dimensional
$\Bbbk _{A}$
to be the one-dimensional
![]() $U_{0}(\mathfrak{b})$
-module on which
$U_{0}(\mathfrak{b})$
-module on which
![]() $\mathfrak{t}$
acts via
$\mathfrak{t}$
acts via
![]() $\unicode[STIX]{x1D706}_{A}-\unicode[STIX]{x1D70C}$
, and the baby Verma module to be
$\unicode[STIX]{x1D706}_{A}-\unicode[STIX]{x1D70C}$
, and the baby Verma module to be
![]() $Z_{\unicode[STIX]{x1D712}}(A)=U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{0}(\mathfrak{b})}\Bbbk _{A}$
. It is known that
$Z_{\unicode[STIX]{x1D712}}(A)=U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{0}(\mathfrak{b})}\Bbbk _{A}$
. It is known that
![]() $Z_{\unicode[STIX]{x1D712}}(A)$
has a unique maximal submodule, and we denote the simple head of
$Z_{\unicode[STIX]{x1D712}}(A)$
has a unique maximal submodule, and we denote the simple head of
![]() $Z_{\unicode[STIX]{x1D712}}(A)$
by
$Z_{\unicode[STIX]{x1D712}}(A)$
by
![]() $L_{\unicode[STIX]{x1D712}}(A)$
. Further, any irreducible
$L_{\unicode[STIX]{x1D712}}(A)$
. Further, any irreducible
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module is isomorphic to
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module is isomorphic to
![]() $L_{\unicode[STIX]{x1D712}}(A)$
for some
$L_{\unicode[STIX]{x1D712}}(A)$
for some
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
, and for
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
, and for
![]() $A,A^{\prime }\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
, we have
$A,A^{\prime }\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
, we have
![]() $L_{\unicode[STIX]{x1D712}}(A)\cong L_{\unicode[STIX]{x1D712}}(A^{\prime })$
if and only if
$L_{\unicode[STIX]{x1D712}}(A)\cong L_{\unicode[STIX]{x1D712}}(A^{\prime })$
if and only if
![]() $A$
is row equivalent to
$A$
is row equivalent to
![]() $A^{\prime }$
. We recall that we say that
$A^{\prime }$
. We recall that we say that
![]() $A$
is row equivalent to
$A$
is row equivalent to
![]() $A^{\prime }$
if we can obtain
$A^{\prime }$
if we can obtain
![]() $A^{\prime }$
from
$A^{\prime }$
from
![]() $A$
by reordering the entries in rows.
$A$
by reordering the entries in rows.
We are now in a position to state our main theorem giving a classification of minimal-dimensional
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-modules.
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-modules.
Theorem 1.1. Let
![]() $\mathfrak{g}=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$
, let
$\mathfrak{g}=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$
, let
![]() $\unicode[STIX]{x1D70B}$
be a pyramid corresponding to a partition
$\unicode[STIX]{x1D70B}$
be a pyramid corresponding to a partition
![]() $\boldsymbol{p}$
of
$\boldsymbol{p}$
of
![]() $N$
, and let
$N$
, and let
![]() $\unicode[STIX]{x1D712}$
be the nilpotent element of
$\unicode[STIX]{x1D712}$
be the nilpotent element of
![]() $\mathfrak{g}^{\ast }$
determined by
$\mathfrak{g}^{\ast }$
determined by
![]() $\unicode[STIX]{x1D70B}$
. For
$\unicode[STIX]{x1D70B}$
. For
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
, we have that
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
, we have that
![]() $L_{\unicode[STIX]{x1D712}}(A)$
is a minimal-dimensional
$L_{\unicode[STIX]{x1D712}}(A)$
is a minimal-dimensional
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module if and only if
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module if and only if
![]() $A$
is row equivalent to a column connected
$A$
is row equivalent to a column connected
![]() $\unicode[STIX]{x1D70B}$
-tableau.
$\unicode[STIX]{x1D70B}$
-tableau.
To state Corollary 1.2, we have to define certain one-dimensional
![]() $U_{0}(\mathfrak{p})$
-modules. As explained in § 2.5, given
$U_{0}(\mathfrak{p})$
-modules. As explained in § 2.5, given
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
, we have that
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
, we have that
![]() $\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}$
is the weight of a one-dimensional
$\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}$
is the weight of a one-dimensional
![]() $U_{0}(\mathfrak{h})$
-module if and only
$U_{0}(\mathfrak{h})$
-module if and only
![]() $A$
is column connected. For column connected
$A$
is column connected. For column connected
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
, we define
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
, we define
![]() $\overline{\Bbbk }_{A}$
to be the one-dimensional
$\overline{\Bbbk }_{A}$
to be the one-dimensional
![]() $U_{0}(\mathfrak{p})$
-module obtained by inflating the one-dimensional
$U_{0}(\mathfrak{p})$
-module obtained by inflating the one-dimensional
![]() $U_{0}(\mathfrak{h})$
-module with weight
$U_{0}(\mathfrak{h})$
-module with weight
![]() $\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}$
. In Theorem 2.2 we show that
$\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}$
. In Theorem 2.2 we show that
![]() $L_{\unicode[STIX]{x1D712}}(A)\cong U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{0}(\mathfrak{p})}\overline{\Bbbk }_{A}$
for column connected
$L_{\unicode[STIX]{x1D712}}(A)\cong U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{0}(\mathfrak{p})}\overline{\Bbbk }_{A}$
for column connected
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
. Combining this with Theorem 1.1, we immediately deduce the following corollary.
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
. Combining this with Theorem 1.1, we immediately deduce the following corollary.
Corollary 1.2. Let
![]() $\mathfrak{g}=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$
, let
$\mathfrak{g}=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$
, let
![]() $\unicode[STIX]{x1D70B}$
be a pyramid corresponding to a partition
$\unicode[STIX]{x1D70B}$
be a pyramid corresponding to a partition
![]() $\boldsymbol{p}$
of
$\boldsymbol{p}$
of
![]() $N$
, let
$N$
, let
![]() $\unicode[STIX]{x1D712}$
be the nilpotent element of
$\unicode[STIX]{x1D712}$
be the nilpotent element of
![]() $\mathfrak{g}^{\ast }$
determined by
$\mathfrak{g}^{\ast }$
determined by
![]() $\unicode[STIX]{x1D70B}$
, and let
$\unicode[STIX]{x1D70B}$
, and let
![]() $\mathfrak{p}$
be the parabolic subalgebra of
$\mathfrak{p}$
be the parabolic subalgebra of
![]() $\mathfrak{g}$
determined by
$\mathfrak{g}$
determined by
![]() $\unicode[STIX]{x1D70B}$
. Let
$\unicode[STIX]{x1D70B}$
. Let
![]() $L$
be a minimal-dimensional
$L$
be a minimal-dimensional
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module. Then
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module. Then
![]() $L\cong U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{0}(\mathfrak{p})}\overline{\Bbbk }_{A}$
for some column connected
$L\cong U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{0}(\mathfrak{p})}\overline{\Bbbk }_{A}$
for some column connected
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
.
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
.
We give an outline of the main ideas in the proof of Theorem 1.1. The key step is to rephrase the problem in terms of
![]() $W$
-algebras through Premet’s equivalence. Let
$W$
-algebras through Premet’s equivalence. Let
![]() $U(\mathfrak{g},e)$
be the finite
$U(\mathfrak{g},e)$
be the finite
![]() $W$
-algebra as in [Reference Goodwin and TopleyGT18, Definition 4.3]; in fact we use an equivalent definition in this paper as a subalgebra of
$W$
-algebra as in [Reference Goodwin and TopleyGT18, Definition 4.3]; in fact we use an equivalent definition in this paper as a subalgebra of
![]() $U(\mathfrak{p})$
as explained in § 2.6. The restricted
$U(\mathfrak{p})$
as explained in § 2.6. The restricted
![]() $W$
-algebra
$W$
-algebra
![]() $U_{0}(\mathfrak{g},e)$
is as in [Reference Goodwin and TopleyGT18, Definition 8.5], though as explained in § 2.6 our notation in this paper differs from that in [Reference Goodwin and TopleyGT18] and we view
$U_{0}(\mathfrak{g},e)$
is as in [Reference Goodwin and TopleyGT18, Definition 8.5], though as explained in § 2.6 our notation in this paper differs from that in [Reference Goodwin and TopleyGT18] and we view
![]() $U_{0}(\mathfrak{g},e)$
as a subalgebra of
$U_{0}(\mathfrak{g},e)$
as a subalgebra of
![]() $U_{0}(\mathfrak{p})$
. The definitions of these
$U_{0}(\mathfrak{p})$
. The definitions of these
![]() $W$
-algebras in [Reference Goodwin and TopleyGT18] are inspired by work of Premet, where
$W$
-algebras in [Reference Goodwin and TopleyGT18] are inspired by work of Premet, where
![]() $U(\mathfrak{g},e)$
has appeared for
$U(\mathfrak{g},e)$
has appeared for
![]() $p$
sufficiently large and is obtained from a finite
$p$
sufficiently large and is obtained from a finite
![]() $W$
-algebra in characteristic 0 via reduction modulo
$W$
-algebra in characteristic 0 via reduction modulo
![]() $p$
; see, for example, [Reference PremetPre10, §2.5].
$p$
; see, for example, [Reference PremetPre10, §2.5].
We recall that Premet’s equivalence, which is stated in Theorem 2.4, gives an equivalence of categories between
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\operatorname{ - mod}$
and
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\operatorname{ - mod}$
and
![]() $U_{0}(\mathfrak{g},e)\operatorname{ - mod}$
. Moreover, through this equivalence a
$U_{0}(\mathfrak{g},e)\operatorname{ - mod}$
. Moreover, through this equivalence a
![]() $U_{0}(\mathfrak{g},e)$
-module of dimension
$U_{0}(\mathfrak{g},e)$
-module of dimension
![]() $m$
corresponds to a
$m$
corresponds to a
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module of dimension
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module of dimension
![]() $mp^{d_{\unicode[STIX]{x1D712}}}$
. Therefore, in order to prove Theorem 1.1, we want to classify the one-dimensional
$mp^{d_{\unicode[STIX]{x1D712}}}$
. Therefore, in order to prove Theorem 1.1, we want to classify the one-dimensional
![]() $U_{0}(\mathfrak{g},e)$
-modules.
$U_{0}(\mathfrak{g},e)$
-modules.
In fact we classify all one-dimensional
![]() $U(\mathfrak{g},e)$
-modules and determine which ones factor through the quotient map
$U(\mathfrak{g},e)$
-modules and determine which ones factor through the quotient map
![]() $U(\mathfrak{g},e){\twoheadrightarrow}U_{0}(\mathfrak{g},e)$
. We show that
$U(\mathfrak{g},e){\twoheadrightarrow}U_{0}(\mathfrak{g},e)$
. We show that
![]() $U(\mathfrak{g},e)$
is a modular truncated shifted Yangian; see Theorem 4.3. This is proved by following the methods of Brundan and Kleshchev in [Reference Brundan and KleshchevBK06], but now using the PBW theorem for
$U(\mathfrak{g},e)$
is a modular truncated shifted Yangian; see Theorem 4.3. This is proved by following the methods of Brundan and Kleshchev in [Reference Brundan and KleshchevBK06], but now using the PBW theorem for
![]() $U(\mathfrak{g},e)$
given in [Reference Goodwin and TopleyGT18, Theorem 7.3] and reduction modulo
$U(\mathfrak{g},e)$
given in [Reference Goodwin and TopleyGT18, Theorem 7.3] and reduction modulo
![]() $p$
arguments. In particular, this allows us to determine the abelianization
$p$
arguments. In particular, this allows us to determine the abelianization
![]() $U(\mathfrak{g},e)^{\operatorname{ab}}$
of
$U(\mathfrak{g},e)^{\operatorname{ab}}$
of
![]() $U(\mathfrak{g},e)$
, by observing that a calculation by Premet from [Reference PremetPre10, Theorem 3.3] applies in characteristic
$U(\mathfrak{g},e)$
, by observing that a calculation by Premet from [Reference PremetPre10, Theorem 3.3] applies in characteristic
![]() $p$
. As mentioned above, we view
$p$
. As mentioned above, we view
![]() $U(\mathfrak{g},e)$
as a subalgebra of
$U(\mathfrak{g},e)$
as a subalgebra of
![]() $U(\mathfrak{p})$
. Thus we obtain one-dimensional
$U(\mathfrak{p})$
. Thus we obtain one-dimensional
![]() $U(\mathfrak{g},e)$
-modules by restricting one-dimensional
$U(\mathfrak{g},e)$
-modules by restricting one-dimensional
![]() $U(\mathfrak{p})$
-modules. Rather than using the labelling of one-dimensional
$U(\mathfrak{p})$
-modules. Rather than using the labelling of one-dimensional
![]() $U(\mathfrak{p})$
-modules as
$U(\mathfrak{p})$
-modules as
![]() $\overline{\Bbbk }_{A}$
for column connected
$\overline{\Bbbk }_{A}$
for column connected
![]() $A$
in
$A$
in
![]() $\operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
above, we in fact consider
$\operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
above, we in fact consider
![]() $U(\mathfrak{p})$
-modules
$U(\mathfrak{p})$
-modules
![]() $\widetilde{\Bbbk }_{A}$
, where a different shift is used. Using the description of
$\widetilde{\Bbbk }_{A}$
, where a different shift is used. Using the description of
![]() $U(\mathfrak{g},e)^{\operatorname{ab}}$
, we are able to deduce that the restriction of the modules
$U(\mathfrak{g},e)^{\operatorname{ab}}$
, we are able to deduce that the restriction of the modules
![]() $\widetilde{\Bbbk }_{A}$
for column connected
$\widetilde{\Bbbk }_{A}$
for column connected
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
gives all of the one-dimensional
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
gives all of the one-dimensional
![]() $U(\mathfrak{g},e)$
-modules. Moreover, for column connected
$U(\mathfrak{g},e)$
-modules. Moreover, for column connected
![]() $A,A^{\prime }\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
we deduce that the restrictions of
$A,A^{\prime }\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
we deduce that the restrictions of
![]() $\widetilde{\Bbbk }_{A}$
and
$\widetilde{\Bbbk }_{A}$
and
![]() $\widetilde{\Bbbk }_{A^{\prime }}$
are isomorphic if and only if
$\widetilde{\Bbbk }_{A^{\prime }}$
are isomorphic if and only if
![]() $A$
is row equivalent to
$A$
is row equivalent to
![]() $A^{\prime }$
. We denote
$A^{\prime }$
. We denote
![]() $\widetilde{\Bbbk }_{A}$
restricted to
$\widetilde{\Bbbk }_{A}$
restricted to
![]() $U(\mathfrak{g},e)$
by
$U(\mathfrak{g},e)$
by
![]() $\widetilde{\Bbbk }_{\overline{A}}$
. Our methods for this classification of one-dimensional
$\widetilde{\Bbbk }_{\overline{A}}$
. Our methods for this classification of one-dimensional
![]() $U(\mathfrak{g},e)$
-modules are similar to those used by Brundan in [Reference BrundanBru11, §2].
$U(\mathfrak{g},e)$
-modules are similar to those used by Brundan in [Reference BrundanBru11, §2].
Our next step is to show, for column connected
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
, that
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
, that
![]() $\widetilde{\Bbbk }_{\overline{A}}$
factors to a module for
$\widetilde{\Bbbk }_{\overline{A}}$
factors to a module for
![]() $U_{0}(\mathfrak{g},e)$
if and only if
$U_{0}(\mathfrak{g},e)$
if and only if
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
. This deduction is not immediate and is given in Theorem 6.1. From here we are in a position to apply Premet’s equivalence to determine the minimal-dimensional
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
. This deduction is not immediate and is given in Theorem 6.1. From here we are in a position to apply Premet’s equivalence to determine the minimal-dimensional
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-modules. A key step for this is given by Theorem 2.2, which says that
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-modules. A key step for this is given by Theorem 2.2, which says that
![]() $L_{\unicode[STIX]{x1D712}}(A)\cong U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{0}(\mathfrak{p})}\overline{\Bbbk }_{A}$
for column connected
$L_{\unicode[STIX]{x1D712}}(A)\cong U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{0}(\mathfrak{p})}\overline{\Bbbk }_{A}$
for column connected
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
. This requires us to identify a vector in
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
. This requires us to identify a vector in
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{0}(\mathfrak{p})}\overline{\Bbbk }_{A}$
, which spans a one-dimensional
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{0}(\mathfrak{p})}\overline{\Bbbk }_{A}$
, which spans a one-dimensional
![]() $U(\mathfrak{b})$
-module with weight
$U(\mathfrak{b})$
-module with weight
![]() $\unicode[STIX]{x1D706}_{A}-\unicode[STIX]{x1D70C}$
. From this we can deduce that
$\unicode[STIX]{x1D706}_{A}-\unicode[STIX]{x1D70C}$
. From this we can deduce that
![]() $L_{\unicode[STIX]{x1D712}}(A)$
is minimal-dimensional if
$L_{\unicode[STIX]{x1D712}}(A)$
is minimal-dimensional if
![]() $A$
is column connected. By applying our classification of one-dimensional
$A$
is column connected. By applying our classification of one-dimensional
![]() $U_{0}(\mathfrak{g},e)$
-modules and Premet’s equivalence, we are thus able to conclude that the set
$U_{0}(\mathfrak{g},e)$
-modules and Premet’s equivalence, we are thus able to conclude that the set
![]() $L_{\unicode[STIX]{x1D712}}(A)$
for
$L_{\unicode[STIX]{x1D712}}(A)$
for
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
column connected (up to row equivalence) gives all of the minimal-dimensional
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
column connected (up to row equivalence) gives all of the minimal-dimensional
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-modules, which proves Theorem 1.1. In fact it is possible to show that through Premet’s equivalence
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-modules, which proves Theorem 1.1. In fact it is possible to show that through Premet’s equivalence
![]() $\widetilde{\Bbbk }_{\overline{A}}$
corresponds to
$\widetilde{\Bbbk }_{\overline{A}}$
corresponds to
![]() $L_{\unicode[STIX]{x1D712}}(A)$
; this is discussed in Remark 7.1.
$L_{\unicode[STIX]{x1D712}}(A)$
; this is discussed in Remark 7.1.
We conclude this introduction with some remarks about minimal-dimensional modules for reduced enveloping algebras
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
for
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
for
![]() $\mathfrak{g}$
the Lie algebra of a reductive algebraic group over
$\mathfrak{g}$
the Lie algebra of a reductive algebraic group over
![]() $\Bbbk$
. The assertion that there is a
$\Bbbk$
. The assertion that there is a
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module of dimension
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module of dimension
![]() $p^{d_{\unicode[STIX]{x1D712}}}$
is now known as Humphreys’ conjecture (see [Reference HumphreysHum98, §8]), though we note that the question was asked earlier by Kac in his review of [Reference PremetPre95] in Mathematical Reviews. There has been lots of progress on this conjecture recently, and thanks to the results of Premet in [Reference PremetPre14] it is now known to be true for
$p^{d_{\unicode[STIX]{x1D712}}}$
is now known as Humphreys’ conjecture (see [Reference HumphreysHum98, §8]), though we note that the question was asked earlier by Kac in his review of [Reference PremetPre95] in Mathematical Reviews. There has been lots of progress on this conjecture recently, and thanks to the results of Premet in [Reference PremetPre14] it is now known to be true for
![]() $p$
sufficiently large; further, Premet states that in forthcoming work he will give an explicit lower bound on
$p$
sufficiently large; further, Premet states that in forthcoming work he will give an explicit lower bound on
![]() $p$
. The questions of whether the minimal-dimensional modules can be classified and whether they are parabolically induced are also of great interest. We plan to consider these in future work, and note that the version of the latter in characteristic 0 is addressed in work of Premet and the second author in [Reference Premet and TopleyPT14].
$p$
. The questions of whether the minimal-dimensional modules can be classified and whether they are parabolically induced are also of great interest. We plan to consider these in future work, and note that the version of the latter in characteristic 0 is addressed in work of Premet and the second author in [Reference Premet and TopleyPT14].
2 Preliminaries
2.1 The general linear Lie algebra and reduced enveloping algebras
Let
![]() $\Bbbk$
be an algebraically closed field of characteristic
$\Bbbk$
be an algebraically closed field of characteristic
![]() $p>0$
and let
$p>0$
and let
![]() $N\in \mathbb{Z}_{{\geqslant}1}$
. Throughout this paper
$N\in \mathbb{Z}_{{\geqslant}1}$
. Throughout this paper
![]() $G:=\text{GL}_{N}(\Bbbk )$
and
$G:=\text{GL}_{N}(\Bbbk )$
and
![]() $\mathfrak{g}:=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$
is the Lie algebra of
$\mathfrak{g}:=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$
is the Lie algebra of
![]() $G$
, which is spanned by the matrix units
$G$
, which is spanned by the matrix units
![]() $\{e_{i,j}\mid 1\leqslant i,j\leqslant N\}$
. Let
$\{e_{i,j}\mid 1\leqslant i,j\leqslant N\}$
. Let
![]() $(\cdot \,,\cdot ):\mathfrak{g}\times \mathfrak{g}\rightarrow \Bbbk$
denote the trace form associated to the natural representation of
$(\cdot \,,\cdot ):\mathfrak{g}\times \mathfrak{g}\rightarrow \Bbbk$
denote the trace form associated to the natural representation of
![]() $G$
, which we use to identify
$G$
, which we use to identify
![]() $\mathfrak{g}\cong \mathfrak{g}^{\ast }$
as
$\mathfrak{g}\cong \mathfrak{g}^{\ast }$
as
![]() $G$
-modules. The universal enveloping algebra of
$G$
-modules. The universal enveloping algebra of
![]() $\mathfrak{g}$
is denoted by
$\mathfrak{g}$
is denoted by
![]() $U(\mathfrak{g})$
.
$U(\mathfrak{g})$
.
We occasionally need to call on some results from characteristic 0 and so we fix some more notation. We let
![]() $\mathfrak{g}_{\mathbb{Z}}$
denote the general linear Lie
$\mathfrak{g}_{\mathbb{Z}}$
denote the general linear Lie
![]() $\mathbb{Z}$
-algebra
$\mathbb{Z}$
-algebra
![]() $\mathfrak{g}\mathfrak{l}_{N}(\mathbb{Z})$
and we write
$\mathfrak{g}\mathfrak{l}_{N}(\mathbb{Z})$
and we write
![]() $\mathfrak{g}_{\mathbb{C}}$
for
$\mathfrak{g}_{\mathbb{C}}$
for
![]() $\mathfrak{g}\mathfrak{l}_{N}(\mathbb{C})$
. Throughout we use the identifications
$\mathfrak{g}\mathfrak{l}_{N}(\mathbb{C})$
. Throughout we use the identifications
![]() $\mathfrak{g}\cong \mathfrak{g}_{\mathbb{Z}}\otimes _{\mathbb{Z}}\Bbbk$
and
$\mathfrak{g}\cong \mathfrak{g}_{\mathbb{Z}}\otimes _{\mathbb{Z}}\Bbbk$
and
![]() $\mathfrak{g}_{\mathbb{C}}\cong \mathfrak{g}_{\mathbb{Z}}\otimes _{\mathbb{Z}}\mathbb{C}$
, and by a slight abuse of notation we view the matrix units
$\mathfrak{g}_{\mathbb{C}}\cong \mathfrak{g}_{\mathbb{Z}}\otimes _{\mathbb{Z}}\mathbb{C}$
, and by a slight abuse of notation we view the matrix units
![]() $e_{i,j}$
as elements of
$e_{i,j}$
as elements of
![]() $\mathfrak{g}_{\mathbb{Z}}$
or
$\mathfrak{g}_{\mathbb{Z}}$
or
![]() $\mathfrak{g}_{\mathbb{C}}$
when it is convenient to do so. We often consider subalgebras of
$\mathfrak{g}_{\mathbb{C}}$
when it is convenient to do so. We often consider subalgebras of
![]() $\mathfrak{g}$
, which are spanned by matrix units, so have analogues inside
$\mathfrak{g}$
, which are spanned by matrix units, so have analogues inside
![]() $\mathfrak{g}_{\mathbb{Z}}$
and
$\mathfrak{g}_{\mathbb{Z}}$
and
![]() $\mathfrak{g}_{\mathbb{C}}$
and we denote them by decorating with subscripts
$\mathfrak{g}_{\mathbb{C}}$
and we denote them by decorating with subscripts
![]() $\mathbb{Z}$
and
$\mathbb{Z}$
and
![]() $\mathbb{C}$
. We mention that since
$\mathbb{C}$
. We mention that since
![]() $\mathfrak{g}_{\mathbb{Z}}$
is a free
$\mathfrak{g}_{\mathbb{Z}}$
is a free
![]() $\mathbb{Z}$
-module the PBW theorem holds for
$\mathbb{Z}$
-module the PBW theorem holds for
![]() $U(\mathfrak{g}_{\mathbb{Z}})$
, so that
$U(\mathfrak{g}_{\mathbb{Z}})$
, so that
![]() $U(\mathfrak{g}_{\mathbb{Z}})$
is a free
$U(\mathfrak{g}_{\mathbb{Z}})$
is a free
![]() $\mathbb{Z}$
-module with a basis consisting of ordered monomials in the matrix units with respect to any choice of total order.
$\mathbb{Z}$
-module with a basis consisting of ordered monomials in the matrix units with respect to any choice of total order.
Let
![]() $g\in G$
,
$g\in G$
,
![]() $x\in \mathfrak{g}$
and
$x\in \mathfrak{g}$
and
![]() $\unicode[STIX]{x1D712}\in \mathfrak{g}^{\ast }$
. We write
$\unicode[STIX]{x1D712}\in \mathfrak{g}^{\ast }$
. We write
![]() $g\cdot x$
for the image of
$g\cdot x$
for the image of
![]() $x$
under the adjoint action of
$x$
under the adjoint action of
![]() $g$
, so as matrices
$g$
, so as matrices
![]() $g\cdot x=gxg^{-1}$
; this action extends to an action on
$g\cdot x=gxg^{-1}$
; this action extends to an action on
![]() $U(\mathfrak{g})$
by algebra automorphisms. The centralizer of
$U(\mathfrak{g})$
by algebra automorphisms. The centralizer of
![]() $x$
in
$x$
in
![]() $G$
is denoted by
$G$
is denoted by
![]() $G^{x}:=\{g\in G\mid g\cdot x=x\}$
and the centralizer of
$G^{x}:=\{g\in G\mid g\cdot x=x\}$
and the centralizer of
![]() $x$
in
$x$
in
![]() $\mathfrak{g}$
is denoted by
$\mathfrak{g}$
is denoted by
![]() $\mathfrak{g}^{x}:=\{y\in \mathfrak{g}\mid [y,x]=0\}$
; we note that
$\mathfrak{g}^{x}:=\{y\in \mathfrak{g}\mid [y,x]=0\}$
; we note that
![]() $\mathfrak{g}^{x}=\operatorname{Lie}(G^{x})$
. We write
$\mathfrak{g}^{x}=\operatorname{Lie}(G^{x})$
. We write
![]() $G\cdot \unicode[STIX]{x1D712}$
for the coadjoint orbit of
$G\cdot \unicode[STIX]{x1D712}$
for the coadjoint orbit of
![]() $\unicode[STIX]{x1D712}$
. It is well known that
$\unicode[STIX]{x1D712}$
. It is well known that
![]() $\dim (G\cdot \unicode[STIX]{x1D712})$
is even and we define
$\dim (G\cdot \unicode[STIX]{x1D712})$
is even and we define
![]() $d_{\unicode[STIX]{x1D712}}:=\frac{1}{2}\dim (G\cdot \unicode[STIX]{x1D712})$
.
$d_{\unicode[STIX]{x1D712}}:=\frac{1}{2}\dim (G\cdot \unicode[STIX]{x1D712})$
.
Let
![]() $T\subseteq B\subseteq G$
be the maximal torus and Borel subgroup consisting of diagonal matrices and upper triangular matrices respectively, and let
$T\subseteq B\subseteq G$
be the maximal torus and Borel subgroup consisting of diagonal matrices and upper triangular matrices respectively, and let
![]() $\mathfrak{t}:=\operatorname{Lie}(T)$
,
$\mathfrak{t}:=\operatorname{Lie}(T)$
,
![]() $\mathfrak{b}:=\operatorname{Lie}(B)$
. We use the notation
$\mathfrak{b}:=\operatorname{Lie}(B)$
. We use the notation
![]() $\operatorname{diag}(d_{1},\ldots ,d_{n})$
to denote the element of
$\operatorname{diag}(d_{1},\ldots ,d_{n})$
to denote the element of
![]() $T$
with
$T$
with
![]() $d_{i}$
in the
$d_{i}$
in the
![]() $i$
th entry of the diagonal. We write
$i$
th entry of the diagonal. We write
![]() $X^{\ast }(T)$
for the group of characters, and let
$X^{\ast }(T)$
for the group of characters, and let
![]() $\{\unicode[STIX]{x1D700}_{1},\ldots ,\unicode[STIX]{x1D700}_{N}\}$
be the standard basis of
$\{\unicode[STIX]{x1D700}_{1},\ldots ,\unicode[STIX]{x1D700}_{N}\}$
be the standard basis of
![]() $X^{\ast }(T)$
defined by
$X^{\ast }(T)$
defined by
![]() $\unicode[STIX]{x1D700}_{i}(\operatorname{diag}(d_{1},\ldots ,d_{n}))=d_{i}$
. Let
$\unicode[STIX]{x1D700}_{i}(\operatorname{diag}(d_{1},\ldots ,d_{n}))=d_{i}$
. Let
![]() $\unicode[STIX]{x1D6F7}\subseteq X^{\ast }(T)$
be the root system of
$\unicode[STIX]{x1D6F7}\subseteq X^{\ast }(T)$
be the root system of
![]() $G$
with respect to
$G$
with respect to
![]() $T$
, so
$T$
, so
![]() $\unicode[STIX]{x1D6F7}=\{\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}\mid 1\leqslant i,j\leqslant n,i\neq j\}$
. We write
$\unicode[STIX]{x1D6F7}=\{\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}\mid 1\leqslant i,j\leqslant n,i\neq j\}$
. We write
![]() $e_{i,j}$
for the matrix unit that spans the root space corresponding to
$e_{i,j}$
for the matrix unit that spans the root space corresponding to
![]() $\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}$
. The root subgroup corresponding to
$\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}$
. The root subgroup corresponding to
![]() $\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}$
is the image of
$\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}$
is the image of
![]() $u_{i,j}:\Bbbk \rightarrow G$
defined by
$u_{i,j}:\Bbbk \rightarrow G$
defined by
![]() $u_{i,j}(s):=1+se_{i,j}$
, and the adjoint action of
$u_{i,j}(s):=1+se_{i,j}$
, and the adjoint action of
![]() $u_{i,j}(s)$
on
$u_{i,j}(s)$
on
![]() $e_{k,l}$
is given by the formula
$e_{k,l}$
is given by the formula
Where it is convenient we allow ourselves to view a character
![]() $\unicode[STIX]{x1D6FC}\in X^{\ast }(T)$
as an element of
$\unicode[STIX]{x1D6FC}\in X^{\ast }(T)$
as an element of
![]() $\mathfrak{t}^{\ast }$
by writing
$\mathfrak{t}^{\ast }$
by writing
![]() $\unicode[STIX]{x1D6FC}$
for
$\unicode[STIX]{x1D6FC}$
for
![]() $d\unicode[STIX]{x1D6FC}:\mathfrak{t}\rightarrow \Bbbk$
; this is a slight abuse of notation, because
$d\unicode[STIX]{x1D6FC}:\mathfrak{t}\rightarrow \Bbbk$
; this is a slight abuse of notation, because
![]() $d\unicode[STIX]{x1D6FC}=0$
for any
$d\unicode[STIX]{x1D6FC}=0$
for any
![]() $\unicode[STIX]{x1D6FC}\in pX^{\ast }(T)$
.
$\unicode[STIX]{x1D6FC}\in pX^{\ast }(T)$
.
There is a natural restricted structure on
![]() $\mathfrak{g}$
, where the
$\mathfrak{g}$
, where the
![]() $p$
-power map
$p$
-power map
![]() $x\mapsto x^{[p]}$
is given by taking the
$x\mapsto x^{[p]}$
is given by taking the
![]() $p$
th power of
$p$
th power of
![]() $x$
as a matrix. In particular, we note that
$x$
as a matrix. In particular, we note that
![]() $e_{i,j}^{[p]}=\unicode[STIX]{x1D6FF}_{i,j}e_{i,j}$
for
$e_{i,j}^{[p]}=\unicode[STIX]{x1D6FF}_{i,j}e_{i,j}$
for
![]() $1\leqslant i,j\leqslant N$
. The
$1\leqslant i,j\leqslant N$
. The
![]() $p$
-centre of
$p$
-centre of
![]() $U(\mathfrak{g})$
is the subalgebra of the centre of
$U(\mathfrak{g})$
is the subalgebra of the centre of
![]() $U(\mathfrak{g})$
generated by
$U(\mathfrak{g})$
generated by
![]() $\{e_{i,j}^{p}-e_{i,j}^{[p]}\mid 1\leqslant i,j\leqslant N\}$
. It follows from the PBW theorem that
$\{e_{i,j}^{p}-e_{i,j}^{[p]}\mid 1\leqslant i,j\leqslant N\}$
. It follows from the PBW theorem that
![]() $U(\mathfrak{g})$
is a free
$U(\mathfrak{g})$
is a free
![]() $Z_{p}(\mathfrak{g})$
-module of rank
$Z_{p}(\mathfrak{g})$
-module of rank
![]() $p^{\dim \mathfrak{g}}$
. Further, there is a natural identification
$p^{\dim \mathfrak{g}}$
. Further, there is a natural identification
![]() $Z_{p}(\mathfrak{g})\cong \Bbbk [(\mathfrak{g}^{\ast })^{(1)}]$
, where
$Z_{p}(\mathfrak{g})\cong \Bbbk [(\mathfrak{g}^{\ast })^{(1)}]$
, where
![]() $(\mathfrak{g}^{\ast })^{(1)}$
denotes the Frobenius twist of
$(\mathfrak{g}^{\ast })^{(1)}$
denotes the Frobenius twist of
![]() $\mathfrak{g}^{\ast }$
. Given
$\mathfrak{g}^{\ast }$
. Given
![]() $\unicode[STIX]{x1D712}\in \mathfrak{g}^{\ast }$
, we define
$\unicode[STIX]{x1D712}\in \mathfrak{g}^{\ast }$
, we define
![]() $J_{\unicode[STIX]{x1D712}}$
to be the ideal of
$J_{\unicode[STIX]{x1D712}}$
to be the ideal of
![]() $U(\mathfrak{g})$
generated by
$U(\mathfrak{g})$
generated by
![]() $\{x^{p}-x^{[p]}-\unicode[STIX]{x1D712}(x)^{p}\mid x\in \mathfrak{g}\}$
, and the reduced enveloping algebra corresponding to
$\{x^{p}-x^{[p]}-\unicode[STIX]{x1D712}(x)^{p}\mid x\in \mathfrak{g}\}$
, and the reduced enveloping algebra corresponding to
![]() $\unicode[STIX]{x1D712}$
to be
$\unicode[STIX]{x1D712}$
to be
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g}):=U(\mathfrak{g})/J_{\unicode[STIX]{x1D712}}$
.
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g}):=U(\mathfrak{g})/J_{\unicode[STIX]{x1D712}}$
.
As stated in the introduction, the Kac–Weisfeiler conjecture, which is a theorem of Premet, states that
![]() $p^{d_{\unicode[STIX]{x1D712}}}$
is a factor of the dimension of any
$p^{d_{\unicode[STIX]{x1D712}}}$
is a factor of the dimension of any
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module. We refer to
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module. We refer to
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-modules of dimension
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-modules of dimension
![]() $p^{d_{\unicode[STIX]{x1D712}}}$
as minimal-dimensional modules, and note that such modules are clearly irreducible.
$p^{d_{\unicode[STIX]{x1D712}}}$
as minimal-dimensional modules, and note that such modules are clearly irreducible.
Let
![]() $\unicode[STIX]{x1D712}\in \mathfrak{g}^{\ast }$
. There is unique
$\unicode[STIX]{x1D712}\in \mathfrak{g}^{\ast }$
. There is unique
![]() $x\in \mathfrak{g}$
such that
$x\in \mathfrak{g}$
such that
![]() $\unicode[STIX]{x1D712}=(x,\cdot )$
. We have a Jordan decomposition
$\unicode[STIX]{x1D712}=(x,\cdot )$
. We have a Jordan decomposition
![]() $x=x_{\text{s}}+x_{\text{n}}$
of
$x=x_{\text{s}}+x_{\text{n}}$
of
![]() $x$
, and thus a corresponding decomposition
$x$
, and thus a corresponding decomposition
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\text{s}}+\unicode[STIX]{x1D712}_{\text{n}}$
. We say that
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\text{s}}+\unicode[STIX]{x1D712}_{\text{n}}$
. We say that
![]() $\unicode[STIX]{x1D712}$
is nilpotent if
$\unicode[STIX]{x1D712}$
is nilpotent if
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\text{n}}$
. Next we recall the ‘reduction’ to the case
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\text{n}}$
. Next we recall the ‘reduction’ to the case
![]() $\unicode[STIX]{x1D712}$
nilpotent in the representation theory of
$\unicode[STIX]{x1D712}$
nilpotent in the representation theory of
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
from [Reference Friedlander and ParshallFP88, §3]; as is noted in [Reference Friedlander and ParshallFP88, §8], this reduction can also be deduced from [Reference Veisfeiler and KatsVK71, Theorem 2]. Let
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
from [Reference Friedlander and ParshallFP88, §3]; as is noted in [Reference Friedlander and ParshallFP88, §8], this reduction can also be deduced from [Reference Veisfeiler and KatsVK71, Theorem 2]. Let
![]() $\mathfrak{l}=\mathfrak{g}^{x_{\text{s}}}$
, let
$\mathfrak{l}=\mathfrak{g}^{x_{\text{s}}}$
, let
![]() $\mathfrak{q}$
be a parabolic subalgebra of
$\mathfrak{q}$
be a parabolic subalgebra of
![]() $\mathfrak{g}$
with Levi factor
$\mathfrak{g}$
with Levi factor
![]() $\mathfrak{l}$
and let
$\mathfrak{l}$
and let
![]() $\mathfrak{u}$
denote the nilradical of
$\mathfrak{u}$
denote the nilradical of
![]() $\mathfrak{q}$
. We can parabolically induce a
$\mathfrak{q}$
. We can parabolically induce a
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{l})$
-module
$U_{\unicode[STIX]{x1D712}}(\mathfrak{l})$
-module
![]() $M$
, to obtain the
$M$
, to obtain the
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{\unicode[STIX]{x1D712}}(\mathfrak{q})}M$
, where
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{\unicode[STIX]{x1D712}}(\mathfrak{q})}M$
, where
![]() $M$
is the
$M$
is the
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{q})$
-module on which
$U_{\unicode[STIX]{x1D712}}(\mathfrak{q})$
-module on which
![]() $\mathfrak{u}$
acts trivially. This gives a functor
$\mathfrak{u}$
acts trivially. This gives a functor
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{l})\operatorname{ - mod}\rightarrow U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\operatorname{ - mod}$
and it is proved in [Reference Friedlander and ParshallFP88, Theorem 3.2] that this is an equivalence of categories; in turn there is an equivalence
$U_{\unicode[STIX]{x1D712}}(\mathfrak{l})\operatorname{ - mod}\rightarrow U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\operatorname{ - mod}$
and it is proved in [Reference Friedlander and ParshallFP88, Theorem 3.2] that this is an equivalence of categories; in turn there is an equivalence
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{l})\operatorname{ - mod}\cong U_{\unicode[STIX]{x1D712}_{\text{n}}}(\mathfrak{l})\operatorname{ - mod}$
as follows from [Reference Friedlander and ParshallFP88, Corollary 3.3]. Further, the theory of Jordan normal forms implies that
$U_{\unicode[STIX]{x1D712}}(\mathfrak{l})\operatorname{ - mod}\cong U_{\unicode[STIX]{x1D712}_{\text{n}}}(\mathfrak{l})\operatorname{ - mod}$
as follows from [Reference Friedlander and ParshallFP88, Corollary 3.3]. Further, the theory of Jordan normal forms implies that
![]() $\dim (G\cdot \unicode[STIX]{x1D712})=\dim (L\cdot \unicode[STIX]{x1D712}_{\text{n}})+2\dim \mathfrak{u}$
. Therefore, through the equivalence of categories
$\dim (G\cdot \unicode[STIX]{x1D712})=\dim (L\cdot \unicode[STIX]{x1D712}_{\text{n}})+2\dim \mathfrak{u}$
. Therefore, through the equivalence of categories
![]() $U_{\unicode[STIX]{x1D712}_{\text{n}}}(\mathfrak{l})\operatorname{ - mod}\cong U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\operatorname{ - mod}$
, minimal-dimensional modules for
$U_{\unicode[STIX]{x1D712}_{\text{n}}}(\mathfrak{l})\operatorname{ - mod}\cong U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\operatorname{ - mod}$
, minimal-dimensional modules for
![]() $U_{\unicode[STIX]{x1D712}_{\text{n}}}(\mathfrak{l})$
correspond to minimal-dimensional modules for
$U_{\unicode[STIX]{x1D712}_{\text{n}}}(\mathfrak{l})$
correspond to minimal-dimensional modules for
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\operatorname{ - mod}$
. This justifies our restriction to nilpotent
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\operatorname{ - mod}$
. This justifies our restriction to nilpotent
![]() $\unicode[STIX]{x1D712}$
in the statements of Theorem 1.1 and Corollary 1.2.
$\unicode[STIX]{x1D712}$
in the statements of Theorem 1.1 and Corollary 1.2.
2.2 Pyramids
We require the combinatorics of pyramids to set up some notation. For more details on this we refer to [Reference Brundan and KleshchevBK06, §7].
We fix a partition
![]() $\boldsymbol{p}=(p_{1},\ldots ,p_{n})$
on
$\boldsymbol{p}=(p_{1},\ldots ,p_{n})$
on
![]() $N$
with
$N$
with
![]() $p_{1}\leqslant \cdots \leqslant p_{n}$
. A pyramid
$p_{1}\leqslant \cdots \leqslant p_{n}$
. A pyramid
![]() $\unicode[STIX]{x1D70B}$
associated to
$\unicode[STIX]{x1D70B}$
associated to
![]() $\boldsymbol{p}$
is a diagram with
$\boldsymbol{p}$
is a diagram with
![]() $p_{n}$
boxes in the bottom row,
$p_{n}$
boxes in the bottom row,
![]() $p_{n-1}$
boxes in the row above it, and so forth, stacked in such a way that every box which is not in the bottom row lies directly above a box in the row beneath it, and boxes occur consecutively in each row. The boxes in the pyramid are numbered along rows from left to right and from top to bottom. For example, the pyramids associated to the partition
$p_{n-1}$
boxes in the row above it, and so forth, stacked in such a way that every box which is not in the bottom row lies directly above a box in the row beneath it, and boxes occur consecutively in each row. The boxes in the pyramid are numbered along rows from left to right and from top to bottom. For example, the pyramids associated to the partition
![]() $\boldsymbol{p}=(2,5)$
are
$\boldsymbol{p}=(2,5)$
are
Let
![]() $l=p_{n}$
. The columns of
$l=p_{n}$
. The columns of
![]() $\unicode[STIX]{x1D70B}$
are labelled
$\unicode[STIX]{x1D70B}$
are labelled
![]() $1,2,\ldots ,l$
from left to right and the rows are labelled
$1,2,\ldots ,l$
from left to right and the rows are labelled
![]() $1,2,\ldots ,n$
from top to bottom. We denote the heights of the columns in
$1,2,\ldots ,n$
from top to bottom. We denote the heights of the columns in
![]() $\unicode[STIX]{x1D70B}$
by
$\unicode[STIX]{x1D70B}$
by
![]() $q_{1},q_{2},\ldots ,q_{l}$
. The box in
$q_{1},q_{2},\ldots ,q_{l}$
. The box in
![]() $\unicode[STIX]{x1D70B}$
containing
$\unicode[STIX]{x1D70B}$
containing
![]() $i$
is referred to as the
$i$
is referred to as the
![]() $i$
th box, and we write
$i$
th box, and we write
![]() $\operatorname{row}(i)$
and
$\operatorname{row}(i)$
and
![]() $\operatorname{col}(i)$
for the row and column of the
$\operatorname{col}(i)$
for the row and column of the
![]() $i$
th box, respectively.
$i$
th box, respectively.
We fix a pyramid
![]() $\unicode[STIX]{x1D70B}$
corresponding to
$\unicode[STIX]{x1D70B}$
corresponding to
![]() $\boldsymbol{p}$
for the rest of this paper. From
$\boldsymbol{p}$
for the rest of this paper. From
![]() $\unicode[STIX]{x1D70B}$
, we define the shift matrix
$\unicode[STIX]{x1D70B}$
, we define the shift matrix
![]() $\unicode[STIX]{x1D70E}=(s_{i,j})$
as follows. For
$\unicode[STIX]{x1D70E}=(s_{i,j})$
as follows. For
![]() $1\leqslant i<j\leqslant n$
we let
$1\leqslant i<j\leqslant n$
we let
![]() $s_{j,i}$
be the left indentation of the
$s_{j,i}$
be the left indentation of the
![]() $i$
th row of
$i$
th row of
![]() $\unicode[STIX]{x1D70B}$
relative to the
$\unicode[STIX]{x1D70B}$
relative to the
![]() $j$
th row, and we let
$j$
th row, and we let
![]() $s_{i,j}$
be the right indentation of the
$s_{i,j}$
be the right indentation of the
![]() $i$
th row of
$i$
th row of
![]() $\unicode[STIX]{x1D70B}$
relative to the
$\unicode[STIX]{x1D70B}$
relative to the
![]() $j$
th row; also we set
$j$
th row; also we set
![]() $s_{i,i}=0$
. For example, the shift matrices associated to the pyramids in (2) are
$s_{i,i}=0$
. For example, the shift matrices associated to the pyramids in (2) are
2.3 The nilpotent element and subalgebras
We define the nilpotent element
For example, for each of the pyramids in (2), we have
![]() $e=e_{1,2}+e_{3,4}+e_{4,5}+e_{5,6}+e_{6,7}$
. Observe that
$e=e_{1,2}+e_{3,4}+e_{4,5}+e_{5,6}+e_{6,7}$
. Observe that
![]() $e$
has Jordan blocks of size
$e$
has Jordan blocks of size
![]() $p_{1},p_{2},\ldots ,p_{n}$
. We define
$p_{1},p_{2},\ldots ,p_{n}$
. We define
![]() $\unicode[STIX]{x1D712}:=(e,\cdot )\in \mathfrak{g}^{\ast }$
. We also note that
$\unicode[STIX]{x1D712}:=(e,\cdot )\in \mathfrak{g}^{\ast }$
. We also note that
![]() $\unicode[STIX]{x1D712}$
is in standard Levi form (in the sense of [Reference Friedlander and ParshallFP90, Definition 3.1]) with respect to the simple roots corresponding to the Borel subalgebra
$\unicode[STIX]{x1D712}$
is in standard Levi form (in the sense of [Reference Friedlander and ParshallFP90, Definition 3.1]) with respect to the simple roots corresponding to the Borel subalgebra
![]() $\mathfrak{b}$
.
$\mathfrak{b}$
.
The first part of the following lemma gives a basis of
![]() $\mathfrak{g}^{e}$
, and can be verified by observing that the proof of [Reference Brundan and KleshchevBK06, Lemma 7.3] is also valid in positive characteristic. The second part of the lemma is verified by direct calculation.
$\mathfrak{g}^{e}$
, and can be verified by observing that the proof of [Reference Brundan and KleshchevBK06, Lemma 7.3] is also valid in positive characteristic. The second part of the lemma is verified by direct calculation.
Lemma 2.1. Let
 $$\begin{eqnarray}c_{i,j}^{(r)}:=\mathop{\sum }_{\substack{ 1\leqslant h,k,\leqslant N \\ \operatorname{row}(h)=i,\operatorname{row}(k)=j \\ \operatorname{col}(k)-\operatorname{col}(h)+1=r}}e_{h,k}\end{eqnarray}$$
$$\begin{eqnarray}c_{i,j}^{(r)}:=\mathop{\sum }_{\substack{ 1\leqslant h,k,\leqslant N \\ \operatorname{row}(h)=i,\operatorname{row}(k)=j \\ \operatorname{col}(k)-\operatorname{col}(h)+1=r}}e_{h,k}\end{eqnarray}$$
for
![]() $0\leqslant i,j\leqslant n$
and
$0\leqslant i,j\leqslant n$
and
![]() $r>s_{i,j}$
.
$r>s_{i,j}$
.
(a) The centralizer
 $\mathfrak{g}^{e}$
of
$\mathfrak{g}^{e}$
of
 $e$
in
$e$
in
 $\mathfrak{g}$
has basis
$\mathfrak{g}$
has basis  $$\begin{eqnarray}\{c_{i,j}^{(r)}\mid 0\leqslant i,j\leqslant n,s_{i,j}<r\leqslant s_{i,j}+p_{\min (i,j)}\}.\end{eqnarray}$$
$$\begin{eqnarray}\{c_{i,j}^{(r)}\mid 0\leqslant i,j\leqslant n,s_{i,j}<r\leqslant s_{i,j}+p_{\min (i,j)}\}.\end{eqnarray}$$
(b) We have
 $$\begin{eqnarray}[c_{i,j}^{(r)},c_{k,l}^{(s)}]=\unicode[STIX]{x1D6FF}_{j,k}c_{i,l}^{(r+s-1)}-\unicode[STIX]{x1D6FF}_{i,l}c_{k,j}^{(r+s-1)}.\end{eqnarray}$$
$$\begin{eqnarray}[c_{i,j}^{(r)},c_{k,l}^{(s)}]=\unicode[STIX]{x1D6FF}_{j,k}c_{i,l}^{(r+s-1)}-\unicode[STIX]{x1D6FF}_{i,l}c_{k,j}^{(r+s-1)}.\end{eqnarray}$$
Consider the cocharacter
![]() $\unicode[STIX]{x1D707}:\Bbbk ^{\times }\rightarrow T\subseteq G$
defined by
$\unicode[STIX]{x1D707}:\Bbbk ^{\times }\rightarrow T\subseteq G$
defined by
![]() $\unicode[STIX]{x1D707}(t)=\operatorname{diag}(t^{\operatorname{col}(1)},\ldots ,t^{\operatorname{col}(n)})$
. Using
$\unicode[STIX]{x1D707}(t)=\operatorname{diag}(t^{\operatorname{col}(1)},\ldots ,t^{\operatorname{col}(n)})$
. Using
![]() $\unicode[STIX]{x1D707}$
, we define the
$\unicode[STIX]{x1D707}$
, we define the
![]() $\mathbb{Z}$
-grading
$\mathbb{Z}$
-grading
Since the adjoint action of
![]() $\unicode[STIX]{x1D707}(t)$
on a matrix unit is given by
$\unicode[STIX]{x1D707}(t)$
on a matrix unit is given by
![]() $\unicode[STIX]{x1D707}(t)\cdot e_{i,j}=t^{\operatorname{col}(j)-\operatorname{col}(i)}e_{i,j}$
, we have
$\unicode[STIX]{x1D707}(t)\cdot e_{i,j}=t^{\operatorname{col}(j)-\operatorname{col}(i)}e_{i,j}$
, we have
![]() $\mathfrak{g}(k)=\operatorname{span}\{e_{i,j}\mid \operatorname{col}(j)-\operatorname{col}(i)=k\}$
. From the classification of good gradings in [Reference Elashvili, Kac and VinbergEK05, §4], we see that the grading in (4) is a good grading for
$\mathfrak{g}(k)=\operatorname{span}\{e_{i,j}\mid \operatorname{col}(j)-\operatorname{col}(i)=k\}$
. From the classification of good gradings in [Reference Elashvili, Kac and VinbergEK05, §4], we see that the grading in (4) is a good grading for
![]() $e$
. In fact to get a good grading we should scale the grading by a factor of 2, as we have
$e$
. In fact to get a good grading we should scale the grading by a factor of 2, as we have
![]() $e\in \mathfrak{g}(1)$
. We refer also to [Reference Goodwin and TopleyGT18, §3] where good gradings are considered in positive characteristic, and it is shown that the ‘same classification’ of good gradings holds. Since the grading in (4) is good we have that
$e\in \mathfrak{g}(1)$
. We refer also to [Reference Goodwin and TopleyGT18, §3] where good gradings are considered in positive characteristic, and it is shown that the ‘same classification’ of good gradings holds. Since the grading in (4) is good we have that
![]() $\mathfrak{g}^{e}\subseteq \bigoplus _{k\geqslant 0}\mathfrak{g}(k)$
, which can also be seen directly from Lemma 2.1, Now it follows from [Reference Elashvili, Kac and VinbergEK05, Theorem 1.4] that
$\mathfrak{g}^{e}\subseteq \bigoplus _{k\geqslant 0}\mathfrak{g}(k)$
, which can also be seen directly from Lemma 2.1, Now it follows from [Reference Elashvili, Kac and VinbergEK05, Theorem 1.4] that
![]() $\dim \mathfrak{g}^{e}=\dim \mathfrak{g}(0)$
; this can also be verified directly from the basis given in Lemma 2.1.
$\dim \mathfrak{g}^{e}=\dim \mathfrak{g}(0)$
; this can also be verified directly from the basis given in Lemma 2.1.
We define the following subalgebras of
![]() $\mathfrak{g}$
:
$\mathfrak{g}$
:
Then
![]() $\mathfrak{p}$
is a parabolic subalgebra of
$\mathfrak{p}$
is a parabolic subalgebra of
![]() $\mathfrak{g}$
, and
$\mathfrak{g}$
, and
![]() $\mathfrak{h}$
is the Levi factor of
$\mathfrak{h}$
is the Levi factor of
![]() $\mathfrak{p}$
containing
$\mathfrak{p}$
containing
![]() $\mathfrak{t}$
. Further,
$\mathfrak{t}$
. Further,
![]() $\mathfrak{m}$
is the nilradical of the opposite parabolic to
$\mathfrak{m}$
is the nilradical of the opposite parabolic to
![]() $\mathfrak{p}$
. We recall that the heights of the columns in
$\mathfrak{p}$
. We recall that the heights of the columns in
![]() $\unicode[STIX]{x1D70B}$
are
$\unicode[STIX]{x1D70B}$
are
![]() $q_{1},q_{2},\ldots ,q_{l}$
, and we see that
$q_{1},q_{2},\ldots ,q_{l}$
, and we see that
![]() $\mathfrak{h}$
is isomorphic to
$\mathfrak{h}$
is isomorphic to
![]() $\mathfrak{g}\mathfrak{l}_{q_{1}}(\Bbbk )\oplus \mathfrak{g}\mathfrak{l}_{q_{2}}(\Bbbk )\oplus \cdots \oplus \mathfrak{g}\mathfrak{l}_{q_{l}}(\Bbbk )$
. Also
$\mathfrak{g}\mathfrak{l}_{q_{1}}(\Bbbk )\oplus \mathfrak{g}\mathfrak{l}_{q_{2}}(\Bbbk )\oplus \cdots \oplus \mathfrak{g}\mathfrak{l}_{q_{l}}(\Bbbk )$
. Also
![]() $\mathfrak{m}$
is the Lie algebra of the closed subgroup
$\mathfrak{m}$
is the Lie algebra of the closed subgroup
![]() $M$
of
$M$
of
![]() $G$
generated by the root subgroups
$G$
generated by the root subgroups
![]() $u_{i,j}(\Bbbk )$
with
$u_{i,j}(\Bbbk )$
with
![]() $\operatorname{col}(j)<\operatorname{col}(i)$
.
$\operatorname{col}(j)<\operatorname{col}(i)$
.
We recall that
![]() $d_{\unicode[STIX]{x1D712}}$
denotes half the dimension of the coadjoint
$d_{\unicode[STIX]{x1D712}}$
denotes half the dimension of the coadjoint
![]() $G$
-orbit of
$G$
-orbit of
![]() $\unicode[STIX]{x1D712}$
. So we also have that
$\unicode[STIX]{x1D712}$
. So we also have that
![]() $d_{\unicode[STIX]{x1D712}}$
is half the dimension of the adjoint
$d_{\unicode[STIX]{x1D712}}$
is half the dimension of the adjoint
![]() $G$
-orbit of
$G$
-orbit of
![]() $e$
, and thus we see that
$e$
, and thus we see that
![]() $d_{\unicode[STIX]{x1D712}}:=\dim \mathfrak{m}$
, because
$d_{\unicode[STIX]{x1D712}}:=\dim \mathfrak{m}$
, because
![]() $\dim \mathfrak{g}^{e}=\dim \mathfrak{g}(0)$
.
$\dim \mathfrak{g}^{e}=\dim \mathfrak{g}(0)$
.
2.4 Tableaux and weights
We require various weights in
![]() $\mathfrak{t}^{\ast }$
, which are used as shifts and to label certain modules. These weights can be encoded by fillings of
$\mathfrak{t}^{\ast }$
, which are used as shifts and to label certain modules. These weights can be encoded by fillings of
![]() $\unicode[STIX]{x1D70B}$
as we explain below. We then move on to give the weights we need.
$\unicode[STIX]{x1D70B}$
as we explain below. We then move on to give the weights we need.
A
![]() $\unicode[STIX]{x1D70B}$
-tableau is a diagram obtained by filling the boxes of
$\unicode[STIX]{x1D70B}$
-tableau is a diagram obtained by filling the boxes of
![]() $\unicode[STIX]{x1D70B}$
with elements of
$\unicode[STIX]{x1D70B}$
with elements of
![]() $\Bbbk$
. The set of all tableaux of shape
$\Bbbk$
. The set of all tableaux of shape
![]() $\unicode[STIX]{x1D70B}$
is denoted
$\unicode[STIX]{x1D70B}$
is denoted
![]() $\operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
, and we write
$\operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
, and we write
![]() $\operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})\subseteq \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
for those tableaux with entries in
$\operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})\subseteq \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
for those tableaux with entries in
![]() $\mathbb{F}_{p}$
. For
$\mathbb{F}_{p}$
. For
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
, we write
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
, we write
![]() $a_{i}$
for the entry in the
$a_{i}$
for the entry in the
![]() $i$
th box of
$i$
th box of
![]() $A$
. Two tableaux are called row equivalent if one can be obtained from the other by permuting the entries in the rows. A tableau
$A$
. Two tableaux are called row equivalent if one can be obtained from the other by permuting the entries in the rows. A tableau
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
is column connected if whenever the
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
is column connected if whenever the
![]() $j$
th box of
$j$
th box of
![]() $\unicode[STIX]{x1D70B}$
is directly below the
$\unicode[STIX]{x1D70B}$
is directly below the
![]() $i$
th box we have
$i$
th box we have
![]() $a_{i}=a_{j}+1$
.
$a_{i}=a_{j}+1$
.
For
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
we define a weight
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
we define a weight
![]() $\unicode[STIX]{x1D706}_{A}\in \mathfrak{t}^{\ast }$
by
$\unicode[STIX]{x1D706}_{A}\in \mathfrak{t}^{\ast }$
by
To understand the required weights it helps for us to give a decomposition of
![]() $\unicode[STIX]{x1D6F7}$
. We define
$\unicode[STIX]{x1D6F7}$
. We define
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{+} & := & \displaystyle \{\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}\in \unicode[STIX]{x1D6F7}\mid \operatorname{row}(i)<\operatorname{row}(j)\},\nonumber\\ \displaystyle \unicode[STIX]{x1D6F7}_{0} & := & \displaystyle \{\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}\in \unicode[STIX]{x1D6F7}\mid \operatorname{row}(i)=\operatorname{row}(j)\},\nonumber\\ \displaystyle \unicode[STIX]{x1D6F7}_{-} & := & \displaystyle \{\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}\in \unicode[STIX]{x1D6F7}\mid \operatorname{row}(i)>\operatorname{row}(j)\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{+} & := & \displaystyle \{\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}\in \unicode[STIX]{x1D6F7}\mid \operatorname{row}(i)<\operatorname{row}(j)\},\nonumber\\ \displaystyle \unicode[STIX]{x1D6F7}_{0} & := & \displaystyle \{\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}\in \unicode[STIX]{x1D6F7}\mid \operatorname{row}(i)=\operatorname{row}(j)\},\nonumber\\ \displaystyle \unicode[STIX]{x1D6F7}_{-} & := & \displaystyle \{\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}\in \unicode[STIX]{x1D6F7}\mid \operatorname{row}(i)>\operatorname{row}(j)\}.\nonumber\end{eqnarray}$$
Also we define
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}(+) & := & \displaystyle \{\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}\in \unicode[STIX]{x1D6F7}\mid \operatorname{col}(i)<\operatorname{col}(j)\},\nonumber\\ \displaystyle \unicode[STIX]{x1D6F7}(0) & := & \displaystyle \{\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}\in \unicode[STIX]{x1D6F7}\mid \operatorname{col}(i)=\operatorname{col}(j)\},\nonumber\\ \displaystyle \unicode[STIX]{x1D6F7}(-) & := & \displaystyle \{\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}\in \unicode[STIX]{x1D6F7}\mid \operatorname{col}(i)>\operatorname{col}(j)\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}(+) & := & \displaystyle \{\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}\in \unicode[STIX]{x1D6F7}\mid \operatorname{col}(i)<\operatorname{col}(j)\},\nonumber\\ \displaystyle \unicode[STIX]{x1D6F7}(0) & := & \displaystyle \{\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}\in \unicode[STIX]{x1D6F7}\mid \operatorname{col}(i)=\operatorname{col}(j)\},\nonumber\\ \displaystyle \unicode[STIX]{x1D6F7}(-) & := & \displaystyle \{\unicode[STIX]{x1D700}_{i}-\unicode[STIX]{x1D700}_{j}\in \unicode[STIX]{x1D6F7}\mid \operatorname{col}(i)>\operatorname{col}(j)\}.\nonumber\end{eqnarray}$$
Then for
![]() $\unicode[STIX]{x1D702},\unicode[STIX]{x1D709}\in \{-,0,+\}$
, we define
$\unicode[STIX]{x1D702},\unicode[STIX]{x1D709}\in \{-,0,+\}$
, we define
We note that
![]() $\unicode[STIX]{x1D6F7}(0)_{0}=\varnothing$
and that
$\unicode[STIX]{x1D6F7}(0)_{0}=\varnothing$
and that
![]() $\unicode[STIX]{x1D6F7}_{+}\cup \unicode[STIX]{x1D6F7}(+)_{0}$
is the system of positive roots corresponding to
$\unicode[STIX]{x1D6F7}_{+}\cup \unicode[STIX]{x1D6F7}(+)_{0}$
is the system of positive roots corresponding to
![]() $\mathfrak{b}$
. Further,
$\mathfrak{b}$
. Further,
![]() $\unicode[STIX]{x1D6F7}(+)\cup \unicode[STIX]{x1D6F7}(0)_{+}$
is the system of positive roots corresponding to a Borel subalgebra contained in
$\unicode[STIX]{x1D6F7}(+)\cup \unicode[STIX]{x1D6F7}(0)_{+}$
is the system of positive roots corresponding to a Borel subalgebra contained in
![]() $\mathfrak{p}$
, and
$\mathfrak{p}$
, and
![]() $\unicode[STIX]{x1D6F7}(-)\cup \unicode[STIX]{x1D6F7}(0)_{+}$
is another system of positive roots.
$\unicode[STIX]{x1D6F7}(-)\cup \unicode[STIX]{x1D6F7}(0)_{+}$
is another system of positive roots.
Having set up this notation, we are in a position to give the weights that we require. First we define
this is a shifted half sum of positive roots for
![]() $\mathfrak{b}$
, and is given by
$\mathfrak{b}$
, and is given by
where
We note that we should be careful in the above formulas when
![]() $p=2$
, though as the final value of
$p=2$
, though as the final value of
![]() $\unicode[STIX]{x1D70C}$
only involves integer coefficients this is not a problem.
$\unicode[STIX]{x1D70C}$
only involves integer coefficients this is not a problem.
We also require a ‘choice of
![]() $\unicode[STIX]{x1D70C}$
’ corresponding to the system of positive roots
$\unicode[STIX]{x1D70C}$
’ corresponding to the system of positive roots
![]() $\unicode[STIX]{x1D6F7}(+)\cup \unicode[STIX]{x1D6F7}(0)_{+}$
, and we define
$\unicode[STIX]{x1D6F7}(+)\cup \unicode[STIX]{x1D6F7}(0)_{+}$
, and we define
More explicitly, we have
The weight
is important for Theorem 2.2, because
We define
and
which is a shifted choice
![]() $\unicode[STIX]{x1D70C}$
for the Borel subalgebra
$\unicode[STIX]{x1D70C}$
for the Borel subalgebra
![]() $\mathfrak{b}\cap \mathfrak{h}$
of
$\mathfrak{b}\cap \mathfrak{h}$
of
![]() $\mathfrak{h}$
. Further, we define
$\mathfrak{h}$
. Further, we define
and
We note that
![]() $\widetilde{\unicode[STIX]{x1D70C}}$
is a shifted choice of
$\widetilde{\unicode[STIX]{x1D70C}}$
is a shifted choice of
![]() $\unicode[STIX]{x1D70C}$
for the system of positive roots
$\unicode[STIX]{x1D70C}$
for the system of positive roots
![]() $\unicode[STIX]{x1D6F7}(-)\cup \unicode[STIX]{x1D6F7}(0)_{+}$
. An important identity for us is
$\unicode[STIX]{x1D6F7}(-)\cup \unicode[STIX]{x1D6F7}(0)_{+}$
. An important identity for us is
2.5 Some modules for
 $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
The weights introduced in the previous subsection are required to define some modules for
![]() $\mathfrak{h}$
and for
$\mathfrak{h}$
and for
![]() $\mathfrak{g}$
. In what follows it is helpful to note that
$\mathfrak{g}$
. In what follows it is helpful to note that
![]() $\unicode[STIX]{x1D712}|_{\mathfrak{p}}=0$
, so that we can view
$\unicode[STIX]{x1D712}|_{\mathfrak{p}}=0$
, so that we can view
![]() $U_{0}(\mathfrak{h})\subseteq U_{0}(\mathfrak{p})\subseteq U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
.
$U_{0}(\mathfrak{h})\subseteq U_{0}(\mathfrak{p})\subseteq U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
.
We note that
![]() $\unicode[STIX]{x1D706}\in \mathfrak{t}^{\ast }$
is the weight of a one-dimensional
$\unicode[STIX]{x1D706}\in \mathfrak{t}^{\ast }$
is the weight of a one-dimensional
![]() $U(\mathfrak{h})$
-module if and only if
$U(\mathfrak{h})$
-module if and only if
![]() $\unicode[STIX]{x1D706}(e_{i,i})=\unicode[STIX]{x1D706}(e_{j,j})$
whenever
$\unicode[STIX]{x1D706}(e_{i,i})=\unicode[STIX]{x1D706}(e_{j,j})$
whenever
![]() $\operatorname{col}(i)=\operatorname{col}(j)$
, and also that
$\operatorname{col}(i)=\operatorname{col}(j)$
, and also that
![]() $\widetilde{\unicode[STIX]{x1D70C}}(e_{i,i})=\widetilde{\unicode[STIX]{x1D70C}}(e_{j,j})-1$
, when the
$\widetilde{\unicode[STIX]{x1D70C}}(e_{i,i})=\widetilde{\unicode[STIX]{x1D70C}}(e_{j,j})-1$
, when the
![]() $i$
th box in
$i$
th box in
![]() $\unicode[STIX]{x1D70B}$
is directly above the
$\unicode[STIX]{x1D70B}$
is directly above the
![]() $j$
th box. Thus, for
$j$
th box. Thus, for
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
, we deduce that
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
, we deduce that
![]() $\unicode[STIX]{x1D706}_{A}-\widetilde{\unicode[STIX]{x1D70C}}$
is the weight of a one-dimensional
$\unicode[STIX]{x1D706}_{A}-\widetilde{\unicode[STIX]{x1D70C}}$
is the weight of a one-dimensional
![]() $U(\mathfrak{h})$
-module if and only if
$U(\mathfrak{h})$
-module if and only if
![]() $A$
is column connected. For column connected
$A$
is column connected. For column connected
![]() $A$
we denote this one-dimensional
$A$
we denote this one-dimensional
![]() $U(\mathfrak{h})$
-module by
$U(\mathfrak{h})$
-module by
![]() $\widetilde{\Bbbk }_{A}$
.
$\widetilde{\Bbbk }_{A}$
.
Similarly, given
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
, we have that
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
, we have that
![]() $\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}$
is the weight of a one-dimensional
$\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}$
is the weight of a one-dimensional
![]() $U(\mathfrak{h})$
-module if and only if
$U(\mathfrak{h})$
-module if and only if
![]() $A$
is column connected. In this case we denote the one-dimensional
$A$
is column connected. In this case we denote the one-dimensional
![]() $U(\mathfrak{h})$
-module by
$U(\mathfrak{h})$
-module by
![]() $\overline{\Bbbk }_{A}$
, and note that it factors to a module for
$\overline{\Bbbk }_{A}$
, and note that it factors to a module for
![]() $U_{0}(\mathfrak{h})$
if and only if
$U_{0}(\mathfrak{h})$
if and only if
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
. For
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
. For
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
, we can inflate
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
, we can inflate
![]() $\overline{\Bbbk }_{A}$
to a
$\overline{\Bbbk }_{A}$
to a
![]() $U_{0}(\mathfrak{p})$
-module and consider the induced module
$U_{0}(\mathfrak{p})$
-module and consider the induced module
![]() $N_{\unicode[STIX]{x1D712}}(A):=U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{0}(\mathfrak{p})}\overline{\Bbbk }_{A}$
. We have that
$N_{\unicode[STIX]{x1D712}}(A):=U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{0}(\mathfrak{p})}\overline{\Bbbk }_{A}$
. We have that
![]() $N_{\unicode[STIX]{x1D712}}(A)\cong U_{\unicode[STIX]{x1D712}}(\mathfrak{m})$
as a
$N_{\unicode[STIX]{x1D712}}(A)\cong U_{\unicode[STIX]{x1D712}}(\mathfrak{m})$
as a
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{m})$
-module, so that
$U_{\unicode[STIX]{x1D712}}(\mathfrak{m})$
-module, so that
![]() $\dim N_{\unicode[STIX]{x1D712}}(A)=p^{\dim \mathfrak{m}}=p^{d_{\unicode[STIX]{x1D712}}}$
and
$\dim N_{\unicode[STIX]{x1D712}}(A)=p^{\dim \mathfrak{m}}=p^{d_{\unicode[STIX]{x1D712}}}$
and
![]() $N_{\unicode[STIX]{x1D712}}(A)$
is a minimal-dimensional
$N_{\unicode[STIX]{x1D712}}(A)$
is a minimal-dimensional
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module.
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module.
Let
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
. We define
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
. We define
![]() $\Bbbk _{A}$
to be the one-dimensional
$\Bbbk _{A}$
to be the one-dimensional
![]() $U_{0}(\mathfrak{b})$
-module where
$U_{0}(\mathfrak{b})$
-module where
![]() $\mathfrak{t}$
acts by
$\mathfrak{t}$
acts by
![]() $\unicode[STIX]{x1D706}_{A}-\unicode[STIX]{x1D70C}$
, and the nilradical of
$\unicode[STIX]{x1D706}_{A}-\unicode[STIX]{x1D70C}$
, and the nilradical of
![]() $\mathfrak{b}$
acts trivially. The baby Verma module
$\mathfrak{b}$
acts trivially. The baby Verma module
![]() $Z_{\unicode[STIX]{x1D712}}(A)$
is defined to be
$Z_{\unicode[STIX]{x1D712}}(A)$
is defined to be
![]() $Z_{\unicode[STIX]{x1D712}}(A):=U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{0}(\mathfrak{b})}\Bbbk _{A}$
. Since
$Z_{\unicode[STIX]{x1D712}}(A):=U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{0}(\mathfrak{b})}\Bbbk _{A}$
. Since
![]() $\unicode[STIX]{x1D712}$
is in standard Levi form for the Levi subalgebra
$\unicode[STIX]{x1D712}$
is in standard Levi form for the Levi subalgebra
![]() $\mathfrak{g}_{0}$
with basis
$\mathfrak{g}_{0}$
with basis
![]() $\{e_{i,j}\mid \operatorname{row}(i)=\operatorname{row}(j)\}$
,
$\{e_{i,j}\mid \operatorname{row}(i)=\operatorname{row}(j)\}$
,
![]() $Z_{\unicode[STIX]{x1D712}}(A)$
has a simple head, which we denote by
$Z_{\unicode[STIX]{x1D712}}(A)$
has a simple head, which we denote by
![]() $L_{\unicode[STIX]{x1D712}}(A)$
; this essentially follows from the results in [Reference Friedlander and ParshallFP90, §3] (see also [Reference Jantzen and BroerJan98, Proposition 10.7]). Moreover, we have that
$L_{\unicode[STIX]{x1D712}}(A)$
; this essentially follows from the results in [Reference Friedlander and ParshallFP90, §3] (see also [Reference Jantzen and BroerJan98, Proposition 10.7]). Moreover, we have that
![]() $L_{\unicode[STIX]{x1D712}}(A)\cong L_{\unicode[STIX]{x1D712}}(A^{\prime })$
if and only if
$L_{\unicode[STIX]{x1D712}}(A)\cong L_{\unicode[STIX]{x1D712}}(A^{\prime })$
if and only if
![]() $A$
is row equivalent to
$A$
is row equivalent to
![]() $A^{\prime }$
; see [Reference Friedlander and ParshallFP90, Corollary 3.5] or [Reference Jantzen and BroerJan98, Proposition 10.8]. To see this we note that the shift by
$A^{\prime }$
; see [Reference Friedlander and ParshallFP90, Corollary 3.5] or [Reference Jantzen and BroerJan98, Proposition 10.8]. To see this we note that the shift by
![]() $\unicode[STIX]{x1D70C}$
in our labelling of the simple modules transforms the dot action of the
$\unicode[STIX]{x1D70C}$
in our labelling of the simple modules transforms the dot action of the
![]() $W_{0}$
on
$W_{0}$
on
![]() $\mathfrak{t}^{\ast }$
in [Reference Friedlander and ParshallFP90] to the standard action, where
$\mathfrak{t}^{\ast }$
in [Reference Friedlander and ParshallFP90] to the standard action, where
![]() $W_{0}$
is the Weyl group of
$W_{0}$
is the Weyl group of
![]() $\mathfrak{g}_{0}$
with respect to
$\mathfrak{g}_{0}$
with respect to
![]() $T$
; and then this action corresponds to permutations of the entries of a row of a tableau. Given a
$T$
; and then this action corresponds to permutations of the entries of a row of a tableau. Given a
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module
![]() $M$
, we say
$M$
, we say
![]() $v\in M$
is a highest weight vector (for
$v\in M$
is a highest weight vector (for
![]() $\mathfrak{b}$
) of weight
$\mathfrak{b}$
) of weight
![]() $\unicode[STIX]{x1D706}\in \mathfrak{t}^{\ast }$
if
$\unicode[STIX]{x1D706}\in \mathfrak{t}^{\ast }$
if
![]() $\mathfrak{b}v\subseteq \Bbbk v$
and
$\mathfrak{b}v\subseteq \Bbbk v$
and
![]() $tv=\unicode[STIX]{x1D706}(t)v$
for all
$tv=\unicode[STIX]{x1D706}(t)v$
for all
![]() $t\in \mathfrak{t}$
; so if
$t\in \mathfrak{t}$
; so if
![]() $v\in M$
is a highest weight vector of weight
$v\in M$
is a highest weight vector of weight
![]() $\unicode[STIX]{x1D706}_{A}-\unicode[STIX]{x1D70C}$
, then there is a homomorphism
$\unicode[STIX]{x1D706}_{A}-\unicode[STIX]{x1D70C}$
, then there is a homomorphism
![]() $Z_{\unicode[STIX]{x1D712}}(A)\rightarrow M$
sending
$Z_{\unicode[STIX]{x1D712}}(A)\rightarrow M$
sending
![]() $1\otimes 1_{A}$
to
$1\otimes 1_{A}$
to
![]() $v$
, where
$v$
, where
![]() $1_{A}$
denotes the generator of
$1_{A}$
denotes the generator of
![]() $\Bbbk _{A}$
.
$\Bbbk _{A}$
.
The following theorem is key to this paper and gives a compatibility between the modules
![]() $L_{\unicode[STIX]{x1D712}}(A)$
and
$L_{\unicode[STIX]{x1D712}}(A)$
and
![]() $N_{\unicode[STIX]{x1D712}}(A)$
.
$N_{\unicode[STIX]{x1D712}}(A)$
.
Theorem 2.2. For column connected
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
we have that
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
we have that
![]() $L_{\unicode[STIX]{x1D712}}(A)\cong N_{\unicode[STIX]{x1D712}}(A)$
which has dimension
$L_{\unicode[STIX]{x1D712}}(A)\cong N_{\unicode[STIX]{x1D712}}(A)$
which has dimension
![]() $p^{d_{\unicode[STIX]{x1D712}}}$
. In particular, for column connected
$p^{d_{\unicode[STIX]{x1D712}}}$
. In particular, for column connected
![]() $A,A^{\prime }\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
, we have that
$A,A^{\prime }\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
, we have that
![]() $N_{\unicode[STIX]{x1D712}}(A)\cong N_{\unicode[STIX]{x1D712}}(A^{\prime })$
if and only if
$N_{\unicode[STIX]{x1D712}}(A)\cong N_{\unicode[STIX]{x1D712}}(A^{\prime })$
if and only if
![]() $A$
is row equivalent to
$A$
is row equivalent to
![]() $A^{\prime }$
.
$A^{\prime }$
.
Proof. From the discussion above, we know that
![]() $N_{\unicode[STIX]{x1D712}}(A)$
has dimension
$N_{\unicode[STIX]{x1D712}}(A)$
has dimension
![]() $p^{d_{\unicode[STIX]{x1D712}}}$
, so it is a minimal module for
$p^{d_{\unicode[STIX]{x1D712}}}$
, so it is a minimal module for
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
and thus simple. It follows that if we can find a highest weight vector
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
and thus simple. It follows that if we can find a highest weight vector
![]() $v\in N_{\unicode[STIX]{x1D712}}(A)$
for
$v\in N_{\unicode[STIX]{x1D712}}(A)$
for
![]() $\mathfrak{b}$
of weight
$\mathfrak{b}$
of weight
![]() $\unicode[STIX]{x1D706}_{A}-\unicode[STIX]{x1D70C}$
, then
$\unicode[STIX]{x1D706}_{A}-\unicode[STIX]{x1D70C}$
, then
![]() $L_{\unicode[STIX]{x1D712}}(A)\cong N_{\unicode[STIX]{x1D712}}(A)$
as required. This can be seen by noting that the homomorphism
$L_{\unicode[STIX]{x1D712}}(A)\cong N_{\unicode[STIX]{x1D712}}(A)$
as required. This can be seen by noting that the homomorphism
![]() $Z_{\unicode[STIX]{x1D712}}(A)\rightarrow N_{\unicode[STIX]{x1D712}}(A)$
will factor to give this isomorphism. The claim regarding row equivalence was justified in the remarks preceding the statement of the theorem.
$Z_{\unicode[STIX]{x1D712}}(A)\rightarrow N_{\unicode[STIX]{x1D712}}(A)$
will factor to give this isomorphism. The claim regarding row equivalence was justified in the remarks preceding the statement of the theorem.
We observe that the root vectors corresponding to roots in
![]() $\unicode[STIX]{x1D6F7}(-)_{+}$
span a
$\unicode[STIX]{x1D6F7}(-)_{+}$
span a
![]() $p$
-nilpotent subalgebra
$p$
-nilpotent subalgebra
![]() $\mathfrak{a}$
of
$\mathfrak{a}$
of
![]() $\mathfrak{g}$
. We let
$\mathfrak{g}$
. We let
so that
![]() $\mathfrak{a}$
has basis
$\mathfrak{a}$
has basis
![]() $\{e_{i,j}\mid (i,j)\in I\}$
. Since all of the elements of this basis have non-zero
$\{e_{i,j}\mid (i,j)\in I\}$
. Since all of the elements of this basis have non-zero
![]() $\mathfrak{t}^{e}$
weight, we see that the restriction of
$\mathfrak{t}^{e}$
weight, we see that the restriction of
![]() $\unicode[STIX]{x1D712}$
to
$\unicode[STIX]{x1D712}$
to
![]() $\mathfrak{a}$
is zero. Hence, the restricted enveloping algebra
$\mathfrak{a}$
is zero. Hence, the restricted enveloping algebra
![]() $U_{0}(\mathfrak{a})$
embeds in
$U_{0}(\mathfrak{a})$
embeds in
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
, and consequently
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
, and consequently
![]() $e_{i,j}^{p}=0$
in
$e_{i,j}^{p}=0$
in
![]() $U_{0}(\mathfrak{a})\subseteq U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
for
$U_{0}(\mathfrak{a})\subseteq U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
for
![]() $(i,j)\in I$
.
$(i,j)\in I$
.
There is an action of
![]() $T$
on
$T$
on
![]() $U_{0}(\mathfrak{a})$
, and
$U_{0}(\mathfrak{a})$
, and
is in the unique weight space of maximal weight (with respect to the positive roots for
![]() $\mathfrak{b}$
). Further, this weight space is one-dimensional, which implies that the product in (11) can be taken in any order (up to rescaling).
$\mathfrak{b}$
). Further, this weight space is one-dimensional, which implies that the product in (11) can be taken in any order (up to rescaling).
Let
![]() $\overline{1}_{A}$
denote the generator of
$\overline{1}_{A}$
denote the generator of
![]() $\overline{\Bbbk }_{A}$
. Observe that under the adjoint action
$\overline{\Bbbk }_{A}$
. Observe that under the adjoint action
![]() $\mathfrak{t}$
acts on
$\mathfrak{t}$
acts on
![]() $u$
with weight
$u$
with weight
![]() $(p-1)\unicode[STIX]{x1D6FE}=-\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D70C}-\overline{\unicode[STIX]{x1D70C}}$
by (8). Therefore,
$(p-1)\unicode[STIX]{x1D6FE}=-\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D70C}-\overline{\unicode[STIX]{x1D70C}}$
by (8). Therefore,
![]() $v:=u\otimes \overline{1}_{A}$
is a weight vector for
$v:=u\otimes \overline{1}_{A}$
is a weight vector for
![]() $\mathfrak{t}$
with weight
$\mathfrak{t}$
with weight
![]() $\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}+(\overline{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D70C})=\unicode[STIX]{x1D706}_{A}-\unicode[STIX]{x1D70C}$
. In order to complete the proof we must show
$\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}+(\overline{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D70C})=\unicode[STIX]{x1D706}_{A}-\unicode[STIX]{x1D70C}$
. In order to complete the proof we must show
![]() $v$
is a highest weight vector for the action of
$v$
is a highest weight vector for the action of
![]() $\mathfrak{b}$
, which requires us to show that
$\mathfrak{b}$
, which requires us to show that
![]() $e_{i,i+1}v=0$
for
$e_{i,i+1}v=0$
for
![]() $i=1,\ldots ,N-1$
.
$i=1,\ldots ,N-1$
.
We first deal with the case where
![]() $\operatorname{row}(i)=\operatorname{row}(i+1)$
and we let
$\operatorname{row}(i)=\operatorname{row}(i+1)$
and we let
![]() $r:=\operatorname{row}(i)$
. We begin by decomposing
$r:=\operatorname{row}(i)$
. We begin by decomposing
![]() $I$
into four subsets:
$I$
into four subsets:
 $$\begin{eqnarray}\displaystyle I_{1} & := & \displaystyle \{(j,k)\in I\mid \operatorname{row}(j)=r\};\nonumber\\ \displaystyle I_{2} & := & \displaystyle \{(j,k)\in I\mid \operatorname{row}(k)=r\};\nonumber\\ \displaystyle I_{3} & := & \displaystyle \{(j,k)\in I\mid \operatorname{row}(j)<r,\operatorname{row}(k)>r\};\nonumber\\ \displaystyle I_{4} & := & \displaystyle \{(j,k)\in I\mid (j,k)\notin I_{1}\cup I_{2}\cup I_{3}\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{1} & := & \displaystyle \{(j,k)\in I\mid \operatorname{row}(j)=r\};\nonumber\\ \displaystyle I_{2} & := & \displaystyle \{(j,k)\in I\mid \operatorname{row}(k)=r\};\nonumber\\ \displaystyle I_{3} & := & \displaystyle \{(j,k)\in I\mid \operatorname{row}(j)<r,\operatorname{row}(k)>r\};\nonumber\\ \displaystyle I_{4} & := & \displaystyle \{(j,k)\in I\mid (j,k)\notin I_{1}\cup I_{2}\cup I_{3}\}.\nonumber\end{eqnarray}$$
We record three facts about commuting elements which are straightforward to verify directly.
Fact 1.
![]() $e_{i,i+1}$
commutes with
$e_{i,i+1}$
commutes with
![]() $e_{j,k}$
for
$e_{j,k}$
for
![]() $(j,k)\in I_{3}\cup I_{4}$
.
$(j,k)\in I_{3}\cup I_{4}$
.
Fact 2. The elements
![]() $\{e_{j,k}\mid (j,k)\in I_{1}\cup I_{3}\}$
pairwise commute.
$\{e_{j,k}\mid (j,k)\in I_{1}\cup I_{3}\}$
pairwise commute.
Fact 3. The elements
![]() $\{e_{j,k}\mid (j,k)\in I_{2}\cup I_{3}\}$
pairwise commute.
$\{e_{j,k}\mid (j,k)\in I_{2}\cup I_{3}\}$
pairwise commute.
For
![]() $s=1,2,3$
, we see that
$s=1,2,3$
, we see that
![]() $\{e_{j,k}\mid (j,k)\in I_{s}\}$
is the basis of an abelian subalgebra of
$\{e_{j,k}\mid (j,k)\in I_{s}\}$
is the basis of an abelian subalgebra of
![]() $\mathfrak{a}$
. Therefore, the element
$\mathfrak{a}$
. Therefore, the element
![]() $u_{s}:=\prod _{(j,k)\in I_{s}}e_{j,k}^{p-1}$
does not depend on the order of the product. We choose an arbitrary ordering of
$u_{s}:=\prod _{(j,k)\in I_{s}}e_{j,k}^{p-1}$
does not depend on the order of the product. We choose an arbitrary ordering of
![]() $I_{4}$
and let
$I_{4}$
and let
![]() $u_{4}:=\prod _{(j,k)\in I_{4}}e_{j,k}^{p-1}$
.
$u_{4}:=\prod _{(j,k)\in I_{4}}e_{j,k}^{p-1}$
.
We proceed with three claims, which we use to show that
![]() $e_{i,i+1}v=0$
.
$e_{i,i+1}v=0$
.
Claim 1.
![]() $(\operatorname{ad}(e_{i,i+1})u_{1})\otimes \overline{1}_{A}=0$
.
$(\operatorname{ad}(e_{i,i+1})u_{1})\otimes \overline{1}_{A}=0$
.
Observe that
![]() $\operatorname{ad}(e_{i,i+1})u_{1}$
is a sum of expressions of the form
$\operatorname{ad}(e_{i,i+1})u_{1}$
is a sum of expressions of the form
where
![]() $(i+1,l)\in I_{1}$
, and the product is taken over all
$(i+1,l)\in I_{1}$
, and the product is taken over all
![]() $(j,k)\neq (i+1,l)\in I_{1}$
. Since all matrix units occurring in (12) are of the form
$(j,k)\neq (i+1,l)\in I_{1}$
. Since all matrix units occurring in (12) are of the form
![]() $e_{a,b}$
with
$e_{a,b}$
with
![]() $\operatorname{row}(a)=r$
and
$\operatorname{row}(a)=r$
and
![]() $\operatorname{row}(b)>r$
, all of these factors commute so can be reordered.
$\operatorname{row}(b)>r$
, all of these factors commute so can be reordered.
We consider two cases to complete the proof of Claim 1. The first case is when
![]() $(i,l)\in I_{1}$
. Then
$(i,l)\in I_{1}$
. Then
![]() $u_{1}^{(i+1,l)}$
contains a factor of
$u_{1}^{(i+1,l)}$
contains a factor of
![]() $e_{i,l}^{p}$
, so that
$e_{i,l}^{p}$
, so that
![]() $u_{1}^{(i+1,l)}=0$
. The second case is when
$u_{1}^{(i+1,l)}=0$
. The second case is when
![]() $\operatorname{col}(i)=\operatorname{col}(l)$
and so
$\operatorname{col}(i)=\operatorname{col}(l)$
and so
![]() $e_{i,l}\in [\mathfrak{h},\mathfrak{h}]$
. In this case
$e_{i,l}\in [\mathfrak{h},\mathfrak{h}]$
. In this case
![]() $e_{i,l}\overline{1}_{A}=0$
and so
$e_{i,l}\overline{1}_{A}=0$
and so
![]() $u_{1}^{(i+1,l)}\otimes \overline{1}_{A}=0$
.
$u_{1}^{(i+1,l)}\otimes \overline{1}_{A}=0$
.
Claim 2.
![]() $u_{3}e_{j,k}u_{1}\otimes \overline{1}_{A}=0$
whenever
$u_{3}e_{j,k}u_{1}\otimes \overline{1}_{A}=0$
whenever
![]() $\operatorname{col}(j)=\operatorname{col}(k)$
and
$\operatorname{col}(j)=\operatorname{col}(k)$
and
![]() $\operatorname{row}(j)<\operatorname{row}(k)=r$
.
$\operatorname{row}(j)<\operatorname{row}(k)=r$
.
We have
![]() $e_{j,k}\in [\mathfrak{h},\mathfrak{h}]$
, so
$e_{j,k}\in [\mathfrak{h},\mathfrak{h}]$
, so
![]() $e_{j,k}\overline{1}_{A}=0$
. Thus it suffices to show that
$e_{j,k}\overline{1}_{A}=0$
. Thus it suffices to show that
![]() $u_{3}(\operatorname{ad}(e_{j,k})u_{1})=0$
. Observe that
$u_{3}(\operatorname{ad}(e_{j,k})u_{1})=0$
. Observe that
![]() $\operatorname{ad}(e_{j,k})u_{1}$
is a sum of monomials of the form
$\operatorname{ad}(e_{j,k})u_{1}$
is a sum of monomials of the form
where
![]() $(k,l)\in I_{1}$
and the product is taken over
$(k,l)\in I_{1}$
and the product is taken over
![]() $(k^{\prime },l^{\prime })\neq (k,l)\in I_{1}$
. Similar to the comments following (12), the matrix units occurring in (13) all commute and so can be reordered. Since
$(k^{\prime },l^{\prime })\neq (k,l)\in I_{1}$
. Similar to the comments following (12), the matrix units occurring in (13) all commute and so can be reordered. Since
![]() $\operatorname{row}(j)<r$
and
$\operatorname{row}(j)<r$
and
![]() $\operatorname{row}(l)>\operatorname{row}(k)=r$
, we have
$\operatorname{row}(l)>\operatorname{row}(k)=r$
, we have
![]() $e_{j,l}\in I_{3}$
. Applying Fact 3 above, we see that
$e_{j,l}\in I_{3}$
. Applying Fact 3 above, we see that
![]() $u_{3}e_{j,l}e_{k,l}^{p-2}\prod e_{k^{\prime },l^{\prime }}^{p-1}$
contains a factor of
$u_{3}e_{j,l}e_{k,l}^{p-2}\prod e_{k^{\prime },l^{\prime }}^{p-1}$
contains a factor of
![]() $e_{j,l}^{p}$
, hence is equal to 0. This proves Claim 2.
$e_{j,l}^{p}$
, hence is equal to 0. This proves Claim 2.
Claim 3.
![]() $u_{3}(\operatorname{ad}(e_{i,i+1})u_{2})u_{1}\otimes \overline{1}_{A}=0$
.
$u_{3}(\operatorname{ad}(e_{i,i+1})u_{2})u_{1}\otimes \overline{1}_{A}=0$
.
Observe that
![]() $\operatorname{ad}(e_{i,i+1})u_{2}$
is a sum of expressions of the form
$\operatorname{ad}(e_{i,i+1})u_{2}$
is a sum of expressions of the form
where
![]() $(l,i)\in I_{2}$
and the product is taken over all
$(l,i)\in I_{2}$
and the product is taken over all
![]() $(j,k)\in I_{2}$
with
$(j,k)\in I_{2}$
with
![]() $(j,k)\neq (l,i)$
. The matrix units occurring here all commute, so can be reordered. We consider two cases. The first case is when
$(j,k)\neq (l,i)$
. The matrix units occurring here all commute, so can be reordered. We consider two cases. The first case is when
![]() $(l,i+1)\in I_{2}$
. Then
$(l,i+1)\in I_{2}$
. Then
![]() $u_{2}^{(l,i)}$
contains a factor of
$u_{2}^{(l,i)}$
contains a factor of
![]() $e_{l,i+1}^{p}$
and
$e_{l,i+1}^{p}$
and
![]() $u_{2}^{(l,i)}=0$
. The second case is when
$u_{2}^{(l,i)}=0$
. The second case is when
![]() $\operatorname{col}(l)=\operatorname{col}(i+1)$
. Then we can use Claim 2 along with Fact 3 to show that
$\operatorname{col}(l)=\operatorname{col}(i+1)$
. Then we can use Claim 2 along with Fact 3 to show that
![]() $u_{3}u_{2}^{(l,i)}u_{1}\otimes \overline{1}_{A}=0$
. This completes the proof of Claim 3.
$u_{3}u_{2}^{(l,i)}u_{1}\otimes \overline{1}_{A}=0$
. This completes the proof of Claim 3.
We now combine these claims to prove that
![]() $e_{i,i+1}v=0$
. Since
$e_{i,i+1}v=0$
. Since
![]() $e_{i,i+1}$
lies in the nilradical of
$e_{i,i+1}$
lies in the nilradical of
![]() $\mathfrak{p}$
, we have that
$\mathfrak{p}$
, we have that
![]() $e_{i,i+1}\overline{1}_{A}=0$
. Thus it suffices to prove
$e_{i,i+1}\overline{1}_{A}=0$
. Thus it suffices to prove
![]() $\operatorname{ad}(e_{i,i+1})(u_{4}u_{3}u_{2}u_{1})\otimes \overline{1}_{A}=0$
. Applying Fact 1, we only need to check
$\operatorname{ad}(e_{i,i+1})(u_{4}u_{3}u_{2}u_{1})\otimes \overline{1}_{A}=0$
. Applying Fact 1, we only need to check
![]() $u_{4}u_{3}(\operatorname{ad}(e_{i,i+1})u_{2})u_{1}\otimes \overline{1}_{A}=0$
and
$u_{4}u_{3}(\operatorname{ad}(e_{i,i+1})u_{2})u_{1}\otimes \overline{1}_{A}=0$
and
![]() $u_{4}u_{3}u_{2}(\operatorname{ad}(e_{i,i+1})u_{1})\otimes \overline{1}_{A}=0$
, which are given by Claim 3 and Claim 1, respectively.
$u_{4}u_{3}u_{2}(\operatorname{ad}(e_{i,i+1})u_{1})\otimes \overline{1}_{A}=0$
, which are given by Claim 3 and Claim 1, respectively.
We move on to deal with the case
![]() $\operatorname{row}(i)<\operatorname{row}(i+1)$
, and show that
$\operatorname{row}(i)<\operatorname{row}(i+1)$
, and show that
![]() $e_{i,i+1}v=0$
.
$e_{i,i+1}v=0$
.
For this case first suppose that
![]() $\operatorname{col}(i)>\operatorname{col}(i+1)$
. Then we have
$\operatorname{col}(i)>\operatorname{col}(i+1)$
. Then we have
![]() $e_{i,i+1}\in \mathfrak{a}$
. By the remarks following (11), we can write
$e_{i,i+1}\in \mathfrak{a}$
. By the remarks following (11), we can write
![]() $u=e_{i,i+1}^{p-1}u_{0}$
for some
$u=e_{i,i+1}^{p-1}u_{0}$
for some
![]() $u_{0}\in U_{0}(\mathfrak{a})$
and so
$u_{0}\in U_{0}(\mathfrak{a})$
and so
![]() $e_{i,i+1}u=0$
, which implies that
$e_{i,i+1}u=0$
, which implies that
![]() $e_{i,i+1}v=0$
.
$e_{i,i+1}v=0$
.
The case where
![]() $\operatorname{col}(i)=\operatorname{col}(i+1)$
only happens when
$\operatorname{col}(i)=\operatorname{col}(i+1)$
only happens when
![]() $p_{\operatorname{row}(i)}=1$
and
$p_{\operatorname{row}(i)}=1$
and
![]() $s_{i+1,i}=0$
. Then we have
$s_{i+1,i}=0$
. Then we have
![]() $e_{i,i+1}\in [\mathfrak{h},\mathfrak{h}]$
and
$e_{i,i+1}\in [\mathfrak{h},\mathfrak{h}]$
and
![]() $e_{i,i+1}\overline{1}_{A}=0$
, so we are just required to show that
$e_{i,i+1}\overline{1}_{A}=0$
, so we are just required to show that
![]() $[e_{i,i+1},u]=0$
. This is done with commutator arguments similar to those used above, so we omit the details.◻
$[e_{i,i+1},u]=0$
. This is done with commutator arguments similar to those used above, so we omit the details.◻
2.6 The
 $W$
-algebra
$W$
-algebra
 $U(\mathfrak{g},e)$
and its
$U(\mathfrak{g},e)$
and its
 $p$
-centre
$p$
-centre
Since
![]() $e\in \mathfrak{g}(1)$
, we have that
$e\in \mathfrak{g}(1)$
, we have that
![]() $\unicode[STIX]{x1D712}$
vanishes on
$\unicode[STIX]{x1D712}$
vanishes on
![]() $\mathfrak{g}(k)$
for
$\mathfrak{g}(k)$
for
![]() $k\neq -1$
. Therefore,
$k\neq -1$
. Therefore,
![]() $\unicode[STIX]{x1D712}$
restricts to a character of
$\unicode[STIX]{x1D712}$
restricts to a character of
![]() $\mathfrak{m}$
. We define
$\mathfrak{m}$
. We define
![]() $\mathfrak{m}_{\unicode[STIX]{x1D712}}:=\{x-\unicode[STIX]{x1D712}(x)\mid x\in \mathfrak{m}\}\subseteq U(\mathfrak{g})$
, which is a Lie subalgebra of
$\mathfrak{m}_{\unicode[STIX]{x1D712}}:=\{x-\unicode[STIX]{x1D712}(x)\mid x\in \mathfrak{m}\}\subseteq U(\mathfrak{g})$
, which is a Lie subalgebra of
![]() $U(\mathfrak{g})$
. By the PBW theorem there is a direct sum decomposition
$U(\mathfrak{g})$
. By the PBW theorem there is a direct sum decomposition
We let
![]() $\operatorname{pr}:U(\mathfrak{g})\rightarrow U(\mathfrak{p})$
be the projection onto the second factor. Also we abbreviate and write
$\operatorname{pr}:U(\mathfrak{g})\rightarrow U(\mathfrak{p})$
be the projection onto the second factor. Also we abbreviate and write
![]() $I:=U(\mathfrak{g})\mathfrak{m}_{\unicode[STIX]{x1D712}}$
, and define
$I:=U(\mathfrak{g})\mathfrak{m}_{\unicode[STIX]{x1D712}}$
, and define
![]() $Q:=U(\mathfrak{g})/I$
.
$Q:=U(\mathfrak{g})/I$
.
As explained in [Reference Goodwin and TopleyGT18, §4.3], the adjoint action of
![]() $M$
on
$M$
on
![]() $U(\mathfrak{g})$
gives an adjoint action of
$U(\mathfrak{g})$
gives an adjoint action of
![]() $M$
on
$M$
on
![]() $Q$
. In [Reference Goodwin and TopleyGT18, Definition 4.3] the
$Q$
. In [Reference Goodwin and TopleyGT18, Definition 4.3] the
![]() $W$
-algebra associated to
$W$
-algebra associated to
![]() $e$
is defined to be
$e$
is defined to be
In this paper, we prefer to work with an equivalent realization of
![]() $U(\mathfrak{g},e)$
as a subalgebra of
$U(\mathfrak{g},e)$
as a subalgebra of
![]() $U(\mathfrak{p})$
. For this we require the twisted adjoint action of
$U(\mathfrak{p})$
. For this we require the twisted adjoint action of
![]() $M$
on
$M$
on
![]() $U(\mathfrak{p})$
, which is defined by
$U(\mathfrak{p})$
, which is defined by
for
![]() $g\in M$
and
$g\in M$
and
![]() $u\in U(\mathfrak{p})$
. By using
$u\in U(\mathfrak{p})$
. By using
![]() $\operatorname{pr}$
to identify
$\operatorname{pr}$
to identify
![]() $U(\mathfrak{g})/I$
with
$U(\mathfrak{g})/I$
with
![]() $U(\mathfrak{p})$
, we can equivalently define the
$U(\mathfrak{p})$
, we can equivalently define the
![]() $W$
-algebra associated to
$W$
-algebra associated to
![]() $e$
to be the invariant subalgebra
$e$
to be the invariant subalgebra
We want to recast some of the material from [Reference Goodwin and TopleyGT18, §8] to our setting where
![]() $U(\mathfrak{g},e)=U(\mathfrak{p})^{\operatorname{tw}(M)}$
. We begin with the
$U(\mathfrak{g},e)=U(\mathfrak{p})^{\operatorname{tw}(M)}$
. We begin with the
![]() $p$
-centre of
$p$
-centre of
![]() $U(\mathfrak{g},e)$
, and to define this we note that the
$U(\mathfrak{g},e)$
, and to define this we note that the
![]() $p$
-centre
$p$
-centre
![]() $Z_{p}(\mathfrak{p})$
of
$Z_{p}(\mathfrak{p})$
of
![]() $U(\mathfrak{p})$
is stable under the twisted adjoint action of
$U(\mathfrak{p})$
is stable under the twisted adjoint action of
![]() $M$
of
$M$
of
![]() $U(\mathfrak{p})$
. The
$U(\mathfrak{p})$
. The
![]() $p$
-centre of
$p$
-centre of
![]() $U(\mathfrak{g},e)$
is defined in [Reference Goodwin and TopleyGT18, Definition 8.1], and in our setting, it is given by
$U(\mathfrak{g},e)$
is defined in [Reference Goodwin and TopleyGT18, Definition 8.1], and in our setting, it is given by
Let
![]() $\unicode[STIX]{x1D713}\in \mathfrak{p}^{\ast }\subseteq \mathfrak{g}^{\ast }$
. We write
$\unicode[STIX]{x1D713}\in \mathfrak{p}^{\ast }\subseteq \mathfrak{g}^{\ast }$
. We write
![]() $J_{\unicode[STIX]{x1D713}}^{\mathfrak{p}}$
for the ideal of
$J_{\unicode[STIX]{x1D713}}^{\mathfrak{p}}$
for the ideal of
![]() $U(\mathfrak{p})$
generated by
$U(\mathfrak{p})$
generated by
![]() $\{x^{p}-x^{[p]}-\unicode[STIX]{x1D713}(x)^{p}\mid x\in \mathfrak{p}\}$
. Then the reduced
$\{x^{p}-x^{[p]}-\unicode[STIX]{x1D713}(x)^{p}\mid x\in \mathfrak{p}\}$
. Then the reduced
![]() $W$
-algebra corresponding to
$W$
-algebra corresponding to
![]() $\unicode[STIX]{x1D713}$
is defined to be
$\unicode[STIX]{x1D713}$
is defined to be
We note that our notation here differs from that used in [Reference Goodwin and TopleyGT18, Definition 8.5] by a shift of
![]() $\unicode[STIX]{x1D712}$
, that is,
$\unicode[STIX]{x1D712}$
, that is,
![]() $U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)$
here would be denoted
$U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)$
here would be denoted
![]() $U_{\unicode[STIX]{x1D712}+\unicode[STIX]{x1D713}}(\mathfrak{g},e)$
there (to make sense of
$U_{\unicode[STIX]{x1D712}+\unicode[STIX]{x1D713}}(\mathfrak{g},e)$
there (to make sense of
![]() $\unicode[STIX]{x1D712}+\unicode[STIX]{x1D713}\in \mathfrak{g}^{\ast }$
we identify
$\unicode[STIX]{x1D712}+\unicode[STIX]{x1D713}\in \mathfrak{g}^{\ast }$
we identify
![]() $\mathfrak{p}^{\ast }=\operatorname{Ann}_{\mathfrak{g}^{\ast }}(\mathfrak{m})\subseteq \mathfrak{g}^{\ast }$
). This change in notation is partly justified by the fact that the kernel of the restriction of the projection
$\mathfrak{p}^{\ast }=\operatorname{Ann}_{\mathfrak{g}^{\ast }}(\mathfrak{m})\subseteq \mathfrak{g}^{\ast }$
). This change in notation is partly justified by the fact that the kernel of the restriction of the projection
![]() $U(\mathfrak{p}){\twoheadrightarrow}U_{\unicode[STIX]{x1D713}}(\mathfrak{p})$
to
$U(\mathfrak{p}){\twoheadrightarrow}U_{\unicode[STIX]{x1D713}}(\mathfrak{p})$
to
![]() $U(\mathfrak{g},e)$
is
$U(\mathfrak{g},e)$
is
![]() $J_{\unicode[STIX]{x1D713}}\cap U(\mathfrak{g},e)$
. Consequently, we can identify
$J_{\unicode[STIX]{x1D713}}\cap U(\mathfrak{g},e)$
. Consequently, we can identify
![]() $U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)$
with the image of
$U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)$
with the image of
![]() $U(\mathfrak{g},e)$
in
$U(\mathfrak{g},e)$
in
![]() $U_{\unicode[STIX]{x1D713}}(\mathfrak{p})$
.
$U_{\unicode[STIX]{x1D713}}(\mathfrak{p})$
.
It turns out that for
![]() $\unicode[STIX]{x1D713}\neq \unicode[STIX]{x1D713}^{\prime }$
we can have
$\unicode[STIX]{x1D713}\neq \unicode[STIX]{x1D713}^{\prime }$
we can have
![]() $J_{\unicode[STIX]{x1D713}}^{\mathfrak{p}}\cap U(\mathfrak{g},e)=J_{\unicode[STIX]{x1D713}^{\prime }}^{\mathfrak{p}}\cap U(\mathfrak{g},e)$
, so that
$J_{\unicode[STIX]{x1D713}}^{\mathfrak{p}}\cap U(\mathfrak{g},e)=J_{\unicode[STIX]{x1D713}^{\prime }}^{\mathfrak{p}}\cap U(\mathfrak{g},e)$
, so that
![]() $U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)=U_{\unicode[STIX]{x1D713}^{\prime }}(\mathfrak{g},e)$
. To explain precisely when this happens we need to translate some of the material from [Reference Goodwin and TopleyGT18, §8.2] to our setting. We write
$U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)=U_{\unicode[STIX]{x1D713}^{\prime }}(\mathfrak{g},e)$
. To explain precisely when this happens we need to translate some of the material from [Reference Goodwin and TopleyGT18, §8.2] to our setting. We write
![]() $\mathfrak{m}^{\bot }\subseteq \mathfrak{g}$
for the annihilator of
$\mathfrak{m}^{\bot }\subseteq \mathfrak{g}$
for the annihilator of
![]() $\mathfrak{m}$
with respect to
$\mathfrak{m}$
with respect to
![]() $(\cdot \,,\cdot )$
, and note that we can identify
$(\cdot \,,\cdot )$
, and note that we can identify
![]() $\mathfrak{p}^{\ast }\cong e+\mathfrak{m}^{\bot }$
via
$\mathfrak{p}^{\ast }\cong e+\mathfrak{m}^{\bot }$
via
![]() $(\cdot \,,\cdot )$
. There is an adjoint action of
$(\cdot \,,\cdot )$
. There is an adjoint action of
![]() $M$
on
$M$
on
![]() $e+\mathfrak{m}^{\bot }$
, and this translates through the identification
$e+\mathfrak{m}^{\bot }$
, and this translates through the identification
![]() $\mathfrak{p}^{\ast }\cong e+\mathfrak{m}^{\bot }$
to an action of
$\mathfrak{p}^{\ast }\cong e+\mathfrak{m}^{\bot }$
to an action of
![]() $M$
on
$M$
on
![]() $\mathfrak{p}^{\ast }$
, which we refer to as the twisted action of
$\mathfrak{p}^{\ast }$
, which we refer to as the twisted action of
![]() $M$
on
$M$
on
![]() $\mathfrak{p}^{\ast }$
. For
$\mathfrak{p}^{\ast }$
. For
![]() $\unicode[STIX]{x1D719}\in \mathfrak{p}^{\ast }$
,
$\unicode[STIX]{x1D719}\in \mathfrak{p}^{\ast }$
,
![]() $g\in M$
and
$g\in M$
and
![]() $x\in \mathfrak{p}$
this twisted adjoint action is given by
$x\in \mathfrak{p}$
this twisted adjoint action is given by
![]() $(\operatorname{tw}(g)\cdot \unicode[STIX]{x1D719})(x)=\unicode[STIX]{x1D712}(g^{-1}\cdot x-x)+\unicode[STIX]{x1D719}(g^{-1}\cdot x)$
.
$(\operatorname{tw}(g)\cdot \unicode[STIX]{x1D719})(x)=\unicode[STIX]{x1D712}(g^{-1}\cdot x-x)+\unicode[STIX]{x1D719}(g^{-1}\cdot x)$
.
Now we state the required part of [Reference Goodwin and TopleyGT18, Lemma 8.6] in our notation.
Lemma 2.3. We have that
![]() $U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)=U_{\unicode[STIX]{x1D713}^{\prime }}(\mathfrak{g},e)$
if and only if
$U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)=U_{\unicode[STIX]{x1D713}^{\prime }}(\mathfrak{g},e)$
if and only if
![]() $\unicode[STIX]{x1D713}$
and
$\unicode[STIX]{x1D713}$
and
![]() $\unicode[STIX]{x1D713}^{\prime }$
are conjugate under the twisted
$\unicode[STIX]{x1D713}^{\prime }$
are conjugate under the twisted
![]() $M$
-action on
$M$
-action on
![]() $\mathfrak{p}^{\ast }$
.
$\mathfrak{p}^{\ast }$
.
Thanks to Quillen’s lemma, an irreducible
![]() $U(\mathfrak{g},e)$
-module
$U(\mathfrak{g},e)$
-module
![]() $L$
factors to a module for
$L$
factors to a module for
![]() $U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)$
for some
$U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)$
for some
![]() $\unicode[STIX]{x1D713}\in \mathfrak{p}^{\ast }$
. Further, it is clear from the definitions that, for
$\unicode[STIX]{x1D713}\in \mathfrak{p}^{\ast }$
. Further, it is clear from the definitions that, for
![]() $\unicode[STIX]{x1D713},\unicode[STIX]{x1D713}^{\prime }\in \mathfrak{p}^{\ast }$
, the module
$\unicode[STIX]{x1D713},\unicode[STIX]{x1D713}^{\prime }\in \mathfrak{p}^{\ast }$
, the module
![]() $L$
factors to a module both for
$L$
factors to a module both for
![]() $U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)$
and for
$U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)$
and for
![]() $U_{\unicode[STIX]{x1D713}^{\prime }}(\mathfrak{g},e)$
if and only if
$U_{\unicode[STIX]{x1D713}^{\prime }}(\mathfrak{g},e)$
if and only if
![]() $J_{\unicode[STIX]{x1D713}}^{\mathfrak{p}}\cap U(\mathfrak{g},e)=J_{\unicode[STIX]{x1D713}^{\prime }}^{\mathfrak{p}}\cap U(\mathfrak{g},e)$
, which by the previous lemma occurs if and only if
$J_{\unicode[STIX]{x1D713}}^{\mathfrak{p}}\cap U(\mathfrak{g},e)=J_{\unicode[STIX]{x1D713}^{\prime }}^{\mathfrak{p}}\cap U(\mathfrak{g},e)$
, which by the previous lemma occurs if and only if
![]() $\unicode[STIX]{x1D713}$
and
$\unicode[STIX]{x1D713}$
and
![]() $\unicode[STIX]{x1D713}^{\prime }$
are conjugate under the twisted
$\unicode[STIX]{x1D713}^{\prime }$
are conjugate under the twisted
![]() $M$
-action.
$M$
-action.
We also recall Premet’s equivalence in Theorem 2.4 below. This theorem is based on [Reference PremetPre02, Theorem 2.4], and the statement here can be deduced from [Reference PremetPre10, Lemma 2.2(c)] and [Reference Goodwin and TopleyGT18, Proposition 8.7 and Lemma 8.8]; see also [Reference Goodwin and TopleyGT18, Remark 9.4]. For the statement, we view
![]() $\unicode[STIX]{x1D713}\in \mathfrak{p}^{\ast }$
as an element of
$\unicode[STIX]{x1D713}\in \mathfrak{p}^{\ast }$
as an element of
![]() $\mathfrak{g}^{\ast }$
via the identification
$\mathfrak{g}^{\ast }$
via the identification
![]() $\mathfrak{p}^{\ast }=\operatorname{Ann}_{\mathfrak{g}^{\ast }}(\mathfrak{m})\subseteq \mathfrak{g}^{\ast }$
. Also we define
$\mathfrak{p}^{\ast }=\operatorname{Ann}_{\mathfrak{g}^{\ast }}(\mathfrak{m})\subseteq \mathfrak{g}^{\ast }$
. Also we define
![]() $Q^{\unicode[STIX]{x1D713}}=Q/J_{\unicode[STIX]{x1D712}+\unicode[STIX]{x1D713}}Q$
and recall that, as explained in [Reference Goodwin and TopleyGT18, §8.3],
$Q^{\unicode[STIX]{x1D713}}=Q/J_{\unicode[STIX]{x1D712}+\unicode[STIX]{x1D713}}Q$
and recall that, as explained in [Reference Goodwin and TopleyGT18, §8.3],
![]() $Q^{\unicode[STIX]{x1D713}}$
is a left
$Q^{\unicode[STIX]{x1D713}}$
is a left
![]() $U_{\unicode[STIX]{x1D712}+\unicode[STIX]{x1D713}}(\mathfrak{g})$
-module and a right
$U_{\unicode[STIX]{x1D712}+\unicode[STIX]{x1D713}}(\mathfrak{g})$
-module and a right
![]() $U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)$
-module.
$U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)$
-module.
Theorem 2.4. Let
![]() $\unicode[STIX]{x1D713}\in \mathfrak{p}^{\ast }$
. Then
$\unicode[STIX]{x1D713}\in \mathfrak{p}^{\ast }$
. Then
(a)
 $U_{\unicode[STIX]{x1D712}+\unicode[STIX]{x1D713}}(\mathfrak{g})\cong \operatorname{Mat}_{p^{d_{\unicode[STIX]{x1D712}}}}U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e);$
$U_{\unicode[STIX]{x1D712}+\unicode[STIX]{x1D713}}(\mathfrak{g})\cong \operatorname{Mat}_{p^{d_{\unicode[STIX]{x1D712}}}}U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e);$
(b) the functor from
 $U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)\operatorname{ - mod}$
to
$U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)\operatorname{ - mod}$
to
 $U_{\unicode[STIX]{x1D712}+\unicode[STIX]{x1D713}}(\mathfrak{g})\operatorname{ - mod}$
given by (15)is an equivalence of categories with quasi-inverse given by
$U_{\unicode[STIX]{x1D712}+\unicode[STIX]{x1D713}}(\mathfrak{g})\operatorname{ - mod}$
given by (15)is an equivalence of categories with quasi-inverse given by $$\begin{eqnarray}\displaystyle M\mapsto Q^{\unicode[STIX]{x1D713}}\otimes _{U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)}M & & \displaystyle\end{eqnarray}$$
(16)
$$\begin{eqnarray}\displaystyle M\mapsto Q^{\unicode[STIX]{x1D713}}\otimes _{U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)}M & & \displaystyle\end{eqnarray}$$
(16) $$\begin{eqnarray}\displaystyle V\mapsto V^{\mathfrak{m}_{\unicode[STIX]{x1D712}}}:=\{v\in V\mid \mathfrak{m}_{\unicode[STIX]{x1D712}}v=0\}; & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V\mapsto V^{\mathfrak{m}_{\unicode[STIX]{x1D712}}}:=\{v\in V\mid \mathfrak{m}_{\unicode[STIX]{x1D712}}v=0\}; & & \displaystyle\end{eqnarray}$$
(c)
 $\dim (Q^{\unicode[STIX]{x1D713}}\otimes _{U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)}M)=p^{d_{\unicode[STIX]{x1D712}}}\dim M$
, for a finite-dimensional
$\dim (Q^{\unicode[STIX]{x1D713}}\otimes _{U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)}M)=p^{d_{\unicode[STIX]{x1D712}}}\dim M$
, for a finite-dimensional
 $U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)$
-module
$U_{\unicode[STIX]{x1D713}}(\mathfrak{g},e)$
-module
 $M$
.
$M$
.
We also recall that
![]() $U(\mathfrak{g},e)$
has a PBW basis, which is described in [Reference Goodwin and TopleyGT18, Theorem 7.3]. We summarize the properties that we require in Proposition 2.5 below and adapt the statement to the case
$U(\mathfrak{g},e)$
has a PBW basis, which is described in [Reference Goodwin and TopleyGT18, Theorem 7.3]. We summarize the properties that we require in Proposition 2.5 below and adapt the statement to the case
![]() $\mathfrak{g}=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$
. For this we first have to give some notation. We fix a basis
$\mathfrak{g}=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$
. For this we first have to give some notation. We fix a basis
![]() $x_{1},\ldots ,x_{r}$
of
$x_{1},\ldots ,x_{r}$
of
![]() $\mathfrak{g}^{e}$
, chosen so that
$\mathfrak{g}^{e}$
, chosen so that
![]() $x_{i}\in \mathfrak{g}(n_{i})$
, where
$x_{i}\in \mathfrak{g}(n_{i})$
, where
![]() $n_{i}\in \mathbb{Z}_{{\geqslant}0}$
. Let
$n_{i}\in \mathbb{Z}_{{\geqslant}0}$
. Let
![]() $I_{\mathfrak{p}}=\{(i,j)\mid 1\leqslant i,j,\leqslant N,e_{i,j}\in \mathfrak{p}\}$
and fix an order on
$I_{\mathfrak{p}}=\{(i,j)\mid 1\leqslant i,j,\leqslant N,e_{i,j}\in \mathfrak{p}\}$
and fix an order on
![]() $I_{\mathfrak{p}}$
. For
$I_{\mathfrak{p}}$
. For
![]() $\boldsymbol{a}=(a_{i,j})\in \mathbb{Z}_{{\geqslant}0}^{I_{\mathfrak{p}}}$
we write
$\boldsymbol{a}=(a_{i,j})\in \mathbb{Z}_{{\geqslant}0}^{I_{\mathfrak{p}}}$
we write
and define
![]() $|\boldsymbol{a}|=\sum _{(i,j)\in I_{\mathfrak{p}}}a_{i,j}$
and
$|\boldsymbol{a}|=\sum _{(i,j)\in I_{\mathfrak{p}}}a_{i,j}$
and
![]() $|\boldsymbol{a}|_{e}=\sum _{(i,j)\in I_{\mathfrak{p}}}(\operatorname{col}(j)-\operatorname{col}(i)+1)a_{i,j}$
.
$|\boldsymbol{a}|_{e}=\sum _{(i,j)\in I_{\mathfrak{p}}}(\operatorname{col}(j)-\operatorname{col}(i)+1)a_{i,j}$
.
We can now state our proposition about the PBW basis of
![]() $U(\mathfrak{g},e)$
; it is a consequence of [Reference Goodwin and TopleyGT18, Lemma 7.1 and Theorem 7.3]. We remind the reader that the graded degrees in this paper differ from those in [Reference Goodwin and TopleyGT18] by a factor of 2.
$U(\mathfrak{g},e)$
; it is a consequence of [Reference Goodwin and TopleyGT18, Lemma 7.1 and Theorem 7.3]. We remind the reader that the graded degrees in this paper differ from those in [Reference Goodwin and TopleyGT18] by a factor of 2.
Proposition 2.5.
![]() $(\text{a})$
There are elements
$(\text{a})$
There are elements
![]() $\unicode[STIX]{x1D6E9}(x_{1}),\ldots ,\unicode[STIX]{x1D6E9}(x_{r})$
of
$\unicode[STIX]{x1D6E9}(x_{1}),\ldots ,\unicode[STIX]{x1D6E9}(x_{r})$
of
![]() $U(\mathfrak{g},e)$
of the form
$U(\mathfrak{g},e)$
of the form
where the
![]() $\unicode[STIX]{x1D706}_{\boldsymbol{a},i}\in \Bbbk$
satisfy
$\unicode[STIX]{x1D706}_{\boldsymbol{a},i}\in \Bbbk$
satisfy
![]() $\unicode[STIX]{x1D706}_{\boldsymbol{a},i}=0$
whenever
$\unicode[STIX]{x1D706}_{\boldsymbol{a},i}=0$
whenever
![]() $|\boldsymbol{a}|_{e}=n_{i}+1$
and
$|\boldsymbol{a}|_{e}=n_{i}+1$
and
![]() $|\boldsymbol{a}|=1$
.
$|\boldsymbol{a}|=1$
.
![]() $(\text{b})$
Given any elements
$(\text{b})$
Given any elements
![]() $\unicode[STIX]{x1D6E9}(x_{1}),\ldots ,\unicode[STIX]{x1D6E9}(x_{r})\in U(\mathfrak{g},e)$
of the form in (18), the ordered monomials in
$\unicode[STIX]{x1D6E9}(x_{1}),\ldots ,\unicode[STIX]{x1D6E9}(x_{r})\in U(\mathfrak{g},e)$
of the form in (18), the ordered monomials in
![]() $\unicode[STIX]{x1D6E9}(x_{1}),\ldots ,\unicode[STIX]{x1D6E9}(x_{r})$
form a basis of
$\unicode[STIX]{x1D6E9}(x_{1}),\ldots ,\unicode[STIX]{x1D6E9}(x_{r})$
form a basis of
![]() $U(\mathfrak{g},e)$
.
$U(\mathfrak{g},e)$
.
Let
![]() $\unicode[STIX]{x1D6E9}(x_{i}),\unicode[STIX]{x1D6E9}(x_{j})$
be elements of
$\unicode[STIX]{x1D6E9}(x_{i}),\unicode[STIX]{x1D6E9}(x_{j})$
be elements of
![]() $U(\mathfrak{g},e)$
of the form (18). Then a commutator calculation shows that
$U(\mathfrak{g},e)$
of the form (18). Then a commutator calculation shows that
where the
![]() $\unicode[STIX]{x1D707}_{\boldsymbol{a}}\in \Bbbk$
satisfy
$\unicode[STIX]{x1D707}_{\boldsymbol{a}}\in \Bbbk$
satisfy
![]() $\unicode[STIX]{x1D707}_{\boldsymbol{a}}=0$
whenever
$\unicode[STIX]{x1D707}_{\boldsymbol{a}}=0$
whenever
![]() $|\boldsymbol{a}|_{e}=n_{i}+n_{j}+1$
and
$|\boldsymbol{a}|_{e}=n_{i}+n_{j}+1$
and
![]() $|\boldsymbol{a}|=1$
. The key ingredient for this calculation is to observe that if we take the commutator
$|\boldsymbol{a}|=1$
. The key ingredient for this calculation is to observe that if we take the commutator
![]() $[\boldsymbol{e}^{\boldsymbol{a}},\boldsymbol{e}^{\boldsymbol{b}}]$
for
$[\boldsymbol{e}^{\boldsymbol{a}},\boldsymbol{e}^{\boldsymbol{b}}]$
for
![]() $\boldsymbol{a},\boldsymbol{b}\in \mathbb{Z}_{{\geqslant}0}^{I_{\mathfrak{p}}}$
, then we get a linear combinations of terms
$\boldsymbol{a},\boldsymbol{b}\in \mathbb{Z}_{{\geqslant}0}^{I_{\mathfrak{p}}}$
, then we get a linear combinations of terms
![]() $\boldsymbol{e}^{\boldsymbol{c}}$
with
$\boldsymbol{e}^{\boldsymbol{c}}$
with
![]() $|\boldsymbol{c}|_{e}=|\boldsymbol{a}|_{e}+|\boldsymbol{b}|_{e}-1$
and
$|\boldsymbol{c}|_{e}=|\boldsymbol{a}|_{e}+|\boldsymbol{b}|_{e}-1$
and
![]() $|\boldsymbol{c}|=|\boldsymbol{a}|+|\boldsymbol{b}|-1$
, plus a linear combination of terms
$|\boldsymbol{c}|=|\boldsymbol{a}|+|\boldsymbol{b}|-1$
, plus a linear combination of terms
![]() $\boldsymbol{e}^{\boldsymbol{d}}$
with
$\boldsymbol{e}^{\boldsymbol{d}}$
with
![]() $|\boldsymbol{d}|_{e}<|\boldsymbol{a}|_{e}+|\boldsymbol{b}|_{e}-1$
.
$|\boldsymbol{d}|_{e}<|\boldsymbol{a}|_{e}+|\boldsymbol{b}|_{e}-1$
.
3 Modular truncated shifted Yangian
In this section we consider the modular shifted Yangian
![]() $Y_{n}(\unicode[STIX]{x1D70E})$
and its truncation
$Y_{n}(\unicode[STIX]{x1D70E})$
and its truncation
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
. The algebras
$Y_{n,l}(\unicode[STIX]{x1D70E})$
. The algebras
![]() $Y_{n}(\unicode[STIX]{x1D70E})$
have been studied in recent work by Brundan and the second author, [Reference Brundan and TopleyBT18]. Here we recall some of the results in [Reference Brundan and TopleyBT18] and go on to verify that the truncation
$Y_{n}(\unicode[STIX]{x1D70E})$
have been studied in recent work by Brundan and the second author, [Reference Brundan and TopleyBT18]. Here we recall some of the results in [Reference Brundan and TopleyBT18] and go on to verify that the truncation
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
has structure theory similar to that in characteristic 0. In the next section we exploit formulas from [Reference Brundan and KleshchevBK06, §9] to show that the modular finite
$Y_{n,l}(\unicode[STIX]{x1D70E})$
has structure theory similar to that in characteristic 0. In the next section we exploit formulas from [Reference Brundan and KleshchevBK06, §9] to show that the modular finite
![]() $W$
-algebra
$W$
-algebra
![]() $U(\mathfrak{g},e)$
is isomorphic to the shifted truncated Yangian
$U(\mathfrak{g},e)$
is isomorphic to the shifted truncated Yangian
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
of level
$Y_{n,l}(\unicode[STIX]{x1D70E})$
of level
![]() $l=p_{n}$
.
$l=p_{n}$
.
We recall that
![]() $\unicode[STIX]{x1D70E}$
is the shift matrix for the pyramid
$\unicode[STIX]{x1D70E}$
is the shift matrix for the pyramid
![]() $\unicode[STIX]{x1D70B}$
. The modular shifted Yangian
$\unicode[STIX]{x1D70B}$
. The modular shifted Yangian
![]() $Y_{n}(\unicode[STIX]{x1D70E})$
is the
$Y_{n}(\unicode[STIX]{x1D70E})$
is the
![]() $\Bbbk$
-algebra with generators
$\Bbbk$
-algebra with generators
and relations
for all admissible
![]() $i,j,r,s,t$
. In the relations, the shorthand
$i,j,r,s,t$
. In the relations, the shorthand
![]() $D_{i}^{(0)}=\widetilde{D}_{i}^{(0)}:=1$
is used, and the elements
$D_{i}^{(0)}=\widetilde{D}_{i}^{(0)}:=1$
is used, and the elements
![]() $\widetilde{D}_{i}^{(r)}$
for
$\widetilde{D}_{i}^{(r)}$
for
![]() $r>0$
are defined recursively by
$r>0$
are defined recursively by
![]() $\widetilde{D}_{i}^{(r)}:=-\sum _{t=1}^{r}D_{i}^{(t)}\widetilde{D}_{i}^{(r-t)}$
.
$\widetilde{D}_{i}^{(r)}:=-\sum _{t=1}^{r}D_{i}^{(t)}\widetilde{D}_{i}^{(r-t)}$
.
This presentation of
![]() $Y_{n}(\unicode[STIX]{x1D70E})$
is given in [Reference Brundan and TopleyBT18, Theorem 4.15] and is modelled on the Drinfeld presentation of the shifted Yangian defined over
$Y_{n}(\unicode[STIX]{x1D70E})$
is given in [Reference Brundan and TopleyBT18, Theorem 4.15] and is modelled on the Drinfeld presentation of the shifted Yangian defined over
![]() $\mathbb{C}$
, as introduced in [Reference Brundan and KleshchevBK06, §2]. It is proved in [Reference Brundan and TopleyBT18, Theorem 4.14] that there is a PBW basis for
$\mathbb{C}$
, as introduced in [Reference Brundan and KleshchevBK06, §2]. It is proved in [Reference Brundan and TopleyBT18, Theorem 4.14] that there is a PBW basis for
![]() $Y_{n}(\unicode[STIX]{x1D70E})$
, whose description does not depend on the characteristic
$Y_{n}(\unicode[STIX]{x1D70E})$
, whose description does not depend on the characteristic
![]() $p$
. Before stating this result it is necessary to introduce some additional elements. We define
$p$
. Before stating this result it is necessary to introduce some additional elements. We define
for
![]() $i=1,\ldots ,n-1$
, and inductively define
$i=1,\ldots ,n-1$
, and inductively define
Then [Reference Brundan and TopleyBT18, Theorem 4.14] says that monomials in the elements
in any fixed order give a basis of
![]() $Y_{n}(\unicode[STIX]{x1D70E})$
.
$Y_{n}(\unicode[STIX]{x1D70E})$
.
The shifted Yangian has the canonical filtration which we denote by
![]() $Y_{n}(\unicode[STIX]{x1D70E})=\bigcup _{r\geqslant 0}{\mathcal{F}}_{r}Y_{n}(\unicode[STIX]{x1D70E})$
and is defined by declaring that
$Y_{n}(\unicode[STIX]{x1D70E})=\bigcup _{r\geqslant 0}{\mathcal{F}}_{r}Y_{n}(\unicode[STIX]{x1D70E})$
and is defined by declaring that
![]() $D_{i}^{(r)},E_{i,j}^{(r)},F_{i,j}^{(r)}\in {\mathcal{F}}_{r}Y_{n}(\unicode[STIX]{x1D70E})$
, that is, that
$D_{i}^{(r)},E_{i,j}^{(r)},F_{i,j}^{(r)}\in {\mathcal{F}}_{r}Y_{n}(\unicode[STIX]{x1D70E})$
, that is, that
![]() ${\mathcal{F}}_{r}Y_{n}(\unicode[STIX]{x1D70E})$
is spanned by the monomials in these elements of total degree less than or equal to
${\mathcal{F}}_{r}Y_{n}(\unicode[STIX]{x1D70E})$
is spanned by the monomials in these elements of total degree less than or equal to
![]() $r$
. It is immediate from the relations (21)–(33) that the associated graded algebra
$r$
. It is immediate from the relations (21)–(33) that the associated graded algebra
![]() $\operatorname{gr}Y_{n}(\unicode[STIX]{x1D70E})$
is commutative.
$\operatorname{gr}Y_{n}(\unicode[STIX]{x1D70E})$
is commutative.
The truncated shifted Yangian of level
![]() $l$
is denoted by
$l$
is denoted by
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
and defined to be the quotient of
$Y_{n,l}(\unicode[STIX]{x1D70E})$
and defined to be the quotient of
![]() $Y_{n}(\unicode[STIX]{x1D70E})$
by the ideal generated by
$Y_{n}(\unicode[STIX]{x1D70E})$
by the ideal generated by
![]() $\{D_{1}^{(r)}\mid r>p_{1}\}$
; this definition is taken from [Reference Brundan and KleshchevBK06, §6] where it is given for characteristic 0. We recall that
$\{D_{1}^{(r)}\mid r>p_{1}\}$
; this definition is taken from [Reference Brundan and KleshchevBK06, §6] where it is given for characteristic 0. We recall that
![]() $l=p_{n}$
, so that
$l=p_{n}$
, so that
![]() $p_{1}=l-s_{1,n}-s_{n,1}$
. The truncated shifted Yangian inherits the canonical filtration from
$p_{1}=l-s_{1,n}-s_{n,1}$
. The truncated shifted Yangian inherits the canonical filtration from
![]() $Y_{n}(\unicode[STIX]{x1D70E})$
and we write
$Y_{n}(\unicode[STIX]{x1D70E})$
and we write
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})=\bigcup _{i\geqslant 0}{\mathcal{F}}_{i}Y_{n,l}(\unicode[STIX]{x1D70E})$
. The associated graded algebra
$Y_{n,l}(\unicode[STIX]{x1D70E})=\bigcup _{i\geqslant 0}{\mathcal{F}}_{i}Y_{n,l}(\unicode[STIX]{x1D70E})$
. The associated graded algebra
![]() $\operatorname{gr}Y_{n,l}(\unicode[STIX]{x1D70E})$
is certainly commutative, as it is a quotient of
$\operatorname{gr}Y_{n,l}(\unicode[STIX]{x1D70E})$
is certainly commutative, as it is a quotient of
![]() $\operatorname{gr}Y_{n}(\unicode[STIX]{x1D70E})$
. When working with
$\operatorname{gr}Y_{n}(\unicode[STIX]{x1D70E})$
. When working with
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
we often abuse notation by using the same symbols
$Y_{n,l}(\unicode[STIX]{x1D70E})$
we often abuse notation by using the same symbols
![]() $D_{i}^{(r)},E_{i,j}^{(r)},F_{i,j}^{(r)}$
to refer to the elements of
$D_{i}^{(r)},E_{i,j}^{(r)},F_{i,j}^{(r)}$
to refer to the elements of
![]() $Y_{n}(\unicode[STIX]{x1D70E})$
and their images in
$Y_{n}(\unicode[STIX]{x1D70E})$
and their images in
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
.
$Y_{n,l}(\unicode[STIX]{x1D70E})$
.
The next lemma gives a spanning set for
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
and should be viewed as a modular version of [Reference Brundan and KleshchevBK06, Lemma 6.1]; though we note that it is less general as we do not deal with parabolic presentations here. We recover the full PBW theorem for
$Y_{n,l}(\unicode[STIX]{x1D70E})$
and should be viewed as a modular version of [Reference Brundan and KleshchevBK06, Lemma 6.1]; though we note that it is less general as we do not deal with parabolic presentations here. We recover the full PBW theorem for
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
, that is, that the spanning set given in the next lemma is actually a basis, once we have clarified the connection with
$Y_{n,l}(\unicode[STIX]{x1D70E})$
, that is, that the spanning set given in the next lemma is actually a basis, once we have clarified the connection with
![]() $U(\mathfrak{g},e)$
in Theorem 4.3.
$U(\mathfrak{g},e)$
in Theorem 4.3.
Lemma 3.1. The monomials in the elements
in any fixed order form a spanning set of
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
.
$Y_{n,l}(\unicode[STIX]{x1D70E})$
.
Proof. Our proof uses the arguments in the proof of [Reference Brundan and KleshchevBK06, Lemma 6.1]. As we are not using the more general parabolic presentations of the Yangian as in that proof, we outline the arguments required for the convenience of the reader.
During the proof we frequently refer to degree, by which we always mean filtered degree for the canonical filtration; on occasion we speak about the total degree of a monomial to make the intended meaning clearer. Until the final paragraph we use the word ‘monomials’ to mean unordered monomials, as this simplifies the exposition. We frequently use the fact that
![]() $\operatorname{gr}Y_{n}(\unicode[STIX]{x1D70E})$
is commutative, so for
$\operatorname{gr}Y_{n}(\unicode[STIX]{x1D70E})$
is commutative, so for
![]() $u\in Y_{n,l}(\unicode[STIX]{x1D70E})$
of degree
$u\in Y_{n,l}(\unicode[STIX]{x1D70E})$
of degree
![]() $r$
and
$r$
and
![]() $v\in Y_{n,l}(\unicode[STIX]{x1D70E})$
of degree
$v\in Y_{n,l}(\unicode[STIX]{x1D70E})$
of degree
![]() $s$
, the commutator
$s$
, the commutator
![]() $[u,v]$
has degree less than or equal to
$[u,v]$
has degree less than or equal to
![]() $r+s-1$
.
$r+s-1$
.
For
![]() $1\leqslant k\leqslant n$
and
$1\leqslant k\leqslant n$
and
![]() $s\geqslant 1$
, we let:
$s\geqslant 1$
, we let:
–
 $\unicode[STIX]{x1D6FA}_{k}$
be the set of generators given in (38) with
$\unicode[STIX]{x1D6FA}_{k}$
be the set of generators given in (38) with
 $i,j\leqslant k$
;
$i,j\leqslant k$
;–
 $\unicode[STIX]{x1D6FA}_{k,E}$
be the generators in
$\unicode[STIX]{x1D6FA}_{k,E}$
be the generators in
 $\unicode[STIX]{x1D6FA}_{k}$
along with the generators
$\unicode[STIX]{x1D6FA}_{k}$
along with the generators
 $E_{i,k+1}^{(r)}$
with
$E_{i,k+1}^{(r)}$
with
 $1\leqslant i\leqslant k$
and
$1\leqslant i\leqslant k$
and
 $s_{i,k+1}<r\leqslant s_{i,k+1}+p_{k+1}$
; and
$s_{i,k+1}<r\leqslant s_{i,k+1}+p_{k+1}$
; and–
 $\widehat{\unicode[STIX]{x1D6FA}}_{k}$
be the set of generators from (37) with
$\widehat{\unicode[STIX]{x1D6FA}}_{k}$
be the set of generators from (37) with
 $i,j\leqslant k$
.
$i,j\leqslant k$
.
A key observation for us is:
- (
 $\ast$
)
$\ast$
) if
 $X\in \unicode[STIX]{x1D6FA}_{k}$
with degree
$X\in \unicode[STIX]{x1D6FA}_{k}$
with degree
 $r-s_{k,k+1}$
, then
$r-s_{k,k+1}$
, then
 $[X,E_{k}^{s_{k,k+1}+1}]$
can be written as a linear combination of monomials in
$[X,E_{k}^{s_{k,k+1}+1}]$
can be written as a linear combination of monomials in
 $\unicode[STIX]{x1D6FA}_{k,E}$
with total degree
$\unicode[STIX]{x1D6FA}_{k,E}$
with total degree
 $r$
.
$r$
.
This can be checked directly from the relations, and the definition of
![]() $E_{i,j}^{(r)}$
in (35). A similar statement holds with ‘
$E_{i,j}^{(r)}$
in (35). A similar statement holds with ‘
![]() $F$
replacing
$F$
replacing
![]() $E$
’. Further, we have:
$E$
’. Further, we have:
- (
 $\dagger$
)
$\dagger$
) if
 $X\in \unicode[STIX]{x1D6FA}_{k,E}$
with degree
$X\in \unicode[STIX]{x1D6FA}_{k,E}$
with degree
 $r-s_{k+1,k}$
, then
$r-s_{k+1,k}$
, then
 $[X,F_{k}^{s_{k+1,k}+1}]$
can be written as a linear combination of monomials in
$[X,F_{k}^{s_{k+1,k}+1}]$
can be written as a linear combination of monomials in
 $\unicode[STIX]{x1D6FA}_{k+1}\cup \{\widetilde{D}_{k}^{(s)}\mid s=p_{k}+1,\ldots ,p_{k+1}\}$
with total degree
$\unicode[STIX]{x1D6FA}_{k+1}\cup \{\widetilde{D}_{k}^{(s)}\mid s=p_{k}+1,\ldots ,p_{k+1}\}$
with total degree
 $r$
.
$r$
.
Again this is checked directly from the relations, and we note that
![]() $\widetilde{D}_{k}^{(s)}$
can be written in terms of
$\widetilde{D}_{k}^{(s)}$
can be written in terms of
![]() $D_{k}^{(t)}$
for
$D_{k}^{(t)}$
for
![]() $t\leqslant s$
.
$t\leqslant s$
.
We show by induction on
![]() $k$
that any element in
$k$
that any element in
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{k}$
of degree
$\widehat{\unicode[STIX]{x1D6FA}}_{k}$
of degree
![]() $r\geqslant 0$
can be written as a linear combination of monomials in the elements of
$r\geqslant 0$
can be written as a linear combination of monomials in the elements of
![]() $\unicode[STIX]{x1D6FA}_{k}$
of total degree
$\unicode[STIX]{x1D6FA}_{k}$
of total degree
![]() $r$
.
$r$
.
To start the induction we note that the case
![]() $k=1$
is trivial, because
$k=1$
is trivial, because
![]() $D_{1}^{(r)}=0$
for
$D_{1}^{(r)}=0$
for
![]() $r>p_{1}$
in
$r>p_{1}$
in
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
. So suppose inductively we have proved the claim for
$Y_{n,l}(\unicode[STIX]{x1D70E})$
. So suppose inductively we have proved the claim for
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{k}$
and we consider elements of
$\widehat{\unicode[STIX]{x1D6FA}}_{k}$
and we consider elements of
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{k+1}$
.
$\widehat{\unicode[STIX]{x1D6FA}}_{k+1}$
.
First consider an element
![]() $E_{i,k+1}^{(r)}$
for
$E_{i,k+1}^{(r)}$
for
![]() $r>s_{i,k+1}+p_{i}$
. For
$r>s_{i,k+1}+p_{i}$
. For
![]() $i<k$
, we use the definition of
$i<k$
, we use the definition of
![]() $E_{i,k+1}^{(r)}$
in (35) to write
$E_{i,k+1}^{(r)}$
in (35) to write
![]() $E_{i,k+1}^{(r)}=[E_{i,k}^{(r-s_{k,k+1})},E_{k}^{(s_{k,k+1}+1)}]$
. Using the inductive hypothesis,
$E_{i,k+1}^{(r)}=[E_{i,k}^{(r-s_{k,k+1})},E_{k}^{(s_{k,k+1}+1)}]$
. Using the inductive hypothesis,
![]() $E_{i,k}^{(r-s_{k,k+1})}$
can be written as a sum of monomials in
$E_{i,k}^{(r-s_{k,k+1})}$
can be written as a sum of monomials in
![]() $\unicode[STIX]{x1D6FA}_{k}$
of total degree
$\unicode[STIX]{x1D6FA}_{k}$
of total degree
![]() $r-s_{k,k+1}$
. Now using (
$r-s_{k,k+1}$
. Now using (
![]() $\ast$
), we deduce that
$\ast$
), we deduce that
![]() $E_{i,k+1}^{(r)}$
can be written as a sum of monomials in
$E_{i,k+1}^{(r)}$
can be written as a sum of monomials in
![]() $\unicode[STIX]{x1D6FA}_{k,E}$
with total degree
$\unicode[STIX]{x1D6FA}_{k,E}$
with total degree
![]() $r$
. For
$r$
. For
![]() $i=k$
, we have
$i=k$
, we have
![]() $E_{i,k+1}^{(r)}=E_{k}^{(r)}$
and we can use the relation (23) to write
$E_{i,k+1}^{(r)}=E_{k}^{(r)}$
and we can use the relation (23) to write
The right-hand side of the above is an expression in elements of
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{k+1}$
of degree
$\widehat{\unicode[STIX]{x1D6FA}}_{k+1}$
of degree
![]() $r$
. We use property (
$r$
. We use property (
![]() $\ast$
) to deduce that the first term above can be written as a sum of monomials in
$\ast$
) to deduce that the first term above can be written as a sum of monomials in
![]() $\unicode[STIX]{x1D6FA}_{k,E}$
with total degree
$\unicode[STIX]{x1D6FA}_{k,E}$
with total degree
![]() $r$
. To deal with the second term we do an induction on
$r$
. To deal with the second term we do an induction on
![]() $r$
.
$r$
.
We can deal with the elements
![]() $F_{i,k+1}^{(r)}$
similarly.
$F_{i,k+1}^{(r)}$
similarly.
We are left to consider the elements
![]() $D_{k+1}^{(r)}$
. Using (22), we write
$D_{k+1}^{(r)}$
. Using (22), we write
For the first term on the right-hand side we use the above to write
![]() $E_{k}^{r-s_{k+1,k}}$
as a linear combination of monomials in
$E_{k}^{r-s_{k+1,k}}$
as a linear combination of monomials in
![]() $\unicode[STIX]{x1D6FA}_{k,E}$
of total degree
$\unicode[STIX]{x1D6FA}_{k,E}$
of total degree
![]() $r-s_{k+1,k}$
. Using (
$r-s_{k+1,k}$
. Using (
![]() $\dagger$
), we rewrite this in terms of monomials in
$\dagger$
), we rewrite this in terms of monomials in
![]() $\unicode[STIX]{x1D6FA}_{k+1}\cup \{\tilde{D}_{k}^{(s)}\mid s=p_{k}+1,\ldots ,p_{k+1}\}$
. Now we can use the inductive hypothesis to write this as linear combination of monomials in
$\unicode[STIX]{x1D6FA}_{k+1}\cup \{\tilde{D}_{k}^{(s)}\mid s=p_{k}+1,\ldots ,p_{k+1}\}$
. Now we can use the inductive hypothesis to write this as linear combination of monomials in
![]() $\unicode[STIX]{x1D6FA}_{k+1}$
. The second term can be dealt with by induction on
$\unicode[STIX]{x1D6FA}_{k+1}$
. The second term can be dealt with by induction on
![]() $r$
.
$r$
.
To finish the proof, we have to observe that for a fixed order on the elements given in (38), an unordered monomial can be written as a linear combination of ordered monomials. This is easily done using the fact that
![]() $\operatorname{gr}Y_{n}(\unicode[STIX]{x1D70E})$
is commutative, an induction on degree, and what has already been proved.◻
$\operatorname{gr}Y_{n}(\unicode[STIX]{x1D70E})$
is commutative, an induction on degree, and what has already been proved.◻
Let
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})^{\operatorname{ab}}$
denote the maximal abelian quotient of
$Y_{n,l}(\unicode[STIX]{x1D70E})^{\operatorname{ab}}$
denote the maximal abelian quotient of
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
obtained by factoring out the ideal generated by all commutators
$Y_{n,l}(\unicode[STIX]{x1D70E})$
obtained by factoring out the ideal generated by all commutators
![]() $\{[u,v]\mid u,v\in Y_{n,l}(\unicode[STIX]{x1D70E})\}$
. So the isomorphism classes of one-dimensional representations of
$\{[u,v]\mid u,v\in Y_{n,l}(\unicode[STIX]{x1D70E})\}$
. So the isomorphism classes of one-dimensional representations of
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
are in one-to-one correspondence with maximal ideals of
$Y_{n,l}(\unicode[STIX]{x1D70E})$
are in one-to-one correspondence with maximal ideals of
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})^{\operatorname{ab}}$
. A calculation due to Premet within the proof of [Reference PremetPre10, Theorem 3.3] shows that
$Y_{n,l}(\unicode[STIX]{x1D70E})^{\operatorname{ab}}$
. A calculation due to Premet within the proof of [Reference PremetPre10, Theorem 3.3] shows that
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})^{\operatorname{ab}}$
is generated by a particular subset of the elements (38) as stated in the following lemma. Although [Reference PremetPre10, Theorem 3.3] is only stated in characteristic 0, the required calculation works directly from the relations and we can observe that it is valid in characteristic
$Y_{n,l}(\unicode[STIX]{x1D70E})^{\operatorname{ab}}$
is generated by a particular subset of the elements (38) as stated in the following lemma. Although [Reference PremetPre10, Theorem 3.3] is only stated in characteristic 0, the required calculation works directly from the relations and we can observe that it is valid in characteristic
![]() $p$
.
$p$
.
Lemma 3.2. The algebra
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})^{\operatorname{ab}}$
is generated by the
$Y_{n,l}(\unicode[STIX]{x1D70E})^{\operatorname{ab}}$
is generated by the
![]() $l$
elements
$l$
elements
where
![]() ${\dot{D}}_{i}^{(r)}$
denotes the image of
${\dot{D}}_{i}^{(r)}$
denotes the image of
![]() $D_{i}^{(r)}$
in
$D_{i}^{(r)}$
in
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})^{\operatorname{ab}}$
.
$Y_{n,l}(\unicode[STIX]{x1D70E})^{\operatorname{ab}}$
.
4
 $U(\mathfrak{g},e)$
as modular truncated shifted Yangian
$U(\mathfrak{g},e)$
as modular truncated shifted Yangian
We proceed with the notation in § 2 and recall that
![]() $U(\mathfrak{g},e)$
is the invariant algebra
$U(\mathfrak{g},e)$
is the invariant algebra
![]() $U(\mathfrak{p})^{\operatorname{tw}(M)}$
for the twisted adjoint action of
$U(\mathfrak{p})^{\operatorname{tw}(M)}$
for the twisted adjoint action of
![]() $M$
on
$M$
on
![]() $U(\mathfrak{p})$
. The goal of the current section is to show that
$U(\mathfrak{p})$
. The goal of the current section is to show that
![]() $U(\mathfrak{g},e)$
is isomorphic to the truncated shifted Yangian
$U(\mathfrak{g},e)$
is isomorphic to the truncated shifted Yangian
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
of level
$Y_{n,l}(\unicode[STIX]{x1D70E})$
of level
![]() $l$
.
$l$
.
First we recall some remarkable formulas from [Reference Brundan and KleshchevBK06, §9] for elements of
![]() $U(\mathfrak{p})$
, which are actually invariants for the twisted adjoint action of
$U(\mathfrak{p})$
, which are actually invariants for the twisted adjoint action of
![]() $M$
as proved in Lemma 4.1. We refer also to [Reference Brundan and KleshchevBK08, §3.3], as our notation is closer to the notation used there. The weight
$M$
as proved in Lemma 4.1. We refer also to [Reference Brundan and KleshchevBK08, §3.3], as our notation is closer to the notation used there. The weight
![]() $\unicode[STIX]{x1D702}\in \mathfrak{t}^{\ast }$
from (9) is required to define these invariants, and we note that
$\unicode[STIX]{x1D702}\in \mathfrak{t}^{\ast }$
from (9) is required to define these invariants, and we note that
![]() $\unicode[STIX]{x1D702}$
extends to a character of
$\unicode[STIX]{x1D702}$
extends to a character of
![]() $\mathfrak{p}$
. For
$\mathfrak{p}$
. For
![]() $e_{i,j}\in \mathfrak{p}$
, we define
$e_{i,j}\in \mathfrak{p}$
, we define
Now for
![]() $1\leqslant i,j\leqslant n$
,
$1\leqslant i,j\leqslant n$
,
![]() $0\leqslant x<n$
and
$0\leqslant x<n$
and
![]() $r\geqslant 1$
, we let
$r\geqslant 1$
, we let
 $$\begin{eqnarray}\displaystyle T_{i,j;x}^{(r)}:=\mathop{\sum }_{s=1}^{r}(-1)^{r-s}\mathop{\sum }_{\substack{ i_{1},\ldots ,i_{s} \\ j_{1},\ldots ,j_{s}}}(-1)^{|\{t=1,\ldots ,s-1\mid \operatorname{row}(j_{t})\leqslant x\}|}\tilde{e}_{i_{1},j_{1}}\cdots \tilde{e}_{i_{s},j_{s}}\in U(\mathfrak{p}) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{i,j;x}^{(r)}:=\mathop{\sum }_{s=1}^{r}(-1)^{r-s}\mathop{\sum }_{\substack{ i_{1},\ldots ,i_{s} \\ j_{1},\ldots ,j_{s}}}(-1)^{|\{t=1,\ldots ,s-1\mid \operatorname{row}(j_{t})\leqslant x\}|}\tilde{e}_{i_{1},j_{1}}\cdots \tilde{e}_{i_{s},j_{s}}\in U(\mathfrak{p}) & & \displaystyle\end{eqnarray}$$
where the sum is taken over all
![]() $1\leqslant i_{1},\ldots ,i_{s},j_{1},\ldots ,j_{s}\leqslant N$
such that
$1\leqslant i_{1},\ldots ,i_{s},j_{1},\ldots ,j_{s}\leqslant N$
such that
(a)
 $\operatorname{col}(j_{1})-\operatorname{col}(i_{1})+\cdots +\operatorname{col}(j_{s})-\operatorname{col}(i_{s})+s=r$
;
$\operatorname{col}(j_{1})-\operatorname{col}(i_{1})+\cdots +\operatorname{col}(j_{s})-\operatorname{col}(i_{s})+s=r$
;(b)
 $\operatorname{col}(i_{t})\leqslant \operatorname{col}(j_{t})$
for each
$\operatorname{col}(i_{t})\leqslant \operatorname{col}(j_{t})$
for each
 $t=1,\ldots ,s$
;
$t=1,\ldots ,s$
;(c) if
 $\operatorname{row}(j_{t})>x$
, then
$\operatorname{row}(j_{t})>x$
, then
 $\operatorname{col}(j_{t})<\operatorname{col}(i_{t+1})$
for each
$\operatorname{col}(j_{t})<\operatorname{col}(i_{t+1})$
for each
 $t=1,\ldots ,s-1$
;
$t=1,\ldots ,s-1$
;(d) if
 $\operatorname{row}(j_{t})\leqslant x$
then
$\operatorname{row}(j_{t})\leqslant x$
then
 $\operatorname{col}(j_{t})\geqslant \operatorname{col}(i_{t+1})$
for each
$\operatorname{col}(j_{t})\geqslant \operatorname{col}(i_{t+1})$
for each
 $t=1,\ldots ,s-1$
;
$t=1,\ldots ,s-1$
;(e)
 $\operatorname{row}(i_{1})=i$
,
$\operatorname{row}(i_{1})=i$
,
 $\operatorname{row}(j_{s})=j$
;
$\operatorname{row}(j_{s})=j$
;(f)
 $\operatorname{row}(j_{t})=\operatorname{row}(i_{t+1})$
for each
$\operatorname{row}(j_{t})=\operatorname{row}(i_{t+1})$
for each
 $t=1,\ldots ,s-1$
.
$t=1,\ldots ,s-1$
.
Now define
These elements are denoted by the same symbols as the generators of the truncated shifted Yangian and this will be justified later. First we prove that they are invariants for the twisted adjoint action of
![]() $M$
and thus are elements of
$M$
and thus are elements of
![]() $U(\mathfrak{g},e)$
.
$U(\mathfrak{g},e)$
.
Lemma 4.1. The elements
![]() $D_{i}^{(r)}$
,
$D_{i}^{(r)}$
,
![]() $E_{i}^{(r)}$
and
$E_{i}^{(r)}$
and
![]() $F_{i}^{(r)}$
of
$F_{i}^{(r)}$
of
![]() $U(\mathfrak{p})$
defined in (40), (41) and (42) are all invariant under the twisted adjoint action of
$U(\mathfrak{p})$
defined in (40), (41) and (42) are all invariant under the twisted adjoint action of
![]() $M$
.
$M$
.
Proof. Recall from § 2.1 that
![]() $\mathfrak{g}_{\mathbb{C}}=\mathfrak{g}\mathfrak{l}_{N}(\mathbb{C})$
and
$\mathfrak{g}_{\mathbb{C}}=\mathfrak{g}\mathfrak{l}_{N}(\mathbb{C})$
and
![]() $\mathfrak{g}_{\mathbb{Z}}=\mathfrak{g}\mathfrak{l}_{N}(\mathbb{Z})$
; and we have the subalgebras
$\mathfrak{g}_{\mathbb{Z}}=\mathfrak{g}\mathfrak{l}_{N}(\mathbb{Z})$
; and we have the subalgebras
![]() $\mathfrak{p}_{\mathbb{C}}$
,
$\mathfrak{p}_{\mathbb{C}}$
,
![]() $\mathfrak{m}_{\mathbb{C}}$
,
$\mathfrak{m}_{\mathbb{C}}$
,
![]() $\mathfrak{p}_{\mathbb{Z}}$
and
$\mathfrak{p}_{\mathbb{Z}}$
and
![]() $\mathfrak{m}_{\mathbb{Z}}$
.
$\mathfrak{m}_{\mathbb{Z}}$
.
Let
![]() $X_{i}^{(r)}\in U(\mathfrak{p})$
be one of the elements defined by (40), (41) or (42). Throughout this proof we abuse notation slightly by simultaneously viewing
$X_{i}^{(r)}\in U(\mathfrak{p})$
be one of the elements defined by (40), (41) or (42). Throughout this proof we abuse notation slightly by simultaneously viewing
![]() $X_{i}^{(r)}$
also as an element of
$X_{i}^{(r)}$
also as an element of
![]() $U(\mathfrak{p}_{\mathbb{Z}})$
and of
$U(\mathfrak{p}_{\mathbb{Z}})$
and of
![]() $U(\mathfrak{p}_{\mathbb{C}})$
.
$U(\mathfrak{p}_{\mathbb{C}})$
.
According to [Reference Brundan and KleshchevBK06, Lemma 10.12], we have that
![]() $X_{i}^{(r)}\in U(\mathfrak{p}_{\mathbb{C}})$
is invariant under the twisted adjoint action of
$X_{i}^{(r)}\in U(\mathfrak{p}_{\mathbb{C}})$
is invariant under the twisted adjoint action of
![]() $\mathfrak{m}_{\mathbb{C}}$
. This twisted adjoint action is defined by
$\mathfrak{m}_{\mathbb{C}}$
. This twisted adjoint action is defined by
for
![]() $x\in \mathfrak{m}_{\mathbb{C}}$
and
$x\in \mathfrak{m}_{\mathbb{C}}$
and
![]() $u\in U(\mathfrak{p}_{\mathbb{C}})$
. We see that the twisted adjoint action of
$u\in U(\mathfrak{p}_{\mathbb{C}})$
. We see that the twisted adjoint action of
![]() $\mathfrak{m}_{\mathbb{C}}$
exponentiates to give the twisted adjoint action of
$\mathfrak{m}_{\mathbb{C}}$
exponentiates to give the twisted adjoint action of
![]() $M_{\mathbb{C}}$
as defined in 2.6. Thus we deduce that
$M_{\mathbb{C}}$
as defined in 2.6. Thus we deduce that
![]() $X_{i}^{(r)}$
is an invariant for the twisted adjoint action of
$X_{i}^{(r)}$
is an invariant for the twisted adjoint action of
![]() $M_{\mathbb{C}}$
.
$M_{\mathbb{C}}$
.
Now let
![]() $1\leqslant i,j\leqslant N$
such that
$1\leqslant i,j\leqslant N$
such that
![]() $e_{i,j}\in \mathfrak{m}_{\mathbb{C}}$
. Let
$e_{i,j}\in \mathfrak{m}_{\mathbb{C}}$
. Let
![]() $t$
be an indeterminate and consider the homomorphism
$t$
be an indeterminate and consider the homomorphism
![]() $U(\mathfrak{g}_{\mathbb{C}})[t]\rightarrow U(\mathfrak{g}_{\mathbb{C}})[t]$
determined by
$U(\mathfrak{g}_{\mathbb{C}})[t]\rightarrow U(\mathfrak{g}_{\mathbb{C}})[t]$
determined by
![]() $e_{k,l}\mapsto e_{k,l}+t\unicode[STIX]{x1D6FF}_{j,k}e_{i,l}-t\unicode[STIX]{x1D6FF}_{l,i}e_{k,j}-t^{2}\unicode[STIX]{x1D6FF}_{j,k}\unicode[STIX]{x1D6FF}_{l,i}e_{i,j}$
, which ‘gives the action of
$e_{k,l}\mapsto e_{k,l}+t\unicode[STIX]{x1D6FF}_{j,k}e_{i,l}-t\unicode[STIX]{x1D6FF}_{l,i}e_{k,j}-t^{2}\unicode[STIX]{x1D6FF}_{j,k}\unicode[STIX]{x1D6FF}_{l,i}e_{i,j}$
, which ‘gives the action of
![]() $u_{i,j}(t)$
on
$u_{i,j}(t)$
on
![]() $e_{k,l}$
’ as in (1). This preserves the integral form
$e_{k,l}$
’ as in (1). This preserves the integral form
![]() $U(\mathfrak{g}_{\mathbb{Z}})[t]$
of
$U(\mathfrak{g}_{\mathbb{Z}})[t]$
of
![]() $U(\mathfrak{g}_{\mathbb{C}})[t]$
and, composing with the projection
$U(\mathfrak{g}_{\mathbb{C}})[t]$
and, composing with the projection
![]() $U(\mathfrak{g}_{\mathbb{Z}})[t]\rightarrow U(\mathfrak{p}_{\mathbb{Z}})[t]$
along the direct sum decomposition
$U(\mathfrak{g}_{\mathbb{Z}})[t]\rightarrow U(\mathfrak{p}_{\mathbb{Z}})[t]$
along the direct sum decomposition
![]() $U(\mathfrak{g}_{\mathbb{Z}})[t]=U(\mathfrak{p}_{\mathbb{Z}})[t]\oplus U(\mathfrak{g}_{\mathbb{Z}})[t]\{x-\unicode[STIX]{x1D712}(x)\mid x\in \mathfrak{m}_{\mathbb{Z}}\}$
, we obtain a
$U(\mathfrak{g}_{\mathbb{Z}})[t]=U(\mathfrak{p}_{\mathbb{Z}})[t]\oplus U(\mathfrak{g}_{\mathbb{Z}})[t]\{x-\unicode[STIX]{x1D712}(x)\mid x\in \mathfrak{m}_{\mathbb{Z}}\}$
, we obtain a
![]() $\mathbb{Z}$
-module homomorphism
$\mathbb{Z}$
-module homomorphism
![]() $\unicode[STIX]{x1D713}_{i,j}:U(\mathfrak{p}_{\mathbb{Z}})[t]\rightarrow U(\mathfrak{p}_{\mathbb{Z}})[t]$
. By the observations of the previous paragraph,
$\unicode[STIX]{x1D713}_{i,j}:U(\mathfrak{p}_{\mathbb{Z}})[t]\rightarrow U(\mathfrak{p}_{\mathbb{Z}})[t]$
. By the observations of the previous paragraph,
![]() $\unicode[STIX]{x1D713}_{i,j}(X_{k}^{(r)})-X_{k}^{(r)}\in (t-s)U(\mathfrak{p}_{\mathbb{C}})[t]$
for every
$\unicode[STIX]{x1D713}_{i,j}(X_{k}^{(r)})-X_{k}^{(r)}\in (t-s)U(\mathfrak{p}_{\mathbb{C}})[t]$
for every
![]() $s\in \mathbb{C}$
. It follows that
$s\in \mathbb{C}$
. It follows that
![]() $\unicode[STIX]{x1D713}_{i,j}(X_{k}^{(r)})-X_{k}^{(r)}=0$
in
$\unicode[STIX]{x1D713}_{i,j}(X_{k}^{(r)})-X_{k}^{(r)}=0$
in
![]() $U(\mathfrak{p}_{\mathbb{C}})[t]$
. Note that
$U(\mathfrak{p}_{\mathbb{C}})[t]$
. Note that
![]() $\bigcap _{s\in \mathbb{C}}(t-s)U(\mathfrak{p}_{\mathbb{C}})[t]=0$
follows from the fact that
$\bigcap _{s\in \mathbb{C}}(t-s)U(\mathfrak{p}_{\mathbb{C}})[t]=0$
follows from the fact that
![]() $U(\mathfrak{p}_{\mathbb{C}})[t]$
is a free
$U(\mathfrak{p}_{\mathbb{C}})[t]$
is a free
![]() $\mathbb{C}[t]$
-module, and
$\mathbb{C}[t]$
-module, and
![]() $\bigcap _{s\in \mathbb{C}}(t-s)\mathbb{C}[t]=0$
.
$\bigcap _{s\in \mathbb{C}}(t-s)\mathbb{C}[t]=0$
.
Now consider the equation
valid in
![]() $U(\mathfrak{p}_{\mathbb{Z}})[t]\otimes _{\mathbb{Z}}\Bbbk \cong U(\mathfrak{p})[t]$
. Examining the image in
$U(\mathfrak{p}_{\mathbb{Z}})[t]\otimes _{\mathbb{Z}}\Bbbk \cong U(\mathfrak{p})[t]$
. Examining the image in
![]() $U(\mathfrak{p})\cong U(\mathfrak{p})[t]/(t-s)U(\mathfrak{p})[t]$
for all
$U(\mathfrak{p})\cong U(\mathfrak{p})[t]/(t-s)U(\mathfrak{p})[t]$
for all
![]() $s\in \Bbbk$
, we deduce that
$s\in \Bbbk$
, we deduce that
![]() $X_{k}^{(r)}\in U(\mathfrak{p})$
is invariant under the twisted adjoint action of the root subgroup
$X_{k}^{(r)}\in U(\mathfrak{p})$
is invariant under the twisted adjoint action of the root subgroup
![]() $u_{i,j}(\Bbbk )$
. Hence,
$u_{i,j}(\Bbbk )$
. Hence,
![]() $X_{k}^{(r)}\in U(\mathfrak{p})$
is invariant under the twisted adjoint action of
$X_{k}^{(r)}\in U(\mathfrak{p})$
is invariant under the twisted adjoint action of
![]() $M$
, and this completes the proof.◻
$M$
, and this completes the proof.◻
We define elements
![]() $E_{i,j}^{(r)}\in U(\mathfrak{p})$
for
$E_{i,j}^{(r)}\in U(\mathfrak{p})$
for
![]() $1\leqslant i<j\leqslant n$
and
$1\leqslant i<j\leqslant n$
and
![]() $r>s_{i,j}$
from the expressions for
$r>s_{i,j}$
from the expressions for
![]() $E_{i}^{(r)}\in U(\mathfrak{p})$
given in (41) and the recursive formula in (35); we define
$E_{i}^{(r)}\in U(\mathfrak{p})$
given in (41) and the recursive formula in (35); we define
![]() $F_{i,j}^{(r)}\in U(\mathfrak{p})$
similarly. From these definitions and Lemma 4.1, we have that these
$F_{i,j}^{(r)}\in U(\mathfrak{p})$
similarly. From these definitions and Lemma 4.1, we have that these
![]() $E_{i,j}^{(r)}$
and
$E_{i,j}^{(r)}$
and
![]() $F_{i,j}^{(r)}$
are actually elements of
$F_{i,j}^{(r)}$
are actually elements of
![]() $U(\mathfrak{g},e)$
. For the next lemma we recall the basis for
$U(\mathfrak{g},e)$
. For the next lemma we recall the basis for
![]() $\mathfrak{g}^{e}$
from Lemma 2.1, and the notation for elements
$\mathfrak{g}^{e}$
from Lemma 2.1, and the notation for elements
![]() $\boldsymbol{e}^{\boldsymbol{a}}$
in
$\boldsymbol{e}^{\boldsymbol{a}}$
in
![]() $U(\mathfrak{p})$
given in (17).
$U(\mathfrak{p})$
given in (17).
Lemma 4.2.
![]() $(\text{a})$
For
$(\text{a})$
For
![]() $1\leqslant i\leqslant n$
and
$1\leqslant i\leqslant n$
and
![]() $1\leqslant r\leqslant p_{i}$
, we have
$1\leqslant r\leqslant p_{i}$
, we have
![]() $D_{i}^{(r)}=(-1)^{r-1}c_{i,i}^{(r)}+u$
, where
$D_{i}^{(r)}=(-1)^{r-1}c_{i,i}^{(r)}+u$
, where
![]() $u$
is a linear combination of terms
$u$
is a linear combination of terms
![]() $\boldsymbol{e}^{\boldsymbol{a}}$
satisfying either
$\boldsymbol{e}^{\boldsymbol{a}}$
satisfying either
![]() $|\boldsymbol{a}|_{e}=r$
and
$|\boldsymbol{a}|_{e}=r$
and
![]() $|\boldsymbol{a}|>1$
, or
$|\boldsymbol{a}|>1$
, or
![]() $|\boldsymbol{a}|_{e}<r$
.
$|\boldsymbol{a}|_{e}<r$
.
![]() $(\text{b})$
For
$(\text{b})$
For
![]() $1\leqslant i<j\leqslant n$
and
$1\leqslant i<j\leqslant n$
and
![]() $s_{i,j}<r\leqslant p_{i}+s_{i,j}$
, we have
$s_{i,j}<r\leqslant p_{i}+s_{i,j}$
, we have
![]() $E_{i,j}^{(r)}=(-1)^{r-1}c_{i,j}^{(r)}+u$
, where
$E_{i,j}^{(r)}=(-1)^{r-1}c_{i,j}^{(r)}+u$
, where
![]() $u$
is a linear combination of terms
$u$
is a linear combination of terms
![]() $\boldsymbol{e}^{\boldsymbol{a}}$
satisfying either
$\boldsymbol{e}^{\boldsymbol{a}}$
satisfying either
![]() $|\boldsymbol{a}|_{e}=r$
and
$|\boldsymbol{a}|_{e}=r$
and
![]() $|\boldsymbol{a}|>1$
, or
$|\boldsymbol{a}|>1$
, or
![]() $|\boldsymbol{a}|_{e}<r$
.
$|\boldsymbol{a}|_{e}<r$
.
![]() $(\text{c})$
For
$(\text{c})$
For
![]() $1\leqslant i<j\leqslant n$
and
$1\leqslant i<j\leqslant n$
and
![]() $s_{j,i}<r\leqslant p_{i}+s_{j,i}$
, we have
$s_{j,i}<r\leqslant p_{i}+s_{j,i}$
, we have
![]() $F_{i,j}^{(r)}=(-1)^{r-1}c_{j,i}^{(r)}+u$
, where
$F_{i,j}^{(r)}=(-1)^{r-1}c_{j,i}^{(r)}+u$
, where
![]() $u$
is a linear combination of terms
$u$
is a linear combination of terms
![]() $\boldsymbol{e}^{\boldsymbol{a}}$
satisfying either
$\boldsymbol{e}^{\boldsymbol{a}}$
satisfying either
![]() $|\boldsymbol{a}|_{e}=r$
and
$|\boldsymbol{a}|_{e}=r$
and
![]() $|\boldsymbol{a}|>1$
, or
$|\boldsymbol{a}|>1$
, or
![]() $|\boldsymbol{a}|_{e}<r$
.
$|\boldsymbol{a}|_{e}<r$
.
![]() $(\text{d})$
The monomials in
$(\text{d})$
The monomials in
taken in any fixed order, form a basis of
![]() $U(\mathfrak{g},e)$
.
$U(\mathfrak{g},e)$
.
Proof. We begin by proving (a). Consider the expression given for
![]() $D_{i}^{(r)}$
given by (39) and (40). We can verify that the terms for
$D_{i}^{(r)}$
given by (39) and (40). We can verify that the terms for
![]() $s>1$
are a linear combination of terms
$s>1$
are a linear combination of terms
![]() $\boldsymbol{e}^{\boldsymbol{a}}$
satisfying
$\boldsymbol{e}^{\boldsymbol{a}}$
satisfying
![]() $|\boldsymbol{a}|_{e}=r$
and
$|\boldsymbol{a}|_{e}=r$
and
![]() $|\boldsymbol{a}|>1$
, or
$|\boldsymbol{a}|>1$
, or
![]() $|\boldsymbol{a}|_{e}<r$
. So we are left to show that the
$|\boldsymbol{a}|_{e}<r$
. So we are left to show that the
![]() $s=1$
part is precisely
$s=1$
part is precisely
![]() $(-1)^{r-1}c_{i,i}^{(r)}$
, and this follows directly from the definitions.
$(-1)^{r-1}c_{i,i}^{(r)}$
, and this follows directly from the definitions.
The cases of (b) and (c) for
![]() $j=i+1$
are proved similarly to (a). Then, using the definitions in (35) and (36), along with Lemma 2.1(b) and (19), we deduce the statement for all
$j=i+1$
are proved similarly to (a). Then, using the definitions in (35) and (36), along with Lemma 2.1(b) and (19), we deduce the statement for all
![]() $i$
and
$i$
and
![]() $j$
.
$j$
.
Part (d) is now an immediate consequence of Lemma 2.1(a) and Proposition 2.5.◻
We are now in a position to prove the main result of the section, showing that
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
is isomorphic to
$Y_{n,l}(\unicode[STIX]{x1D70E})$
is isomorphic to
![]() $U(\mathfrak{g},e)$
, which is a modular analogue of [Reference Brundan and KleshchevBK06, Theorem 10.1].
$U(\mathfrak{g},e)$
, which is a modular analogue of [Reference Brundan and KleshchevBK06, Theorem 10.1].
Theorem 4.3. The map from
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
to
$Y_{n,l}(\unicode[STIX]{x1D70E})$
to
![]() $U(\mathfrak{g},e)$
, determined by sending each element of
$U(\mathfrak{g},e)$
, determined by sending each element of
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
in
$Y_{n,l}(\unicode[STIX]{x1D70E})$
in
to the element of
![]() $U(\mathfrak{g},e)$
denoted by the same symbol, defines an isomorphism
$U(\mathfrak{g},e)$
denoted by the same symbol, defines an isomorphism
Proof. Consider the elements
![]() $D_{i}^{(r)},E_{i}^{(r)},F_{i}^{(r)}$
defined in
$D_{i}^{(r)},E_{i}^{(r)},F_{i}^{(r)}$
defined in
![]() $U(\mathfrak{p}_{\mathbb{C}})$
by formulas (39)–(42). It follows from [Reference Brundan and KleshchevBK06, Theorem 10.1] that these elements satisfy relations (21)–(32). Also they satisfy (33) and (34) as these follow over
$U(\mathfrak{p}_{\mathbb{C}})$
by formulas (39)–(42). It follows from [Reference Brundan and KleshchevBK06, Theorem 10.1] that these elements satisfy relations (21)–(32). Also they satisfy (33) and (34) as these follow over
![]() $\mathbb{C}$
from [Reference Brundan and KleshchevBK06, (2.14), (2.15)]. Since all of these relations have integral coefficients, they hold in
$\mathbb{C}$
from [Reference Brundan and KleshchevBK06, (2.14), (2.15)]. Since all of these relations have integral coefficients, they hold in
![]() $U(\mathfrak{p}_{\mathbb{Z}})$
, and thus also in
$U(\mathfrak{p}_{\mathbb{Z}})$
, and thus also in
![]() $U(\mathfrak{p})\cong U(\mathfrak{p}_{\mathbb{Z}})\otimes \Bbbk$
. In addition, it is clear from the definition of
$U(\mathfrak{p})\cong U(\mathfrak{p}_{\mathbb{Z}})\otimes \Bbbk$
. In addition, it is clear from the definition of
![]() $D_{1}^{(r)}\in U(\mathfrak{g},e)$
given in (39) and (40) that
$D_{1}^{(r)}\in U(\mathfrak{g},e)$
given in (39) and (40) that
![]() $D_{1}^{(r)}=0$
for
$D_{1}^{(r)}=0$
for
![]() $r>p_{1}$
.
$r>p_{1}$
.
Hence, the map described in the statement does give a homomorphism
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})\rightarrow U(\mathfrak{g},e)$
. By Lemma 4.2(d), we see that this homomorphism is surjective, and, using Lemma 3.1, we deduce that it is injective.◻
$Y_{n,l}(\unicode[STIX]{x1D70E})\rightarrow U(\mathfrak{g},e)$
. By Lemma 4.2(d), we see that this homomorphism is surjective, and, using Lemma 3.1, we deduce that it is injective.◻
As mentioned before Lemma 3.1, we are now able to deduce a PBW theorem for
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
, as given in [Reference Brundan and KleshchevBK06, Corollary 6.3]. This says that the monomials in the elements given in (38), taken in any fixed order, form a basis of
$Y_{n,l}(\unicode[STIX]{x1D70E})$
, as given in [Reference Brundan and KleshchevBK06, Corollary 6.3]. This says that the monomials in the elements given in (38), taken in any fixed order, form a basis of
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
, and follows immediately from Lemma 4.2 and Theorem 4.3.
$Y_{n,l}(\unicode[STIX]{x1D70E})$
, and follows immediately from Lemma 4.2 and Theorem 4.3.
5 One-dimensional modules for
 $U(\mathfrak{g},e)$
$U(\mathfrak{g},e)$
We follow similar methods to those in [Reference BrundanBru11, §2] to classify the one-dimensional modules for
![]() $U(\mathfrak{g},e)$
. Before stating this in Theorem 5.1 we require some notation, and we also use the generators and relations for
$U(\mathfrak{g},e)$
. Before stating this in Theorem 5.1 we require some notation, and we also use the generators and relations for
![]() $U(\mathfrak{g},e)$
given by Theorem 4.3 to make some initial deductions about one-dimensional modules for
$U(\mathfrak{g},e)$
given by Theorem 4.3 to make some initial deductions about one-dimensional modules for
![]() $U(\mathfrak{g},e)$
.
$U(\mathfrak{g},e)$
.
It follows from (21) and Lemma 4.2 that
![]() $\{D_{i}^{(r)}\mid i=1,\ldots ,n,1\leqslant r\leqslant p_{i}\}$
generates a subalgebra of
$\{D_{i}^{(r)}\mid i=1,\ldots ,n,1\leqslant r\leqslant p_{i}\}$
generates a subalgebra of
![]() $U(\mathfrak{g},e)$
isomorphic to a polynomial algebra in
$U(\mathfrak{g},e)$
isomorphic to a polynomial algebra in
![]() $N$
variables; we denote this subalgebra by
$N$
variables; we denote this subalgebra by
![]() $U(\mathfrak{g},e)^{0}$
.
$U(\mathfrak{g},e)^{0}$
.
Let
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
. For
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
. For
![]() $i=1,\ldots ,n$
, we write
$i=1,\ldots ,n$
, we write
![]() $a_{i,1},\ldots ,a_{i,p_{i}}$
for the entries in the
$a_{i,1},\ldots ,a_{i,p_{i}}$
for the entries in the
![]() $i$
th row of
$i$
th row of
![]() $A$
from left to right. We define the one-dimensional
$A$
from left to right. We define the one-dimensional
![]() $U(\mathfrak{g},e)^{0}$
-module
$U(\mathfrak{g},e)^{0}$
-module
![]() $\Bbbk _{\overline{A}}$
by saying that
$\Bbbk _{\overline{A}}$
by saying that
![]() $D_{i}^{(r)}$
acts on
$D_{i}^{(r)}$
acts on
![]() $\Bbbk _{A}$
by
$\Bbbk _{A}$
by
![]() $e_{r}(a_{i,1}+i,\ldots ,a_{i,p_{i}}+i)$
; here
$e_{r}(a_{i,1}+i,\ldots ,a_{i,p_{i}}+i)$
; here
![]() $e_{r}(x_{1},\ldots ,x_{p_{i}})$
is the
$e_{r}(x_{1},\ldots ,x_{p_{i}})$
is the
![]() $r$
th elementary symmetric polynomial in the indeterminates
$r$
th elementary symmetric polynomial in the indeterminates
![]() $x_{1},\ldots ,x_{p_{i}}$
. It is clear that
$x_{1},\ldots ,x_{p_{i}}$
. It is clear that
![]() $\Bbbk _{\overline{A}}$
depends only on the row equivalence class of
$\Bbbk _{\overline{A}}$
depends only on the row equivalence class of
![]() $A$
. We note that, given
$A$
. We note that, given
![]() $b_{1},\ldots ,b_{p_{i}}\in \Bbbk$
, finding
$b_{1},\ldots ,b_{p_{i}}\in \Bbbk$
, finding
![]() $c_{i,1},\ldots ,c_{i,p_{i}}$
such that
$c_{i,1},\ldots ,c_{i,p_{i}}$
such that
![]() $e_{r}(c_{1},\ldots ,c_{p_{i}})=b_{r}$
for each
$e_{r}(c_{1},\ldots ,c_{p_{i}})=b_{r}$
for each
![]() $r$
is equivalent to finding solutions of the polynomial
$r$
is equivalent to finding solutions of the polynomial
![]() $t^{p_{i}}-b_{1}t^{p_{i}-1}+\cdots +(-1)^{p_{i}-1}b_{p_{i}-1}t+(-1)^{p_{i}}b_{p_{i}}$
. Therefore, since
$t^{p_{i}}-b_{1}t^{p_{i}-1}+\cdots +(-1)^{p_{i}-1}b_{p_{i}-1}t+(-1)^{p_{i}}b_{p_{i}}$
. Therefore, since
![]() $\Bbbk$
is algebraically closed, we see that any one-dimensional
$\Bbbk$
is algebraically closed, we see that any one-dimensional
![]() $U(\mathfrak{g},e)^{0}$
-module is isomorphic to
$U(\mathfrak{g},e)^{0}$
-module is isomorphic to
![]() $\Bbbk _{\overline{A}}$
for some
$\Bbbk _{\overline{A}}$
for some
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
. Thus we see that the restriction of any one-dimensional
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
. Thus we see that the restriction of any one-dimensional
![]() $U(\mathfrak{g},e)$
-module to
$U(\mathfrak{g},e)$
-module to
![]() $U(\mathfrak{g},e)^{0}$
is isomorphic to
$U(\mathfrak{g},e)^{0}$
is isomorphic to
![]() $\Bbbk _{\overline{A}}$
for some
$\Bbbk _{\overline{A}}$
for some
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
, and that such
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
, and that such
![]() $A$
is defined up to row equivalence. Using the relations (23) and (24) for
$A$
is defined up to row equivalence. Using the relations (23) and (24) for
![]() $r=1$
, we see that the generators
$r=1$
, we see that the generators
![]() $E_{i}^{(s)}$
and
$E_{i}^{(s)}$
and
![]() $F_{i}^{(s)}$
act as 0 on any one-dimensional
$F_{i}^{(s)}$
act as 0 on any one-dimensional
![]() $U(\mathfrak{g},e)$
-module, for all
$U(\mathfrak{g},e)$
-module, for all
![]() $i$
and
$i$
and
![]() $s$
. If the action of
$s$
. If the action of
![]() $U(\mathfrak{g},e)^{0}$
on
$U(\mathfrak{g},e)^{0}$
on
![]() $\Bbbk _{\overline{A}}$
can be extended to a
$\Bbbk _{\overline{A}}$
can be extended to a
![]() $U(\mathfrak{g},e)$
-module, on which
$U(\mathfrak{g},e)$
-module, on which
![]() $E_{i}^{(s)}$
and
$E_{i}^{(s)}$
and
![]() $F_{i}^{(s)}$
act as 0, then we denote this module by
$F_{i}^{(s)}$
act as 0, then we denote this module by
![]() $\widetilde{\Bbbk }_{\overline{A}}$
. Our goal is thus to determine when
$\widetilde{\Bbbk }_{\overline{A}}$
. Our goal is thus to determine when
![]() $\widetilde{\Bbbk }_{\overline{A}}$
exists, and this is achieved in the following theorem.
$\widetilde{\Bbbk }_{\overline{A}}$
exists, and this is achieved in the following theorem.
Theorem 5.1. Let
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
. There is a one-dimensional
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
. There is a one-dimensional
![]() $U(\mathfrak{g},e)$
-module
$U(\mathfrak{g},e)$
-module
![]() $\widetilde{\Bbbk }_{\overline{A}}$
, which extends the action of
$\widetilde{\Bbbk }_{\overline{A}}$
, which extends the action of
![]() $U(\mathfrak{g},e)^{0}$
on
$U(\mathfrak{g},e)^{0}$
on
![]() $\Bbbk _{\overline{A}}$
if and only if
$\Bbbk _{\overline{A}}$
if and only if
![]() $A$
is row equivalent to a column connected tableau.
$A$
is row equivalent to a column connected tableau.
Proof. First let
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
be column connected, with entries in the
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
be column connected, with entries in the
![]() $i$
th row labelled
$i$
th row labelled
![]() $a_{i,1},\ldots ,a_{i,p_{i}}$
for
$a_{i,1},\ldots ,a_{i,p_{i}}$
for
![]() $i=1,\ldots ,n$
. Recall the one-dimensional
$i=1,\ldots ,n$
. Recall the one-dimensional
![]() $U(\mathfrak{h})$
-module
$U(\mathfrak{h})$
-module
![]() $\widetilde{\Bbbk }_{A}$
defined in § 2.5; this can be inflated to a
$\widetilde{\Bbbk }_{A}$
defined in § 2.5; this can be inflated to a
![]() $U(\mathfrak{p})$
module, which we also denote by
$U(\mathfrak{p})$
module, which we also denote by
![]() $\widetilde{\Bbbk }_{A}$
. Consider the action of the explicit elements
$\widetilde{\Bbbk }_{A}$
. Consider the action of the explicit elements
![]() $D_{i}^{(r)}\in U(\mathfrak{p})$
given in (39) and (40) on the module
$D_{i}^{(r)}\in U(\mathfrak{p})$
given in (39) and (40) on the module
![]() $\widetilde{\Bbbk }_{A}$
. The only summands in the expression for
$\widetilde{\Bbbk }_{A}$
. The only summands in the expression for
![]() $D_{i}^{(r)}$
that do not act as zero on
$D_{i}^{(r)}$
that do not act as zero on
![]() $\widetilde{\Bbbk }_{A}$
are those which are products
$\widetilde{\Bbbk }_{A}$
are those which are products
![]() $\tilde{e}_{i_{1},j_{1}}\cdots \tilde{e}_{i_{s},j_{s}}$
such that
$\tilde{e}_{i_{1},j_{1}}\cdots \tilde{e}_{i_{s},j_{s}}$
such that
![]() $i_{1}=j_{1},\ldots ,i_{s}=j_{s}$
: terms of this form only occur for
$i_{1}=j_{1},\ldots ,i_{s}=j_{s}$
: terms of this form only occur for
![]() $s=r$
and their sum is precisely
$s=r$
and their sum is precisely
![]() $e_{r}(\tilde{e}_{i_{1},j_{1}},\ldots ,\tilde{e}_{ir_{,}j_{r}})$
. The
$e_{r}(\tilde{e}_{i_{1},j_{1}},\ldots ,\tilde{e}_{ir_{,}j_{r}})$
. The
![]() $\mathfrak{t}$
-weight of
$\mathfrak{t}$
-weight of
![]() $\widetilde{\Bbbk }_{A}$
is
$\widetilde{\Bbbk }_{A}$
is
![]() $\unicode[STIX]{x1D706}_{A}-\widetilde{\unicode[STIX]{x1D70C}}$
, and we have
$\unicode[STIX]{x1D706}_{A}-\widetilde{\unicode[STIX]{x1D70C}}$
, and we have
![]() $\widetilde{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D702}+\unicode[STIX]{x1D70C}_{\mathfrak{h}}$
by (10). Thus we see that each
$\widetilde{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D702}+\unicode[STIX]{x1D70C}_{\mathfrak{h}}$
by (10). Thus we see that each
![]() $\tilde{e}_{i,i}$
acts on
$\tilde{e}_{i,i}$
acts on
![]() $\widetilde{\Bbbk }_{A}$
by
$\widetilde{\Bbbk }_{A}$
by
![]() $(\unicode[STIX]{x1D706}_{A}+\unicode[STIX]{x1D70C}_{\mathfrak{h}})(e_{i,i})$
, because of the shift of
$(\unicode[STIX]{x1D706}_{A}+\unicode[STIX]{x1D70C}_{\mathfrak{h}})(e_{i,i})$
, because of the shift of
![]() $\unicode[STIX]{x1D702}$
in the definition of
$\unicode[STIX]{x1D702}$
in the definition of
![]() $\tilde{e}_{i,j}$
. Combining all of these observations shows that the action of
$\tilde{e}_{i,j}$
. Combining all of these observations shows that the action of
![]() $D_{i}^{(r)}$
on
$D_{i}^{(r)}$
on
![]() $\widetilde{\Bbbk }_{A}$
is given by
$\widetilde{\Bbbk }_{A}$
is given by
![]() $e_{r}(a_{i,1}+i,\ldots ,a_{i,p_{i}}+i)$
. This proves that
$e_{r}(a_{i,1}+i,\ldots ,a_{i,p_{i}}+i)$
. This proves that
![]() $\widetilde{\Bbbk }_{\overline{A}}$
exists, under the assumption that
$\widetilde{\Bbbk }_{\overline{A}}$
exists, under the assumption that
![]() $A$
is column connected.
$A$
is column connected.
We move on to prove that
![]() $\widetilde{\Bbbk }_{\overline{A}}$
exists only if
$\widetilde{\Bbbk }_{\overline{A}}$
exists only if
![]() $A$
is column connected. To do this, first note that the action
$A$
is column connected. To do this, first note that the action
![]() $U(\mathfrak{g},e)$
on any one-dimensional module factors to an action of the abelianization
$U(\mathfrak{g},e)$
on any one-dimensional module factors to an action of the abelianization
![]() $U(\mathfrak{g},e)^{\operatorname{ab}}$
of
$U(\mathfrak{g},e)^{\operatorname{ab}}$
of
![]() $U(\mathfrak{g},e)$
. By Lemma 3.2 and Theorem 4.3, we know that
$U(\mathfrak{g},e)$
. By Lemma 3.2 and Theorem 4.3, we know that
![]() $U(\mathfrak{g},e)^{\operatorname{ab}}$
is generated by the images of the
$U(\mathfrak{g},e)^{\operatorname{ab}}$
is generated by the images of the
![]() $l$
elements
$l$
elements
So any one-dimensional
![]() $U(\mathfrak{g},e)$
-module is determined uniquely by the action of these elements. Thus to show that any one-dimensional
$U(\mathfrak{g},e)$
-module is determined uniquely by the action of these elements. Thus to show that any one-dimensional
![]() $U(\mathfrak{g},e)$
-module is of the form
$U(\mathfrak{g},e)$
-module is of the form
![]() $\widetilde{\Bbbk }_{\overline{A}}$
for some column connected
$\widetilde{\Bbbk }_{\overline{A}}$
for some column connected
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
, it suffices to show that for any set
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
, it suffices to show that for any set
where
![]() $a_{i}^{(r)}\in \Bbbk$
, there is a column connected
$a_{i}^{(r)}\in \Bbbk$
, there is a column connected
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
such that the action of
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
such that the action of
![]() $D_{i}^{(r)}$
on
$D_{i}^{(r)}$
on
![]() $\widetilde{\Bbbk }_{\overline{A}}$
is given by
$\widetilde{\Bbbk }_{\overline{A}}$
is given by
![]() $a_{i}^{(r)}$
for
$a_{i}^{(r)}$
for
![]() $i=1,\ldots ,n$
and
$i=1,\ldots ,n$
and
![]() $0\leqslant r\leqslant p_{i}-p_{i-1}$
. This is proved ‘over the complex numbers’ at the end of [Reference BrundanBru11, §2], and depends crucially on [Reference BrundanBru11, Lemma 2.6]. It can be observed that the proof of this lemma is also valid over an algebraically closed field of characteristic
$0\leqslant r\leqslant p_{i}-p_{i-1}$
. This is proved ‘over the complex numbers’ at the end of [Reference BrundanBru11, §2], and depends crucially on [Reference BrundanBru11, Lemma 2.6]. It can be observed that the proof of this lemma is also valid over an algebraically closed field of characteristic
![]() $p$
. From this we can deduce that all one-dimensional
$p$
. From this we can deduce that all one-dimensional
![]() $U(\mathfrak{g},e)$
-modules are of the form
$U(\mathfrak{g},e)$
-modules are of the form
![]() $\tilde{\Bbbk }_{\overline{A}}$
for some column connected
$\tilde{\Bbbk }_{\overline{A}}$
for some column connected
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
.◻
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
.◻
As mentioned after the statement of Lemma 3.2, the abelianization of
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
is actually a polynomial algebra on the generators given in that lemma. This can now be deduced immediately from the proof of Theorem 5.1, which shows that there are one-dimensional modules for
$Y_{n,l}(\unicode[STIX]{x1D70E})$
is actually a polynomial algebra on the generators given in that lemma. This can now be deduced immediately from the proof of Theorem 5.1, which shows that there are one-dimensional modules for
![]() $Y_{n,l}(\unicode[STIX]{x1D70E})$
on which these generators can act by arbitrary elements of
$Y_{n,l}(\unicode[STIX]{x1D70E})$
on which these generators can act by arbitrary elements of
![]() $\Bbbk$
.
$\Bbbk$
.
6 One-dimensional modules for
 $U_{0}(\mathfrak{g},e)$
$U_{0}(\mathfrak{g},e)$
From Theorem 5.1 we have a classification of one-dimensional
![]() $U(\mathfrak{g},e)$
-modules given by the modules
$U(\mathfrak{g},e)$
-modules given by the modules
![]() $\widetilde{\Bbbk }_{\overline{A}}$
for
$\widetilde{\Bbbk }_{\overline{A}}$
for
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
ranging over a set of representatives of row equivalence classes of column connected tableaux. Our next theorem determines for which of these one-dimensional modules the action of
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
ranging over a set of representatives of row equivalence classes of column connected tableaux. Our next theorem determines for which of these one-dimensional modules the action of
![]() $U(\mathfrak{g},e)$
factors through the quotient
$U(\mathfrak{g},e)$
factors through the quotient
![]() $U(\mathfrak{g},e){\twoheadrightarrow}U_{0}(\mathfrak{g},e)$
to give a one-dimensional
$U(\mathfrak{g},e){\twoheadrightarrow}U_{0}(\mathfrak{g},e)$
to give a one-dimensional
![]() $U_{0}(\mathfrak{g},e)$
-module. Therefore, we obtain a classification of the one-dimensional
$U_{0}(\mathfrak{g},e)$
-module. Therefore, we obtain a classification of the one-dimensional
![]() $U_{0}(\mathfrak{g},e)$
-modules.
$U_{0}(\mathfrak{g},e)$
-modules.
Theorem 6.1. Let
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
be column connected. Then
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
be column connected. Then
![]() $\widetilde{\Bbbk }_{\overline{A}}$
factors to a module for
$\widetilde{\Bbbk }_{\overline{A}}$
factors to a module for
![]() $U_{0}(\mathfrak{g},e)$
if and only if
$U_{0}(\mathfrak{g},e)$
if and only if
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
.
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
.
Proof. Let
![]() $A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
be column connected with entries labelled
$A\in \operatorname{Tab}_{\Bbbk }(\unicode[STIX]{x1D70B})$
be column connected with entries labelled
![]() $a_{1},\ldots ,a_{N}$
as usual. We see that
$a_{1},\ldots ,a_{N}$
as usual. We see that
![]() $\widetilde{\Bbbk }_{A}$
factors through
$\widetilde{\Bbbk }_{A}$
factors through
![]() $U_{\unicode[STIX]{x1D713}_{A}}(\mathfrak{p})$
, where
$U_{\unicode[STIX]{x1D713}_{A}}(\mathfrak{p})$
, where
![]() $\unicode[STIX]{x1D713}_{A}\in \mathfrak{p}^{\ast }$
is defined by
$\unicode[STIX]{x1D713}_{A}\in \mathfrak{p}^{\ast }$
is defined by
![]() $\unicode[STIX]{x1D713}_{A}(e_{i,j})=0$
for
$\unicode[STIX]{x1D713}_{A}(e_{i,j})=0$
for
![]() $i\neq j$
, and
$i\neq j$
, and
![]() $\unicode[STIX]{x1D713}_{A}(e_{i,i})=a_{i}^{p}-a_{i}$
. Therefore,
$\unicode[STIX]{x1D713}_{A}(e_{i,i})=a_{i}^{p}-a_{i}$
. Therefore,
![]() $\widetilde{\Bbbk }_{\overline{A}}$
is a module for the reduced
$\widetilde{\Bbbk }_{\overline{A}}$
is a module for the reduced
![]() $W$
-algebra
$W$
-algebra
![]() $U_{\unicode[STIX]{x1D713}_{A}}(\mathfrak{g},e)$
as defined in § 2.6. From the discussion after Lemma 2.3, we see that
$U_{\unicode[STIX]{x1D713}_{A}}(\mathfrak{g},e)$
as defined in § 2.6. From the discussion after Lemma 2.3, we see that
![]() $\widetilde{\Bbbk }_{\overline{A}}$
factors to a module for
$\widetilde{\Bbbk }_{\overline{A}}$
factors to a module for
![]() $U_{0}(\mathfrak{g},e)$
if and only if
$U_{0}(\mathfrak{g},e)$
if and only if
![]() $0$
and
$0$
and
![]() $\unicode[STIX]{x1D713}_{A}$
are conjugate under the twisted
$\unicode[STIX]{x1D713}_{A}$
are conjugate under the twisted
![]() $M$
-action.
$M$
-action.
We next show that
![]() $\unicode[STIX]{x1D713}_{A}$
is conjugate to 0 under the twisted
$\unicode[STIX]{x1D713}_{A}$
is conjugate to 0 under the twisted
![]() $M$
-action only if
$M$
-action only if
![]() $\unicode[STIX]{x1D713}_{A}=0$
. To do this, note that under the identification
$\unicode[STIX]{x1D713}_{A}=0$
. To do this, note that under the identification
![]() $\mathfrak{p}^{\ast }\cong e+\mathfrak{m}^{\bot }$
we have that
$\mathfrak{p}^{\ast }\cong e+\mathfrak{m}^{\bot }$
we have that
![]() $0$
corresponds to
$0$
corresponds to
![]() $e$
and
$e$
and
![]() $\unicode[STIX]{x1D713}_{A}$
corresponds to an element
$\unicode[STIX]{x1D713}_{A}$
corresponds to an element
![]() $e+\operatorname{diag}(a_{1}^{p}-a_{1},\ldots ,a_{N}^{p}-a_{N})$
, where we recall that
$e+\operatorname{diag}(a_{1}^{p}-a_{1},\ldots ,a_{N}^{p}-a_{N})$
, where we recall that
![]() $\operatorname{diag}(d_{1},\ldots ,d_{N})$
denotes the diagonal matrix with
$\operatorname{diag}(d_{1},\ldots ,d_{N})$
denotes the diagonal matrix with
![]() $i$
th entry
$i$
th entry
![]() $d_{i}$
. We have that
$d_{i}$
. We have that
![]() $e+\operatorname{diag}(a_{1}^{p}-a_{1},\ldots ,a_{N}^{p}-a_{N})$
is nilpotent only if
$e+\operatorname{diag}(a_{1}^{p}-a_{1},\ldots ,a_{N}^{p}-a_{N})$
is nilpotent only if
![]() $\operatorname{diag}(a_{1}^{p}-a_{1},\ldots ,a_{N}^{p}-a_{N})=0$
. Therefore,
$\operatorname{diag}(a_{1}^{p}-a_{1},\ldots ,a_{N}^{p}-a_{N})=0$
. Therefore,
![]() $e$
is not in the same
$e$
is not in the same
![]() $M$
-orbit as
$M$
-orbit as
![]() $e+\operatorname{diag}(a_{1}^{p}-a_{1},\ldots ,a_{N}^{p}-a_{N})$
unless
$e+\operatorname{diag}(a_{1}^{p}-a_{1},\ldots ,a_{N}^{p}-a_{N})$
unless
![]() $a_{i}^{p}-a_{i}=0$
for all
$a_{i}^{p}-a_{i}=0$
for all
![]() $i$
.
$i$
.
Hence, we deduce that
![]() $\widetilde{\Bbbk }_{\overline{A}}$
factors to a module for
$\widetilde{\Bbbk }_{\overline{A}}$
factors to a module for
![]() $U_{0}(\mathfrak{g},e)$
if only if
$U_{0}(\mathfrak{g},e)$
if only if
![]() $a_{i}^{p}-a_{i}=0$
for all
$a_{i}^{p}-a_{i}=0$
for all
![]() $i$
. This is the case if and only if
$i$
. This is the case if and only if
![]() $a_{i}\in \mathbb{F}_{p}$
for all
$a_{i}\in \mathbb{F}_{p}$
for all
![]() $i$
, so that
$i$
, so that
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
.◻
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
.◻
7 Minimal-dimensional modules for
 $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
Armed with Premet’s equivalence (Theorem 2.4) and Theorems 2.2 and 6.1, we are ready to prove our main theorem.
Proof of Theorem 1.1.
Let
![]() $c_{\unicode[STIX]{x1D70B}}$
be the number of row equivalence classes in
$c_{\unicode[STIX]{x1D70B}}$
be the number of row equivalence classes in
![]() $\operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
containing a column connected tableau. By Theorem 6.1, we know that the number of isomorphism classes of
$\operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
containing a column connected tableau. By Theorem 6.1, we know that the number of isomorphism classes of
![]() $1$
-dimensional modules for
$1$
-dimensional modules for
![]() $U_{0}(\mathfrak{g},e)$
-modules is
$U_{0}(\mathfrak{g},e)$
-modules is
![]() $c_{\unicode[STIX]{x1D70B}}$
. Thus by Theorem 2.4 the number of minimal-dimensional
$c_{\unicode[STIX]{x1D70B}}$
. Thus by Theorem 2.4 the number of minimal-dimensional
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-modules is
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-modules is
![]() $c_{\unicode[STIX]{x1D70B}}$
.
$c_{\unicode[STIX]{x1D70B}}$
.
Given column connected
![]() $A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
, we have that
$A\in \operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
, we have that
![]() $L_{\unicode[STIX]{x1D712}}(A)$
is
$L_{\unicode[STIX]{x1D712}}(A)$
is
![]() $p^{d_{\unicode[STIX]{x1D712}}}$
-dimensional by Theorem 2.2. Also up to isomorphism
$p^{d_{\unicode[STIX]{x1D712}}}$
-dimensional by Theorem 2.2. Also up to isomorphism
![]() $L_{\unicode[STIX]{x1D712}}(A)$
depends only on the row equivalence class of
$L_{\unicode[STIX]{x1D712}}(A)$
depends only on the row equivalence class of
![]() $A$
. Therefore, the modules
$A$
. Therefore, the modules
![]() $L_{\unicode[STIX]{x1D712}}(A)$
for
$L_{\unicode[STIX]{x1D712}}(A)$
for
![]() $A$
ranging over a set of row equivalence classes of column connected tableaux in
$A$
ranging over a set of row equivalence classes of column connected tableaux in
![]() $\operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
give all
$\operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
give all
![]() $c_{\unicode[STIX]{x1D70B}}$
isomorphism classes of minimal-dimensional modules.◻
$c_{\unicode[STIX]{x1D70B}}$
isomorphism classes of minimal-dimensional modules.◻
Now that Theorem 1.1 is proved, Corollary 1.2 follows, as explained in the introduction.
Remark 7.1. It is interesting to know the bijection given by Premet’s equivalence between the sets of isomorphism classes of the one-dimensional
![]() $U_{0}(\mathfrak{g},e)$
-modules
$U_{0}(\mathfrak{g},e)$
-modules
![]() $\widetilde{\Bbbk }_{\overline{A}}$
and those of the minimal-dimensional
$\widetilde{\Bbbk }_{\overline{A}}$
and those of the minimal-dimensional
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-modules
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-modules
![]() $L_{\unicode[STIX]{x1D712}}(A)$
, as
$L_{\unicode[STIX]{x1D712}}(A)$
, as
![]() $A$
ranges over a set of representatives of row equivalence classes of column connected tableaux in
$A$
ranges over a set of representatives of row equivalence classes of column connected tableaux in
![]() $\operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
. It turns out that this bijection sends
$\operatorname{Tab}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D70B})$
. It turns out that this bijection sends
![]() $\widetilde{\Bbbk }_{\overline{A}}$
to
$\widetilde{\Bbbk }_{\overline{A}}$
to
![]() $L_{\unicode[STIX]{x1D712}}(A)$
and we briefly outline some steps that can be used to verify this.
$L_{\unicode[STIX]{x1D712}}(A)$
and we briefly outline some steps that can be used to verify this.
Use the fact that
![]() $L_{\unicode[STIX]{x1D712}}(A)\cong N_{\unicode[STIX]{x1D712}}(A)=U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{0}(\mathfrak{p})}\overline{\Bbbk }_{A}$
as is given in Theorem 2.2. Then show that
$L_{\unicode[STIX]{x1D712}}(A)\cong N_{\unicode[STIX]{x1D712}}(A)=U_{\unicode[STIX]{x1D712}}(\mathfrak{g})\otimes _{U_{0}(\mathfrak{p})}\overline{\Bbbk }_{A}$
as is given in Theorem 2.2. Then show that
![]() $N_{\unicode[STIX]{x1D712}}(A)^{\mathfrak{m}_{\unicode[STIX]{x1D712}}}\cong \widetilde{\Bbbk }_{\overline{A}}$
using the following arguments; we recall here that
$N_{\unicode[STIX]{x1D712}}(A)^{\mathfrak{m}_{\unicode[STIX]{x1D712}}}\cong \widetilde{\Bbbk }_{\overline{A}}$
using the following arguments; we recall here that
![]() $N_{\unicode[STIX]{x1D712}}(A)^{\mathfrak{m}_{\unicode[STIX]{x1D712}}}$
is defined in (16).
$N_{\unicode[STIX]{x1D712}}(A)^{\mathfrak{m}_{\unicode[STIX]{x1D712}}}$
is defined in (16).
Consider the dual
![]() $N_{\unicode[STIX]{x1D712}}(A)^{\ast }$
viewed as a right module for
$N_{\unicode[STIX]{x1D712}}(A)^{\ast }$
viewed as a right module for
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
. We observe that
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
. We observe that
![]() $\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D706}-\tilde{\unicode[STIX]{x1D70C}}$
is the weight of a
$\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D706}-\tilde{\unicode[STIX]{x1D70C}}$
is the weight of a
![]() $1$
-dimensional right
$1$
-dimensional right
![]() $U_{0}(\mathfrak{h})$
-module, which we denote by
$U_{0}(\mathfrak{h})$
-module, which we denote by
![]() $\Bbbk _{\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D6FD}}$
. Using the fact that any
$\Bbbk _{\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D6FD}}$
. Using the fact that any
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module is free as a
$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
-module is free as a
![]() $U_{\unicode[STIX]{x1D712}}(\mathfrak{m})$
-module, it can be proved that
$U_{\unicode[STIX]{x1D712}}(\mathfrak{m})$
-module, it can be proved that
![]() $N_{\unicode[STIX]{x1D712}}(A)^{\ast }\cong \Bbbk _{\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D6FD}}\otimes _{U_{0}(\mathfrak{p})}U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
. Note that it is more natural to consider the weight
$N_{\unicode[STIX]{x1D712}}(A)^{\ast }\cong \Bbbk _{\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D6FD}}\otimes _{U_{0}(\mathfrak{p})}U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
. Note that it is more natural to consider the weight
![]() $\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}+(p-1)\unicode[STIX]{x1D6FD}$
to prove this isomorphism, and use that this is the
$\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}+(p-1)\unicode[STIX]{x1D6FD}$
to prove this isomorphism, and use that this is the
![]() $\mathfrak{t}$
-weight of
$\mathfrak{t}$
-weight of
![]() $\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}(-)}e_{\unicode[STIX]{x1D6FC}}^{p-1}\overline{1}_{A}\in N_{\unicode[STIX]{x1D712}}(A)$
, where
$\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}(-)}e_{\unicode[STIX]{x1D6FC}}^{p-1}\overline{1}_{A}\in N_{\unicode[STIX]{x1D712}}(A)$
, where
![]() $\overline{1}_{A}$
is the generator of
$\overline{1}_{A}$
is the generator of
![]() $\overline{\Bbbk }_{A}$
.
$\overline{\Bbbk }_{A}$
.
Next consider the space of Whittaker coinvariants of
![]() $N_{\unicode[STIX]{x1D712}}(A)^{\ast }$
. This is defined by
$N_{\unicode[STIX]{x1D712}}(A)^{\ast }$
. This is defined by
![]() $N_{\unicode[STIX]{x1D712}}(A)^{\ast }/N_{\unicode[STIX]{x1D712}}(A)^{\ast }\mathfrak{m}_{\unicode[STIX]{x1D712}}$
and is a right module for
$N_{\unicode[STIX]{x1D712}}(A)^{\ast }/N_{\unicode[STIX]{x1D712}}(A)^{\ast }\mathfrak{m}_{\unicode[STIX]{x1D712}}$
and is a right module for
![]() $U(\mathfrak{g},e)$
. It is quite straightforward to show that the space of Whittaker coinvariants of
$U(\mathfrak{g},e)$
. It is quite straightforward to show that the space of Whittaker coinvariants of
![]() $\Bbbk _{\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D6FD}}\otimes _{U_{0}(\mathfrak{p})}U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
is isomorphic to the restriction of the right
$\Bbbk _{\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D6FD}}\otimes _{U_{0}(\mathfrak{p})}U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$
is isomorphic to the restriction of the right
![]() $U_{0}(\mathfrak{p})$
-module
$U_{0}(\mathfrak{p})$
-module
![]() $\Bbbk _{\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D6FD}}$
to
$\Bbbk _{\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D6FD}}$
to
![]() $U(\mathfrak{g},e)$
, so the same is true for the space of Whittaker coinvariants of
$U(\mathfrak{g},e)$
, so the same is true for the space of Whittaker coinvariants of
![]() $N_{\unicode[STIX]{x1D712}}(A)^{\ast }$
. Standard arguments show that
$N_{\unicode[STIX]{x1D712}}(A)^{\ast }$
. Standard arguments show that
![]() $N_{\unicode[STIX]{x1D712}}(A)^{\mathfrak{m}_{\unicode[STIX]{x1D712}}}\cong (N_{\unicode[STIX]{x1D712}}(A)^{\ast }/\mathfrak{m}_{\unicode[STIX]{x1D712}}N_{\unicode[STIX]{x1D712}}(A)^{\ast })^{\ast }$
. Then it can be deduced that
$N_{\unicode[STIX]{x1D712}}(A)^{\mathfrak{m}_{\unicode[STIX]{x1D712}}}\cong (N_{\unicode[STIX]{x1D712}}(A)^{\ast }/\mathfrak{m}_{\unicode[STIX]{x1D712}}N_{\unicode[STIX]{x1D712}}(A)^{\ast })^{\ast }$
. Then it can be deduced that
![]() $N_{\unicode[STIX]{x1D712}}(A)^{\mathfrak{m}_{\unicode[STIX]{x1D712}}}$
is isomorphic to the restriction of the left
$N_{\unicode[STIX]{x1D712}}(A)^{\mathfrak{m}_{\unicode[STIX]{x1D712}}}$
is isomorphic to the restriction of the left
![]() $U_{0}(\mathfrak{p})$
-module
$U_{0}(\mathfrak{p})$
-module
![]() $\Bbbk _{\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D6FD}}$
to
$\Bbbk _{\unicode[STIX]{x1D706}_{A}-\overline{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D6FD}}$
to
![]() $U_{0}(\mathfrak{g},e)$
.
$U_{0}(\mathfrak{g},e)$
.
It just remains to use the fact that
![]() $\overline{\unicode[STIX]{x1D70C}}+\unicode[STIX]{x1D6FD}=\widetilde{\unicode[STIX]{x1D70C}}$
to deduce that
$\overline{\unicode[STIX]{x1D70C}}+\unicode[STIX]{x1D6FD}=\widetilde{\unicode[STIX]{x1D70C}}$
to deduce that
![]() $N_{\unicode[STIX]{x1D712}}(A)^{\mathfrak{m}_{\unicode[STIX]{x1D712}}}\cong \widetilde{\Bbbk }_{\overline{A}}$
.
$N_{\unicode[STIX]{x1D712}}(A)^{\mathfrak{m}_{\unicode[STIX]{x1D712}}}\cong \widetilde{\Bbbk }_{\overline{A}}$
.
Acknowledgements
Both authors would like to thank the University of Padova and the Erwin Schrödinger Institute, Vienna, where parts of this work were carried out. The first author is supported in part by EPSRC grant EP/R018952/1. The second author gratefully acknowledges funding from the European Commission Seventh Framework Programme, Grant Agreement 600376, as well as EPSRC grant EP/N034449/1. We thank Alexander Premet for helpful correspondence about this work, and the referee for useful comments.