The notion of Hochschild cochains induces an assignment from 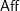 $\mathsf{Aff}$, affine DG schemes, to monoidal DG categories. We show that this assignment extends, under appropriate finiteness conditions, to a functor
$\mathsf{Aff}$, affine DG schemes, to monoidal DG categories. We show that this assignment extends, under appropriate finiteness conditions, to a functor 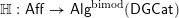 $\mathbb{H}:\mathsf{Aff}\rightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$, where the latter denotes the category of monoidal DG categories and bimodules. Any functor
$\mathbb{H}:\mathsf{Aff}\rightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$, where the latter denotes the category of monoidal DG categories and bimodules. Any functor 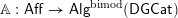 $\mathbb{A}:\mathsf{Aff}\rightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$ gives rise, by taking modules, to a theory of sheaves of categories
$\mathbb{A}:\mathsf{Aff}\rightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$ gives rise, by taking modules, to a theory of sheaves of categories 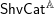 $\mathsf{ShvCat}^{\mathbb{A}}$. In this paper, we study
$\mathsf{ShvCat}^{\mathbb{A}}$. In this paper, we study 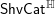 $\mathsf{ShvCat}^{\mathbb{H}}$. Loosely speaking, this theory categorifies the theory of
$\mathsf{ShvCat}^{\mathbb{H}}$. Loosely speaking, this theory categorifies the theory of 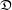 $\mathfrak{D}$-modules, in the same way as Gaitsgory’s original
$\mathfrak{D}$-modules, in the same way as Gaitsgory’s original 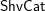 $\mathsf{ShvCat}$ categorifies the theory of quasi-coherent sheaves. We develop the functoriality of
$\mathsf{ShvCat}$ categorifies the theory of quasi-coherent sheaves. We develop the functoriality of 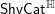 $\mathsf{ShvCat}^{\mathbb{H}}$, its descent properties and the notion of
$\mathsf{ShvCat}^{\mathbb{H}}$, its descent properties and the notion of 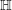 $\mathbb{H}$-affineness. We then prove the
$\mathbb{H}$-affineness. We then prove the 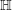 $\mathbb{H}$-affineness of algebraic stacks: for
$\mathbb{H}$-affineness of algebraic stacks: for 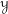 ${\mathcal{Y}}$ a stack satisfying some mild conditions, the
${\mathcal{Y}}$ a stack satisfying some mild conditions, the 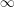 $\infty$-category
$\infty$-category 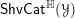 $\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$ is equivalent to the
$\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$ is equivalent to the  $\infty$-category of modules for
$\infty$-category of modules for 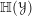 $\mathbb{H}({\mathcal{Y}})$, the monoidal DG category of higher differential operators. The main consequence, for
$\mathbb{H}({\mathcal{Y}})$, the monoidal DG category of higher differential operators. The main consequence, for  ${\mathcal{Y}}$ quasi-smooth, is the following: if
${\mathcal{Y}}$ quasi-smooth, is the following: if 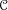 ${\mathcal{C}}$ is a DG category acted on by
${\mathcal{C}}$ is a DG category acted on by 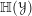 $\mathbb{H}({\mathcal{Y}})$, then
$\mathbb{H}({\mathcal{Y}})$, then 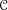 ${\mathcal{C}}$ admits a theory of singular support in
${\mathcal{C}}$ admits a theory of singular support in 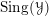 $\operatorname{Sing}({\mathcal{Y}})$, where
$\operatorname{Sing}({\mathcal{Y}})$, where 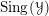 $\operatorname{Sing}({\mathcal{Y}})$ is the space of singularities of
$\operatorname{Sing}({\mathcal{Y}})$ is the space of singularities of 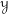 ${\mathcal{Y}}$. As an application to the geometric Langlands programme, we indicate how derived Satake yields an action of
${\mathcal{Y}}$. As an application to the geometric Langlands programme, we indicate how derived Satake yields an action of 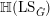 $\mathbb{H}(\operatorname{LS}_{{\check{G}}})$ on
$\mathbb{H}(\operatorname{LS}_{{\check{G}}})$ on 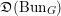 $\mathfrak{D}(\operatorname{Bun}_{G})$, thereby equipping objects of
$\mathfrak{D}(\operatorname{Bun}_{G})$, thereby equipping objects of 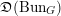 $\mathfrak{D}(\operatorname{Bun}_{G})$ with singular support in
$\mathfrak{D}(\operatorname{Bun}_{G})$ with singular support in 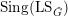 $\operatorname{Sing}(\operatorname{LS}_{{\check{G}}})$.
$\operatorname{Sing}(\operatorname{LS}_{{\check{G}}})$.
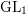 $\text{GL}_{1}$
$\text{GL}_{1}$
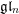 $\mathfrak{g}\mathfrak{l}_{n}$
$\mathfrak{g}\mathfrak{l}_{n}$
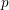 $p$-groups
$p$-groups