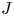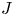1 Introduction
In a recent series of papers (Helander & Plunk Reference Helander and Plunk2021, Reference Helander and Plunk2022; Plunk & Helander Reference Plunk and Helander2022, Reference Plunk and Helander2023) a new theory has been developed that bounds the growth of linear and nonlinear instabilities in gyrokinetic systems by considering the energy balance that must be obeyed by these systems (from now on we will refer to these publications as Parts 1, 2 and 3, respectively). These upper bounds are attained by the optimal modes of the system – states of the gyrokinetic system that maximise the growth of a chosen ‘energy norm’ within the limits allowed by energy balance. The optimal modes form a complete orthogonal basis for the space of distribution functions. Unlike the ‘normal’ modes of the linear gyrokinetic operator (solutions to the gyrokinetic system which evolve as $\exp ({-{\rm i} \omega t})$![]() ), the velocity space dependence of the optimal modes is significantly simpler. Moreover, the optimal modes possess a closed-form solution in terms of a finite set of gyrofluid-like moments, without any closure approximation, resulting in a low-dimensionality eigenvalue problem for the optimal growth rate, which can be solved at low computational cost. This makes the optimal modes an attractive lens with which to explore gyrokinetic systems.
), the velocity space dependence of the optimal modes is significantly simpler. Moreover, the optimal modes possess a closed-form solution in terms of a finite set of gyrofluid-like moments, without any closure approximation, resulting in a low-dimensionality eigenvalue problem for the optimal growth rate, which can be solved at low computational cost. This makes the optimal modes an attractive lens with which to explore gyrokinetic systems.
There is a wide range of energy norms that can be used in these optimal mode analyses. In Parts 1 and 2 the bounds were developed using the Helmholtz free energy as an energy norm, culminating in upper bounds on fully electromagnetic, multispecies instabilities. Part 3 extended the optimal mode analysis by considering the generalised free energy, a linear combination of the Helmholtz free energy and the electrostatic energy, for a single kinetic species (kinetic ions with adiabatic electrons). The optimal growth of this generalised free energy yields the lowest possible upper bound that can be formed from the balance of these two energies, as will become clearer below. Importantly, the generalised free energy adds an explicit dependence on magnetic geometry into the optimal mode analysis by retaining the wave–particle interaction effects, including magnetic drifts, which contribute in a physically transparent way to the evolution of the field energy of the system.
While the bounds derived for the system with kinetic ions and adiabatic electrons have been found to be quite close to the results of linear gyrokinetic simulations in tokamaks and stellarators, the upper bounds for two kinetic species in the electrostatic limit derived in Part 2 tends to be several times larger than the simulated linear instability growth in these geometries (Podavini et al. Reference Podavini, Plunk, Helander and Zocco2025). This is most evident at small values of the perpendicular wavenumber $k_\perp$![]() , where the simulated growth rates in the toroidal geometries tend to zero, and the upper bound tends to a non-zero value of considerable size. This discrepancy in qualitative behaviour is because the upper bound of Part 2 is geometry independent and must also bound the growth of instabilities in closed-field-line geometries, like the z-pinch (Ricci et al. Reference Ricci, Rogers, Dorland and Barnes2006), which exhibit finite growth as $k_\perp \to 0$
, where the simulated growth rates in the toroidal geometries tend to zero, and the upper bound tends to a non-zero value of considerable size. This discrepancy in qualitative behaviour is because the upper bound of Part 2 is geometry independent and must also bound the growth of instabilities in closed-field-line geometries, like the z-pinch (Ricci et al. Reference Ricci, Rogers, Dorland and Barnes2006), which exhibit finite growth as $k_\perp \to 0$![]() . As we will see, the difference in these geometries lies in the transit average of the passing-electron response, which may be non-adiabatic in closed-field-line geometry but is largely adiabatic on the typical instability time scale in toroidal geometry, where the trapped electrons dominate the non-adiabatic electron response.
. As we will see, the difference in these geometries lies in the transit average of the passing-electron response, which may be non-adiabatic in closed-field-line geometry but is largely adiabatic on the typical instability time scale in toroidal geometry, where the trapped electrons dominate the non-adiabatic electron response.
In this work, we aim to increase the applicability of the optimal mode theory with a kinetic electron response to stellarator and tokamak geometry. This is done by considering a reduced two-species system, in the electrostatic limit, in which the electron transit time along the magnetic field is assumed to be much faster than the evolution of the instabilities. In toroidal geometry, this eliminates the passing-electron contribution to instabilities, at lowest order, leaving only a bounce-averaged trapped electron response. The resulting gyrokinetic system is often used to describe electrostatic instabilities such as trapped-electron modes (TEMs) (Helander, Proll & Plunk Reference Helander, Proll and Plunk2013) and ion-driven TEMs (ITEMs) (Plunk, Connor & Helander Reference Plunk, Connor and Helander2017), but is also applicable to ion-temperature gradient modes (ITGs) (Proll et al. Reference Proll, Plunk, Faber, Görler, Helander, McKinney, Pueschel, Smith and Xanthopoulos2022). We note that we exclude modes such as the electron-temperature-gradient mode (ETG) (Dorland et al. Reference Dorland, Jenko, Kotschenreuther and Rogers2000; Plunk et al. Reference Plunk2019) and the universal mode (Helander & Plunk Reference Helander and Plunk2015; Landreman, Plunk & Dorland Reference Landreman, Plunk and Dorland2015) which evolve on time scales comparable to, or shorter than, the electron transit time.
To include wave–particle resonance effects, particularly involving the magnetic drifts, we construct the generalised free energy (of which the Helmholtz free energy is a special case) of the system with gyrokinetic ions and bounce-averaged electrons. We first study the Helmholtz free energy limit, which is directly comparable with the two-species result of Part 2. We then consider the full generalised free energy and explore the impact of magnetic curvature on the optimal modes and the resulting upper bounds. We confirm that the previously known linear stability benefits of maximum-$J$![]() magnetic geometries associated with the presence of an electron free energy source (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander et al. Reference Helander, Proll and Plunk2013) are exhibited by the optimal modes. The optimal mode analysis also reveals an additional stabilising effect that the maximum-$J$
magnetic geometries associated with the presence of an electron free energy source (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander et al. Reference Helander, Proll and Plunk2013) are exhibited by the optimal modes. The optimal mode analysis also reveals an additional stabilising effect that the maximum-$J$![]() property has on ITGs – even in the absence of an electron free energy source. We explain this effect through the concept of mode inertia, which is sensitive to the degree of depletion of the Boltzmann response by the trapped electrons. This is distinct from other mechanisms described in previous works that enhance microstability in maximum-$J$
property has on ITGs – even in the absence of an electron free energy source. We explain this effect through the concept of mode inertia, which is sensitive to the degree of depletion of the Boltzmann response by the trapped electrons. This is distinct from other mechanisms described in previous works that enhance microstability in maximum-$J$![]() stellarators, which involve a lack of resonance between bounce-averaged curvature and diamagnetic drifts.
stellarators, which involve a lack of resonance between bounce-averaged curvature and diamagnetic drifts.
2 Gyrokinetic system
To begin, we consider a local, electrostatic gyrokinetic system, where the domain is a narrow flux tube centred around a magnetic field line in the plasma. In this local approximation, a Fourier decomposition may be applied in the directions perpendicular to the magnetic field assuming periodicity in these coordinates. The electrostatic gyrokinetic equation for a species $a$![]() , and the Fourier component $\boldsymbol {k}$
, and the Fourier component $\boldsymbol {k}$![]() is
is

where $g_{a,\boldsymbol {k}}$![]() is the non-adiabatic part of the perturbed distribution function $g_a(\boldsymbol {R}, E_a, \mu _a, t) = \delta f(\boldsymbol {r}, \boldsymbol {v}, t) + e_a\delta \phi (\boldsymbol {r}, t) F_{a0}/T_a$
is the non-adiabatic part of the perturbed distribution function $g_a(\boldsymbol {R}, E_a, \mu _a, t) = \delta f(\boldsymbol {r}, \boldsymbol {v}, t) + e_a\delta \phi (\boldsymbol {r}, t) F_{a0}/T_a$![]() , $F_{a0}$
, $F_{a0}$![]() is the background Maxwellian distribution and $\delta \phi$
is the background Maxwellian distribution and $\delta \phi$![]() is the electrostatic potential. The phase-space coordinates for the gyrocentre distribution function $g_a$
is the electrostatic potential. The phase-space coordinates for the gyrocentre distribution function $g_a$![]() are the magnetic moment, $\mu _a = m_a v_\perp ^2/(2B)$
are the magnetic moment, $\mu _a = m_a v_\perp ^2/(2B)$![]() and the kinetic energy, $E_a = m_a v^2/2$
and the kinetic energy, $E_a = m_a v^2/2$![]() . We also use Clebsch magnetic coordinates, in which the magnetic field is of the form $\boldsymbol {B} = \boldsymbol {\nabla } \psi \times \boldsymbol {\nabla } \alpha$
. We also use Clebsch magnetic coordinates, in which the magnetic field is of the form $\boldsymbol {B} = \boldsymbol {\nabla } \psi \times \boldsymbol {\nabla } \alpha$![]() , where $\psi$
, where $\psi$![]() is the toroidal magnetic flux (acting as a radial coordinate in toroidal geometry), and $\alpha$
is the toroidal magnetic flux (acting as a radial coordinate in toroidal geometry), and $\alpha$![]() is the binormal coordinate, which labels different field lines on surfaces of constant $\psi$
is the binormal coordinate, which labels different field lines on surfaces of constant $\psi$![]() . In these coordinates, the field-line following coordinate is $l$
. In these coordinates, the field-line following coordinate is $l$![]() , the unit vector along the magnetic field is $\boldsymbol {b} = \boldsymbol {B}/B$
, the unit vector along the magnetic field is $\boldsymbol {b} = \boldsymbol {B}/B$![]() and the perpendicular wavenumber is ${\boldsymbol{k}} ={\boldsymbol{k}}_\perp = k_\alpha \nabla \alpha + k_\psi \nabla \psi$
and the perpendicular wavenumber is ${\boldsymbol{k}} ={\boldsymbol{k}}_\perp = k_\alpha \nabla \alpha + k_\psi \nabla \psi$![]() . The argument of the Bessel function is ${\rm J}_0 = {\rm J}_0(k_\perp v_\perp /\varOmega _a)$
. The argument of the Bessel function is ${\rm J}_0 = {\rm J}_0(k_\perp v_\perp /\varOmega _a)$![]() with the gyrofrequency defined as $\varOmega _a = e_a B/m_a$
with the gyrofrequency defined as $\varOmega _a = e_a B/m_a$![]() . The magnetic drift frequency is $\omega _{da}= \boldsymbol {k}_\perp \boldsymbol {\cdot } \boldsymbol {v}_d$
. The magnetic drift frequency is $\omega _{da}= \boldsymbol {k}_\perp \boldsymbol {\cdot } \boldsymbol {v}_d$![]() , where $\boldsymbol {v}_d = {\boldsymbol {b}}\times (v_\perp ^2/2 \boldsymbol {\nabla } \ln B + v_\|^2 \boldsymbol {\kappa })/{\varOmega _a}$
, where $\boldsymbol {v}_d = {\boldsymbol {b}}\times (v_\perp ^2/2 \boldsymbol {\nabla } \ln B + v_\|^2 \boldsymbol {\kappa })/{\varOmega _a}$![]() . In the low-plasma pressure limit (assuming $\boldsymbol {\nabla } \ln B \approx \boldsymbol {\kappa }$
. In the low-plasma pressure limit (assuming $\boldsymbol {\nabla } \ln B \approx \boldsymbol {\kappa }$![]() ), the drift frequency can be approximated by
), the drift frequency can be approximated by

where $v_{{\rm Ta}} = \sqrt {2T_a/m_a}$![]() is the thermal speed and $\hat {\omega }_{{\rm da}}(l)$
is the thermal speed and $\hat {\omega }_{{\rm da}}(l)$![]() is a geometry dependent factor. The energy-dependent diamagnetic drift frequency is
is a geometry dependent factor. The energy-dependent diamagnetic drift frequency is
where the plasma gradients enter via $\omega _{*a} = (k_\alpha T_a/e_a)\,\mathrm {d} \ln n_a /\mathrm {d} \psi$![]() and the gradient ratio $\eta _a = \mathrm {d}\ln T_a/ \mathrm {d} \ln n_a$
and the gradient ratio $\eta _a = \mathrm {d}\ln T_a/ \mathrm {d} \ln n_a$![]() . In the electrostatic limit, the system is closed by the quasineutrality condition
. In the electrostatic limit, the system is closed by the quasineutrality condition

In Clebsch coordinates, we may write the nonlinear term of (2.1) in the more convenient form
3 Bounce-averaged electrons
To simplify the electron gyrokinetic equation, we employ a standard ordering. We assume that the time scale of the dynamics of interest in the gyrokinetic system $\tau _D$![]() (i.e. the growth time of an instability) is much longer than the time scale on which thermal electrons transit the typical parallel length scale of the system, such that $\tau _D \gg L/v_{{\rm Te}}$
(i.e. the growth time of an instability) is much longer than the time scale on which thermal electrons transit the typical parallel length scale of the system, such that $\tau _D \gg L/v_{{\rm Te}}$![]() . Expanding the electron distribution in orders of $L/(v_{{\rm Te}}\tau _D)$
. Expanding the electron distribution in orders of $L/(v_{{\rm Te}}\tau _D)$![]() as $g_{e,\boldsymbol {k}} = g_{e,\boldsymbol {k}}^0 + g_{e,\boldsymbol {k}}^1 \ldots$
as $g_{e,\boldsymbol {k}} = g_{e,\boldsymbol {k}}^0 + g_{e,\boldsymbol {k}}^1 \ldots$![]() we find that, to leading order,
we find that, to leading order,
such that the lowest-order electron distribution function is constant along the magnetic field line. This, it turns out, is a highly consequential result of this ordering, and how it is interpreted is the key to tailoring the forthcoming optimal mode analysis to capture the behaviour of the electron response for ion-scale instabilities that satisfy our ordering in toroidal geometry.
The constancy of $g_{e}^0 = g_e^0(E_e,\mu _e, \psi, \alpha )$![]() in $l$
in $l$![]() implies that its value is entirely determined by the parallel boundary conditions. For the passing particles in toroidal geometry, and for $k_\alpha \neq 0$
implies that its value is entirely determined by the parallel boundary conditions. For the passing particles in toroidal geometry, and for $k_\alpha \neq 0$![]() , the relevant boundary conditions are the so-called ‘incoming’ boundary conditions of ballooning space where
, the relevant boundary conditions are the so-called ‘incoming’ boundary conditions of ballooning space where
As explained in an appendix by Plunk et al. (Reference Plunk, Helander, Xanthopoulos and Connor2014), these boundary conditions are required to preserve causality (Connor, Hastie & Taylor Reference Connor, Hastie and Taylor1980), such that information from the boundary, which is infinitely far away, cannot be communicated in a finite time. Therefore, it must be the case that $g_{e}^0(k_\alpha \neq 0) = 0$![]() in the passing region of velocity space to satisfy the boundary conditions. For the $k_\alpha = 0$
in the passing region of velocity space to satisfy the boundary conditions. For the $k_\alpha = 0$![]() component, ballooning space boundary conditions are not appropriate because there is no mechanism that should cause the mode to decay along the flux tube. Thus, for $k_\alpha = 0$
component, ballooning space boundary conditions are not appropriate because there is no mechanism that should cause the mode to decay along the flux tube. Thus, for $k_\alpha = 0$![]() the electron distribution function has a zeroth-order contribution from the passing electrons.
the electron distribution function has a zeroth-order contribution from the passing electrons.
The trapped particles on the other hand (in the absence of collisions), are confined to a limited region of ballooning space. As such, the appropriate boundary conditions for these particles are the ‘turning-point’ boundary conditions (Connor et al. Reference Connor, Hastie and Taylor1980),
where $l_{1,2}$![]() are the bounce points for a particle defined by $\lambda B(l_{1,2}) =1$
are the bounce points for a particle defined by $\lambda B(l_{1,2}) =1$![]() , where $\lambda$
, where $\lambda$![]() is the particle pitch angle, $\lambda = v_\perp ^2/(v^2 B)$
is the particle pitch angle, $\lambda = v_\perp ^2/(v^2 B)$![]() . These boundary conditions can be satisfied with $g_{e,\boldsymbol {k}}^0 \neq 0$
. These boundary conditions can be satisfied with $g_{e,\boldsymbol {k}}^0 \neq 0$![]() , and so, for $k_\alpha \neq 0$
, and so, for $k_\alpha \neq 0$![]() , only the trapped electrons contribute to the non-adiabatic electron response in this limit. Note that this is not the case in closed-field-line geometries where the parallel boundary conditions can be periodic, allowing $g_{e,\boldsymbol {k}}^0$
, only the trapped electrons contribute to the non-adiabatic electron response in this limit. Note that this is not the case in closed-field-line geometries where the parallel boundary conditions can be periodic, allowing $g_{e,\boldsymbol {k}}^0$![]() to be non-zero in the passing region of velocity space to zeroth order.
to be non-zero in the passing region of velocity space to zeroth order.
At next order in $L/(v_{\rm Te}\tau _D)$![]() , we find
, we find

We now define the bounce average as

where we have introduced the bounce time $\tau _B = \int _{l_1}^{l_2}({\mathrm {d}l}/{\sqrt {1 -\lambda B}})$![]() .Footnote 1 In pitch-angle coordinates, the velocity space element is defined as
.Footnote 1 In pitch-angle coordinates, the velocity space element is defined as

where $\sigma = v_\parallel /|v_\parallel |$![]() . Applying the bounce average to (3.6) annihilates the $g_{e, \boldsymbol {k}}^1$
. Applying the bounce average to (3.6) annihilates the $g_{e, \boldsymbol {k}}^1$![]() contribution, leaving an equation for $g^0_{e,\boldsymbol {k}}$
contribution, leaving an equation for $g^0_{e,\boldsymbol {k}}$![]() . Additionally ordering $k_\perp \rho _e\ll 1$
. Additionally ordering $k_\perp \rho _e\ll 1$![]() , where $\rho _a = v_{{\rm Ta}}/|\varOmega _a|$
, where $\rho _a = v_{{\rm Ta}}/|\varOmega _a|$![]() , for simplicity and omitting the superscript ‘$0$
, for simplicity and omitting the superscript ‘$0$![]() ’ for brevity gives
’ for brevity gives

We now consider (3.9) as the governing equation for the bounce-averaged electrons in our gyrokinetic system, which is accurate to lowest order in $L/(v_{{\rm Te}}\tau _D)$![]() . Here, we restrict our view to toroidal geometry such that, for $k_\alpha \neq 0$
. Here, we restrict our view to toroidal geometry such that, for $k_\alpha \neq 0$![]() , $g_e$
, $g_e$![]() is only non-zero in the trapped region of velocity space.
is only non-zero in the trapped region of velocity space.
4 Energy balance
In the limit of $\tau _D \gg L/v_{\rm Te}$![]() , we have a gyrokinetic system comprised of ions described by (2.1), with finite ion-Larmor-radius effects, and bounce-averaged electrons described by (3.9). As described in Parts 1, 2 and 3, we can construct energy norms for this two-species system that are conserved by the nonlinear terms of the gyrokinetic equations. These nonlinear invariants are the Helmholtz free energy, detailed in Parts 1 and 2, and the electrostatic energy, described in Part 3. We now derive these invariants in our system with bounce-averaged electrons.
, we have a gyrokinetic system comprised of ions described by (2.1), with finite ion-Larmor-radius effects, and bounce-averaged electrons described by (3.9). As described in Parts 1, 2 and 3, we can construct energy norms for this two-species system that are conserved by the nonlinear terms of the gyrokinetic equations. These nonlinear invariants are the Helmholtz free energy, detailed in Parts 1 and 2, and the electrostatic energy, described in Part 3. We now derive these invariants in our system with bounce-averaged electrons.
4.1 Helmholtz free energy
For simplicity, we will consider a two-species hydrogen plasma with $n_i = n_e = n$![]() , but the following can be easily generalised to multiple ion species. Constructing the Helmholtz free energy of this system proceeds in the same manner as in the general multispecies case, shown in Part 2, except for our assumption that $k_\perp \rho _e\ll 1$
, but the following can be easily generalised to multiple ion species. Constructing the Helmholtz free energy of this system proceeds in the same manner as in the general multispecies case, shown in Part 2, except for our assumption that $k_\perp \rho _e\ll 1$![]() . This is done by multiplying the gyrokinetic equation for each species by the factor $T_a g_{a,\boldsymbol {k}}^*/F_{a0}$
. This is done by multiplying the gyrokinetic equation for each species by the factor $T_a g_{a,\boldsymbol {k}}^*/F_{a0}$![]() , integrating over velocity space, applying the flux-tube average defined by
, integrating over velocity space, applying the flux-tube average defined by

summing the equations for both species, and taking the real part. Applying the flux-tube average has no impact on the bounce-averaged electron equation, but we leverage the identity
to allow us to combine the electron and ion contributions to the Helmholtz free energy. After using quasineutrality, we arrive at the Helmholtz free energy, which looks similar to that of Parts 1 and 2,

The Helmholtz free energy balance reads, as before,

the only difference here is that we have considered the limit ${\rm J}_{0e} \approx 1$![]() and $g_e = g_e(E_e,\mu _e, \psi, \alpha )$
and $g_e = g_e(E_e,\mu _e, \psi, \alpha )$![]() with $g_e = 0$
with $g_e = 0$![]() for $\lambda < 1/B_{\mathrm {max}}$
for $\lambda < 1/B_{\mathrm {max}}$![]() . We have denoted the electron contribution with a ‘tr’ superscript to signify that only the trapped region of velocity space contributes. The total free energy drive for a given $\boldsymbol {k}$
. We have denoted the electron contribution with a ‘tr’ superscript to signify that only the trapped region of velocity space contributes. The total free energy drive for a given $\boldsymbol {k}$![]() is then given by $D(\boldsymbol {k}, t) = D_i(\boldsymbol {k},t) + D_e^{\mathrm {tr}}(\boldsymbol {k},t)$
is then given by $D(\boldsymbol {k}, t) = D_i(\boldsymbol {k},t) + D_e^{\mathrm {tr}}(\boldsymbol {k},t)$![]() , which determines the rate at which the system can grow given the presence of gradients in the plasma.
, which determines the rate at which the system can grow given the presence of gradients in the plasma.
4.2 Electrostatic energy
To construct the generalised free energy, as demonstrated for a single kinetic species in Part 3, we first need to derive the electrostatic energy balance of the system with bounce-averaged electrons. As shown in Appendix A of Part 3, the electrostatic energy balance equation of a multispecies system may be constructed by applying the operator

to the gyrokinetic equations for each species and summing over species. When this operator is applied to the electron equation, the nonlinear term is annihilated. This can be shown by noticing that its contribution,

when expressed in pitch-angle coordinates (3.8) and using the identity (Helander et al. Reference Helander, Proll and Plunk2013)

where the subscript $j$![]() denotes the different magnetic trapping wells along the flux tube, becomes
denotes the different magnetic trapping wells along the flux tube, becomes

Since $\delta \phi ^*_{\boldsymbol {k}} = \delta \phi _{-\boldsymbol {k}}$![]() and $g_{e,\boldsymbol {k}}^* = g_{e,-\boldsymbol {k}}$
and $g_{e,\boldsymbol {k}}^* = g_{e,-\boldsymbol {k}}$![]() , upon taking the real part, this contribution is proportional to
, upon taking the real part, this contribution is proportional to
which changes sign if $\boldsymbol {k}$![]() and $\boldsymbol {k}'$
and $\boldsymbol {k}'$![]() are swapped, such that this term vanishes upon summation over $\boldsymbol {k}$
are swapped, such that this term vanishes upon summation over $\boldsymbol {k}$![]() and $\boldsymbol {k}'$
and $\boldsymbol {k}'$![]() .
.
What remains of the electron equation when this operator is applied is

We may also use the identity (4.7) to rewrite the right-hand side of this expression. Upon taking the real part of the right-hand side, the term proportional to $\omega _{*e}^T$![]() vanishes leaving
vanishes leaving

Applying the operator (4.5) to the ion gyrokinetic equation proceeds similarly, albeit without bounce averages, yielding

where $\varGamma _{0i}(b) = {\rm I}_0(b)\exp (-b)$![]() and $b = k_\perp ^2\rho _i^2$
and $b = k_\perp ^2\rho _i^2$![]() . If we now sum the contributions from the ions and the electrons, given by (4.12) and (4.11), after using quasineutrality, we arrive at electrostatic energy balance,
. If we now sum the contributions from the ions and the electrons, given by (4.12) and (4.11), after using quasineutrality, we arrive at electrostatic energy balance,
Here, $E(\boldsymbol {k}, t)$![]() is electrostatic energy contained in the potential fluctuations in this system given by
is electrostatic energy contained in the potential fluctuations in this system given by

where $\tau = T_i/T_e$![]() . The drive terms ${\rm K}_i(\boldsymbol {k}, t)$
. The drive terms ${\rm K}_i(\boldsymbol {k}, t)$![]() and ${\rm K}_e^{\mathrm {tr}}(\boldsymbol {k},t)$
and ${\rm K}_e^{\mathrm {tr}}(\boldsymbol {k},t)$![]() are the work performed by the ions and trapped electrons on the electric field, respectively, and are given by
are the work performed by the ions and trapped electrons on the electric field, respectively, and are given by
and
The total electrostatic energy drive is then $K(\boldsymbol {k}, t) = {\rm K}_i(\boldsymbol {k},t) + {\rm K}_e^{\mathrm {tr}}(\boldsymbol {k},t)$![]() . The drive, $K$
. The drive, $K$![]() , determines the rate at which the electrostatic energy of the system can grow, given the energy transfer possible by wave–particle interactions. This form of electrostatic energy balance is similar to forms derived by Helander et al. (Reference Helander, Proll and Plunk2013) and Plunk et al. (Reference Plunk, Connor and Helander2017), where they were concerned with normal modes.
, determines the rate at which the electrostatic energy of the system can grow, given the energy transfer possible by wave–particle interactions. This form of electrostatic energy balance is similar to forms derived by Helander et al. (Reference Helander, Proll and Plunk2013) and Plunk et al. (Reference Plunk, Connor and Helander2017), where they were concerned with normal modes.
4.3 Generalised free energy
Now that we have found forms for both the electrostatic energy and the Helmholtz free energy, we can construct the generalised free energy, as shown in Part 3, by considering the linear combination
where $\varDelta$![]() is a real constant. Here $\tilde {H}$
is a real constant. Here $\tilde {H}$![]() can be guaranteed to be a positive-definite energy norm if $\varDelta$
can be guaranteed to be a positive-definite energy norm if $\varDelta$![]() is chosen correctly; for example, any negative real choice of $\varDelta$
is chosen correctly; for example, any negative real choice of $\varDelta$![]() gives a positive definite energy measure. However, positive-definiteness will not be fulfilled beyond a certain magnitude of positive $\varDelta$
gives a positive definite energy measure. However, positive-definiteness will not be fulfilled beyond a certain magnitude of positive $\varDelta$![]() . Note that $\tilde {H}$
. Note that $\tilde {H}$![]() does not define a single energetic norm, but rather an infinite set of norms for each allowable value of $\varDelta$
does not define a single energetic norm, but rather an infinite set of norms for each allowable value of $\varDelta$![]() , all of which are invariant under nonlinear interactions between different wavenumbers if $\varDelta$
, all of which are invariant under nonlinear interactions between different wavenumbers if $\varDelta$![]() is chosen to be independent of $k$
is chosen to be independent of $k$![]() (Plunk & Helander Reference Plunk and Helander2023). The Helmholtz free energy is a special case in this set of energy norms for which $\varDelta = 0$
(Plunk & Helander Reference Plunk and Helander2023). The Helmholtz free energy is a special case in this set of energy norms for which $\varDelta = 0$![]() .
.
The energy balance equation for $\tilde {H}$![]() is
is
This energy balance is now ‘aware’ of both the source of free energy growth (the gradients), and the mechanism by which it is extracted (wave–particle interactions). As defined in Part 3, the instantaneous growth rate of the generalised free energy is
Note that because $\tilde {H}$![]() defines a positive definite square norm, the linear, normal mode growth $\gamma _L$
defines a positive definite square norm, the linear, normal mode growth $\gamma _L$![]() is bounded by the maximum possible value of $\varLambda$
is bounded by the maximum possible value of $\varLambda$![]() ,
,
5 Optimal modes
We now seek the distribution functions $g_i$![]() and $g_e$
and $g_e$![]() which extremise the value of $\varLambda$
which extremise the value of $\varLambda$![]() – the optimal modes. These optimal modes are found by varying (4.19) with respect to the distribution function for each species and seeking an extremum ($\delta \varLambda = 0$
– the optimal modes. These optimal modes are found by varying (4.19) with respect to the distribution function for each species and seeking an extremum ($\delta \varLambda = 0$![]() ). This optimisation procedure yields two coupled variational problems, one for each species, given by
). This optimisation procedure yields two coupled variational problems, one for each species, given by
However, when performing the variation, we must take into consideration that the electron distribution function is independent of the field-line-following coordinate $l$![]() . To enforce this, when computing the variation of a functional $F[g_e]$
. To enforce this, when computing the variation of a functional $F[g_e]$![]() as
as
the perturbation $h_e$![]() is taken to be independent of $l$
is taken to be independent of $l$![]() . To make the impact of $l$
. To make the impact of $l$![]() -independence clearer, we define the inner product on the space of trapped-electron distribution functions as
-independence clearer, we define the inner product on the space of trapped-electron distribution functions as

which can be derived from the inner product for ion distributions (which we also use for the ion distributions here) defined in Part 3,
by expressing the velocity space integration in pitch-angle coordinates, under the assumptions of $l$![]() -independence, and $g_e$
-independence, and $g_e$![]() being zero in the passing region of velocity space.
being zero in the passing region of velocity space.
Evaluating the two variational problems (5.1) and expressing the result in terms of the inner products defined above, for the respective species over which the variation is performed, yields two coupled eigenvalue problems for the optimal modes and the growth rate $\varLambda$![]() ,
,
where the operators $\tilde {\mathcal {H}}_{{\rm ab}}$![]() , ${\mathcal {D}}_{{\rm ab}}$
, ${\mathcal {D}}_{{\rm ab}}$![]() and $\mathcal {K}_{{\rm ab}}$
and $\mathcal {K}_{{\rm ab}}$![]() are given in Appendix A. Here, and from now on, we will omit the subscript ‘$\boldsymbol {k}$
are given in Appendix A. Here, and from now on, we will omit the subscript ‘$\boldsymbol {k}$![]() ’ for simplicity. These operators are expressed in terms of a finite set of velocity-space moments of the distributions,
’ for simplicity. These operators are expressed in terms of a finite set of velocity-space moments of the distributions,

where we have written $\hat {\omega }_{{\rm de}}(l) = \tilde {\omega }_{{\rm de}} f(l)$![]() , $f(l)$
, $f(l)$![]() is a dimensionless function which captures the $l$
is a dimensionless function which captures the $l$![]() -dependence of $\hat {\omega }_{{\rm de}}$
-dependence of $\hat {\omega }_{{\rm de}}$![]() , and $\tilde {\omega }_{{\rm de}}$
, and $\tilde {\omega }_{{\rm de}}$![]() is a constant with units of inverse time. Note that, due to the appearance of the bounce average in each of the electron operators in Appendix A, the equation which results from the variation of the electron distribution function gives an optimal $g_e$
is a constant with units of inverse time. Note that, due to the appearance of the bounce average in each of the electron operators in Appendix A, the equation which results from the variation of the electron distribution function gives an optimal $g_e$![]() which is independent of $l$
which is independent of $l$![]() as required.
as required.
This eigenvalue problem for the optimal mode growth has ‘full’ dependence on the magnetic geometry of the flux tube, i.e. the magnetic field strength, the curvature and the metric coefficients, all as a function of $l$![]() . The system can be closed exactly in terms of the moments $\kappa _{n a}$
. The system can be closed exactly in terms of the moments $\kappa _{n a}$![]() by taking moments of the two equations given by (5.5). This results in an $8\times 8$
by taking moments of the two equations given by (5.5). This results in an $8\times 8$![]() system of integrodifferential equations which must be solved for the eigenvalue $\varLambda$
system of integrodifferential equations which must be solved for the eigenvalue $\varLambda$![]() .
.
This system of equations can be solved for any choice of $\varDelta$![]() , for which $\tilde {H}$
, for which $\tilde {H}$![]() is positive definite, allowing us to compute the optimal mode growth rate for any element in the set of energy norms defined by $\tilde {H}$
is positive definite, allowing us to compute the optimal mode growth rate for any element in the set of energy norms defined by $\tilde {H}$![]() . Thus, for a given scenario (e.g. plasma parameters and geometry), we can seek the value of $\varDelta$
. Thus, for a given scenario (e.g. plasma parameters and geometry), we can seek the value of $\varDelta$![]() which corresponds to the most restrictive norm on the dynamics of the system within this set. This will give the tightest possible bound on linear instability growth in accordance with (4.20).
which corresponds to the most restrictive norm on the dynamics of the system within this set. This will give the tightest possible bound on linear instability growth in accordance with (4.20).
In practical terms, this means that for each scenario we can optimise over $\varDelta$![]() to find the tightest upper bound on instability growth in the system. Here, this optimisation will be carried out numerically. As explained in Part 3, this tightest upper bound is guaranteed to be less than (or equal to) that of the Helmholtz free energy at $\varDelta = 0$
to find the tightest upper bound on instability growth in the system. Here, this optimisation will be carried out numerically. As explained in Part 3, this tightest upper bound is guaranteed to be less than (or equal to) that of the Helmholtz free energy at $\varDelta = 0$![]() and the magnitude of the optimal $\varDelta$
and the magnitude of the optimal $\varDelta$![]() can be thought of as the relative importance of wave–particle effects in restricting the optimal growth for a given scenario.
can be thought of as the relative importance of wave–particle effects in restricting the optimal growth for a given scenario.
Note that, due to the complexity of the system in general magnetic geometry, we are unable to derive generally the limiting value of $\varDelta$![]() beyond which positive definiteness is no longer guaranteed. However, this does not pose a problem when solving the system numerically as positive definiteness can be checked at each step when optimising over $\varDelta$
beyond which positive definiteness is no longer guaranteed. However, this does not pose a problem when solving the system numerically as positive definiteness can be checked at each step when optimising over $\varDelta$![]() .
.
6 Solving the system in the slow-ion-transit limit
To make finding the solution to the eigenvalue problem more straightforward, we consider the limit $L/v_{{\rm Ti}} \gg \tau _D$![]() , where the ion transit time is much longer than the typical instability time scale. In this limit, we can neglect the derivatives along the magnetic field line that arise due to the parallel ion motion. This reduces the dimensionality of the system by removing $\kappa _{4i}$
, where the ion transit time is much longer than the typical instability time scale. In this limit, we can neglect the derivatives along the magnetic field line that arise due to the parallel ion motion. This reduces the dimensionality of the system by removing $\kappa _{4i}$![]() and $\kappa _{5i}$
and $\kappa _{5i}$![]() from the problem, leaving a $6 \times 6$
from the problem, leaving a $6 \times 6$![]() system of integroalgebraic equations. Note that this ordering is the typical ‘toroidal’ ITG and TEM ordering often applied in linear, normal-mode analyses (Biglari, Diamond & Rosenbluth Reference Biglari, Diamond and Rosenbluth1989; Helander et al. Reference Helander, Proll and Plunk2013; Plunk et al. Reference Plunk, Connor and Helander2017). The system of moment equations in this limit is given in Appendix B.
system of integroalgebraic equations. Note that this ordering is the typical ‘toroidal’ ITG and TEM ordering often applied in linear, normal-mode analyses (Biglari, Diamond & Rosenbluth Reference Biglari, Diamond and Rosenbluth1989; Helander et al. Reference Helander, Proll and Plunk2013; Plunk et al. Reference Plunk, Connor and Helander2017). The system of moment equations in this limit is given in Appendix B.
6.1 A square magnetic well
We cannot make much progress towards an analytical solution of this system for a general magnetic geometry. Thus, to gain some insight into the behaviour of the system, we consider a ‘square’ magnetic field of the form

with $\omega _{{\rm da}}(l) = \mathrm {const.}$![]() and $k_\perp = \mathrm {const}$
and $k_\perp = \mathrm {const}$![]() . In this simplified geometry, the $\kappa _{{\rm na}}$
. In this simplified geometry, the $\kappa _{{\rm na}}$![]() eigenfunctions are constant inside the magnetic well between $-L/2 < l < L/2$
eigenfunctions are constant inside the magnetic well between $-L/2 < l < L/2$![]() and the $\kappa _{ne}$
and the $\kappa _{ne}$![]() moments must vanish for $|l|\geqslant L/2$
moments must vanish for $|l|\geqslant L/2$![]() . In this case, there are two possibilities, either the ion moments must also vanish in this region, or the electron moments are zero everywhere, corresponding to the system with adiabatic electrons. Both of these solutions are realisable, with the adiabatic electron solution being described in Part 3. Here, we concern ourselves with the eigenfunctions that vanish at $B_\mathrm {max}$
. In this case, there are two possibilities, either the ion moments must also vanish in this region, or the electron moments are zero everywhere, corresponding to the system with adiabatic electrons. Both of these solutions are realisable, with the adiabatic electron solution being described in Part 3. Here, we concern ourselves with the eigenfunctions that vanish at $B_\mathrm {max}$![]() , whilst keeping in mind that the adiabatic electron solution is also present in the system outside the well.
, whilst keeping in mind that the adiabatic electron solution is also present in the system outside the well.
The solution to the eigenvalue problem in this square magnetic geometry is given in appendix C and is denoted as $\varLambda _{\mathrm {SW}}$![]() . We find that the value of $\varDelta$
. We find that the value of $\varDelta$![]() beyond which the system is not guaranteed to be Hermitian (i.e. implying a violation of positive-definiteness) is
beyond which the system is not guaranteed to be Hermitian (i.e. implying a violation of positive-definiteness) is
where $\varepsilon = \sqrt {1 - B_{\textrm {min}}/B_{\textrm {max}}}$![]() . While we will mostly employ this solution as a benchmark for comparison with numerical solutions, it can provide some insight into the behaviour of the optimal mode system in this limit. Firstly, in the Helmholtz limit with $\varDelta =0$
. While we will mostly employ this solution as a benchmark for comparison with numerical solutions, it can provide some insight into the behaviour of the optimal mode system in this limit. Firstly, in the Helmholtz limit with $\varDelta =0$![]() , we see that $\varLambda _{\mathrm {SW}}$
, we see that $\varLambda _{\mathrm {SW}}$![]() reduces to an expression of the same form as the fully kinetic electron Helmholtz bound derived in Appendix D of Part 2, with the only difference being the lack of finite-electron-Larmor-radius effects in the solution here, and the reduction of the size of the electron response by the trapped-particle fraction $\varepsilon$
reduces to an expression of the same form as the fully kinetic electron Helmholtz bound derived in Appendix D of Part 2, with the only difference being the lack of finite-electron-Larmor-radius effects in the solution here, and the reduction of the size of the electron response by the trapped-particle fraction $\varepsilon$![]() . Later, we will see that this reduction of the population of electrons which contributes to instability growth has a profound impact on the qualitative behaviour of the bound. Moreover, in the limit of $\varepsilon \to 0$
. Later, we will see that this reduction of the population of electrons which contributes to instability growth has a profound impact on the qualitative behaviour of the bound. Moreover, in the limit of $\varepsilon \to 0$![]() , we recover the adiabatic electron Helmholtz bound of Part 1. Thus, the system studied here behaves like an intermediate limit between the fully kinetic and adiabatic electron limits.
, we recover the adiabatic electron Helmholtz bound of Part 1. Thus, the system studied here behaves like an intermediate limit between the fully kinetic and adiabatic electron limits.
For the generalised free energy case, with $\varDelta \neq 0$![]() , we also note that, in the limit of $\varepsilon \to 0$
, we also note that, in the limit of $\varepsilon \to 0$![]() , $\varLambda _{\textrm {SW}}$
, $\varLambda _{\textrm {SW}}$![]() reduces to the adiabatic electron result of Part 3 in the toroidal ITG limit.
reduces to the adiabatic electron result of Part 3 in the toroidal ITG limit.
6.2 Numerically solving the system
The analytical solution in the square well, $\varLambda _{\mathrm {SW}}$![]() , already provides some insight into the behaviour of the eigenvalue problem but does not capture the subtleties of the bounce-averaged electron response. In realistic magnetic geometries, the local curvature along the field line may differ vastly from the bounce-averaged curvature felt by trapped electrons due to the variation of the magnetic field strength along the field line. As a result, the ions and electrons in the bounce-averaged limit can experience drifts which are vastly different. This could be captured in the square well geometry by stipulating that the ions and electrons experience different curvatures in the well, but this would be a coarse approximation of the realistic situation.
, already provides some insight into the behaviour of the eigenvalue problem but does not capture the subtleties of the bounce-averaged electron response. In realistic magnetic geometries, the local curvature along the field line may differ vastly from the bounce-averaged curvature felt by trapped electrons due to the variation of the magnetic field strength along the field line. As a result, the ions and electrons in the bounce-averaged limit can experience drifts which are vastly different. This could be captured in the square well geometry by stipulating that the ions and electrons experience different curvatures in the well, but this would be a coarse approximation of the realistic situation.
To get a better sense of the behaviour of the system in more realistic geometries, we resort to numerically solving the system of integroalgebraic equations given by the moment form of the kinetic eigenvalue problem (5.5) in the slow-ion-transit limit ($L/v_{{\rm Ti}} \gg \tau _D$![]() ). For the sake of simplicity, we do this in simple, toy-model magnetic fields. Here, we discretise the system on a basis of cosines in $l$
). For the sake of simplicity, we do this in simple, toy-model magnetic fields. Here, we discretise the system on a basis of cosines in $l$![]() , with zeros at the maximum of magnetic field strength (the eigenfunctions of interest are purely even in a symmetric geometry, and must vanish at $B = B_{\mathrm {max}}$
, with zeros at the maximum of magnetic field strength (the eigenfunctions of interest are purely even in a symmetric geometry, and must vanish at $B = B_{\mathrm {max}}$![]() ), and use a recently developed numerical package to evaluate the bounce averages and integrals over $\lambda$
), and use a recently developed numerical package to evaluate the bounce averages and integrals over $\lambda$![]() (Mackenbach et al. Reference Mackenbach, Duff, Gerard, Proll, Helander and Hegna2023a).
(Mackenbach et al. Reference Mackenbach, Duff, Gerard, Proll, Helander and Hegna2023a).
7 Helmholtz free energy ($\varDelta = 0$ ) bounds
) bounds
For the case of $\varDelta = 0$![]() , the generalised free energy reduces to the Helmholtz free energy, and the $\kappa _{3a}$
, the generalised free energy reduces to the Helmholtz free energy, and the $\kappa _{3a}$![]() moments do not contribute to the system of equations. This reduces the dimensionality of the system to $4\times 4$
moments do not contribute to the system of equations. This reduces the dimensionality of the system to $4\times 4$![]() . In this limit, the optimal modes do not depend on magnetic curvature, but retain dependency on $B(l)$
. In this limit, the optimal modes do not depend on magnetic curvature, but retain dependency on $B(l)$![]() and the variation of $k_\perp$
and the variation of $k_\perp$![]() with $l$
with $l$![]() . We will refer to the optimal mode growth rate of this system with $\varDelta = 0$
. We will refer to the optimal mode growth rate of this system with $\varDelta = 0$![]() as the Helmholtz bound. To get a sense of how the optimal modes behave in response to the presence of different plasma gradients, we consider three cases: the case of a pure ion-temperature gradient in the plasma ($\boldsymbol {\nabla } n = 0$
as the Helmholtz bound. To get a sense of how the optimal modes behave in response to the presence of different plasma gradients, we consider three cases: the case of a pure ion-temperature gradient in the plasma ($\boldsymbol {\nabla } n = 0$![]() , $\boldsymbol {\nabla } T_e = 0$
, $\boldsymbol {\nabla } T_e = 0$![]() ) that we refer to as the ‘pure ITG case’; a pure density gradient ($\boldsymbol {\nabla } T_i = 0$
) that we refer to as the ‘pure ITG case’; a pure density gradient ($\boldsymbol {\nabla } T_i = 0$![]() , $\boldsymbol {\nabla } T_e = 0$
, $\boldsymbol {\nabla } T_e = 0$![]() ) case that we refer to as the ‘pure TEM case’; and a case with only an electron temperature gradient ($\boldsymbol {\nabla } n = 0$
) case that we refer to as the ‘pure TEM case’; and a case with only an electron temperature gradient ($\boldsymbol {\nabla } n = 0$![]() , $\boldsymbol {\nabla } T_i = 0$
, $\boldsymbol {\nabla } T_i = 0$![]() which we refer to as the ‘pure ETG-TEM case’. While we have only considered single gradients here for simplicity, we note that the optimal modes can equally be applied to mixed gradient cases.
which we refer to as the ‘pure ETG-TEM case’. While we have only considered single gradients here for simplicity, we note that the optimal modes can equally be applied to mixed gradient cases.
In figure 1, we show the Helmholtz bound of the system as a function of $b_i = k_\perp ^2\rho _i^2$![]() . Here, for the numerical solution, we consider a magnetic field of the form $B(l) = B_0 - B_1 \cos (l)$
. Here, for the numerical solution, we consider a magnetic field of the form $B(l) = B_0 - B_1 \cos (l)$![]() with $B_0 = 1$
with $B_0 = 1$![]() and $B_1= 0.2$
and $B_1= 0.2$![]() , and use $k_\perp = \mathrm {const.}$
, and use $k_\perp = \mathrm {const.}$![]() for simplicity. In a sinusoidal field such as this, the magnetic trapping wells are identical and are separated by identical maxima (like in an omnigenous field), thus we need only solve the system in a single well with $-{\rm \pi} \leqslant l \leqslant {\rm \pi}$
for simplicity. In a sinusoidal field such as this, the magnetic trapping wells are identical and are separated by identical maxima (like in an omnigenous field), thus we need only solve the system in a single well with $-{\rm \pi} \leqslant l \leqslant {\rm \pi}$![]() . Note that numerically solving the integroalgebraic system results in a spectrum of eigenvalues (an example of which can be seen in figure 2), which are all real due to the Hermiticy of the system, and come in pairs of positive and negative values of equal magnitude due to the time reversibility of the system (Plunk & Helander Reference Plunk and Helander2022). In figure 1 we only show the fastest-growing optimal mode growth rate (the largest positive eigenvalue) for clarity.
. Note that numerically solving the integroalgebraic system results in a spectrum of eigenvalues (an example of which can be seen in figure 2), which are all real due to the Hermiticy of the system, and come in pairs of positive and negative values of equal magnitude due to the time reversibility of the system (Plunk & Helander Reference Plunk and Helander2022). In figure 1 we only show the fastest-growing optimal mode growth rate (the largest positive eigenvalue) for clarity.

Figure 1. Optimal mode growth rates $\varLambda$![]() of the Helmholtz free energy with $\tau = 1$
of the Helmholtz free energy with $\tau = 1$![]() as a function of $k_\perp ^2\rho _i^2$
as a function of $k_\perp ^2\rho _i^2$![]() for the various electron models. Panel (a) shows the pure ITG case, (b) shows the pure TEM case and (c) shows the pure ETG-TEM case.
for the various electron models. Panel (a) shows the pure ITG case, (b) shows the pure TEM case and (c) shows the pure ETG-TEM case.

Figure 2. Spectrum of numerical solutions to the kinetic eigenvalue problem (5.5) for a sinusoidal magnetic field strength with $\tau = 1$![]() for the pure-ITG case alongside the adiabatic electron optimal growth rate. Shown are the six largest eigenvalues found numerically.
for the pure-ITG case alongside the adiabatic electron optimal growth rate. Shown are the six largest eigenvalues found numerically.
We also show the analytical Helmholtz bound of the system in a square magnetic trapping well of the same depth, $\varLambda _{\mathrm {SW}}$![]() , given by (C18) with $\varDelta = 0$
, given by (C18) with $\varDelta = 0$![]() . We compare these Helmholtz bounds with the bounce-averaged trapped electron response to the Helmholtz bounds with adiabatic electrons, given by (6.20) in Helander & Plunk (Reference Helander and Plunk2022), and the Helmholtz bound with fully kinetic electrons, taken from Appendix C of Plunk & Helander (Reference Plunk and Helander2022). For all gradients considered, we find that the numerical solution in the sinusoidal magnetic field closely follows the analytical solution for the square magnetic trapping well.
. We compare these Helmholtz bounds with the bounce-averaged trapped electron response to the Helmholtz bounds with adiabatic electrons, given by (6.20) in Helander & Plunk (Reference Helander and Plunk2022), and the Helmholtz bound with fully kinetic electrons, taken from Appendix C of Plunk & Helander (Reference Plunk and Helander2022). For all gradients considered, we find that the numerical solution in the sinusoidal magnetic field closely follows the analytical solution for the square magnetic trapping well.
For the pure ITG case (figure 1a), we find that the Helmholtz bound of the system with the bounce-averaged trapped electron response lies between the bounds for the adiabatic and fully kinetic electron systems. Moreover, in figure 2 we see that this is true of the entire spectrum of solutions, which appear to be bounded from below in magnitude by the adiabatic electron bound. We note that, for all gradients, the optimal mode growth rate tends to zero as $k_\perp \to 0$![]() in the bounce-averaged system. This signifies the removal of the ‘magnetohydrodynamic-like’ instability mechanism present in the fully kinetic electron Helmholtz bound, which causes the bound to approach a finite value in this limit. Mathematically, the cause of this difference is illustrated by the square well solution $\varLambda _{\mathrm {SW}}$
in the bounce-averaged system. This signifies the removal of the ‘magnetohydrodynamic-like’ instability mechanism present in the fully kinetic electron Helmholtz bound, which causes the bound to approach a finite value in this limit. Mathematically, the cause of this difference is illustrated by the square well solution $\varLambda _{\mathrm {SW}}$![]() where as $k_\perp \to 0$
where as $k_\perp \to 0$![]() , the numerator tends to zero and the denominator is proportional to $(1 - \varepsilon )$
, the numerator tends to zero and the denominator is proportional to $(1 - \varepsilon )$![]() , which is finite unless the trapped particle fraction is unity. Thus, we have $\varLambda _{\mathrm {SW}} \to$
, which is finite unless the trapped particle fraction is unity. Thus, we have $\varLambda _{\mathrm {SW}} \to$![]() 0 as $k_\perp \to 0$
0 as $k_\perp \to 0$![]() . This is in contrast to the fully kinetic electron bound of Part 2, whose denominator goes to zero in the limit $k_\perp \to 0$
. This is in contrast to the fully kinetic electron bound of Part 2, whose denominator goes to zero in the limit $k_\perp \to 0$![]() in such a way that the bound remains finite. Physically, the Helmholtz bound with fully kinetic electrons overestimates the degree of instability because it contains a contribution from non-adiabatic passing electrons which, in toroidal geometry, does not contribute on time scales longer than the electron transit time.
in such a way that the bound remains finite. Physically, the Helmholtz bound with fully kinetic electrons overestimates the degree of instability because it contains a contribution from non-adiabatic passing electrons which, in toroidal geometry, does not contribute on time scales longer than the electron transit time.
The bounce-averaged electron system also yields a Helmholtz bound for the pure TEM case and the pure ETG-TEM case; see figures 1(b) and 1(c). In this bounce-averaged electron system, this provides a bound on the growth of $\boldsymbol {\nabla } n$![]() and $\boldsymbol {\nabla } T_e$
and $\boldsymbol {\nabla } T_e$![]() -driven TEMs (this does not extend to ‘true’ ETGs, which exist at larger values of $k_\perp$
-driven TEMs (this does not extend to ‘true’ ETGs, which exist at larger values of $k_\perp$![]() thus violating our assumption of $k_\perp \rho _e \ll 1$
thus violating our assumption of $k_\perp \rho _e \ll 1$![]() and require a non-adiabatic passing electron response).
and require a non-adiabatic passing electron response).
In figure 3, an example of two of the fastest-growing eigenmodes is shown for the pure TEM case. The eigenfunctions are similar (in $l$![]() -variation) to the expectation from the linear theory, with the fastest growing mode having a maximum where the largest fraction of trapped electrons reside at the minimum of the magnetic field strength. The fastest-growing eigenmode has a significant contribution from the $\kappa _{{\rm ne}}$
-variation) to the expectation from the linear theory, with the fastest growing mode having a maximum where the largest fraction of trapped electrons reside at the minimum of the magnetic field strength. The fastest-growing eigenmode has a significant contribution from the $\kappa _{{\rm ne}}$![]() moments, indicating their importance for extracting free energy at these parameters.
moments, indicating their importance for extracting free energy at these parameters.

Figure 3. Eigenfunctions of the kinetic eigenvalue problem (5.5), obtained numerically, for $\varDelta = 0$![]() (Helmholtz limit of the generalised free energy) with $\tau = 1$
(Helmholtz limit of the generalised free energy) with $\tau = 1$![]() , $b_i = 1.5$
, $b_i = 1.5$![]() , in the pure TEM case. Here, the absolute values of the $\kappa _{{\rm na}}$
, in the pure TEM case. Here, the absolute values of the $\kappa _{{\rm na}}$![]() moments are shown as a function of $l$
moments are shown as a function of $l$![]() , alongside the magnetic field strength $B(l)$
, alongside the magnetic field strength $B(l)$![]() , for the eigenfunction with the largest eigenvalue (a) and the second largest (b).
, for the eigenfunction with the largest eigenvalue (a) and the second largest (b).
8 Generalised free energy bounds
We now turn our attention to the general problem in which $\varDelta$![]() is a free parameter. For this case where $\varDelta \neq 0$
is a free parameter. For this case where $\varDelta \neq 0$![]() , the species moments $\kappa _{3a}$
, the species moments $\kappa _{3a}$![]() , are retained. Thus, the optimal modes of this system depend on the magnetic curvature drift, $\omega _{{\rm da}}$
, are retained. Thus, the optimal modes of this system depend on the magnetic curvature drift, $\omega _{{\rm da}}$![]() , for each species. We seek values of $\varDelta$
, for each species. We seek values of $\varDelta$![]() which minimise the maximum growth rate $\varLambda$
which minimise the maximum growth rate $\varLambda$![]() of the generalised free energy, giving the lowest possible upper bound. The largest resulting optimal growth rate, at this minimising value of $\varDelta$
of the generalised free energy, giving the lowest possible upper bound. The largest resulting optimal growth rate, at this minimising value of $\varDelta$![]() , gives an upper bound on instabilities, in the considered limit, that depends on the magnetic curvature.
, gives an upper bound on instabilities, in the considered limit, that depends on the magnetic curvature.
Because of the complexity of the general system, we perform the optimisation over $\varDelta$![]() numerically and exclude values for which positive definiteness is violated. However, we have found that the optimisation space of $\varLambda ( \varDelta )$
numerically and exclude values for which positive definiteness is violated. However, we have found that the optimisation space of $\varLambda ( \varDelta )$![]() is very smooth and that a global minimum is easily found.
is very smooth and that a global minimum is easily found.
As a first test for the numerical solution, to facilitate comparison with the analytical solution for square magnetic trapping well with constant curvature, we solve the system numerically for the case of a magnetic field of the form $B(l) = B_0 - B_1 \cos (l)$![]() with $B_0 = 1$
with $B_0 = 1$![]() and $B_1= 0.1$
and $B_1= 0.1$![]() with constant curvature, $\hat {\omega }_{{\rm da}}(l) = \mathrm {const}$
with constant curvature, $\hat {\omega }_{{\rm da}}(l) = \mathrm {const}$![]() . Following the analysis of the generalised free energy with adiabatic electrons of Part 3, we consider the instability drive parameter $\kappa _d = \omega _{*i}/\hat {\omega }_{{\rm di}}$
. Following the analysis of the generalised free energy with adiabatic electrons of Part 3, we consider the instability drive parameter $\kappa _d = \omega _{*i}/\hat {\omega }_{{\rm di}}$![]() or ($\kappa _d= \omega _{*i}\eta _i/\hat {\omega }_{{\rm di}}$
or ($\kappa _d= \omega _{*i}\eta _i/\hat {\omega }_{{\rm di}}$![]() for the pure ITG case and $\kappa _d= |\omega _{*e}\eta _e|/\hat {\omega }_{{\rm di}}$
for the pure ITG case and $\kappa _d= |\omega _{*e}\eta _e|/\hat {\omega }_{{\rm di}}$![]() for the pure ETG-TEM case). We thus have $\hat {\omega }_{{\rm da}}/\omega _{*i} = \mathrm {sign}(e_a)\kappa _d^{-1}T_a/{T_i}$
for the pure ETG-TEM case). We thus have $\hat {\omega }_{{\rm da}}/\omega _{*i} = \mathrm {sign}(e_a)\kappa _d^{-1}T_a/{T_i}$![]() for each species. Under this normalisation, if $\kappa _d > 0$
for each species. Under this normalisation, if $\kappa _d > 0$![]() , then $\hat {\omega }_{{\rm da}}\omega _{*a} > 0$
, then $\hat {\omega }_{{\rm da}}\omega _{*a} > 0$![]() for both species, corresponding to ‘bad’ curvature where linear instability is expected. The case of $\kappa _d < 0$
for both species, corresponding to ‘bad’ curvature where linear instability is expected. The case of $\kappa _d < 0$![]() corresponds to ‘good’ curvature, where the system is expected to be linearly stable.
corresponds to ‘good’ curvature, where the system is expected to be linearly stable.
In figure 4, we show the optimal mode growth for the pure TEM case, the pure ETG-TEM case, and for the pure ITG case, as the curvature-drive parameter $\kappa _d$![]() is varied. We see that the square and the cosine trapping wells follow similar trends with $\kappa _d$
is varied. We see that the square and the cosine trapping wells follow similar trends with $\kappa _d$![]() , attaining a maximum for a finite positive value of $\kappa _d$
, attaining a maximum for a finite positive value of $\kappa _d$![]() , where the optimal bound is obtained for $\varDelta = 0$
, where the optimal bound is obtained for $\varDelta = 0$![]() and therefore coincides with the Helmholtz bound. This feature of the generalised free energy bound overlapping with the Helmholtz bound at a particular value of the curvature drive was also found for the adiabatic electron analysis in Part 3. The optimal bound decreases monotonically away from this maximum towards the ‘strongly driven’ limit of large positive $\kappa _d$
and therefore coincides with the Helmholtz bound. This feature of the generalised free energy bound overlapping with the Helmholtz bound at a particular value of the curvature drive was also found for the adiabatic electron analysis in Part 3. The optimal bound decreases monotonically away from this maximum towards the ‘strongly driven’ limit of large positive $\kappa _d$![]() and in the direction of small $\kappa _d$
and in the direction of small $\kappa _d$![]() in the ‘resonant limit’. The bound also decreases for $\kappa _d \leqslant 0$
in the ‘resonant limit’. The bound also decreases for $\kappa _d \leqslant 0$![]() where the curvature is favourable (‘good’).
where the curvature is favourable (‘good’).

Figure 4. The optimal mode growth rate of generalised free energy, at the minimising value of $\varDelta$![]() , versus the drive parameter $\kappa _d$
, versus the drive parameter $\kappa _d$![]() at $\tau = 1$
at $\tau = 1$![]() . The analytical square well with constant curvature solution is shown alongside the numerical solutions of the eigenvalue problem in a cosine magnetic well with constant curvature. These are computed for a density-gradient-driven case (pure TEM case), an ion-temperature-gradient-driven case (pure ITG case) and an electron-temperature-gradient-driven case (pure ETG-TEM case).
. The analytical square well with constant curvature solution is shown alongside the numerical solutions of the eigenvalue problem in a cosine magnetic well with constant curvature. These are computed for a density-gradient-driven case (pure TEM case), an ion-temperature-gradient-driven case (pure ITG case) and an electron-temperature-gradient-driven case (pure ETG-TEM case).
In figure 5, we compare the optimal mode growth in the square well, $\varLambda _{\mathrm {SW}}$![]() , with constant curvature to the solution to the linear dispersion relation with bounce-averaged electrons (details given in appendix D) in the same geometry, in the pure ITG case. Once again, we vary the drive parameter $\kappa _d$
, with constant curvature to the solution to the linear dispersion relation with bounce-averaged electrons (details given in appendix D) in the same geometry, in the pure ITG case. Once again, we vary the drive parameter $\kappa _d$![]() to compare how each solution depends on the curvature inside the well. We confirm that the linear result lies below the upper bound, and we find that, much like the behaviour of the upper bound, the presence of bounce-averaged electrons in the linear dispersion relation ‘lifts up’ the linear growth rate of the ITG. In regions where the normal modes are stable, the optimal modes have a finite but reduced growth rate, as was found in Part 3 for the adiabatic electron system.
to compare how each solution depends on the curvature inside the well. We confirm that the linear result lies below the upper bound, and we find that, much like the behaviour of the upper bound, the presence of bounce-averaged electrons in the linear dispersion relation ‘lifts up’ the linear growth rate of the ITG. In regions where the normal modes are stable, the optimal modes have a finite but reduced growth rate, as was found in Part 3 for the adiabatic electron system.

Figure 5. Comparison between the generalised upper bound $\varLambda _{\mathrm {SW}}$![]() , and the linear growth rate, for a pure ITG case in a square magnetic well with $B_{\mathrm {min}}/B_\mathrm {max} = 0.1$
, and the linear growth rate, for a pure ITG case in a square magnetic well with $B_{\mathrm {min}}/B_\mathrm {max} = 0.1$![]() , $\tau = 1$
, $\tau = 1$![]() , and constant curvature (see Appendix D). Here, the drift-kinetic limit has been considered for simplicity (${\rm J}_{0i} \approx 1$
, and constant curvature (see Appendix D). Here, the drift-kinetic limit has been considered for simplicity (${\rm J}_{0i} \approx 1$![]() ).
).
8.1 Impact of the maximum-$J$ property
property
A class of magnetic configurations in which the gyrokinetic system with bounce-averaged electrons is particularly interesting is provided by so-called ‘maximum-$J$![]() ’ geometries, where the radial profile of the parallel adiabatic invariant,
’ geometries, where the radial profile of the parallel adiabatic invariant,
has a maximum at the magnetic axis, and decreases radially (Rosenbluth Reference Rosenbluth1968). In such geometries, the electrons experience good curvature everywhere because
is negative for all trapped electrons if $\partial J / \partial \psi < 0$![]() and ${\mathrm {d}\ln n}/{\mathrm {d}\psi } < 0$
and ${\mathrm {d}\ln n}/{\mathrm {d}\psi } < 0$![]() , as is usually the case in fusion plasmas (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander et al. Reference Helander, Proll and Plunk2013). Quasi-isodynamic stellarators are a particular type of optimised stellarator (Helander & Nührenberg Reference Helander and Nührenberg2009; Nührenberg Reference Nührenberg2010) which can be designed to have this property (Sánchez et al. Reference Sánchez, Velasco, Calvo and Mulas2023; Rodríguez, Helander & Goodman Reference Rodríguez, Helander and Goodman2024). In such devices, the local curvature (as seen by the ions) may be unfavourable, but the bounce-averaged curvature for trapped electrons is always favourable. Many results from normal-mode theory, as well as gyrokinetic simulations, have found that the trapped electron population in these geometries have a stabilising influence if a plasma density gradient is present (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Plunk et al. Reference Plunk, Helander, Xanthopoulos and Connor2014; Alcusón et al. Reference Alcusón, Xanthopoulos, Plunk, Helander, Wilms, Turkin, von Stechow and Grulke2020; Proll et al. Reference Proll, Plunk, Faber, Görler, Helander, McKinney, Pueschel, Smith and Xanthopoulos2022). The physical reason for this enhanced stability can be traced back to the fact that relatively little of the thermal energy is ‘available’ for conversion to instabilities (Helander Reference Helander2017; Mackenbach et al. Reference Mackenbach, Proll, Wakelkamp and Helander2023b).
, as is usually the case in fusion plasmas (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander et al. Reference Helander, Proll and Plunk2013). Quasi-isodynamic stellarators are a particular type of optimised stellarator (Helander & Nührenberg Reference Helander and Nührenberg2009; Nührenberg Reference Nührenberg2010) which can be designed to have this property (Sánchez et al. Reference Sánchez, Velasco, Calvo and Mulas2023; Rodríguez, Helander & Goodman Reference Rodríguez, Helander and Goodman2024). In such devices, the local curvature (as seen by the ions) may be unfavourable, but the bounce-averaged curvature for trapped electrons is always favourable. Many results from normal-mode theory, as well as gyrokinetic simulations, have found that the trapped electron population in these geometries have a stabilising influence if a plasma density gradient is present (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Plunk et al. Reference Plunk, Helander, Xanthopoulos and Connor2014; Alcusón et al. Reference Alcusón, Xanthopoulos, Plunk, Helander, Wilms, Turkin, von Stechow and Grulke2020; Proll et al. Reference Proll, Plunk, Faber, Görler, Helander, McKinney, Pueschel, Smith and Xanthopoulos2022). The physical reason for this enhanced stability can be traced back to the fact that relatively little of the thermal energy is ‘available’ for conversion to instabilities (Helander Reference Helander2017; Mackenbach et al. Reference Mackenbach, Proll, Wakelkamp and Helander2023b).
To investigate if this property is present in the optimal mode system, we require a test geometry where the ions may experience bad curvature locally, while the bounce-averaged curvature of the electrons can be independently varied. A simple model magnetic geometry can be seen in figure 6. In this geometry, we choose a curvature of the form $\hat {\omega }_{{\rm da}}(l)/\omega _{*i} = \mathrm {sign}(e_a)\sigma _d \cos (l) T_a/{T_i}$![]() and $B(l) = B_0 + B_1\cos (l)$
and $B(l) = B_0 + B_1\cos (l)$![]() , where once again, we take $B_0 = 1.0$
, where once again, we take $B_0 = 1.0$![]() and $B_1 = 0.1$
and $B_1 = 0.1$![]() . In this toy geometry, $\sigma _d$
. In this toy geometry, $\sigma _d$![]() is a parameter which determines the relative magnitude of the gradient length scale and the maximum radius of curvature, similar to the familiar $R/L_n$
is a parameter which determines the relative magnitude of the gradient length scale and the maximum radius of curvature, similar to the familiar $R/L_n$![]() or $R/L_{T_a}$
or $R/L_{T_a}$![]() normalisation, where $R$
normalisation, where $R$![]() is the major radius of the torus and $L_{n,T_i}$
is the major radius of the torus and $L_{n,T_i}$![]() is the scale length of the density or temperature gradients, respectively. With this model geometry, by changing the sign of $\sigma _d$
is the scale length of the density or temperature gradients, respectively. With this model geometry, by changing the sign of $\sigma _d$![]() we can choose between a mostly maximum-$J$
we can choose between a mostly maximum-$J$![]() geometry for $\sigma _d < 0$
geometry for $\sigma _d < 0$![]() , where most trapped electrons, particularly those which are deeply trapped, experience bounce-averaged good curvature, and a mostly minimum-$J$
, where most trapped electrons, particularly those which are deeply trapped, experience bounce-averaged good curvature, and a mostly minimum-$J$![]() geometry for $\sigma _d > 0$
geometry for $\sigma _d > 0$![]() . Importantly, we can make this change between maximum-$J$
. Importantly, we can make this change between maximum-$J$![]() and minimum-$J$
and minimum-$J$![]() geometry without changing the field-line-average curvature (zero in this case), whilst always having a region of unfavourable curvature along the field line.
geometry without changing the field-line-average curvature (zero in this case), whilst always having a region of unfavourable curvature along the field line.

Figure 6. An example of an approximately maximum-$J$![]() toy geometry, where most trapped electrons, particularly those that are deeply trapped, experience bounce-averaged good curvature. (a) The curvature is shown alongside the magnetic field strength, where negative values indicate bad curvature. (b) The $\lambda$
toy geometry, where most trapped electrons, particularly those that are deeply trapped, experience bounce-averaged good curvature. (a) The curvature is shown alongside the magnetic field strength, where negative values indicate bad curvature. (b) The $\lambda$![]() -dependence of the bounce-averaged electron drift is shown.
-dependence of the bounce-averaged electron drift is shown.
In figure 7, we show the optimal growth rate $\varLambda$![]() as $\sigma _d$
as $\sigma _d$![]() is varied, the pure ITG case, pure TEM case and pure ETG-TEM case. The upper bound in the pure TEM case is lower in the maximum-$J$
is varied, the pure ITG case, pure TEM case and pure ETG-TEM case. The upper bound in the pure TEM case is lower in the maximum-$J$![]() geometries (negative $\sigma _d$
geometries (negative $\sigma _d$![]() ) than in the equivalent minimum-$J$
) than in the equivalent minimum-$J$![]() geometries (positive $\sigma _d$
geometries (positive $\sigma _d$![]() ). To explore the physical mechanism at play, we also test the dependence of the optimal mode growth on the curvature drift for each species separately. For $\sigma _d<0$
). To explore the physical mechanism at play, we also test the dependence of the optimal mode growth on the curvature drift for each species separately. For $\sigma _d<0$![]() (maximum-$J$
(maximum-$J$![]() ), removing the electron drift frequency (the instability mechanism that remains is analogous to the ITEM of Plunk et al. (Reference Plunk, Connor and Helander2017)) increases growth rates if $|\sigma _d|$
), removing the electron drift frequency (the instability mechanism that remains is analogous to the ITEM of Plunk et al. (Reference Plunk, Connor and Helander2017)) increases growth rates if $|\sigma _d|$![]() is small, and has little effect for $\sigma _d$
is small, and has little effect for $\sigma _d$![]() large and negative. Thus, $\overline {\omega }_{{\rm de}}$
large and negative. Thus, $\overline {\omega }_{{\rm de}}$![]() has a stabilising effect in the maximum-$J$
has a stabilising effect in the maximum-$J$![]() geometries, in agreement with the expectation linear theory. Moreover, in maximum-$J$
geometries, in agreement with the expectation linear theory. Moreover, in maximum-$J$![]() geometries at large negative values of $\sigma _d$
geometries at large negative values of $\sigma _d$![]() , the instability mechanism is largely reliant on the ion curvature drift, as is expected from the linear ITEM or ubiquitous mode (Coppi & Pegoraro Reference Coppi and Pegoraro1977).
, the instability mechanism is largely reliant on the ion curvature drift, as is expected from the linear ITEM or ubiquitous mode (Coppi & Pegoraro Reference Coppi and Pegoraro1977).

Figure 7. The optimal mode growth rate of generalised free energy, for the minimising $\varDelta$![]() , versus the drive parameter $\sigma _d$
, versus the drive parameter $\sigma _d$![]() . Negative and positive values of this parameter correspond to the ‘maximum-$J$
. Negative and positive values of this parameter correspond to the ‘maximum-$J$![]() ’ and ‘minimum-$J$
’ and ‘minimum-$J$![]() ’ cases of the model geometry shown in figure 6. (a) The pure TEM case is shown at $k_\perp \rho _i = 1.5$
’ cases of the model geometry shown in figure 6. (a) The pure TEM case is shown at $k_\perp \rho _i = 1.5$![]() , (b) the pure ITG case in the drift kinetic limit (${\rm J}_{0i} \approx 1$
, (b) the pure ITG case in the drift kinetic limit (${\rm J}_{0i} \approx 1$![]() ) is shown and (c) shows the pure ETG-TEM case at $k_\perp \rho _i = 1.5$
) is shown and (c) shows the pure ETG-TEM case at $k_\perp \rho _i = 1.5$![]() . The impact of species-dependent curvature drifts on each case is explored by zeroing out $\hat {\omega }_{{\rm di}}$
. The impact of species-dependent curvature drifts on each case is explored by zeroing out $\hat {\omega }_{{\rm di}}$![]() or $\overline {\omega }_{{\rm de}}$
or $\overline {\omega }_{{\rm de}}$![]() independently.
independently.
For $\sigma _d > 0$![]() (minimum-$J$
(minimum-$J$![]() ), the removal of the curvature drift for either species in the pure TEM case serves to move the maximum value of the optimal growth rate towards lower values of $\sigma _d$
), the removal of the curvature drift for either species in the pure TEM case serves to move the maximum value of the optimal growth rate towards lower values of $\sigma _d$![]() and greatly reduces the growth rate for large $\sigma _d$
and greatly reduces the growth rate for large $\sigma _d$![]() . This suggests that the drifts of both species are important for the optimal extraction of free energy from the gradients.
. This suggests that the drifts of both species are important for the optimal extraction of free energy from the gradients.
In the pure ETG-TEM case, we see a reduction of the optimal mode growth for $\sigma _d < 0$![]() . This is in keeping with the expectation from the dispersion relation of Plunk et al. (Reference Plunk, Connor and Helander2017), which shows that the maximum-$J$
. This is in keeping with the expectation from the dispersion relation of Plunk et al. (Reference Plunk, Connor and Helander2017), which shows that the maximum-$J$![]() property, associated with the relative direction of the bounce-averaged drift to the electron diamagnetic frequency, also exerts a stabilising influence in the strongly driven limit when $\eta _e$
property, associated with the relative direction of the bounce-averaged drift to the electron diamagnetic frequency, also exerts a stabilising influence in the strongly driven limit when $\eta _e$![]() is finite. The optimal mode analysis here suggests that this benefit extends into the resonant limit (small $\sigma _d$
is finite. The optimal mode analysis here suggests that this benefit extends into the resonant limit (small $\sigma _d$![]() ).
).
We observe that maximum-$J$![]() configurations also exhibit lower optimal growth in the ITG scenario ($\boldsymbol {\nabla } n = 0$
configurations also exhibit lower optimal growth in the ITG scenario ($\boldsymbol {\nabla } n = 0$![]() , $\boldsymbol {\nabla } T_e = 0$
, $\boldsymbol {\nabla } T_e = 0$![]() ). This is despite the absence of any electron free energy source, something which has not been predicted previously from linear normal-mode theory. It is found that beyond a negative value of $\sigma _d$
). This is despite the absence of any electron free energy source, something which has not been predicted previously from linear normal-mode theory. It is found that beyond a negative value of $\sigma _d$![]() of sufficient magnitude, the ITG upper bound with bounce-averaged electrons coincides with that of the adiabatic electron upper bound of Part 3 computed in this geometry (because the bound with adiabatic electrons is local in this limit, here we evaluate the bound at each point in $l$
of sufficient magnitude, the ITG upper bound with bounce-averaged electrons coincides with that of the adiabatic electron upper bound of Part 3 computed in this geometry (because the bound with adiabatic electrons is local in this limit, here we evaluate the bound at each point in $l$![]() in the toy geometry and plot the largest value found). This is also reflected in the eigenfunction (not shown), which tends towards a delta function at the location of maximum magnetic field strength, where the trapped electron contribution is zero, suggesting that the adiabatic ITG solution to (5.5) becomes the solution with the largest $\varLambda$
in the toy geometry and plot the largest value found). This is also reflected in the eigenfunction (not shown), which tends towards a delta function at the location of maximum magnetic field strength, where the trapped electron contribution is zero, suggesting that the adiabatic ITG solution to (5.5) becomes the solution with the largest $\varLambda$![]() for these values of $\sigma _d$
for these values of $\sigma _d$![]() . As shown in figure 7, this mechanism of stabilisation in maximum-$J$
. As shown in figure 7, this mechanism of stabilisation in maximum-$J$![]() geometry is present even if $\overline{\omega }_{\rm de} = 0$
geometry is present even if $\overline{\omega }_{\rm de} = 0$![]() . Thus, this stabilising mechanism in maximum-$J$
. Thus, this stabilising mechanism in maximum-$J$![]() geometries is distinct from the known mechanism that follows from the difference in sign between $\overline {\omega }_{\rm de}$
geometries is distinct from the known mechanism that follows from the difference in sign between $\overline {\omega }_{\rm de}$![]() and $\omega _{*e}^T$
and $\omega _{*e}^T$![]() (Proll et al. Reference Proll, Plunk, Faber, Görler, Helander, McKinney, Pueschel, Smith and Xanthopoulos2022).
(Proll et al. Reference Proll, Plunk, Faber, Görler, Helander, McKinney, Pueschel, Smith and Xanthopoulos2022).
8.1.1 Interpreting with linear theory
To interpret the observed reduction of the ITG-driven optimal mode growth in maximum-$J$![]() geometries without a source of electron free energy, we turn to expressions from linear normal-mode theory (i.e solutions to the gyokinetic equation which evolve in time like $\exp ({-{\rm i} \omega t})$
geometries without a source of electron free energy, we turn to expressions from linear normal-mode theory (i.e solutions to the gyokinetic equation which evolve in time like $\exp ({-{\rm i} \omega t})$![]() , where $\omega$
, where $\omega$![]() is the complex frequency). The comparable linear dispersion relation is given by (3.5) in Plunk et al. (Reference Plunk, Connor and Helander2017), for the case of a pure ITG, which is valid if the mode frequency satisfies $\omega /(\omega _{*i}\eta _i) \sim (\omega _{{\rm di}}/\omega _{*i}\eta _i)^{1/2} \ll 1$
is the complex frequency). The comparable linear dispersion relation is given by (3.5) in Plunk et al. (Reference Plunk, Connor and Helander2017), for the case of a pure ITG, which is valid if the mode frequency satisfies $\omega /(\omega _{*i}\eta _i) \sim (\omega _{{\rm di}}/\omega _{*i}\eta _i)^{1/2} \ll 1$![]() (i.e. in the regime of large $\kappa _d$
(i.e. in the regime of large $\kappa _d$![]() ). Taking the drift-kinetic limit (${\rm J}_{0i} \approx 1)$
). Taking the drift-kinetic limit (${\rm J}_{0i} \approx 1)$![]() , the normal mode frequency is given by
, the normal mode frequency is given by

where instability growth is given by a positive imaginary part of $\omega$![]() which arises due to regions of bad curvature along the magnetic field ($\omega _{*i}\eta _i \hat {\omega }_{{\rm di}} > 0$
which arises due to regions of bad curvature along the magnetic field ($\omega _{*i}\eta _i \hat {\omega }_{{\rm di}} > 0$![]() ). We see that when the ITG is unstable, the trapped electron contribution in the denominator acts to further destabilise the mode by making the denominator (which is always positive (Helander et al. Reference Helander, Proll and Plunk2013)) smaller. This destabilising effect is due to the depletion of the Boltzmann response by the population of non-adiabatic trapped electrons.
). We see that when the ITG is unstable, the trapped electron contribution in the denominator acts to further destabilise the mode by making the denominator (which is always positive (Helander et al. Reference Helander, Proll and Plunk2013)) smaller. This destabilising effect is due to the depletion of the Boltzmann response by the population of non-adiabatic trapped electrons.
The effect of the maximum-$J$![]() property on this dispersion relation is most easily illustrated when the case of the ‘square well’ magnetic field with constant curvature inside the well is considered. Inside the well, the ITG frequency becomes $\omega = \pm \sqrt {-\omega _{*i}\eta _i \hat {\omega }_{{\rm di}}/ (\tau (1- \varepsilon ))}$
property on this dispersion relation is most easily illustrated when the case of the ‘square well’ magnetic field with constant curvature inside the well is considered. Inside the well, the ITG frequency becomes $\omega = \pm \sqrt {-\omega _{*i}\eta _i \hat {\omega }_{{\rm di}}/ (\tau (1- \varepsilon ))}$![]() , where $\varepsilon$
, where $\varepsilon$![]() is the trapped particle fraction, and outside the well it is given by $\omega = \pm \sqrt {-\omega _{*i}\eta _i \hat {\omega }_{{\rm di}}/\tau }$
is the trapped particle fraction, and outside the well it is given by $\omega = \pm \sqrt {-\omega _{*i}\eta _i \hat {\omega }_{{\rm di}}/\tau }$![]() . If we consider a series of these square magnetic trapping wells with minima of $B = B_{\mathrm {min}}$
. If we consider a series of these square magnetic trapping wells with minima of $B = B_{\mathrm {min}}$![]() separated by regions of $B = B_{\mathrm {max}}$
separated by regions of $B = B_{\mathrm {max}}$![]() , with a magnetic curvature that alternates sign (from ‘good’ curvature to ‘bad’ curvature) between regions of $B = B_{\mathrm {max}}$
, with a magnetic curvature that alternates sign (from ‘good’ curvature to ‘bad’ curvature) between regions of $B = B_{\mathrm {max}}$![]() and $B = B_{\mathrm {min}}$
and $B = B_{\mathrm {min}}$![]() , then there are two possibilities: either the bad curvature is located at the minimum of magnetic field strength, corresponding to a minimum-$J$
, then there are two possibilities: either the bad curvature is located at the minimum of magnetic field strength, corresponding to a minimum-$J$![]() geometry; or the bad curvature is located outside the well, corresponding to a maximum-$J$
geometry; or the bad curvature is located outside the well, corresponding to a maximum-$J$![]() geometry.
geometry.
In the minimum-$J$![]() case, the ITG is unstable inside the well, with a growth rate given by $\omega = \pm \sqrt {-\omega _{*i}\eta _i \hat {\omega }_{{\rm di}}/ (\tau (1- \varepsilon ))}$
case, the ITG is unstable inside the well, with a growth rate given by $\omega = \pm \sqrt {-\omega _{*i}\eta _i \hat {\omega }_{{\rm di}}/ (\tau (1- \varepsilon ))}$![]() . In this scenario, the non-adiabatic population of trapped electrons can raise the ITG growth rate by depleting the Boltzmann response. On the other hand, in the maximum-$J$
. In this scenario, the non-adiabatic population of trapped electrons can raise the ITG growth rate by depleting the Boltzmann response. On the other hand, in the maximum-$J$![]() case, the ITG is stable inside the well because the curvature is favourable there ($\hat {\omega }_{{\rm di}} \omega _{*i}\eta _i> 0$
case, the ITG is stable inside the well because the curvature is favourable there ($\hat {\omega }_{{\rm di}} \omega _{*i}\eta _i> 0$![]() ). Instead, the unstable ITG is outside of the well at $B= B_{\mathrm {max}}$
). Instead, the unstable ITG is outside of the well at $B= B_{\mathrm {max}}$![]() and the growth rate is $\omega = \pm \sqrt {-\omega _{*i}\eta _i \hat {\omega }_{{\rm di}}/\tau }$
and the growth rate is $\omega = \pm \sqrt {-\omega _{*i}\eta _i \hat {\omega }_{{\rm di}}/\tau }$![]() , corresponding to the ITG growth rate if the electrons are treated adiabatically.
, corresponding to the ITG growth rate if the electrons are treated adiabatically.
This behaviour can also be inferred from the ITG growth rate in general geometry (8.3), in which it can be seen that for instability to occur, the average of $\omega _{*i}\eta _i\hat {\omega }_{{\rm di}}| \delta \phi |^2$![]() along the magnetic field line must be positive, such that $\delta \phi$
along the magnetic field line must be positive, such that $\delta \phi$![]() must have large amplitude in the regions of bad curvature. In maximum-$J$
must have large amplitude in the regions of bad curvature. In maximum-$J$![]() geometry, the regions of bad curvature are at different locations in $l$
geometry, the regions of bad curvature are at different locations in $l$![]() than the minima of magnetic field strength. In these geometries, for the instability criterion to be fulfilled, the non-adiabatic electron response, which is proportional to the average potential seen by the trapped electrons as they bounce in the magnetic well, will be necessarily small. Otherwise, if the electron contribution were large, the potential would have a large amplitude in a region of favourable curvature, thus impacting the instability criterion. As a result, the destabilising impact of trapped electrons on the ITG is diminished in such geometries.
than the minima of magnetic field strength. In these geometries, for the instability criterion to be fulfilled, the non-adiabatic electron response, which is proportional to the average potential seen by the trapped electrons as they bounce in the magnetic well, will be necessarily small. Otherwise, if the electron contribution were large, the potential would have a large amplitude in a region of favourable curvature, thus impacting the instability criterion. As a result, the destabilising impact of trapped electrons on the ITG is diminished in such geometries.
This is not the case in minimum-$J$![]() geometries, where the regions of bad curvature are located at the minima of $B$
geometries, where the regions of bad curvature are located at the minima of $B$![]() along the field line. In these geometries, the instability criterion and the magnitude of the trapped electron contribution are not in conflict, thus the ITG growth can be increased by the trapped electron population without impacting the instability mechanism.
along the field line. In these geometries, the instability criterion and the magnitude of the trapped electron contribution are not in conflict, thus the ITG growth can be increased by the trapped electron population without impacting the instability mechanism.
In the optimal mode analysis, this effect is slightly obscured due to the optimisation over the $\varDelta$![]() parameter, but the same basic behaviour can be observed in the expression for $E(\boldsymbol {k}, t)$
parameter, but the same basic behaviour can be observed in the expression for $E(\boldsymbol {k}, t)$![]() given by (4.14), which is of the same form as the denominator in (8.3). Thus, the magnitude of $E(\boldsymbol {k},t)$
given by (4.14), which is of the same form as the denominator in (8.3). Thus, the magnitude of $E(\boldsymbol {k},t)$![]() affects the magnitude of $\varLambda$
affects the magnitude of $\varLambda$![]() via the denominator of (4.19), for non-zero values of $\varDelta$
via the denominator of (4.19), for non-zero values of $\varDelta$![]() . This stabilising effect of maximum-$J$
. This stabilising effect of maximum-$J$![]() can be seen in figure 7, where for the ITG scenario, the upper bound with bounce averaged electrons approaches the adiabatic electron result for large negative values of $\sigma _d$
can be seen in figure 7, where for the ITG scenario, the upper bound with bounce averaged electrons approaches the adiabatic electron result for large negative values of $\sigma _d$![]() , corresponding to an approximately maximum-$J$
, corresponding to an approximately maximum-$J$![]() geometry.
geometry.
To summarise this section, the impact of the trapped electron response on ITG instability in the absence of electron free energy is always destabilising, but the amount of destabilisation is impacted by the location of the most deeply trapped particles relative to the regions of bad curvature. To use a term coined in the literature for zonal-flows (Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005), the location of the trapped particles changes the inertia of the ITG mode, with ITGs possessing lower inertia in minimum-$J$![]() configurations than in those which are maximum-$J$
configurations than in those which are maximum-$J$![]() . This may go some way towards explaining why simulations performed in newly optimised, highly maximum-$J$
. This may go some way towards explaining why simulations performed in newly optimised, highly maximum-$J$![]() stellarators (Goodman et al. Reference Goodman, Xanthopoulos, Plunk, Smith, Nührenberg, Beidler, Henneberg, Roberg-Clark, Drevlak and Helander2024) show a smaller increase in ITG-driven heat fluxes with the addition of kinetic electrons in comparison with configurations which do not satisfy the maximum-$J$
stellarators (Goodman et al. Reference Goodman, Xanthopoulos, Plunk, Smith, Nührenberg, Beidler, Henneberg, Roberg-Clark, Drevlak and Helander2024) show a smaller increase in ITG-driven heat fluxes with the addition of kinetic electrons in comparison with configurations which do not satisfy the maximum-$J$![]() property to the same degree.
property to the same degree.
9 Conclusion
We have studied the optimal modes of the generalised free energy for the case of a two-species system with fully gyrokinetic ions and bounce-averaged electrons. The central result of this effort is a system of integrodifferential equations (B1)–(B3) and (B10)–(B12), the solutions to which provide an upper bound on the possible instantaneous growth of any instabilities which satisfy $L/v_{{\rm Te}} \ll \tau _D$![]() . These bounds depend explicitly on the magnetic field strength of the chosen flux tube. Despite being more difficult to solve than the optimal mode systems of Parts 1–3 (requiring a numerical treatment for all but the simplest of magnetic fields), the eigenvalue problem here, which involves a relatively small number of velocity space moments of the distribution function, is still much simpler than the equivalent normal mode problem, which involves computing the full distribution function as a function of velocity space.
. These bounds depend explicitly on the magnetic field strength of the chosen flux tube. Despite being more difficult to solve than the optimal mode systems of Parts 1–3 (requiring a numerical treatment for all but the simplest of magnetic fields), the eigenvalue problem here, which involves a relatively small number of velocity space moments of the distribution function, is still much simpler than the equivalent normal mode problem, which involves computing the full distribution function as a function of velocity space.
As is discussed in Parts 1–3, the upper bounds given by the fastest growing optimal modes not only give an upper bound on linear instability, but also have nonlinear implications. This is because the nonlinear growth of the system is bounded by the growth of the fastest growing optimal mode. Here, however, the removal of the ‘finite-electron-Larmor-radius’ effects associated with retaining $k_\perp \rho _e$![]() results in an unbounded growth of $\varLambda$
results in an unbounded growth of $\varLambda$![]() as $k_\perp \to \infty$
as $k_\perp \to \infty$![]() . As a result, the nonlinear growth is also unbounded if all values of $k_\perp$
. As a result, the nonlinear growth is also unbounded if all values of $k_\perp$![]() are considered. Thus, when seeking a bound on nonlinear growth, the spectrum in $k_\perp$
are considered. Thus, when seeking a bound on nonlinear growth, the spectrum in $k_\perp$![]() must be cut off at a chosen value, limiting its applicability to cases in which only the ion-scale dynamics are of interest, as is often done in gyrokinetic simulations. Other nonlinear implications of optimal modes also discussed in Part 2, such as their required presence in statistically steady turbulence (DelSole Reference DelSole2004; Landreman et al. Reference Landreman, Plunk and Dorland2015), also hold true for the optimal modes studied here.
must be cut off at a chosen value, limiting its applicability to cases in which only the ion-scale dynamics are of interest, as is often done in gyrokinetic simulations. Other nonlinear implications of optimal modes also discussed in Part 2, such as their required presence in statistically steady turbulence (DelSole Reference DelSole2004; Landreman et al. Reference Landreman, Plunk and Dorland2015), also hold true for the optimal modes studied here.
The upper bounds computed here are specific to toroidal geometries with non-periodic flux tubes (i.e. tokamaks and stellarators) and as such, the Helmholtz bound we find behaves as expected in these geometries at small values of $k_\perp \rho _i$![]() . This is in contrast to the fully kinetic electron Helmholtz bound of Part 2 which, in its generality, must also bound growth in closed-field-line geometries. The Helmholtz bounds of the bounce-averaged system are significantly lower than the Part 2 result for all gradients, as long as $k_\perp \rho _e \ll 1$
. This is in contrast to the fully kinetic electron Helmholtz bound of Part 2 which, in its generality, must also bound growth in closed-field-line geometries. The Helmholtz bounds of the bounce-averaged system are significantly lower than the Part 2 result for all gradients, as long as $k_\perp \rho _e \ll 1$![]() .
.
Moreover, the generalised bound, which is optimised over the free parameter $\varDelta$![]() , depends explicitly on all the geometry quantities associated with the flux-tube domain. Here, we neglected parallel ion motion in our system of equations for the sake of simplicity, focusing on the typical toroidal ITG-TEM limits familiar from normal-mode theory. We have found that the optimal modes exhibit much of the behaviour expected from normal modes, attaining a maximum growth rate (relative to the strength of the plasma gradients) when the curvature drift for both species is unfavourable and when the ratios of the diamagnetic frequencies and drift frequencies are close to unity. We have also demonstrated that the beneficial properties of maximum-$J$
, depends explicitly on all the geometry quantities associated with the flux-tube domain. Here, we neglected parallel ion motion in our system of equations for the sake of simplicity, focusing on the typical toroidal ITG-TEM limits familiar from normal-mode theory. We have found that the optimal modes exhibit much of the behaviour expected from normal modes, attaining a maximum growth rate (relative to the strength of the plasma gradients) when the curvature drift for both species is unfavourable and when the ratios of the diamagnetic frequencies and drift frequencies are close to unity. We have also demonstrated that the beneficial properties of maximum-$J$![]() configurations expected from normal-mode theory are also captured by the optimal modes. This was also found to be the case for another measure of turbulent transport that is valid nonlinearly, the available energy of trapped electrons (Helander Reference Helander2017; Mackenbach et al. Reference Mackenbach, Proll, Wakelkamp and Helander2023b).
configurations expected from normal-mode theory are also captured by the optimal modes. This was also found to be the case for another measure of turbulent transport that is valid nonlinearly, the available energy of trapped electrons (Helander Reference Helander2017; Mackenbach et al. Reference Mackenbach, Proll, Wakelkamp and Helander2023b).
An unexpected consequence of this work was the observation of reduced ITG mode growth rates in maximum-$J$![]() configurations in comparison with a similar minimum-$J$
configurations in comparison with a similar minimum-$J$![]() configuration when trapped electrons are included, even in the absence of a source of free energy in the electron equation. This effect, observed in both the optimal modes and the normal modes, was found to be related to the ‘inertia’ of the ITG mode, which is larger in maximum-$J$
configuration when trapped electrons are included, even in the absence of a source of free energy in the electron equation. This effect, observed in both the optimal modes and the normal modes, was found to be related to the ‘inertia’ of the ITG mode, which is larger in maximum-$J$![]() devices.
devices.
The optimal modes presented in this work could form the basis of a ‘target function’ for stellarator optimisation, given that they depend explicitly on the magnetic geometry and plasma parameters. The optimal modes studied here exhibit the effects present in the adiabatic electron optimal modes of Part 3. In particular, the two-species upper bound here shows a reduction of instability in both the ‘strongly driven’ and ‘resonant’ limits of the drive parameter $\kappa _d$![]() (or $\sigma _d$
(or $\sigma _d$![]() ); these limits are also visible in the available energy analysis of Mackenbach et al. (Reference Mackenbach, Proll, Wakelkamp and Helander2023b). This suggests that, for fixed plasma gradients, one could choose to reduce the amount of bad curvature experienced by both species thus increasing $\kappa _d$
); these limits are also visible in the available energy analysis of Mackenbach et al. (Reference Mackenbach, Proll, Wakelkamp and Helander2023b). This suggests that, for fixed plasma gradients, one could choose to reduce the amount of bad curvature experienced by both species thus increasing $\kappa _d$![]() (or $\sigma _d$
(or $\sigma _d$![]() ). Alternatively, in so-called ‘critical-gradient optimisation’, the amount of bad curvature could be increased (decreasing $\kappa _d$
). Alternatively, in so-called ‘critical-gradient optimisation’, the amount of bad curvature could be increased (decreasing $\kappa _d$![]() into the resonant limit), as performed by Roberg-Clark et al. (Reference Roberg-Clark, Plunk, Xanthopoulos, Nührenberg, Henneberg and Smith2023) for ITG-driven turbulence with adiabatic electrons. Our findings suggest that both strategies are viable for reducing the growth of instabilities including the response of trapped electrons. Moreover, as we have seen, these optimal modes capture the interaction of several physical effects associated with the maximum-$J$
into the resonant limit), as performed by Roberg-Clark et al. (Reference Roberg-Clark, Plunk, Xanthopoulos, Nührenberg, Henneberg and Smith2023) for ITG-driven turbulence with adiabatic electrons. Our findings suggest that both strategies are viable for reducing the growth of instabilities including the response of trapped electrons. Moreover, as we have seen, these optimal modes capture the interaction of several physical effects associated with the maximum-$J$![]() property and thus may directly inform the optimisation of the benefits of this property in a way that is not captured by present maximum-$J$
property and thus may directly inform the optimisation of the benefits of this property in a way that is not captured by present maximum-$J$![]() targets, which are generally not designed with turbulence in mind.
targets, which are generally not designed with turbulence in mind.
Acknowledgements
The authors would like to thank P. Helander, L. Podavini, R. Mackenbach and E. Rodríguez for their useful discussions and comments regarding this work.
Editor P. Catto thanks the referees for their advice in evaluating this article.
Funding
This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (grant agreement no. 101052200 – EUROfusion). Views and opinions expressed are those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Determining the Hermitian linear operators
The Hermitian linear operators in (5.5) can be identified from the variational problem (5.1). To make the variation of $\tilde {H}$![]() more straightforward we invert the identity (4.7) to arrive at
more straightforward we invert the identity (4.7) to arrive at

where we have defined $\alpha = 1+ \tau + \varDelta ( 1 + \tau - \varGamma _{0i})$![]() . Written in this form, all that remains is to insert $\delta \phi$
. Written in this form, all that remains is to insert $\delta \phi$![]() from quasineutrality,
from quasineutrality,
and perform the variation over $g_i$![]() and $g_e$
and $g_e$![]() , writing the result in terms of the inner product defined for each species given by (5.3) and (5.4) yielding
, writing the result in terms of the inner product defined for each species given by (5.3) and (5.4) yielding

and

from which the operators can be identified. The construction of the operators associated with $D$![]() proceeds similarly. However, due to the derivatives with respect to $l$
proceeds similarly. However, due to the derivatives with respect to $l$![]() , care must be taken when finding the operators associated with $K$
, care must be taken when finding the operators associated with $K$![]() . This involves integration by parts, and because the derivatives with $l$
. This involves integration by parts, and because the derivatives with $l$![]() are taken at constant ${E}_a$
are taken at constant ${E}_a$![]() and $\mu _a$
and $\mu _a$![]() , we require the identity given in an appendix of Plunk & Helander (Reference Plunk and Helander2023),
, we require the identity given in an appendix of Plunk & Helander (Reference Plunk and Helander2023),
After some manipulation, the Hermitian linear operators can be found to be






where we have used the moment representation given by (5.6)–(5.11). Inserting these operators into (5.5), for $a = i$![]() and $a = e$
and $a = e$![]() , gives the equation for the optimal distribution function for ions and electrons, respectively.
, gives the equation for the optimal distribution function for ions and electrons, respectively.
Appendix B. Moment form of eigenvalue problem
Here, we give the (quite lengthy) closed set of equations which arise upon taking moments of (5.5). The moment equations which come from the optimal ion distribution function equation are



Here, the functions $G_{ni} = G_{{\rm ni}}(b)$![]() come from evaluating the integrals over velocity space which contain ${\rm J}_{0i}^2$
come from evaluating the integrals over velocity space which contain ${\rm J}_{0i}^2$![]() in the integrand. We use the same notation as was used in Part 3, where, in an appendix, these functions were computed and are given as
in the integrand. We use the same notation as was used in Part 3, where, in an appendix, these functions were computed and are given as
where $\varGamma _{n}(b) = {\rm I}_n(b)\exp (-b)$![]() and ${\rm I}_n$
and ${\rm I}_n$![]() is the modified Bessel function of the first kind.
is the modified Bessel function of the first kind.
The equations which arise upon taking velocity space moments of the optimal electron distribution are



Appendix C. Eigenvalue problem in the square magnetic well
In the slow-ion-transit limit with a square magnetic trapping well, the $l$![]() -dependence of the eigenvalue problem (5.5) is trivial. This makes the system of moment equations purely algebraic, allowing us to adopt a ‘supermoment’ representation akin to that of Part 2. We define
-dependence of the eigenvalue problem (5.5) is trivial. This makes the system of moment equations purely algebraic, allowing us to adopt a ‘supermoment’ representation akin to that of Part 2. We define

where we have introduced the normalisation $\omega _{*a}' = \omega _{*a}/\omega _{*i}$![]() and $\omega _{\rm da}' = \hat {\omega }_{\rm da}/\omega _{*i}$
and $\omega _{\rm da}' = \hat {\omega }_{\rm da}/\omega _{*i}$![]() . We may also define the following velocity-space-dependent factors:
. We may also define the following velocity-space-dependent factors:

where we once again take ${\rm J}_{0e} \approx 1$![]() . If we adopt the compact notation
. If we adopt the compact notation

then (5.5) for the species ‘$a$![]() ’ can be written as
’ can be written as

Here, we have evaluated the integral,

and defined $\tilde {\alpha } = (\alpha - \Delta \tau \varepsilon (l))/(1 + \tau )$![]() . We can take moments of (C8) by multiplying by the constant $c_{mn}^{(a)}$
. We can take moments of (C8) by multiplying by the constant $c_{mn}^{(a)}$![]() and the function $\psi _{\rm ma}$
and the function $\psi _{\rm ma}$![]() , summing over the index $n$
, summing over the index $n$![]() and the species label, and integrating over velocity space to arrive at
and the species label, and integrating over velocity space to arrive at

where the factors $X_{\rm mn}^{(a)}$![]() are integrals over velocity space defined by
are integrals over velocity space defined by
where, for the electron species, the velocity space integral is carried out in the trapped region of velocity space, defined by $1/B_{\mathrm {max}} \leqslant \lambda \leqslant 1/B_{\mathrm {min}}$![]() .
.
Written in this form, the system reduces to a simple $3\times 3$![]() generalised eigenvalue problem which may be solved for the eigenvalue $\varLambda$
generalised eigenvalue problem which may be solved for the eigenvalue $\varLambda$![]() . The $X_{nm}^{(a)}$
. The $X_{nm}^{(a)}$![]() s are given by
s are given by
where the functions $G_n(b)$![]() are given in appendix B. In this simple limit, the eigenvalue problem can be solved analytically to yield
are given in appendix B. In this simple limit, the eigenvalue problem can be solved analytically to yield

where we define the following factors:
Appendix D. Linear theory
To make a comparison between the upper bounds derived here in the bounce-averaged electron response limit, we must solve the integral equation

where $\xi _i = \omega /\hat {\omega }_{{\rm di}}(l)$![]() , $\xi _e = \omega /(\overline {\hat {\omega }_{\rm de}(1 -\lambda B/2)})$
, $\xi _e = \omega /(\overline {\hat {\omega }_{\rm de}(1 -\lambda B/2)})$![]() and the ion response $R_i$
and the ion response $R_i$![]() is given by the standard expression of Biglari et al. (Reference Biglari, Diamond and Rosenbluth1989),
is given by the standard expression of Biglari et al. (Reference Biglari, Diamond and Rosenbluth1989),
where $\kappa _{{\rm di}} = \omega _{*i}/\hat {\omega }_{{\rm di}}(l)$![]() and $Y(\xi _i) = -\sqrt {\xi _i}Z(\sqrt {\xi _i})$
and $Y(\xi _i) = -\sqrt {\xi _i}Z(\sqrt {\xi _i})$![]() with $Z$
with $Z$![]() being the plasma dispersion function and where the principal branch of $\sqrt {\xi _i}$
being the plasma dispersion function and where the principal branch of $\sqrt {\xi _i}$![]() has been selected. The electron response function $R_e$
has been selected. The electron response function $R_e$![]() is
is
where $x = v/v_{\rm Te}$![]() , $\kappa _{\rm de} = \omega _{*e}/(\overline {\hat {\omega }_{\rm de}(1 -\lambda B/2)})$
, $\kappa _{\rm de} = \omega _{*e}/(\overline {\hat {\omega }_{\rm de}(1 -\lambda B/2)})$![]() and we have taken $\eta _e = 0$
and we have taken $\eta _e = 0$![]() for simplicity. Here, because the integrand is even in $x$
for simplicity. Here, because the integrand is even in $x$![]() , the integration domain can be extended to $x \in [-\infty, \infty ]$
, the integration domain can be extended to $x \in [-\infty, \infty ]$![]() . Additionally, a partial fraction expansion can be employed to yield
. Additionally, a partial fraction expansion can be employed to yield
where we have selected the principal branch of $\sqrt {\xi _e}$![]() . The above integrals can be written in terms of the standard definition of the plasma dispersion function, but care must be taken. Because we are interested in unstable eigenmodes, defined as $\mathrm {Im} \, \xi _i > 0$
. The above integrals can be written in terms of the standard definition of the plasma dispersion function, but care must be taken. Because we are interested in unstable eigenmodes, defined as $\mathrm {Im} \, \xi _i > 0$![]() (which corresponds to $\mathrm {Im}\,\xi _e < 0$
(which corresponds to $\mathrm {Im}\,\xi _e < 0$![]() ), we can express the integral in terms of the plasma dispersion function by evaluating $Z$
), we can express the integral in terms of the plasma dispersion function by evaluating $Z$![]() in the complex-conjugate plane when the imaginary component of its argument is negative and then taking the complex conjugate of the output. This avoids the contribution from analytic continuation into the lower-half of the complex plane which is included in the definition of $Z$
in the complex-conjugate plane when the imaginary component of its argument is negative and then taking the complex conjugate of the output. This avoids the contribution from analytic continuation into the lower-half of the complex plane which is included in the definition of $Z$![]() but is not relevant here;
but is not relevant here;
Which is equivalent to previous derivations by Connor et al. (Reference Connor, Hastie and Taylor1980). For this work, we only consider the solution to this equation in a square magnetic trapping well with constant curvature. In this case, $\phi = \bar {\phi }$![]() and $\hat {\omega }_{da}(l) = \mathrm {const.}$
and $\hat {\omega }_{da}(l) = \mathrm {const.}$![]() The integral over $\lambda$
The integral over $\lambda$![]() and the roots of the dispersion relation can both be computed numerically. The solution is shown in figure 5.
and the roots of the dispersion relation can both be computed numerically. The solution is shown in figure 5.