1 Introduction
Cryogenic solid-state lasers have come to the fore recently, in large part because cryogenic laser technology has been shown to be capable of providing concomitant high average and peak powers with very good beam quality and without the need for any beam-correction optics or nonlinear beam-correction schemes. The progress made has been well documented in two landmark papers[Reference Brown1, Reference Fan, Ripin, Aggarwal, Ochoa, Chann, Tilleman and Spitzberg2], and more recently in a comprehensive review of the technology[Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3], including its applicability to ultrafast lasers. In this paper, we discuss cryogenic nanosecond and picosecond lasers, the former having the potential to substantially increase the performance of traditional Ti:![]() $\text{Al}_{2}\text{O}_{3}$ lasers, and the latter to provide powerful pump sources for optical parametric chirped pulse amplification (OPCPA) systems. For nanosecond pulse durations, large laser-induced damage thresholds (LIDTs) are the norm, and one can build powerful pump sources using direct amplification only. For picosecond lasers, direct and chirped pulse amplification (CPA) approaches have been used[Reference Brown, Singley, Kowalewski, Guelzow and Vitali4, Reference Miller, Zapata, Ripin and Fan5]. For pulsewidths greater than 5–10 ps, direct amplification may be used consistent with the reduced LIDTs found for ps pulse durations; however, pulsewidths of about 1 ps are desired for pumping OPCPA systems[Reference Fattahi, Barros, Gorjan, Nubbemeyer, Alsaif, Teisset, Schultze, Prinz, Haefner, Ueffing, Alismail, Vámos, Schwarz, Pronin, Brons, Geng, Arisholm, Ciappina, Yalolev, Kim, Azzeer, Karpowicz, Sutter, Major, Metzger and Krausz6, Reference Vaupel, Bodnar, Webb, Shah and Richardson7], and to obtain large energy/pulse one must use the CPA approach, stretching low power seed lasers into the hundreds of ps or even into the ns regime to obtain larger damage thresholds, and then compressing the pulses after amplification. For short pulse ps systems, dispersion begins to play an important role, although not as important as for fs laser systems. Successful compression of 1 to a few ps pulses requires a knowledge of the dispersion accumulated in the system and the use of compression methods that compensate such dispersion.
$\text{Al}_{2}\text{O}_{3}$ lasers, and the latter to provide powerful pump sources for optical parametric chirped pulse amplification (OPCPA) systems. For nanosecond pulse durations, large laser-induced damage thresholds (LIDTs) are the norm, and one can build powerful pump sources using direct amplification only. For picosecond lasers, direct and chirped pulse amplification (CPA) approaches have been used[Reference Brown, Singley, Kowalewski, Guelzow and Vitali4, Reference Miller, Zapata, Ripin and Fan5]. For pulsewidths greater than 5–10 ps, direct amplification may be used consistent with the reduced LIDTs found for ps pulse durations; however, pulsewidths of about 1 ps are desired for pumping OPCPA systems[Reference Fattahi, Barros, Gorjan, Nubbemeyer, Alsaif, Teisset, Schultze, Prinz, Haefner, Ueffing, Alismail, Vámos, Schwarz, Pronin, Brons, Geng, Arisholm, Ciappina, Yalolev, Kim, Azzeer, Karpowicz, Sutter, Major, Metzger and Krausz6, Reference Vaupel, Bodnar, Webb, Shah and Richardson7], and to obtain large energy/pulse one must use the CPA approach, stretching low power seed lasers into the hundreds of ps or even into the ns regime to obtain larger damage thresholds, and then compressing the pulses after amplification. For short pulse ps systems, dispersion begins to play an important role, although not as important as for fs laser systems. Successful compression of 1 to a few ps pulses requires a knowledge of the dispersion accumulated in the system and the use of compression methods that compensate such dispersion.
In this paper, we first give Section 2. A succinct review of the important thermal, thermo-optic and elastic properties including figures of merit found helpful in evaluating candidate laser materials. Spectroscopic, laser, linear and nonlinear indices for a variety of legacy and newer laser materials are presented. An up-to-date compilation of most Yb-based laser materials is included. Section 3 discusses HAPP laser design considerations. In Section 3.1, we discuss the two distinctly different operating modes of cryogenic lasers: stress-limited and aberration-limited operation. For aberration-limited operation we define a very useful new performance parameter, the extracted power output per unit phase distortion, that allows for example the calculation of the expected thermal phase distortion from a laser amplifier operating at two different temperatures and identical output power, that is applied to Yb:YAG operating at 300 and 77 K. In Section 3.2, we present a new pulse-pumped extraction and kinetics model that may be used for any pump pulsewidth and repetition rate. In Section 3.3, we discuss the use of the generalized Frantz–Nodvik equation. In Section 3.4, we present a review of the calculational methods that may be employed for the accumulated nonlinear phase (![]() $B$-integral) in a laser amplifier, using the Frantz–Nodvik equation. A discussion of LIDTs is shown in Section 3.5 and some sample results from a first-order ray-tracing extraction code developed to aid in the design of HAPP cryogenic laser systems are presented in Section 3.6. Finally, in Section 4, we summarize the results contained in this article.
$B$-integral) in a laser amplifier, using the Frantz–Nodvik equation. A discussion of LIDTs is shown in Section 3.5 and some sample results from a first-order ray-tracing extraction code developed to aid in the design of HAPP cryogenic laser systems are presented in Section 3.6. Finally, in Section 4, we summarize the results contained in this article.
2 Review of important laser materials properties
The development of modern cryogenic solid-state lasers began with the publications of the first experimental cryogenic Yb:YAG laser[Reference Lacovara, Choi, Wang, Aggarwal and Fan8], and a significantly performance-enhanced Ti:![]() $\text{Al}_{2}\text{O}_{3}$ laser[Reference Schulz9], both in 1991. Subsequent theoretical and experimental work confirmed that not only can enhanced laser properties be obtained by cryogenic cooling, but that dramatic reductions in thermo-optic distortion and enhanced mechanical properties can be realized as well[Reference Brown1–Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3, Reference Brown10–Reference Glur, Lavi and Graf14]. Cryogenic cooling was employed prior to 1991; however, thermo-optic properties were not emphasized and the focus was mainly on laser physics, kinetics and spectroscopy. Since 1991, laser physicists, designers and engineers have for the first time fully appreciated that the entire set of physical crystal properties (optical, laser kinetics, thermal, thermo-optic, and elastic) must be taken into account to effect successful laser outcomes. Appreciation of this reality has and will continue to drive the demonstration of much higher average power cryogenic lasers, as well as HAPP lasers, in the future. The manipulation of the thermo-optic properties of solid-state laser hosts through the use of cryogenic cooling has been proven capable of providing both high average power and near-vanishing thermally induced aberrations. This results in output beams whose divergence and transverse beam size are virtually constant, without the use of any external beam correction. Beam-parameter-independent lasers are highly desirable for harmonic generation, as well as for many other scientific, commercial and military applications.
$\text{Al}_{2}\text{O}_{3}$ laser[Reference Schulz9], both in 1991. Subsequent theoretical and experimental work confirmed that not only can enhanced laser properties be obtained by cryogenic cooling, but that dramatic reductions in thermo-optic distortion and enhanced mechanical properties can be realized as well[Reference Brown1–Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3, Reference Brown10–Reference Glur, Lavi and Graf14]. Cryogenic cooling was employed prior to 1991; however, thermo-optic properties were not emphasized and the focus was mainly on laser physics, kinetics and spectroscopy. Since 1991, laser physicists, designers and engineers have for the first time fully appreciated that the entire set of physical crystal properties (optical, laser kinetics, thermal, thermo-optic, and elastic) must be taken into account to effect successful laser outcomes. Appreciation of this reality has and will continue to drive the demonstration of much higher average power cryogenic lasers, as well as HAPP lasers, in the future. The manipulation of the thermo-optic properties of solid-state laser hosts through the use of cryogenic cooling has been proven capable of providing both high average power and near-vanishing thermally induced aberrations. This results in output beams whose divergence and transverse beam size are virtually constant, without the use of any external beam correction. Beam-parameter-independent lasers are highly desirable for harmonic generation, as well as for many other scientific, commercial and military applications.
We have recently provided a detailed comprehensive review of the important thermal, thermo-optic, elastic, laser, optical, nonlinear and dispersion effects for a number of laser materials[Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3], and will not repeat that discussion here. Previous publications also provide a wealth of information[Reference Brown1–Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3, Reference Fan and Daneu15–Reference Cardinalli, Marmois, Le Garrec and Bourdet22]. It is now well known that the value of the thermal conductivity increases as temperature is lowered, for all measured single crystals as well as for their ceramic counterparts. The increase in thermal conductivity is however reduced in some materials as the rare-earth doping density is increased[Reference Aggarwal, Ripin, Ochoa and Fan18, Reference McMillen, Thompson, Tritt and Kolis23]. The two other major determinants of the magnitude of thermally induced aberrations, the thermal expansion coefficient, and the thermo-optic coefficient ![]() $(dn/dT)$, have also been found to be dramatically decreased in most single-crystal and ceramic optical and laser materials as temperature is lowered[Reference Brown1, Reference Fan, Ripin, Aggarwal, Ochoa, Chann, Tilleman and Spitzberg2, Reference Fan and Daneu15, Reference Wynne, Daneu and Fan16, Reference Aggarwal, Ripin, Ochoa and Fan18, Reference Rand, Miller, Ripin and Fan19]. In combination, the net result is that at temperatures of
$(dn/dT)$, have also been found to be dramatically decreased in most single-crystal and ceramic optical and laser materials as temperature is lowered[Reference Brown1, Reference Fan, Ripin, Aggarwal, Ochoa, Chann, Tilleman and Spitzberg2, Reference Fan and Daneu15, Reference Wynne, Daneu and Fan16, Reference Aggarwal, Ripin, Ochoa and Fan18, Reference Rand, Miller, Ripin and Fan19]. In combination, the net result is that at temperatures of ![]() ${<}100~\text{K}$, the thermal aberrations are reduced in most cases by at least one order of magnitude. In addition, thermally induced stresses are nearly eliminated, significantly increasing the value of the rupture modulus and leading to only residual values for the stress-induced contribution to thermal aberrations. Section 2.1 provides a summary, in graphical form, of much of the recently published data for the thermal conductivity, thermo-optic coefficient and thermal expansion coefficient. In Section 2.2, we present recently derived figures of merits for thermal and stress effects[Reference Brown1]. A summary of relevant laser material elastic parameters can be found in Section 2.3. Section 2.4 presents calculations of the figures of merit for temperatures of 300 and 77 K. In Section 2.5, we discuss the spectral and laser parameters for a number of laser materials at 300 and 77 K, and summarized in Table 3. Section 2.6 contains a brief discussion of the intensity-dependent nonlinear index of refraction and nonlinear coefficient; Table 4 summarizes many known values for the linear index, nonlinear index and nonlinear coefficients for various laser and optical materials.
${<}100~\text{K}$, the thermal aberrations are reduced in most cases by at least one order of magnitude. In addition, thermally induced stresses are nearly eliminated, significantly increasing the value of the rupture modulus and leading to only residual values for the stress-induced contribution to thermal aberrations. Section 2.1 provides a summary, in graphical form, of much of the recently published data for the thermal conductivity, thermo-optic coefficient and thermal expansion coefficient. In Section 2.2, we present recently derived figures of merits for thermal and stress effects[Reference Brown1]. A summary of relevant laser material elastic parameters can be found in Section 2.3. Section 2.4 presents calculations of the figures of merit for temperatures of 300 and 77 K. In Section 2.5, we discuss the spectral and laser parameters for a number of laser materials at 300 and 77 K, and summarized in Table 3. Section 2.6 contains a brief discussion of the intensity-dependent nonlinear index of refraction and nonlinear coefficient; Table 4 summarizes many known values for the linear index, nonlinear index and nonlinear coefficients for various laser and optical materials.

Figure 1. Thermal conductivity for ![]() $\text{Al}_{2}\text{O}_{3}$ as a function of temperature for the
$\text{Al}_{2}\text{O}_{3}$ as a function of temperature for the ![]() $c$-axis (green circles) and the
$c$-axis (green circles) and the ![]() $a$-axis (blue squares); also shown are the thermal expansion coefficient values for the
$a$-axis (blue squares); also shown are the thermal expansion coefficient values for the ![]() $c$-axis (pink triangles) and the
$c$-axis (pink triangles) and the ![]() $a$-axis (red squares).
$a$-axis (red squares).
2.1 Thermal conductivity, thermal expansion coefficient and thermo-optic coefficient
In this section, we present published numerical data for the thermal conductivity ![]() $k$, thermal expansion coefficient
$k$, thermal expansion coefficient ![]() ${\it\alpha}$, and the thermo-optic coefficient
${\it\alpha}$, and the thermo-optic coefficient ![]() $(dn/dT)$, all on the same graph, as a function of absolute temperature, for a number of anaxial, uniaxial and biaxial laser materials. All the materials presented here have published complete datasets between 300 and 77 K or lower, with the exception of
$(dn/dT)$, all on the same graph, as a function of absolute temperature, for a number of anaxial, uniaxial and biaxial laser materials. All the materials presented here have published complete datasets between 300 and 77 K or lower, with the exception of ![]() $\text{Al}_{2}\text{O}_{3}$ for which little
$\text{Al}_{2}\text{O}_{3}$ for which little ![]() $(dn/dT)$ data is known. We do not include single value data points that may be found in the literature, with the exception of
$(dn/dT)$ data is known. We do not include single value data points that may be found in the literature, with the exception of ![]() $\text{Al}_{2}\text{O}_{3}$. The thermal conductivity values are, except where noted, for un-doped crystals only. Those parameters are most important in determining the value of the low temperature thermal aberrations and play a significant role in scaling the average power of solid-state lasers at cryogenic temperatures. This data, as well as data presented in Section 2.3 for Young’s modulus and Poisson’s ratio, are used in Section 2.4 to calculate figures of merit that may be used to compare various laser materials.
$\text{Al}_{2}\text{O}_{3}$. The thermal conductivity values are, except where noted, for un-doped crystals only. Those parameters are most important in determining the value of the low temperature thermal aberrations and play a significant role in scaling the average power of solid-state lasers at cryogenic temperatures. This data, as well as data presented in Section 2.3 for Young’s modulus and Poisson’s ratio, are used in Section 2.4 to calculate figures of merit that may be used to compare various laser materials.
Figure 1 shows the thermal conductivity for ![]() $\text{Al}_{2}\text{O}_{3}$ along the
$\text{Al}_{2}\text{O}_{3}$ along the ![]() $a$ and
$a$ and ![]() $c$ axes[Reference Touloukian, Kirby, Taylor and Lee24], as well as the thermal expansion coefficient along the same axes[Reference Reeber and Wang25], both as a function of absolute temperature. The thermal conductivity increases for both axes from a value of about
$c$ axes[Reference Touloukian, Kirby, Taylor and Lee24], as well as the thermal expansion coefficient along the same axes[Reference Reeber and Wang25], both as a function of absolute temperature. The thermal conductivity increases for both axes from a value of about ![]() $0.36~\text{W}/(\text{cm}~\text{K})$ near room temperature to about
$0.36~\text{W}/(\text{cm}~\text{K})$ near room temperature to about ![]() $7.35~\text{W}/(\text{cm}~\text{K})$ at 80 K. The thermal expansion coefficient of the
$7.35~\text{W}/(\text{cm}~\text{K})$ at 80 K. The thermal expansion coefficient of the ![]() $c$-axis is reduced from about
$c$-axis is reduced from about ![]() $5.9\times 10^{-6}/\text{K}$ at room temperature to about
$5.9\times 10^{-6}/\text{K}$ at room temperature to about ![]() $0.38\times 10^{-6}/\text{K}$ at 80 K.
$0.38\times 10^{-6}/\text{K}$ at 80 K. ![]() $(dn/dT)$ values can be estimated at 300 and 77 K from literature values[Reference Schulz9], but are not shown in Figure 1. In Figure 2, we show thermal conductivity
$(dn/dT)$ values can be estimated at 300 and 77 K from literature values[Reference Schulz9], but are not shown in Figure 1. In Figure 2, we show thermal conductivity ![]() $k$, thermal expansion coefficient
$k$, thermal expansion coefficient ![]() ${\it\alpha}$, and thermo-optic coefficient
${\it\alpha}$, and thermo-optic coefficient ![]() ${\it\beta}$ as a function of absolute temperature for the legacy anaxial laser material YAG[Reference Aggarwal, Ripin, Ochoa and Fan18]. Figure 3 shows
${\it\beta}$ as a function of absolute temperature for the legacy anaxial laser material YAG[Reference Aggarwal, Ripin, Ochoa and Fan18]. Figure 3 shows ![]() $k$,
$k$, ![]() ${\it\alpha}$ and
${\it\alpha}$ and ![]() ${\it\beta}$ for the homologous laser material Yb:LuAG[Reference Aggarwal, Ripin, Ochoa and Fan18]. Both YAG and LuAG display very similar functional dependences, and both experience increased thermal conductivities and reduced thermal expansion and thermo-optic coefficients as temperature is lowered. Figure 4 plots
${\it\beta}$ for the homologous laser material Yb:LuAG[Reference Aggarwal, Ripin, Ochoa and Fan18]. Both YAG and LuAG display very similar functional dependences, and both experience increased thermal conductivities and reduced thermal expansion and thermo-optic coefficients as temperature is lowered. Figure 4 plots ![]() $k$,
$k$, ![]() ${\it\alpha}$ and
${\it\alpha}$ and ![]() ${\it\beta}$ for the fluoride uniaxial laser material YLF[Reference Aggarwal, Ripin, Ochoa and Fan18], along the
${\it\beta}$ for the fluoride uniaxial laser material YLF[Reference Aggarwal, Ripin, Ochoa and Fan18], along the ![]() $a$ and
$a$ and ![]() $c$ axes. For this laser material, the thermo-optic coefficients are negative, converging toward 0 as temperature is lowered. This same behavior is seen for the homologous laser material LuLF in Figure 5; however, for LuLF the thermo-optic coefficient displays a more complicated behavior[Reference Aggarwal, Ripin, Ochoa and Fan18]. Both YLF and LuLF display increasing thermal conductivities and decreasing thermal expansion coefficients as temperature is lowered. In Figure 6, we show
$c$ axes. For this laser material, the thermo-optic coefficients are negative, converging toward 0 as temperature is lowered. This same behavior is seen for the homologous laser material LuLF in Figure 5; however, for LuLF the thermo-optic coefficient displays a more complicated behavior[Reference Aggarwal, Ripin, Ochoa and Fan18]. Both YLF and LuLF display increasing thermal conductivities and decreasing thermal expansion coefficients as temperature is lowered. In Figure 6, we show ![]() $k$,
$k$, ![]() ${\it\alpha}$ and
${\it\alpha}$ and ![]() ${\it\beta}$ for the biaxial oxide laser material YALO (YAP)[Reference Aggarwal, Ripin, Ochoa and Fan18]; values for the three parameters are plotted for the
${\it\beta}$ for the biaxial oxide laser material YALO (YAP)[Reference Aggarwal, Ripin, Ochoa and Fan18]; values for the three parameters are plotted for the ![]() $a,b$ and
$a,b$ and ![]() $c$ axes. For each axis we see an increasing thermal conductivity and decreasing values of the thermal expansion and thermo-optic coefficients as temperature is lowered, similar to the oxide materials YAG and LuAG. Figures 7 and 8 show
$c$ axes. For each axis we see an increasing thermal conductivity and decreasing values of the thermal expansion and thermo-optic coefficients as temperature is lowered, similar to the oxide materials YAG and LuAG. Figures 7 and 8 show ![]() $k$,
$k$, ![]() ${\it\alpha}$ and
${\it\alpha}$ and ![]() ${\it\beta}$ for the anaxial sesquioxide laser materials
${\it\beta}$ for the anaxial sesquioxide laser materials ![]() $\text{Y}_{2}\text{O}_{3}$[Reference Fan, Ripin, Aggarwal, Ochoa, Chann, Tilleman and Spitzberg2, Reference Cardinalli, Marmois, Le Garrec and Bourdet22] and
$\text{Y}_{2}\text{O}_{3}$[Reference Fan, Ripin, Aggarwal, Ochoa, Chann, Tilleman and Spitzberg2, Reference Cardinalli, Marmois, Le Garrec and Bourdet22] and ![]() $\text{Sc}_{2}\text{O}_{3}$[Reference Fan, Ripin, Aggarwal, Ochoa, Chann, Tilleman and Spitzberg2, Reference McMillen, Thompson, Tritt and Kolis23]. Figure 9 plots
$\text{Sc}_{2}\text{O}_{3}$[Reference Fan, Ripin, Aggarwal, Ochoa, Chann, Tilleman and Spitzberg2, Reference McMillen, Thompson, Tritt and Kolis23]. Figure 9 plots ![]() $k$,
$k$, ![]() ${\it\alpha}$ and
${\it\alpha}$ and ![]() ${\it\beta}$ for the uniaxial laser material
${\it\beta}$ for the uniaxial laser material ![]() $\text{GdVO}_{4}$[Reference Fan, Ripin, Aggarwal, Ochoa, Chann, Tilleman and Spitzberg2, Reference Rand, Miller, Ripin and Fan19].
$\text{GdVO}_{4}$[Reference Fan, Ripin, Aggarwal, Ochoa, Chann, Tilleman and Spitzberg2, Reference Rand, Miller, Ripin and Fan19].

Figure 2. YAG thermal conductivity (blue diamonds), thermal expansion coefficient (red squares) and ![]() $(dn/dT)$ (green triangles) as a function of absolute temperature.
$(dn/dT)$ (green triangles) as a function of absolute temperature.

Figure 3. LuAG thermal conductivity (red squares), thermal expansion coefficient (blue diamonds) and ![]() $(dn/dT)$ (green triangles) as a function of absolute temperature.
$(dn/dT)$ (green triangles) as a function of absolute temperature.

Figure 4. YLF thermal conductivity along ![]() $a$-axis (blue diamonds) and
$a$-axis (blue diamonds) and ![]() $c$-axis (green triangles), thermal expansion coefficient along
$c$-axis (green triangles), thermal expansion coefficient along ![]() $a$-axis (red squares) and
$a$-axis (red squares) and ![]() $c$-axis (black diamonds), and
$c$-axis (black diamonds), and ![]() $(dn/dT)$ along the
$(dn/dT)$ along the ![]() $a$-axis (pink circles) and the
$a$-axis (pink circles) and the ![]() $c$-axis (orange circles), all as a function of absolute temperature.
$c$-axis (orange circles), all as a function of absolute temperature.

Figure 5. LuLF thermal conductivity along ![]() $a$-axis (blue diamonds) and
$a$-axis (blue diamonds) and ![]() $c$-axis (green triangles), thermal expansion coefficient along
$c$-axis (green triangles), thermal expansion coefficient along ![]() $a$-axis (red squares) and
$a$-axis (red squares) and ![]() $c$-axis (black triangles), and
$c$-axis (black triangles), and ![]() $(dn/dT)$ along the
$(dn/dT)$ along the ![]() $a$-axis (pink circles) and the
$a$-axis (pink circles) and the ![]() $c$-axis (orange circles), all as a function of absolute temperature.
$c$-axis (orange circles), all as a function of absolute temperature.

Figure 6. YALO thermal conductivity along ![]() $a$-axis (blue diamonds),
$a$-axis (blue diamonds), ![]() $b$-axis (red squares) and
$b$-axis (red squares) and ![]() $c$-axis (green triangles), thermal expansion coefficient along the
$c$-axis (green triangles), thermal expansion coefficient along the ![]() $a$-axis (black crosses),
$a$-axis (black crosses), ![]() $b$-axis (blue squares) and
$b$-axis (blue squares) and ![]() $c$-axis (long dashes), and
$c$-axis (long dashes), and ![]() $(dn/dT)$ along the
$(dn/dT)$ along the ![]() $a$-axis (light blue diamonds),
$a$-axis (light blue diamonds), ![]() $b$-axis (short dashes) and
$b$-axis (short dashes) and ![]() $c\text{-}\text{axis}(\text{pink}~\text{triangles})$, all as a function of absolute temperature.
$c\text{-}\text{axis}(\text{pink}~\text{triangles})$, all as a function of absolute temperature.

Figure 7. ![]() $\text{Y}_{2}\text{O}_{3}$ thermal conductivity (red circles), thermal expansion coefficient (blue diamonds) and
$\text{Y}_{2}\text{O}_{3}$ thermal conductivity (red circles), thermal expansion coefficient (blue diamonds) and ![]() $(dn/dT)$ (green triangles) as a function of absolute temperature.
$(dn/dT)$ (green triangles) as a function of absolute temperature.

Figure 8. ![]() $\text{Sc}_{2}\text{O}_{3}$ thermal conductivity (blue circles), thermal expansion coefficient (green diamonds) and
$\text{Sc}_{2}\text{O}_{3}$ thermal conductivity (blue circles), thermal expansion coefficient (green diamonds) and ![]() $(dn/dT)$ (red squares) as a function of absolute temperature.
$(dn/dT)$ (red squares) as a function of absolute temperature.

Figure 9. ![]() $\text{GdVO}_{4}$ thermal conductivity along
$\text{GdVO}_{4}$ thermal conductivity along ![]() $a$-axis (blue diamonds) and
$a$-axis (blue diamonds) and ![]() $c$-axis (green triangles), thermal expansion coefficient along
$c$-axis (green triangles), thermal expansion coefficient along ![]() $a$-axis (black triangles) and
$a$-axis (black triangles) and ![]() $c$-axis (red triangles), and
$c$-axis (red triangles), and ![]() $(dn/dT)$ along the
$(dn/dT)$ along the ![]() $a$-axis (orange circles) and the
$a$-axis (orange circles) and the ![]() $c$-axis (pink squares), all as a function of absolute temperature.
$c$-axis (pink squares), all as a function of absolute temperature.

Figure 10. ![]() $\text{CaF}_{2}$ thermal conductivity (red squares, blue diamonds and pink circles), thermal expansion coefficient green triangles) and
$\text{CaF}_{2}$ thermal conductivity (red squares, blue diamonds and pink circles), thermal expansion coefficient green triangles) and ![]() $(dn/dT)$ (black circles) as a function of absolute temperature.
$(dn/dT)$ (black circles) as a function of absolute temperature.
Finally, in Figure 10 we show measured values of ![]() $k$,
$k$, ![]() ${\it\alpha}$ and
${\it\alpha}$ and ![]() ${\it\beta}$[Reference Le Garrec, Cardinali and Bourdet21, Reference Cardinalli, Marmois, Le Garrec and Bourdet22, Reference Nikogosyan26, Reference Slack27] for the anaxial laser and optical material
${\it\beta}$[Reference Le Garrec, Cardinali and Bourdet21, Reference Cardinalli, Marmois, Le Garrec and Bourdet22, Reference Nikogosyan26, Reference Slack27] for the anaxial laser and optical material ![]() $\text{CaF}_{2}$. The values of
$\text{CaF}_{2}$. The values of ![]() ${\it\alpha}$ and
${\it\alpha}$ and ![]() ${\it\beta}$ were measured at a wavelength of 632.8 nm[Reference Cardinalli, Marmois, Le Garrec and Bourdet22]. Like other laser materials, the thermal conductivity increases and the thermal expansion coefficient decreases as temperature is lowered. The values of
${\it\beta}$ were measured at a wavelength of 632.8 nm[Reference Cardinalli, Marmois, Le Garrec and Bourdet22]. Like other laser materials, the thermal conductivity increases and the thermal expansion coefficient decreases as temperature is lowered. The values of ![]() ${\it\beta}$ however, are negative and show a complicated temperature dependence. Yb:
${\it\beta}$ however, are negative and show a complicated temperature dependence. Yb:![]() $\text{CaF}_{2}$ has been shown to be a laser material with much promise as an ultrafast laser, capable of reaching pulsewidths
$\text{CaF}_{2}$ has been shown to be a laser material with much promise as an ultrafast laser, capable of reaching pulsewidths ![]() ${<}100~\text{fs}$[Reference Friebel, Druon, Boudeile, Papadopoulus, Hanna, Georges, Camy, Doualon, Benayad, Moncorgé, Cassagne and Boudebs28]. As discussed in more detail in Refs. [Reference Le Garrec, Cardinali and Bourdet21, Reference Popov, Federov, Kuznetsov, Konyushkin, Osiko and Basiev29], however, very low Yb doping levels lead to clustering and to a reduction in thermal conductivity as temperature is lowered. It has been surmised that
${<}100~\text{fs}$[Reference Friebel, Druon, Boudeile, Papadopoulus, Hanna, Georges, Camy, Doualon, Benayad, Moncorgé, Cassagne and Boudebs28]. As discussed in more detail in Refs. [Reference Le Garrec, Cardinali and Bourdet21, Reference Popov, Federov, Kuznetsov, Konyushkin, Osiko and Basiev29], however, very low Yb doping levels lead to clustering and to a reduction in thermal conductivity as temperature is lowered. It has been surmised that ![]() $\text{CaF}_{2}$ in that situation transitions from a crystalline to a glassy state, thus displaying the characteristic reduction in thermal conductivity as temperature is lowered. Such behavior is well known for
$\text{CaF}_{2}$ in that situation transitions from a crystalline to a glassy state, thus displaying the characteristic reduction in thermal conductivity as temperature is lowered. Such behavior is well known for ![]() $\text{SiO}_{2}$, for example[Reference Brown1].
$\text{SiO}_{2}$, for example[Reference Brown1].
2.2 Thermal and stress figures of merit
For the case where a major design goal is to eliminate or reduce aberrations to residual levels, we can define two figures of merit ![]() ${\rm\Gamma}$ as follows[Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3]:
${\rm\Gamma}$ as follows[Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3]:
Figure of merit ![]() ${\rm\Gamma}_{T}$ addresses changes in the index of refraction due to temperature gradients, and
${\rm\Gamma}_{T}$ addresses changes in the index of refraction due to temperature gradients, and ![]() ${\rm\Gamma}_{S}$ applies to changes in the index due to stress (or strain) effects. For a detailed discussion of Equations (1) and (2) please consult[Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3]. To reduce thermal aberrations, we wish to maximize the value of
${\rm\Gamma}_{S}$ applies to changes in the index due to stress (or strain) effects. For a detailed discussion of Equations (1) and (2) please consult[Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3]. To reduce thermal aberrations, we wish to maximize the value of ![]() ${\rm\Gamma}_{T}$. This is achieved by maximizing the value of
${\rm\Gamma}_{T}$. This is achieved by maximizing the value of ![]() $k$ to minimize the thermal gradients, minimizing the values of
$k$ to minimize the thermal gradients, minimizing the values of ![]() ${\it\alpha}$ and
${\it\alpha}$ and ![]() ${\it\beta}$, and by minimizing the amount of heat generated by minimizing the value of the total heat fraction
${\it\beta}$, and by minimizing the amount of heat generated by minimizing the value of the total heat fraction ![]() ${\it\eta}_{h}$. Minimizing the thermal expansion coefficient
${\it\eta}_{h}$. Minimizing the thermal expansion coefficient ![]() ${\it\alpha}$ minimizes thermal distortions in large aspect ratio, rod lasers (plane-strain approximation) in which the bulging of the end faces is ignored. However, since end face bulging is primarily due to the thermal expansion, minimizing
${\it\alpha}$ minimizes thermal distortions in large aspect ratio, rod lasers (plane-strain approximation) in which the bulging of the end faces is ignored. However, since end face bulging is primarily due to the thermal expansion, minimizing ![]() ${\it\alpha}$ also minimizes the magnitude of the bulging as well. The heat fraction is formally defined as the fraction of the absorbed light converted to heat. It includes contributions from the quantum defect, fluorescence and stimulated emission. Yb-based materials are particularly attractive for producing low
${\it\alpha}$ also minimizes the magnitude of the bulging as well. The heat fraction is formally defined as the fraction of the absorbed light converted to heat. It includes contributions from the quantum defect, fluorescence and stimulated emission. Yb-based materials are particularly attractive for producing low ![]() ${\it\eta}_{h}$ values, due to the lack of concentration-quenching, excited-state absorption and upconversion, processes that plague other laser materials like Nd:YAG or Nd:
${\it\eta}_{h}$ values, due to the lack of concentration-quenching, excited-state absorption and upconversion, processes that plague other laser materials like Nd:YAG or Nd:![]() $\text{YVO}_{4}$ and Nd:YLF, for example. The thermal conductivity
$\text{YVO}_{4}$ and Nd:YLF, for example. The thermal conductivity ![]() $k$, thermal expansion coefficient
$k$, thermal expansion coefficient ![]() ${\it\alpha}$ and thermo-optic coefficient
${\it\alpha}$ and thermo-optic coefficient ![]() ${\it\beta}$ were previously defined and discussed in Section 2.1.
${\it\beta}$ were previously defined and discussed in Section 2.1.
Table 1. Young’s modulus, bulk modulus and Poisson’s ratio for selected laser materials (from Ref. [Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3]).

Equation (2) is the figure of merit for considering stress effects only. It arises naturally from the consideration of the stresses generated in laser crystals due to thermal gradients. Calculation shows[Reference Brown11] that the obtained thermally induced stress in laser materials is proportional to the heat density ![]() $Q_{0}$ and inversely proportional to
$Q_{0}$ and inversely proportional to ![]() $M_{s}$, a quantity known as the materials parameter, expressed as
$M_{s}$, a quantity known as the materials parameter, expressed as
where ![]() $E$ is Young’s modulus and
$E$ is Young’s modulus and ![]() ${\it\nu}$ Poisson’s ratio. The materials parameter is then a mixture of thermal and elastic constants. To reduce the stress one wants to maximize the value of
${\it\nu}$ Poisson’s ratio. The materials parameter is then a mixture of thermal and elastic constants. To reduce the stress one wants to maximize the value of ![]() $M_{s}$, and that is the motivation for the use of the figure of merit
$M_{s}$, and that is the motivation for the use of the figure of merit ![]() ${\rm\Gamma}_{S}$. To minimize stress contributions to the change in the index of refraction, the appropriate strategy is to maximize
${\rm\Gamma}_{S}$. To minimize stress contributions to the change in the index of refraction, the appropriate strategy is to maximize ![]() $k$, minimize
$k$, minimize ![]() ${\it\alpha}$,
${\it\alpha}$, ![]() $E$ and
$E$ and ![]() ${\it\eta}_{h}$, and minimize the value of
${\it\eta}_{h}$, and minimize the value of ![]() ${\it\nu}$. While other similar figures of merit have been used[Reference Fan, Ripin, Aggarwal, Ochoa, Chann, Tilleman and Spitzberg2], we prefer our approach where the contributing factors to the change in index of refraction from purely thermal effects and thermally induced stress are clearly separated. If desired, however, after eliminating duplicate parameters we can write a simple overall multiplicative figure of merit
${\it\nu}$. While other similar figures of merit have been used[Reference Fan, Ripin, Aggarwal, Ochoa, Chann, Tilleman and Spitzberg2], we prefer our approach where the contributing factors to the change in index of refraction from purely thermal effects and thermally induced stress are clearly separated. If desired, however, after eliminating duplicate parameters we can write a simple overall multiplicative figure of merit ![]() ${\rm\Gamma}$ as
${\rm\Gamma}$ as
Laser materials with the highest figure of merit therefore should have a large value for ![]() $M_{S}$, and minimum values for
$M_{S}$, and minimum values for ![]() ${\it\beta}$ and
${\it\beta}$ and ![]() ${\it\eta}_{h}$. Values of the figures of merit are provided for a number of laser materials in Section 2.4 at 300 and 100 K.
${\it\eta}_{h}$. Values of the figures of merit are provided for a number of laser materials in Section 2.4 at 300 and 100 K.
2.3 Elastic parameters
The elastic parameters Young’s Modulus (![]() $E$), Poisson’s ratio (
$E$), Poisson’s ratio (![]() ${\it\nu}$), the bulk modulus
${\it\nu}$), the bulk modulus ![]() $B$ and the related moduli
$B$ and the related moduli ![]() $K$ and
$K$ and ![]() $G$ have been investigated by a number of researchers. The most comprehensive study was published by Munro[Reference Munro30] who treated single-crystal and ceramic materials with varying porosity, and whose data for single crystals we include in Table 1, which lists values for
$G$ have been investigated by a number of researchers. The most comprehensive study was published by Munro[Reference Munro30] who treated single-crystal and ceramic materials with varying porosity, and whose data for single crystals we include in Table 1, which lists values for ![]() $E_{0}$ (0 K),
$E_{0}$ (0 K), ![]() $a$,
$a$, ![]() $E$ (300 K),
$E$ (300 K), ![]() ${\it\nu}$ and
${\it\nu}$ and ![]() $B$. In Ref. [Reference Munro30], the Young’s modulus values were generated for a temperature of absolute zero, and the values at higher temperatures are determined using the relationship
$B$. In Ref. [Reference Munro30], the Young’s modulus values were generated for a temperature of absolute zero, and the values at higher temperatures are determined using the relationship
where ![]() $E$ is Young’s modulus at temperature
$E$ is Young’s modulus at temperature ![]() $T$ and
$T$ and ![]() $a$ is a constant. The bulk moduli values
$a$ is a constant. The bulk moduli values ![]() $B_{0}$ and
$B_{0}$ and ![]() $B$ at 300 K in Table 2 are taken from Ref. [Reference Munro30] as well, with
$B$ at 300 K in Table 2 are taken from Ref. [Reference Munro30] as well, with ![]() $B(T)$ calculated from the relationship
$B(T)$ calculated from the relationship
Other values in Table 2 were obtained from Refs. [Reference Zhou, Xiang and Feng31, Reference Krupke, Shinn, Marion, Caird and Stokowski32]. The Poisson’s ratio values in Table 2 were either calculated at 300 K using the relationship
or taken from Ref. [Reference Zhou, Xiang and Feng31, Reference Krupke, Shinn, Marion, Caird and Stokowski32].
Table 2. Thermal conductivity ![]() $k$, thermal expansion coefficient
$k$, thermal expansion coefficient ![]() ${\it\alpha}$, thermo-optic coefficient
${\it\alpha}$, thermo-optic coefficient ![]() ${\it\beta}$, quantum-defect heat fraction
${\it\beta}$, quantum-defect heat fraction ![]() ${\it\eta}_{h}^{\text{QD}}$, Poisson’s ratio
${\it\eta}_{h}^{\text{QD}}$, Poisson’s ratio ![]() ${\it\nu}$, Young’s modulus
${\it\nu}$, Young’s modulus ![]() $E$, and calculated figures of merit
$E$, and calculated figures of merit ![]() ${\rm\Gamma}_{T}$,
${\rm\Gamma}_{T}$, ![]() ${\rm\Gamma}_{S}$ and
${\rm\Gamma}_{S}$ and ![]() ${\rm\Gamma}$ for selected laser crystals at 100 and 300 K. Absolute values of negative parameter values were used to calculate figures of merit. Table is reproduced from Ref. [Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3].
${\rm\Gamma}$ for selected laser crystals at 100 and 300 K. Absolute values of negative parameter values were used to calculate figures of merit. Table is reproduced from Ref. [Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3].

* Estimated values.
2.4 Figures-of-merit calculations
Table 2 shows the values of ![]() $k$,
$k$, ![]() ${\it\alpha}$,
${\it\alpha}$, ![]() ${\it\beta}$,
${\it\beta}$, ![]() ${\it\nu}$ and
${\it\nu}$ and ![]() $E$ at 300 and 100 K. The heat fraction was in all cases for simple comparison taken equal to the quantum-defect value. The figures of merit
$E$ at 300 and 100 K. The heat fraction was in all cases for simple comparison taken equal to the quantum-defect value. The figures of merit ![]() ${\rm\Gamma}_{T}$,
${\rm\Gamma}_{T}$, ![]() ${\rm\Gamma}_{S}$ and
${\rm\Gamma}_{S}$ and ![]() ${\rm\Gamma}$ are also shown at 300 and 100 K. Large increases in the figures of merit are obtained at 100 K relative to 300 K. Materials like YAG,
${\rm\Gamma}$ are also shown at 300 and 100 K. Large increases in the figures of merit are obtained at 100 K relative to 300 K. Materials like YAG, ![]() $\text{Sc}_{2}\text{O}_{3}$, the
$\text{Sc}_{2}\text{O}_{3}$, the ![]() $c$-axis of YLF, the
$c$-axis of YLF, the ![]() $a$-axis of YALO and the
$a$-axis of YALO and the ![]() $a$ and
$a$ and ![]() $c$ axes of
$c$ axes of ![]() $\text{Al}_{2}\text{O}_{3}$ show the largest increases in the figures of merit, while
$\text{Al}_{2}\text{O}_{3}$ show the largest increases in the figures of merit, while ![]() $\text{CaF}_{2}$ shows the smallest increase. We can conclude from this simple comparison that the most suitable materials for high-average-power and HAPP cryogenic lasers, of the materials investigated to date, are YAG, YLF, YALO,
$\text{CaF}_{2}$ shows the smallest increase. We can conclude from this simple comparison that the most suitable materials for high-average-power and HAPP cryogenic lasers, of the materials investigated to date, are YAG, YLF, YALO, ![]() $\text{Sc}_{2}\text{O}_{3}$ and
$\text{Sc}_{2}\text{O}_{3}$ and ![]() $\text{Al}_{2}\text{O}_{3}$.
$\text{Al}_{2}\text{O}_{3}$. ![]() $\text{CaF}_{2}$ on the other hand may be very useful as a low-average-power mode-locked laser material (Yb:
$\text{CaF}_{2}$ on the other hand may be very useful as a low-average-power mode-locked laser material (Yb:![]() $\text{CaF}_{2}$), but is unlikely to be used for amplifiers in HAPP cryogenic laser systems.
$\text{CaF}_{2}$), but is unlikely to be used for amplifiers in HAPP cryogenic laser systems.
2.5 Spectroscopic and lasing parameters
Table 3, taken from Ref. [Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3], shows the spectral properties of a number of important laser materials, including a number of legacy ultrafast materials as well as some newer laser materials, all based upon the ![]() $\text{Yb}^{3+}$ lasing ion. We show only Yb materials for which both room and cryogenic temperature data are available. Table 3 shows the laser material, the crystal classification (anaxial (A) and uniaxial (U)), the absorption span
$\text{Yb}^{3+}$ lasing ion. We show only Yb materials for which both room and cryogenic temperature data are available. Table 3 shows the laser material, the crystal classification (anaxial (A) and uniaxial (U)), the absorption span ![]() ${\it\delta}{\bf\lambda}_{\mathbf{abs}}$ (FWHM) and wavelength of peak absorption
${\it\delta}{\bf\lambda}_{\mathbf{abs}}$ (FWHM) and wavelength of peak absorption ![]() ${\it\lambda}_{\text{abs}}^{P}$, the absorption bandwidth
${\it\lambda}_{\text{abs}}^{P}$, the absorption bandwidth ![]() ${\rm\Delta}{\it\lambda}_{\text{abs}}$ (FWHM), peak absorption cross-section
${\rm\Delta}{\it\lambda}_{\text{abs}}$ (FWHM), peak absorption cross-section ![]() ${\it\sigma}_{\text{abs}}^{P}$, the wavelength of the peak stimulated-emission cross-section
${\it\sigma}_{\text{abs}}^{P}$, the wavelength of the peak stimulated-emission cross-section ![]() ${\it\lambda}_{\text{em}}^{P}$, the emission bandwidth
${\it\lambda}_{\text{em}}^{P}$, the emission bandwidth ![]() ${\rm\Delta}{\it\lambda}_{\text{em}}$ (FWHM), the value of the peak stimulated-emission cross-section
${\rm\Delta}{\it\lambda}_{\text{em}}$ (FWHM), the value of the peak stimulated-emission cross-section ![]() ${\it\sigma}_{\text{em}}^{P}$, the upper level
${\it\sigma}_{\text{em}}^{P}$, the upper level ![]() $(\text{}^{2}\text{F}_{5/2})$ fluorescence lifetime
$(\text{}^{2}\text{F}_{5/2})$ fluorescence lifetime ![]() ${\it\tau}_{F}$, the absolute temperature, and the references from whence the data were taken. While we will not detail the enhanced laser properties of laser materials at cryogenic temperatures, and instead refer the reader to the discussion in Ref. [Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3], we mention here that Yb laser materials become more four-level like at temperatures below about 150 K, negating the need to first pump to transparency as is required for room-temperature operation. Spectral absorption and emission lines narrow as well; the stimulated-emission cross-section becomes substantially larger at cryogenic temperatures, resulting in a much reduced saturation fluence and intensity. While the absorption bands narrow, in the pump region around 940 nm the narrowing is moderate, and the band remains broad enough to be pumped by common diode laser sources. For many laser materials such as Yb:YAG, the zero-phonon absorption line near 969 nm becomes extremely narrow at low temperatures, so that even narrowband volume Bragg grating stabilized diode laser sources have inefficient absorption. For Yb:
${\it\tau}_{F}$, the absolute temperature, and the references from whence the data were taken. While we will not detail the enhanced laser properties of laser materials at cryogenic temperatures, and instead refer the reader to the discussion in Ref. [Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3], we mention here that Yb laser materials become more four-level like at temperatures below about 150 K, negating the need to first pump to transparency as is required for room-temperature operation. Spectral absorption and emission lines narrow as well; the stimulated-emission cross-section becomes substantially larger at cryogenic temperatures, resulting in a much reduced saturation fluence and intensity. While the absorption bands narrow, in the pump region around 940 nm the narrowing is moderate, and the band remains broad enough to be pumped by common diode laser sources. For many laser materials such as Yb:YAG, the zero-phonon absorption line near 969 nm becomes extremely narrow at low temperatures, so that even narrowband volume Bragg grating stabilized diode laser sources have inefficient absorption. For Yb:![]() $\text{CaF}_{2}$, however, even at cryogenic temperatures the zero-phonon line remains broad enough to be pumped with conventional diode sources, leading to a very low quantum defect.
$\text{CaF}_{2}$, however, even at cryogenic temperatures the zero-phonon line remains broad enough to be pumped with conventional diode sources, leading to a very low quantum defect.
The three legacy laser materials shown, Ti:![]() $\text{Al}_{2}\text{O}_{3}$,Cr:LiSAF and Cr:LiCAF, are uniaxial and we show data for the cases
$\text{Al}_{2}\text{O}_{3}$,Cr:LiSAF and Cr:LiCAF, are uniaxial and we show data for the cases ![]() $E\Vert c$ and
$E\Vert c$ and ![]() $E\Vert a$, and at room temperature. While Ti:
$E\Vert a$, and at room temperature. While Ti:![]() $\text{Al}_{2}\text{O}_{3}$ is often cooled to near 77 K to reduce thermal aberrations[Reference Backus, Durfee, Mourou, Kapteyn and Murnane33–Reference Planchon, Amir, Childress, Squier and Durfee36], little data is available in the literature regarding the spectral properties at that temperature. For Cr:LiSAF and Cr:LiCAF, we were not able to find any cryogenic data available in the literature. The bandwidths for these materials indicate that for transform-limited Gaussian pulses, pulsewidths of as short as 4, 6 and 7 fs can be achieved, respectively, in the absence of gain narrowing.
$\text{Al}_{2}\text{O}_{3}$ is often cooled to near 77 K to reduce thermal aberrations[Reference Backus, Durfee, Mourou, Kapteyn and Murnane33–Reference Planchon, Amir, Childress, Squier and Durfee36], little data is available in the literature regarding the spectral properties at that temperature. For Cr:LiSAF and Cr:LiCAF, we were not able to find any cryogenic data available in the literature. The bandwidths for these materials indicate that for transform-limited Gaussian pulses, pulsewidths of as short as 4, 6 and 7 fs can be achieved, respectively, in the absence of gain narrowing.
Table 3. Spectral properties of legacy and Yb-based ultrafast laser materials at room and cryogenic temperatures. Part of Table 3 is reproduced from Ref. [Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3].

* Reported data is incomplete or crystal axes orientation not identified.
2.6 Linear and nonlinear indices of refraction
Other than laser-induced optical damage, a subject that we shall discuss in Section 3.5, the major performance-limiting factor affecting ultrafast performance in solid-state laser systems is the existence of a finite nonlinear index of refraction ![]() $n_{2}$. Much of the early work on inertial-confinement fusion involved the use of flashlamp-pumped laser glasses doped with Nd, driven by picosecond duration Nd:YLF mode-locked oscillators with typical FWHM pulse durations in the range 50–200 ps. When scaling such systems to ever larger energy/pulse and peak powers, it was discovered that whole-beam and small-scale self-focusing, caused by the nonlinear index, were the principal limiting factors, and managing and reducing such effects was a major design goal. Good summaries of the understanding and design tools used to design picosecond high-peak-power laser systems may be found in Refs. [Reference Brown58, Reference Boyd and Lukishova59]; in addition, a very good summary of the most important papers addressing the phenomena of self-focusing and the design and performance of such systems may be found in Ref. [Reference Soures60]. It should be pointed out that in those early systems dispersion management was not a significant design issue and the technique of CPA was just in its infancy.
$n_{2}$. Much of the early work on inertial-confinement fusion involved the use of flashlamp-pumped laser glasses doped with Nd, driven by picosecond duration Nd:YLF mode-locked oscillators with typical FWHM pulse durations in the range 50–200 ps. When scaling such systems to ever larger energy/pulse and peak powers, it was discovered that whole-beam and small-scale self-focusing, caused by the nonlinear index, were the principal limiting factors, and managing and reducing such effects was a major design goal. Good summaries of the understanding and design tools used to design picosecond high-peak-power laser systems may be found in Refs. [Reference Brown58, Reference Boyd and Lukishova59]; in addition, a very good summary of the most important papers addressing the phenomena of self-focusing and the design and performance of such systems may be found in Ref. [Reference Soures60]. It should be pointed out that in those early systems dispersion management was not a significant design issue and the technique of CPA was just in its infancy.
For a laser pulse traveling through a nonlinear medium, a finite nonlinear index leads to the temporal phenomenon of self-phase modulation, resulting in a temporally dependent phase modulation. Spatial phase modulation can lead to whole-beam and small-scale self-focusing[Reference Brown58, Reference Boyd and Lukishova59]. In general, the threshold for the formation of small-scale self-focusing is significantly lower than that for whole-beam self-focusing. Calculating in advance the susceptibility of an ultrafast system to nonlinear and damage effects is an important part of ultrafast laser system design, and here we discuss the standard method for doing so.
To manage whole-beam and small-scale self-focusing in high-peak-power laser ultrafast systems, a knowledge of the nonlinear index ![]() $n_{2}$ and the corresponding nonlinear coefficient
$n_{2}$ and the corresponding nonlinear coefficient ![]() ${\it\gamma}_{N}$ is essential. A standard and often-used measure of the severity of nonlinear effects in laser systems is the
${\it\gamma}_{N}$ is essential. A standard and often-used measure of the severity of nonlinear effects in laser systems is the ![]() $B$-integral[Reference Brown58, Reference Boyd and Lukishova59], formally defined as
$B$-integral[Reference Brown58, Reference Boyd and Lukishova59], formally defined as
where ![]() $B$ is in general a function of the beam radius
$B$ is in general a function of the beam radius ![]() $r$, propagation location
$r$, propagation location ![]() $z$ and time
$z$ and time ![]() $t,I(r,z,t)$ is the radially, longitudinally and temporally varying laser intensity, the wavelength
$t,I(r,z,t)$ is the radially, longitudinally and temporally varying laser intensity, the wavelength ![]() ${\it\lambda}$, and
${\it\lambda}$, and ![]() $z$ is the propagation length parameter. The
$z$ is the propagation length parameter. The ![]() $B$-integral is the nonlinear phase accumulation
$B$-integral is the nonlinear phase accumulation ![]() ${\rm\Delta}{\it\varphi}_{NL}(r,z,t)$ due to the nonlinear index
${\rm\Delta}{\it\varphi}_{NL}(r,z,t)$ due to the nonlinear index ![]() $n_{2}$, and in laser systems must be calculated for all optical and gain elements encountered by the propagating beam. It is customary to calculate the maximum value of the
$n_{2}$, and in laser systems must be calculated for all optical and gain elements encountered by the propagating beam. It is customary to calculate the maximum value of the ![]() $B$-integral where the intensity
$B$-integral where the intensity ![]() $I$ is maximum (
$I$ is maximum (![]() $t=0$). For spatially Gaussian beams, the
$t=0$). For spatially Gaussian beams, the ![]() $B$-integral value at the beam edge is typically very small, and only the on-axis value is normally specified. The same holds true for higher-order super-Gaussian beams where the intensity at the beam edge becomes insignificant. For any arbitrary spatial beam profile, it is easy to use Equation (8) in a computer code and calculate the
$B$-integral value at the beam edge is typically very small, and only the on-axis value is normally specified. The same holds true for higher-order super-Gaussian beams where the intensity at the beam edge becomes insignificant. For any arbitrary spatial beam profile, it is easy to use Equation (8) in a computer code and calculate the ![]() $B$-integral profile at any location in a laser amplifier or system. The nonlinear index can be calculated using the relationship[Reference Brown58, Reference Boyd and Lukishova59]
$B$-integral profile at any location in a laser amplifier or system. The nonlinear index can be calculated using the relationship[Reference Brown58, Reference Boyd and Lukishova59]
Here, ![]() ${\it\chi}^{(3)}$ is the third-order susceptibility, and both
${\it\chi}^{(3)}$ is the third-order susceptibility, and both ![]() $n_{2}$ and
$n_{2}$ and ![]() ${\it\chi}^{(3)}$ are expressed in electrostatic units (esu). The relationship between
${\it\chi}^{(3)}$ are expressed in electrostatic units (esu). The relationship between ![]() $n_{2}$ and
$n_{2}$ and ![]() ${\it\gamma}_{N}$ is given by the simple formula[Reference Moulton37, Reference DeSalvo, Said, Hagan, Van Stryland and Sheik-Bahae61]
${\it\gamma}_{N}$ is given by the simple formula[Reference Moulton37, Reference DeSalvo, Said, Hagan, Van Stryland and Sheik-Bahae61]
and ![]() ${\it\gamma}_{N}$ is expressed in (
${\it\gamma}_{N}$ is expressed in (![]() $\text{cm}^{2}/\text{W}$). We note that in some contributions to the laser literature,
$\text{cm}^{2}/\text{W}$). We note that in some contributions to the laser literature, ![]() $n_{2}$ is often used to describe
$n_{2}$ is often used to describe ![]() ${\it\gamma}_{N}$, a confusing practice since they have distinctly different values and units. Table 4 shows reported values for the nonlinear index
${\it\gamma}_{N}$, a confusing practice since they have distinctly different values and units. Table 4 shows reported values for the nonlinear index ![]() $n_{2}$ and for the nonlinear coefficient
$n_{2}$ and for the nonlinear coefficient ![]() ${\it\gamma}_{N}$. The table also shows the linear index
${\it\gamma}_{N}$. The table also shows the linear index ![]() $n_{0}$, the measurement wavelength, the crystal type and the orientation of the electric field. All values are reported at room temperature.
$n_{0}$, the measurement wavelength, the crystal type and the orientation of the electric field. All values are reported at room temperature.
Table 4. Reported room-temperature values of the linear index, nonlinear index and nonlinear coefficient for a number of important laser crystals and optical materials. Also shown are the crystal type (SC – single crystal, GM – glassy material, or CER – ceramic), the ![]() $E$-field orientation (parallel to specified crystal axis, unspecified, and I – isotropic), and the measurement wavelength. Table reproduced from Ref. [Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3].
$E$-field orientation (parallel to specified crystal axis, unspecified, and I – isotropic), and the measurement wavelength. Table reproduced from Ref. [Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3].

* Measurements of ![]() ${\it\gamma}_{N}$ along
${\it\gamma}_{N}$ along ![]() $c$-axis and orthogonal
$c$-axis and orthogonal ![]() $b$-axis found to be the same.
$b$-axis found to be the same.
![]() $\text{Al}_{2}\text{O}_{3}$, LiSAF, LiCAF, LiSGAF,
$\text{Al}_{2}\text{O}_{3}$, LiSAF, LiCAF, LiSGAF, ![]() $\text{Mg}_{2}\text{SiO}_{4}$,
$\text{Mg}_{2}\text{SiO}_{4}$, ![]() $\text{SiO}_{2}$, YLF, MgO,
$\text{SiO}_{2}$, YLF, MgO, ![]() $\text{MgAl}_{2}\text{O}_{4}$ and
$\text{MgAl}_{2}\text{O}_{4}$ and ![]() $\text{CaF}_{2}$ all exhibit rather small nonlinear index values in the spectral region 800–1100 nm. YAG, YALO and LuAG display somewhat larger values, while the sesquioxides
$\text{CaF}_{2}$ all exhibit rather small nonlinear index values in the spectral region 800–1100 nm. YAG, YALO and LuAG display somewhat larger values, while the sesquioxides ![]() $\text{Y}_{2}\text{O}_{3}$,
$\text{Y}_{2}\text{O}_{3}$, ![]() $\text{Sc}_{2}\text{O}_{3}$ and
$\text{Sc}_{2}\text{O}_{3}$ and ![]() $\text{Lu}_{2}\text{O}_{3}$ show a substantial increase, followed by the vanadates
$\text{Lu}_{2}\text{O}_{3}$ show a substantial increase, followed by the vanadates ![]() $\text{YVO}_{4}$ and
$\text{YVO}_{4}$ and ![]() $\text{GdVO}_{4}$ and the tungstates KGW and KYW which display the largest nonlinear index values. A much larger nonlinear index for many commonly mode-locked materials like
$\text{GdVO}_{4}$ and the tungstates KGW and KYW which display the largest nonlinear index values. A much larger nonlinear index for many commonly mode-locked materials like ![]() $\text{YVO}_{4}$, KGW and KYW makes Kerr lens mode locking easier to achieve, but will provide challenges to suppress nonlinear effects in scaled up ultrafast systems consisting of multiple amplifiers. Minimizing
$\text{YVO}_{4}$, KGW and KYW makes Kerr lens mode locking easier to achieve, but will provide challenges to suppress nonlinear effects in scaled up ultrafast systems consisting of multiple amplifiers. Minimizing ![]() $B$-integral contributions in ultrafast systems utilizing some of these newer materials will likely force designers to consider thin lasing elements such as thin-disk lasers for some applications; however, the thinner the lasing element the more troublesome the suppression of parasitics and amplified spontaneous emission (ASE), so undoubtedly tradeoffs will need to be made. Also, thin lasing elements have low gain as well, and require multi-passing of the element for good extraction, thus increasing the
$B$-integral contributions in ultrafast systems utilizing some of these newer materials will likely force designers to consider thin lasing elements such as thin-disk lasers for some applications; however, the thinner the lasing element the more troublesome the suppression of parasitics and amplified spontaneous emission (ASE), so undoubtedly tradeoffs will need to be made. Also, thin lasing elements have low gain as well, and require multi-passing of the element for good extraction, thus increasing the ![]() $B$-integral and often negating any advantage.
$B$-integral and often negating any advantage.
3 HAPP cryogenic laser design considerations
3.1 Operating modes of cryogenic lasers
It is generally assumed that a diode-pumped laser system operating at room temperature, upon being cooled to cryogenic temperatures, will have superior performance characteristics. In particular, thermal effects are lessened due to improved thermal conductivity and reduced values of the thermal expansion coefficient and ![]() $(dn/dT)$. It is also assumed that a cryogenically cooled device will behave as a nearly 4-level laser, that stimulated-emission cross-sections will increase, reducing the saturation fluence, and that stress-induced birefringence will be absent. While much experimental evidence exists in the laser literature to support those assumptions, surprisingly little work has been done to quantify the improvement in beam quality relative to room-temperature operation. It is also not generally appreciated that there exist two distinctly different operating modes for cryogenic lasers, here referred to as stress-limited operation and aberration-limited operation. We briefly describe both modes.
$(dn/dT)$. It is also assumed that a cryogenically cooled device will behave as a nearly 4-level laser, that stimulated-emission cross-sections will increase, reducing the saturation fluence, and that stress-induced birefringence will be absent. While much experimental evidence exists in the laser literature to support those assumptions, surprisingly little work has been done to quantify the improvement in beam quality relative to room-temperature operation. It is also not generally appreciated that there exist two distinctly different operating modes for cryogenic lasers, here referred to as stress-limited operation and aberration-limited operation. We briefly describe both modes.
3.1.1 Stress-limited operation
Both room-temperature and cryogenic lasers can be operated at the stress limit, and both cases were examined in an early cryogenic laser paper[Reference Brown10]. For a rod laser, the stress limit is defined as the heat density at which the barrel surface stress is equal to the fracture stress. Stress at the barrel surface is most important because surfaces are always weaker than the crystalline bulk due to the presence of micro-fractures, scratches and voids. The relationship between crack size and surface strength has been discussed in the literature[Reference Krupke, Shinn, Marion, Caird and Stokowski32]. If we define the heat fraction ![]() ${\it\eta}_{h}$ as the fraction of the incident pump power converted to heat, and
${\it\eta}_{h}$ as the fraction of the incident pump power converted to heat, and ![]() ${\it\eta}_{i}$ as the inversion fraction, then we have
${\it\eta}_{i}$ as the inversion fraction, then we have
where ![]() $P_{\text{abs}}$ is the absorbed pump power, and
$P_{\text{abs}}$ is the absorbed pump power, and ![]() $P_{h}$ and
$P_{h}$ and ![]() $P_{i}$ are the absorbed total heat power and inversion power, respectively. We also have from power conservation,
$P_{i}$ are the absorbed total heat power and inversion power, respectively. We also have from power conservation,
We can write the ratio of heat to inversion powers ![]() ${\it\chi}$ as
${\it\chi}$ as
If ![]() $Q_{0}$ is the heat per unit volume, then the extractable power per unit length is
$Q_{0}$ is the heat per unit volume, then the extractable power per unit length is
where ![]() $A_{P}$ is the pump area/for the case where the rod tangential stress
$A_{P}$ is the pump area/for the case where the rod tangential stress ![]() ${\it\sigma}_{{\it\theta}{\it\theta}}$ is equal to the fracture stress
${\it\sigma}_{{\it\theta}{\it\theta}}$ is equal to the fracture stress ![]() ${\it\sigma}_{f}$, and using the explicit expression for
${\it\sigma}_{f}$, and using the explicit expression for ![]() ${\it\sigma}_{{\it\theta}{\it\theta}}$ in a rod laser (in the plane-strain approximation) as a function of the rod radius
${\it\sigma}_{{\it\theta}{\it\theta}}$ in a rod laser (in the plane-strain approximation) as a function of the rod radius ![]() $r$ and diameter
$r$ and diameter ![]() $D$[Reference Brown11],
$D$[Reference Brown11],
we find the maximum tolerable heat density ![]() $Q_{0}^{M}$ to be, evaluating Equation (16) for
$Q_{0}^{M}$ to be, evaluating Equation (16) for ![]() $r=(D/2)$,
$r=(D/2)$,
Substituting Equations (17) into (15), the extractable power/length is then given by
 $$\begin{eqnarray}\displaystyle \left(\frac{P_{\text{ex}}}{L}\right) & = & \displaystyle 8{\it\pi}{\it\eta}_{\text{ex}}\left(\frac{1-{\it\eta}_{h}}{{\it\eta}_{h}}\right)\left({\it\sigma}_{f}M_{s}\right)\nonumber\\ \displaystyle & = & \displaystyle 8{\it\pi}{\it\eta}_{\text{ex}}\left(\frac{1-{\it\eta}_{h}}{{\it\eta}_{h}}\right)R_{m}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{P_{\text{ex}}}{L}\right) & = & \displaystyle 8{\it\pi}{\it\eta}_{\text{ex}}\left(\frac{1-{\it\eta}_{h}}{{\it\eta}_{h}}\right)\left({\it\sigma}_{f}M_{s}\right)\nonumber\\ \displaystyle & = & \displaystyle 8{\it\pi}{\it\eta}_{\text{ex}}\left(\frac{1-{\it\eta}_{h}}{{\it\eta}_{h}}\right)R_{m}.\end{eqnarray}$$ The quantity ![]() $R_{m}$, the product of the materials parameter times the fracture stress, is known in the literature as the rupture modulus. The heat fraction can be obtained explicitly as a function of the extraction efficiency. For Yb:YAG, for example, we have shown previously that
$R_{m}$, the product of the materials parameter times the fracture stress, is known in the literature as the rupture modulus. The heat fraction can be obtained explicitly as a function of the extraction efficiency. For Yb:YAG, for example, we have shown previously that ![]() ${\it\eta}_{h}$ can be found from the relationship[Reference Brown and Vitali72]
${\it\eta}_{h}$ can be found from the relationship[Reference Brown and Vitali72]
Upon substituting Equations (19) into (18), we find a final simple expression for the extractable power per unit length as a function of the heat fraction:
The constants ![]() $A,B$ and
$A,B$ and ![]() $C$ have been calculated for Yb:YAG and are tabulated at 300 and 77 K in Ref. [Reference Brown and Vitali72]. The maximum extractable power per unit length is then seen to be a function of the heat fraction only, as the rupture modulus is a constant in this treatment. The maximum tolerable surface stress has been discussed in the literature, and is a function of the fracture toughness, a geometry factor, and the surface flaw radius that initiates a crack[Reference Krupke, Shinn, Marion, Caird and Stokowski32]. A number of techniques have been used to decrease the surface flaw radius and increase the fracture stress, including advanced surface polishing techniques and acid etching[Reference Krupke, Shinn, Marion, Caird and Stokowski32]. In the case of rod amplifiers, however, it is often the case that the barrel is ground to suppress parasitic oscillations. This leads to a much reduced rupture modulus. Recently, an alternative technique has been developed to suppress parasitics, in which a ceramic or single-crystal layer is grown in an absorbing annulus onto the rod barrel. The layer may contain Sm,
$C$ have been calculated for Yb:YAG and are tabulated at 300 and 77 K in Ref. [Reference Brown and Vitali72]. The maximum extractable power per unit length is then seen to be a function of the heat fraction only, as the rupture modulus is a constant in this treatment. The maximum tolerable surface stress has been discussed in the literature, and is a function of the fracture toughness, a geometry factor, and the surface flaw radius that initiates a crack[Reference Krupke, Shinn, Marion, Caird and Stokowski32]. A number of techniques have been used to decrease the surface flaw radius and increase the fracture stress, including advanced surface polishing techniques and acid etching[Reference Krupke, Shinn, Marion, Caird and Stokowski32]. In the case of rod amplifiers, however, it is often the case that the barrel is ground to suppress parasitic oscillations. This leads to a much reduced rupture modulus. Recently, an alternative technique has been developed to suppress parasitics, in which a ceramic or single-crystal layer is grown in an absorbing annulus onto the rod barrel. The layer may contain Sm, ![]() $\text{Cr}^{4+}$ or any other number of ions to absorb fluorescence and ASE to both suppress parasitics and minimize ASE losses[Reference Brown, Kowalewski, Envid, Zembeck, Kolis, McMillen and Geisber73]. This solution allows rod barrels to be polished, substantially increasing the fracture stress.
$\text{Cr}^{4+}$ or any other number of ions to absorb fluorescence and ASE to both suppress parasitics and minimize ASE losses[Reference Brown, Kowalewski, Envid, Zembeck, Kolis, McMillen and Geisber73]. This solution allows rod barrels to be polished, substantially increasing the fracture stress.
Equation (18) takes the following values for ![]() ${\it\eta}_{\text{ex}}=0,1$
${\it\eta}_{\text{ex}}=0,1$
Calculation shows that the rupture modulus can be much larger at 77 K than at 300 K[Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3]. If we assume that ![]() ${\it\eta}_{\text{ex}}=1$, then the extractable power per unit length obtained at 77 K can be calculated from Equation (22) to be about 9.31 times the extractable power at 300 K, assuming that the fracture stress values are the same in both cases. We evaluated the
${\it\eta}_{\text{ex}}=1$, then the extractable power per unit length obtained at 77 K can be calculated from Equation (22) to be about 9.31 times the extractable power at 300 K, assuming that the fracture stress values are the same in both cases. We evaluated the ![]() $R_{m}$ values at 300 and 77 K using the data from Table 2 and assuming that the values for Young’s modulus and Poisson’s ratio are approximately the same at both temperatures.
$R_{m}$ values at 300 and 77 K using the data from Table 2 and assuming that the values for Young’s modulus and Poisson’s ratio are approximately the same at both temperatures.
Stress-limited operation can, in this case, result in an increase of average power at 77 K by approximately an order of magnitude compared to room-temperature operation. We note that in stress-limited operation, laser amplifiers will have very large thermal aberrations. Stress values are large and will contribute strongly to the change in index of refraction. Such amplifiers display large changes in the beam parameters (beam waist and divergence angle) as pump power is increased to the maximum value.
3.1.2 Aberration-limited operation
In contrast to stress-limited operation, for aberration-limited operation the contribution to the change in the index of refraction from stresses is near-zero. We begin by writing the change in phase ![]() ${\rm\Delta}{\it\varphi}$ due to thermal effects in a rod amplifier as[Reference Brown11]:
${\rm\Delta}{\it\varphi}$ due to thermal effects in a rod amplifier as[Reference Brown11]:
 $$\begin{eqnarray}\displaystyle {\rm\Delta}{\it\varphi} & = & \displaystyle \left(\frac{2{\it\pi}L}{{\it\lambda}}\right)\left[\left({\it\beta}+\left(n_{0}-1\right){\it\alpha}\right){\rm\Delta}T_{c-e}+(n_{0}-1)\phantom{\frac{{\it\sigma}_{zz}}{E}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\times \left(\frac{{\it\sigma}_{zz}}{E}-\frac{{\it\nu}}{E}\left({\it\sigma}_{rr}+{\it\sigma}_{{\it\theta}{\it\theta}}\right)\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\rm\Delta}{\it\varphi} & = & \displaystyle \left(\frac{2{\it\pi}L}{{\it\lambda}}\right)\left[\left({\it\beta}+\left(n_{0}-1\right){\it\alpha}\right){\rm\Delta}T_{c-e}+(n_{0}-1)\phantom{\frac{{\it\sigma}_{zz}}{E}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\times \left(\frac{{\it\sigma}_{zz}}{E}-\frac{{\it\nu}}{E}\left({\it\sigma}_{rr}+{\it\sigma}_{{\it\theta}{\it\theta}}\right)\right)\right],\end{eqnarray}$$ where ![]() $L$ is the amplifier length;
$L$ is the amplifier length; ![]() ${\it\beta}$ the value of
${\it\beta}$ the value of ![]() $(dn/dT)$;
$(dn/dT)$; ![]() ${\it\alpha}$ the thermal expansion coefficient and
${\it\alpha}$ the thermal expansion coefficient and ![]() ${\it\sigma}_{rr}$,
${\it\sigma}_{rr}$, ![]() ${\it\sigma}_{{\it\theta}{\it\theta}}$ and
${\it\sigma}_{{\it\theta}{\it\theta}}$ and ![]() ${\it\sigma}_{zz}$ are the radial, tangential, and
${\it\sigma}_{zz}$ are the radial, tangential, and ![]() $z$ stress components. The quantity
$z$ stress components. The quantity ![]() ${\rm\Delta}T_{c-e}$ is the rod center-edge temperature difference. At cryogenic temperatures, it can be shown that the stress term is very small and may be ignored[Reference Brown11]. Equation (23) then reverts to the much simpler equation
${\rm\Delta}T_{c-e}$ is the rod center-edge temperature difference. At cryogenic temperatures, it can be shown that the stress term is very small and may be ignored[Reference Brown11]. Equation (23) then reverts to the much simpler equation
that involves only changes in the index of refraction with temperature, ![]() ${\it\beta}$, and changes in physical path length due to
${\it\beta}$, and changes in physical path length due to ![]() ${\it\alpha}$.
${\it\alpha}$. ![]() $Q_{0}$ is the heat density,
$Q_{0}$ is the heat density, ![]() $D$ the rod diameter and
$D$ the rod diameter and ![]() $k$ the thermal conductivity. We define a new parameter
$k$ the thermal conductivity. We define a new parameter ![]() ${\it\xi}$, the extractable power per unit thermal phase distortion, as
${\it\xi}$, the extractable power per unit thermal phase distortion, as
 $$\begin{eqnarray}{\it\xi}=\left(\frac{P_{\text{ex}}}{{\rm\Delta}{\it\varphi}}\right)=\frac{{\it\eta}_{\text{ex}}\left(\frac{1-{\it\eta}_{h}}{{\it\eta}_{h}}\right)Q_{0}V_{p}}{\left(\frac{2{\it\pi}L}{{\it\lambda}}\right)\left(\frac{Q_{0}D^{2}}{16k}\right)\left[\left({\it\beta}+\left(n_{0}-1\right){\it\alpha}\right)\right]}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\xi}=\left(\frac{P_{\text{ex}}}{{\rm\Delta}{\it\varphi}}\right)=\frac{{\it\eta}_{\text{ex}}\left(\frac{1-{\it\eta}_{h}}{{\it\eta}_{h}}\right)Q_{0}V_{p}}{\left(\frac{2{\it\pi}L}{{\it\lambda}}\right)\left(\frac{Q_{0}D^{2}}{16k}\right)\left[\left({\it\beta}+\left(n_{0}-1\right){\it\alpha}\right)\right]}.\end{eqnarray}$$ We use the phase relationship ![]() $N={\rm\Delta}{\it\varphi}/2{\it\pi}$ where
$N={\rm\Delta}{\it\varphi}/2{\it\pi}$ where ![]() $N$ is the number of waves of thermal distortion, which leads to the final expression
$N$ is the number of waves of thermal distortion, which leads to the final expression
 $$\begin{eqnarray}\displaystyle {\it\xi} & = & \displaystyle 4{\it\pi}\left(\frac{{\it\lambda}k}{({\it\beta}+(n_{0}-1)){\it\alpha}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \left[\frac{A+B{\it\eta}_{\text{ex}}+C(1-{\it\eta}_{\text{ex}})}{1-A-B{\it\eta}_{\text{ex}}-C(1-{\it\eta}_{\text{ex}})}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\xi} & = & \displaystyle 4{\it\pi}\left(\frac{{\it\lambda}k}{({\it\beta}+(n_{0}-1)){\it\alpha}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \left[\frac{A+B{\it\eta}_{\text{ex}}+C(1-{\it\eta}_{\text{ex}})}{1-A-B{\it\eta}_{\text{ex}}-C(1-{\it\eta}_{\text{ex}})}\right].\end{eqnarray}$$ This new equation allows the (idealized) calculation of the output power per unit phase distortion, or if preferred, the magnitude of the thermally induced phase distortion for a given amount of laser output power, at cryogenic temperatures. (This equation obviously ignores the effects of gain or a resonator.) Note that ![]() ${\it\xi}$ is independent of the heat density, the rod diameter and the rod length. We can use this relationship to estimate for example how much phase aberration will be produced at two temperatures for the same amount of output power. It is instructive to ignore the stress contribution to the phase aberration at room temperature, and to simply calculate the ratio
${\it\xi}$ is independent of the heat density, the rod diameter and the rod length. We can use this relationship to estimate for example how much phase aberration will be produced at two temperatures for the same amount of output power. It is instructive to ignore the stress contribution to the phase aberration at room temperature, and to simply calculate the ratio
 $$\begin{eqnarray}R_{{\it\varphi}}=\frac{\left(\frac{1}{{\it\xi}}\right)_{300}}{\left(\frac{1}{{\it\xi}}\right)_{77}},\end{eqnarray}$$
$$\begin{eqnarray}R_{{\it\varphi}}=\frac{\left(\frac{1}{{\it\xi}}\right)_{300}}{\left(\frac{1}{{\it\xi}}\right)_{77}},\end{eqnarray}$$ to find the ratio of the phase aberration at 300 K relative to 77 K. While we prefer in this paper to calculate Equation (27), note that we could also have calculated the ratio of ![]() ${\it\xi}$ at 300 K to that at 77 K to find the ratio of power output at 300 K relative to that at 77 K for 1 unit of wave distortion. Using the values of A, B and C found in Ref. [Reference Brown and Vitali72] for Yb:YAG, as well as values of
${\it\xi}$ at 300 K to that at 77 K to find the ratio of power output at 300 K relative to that at 77 K for 1 unit of wave distortion. Using the values of A, B and C found in Ref. [Reference Brown and Vitali72] for Yb:YAG, as well as values of ![]() ${\it\beta}$ and
${\it\beta}$ and ![]() ${\it\alpha}$ from Table 2, a wavelength of 1029 nm, and an index of refraction of 1.817, we have calculated the reciprocal of
${\it\alpha}$ from Table 2, a wavelength of 1029 nm, and an index of refraction of 1.817, we have calculated the reciprocal of ![]() ${\it\xi}$ at 300 and 77 K,
${\it\xi}$ at 300 and 77 K, ![]() $\left(1/{\it\xi}\right)_{300}$ and
$\left(1/{\it\xi}\right)_{300}$ and ![]() $\left(1/{\it\xi}\right)_{77}$, and the ratio
$\left(1/{\it\xi}\right)_{77}$, and the ratio ![]() $R_{{\it\varphi}}$ as a function of
$R_{{\it\varphi}}$ as a function of ![]() ${\it\eta}_{\text{ex}}$ and show the results in Figure 11. Examination of Figure 11 reveals that the number of waves distortion at 300 K, for the same heat density and rod radius and length is about 16.4 to 15.9 times the number of waves generated at 77 K. This result explicitly shows that for any extraction efficiency, operating an amplifier at 77 K will always result in much lower thermal aberrations, by over an order of magnitude for Yb:YAG. Similar results will be obtained for other laser materials. We have not included the stress contribution to the thermal phase change at 300 K in Yb:YAG here for brevity, but doing so will increase the value of
${\it\eta}_{\text{ex}}$ and show the results in Figure 11. Examination of Figure 11 reveals that the number of waves distortion at 300 K, for the same heat density and rod radius and length is about 16.4 to 15.9 times the number of waves generated at 77 K. This result explicitly shows that for any extraction efficiency, operating an amplifier at 77 K will always result in much lower thermal aberrations, by over an order of magnitude for Yb:YAG. Similar results will be obtained for other laser materials. We have not included the stress contribution to the thermal phase change at 300 K in Yb:YAG here for brevity, but doing so will increase the value of ![]() $R_{{\it\varphi}}$. Equation (24) represents a rational way to compare the performance of laser amplifiers at different temperatures, and may be used to quantify the expected improvement in power output per unit thermal phase distortion at cryogenic temperatures.
$R_{{\it\varphi}}$. Equation (24) represents a rational way to compare the performance of laser amplifiers at different temperatures, and may be used to quantify the expected improvement in power output per unit thermal phase distortion at cryogenic temperatures.
3.2 Pulse-pumped laser extraction model
We have developed a very useful pulsed-pumping model that enables modeling of picosecond and nanosecond cryogenic laser systems that are used for pumping ultrafast lasers, whether broadband Ti:![]() $\text{Al}_{2}\text{O}_{3}$ or other tunable broad-bandwidth systems or broadband OPCPA systems. The model treats four-level diode-pumped lasers like cryogenic Yb:YAG that use square-wave pumping into the upper laser manifold. We begin by showing in Figure 12 a timing diagram for a typical diode-pumped laser.
$\text{Al}_{2}\text{O}_{3}$ or other tunable broad-bandwidth systems or broadband OPCPA systems. The model treats four-level diode-pumped lasers like cryogenic Yb:YAG that use square-wave pumping into the upper laser manifold. We begin by showing in Figure 12 a timing diagram for a typical diode-pumped laser.
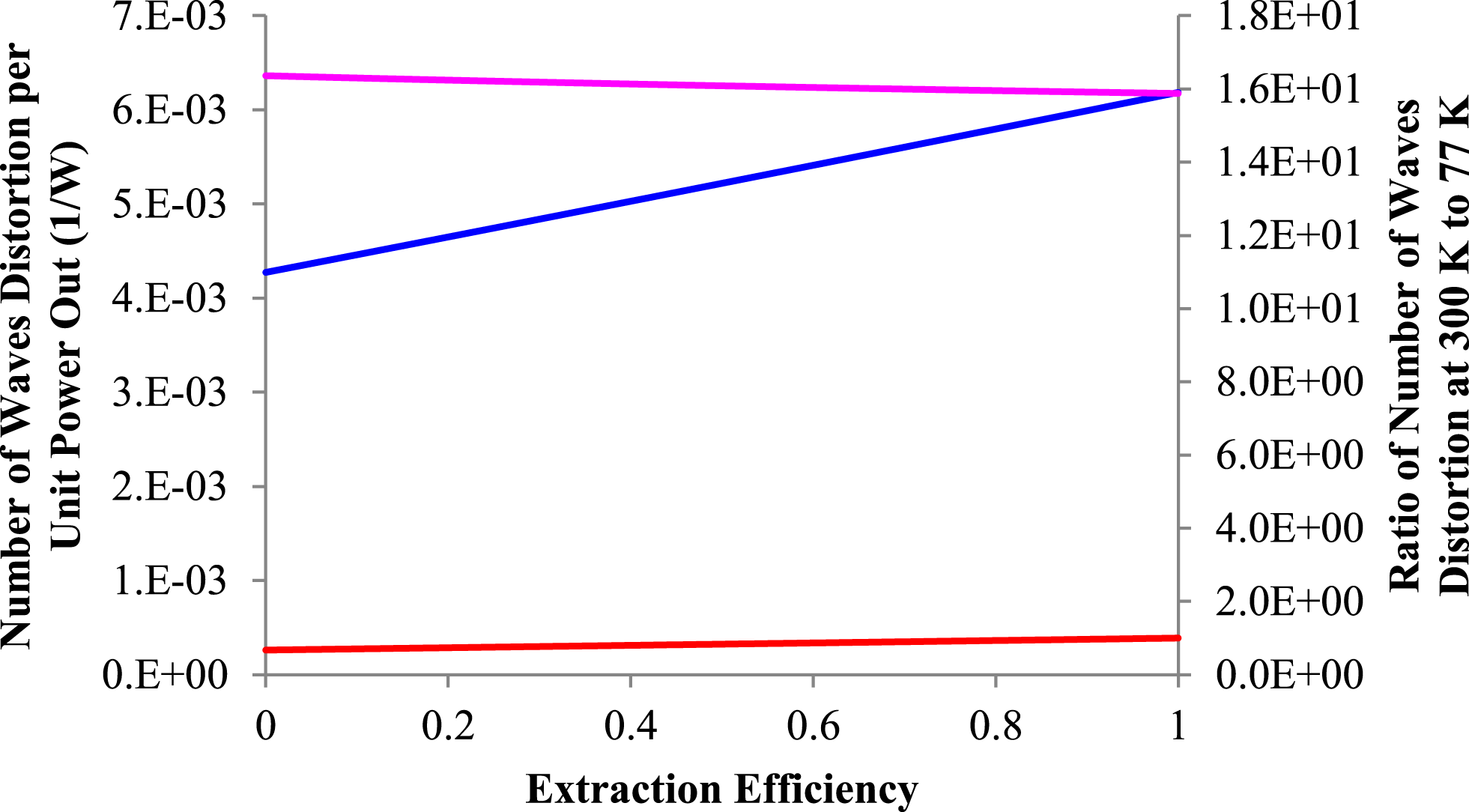
Figure 11. Number of waves distortion per unit output power for Yb:YAG at 300 (blue line) and 77 K (red line), and the ratio of the number of waves at 300 to 77 K pink), all as a function of laser extraction efficiency.

Figure 12. Temporal repetitively diode-pumped sequence showing pump pulses of duration ![]() $T$, repetition rate
$T$, repetition rate ![]() ${\it\nu}_{R}$, the temporal variation of the initial inversion density
${\it\nu}_{R}$, the temporal variation of the initial inversion density ![]() $n_{i}$ and the inversion from a previous pulse
$n_{i}$ and the inversion from a previous pulse ![]() $n_{\text{fp}}$, and the difference inversion density
$n_{\text{fp}}$, and the difference inversion density ![]() ${\rm\Delta}n$ due to extraction.
${\rm\Delta}n$ due to extraction.
The pump pulse, of duration ![]() $T$, produces an initial inversion density
$T$, produces an initial inversion density ![]() $n_{i}$ that is the sum of the inversion left from the fluorescence decay of the final inversion density from the previous pulse (pink)
$n_{i}$ that is the sum of the inversion left from the fluorescence decay of the final inversion density from the previous pulse (pink) ![]() $n_{\text{fp}}$, plus the inversion created from the current pulse (solid blue line). The final inversion density after the passage of an extracting pulse is
$n_{\text{fp}}$, plus the inversion created from the current pulse (solid blue line). The final inversion density after the passage of an extracting pulse is ![]() $n_{\!f}$, and the difference inversion density is
$n_{\!f}$, and the difference inversion density is ![]() ${\rm\Delta}n=n_{i}-n_{\!f}$. The time between pulses,
${\rm\Delta}n=n_{i}-n_{\!f}$. The time between pulses, ![]() $T_{\text{bp}}$, is the inverse of the repetition rate
$T_{\text{bp}}$, is the inverse of the repetition rate ![]() ${\it\nu}_{R}$. We can then write the initial inversion density as
${\it\nu}_{R}$. We can then write the initial inversion density as
and recognizing that in steady-state ![]() $n_{\text{fp}}=n_{\!f}$, we have
$n_{\text{fp}}=n_{\!f}$, we have
The CW inversion density is given by
The quantity ![]() ${\it\tau}$ is fluorescence lifetime,
${\it\tau}$ is fluorescence lifetime, ![]() $R_{e}$ the excitation density, A the pump absorption,
$R_{e}$ the excitation density, A the pump absorption, ![]() $P_{P}$ the pump power,
$P_{P}$ the pump power, ![]() ${\it\lambda}_{P}$ the pump wavelength,
${\it\lambda}_{P}$ the pump wavelength, ![]() $h$ Planck’s constant,
$h$ Planck’s constant, ![]() $c$ the speed of light and
$c$ the speed of light and ![]() $V_{P}$ the pump volume that may be calculated from
$V_{P}$ the pump volume that may be calculated from
where ![]() $a$ is the assumed cylindrical pump volume radius and
$a$ is the assumed cylindrical pump volume radius and ![]() $L$ the length. We assume in all that follows that the excitation and inversion densities are constant in the pump volume. We can relate the change in excitation after pulse extraction to the change in the extracting beam fluence
$L$ the length. We assume in all that follows that the excitation and inversion densities are constant in the pump volume. We can relate the change in excitation after pulse extraction to the change in the extracting beam fluence ![]() ${\rm\Delta}J$ through the relationship
${\rm\Delta}J$ through the relationship
with the change in the fluence given by
The quantity ![]() $n_{\text{ex}}$, the extracted inversion density, can then be written
$n_{\text{ex}}$, the extracted inversion density, can then be written
Substituting ![]() $n_{\!f}=n_{i}-n_{\text{ex}}$ in Equation (29), we find
$n_{\!f}=n_{i}-n_{\text{ex}}$ in Equation (29), we find
 $$\begin{eqnarray}\displaystyle n_{i}=\frac{n_{\text{cw}}(1-e^{-(\frac{T}{{\it\tau}})})-n_{\text{ex }}e^{-\left(\frac{T_{\text{bp}}}{{\it\tau}}\right)}}{\biggl(1-e^{-(\frac{T_{\text{bp}}}{{\it\tau}})}\biggr)}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n_{i}=\frac{n_{\text{cw}}(1-e^{-(\frac{T}{{\it\tau}})})-n_{\text{ex }}e^{-\left(\frac{T_{\text{bp}}}{{\it\tau}}\right)}}{\biggl(1-e^{-(\frac{T_{\text{bp}}}{{\it\tau}})}\biggr)}. & & \displaystyle\end{eqnarray}$$Now, using Equation (31), we find a similar equation for the final inversion density:
 $$\begin{eqnarray}n_{\!f}=\frac{n_{\text{cw}}(1-e^{-(\frac{T}{{\it\tau}})})-n_{\text{ex}}}{(1-e^{-(\frac{T_{\text{bp}}}{{\it\tau}})})}.\end{eqnarray}$$
$$\begin{eqnarray}n_{\!f}=\frac{n_{\text{cw}}(1-e^{-(\frac{T}{{\it\tau}})})-n_{\text{ex}}}{(1-e^{-(\frac{T_{\text{bp}}}{{\it\tau}})})}.\end{eqnarray}$$Equations (34) and (35), which express the initial and final inversion densities in terms of the CW inversion density and the extracted inversion density, will be found to be useful in the following derivations. Using Equation (31), we write the extracted inversion density as
![]() $G_{s}$ is the saturated gain which is defined as:
$G_{s}$ is the saturated gain which is defined as:
We will use the Frantz–Nodvik Equation, written in the form
![]() $G_{0}$ is the small-signal gain, given by
$G_{0}$ is the small-signal gain, given by
and ![]() ${\it\sigma}_{e}$ is the stimulated-emission cross-section. Substituting Equation (38) into (36), we find the very useful relationship
${\it\sigma}_{e}$ is the stimulated-emission cross-section. Substituting Equation (38) into (36), we find the very useful relationship
This equation allows us to calculate the extracted inversion density ![]() $n_{\text{ex}}$ as a function of the small-signal gain
$n_{\text{ex}}$ as a function of the small-signal gain ![]() $G_{0}$, the saturation fluence, and the input fluence of the amplifier,
$G_{0}$, the saturation fluence, and the input fluence of the amplifier, ![]() $J_{\text{in}}$. We can now re-write Equation (34) as
$J_{\text{in}}$. We can now re-write Equation (34) as
 $$\begin{eqnarray}n_{i}=n_{i}^{0}-\frac{n_{\text{ex }}e^{-\left(\frac{T_{\text{bp}}}{{\it\tau}}\right)}}{(1-e^{-(\frac{T_{\text{bp}}}{{\it\tau}})})},\end{eqnarray}$$
$$\begin{eqnarray}n_{i}=n_{i}^{0}-\frac{n_{\text{ex }}e^{-\left(\frac{T_{\text{bp}}}{{\it\tau}}\right)}}{(1-e^{-(\frac{T_{\text{bp}}}{{\it\tau}})})},\end{eqnarray}$$or, finally, as
The quantity ![]() $n_{i}^{0}$ is the initial starting density without extraction, and is calculated according to
$n_{i}^{0}$ is the initial starting density without extraction, and is calculated according to
 $$\begin{eqnarray}n_{i}^{0}=\frac{n_{\text{cw}}(1-e^{-(\frac{T}{{\it\tau}})})}{(1-e^{-(\frac{T_{b_{p}}}{{\it\tau}})})}.\end{eqnarray}$$
$$\begin{eqnarray}n_{i}^{0}=\frac{n_{\text{cw}}(1-e^{-(\frac{T}{{\it\tau}})})}{(1-e^{-(\frac{T_{b_{p}}}{{\it\tau}})})}.\end{eqnarray}$$ Thus, by knowing the time between the pump pulses (repetition rate), the fluorescence lifetime and the CW inversion density, we may calculate the initial inversion density with no extraction. We define the starting small-signal gain ![]() $G_{0}^{0}$ by the following relationship:
$G_{0}^{0}$ by the following relationship:
The starting small-signal gain is then calculated with re-pumping, but with no extraction. Similarly, we can calculate the small-signal gain after extraction, ![]() $G_{0}$, using
$G_{0}$, using
This equation allows us to calculate the remaining small-signal gain with re-pumping but after extraction. We now define two new variables, ![]() ${\it\beta}$ and
${\it\beta}$ and ![]() $f$ as follows:
$f$ as follows:
Multiplying Equation (42) by ![]() ${\it\sigma}_{e}L$, we find
${\it\sigma}_{e}L$, we find
This equation may be manipulated to yield the relationship
Using Equations (36) and (38) we then arrive at
or, upon further arrangement:
 $$\begin{eqnarray}\ln \left(\left(\frac{G_{0}}{G_{0}^{0}}\right)^{f}\right)={\it\beta}_{\text{in}}-\ln \left(1+G_{0}\left(e^{{\it\beta}_{\text{in}}}-1\right)\right).\end{eqnarray}$$
$$\begin{eqnarray}\ln \left(\left(\frac{G_{0}}{G_{0}^{0}}\right)^{f}\right)={\it\beta}_{\text{in}}-\ln \left(1+G_{0}\left(e^{{\it\beta}_{\text{in}}}-1\right)\right).\end{eqnarray}$$ There are no closed form solutions to this transcendental equation; however, the equations may be solved numerically. Knowing ![]() ${\it\beta}$,
${\it\beta}$, ![]() $G_{0}^{0}$ and f, we can solve for
$G_{0}^{0}$ and f, we can solve for ![]() $G_{0}$, and then using the Frantz–Nodvik Equation (38), we can calculate the saturated gain as well as
$G_{0}$, and then using the Frantz–Nodvik Equation (38), we can calculate the saturated gain as well as ![]() $J_{\text{out}}$. The formalism above can be used to solve for the initial and final inversion densities, the extracted inversion density, the starting and final small-signal gains, the saturated gain, and the output fluence for any pump pulse duration
$J_{\text{out}}$. The formalism above can be used to solve for the initial and final inversion densities, the extracted inversion density, the starting and final small-signal gains, the saturated gain, and the output fluence for any pump pulse duration ![]() $T$ and repetition rate
$T$ and repetition rate ![]() ${\it\nu}_{R}$. We have developed a computer code to implement these results, as applied to spatially flat-topped or Gaussian distributions. Equation (51) is solved in the form
${\it\nu}_{R}$. We have developed a computer code to implement these results, as applied to spatially flat-topped or Gaussian distributions. Equation (51) is solved in the form
 $$\begin{eqnarray}\displaystyle \ln \left(\left(\frac{G_{0}}{G_{0}^{0}}\right)^{f}\right)-{\it\beta}_{\text{in}}+\ln \left(1+G_{0}\left(e^{{\it\beta}_{\text{in}}}-1\right)\right)=0.\quad & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \ln \left(\left(\frac{G_{0}}{G_{0}^{0}}\right)^{f}\right)-{\it\beta}_{\text{in}}+\ln \left(1+G_{0}\left(e^{{\it\beta}_{\text{in}}}-1\right)\right)=0.\quad & & \displaystyle\end{eqnarray}$$ In addition to the above relationships, the code keeps tracks of a number of other quantities as well, including the CW small-signal gain given by ![]() $G_{0}^{\text{cw}}$,
$G_{0}^{\text{cw}}$,
the CW total energy stored in pumped volume ![]() $V_{p}$,
$V_{p}$, ![]() $E_{T}^{\text{cw}}$,
$E_{T}^{\text{cw}}$,
the total energy stored with re-pumping and just before extraction, ![]() $E_{T}^{i}$
$E_{T}^{i}$
 $$\begin{eqnarray}E_{T}^{i}=\frac{n_{\text{cw}}\left(1-e^{-\left(\frac{T}{{\it\tau}}\right)}\right)}{\left(1-e^{-\left(\frac{T_{\text{bp}}}{{\it\tau}}\right)}\right)}\left(\frac{hc}{{\it\lambda}_{L}}\right)V_{p},\end{eqnarray}$$
$$\begin{eqnarray}E_{T}^{i}=\frac{n_{\text{cw}}\left(1-e^{-\left(\frac{T}{{\it\tau}}\right)}\right)}{\left(1-e^{-\left(\frac{T_{\text{bp}}}{{\it\tau}}\right)}\right)}\left(\frac{hc}{{\it\lambda}_{L}}\right)V_{p},\end{eqnarray}$$ and the total energy remaining after extraction, ![]() $E_{T}^{f}$,
$E_{T}^{f}$,
An additional quantity of interest is the energy extraction efficiency ![]() ${\it\eta}_{\text{ex}}$, given by
${\it\eta}_{\text{ex}}$, given by
![]() $E_{\text{out}}$ and
$E_{\text{out}}$ and ![]() $E_{\text{in}}$ are found from the obvious relationships
$E_{\text{in}}$ are found from the obvious relationships
and ![]() $E_{\text{Stored}}=E_{T}^{i}$. Then
$E_{\text{Stored}}=E_{T}^{i}$. Then ![]() ${\it\eta}_{\text{ex}}$ can be expressed as
${\it\eta}_{\text{ex}}$ can be expressed as
 $$\begin{eqnarray}{\it\eta}_{\text{ex}}=(J_{\text{out}}-J_{\text{in}})\left(\frac{{\it\lambda}_{L}}{hcL}\right)\frac{(1-e^{-(\frac{T_{\text{bp}}}{{\it\tau}})})}{n_{\text{cw}}(1-e^{-(\frac{T}{{\it\tau}})})}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\eta}_{\text{ex}}=(J_{\text{out}}-J_{\text{in}})\left(\frac{{\it\lambda}_{L}}{hcL}\right)\frac{(1-e^{-(\frac{T_{\text{bp}}}{{\it\tau}})})}{n_{\text{cw}}(1-e^{-(\frac{T}{{\it\tau}})})}.\end{eqnarray}$$3.3 Use of Frantz–Nodvik equation in system modeling: generalized form
We begin this Section by first writing the well-known Avizonis–Grotbeck equation describing the variation of the pulse fluence ![]() $J$ with distance z in an amplifier as:
$J$ with distance z in an amplifier as:
In Equation (60), ![]() $J$ is the fluence,
$J$ is the fluence, ![]() $J_{S}$ the saturation fluence,
$J_{S}$ the saturation fluence, ![]() $g_{0}$ the gain/length, and
$g_{0}$ the gain/length, and ![]() ${\it\alpha}_{L}$ is a general loss coefficient per unit length. By assuming
${\it\alpha}_{L}$ is a general loss coefficient per unit length. By assuming ![]() ${\it\alpha}_{L}=0$, Equation (60) is easily integrated to give the Frantz–Nodvik equation for the saturated gain, given by
${\it\alpha}_{L}=0$, Equation (60) is easily integrated to give the Frantz–Nodvik equation for the saturated gain, given by
 $$\begin{eqnarray}\displaystyle G_{S} & = & \displaystyle \left(\frac{J_{S}}{J_{\text{in}}}\right)\ln \left[1+e^{g_{0}L}\left(e^{\left(\frac{J_{\text{in}}}{J_{S}}\right)}-1\right)\right]\nonumber\\ \displaystyle & = & \displaystyle \left(\frac{J_{S}}{J_{\text{in}}}\right)\ln \left[1+G_{0}\left(e^{\left(\frac{J_{\text{in}}}{J_{S}}\right)}-1\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G_{S} & = & \displaystyle \left(\frac{J_{S}}{J_{\text{in}}}\right)\ln \left[1+e^{g_{0}L}\left(e^{\left(\frac{J_{\text{in}}}{J_{S}}\right)}-1\right)\right]\nonumber\\ \displaystyle & = & \displaystyle \left(\frac{J_{S}}{J_{\text{in}}}\right)\ln \left[1+G_{0}\left(e^{\left(\frac{J_{\text{in}}}{J_{S}}\right)}-1\right)\right],\end{eqnarray}$$ ![]() $G_{0}$ is the exponential small-signal gain; by knowing the input fluence and the small-signal gain, one can then calculate the saturated gain for an amplifier of length
$G_{0}$ is the exponential small-signal gain; by knowing the input fluence and the small-signal gain, one can then calculate the saturated gain for an amplifier of length ![]() $L$. In most laser systems, a number of amplifiers are usually required to meet performance goals. For systems we have demonstrated or are presently demonstrating, for example, as many as 15 laser disks may be used. To simplify the laser pulse extraction modeling using the Frantz–Nodvik equation, it is convenient to use a cascaded Frantz–Nodvik approach where the output of the first amplifier for example is incident on a second amplifier. If the amplifiers are identical, then we have as the equations for the output fluences of the first and second amplifiers:
$L$. In most laser systems, a number of amplifiers are usually required to meet performance goals. For systems we have demonstrated or are presently demonstrating, for example, as many as 15 laser disks may be used. To simplify the laser pulse extraction modeling using the Frantz–Nodvik equation, it is convenient to use a cascaded Frantz–Nodvik approach where the output of the first amplifier for example is incident on a second amplifier. If the amplifiers are identical, then we have as the equations for the output fluences of the first and second amplifiers:
 $$\begin{eqnarray}\displaystyle J_{\text{out}}^{1}=G_{S}^{1}J_{\text{in}}^{1}=J_{S}\ln \left[1+G_{0}^{1}\left(e^{\left(\frac{J_{\text{in}}^{1}}{J_{S}}\right)}-1\right)\right], & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{\text{out}}^{1}=G_{S}^{1}J_{\text{in}}^{1}=J_{S}\ln \left[1+G_{0}^{1}\left(e^{\left(\frac{J_{\text{in}}^{1}}{J_{S}}\right)}-1\right)\right], & & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle J_{\text{out}}^{2}=G_{S}^{2}J_{\text{in}}^{2}=J_{S}\ln \left[1+G_{0}^{2}\left(e^{\left(\frac{J_{\text{in}}^{2}}{J_{S}}\right)}-1\right)\right]. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{\text{out}}^{2}=G_{S}^{2}J_{\text{in}}^{2}=J_{S}\ln \left[1+G_{0}^{2}\left(e^{\left(\frac{J_{\text{in}}^{2}}{J_{S}}\right)}-1\right)\right]. & & \displaystyle\end{eqnarray}$$ If we now use ![]() $J_{\text{out}}^{1}=J_{\text{in}}^{2}$, and substitute Equation (62) for
$J_{\text{out}}^{1}=J_{\text{in}}^{2}$, and substitute Equation (62) for ![]() $J_{\text{in}}^{2}$ in the exponential of Equation (63), we find the following equation:
$J_{\text{in}}^{2}$ in the exponential of Equation (63), we find the following equation:
 $$\begin{eqnarray}J_{\text{out}}^{2}=G_{S}^{2}J_{\text{in}}^{2}=J_{S}\ln \left[1+G_{0}^{2}G_{0}^{1}\left(e^{\left(\frac{J_{\text{in}}^{1}}{J_{S}}\right)}-1\right)\right].\end{eqnarray}$$
$$\begin{eqnarray}J_{\text{out}}^{2}=G_{S}^{2}J_{\text{in}}^{2}=J_{S}\ln \left[1+G_{0}^{2}G_{0}^{1}\left(e^{\left(\frac{J_{\text{in}}^{1}}{J_{S}}\right)}-1\right)\right].\end{eqnarray}$$Thus we can see that by utilizing the two Frantz–Nodvik equations, it is possible to combine the effect of the two amplifiers into a single gain equation simply by multiplying the two small-signal gains together. For identical amplifiers, each having the same small-signal gain, Equation (64) becomes
 $$\begin{eqnarray}J_{\text{out}}^{2}=G_{S}^{2}J_{\text{in}}^{2}=J_{S}\ln \left[1+\left(G_{0}\right)^{2}\left(e^{\left(\frac{J_{\text{in}}^{1}}{J_{S}}\right)}-1\right)\right].\end{eqnarray}$$
$$\begin{eqnarray}J_{\text{out}}^{2}=G_{S}^{2}J_{\text{in}}^{2}=J_{S}\ln \left[1+\left(G_{0}\right)^{2}\left(e^{\left(\frac{J_{\text{in}}^{1}}{J_{S}}\right)}-1\right)\right].\end{eqnarray}$$The saturated gain is then
 $$\begin{eqnarray}G_{S}^{T}=\frac{J_{\text{out}}^{2}}{J_{\text{in}}^{1}}=\left(\frac{J_{S}}{J_{\text{in}}^{1}}\right)\ln \left[1+\left(G_{0}\right)^{2}\left(e^{\left(\frac{J_{\text{in}}^{1}}{J_{S}}\right)}-1\right)\right].\end{eqnarray}$$
$$\begin{eqnarray}G_{S}^{T}=\frac{J_{\text{out}}^{2}}{J_{\text{in}}^{1}}=\left(\frac{J_{S}}{J_{\text{in}}^{1}}\right)\ln \left[1+\left(G_{0}\right)^{2}\left(e^{\left(\frac{J_{\text{in}}^{1}}{J_{S}}\right)}-1\right)\right].\end{eqnarray}$$ It is easy to show that the saturated gain from ![]() $N$ identical amplifiers is then
$N$ identical amplifiers is then
 $$\begin{eqnarray}G_{S}^{N}=\frac{J_{\text{out}}^{N}}{J_{\text{in}}^{1}}=\left(\frac{J_{S}}{J_{\text{in}}^{1}}\right)\ln \left[1+\left(G_{0}\right)^{N}\left(e^{\left(\frac{J_{\text{in}}^{1}}{J_{S}}\right)}-1\right)\right].\end{eqnarray}$$
$$\begin{eqnarray}G_{S}^{N}=\frac{J_{\text{out}}^{N}}{J_{\text{in}}^{1}}=\left(\frac{J_{S}}{J_{\text{in}}^{1}}\right)\ln \left[1+\left(G_{0}\right)^{N}\left(e^{\left(\frac{J_{\text{in}}^{1}}{J_{S}}\right)}-1\right)\right].\end{eqnarray}$$Equation (67) works for nonidentical amplifiers as well; it is also easy to include a transmission factor to account for any losses between the amplifier stages. We refer to this equation as the cascaded Frantz–Nodvik equation.
Another application for Equation (67) is in modeling double-passed active-mirror or other types of amplifiers. If we ignore any overlap effects, and assume that the first and second extraction pulses are completely separated in time, then the active-mirror gain can be written
 $$\begin{eqnarray}\displaystyle G_{S}^{\text{AM}}=\left(\frac{J_{S}}{J_{\text{in}}^{1}}\right)\ln \left[1+G_{0}^{2}G_{0}^{1}\left(e^{\left(\frac{J_{\text{in}}^{1}}{J_{S}}\right)}-1\right)\right]. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G_{S}^{\text{AM}}=\left(\frac{J_{S}}{J_{\text{in}}^{1}}\right)\ln \left[1+G_{0}^{2}G_{0}^{1}\left(e^{\left(\frac{J_{\text{in}}^{1}}{J_{S}}\right)}-1\right)\right]. & & \displaystyle\end{eqnarray}$$ In this case, the small-signal gain of the first pass, ![]() $G_{0}^{1}$, is greater than the second-pass small-signal gain
$G_{0}^{1}$, is greater than the second-pass small-signal gain ![]() $G_{0}^{2}$ since the first pass reduces the stored inversion density; it is then necessary to find the remaining inversion and to calculate the remaining small-signal gain
$G_{0}^{2}$ since the first pass reduces the stored inversion density; it is then necessary to find the remaining inversion and to calculate the remaining small-signal gain ![]() $G_{0}^{2}$ available for pass two, a feat that is easily accomplished. Equation (68) is then convenient to use in modeling the extraction from active-mirror amplifiers; a second way to accomplish the same task is to use two Frantz–Nodvik equations serially. The two approaches agree exactly.
$G_{0}^{2}$ available for pass two, a feat that is easily accomplished. Equation (68) is then convenient to use in modeling the extraction from active-mirror amplifiers; a second way to accomplish the same task is to use two Frantz–Nodvik equations serially. The two approaches agree exactly.
For pulses that overlap in time, Equation (68) still applies. It has been shown that the Frantz–Nodvik equation is invariant to any starting pulse shape. This is because the extracted inversion is proportional to the total fluence only, and is thus not sensitive to pulse shape. This means that two pulses with exactly the same total fluence, but with widely different pulsewidths, will produce exactly the same Frantz–Nodvik saturated gain. Because of this pulsewidth invariant property, we can see that even overlapped pulses in the active-mirror extraction volume with nanosecond durations and extracting a ![]() ${\sim}1~\text{cm}$ thick disk must have the same extraction efficiency as a pulse, that is, say only 1 ps duration, and that the overlap does not affect the extraction efficiency. Thus, calculating the extraction efficiency serially, using two pulses that are assumed not to overlap in time, results in the same extraction efficiency as for two temporally overlapped pulses. We of course ignore any gain narrowing that may occur at a pulse leading edge for example; in that case a more sophisticated finite-element approach is needed.
${\sim}1~\text{cm}$ thick disk must have the same extraction efficiency as a pulse, that is, say only 1 ps duration, and that the overlap does not affect the extraction efficiency. Thus, calculating the extraction efficiency serially, using two pulses that are assumed not to overlap in time, results in the same extraction efficiency as for two temporally overlapped pulses. We of course ignore any gain narrowing that may occur at a pulse leading edge for example; in that case a more sophisticated finite-element approach is needed.
3.4 Calculating nonlinear phase with the Frantz–Nodvik equation
As discussed previously in Section 2.6, the ![]() $B$-integral defined by Equation (8) is an important system design parameter.
$B$-integral defined by Equation (8) is an important system design parameter. ![]() $B$ is in general a function of the beam radius
$B$ is in general a function of the beam radius ![]() $r$, propagation location
$r$, propagation location ![]() $z$ and time
$z$ and time ![]() $t$,
$t$, ![]() $I(r,z,t)$ is the radially, longitudinally and temporally varying laser intensity, the wavelength
$I(r,z,t)$ is the radially, longitudinally and temporally varying laser intensity, the wavelength ![]() ${\it\lambda}$, and
${\it\lambda}$, and ![]() $z$ is the propagation length parameter. The
$z$ is the propagation length parameter. The ![]() $B$-integral is the nonlinear phase accumulation
$B$-integral is the nonlinear phase accumulation ![]() ${\rm\Delta}{\it\varphi}_{NL}(r,z,t)$ due to the nonlinear index
${\rm\Delta}{\it\varphi}_{NL}(r,z,t)$ due to the nonlinear index ![]() $n_{2}$, and in laser systems must be calculated for all optical and gain elements encountered by the propagating beam. It is customary to calculate the maximum value of the
$n_{2}$, and in laser systems must be calculated for all optical and gain elements encountered by the propagating beam. It is customary to calculate the maximum value of the ![]() $B$-integral where the intensity
$B$-integral where the intensity ![]() $I$ is maximum (
$I$ is maximum (![]() $t=0$). For spatially Gaussian beams, the
$t=0$). For spatially Gaussian beams, the ![]() $B$-integral value at the beam edge is typically very small, and only the on-axis value for
$B$-integral value at the beam edge is typically very small, and only the on-axis value for ![]() $r=0$ is normally specified. For any arbitrary spatial beam profile, is easy to use Equation (8) in a computer code to calculate the
$r=0$ is normally specified. For any arbitrary spatial beam profile, is easy to use Equation (8) in a computer code to calculate the ![]() $B$-integral profile at any location in a laser amplifier or system. In order to calculate
$B$-integral profile at any location in a laser amplifier or system. In order to calculate ![]() $B(r,z,t)={\rm\Delta}{\it\varphi}_{NL}(r,z,t)$, a very important design parameter in HAPP lasers, we have developed an approach that uses the Frantz–Nodvik Equation (38), previously discussed in this paper. We start by explicitly showing the Gaussian intensity distribution as a function or radius and time:
$B(r,z,t)={\rm\Delta}{\it\varphi}_{NL}(r,z,t)$, a very important design parameter in HAPP lasers, we have developed an approach that uses the Frantz–Nodvik Equation (38), previously discussed in this paper. We start by explicitly showing the Gaussian intensity distribution as a function or radius and time:
where ![]() $I_{\text{0P}}$ is the peak intensity on axis
$I_{\text{0P}}$ is the peak intensity on axis ![]() $(r=0)$ and at pulse center for
$(r=0)$ and at pulse center for ![]() $t=0$,
$t=0$, ![]() ${\it\omega}_{0}$ is the
${\it\omega}_{0}$ is the ![]() $1/e^{2}$ radius and
$1/e^{2}$ radius and ![]() $t_{0}$ is the
$t_{0}$ is the ![]() $1/e^{2}$ time half-width. By integrating Equation (69) over the beam area and time, we arrive at an expression for the pulse energy
$1/e^{2}$ time half-width. By integrating Equation (69) over the beam area and time, we arrive at an expression for the pulse energy ![]() $E_{0}$:
$E_{0}$:
We also note that for a Gaussian beam, the ![]() $1/e^{2}$ half-width
$1/e^{2}$ half-width ![]() $t_{0}$ is related to the full width at half maximum pulsewidth
$t_{0}$ is related to the full width at half maximum pulsewidth ![]() $t_{p}$ by the relationship
$t_{p}$ by the relationship
By combining Equations (70) and (72), we find an expression for the peak intensity ![]() $I_{\text{0P}}$ as a function of the pulse energy, full width at half maximum pulsewidth and beam radius:
$I_{\text{0P}}$ as a function of the pulse energy, full width at half maximum pulsewidth and beam radius:
To find the peak fluence ![]() $J_{0}$ for
$J_{0}$ for ![]() $r=0$, we integrate the intensity over time to find
$r=0$, we integrate the intensity over time to find
We now write the general expression for the passive ![]() $B$-integral as
$B$-integral as
or, if gain is present in the propagation medium,
If we now restrict the calculated value to the peak value for ![]() $r=0$ and
$r=0$ and ![]() $t=0$, we have
$t=0$, we have
Using the previous Equations (72) and (75), we then find an equation for calculating ![]() $B$:
$B$:
We have set ![]() $J_{0}=J_{\text{in}}$ in Equation (77). For passive (nonamplifying) optical elements in a laser system, the
$J_{0}=J_{\text{in}}$ in Equation (77). For passive (nonamplifying) optical elements in a laser system, the ![]() $B$-integral becomes simply
$B$-integral becomes simply
Now, using the Frantz–Nodvik equation (Equation (61)), we can then write the final expression for ![]() $B$, evaluated at
$B$, evaluated at ![]() $z=L$:
$z=L$:
 $$\begin{eqnarray}\displaystyle B\left(L\right) & = & \displaystyle \left(\frac{4\left({\it\pi}\ln (2)\right)^{1/2}{\it\gamma}_{NL}J_{s}}{{\it\lambda}_{L}t_{p}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{0}^{L}\ln \left[1+e^{g_{0}L}\left(e^{\left(\frac{J_{\text{in}}}{J_{S}}\right)}-1\right)\right]dz.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B\left(L\right) & = & \displaystyle \left(\frac{4\left({\it\pi}\ln (2)\right)^{1/2}{\it\gamma}_{NL}J_{s}}{{\it\lambda}_{L}t_{p}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{0}^{L}\ln \left[1+e^{g_{0}L}\left(e^{\left(\frac{J_{\text{in}}}{J_{S}}\right)}-1\right)\right]dz.\end{eqnarray}$$The integral in Equation (79) can be solved analytically; the result is shown below:
 $$\begin{eqnarray}\displaystyle B\left(L\right) & = & \displaystyle \left(\frac{4\left({\it\pi}\ln (2)\right)^{1/2}{\it\gamma}_{NL}J_{s}}{{\it\lambda}_{L}t_{p}g_{0}}\right)\left\{\text{Li}_{2}\left(1-e^{\left(\frac{J_{\text{in}}}{J_{S}}\right)}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\text{Li}_{2}\left(\left(1-e^{\left(\frac{J_{\text{in}}}{J_{S}}\right)}\right)e^{\left(g_{0}L\right)}\right)\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B\left(L\right) & = & \displaystyle \left(\frac{4\left({\it\pi}\ln (2)\right)^{1/2}{\it\gamma}_{NL}J_{s}}{{\it\lambda}_{L}t_{p}g_{0}}\right)\left\{\text{Li}_{2}\left(1-e^{\left(\frac{J_{\text{in}}}{J_{S}}\right)}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\text{Li}_{2}\left(\left(1-e^{\left(\frac{J_{\text{in}}}{J_{S}}\right)}\right)e^{\left(g_{0}L\right)}\right)\right\}.\end{eqnarray}$$ ![]() $\text{Li}_{2}(z)$ is the dilogarithm, which may be calculated from the polylogarithm infinite sum with
$\text{Li}_{2}(z)$ is the dilogarithm, which may be calculated from the polylogarithm infinite sum with ![]() $n=2$:
$n=2$:
While the polylogarithm may be calculated using computer programs such as Mathematica, it can be difficult to integrate into stand-alone laser amplifier extraction programs.
Limiting solutions:
It is well known that the Frantz–Nodvik equation has two limiting solutions for ![]() $J_{\text{in}}/J_{S}\ll 1$, and for
$J_{\text{in}}/J_{S}\ll 1$, and for ![]() $J_{\text{in}}/J_{S}\gg 1$. In the former case the gain is equal to the small-signal gain
$J_{\text{in}}/J_{S}\gg 1$. In the former case the gain is equal to the small-signal gain ![]() $G_{0}$, and Equation (79) for the
$G_{0}$, and Equation (79) for the ![]() $B$-integral reverts to
$B$-integral reverts to
For the latter case, we obtain
First-order computer laser design codes that ray-trace assumed Gaussian beams through a sequence of amplifiers are very useful in determining whether or not an estimated laser system configuration has the potential to achieve a prescribed set of laser system output parameters, and can be used to determine for example the number of finite amplification stages required, and to determine what beam sizes are required to achieve a reasonably efficient system, as well as to determine how close required fluences might be to damage thresholds. More detailed system simulations usually then follow to include finite-element beam propagation, diffraction effects, and an accurate calculation of the ![]() $B$-integral. It is then usually sufficient for first-order laser design codes to only estimate the value of the
$B$-integral. It is then usually sufficient for first-order laser design codes to only estimate the value of the ![]() $B$-integral in amplification stages. As we have seen, no truly simple calculation approaches are presently available to do so, except in the case where the amplifier fluence is greater than or approximately equal to the saturation fluence, in which case Equation (83) may be employed. Another method that we have employed is to calculate the fluences at the input and output faces of an amplifier,
$B$-integral in amplification stages. As we have seen, no truly simple calculation approaches are presently available to do so, except in the case where the amplifier fluence is greater than or approximately equal to the saturation fluence, in which case Equation (83) may be employed. Another method that we have employed is to calculate the fluences at the input and output faces of an amplifier, ![]() $J_{\text{in}}$ and
$J_{\text{in}}$ and ![]() $J_{\text{out}}$, and to then estimate the average
$J_{\text{out}}$, and to then estimate the average ![]() $B$-integral value using the equation
$B$-integral value using the equation
 $$\begin{eqnarray}\displaystyle B\left(L\right) & = & \displaystyle \left(\frac{4\left({\it\pi}\ln (2)\right)^{1/2}{\it\gamma}_{NL}L}{{\it\lambda}_{L}t_{p}}\right)\left[\frac{J_{\text{out}}+J_{\text{in}}}{2}\right]\nonumber\\ \displaystyle & = & \displaystyle \left(\frac{4\left({\it\pi}\ln (2)\right)^{1/2}{\it\gamma}_{NL}L}{{\it\lambda}_{L}t_{p}}\right)\left(\frac{G_{S}+1}{2}\right)J_{\text{in}}.\quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B\left(L\right) & = & \displaystyle \left(\frac{4\left({\it\pi}\ln (2)\right)^{1/2}{\it\gamma}_{NL}L}{{\it\lambda}_{L}t_{p}}\right)\left[\frac{J_{\text{out}}+J_{\text{in}}}{2}\right]\nonumber\\ \displaystyle & = & \displaystyle \left(\frac{4\left({\it\pi}\ln (2)\right)^{1/2}{\it\gamma}_{NL}L}{{\it\lambda}_{L}t_{p}}\right)\left(\frac{G_{S}+1}{2}\right)J_{\text{in}}.\quad\end{eqnarray}$$3.5 LIDTs
Perhaps the most important parameter in the design of any laser system is the LIDT, the value of fluence, intensity, or average power that if exceeded, will result in irreversible damage to at least one optical or lasing element in the laser system. If the weakest component in a laser system has an LIDT that is a fraction of the laser saturation fluence, one cannot obtain a high overall system efficiency because for high extraction efficiency the input laser fluence must be at least equal to the saturation fluence, and in the case of Gaussian beams, many times the saturation fluence. A small saturation fluence is obtained for laser materials with a large stimulated-emission cross-section. The LIDT has a strong laser pulsewidth dependence that results in picosecond pulses having a smaller damage threshold than nanosecond pulses, and femtosecond less than picosecond. It was a challenge in early ultrafast lasers to scale laser output due to the limiting value of LIDT’s in the picosecond and particularly in the femtosecond regime. It was because of those damage limitations, as well as to avoid the type of nonlinear effects discussed in the aforementioned, that the technique of CPA was invented[Reference Strickland and Mourou74]. Using CPA, a short femtosecond pulse for example is stretched using diffraction gratings or other means, to the picosecond regime where damage thresholds are substantially larger, After stretching, the initial pulse is amplified in a following beam line of amplifiers where the larger pulsewidth allows nonlinear effects to be avoided or minimized, and where more efficient extraction can be obtained due to the larger damage threshold. After amplification, the stretched pulse is compressed, in many cases using a diffraction-grating compressor, to restore the pulsewidth close to its initial value. Managing the accumulated dispersion, and compensating for it using certain types of compressor configurations determines how close to the initial pulsewidth the final compressed pulse comes. Reducing gain narrowing is also an important contributing factor to the compressed pulse duration.
The literature of LIDT’s is vast. Interested readers that have a need to thoroughly explore the field may consult the book by Wood[Reference Wood75], as well as the many publications of the Annual Boulder Damage Symposium (Boulder, Colorado, USA), a conference that celebrated it’s 45th year in 2013. The LIDT of laser and optical materials is a consequence of the many physical mechanisms connected with the high fields achievable with laser. When intense beams are transmitted through crystals or glasses, many nonlinear effects such as harmonic generation, self-focusing and self-phase modulation, nonlinear absorption, excited-state absorption, stimulated Brillouin or Raman scattering and others may occur, and contribute to irreversible damage. In addition, electron avalanches may occur in response to a strong E field, and plasmas may form on a crystal surface or internally. High-average-power effects, that are now becoming more and more important, can be caused by absorption and melting of dielectric crystals or dielectric coatings, and can lead to distortion de-polarization, and ultimately fracture of crystals or other optics. It is a general observation, supported by measurements, that the LIDT of surfaces are substantially smaller than bulk LIDT’s. LIDT’s are a strong function of the laser wavelength, with visible and UV LIDT’s much less than those obtained around 1000 nm[Reference Wood75, Reference Koechner76].
The pulsewidth dependence of surface LIDT’s is rather simple in the picosecond–nanosecond-long-pulse regime, varying as the pulsewidth to the ![]() $\frac{1}{2}$ power[Reference Wood75, Reference Koechner76] for pulsewidths
$\frac{1}{2}$ power[Reference Wood75, Reference Koechner76] for pulsewidths ![]() ${\it\tau}_{P}$
${\it\tau}_{P}$ ![]() ${>}$ about 20 ps. For picosecond pulses
${>}$ about 20 ps. For picosecond pulses ![]() ${<}20$ ps in duration and femtosecond pulses, the dependence is however more complicated[Reference Stuart, Feit, Rubenchik, Shore and Perry77, Reference Stuart, Feit, Herman, Rubenchik, Shore and Perry78]. For
${<}20$ ps in duration and femtosecond pulses, the dependence is however more complicated[Reference Stuart, Feit, Rubenchik, Shore and Perry77, Reference Stuart, Feit, Herman, Rubenchik, Shore and Perry78]. For ![]() ${\it\tau}_{P}>20$ ps, the damage morphology is thermal in nature, and usually accompanied by surface melting and boiling; electronic kinetic energy is transferred to the crystal lattice via avalanche multi-photon ionization and inverse Bremsstrahlung free carrier absorption, and diffuses in the lattice during the pulsewidth
${\it\tau}_{P}>20$ ps, the damage morphology is thermal in nature, and usually accompanied by surface melting and boiling; electronic kinetic energy is transferred to the crystal lattice via avalanche multi-photon ionization and inverse Bremsstrahlung free carrier absorption, and diffuses in the lattice during the pulsewidth ![]() ${\it\tau}_{P}$. For short ps and femtosecond pulsewidths (
${\it\tau}_{P}$. For short ps and femtosecond pulsewidths (![]() ${\it\tau}_{P}<20~\text{ps}$), the LIDT is explained by the nonlinear excitation of electrons to the conduction band from avalanche ionization, tunneling ionization, and multi-photon absorption. After reaching a critical plasma density of
${\it\tau}_{P}<20~\text{ps}$), the LIDT is explained by the nonlinear excitation of electrons to the conduction band from avalanche ionization, tunneling ionization, and multi-photon absorption. After reaching a critical plasma density of ![]() ${\approx}10^{21}/\text{cm}^{3}$, strong absorption occurs due to inverse Bremsstrahlung, that results in ablation and permanent structural changes. Measurements of the LIDT using the standard high-purity material
${\approx}10^{21}/\text{cm}^{3}$, strong absorption occurs due to inverse Bremsstrahlung, that results in ablation and permanent structural changes. Measurements of the LIDT using the standard high-purity material ![]() $\text{SiO}_{2}$ or
$\text{SiO}_{2}$ or ![]() $\text{CaF}_{2}$, have resulted in rather complete sets of data showing the LIDT dependence on
$\text{CaF}_{2}$, have resulted in rather complete sets of data showing the LIDT dependence on ![]() ${\it\tau}_{P}$ from 140 fs to 1 ns. In general, the LIDT value decreases in a monotonic fashion over the entire range of pulsewidths. A more recent publication shows the
${\it\tau}_{P}$ from 140 fs to 1 ns. In general, the LIDT value decreases in a monotonic fashion over the entire range of pulsewidths. A more recent publication shows the ![]() $\text{SiO}_{2}$ LIDT dependence on the pulsewidth over the more limited range of 7–350 fs. While the pulsewidth dependence of all dielectric elements such as crystals and dielectric coatings have been found to show a similar pulsewidth dependence, from a laser designers perspective every optic in a HAPP systems should be LIDT tested before installation, at the expected operating pulsewidth and average power. Fortunately, many laser optics fabricators are now beginning to offer such measurements.
$\text{SiO}_{2}$ LIDT dependence on the pulsewidth over the more limited range of 7–350 fs. While the pulsewidth dependence of all dielectric elements such as crystals and dielectric coatings have been found to show a similar pulsewidth dependence, from a laser designers perspective every optic in a HAPP systems should be LIDT tested before installation, at the expected operating pulsewidth and average power. Fortunately, many laser optics fabricators are now beginning to offer such measurements.
It is a shortcoming of the present state of the art that high-average-power effects have received far less attention than high-peak-power effects. Now that we are witnessing the advent of HAPP laser systems, much attention will be focused in the near future on determining the LIDT’s of laser crystals and optics under very extreme conditions. LIDT’s at low temperature are scarce and in most cases have not been measured. Recently a publication reported a reduced damage threshold at cryogenic temperatures relative to the room-temperature value[Reference Wang, Zhang and He79]. This is in contrast to a number of publications that have reported increased damage thresholds at cryogenic temperatures[Reference Yang, Yuan, Deng, Xiang, Zheng, He, Jiang, Lv, Ye, Wang and Zu80–Reference Mikami, Motokoshi, Somekawa, Jitsuno, Fujita and Tanake82]. Increased laser damage threshold measurement efforts at cryogenic temperatures are needed to further our understanding of the design of cryogenic laser devices and to increase our knowledge of the scaling of the damage threshold with temperature.
Table 5. Calculated room-temperature values of the linear index and the first-, second-, third- and fourth-order dispersion parameters for legacy and newer laser crystals of length 1 mm. Also shown are the operating laser wavelengths, as well as references to allow readers to know what Sellmeier or alternative index equation was used in the calculations. Table reproduced from Ref. [Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3].

3.6 Dispersion effects
Dispersion effects in high-peak-power laser systems are negligible for nanosecond pulsewidths, slightly important for picosecond pulsewidths, and critically important for femtosecond lasers. The following well-known equation may be used to estimate the importance of the operating pulsewidth:
 $$\begin{eqnarray}\frac{{\it\tau}_{P}\left(z\right)}{{\it\tau}_{P0}}=\sqrt{1+\left(\frac{{\it\beta}_{2}z}{{\it\tau}_{PO}^{2}}\right)^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{{\it\tau}_{P}\left(z\right)}{{\it\tau}_{P0}}=\sqrt{1+\left(\frac{{\it\beta}_{2}z}{{\it\tau}_{PO}^{2}}\right)^{2}}.\end{eqnarray}$$ ![]() ${\it\tau}_{P0}$ is the pulsewidth entering a dispersive medium,
${\it\tau}_{P0}$ is the pulsewidth entering a dispersive medium, ![]() ${\it\beta}_{2}$ is the second-order dispersion coefficient (GVD) and
${\it\beta}_{2}$ is the second-order dispersion coefficient (GVD) and ![]() $z$ the propagation distance.
$z$ the propagation distance. ![]() ${\it\tau}_{P}(z)$ is the pulsewidth after propagating a distance
${\it\tau}_{P}(z)$ is the pulsewidth after propagating a distance ![]() $z$, and is broadened by the effect of the second-order dispersion. This approach ignores any broadening effects due to the higher-order dispersion terms. If we examine a laser system using the laser material Yb:YAG for example, and assume that the total path length is typically 10 cm for the amplification stages, then about 6,700
$z$, and is broadened by the effect of the second-order dispersion. This approach ignores any broadening effects due to the higher-order dispersion terms. If we examine a laser system using the laser material Yb:YAG for example, and assume that the total path length is typically 10 cm for the amplification stages, then about 6,700![]() $~\text{fs}^{2}$ of GVD are accumulated in a single pass. For a 1 ns pulsewidth, the pulse broadening term
$~\text{fs}^{2}$ of GVD are accumulated in a single pass. For a 1 ns pulsewidth, the pulse broadening term ![]() ${\it\beta}_{2}z/{\it\tau}_{PO}^{2}$ amounts to
${\it\beta}_{2}z/{\it\tau}_{PO}^{2}$ amounts to ![]() ${\approx}2\times 10^{-8}$, so the square root in Equation (85) is close to 1, and the pulsewidth unaffected. For a 1 ps pulsewidth,
${\approx}2\times 10^{-8}$, so the square root in Equation (85) is close to 1, and the pulsewidth unaffected. For a 1 ps pulsewidth, ![]() ${\it\beta}_{2}z/{\it\tau}_{PO}^{2}$ is 0.0186, and the square root takes the value 1.00017, so the pulsewidth is still hardly affected. For a 10 fs pulsewidth, however,
${\it\beta}_{2}z/{\it\tau}_{PO}^{2}$ is 0.0186, and the square root takes the value 1.00017, so the pulsewidth is still hardly affected. For a 10 fs pulsewidth, however, ![]() ${\it\beta}_{2}z/{\it\tau}_{PO}^{2}$ is calculated to be about 185.8, and the pulse is significantly broadened to about 137 fs. Now, when other system components such as windows and wave plates are included in the calculation, pulse broadening may become significant at 1 ps as well; however, direct pulse amplification may be used in common cryogenic laser systems with a pulsewidth
${\it\beta}_{2}z/{\it\tau}_{PO}^{2}$ is calculated to be about 185.8, and the pulse is significantly broadened to about 137 fs. Now, when other system components such as windows and wave plates are included in the calculation, pulse broadening may become significant at 1 ps as well; however, direct pulse amplification may be used in common cryogenic laser systems with a pulsewidth ![]() ${>}5$–10 ps, as long as there are no laser-induced damage constraints. This approach has been successfully used in a high repetition rate, low energy/pulse cryogenic laser system for example[Reference Brown, Singley, Kowalewski, Guelzow and Vitali83]. For repetition rates less than a few kHz in which the energy/pulse is typically large, CPA must be used to increase the available damage threshold. In that case the dispersion used to stretch the pulse, typically by a diffraction-grating pair, as well as the accumulated dispersion from pulse propagation through the laser system must be compensated in the compressor stage, typically up to at least to the second order, and in some cases the third-order dispersion term.
${>}5$–10 ps, as long as there are no laser-induced damage constraints. This approach has been successfully used in a high repetition rate, low energy/pulse cryogenic laser system for example[Reference Brown, Singley, Kowalewski, Guelzow and Vitali83]. For repetition rates less than a few kHz in which the energy/pulse is typically large, CPA must be used to increase the available damage threshold. In that case the dispersion used to stretch the pulse, typically by a diffraction-grating pair, as well as the accumulated dispersion from pulse propagation through the laser system must be compensated in the compressor stage, typically up to at least to the second order, and in some cases the third-order dispersion term.

Figure 13. Schematic diagram of the Thor-300 Cryo Amplifier system; the gray boxes represent copper heat sinks that are coupled to closed-cycle cryogenic coolers, the disks are shown on opposite faces of the heat sinks. Green arrows represent 940 nm pump beams used to optically pump the disks, A more detailed description may be found in the text.
Table 5, reproduced from Ref. [Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3], shows calculated values of the index of refraction, the wavelength the values were calculated at, and the first-, second-, third- and fourth-order dispersion coefficients. In addition, references are provided to allow interested readers to know what form of the index equation was used, as well as the values of the constants. We have included crystals and optical materials often used in ultrafast lasers, including Ti:![]() $\text{Al}_{2}\text{O}_{3}$, Cr:LiSAF, Cr:LiCAF and a number of Yb laser materials. Some entries in Table 5 have also served as a check on the calculational accuracy. For example, for BK-7 at 800 nm and fused silica
$\text{Al}_{2}\text{O}_{3}$, Cr:LiSAF, Cr:LiCAF and a number of Yb laser materials. Some entries in Table 5 have also served as a check on the calculational accuracy. For example, for BK-7 at 800 nm and fused silica ![]() $(\text{SiO}_{2})$ at 800 nm, the calculated dispersion parameter values agree closely with previously published results[Reference Krupke, Shinn, Marion, Caird and Stokowski32]. For Ti:
$(\text{SiO}_{2})$ at 800 nm, the calculated dispersion parameter values agree closely with previously published results[Reference Krupke, Shinn, Marion, Caird and Stokowski32]. For Ti:![]() $\text{Al}_{2}\text{O}_{3}$, the dispersion parameters were calculated for a Sellmeier equation used for sapphire grown using the heat exchanger method (HEM), and are similar to previously published results[Reference Backus, Durfee, Murnane and Kapteyn84], but a one-to-one comparison cannot be made because the data and Sellmeier equations used in Ref. [Reference Krupke, Shinn, Marion, Caird and Stokowski32] were not revealed. The variation of the index of refraction with wavelength can also be slightly different depending upon the crystal growth method, and the corresponding Sellmeier equations will be somewhat different as well, and it is likely that such differences explain the variation between our calculations and Ref. [Reference Backus, Durfee, Murnane and Kapteyn84]. We have endeavored to calculate accurate values for the dispersion parameters reported in Table 5, and have checked and compared our results to other values found in the literature where available. Readers should be aware however that coding long and tedious Sellmeier, Cauchy, Laurent and other equations and their derivatives up to the fourth order may lead to some inadvertent errors being present.
$\text{Al}_{2}\text{O}_{3}$, the dispersion parameters were calculated for a Sellmeier equation used for sapphire grown using the heat exchanger method (HEM), and are similar to previously published results[Reference Backus, Durfee, Murnane and Kapteyn84], but a one-to-one comparison cannot be made because the data and Sellmeier equations used in Ref. [Reference Krupke, Shinn, Marion, Caird and Stokowski32] were not revealed. The variation of the index of refraction with wavelength can also be slightly different depending upon the crystal growth method, and the corresponding Sellmeier equations will be somewhat different as well, and it is likely that such differences explain the variation between our calculations and Ref. [Reference Backus, Durfee, Murnane and Kapteyn84]. We have endeavored to calculate accurate values for the dispersion parameters reported in Table 5, and have checked and compared our results to other values found in the literature where available. Readers should be aware however that coding long and tedious Sellmeier, Cauchy, Laurent and other equations and their derivatives up to the fourth order may lead to some inadvertent errors being present.
3.7 Computer code design results
We have written a number of VBA (Visual Basic Application) computer codes to model single- and double-passed active-mirror chains as well as straight-through laser disks, and regenerative amplifiers, based on the pulsed pump extraction model (PPEM) described in Section 3.2, and have used the code to investigate the pulse energy scaling in excess of 1 J![]() $/$pulse at 1 kHz. In this section, we will review some of the features and results of the code, which we refer to as PPEM-8.0.
$/$pulse at 1 kHz. In this section, we will review some of the features and results of the code, which we refer to as PPEM-8.0.
One system we have modeled, the Thor 300 cryogenic amplifier, is shown in Figure 13. Eight active-mirror disks are used to amplify an initial beam, that is imaged and double-passed through the first stage using a series of HR mirrors and a final HR mirror and quarter-wave plate. A positive and negative lens pair (not shown in Figure 13) is used to image the beam through the stage. After rejection from the first thin-film polarizer (TFP), the beam is further imaged and magnified using the vacuum beam expander to the second TFP. The beam is then imaged through the second double pass which also includes a final HR mirror and quarter-wave plate, using a second positive–negative lens pair, and rejected from the second TFP and exits the system. The system architecture is largely driven by the limited heat removal capacity of the closed-cycle cryogenic coolers.

Figure 14. Thor-300 Yb:YAG pump chamber showing entrance window, vacuum, window, and mounting flanges, and a pulse-tube He closed-cycle cryocooler mounted on top.

Figure 15. Evolution of the energy/pulse in Thor-300 cryogenic laser system as a function of the optical element number and at a 1 kHz repetition rate. The pump pulse duration is ![]() $500~{\rm\mu}\text{s}$. The Gaussian beam radius in elements 1-82 is 2 mm; after beam expansion at element 82, the beam radius is 3.5 mm.
$500~{\rm\mu}\text{s}$. The Gaussian beam radius in elements 1-82 is 2 mm; after beam expansion at element 82, the beam radius is 3.5 mm.
The system uses 200 W of pump peak power per active-mirror disk, for a total pump power of 1600 W. The pump pulse duration is ![]() $500~{\rm\mu}\text{s}$ and the repetition rate 1 kHz. Each active-mirror disk is 25 mm in diameter and has a 3.75 mm thick Yb:YAG section with 10 at.% doping. A second 2 mm thick clear YAG disk is diffusion-bonded to the doped disk forming a 25 mm diameter
$500~{\rm\mu}\text{s}$ and the repetition rate 1 kHz. Each active-mirror disk is 25 mm in diameter and has a 3.75 mm thick Yb:YAG section with 10 at.% doping. A second 2 mm thick clear YAG disk is diffusion-bonded to the doped disk forming a 25 mm diameter ![]() $\times$ 5.75 mm bonded crystal assembly. The rear surface of each disk has a high reflection (HR) dielectric coating at 940 and 1029 nm and is typically cooled through a thin indium foil by use of a pulse-tube cryocooler that maintains temperature
$\times$ 5.75 mm bonded crystal assembly. The rear surface of each disk has a high reflection (HR) dielectric coating at 940 and 1029 nm and is typically cooled through a thin indium foil by use of a pulse-tube cryocooler that maintains temperature ![]() ${<}120~\text{K}$ at full power pumping. The opposite disk face has an anti-reflection (AR) coating at 940 and 1029 nm. The Thor 300 cryogenic amplifier system modeled, under development by our group, consists of eight active-mirror disks with two disks cooled per closed-cycle pulsed cryocooler. A photograph of one Thor 300 vacuum pump chamber is shown in Figure 14. Each of the four disks on the first double-pass side are pumped with a 4f imaging system that provides a 1:1 magnification from a pump source fiber collimator, with a
${<}120~\text{K}$ at full power pumping. The opposite disk face has an anti-reflection (AR) coating at 940 and 1029 nm. The Thor 300 cryogenic amplifier system modeled, under development by our group, consists of eight active-mirror disks with two disks cooled per closed-cycle pulsed cryocooler. A photograph of one Thor 300 vacuum pump chamber is shown in Figure 14. Each of the four disks on the first double-pass side are pumped with a 4f imaging system that provides a 1:1 magnification from a pump source fiber collimator, with a ![]() $1/e^{2}$ pump beam diameter of 4 mm. The seed beam used to drive the amplifier system is double-passed on both sides using polarization multiplexing. Between the two double passes of the system, the beam is imaged using a vacuum telescope magnifier to a
$1/e^{2}$ pump beam diameter of 4 mm. The seed beam used to drive the amplifier system is double-passed on both sides using polarization multiplexing. Between the two double passes of the system, the beam is imaged using a vacuum telescope magnifier to a ![]() $1/e^{2}$ beam diameter of 7 mm (magnification of 1.75). The design assumes that the seed beam diameter
$1/e^{2}$ beam diameter of 7 mm (magnification of 1.75). The design assumes that the seed beam diameter ![]() $2{\it\omega}_{0}$ is matched to the
$2{\it\omega}_{0}$ is matched to the ![]() $1/e^{2}$ pump beam diameter.
$1/e^{2}$ pump beam diameter.

Figure 16. Evolution of the intensity in Thor-300 cryogenic laser system as a function of the optical element number and at a 1 kHz repetition rate. The pump pulse duration is ![]() $500~{\rm\mu}\text{s}$. The Gaussian beam radius in elements 1-82 is 2 mm; after beam expansion at element 82, the beam radius is 3.5 mm.
$500~{\rm\mu}\text{s}$. The Gaussian beam radius in elements 1-82 is 2 mm; after beam expansion at element 82, the beam radius is 3.5 mm.

Figure 17. Evolution of the intensity (blue line) in Thor-300 cryogenic laser system as a function of the optical element number and at a 1 kHz repetition rate. Also shown is the laser damage threshold for each optical element (red line). The pump pulse duration is ![]() $500~{\rm\mu}\text{s}$. The Gaussian beam radius in elements 1-82 is 2 mm; after beam expansion at element 82, the beam radius is 3.5 mm.
$500~{\rm\mu}\text{s}$. The Gaussian beam radius in elements 1-82 is 2 mm; after beam expansion at element 82, the beam radius is 3.5 mm.

Figure 18. Evolution of the energy/pulse in Thor-300 cryogenic laser system as a function of the optical element number and at a 1 kHz repetition rate. The pump pulse duration is ![]() $500~{\rm\mu}\text{s}$. The Gaussian beam radius in elements 1-82 is 2 mm; after beam expansion at element 82, the beam radius is 3.5 mm.
$500~{\rm\mu}\text{s}$. The Gaussian beam radius in elements 1-82 is 2 mm; after beam expansion at element 82, the beam radius is 3.5 mm.

Figure 19. Evolution of the intensity in Thor-300 cryogenic laser system as a function of the optical element number and at a 1 kHz repetition rate. The pump pulse duration is ![]() $500~{\rm\mu}\text{s}$. The Gaussian beam radius in elements 1-82 is 2 mm; after beam expansion at element 82, the beam radius is 3.5 mm.
$500~{\rm\mu}\text{s}$. The Gaussian beam radius in elements 1-82 is 2 mm; after beam expansion at element 82, the beam radius is 3.5 mm.

Figure 20. Evolution of the intensity (blue line) in Thor-300 cryogenic laser system as a function of the optical element number and at a 1 kHz repetition rate. Also shown is the laser damage threshold for each optical element (red line). The pump pulse duration is ![]() $500~{\rm\mu}\text{s}$. The Gaussian beam radius in elements 1-82 is 2 mm; after beam expansion at element 82, the beam radius is 3.5 mm.
$500~{\rm\mu}\text{s}$. The Gaussian beam radius in elements 1-82 is 2 mm; after beam expansion at element 82, the beam radius is 3.5 mm.
The entire Thor amplifier system will be discussed in much more detail in a future publication. Here we show some typical results obtained with our laser extraction computer code, used to ascertain the expected output energy/pulse, the intensities expected at each optical element, where the peak intensities occur, and which elements are most susceptible to laser-induced damage. Figure 15 shows a plot of the energy/pulse as a function of the optical element number. There are 182 optical elements in the entire system, including many optical elements that are double-passed and counted twice. The input energy/pulse at 1 kHz is 10 mJ, and the FWHM Gaussian pulsewidth is 1 ns. The seed beam driving the system is assumed to be Gaussian spatially and temporally. Passive losses associated with optical elements are included in the calculations. After propagation through the entire system the calculated energy/pulse exiting is about 293 mJ, close to our design goal of 300 mJ. The second plot, Figure 16, shows the intensity as a function of optical element number. The peak intensity reaches about ![]() $3~\text{GW}/\text{cm}^{2}$ just before the amplified beam is expanded after the first double pass. To determine what optical elements are most susceptible to laser-induced optical damage, we show in Figure 17 the same data used for Figure 16 plus the damage threshold for each optical element in the system, as obtained from the manufacturers of all the optical elements. As expected, the optics for which the probability of damage is highest is at the location of the TFPs used to inject and reject the amplifier beam from the first and second double passes and for some lower damage threshold half- and quarter-wave plates. Calculated intensity values for TFPs were reduced by taking the increased area of the polarizer at Brewster’s angle into account. While the damage thresholds shown in Figure 17 appear to be a piecewise continuous function, note that the individual damage thresholds for each optic in the system are simply linked together using the plotting program, making it much easier to visualize the wide variation in damage thresholds encountered by a beam propagating through the system.
$3~\text{GW}/\text{cm}^{2}$ just before the amplified beam is expanded after the first double pass. To determine what optical elements are most susceptible to laser-induced optical damage, we show in Figure 17 the same data used for Figure 16 plus the damage threshold for each optical element in the system, as obtained from the manufacturers of all the optical elements. As expected, the optics for which the probability of damage is highest is at the location of the TFPs used to inject and reject the amplifier beam from the first and second double passes and for some lower damage threshold half- and quarter-wave plates. Calculated intensity values for TFPs were reduced by taking the increased area of the polarizer at Brewster’s angle into account. While the damage thresholds shown in Figure 17 appear to be a piecewise continuous function, note that the individual damage thresholds for each optic in the system are simply linked together using the plotting program, making it much easier to visualize the wide variation in damage thresholds encountered by a beam propagating through the system.
Figures 18–20 show the same plots of energy/pulse, intensity, and intensity and damage threshold, respectively for a much smaller seed energy/pulse of 0.1 mJ, and for a FWHM pulsewidth of 400 ps. All other system parameters are identical to those used for Figures 15–17. Figure 20 shows that for this case, laser-induced damage is not an issue anywhere in the system.
It should be pointed out that the PPEM-8.0 results shown in Figures 15–20 do not represent optimized systems, but rather individual runs that demonstrate the utility of the PPEM-8.0 code and its usefulness in identifying damage sensitive optics in the laser system.
The development of the PPEM-8.0 computer code allows us to quickly obtain the expected first-order performance of any single- or double-pass laser disk system with an arbitrary number of disks. The ease with which the repetition rate, pump pulse duration, input energy/pulse, peak pump power, pump and seed beam spot sizes and other critical parameters can be changed allows optimum system configurations to be determined time efficiently. The code has also been applied to cryogenic Yb:YAG lasers with high repetition rates (MHz), to systems that use other laser crystals such as Yb:![]() $\text{Lu}_{2}\text{O}_{3}$ and Yb:LuAG, to single- and double-passed rod amplifier systems, and to regenerative amplifiers. Once near-optimum system configurations have been determined, more sophisticated diffraction-based codes may be used to refine the expected results.
$\text{Lu}_{2}\text{O}_{3}$ and Yb:LuAG, to single- and double-passed rod amplifier systems, and to regenerative amplifiers. Once near-optimum system configurations have been determined, more sophisticated diffraction-based codes may be used to refine the expected results.
4 Summary
In this paper, we have endeavored to provide readers with an overview of the most important laser materials parameters needed to design nanosecond and picosecond cryogenic laser systems, with useful Tables tabulating the known values of those parameters. Thermal, thermo-optic, elastic, optical, nonlinear and laser properties are discussed. Representative plots of the thermal conductivity, thermal expansion coefficient and thermo-optic coefficients as a function of absolute temperature have been included for ten anaxial, uniaxial and biaxial laser materials. We have also reviewed the use of figures of merit to evaluate the average power potential of laser materials, and show in Table 2 representative values for a number of legacy and Yb-based laser materials. The relevant spectral properties of a number of laser materials at 300 and 77 K are shown in Table 2, including many legacy materials and a more comprehensive sample of Yb-based laser materials than previously published[Reference Brown, Tornegard, Kolis, McMillen, Moore, Samjeewa and Hancock3].
In Section 3, we discussed the important design considerations for HAPP lasers. Section 3.1 discussed the two major operating modes of cryogenic lasers, referred to as fracture-limited and aberration-limited. For aberration-limited operating we defined a new parameter ![]() ${\it\xi}$, the extractable output power obtained per unit thermal phase aberration, that allows designers to easily evaluate the benefits that can be obtained by operating a laser amplifier at cryogenic temperatures. Also, in Section 3.2, we present a useful new pulse-pumped laser extraction model based on the use of the Frantz–Nodvik equation that is an efficient tool for generating first-order ray-tracing designs for cryogenically cooled amplifiers or amplifier chains, whether they be straight-through single-pass or double-passed active-mirror amplifiers. Section 3.3 gives the derivation of the cascaded Frantz–Nodvik equation and discusses active-mirror modeling as well. In Section 3.4, we discuss methods of calculating the nonlinear phase or
${\it\xi}$, the extractable output power obtained per unit thermal phase aberration, that allows designers to easily evaluate the benefits that can be obtained by operating a laser amplifier at cryogenic temperatures. Also, in Section 3.2, we present a useful new pulse-pumped laser extraction model based on the use of the Frantz–Nodvik equation that is an efficient tool for generating first-order ray-tracing designs for cryogenically cooled amplifiers or amplifier chains, whether they be straight-through single-pass or double-passed active-mirror amplifiers. Section 3.3 gives the derivation of the cascaded Frantz–Nodvik equation and discusses active-mirror modeling as well. In Section 3.4, we discuss methods of calculating the nonlinear phase or ![]() $B$-integral by use of the Frantz–Nodvik equation, and in Section 3.5 LIDTs. The damage of optical elements is the most limiting effect to consider in high-peak-power laser designs. The CPA technique was invented to circumvent this limitation by stretching pulses to obtain a larger damage threshold, and than compressing after amplification. Section 3.6 discusses dispersion effects in high-peak-power lasers; it was shown that dispersion management and compensation are not important for nanosecond lasers, but need to be considered for short pulse picosecond lasers (
$B$-integral by use of the Frantz–Nodvik equation, and in Section 3.5 LIDTs. The damage of optical elements is the most limiting effect to consider in high-peak-power laser designs. The CPA technique was invented to circumvent this limitation by stretching pulses to obtain a larger damage threshold, and than compressing after amplification. Section 3.6 discusses dispersion effects in high-peak-power lasers; it was shown that dispersion management and compensation are not important for nanosecond lasers, but need to be considered for short pulse picosecond lasers (![]() ${<}10~\text{ps}$), and are very important in femtosecond lasers. Finally, in Section 3, we showed representative computer design results obtained in connection with the design of our Thor-300 Yb:YAG cryogenic amplifier system, including plots for operation at 1 kHz using a 1 ns pulsewidth,
${<}10~\text{ps}$), and are very important in femtosecond lasers. Finally, in Section 3, we showed representative computer design results obtained in connection with the design of our Thor-300 Yb:YAG cryogenic amplifier system, including plots for operation at 1 kHz using a 1 ns pulsewidth, ![]() $10~\text{mJ}/\text{pulse}$ seed pulse that produces near 300 mJ of output energy/pulse, and for a
$10~\text{mJ}/\text{pulse}$ seed pulse that produces near 300 mJ of output energy/pulse, and for a ![]() $0.1~\text{mJ}/\text{pulse}$, 400 ps seed pulse that produces close to
$0.1~\text{mJ}/\text{pulse}$, 400 ps seed pulse that produces close to ![]() $100~\text{mJ}/\text{pulse}$.
$100~\text{mJ}/\text{pulse}$.



























