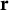1 Introduction
Affine isoperimetric inequalities provide a rich foundation for understanding principles in geometry and analysis that arise in the presence of symmetries. Among the most fundamental examples is the Blaschke–Santaló inequality [Reference Santaló48] on the product of volumes of an origin-symmetric convex body L in
![]() $\mathbb {R}^n$
and its polar
$\mathbb {R}^n$
and its polar
![]() $L^{\circ }=\{x\in \mathbb {R}^n:\langle x, y\rangle \leq 1, \;\forall y\in L\}$
. The latter asserts that this product is maximized for ellipsoids, i.e.,
$L^{\circ }=\{x\in \mathbb {R}^n:\langle x, y\rangle \leq 1, \;\forall y\in L\}$
. The latter asserts that this product is maximized for ellipsoids, i.e.,
where
![]() $\omega _n$
is the volume of the unit Euclidean ball
$\omega _n$
is the volume of the unit Euclidean ball
![]() $B_2^n$
, and
$B_2^n$
, and
![]() $\left \lvert \cdot \right \rvert $
denotes Lebesgue measure. The Blaschke–Santaló inequality, and its version for non-origin-symmetric bodies, is one of several equivalent forms of the affine isoperimetric inequality; see, e.g., the survey [Reference Lutwak34]. Moreover, it admits numerous extensions: for example,
$\left \lvert \cdot \right \rvert $
denotes Lebesgue measure. The Blaschke–Santaló inequality, and its version for non-origin-symmetric bodies, is one of several equivalent forms of the affine isoperimetric inequality; see, e.g., the survey [Reference Lutwak34]. Moreover, it admits numerous extensions: for example,
![]() $L_p$
versions [Reference Lutwak and Zhang37], generalizations from convex bodies to functions, e.g., [Reference Artstein-Avidan, Klartag and Milman1, Reference Ball3, Reference Fradelizi and Meyer14] with applications to concentration of measure [Reference Artstein-Avidan, Klartag and Milman1, Reference Lehec27]; further functional affine isoperimetric inequalities, e.g., [Reference Artstein-Avidan, Klartag, Schütt and Werner2]; stronger versions in which stochastic dominance holds [Reference Cordero-Erausquin, Fradelizi, Paouris and Pivovarov10].
$L_p$
versions [Reference Lutwak and Zhang37], generalizations from convex bodies to functions, e.g., [Reference Artstein-Avidan, Klartag and Milman1, Reference Ball3, Reference Fradelizi and Meyer14] with applications to concentration of measure [Reference Artstein-Avidan, Klartag and Milman1, Reference Lehec27]; further functional affine isoperimetric inequalities, e.g., [Reference Artstein-Avidan, Klartag, Schütt and Werner2]; stronger versions in which stochastic dominance holds [Reference Cordero-Erausquin, Fradelizi, Paouris and Pivovarov10].
Another fundamental affine isoperimetric inequality is the Petty projection inequality [Reference Petty44]. This concerns projection bodies, which are special zonoids that play a fundamental role in convex geometry and functional analysis, among other fields, e.g., [Reference Gardner17, Reference Schneider49, Reference Schneider and Weil50]. The projection body of a convex body
![]() $L\subseteq \mathbb {R}^n$
is the convex body
$L\subseteq \mathbb {R}^n$
is the convex body
![]() $\Pi L$
defined by its support function in direction
$\Pi L$
defined by its support function in direction
![]() $\theta \in S^{n-1}$
as
$\theta \in S^{n-1}$
as
![]() $h_{\Pi L}(\theta )=\left \lvert P_{\theta ^{\perp }}L\right \rvert $
, where
$h_{\Pi L}(\theta )=\left \lvert P_{\theta ^{\perp }}L\right \rvert $
, where
![]() $P_{\theta ^{\perp }}$
is the orthogonal projection onto
$P_{\theta ^{\perp }}$
is the orthogonal projection onto
![]() $\theta ^{\perp }$
, the central hyperplane perpendicular to
$\theta ^{\perp }$
, the central hyperplane perpendicular to
![]() $\theta $
. The Petty projection inequality asserts that the affine-invariant quantity
$\theta $
. The Petty projection inequality asserts that the affine-invariant quantity
![]() $\left \lvert L\right \rvert ^{n-1}\left \lvert (\Pi L)^{\circ }\right \rvert $
is maximized by ellipsoids, i.e.,
$\left \lvert L\right \rvert ^{n-1}\left \lvert (\Pi L)^{\circ }\right \rvert $
is maximized by ellipsoids, i.e.,
The Petty projection inequality is the geometric foundation for Zhang’s affine Sobolev inequality [Reference Zhang53]. Its equivalent forms and extensions have given rise to fundamental inequalities in analysis, geometry, and information theory, e.g., [Reference Lutwak, Yang and Zhang35, Reference Lutwak, Yang and Zhang36].
The affine invariance in inequalities (1) and (2) follows from volumetric considerations. However, as we will review below, the underlying principle goes much deeper and extends to the family of affine quermassintegrals, of which
![]() $\left \lvert L^{\circ }\right \rvert $
and
$\left \lvert L^{\circ }\right \rvert $
and
![]() $\left \lvert (\Pi L)^{\circ }\right \rvert $
are just two special cases, up to normalization. Formally, the affine quermassintegrals are defined for compact bodies L in
$\left \lvert (\Pi L)^{\circ }\right \rvert $
are just two special cases, up to normalization. Formally, the affine quermassintegrals are defined for compact bodies L in
![]() $\mathbb {R}^n$
(i.e., compact sets with non-empty interior), and
$\mathbb {R}^n$
(i.e., compact sets with non-empty interior), and
![]() $1\leq k\leq n$
, by
$1\leq k\leq n$
, by
 $$ \begin{align} \Phi_{[k]}(L)= \left(\int_{G_{n,k}}\left\lvert P_EL\right\rvert^{-n}d\nu_{n,k}(E)\right)^{-\frac{1}{kn}}, \end{align} $$
$$ \begin{align} \Phi_{[k]}(L)= \left(\int_{G_{n,k}}\left\lvert P_EL\right\rvert^{-n}d\nu_{n,k}(E)\right)^{-\frac{1}{kn}}, \end{align} $$
where
![]() $G_{n,k}$
is the Grassmannian manifold of k-dimensional linear subspaces equipped with the Haar probability measure
$G_{n,k}$
is the Grassmannian manifold of k-dimensional linear subspaces equipped with the Haar probability measure
![]() $\nu _{n,k}$
(see [Reference Lutwak30]). Writing
$\nu _{n,k}$
(see [Reference Lutwak30]). Writing
![]() $\left \lvert L^{\circ }\right \rvert $
and
$\left \lvert L^{\circ }\right \rvert $
and
![]() $\left \lvert (\Pi L)^{\circ }\right \rvert $
in polar coordinates shows a direct connection to
$\left \lvert (\Pi L)^{\circ }\right \rvert $
in polar coordinates shows a direct connection to
![]() $k=1$
and
$k=1$
and
![]() $k=n-1$
in (3), respectively. As the name suggests, they are affine-invariant, i.e.,
$k=n-1$
in (3), respectively. As the name suggests, they are affine-invariant, i.e.,
![]() $\Phi _{[k]}(TL)=\Phi _{[k]}(L)$
for each volume preserving affine transformation T, as proved by Grinberg [Reference Grinberg20], extending earlier work on ellipsoids by Furstenberg and Tzkoni [Reference Furstenberg and Tzkoni16] and Lutwak [Reference Lutwak32].
$\Phi _{[k]}(TL)=\Phi _{[k]}(L)$
for each volume preserving affine transformation T, as proved by Grinberg [Reference Grinberg20], extending earlier work on ellipsoids by Furstenberg and Tzkoni [Reference Furstenberg and Tzkoni16] and Lutwak [Reference Lutwak32].
The quantities
![]() $\Phi _{[k]}(L)$
are affine versions of quermassintegrals or intrinsic volumes, which play a central role in Brunn–Minkowski theory [Reference Schneider49]. In particular, the intrinsic volumes
$\Phi _{[k]}(L)$
are affine versions of quermassintegrals or intrinsic volumes, which play a central role in Brunn–Minkowski theory [Reference Schneider49]. In particular, the intrinsic volumes
![]() $V_1(L),\ldots , V_n(L)$
of a convex body L admit similar representations through Kubota’s integral recursion as
$V_1(L),\ldots , V_n(L)$
of a convex body L admit similar representations through Kubota’s integral recursion as
where
![]() $c_{n,k}$
is a constant that depends only on n and k. They enjoy many fundamental inequalities, such as
$c_{n,k}$
is a constant that depends only on n and k. They enjoy many fundamental inequalities, such as
for
![]() $k=1,\ldots ,n-1$
, where
$k=1,\ldots ,n-1$
, where
![]() $r_L$
is the radius of a Euclidean ball in
$r_L$
is the radius of a Euclidean ball in
![]() $\mathbb {R}^n$
having the same volume as L. Taking
$\mathbb {R}^n$
having the same volume as L. Taking
![]() $k=1$
in (4) corresponds to Urysohn’s inequality, while
$k=1$
in (4) corresponds to Urysohn’s inequality, while
![]() $k=n-1$
is the standard isoperimetric inequality. From Jensen’s inequality, one sees that (1) and (2) provide stronger affine-invariant analogues of (4) for
$k=n-1$
is the standard isoperimetric inequality. From Jensen’s inequality, one sees that (1) and (2) provide stronger affine-invariant analogues of (4) for
![]() $k=1$
and
$k=1$
and
![]() $k=n-1$
, respectively. For the intermediary values
$k=n-1$
, respectively. For the intermediary values
![]() $1<k<n-1$
, the inequalities in (4) are well-known consequences of Alexandrov–Fenchel inequality (e.g., [Reference Schneider49]). It was a long-standing problem posed by Lutwak [Reference Lutwak32] whether affine quermassintegrals are minimized by ellipsoids. In a recent breakthrough, this has been resolved by E. Milman and Yehudayoff in [Reference Milman and Yehudayoff38]; namely, for any convex body L, and
$1<k<n-1$
, the inequalities in (4) are well-known consequences of Alexandrov–Fenchel inequality (e.g., [Reference Schneider49]). It was a long-standing problem posed by Lutwak [Reference Lutwak32] whether affine quermassintegrals are minimized by ellipsoids. In a recent breakthrough, this has been resolved by E. Milman and Yehudayoff in [Reference Milman and Yehudayoff38]; namely, for any convex body L, and
![]() $1<k<n-1$
,
$1<k<n-1$
,
In the last 40 years, a compelling dual theory, initiated by Lutwak in [Reference Lutwak29], has flourished (see, e.g., [Reference Gardner17, Reference Schneider49]). Rather than convex bodies and projections onto lower-dimensional subspaces, this involves star-shaped sets and intersections with subspaces. As above, a key isoperimetric inequality lies at its foundation. The intersection body of a star-shaped body L is the star-shaped body
![]() $IL$
with radial function
$IL$
with radial function
![]() $\rho _{IL} (\theta ) := | L \cap \theta ^{\perp } |$
. The Busemann intersection inequality [Reference Busemann8], proved originally for convex bodies L, states that
$\rho _{IL} (\theta ) := | L \cap \theta ^{\perp } |$
. The Busemann intersection inequality [Reference Busemann8], proved originally for convex bodies L, states that
The volume of the intersection body lies at one endpoint of a sequence of
![]() $SL_{n}$
-invariant quantities that are called the dual affine quermassintegrals. These are
$SL_{n}$
-invariant quantities that are called the dual affine quermassintegrals. These are
![]() $SL_{n}$
-invariant analogues of the dual quermassintegrals introduced by Lutwak [Reference Lutwak31]. Formally, for a compact body
$SL_{n}$
-invariant analogues of the dual quermassintegrals introduced by Lutwak [Reference Lutwak31]. Formally, for a compact body
![]() $L\subseteq \mathbb {R}^n$
and
$L\subseteq \mathbb {R}^n$
and
![]() $1\leq k\leq n$
, the dual affine quermassintegralsFootnote
1
of L are defined by
$1\leq k\leq n$
, the dual affine quermassintegralsFootnote
1
of L are defined by
 $$ \begin{align} \Psi_{[k]}(L) = \left(\int_{G_{n,k}}\left\lvert L\cap E\right\rvert^nd\nu_{n,k}(E)\right)^{\frac{1}{kn}}. \end{align} $$
$$ \begin{align} \Psi_{[k]}(L) = \left(\int_{G_{n,k}}\left\lvert L\cap E\right\rvert^nd\nu_{n,k}(E)\right)^{\frac{1}{kn}}. \end{align} $$
As above, Grinberg [Reference Grinberg20], drawing on [Reference Furstenberg and Tzkoni16], showed that these enjoy invariance under volume-preserving linear transformations, i.e.,
![]() $\Psi _{[k]}(TL)= \Psi _{[k]}(L)$
for
$\Psi _{[k]}(TL)= \Psi _{[k]}(L)$
for
![]() $T\in SL_{n}$
. They also satisfy the following extension of (6), proved by Busemann and Straus [Reference Busemann and Straus9] and Grinberg [Reference Grinberg20]:
$T\in SL_{n}$
. They also satisfy the following extension of (6), proved by Busemann and Straus [Reference Busemann and Straus9] and Grinberg [Reference Grinberg20]:
While the dual theory has been developed for star-shaped bodies, the investigation of these quantities goes deeper and can be extended to bounded Borel sets and non-negative measurable functions [Reference Dann, Paouris and Pivovarov12, Reference Gardner18]. For recent developments on dual Brunn–Minkowski theory, see [Reference Gardner17, Reference Huang, Lutwak, Yang and Zhang22, Reference Schneider49] and the references therein.
Affine and dual affine quermassintegrals have implications well outside of integral geometry, convexity, and isoperimetry. They are essential for understanding phenomena in high-dimensional probability. Indeed, functional versions of (8) lead to sharp asymptotics for small-ball probabilities for marginal densities of probability measures [Reference Dann, Paouris and Pivovarov12]. They also govern key parameters of marginals of
![]() $\log $
-concave probability measures connected to the Slicing Problem [Reference Paouris and Valettas43]. Furthermore, small-ball probabilities for the volume of random convex sets in [Reference Paouris and Pivovarov42] also depend on quantifying volumetric bounds for random projections and sections of convex bodies. Each of these applications to high-dimensional probability boils down to understanding affine invariant quantities on Grassmannians.
$\log $
-concave probability measures connected to the Slicing Problem [Reference Paouris and Valettas43]. Furthermore, small-ball probabilities for the volume of random convex sets in [Reference Paouris and Pivovarov42] also depend on quantifying volumetric bounds for random projections and sections of convex bodies. Each of these applications to high-dimensional probability boils down to understanding affine invariant quantities on Grassmannians.
1.1 A return to flag manifolds
The work of Furstenberg and Tzkoni [Reference Furstenberg and Tzkoni16] that established the
![]() $SL_{n}$
-invariance of (7) for ellipsoids on the Grassmannian provided the impetus for the development of affine and dual affine quermassintegrals. However, Furstenberg and Tzkoni went well beyond the Grassmannian and derived kindred integral geometric formulas for ellipsoids on flag manifolds. They established deeper connections to representation of spherical functions on symmetric spaces. Their work was motivated by results in ergodic theory of Furstenberg and Keston [Reference Furstenberg and Keston15]. Recently, Hanin and the second-named author studied randomness on flag manifolds and implications for high-dimensional frames and products of random matrices. They derived non-asymptotic results in the ergodic theorem [Reference Hanin and Paouris21] that ultimately rely on notions for affine quantities on flag manifolds.
$SL_{n}$
-invariance of (7) for ellipsoids on the Grassmannian provided the impetus for the development of affine and dual affine quermassintegrals. However, Furstenberg and Tzkoni went well beyond the Grassmannian and derived kindred integral geometric formulas for ellipsoids on flag manifolds. They established deeper connections to representation of spherical functions on symmetric spaces. Their work was motivated by results in ergodic theory of Furstenberg and Keston [Reference Furstenberg and Keston15]. Recently, Hanin and the second-named author studied randomness on flag manifolds and implications for high-dimensional frames and products of random matrices. They derived non-asymptotic results in the ergodic theorem [Reference Hanin and Paouris21] that ultimately rely on notions for affine quantities on flag manifolds.
Unlike for affine or dual affine quermassintegrals, the corresponding notions for convex bodies, compact bodies, and functions have not been investigated in the setting of flag manifolds. Our main goal is to initiate such a study in this paper. We extend and develop fundamental notions that are currently only available on Grassmannians to the setting of flag manifolds. We introduce flag versions of (dual) affine quermassintegrals (cf. (3) and (7)). Our investigation includes (i) affine invariance properties, (ii) sharp extremal inequalities, (iii) approximate reverse isoperimetric inequalities, and (iv) functional versions. As mentioned, each of these notions on the Grassmannian has played an important role in high-dimensional convex geometry and probability. New connections discovered in [Reference Hanin and Paouris21] suggest that corresponding flag versions are needed and will have broader applicability.
As flag manifolds are natural generalizations of Grassmannians, they have been studied from several different perspectives. In convex geometry, mixed volumes admit representations in terms of certain flag measures (e.g., [Reference Hug, Rataj and Weil23]). Recently, there is increasing interest in other probabilistic aspects of Grassmannians and flag manifolds such as topological properties of random sets in real algebraic geometry (see [Reference Bürgisser and Lerario7] and the references therein). Our aim here is to develop a corresponding theory within high-dimensional convex geometry.
1.2 Main results
We start by recalling the setting from work of Furstenberg and Tzkoni [Reference Furstenberg and Tzkoni16]. Let
![]() $ 1\leq r \leq n-1$
, and let
$ 1\leq r \leq n-1$
, and let
![]() $ \mathbf {r}:= ( i_{1}, i_{2}, \ldots , i_{r})$
be a strictly increasing sequence of integers,
$ \mathbf {r}:= ( i_{1}, i_{2}, \ldots , i_{r})$
be a strictly increasing sequence of integers,
![]() $1\leq i_{1} < i_{2} < \cdots < i_{r} \leq n-1$
. Let
$1\leq i_{1} < i_{2} < \cdots < i_{r} \leq n-1$
. Let
![]() $ \xi _{\mathbf {r}} := ( F_{1}, \ldots , F_{r})$
be a (partial) flag of subspaces; i.e.,
$ \xi _{\mathbf {r}} := ( F_{1}, \ldots , F_{r})$
be a (partial) flag of subspaces; i.e.,
![]() $ F_{1} \subset F_{2} \subset \cdots \subset F_{r}$
with each
$ F_{1} \subset F_{2} \subset \cdots \subset F_{r}$
with each
![]() $F_{j} $
an
$F_{j} $
an
![]() $i_{j}$
-dimensional subspace. We denote by
$i_{j}$
-dimensional subspace. We denote by
![]() $ F_{\mathbf {r}}^{n} $
the flag manifold (with indices
$ F_{\mathbf {r}}^{n} $
the flag manifold (with indices
![]() $\mathbf {r}$
) as the set of all partial flags
$\mathbf {r}$
) as the set of all partial flags
![]() $\xi _{\mathbf {r}}$
.
$\xi _{\mathbf {r}}$
.
![]() $F_{\mathbf {r}}^{n} $
is equipped with the unique Haar probability measure that is invariant under the action of
$F_{\mathbf {r}}^{n} $
is equipped with the unique Haar probability measure that is invariant under the action of
![]() $SO_{n}$
and all integrations on this set in this note are meant with respect to this measure.
$SO_{n}$
and all integrations on this set in this note are meant with respect to this measure.
In the special case when
![]() $r=1$
and
$r=1$
and
![]() $i_{1}=k$
, the partial flag manifold
$i_{1}=k$
, the partial flag manifold
![]() $F^{n}_{\mathbf {r}}$
is just the Grassmann manifold
$F^{n}_{\mathbf {r}}$
is just the Grassmann manifold
![]() $G_{n,k}$
. Hence, (partial) flag-manifolds can be considered as generalizations of Grassmannians. When
$G_{n,k}$
. Hence, (partial) flag-manifolds can be considered as generalizations of Grassmannians. When
![]() $r=n-1$
, so that
$r=n-1$
, so that
![]() $ \mathbf {r}:= (1, 2, \ldots , n-1)$
, we write
$ \mathbf {r}:= (1, 2, \ldots , n-1)$
, we write
![]() $F^{n}:= F_{\mathbf {r}}^{n}$
for the complete flag manifold. We follow the convention that
$F^{n}:= F_{\mathbf {r}}^{n}$
for the complete flag manifold. We follow the convention that
![]() $i_{0} = 0$
and
$i_{0} = 0$
and
![]() $i_{r+1}= n$
; hence,
$i_{r+1}= n$
; hence,
 $$ \begin{align} \sum_{j=1}^{r} i_{j} ( i_{j+1} - i_{j-1}) = i_{r} n. \end{align} $$
$$ \begin{align} \sum_{j=1}^{r} i_{j} ( i_{j+1} - i_{j-1}) = i_{r} n. \end{align} $$
Let L be a compact body in
![]() ${\mathbb R}^{n}$
, and let
${\mathbb R}^{n}$
, and let
![]() $ 1\leq r \leq n-1$
and
$ 1\leq r \leq n-1$
and
![]() $\mathbf {r}$
be a set of indices as above. We define the
$\mathbf {r}$
be a set of indices as above. We define the
![]() $\mathbf {r}$
-flag affine quermassintegral of L by
$\mathbf {r}$
-flag affine quermassintegral of L by
 $$ \begin{align} \Phi_{\mathbf{r}} (L) := \left( \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | P_{F_{j}} L |^{ i_{j-1}- i_{j+1}} d\xi_{\mathbf{r}} \right)^{-\frac{1}{i_{r} n}}. \end{align} $$
$$ \begin{align} \Phi_{\mathbf{r}} (L) := \left( \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | P_{F_{j}} L |^{ i_{j-1}- i_{j+1}} d\xi_{\mathbf{r}} \right)^{-\frac{1}{i_{r} n}}. \end{align} $$
Similarly, we define the dual
![]() $\mathbf {r}$
-flag affine quermassintegral of L by
$\mathbf {r}$
-flag affine quermassintegral of L by
 $$ \begin{align} \Psi_{\mathbf{r}} (L) := \left( \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | L\cap F_{j} |^{ i_{j+1}- i_{j-1}} d\xi_{\mathbf{r}} \right)^{\frac{1}{i_{r} n}}. \end{align} $$
$$ \begin{align} \Psi_{\mathbf{r}} (L) := \left( \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | L\cap F_{j} |^{ i_{j+1}- i_{j-1}} d\xi_{\mathbf{r}} \right)^{\frac{1}{i_{r} n}}. \end{align} $$
In [Reference Furstenberg and Tzkoni16], it was shown that when
![]() $L=\cal {E}$
is an ellipsoid,
$L=\cal {E}$
is an ellipsoid,
![]() $\Psi _{\mathbf {r}}(\cal {E})$
is invariant under
$\Psi _{\mathbf {r}}(\cal {E})$
is invariant under
![]() $SL_{n}$
. When
$SL_{n}$
. When
![]() $r=1$
, the
$r=1$
, the
![]() $\mathbf {r}$
-flag affine quermassintegrals are exactly the affine quermassintegrals; similarly for the dual case. Thus, the latter quantities can be considered as extensions of the (dual) affine quermassintegrals to flag manifolds. For complete flag manifolds, we similarly define
$\mathbf {r}$
-flag affine quermassintegrals are exactly the affine quermassintegrals; similarly for the dual case. Thus, the latter quantities can be considered as extensions of the (dual) affine quermassintegrals to flag manifolds. For complete flag manifolds, we similarly define
 $$ \begin{align} \Psi_{\mathbf{F^{n}}}(L) := \left( \int_{F^{n}} \prod_{i=1}^{n-1} |L \cap F_{i} |^{2} d \xi\right)^{\frac{1}{n(n-1)}} \mathrm{and } \quad \Phi_{\mathbf{F^{n}}}(L) := \left( \int_{F^{n}} \prod_{i=1}^{n-1} | P_{F_{i}} L |^{-2} d \xi\right)^{-\frac{1}{n(n-1)}}. \end{align} $$
$$ \begin{align} \Psi_{\mathbf{F^{n}}}(L) := \left( \int_{F^{n}} \prod_{i=1}^{n-1} |L \cap F_{i} |^{2} d \xi\right)^{\frac{1}{n(n-1)}} \mathrm{and } \quad \Phi_{\mathbf{F^{n}}}(L) := \left( \int_{F^{n}} \prod_{i=1}^{n-1} | P_{F_{i}} L |^{-2} d \xi\right)^{-\frac{1}{n(n-1)}}. \end{align} $$
Clearly, by (9),
Our first result extends the invariance results of Grinberg [Reference Grinberg20] that give invariance of (3) and (7) under volume-preserving affine and linear transformations, respectively.
Theorem 1.1 Let L be a compact body in
![]() ${\mathbb R}^{n}$
,
${\mathbb R}^{n}$
,
![]() $ 1\leq r \leq n-1$
, and let
$ 1\leq r \leq n-1$
, and let
![]() $ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
$ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
![]() $1$
and
$1$
and
![]() $n-1$
. Let A be an affine map that preserves volume and
$n-1$
. Let A be an affine map that preserves volume and
![]() $T\in SL_{n}$
. Then
$T\in SL_{n}$
. Then
With such invariance properties, it is natural to seek extremizers of
![]() $\Phi _{\mathbf {r}}(L)$
and
$\Phi _{\mathbf {r}}(L)$
and
![]() $\Psi _{\mathbf {r}}(L)$
, especially over convex bodies
$\Psi _{\mathbf {r}}(L)$
, especially over convex bodies
![]() $L \subseteq \mathbb {R}^n$
. However, even for the Grassmannian, very few such results are known; cf. (5) and (8), with (5) established only recently in [Reference Milman and Yehudayoff38]. Previously, (5) was shown to hold at the expense of a universal constant in [Reference Paouris and Pivovarov42] by the second- and third-named authors. It is easy to construct compact sets
$L \subseteq \mathbb {R}^n$
. However, even for the Grassmannian, very few such results are known; cf. (5) and (8), with (5) established only recently in [Reference Milman and Yehudayoff38]. Previously, (5) was shown to hold at the expense of a universal constant in [Reference Paouris and Pivovarov42] by the second- and third-named authors. It is easy to construct compact sets
![]() $L \subseteq \mathbb {R}^n$
of a given volume such that
$L \subseteq \mathbb {R}^n$
of a given volume such that
![]() $\Phi _{[k]}(L)$
is arbitrarily large. This, however, cannot happen when L is convex: in [Reference Dafnis and Paouris11], it was shown that up to a logarithmic factor in the dimension n,
$\Phi _{[k]}(L)$
is arbitrarily large. This, however, cannot happen when L is convex: in [Reference Dafnis and Paouris11], it was shown that up to a logarithmic factor in the dimension n,
![]() $\Phi _{[k]}(L)$
does not exceed
$\Phi _{[k]}(L)$
does not exceed
![]() $\Phi _{[k]}(r_L B_2^n)$
(where, as above,
$\Phi _{[k]}(r_L B_2^n)$
(where, as above,
![]() $r_L$
is the radius of a Euclidean ball in
$r_L$
is the radius of a Euclidean ball in
![]() $\mathbb {R}^n$
with the same volume as L).
$\mathbb {R}^n$
with the same volume as L).
We extend the aforementioned results to the setting of flag manifolds. In this note,
![]() $c, c^{\prime }, c_{0},\ldots $
etc. will denote universal constants (not necessarily the same at each occurrence).
$c, c^{\prime }, c_{0},\ldots $
etc. will denote universal constants (not necessarily the same at each occurrence).
Theorem 1.2 Let L be a compact body in
![]() ${\mathbb R}^{n}$
,
${\mathbb R}^{n}$
,
![]() $ 1\leq r \leq n-1$
and
$ 1\leq r \leq n-1$
and
![]() $\mathbf {r}:= (i_{1}, \ldots , i_{r})$
an increasing sequence of integers between
$\mathbf {r}:= (i_{1}, \ldots , i_{r})$
an increasing sequence of integers between
![]() $1$
and
$1$
and
![]() $n-1$
. Then
$n-1$
. Then
If L is an origin-symmetric convex body, then
 $$ \begin{align} \Psi_{\mathbf{r}} (L) \geq \frac{ c}{\min\left\{ \sqrt{\frac{n}{i_{r}}} , \log{n}\right\} }\Psi_{\mathbf{r}} (r_L B_2^n). \end{align} $$
$$ \begin{align} \Psi_{\mathbf{r}} (L) \geq \frac{ c}{\min\left\{ \sqrt{\frac{n}{i_{r}}} , \log{n}\right\} }\Psi_{\mathbf{r}} (r_L B_2^n). \end{align} $$
If L is a convex body, then
 $$ \begin{align} \Phi_{\mathbf{r}} (r_L B_2^n) \color{black} \leq \Phi_{\mathbf{r}} (L) \leq c \min\left\{ \sqrt{\frac{n}{i_{r}}} , \log{n}\right\} \Phi_{\mathbf{r}} (r_L B_2^n). \end{align} $$
$$ \begin{align} \Phi_{\mathbf{r}} (r_L B_2^n) \color{black} \leq \Phi_{\mathbf{r}} (L) \leq c \min\left\{ \sqrt{\frac{n}{i_{r}}} , \log{n}\right\} \Phi_{\mathbf{r}} (r_L B_2^n). \end{align} $$
The necessity of the logarithmic factors appearing in (14) and (15) remains an open question. For
![]() $\Phi _{[k]}$
, the analogous theorem was proved in [Reference Dafnis and Paouris11]. For
$\Phi _{[k]}$
, the analogous theorem was proved in [Reference Dafnis and Paouris11]. For
![]() $\Phi _{\mathbf {r}}$
and
$\Phi _{\mathbf {r}}$
and
![]() $\Psi _{\mathbf {r}}$
, the result is new and the path that we use to prove Theorem 1.2 is quite different than that of [Reference Dafnis and Paouris11]. We use isotropic position and the theory of isotropic convex bodies. In particular, we use the isomorphic solution to the Slicing Problem, due to B. Klartag. We believe this is of its own independent interest.
$\Psi _{\mathbf {r}}$
, the result is new and the path that we use to prove Theorem 1.2 is quite different than that of [Reference Dafnis and Paouris11]. We use isotropic position and the theory of isotropic convex bodies. In particular, we use the isomorphic solution to the Slicing Problem, due to B. Klartag. We believe this is of its own independent interest.
Further drawing on [Reference Furstenberg and Tzkoni16], we also consider variants of (dual)
![]() $\mathbf { r}$
-flag affine quermassintegrals involving permutations
$\mathbf { r}$
-flag affine quermassintegrals involving permutations
![]() $\omega $
of
$\omega $
of
![]() $\{1,\ldots ,n\}$
. We define the
$\{1,\ldots ,n\}$
. We define the
![]() $\omega $
-flag quermassintegral and dual
$\omega $
-flag quermassintegral and dual
![]() $\omega $
-flag quermassintegral as follows: for every compact body L in
$\omega $
-flag quermassintegral as follows: for every compact body L in
![]() ${\mathbb R}^{n}$
,
${\mathbb R}^{n}$
,
 $$ \begin{align} \Phi_{\omega} (L) := \begin{cases} \left( \int_{F^{n}} \prod_{j=1}^{n-1} | P_{F_{j}}L|^{- \omega(j) + \omega(j+1)-1} d \xi \right)^{-\frac{1}{n( n- \omega(n))}}, &\ \mathrm{if } \ \omega(n) \neq n,\\ \int_{F^{n}} \prod_{j=1}^{n-1} | P_{F_{j}}L|^{- \omega(j) + \omega(j+1)-1} d \xi, &\ \mathrm{if } \ \omega(n) = n, \end{cases} \end{align} $$
$$ \begin{align} \Phi_{\omega} (L) := \begin{cases} \left( \int_{F^{n}} \prod_{j=1}^{n-1} | P_{F_{j}}L|^{- \omega(j) + \omega(j+1)-1} d \xi \right)^{-\frac{1}{n( n- \omega(n))}}, &\ \mathrm{if } \ \omega(n) \neq n,\\ \int_{F^{n}} \prod_{j=1}^{n-1} | P_{F_{j}}L|^{- \omega(j) + \omega(j+1)-1} d \xi, &\ \mathrm{if } \ \omega(n) = n, \end{cases} \end{align} $$
and
 $$ \begin{align} \Psi_{\omega} (L) := \begin{cases}\left( \int_{F^{n}} \prod_{j=1}^{n-1} | L \cap F_{j}|^{ \omega(j) - \omega(j+1)+1} d \xi \right)^{\frac{1}{ n(n- \omega(n))}}, &\ \mathrm{if} \ \omega(n) \neq n,\\ \int_{F^{n}} \prod_{j=1}^{n-1} | L \cap F_{j}|^{ \omega(j) - \omega(j+1)+1} d \xi, &\ \mathrm{if } \ \omega(n) = n. \end{cases} \end{align} $$
$$ \begin{align} \Psi_{\omega} (L) := \begin{cases}\left( \int_{F^{n}} \prod_{j=1}^{n-1} | L \cap F_{j}|^{ \omega(j) - \omega(j+1)+1} d \xi \right)^{\frac{1}{ n(n- \omega(n))}}, &\ \mathrm{if} \ \omega(n) \neq n,\\ \int_{F^{n}} \prod_{j=1}^{n-1} | L \cap F_{j}|^{ \omega(j) - \omega(j+1)+1} d \xi, &\ \mathrm{if } \ \omega(n) = n. \end{cases} \end{align} $$
Furstenberg and Tzkoni showed
![]() $SL_{n}$
-invariance of
$SL_{n}$
-invariance of
![]() $\Psi _{\omega }$
for ellipsoids. We investigate the extent to which this invariance carries over to compact bodies. Moreover, in the case of convex bodies, we show that such quantities cannot be too degenerate in the sense that they admit uniform upper and lower bounds, independent of the body. We apply V. D. Milman’s M-ellipsoids [Reference Milman40], together with the aforementioned
$\Psi _{\omega }$
for ellipsoids. We investigate the extent to which this invariance carries over to compact bodies. Moreover, in the case of convex bodies, we show that such quantities cannot be too degenerate in the sense that they admit uniform upper and lower bounds, independent of the body. We apply V. D. Milman’s M-ellipsoids [Reference Milman40], together with the aforementioned
![]() $SL_n$
-invariance of Furstenberg–Tzkoni to establish these bounds (see Corollary 4.4).
$SL_n$
-invariance of Furstenberg–Tzkoni to establish these bounds (see Corollary 4.4).
In Section 5, we introduce functional analogues of the dual
![]() $\mathbf {r}$
-flag affine quermassintegrals. We show that more general quantities share the
$\mathbf {r}$
-flag affine quermassintegrals. We show that more general quantities share the
![]() $SL_{n}$
-invariance properties, and we prove sharp isoperimetric inequalities. In this section, we invoke techniques and results from our previous work [Reference Dann, Paouris and Pivovarov12]. Lastly, in Section 5, we also introduce a functional form of
$SL_{n}$
-invariance properties, and we prove sharp isoperimetric inequalities. In this section, we invoke techniques and results from our previous work [Reference Dann, Paouris and Pivovarov12]. Lastly, in Section 5, we also introduce a functional form of
![]() $\mathbf {r}$
-flag affine quermassintegrals. There is much recent interest in extending fundamental geometric inequalities from convex bodies to certain classes of functions (e.g., [Reference Bobkov, Colesanti and Fragalá4, Reference Klartag and Milman25, Reference Milman and Rotem39]). The latter works have treated variants of inequalities for intrinsic volumes, or even mixed volumes, and other general quantities; for example, they establish functional analogues of (4). Here, we establish a functional generalization of (15), using E. Milman and Yehudayoff’s result (5). Invariance properties and bounds for these quantities are treated in Section 5.2.
$\mathbf {r}$
-flag affine quermassintegrals. There is much recent interest in extending fundamental geometric inequalities from convex bodies to certain classes of functions (e.g., [Reference Bobkov, Colesanti and Fragalá4, Reference Klartag and Milman25, Reference Milman and Rotem39]). The latter works have treated variants of inequalities for intrinsic volumes, or even mixed volumes, and other general quantities; for example, they establish functional analogues of (4). Here, we establish a functional generalization of (15), using E. Milman and Yehudayoff’s result (5). Invariance properties and bounds for these quantities are treated in Section 5.2.
2 Affine invariance
In this section, we will present the proof of Theorem 1.1. The following proposition relates integration on a flag manifold to integration on nested Grassmannians (see [Reference Schneider and Weil51, Theorem 7.1.1 on p. 267] for such a result for flags of elements consisting of two subspaces). Since we will use this fact many times throughout this paper, we include the proof. For a subspace
![]() $F \subset \mathbb {R}^n$
, we denote by
$F \subset \mathbb {R}^n$
, we denote by
![]() $G_{F,i}$
the Grassmannian of all i-dimensional subspaces contained in F.
$G_{F,i}$
the Grassmannian of all i-dimensional subspaces contained in F.
Proposition 2.1 Let
![]() $ 1\leq r \leq n-1$
and
$ 1\leq r \leq n-1$
and
![]() $ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
$ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
![]() $1$
and
$1$
and
![]() $n-1$
. For
$n-1$
. For
![]() $G \in L^1(F^n_{\mathbf {r}})$
,
$G \in L^1(F^n_{\mathbf {r}})$
,
 $$ \begin{align} \int\limits_{F^n_{\mathbf{r}}} G (\xi_{\mathbf{r}}) d\xi_{\mathbf{r}} = \int\limits_{G_{n,i_{r}} } \int\limits_{G_{F_{r}, i_{r-1}}} \ldots \int\limits_{G_{ F_{2}}, i_{1}} G ( F_{1}, \ldots, F_{r-1}, F_{r}) \, d F_{1} \ldots d F_{r-1} dF_{r}. \end{align} $$
$$ \begin{align} \int\limits_{F^n_{\mathbf{r}}} G (\xi_{\mathbf{r}}) d\xi_{\mathbf{r}} = \int\limits_{G_{n,i_{r}} } \int\limits_{G_{F_{r}, i_{r-1}}} \ldots \int\limits_{G_{ F_{2}}, i_{1}} G ( F_{1}, \ldots, F_{r-1}, F_{r}) \, d F_{1} \ldots d F_{r-1} dF_{r}. \end{align} $$
For simplicity, we have suppressed the notation to write
![]() $dF_1$
rather than
$dF_1$
rather than
![]() $d\mu _{G_{F_2,i_1}}(F_1)$
, which is the Haar probability measure on the Grassmannian of all
$d\mu _{G_{F_2,i_1}}(F_1)$
, which is the Haar probability measure on the Grassmannian of all
![]() $i_1$
-dimensional subspaces of the ambient space
$i_1$
-dimensional subspaces of the ambient space
![]() $F_2$
; similarly for all other indices. This convention will be used throughout.
$F_2$
; similarly for all other indices. This convention will be used throughout.
Proof Fix
![]() $i_j$
. Denote by
$i_j$
. Denote by
![]() $SO(F_{j})$
the subgroup of
$SO(F_{j})$
the subgroup of
![]() $SO_n$
acting transitively on
$SO_n$
acting transitively on
![]() $G_{F_{j},{i_{j-1}}}$
. For example, if
$G_{F_{j},{i_{j-1}}}$
. For example, if
![]() $F_o=\mathop{\mathrm{span}}\{e_1, \ldots , e_{i_j}\}$
and
$F_o=\mathop{\mathrm{span}}\{e_1, \ldots , e_{i_j}\}$
and
![]() $E_o=\mathop{\mathrm{span}}\{e_1, \ldots , e_{i_{j-1}}\}$
, then elements of
$E_o=\mathop{\mathrm{span}}\{e_1, \ldots , e_{i_{j-1}}\}$
, then elements of
![]() $SO(F_o)$
are given by
$SO(F_o)$
are given by
 $$\begin{align*}\left( \begin{array}{cc} SO_{i_j} & 0 \\ 0 & I_{n-i_j} \end{array} \right) .\end{align*}$$
$$\begin{align*}\left( \begin{array}{cc} SO_{i_j} & 0 \\ 0 & I_{n-i_j} \end{array} \right) .\end{align*}$$
And, the stabilizer of
![]() $E_o$
in
$E_o$
in
![]() $SO(F_o)$
is
$SO(F_o)$
is
 $$\begin{align*}\left( \begin{array}{ccc} SO_{i_{j-1}} & 0 & 0 \\ 0 & SO_{i_j - i_{j-1}} & 0 \\ 0 & 0 & I_{n-i_j} \end{array} \right) .\end{align*}$$
$$\begin{align*}\left( \begin{array}{ccc} SO_{i_{j-1}} & 0 & 0 \\ 0 & SO_{i_j - i_{j-1}} & 0 \\ 0 & 0 & I_{n-i_j} \end{array} \right) .\end{align*}$$
The measure
![]() $\mu _{G_{F_j},i_{j-1}}$
is invariant under
$\mu _{G_{F_j},i_{j-1}}$
is invariant under
![]() $SO(F_{j})$
. Further, for
$SO(F_{j})$
. Further, for
![]() $g\in SO_n$
and a Borel subset
$g\in SO_n$
and a Borel subset
![]() $A \subset G_{F_j,i_{j-1}}$
, we have
$A \subset G_{F_j,i_{j-1}}$
, we have
![]() $ \mu _{G_{g F_j,i_{j-1}}} (gA) = \mu _{G_{F_j,i_{j-1}}} (A)$
.
$ \mu _{G_{g F_j,i_{j-1}}} (gA) = \mu _{G_{F_j,i_{j-1}}} (A)$
.
We will show that both integrals are invariant under the action of
![]() $SO_n$
. Fix
$SO_n$
. Fix
![]() $g\in SO_n$
. We start with the integral on the right-hand side of (18):
$g\in SO_n$
. We start with the integral on the right-hand side of (18):
 $$ \begin{align*} \int_{G_{n,i_r} } & \int_{G_{ F_r, i_{r-1} }} \ldots \int_{G_{ F_2,i_1 }} G (g^{-1} \cdot(F_{1}, \ldots, F_{r})) \, d F_1\ldots dF_{r-1} dF_r \\ &= \int_{G_{n,i_r} } \int_{G_{ g F_r, i_{r-1} }} \ldots \int_{G_{ g F_2, i_1 }} G (F_{1}, \ldots, F_{r}) \, d (g F_1)\ldots d (g F_{r-1}) d (g F_r) \\ &= \int_{G_{n,i_r} } \int_{G_{g F_r, i_{r-1} }} \ldots \int_{G_{gF_3,i_2}}\int_{G_{ F_2, i_1 }} G (F_{1}, \ldots, F_{r}) \, dF_1 d(gF_2)\ldots d (g F_{r-1}) d (g F_r), \end{align*} $$
$$ \begin{align*} \int_{G_{n,i_r} } & \int_{G_{ F_r, i_{r-1} }} \ldots \int_{G_{ F_2,i_1 }} G (g^{-1} \cdot(F_{1}, \ldots, F_{r})) \, d F_1\ldots dF_{r-1} dF_r \\ &= \int_{G_{n,i_r} } \int_{G_{ g F_r, i_{r-1} }} \ldots \int_{G_{ g F_2, i_1 }} G (F_{1}, \ldots, F_{r}) \, d (g F_1)\ldots d (g F_{r-1}) d (g F_r) \\ &= \int_{G_{n,i_r} } \int_{G_{g F_r, i_{r-1} }} \ldots \int_{G_{gF_3,i_2}}\int_{G_{ F_2, i_1 }} G (F_{1}, \ldots, F_{r}) \, dF_1 d(gF_2)\ldots d (g F_{r-1}) d (g F_r), \end{align*} $$
where we have sent
![]() $(F_{1}, \ldots , F_{r}) \to g \cdot (F_{1}, \ldots , F_{r})$
and then used the invariance property
$(F_{1}, \ldots , F_{r}) \to g \cdot (F_{1}, \ldots , F_{r})$
and then used the invariance property
Continuing this way for all inner integrals and using the
![]() $SO_n$
-invariance of the measure
$SO_n$
-invariance of the measure
![]() $\mu _{G_{n,i_r}}$
for the outer integral, the above expression reduces to
$\mu _{G_{n,i_r}}$
for the outer integral, the above expression reduces to
Note that at each step
![]() $(F_{1}, \ldots , F_{r})$
remains an element of
$(F_{1}, \ldots , F_{r})$
remains an element of
![]() $F^n_{\mathbf {r}}$
, this is to say that the inclusion relation is preserved. The invariance of the integral on the left-hand side of (18) is a consequence of the
$F^n_{\mathbf {r}}$
, this is to say that the inclusion relation is preserved. The invariance of the integral on the left-hand side of (18) is a consequence of the
![]() $SO_n$
-invariance of the measure
$SO_n$
-invariance of the measure
![]() $\mu _{F^n_{\mathbf {r}}}$
. The proposition now follows by the uniqueness of the
$\mu _{F^n_{\mathbf {r}}}$
. The proposition now follows by the uniqueness of the
![]() $SO_n$
-invariant probability measure on
$SO_n$
-invariant probability measure on
![]() $F^n_{\mathbf {r}}$
(see, for example, Section 13.3 in [Reference Schneider and Weil51]).
$F^n_{\mathbf {r}}$
(see, for example, Section 13.3 in [Reference Schneider and Weil51]).
The following fact allows one to view an integral of a function on a partial flag as an integral over the full flag manifold. In this case, to avoid confusion, the subspaces of flag manifolds are indexed by their dimension.
Proposition 2.2 Let
![]() $ 1\leq r \leq n-1$
and
$ 1\leq r \leq n-1$
and
![]() $ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
$ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
![]() $1$
and
$1$
and
![]() $n-1$
. For a function
$n-1$
. For a function
![]() $ G $
on the partial flag
$ G $
on the partial flag
![]() $F_{\mathbf {r}}^{n}$
, denote by
$F_{\mathbf {r}}^{n}$
, denote by
![]() $\widetilde {G}$
its trivial extension to the full flag manifold
$\widetilde {G}$
its trivial extension to the full flag manifold
![]() $F^{n}$
, i.e.,
$F^{n}$
, i.e.,
![]() $\widetilde {G}(F_1, \ldots , F_{n-1}) := G(F_{i_1}, \ldots , F_{i_r})$
. Then
$\widetilde {G}(F_1, \ldots , F_{n-1}) := G(F_{i_1}, \ldots , F_{i_r})$
. Then
Proof We “integrate out” the Grassmannians that do not contain subspaces that G depends on by repeatedly using the identity
On the right-hand side, we integrate over the set of all
![]() $(j-1)$
-dimensional subspaces in the ambient
$(j-1)$
-dimensional subspaces in the ambient
![]() $(j+1)$
-dimensional space. On the left-hand side, we integrate over the same set of planes (up to a null set) stepwise, we step from one j-dimensional subspace in the ambient
$(j+1)$
-dimensional space. On the left-hand side, we integrate over the same set of planes (up to a null set) stepwise, we step from one j-dimensional subspace in the ambient
![]() $(j+1)$
-dimensional space to the next, and in each such subspace, we consider all
$(j+1)$
-dimensional space to the next, and in each such subspace, we consider all
![]() $(j-1)$
-dimensional subspaces. The above identity holds since we are using probability measures on each nested Grassmannian. Applying the latter iteratively, we get
$(j-1)$
-dimensional subspaces. The above identity holds since we are using probability measures on each nested Grassmannian. Applying the latter iteratively, we get
 $$ \begin{align*} & \int_{F^{n}} \widetilde{G}( \eta) d \eta \\ &= \int_{G_{n,n-1} } \int_{G_{ F_{n-1}, n-2 }} \ldots \int_{G_{ F_2, 1 }} \widetilde{G} (F_{1}, \ldots , F_{n-1}) d F_1\ldots d F_{n-2} d F_{n-1} \\ &= \int_{G_{n,n-1} } \int_{G_{ F_{n-1}, n-2 }} \ldots \int_{G_{ F_2, 1}} G (F_{i_1}, \ldots, F_{i_r}) dF_1\ldots d F_{n-2} d F_{n-1} \\ & = \int_{G_{n,n-1} } \ldots \int_{G_{ F_{i_1+1}, i_1 }} G (F_{i_1}, \ldots, F_{i_r}) \left( \int_{G_{F_{i_1},i_1-1}} \ldots \int_{G_{F_2,1}} dF_1 \ldots dF_{i_1-1} \right) d F_{i_1} \ldots dF_{n-1} \\ &= \int_{G_{n,n-1} } \ldots \int_{G_{ F_{i_1+1}, i_1 }} G (F_{i_1}, \ldots, F_{i_r}) d F_{i_1} \ldots dF_{n-1} \\ &= \int_{G_{n,n-1} } \ldots \left( \int_{G_{ F_{i_2}, i_2-1 }} \ldots \int_{G_{ F_{i_1+1}, i_1}} G(F_{i_1}, \ldots, F_{i_r}) d F_{i_1} \ldots dF_{i_2-1} \right) \ldots d F_{n-1} \\ &= \int_{G_{n,n-1} } \ldots \left( \int_{G_{F_{i_2}, i_1 }} G (F_{i_1}, \ldots, F_{i_r}) d F_{i_1} \right) \ldots dF_{n-1} \\ &= \cdots \\ &= \int_{G_{n,i_r} } \int_{G_{F_{i_r}, i_{r-1} }} \ldots \int_{G_{ F_{i_2}, i_1 }} G (F_{i_1}, \ldots, F_{i_r}) d F_{i_1}\ldots dF_{i_{r-1}}d F_{i_r} \\ &=\int_{F_{\mathbf{r}}^{n}} G(\xi_{\mathbf{r}}) d \xi_{\mathbf{r}}.\\[-37pt] \end{align*} $$
$$ \begin{align*} & \int_{F^{n}} \widetilde{G}( \eta) d \eta \\ &= \int_{G_{n,n-1} } \int_{G_{ F_{n-1}, n-2 }} \ldots \int_{G_{ F_2, 1 }} \widetilde{G} (F_{1}, \ldots , F_{n-1}) d F_1\ldots d F_{n-2} d F_{n-1} \\ &= \int_{G_{n,n-1} } \int_{G_{ F_{n-1}, n-2 }} \ldots \int_{G_{ F_2, 1}} G (F_{i_1}, \ldots, F_{i_r}) dF_1\ldots d F_{n-2} d F_{n-1} \\ & = \int_{G_{n,n-1} } \ldots \int_{G_{ F_{i_1+1}, i_1 }} G (F_{i_1}, \ldots, F_{i_r}) \left( \int_{G_{F_{i_1},i_1-1}} \ldots \int_{G_{F_2,1}} dF_1 \ldots dF_{i_1-1} \right) d F_{i_1} \ldots dF_{n-1} \\ &= \int_{G_{n,n-1} } \ldots \int_{G_{ F_{i_1+1}, i_1 }} G (F_{i_1}, \ldots, F_{i_r}) d F_{i_1} \ldots dF_{n-1} \\ &= \int_{G_{n,n-1} } \ldots \left( \int_{G_{ F_{i_2}, i_2-1 }} \ldots \int_{G_{ F_{i_1+1}, i_1}} G(F_{i_1}, \ldots, F_{i_r}) d F_{i_1} \ldots dF_{i_2-1} \right) \ldots d F_{n-1} \\ &= \int_{G_{n,n-1} } \ldots \left( \int_{G_{F_{i_2}, i_1 }} G (F_{i_1}, \ldots, F_{i_r}) d F_{i_1} \right) \ldots dF_{n-1} \\ &= \cdots \\ &= \int_{G_{n,i_r} } \int_{G_{F_{i_r}, i_{r-1} }} \ldots \int_{G_{ F_{i_2}, i_1 }} G (F_{i_1}, \ldots, F_{i_r}) d F_{i_1}\ldots dF_{i_{r-1}}d F_{i_r} \\ &=\int_{F_{\mathbf{r}}^{n}} G(\xi_{\mathbf{r}}) d \xi_{\mathbf{r}}.\\[-37pt] \end{align*} $$
We now turn to the invariance properties of the functionals
![]() $\Phi _{\mathbf {r}}$
and
$\Phi _{\mathbf {r}}$
and
![]() $\Psi _{\mathbf {r}}$
. Although self-contained proofs are possible, they require somewhat involved machinery. Since all of the ingredients are available in the literature [Reference Dann, Paouris and Pivovarov12, Reference Furstenberg and Tzkoni16, Reference Grinberg20], we have chosen to gather the essentials without proofs. For readers less familiar with the relevant work, we will explain the main points behind the affine invariance of the functionals
$\Psi _{\mathbf {r}}$
. Although self-contained proofs are possible, they require somewhat involved machinery. Since all of the ingredients are available in the literature [Reference Dann, Paouris and Pivovarov12, Reference Furstenberg and Tzkoni16, Reference Grinberg20], we have chosen to gather the essentials without proofs. For readers less familiar with the relevant work, we will explain the main points behind the affine invariance of the functionals
![]() $\Phi _{{[k]}}(K)$
and
$\Phi _{{[k]}}(K)$
and
![]() $\Psi _{{[k]}}(K)$
along the way. There are two important changes of variables: a “global” change of variables on the Grassmannian
$\Psi _{{[k]}}(K)$
along the way. There are two important changes of variables: a “global” change of variables on the Grassmannian
![]() $G_{n,k}$
or the flag manifold
$G_{n,k}$
or the flag manifold
![]() $F^n_{\mathbf {r}}$
and a “local” change of variables on each element
$F^n_{\mathbf {r}}$
and a “local” change of variables on each element
![]() $F\in G_{n,k}$
or
$F\in G_{n,k}$
or
![]() $\xi _{\mathbf {r}} \in F^n_{\mathbf {r}}$
.
$\xi _{\mathbf {r}} \in F^n_{\mathbf {r}}$
.
Let
![]() $g\in SL_n$
,
$g\in SL_n$
,
![]() $F\in G_{n,k}$
, and
$F\in G_{n,k}$
, and
![]() $A\subset F$
be a full-dimensional Borel set, then
$A\subset F$
be a full-dimensional Borel set, then
![]() $|g A| = |\det (g|_F)| |A|$
. This determinant of the transformation g restricted to the subspace F,
$|g A| = |\det (g|_F)| |A|$
. This determinant of the transformation g restricted to the subspace F,
![]() $\det (g|_F)$
, is the Jacobian in the following change of variables:
$\det (g|_F)$
, is the Jacobian in the following change of variables:
Denote it as in [Reference Furstenberg and Tzkoni16] by
![]() $\sigma _k(g,F):= |\det (g|_F)| = \frac {|g A|}{|A|}$
.
$\sigma _k(g,F):= |\det (g|_F)| = \frac {|g A|}{|A|}$
.
For the relevant manifolds M considered in this paper, denote by
![]() $\sigma _M(g,F)$
the Jacobian determinant in the following change of variables:
$\sigma _M(g,F)$
the Jacobian determinant in the following change of variables:
Furstenberg and Tzkoni proved in [Reference Furstenberg and Tzkoni16] that
and
where
![]() $\mathbf {r}:= (i_{1}, \ldots , i_{r})$
. The linear invariance of the dual affine quermassintegrals
$\mathbf {r}:= (i_{1}, \ldots , i_{r})$
. The linear invariance of the dual affine quermassintegrals
![]() $ \Psi _{[k]} $
now follows immediately. Indeed, for
$ \Psi _{[k]} $
now follows immediately. Indeed, for
![]() $g\in SL_n$
,
$g\in SL_n$
,
 $$ \begin{align*} \Psi^{kn}_{[k]}(gL) &=\int_{G_{n,k}} |gL\cap F|^n dF = \int_{G_{n,k}} |gL\cap gF|^n \sigma_{G_{n,k}}(g,F) dF \\ &= \int_{G_{n,k}} \left(\sigma_{k}(g,F) |L\cap F|\right)^n \sigma_{k}^{-n} (g,F) dF = \Psi^{kn}_{[k]}(L), \end{align*} $$
$$ \begin{align*} \Psi^{kn}_{[k]}(gL) &=\int_{G_{n,k}} |gL\cap F|^n dF = \int_{G_{n,k}} |gL\cap gF|^n \sigma_{G_{n,k}}(g,F) dF \\ &= \int_{G_{n,k}} \left(\sigma_{k}(g,F) |L\cap F|\right)^n \sigma_{k}^{-n} (g,F) dF = \Psi^{kn}_{[k]}(L), \end{align*} $$
where we have used (21), (20) with
![]() $f=1_L$
, and (22). Now we turn toward the proof of Theorem 1.1. We start with the case of dual
$f=1_L$
, and (22). Now we turn toward the proof of Theorem 1.1. We start with the case of dual
![]() $\mathbf {r}$
-flag affine quermassintegrals.
$\mathbf {r}$
-flag affine quermassintegrals.
Proposition 2.3 Let
![]() $ 1\leq r \leq n-1$
and
$ 1\leq r \leq n-1$
and
![]() $ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
$ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
![]() $1$
and
$1$
and
![]() $n-1$
. For every compact body L in
$n-1$
. For every compact body L in
![]() ${\mathbb R}^{n}$
and every
${\mathbb R}^{n}$
and every
![]() $g \in SL_{n}$
,
$g \in SL_{n}$
,
Proof Let us start by expressing
![]() $\sigma _{F_{\mathbf {r}}^{n} }(g, \xi _{\mathbf {r}})$
in terms of sections. For this, note that
$\sigma _{F_{\mathbf {r}}^{n} }(g, \xi _{\mathbf {r}})$
in terms of sections. For this, note that
 $$ \begin{align*}\sigma_{i_{j}}(g, F_{j}) = \frac{ |g( L \cap F_{j})|}{ | L\cap F_{j}|},\end{align*} $$
$$ \begin{align*}\sigma_{i_{j}}(g, F_{j}) = \frac{ |g( L \cap F_{j})|}{ | L\cap F_{j}|},\end{align*} $$
where as a subset of
![]() $F_{j}$
we use the section
$F_{j}$
we use the section
![]() $ L \cap F_{j}$
. By (23) with
$ L \cap F_{j}$
. By (23) with
![]() $i_0=0$
and
$i_0=0$
and
![]() $i_{r+1}=n$
, we have
$i_{r+1}=n$
, we have
 $$ \begin{align*}\sigma_{F_{\mathbf{r}}^{n} } ( g, \xi_{\mathbf{r}}):= \prod_{j=1}^{r} \sigma_{i_{j}}^{-i_{j+1}+ i_{j-1}} (g, F_{j})=\prod_{j=1}^{r} \frac{ |L \cap F_{j}|^{ i_{j+1}- i_{j-1}} }{ |gL \cap g F_{j}|^{ i_{j+1}-i_{j-1}}} .\end{align*} $$
$$ \begin{align*}\sigma_{F_{\mathbf{r}}^{n} } ( g, \xi_{\mathbf{r}}):= \prod_{j=1}^{r} \sigma_{i_{j}}^{-i_{j+1}+ i_{j-1}} (g, F_{j})=\prod_{j=1}^{r} \frac{ |L \cap F_{j}|^{ i_{j+1}- i_{j-1}} }{ |gL \cap g F_{j}|^{ i_{j+1}-i_{j-1}}} .\end{align*} $$
Using the change of variables (21) with the above expression for
![]() $\sigma _{F_{\mathbf {r}}^{n} }$
, yields
$\sigma _{F_{\mathbf {r}}^{n} }$
, yields
 $$ \begin{align*} \Psi_{\mathbf{r}}^{ni_{r}} ( gL) &= \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | gL \cap F_{j}|^{ i_{j+1}- i_{j-1}} d\xi_{\mathbf{r}} \\ &= \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | gL \cap g F_{j}|^{ i_{j+1}- i_{j-1}} \sigma_{F_{\mathbf{r}}^{n}} (g,\xi_{\mathbf{r}}) d\xi_{\mathbf{r}} \\ &= \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | gL \cap g F_{j}|^{ i_{j+1}- i_{j-1}}\prod_{j=1}^{r} \frac{ | L \cap F_{j}|^{ i_{j+1}- i_{j-1}} }{ |gL \cap g F_{j}|^{i_{j+1}- i_{j-1}}} d\xi_{\mathbf{r}} \\ &=\int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | L \cap F_{j}|^{ i_{j+1}- i_{j-1}} d\xi_{\mathbf{r}} \\ &=\Psi_{\mathbf{r}}^{ni_{r}} (L).\\[-34pt] \end{align*} $$
$$ \begin{align*} \Psi_{\mathbf{r}}^{ni_{r}} ( gL) &= \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | gL \cap F_{j}|^{ i_{j+1}- i_{j-1}} d\xi_{\mathbf{r}} \\ &= \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | gL \cap g F_{j}|^{ i_{j+1}- i_{j-1}} \sigma_{F_{\mathbf{r}}^{n}} (g,\xi_{\mathbf{r}}) d\xi_{\mathbf{r}} \\ &= \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | gL \cap g F_{j}|^{ i_{j+1}- i_{j-1}}\prod_{j=1}^{r} \frac{ | L \cap F_{j}|^{ i_{j+1}- i_{j-1}} }{ |gL \cap g F_{j}|^{i_{j+1}- i_{j-1}}} d\xi_{\mathbf{r}} \\ &=\int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | L \cap F_{j}|^{ i_{j+1}- i_{j-1}} d\xi_{\mathbf{r}} \\ &=\Psi_{\mathbf{r}}^{ni_{r}} (L).\\[-34pt] \end{align*} $$
To recall the linear invariance of the operator
![]() $\Phi _{[k]}$
, we follow Grinberg [Reference Grinberg20]. Observe that for
$\Phi _{[k]}$
, we follow Grinberg [Reference Grinberg20]. Observe that for
![]() $F\in G_{n,k}$
and
$F\in G_{n,k}$
and
![]() $g\in SL_n$
upper-triangular with respect to the decomposition
$g\in SL_n$
upper-triangular with respect to the decomposition
![]() $\mathbb {R}^n=F+F^{\perp }$
, we have
$\mathbb {R}^n=F+F^{\perp }$
, we have
where
![]() $g^t$
stands for the transpose of g. While for
$g^t$
stands for the transpose of g. While for
![]() $l\in SO_n$
, we have
$l\in SO_n$
, we have
![]() $P_F(l^t L)=P_{l F}(L)$
. Since any
$P_F(l^t L)=P_{l F}(L)$
. Since any
![]() $g\in SL_n$
can be written as a product of a rotation and an upper-triangular matrix, combining the two observations yields the following.
$g\in SL_n$
can be written as a product of a rotation and an upper-triangular matrix, combining the two observations yields the following.
Lemma 2.4 [Reference Grinberg20]
Let L be a compact body in
![]() ${\mathbb R}^{n}$
,
${\mathbb R}^{n}$
,
![]() $F\in G_{n,k}$
, and
$F\in G_{n,k}$
, and
![]() $g \in SL_{n}$
. Then
$g \in SL_{n}$
. Then
The linear invariance of the affine quermassintegrals
![]() $ \Phi _{[k]} $
can now be seen as follows: let
$ \Phi _{[k]} $
can now be seen as follows: let
![]() $g\in SL_n$
,
$g\in SL_n$
,
where we have used (25) and (21) taking into account (22).
Proposition 2.5 Let
![]() $ 1\leq r \leq n-1$
and
$ 1\leq r \leq n-1$
and
![]() $ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
$ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
![]() $1$
and
$1$
and
![]() $n-1$
. Let A be an affine volume preserving map in
$n-1$
. Let A be an affine volume preserving map in
![]() ${\mathbb R}^{n}$
. Then, for every compact body L in
${\mathbb R}^{n}$
. Then, for every compact body L in
![]() ${\mathbb R}^{n}$
,
${\mathbb R}^{n}$
,
Proof We will first prove the theorem in the case
![]() $A:= g\in SL_{n}$
. Using (25) for the projection onto each
$A:= g\in SL_{n}$
. Using (25) for the projection onto each
![]() $F_j$
, (23), and making the change of variables (21), we get
$F_j$
, (23), and making the change of variables (21), we get
 $$ \begin{align*} \Phi^{-n i_r}_{\mathbf{r}} ( g^t L) &= \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | P_{F_{j}}(g^t L)|^{- i_{j+1}+ i_{j-1}} d\xi_{\mathbf{r}} \\ &= \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} \left( |P_{g F_j} L| \sigma_{i_j}(g,F_j) \right)^{- i_{j+1}+ i_{j-1}} d\xi_{\mathbf{r}} \\ &= \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} |P_{g F_j} L|^{- i_{j+1}+ i_{j-1}} \prod_{j=1}^{r} \sigma^{- i_{j+1}+ i_{j-1}}_{i_j}(g,F_j) d\xi_{\mathbf{r}} \\ &= \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} |P_{g F_j} L|^{- i_{j+1}+ i_{j-1}} \sigma_{F_{\mathbf{r}}^{n} } ( g, \xi_{\mathbf{r}}) d\xi_{\mathbf{r}} \\ &= \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | P_{F_{j}} L|^{- i_{j+1}+i_{j-1}} d\xi_{\mathbf{r}} \\ &= \Phi^{-n i_r}_{\mathbf{r}} (L). \end{align*} $$
$$ \begin{align*} \Phi^{-n i_r}_{\mathbf{r}} ( g^t L) &= \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | P_{F_{j}}(g^t L)|^{- i_{j+1}+ i_{j-1}} d\xi_{\mathbf{r}} \\ &= \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} \left( |P_{g F_j} L| \sigma_{i_j}(g,F_j) \right)^{- i_{j+1}+ i_{j-1}} d\xi_{\mathbf{r}} \\ &= \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} |P_{g F_j} L|^{- i_{j+1}+ i_{j-1}} \prod_{j=1}^{r} \sigma^{- i_{j+1}+ i_{j-1}}_{i_j}(g,F_j) d\xi_{\mathbf{r}} \\ &= \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} |P_{g F_j} L|^{- i_{j+1}+ i_{j-1}} \sigma_{F_{\mathbf{r}}^{n} } ( g, \xi_{\mathbf{r}}) d\xi_{\mathbf{r}} \\ &= \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | P_{F_{j}} L|^{- i_{j+1}+i_{j-1}} d\xi_{\mathbf{r}} \\ &= \Phi^{-n i_r}_{\mathbf{r}} (L). \end{align*} $$
The general case follows easily. This proves (26).
The proof of Theorem 1.1 is now complete.
3 Inequalities
We start by proving an extension of the inequality of Busemann–Straus and Grinberg (8) to flag manifolds.
Proposition 3.1 Let
![]() $ 1 < r \leq n-1$
and
$ 1 < r \leq n-1$
and
![]() $ \mathbf {r} := (i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
$ \mathbf {r} := (i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
![]() $1$
and
$1$
and
![]() $n-1$
. Then, for every compact body L in
$n-1$
. Then, for every compact body L in
![]() $\mathbb {R}^n$
,
$\mathbb {R}^n$
,
with equality if and only if L is an origin-symmetric ellipsoid (up to a set of measure zero).
Proof Inequality (8) implies that for every n, every
![]() $ E\in G_{n,m}$
, any
$ E\in G_{n,m}$
, any
![]() $1\leq \ell \leq m-1$
and every compact body
$1\leq \ell \leq m-1$
and every compact body
![]() $L \subseteq {\mathbb R}^{n}$
,
$L \subseteq {\mathbb R}^{n}$
,
 $$ \begin{align} \int_{G_{E,\ell} } | (L \cap E) \cap F |^{ m} d \mu_{G_{E, \ell}} (F) \leq \frac{\omega_{\ell}^m}{\omega_m^{\ell}} | L \cap E|^{\ell} , \end{align} $$
$$ \begin{align} \int_{G_{E,\ell} } | (L \cap E) \cap F |^{ m} d \mu_{G_{E, \ell}} (F) \leq \frac{\omega_{\ell}^m}{\omega_m^{\ell}} | L \cap E|^{\ell} , \end{align} $$
with equality iff
![]() $L \cap E $
is an ellipsoid (up to a measure
$L \cap E $
is an ellipsoid (up to a measure
![]() $0$
set; see [Reference Gardner18]). Using (18) and (28), we have that
$0$
set; see [Reference Gardner18]). Using (18) and (28), we have that
 $$ \begin{align*} \Psi_{\mathbf{r}}^{ i_{r} n} (L) & = \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} |L\cap F_{{j}} |^{ i_{j+1}- i_{j-1}} d \xi_{\mathbf{r}} \\ & = \int_{ G_{n, i_{r}} } \int_{G_{F_{r}, i_{r-1}}} \ldots \int_{ G_{F_{2}, i_{1}}} \prod_{j=1}^{r} |L\cap F_{{j}} |^{ i_{j+1}- i_{j-1}} dF_{1} \ldots dF_{r-1} dF_{r} \\ & = \int_{ G_{n, i_{r}} } \int_{G_{F_{r}, i_{r-1}}} \ldots\int_{G_{F_{3}, i_{2}}} \prod_{j=2}^{r} |L\cap F_{{j}} |^{ i_{j+1}- i_{j-1}} \times \\ & \qquad \times \left( \int_{ G_{F_{2}, i_{1}}} |L\cap F_{1} |^{ i_{2}} dF_{1} \right) dF_{2} \ldots dF_{r-1} dF_{r}\\ & = \int_{ G_{n, i_{r}} } \int_{G_{F_{r}, i_{r-1}}} \ldots\int_{G_{F_{3}, i_{2}}} \prod_{j=2}^{r} |L\cap F_{{j}} |^{i_{j+1}- i_{j-1}} \times \\ & \qquad \times \left( \int_{ G_{F_{2}, i_{1}}} |(L\cap F_{2}) \cap F_{1} |^{ i_{2}} dF_{1} \right) dF_{2} \ldots dF_{r-1} dF_{r} \\ & \leq \frac{\omega_{i_1}^{i_2}}{\omega_{i_2}^{i_1}} \int_{ G_{n, i_{r}} } \int_{G_{F_{r}, i_{r-1}}} \ldots\int_{G_{F_{3}, i_{2}}} \prod_{j=2}^{r} |L\cap F_{{j}} |^{ i_{j+1}- i_{j-1}} \times \\ &\qquad \times |L \cap F_{2} |^{ i_{1}} dF_{2} \ldots dF_{r-1} dF_{r} \\ &\leq \cdots \\ &\leq |L|^{i_{r}} \prod_{j=1}^{r} \frac{\omega_{i_j}^{i_{j+1}}}{\omega_{i_{j+1}}^{i_j}}. \end{align*} $$
$$ \begin{align*} \Psi_{\mathbf{r}}^{ i_{r} n} (L) & = \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} |L\cap F_{{j}} |^{ i_{j+1}- i_{j-1}} d \xi_{\mathbf{r}} \\ & = \int_{ G_{n, i_{r}} } \int_{G_{F_{r}, i_{r-1}}} \ldots \int_{ G_{F_{2}, i_{1}}} \prod_{j=1}^{r} |L\cap F_{{j}} |^{ i_{j+1}- i_{j-1}} dF_{1} \ldots dF_{r-1} dF_{r} \\ & = \int_{ G_{n, i_{r}} } \int_{G_{F_{r}, i_{r-1}}} \ldots\int_{G_{F_{3}, i_{2}}} \prod_{j=2}^{r} |L\cap F_{{j}} |^{ i_{j+1}- i_{j-1}} \times \\ & \qquad \times \left( \int_{ G_{F_{2}, i_{1}}} |L\cap F_{1} |^{ i_{2}} dF_{1} \right) dF_{2} \ldots dF_{r-1} dF_{r}\\ & = \int_{ G_{n, i_{r}} } \int_{G_{F_{r}, i_{r-1}}} \ldots\int_{G_{F_{3}, i_{2}}} \prod_{j=2}^{r} |L\cap F_{{j}} |^{i_{j+1}- i_{j-1}} \times \\ & \qquad \times \left( \int_{ G_{F_{2}, i_{1}}} |(L\cap F_{2}) \cap F_{1} |^{ i_{2}} dF_{1} \right) dF_{2} \ldots dF_{r-1} dF_{r} \\ & \leq \frac{\omega_{i_1}^{i_2}}{\omega_{i_2}^{i_1}} \int_{ G_{n, i_{r}} } \int_{G_{F_{r}, i_{r-1}}} \ldots\int_{G_{F_{3}, i_{2}}} \prod_{j=2}^{r} |L\cap F_{{j}} |^{ i_{j+1}- i_{j-1}} \times \\ &\qquad \times |L \cap F_{2} |^{ i_{1}} dF_{2} \ldots dF_{r-1} dF_{r} \\ &\leq \cdots \\ &\leq |L|^{i_{r}} \prod_{j=1}^{r} \frac{\omega_{i_j}^{i_{j+1}}}{\omega_{i_{j+1}}^{i_j}}. \end{align*} $$
The last inequality is an equality only when L is an origin-symmetric ellipsoid, up to a set of measure zero (see [Reference Gardner18]). Since for the Euclidean ball all inequalities in the previous chain are actually equalities, we can compute the constants and by the linear-invariance property established by Furstenberg and Tzkoni, we conclude the proof.
Our next result is a type of Blaschke–Santaló and reverse Blaschke–Santaló inequality for
![]() $\mathbf {r}$
-flag affine quermassintegrals. These inequalities concern the volume of the polar body. For a compact set L, we define the polar body
$\mathbf {r}$
-flag affine quermassintegrals. These inequalities concern the volume of the polar body. For a compact set L, we define the polar body
![]() $L^{\circ }$
(with respect to the origin) as the convex body
$L^{\circ }$
(with respect to the origin) as the convex body
It is straightforward to check the following inclusion: for every compact set L in
![]() ${\mathbb R}^{n}$
and
${\mathbb R}^{n}$
and
![]() $F\in G_{n,k}$
,
$F\in G_{n,k}$
,
If, in addition, L is convex and
![]() $0$
is in the interior of L,
$0$
is in the interior of L,
Recall that the Blaschke–Santaló inequality (e.g., [Reference Gardner17, Reference Schneider49]) states that for every origin-symmetric convex body L in
![]() $\mathbb R^{n}$
,
$\mathbb R^{n}$
,
Moreover, (31) holds when L is a convex body and
![]() $L^{\circ }$
is centered, i.e., the centroid of
$L^{\circ }$
is centered, i.e., the centroid of
![]() $L^{\circ }$
is at the origin (see [Reference Schneider49]). We do not know the first reference for (31) in case of compact sets; (31) for centered star-shaped sets appears in [Reference Lutwak33]. For origin-symmetric compact sets with interior points, (31) follows from a more general result in [Reference Cordero-Erausquin, Fradelizi, Paouris and Pivovarov10] (as a limiting case of Theorem 1.1 with
$L^{\circ }$
is at the origin (see [Reference Schneider49]). We do not know the first reference for (31) in case of compact sets; (31) for centered star-shaped sets appears in [Reference Lutwak33]. For origin-symmetric compact sets with interior points, (31) follows from a more general result in [Reference Cordero-Erausquin, Fradelizi, Paouris and Pivovarov10] (as a limiting case of Theorem 1.1 with
![]() $f=1_{L^{\prime }}$
, where
$f=1_{L^{\prime }}$
, where
![]() $L^{\prime }$
is the closure of the interior of L). For a general proof, see [Reference Milman and Yehudayoff38]. An approximate reverse form of this inequality is known as the Bourgain–Milman theorem [Reference Bourgain and Milman5]: for every compact, convex set L with
$L^{\prime }$
is the closure of the interior of L). For a general proof, see [Reference Milman and Yehudayoff38]. An approximate reverse form of this inequality is known as the Bourgain–Milman theorem [Reference Bourgain and Milman5]: for every compact, convex set L with
![]() $ 0 \in \mathrm {int}(L)$
,
$ 0 \in \mathrm {int}(L)$
,
for some absolute constant
![]() $c>0$
. For further background and alternate proofs of this inequality, see [Reference Giannopoulos, Paouris and Vritsiou19, Reference Kuperberg26, Reference Milman40, Reference Nazarov41].
$c>0$
. For further background and alternate proofs of this inequality, see [Reference Giannopoulos, Paouris and Vritsiou19, Reference Kuperberg26, Reference Milman40, Reference Nazarov41].
The next proposition is the aforementioned Blaschke–Santaló inequality and its (approximate) reversal in the setting of
![]() $\mathbf {r}$
-flag manifolds:
$\mathbf {r}$
-flag manifolds:
Proposition 3.2 Let
![]() $ 1 \leq r \leq n-1$
and
$ 1 \leq r \leq n-1$
and
![]() $ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
$ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
![]() $1$
and
$1$
and
![]() $n-1$
. Then, for an origin-symmetric compact body L in
$n-1$
. Then, for an origin-symmetric compact body L in
![]() ${\mathbb R}^{n}$
,
${\mathbb R}^{n}$
,
Moreover, if L is a convex body in
![]() ${\mathbb R}^{n}$
with
${\mathbb R}^{n}$
with
![]() $ 0 \in \mathrm { int}(L)$
, we have that
$ 0 \in \mathrm { int}(L)$
, we have that
where
![]() $c>0$
is an absolute constant (from the reverse Santaló inequality (32)).
$c>0$
is an absolute constant (from the reverse Santaló inequality (32)).
Proof First, note that
 $$ \begin{align*}\Phi_{\mathbf{r}}^{i_{r} n} ( B_{2}^{n} ) \Psi_{\mathbf{r}}^{i_{r} n} (B_{2}^{n}) = \left( \prod_{j=1}^{r} | B_{2}^{n} \cap F_j|^{i_{j+1}- i_{j-1}} \right)^{2},\end{align*} $$
$$ \begin{align*}\Phi_{\mathbf{r}}^{i_{r} n} ( B_{2}^{n} ) \Psi_{\mathbf{r}}^{i_{r} n} (B_{2}^{n}) = \left( \prod_{j=1}^{r} | B_{2}^{n} \cap F_j|^{i_{j+1}- i_{j-1}} \right)^{2},\end{align*} $$
where
![]() $F_j$
are
$F_j$
are
![]() $i_j$
-dimensional subspaces as defined in Section 1.2 and the expression is independent of
$i_j$
-dimensional subspaces as defined in Section 1.2 and the expression is independent of
![]() $ \xi _{\mathbf {r}} := (F_{1}, \ldots , F_{r})$
. Replacing
$ \xi _{\mathbf {r}} := (F_{1}, \ldots , F_{r})$
. Replacing
![]() $L \cap F_j$
by its convex hull in
$L \cap F_j$
by its convex hull in
![]() $F_j$
, using the Blaschke–Santaló inequality (31) and (29), we have
$F_j$
, using the Blaschke–Santaló inequality (31) and (29), we have
 $$ \begin{align*} \Psi_{\mathbf{r}}^{i_{r}n} (L)&=\int_{F_{\mathbf{r}}^{n}}\prod_{j=1}^{r}|L \cap F_j|^{ i_{j+1}- i_{j-1}} d \xi_{\mathbf{r}} \\ &\leq \int_{F_{\mathbf{r}}^{n}}\left(\prod_{j=1}^{r} | B_{2}^{n} \cap F_j|^{i_{j+1}- i_{j-1}}\right)^{2} \prod_{j=1}^{r} \frac{1}{ |(L \cap F_j)^{\circ}|^{ i_{j+1}- i_{j-1}} } d \xi_{\mathbf{r}} \\ & \leq \int_{F_{y r}^{n}}\left( \prod_{j=1}^{r} | B_{2}^{n} \cap F_j|^{i_{j+1}-i_{j-1}}\right)^{2} \prod_{j=1}^{r} \frac{1}{|P_{F_j}L^{\circ}|^{ i_{j+1}- i_{j-1}} } d \xi_{\mathbf{r}} \\ & = \Phi_{\mathbf{r}}^{i_{r} n} ( B_{2}^{n} ) \Psi_{\mathbf{r}}^{i_{r} n} (B_{2}^{n}) \Phi_{\mathbf{r}}^{-i_{r}n} (L^{\circ}). \end{align*} $$
$$ \begin{align*} \Psi_{\mathbf{r}}^{i_{r}n} (L)&=\int_{F_{\mathbf{r}}^{n}}\prod_{j=1}^{r}|L \cap F_j|^{ i_{j+1}- i_{j-1}} d \xi_{\mathbf{r}} \\ &\leq \int_{F_{\mathbf{r}}^{n}}\left(\prod_{j=1}^{r} | B_{2}^{n} \cap F_j|^{i_{j+1}- i_{j-1}}\right)^{2} \prod_{j=1}^{r} \frac{1}{ |(L \cap F_j)^{\circ}|^{ i_{j+1}- i_{j-1}} } d \xi_{\mathbf{r}} \\ & \leq \int_{F_{y r}^{n}}\left( \prod_{j=1}^{r} | B_{2}^{n} \cap F_j|^{i_{j+1}-i_{j-1}}\right)^{2} \prod_{j=1}^{r} \frac{1}{|P_{F_j}L^{\circ}|^{ i_{j+1}- i_{j-1}} } d \xi_{\mathbf{r}} \\ & = \Phi_{\mathbf{r}}^{i_{r} n} ( B_{2}^{n} ) \Psi_{\mathbf{r}}^{i_{r} n} (B_{2}^{n}) \Phi_{\mathbf{r}}^{-i_{r}n} (L^{\circ}). \end{align*} $$
On the other hand, using the reverse Blaschke–Santaló inequality (32), (30), and (9), we get
 $$ \begin{align*} \Psi_{\mathbf{r}}^{i_{r}n}(L) & = \int_{F_{\mathbf{r}}^{n}}\prod_{j=1}^{r} |L \cap F_j|^{ i_{j+1}- i_{j-1}} d \xi_{\mathbf{r}}\\ &\geq c^{ \sum_{j=1}^{r} i_{j} (i_{j+1}-i_{j-1}) } \int_{F_{\mathbf{r}}^n } \left( \prod_{j=1}^{r} | B_{2}^{n} \cap F_j|^{i_{j+1}- i_{j-1}} \right)^{2}\prod_{j=1}^{r} \frac{1}{|(L \cap F_j)^{\circ}|^{ i_{j+1}- i_{j-1}} } d \xi_{\mathbf{r}} \\ & = c^{i_{r}n} \int_{F_{\mathbf{r}}^{n}}\left( \prod_{j=1}^{r} | B_{2}^{n} \cap F_j|^{i_{j+1}- i_{j-1}}\right)^{2} \prod_{j=1}^{r} \frac{1}{ | P_{F_j}L^{\circ}|^{ i_{j+1}-i_{j-1}} } d \xi_{\mathbf{r}}\\ &= c^{i_{r}n} \Phi_{\mathbf{r}}^{i_{r} n} ( B_{2}^{n} ) \Psi_{\mathbf{r}}^{i_{r} n} (B_{2}^{n})\Phi_{\mathbf{r}}^{-i_{r}n}(L^{\circ}). \end{align*} $$
$$ \begin{align*} \Psi_{\mathbf{r}}^{i_{r}n}(L) & = \int_{F_{\mathbf{r}}^{n}}\prod_{j=1}^{r} |L \cap F_j|^{ i_{j+1}- i_{j-1}} d \xi_{\mathbf{r}}\\ &\geq c^{ \sum_{j=1}^{r} i_{j} (i_{j+1}-i_{j-1}) } \int_{F_{\mathbf{r}}^n } \left( \prod_{j=1}^{r} | B_{2}^{n} \cap F_j|^{i_{j+1}- i_{j-1}} \right)^{2}\prod_{j=1}^{r} \frac{1}{|(L \cap F_j)^{\circ}|^{ i_{j+1}- i_{j-1}} } d \xi_{\mathbf{r}} \\ & = c^{i_{r}n} \int_{F_{\mathbf{r}}^{n}}\left( \prod_{j=1}^{r} | B_{2}^{n} \cap F_j|^{i_{j+1}- i_{j-1}}\right)^{2} \prod_{j=1}^{r} \frac{1}{ | P_{F_j}L^{\circ}|^{ i_{j+1}-i_{j-1}} } d \xi_{\mathbf{r}}\\ &= c^{i_{r}n} \Phi_{\mathbf{r}}^{i_{r} n} ( B_{2}^{n} ) \Psi_{\mathbf{r}}^{i_{r} n} (B_{2}^{n})\Phi_{\mathbf{r}}^{-i_{r}n}(L^{\circ}). \end{align*} $$
The proof is complete.
We now turn to the proof of (5) in the setting of r-flag manifolds. Let us first prove an analogue of (5) for r-flag affine quermassintegrals at the expense of a universal constant using known techniques. The case
![]() $r=1$
of the following corollary has been proved in [Reference Paouris and Pivovarov42] before.
$r=1$
of the following corollary has been proved in [Reference Paouris and Pivovarov42] before.
Corollary 3.3 Let
![]() $ 1 \leq r \leq n-1$
and
$ 1 \leq r \leq n-1$
and
![]() $ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
$ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
![]() $1$
and
$1$
and
![]() $n-1$
. Then, for every convex body L,
$n-1$
. Then, for every convex body L,
where
![]() $c>0$
is an absolute constant.
$c>0$
is an absolute constant.
Proof As
![]() $\Phi _{\mathbf {r}}(L)$
is translation-invariant, we may assume that L is centered. The Blaschke–Santaló inequality implies
$\Phi _{\mathbf {r}}(L)$
is translation-invariant, we may assume that L is centered. The Blaschke–Santaló inequality implies
![]() $r_L r_{L^{\circ }}\leq 1$
, so with (34) and (27), we obtain
$r_L r_{L^{\circ }}\leq 1$
, so with (34) and (27), we obtain
 $$ \begin{align*}\Phi_{\mathbf{r}} (L) \geq c \frac{ \Phi_{\mathbf{r} } (B_{2}^{n}) \Psi_{\mathbf{r}} (B_{2}^{n}) }{ \Psi_{\mathbf{r}}(L^{\circ})} \geq c \frac{ \Phi_{\mathbf{r} } (B_{2}^{n}) \Psi_{\mathbf{r}} (B_{2}^{n}) }{ \Psi_{\mathbf{r}}( r_{L^{\circ}} B_{2}^{n})} = \frac{c}{ r_{L^{\circ}}} \Phi_{\mathbf{r}} ( B_{2}^{n}) \geq c \, \Phi_{\mathbf{r}} (r_{L} B_{2}^{n}).\end{align*} $$
$$ \begin{align*}\Phi_{\mathbf{r}} (L) \geq c \frac{ \Phi_{\mathbf{r} } (B_{2}^{n}) \Psi_{\mathbf{r}} (B_{2}^{n}) }{ \Psi_{\mathbf{r}}(L^{\circ})} \geq c \frac{ \Phi_{\mathbf{r} } (B_{2}^{n}) \Psi_{\mathbf{r}} (B_{2}^{n}) }{ \Psi_{\mathbf{r}}( r_{L^{\circ}} B_{2}^{n})} = \frac{c}{ r_{L^{\circ}}} \Phi_{\mathbf{r}} ( B_{2}^{n}) \geq c \, \Phi_{\mathbf{r}} (r_{L} B_{2}^{n}).\end{align*} $$
The proof is complete.
The constant in the above corollary can be made
![]() $1$
using (5) and an argument similar to that of Proposition 3.1, as we argue next.
$1$
using (5) and an argument similar to that of Proposition 3.1, as we argue next.
Proposition 3.4 Let
![]() $ 1 < r \leq n-1$
and
$ 1 < r \leq n-1$
and
![]() $ \mathbf {r} := (i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
$ \mathbf {r} := (i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
![]() $1$
and
$1$
and
![]() $n-1$
. Then, for every convex body L in
$n-1$
. Then, for every convex body L in
![]() $\mathbb {R}^n$
,
$\mathbb {R}^n$
,
with equality if and only if L is an ellipsoid.
Proof First, note that (5) can be written equivalently as
and
 $$ \begin{align} \Phi_{\mathbf{r}}^{- i_{r} n} (r_L B^n_2) = \prod_{j=1}^{r} |r_L B^{i_j}_2|^{{i_{j-1} -i_{j+1}}} = \left( \prod_{j=1}^{r} \omega_{i_j}^{i_{j-1} -i_{j+1}} \right) \omega_n^{i_r} |L|^{-i_r} \,. \end{align} $$
$$ \begin{align} \Phi_{\mathbf{r}}^{- i_{r} n} (r_L B^n_2) = \prod_{j=1}^{r} |r_L B^{i_j}_2|^{{i_{j-1} -i_{j+1}}} = \left( \prod_{j=1}^{r} \omega_{i_j}^{i_{j-1} -i_{j+1}} \right) \omega_n^{i_r} |L|^{-i_r} \,. \end{align} $$
We repeatedly use the following simple reformulation of (36) that for every n, every
![]() $ E\in G_{n,m}$
, and any
$ E\in G_{n,m}$
, and any
![]() $1\leq \ell \leq m-1$
,
$1\leq \ell \leq m-1$
,
Using (18) and (36)–(38), we obtain
 $$ \begin{align*} &\Phi_{\mathbf{r}}^{- i_{r} n} (L)\\ &\quad = \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} |P_{F_{j}} L|^{i_{j-1}-i_{j+1}} d \xi_{\mathbf{r}} \\ &\quad = \int_{ G_{n, i_{r}} } \ldots\int_{G_{F_{3}, i_{2}}} \prod_{j=2}^{r} |P_{F_j}L|^{i_{j-1}-i_{j+1}} \left( \int_{ G_{F_{2}, i_{1}}} |P_{F_1}(P_{F_2}L)|^{-i_{2}} dF_{1} \right) dF_{2} \ldots dF_{r} \\ &\quad \leq \omega^{i_1}_{i_2} \omega_{i_1}^{-i_2} \int_{ G_{n, i_{r}} } \ldots\int_{G_{F_{3}, i_{2}}} \prod_{j=2}^{r} |P_{F_j}L|^{i_{j-1}-i_{j+1}} \left( |P_{F_2}L|^{-i_{1}} \right) dF_{2} \ldots dF_{r} \\ &\quad = \omega^{i_1}_{i_2} \omega_{i_1}^{-i_2} \int_{ G_{n, i_{r}} } \ldots\int_{G_{F_{4}, i_{3}}} \prod_{j=3}^{r} |P_{F_j}L|^{i_{j-1}-i_{j+1}} \left( \int_{G_{F_{3}, i_{2}}} |P_{F_2}(P_{F_3}L)|^{-i_3} dF_{2} \right) dF_{3} \ldots dF_{r} \\ &\quad \leq (\omega^{i_1}_{i_2} \omega_{i_1}^{-i_2}) (\omega^{i_2}_{i_3} \omega_{i_2}^{-i_3}) \int_{ G_{n, i_{r}} } \ldots\int_{G_{F_{4}, i_{3}}} \prod_{j=3}^{r} |P_{F_j}L|^{i_{j-1}-i_{j+1}} \left( |P_{F_3}L|^{-i_2} \right) dF_{3} \ldots dF_{r} \\ &\quad \cdots\\ &\quad\leq \prod_{j=1}^{r} \omega^{i_j}_{i_{j+1}} \omega_{i_j}^{-i_{j+1}} \quad |L|^{-i_{r}} = \left( \prod_{j=1}^{r} \omega_{i_j}^{i_{j-1} -i_{j+1}} \right) \omega_n^{i_r} \quad |L|^{-i_{r}} = \Phi_{\mathbf{r}}^{- i_{r} n} (r_L B^n_2) \, , \end{align*} $$
$$ \begin{align*} &\Phi_{\mathbf{r}}^{- i_{r} n} (L)\\ &\quad = \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} |P_{F_{j}} L|^{i_{j-1}-i_{j+1}} d \xi_{\mathbf{r}} \\ &\quad = \int_{ G_{n, i_{r}} } \ldots\int_{G_{F_{3}, i_{2}}} \prod_{j=2}^{r} |P_{F_j}L|^{i_{j-1}-i_{j+1}} \left( \int_{ G_{F_{2}, i_{1}}} |P_{F_1}(P_{F_2}L)|^{-i_{2}} dF_{1} \right) dF_{2} \ldots dF_{r} \\ &\quad \leq \omega^{i_1}_{i_2} \omega_{i_1}^{-i_2} \int_{ G_{n, i_{r}} } \ldots\int_{G_{F_{3}, i_{2}}} \prod_{j=2}^{r} |P_{F_j}L|^{i_{j-1}-i_{j+1}} \left( |P_{F_2}L|^{-i_{1}} \right) dF_{2} \ldots dF_{r} \\ &\quad = \omega^{i_1}_{i_2} \omega_{i_1}^{-i_2} \int_{ G_{n, i_{r}} } \ldots\int_{G_{F_{4}, i_{3}}} \prod_{j=3}^{r} |P_{F_j}L|^{i_{j-1}-i_{j+1}} \left( \int_{G_{F_{3}, i_{2}}} |P_{F_2}(P_{F_3}L)|^{-i_3} dF_{2} \right) dF_{3} \ldots dF_{r} \\ &\quad \leq (\omega^{i_1}_{i_2} \omega_{i_1}^{-i_2}) (\omega^{i_2}_{i_3} \omega_{i_2}^{-i_3}) \int_{ G_{n, i_{r}} } \ldots\int_{G_{F_{4}, i_{3}}} \prod_{j=3}^{r} |P_{F_j}L|^{i_{j-1}-i_{j+1}} \left( |P_{F_3}L|^{-i_2} \right) dF_{3} \ldots dF_{r} \\ &\quad \cdots\\ &\quad\leq \prod_{j=1}^{r} \omega^{i_j}_{i_{j+1}} \omega_{i_j}^{-i_{j+1}} \quad |L|^{-i_{r}} = \left( \prod_{j=1}^{r} \omega_{i_j}^{i_{j-1} -i_{j+1}} \right) \omega_n^{i_r} \quad |L|^{-i_{r}} = \Phi_{\mathbf{r}}^{- i_{r} n} (r_L B^n_2) \, , \end{align*} $$
where for the penultimate equality we have used the convention that
![]() $i_0=0$
and
$i_0=0$
and
![]() $i_{r+1}=n$
. This proves (35). For the Euclidean ball, all inequalities in the above argument are equalities [Reference Milman and Yehudayoff38]. By the affine invariance of
$i_{r+1}=n$
. This proves (35). For the Euclidean ball, all inequalities in the above argument are equalities [Reference Milman and Yehudayoff38]. By the affine invariance of
![]() $\Phi _{\mathbf {r}}$
, the equality holds only when L is an ellipsoid.
$\Phi _{\mathbf {r}}$
, the equality holds only when L is an ellipsoid.
The next proposition shows that for a convex body L in
![]() $\mathbb {R}^n$
, all the quantities
$\mathbb {R}^n$
, all the quantities
![]() $\Phi _{\mathbf {r}}(L)$
lie between the volume-radius
$\Phi _{\mathbf {r}}(L)$
lie between the volume-radius
![]() $r_{L}$
and the mean width
$r_{L}$
and the mean width
![]() $W(L)=2\int _{S^{n-1}}h_L(\theta )d\sigma (\theta )$
; here,
$W(L)=2\int _{S^{n-1}}h_L(\theta )d\sigma (\theta )$
; here,
![]() $h_L$
is the support function of L, i.e.,
$h_L$
is the support function of L, i.e.,
![]() $h_L(\theta )=\sup _{x\in L}\langle x,\theta \rangle $
. We also set
$h_L(\theta )=\sup _{x\in L}\langle x,\theta \rangle $
. We also set
It will be convenient to use Urysohn’s inequality (
![]() $k=1$
in (4)) in the following form. For any convex body K in
$k=1$
in (4)) in the following form. For any convex body K in
![]() $\mathbb {R}^n$
,
$\mathbb {R}^n$
,
 $$ \begin{align*} \left(\frac{\left\lvert K\right\rvert}{\left\lvert B_2^n\right\rvert}\right)^{1/n}\leq \frac{W(K)}{2}. \end{align*} $$
$$ \begin{align*} \left(\frac{\left\lvert K\right\rvert}{\left\lvert B_2^n\right\rvert}\right)^{1/n}\leq \frac{W(K)}{2}. \end{align*} $$
Proposition 3.5 Let
![]() $ 1 \leq r \leq n-1$
and
$ 1 \leq r \leq n-1$
and
![]() $ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
$ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
![]() $1$
and
$1$
and
![]() $n-1$
. Then, for any convex body L in
$n-1$
. Then, for any convex body L in
![]() ${\mathbb R}^{n}$
,
${\mathbb R}^{n}$
,
 $$ \begin{align} r_L \leq \frac{ \Phi_{\mathbf{r}}(L) }{ \Phi_{\mathbf{r}} (B_{2}^{n}) }\leq \frac{W_{L}}{2}. \end{align} $$
$$ \begin{align} r_L \leq \frac{ \Phi_{\mathbf{r}}(L) }{ \Phi_{\mathbf{r}} (B_{2}^{n}) }\leq \frac{W_{L}}{2}. \end{align} $$
Proof The left-most inequality follows from (35). Next, for
![]() $s>0$
, Hölder’s inequality and the fact that
$s>0$
, Hölder’s inequality and the fact that
![]() $h_{L} (x) = h_{P_{F}L}(x)$
for
$h_{L} (x) = h_{P_{F}L}(x)$
for
![]() $x\in F$
, give
$x\in F$
, give
 $$ \begin{align} \left(\int_{G_{n,k}}W(P_{F}L)^{-s}dF\right)^{-1/s}\leq \int_{G_{n,k}} W(P_{F} L) \, d F = W(L). \end{align} $$
$$ \begin{align} \left(\int_{G_{n,k}}W(P_{F}L)^{-s}dF\right)^{-1/s}\leq \int_{G_{n,k}} W(P_{F} L) \, d F = W(L). \end{align} $$
Toward proving the right-hand side, we write
 $$ \begin{align} \Phi_{\mathbf{r}}^{-ni_r}(L) & = \int_{ G_{n, i_{r}} } \ldots\int_{G_{F_{3}, i_{2}}}\int_{G_{F_{2}, i_{1}}} \prod_{j=1}^{r} |P_{F_j}L|^{i_{j-1}-i_{j+1}} dF_{1}dF_{2} \ldots dF_{r}. \end{align} $$
$$ \begin{align} \Phi_{\mathbf{r}}^{-ni_r}(L) & = \int_{ G_{n, i_{r}} } \ldots\int_{G_{F_{3}, i_{2}}}\int_{G_{F_{2}, i_{1}}} \prod_{j=1}^{r} |P_{F_j}L|^{i_{j-1}-i_{j+1}} dF_{1}dF_{2} \ldots dF_{r}. \end{align} $$
Working with the inner-most integral (recall
![]() $i_0=0$
), we invoke Urysohn’s inequality, followed by (41) to obtain
$i_0=0$
), we invoke Urysohn’s inequality, followed by (41) to obtain
 $$ \begin{align*} \int_{G_{F_2,i_1}}\frac{1}{|P_{F_1}L|^{i_2}}dF_{1} \geq \int_{G_{F_2,i_1}} \frac{2^{i_1i_2}}{\omega_{i_1}^{i_2}W(P_{F_1}L)^{i_1i_2}}dF_{1} \geq \frac{2^{i_1i_2}}{\omega_{i_1}^{i_2}W(P_{F_2}L)^{i_1i_2}}. \end{align*} $$
$$ \begin{align*} \int_{G_{F_2,i_1}}\frac{1}{|P_{F_1}L|^{i_2}}dF_{1} \geq \int_{G_{F_2,i_1}} \frac{2^{i_1i_2}}{\omega_{i_1}^{i_2}W(P_{F_1}L)^{i_1i_2}}dF_{1} \geq \frac{2^{i_1i_2}}{\omega_{i_1}^{i_2}W(P_{F_2}L)^{i_1i_2}}. \end{align*} $$
Similarly, by Urysohn’s inequality,
 $$ \begin{align*} \frac{1}{|P_{F_2}L|^{i_3-i_1}}\geq \frac{2^{i_2(i_3-i_1)}}{\omega_{i_2}^{i_3-i_1}W(P_{F_2}L)^{i_2(i_3-i_1)}}. \end{align*} $$
$$ \begin{align*} \frac{1}{|P_{F_2}L|^{i_3-i_1}}\geq \frac{2^{i_2(i_3-i_1)}}{\omega_{i_2}^{i_3-i_1}W(P_{F_2}L)^{i_2(i_3-i_1)}}. \end{align*} $$
Inserting the last two inequalities into (42) and applying the same argument iteratively, we have
 $$ \begin{align*} \Phi_{\mathbf{r}}^{-ni_r}(L) &\geq \int_{ G_{n, i_{r}} } \ldots\int_{G_{F_{4}, i_{3}}} \prod_{j=3}^{r} |P_{F_j}L|^{i_{j-1}-i_{j+1}} \int_{G_{F_3,i_2}}\frac{2^{i_2i_3}}{\omega_{i_2}^{i_3-i_1}\omega_{i_1}^{i_2}W(P_{F_2}L)^{i_2i_3}} dF_{2}dF_{3} \ldots dF_{r}\\ &\geq \int_{ G_{n, i_{r}} } \ldots\int_{G_{F_{4}, i_{3}}} \prod_{j=3}^{r} |P_{F_j}L|^{i_{j-1}-i_{j+1}} \frac{2^{i_2i_3}}{\omega_{i_2}^{i_3-i_1}\omega_{i_1}^{i_2}W(P_{F_3}L)^{i_2i_3}} dF_{3} \ldots dF_{r}\\ &\geq \ldots\\ &\geq 2^{ni_r}\Phi^{-ni_r}_{\mathbf{ r}}(B_2^n)\int_{G_{n,i_r}}\frac{1}{W(P_{F_r}L)^{ni_r}}dF_r\\ &\geq 2^{ni_r}\Phi^{-ni_r}_{\mathbf{ r}}(B_2^n)W(L)^{-ni_r}.\\ \end{align*} $$
$$ \begin{align*} \Phi_{\mathbf{r}}^{-ni_r}(L) &\geq \int_{ G_{n, i_{r}} } \ldots\int_{G_{F_{4}, i_{3}}} \prod_{j=3}^{r} |P_{F_j}L|^{i_{j-1}-i_{j+1}} \int_{G_{F_3,i_2}}\frac{2^{i_2i_3}}{\omega_{i_2}^{i_3-i_1}\omega_{i_1}^{i_2}W(P_{F_2}L)^{i_2i_3}} dF_{2}dF_{3} \ldots dF_{r}\\ &\geq \int_{ G_{n, i_{r}} } \ldots\int_{G_{F_{4}, i_{3}}} \prod_{j=3}^{r} |P_{F_j}L|^{i_{j-1}-i_{j+1}} \frac{2^{i_2i_3}}{\omega_{i_2}^{i_3-i_1}\omega_{i_1}^{i_2}W(P_{F_3}L)^{i_2i_3}} dF_{3} \ldots dF_{r}\\ &\geq \ldots\\ &\geq 2^{ni_r}\Phi^{-ni_r}_{\mathbf{ r}}(B_2^n)\int_{G_{n,i_r}}\frac{1}{W(P_{F_r}L)^{ni_r}}dF_r\\ &\geq 2^{ni_r}\Phi^{-ni_r}_{\mathbf{ r}}(B_2^n)W(L)^{-ni_r}.\\ \end{align*} $$
In the above argument, we may replace L by
![]() $TL$
, where
$TL$
, where
![]() $T\in SL_n$
. Since the left-hand side of this inequality remains the same for all T by Theorem 1.1, we may take the infimum over all T on the right-hand side. This completes the proof.
$T\in SL_n$
. Since the left-hand side of this inequality remains the same for all T by Theorem 1.1, we may take the infimum over all T on the right-hand side. This completes the proof.
We conclude this subsection with a discussion of inequalities of isomorphic nature. For convex bodies L in
![]() $\mathbb {R}^n$
, we define the Banach–Mazur distance to the Euclidean ball
$\mathbb {R}^n$
, we define the Banach–Mazur distance to the Euclidean ball
![]() $B_2^n$
by
$B_2^n$
by
For origin-symmetric convex bodies, this coincides with the standard notion of Banach–Mazur distance (for more information, see, e.g., [Reference Tomczak-Jaegermann52]).
Proposition 3.6 Let
![]() $ 1 \leq r \leq n-1$
and
$ 1 \leq r \leq n-1$
and
![]() $ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
$ \mathbf {r} := ( i_{1}, \ldots , i_{r})$
be an increasing sequence of integers between
![]() $1$
and
$1$
and
![]() $n-1$
. Then, for any convex body L in
$n-1$
. Then, for any convex body L in
![]() $\mathbb {R}^n$
,
$\mathbb {R}^n$
,
 $$ \begin{align} \Phi_{\mathbf{r}}(L) \leq c_1 \min\left\{ \sqrt{\frac{n}{i_{r}}}, \log{(1+ d_{BM}(L))} \right\} \Phi_{\mathbf{r}} (r_{L} B_{2}^{n}), \end{align} $$
$$ \begin{align} \Phi_{\mathbf{r}}(L) \leq c_1 \min\left\{ \sqrt{\frac{n}{i_{r}}}, \log{(1+ d_{BM}(L))} \right\} \Phi_{\mathbf{r}} (r_{L} B_{2}^{n}), \end{align} $$
and, if L is also symmetric, then
 $$ \begin{align} \Psi_{\mathbf{r}}(L) \geq \frac{c_2}{\min\left\{ \sqrt{\frac{n}{i_{r}}} , \log{(1+ d_{BM}(L))} \right\} }\Psi_{\mathbf{r}} (r_{L} B_{2}^{n}), \end{align} $$
$$ \begin{align} \Psi_{\mathbf{r}}(L) \geq \frac{c_2}{\min\left\{ \sqrt{\frac{n}{i_{r}}} , \log{(1+ d_{BM}(L))} \right\} }\Psi_{\mathbf{r}} (r_{L} B_{2}^{n}), \end{align} $$
where
![]() $c_1,c_2>0$
are absolute constants.
$c_1,c_2>0$
are absolute constants.
The proof relies on several different tools. We draw on ideas from Dafnis and the second-named author [Reference Dafnis and Paouris11] to exploit the affine invariance of
![]() $\Phi _{\mathbf {r}}(L)$
,
$\Phi _{\mathbf {r}}(L)$
,
![]() $\Psi _{\mathbf { r}}(L)$
by using appropriately chosen affine images of L. To this end, recall the following fundamental theorem, which combines work of Figiel–Tomczak-Jaegermann [Reference Figiel and Tomczak-Jaegermann13], Lewis [Reference Lewis28], Pisier [Reference Pisier45], and Rogers–Shephard [Reference Rogers and Shephard47] (see Theorem 1.11.5 on page 52 in [Reference Brazitikos, Giannopoulos, Valettas and Vritsiou6]).
$\Psi _{\mathbf { r}}(L)$
by using appropriately chosen affine images of L. To this end, recall the following fundamental theorem, which combines work of Figiel–Tomczak-Jaegermann [Reference Figiel and Tomczak-Jaegermann13], Lewis [Reference Lewis28], Pisier [Reference Pisier45], and Rogers–Shephard [Reference Rogers and Shephard47] (see Theorem 1.11.5 on page 52 in [Reference Brazitikos, Giannopoulos, Valettas and Vritsiou6]).
Theorem 3.7 Let L be a centered convex body in
![]() $\mathbb {R}^n$
. Then there exists a linear map
$\mathbb {R}^n$
. Then there exists a linear map
![]() $T\in SL_{n}$
such that
$T\in SL_{n}$
such that
for some absolute constant
![]() $c> 0$
.
$c> 0$
.
We will also use recent results on isotropic convex bodies. For background, the reader may consult [Reference Brazitikos, Giannopoulos, Valettas and Vritsiou6], but we will recall all facts that we need here. To each convex body
![]() $M\subseteq \mathbb {R}^n$
with unit volume, one can associate an ellipsoid
$M\subseteq \mathbb {R}^n$
with unit volume, one can associate an ellipsoid
![]() $Z_{2}(M)$
, called the
$Z_{2}(M)$
, called the
![]() $L_{2}$
-centroid body of M, which is defined by its support function as
$L_{2}$
-centroid body of M, which is defined by its support function as
 $$ \begin{align*}h_{Z_{2}(M)} (\theta) := \left( \int_{M} | \langle x, \theta \rangle |^{2} dx \right)^{\frac{1}{2}}.\end{align*} $$
$$ \begin{align*}h_{Z_{2}(M)} (\theta) := \left( \int_{M} | \langle x, \theta \rangle |^{2} dx \right)^{\frac{1}{2}}.\end{align*} $$
The isotropic constant of M is defined by
![]() $L_{M} := r_{Z_{2}(M)}$
. We say that M is isotropic if it is centered and
$L_{M} := r_{Z_{2}(M)}$
. We say that M is isotropic if it is centered and
![]() $Z_{2}(M) = L_{M} B_{2}^{n}$
. Fix an isotropic convex body M and a k-dimensional subspace F. Ball [Reference Ball3] proved that
$Z_{2}(M) = L_{M} B_{2}^{n}$
. Fix an isotropic convex body M and a k-dimensional subspace F. Ball [Reference Ball3] proved that
a corresponding inequality for projections,
 $$ \begin{align} |P_{F} M| \leq \left(c \frac{n}{k} L_{M}\right)^{k}, \end{align} $$
$$ \begin{align} |P_{F} M| \leq \left(c \frac{n}{k} L_{M}\right)^{k}, \end{align} $$
follows immediately from (45) and the Rogers–Shephard inequality [Reference Rogers and Shephard47]:
Next, we recall a variant of
![]() $\Psi _{[k]}(M)$
studied by Dafnis and the second-named author [Reference Dafnis and Paouris11]. For every
$\Psi _{[k]}(M)$
studied by Dafnis and the second-named author [Reference Dafnis and Paouris11]. For every
![]() $ 1\leq k \leq n-1$
and a compact body M in
$ 1\leq k \leq n-1$
and a compact body M in
![]() ${\mathbb R}^{n}$
with
${\mathbb R}^{n}$
with
![]() $|M|=1$
, we define
$|M|=1$
, we define
 $$ \begin{align} \widetilde{\Phi}_{[k]}(M) := \left( \int_{G_{n,k}} |M\cap F^{\perp}|^{n} d\mu_{G_{n,k}}(F) \right)^{\frac{1}{nk}}. \end{align} $$
$$ \begin{align} \widetilde{\Phi}_{[k]}(M) := \left( \int_{G_{n,k}} |M\cap F^{\perp}|^{n} d\mu_{G_{n,k}}(F) \right)^{\frac{1}{nk}}. \end{align} $$
In [Reference Dafnis and Paouris11], it is shown that for every centered convex body M in
![]() $\mathbb {R}^n$
of unit volume,
$\mathbb {R}^n$
of unit volume,
where
![]() $D_n$
is the Euclidean ball of volume one.
$D_n$
is the Euclidean ball of volume one.
We also invoke Klartag’s [Reference Klartag24] fundamental result on perturbations of isotropic convex bodies having a well-bounded isotropic constant.
Theorem 3.8 Let M be a convex body in
![]() ${\mathbb R}^{n}$
. For every
${\mathbb R}^{n}$
. For every
![]() $\varepsilon \in (0,1)$
, there exists a centered convex body
$\varepsilon \in (0,1)$
, there exists a centered convex body
![]() $M_{Kl} \subset {\mathbb R}^{n}$
and a point
$M_{Kl} \subset {\mathbb R}^{n}$
and a point
![]() $x\in {\mathbb R}^{n}$
such that
$x\in {\mathbb R}^{n}$
such that
and
We are now ready to complete the proof.
Proof of Proposition 3.6
By homogeneity of the operators
![]() $\Phi _{\mathbf {r}}$
and
$\Phi _{\mathbf {r}}$
and
![]() $\Psi _{\mathbf {r}}$
, we can assume that L has unit volume.
$\Psi _{\mathbf {r}}$
, we can assume that L has unit volume.
First, we will prove the bound (43) for
![]() $\mathbf {r}$
-flag affine quermassintegrals. By translation invariance of projections, we may further assume that L is centered. Bounding
$\mathbf {r}$
-flag affine quermassintegrals. By translation invariance of projections, we may further assume that L is centered. Bounding
![]() $\Phi _{\mathbf {r}}(L)$
by
$\Phi _{\mathbf {r}}(L)$
by
![]() $W(L)$
according to (40), using affine invariance of
$W(L)$
according to (40), using affine invariance of
![]() $\Phi _{\mathbf {r}}$
and reverse Urysohn inequality from Theorem 3.7, we get
$\Phi _{\mathbf {r}}$
and reverse Urysohn inequality from Theorem 3.7, we get
For the Euclidean ball
![]() $D_n$
of unit volume, we have
$D_n$
of unit volume, we have
![]() $|P_{F} D_{n}|^{\frac {1}{k}}=| D_{n} \cap F|^{\frac {1}{k}}\simeq \sqrt {\frac {n}{k}}$
for every
$|P_{F} D_{n}|^{\frac {1}{k}}=| D_{n} \cap F|^{\frac {1}{k}}\simeq \sqrt {\frac {n}{k}}$
for every
![]() $F\in G_{n,k}$
, so
$F\in G_{n,k}$
, so
 $$ \begin{align*}\Phi_{\mathbf{r}} ( D_{n}) \simeq \left( \prod_{j=1}^{r} \left(\frac{n}{ i_{j}}\right)^{i_{j} (i_{j+1}-i_{j-1}) }\right)^{\frac{1}{2i_{r} n}}.\end{align*} $$
$$ \begin{align*}\Phi_{\mathbf{r}} ( D_{n}) \simeq \left( \prod_{j=1}^{r} \left(\frac{n}{ i_{j}}\right)^{i_{j} (i_{j+1}-i_{j-1}) }\right)^{\frac{1}{2i_{r} n}}.\end{align*} $$
The AM/GM inequality implies
 $$ \begin{align*}\left( \prod_{j=1}^{r} \left( \frac{n}{ i_{j}}\right)^{i_{j} (i_{j+1}-i_{j-1}) }\right)^{\frac{1}{ 2i_{r} n}} \leq \sqrt{\frac{n}{i_{r}n} \sum_{j=1}^{r} \frac{i_{j} (i_{j+1}-j_{j-1})}{i_{j}} }\leq \sqrt{ \frac{n}{ i_{r}} }.\end{align*} $$
$$ \begin{align*}\left( \prod_{j=1}^{r} \left( \frac{n}{ i_{j}}\right)^{i_{j} (i_{j+1}-i_{j-1}) }\right)^{\frac{1}{ 2i_{r} n}} \leq \sqrt{\frac{n}{i_{r}n} \sum_{j=1}^{r} \frac{i_{j} (i_{j+1}-j_{j-1})}{i_{j}} }\leq \sqrt{ \frac{n}{ i_{r}} }.\end{align*} $$
Thus,
 $$ \begin{align} \Phi_{\mathbf{r}} (D_{n}) = \Psi_{\mathbf{r}}( D_{n}) \simeq \left( \prod_{j=1}^{r} \left( \frac{n}{ i_{j}}\right)^{i_{j} ( i_{j+1}-i_{j-1}) }\right)^{\frac{1}{ 2i_{r} n}} \leq \sqrt{\frac{n}{i_{r}}}. \end{align} $$
$$ \begin{align} \Phi_{\mathbf{r}} (D_{n}) = \Psi_{\mathbf{r}}( D_{n}) \simeq \left( \prod_{j=1}^{r} \left( \frac{n}{ i_{j}}\right)^{i_{j} ( i_{j+1}-i_{j-1}) }\right)^{\frac{1}{ 2i_{r} n}} \leq \sqrt{\frac{n}{i_{r}}}. \end{align} $$
Let
![]() $K_{1} \subset \mathbb {R}^n$
be a centered convex body and
$K_{1} \subset \mathbb {R}^n$
be a centered convex body and
![]() $x\in \mathbb {R}^n$
from the conclusion of Theorem 3.8 corresponding to
$x\in \mathbb {R}^n$
from the conclusion of Theorem 3.8 corresponding to
![]() $\varepsilon =\frac {1}{2}$
. Then (48) implies
$\varepsilon =\frac {1}{2}$
. Then (48) implies
![]() $1=|L|^{1/n} \geq \frac {2}{3} | K_{1}|^{1/n}$
, while (49) implies
$1=|L|^{1/n} \geq \frac {2}{3} | K_{1}|^{1/n}$
, while (49) implies
![]() $L_{K_1} \simeq 1$
. Let
$L_{K_1} \simeq 1$
. Let
![]() $ K_{2} := \frac {K_{1}}{ |K_{1}|^{\frac {1}{n}} }$
. Then
$ K_{2} := \frac {K_{1}}{ |K_{1}|^{\frac {1}{n}} }$
. Then
![]() $L_{K_2} = L_{K_1} \simeq 1$
and our choice of
$L_{K_2} = L_{K_1} \simeq 1$
and our choice of
![]() $\varepsilon $
and the latter volume bound give
$\varepsilon $
and the latter volume bound give
Affine invariance of
![]() $\Phi _{\mathbf {r}}$
(Theorem 1.1) allows us to assume that
$\Phi _{\mathbf {r}}$
(Theorem 1.1) allows us to assume that
![]() $K_{2}$
is isotropic. Using (46), (51),
$K_{2}$
is isotropic. Using (46), (51),
![]() $L_{K_2} \simeq 1$
, and (51) one more time, we obtain
$L_{K_2} \simeq 1$
, and (51) one more time, we obtain
 $$ \begin{align*} \Phi_{\mathbf{r}}(K_{2}) &= \left( \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | P_{F_{j}} K_2|^{-i_{j+1}+i_{j-1}} d\xi_{\mathbf{r}} \right)^{-\frac{1}{i_{r} n}} \\ &\leq \left(\prod_{j=1}^{r} \left( \frac{n}{ i_{j}}\right)^{i_{j}(i_{j+1}-i_{j-1})} \right)^{\frac{1}{i_{r}n}} (cL_{K_{2}})^{\frac{1}{i_{r}n}\sum_{j=1}^{r} i_{j}(i_{j+1}-i_{j-1}) }\\ & \leq c \, L_{K_{2}} \Phi_{\mathbf{r}}(D_n)^{2} \\ &\leq c \, \sqrt{\frac{n}{i_{r}}} \, \Phi_{\mathbf{r}}(D_n). \end{align*} $$
$$ \begin{align*} \Phi_{\mathbf{r}}(K_{2}) &= \left( \int_{F_{\mathbf{r}}^{n}} \prod_{j=1}^{r} | P_{F_{j}} K_2|^{-i_{j+1}+i_{j-1}} d\xi_{\mathbf{r}} \right)^{-\frac{1}{i_{r} n}} \\ &\leq \left(\prod_{j=1}^{r} \left( \frac{n}{ i_{j}}\right)^{i_{j}(i_{j+1}-i_{j-1})} \right)^{\frac{1}{i_{r}n}} (cL_{K_{2}})^{\frac{1}{i_{r}n}\sum_{j=1}^{r} i_{j}(i_{j+1}-i_{j-1}) }\\ & \leq c \, L_{K_{2}} \Phi_{\mathbf{r}}(D_n)^{2} \\ &\leq c \, \sqrt{\frac{n}{i_{r}}} \, \Phi_{\mathbf{r}}(D_n). \end{align*} $$
By (52), we have
![]() $ \Phi _{\mathbf {r}} (L) \leq c^{\prime } \sqrt {\frac {n}{i_{r}}} \, \Phi _{\mathbf {r}} (D_n) $
, which together with (50) implies (43).
$ \Phi _{\mathbf {r}} (L) \leq c^{\prime } \sqrt {\frac {n}{i_{r}}} \, \Phi _{\mathbf {r}} (D_n) $
, which together with (50) implies (43).
Applying (34), (43) for
![]() $L^{\circ }$
, and the Blaschke–Santaló inequality
$L^{\circ }$
, and the Blaschke–Santaló inequality
![]() $r_L r_{L^{\circ }}\leq 1$
, we get
$r_L r_{L^{\circ }}\leq 1$
, we get
 $$ \begin{align*} \Psi_{\mathbf{r}} (L) &\geq c\frac{ \Phi_{\mathbf{r}} (B_{2}^{n}) \Psi_{\mathbf{r}}(B_{2}^{n}) }{ \Phi_{\mathbf{r}} ( L^{\circ}) } \\ &\geq \frac{c}{r_{L^{\circ}}} \frac{1}{ \min\left\{ \log{(1+ d_{BM}(L^{\circ}))}, \sqrt{\frac{n}{i_r}}\right\}} \frac{\Phi_{\mathbf{r}} (B_{2}^{n}) \Psi_{\mathbf{r}}(B_{2}^{n}) }{ \Phi_{\mathbf{r}} ( B_{2}^{n})} \\ & \geq \frac{c}{ \min\left\{ \log{(1+ d_{BM}(L))}, \sqrt{\frac{n}{i_{r}}}\right\}} \Psi_{\mathbf{r}} ( r_{L} B_{2}^{n}), \end{align*} $$
$$ \begin{align*} \Psi_{\mathbf{r}} (L) &\geq c\frac{ \Phi_{\mathbf{r}} (B_{2}^{n}) \Psi_{\mathbf{r}}(B_{2}^{n}) }{ \Phi_{\mathbf{r}} ( L^{\circ}) } \\ &\geq \frac{c}{r_{L^{\circ}}} \frac{1}{ \min\left\{ \log{(1+ d_{BM}(L^{\circ}))}, \sqrt{\frac{n}{i_r}}\right\}} \frac{\Phi_{\mathbf{r}} (B_{2}^{n}) \Psi_{\mathbf{r}}(B_{2}^{n}) }{ \Phi_{\mathbf{r}} ( B_{2}^{n})} \\ & \geq \frac{c}{ \min\left\{ \log{(1+ d_{BM}(L))}, \sqrt{\frac{n}{i_{r}}}\right\}} \Psi_{\mathbf{r}} ( r_{L} B_{2}^{n}), \end{align*} $$
where we have also used the identity
![]() $d_{BM} (L^{\circ }) = d_{BM}(L)$
for origin-symmetric convex bodies. This proves (44).
$d_{BM} (L^{\circ }) = d_{BM}(L)$
for origin-symmetric convex bodies. This proves (44).
4 Flag manifolds and permutations
In this section, we discuss more general quantities involving permutations. We investigate the extent to which
![]() $SL_{n}$
-invariance properties established by Furstenberg and Tzkoni [Reference Furstenberg and Tzkoni16] carry over from ellipsoids to compact bodies. In particular, we provide an example of a convex body for which
$SL_{n}$
-invariance properties established by Furstenberg and Tzkoni [Reference Furstenberg and Tzkoni16] carry over from ellipsoids to compact bodies. In particular, we provide an example of a convex body for which
![]() $SL_{n}$
-invariance fails. Nevertheless, we show that for convex bodies, such quantities cannot be too degenerate in the sense that they admit uniform upper and lower bounds, independent of the body. The key ingredient is the notion of M-ellipsoids, introduced by V. D. Milman [Reference Milman40].
$SL_{n}$
-invariance fails. Nevertheless, we show that for convex bodies, such quantities cannot be too degenerate in the sense that they admit uniform upper and lower bounds, independent of the body. The key ingredient is the notion of M-ellipsoids, introduced by V. D. Milman [Reference Milman40].
The next definition is motivated by the work of Furstenberg and Tzkoni [Reference Furstenberg and Tzkoni16] for ellipsoids.
Definition 4.1 Let
![]() $\Pi _{n}$
be the set of permutations of
$\Pi _{n}$
be the set of permutations of
![]() $\{1,2,\ldots ,n\}$
and
$\{1,2,\ldots ,n\}$
and
![]() $\omega \in \Pi _{n}$
. For compact bodies L in
$\omega \in \Pi _{n}$
. For compact bodies L in
![]() $\mathbb {R}^n$
, we define the
$\mathbb {R}^n$
, we define the
![]() $\omega $
-flag quermassintegral and dual
$\omega $
-flag quermassintegral and dual
![]() $\omega $
-flag quermassintegrals as follows: if
$\omega $
-flag quermassintegrals as follows: if
![]() $\omega (n) \neq n$
, then
$\omega (n) \neq n$
, then
 $$ \begin{align} \Phi_{\omega} (L) := \left( \int_{F^{n}} \prod_{j=1}^{n-1} | P_{F_{j}} L|^{- \omega(j) + \omega(j+1)-1} d \xi \right)^{-\frac{1}{n( n- \omega(n))}} \end{align} $$
$$ \begin{align} \Phi_{\omega} (L) := \left( \int_{F^{n}} \prod_{j=1}^{n-1} | P_{F_{j}} L|^{- \omega(j) + \omega(j+1)-1} d \xi \right)^{-\frac{1}{n( n- \omega(n))}} \end{align} $$
and
 $$ \begin{align} \Psi_{\omega} (L) := \left( \int_{F^{n}} \prod_{j=1}^{n-1} | L \cap F_{j}|^{ \omega(j) - \omega(j+1)+1} d \xi \right)^{\frac{1}{ n(n- \omega(n))}}. \end{align} $$
$$ \begin{align} \Psi_{\omega} (L) := \left( \int_{F^{n}} \prod_{j=1}^{n-1} | L \cap F_{j}|^{ \omega(j) - \omega(j+1)+1} d \xi \right)^{\frac{1}{ n(n- \omega(n))}}. \end{align} $$
When
![]() $\omega (n)=n$
, we set
$\omega (n)=n$
, we set
 $$ \begin{align} \Phi_{\omega} (L) := \int_{F^{n}} \prod_{j=1}^{n-1} | P_{F_{j}} L|^{- \omega(j) + \omega(j+1)-1} d \xi \end{align} $$
$$ \begin{align} \Phi_{\omega} (L) := \int_{F^{n}} \prod_{j=1}^{n-1} | P_{F_{j}} L|^{- \omega(j) + \omega(j+1)-1} d \xi \end{align} $$
and
 $$ \begin{align} \Psi_{\omega} (L) := \int_{F^{n}} \prod_{j=1}^{n-1} | L \cap F_{j}|^{ \omega(j) - \omega(j+1)+1} d \xi. \end{align} $$
$$ \begin{align} \Psi_{\omega} (L) := \int_{F^{n}} \prod_{j=1}^{n-1} | L \cap F_{j}|^{ \omega(j) - \omega(j+1)+1} d \xi. \end{align} $$
Note that
 $$ \begin{align} \sum_{j=1}^{n-1} \left( \omega(j) - \omega(j+1) +1\right) = n-\omega(n)+ \omega(1)-1 \end{align} $$
$$ \begin{align} \sum_{j=1}^{n-1} \left( \omega(j) - \omega(j+1) +1\right) = n-\omega(n)+ \omega(1)-1 \end{align} $$
and
 $$ \begin{align} \sum_{j=1}^{n-1} j\left( \omega(j) - \omega(j+1) +1\right) = n(n-\omega(n)). \end{align} $$
$$ \begin{align} \sum_{j=1}^{n-1} j\left( \omega(j) - \omega(j+1) +1\right) = n(n-\omega(n)). \end{align} $$
Identity (58) guarantees that
![]() $\Psi _{\omega }(L)$
and
$\Psi _{\omega }(L)$
and
![]() $ \Phi _{\omega }(L)$
are
$ \Phi _{\omega }(L)$
are
![]() $1$
-homogeneous when
$1$
-homogeneous when
![]() $\omega (n)\neq n$
and
$\omega (n)\neq n$
and
![]() $0$
-homogeneous when
$0$
-homogeneous when
![]() $ \omega (n)=n$
.
$ \omega (n)=n$
.
The following fact for dual
![]() $\omega $
-flag quermassintegrals is from [Reference Furstenberg and Tzkoni16]. For
$\omega $
-flag quermassintegrals is from [Reference Furstenberg and Tzkoni16]. For
![]() $\omega $
-flag quermassintegrals, it follows, for example, by duality.
$\omega $
-flag quermassintegrals, it follows, for example, by duality.
Theorem 4.2 Let
![]() ${\cal {E}}$
be an ellipsoid in
${\cal {E}}$
be an ellipsoid in
![]() ${\mathbb R}^{n}$
and
${\mathbb R}^{n}$
and
![]() $\omega \in \Pi _{n}$
. Then
$\omega \in \Pi _{n}$
. Then
An equivalent formulation of the latter result is that for every ellipsoid
![]() ${\cal {E}}$
,
${\cal {E}}$
,
where
![]() $c_{\omega } $
is a constant that depends only on
$c_{\omega } $
is a constant that depends only on
![]() $\omega $
. An analogous statement holds for
$\omega $
. An analogous statement holds for
![]() $\Phi _{\omega }(\cal {E})$
(see the proof of Proposition 3.2).
$\Phi _{\omega }(\cal {E})$
(see the proof of Proposition 3.2).
The operators
![]() $\Psi _{\omega }$
and
$\Psi _{\omega }$
and
![]() $\Phi _{\omega }$
are generalizations of
$\Phi _{\omega }$
are generalizations of
![]() $\Psi _{\mathbf {r}}$
and
$\Psi _{\mathbf {r}}$
and
![]() $\Phi _{\mathbf {r}}$
. Indeed, let
$\Phi _{\mathbf {r}}$
. Indeed, let
![]() $1\leq r \leq n-1$
,
$1\leq r \leq n-1$
,
![]() $1\leq i_{1}< i_{2} < \cdots < i_{r}\leq n-1$
, and
$1\leq i_{1}< i_{2} < \cdots < i_{r}\leq n-1$
, and
![]() $ \mathbf {r}:= (i_{1}, \ldots , i_{r}). $
Define
$ \mathbf {r}:= (i_{1}, \ldots , i_{r}). $
Define
![]() $\omega $
by
$\omega $
by
![]() $\omega (1) = n-i_{1}+1$
, and
$\omega (1) = n-i_{1}+1$
, and
![]() $\omega (t+1)= \omega (t) +1$
, for
$\omega (t+1)= \omega (t) +1$
, for
![]() $ t\neq i_{j}$
,
$ t\neq i_{j}$
,
![]() $1\leq j \leq r$
, and
$1\leq j \leq r$
, and
![]() $\omega ( i_{j}+1)= \omega (i_{j}) +1 - i_{j+1}+ i_{j-1}$
for
$\omega ( i_{j}+1)= \omega (i_{j}) +1 - i_{j+1}+ i_{j-1}$
for
![]() $ 1\leq j \leq r$
. Then
$ 1\leq j \leq r$
. Then
![]() $\omega \in \Pi _n$
with
$\omega \in \Pi _n$
with
![]() $ \omega (i_{j} ) - \omega (i_{j}+1) +1 = i_{j+1}- i_{j-1}$
for
$ \omega (i_{j} ) - \omega (i_{j}+1) +1 = i_{j+1}- i_{j-1}$
for
![]() $1\leq j\leq r$
and
$1\leq j\leq r$
and
![]() $ \omega ( t) - \omega ( t+1) +1 = 0 , \ t\neq i_{j}$
, for
$ \omega ( t) - \omega ( t+1) +1 = 0 , \ t\neq i_{j}$
, for
![]() $1\leq j \leq r.$
Since
$1\leq j \leq r.$
Since
![]() $\omega (n) = n-i_{r}$
, for a compact body L in
$\omega (n) = n-i_{r}$
, for a compact body L in
![]() ${\mathbb R}^{n}$
, we have
${\mathbb R}^{n}$
, we have
 $$ \begin{align*} \Psi^{n i_{r}}_{\omega} (L) = \int_{F^{n} } \prod_{j=1}^{n-1} |L \cap F_{j}|^{\omega(j)-\omega(j+1)+1} d \xi = \int_{F^{n} } \prod_{j=1}^{r} |L \cap F_{i_{j}}|^{i_{j+1}-i_{j-1}} d \xi = \Psi^{n i_{r}}_{\mathbf{r}}(L), \end{align*} $$
$$ \begin{align*} \Psi^{n i_{r}}_{\omega} (L) = \int_{F^{n} } \prod_{j=1}^{n-1} |L \cap F_{j}|^{\omega(j)-\omega(j+1)+1} d \xi = \int_{F^{n} } \prod_{j=1}^{r} |L \cap F_{i_{j}}|^{i_{j+1}-i_{j-1}} d \xi = \Psi^{n i_{r}}_{\mathbf{r}}(L), \end{align*} $$
where, in the last equality, we have used (19). Correspondingly, we also have
![]() $ \Phi _{\omega }(L) = \Phi _{\mathbf {r}} (L)$
. In particular, for this permutation
$ \Phi _{\omega }(L) = \Phi _{\mathbf {r}} (L)$
. In particular, for this permutation
![]() $\omega $
,
$\omega $
,
![]() $\Psi _{\omega }(L)$
is
$\Psi _{\omega }(L)$
is
![]() $SL_{n}$
-invariant and
$SL_{n}$
-invariant and
![]() $\Phi _{\omega }(L)$
is affine invariant. As a particular case of the preceding discussion, let
$\Phi _{\omega }(L)$
is affine invariant. As a particular case of the preceding discussion, let
![]() $r=1$
,
$r=1$
,
![]() $i_{1}= k$
,
$i_{1}= k$
,
![]() $1\leq k \leq n$
, and let
$1\leq k \leq n$
, and let
![]() $\omega (1)= n-k+1$
and
$\omega (1)= n-k+1$
and
![]() $\omega (t+1)= \omega (t)+1$
for
$\omega (t+1)= \omega (t)+1$
for
![]() $t\neq k$
and
$t\neq k$
and
![]() $ \omega (k+1) = \omega (k) - n +1$
. Then
$ \omega (k+1) = \omega (k) - n +1$
. Then
![]() $\Phi _{\omega }(L) = \Phi _{[k]}(L).$
$\Phi _{\omega }(L) = \Phi _{[k]}(L).$
Given that
![]() $\Psi _{\mathbf {r}}(L)$
and
$\Psi _{\mathbf {r}}(L)$
and
![]() $\Phi _{\mathbf {r}}(L)$
enjoy invariance properties and arise as permutations, it is natural to investigate the extent to which the invariance from Theorem 4.2 carries over to compact bodies. We do not have a complete answer. However, there are cases outside of those considered above where the invariance holds and also counter-examples where it fails as the next two examples show. It will be convenient to recall that a star-body L is a compact body with
$\Phi _{\mathbf {r}}(L)$
enjoy invariance properties and arise as permutations, it is natural to investigate the extent to which the invariance from Theorem 4.2 carries over to compact bodies. We do not have a complete answer. However, there are cases outside of those considered above where the invariance holds and also counter-examples where it fails as the next two examples show. It will be convenient to recall that a star-body L is a compact body with
![]() $0\in \mathop{\mathrm{int}}(L)$
such that
$0\in \mathop{\mathrm{int}}(L)$
such that
![]() $\alpha x\in L$
whenever
$\alpha x\in L$
whenever
![]() $x\in L$
and
$x\in L$
and
![]() $\alpha \in [0,1]$
, with continuous radial function
$\alpha \in [0,1]$
, with continuous radial function
![]() $\rho _L(\theta )=\sup \{r\geq 0:r\theta \in L\}$
(
$\rho _L(\theta )=\sup \{r\geq 0:r\theta \in L\}$
(
![]() $\theta \in S^{n-1}$
).
$\theta \in S^{n-1}$
).
Example 1 Let
![]() $n\geq 3$
. Define
$n\geq 3$
. Define
![]() $\omega $
by
$\omega $
by
![]() $\omega (1)=2$
,
$\omega (1)=2$
,
![]() $\omega (2)=1$
and
$\omega (2)=1$
and
![]() $\omega (t)=t$
for all
$\omega (t)=t$
for all
![]() $ 3\leq t \leq n$
. We will show that for every origin-symmetric star-body L in
$ 3\leq t \leq n$
. We will show that for every origin-symmetric star-body L in
![]() ${\mathbb R}^{n}$
,
${\mathbb R}^{n}$
,
In particular,
![]() $\Psi _{\omega }(L)$
is
$\Psi _{\omega }(L)$
is
![]() $SL_{n}$
-invariant. Note that our choice of the permutation
$SL_{n}$
-invariant. Note that our choice of the permutation
![]() $\omega $
satisfies
$\omega $
satisfies
or equivalently
Moreover,
![]() $\omega $
is the unique permutation satisfying the latter equations, as
$\omega $
is the unique permutation satisfying the latter equations, as
![]() $1\leq \omega (j)\leq n$
for all
$1\leq \omega (j)\leq n$
for all
![]() $1\leq j\leq n$
. For a k-dimensional subspace
$1\leq j\leq n$
. For a k-dimensional subspace
![]() $F_k$
of
$F_k$
of
![]() $\mathbb {R}^n$
, denote by
$\mathbb {R}^n$
, denote by
![]() $S_{F_k}$
the unit sphere in
$S_{F_k}$
the unit sphere in
![]() $F_k$
. Now, using (19) and recalling the notation for
$F_k$
. Now, using (19) and recalling the notation for
![]() $\rho _L$
above, we compute
$\rho _L$
above, we compute
 $$ \begin{align*} \Psi_{\omega} (L) &= \int_{F^{n}} \prod_{j=1}^{n-1} |L \cap F_{j}|^{\omega(j)-\omega(j+1)+1} d\xi \\ &= \int_{F^{n}} |L \cap F_1|^2 |L \cap F_2|^{-1} d\xi \\ &= \int_{G_{n,2}} |L \cap F_2|^{-1} \int_{G_{F_2,1}} |(L \cap F_2) \cap F_1|^2 dF_1 dF_2 \\ &= \int_{G_{n,2}} |L \cap F_2|^{-1} \int_{S_{F_2}} (2 \rho_{L \cap F_2}(\theta))^2 d\sigma(\theta) dF_2 \\ &= \int_{G_{n,2}} |L \cap F_2|^{-1} \frac{4}{|S_{F_2}|} \int_{S_{F_2}} \rho^2_{L \cap F_2}(\theta) d\theta \, dF_2 \\ &= \frac{4}{\pi} \int_{G_{n,2}} |L \cap F_2|^{-1} |L \cap F_2| dF_2 \\ &= \frac{4}{\pi}. \end{align*} $$
$$ \begin{align*} \Psi_{\omega} (L) &= \int_{F^{n}} \prod_{j=1}^{n-1} |L \cap F_{j}|^{\omega(j)-\omega(j+1)+1} d\xi \\ &= \int_{F^{n}} |L \cap F_1|^2 |L \cap F_2|^{-1} d\xi \\ &= \int_{G_{n,2}} |L \cap F_2|^{-1} \int_{G_{F_2,1}} |(L \cap F_2) \cap F_1|^2 dF_1 dF_2 \\ &= \int_{G_{n,2}} |L \cap F_2|^{-1} \int_{S_{F_2}} (2 \rho_{L \cap F_2}(\theta))^2 d\sigma(\theta) dF_2 \\ &= \int_{G_{n,2}} |L \cap F_2|^{-1} \frac{4}{|S_{F_2}|} \int_{S_{F_2}} \rho^2_{L \cap F_2}(\theta) d\theta \, dF_2 \\ &= \frac{4}{\pi} \int_{G_{n,2}} |L \cap F_2|^{-1} |L \cap F_2| dF_2 \\ &= \frac{4}{\pi}. \end{align*} $$
When
![]() $n=3$
, for permutations
$n=3$
, for permutations
![]() $\omega $
with
$\omega $
with
![]() $\omega (3)=3$
,
$\omega (3)=3$
,
![]() $\Psi _{\omega }(L)$
are absolute constants. Moreover, the discussion following Theorem 4.2 shows that for three of the remaining four permutations
$\Psi _{\omega }(L)$
are absolute constants. Moreover, the discussion following Theorem 4.2 shows that for three of the remaining four permutations
![]() $\omega $
in
$\omega $
in
![]() $\Pi _3$
,
$\Pi _3$
,
![]() $\Psi _{\omega }(L)=\Psi _{\mathbf {r}}(L)$
. Altogether, for
$\Psi _{\omega }(L)=\Psi _{\mathbf {r}}(L)$
. Altogether, for
![]() $n=3$
, for five out of six permutations
$n=3$
, for five out of six permutations
![]() $\omega $
,
$\omega $
,
![]() $\Psi _{\omega }(L)$
are
$\Psi _{\omega }(L)$
are
![]() $SL_n$
-invariant. The next example shows that for the remaining permutation, the invariance does not carry over for all convex bodies.
$SL_n$
-invariant. The next example shows that for the remaining permutation, the invariance does not carry over for all convex bodies.
Example 2 Let
![]() $\omega \in \Pi _3$
with
$\omega \in \Pi _3$
with
![]() $\omega (1)=1, \, \omega (2)=3$
, and
$\omega (1)=1, \, \omega (2)=3$
, and
![]() $\omega (3)=2$
. We claim that for a centered cube
$\omega (3)=2$
. We claim that for a centered cube
![]() $Q:=[-1,1]^3$
and the diagonal matrix
$Q:=[-1,1]^3$
and the diagonal matrix
![]() $D=\mathop{\mathrm{diag}}(1,2,1/2)$
,
$D=\mathop{\mathrm{diag}}(1,2,1/2)$
,
![]() $\Phi _{\omega }(DQ)>\Phi _{\omega }(Q)$
. Since
$\Phi _{\omega }(DQ)>\Phi _{\omega }(Q)$
. Since
![]() $D \in SL_3$
, this shows that the operator
$D \in SL_3$
, this shows that the operator
![]() $\Phi _{\omega }$
is not invariant under volume-preserving transformations.
$\Phi _{\omega }$
is not invariant under volume-preserving transformations.
To show this, we first note that for any convex body
![]() $L \subset {\mathbb R}^{3}$
$L \subset {\mathbb R}^{3}$
 $$ \begin{align*} \Phi^{-3}_{\omega}(L) = \int_{G_{3,2}}\left\lvert P_{F_2}L\right\rvert^{-2}\int_{G_{F_2,1}}\left\lvert P_{F_1} L\right\rvert dF_1dF_2 = \int_{S^{2} } \frac{ W( P_{\phi^{\perp}}L)}{ h_{\Pi L}^{2} (\phi) } d\sigma (\phi), \end{align*} $$
$$ \begin{align*} \Phi^{-3}_{\omega}(L) = \int_{G_{3,2}}\left\lvert P_{F_2}L\right\rvert^{-2}\int_{G_{F_2,1}}\left\lvert P_{F_1} L\right\rvert dF_1dF_2 = \int_{S^{2} } \frac{ W( P_{\phi^{\perp}}L)}{ h_{\Pi L}^{2} (\phi) } d\sigma (\phi), \end{align*} $$
where
![]() $h_{\Pi L}(\phi )=\left \lvert P_{\phi ^{\perp }}L\right \rvert $
. For
$h_{\Pi L}(\phi )=\left \lvert P_{\phi ^{\perp }}L\right \rvert $
. For
![]() $\theta \in S^{2}$
, we have
$\theta \in S^{2}$
, we have
![]() $h_Q(\theta )=\sum _{i=1}^3 |\theta _i|$
and, for
$h_Q(\theta )=\sum _{i=1}^3 |\theta _i|$
and, for
![]() $g\in GL_3$
,
$g\in GL_3$
,
![]() $h_{gL}(\theta ) = h_L(g^{t}\theta )$
. We will also use the following facts about projection bodies (see, e.g., [Reference Gardner17]). The projection body of a cube is again a cube,
$h_{gL}(\theta ) = h_L(g^{t}\theta )$
. We will also use the following facts about projection bodies (see, e.g., [Reference Gardner17]). The projection body of a cube is again a cube,
![]() $\Pi Q = 2 Q$
, and for
$\Pi Q = 2 Q$
, and for
![]() $g\in GL_3$
,
$g\in GL_3$
,
Let
![]() $ A=[a_{1} \ a_{2} \ a_{3} ] \in SL_3$
with columns
$ A=[a_{1} \ a_{2} \ a_{3} ] \in SL_3$
with columns
![]() $a_i$
. Fix
$a_i$
. Fix
![]() $ \phi \in S^{2}$
. Let
$ \phi \in S^{2}$
. Let
![]() $U \in O_3$
be given in column form by
$U \in O_3$
be given in column form by
![]() $ U = [ u \ v \ \phi ] $
. Since
$ U = [ u \ v \ \phi ] $
. Since
![]() $ U $
is orthogonal,
$ U $
is orthogonal,
![]() $ U^{t} \phi = e_{3} $
and
$ U^{t} \phi = e_{3} $
and
![]() $ U^{t} \phi ^{\perp } = \mathrm {span}\{ e_{1}, e_{2} \} = \mathbb R^{2} $
. Then
$ U^{t} \phi ^{\perp } = \mathrm {span}\{ e_{1}, e_{2} \} = \mathbb R^{2} $
. Then
Thus, denoting by P the orthogonal projection onto
![]() ${\mathbb R}^{2}$
, we have
${\mathbb R}^{2}$
, we have
 $$ \begin{align*}W( P_{\phi^{\perp}} A Q) = 2 \sum_{i=1}^{3} \int_{S^{1}} | \langle \theta , U^{t} A e_{i} \rangle | d\sigma( \theta ) = 2 \sum_{i=1}^{3} \int_{S^{1}} | \langle \theta , P U^{t} A e_{i} \rangle | d\sigma( \theta ) = \frac{4}{\pi} \sum_{i=1}^{3} \| P U^{t} A e_{i} \|_{2} .\end{align*} $$
$$ \begin{align*}W( P_{\phi^{\perp}} A Q) = 2 \sum_{i=1}^{3} \int_{S^{1}} | \langle \theta , U^{t} A e_{i} \rangle | d\sigma( \theta ) = 2 \sum_{i=1}^{3} \int_{S^{1}} | \langle \theta , P U^{t} A e_{i} \rangle | d\sigma( \theta ) = \frac{4}{\pi} \sum_{i=1}^{3} \| P U^{t} A e_{i} \|_{2} .\end{align*} $$
One can verify the last equality in this setting by a direct computation as follows. We realize integration over
![]() $S^{1}$
as integration over
$S^{1}$
as integration over
![]() $[0, 2\pi ]$
. Hence, we write
$[0, 2\pi ]$
. Hence, we write
![]() $\theta =(\cos \alpha , \sin \alpha )$
,
$\theta =(\cos \alpha , \sin \alpha )$
,
![]() $v \in \mathbb {R}^2$
as
$v \in \mathbb {R}^2$
as
![]() $v = \| v \|_2 (\cos \beta , \sin \beta )$
and
$v = \| v \|_2 (\cos \beta , \sin \beta )$
and
 $\int _{S^{1}} | \langle \theta , v \rangle | d\sigma ( \theta ) = \frac {\| v \|_2}{2\pi } \int _0^{2\pi } | \cos \alpha \cos \beta + \sin \alpha \sin \beta | d\alpha = \frac {\| v \|_2}{2\pi } \int _0^{2\pi } | \cos (\alpha - \beta ) | d\alpha = \frac {\| v \|_2}{2\pi } \int _0^{2\pi } | \cos \alpha | d\alpha = \frac {2}{\pi } \| v \|_2$
. We have that
$\int _{S^{1}} | \langle \theta , v \rangle | d\sigma ( \theta ) = \frac {\| v \|_2}{2\pi } \int _0^{2\pi } | \cos \alpha \cos \beta + \sin \alpha \sin \beta | d\alpha = \frac {\| v \|_2}{2\pi } \int _0^{2\pi } | \cos (\alpha - \beta ) | d\alpha = \frac {\| v \|_2}{2\pi } \int _0^{2\pi } | \cos \alpha | d\alpha = \frac {2}{\pi } \| v \|_2$
. We have that
![]() $ A e_{i} = a_{i}$
,
$ A e_{i} = a_{i}$
,
![]() $ U^{t} a_{i} = \left ( \langle u, a_{i} \rangle , \langle v, a_{i} \rangle , \langle \phi , a_{i} \rangle \right )^{t} $
and
$ U^{t} a_{i} = \left ( \langle u, a_{i} \rangle , \langle v, a_{i} \rangle , \langle \phi , a_{i} \rangle \right )^{t} $
and
Therefore,
 $$ \begin{align*} W( P_{\phi^{\perp}} A Q)= \frac{4}{\pi} \sum_{i=1}^{3} \sqrt{ \|a_{i}\|_{2}^{2} - \langle \phi, a_{i} \rangle^{2} }. \end{align*} $$
$$ \begin{align*} W( P_{\phi^{\perp}} A Q)= \frac{4}{\pi} \sum_{i=1}^{3} \sqrt{ \|a_{i}\|_{2}^{2} - \langle \phi, a_{i} \rangle^{2} }. \end{align*} $$
Moreover, by the aforementioned properties of a centered cube,
![]() $ h_{\Pi (A Q) } ( \phi ) = h_{\Pi Q} ( A^{-1} \phi ) = 2 \sum _{i=1}^{3} | \langle A^{-1} \phi , e_{i} \rangle | $
. Thus,
$ h_{\Pi (A Q) } ( \phi ) = h_{\Pi Q} ( A^{-1} \phi ) = 2 \sum _{i=1}^{3} | \langle A^{-1} \phi , e_{i} \rangle | $
. Thus,
 $$ \begin{align*} \Phi^{-3}_{\omega}(AQ) = \frac{1}{\pi} \int_{S^{2}} \frac{ \sum_{i=1}^{3} \sqrt{ \|a_{i}\|_{2}^{2} - \langle \phi, a_{i} \rangle^{2} }}{\left(\sum_{j=1}^{3} | \langle A^{-1} \phi, e_{j} \rangle | \right)^{2} } d\sigma ( \phi). \end{align*} $$
$$ \begin{align*} \Phi^{-3}_{\omega}(AQ) = \frac{1}{\pi} \int_{S^{2}} \frac{ \sum_{i=1}^{3} \sqrt{ \|a_{i}\|_{2}^{2} - \langle \phi, a_{i} \rangle^{2} }}{\left(\sum_{j=1}^{3} | \langle A^{-1} \phi, e_{j} \rangle | \right)^{2} } d\sigma ( \phi). \end{align*} $$
Set
![]() $ A:= \mathrm {diag} ( d_{1}, d_{2}, d_{3})$
with
$ A:= \mathrm {diag} ( d_{1}, d_{2}, d_{3})$
with
![]() $\prod _{i=1}^{3} d_{i}= 1$
and
$\prod _{i=1}^{3} d_{i}= 1$
and
![]() $ d_{i}>0$
. Then the quantity
$ d_{i}>0$
. Then the quantity
 $$ \begin{align*} {\cal{A}}( d_{1}, d_{2}, d_{3}) := \int_{S^{2}} \frac{\sum_{i=1}^{3} d_{i} \sqrt{ 1- \phi_{i}^{2} }}{ \left(\sum_{j=1}^{3}\frac{|\phi_{j}|}{ d_{j}}\right)^{2} } d\sigma ( \phi) \end{align*} $$
$$ \begin{align*} {\cal{A}}( d_{1}, d_{2}, d_{3}) := \int_{S^{2}} \frac{\sum_{i=1}^{3} d_{i} \sqrt{ 1- \phi_{i}^{2} }}{ \left(\sum_{j=1}^{3}\frac{|\phi_{j}|}{ d_{j}}\right)^{2} } d\sigma ( \phi) \end{align*} $$
is not constant. Indeed, using MATLAB, for example, one can verify that
![]() ${\cal {A}}(1,2,1/2)<{\cal {A}}(1,1,1)$
.
${\cal {A}}(1,2,1/2)<{\cal {A}}(1,1,1)$
.
In the case of convex bodies, the quantities
![]() $\Psi _{\omega }(K)$
,
$\Psi _{\omega }(K)$
,
![]() $\Phi _{\omega }(K)$
are uniformly bounded by a constant that depends on
$\Phi _{\omega }(K)$
are uniformly bounded by a constant that depends on
![]() $\omega $
only. We will use the following well-known consequence of the celebrated “existence of M-ellipsoids” by V. D. Milman [Reference Milman40].
$\omega $
only. We will use the following well-known consequence of the celebrated “existence of M-ellipsoids” by V. D. Milman [Reference Milman40].
Theorem 4.3 Let K be an origin-symmetric convex body in
![]() ${\mathbb R}^{n}$
. Then there exists an ellipsoid
${\mathbb R}^{n}$
. Then there exists an ellipsoid
![]() ${\cal {E}}$
such that
${\cal {E}}$
such that
![]() $|{\cal {E}}|^{1/n} \leq e^{c} |K|^{1/n}$
and for every
$|{\cal {E}}|^{1/n} \leq e^{c} |K|^{1/n}$
and for every
![]() $F\in G_{n,k}$
,
$F\in G_{n,k}$
,
and
where
![]() $c>0$
is an absolute constant.
$c>0$
is an absolute constant.
Corollary 4.4 Let
![]() $\omega \in \Pi _{n}$
such that
$\omega \in \Pi _{n}$
such that
![]() $\omega (n)\neq n$
. Let
$\omega (n)\neq n$
. Let
![]() $ \delta _{\omega } (j) := \omega (j) - \omega (j+1) + 1$
. Set
$ \delta _{\omega } (j) := \omega (j) - \omega (j+1) + 1$
. Set
 $$ \begin{align*}I_{\omega} := \{ j\leq n : \delta_{\omega} ( j) \geq 0 \} \ \mathrm{and } \ \Delta(\omega):=\frac{\min\{ \sum_{j\in I_{\omega} } \delta_{\omega}(j) , \sum_{j\in I_{\omega}^{c} } |\delta_{\omega}(j)|\} }{n - \omega(n)} + 1 .\end{align*} $$
$$ \begin{align*}I_{\omega} := \{ j\leq n : \delta_{\omega} ( j) \geq 0 \} \ \mathrm{and } \ \Delta(\omega):=\frac{\min\{ \sum_{j\in I_{\omega} } \delta_{\omega}(j) , \sum_{j\in I_{\omega}^{c} } |\delta_{\omega}(j)|\} }{n - \omega(n)} + 1 .\end{align*} $$
We have that
and
where
![]() $c>0$
is an absolute constant.
$c>0$
is an absolute constant.
Proof Set
![]() $ \Delta _{+}(\omega ) := \frac { \sum _{j\in I_{\omega } } \delta _{\omega }(j) }{n - \omega (n)}$
and
$ \Delta _{+}(\omega ) := \frac { \sum _{j\in I_{\omega } } \delta _{\omega }(j) }{n - \omega (n)}$
and
![]() $ \Delta _{-} ( \omega ):= \frac { \sum _{j\in I_{\omega }^{c}} |\delta _{\omega }(j) |}{n - \omega (n)}$
. In the ensuing computation, we use the bounds on
$ \Delta _{-} ( \omega ):= \frac { \sum _{j\in I_{\omega }^{c}} |\delta _{\omega }(j) |}{n - \omega (n)}$
. In the ensuing computation, we use the bounds on
![]() $|K\cap F|$
in (60): for
$|K\cap F|$
in (60): for
![]() $j\in I_{\omega }$
, we use the upper bound, while for
$j\in I_{\omega }$
, we use the upper bound, while for
![]() $j \notin I_{\omega }$
, we use the lower bound. Thus, we obtain
$j \notin I_{\omega }$
, we use the lower bound. Thus, we obtain
 $$ \begin{align*} \Psi_{\omega} (K) &= \left( \int_{F_{n}} \prod_{j=1}^{n-1} | K \cap F_{j}|^{ \omega(j) - \omega(j+1)+1} d \xi \right)^{\frac{1}{n(n- \omega(n))}}\\ &\leq \left( \int_{F_{n}} e^{cn \sum_{j\in I_{\omega}} (\omega(j) - \omega(j+1) +1)} \prod_{j=1}^{n-1} | {\cal{E}} \cap F_{j}|^{ \omega(j) - \omega(j+1)+1} d \xi \right)^{\frac{1}{ n(n- \omega(n))}} \\ & = e^{ c\Delta_{+}(\omega) } \left( \int_{F_{n}} \prod_{j=1}^{n-1} | {\cal{E}} \cap F_{j}|^{ \omega(j) - \omega(j+1)+1} d \xi \right)^{\frac{1}{ n(n- \omega(n))}}\\ &=e^{ c\Delta_{+}(\omega) }c_{\omega} | {\cal{E}}|^{\frac{1}{n}} \\ &\leq e^{ c ( \Delta_{+}( \omega) + 1 )}c_{\omega} | K |^{\frac{1}{ n}}. \end{align*} $$
$$ \begin{align*} \Psi_{\omega} (K) &= \left( \int_{F_{n}} \prod_{j=1}^{n-1} | K \cap F_{j}|^{ \omega(j) - \omega(j+1)+1} d \xi \right)^{\frac{1}{n(n- \omega(n))}}\\ &\leq \left( \int_{F_{n}} e^{cn \sum_{j\in I_{\omega}} (\omega(j) - \omega(j+1) +1)} \prod_{j=1}^{n-1} | {\cal{E}} \cap F_{j}|^{ \omega(j) - \omega(j+1)+1} d \xi \right)^{\frac{1}{ n(n- \omega(n))}} \\ & = e^{ c\Delta_{+}(\omega) } \left( \int_{F_{n}} \prod_{j=1}^{n-1} | {\cal{E}} \cap F_{j}|^{ \omega(j) - \omega(j+1)+1} d \xi \right)^{\frac{1}{ n(n- \omega(n))}}\\ &=e^{ c\Delta_{+}(\omega) }c_{\omega} | {\cal{E}}|^{\frac{1}{n}} \\ &\leq e^{ c ( \Delta_{+}( \omega) + 1 )}c_{\omega} | K |^{\frac{1}{ n}}. \end{align*} $$
One can verify that a similar inequality with the quantity
![]() $ \Delta _{-} (\omega )$
holds as well, which leads to the right-hand side in (61). The proof of the other inequalities is identical and hence is omitted.
$ \Delta _{-} (\omega )$
holds as well, which leads to the right-hand side in (61). The proof of the other inequalities is identical and hence is omitted.
Remark A similar proposition (with the same proof) holds for the case
![]() $\omega (n)=n$
. Moreover, using Pisier’s regular M-position (see [Reference Pisier46]), one can get more precise estimates.
$\omega (n)=n$
. Moreover, using Pisier’s regular M-position (see [Reference Pisier46]), one can get more precise estimates.
5 Functional forms
In this section, we derive functional forms of some of the previous geometric inequalities. Section 5.1 concerns the dual setting with sharp inequalities for restrictions of functions to flags of subspaces; these do not depend on their counterparts for sets. In Section 5.2, we define a new notion of
![]() $\mathbf {r}$
-flag affine quermassintegrals for functions and establish a double-sided approximate isoperimetric inequality.
$\mathbf {r}$
-flag affine quermassintegrals for functions and establish a double-sided approximate isoperimetric inequality.
5.1 Functional forms of dual
 $\mathbf {r}$
-flag affine quermassintegrals
$\mathbf {r}$
-flag affine quermassintegrals
Let
![]() $ f $
be a bounded integrable function on
$ f $
be a bounded integrable function on
![]() $\mathbb {R}^{n}$
. We denote by
$\mathbb {R}^{n}$
. We denote by
![]() $I(f)$
the functional form of the dual
$I(f)$
the functional form of the dual
![]() $\mathbf {r}$
-flag affine quermassintegral
$\mathbf {r}$
-flag affine quermassintegral
 $$ \begin{align*}I(f) := \int_{ F_{\mathbf{r}}^n } \prod_{j=1}^{r} \| f |_{F_j}\|^{i_{j+1}-i_{j-1}}_{1} d\xi_{\mathbf{r}} .\end{align*} $$
$$ \begin{align*}I(f) := \int_{ F_{\mathbf{r}}^n } \prod_{j=1}^{r} \| f |_{F_j}\|^{i_{j+1}-i_{j-1}}_{1} d\xi_{\mathbf{r}} .\end{align*} $$
Theorem 5.1 For every
![]() $ g \in SL_{n}$
,
$ g \in SL_{n}$
,
![]() $ I( g\cdot f) = I( f)$
, where
$ I( g\cdot f) = I( f)$
, where
![]() $g\cdot f(x)=f(g^{-1}x)$
.
$g\cdot f(x)=f(g^{-1}x)$
.
Proof Starting with the left-hand side,
![]() $I( g\cdot f)$
, we do a global change of variables (21) on the flag manifold:
$I( g\cdot f)$
, we do a global change of variables (21) on the flag manifold:
 $$ \begin{align*} I( g\cdot f) = \int_{ F_{\mathbf{r}}^n } \prod_{j=1}^{r} \| g\cdot f |_{F_j}\|^{i_{j+1}-i_{j-1}}_{1} d\xi_{\mathbf{r}} = \int_{ F_{\mathbf{r}}^n } \prod_{j=1}^{r} \| g\cdot f |_{g\cdot F_j}\|^{i_{j+1}-i_{j-1}}_{1} \sigma_{F_{\mathbf{r}}^{n} }(g, \xi) d\xi_{\mathbf{r}}, \end{align*} $$
$$ \begin{align*} I( g\cdot f) = \int_{ F_{\mathbf{r}}^n } \prod_{j=1}^{r} \| g\cdot f |_{F_j}\|^{i_{j+1}-i_{j-1}}_{1} d\xi_{\mathbf{r}} = \int_{ F_{\mathbf{r}}^n } \prod_{j=1}^{r} \| g\cdot f |_{g\cdot F_j}\|^{i_{j+1}-i_{j-1}}_{1} \sigma_{F_{\mathbf{r}}^{n} }(g, \xi) d\xi_{\mathbf{r}}, \end{align*} $$
where by (23)
![]() $\sigma _{F_{\mathbf {r}}^{n} }(g, \xi ) = \sigma _{i_{1}}^{-i_{2}}(g, F_1) \sigma _{i_{2}}^{i_{1}-i_{3}}(g, F_2) \cdots \sigma _{i_{r}}^{i_{r-1}-n}(g, F_r) $
. Now we do r local changes of variables (20) on each nested subspace
$\sigma _{F_{\mathbf {r}}^{n} }(g, \xi ) = \sigma _{i_{1}}^{-i_{2}}(g, F_1) \sigma _{i_{2}}^{i_{1}-i_{3}}(g, F_2) \cdots \sigma _{i_{r}}^{i_{r-1}-n}(g, F_r) $
. Now we do r local changes of variables (20) on each nested subspace
![]() $F_j$
in the product. For each
$F_j$
in the product. For each
![]() $1\leq j \leq r$
, we thus have
$1\leq j \leq r$
, we thus have
For the product under the integral, we obtain
 $$ \begin{align*}\prod_{j=1}^{r} \| g\cdot f |_{g\cdot F_j}\|^{i_{j+1}-i_{j-1}}_{1} = \prod_{j=1}^{r} \left( \|f|_{F_j}\|_{1} \, \sigma_{i_j}(g,F_j) \right)^{i_{j+1}-i_{j-1}} = \prod_{j=1}^{r} \|f|_{F_j}\|^{i_{j+1}-i_{j-1}}_{1} \sigma_{F_{\mathbf{r}}^{n} }^{-1}(g, \xi).\end{align*} $$
$$ \begin{align*}\prod_{j=1}^{r} \| g\cdot f |_{g\cdot F_j}\|^{i_{j+1}-i_{j-1}}_{1} = \prod_{j=1}^{r} \left( \|f|_{F_j}\|_{1} \, \sigma_{i_j}(g,F_j) \right)^{i_{j+1}-i_{j-1}} = \prod_{j=1}^{r} \|f|_{F_j}\|^{i_{j+1}-i_{j-1}}_{1} \sigma_{F_{\mathbf{r}}^{n} }^{-1}(g, \xi).\end{align*} $$
The latter result admits several generalizations as in [Reference Dann, Paouris and Pivovarov12] for functional forms of dual quermassintegrals. Rather than taking
![]() $L_1(F_j)$
norms, one can take
$L_1(F_j)$
norms, one can take
![]() $L_{p_j}(F_j)$
norms and replace the powers
$L_{p_j}(F_j)$
norms and replace the powers
![]() $i_{j+1}-i_{j-1}$
by
$i_{j+1}-i_{j-1}$
by
![]() $\alpha _j$
. As long as
$\alpha _j$
. As long as
![]() $\frac {\alpha _j}{p_j}=i_{j+1}-i_{j-1}$
and the integrals exist, the conclusion of Theorem 5.1 will hold. Theorem 5.1 also generalizes to a product of m functions. One can replace
$\frac {\alpha _j}{p_j}=i_{j+1}-i_{j-1}$
and the integrals exist, the conclusion of Theorem 5.1 will hold. Theorem 5.1 also generalizes to a product of m functions. One can replace
![]() $ \| f |_{F_j}\|^{i_{j+1}-i_{j-1}}_{1} $
by
$ \| f |_{F_j}\|^{i_{j+1}-i_{j-1}}_{1} $
by
![]() $ \prod _{i=1}^m \| f_i |_{E_j} \|^{\alpha _{i,j}}_{p_{i,j}} $
. For the analogue of Theorem 5.1 to hold in this case, we have to require
$ \prod _{i=1}^m \| f_i |_{E_j} \|^{\alpha _{i,j}}_{p_{i,j}} $
. For the analogue of Theorem 5.1 to hold in this case, we have to require
![]() $\sum _{i=1}^m \frac {\alpha _{i,j}}{p_{i,j}} = i_{j+1}-i_{j-1}$
. Another way to generalize functional forms of dual quermassintegrals is to replace
$\sum _{i=1}^m \frac {\alpha _{i,j}}{p_{i,j}} = i_{j+1}-i_{j-1}$
. Another way to generalize functional forms of dual quermassintegrals is to replace
 $$ \begin{align*}\| f |_{F_j}\|^{i_{j+1}-i_{j-1}}_{1} \quad \text{ by } \quad \frac{ \| f |_{F_j} \|^{\alpha_j}_{p_j}}{{\| g |_{F_j}\|^{\beta_j}_{q_j}}} \quad \text{ with } \quad \frac{\alpha_j}{p_j} - \frac{\beta_j}{q_j} = i_{j+1}-i_{j-1},\end{align*} $$
$$ \begin{align*}\| f |_{F_j}\|^{i_{j+1}-i_{j-1}}_{1} \quad \text{ by } \quad \frac{ \| f |_{F_j} \|^{\alpha_j}_{p_j}}{{\| g |_{F_j}\|^{\beta_j}_{q_j}}} \quad \text{ with } \quad \frac{\alpha_j}{p_j} - \frac{\beta_j}{q_j} = i_{j+1}-i_{j-1},\end{align*} $$
to ensure they remain invariant under volume-preserving transformations. Letting
![]() $q_j \to \infty $
modifies the integrand to
$q_j \to \infty $
modifies the integrand to
 $\frac { \| f |_{F_j} \|^{\alpha _j}_{p_j}}{{\| f |_{F_j}\|^{\beta _j}_{\infty }}}$
and the condition on the powers and norms to
$\frac { \| f |_{F_j} \|^{\alpha _j}_{p_j}}{{\| f |_{F_j}\|^{\beta _j}_{\infty }}}$
and the condition on the powers and norms to
![]() $\frac {\alpha _j}{p_j} = i_{j+1}-i_{j-1} $
. Note that in this case the invariance holds for arbitrary powers
$\frac {\alpha _j}{p_j} = i_{j+1}-i_{j-1} $
. Note that in this case the invariance holds for arbitrary powers
![]() $\beta _j$
. As a particular case, this proves invariance under volume-preserving transformations of the integrand appearing in the next theorem. One can also take the quotient of products of functions, replacing
$\beta _j$
. As a particular case, this proves invariance under volume-preserving transformations of the integrand appearing in the next theorem. One can also take the quotient of products of functions, replacing
 $$ \begin{align*}\| f |_{F_j}\|^{i_{j+1}-i_{j-1}}_{1} \quad \text{ by } \quad \frac{ \prod_{i=1}^m \| f_i |_{F_j} \|^{\alpha_{i,j}}_{p_{i,j}} }{ \prod_{l=1}^{m^{\prime}} \| g_l |_{F_j} \|^{\beta_{l,j}}_{q_{l,j}} } \quad \text{ with } \quad \sum_{i=1}^m \frac{\alpha_{i,j}}{p_{i,j}} - \sum_{l=1}^{m^{\prime}} \frac{\beta_{l,j}}{q_{l,j}}=i_{j+1}-i_{j-1}.\end{align*} $$
$$ \begin{align*}\| f |_{F_j}\|^{i_{j+1}-i_{j-1}}_{1} \quad \text{ by } \quad \frac{ \prod_{i=1}^m \| f_i |_{F_j} \|^{\alpha_{i,j}}_{p_{i,j}} }{ \prod_{l=1}^{m^{\prime}} \| g_l |_{F_j} \|^{\beta_{l,j}}_{q_{l,j}} } \quad \text{ with } \quad \sum_{i=1}^m \frac{\alpha_{i,j}}{p_{i,j}} - \sum_{l=1}^{m^{\prime}} \frac{\beta_{l,j}}{q_{l,j}}=i_{j+1}-i_{j-1}.\end{align*} $$
Here again, we can let
![]() $q_{l,j} \rightarrow \infty $
, obtaining the corresponding generalization with no restrictions on
$q_{l,j} \rightarrow \infty $
, obtaining the corresponding generalization with no restrictions on
![]() $\beta _{l,j}$
.
$\beta _{l,j}$
.
Theorem 5.2 Let f be a non-negative bounded integrable function on
![]() $\mathbb R^n$
, then
$\mathbb R^n$
, then
 $$ \begin{align*}\int_{F_{\mathbf{r}}^n} \prod_{j=1}^r \frac{\|f|_{F_j}\|^{i_{j+1}-i_{j-1}}_1}{\|f|_{F_j}\|^{i_{j+1}-i_{j}}_{\infty}} d \xi_{\mathbf{r}} \leq \prod_{j=1}^r \frac{\omega_{i_j}^{i_{j+1}}}{\omega_{i_{j+1}}^{i_j}} \|f\|_1^{i_r}.\end{align*} $$
$$ \begin{align*}\int_{F_{\mathbf{r}}^n} \prod_{j=1}^r \frac{\|f|_{F_j}\|^{i_{j+1}-i_{j-1}}_1}{\|f|_{F_j}\|^{i_{j+1}-i_{j}}_{\infty}} d \xi_{\mathbf{r}} \leq \prod_{j=1}^r \frac{\omega_{i_j}^{i_{j+1}}}{\omega_{i_{j+1}}^{i_j}} \|f\|_1^{i_r}.\end{align*} $$
Proof The result follows by iteration of an inequality on
![]() $G_{n,k}$
for one function from our previous work [Reference Dann, Paouris and Pivovarov12, Theorem 1.2]:
$G_{n,k}$
for one function from our previous work [Reference Dann, Paouris and Pivovarov12, Theorem 1.2]:
 $$ \begin{align} \int_{G_{n,k}}\frac{\|f|_{E}\|^{n}_1}{\|f|_{E}\|^{n-k}_{\infty}} dE \leq \frac{\omega_k^{n}}{\omega_n^k}\|f\|^k_1. \end{align} $$
$$ \begin{align} \int_{G_{n,k}}\frac{\|f|_{E}\|^{n}_1}{\|f|_{E}\|^{n-k}_{\infty}} dE \leq \frac{\omega_k^{n}}{\omega_n^k}\|f\|^k_1. \end{align} $$
Applying the latter inequality repeatedly, we get
 $$ \begin{align*} \int_{F_{\mathbf{r}}^n} &\prod_{j=1}^r \frac{\|f|_{F_j}\|^{i_{j+1}-i_{j-1}}_1}{\|f|_{F_j}\|^{i_{j+1}-i_{j}}_{\infty}} d \xi_{\mathbf{r}} \\ &= \int_{G_{n,i_r}} \ldots \int_{G_{F_3,i_2}} \prod_{j=2}^r \frac{\|f|_{F_j}\|^{i_{j+1}-i_{j-1}}_1}{\|f|_{F_j}\|^{i_{j+1}-i_{j}}_{\infty}} \int_{G_{F_2,i_1}} \frac{\|f|_{F_1}\|^{i_{2}}_1}{\|f|_{F_1}\|^{i_{2}-i_{1}}_{\infty}} dF_1 dF_2 \ldots dF_r\\ &\leq \frac{\omega_{i_1}^{i_2}}{\omega^{i_1}_{i_2}} \int_{G_{n,i_r}} \ldots \int_{G_{F_3,i_2}} \prod_{j=2}^r \frac{\|f|_{F_j}\|^{i_{j+1}-i_{j-1}}_1}{\|f|_{F_j}\|^{i_{j+1}-i_{j}}_{\infty}} \|f|_{F_2}\|^{i_{1}}_1 dF_2 \ldots dF_r \\ &= \frac{\omega_{i_1}^{i_2}}{\omega^{i_1}_{i_2}} \int_{G_{n,i_r}} \ldots \int_{G_{F_4,i_3}} \prod_{j=3}^r \frac{\|f|_{F_j}\|^{i_{j+1}-i_{j-1}}_1}{\|f|_{F_j}\|^{i_{j+1}-i_{j}}_{\infty}} \int_{G_{F_3,i_2}} \frac{\|f|_{F_2}\|^{i_{3}}_1}{\|f|_{F_2}\|^{i_{3}-i_{2}}_{\infty}} dF_2 dF_3 \ldots dF_r \\ &\leq \frac{\omega_{i_1}^{i_2}}{\omega^{i_1}_{i_2}} \frac{\omega_{i_2}^{i_3}}{\omega^{i_2}_{i_3}} \int_{G_{n,i_r}} \ldots \int_{G_{F_4,i_3}} \prod_{j=3}^r \frac{\|f|_{F_j\|^{i_{j+1}-i_{j-1}}_1}}{\|f|_{F_j}\|^{i_{j+1}-i_{j}}_{\infty}} \|f|_{F_3}\|^{i_{2}}_1 dF_3 \ldots dF_r\\ &=\cdots \\ &\leq \prod_{j=1}^r \frac{\omega_{i_j}^{i_{j+1}}}{\omega_{i_{j+1}}^{i_j}} \|f\|_1^{i_r}.\\[-34pt] \end{align*} $$
$$ \begin{align*} \int_{F_{\mathbf{r}}^n} &\prod_{j=1}^r \frac{\|f|_{F_j}\|^{i_{j+1}-i_{j-1}}_1}{\|f|_{F_j}\|^{i_{j+1}-i_{j}}_{\infty}} d \xi_{\mathbf{r}} \\ &= \int_{G_{n,i_r}} \ldots \int_{G_{F_3,i_2}} \prod_{j=2}^r \frac{\|f|_{F_j}\|^{i_{j+1}-i_{j-1}}_1}{\|f|_{F_j}\|^{i_{j+1}-i_{j}}_{\infty}} \int_{G_{F_2,i_1}} \frac{\|f|_{F_1}\|^{i_{2}}_1}{\|f|_{F_1}\|^{i_{2}-i_{1}}_{\infty}} dF_1 dF_2 \ldots dF_r\\ &\leq \frac{\omega_{i_1}^{i_2}}{\omega^{i_1}_{i_2}} \int_{G_{n,i_r}} \ldots \int_{G_{F_3,i_2}} \prod_{j=2}^r \frac{\|f|_{F_j}\|^{i_{j+1}-i_{j-1}}_1}{\|f|_{F_j}\|^{i_{j+1}-i_{j}}_{\infty}} \|f|_{F_2}\|^{i_{1}}_1 dF_2 \ldots dF_r \\ &= \frac{\omega_{i_1}^{i_2}}{\omega^{i_1}_{i_2}} \int_{G_{n,i_r}} \ldots \int_{G_{F_4,i_3}} \prod_{j=3}^r \frac{\|f|_{F_j}\|^{i_{j+1}-i_{j-1}}_1}{\|f|_{F_j}\|^{i_{j+1}-i_{j}}_{\infty}} \int_{G_{F_3,i_2}} \frac{\|f|_{F_2}\|^{i_{3}}_1}{\|f|_{F_2}\|^{i_{3}-i_{2}}_{\infty}} dF_2 dF_3 \ldots dF_r \\ &\leq \frac{\omega_{i_1}^{i_2}}{\omega^{i_1}_{i_2}} \frac{\omega_{i_2}^{i_3}}{\omega^{i_2}_{i_3}} \int_{G_{n,i_r}} \ldots \int_{G_{F_4,i_3}} \prod_{j=3}^r \frac{\|f|_{F_j\|^{i_{j+1}-i_{j-1}}_1}}{\|f|_{F_j}\|^{i_{j+1}-i_{j}}_{\infty}} \|f|_{F_3}\|^{i_{2}}_1 dF_3 \ldots dF_r\\ &=\cdots \\ &\leq \prod_{j=1}^r \frac{\omega_{i_j}^{i_{j+1}}}{\omega_{i_{j+1}}^{i_j}} \|f\|_1^{i_r}.\\[-34pt] \end{align*} $$
In [Reference Dann, Paouris and Pivovarov12], more general versions of (63) are proved with several functions and different powers. These also carry over to extremal inequalities on flag manifolds by mimicking the previous proof. As a sample, we mention just one statement. Let
![]() $1 \leq q \leq i_1$
and let
$1 \leq q \leq i_1$
and let
![]() $f_1, \ldots , f_q$
be non-negative bounded integrable functions on
$f_1, \ldots , f_q$
be non-negative bounded integrable functions on
![]() ${\mathbb R}^n$
, then
${\mathbb R}^n$
, then
 $$ \begin{align*} \int_{F_{\mathbf{r }}^n} \prod_{k=1}^q \prod_{j=2}^r \frac{\|f_k|_{F_j}\|^{\frac{i_{j+1}-i_{j}}{i_j}}_1}{\|f_k|_{F_j}\|^{\frac{i_{j+1}-i_{j}}{i_j}}_{\infty}} \frac{\left\lVert f_k|_{F_1}\right\rVert_1^{\frac{i_2}{i_1}}}{\left\lVert f_k|_{F_1}\right\rVert^{\frac{i_2-i_1}{i_1}}_{\infty}} d \xi_{\mathbf{r}} \leq \prod_{j=1}^r \frac{\omega_{i_j}^{i_{j+1}} }{\omega_{i_{j+1}}^{i_j}} \prod_{k=1}^q \|f_k\|_1. \end{align*} $$
$$ \begin{align*} \int_{F_{\mathbf{r }}^n} \prod_{k=1}^q \prod_{j=2}^r \frac{\|f_k|_{F_j}\|^{\frac{i_{j+1}-i_{j}}{i_j}}_1}{\|f_k|_{F_j}\|^{\frac{i_{j+1}-i_{j}}{i_j}}_{\infty}} \frac{\left\lVert f_k|_{F_1}\right\rVert_1^{\frac{i_2}{i_1}}}{\left\lVert f_k|_{F_1}\right\rVert^{\frac{i_2-i_1}{i_1}}_{\infty}} d \xi_{\mathbf{r}} \leq \prod_{j=1}^r \frac{\omega_{i_j}^{i_{j+1}} }{\omega_{i_{j+1}}^{i_j}} \prod_{k=1}^q \|f_k\|_1. \end{align*} $$
5.2 Functional forms of the
 $\mathbf {r}$
-flag affine quermassintegrals
$\mathbf {r}$
-flag affine quermassintegrals
In this subsection, we extend the notion of
![]() $\mathbf {r}$
-flag affine quermassintegrals to functions. In particular, this will lead to functional versions of affine quermassintegrals. This is motivated by recent work of Bobkov, Colesanti, and Fragalá [Reference Bobkov, Colesanti and Fragalá4] and V. Milman and Rotem [Reference Milman and Rotem39]. The latter authors proposed and studied a notion of quermassintegrals for
$\mathbf {r}$
-flag affine quermassintegrals to functions. In particular, this will lead to functional versions of affine quermassintegrals. This is motivated by recent work of Bobkov, Colesanti, and Fragalá [Reference Bobkov, Colesanti and Fragalá4] and V. Milman and Rotem [Reference Milman and Rotem39]. The latter authors proposed and studied a notion of quermassintegrals for
![]() $\log $
-concave or even quasi-concave functions, which we now recall.
$\log $
-concave or even quasi-concave functions, which we now recall.
Definition 5.3 Suppose that
![]() $f:\mathbb {R}^n\rightarrow [0,\infty )$
is upper-semicontinuous and quasi-concave. For
$f:\mathbb {R}^n\rightarrow [0,\infty )$
is upper-semicontinuous and quasi-concave. For
![]() $ 1\leq k \leq n$
, let
$ 1\leq k \leq n$
, let
The above definition is consistent with the notion of projection of a function onto a subspace as introduced by Klartag and V. Milman in [Reference Klartag and Milman25]. Namely, let
![]() $f:\mathbb R^{n}\rightarrow [0,\infty ] $
be a non-negative function and
$f:\mathbb R^{n}\rightarrow [0,\infty ] $
be a non-negative function and
![]() $F\in G_{n,k}$
. Define the orthogonal projection of f onto F as the function
$F\in G_{n,k}$
. Define the orthogonal projection of f onto F as the function
![]() $P_{F} f: F\rightarrow [0,\infty ]$
given by
$P_{F} f: F\rightarrow [0,\infty ]$
given by
Note that if K is compact and
![]() $ f:= \mathbf {1}_{K}$
, then
$ f:= \mathbf {1}_{K}$
, then
![]() $P_{F}f := \mathbf {1}_{P_{F}(K)}$
. Moreover, from the definition, one has
$P_{F}f := \mathbf {1}_{P_{F}(K)}$
. Moreover, from the definition, one has
Assume from now on that
![]() $f:{\mathbb R}^{n} \rightarrow [0,\infty )$
and
$f:{\mathbb R}^{n} \rightarrow [0,\infty )$
and
For
![]() $1\leq k \leq n-1$
, we define the affine quermassintegral of f by
$1\leq k \leq n-1$
, we define the affine quermassintegral of f by
 $$ \begin{align} \Phi_{[k]} (f) := \int_{0}^{\infty} \Phi_{[k]} ( \{ f\geq t\}) dt = \int_{0}^{\infty} \left(\int_{G_{n,k}} | \{ P_{F} f\geq t\} |^{-n} d F \right)^{-\frac{1}{ nk}} dt. \end{align} $$
$$ \begin{align} \Phi_{[k]} (f) := \int_{0}^{\infty} \Phi_{[k]} ( \{ f\geq t\}) dt = \int_{0}^{\infty} \left(\int_{G_{n,k}} | \{ P_{F} f\geq t\} |^{-n} d F \right)^{-\frac{1}{ nk}} dt. \end{align} $$
Note that for
![]() $f=\mathbf {1}_K$
, we have
$f=\mathbf {1}_K$
, we have
![]() $\Phi _{[k]}(\mathbf {1}_K) = \int _{0}^1 \Phi _{[k]}(K)dt= \Phi _{[k]}(K)$
; hence, the notions coincide for sets. For
$\Phi _{[k]}(\mathbf {1}_K) = \int _{0}^1 \Phi _{[k]}(K)dt= \Phi _{[k]}(K)$
; hence, the notions coincide for sets. For
![]() $1\leq r\leq n-1$
and
$1\leq r\leq n-1$
and
![]() $ 1\leq i_{1} < i_{2} < \cdots < i_{r} \leq n-1$
,
$ 1\leq i_{1} < i_{2} < \cdots < i_{r} \leq n-1$
,
![]() $\mathbf {r}:= (i_{1}, \cdots , i_{r})$
, we define the
$\mathbf {r}:= (i_{1}, \cdots , i_{r})$
, we define the
![]() $\mathbf {r}$
-flag affine quermassintegrals of f by
$\mathbf {r}$
-flag affine quermassintegrals of f by
For comparison, we recall that for every
![]() $f:{\mathbb R}^{n} \rightarrow [0,\infty ] $
,
$f:{\mathbb R}^{n} \rightarrow [0,\infty ] $
,
For
![]() $\lambda \in {\mathbb R}\setminus \{0\}$
and f as above, we write
$\lambda \in {\mathbb R}\setminus \{0\}$
and f as above, we write
and if
![]() $T\in GL_{n}$
,
$T\in GL_{n}$
,
Note that if
![]() $f:= \mathbf {1}_{K}$
, then
$f:= \mathbf {1}_{K}$
, then
For
![]() $ f:{\mathbb R}^{n} \rightarrow [0, \infty ]$
,
$ f:{\mathbb R}^{n} \rightarrow [0, \infty ]$
,
![]() $\lambda>0$
, and
$\lambda>0$
, and
![]() $ T\in GL_{n}$
, we have
$ T\in GL_{n}$
, we have
Thus, by the
![]() $1$
-homogeneity of the
$1$
-homogeneity of the
![]() $\mathbf {r}$
-flag affine quermassintegrals for sets, and the affine invariance of these quantities, we obtain the following theorem.
$\mathbf {r}$
-flag affine quermassintegrals for sets, and the affine invariance of these quantities, we obtain the following theorem.
Theorem 5.4 Let
![]() $f:{\mathbb R}^{n}\rightarrow [0,\infty ]$
satisfy (64). Let
$f:{\mathbb R}^{n}\rightarrow [0,\infty ]$
satisfy (64). Let
![]() $\lambda>0$
and T be an affine volume-preserving map. Then
$\lambda>0$
and T be an affine volume-preserving map. Then
We recall the symmetric decreasing rearrangement of an integrable function f. For a set
![]() $A\subseteq {\mathbb R}^{n}$
with finite volume, the decreasing rearrangement
$A\subseteq {\mathbb R}^{n}$
with finite volume, the decreasing rearrangement
![]() $A^{\ast }$
is defined as
$A^{\ast }$
is defined as
![]() $ A^{\ast } := r_{A} B_{2}^{n},$
where
$ A^{\ast } := r_{A} B_{2}^{n},$
where
![]() $r_A$
is the volume-radius of A. The symmetric decreasing rearrangement
$r_A$
is the volume-radius of A. The symmetric decreasing rearrangement
![]() $f^{\ast }$
of f is defined as the radial function
$f^{\ast }$
of f is defined as the radial function
![]() $f^{\ast }$
such that, for
$f^{\ast }$
such that, for
![]() $t>0$
,
$t>0$
,
In particular,
![]() $r_{\{ f\geq t\} } B_{2}^{n} = \{ f^{\ast } \geq t \}$
. Using (66) and (35), we have, for non-negative quasi-concave functions f on
$r_{\{ f\geq t\} } B_{2}^{n} = \{ f^{\ast } \geq t \}$
. Using (66) and (35), we have, for non-negative quasi-concave functions f on
![]() ${\mathbb R}^{n}$
,
${\mathbb R}^{n}$
,
Lastly, let f be a non-negative quasi-concave function on
![]() $\mathbb R^{n}$
satisfying (64). We define
$\mathbb R^{n}$
satisfying (64). We define
The results of Section 3 lead to the following double-sided inequality for
![]() $\Phi _{\mathbf {r}}(f)$
:
$\Phi _{\mathbf {r}}(f)$
:
Theorem 5.5 Let f be a non-negative quasi-concave function on
![]() ${\mathbb R}^{n}$
satisfying (64). Then
${\mathbb R}^{n}$
satisfying (64). Then
 $$ \begin{align*} \Phi_{\mathbf{r}} (f^{\ast} ) \leq \Phi_{\mathbf{r}} ( f) \leq c^{\prime} \min\left\{ \sqrt{ \frac{n}{i_r} }, \log( 1+d_{BM}(f)) \right\} \Phi_{\mathbf{r}} (f^{\ast} ). \end{align*} $$
$$ \begin{align*} \Phi_{\mathbf{r}} (f^{\ast} ) \leq \Phi_{\mathbf{r}} ( f) \leq c^{\prime} \min\left\{ \sqrt{ \frac{n}{i_r} }, \log( 1+d_{BM}(f)) \right\} \Phi_{\mathbf{r}} (f^{\ast} ). \end{align*} $$
Acknowledgments
We thank the anonymous referee for careful reading and helpful comments.