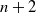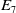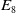1. Introduction
That there is a connection between the Apollonian packing and rational curves on algebraic surfaces has only recently been explored (see [Reference Baragar2, Reference Dolgachev10]). The connection so far has seemed a bit distant. In this paper, we show a rather spectacular connection. Let X be an Enriques surface that contains a smooth rational curve (a nodal curve), but is otherwise generic. Let
![]() $\Lambda$
be its Picard group, modulo torsion. Then
$\Lambda$
be its Picard group, modulo torsion. Then
![]() $\Lambda$
is isomorphic to the Enriques lattice
$\Lambda$
is isomorphic to the Enriques lattice
![]() $E_{10}$
, which is an even unimodular lattice of signature (1, 9). Since
$E_{10}$
, which is an even unimodular lattice of signature (1, 9). Since
![]() $\Lambda\otimes {\mathbb{R}}$
is a Lorentz space
$\Lambda\otimes {\mathbb{R}}$
is a Lorentz space
![]() ${\mathbb{R}}^{1,9}$
, it has a 9-dimensional copy of hyperbolic space
${\mathbb{R}}^{1,9}$
, it has a 9-dimensional copy of hyperbolic space
![]() ${\mathbb{H}}^9$
naturally imbedded in it. Any nodal curve on X has self intersection
${\mathbb{H}}^9$
naturally imbedded in it. Any nodal curve on X has self intersection
![]() $-2$
, so represents a plane in
$-2$
, so represents a plane in
![]() ${\mathbb{H}}^9$
, which in the Poincaré upper-half hyperspace model is represented by an 8-dimensional hemi-sphere. The boundary
${\mathbb{H}}^9$
, which in the Poincaré upper-half hyperspace model is represented by an 8-dimensional hemi-sphere. The boundary
![]() $\partial {\mathbb{H}}^9$
of
$\partial {\mathbb{H}}^9$
of
![]() ${\mathbb{H}}^9$
, not including the point at infinity, is isomorphic to
${\mathbb{H}}^9$
, not including the point at infinity, is isomorphic to
![]() ${\mathbb{R}}^8$
, and its intersection with a hyperbolic plane in
${\mathbb{R}}^8$
, and its intersection with a hyperbolic plane in
![]() ${\mathbb{H}}^9$
is a 7-dimensional hypersphere. In this way, the set of nodal curves on X gives us a configuration of hyperspheres in
${\mathbb{H}}^9$
is a 7-dimensional hypersphere. In this way, the set of nodal curves on X gives us a configuration of hyperspheres in
![]() ${\mathbb{R}}^8$
. In this paper, we show that this configuration is an Apollonian packing, by which we mean the hyperspheres intersect tangentially or not at all, they fill
${\mathbb{R}}^8$
. In this paper, we show that this configuration is an Apollonian packing, by which we mean the hyperspheres intersect tangentially or not at all, they fill
![]() ${\mathbb{R}}^8$
, the packing is crystallographic, and it satisfies the fundamental property that makes it Apollonian, which is that every sphere in the configuration is a member of a cluster of ten hyperspheres that are mutually tangent. (See Section 2.4 for precise definitions.)
${\mathbb{R}}^8$
, the packing is crystallographic, and it satisfies the fundamental property that makes it Apollonian, which is that every sphere in the configuration is a member of a cluster of ten hyperspheres that are mutually tangent. (See Section 2.4 for precise definitions.)
Though the connection to Enriques surfaces is fascinating, this paper is really a study of sphere packings. The underlying algebraic geometry is explained in [Reference Allcock1, 11]. Our starting point is the following Coxeter graph (also known as a Dynkin diagram):

Some may recognize that it generates the Reye Lattice. The graph also appears in Maxwell’s paper [Reference Maxwell16, Table II,
![]() $N=10$
], in which it is described as generating a sphere packing, meaning the spheres intersect tangentially or not at all. It is one of many examples of what are sometimes called Boyd-Maxwell packings (see also [Reference Chen and Labbé7]). Up until recently (see [Reference Baragar4, Reference Baragar5]), it was believed that no Boyd-Maxwell packing in dimension
$N=10$
], in which it is described as generating a sphere packing, meaning the spheres intersect tangentially or not at all. It is one of many examples of what are sometimes called Boyd-Maxwell packings (see also [Reference Chen and Labbé7]). Up until recently (see [Reference Baragar4, Reference Baragar5]), it was believed that no Boyd-Maxwell packing in dimension
![]() $n\geq 4$
is Apollonian (see the Mathematical Review for [Reference Boyd6], [Reference Lagarias, Mallows and Wilks15, p. 356], and [Reference Dolgachev10, p. 33]). In [Reference Baragar5], we describe a different Apollonian packing (though not a Boyd-Maxwell packing) in eight dimensions. The packing in this paper is more efficient, in the sense that its residual set is a subset of the residual set of the packing in [Reference Baragar5]. This also shows that there can be different Apollonian packings in the same dimension.
$n\geq 4$
is Apollonian (see the Mathematical Review for [Reference Boyd6], [Reference Lagarias, Mallows and Wilks15, p. 356], and [Reference Dolgachev10, p. 33]). In [Reference Baragar5], we describe a different Apollonian packing (though not a Boyd-Maxwell packing) in eight dimensions. The packing in this paper is more efficient, in the sense that its residual set is a subset of the residual set of the packing in [Reference Baragar5]. This also shows that there can be different Apollonian packings in the same dimension.
In Section 2.4, we give a precise definition of higher dimensional Apollonian packings. This is the author’s attempt to define what was likely meant or understood by Boyd, Maxwell, and their contemporaries. Note that it is different from the definition given in [Reference Baragar4] (see Remark 2), and that our definition may still evolve as we better understand the subject.
A cross section of a sphere packing gives a sphere packing in a lower dimension. By taking a co-dimension one cross section perpendicular to nine of the ten mutually tangent spheres of our new packing in eight dimensions, we get a weakly Apollonian packing in seven dimensions, meaning there is a cluster of nine mutually tangent spheres, but not all spheres are a member of such a cluster. It too is described by Maxwell [Reference Maxwell16, Table II,
![]() $N=9$
, last line, first graph]. The resulting packing is different from and more efficient than the example in [Reference Baragar5], which is Apollonian.
$N=9$
, last line, first graph]. The resulting packing is different from and more efficient than the example in [Reference Baragar5], which is Apollonian.
For Euclidean lattices, eight dimensions are special as it admits the even unimodular lattice
![]() $E_8$
. The uniradial sphere packing (i.e., all spheres have the same radius) with spheres of radius
$E_8$
. The uniradial sphere packing (i.e., all spheres have the same radius) with spheres of radius
![]() $1/\sqrt{2}$
and centered at vertices of the lattice gives the densest uniradial sphere packing in eight dimensions [Reference Viazovska23]. With an appropriate choice of point at infinity, the Apollonian packing of this paper includes this uniradial sphere packing.
$1/\sqrt{2}$
and centered at vertices of the lattice gives the densest uniradial sphere packing in eight dimensions [Reference Viazovska23]. With an appropriate choice of point at infinity, the Apollonian packing of this paper includes this uniradial sphere packing.
In [Reference Baragar4], we generated Apollonian packings in dimension n from uniradial sphere packings in dimension
![]() $n-1$
. Using a similar procedure and the
$n-1$
. Using a similar procedure and the
![]() $E_8$
lattice, we generate an Apollonian packing in nine dimensions. This too appears in Maxwell’s paper [Reference Maxwell16, Table II,
$E_8$
lattice, we generate an Apollonian packing in nine dimensions. This too appears in Maxwell’s paper [Reference Maxwell16, Table II,
![]() $N=11$
, second graph].
$N=11$
, second graph].
This paper was directly inspired by a paper by Daniel Allcock [Reference Allcock1], who reproved a result (see Theorem 2.1 below) that appears in [Reference Cossec and Dolgachev9]. Dolgachev attributes the original proof to Looijenga, based on an incomplete proof by Coble [Reference Coble8] from 1919.
The descriptions of the Apollonian packings of this paper do not require any background in algebraic geometry. We will therefore keep the algebraic geometry to a minimum, restricting it as much as possible to Subsection 2.5 and to remarks.
With respect to the organization of this paper, Section 2 on background includes a definition of higher dimensional analogs of the Apollonian circle packings, and the main result concerning Enriques surfaces from which the packing is derived; Section 3 is devoted to producing the Apollonian packing in eight dimensions; in Section 5, we look at a cross section; and in Section 6, we build an example in nine-dimensions. In Section 4, we describe a sufficient condition for a packing to have the (weak) Apollonian property and use it to find examples in Maxwell’s list of packings, including a sphere packing in three dimensions that has the Apollonian property but is not the Soddy sphere packing.
2. Background
2.1. The pseudosphere in Lorentz space
Hyperspheres in
![]() ${\mathbb{R}}^n$
can be represented by
${\mathbb{R}}^n$
can be represented by
![]() $(n+2)$
-dimensional vectors. Boyd calls such coordinates polyspherical coordinates and attributes them to Clifford and Darboux from the late 19th century [Reference Boyd6]. The more modern interpretation is that they represent planes in
$(n+2)$
-dimensional vectors. Boyd calls such coordinates polyspherical coordinates and attributes them to Clifford and Darboux from the late 19th century [Reference Boyd6]. The more modern interpretation is that they represent planes in
![]() ${\mathbb{H}}^{n+1}$
imbedded in an
${\mathbb{H}}^{n+1}$
imbedded in an
![]() $(n+2)$
-dimensional Lorentz space, which in turn represent hyperspheres on the boundary
$(n+2)$
-dimensional Lorentz space, which in turn represent hyperspheres on the boundary
![]() $\partial {\mathbb{H}}^{n+1}$
. We refer the reader to [Reference Ratcliffe20] for more details.
$\partial {\mathbb{H}}^{n+1}$
. We refer the reader to [Reference Ratcliffe20] for more details.
Let us set
![]() $N=n+2$
.
$N=n+2$
.
Given a symmetric matrix J with signature
![]() $(1,N-1)$
, we define the Lorentz space,
$(1,N-1)$
, we define the Lorentz space,
![]() ${\mathbb{R}}^{1,N-1} $
to be the set of N-tuples over
${\mathbb{R}}^{1,N-1} $
to be the set of N-tuples over
![]() ${\mathbb{R}}$
equipped with the negative Lorentz product
${\mathbb{R}}$
equipped with the negative Lorentz product
The surface
![]() $\mathbf x\cdot \mathbf x=1$
is a hyperboloid of two sheets. Let us distinguish a vector D with
$\mathbf x\cdot \mathbf x=1$
is a hyperboloid of two sheets. Let us distinguish a vector D with
![]() $D\cdot D>0$
and select the sheet
$D\cdot D>0$
and select the sheet
![]() ${\mathcal H}$
by
${\mathcal H}$
by
We define a distance on
![]() ${\mathcal H}$
by
${\mathcal H}$
by
Then
![]() ${\mathcal H}$
equipped with this metric is a model of
${\mathcal H}$
equipped with this metric is a model of
![]() ${\mathbb{H}}^{N-1}$
, sometimes known as the vector model. Equivalently, one can define
${\mathbb{H}}^{N-1}$
, sometimes known as the vector model. Equivalently, one can define
and
![]() ${\mathcal H}=V^+/{\mathbb{R}}^+$
, together with the metric defined by
${\mathcal H}=V^+/{\mathbb{R}}^+$
, together with the metric defined by
where
![]() $|\mathbf x|=\sqrt{\mathbf x\cdot \mathbf x}$
for
$|\mathbf x|=\sqrt{\mathbf x\cdot \mathbf x}$
for
![]() $\mathbf x\in V$
. For
$\mathbf x\in V$
. For
![]() $\mathbf x\cdot \mathbf x<0$
, we define
$\mathbf x\cdot \mathbf x<0$
, we define
![]() $|\mathbf x|=i\sqrt{-\mathbf x\cdot \mathbf x}$
.
$|\mathbf x|=i\sqrt{-\mathbf x\cdot \mathbf x}$
.
Hyperplanes in
![]() ${\mathcal H}$
are the intersection of
${\mathcal H}$
are the intersection of
![]() ${\mathcal H}$
with hyperplanes
${\mathcal H}$
with hyperplanes
![]() $\mathbf n\cdot \mathbf x=0$
in
$\mathbf n\cdot \mathbf x=0$
in
![]() ${\mathbb{R}}^{1,N-1}$
. Such a plane intersects
${\mathbb{R}}^{1,N-1}$
. Such a plane intersects
![]() ${\mathcal H}$
if and only if
${\mathcal H}$
if and only if
![]() $\mathbf n\cdot \mathbf n<0$
. Let
$\mathbf n\cdot \mathbf n<0$
. Let
![]() $H_{\mathbf n}$
represent both the plane
$H_{\mathbf n}$
represent both the plane
![]() $\mathbf n\cdot \mathbf x=0$
in
$\mathbf n\cdot \mathbf x=0$
in
![]() ${\mathbb{R}}^{1,N-1}$
and its intersection with
${\mathbb{R}}^{1,N-1}$
and its intersection with
![]() ${\mathcal H}$
. The direction of
${\mathcal H}$
. The direction of
![]() $\mathbf n$
distinguishes a half space
$\mathbf n$
distinguishes a half space
in either
![]() ${\mathbb{R}}^{1,N-1}$
or
${\mathbb{R}}^{1,N-1}$
or
![]() ${\mathcal H}$
.
${\mathcal H}$
.
The angle
![]() $\theta$
between two intersecting planes
$\theta$
between two intersecting planes
![]() $H_{\mathbf n}$
and
$H_{\mathbf n}$
and
![]() $H_{\mathbf m}$
in
$H_{\mathbf m}$
in
![]() ${\mathcal H}$
is given by
${\mathcal H}$
is given by
where
![]() $\theta$
is the angle in
$\theta$
is the angle in
![]() $H_{\mathbf n}^+\cap H_{\mathbf m}^+$
. If
$H_{\mathbf n}^+\cap H_{\mathbf m}^+$
. If
![]() $|\mathbf n\cdot \mathbf m|=|\,|\mathbf n||\mathbf m|\,|$
, then the planes are parallel (i.e. tangent at infinity). If
$|\mathbf n\cdot \mathbf m|=|\,|\mathbf n||\mathbf m|\,|$
, then the planes are parallel (i.e. tangent at infinity). If
![]() $|\mathbf n\cdot \mathbf m|>|\,|\mathbf n||\mathbf m|\,|$
, then the planes are ultraparallel, and the quantity
$|\mathbf n\cdot \mathbf m|>|\,|\mathbf n||\mathbf m|\,|$
, then the planes are ultraparallel, and the quantity
![]() $\psi$
in
$\psi$
in
![]() $|\mathbf n||\mathbf m|\cosh \psi=|\mathbf n\cdot \mathbf m |$
is the shortest hyperbolic distance between the two planes.
$|\mathbf n||\mathbf m|\cosh \psi=|\mathbf n\cdot \mathbf m |$
is the shortest hyperbolic distance between the two planes.
The group of isometries of
![]() ${\mathcal H}$
is given by
${\mathcal H}$
is given by
Reflection in the plane
![]() $H_{\mathbf n}$
is given by
$H_{\mathbf n}$
is given by
The group of isometries is generated by the reflections.
Let
![]() $\partial {\mathcal H}$
represent the boundary of
$\partial {\mathcal H}$
represent the boundary of
![]() ${\mathcal H}$
, which is an
${\mathcal H}$
, which is an
![]() $(N-2)$
-sphere. It is represented by
$(N-2)$
-sphere. It is represented by
![]() ${\mathcal L}^+/\Bbb R^+$
where
${\mathcal L}^+/\Bbb R^+$
where
Given an
![]() $E\in{\mathcal L}^+$
, let
$E\in{\mathcal L}^+$
, let
![]() $\partial {\mathcal H}_E=\partial {\mathcal H} \setminus E{\mathbb{R}}^+$
. Then
$\partial {\mathcal H}_E=\partial {\mathcal H} \setminus E{\mathbb{R}}^+$
. Then
![]() $\partial {\mathcal H}_E$
equipped with the metric
$\partial {\mathcal H}_E$
equipped with the metric
![]() $|\cdot |_E$
defined by
$|\cdot |_E$
defined by
is the
![]() $(N-2)$
-dimensional Euclidean space that is the boundary of the Poincaré upper half hyperspace model of
$(N-2)$
-dimensional Euclidean space that is the boundary of the Poincaré upper half hyperspace model of
![]() ${\mathcal H}$
with E the point at infinity. In
${\mathcal H}$
with E the point at infinity. In
![]() $\partial {\mathcal H}_E$
, the plane
$\partial {\mathcal H}_E$
, the plane
![]() $H_{\mathbf n}$
is represented by an
$H_{\mathbf n}$
is represented by an
![]() $(N-3)$
-sphere, which we denote with
$(N-3)$
-sphere, which we denote with
![]() $H_{\mathbf n,E}$
(or just
$H_{\mathbf n,E}$
(or just
![]() $H_{\mathbf n}$
if E is understood, or sometimes just
$H_{\mathbf n}$
if E is understood, or sometimes just
![]() $\mathbf n$
).
$\mathbf n$
).
The curvature (the inverse of the radius, together with a sign) of
![]() $H_{\mathbf n, E}$
is given by the formula
$H_{\mathbf n, E}$
is given by the formula
using the metric
![]() $|\cdot |_E$
[Reference Baragar4]. Here,
$|\cdot |_E$
[Reference Baragar4]. Here,
![]() $||\mathbf n||=-i|\mathbf n|=\sqrt{-\mathbf n\cdot \mathbf n}$
. By choosing a suitable orientation for
$||\mathbf n||=-i|\mathbf n|=\sqrt{-\mathbf n\cdot \mathbf n}$
. By choosing a suitable orientation for
![]() $\mathbf n$
, we get the appropriate sign for the curvature.
$\mathbf n$
, we get the appropriate sign for the curvature.
2.2. Coxeter graphs
Coxeter graphs can represent lattices in
![]() ${\mathbb{R}}^n$
or
${\mathbb{R}}^n$
or
![]() ${\mathbb{R}}^{1,n-1}$
, or groups of isometries of
${\mathbb{R}}^{1,n-1}$
, or groups of isometries of
![]() ${\mathbb{S}}^{n-1}$
or
${\mathbb{S}}^{n-1}$
or
![]() ${\mathbb{H}}^{n-1}$
. Each node in a Coxeter graph represents a plane, which can be represented by its normal vector. Two nodes are not connected if their corresponding planes are perpendicular. A regular edge between two nodes indicates that those planes intersect at an angle of
${\mathbb{H}}^{n-1}$
. Each node in a Coxeter graph represents a plane, which can be represented by its normal vector. Two nodes are not connected if their corresponding planes are perpendicular. A regular edge between two nodes indicates that those planes intersect at an angle of
![]() $\pi/3$
, so their normal vectors are at an angle of
$\pi/3$
, so their normal vectors are at an angle of
![]() $2\pi/3$
(some ambiguity here). If the angle between two planes is
$2\pi/3$
(some ambiguity here). If the angle between two planes is
![]() $\pi/4$
, then we indicate that with an edge subscripted (or superscripted) with a 4, or sometimes a double edge. In general, an edge with a superscript of m (or of multiplicity
$\pi/4$
, then we indicate that with an edge subscripted (or superscripted) with a 4, or sometimes a double edge. In general, an edge with a superscript of m (or of multiplicity
![]() $m-2$
) means the order of the composition of reflections in the two planes represented by the two nodes is m. A thick line, like the one in (1.1), means the two planes are parallel, and this is sometimes indicated with a superscript of
$m-2$
) means the order of the composition of reflections in the two planes represented by the two nodes is m. A thick line, like the one in (1.1), means the two planes are parallel, and this is sometimes indicated with a superscript of
![]() $\infty$
. A dotted edge means the two planes are ultraparallel.
$\infty$
. A dotted edge means the two planes are ultraparallel.
The Coxeter graph represents the lattice
![]() $\mathbf v_1{\mathbb{Z}}\oplus \cdots \oplus \mathbf v_n{\mathbb{Z}}$
, where the
$\mathbf v_1{\mathbb{Z}}\oplus \cdots \oplus \mathbf v_n{\mathbb{Z}}$
, where the
![]() $\mathbf v_i$
are the nodes of the graph. Note that not all graphs give lattices, as the vectors may be linearly dependent. When the nodes are linearly independent (and sometimes when they are not), we get the bilinear form defined by the incidence matrix
$\mathbf v_i$
are the nodes of the graph. Note that not all graphs give lattices, as the vectors may be linearly dependent. When the nodes are linearly independent (and sometimes when they are not), we get the bilinear form defined by the incidence matrix
![]() $[\mathbf v_i\cdot \mathbf v_j]$
. We can normalize the vectors
$[\mathbf v_i\cdot \mathbf v_j]$
. We can normalize the vectors
![]() $\mathbf v_i$
(say) so that
$\mathbf v_i$
(say) so that
![]() $\mathbf v_i\cdot \mathbf v_i=-1$
. Then the angles noted by the edges define
$\mathbf v_i\cdot \mathbf v_i=-1$
. Then the angles noted by the edges define
![]() $\mathbf v_i\cdot \mathbf v_j$
, where we take the angle between the normal vectors of the planes to be obtuse (so
$\mathbf v_i\cdot \mathbf v_j$
, where we take the angle between the normal vectors of the planes to be obtuse (so
![]() $\mathbf v_i\cdot\mathbf v_j\geq 0$
).
$\mathbf v_i\cdot\mathbf v_j\geq 0$
).
The Coxeter graph can also represent a group, the Weyl group
![]() $\langle R_{\mathbf v_1},...,R_{\mathbf v_n}\rangle$
. When representing a group, it is often necessary for the vectors to be linearly dependent.
$\langle R_{\mathbf v_1},...,R_{\mathbf v_n}\rangle$
. When representing a group, it is often necessary for the vectors to be linearly dependent.
We will explain the notion of weights in the next subsection, which will give us an example to investigate.
2.3. The Apollonian circle packing
The Apollonian circle packing is a well- known object, and we assume the reader is already familiar with it. The goal of this section is to think of it in a way that more naturally generalizes to higher dimensions.
Let us consider the strip version of the Apollonian circle packing shown in Figure 1, and think of the picture as lying on the boundary
![]() $\partial {\mathbb{H}}^3$
of hyperbolic space. Then each circle (and the two lines) represents a plane in
$\partial {\mathbb{H}}^3$
of hyperbolic space. Then each circle (and the two lines) represents a plane in
![]() ${\mathbb{H}}^3$
, which in turn are represented by their normal vectors. Let us represent four of the hyperbolic planes with the vectors
${\mathbb{H}}^3$
, which in turn are represented by their normal vectors. Let us represent four of the hyperbolic planes with the vectors
![]() $\mathbf e_i$
for
$\mathbf e_i$
for
![]() $i=1,...,4$
, as shown in Figure 1. We orient
$i=1,...,4$
, as shown in Figure 1. We orient
![]() $\mathbf e_i$
so that
$\mathbf e_i$
so that
![]() $H_{\mathbf e_i}^+$
contains
$H_{\mathbf e_i}^+$
contains
![]() $H_{\mathbf e_j}$
for
$H_{\mathbf e_j}$
for
![]() $i\neq j$
, and assign them norms of
$i\neq j$
, and assign them norms of
![]() $-2$
, meaning
$-2$
, meaning
![]() $\mathbf e_i\cdot \mathbf e_i=-2$
. Then, by the tangency conditions,
$\mathbf e_i\cdot \mathbf e_i=-2$
. Then, by the tangency conditions,
![]() $\mathbf e_i\cdot \mathbf e_j=2$
for
$\mathbf e_i\cdot \mathbf e_j=2$
for
![]() $i\neq j$
(see equation (2.1)). We define
$i\neq j$
(see equation (2.1)). We define
![]() $J_4=[\mathbf e_i\cdot \mathbf e_j]$
, which has signature (1, 3). (It is easy to see that 4 and
$J_4=[\mathbf e_i\cdot \mathbf e_j]$
, which has signature (1, 3). (It is easy to see that 4 and
![]() $-4$
are eigenvalues, the latter with a 3-dimensional eigenspace.) Thus,
$-4$
are eigenvalues, the latter with a 3-dimensional eigenspace.) Thus,
![]() $J_4$
defines a Lorentz product in
$J_4$
defines a Lorentz product in
![]() ${\mathbb{R}}^{1,3}$
.
${\mathbb{R}}^{1,3}$
.

Figure 1. The strip version of the Apollonian packing. The dotted curves
![]() $\alpha_i$
represent symmetries of the packing. The fundamental domain
$\alpha_i$
represent symmetries of the packing. The fundamental domain
![]() ${\mathcal F}_4$
for the group
${\mathcal F}_4$
for the group
![]() ${\mathcal O}^+_{\Lambda_4}$
is the region above the shaded square and above the plane
${\mathcal O}^+_{\Lambda_4}$
is the region above the shaded square and above the plane
![]() $H_{\alpha_3}$
(represented by the dotted circle).
$H_{\alpha_3}$
(represented by the dotted circle).
Note that
![]() $\mathbf e_i\cdot(\mathbf e_i+\mathbf e_j)=0$
, so
$\mathbf e_i\cdot(\mathbf e_i+\mathbf e_j)=0$
, so
![]() $\mathbf e_i+\mathbf e_j$
is the point of tangency between the circles represented by
$\mathbf e_i+\mathbf e_j$
is the point of tangency between the circles represented by
![]() $\mathbf e_i$
and
$\mathbf e_i$
and
![]() $\mathbf e_j$
. Thus, our point at infinity is
$\mathbf e_j$
. Thus, our point at infinity is
![]() $E=\mathbf e_1+\mathbf e_2$
, and the circle represented by
$E=\mathbf e_1+\mathbf e_2$
, and the circle represented by
![]() $\mathbf e_i$
is
$\mathbf e_i$
is
![]() $H_{\mathbf e_i,E}$
.
$H_{\mathbf e_i,E}$
.
There are obvious symmetries of the Apollonian packing, as shown in Figure 1. In the plane, the symmetries are reflection in the lines
![]() $\alpha_1$
,
$\alpha_1$
,
![]() $\alpha_2$
, and
$\alpha_2$
, and
![]() $\alpha_4$
and inversion in the circle
$\alpha_4$
and inversion in the circle
![]() $\alpha_3$
. The Apollonian packing is the orbit of
$\alpha_3$
. The Apollonian packing is the orbit of
![]() $\mathbf e_1$
under the action of the group generated by these symmetries.
$\mathbf e_1$
under the action of the group generated by these symmetries.
Thought of as actions in
![]() ${\mathbb{H}}^3$
, the symmetries are reflection in the planes
${\mathbb{H}}^3$
, the symmetries are reflection in the planes
![]() $H_{\alpha_i}$
, so the packing is the
$H_{\alpha_i}$
, so the packing is the
![]() ${\Gamma}_4$
-orbit of
${\Gamma}_4$
-orbit of
![]() $H_{\mathbf e_1}$
, where
$H_{\mathbf e_1}$
, where
It is fairly easy to solve for
![]() $\alpha_i$
in the basis
$\alpha_i$
in the basis
![]() $\mathbf e=\{\mathbf e_1,...,\mathbf e_4\}$
. For example, we note that
$\mathbf e=\{\mathbf e_1,...,\mathbf e_4\}$
. For example, we note that
![]() $\alpha_1\cdot \mathbf e_i=0$
for
$\alpha_1\cdot \mathbf e_i=0$
for
![]() $i\neq 4$
, since it is perpendicular to those planes. Solving, we get
$i\neq 4$
, since it is perpendicular to those planes. Solving, we get
![]() $\alpha_1=(1,1,1,-1)$
, up to scalars. The others are
$\alpha_1=(1,1,1,-1)$
, up to scalars. The others are
![]() $\alpha_2=(0,0,-1,1)$
,
$\alpha_2=(0,0,-1,1)$
,
![]() $\alpha_3=(0,-1,1,0)$
, and
$\alpha_3=(0,-1,1,0)$
, and
![]() $\alpha_4=(\!-1,1,0,0)$
.
$\alpha_4=(\!-1,1,0,0)$
.
We let
![]() $\Lambda_4=\mathbf e_1{\mathbb{Z}}\oplus ...\oplus \mathbf e_4{\mathbb{Z}}$
, which we call the Apollonian lattice. Let
$\Lambda_4=\mathbf e_1{\mathbb{Z}}\oplus ...\oplus \mathbf e_4{\mathbb{Z}}$
, which we call the Apollonian lattice. Let
It is straight forward to verify that
![]() $R_{\mathbf e_i}$
and
$R_{\mathbf e_i}$
and
![]() $R_{\mathbf \alpha_i}\in {\mathcal O}^+_{\Lambda_4}$
. Let
$R_{\mathbf \alpha_i}\in {\mathcal O}^+_{\Lambda_4}$
. Let
![]() $G_4=\langle {\Gamma}_4, R_{\mathbf e_1}\rangle$
. A fundamental domain
$G_4=\langle {\Gamma}_4, R_{\mathbf e_1}\rangle$
. A fundamental domain
![]() ${\mathcal F}_4$
for this group is the region bounded by the four planes
${\mathcal F}_4$
for this group is the region bounded by the four planes
![]() $H_{\alpha_i}$
, the pane
$H_{\alpha_i}$
, the pane
![]() $H_{\mathbf e_1}$
, and with cusp E at the point at infinity:
$H_{\mathbf e_1}$
, and with cusp E at the point at infinity:
Since
![]() ${\mathcal F}_4$
has finite volume, we know
${\mathcal F}_4$
has finite volume, we know
![]() $G_4$
has finite index in
$G_4$
has finite index in
![]() ${\mathcal O}^+_{\Lambda_4}$
, and it is not hard to verify that the two are equal.
${\mathcal O}^+_{\Lambda_4}$
, and it is not hard to verify that the two are equal.
Let us also use this example to learn a little about Coxeter graphs. The Coxeter graph for the planes that bound
![]() ${\mathcal F}_4$
is the following:
${\mathcal F}_4$
is the following:
We note, from our earlier calculations, that
![]() $\alpha_i\cdot \alpha_i=-8$
. From the Coxeter graph, we therefore get
$\alpha_i\cdot \alpha_i=-8$
. From the Coxeter graph, we therefore get
![]() $\alpha_1\cdot \alpha_2=8$
,
$\alpha_1\cdot \alpha_2=8$
,
![]() $\alpha_2\cdot \alpha_3=4$
,
$\alpha_2\cdot \alpha_3=4$
,
![]() $\alpha_3\cdot \alpha_4=4$
, and all other products
$\alpha_3\cdot \alpha_4=4$
, and all other products
![]() $\alpha_i\cdot \alpha_j$
for
$\alpha_i\cdot \alpha_j$
for
![]() $i<j$
are zero. This gives us the matrix
$i<j$
are zero. This gives us the matrix
 \begin{equation*}J_\alpha=[\alpha_i\cdot \alpha_j]=\left[\begin{array}{lccccccccc}-8&8&0&0 \\ 8&-8&4&0 \\ 0&4&-8&4 \\ 0&0&4&-8\end{array}\right].\end{equation*}
\begin{equation*}J_\alpha=[\alpha_i\cdot \alpha_j]=\left[\begin{array}{lccccccccc}-8&8&0&0 \\ 8&-8&4&0 \\ 0&4&-8&4 \\ 0&0&4&-8\end{array}\right].\end{equation*}
Our Lorentz product, in this basis, is
![]() $\mathbf x \cdot \mathbf y=\mathbf x^tJ_{\alpha}\mathbf y$
. Let
$\mathbf x \cdot \mathbf y=\mathbf x^tJ_{\alpha}\mathbf y$
. Let
![]() $\Lambda_{\alpha}=\alpha_1{\mathbb{Z}}\oplus \cdots \oplus \alpha_4{\mathbb{Z}}$
, so
$\Lambda_{\alpha}=\alpha_1{\mathbb{Z}}\oplus \cdots \oplus \alpha_4{\mathbb{Z}}$
, so
![]() $\Lambda_{\alpha}\subset \Lambda_{4}$
. Since
$\Lambda_{\alpha}\subset \Lambda_{4}$
. Since
![]() $\det\!(J_\alpha)=4\det\!(J_4)$
, the index is two.
$\det\!(J_\alpha)=4\det\!(J_4)$
, the index is two.
The fundamental domain
![]() ${\mathcal F}_4$
has five vertices: The point E at infinity, and the four vertices on
${\mathcal F}_4$
has five vertices: The point E at infinity, and the four vertices on
![]() $H_{\alpha_3}$
, the hemisphere above the dotted circle (see Figure 1). Let
$H_{\alpha_3}$
, the hemisphere above the dotted circle (see Figure 1). Let
![]() $w_i$
be the intersection of the three
$w_i$
be the intersection of the three
![]() $\alpha_j$
with
$\alpha_j$
with
![]() $j\neq i$
, so
$j\neq i$
, so
![]() $w_i$
is a vertex of
$w_i$
is a vertex of
![]() ${\mathcal F}_4$
for
${\mathcal F}_4$
for
![]() $i=1$
and 2, and
$i=1$
and 2, and
![]() $w_3$
is the point at infinity. The
$w_3$
is the point at infinity. The
![]() $w_i$
’s satisfy
$w_i$
’s satisfy
![]() $w_i\cdot \alpha_j=0$
for
$w_i\cdot \alpha_j=0$
for
![]() $i\neq j$
, so in the basis
$i\neq j$
, so in the basis
![]() $\alpha=\{\alpha_1,...,\alpha_4\}$
, are the rows of
$\alpha=\{\alpha_1,...,\alpha_4\}$
, are the rows of
![]() $J_{\alpha}^{-1}$
, up to scalars. To express these points in the basis
$J_{\alpha}^{-1}$
, up to scalars. To express these points in the basis
![]() $\mathbf e$
, we multiply on the left by the change of basis matrix
$\mathbf e$
, we multiply on the left by the change of basis matrix
![]() $Q=[\alpha_1|\alpha_2|\alpha_3|\alpha_4]$
whose columns are
$Q=[\alpha_1|\alpha_2|\alpha_3|\alpha_4]$
whose columns are
![]() $\alpha_i$
; the columns of the resulting matrix are the
$\alpha_i$
; the columns of the resulting matrix are the
![]() $w_i$
’s. The
$w_i$
’s. The
![]() $w_i$
’s are called weights. The incidence matrix for the
$w_i$
’s are called weights. The incidence matrix for the
![]() $w_i$
s is
$w_i$
s is
![]() $[w_i\cdot w_j]=J_\alpha^{-1}J_\alpha (J_\alpha^{-1})^t=(J_\alpha^{-1})^t=J_\alpha^{-1}$
. The first and second diagonal elements of
$[w_i\cdot w_j]=J_\alpha^{-1}J_\alpha (J_\alpha^{-1})^t=(J_\alpha^{-1})^t=J_\alpha^{-1}$
. The first and second diagonal elements of
![]() $J_\alpha^{-1}$
are positive, indicating that
$J_\alpha^{-1}$
are positive, indicating that
![]() $w_1$
and
$w_1$
and
![]() $w_2$
lie in
$w_2$
lie in
![]() ${\mathcal H}$
. The third diagonal element is 0, indicating
${\mathcal H}$
. The third diagonal element is 0, indicating
![]() $w_3$
lies on
$w_3$
lies on
![]() $\partial {\mathcal H}$
, so is a cusp (it is the point E at infinity). The last diagonal element is negative, so
$\partial {\mathcal H}$
, so is a cusp (it is the point E at infinity). The last diagonal element is negative, so
![]() $w_4$
represents a plane in
$w_4$
represents a plane in
![]() ${\mathcal H}$
. That plane is perpendicular to
${\mathcal H}$
. That plane is perpendicular to
![]() $H_{\alpha_1}$
,
$H_{\alpha_1}$
,
![]() $H_{\alpha_2}$
, and
$H_{\alpha_2}$
, and
![]() $H_{\alpha_3}$
, so is the plane
$H_{\alpha_3}$
, so is the plane
![]() $H_{\mathbf e_1}$
.
$H_{\mathbf e_1}$
.
The other two vertices of
![]() ${\mathcal F}_4$
can be found in a similar way by replacing
${\mathcal F}_4$
can be found in a similar way by replacing
![]() $\alpha_4$
with
$\alpha_4$
with
![]() $\mathbf e_1$
. This is plain to see from the picture (see Figure 1). Combinatorially, the intersection of any three of the five faces should give us a potential vertex, but since
$\mathbf e_1$
. This is plain to see from the picture (see Figure 1). Combinatorially, the intersection of any three of the five faces should give us a potential vertex, but since
![]() $H_{\alpha_4}$
and
$H_{\alpha_4}$
and
![]() $H_{\mathbf e_1}$
are parallel, any combination that includes those two will give at most their point of tangency.
$H_{\mathbf e_1}$
are parallel, any combination that includes those two will give at most their point of tangency.
Remark 1. The symmetry of the Coxeter graph about the node
![]() $\alpha_3$
suggests that there is a symmetry that sends
$\alpha_3$
suggests that there is a symmetry that sends
![]() $\mathbf e_1$
to
$\mathbf e_1$
to
![]() $\alpha_1$
, etc. That symmetry is reflection in the diagonal of slope one of the shaded square in Figure 1. However, since the norms of
$\alpha_1$
, etc. That symmetry is reflection in the diagonal of slope one of the shaded square in Figure 1. However, since the norms of
![]() $\mathbf e_1$
and
$\mathbf e_1$
and
![]() $\alpha_1$
are different, it is not a symmetry of the lattice
$\alpha_1$
are different, it is not a symmetry of the lattice
![]() $\Lambda_4$
. There is a different lattice that we could have considered, namely the one generated by the Coxeter graph (2.2) but with
$\Lambda_4$
. There is a different lattice that we could have considered, namely the one generated by the Coxeter graph (2.2) but with
![]() $\alpha_i^2=-2$
. There are some advantages to looking at that graph. Reflection in the diagonal is a symmetry of that lattice.
$\alpha_i^2=-2$
. There are some advantages to looking at that graph. Reflection in the diagonal is a symmetry of that lattice.
2.4. Sphere packings
A sphere packing in
![]() ${\mathbb{R}}^n$
is a configuration of oriented
${\mathbb{R}}^n$
is a configuration of oriented
![]() $(n-1)$
-spheres that intersect tangentially or not at all. By oriented, we mean each sphere includes either the inside (a ball) or the outside. The trivial sphere packing is a sphere and its complement. We will not consider trivial sphere packings.
$(n-1)$
-spheres that intersect tangentially or not at all. By oriented, we mean each sphere includes either the inside (a ball) or the outside. The trivial sphere packing is a sphere and its complement. We will not consider trivial sphere packings.
Maxwell calls
![]() ${\mathcal{P}}\subset {\mathbb{R}}^{1,N-1}$
a packing if for all
${\mathcal{P}}\subset {\mathbb{R}}^{1,N-1}$
a packing if for all
![]() $\mathbf n, \mathbf n'\in {\mathcal{P}}$
, there exists a positive constant k such that
$\mathbf n, \mathbf n'\in {\mathcal{P}}$
, there exists a positive constant k such that
![]() $\mathbf n\cdot \mathbf n=-k$
and
$\mathbf n\cdot \mathbf n=-k$
and
![]() $\mathbf n\cdot \mathbf n'\geq k$
[Reference Maxwell16]. Given a point E for the point at infinity, the packing
$\mathbf n\cdot \mathbf n'\geq k$
[Reference Maxwell16]. Given a point E for the point at infinity, the packing
![]() ${\mathcal{P}}$
defines a sphere packing
${\mathcal{P}}$
defines a sphere packing
We call
![]() ${\mathcal{P}}_E$
a perspective of
${\mathcal{P}}_E$
a perspective of
![]() ${\mathcal{P}}$
.
${\mathcal{P}}$
.
For example, the Apollonian packing in
![]() ${\mathbb{R}}^{1,3}$
is
${\mathbb{R}}^{1,3}$
is
![]() ${\mathcal{P}}_4={\Gamma}_4(\mathbf e_1) $
(the
${\mathcal{P}}_4={\Gamma}_4(\mathbf e_1) $
(the
![]() ${\Gamma}_4$
-orbit of
${\Gamma}_4$
-orbit of
![]() $\mathbf e_1$
) and the strip packing of Figure 1 is
$\mathbf e_1$
) and the strip packing of Figure 1 is
![]() ${\mathcal{P}}_{4,\mathbf e_1+\mathbf e_2}$
. An Apollonian packing derived from a different initial cluster of four mutually tangent circles is a different perspective of
${\mathcal{P}}_{4,\mathbf e_1+\mathbf e_2}$
. An Apollonian packing derived from a different initial cluster of four mutually tangent circles is a different perspective of
![]() ${\mathcal{P}}_4$
.
${\mathcal{P}}_4$
.
We think of
![]() ${\mathcal{P}}$
as defining a cone
${\mathcal{P}}$
as defining a cone
in
![]() ${\mathbb{R}}^{1,N-1}$
, or a polyhedron
${\mathbb{R}}^{1,N-1}$
, or a polyhedron
in
![]() ${\mathbb{H}}^{N-1}$
. The residual set of a sphere packing is the complement of the sphere packing in
${\mathbb{H}}^{N-1}$
. The residual set of a sphere packing is the complement of the sphere packing in
![]() $\partial {\mathcal H}_E\cong {\mathbb{R}}^n$
and is the intersection of
$\partial {\mathcal H}_E\cong {\mathbb{R}}^n$
and is the intersection of
![]() ${\mathcal K}_{{\mathcal{P}}}$
with
${\mathcal K}_{{\mathcal{P}}}$
with
![]() $\partial {\mathcal H}_E$
. A sphere packing is maximal or dense if there is no space in the residual set where one can place another sphere of positive radius. It is complete if the residual set is of measure zero. A packing that is maximal (respectively complete) in one perspective is maximal (complete) in any perspective.
$\partial {\mathcal H}_E$
. A sphere packing is maximal or dense if there is no space in the residual set where one can place another sphere of positive radius. It is complete if the residual set is of measure zero. A packing that is maximal (respectively complete) in one perspective is maximal (complete) in any perspective.
We call a packing of lattice type if
![]() ${\mathcal{P}}{\mathbb{Z}}$
forms a lattice in
${\mathcal{P}}{\mathbb{Z}}$
forms a lattice in
![]() ${\mathbb{R}}^{1,N-1}$
[Reference Maxwell16]. We call a packing of general lattice type if there exists a lattice
${\mathbb{R}}^{1,N-1}$
[Reference Maxwell16]. We call a packing of general lattice type if there exists a lattice
![]() $\Lambda\subset {\mathbb{R}}^{1,N-1}$
so that a scalar multiple of
$\Lambda\subset {\mathbb{R}}^{1,N-1}$
so that a scalar multiple of
![]() $\mathbf n$
is in
$\mathbf n$
is in
![]() $\Lambda$
for all
$\Lambda$
for all
![]() $\mathbf n\in {\mathcal{P}}$
, and
$\mathbf n\in {\mathcal{P}}$
, and
![]() ${\mathcal{P}}$
spans
${\mathcal{P}}$
spans
![]() ${\mathbb{R}}^{1,N-1}$
.
${\mathbb{R}}^{1,N-1}$
.
A subgroup
![]() ${\Gamma} \leq {\mathcal O}_\Lambda^+$
is called geometrically finite if it has a convex fundamental domain with a finite number of faces. A packing is called crystallographic if there exists a geometrically finite group
${\Gamma} \leq {\mathcal O}_\Lambda^+$
is called geometrically finite if it has a convex fundamental domain with a finite number of faces. A packing is called crystallographic if there exists a geometrically finite group
![]() ${\Gamma}\leq {\mathcal O}_{\Lambda}^+$
and a finite set
${\Gamma}\leq {\mathcal O}_{\Lambda}^+$
and a finite set
![]() $S\subset \Lambda$
so that
$S\subset \Lambda$
so that
As the normality condition is not necessary, we will write
![]() ${\mathcal{P}}={\Gamma}(S)$
, the
${\mathcal{P}}={\Gamma}(S)$
, the
![]() ${\Gamma}$
-orbit of S. The residual set for the packing is the limit set of
${\Gamma}$
-orbit of S. The residual set for the packing is the limit set of
![]() ${\Gamma}$
.
${\Gamma}$
.
Crystallographic packings are not always of lattice type, as was noted by Maxwell.
A crystallographic packing that is maximal is known to be complete. Furthermore, the Hausdorff dimension of the residual set is strictly less than
![]() $N-2$
[Reference Sullivan22].
$N-2$
[Reference Sullivan22].
The packings that are known as Boyd-Maxwell packings are crystallographic packings with the restriction that
![]() ${\Gamma}$
be a reflective group (i.e. is generated by a finite number of reflections). Kontorovich and Nakamura include this requirement in their definition of a crystallographic packing [Reference Kontorovich and Nakamura13].
${\Gamma}$
be a reflective group (i.e. is generated by a finite number of reflections). Kontorovich and Nakamura include this requirement in their definition of a crystallographic packing [Reference Kontorovich and Nakamura13].
We say a packing has the weak Apollonian property if it contains a cluster of
![]() $N=n+2$
mutually tangent spheres. We say it has the Apollonian property if every sphere is a member of a cluster of N mutually tangent spheres. We call a packing Apollonian if it is crystallographic, maximal, and has the Apollonian property.
$N=n+2$
mutually tangent spheres. We say it has the Apollonian property if every sphere is a member of a cluster of N mutually tangent spheres. We call a packing Apollonian if it is crystallographic, maximal, and has the Apollonian property.
Missing in this definition is a notion of efficiency. It is conjectured that the residual set for the Apollonian circle packing in two dimensions has minimal Hausdorff dimension among all nontrivial circle packings [Reference Melzak18], so an alternative definition would be that a packing is Apollonian if it is optimally efficient in that dimension. In
![]() ${\mathbb{R}}^7$
, there exists a weakly Apollonian packing that is more efficient than a known Apollonian packing (see Section 3.3), suggesting that there is still much to learn about the subject.
${\mathbb{R}}^7$
, there exists a weakly Apollonian packing that is more efficient than a known Apollonian packing (see Section 3.3), suggesting that there is still much to learn about the subject.
Remark 2. In [Reference Baragar4], we give a different definition for an Apollonian packing. We begin with a set
![]() $\{\mathbf e_1,...,\mathbf e_{N}\}$
with
$\{\mathbf e_1,...,\mathbf e_{N}\}$
with
![]() $\mathbf e_i\cdot \mathbf e_i=-1$
and
$\mathbf e_i\cdot \mathbf e_i=-1$
and
![]() $\mathbf e_i\cdot \mathbf e_j=1$
for
$\mathbf e_i\cdot \mathbf e_j=1$
for
![]() $i\neq j$
(so a cluster of N mutually tangent spheres), and define the lattice
$i\neq j$
(so a cluster of N mutually tangent spheres), and define the lattice
We pick
![]() $D\in \Lambda_N$
with
$D\in \Lambda_N$
with
![]() $D\cdot D>0$
and such that
$D\cdot D>0$
and such that
![]() $D\cdot \mathbf n\neq 0$
for any
$D\cdot \mathbf n\neq 0$
for any
![]() $\mathbf n\in \Lambda_N$
with
$\mathbf n\in \Lambda_N$
with
![]() $\mathbf n\cdot \mathbf n=-1$
. (Such a D exists.) We define
$\mathbf n\cdot \mathbf n=-1$
. (Such a D exists.) We define
We define the cone
and the set
The set
![]() ${\mathcal E}_{-1}^*$
is what is called an Apollonian packing in that paper. It gives the Apollonian circle packing when
${\mathcal E}_{-1}^*$
is what is called an Apollonian packing in that paper. It gives the Apollonian circle packing when
![]() $N=4$
, the Soddy sphere packing when
$N=4$
, the Soddy sphere packing when
![]() $N=5$
, and yields Apollonian packings (as defined in this paper) in dimensions
$N=5$
, and yields Apollonian packings (as defined in this paper) in dimensions
![]() $n=4$
through 8 [Reference Baragar4, Reference Baragar5].
$n=4$
through 8 [Reference Baragar4, Reference Baragar5].
It is not clear that
![]() ${\mathcal E}_{-1}^*$
is a packing for all N, as it is a priori possible that spheres in the set properly intersect. There is a very nice modularity argument to show that this cannot happen. We first note that if
${\mathcal E}_{-1}^*$
is a packing for all N, as it is a priori possible that spheres in the set properly intersect. There is a very nice modularity argument to show that this cannot happen. We first note that if
![]() $\mathbf n,\ \mathbf n'\in {\mathcal E}_{-1}^*$
, then
$\mathbf n,\ \mathbf n'\in {\mathcal E}_{-1}^*$
, then
![]() $\mathbf n\cdot \mathbf n'\in {\mathbb{Z}}$
, so if the spheres intersect but not tangentially, then
$\mathbf n\cdot \mathbf n'\in {\mathbb{Z}}$
, so if the spheres intersect but not tangentially, then
![]() $\mathbf n\cdot \mathbf n'=0$
(so they intersect perpendicularly). Consider the difference
$\mathbf n\cdot \mathbf n'=0$
(so they intersect perpendicularly). Consider the difference
![]() $\mathbf m=\mathbf n-\mathbf n'$
. If
$\mathbf m=\mathbf n-\mathbf n'$
. If
![]() $\mathbf n\cdot \mathbf n'=0$
, then
$\mathbf n\cdot \mathbf n'=0$
, then
![]() $\mathbf m\cdot \mathbf m=-2$
. Let
$\mathbf m\cdot \mathbf m=-2$
. Let
![]() $\mathbf m=(m_1,...,m_N)$
so
$\mathbf m=(m_1,...,m_N)$
so
We consider this modulo four, which means we need only worry about the parity of each
![]() $m_k$
. Suppose there are K odd
$m_k$
. Suppose there are K odd
![]() $m_k$
. Then
$m_k$
. Then
Thus,
![]() $\mathbf m\cdot \mathbf m \neq 2 \pmod 4$
, so there are no spheres that intersect perpendicularly.
$\mathbf m\cdot \mathbf m \neq 2 \pmod 4$
, so there are no spheres that intersect perpendicularly.
Remark 3. For a K3 surface X, let
![]() $\Lambda=\mathop{\textrm{Pic}}\nolimits(X)$
and let
$\Lambda=\mathop{\textrm{Pic}}\nolimits(X)$
and let
![]() ${\mathcal E}_{-2}^*$
be the set of irreducible
${\mathcal E}_{-2}^*$
be the set of irreducible
![]() $-2$
curves on X. Then
$-2$
curves on X. Then
![]() ${\mathcal K}_{{\mathcal E}_{-2}^*}$
is the ample cone for X. This was the motivation for the definitions given in [Reference Baragar4].
${\mathcal K}_{{\mathcal E}_{-2}^*}$
is the ample cone for X. This was the motivation for the definitions given in [Reference Baragar4].
Using a result of Morrison [19], there exist K3 surfaces with intersection matrix
![]() $[J_{ij}]$
with
$[J_{ij}]$
with
![]() $J_{ij}=2-4\delta_{ij}$
and
$J_{ij}=2-4\delta_{ij}$
and
![]() $N\leq 10$
. The set
$N\leq 10$
. The set
![]() ${\mathcal E}_{-2}^*$
gives the same packing as described in Remark 2. By [Reference Kovács14], the ample cone has no circular part for
${\mathcal E}_{-2}^*$
gives the same packing as described in Remark 2. By [Reference Kovács14], the ample cone has no circular part for
![]() $N\geq 4$
, so these packings are maximal.
$N\geq 4$
, so these packings are maximal.
2.5. Enriques surfaces
For a nice introduction to Enriques surfaces, see [11]. Let X be an Enriques surface and let
![]() $\Lambda$
be its Picard group modulo torsion. Then
$\Lambda$
be its Picard group modulo torsion. Then
![]() $\Lambda$
is independent of the choice of X and is sometimes called the Enriques lattice
$\Lambda$
is independent of the choice of X and is sometimes called the Enriques lattice
![]() $E_{10}$
. It is an even unimodular lattice of signature (1, 9) and can be decomposed as the orthogonal product of the
$E_{10}$
. It is an even unimodular lattice of signature (1, 9) and can be decomposed as the orthogonal product of the
![]() $E_8$
lattice (with negative definite inner product) and the plane U equipped with the Lorentz product
$E_8$
lattice (with negative definite inner product) and the plane U equipped with the Lorentz product
![]() $\left[\begin{array}{lcl}0&1 \\ 1&0\end{array}\right]$
:
$\left[\begin{array}{lcl}0&1 \\ 1&0\end{array}\right]$
:
![]() $\Lambda=E_8\oplus U$
.
$\Lambda=E_8\oplus U$
.
A nice representation of
![]() $E_{10}$
is given by the Coxeter graph
$E_{10}$
is given by the Coxeter graph
![]() $T_{237}$
whose nodes have norm
$T_{237}$
whose nodes have norm
![]() $-2$
:
$-2$
:

The subscript in
![]() $T_{237}$
means the graph is a tree with three branches of length 2, 3, and 7, as above. The lattice is
$T_{237}$
means the graph is a tree with three branches of length 2, 3, and 7, as above. The lattice is
![]() $\Lambda=\alpha_0{\mathbb{Z}}\oplus \cdots \oplus \alpha_9{\mathbb{Z}}$
. Since
$\Lambda=\alpha_0{\mathbb{Z}}\oplus \cdots \oplus \alpha_9{\mathbb{Z}}$
. Since
![]() $\alpha_i\cdot \alpha_i=-2$
, we know
$\alpha_i\cdot \alpha_i=-2$
, we know
![]() $\alpha_i\cdot \alpha_j=1$
if
$\alpha_i\cdot \alpha_j=1$
if
![]() $\alpha_i\alpha_j$
is an edge of the graph, and 0 otherwise. Let
$\alpha_i\alpha_j$
is an edge of the graph, and 0 otherwise. Let
![]() $J=[\alpha_i\cdot \alpha_j]$
, so for
$J=[\alpha_i\cdot \alpha_j]$
, so for
![]() $\mathbf x,\ \mathbf y\in \Lambda$
written in this basis,
$\mathbf x,\ \mathbf y\in \Lambda$
written in this basis,
![]() $\mathbf x\cdot \mathbf y=\mathbf x^tJ\mathbf y$
. Since J has integer entries and
$\mathbf x\cdot \mathbf y=\mathbf x^tJ\mathbf y$
. Since J has integer entries and
![]() $-2$
’s along the diagonal, the lattice is even, meaning
$-2$
’s along the diagonal, the lattice is even, meaning
![]() $\mathbf x\cdot \mathbf x$
is even for all
$\mathbf x\cdot \mathbf x$
is even for all
![]() $\mathbf x\in \Lambda$
. One can verify
$\mathbf x\in \Lambda$
. One can verify
![]() $\det(J)=-1$
, so the lattice is unimodular.
$\det(J)=-1$
, so the lattice is unimodular.
The reflections
have integer entries, so are in
![]() ${\mathcal O}_\Lambda^+$
. The inverse of J (which appears in [11, p.11]) has non-negative entries along the diagonal, so the polytope bounded by the faces
${\mathcal O}_\Lambda^+$
. The inverse of J (which appears in [11, p.11]) has non-negative entries along the diagonal, so the polytope bounded by the faces
![]() $H_{\alpha_i}$
has finite volume. Thus, the Weyl group
$H_{\alpha_i}$
has finite volume. Thus, the Weyl group
has finite index in
![]() ${\mathcal O}_{\Lambda}^+$
.
${\mathcal O}_{\Lambda}^+$
.
A generic Enriques surface has no nodal curves, meaning it has no smooth rational curves. The moduli space of Enriques surfaces is ten dimensional. If X contains a nodal curve
![]() $\nu$
, then we call it a nodal Enriques surface. By the adjunction formula,
$\nu$
, then we call it a nodal Enriques surface. By the adjunction formula,
![]() $\nu\cdot \nu=-2$
. Here we have abused notation by letting
$\nu\cdot \nu=-2$
. Here we have abused notation by letting
![]() $\nu$
represent both the curve on X and its representation in
$\nu$
represent both the curve on X and its representation in
![]() $\Lambda$
. Since distinct irreducible curves on X have non-negative intersection, an element of
$\Lambda$
. Since distinct irreducible curves on X have non-negative intersection, an element of
![]() $\Lambda$
represents at most one nodal curve on X. The moduli space of nodal Enriques surfaces is nine dimensional. The following is a rewording of a portion of [Reference Allcock1, Theorem 1.2]:
$\Lambda$
represents at most one nodal curve on X. The moduli space of nodal Enriques surfaces is nine dimensional. The following is a rewording of a portion of [Reference Allcock1, Theorem 1.2]:
Theorem 2.1 (Coble, Looijenga, Cossec, Dolgachev, Allcock). Suppose X is a generic nodal Enriques surface with nodal curve
![]() $\nu$
. Let
$\nu$
. Let
![]() $\Lambda$
be its Picard group modulo torsion. Then there exist
$\Lambda$
be its Picard group modulo torsion. Then there exist
![]() $\beta_0,..., \beta_9\in \Lambda$
so that
$\beta_0,..., \beta_9\in \Lambda$
so that
![]() $\beta_i\cdot\beta_i=-2$
and
$\beta_i\cdot\beta_i=-2$
and
![]() $\beta_0,...,\beta_9,\nu$
are the nodes of the Coxeter graph (1.1). Let
$\beta_0,...,\beta_9,\nu$
are the nodes of the Coxeter graph (1.1). Let
Then the image in
![]() $\Lambda$
of all nodal curves on X is the
$\Lambda$
of all nodal curves on X is the
![]() ${\Gamma}_{\beta}$
-orbit of
${\Gamma}_{\beta}$
-orbit of
![]() $\nu$
.
$\nu$
.
As this version does not look much like Allcock’s result, let us show how it follows. By (5) (of [Reference Allcock1, Theorem 1.2]),
![]() $\mathop{\textrm{Aut}}\nolimits(X)$
acts transitively on the nodal curves on X. The image of
$\mathop{\textrm{Aut}}\nolimits(X)$
acts transitively on the nodal curves on X. The image of
![]() $\mathop{\textrm{Aut}}\nolimits(X)$
in
$\mathop{\textrm{Aut}}\nolimits(X)$
in
![]() ${\mathcal O}_{\Lambda}^+$
is a subgroup of
${\mathcal O}_{\Lambda}^+$
is a subgroup of
![]() ${\Gamma}_{\beta}=W_{246}$
by (2), and by (3), contains a group identified as
${\Gamma}_{\beta}=W_{246}$
by (2), and by (3), contains a group identified as
![]() $\overline{W}_{246}(2)$
(see [Reference Allcock1] for the definition of this group). By (4),
$\overline{W}_{246}(2)$
(see [Reference Allcock1] for the definition of this group). By (4),
![]() $\overline{W}_{246}(2)$
acts transitively on the faces of the ample cone (the interior of
$\overline{W}_{246}(2)$
acts transitively on the faces of the ample cone (the interior of
![]() $\mathop{\textrm{nef}}\nolimits(X)$
), so the image of the nodal curves on X includes all of them. By (1),
$\mathop{\textrm{nef}}\nolimits(X)$
), so the image of the nodal curves on X includes all of them. By (1),
![]() $\mathop{\textrm{nef}}\nolimits(X)$
is the union of the
$\mathop{\textrm{nef}}\nolimits(X)$
is the union of the
![]() ${\Gamma}_{\beta}$
-translates of the fundamental domain of the Coxeter group generated by the Coxeter graph (1.1) on page 2. The faces of the ample cone are therefore the
${\Gamma}_{\beta}$
-translates of the fundamental domain of the Coxeter group generated by the Coxeter graph (1.1) on page 2. The faces of the ample cone are therefore the
![]() ${\Gamma}_{\beta}$
image of
${\Gamma}_{\beta}$
image of
![]() $\nu$
, as all other faces of the fundamental domain correspond to reflections in
$\nu$
, as all other faces of the fundamental domain correspond to reflections in
![]() $W_{246}$
. Hence, the nodal curves on X generate exactly the faces of the ample cone and is the
$W_{246}$
. Hence, the nodal curves on X generate exactly the faces of the ample cone and is the
![]() ${\Gamma}_{\beta}$
-orbit of
${\Gamma}_{\beta}$
-orbit of
![]() $\nu$
.
$\nu$
.
3. The Apollonian packing in eight dimensions
Theorem 3.1. The packing
![]() ${\mathcal{P}}_\beta={\Gamma}_{\beta}(\nu)$
is Apollonian.
${\mathcal{P}}_\beta={\Gamma}_{\beta}(\nu)$
is Apollonian.
Proof. From Maxwell [Reference Maxwell16, Table II,
![]() $N=10$
], we know that this is a Boyd-Maxwell packing, so all we must verify is that it is maximal and that it contains a cluster of ten mutually tangent spheres. (Because
$N=10$
], we know that this is a Boyd-Maxwell packing, so all we must verify is that it is maximal and that it contains a cluster of ten mutually tangent spheres. (Because
![]() ${\Gamma}$
acts transitively on
${\Gamma}$
acts transitively on
![]() ${\mathcal{P}}_\beta$
, the weak Apollonian property implies the Apollonian property.)
${\mathcal{P}}_\beta$
, the weak Apollonian property implies the Apollonian property.)
We define
![]() $J_\beta=[\beta_i\cdot \beta_j]$
, which has
$J_\beta=[\beta_i\cdot \beta_j]$
, which has
![]() $-2$
along the diagonal, 1 if
$-2$
along the diagonal, 1 if
![]() $\beta_i\beta_j$
is an edge in Coxeter graph (1.1), and 0 otherwise. Taking the inverse,
$\beta_i\beta_j$
is an edge in Coxeter graph (1.1), and 0 otherwise. Taking the inverse,
 \begin{equation*}J_\beta^{-1}=\frac{1}{2}\left[\begin{array}{lccccccccccccccccccccccccccc}5&3&6&9&12&10&8&6&4&2 \\3&0&2&4& 6& 5&4&3&2&1 \\6&2&4&8&12&10&8&6&4&2 \\9&4&8&12&18&15&12&9&6&3 \\12&6&12&18&24&20&16&12&8&4 \\10&5&10&15&20&15&12&9&6&3 \\8&4&8&12&16&12&8&6&4&2 \\6&3&6&9&12&9&6&3&2&1 \\4&2&4&6&8&6&4&2&0&0 \\2&1&2&3&4&3&2&1&0&-1 \end{array}\right],\end{equation*}
\begin{equation*}J_\beta^{-1}=\frac{1}{2}\left[\begin{array}{lccccccccccccccccccccccccccc}5&3&6&9&12&10&8&6&4&2 \\3&0&2&4& 6& 5&4&3&2&1 \\6&2&4&8&12&10&8&6&4&2 \\9&4&8&12&18&15&12&9&6&3 \\12&6&12&18&24&20&16&12&8&4 \\10&5&10&15&20&15&12&9&6&3 \\8&4&8&12&16&12&8&6&4&2 \\6&3&6&9&12&9&6&3&2&1 \\4&2&4&6&8&6&4&2&0&0 \\2&1&2&3&4&3&2&1&0&-1 \end{array}\right],\end{equation*}
we find that the weights all have non-negative norm except
![]() $w_9$
, which gives us
$w_9$
, which gives us
![]() $\nu=2w_9=[2,1,2,3,4,3,2,1,0,-1]$
. (Recall that the weights are the rows of
$\nu=2w_9=[2,1,2,3,4,3,2,1,0,-1]$
. (Recall that the weights are the rows of
![]() $J_{\beta}^{-1}$
, and that the diagonal elements are their norms
$J_{\beta}^{-1}$
, and that the diagonal elements are their norms
![]() $w_i\cdot w_i$
.) Since
$w_i\cdot w_i$
.) Since
![]() $w_9\cdot \beta_i=\delta_{i9}$
, we get
$w_9\cdot \beta_i=\delta_{i9}$
, we get
![]() $\nu\cdot\beta_9=2$
and
$\nu\cdot\beta_9=2$
and
![]() $\nu\cdot \beta_i=0$
for
$\nu\cdot \beta_i=0$
for
![]() $i\neq 9$
, as expected. This is our first sphere, which we label
$i\neq 9$
, as expected. This is our first sphere, which we label
![]() $s_0=\nu=2w_9$
. We get
$s_0=\nu=2w_9$
. We get
![]() $s_1$
by reflecting
$s_1$
by reflecting
![]() $s_0$
across
$s_0$
across
![]() $H_{\beta_9}$
:
$H_{\beta_9}$
:
![]() $s_1=R_{\beta_9}(s_0)$
. We define
$s_1=R_{\beta_9}(s_0)$
. We define
![]() $s_i$
through
$s_i$
through
![]() $i=9$
recursively by reflecting in subsequent planes:
$i=9$
recursively by reflecting in subsequent planes:
![]() $s_{i+1}=R_{\beta_{9-i}}(s_i)$
. It is straight forward to verify that
$s_{i+1}=R_{\beta_{9-i}}(s_i)$
. It is straight forward to verify that
![]() $s_i\cdot s_j=2$
if
$s_i\cdot s_j=2$
if
![]() $i\neq j$
, and of course,
$i\neq j$
, and of course,
![]() $s_i\cdot s_i=\nu\cdot\nu=-2$
, so the set
$s_i\cdot s_i=\nu\cdot\nu=-2$
, so the set
![]() $\{s_0,...,s_9\}$
is a cluster of ten mutually tangent spheres.
$\{s_0,...,s_9\}$
is a cluster of ten mutually tangent spheres.
To show it is maximal, we can appeal to arguments like those in [Reference Baragar4] and [Reference Baragar5]. Let us instead appeal to Maxwell’s Theorem 3.3 [Reference Maxwell16]. By this result, it is enough to show that all weights
![]() $w_i$
are in the convex closure of
$w_i$
are in the convex closure of
![]() ${\Gamma}(w_9)$
. Following Maxwell’s example, we note
${\Gamma}(w_9)$
. Following Maxwell’s example, we note
for
![]() $5\leq i \leq 9$
, so these are all in the convex hull of
$5\leq i \leq 9$
, so these are all in the convex hull of
![]() ${\Gamma}(w_9)$
. This leaves us with four more to check, of which
${\Gamma}(w_9)$
. This leaves us with four more to check, of which
![]() $w_1$
is different, as it is a cusp and no spheres go through it.
$w_1$
is different, as it is a cusp and no spheres go through it.
We will use the map
![]() $R_{2w_1-\beta_9}$
, which we verify is in
$R_{2w_1-\beta_9}$
, which we verify is in
![]() ${\Gamma}$
using a method of descent. Our method of descent is as follows: Given a vector
${\Gamma}$
using a method of descent. Our method of descent is as follows: Given a vector
![]() $\mathbf n$
, we descend to
$\mathbf n$
, we descend to
![]() $R_{\beta_j}(\mathbf n)$
if
$R_{\beta_j}(\mathbf n)$
if
![]() $\mathbf n\cdot \beta_j<0$
, and repeat if necessary. For
$\mathbf n\cdot \beta_j<0$
, and repeat if necessary. For
![]() $\mathbf n\cdot \mathbf n>0$
(a point in
$\mathbf n\cdot \mathbf n>0$
(a point in
![]() ${\mathcal H}$
), it is clear that at each step we are getting closer to the fundamental domain, and that descent stops when we reach it. What this method does for
${\mathcal H}$
), it is clear that at each step we are getting closer to the fundamental domain, and that descent stops when we reach it. What this method does for
![]() $\mathbf n\cdot \mathbf n<0$
is less obvious, but is never-the-less useful.
$\mathbf n\cdot \mathbf n<0$
is less obvious, but is never-the-less useful.
With
![]() $\mathbf n=2w_1-\beta_9$
, we eventually descend to
$\mathbf n=2w_1-\beta_9$
, we eventually descend to
![]() $\mathbf \beta_8$
, so there exists
$\mathbf \beta_8$
, so there exists
![]() $\gamma\in {\Gamma}$
so that
$\gamma\in {\Gamma}$
so that
![]() $\mathbf n=\gamma\beta_8$
. Thus,
$\mathbf n=\gamma\beta_8$
. Thus,
![]() $R_{\mathbf n}=R_{\gamma \beta_8}=\gamma R_{\beta_8}\gamma^{-1}\in {\Gamma}$
. The composition
$R_{\mathbf n}=R_{\gamma \beta_8}=\gamma R_{\beta_8}\gamma^{-1}\in {\Gamma}$
. The composition
![]() $R_{2w_1-\beta_9}\circ R_{\beta_9}$
is a parabolic translation with fixed point
$R_{2w_1-\beta_9}\circ R_{\beta_9}$
is a parabolic translation with fixed point
![]() $w_1$
on
$w_1$
on
![]() $\partial {\mathcal H}$
, so repeated applications converge to the line
$\partial {\mathcal H}$
, so repeated applications converge to the line
![]() $\lambda w_1$
. More precisely, a messy but straightforward calculation shows
$\lambda w_1$
. More precisely, a messy but straightforward calculation shows
Thus
![]() $w_1$
is in the convex closure of
$w_1$
is in the convex closure of
![]() ${\Gamma}(w_9)$
.
${\Gamma}(w_9)$
.
Finally, we note that
 \begin{align*}w_2&=(R_{\beta_0}(s_6)+R_{\beta_2}(s_8))/2\\w_0&=w_1+s_9/2 \\w_3&=R_{\beta_2}(w_2)+R_{\beta_1}(w_1).\end{align*}
\begin{align*}w_2&=(R_{\beta_0}(s_6)+R_{\beta_2}(s_8))/2\\w_0&=w_1+s_9/2 \\w_3&=R_{\beta_2}(w_2)+R_{\beta_1}(w_1).\end{align*}
Thus,
![]() ${\mathcal{P}}_\beta$
is an Apollonian sphere packing.
${\mathcal{P}}_\beta$
is an Apollonian sphere packing.
3.1. The strip version and the
 $\boldsymbol{E}_7$
lattice
$\boldsymbol{E}_7$
lattice
To better understand this packing, we describe it in a couple of ways. Let us begin with a strip version, which is an analog of Figure 1. We can think of Figure 1 as an infinite set of circles of constant diameter that are each centered at lattice points of a one-dimensional lattice, then sandwiched between two lines, and filled in using the symmetries of the lattice together with inversion in
![]() $\alpha_3$
and reflection in
$\alpha_3$
and reflection in
![]() $\alpha_4$
. We can describe
$\alpha_4$
. We can describe
![]() ${\mathcal{P}}_\beta$
in a similar way:
${\mathcal{P}}_\beta$
in a similar way:
Theorem 3.2. Consider the
![]() $E_7$
lattice imbedded in a 7-dimensional subspace V of
$E_7$
lattice imbedded in a 7-dimensional subspace V of
![]() ${\mathbb{R}}^8$
. Centered at each lattice point, place a hypersphere of radius
${\mathbb{R}}^8$
. Centered at each lattice point, place a hypersphere of radius
![]() $1/\sqrt{2}$
, and bound these hyperspheres by two hyperplanes parallel to V and a distance
$1/\sqrt{2}$
, and bound these hyperspheres by two hyperplanes parallel to V and a distance
![]() $1/\sqrt{2}$
away from V, so that all the spheres are tangent to the two hyperplanes. Let one of the spheres be tangent to the two hyperplanes at A and B, and let
$1/\sqrt{2}$
away from V, so that all the spheres are tangent to the two hyperplanes. Let one of the spheres be tangent to the two hyperplanes at A and B, and let
![]() $\sigma$
be inversion in the hypersphere centered at A that goes through B. Consider the image of these spheres in the group generated by the symmetries of the
$\sigma$
be inversion in the hypersphere centered at A that goes through B. Consider the image of these spheres in the group generated by the symmetries of the
![]() $E_7$
lattice, the inversion
$E_7$
lattice, the inversion
![]() $\sigma$
, and reflection across the hyperplane V. The resulting configuration of hyperspheres is a perspective of
$\sigma$
, and reflection across the hyperplane V. The resulting configuration of hyperspheres is a perspective of
![]() ${\mathcal{P}}_\beta$
.
${\mathcal{P}}_\beta$
.
The
![]() $E_7$
lattice has the Coxeter diagram
$E_7$
lattice has the Coxeter diagram
![]() $T_{234}$
:
$T_{234}$
:
It is common to assign each node the norm 2 so that the resulting bilinear form has integer entries, is even, and has determinant 2. Thus, the generating vectors have length
![]() $\sqrt 2$
, which is why the spheres above have radius
$\sqrt 2$
, which is why the spheres above have radius
![]() $\sqrt 2/2$
. Adding a node to the appropriate branch gives us the group
$\sqrt 2/2$
. Adding a node to the appropriate branch gives us the group
![]() $W_{244}$
, which acts transitively on the
$W_{244}$
, which acts transitively on the
![]() $E_7$
lattice [Reference Vinberg24, Table 2]. Alternatively, the
$E_7$
lattice [Reference Vinberg24, Table 2]. Alternatively, the
![]() $E_7$
lattice can be thought of as the
$E_7$
lattice can be thought of as the
![]() $W_{244}$
orbit of the point O, where O is the vertex of the canonical fundamental domain for
$W_{244}$
orbit of the point O, where O is the vertex of the canonical fundamental domain for
![]() $W_{244}$
that lies at the intersection of the planes represented by the
$W_{244}$
that lies at the intersection of the planes represented by the
![]() $T_{234}$
subgraph. This is the representation we shall use.
$T_{234}$
subgraph. This is the representation we shall use.
Proof. Referring to
![]() $J_\beta^{-1}$
, we note that
$J_\beta^{-1}$
, we note that
![]() $w_8$
has norm zero, so is a point on
$w_8$
has norm zero, so is a point on
![]() $\partial {\mathcal H}$
. Let us consider the perspective
$\partial {\mathcal H}$
. Let us consider the perspective
![]() ${\mathcal{P}}_{\beta,w_8}$
, which lies in
${\mathcal{P}}_{\beta,w_8}$
, which lies in
![]() $\partial {\mathcal H}_{w_8}\cong {\mathbb{R}}^8$
. Note that the spheres
$\partial {\mathcal H}_{w_8}\cong {\mathbb{R}}^8$
. Note that the spheres
![]() $s_0$
and
$s_0$
and
![]() $s_1$
are tangent at
$s_1$
are tangent at
![]() $w_8$
, so are parallel Euclidean hyperplanes in
$w_8$
, so are parallel Euclidean hyperplanes in
![]() $\partial {\mathcal H}_{w_8}$
. These are our analogs of
$\partial {\mathcal H}_{w_8}$
. These are our analogs of
![]() $\mathbf e_1$
and
$\mathbf e_1$
and
![]() $\mathbf e_2$
, respectively, in Figure 1. Since
$\mathbf e_2$
, respectively, in Figure 1. Since
![]() $s_1=R_{\beta_9}\!(s_0)$
, the reflection
$s_1=R_{\beta_9}\!(s_0)$
, the reflection
![]() $R_{\beta_9}$
is the analog of the symmetry represented by
$R_{\beta_9}$
is the analog of the symmetry represented by
![]() $\alpha_4$
, and we take V to be
$\alpha_4$
, and we take V to be
![]() $H_{\beta_9}\cap \partial {\mathcal H}_{w_8}$
. Since
$H_{\beta_9}\cap \partial {\mathcal H}_{w_8}$
. Since
![]() $s_2=R_{\beta_8}(s_1)$
, the reflection
$s_2=R_{\beta_8}(s_1)$
, the reflection
![]() $R_{\beta_8}$
is
$R_{\beta_8}$
is
![]() $\sigma$
, the analog of inversion in
$\sigma$
, the analog of inversion in
![]() $\alpha_3$
. The sphere
$\alpha_3$
. The sphere
![]() $s_2$
is the analog of
$s_2$
is the analog of
![]() $\mathbf e_3$
, and the points A and B are the points of tangency
$\mathbf e_3$
, and the points A and B are the points of tangency
![]() $s_0+s_2$
and
$s_0+s_2$
and
![]() $s_1+s_2$
, respectively. The rest of the generators are the analogs of
$s_1+s_2$
, respectively. The rest of the generators are the analogs of
![]() $\alpha_1$
and
$\alpha_1$
and
![]() $\alpha_2$
. They form the group
$\alpha_2$
. They form the group
![]() ${\Gamma}_7=\langle R_{\beta_0},...,R_{\beta_7}\rangle \cong W_{244}$
. It remains to understand what the orbit
${\Gamma}_7=\langle R_{\beta_0},...,R_{\beta_7}\rangle \cong W_{244}$
. It remains to understand what the orbit
![]() ${\Gamma}_7(s_2)$
looks like.
${\Gamma}_7(s_2)$
looks like.
Note that the generators of
![]() ${\Gamma}_7$
fix
${\Gamma}_7$
fix
![]() $w_8$
, so are Euclidean reflections in
$w_8$
, so are Euclidean reflections in
![]() $\partial {\mathcal H}_{w_8}\cong {\mathbb{R}}^8$
. The planes through which they reflect are all perpendicular to
$\partial {\mathcal H}_{w_8}\cong {\mathbb{R}}^8$
. The planes through which they reflect are all perpendicular to
![]() $V=H_{\beta_9}\cap \partial {\mathcal H}_{w_8}\cong {\mathbb{R}}^7$
, so act as a group of reflections on V. Let O in V be the point of intersection of
$V=H_{\beta_9}\cap \partial {\mathcal H}_{w_8}\cong {\mathbb{R}}^7$
, so act as a group of reflections on V. Let O in V be the point of intersection of
![]() $H_{\beta_i}$
for
$H_{\beta_i}$
for
![]() $i\leq 6$
. Since the planes
$i\leq 6$
. Since the planes
![]() $H_{\beta_i}$
are perpendicular to
$H_{\beta_i}$
are perpendicular to
![]() $s_2$
for
$s_2$
for
![]() $i\leq 6$
(since
$i\leq 6$
(since
![]() $\beta_i\cdot s_2=0$
for
$\beta_i\cdot s_2=0$
for
![]() $i\leq 6$
), the point O must be the center of the sphere
$i\leq 6$
), the point O must be the center of the sphere
![]() $s_2$
. Thus, the
$s_2$
. Thus, the
![]() ${\Gamma}_7$
-orbit of
${\Gamma}_7$
-orbit of
![]() $s_2$
is a set of congruent spheres that are centered on the lattice points of an
$s_2$
is a set of congruent spheres that are centered on the lattice points of an
![]() $E_7$
lattice. Finally, since
$E_7$
lattice. Finally, since
![]() $s_3=R_{\beta_7}(s_2)$
, and
$s_3=R_{\beta_7}(s_2)$
, and
![]() $s_3$
is tangent to
$s_3$
is tangent to
![]() $s_2$
, the spheres must be of maximal radius so that they intersect tangentially or not at all. That is, scaling so that the generating vectors of the
$s_2$
, the spheres must be of maximal radius so that they intersect tangentially or not at all. That is, scaling so that the generating vectors of the
![]() $E_7$
lattice have length
$E_7$
lattice have length
![]() $\sqrt 2$
, the spheres all have radius
$\sqrt 2$
, the spheres all have radius
![]() $\sqrt 2/2$
.
$\sqrt 2/2$
.
3.2. The
 $\boldsymbol{E}_8$
structure
$\boldsymbol{E}_8$
structure
The
![]() $E_8$
lattice has the Coxeter diagram
$E_8$
lattice has the Coxeter diagram
![]() $T_{235}$
, and the group
$T_{235}$
, and the group
![]() $W_{236}$
acts transitively on it [Reference Vinberg24, Table 2]. The lattice can also be thought of as the
$W_{236}$
acts transitively on it [Reference Vinberg24, Table 2]. The lattice can also be thought of as the
![]() $W_{236}$
orbit of the point O, where O is the vertex of the canonical fundamental domain for
$W_{236}$
orbit of the point O, where O is the vertex of the canonical fundamental domain for
![]() $W_{236}$
that lies at the intersection of the planes represented by the
$W_{236}$
that lies at the intersection of the planes represented by the
![]() $T_{235}$
subgraph. Let us distinguish another vertex of the fundamental domain, the point P that lies at the intersection of the planes represented by the
$T_{235}$
subgraph. Let us distinguish another vertex of the fundamental domain, the point P that lies at the intersection of the planes represented by the
![]() $T_{226}$
subgraph.
$T_{226}$
subgraph.
Theorem 3.3. Consider an arrangement of hyperspheres all of radius
![]() $1/\sqrt 2$
and centered at the lattice points of the
$1/\sqrt 2$
and centered at the lattice points of the
![]() $E_8$
lattice in
$E_8$
lattice in
![]() ${\mathbb{R}}^8$
. (This is the densest uniradial sphere packing in
${\mathbb{R}}^8$
. (This is the densest uniradial sphere packing in
![]() ${\mathbb{R}}^8$
.) Let
${\mathbb{R}}^8$
.) Let
![]() $\sigma$
be inversion in the sphere centered at P (described above) and with radius
$\sigma$
be inversion in the sphere centered at P (described above) and with radius
![]() $1/\sqrt 2$
. Consider the image of this arrangement of spheres in the group generated by
$1/\sqrt 2$
. Consider the image of this arrangement of spheres in the group generated by
![]() $\sigma$
and the symmetries of the
$\sigma$
and the symmetries of the
![]() $E_8$
lattice. The resulting configuration is a perspective of
$E_8$
lattice. The resulting configuration is a perspective of
![]() ${\mathcal{P}}_\beta$
.
${\mathcal{P}}_\beta$
.
Proof. Referring to
![]() $J_\beta^{-1}$
, we see that
$J_\beta^{-1}$
, we see that
![]() $w_1$
is also on
$w_1$
is also on
![]() $\partial {\mathcal H}$
, as
$\partial {\mathcal H}$
, as
![]() $w_1\cdot w_1=0$
. Let us consider the perspective
$w_1\cdot w_1=0$
. Let us consider the perspective
![]() ${\mathcal{P}}_{\beta, w_1}$
. The planes
${\mathcal{P}}_{\beta, w_1}$
. The planes
![]() $H_{\beta_i}$
for
$H_{\beta_i}$
for
![]() $i\neq 1$
all go through
$i\neq 1$
all go through
![]() $w_1$
(by the definition of
$w_1$
(by the definition of
![]() $w_1$
), so the corresponding reflections
$w_1$
), so the corresponding reflections
![]() $R_{\beta_i}$
are Euclidean symmetries of
$R_{\beta_i}$
are Euclidean symmetries of
![]() ${\mathbb{R}}^8\cong \partial {\mathcal H}_{w_1}$
. Let us first consider the group
${\mathbb{R}}^8\cong \partial {\mathcal H}_{w_1}$
. Let us first consider the group
![]() ${\Gamma}_8=\langle R_{\beta_0}, R_{\beta_2},...,R_{\beta_9}\rangle\cong W_{236}$
.
${\Gamma}_8=\langle R_{\beta_0}, R_{\beta_2},...,R_{\beta_9}\rangle\cong W_{236}$
.
We let O be the point on
![]() $\partial {\mathcal H}_{w_1}$
where the planes
$\partial {\mathcal H}_{w_1}$
where the planes
![]() $H_{\beta_0}$
,
$H_{\beta_0}$
,
![]() $H_{\beta_2}$
, …,
$H_{\beta_2}$
, …,
![]() $H_{\beta_8}$
intersect, so
$H_{\beta_8}$
intersect, so
![]() ${\Gamma}_8(O)$
is an
${\Gamma}_8(O)$
is an
![]() $E_8$
lattice in
$E_8$
lattice in
![]() $\partial {\mathcal H}_{w_1}$
. Since these planes intersect
$\partial {\mathcal H}_{w_1}$
. Since these planes intersect
![]() $s_0=\nu$
perpendicularly, we know O is the center of
$s_0=\nu$
perpendicularly, we know O is the center of
![]() $s_0$
. The
$s_0$
. The
![]() ${\Gamma}_8$
-orbit of
${\Gamma}_8$
-orbit of
![]() $s_0$
is therefore a set of spheres of constant radius centered on the vertices of an
$s_0$
is therefore a set of spheres of constant radius centered on the vertices of an
![]() $E_8$
lattice. Since
$E_8$
lattice. Since
![]() $R_{\beta_9}\!(s_0)=s_1$
is tangent to
$R_{\beta_9}\!(s_0)=s_1$
is tangent to
![]() $s_0$
, these spheres are of maximal radius such that any pair intersect tangentially or not at all. They give the densest uniradial sphere packing of
$s_0$
, these spheres are of maximal radius such that any pair intersect tangentially or not at all. They give the densest uniradial sphere packing of
![]() ${\mathbb{R}}^8$
[Reference Viazovska23].
${\mathbb{R}}^8$
[Reference Viazovska23].
It remains to understand the action of
![]() $R_{\beta_1}$
. The plane
$R_{\beta_1}$
. The plane
![]() $H_{\beta_1}$
represents a sphere in
$H_{\beta_1}$
represents a sphere in
![]() $\partial {\mathcal H}_{w_1}$
. Since
$\partial {\mathcal H}_{w_1}$
. Since
![]() $\beta_1\cdot w_1=1=s_0\cdot w_1$
and
$\beta_1\cdot w_1=1=s_0\cdot w_1$
and
![]() $\beta_1\cdot \beta_1=-2=s_0\cdot s_0$
, the spheres have the same radii. Finally,
$\beta_1\cdot \beta_1=-2=s_0\cdot s_0$
, the spheres have the same radii. Finally,
![]() $\beta_1\cdot \beta_i=0$
for
$\beta_1\cdot \beta_i=0$
for
![]() $i=0$
,
$i=0$
,
![]() $3,...,9$
, so is centered at the point of intersection on V of the planes
$3,...,9$
, so is centered at the point of intersection on V of the planes
![]() $H_{\beta_0}$
,
$H_{\beta_0}$
,
![]() $H_{\beta_3}$
, …,
$H_{\beta_3}$
, …,
![]() $H_{\beta_9}$
, which corresponds to the vertex P of the fundamental domain for
$H_{\beta_9}$
, which corresponds to the vertex P of the fundamental domain for
![]() $W_{236}$
. Thus, the described configuration is congruent to the perspective
$W_{236}$
. Thus, the described configuration is congruent to the perspective
![]() ${\mathcal{P}}_{\beta,w_1}$
.
${\mathcal{P}}_{\beta,w_1}$
.
3.3. Comparison with the packing in [Reference Baragar4]
Let
and let
![]() $J_{10}=[s_i\cdot s_j]$
. Then
$J_{10}=[s_i\cdot s_j]$
. Then
![]() $\det\!(J_{10})=-2^{22}$
while
$\det\!(J_{10})=-2^{22}$
while
![]() $\det\!(J_\beta)=-4$
. It would appear that the packing
$\det\!(J_\beta)=-4$
. It would appear that the packing
![]() ${\mathcal{P}}_{10}={\mathcal E}_{-2}^*$
generated by
${\mathcal{P}}_{10}={\mathcal E}_{-2}^*$
generated by
![]() $\Lambda_{10}$
(see Remark 2) is very different than
$\Lambda_{10}$
(see Remark 2) is very different than
![]() ${\mathcal{P}}_\beta$
. However, we can modify the underlying lattice for
${\mathcal{P}}_\beta$
. However, we can modify the underlying lattice for
![]() ${\mathcal{P}}_\beta$
in the following way. Consider the sublattice
${\mathcal{P}}_\beta$
in the following way. Consider the sublattice
and its incidence matrix
![]() $J'_{\!\!\beta}$
. Then
$J'_{\!\!\beta}$
. Then
![]() $\Lambda_{10}\subset \Lambda'_{\!\!\beta}\subset \Lambda_{\beta}$
and
$\Lambda_{10}\subset \Lambda'_{\!\!\beta}\subset \Lambda_{\beta}$
and
![]() $\det\!(J'_{\!\!\beta})=-2^{20}$
. Thus,
$\det\!(J'_{\!\!\beta})=-2^{20}$
. Thus,
![]() $\Lambda_{10}$
is a sublattice of
$\Lambda_{10}$
is a sublattice of
![]() $\Lambda'_{\!\!\beta}$
of index two. Though we have changed the underlying lattice for
$\Lambda'_{\!\!\beta}$
of index two. Though we have changed the underlying lattice for
![]() ${\mathcal{P}}_\beta$
, we have not changed its geometry. Furthermore, in this basis,
${\mathcal{P}}_\beta$
, we have not changed its geometry. Furthermore, in this basis,
![]() ${\mathcal{P}}_\beta={\mathcal E}_{-2}^*$
. Thus,
${\mathcal{P}}_\beta={\mathcal E}_{-2}^*$
. Thus,
![]() ${\mathcal K}_{{\mathcal{P}}_{10}}\supset {\mathcal K}_{{\mathcal{P}}_\beta}$
, so the residual set for the packing
${\mathcal K}_{{\mathcal{P}}_{10}}\supset {\mathcal K}_{{\mathcal{P}}_\beta}$
, so the residual set for the packing
![]() ${\mathcal{P}}_\beta$
is a subset of the residual set for
${\mathcal{P}}_\beta$
is a subset of the residual set for
![]() ${\mathcal{P}}_{10}$
. Thus,
${\mathcal{P}}_{10}$
. Thus,
![]() ${\mathcal{P}}_\beta$
is a more efficient packing than
${\mathcal{P}}_\beta$
is a more efficient packing than
![]() ${\mathcal{P}}_{10}$
.
${\mathcal{P}}_{10}$
.
Remark 4. There exists a K3 surface X with
![]() $\mathop{\textrm{Pic}}\nolimits(X)=\Lambda'_{\beta}$
, so we can think of
$\mathop{\textrm{Pic}}\nolimits(X)=\Lambda'_{\beta}$
, so we can think of
![]() ${\mathcal{P}}_\beta$
as the ample cone for some K3 surface.
${\mathcal{P}}_\beta$
as the ample cone for some K3 surface.
4. The Apollonian property and Maxwell’s paper
In this section, we identify the relevant property of the Coxeter graph (1.1) that implies the existence of a maximal cluster of mutually tangent spheres and use this to identify the Apollonian sphere packings in Maxwell’s paper [Reference Maxwell16].
Theorem 4.1. Let
![]() ${\mathcal{P}}={\Gamma}(S)$
be a crystallographic sphere packing. Suppose there exists an element
${\mathcal{P}}={\Gamma}(S)$
be a crystallographic sphere packing. Suppose there exists an element
![]() $\nu$
of
$\nu$
of
![]() ${\mathcal{P}}$
and a reflective subgroup of
${\mathcal{P}}$
and a reflective subgroup of
![]() ${\Gamma}$
that generates a Coxeter graph of the form
${\Gamma}$
that generates a Coxeter graph of the form
![]() $T_{k}$
with
$T_{k}$
with
![]() $\nu$
attached to one of the ends by a bold edge. Then
$\nu$
attached to one of the ends by a bold edge. Then
![]() ${\mathcal{P}}$
includes a cluster of
${\mathcal{P}}$
includes a cluster of
![]() $k+1$
mutually tangent spheres.
$k+1$
mutually tangent spheres.
The notation
![]() $T_k$
represents a tree with one branch of length k, which is consistent with our notation used earlier. When used to represent a Coxeter graph or lattice, it is sometimes denoted
$T_k$
represents a tree with one branch of length k, which is consistent with our notation used earlier. When used to represent a Coxeter graph or lattice, it is sometimes denoted
![]() $A_k$
, which is Vinberg’s notation (see [Reference Vinberg24, Table I]).
$A_k$
, which is Vinberg’s notation (see [Reference Vinberg24, Table I]).
Proof. Let us label the graph
![]() $T_k$
and
$T_k$
and
![]() $\nu$
as follows:
$\nu$
as follows:
and set
![]() $\alpha_i\cdot \alpha_i=\nu\cdot \nu=-2$
. Let
$\alpha_i\cdot \alpha_i=\nu\cdot \nu=-2$
. Let
![]() $s_1=\nu$
and
$s_1=\nu$
and
![]() $s_{i+1}=R_{\alpha_i}(s_i)$
for
$s_{i+1}=R_{\alpha_i}(s_i)$
for
![]() $i=1, ... , k$
. Then
$i=1, ... , k$
. Then
![]() $s_i\cdot s_i=-2$
for all i. To show the set
$s_i\cdot s_i=-2$
for all i. To show the set
![]() $\{s_1,...,s_{k+1}\}$
is a cluster of
$\{s_1,...,s_{k+1}\}$
is a cluster of
![]() $k+1$
mutually tangent spheres, we need to show
$k+1$
mutually tangent spheres, we need to show
![]() $s_i\cdot s_j=2$
for
$s_i\cdot s_j=2$
for
![]() $i\neq j$
. We prove this using induction on the following statements: (a)
$i\neq j$
. We prove this using induction on the following statements: (a)
![]() $s_i=s_{i-1}+2\alpha_{i-1}$
; (b)
$s_i=s_{i-1}+2\alpha_{i-1}$
; (b)
![]() $\alpha_i\cdot s_i=2$
; (c)
$\alpha_i\cdot s_i=2$
; (c)
![]() $\alpha_j\cdot s_i=0$
for
$\alpha_j\cdot s_i=0$
for
![]() $j>i$
; and (d)
$j>i$
; and (d)
![]() $s_i\cdot s_j=2$
for
$s_i\cdot s_j=2$
for
![]() $i<j$
. We leave the details to the reader.
$i<j$
. We leave the details to the reader.
While this result may not be surprising, and may even be obvious, it nevertheless seems to have escaped any serious notice. With this result in mind, we look at Maxwell’s Table II [Reference Maxwell16] and Chen and Labbé’s Appendix [Reference Chen and Labbé7] in search of candidates for Apollonian packings. We find twelve candidates: The one in the introduction and the eleven listed in Figure 2. The hollow node indicates that removing it yields the desired subgraph. The
![]() $+$
is Maxwell’s notation to indicate that the weight at that point is real, so represents a plane. We have modified his notation a bit, using
$+$
is Maxwell’s notation to indicate that the weight at that point is real, so represents a plane. We have modified his notation a bit, using
![]() $+_\infty$
to indicate that the weight is a plane that is parallel to its associated node, while
$+_\infty$
to indicate that the weight is a plane that is parallel to its associated node, while
![]() $+$
indicates that the plane is ultraparallel to its associated node.
$+$
indicates that the plane is ultraparallel to its associated node.
Maxwell notes that the first four graphs for
![]() $N=5$
yield the same sphere packing [Reference Maxwell16, Table I], which is the Soddy sphere packing [Reference Soddy21]. The two graphs in
$N=5$
yield the same sphere packing [Reference Maxwell16, Table I], which is the Soddy sphere packing [Reference Soddy21]. The two graphs in
![]() $N=6$
also give the same packing. The packings for
$N=6$
also give the same packing. The packings for
![]() $N=6$
, 7, and 8 are the subject of [Reference Baragar4], and their Coxeter graphs are given in [Reference Baragar5]. The graphs for
$N=6$
, 7, and 8 are the subject of [Reference Baragar4], and their Coxeter graphs are given in [Reference Baragar5]. The graphs for
![]() $N=9$
and
$N=9$
and
![]() $N=11$
are the subjects of the next two sections.
$N=11$
are the subjects of the next two sections.
The last graph for
![]() $N=5$
is a pleasant surprise, as it shows that there are different ways of filling in the voids of an initial configuration of five mutually tangent spheres in
$N=5$
is a pleasant surprise, as it shows that there are different ways of filling in the voids of an initial configuration of five mutually tangent spheres in
![]() ${\mathbb{R}}^3$
, yet still get a sphere packing where every sphere is a member of a cluster of five mutually tangent spheres. The packing is Apollonian, but not lattice like. Unlike the Soddy packing, there is no perspective where all the spheres have integer curvature.
${\mathbb{R}}^3$
, yet still get a sphere packing where every sphere is a member of a cluster of five mutually tangent spheres. The packing is Apollonian, but not lattice like. Unlike the Soddy packing, there is no perspective where all the spheres have integer curvature.

Figure 2. The eleven other graphs in [Reference Chen and Labbé7] that satisfy the conditions of Theorem 4.1 for
![]() $k=N-1$
.
$k=N-1$
.
Let us label the Coxeter graph as follows:

so
 \begin{equation*}J_\alpha=\left[\begin{array}{lcccccccccccc}-2&1&0&0&0 \\ 1&-2&1&0&1 \\ 0&1&-2&1&0 \\ 0&0&1&-2&\sqrt 3 \\ 0&1&0&\sqrt 3&-2\end{array}\right].\end{equation*}
\begin{equation*}J_\alpha=\left[\begin{array}{lcccccccccccc}-2&1&0&0&0 \\ 1&-2&1&0&1 \\ 0&1&-2&1&0 \\ 0&0&1&-2&\sqrt 3 \\ 0&1&0&\sqrt 3&-2\end{array}\right].\end{equation*}
We let
![]() $s_1=w_1$
,
$s_1=w_1$
,
![]() $s_2=R_{\alpha_1}\!(s_1)$
, …,
$s_2=R_{\alpha_1}\!(s_1)$
, …,
![]() $s_5=R_{\alpha_4}\!(s_4)$
. We note
$s_5=R_{\alpha_4}\!(s_4)$
. We note
![]() $w_2=s_1+s_2$
and let it be the point at infinity, giving us a strip version of the packing. The cross section on the plane
$w_2=s_1+s_2$
and let it be the point at infinity, giving us a strip version of the packing. The cross section on the plane
![]() $\alpha_1$
is shown in Figure 3, and the cross section on the plane
$\alpha_1$
is shown in Figure 3, and the cross section on the plane
![]() $\alpha_4$
is shown in Figure 4.
$\alpha_4$
is shown in Figure 4.
Remark 5. If we invert the strip packing in the sphere
![]() $w_3$
and scale to get a sphere of curvature
$w_3$
and scale to get a sphere of curvature
![]() $-1$
, then the planes
$-1$
, then the planes
![]() $s_1$
and
$s_1$
and
![]() $s_2$
become spheres with curvature 2 tangent at the center of the sphere
$s_2$
become spheres with curvature 2 tangent at the center of the sphere
![]() $w_3$
. The six spheres surrounding
$w_3$
. The six spheres surrounding
![]() $w_3$
become a hexlet of spheres with curvature 3, just like those in the sphere packing described by Soddy [Reference Soddy21]. How the space between these spheres is filled in, though, is different from how Soddy does it. The spheres
$w_3$
become a hexlet of spheres with curvature 3, just like those in the sphere packing described by Soddy [Reference Soddy21]. How the space between these spheres is filled in, though, is different from how Soddy does it. The spheres
![]() $s_3$
and
$s_3$
and
![]() $s_4$
, in this perspective, have curvature
$s_4$
, in this perspective, have curvature
![]() $7+4\sqrt 3$
.
$7+4\sqrt 3$
.

Figure 3. The horizontal cross section of the strip version of the non-Soddy Apollonian sphere packing with Coxeter graph (4.1). The dotted lines represent the symmetries. Note that the dotted circle represents inversion in a sphere that intersects this plane at an angle of
![]() $\pi/3$
. This picture and the one in Figure 4 were generated using McMullen’s Kleinian groups program [Reference McMullen17].
$\pi/3$
. This picture and the one in Figure 4 were generated using McMullen’s Kleinian groups program [Reference McMullen17].

Figure 4. The cross section on the plane
![]() $H_{\alpha_4}$
of the strip version of the non-Soddy Apollonian sphere packing. As a circle packing, this cross section is weakly Apollonian.
$H_{\alpha_4}$
of the strip version of the non-Soddy Apollonian sphere packing. As a circle packing, this cross section is weakly Apollonian.
5. A cross section in
 ${\mathbb{R}}^7$
${\mathbb{R}}^7$
Given a sphere packing in dimension n, a codimension one cross section is a sphere packing in dimension
![]() $n-1$
. If the sphere packing contains a cluster of
$n-1$
. If the sphere packing contains a cluster of
![]() $n+2$
mutually tangent spheres (i.e. has the Apollonian property), then by choosing a cross section perpendicular to
$n+2$
mutually tangent spheres (i.e. has the Apollonian property), then by choosing a cross section perpendicular to
![]() $n+1$
of these spheres, we get a sphere packing in one lower dimension that has (at least) the weak Apollonian property.
$n+1$
of these spheres, we get a sphere packing in one lower dimension that has (at least) the weak Apollonian property.
Theorem 5.1. A cross section perpendicular to nine spheres in a cluster of ten mutually tangent spheres in
![]() ${\mathcal{P}}_\beta$
yields the sphere packing in
${\mathcal{P}}_\beta$
yields the sphere packing in
![]() ${\mathbb{R}}^7$
with Coxeter graph labeled
${\mathbb{R}}^7$
with Coxeter graph labeled
![]() $N=9$
in Figure 2. This packing is of general lattice type.
$N=9$
in Figure 2. This packing is of general lattice type.
Proof. Let H be the plane perpendicular to
![]() $s_i$
for
$s_i$
for
![]() $i=0$
, …, 8. Then H has normal vector
$i=0$
, …, 8. Then H has normal vector
Note that
![]() $h\cdot \beta_i=0$
for
$h\cdot \beta_i=0$
for
![]() $i=2$
,…,9. Knowing the expected Coxeter graph, we solve for
$i=2$
,…,9. Knowing the expected Coxeter graph, we solve for
![]() $\beta'_{\!\!1}$
so that we get:
$\beta'_{\!\!1}$
so that we get:

Thus we want
![]() $\beta'_{\!\!1}\cdot \beta_i=0$
for
$\beta'_{\!\!1}\cdot \beta_i=0$
for
![]() $i\neq 0$
, 2, or 7;
$i\neq 0$
, 2, or 7;
![]() $\beta'_{\!\!1}\cdot h=0$
;
$\beta'_{\!\!1}\cdot h=0$
;
![]() $\beta'_{\!\!1}\cdot \beta_2=\beta'_{\!\!1}\cdot \beta_7=1$
; and
$\beta'_{\!\!1}\cdot \beta_2=\beta'_{\!\!1}\cdot \beta_7=1$
; and
![]() $\beta'_{\!\!1}\cdot \beta'_{\!\!1}=-2$
. We get
$\beta'_{\!\!1}\cdot \beta'_{\!\!1}=-2$
. We get
![]() $\beta'_{\!\!1}=[2,1,1,2,3,2,1,0,0,0]$
. Using descent, we show
$\beta'_{\!\!1}=[2,1,1,2,3,2,1,0,0,0]$
. Using descent, we show
![]() $R_{\beta'_{\!\!1}}\in {\Gamma}$
. The set
$R_{\beta'_{\!\!1}}\in {\Gamma}$
. The set
![]() $\{\beta'_{\!\!1},\beta_2,...,\beta_9\}$
forms a basis of the subspace H. Let
$\{\beta'_{\!\!1},\beta_2,...,\beta_9\}$
forms a basis of the subspace H. Let
![]() $J_7$
be the incidence matrix for this basis of H, and let
$J_7$
be the incidence matrix for this basis of H, and let
![]() $w_i'$
be the weights. Since
$w_i'$
be the weights. Since
![]() $s_0\cdot h=0$
, we get
$s_0\cdot h=0$
, we get
![]() $s_0=2w'_{\!\!9}$
(so
$s_0=2w'_{\!\!9}$
(so
![]() $w_9=w'_{\!\!9}$
). Let
$w_9=w'_{\!\!9}$
). Let
![]() ${\Gamma}_7=\langle R_{\beta'_{\!\!1}},R_{\beta_2},...,R_{\beta_9}\rangle$
. Then the spheres in
${\Gamma}_7=\langle R_{\beta'_{\!\!1}},R_{\beta_2},...,R_{\beta_9}\rangle$
. Then the spheres in
![]() ${\Gamma}_7(s_0)$
all intersect H perpendicularly. Most spheres in
${\Gamma}_7(s_0)$
all intersect H perpendicularly. Most spheres in
![]() ${\mathcal{P}}_\beta$
miss H and some are tangent to H, but there are some that intersect H at an angle that is not right. In particular, let
${\mathcal{P}}_\beta$
miss H and some are tangent to H, but there are some that intersect H at an angle that is not right. In particular, let
![]() $s_{10}=R_{\beta_0}\!(s_6)$
and
$s_{10}=R_{\beta_0}\!(s_6)$
and
![]() $s_{11}=R_{\beta_0}\!(s_{9})$
. Then,
$s_{11}=R_{\beta_0}\!(s_{9})$
. Then,
![]() $s_{10}\cdot h=4$
and
$s_{10}\cdot h=4$
and
![]() $s_{11}\cdot h=-4$
, while
$s_{11}\cdot h=-4$
, while
![]() $h\cdot h=-14$
, so these two spheres intersect H but not perpendicularly nor tangentially. The difference in signs (the
$h\cdot h=-14$
, so these two spheres intersect H but not perpendicularly nor tangentially. The difference in signs (the
![]() $\pm 4$
) indicates that the centers of the spheres are on opposite sides of H. The intersection of
$\pm 4$
) indicates that the centers of the spheres are on opposite sides of H. The intersection of
![]() $s_{10}$
with H is found by projecting the vector
$s_{10}$
with H is found by projecting the vector
![]() $s_{10}$
onto H to get
$s_{10}$
onto H to get
We note that
![]() $n\cdot h=0$
,
$n\cdot h=0$
,
![]() $n\cdot \beta'_{\!\!1}=0$
, and
$n\cdot \beta'_{\!\!1}=0$
, and
![]() $n\cdot \beta_i=0$
for
$n\cdot \beta_i=0$
for
![]() $i\neq 0$
, 1, or 4, so n is a scalar multiple of
$i\neq 0$
, 1, or 4, so n is a scalar multiple of
![]() $w'_{\!\!3}$
. Similarly, the projection of
$w'_{\!\!3}$
. Similarly, the projection of
![]() $s_{11}$
onto H is a scalar multiple of
$s_{11}$
onto H is a scalar multiple of
![]() $w'_{\!\!4}$
. Thus, the intersection of
$w'_{\!\!4}$
. Thus, the intersection of
![]() ${\mathcal{P}}_\beta$
with H contains the packing
${\mathcal{P}}_\beta$
with H contains the packing
To show that they are equal, we show that
![]() ${\mathcal{P}}_7$
is maximal, so there is no room for the intersection to include anything more than
${\mathcal{P}}_7$
is maximal, so there is no room for the intersection to include anything more than
![]() ${\mathcal{P}}_7$
. We use Maxwell’s technique again (see the proof of Theorem 3.1). That is, we show that the nonreal weights
${\mathcal{P}}_7$
. We use Maxwell’s technique again (see the proof of Theorem 3.1). That is, we show that the nonreal weights
![]() $w_i'$
are in the convex closure of the
$w_i'$
are in the convex closure of the
![]() ${\Gamma}_7$
-orbit of the real weights
${\Gamma}_7$
-orbit of the real weights
![]() $w'_{\!\!9}$
,
$w'_{\!\!9}$
,
![]() $w_3$
, and
$w_3$
, and
![]() $w'_{\!\!4}$
. We note that
$w'_{\!\!4}$
. We note that
 \begin{align*}w'_{\!\!8}&=w_8=(s_0+s_1)/2 \\w'_{\!\!7}&=w_7=(s_0+s_1+s_2)/2 \\w'_{\!\!1}&=(s_0+s_1+s_2+s_3+s_4+s_5+s_6+s_7+s_8)/14.\end{align*}
\begin{align*}w'_{\!\!8}&=w_8=(s_0+s_1)/2 \\w'_{\!\!7}&=w_7=(s_0+s_1+s_2)/2 \\w'_{\!\!1}&=(s_0+s_1+s_2+s_3+s_4+s_5+s_6+s_7+s_8)/14.\end{align*}
By symmetry, we get
![]() $w'_{\!\!6}$
by going the other way around the loop in the Coxeter graph. That is,
$w'_{\!\!6}$
by going the other way around the loop in the Coxeter graph. That is,
where
![]() $s'_{\!\!4}=R_{\beta'_{\!\!1}}\!(s_3)$
,
$s'_{\!\!4}=R_{\beta'_{\!\!1}}\!(s_3)$
,
![]() $s'_{\!\!5}=R_{\beta_2}\!(s'_{\!\!4})$
, …,
$s'_{\!\!5}=R_{\beta_2}\!(s'_{\!\!4})$
, …,
![]() $s'_{\!\!8}=R_{\beta_5}\!(s'_{\!\!7})$
. Finally, to get
$s'_{\!\!8}=R_{\beta_5}\!(s'_{\!\!7})$
. Finally, to get
![]() $w'_{\!\!2}$
, we first note that
$w'_{\!\!2}$
, we first note that
The map
![]() $R_{\mathbf n}$
is a reflection for
$R_{\mathbf n}$
is a reflection for
![]() $\mathbf n\cdot \mathbf n<0$
. The map
$\mathbf n\cdot \mathbf n<0$
. The map
![]() $-R_{\mathbf n}$
for
$-R_{\mathbf n}$
for
![]() $\mathbf n\cdot \mathbf n>0$
is a Cartan involution, which is the
$\mathbf n\cdot \mathbf n>0$
is a Cartan involution, which is the
![]() $-1$
map on
$-1$
map on
![]() ${\mathcal H}$
through the point
${\mathcal H}$
through the point
![]() $\mathbf n\in {\mathcal H}$
. There is no reason to expect
$\mathbf n\in {\mathcal H}$
. There is no reason to expect
![]() $-R_{w'_{\!\!2}}(w_9)$
to be in
$-R_{w'_{\!\!2}}(w_9)$
to be in
![]() ${\Gamma}_7(w_9)$
(similar quantities are not), but we prove it is by using our method of descent. By symmetry,
${\Gamma}_7(w_9)$
(similar quantities are not), but we prove it is by using our method of descent. By symmetry,
![]() $w'_{\!\!5}$
is also in the convex closure of
$w'_{\!\!5}$
is also in the convex closure of
![]() ${\Gamma}_7(w_9)$
.
${\Gamma}_7(w_9)$
.
The spheres in
![]() ${\Gamma}_7(s_0)$
in the perspective with
${\Gamma}_7(s_0)$
in the perspective with
![]() $w_8$
the point at infinity (or any other lattice point for the point at infinity) all have curvature an integer multiple of
$w_8$
the point at infinity (or any other lattice point for the point at infinity) all have curvature an integer multiple of
![]() $\sqrt 2$
, while those in
$\sqrt 2$
, while those in
![]() ${\Gamma}_7(w'_{\!\!3})$
and
${\Gamma}_7(w'_{\!\!3})$
and
![]() ${\Gamma}_7(w'_{\!\!4})$
all have curvature an integer multiple of
${\Gamma}_7(w'_{\!\!4})$
all have curvature an integer multiple of
![]() $\sqrt{42}/3$
. Thus, the packing is not of lattice type, though it is of general lattice type, since all spheres have integer coordinates in the basis
$\sqrt{42}/3$
. Thus, the packing is not of lattice type, though it is of general lattice type, since all spheres have integer coordinates in the basis
![]() $\{\beta'_{\!\!1},\beta_2,...,\beta_9\}$
.
$\{\beta'_{\!\!1},\beta_2,...,\beta_9\}$
.
Remark 6. Every sphere in
![]() ${\Gamma}_7(s_0)$
is a member of a cluster of 9 mutually tangent spheres. The same cannot be said of the spheres in the orbits of
${\Gamma}_7(s_0)$
is a member of a cluster of 9 mutually tangent spheres. The same cannot be said of the spheres in the orbits of
![]() $w'_{\!\!3}$
and
$w'_{\!\!3}$
and
![]() $w'_{\!\!4}$
.
$w'_{\!\!4}$
.
Remark 7. A similar cross section of the Apollonian packings in [Reference Baragar4] and [Reference Baragar5] intersect all spheres perpendicularly, so give the related Apollonian packing in one dimension lower. A similar cross section of the example in Section 4 gives the packing in Figure 4, which is a weakly Apollonian packing.
Remark 8. The spheres
![]() $s_{10}$
and
$s_{10}$
and
![]() $s_{11}$
are tangent at the point
$s_{11}$
are tangent at the point
![]() $P_1=s_{10}+s_{11}$
, which lies in the subspace H and is on
$P_1=s_{10}+s_{11}$
, which lies in the subspace H and is on
![]() $\partial {\mathcal H}$
. Let
$\partial {\mathcal H}$
. Let
![]() $P_2=R_{\beta_3}\!(P_1)$
.
$P_2=R_{\beta_3}\!(P_1)$
.
For two points A and B on
![]() $\partial {\mathcal H}$
, define the Bertini involution to be
$\partial {\mathcal H}$
, define the Bertini involution to be
This is the map that is
![]() $-1$
on
$-1$
on
![]() $\partial {\mathcal H}_A$
through the point B.
$\partial {\mathcal H}_A$
through the point B.
The Bertini involutions
![]() $\phi_{P_1,w_8}$
and
$\phi_{P_1,w_8}$
and
![]() $\phi_{P_1,P_2}$
both preserve the lattice
$\phi_{P_1,P_2}$
both preserve the lattice
![]() $\beta'_{\!\!1}{\mathbb{Z}}\oplus \beta_2{\mathbb{Z}}\oplus \cdots \oplus \beta_9{\mathbb{Z}}$
. Note that
$\beta'_{\!\!1}{\mathbb{Z}}\oplus \beta_2{\mathbb{Z}}\oplus \cdots \oplus \beta_9{\mathbb{Z}}$
. Note that
![]() $\phi_{P_1,P_2}(w'_{\!\!4})=-w'_{\!\!4}$
, so
$\phi_{P_1,P_2}(w'_{\!\!4})=-w'_{\!\!4}$
, so
![]() $\phi_{P_1,P_2}$
sends everything on one side of the plane
$\phi_{P_1,P_2}$
sends everything on one side of the plane
![]() $H_{w'_{\!\!4}}$
to the other side. The map
$H_{w'_{\!\!4}}$
to the other side. The map
![]() $\phi_{P_1,w_8}$
sends
$\phi_{P_1,w_8}$
sends
![]() $w'_{\!\!3}$
to
$w'_{\!\!3}$
to
![]() $w'_{\!\!4}$
. Let
$w'_{\!\!4}$
. Let
Since
![]() ${\Gamma}_7(s_0)$
does not intersect
${\Gamma}_7(s_0)$
does not intersect
![]() $H_{w'_{\!\!3}}$
or
$H_{w'_{\!\!3}}$
or
![]() $H_{w'_{\!\!4}}$
,
$H_{w'_{\!\!4}}$
,
![]() ${\Gamma'}_{\!\!7}(s_0)$
is a sphere packing. Because
${\Gamma'}_{\!\!7}(s_0)$
is a sphere packing. Because
![]() ${\mathcal{P}}_7$
is maximal,
${\mathcal{P}}_7$
is maximal,
![]() ${\Gamma'}_{\!\!7}(s_0)$
is also maximal. It is lattice like and Apollonian. Since
${\Gamma'}_{\!\!7}(s_0)$
is also maximal. It is lattice like and Apollonian. Since
![]() ${\Gamma}_7\leq {\Gamma'}_{\!\!7}$
, the limit set of
${\Gamma}_7\leq {\Gamma'}_{\!\!7}$
, the limit set of
![]() ${\Gamma}_7$
is a subset of the limit set of
${\Gamma}_7$
is a subset of the limit set of
![]() ${\Gamma'}_{\!\!7}$
. Since these are the residual sets of the respective packings, the packing
${\Gamma'}_{\!\!7}$
. Since these are the residual sets of the respective packings, the packing
![]() ${\mathcal{P}}_7$
, which is only weakly Apollonian, is more efficient than the Apollonian packing
${\mathcal{P}}_7$
, which is only weakly Apollonian, is more efficient than the Apollonian packing
![]() ${\Gamma'}_{\!\!7}(s_0)$
.
${\Gamma'}_{\!\!7}(s_0)$
.
The packing
![]() ${\Gamma'}_{\!\!7}(s_0)$
is the packing described in [Reference Baragar5]. The cone
${\Gamma'}_{\!\!7}(s_0)$
is the packing described in [Reference Baragar5]. The cone
![]() ${\mathcal K}_{{\Gamma'}_{\!\!7}(s_0)}$
is the ample cone for a class of K3 surfaces. The packing
${\mathcal K}_{{\Gamma'}_{\!\!7}(s_0)}$
is the ample cone for a class of K3 surfaces. The packing
![]() ${\mathcal{P}}_7$
, though, cannot be the ample cone of any K3 surface.
${\mathcal{P}}_7$
, though, cannot be the ample cone of any K3 surface.
6. A sphere packing in
 ${\mathbb{R}}^9$
${\mathbb{R}}^9$
The sphere packing generated by the Coxeter graph with
![]() $N=11$
in Figure 2 can be described as follows: Let H be an 8-dimensional subspace of
$N=11$
in Figure 2 can be described as follows: Let H be an 8-dimensional subspace of
![]() ${\mathbb{R}}^9$
(with normal vector h) and let us place spheres of radius
${\mathbb{R}}^9$
(with normal vector h) and let us place spheres of radius
![]() $1/\sqrt 2$
at each vertex of a copy of the
$1/\sqrt 2$
at each vertex of a copy of the
![]() $E_8$
lattice imbedded in H. Let us place two hyperplanes parallel to H a distance of
$E_8$
lattice imbedded in H. Let us place two hyperplanes parallel to H a distance of
![]() $1/\sqrt 2$
on either side, so that they are tangent to all the spheres. Let us distinguish the sphere
$1/\sqrt 2$
on either side, so that they are tangent to all the spheres. Let us distinguish the sphere
![]() $s_0$
centered at the origin of the
$s_0$
centered at the origin of the
![]() $E_8$
lattice and let its points of tangencies with the hyperplanes be A and B. Let
$E_8$
lattice and let its points of tangencies with the hyperplanes be A and B. Let
![]() $\sigma$
be inversion in the sphere centered at A and through B. The packing is the image of these spheres under the group generated by
$\sigma$
be inversion in the sphere centered at A and through B. The packing is the image of these spheres under the group generated by
![]() $\sigma$
, the symmetries of the
$\sigma$
, the symmetries of the
![]() $E_8$
lattice, and reflection
$E_8$
lattice, and reflection
![]() $R_h$
in H.
$R_h$
in H.
To see this, recall that the spheres centered on the vertices of the
![]() $E_8$
lattice are generated by the image of
$E_8$
lattice are generated by the image of
![]() $s_0$
under the action of the Weyl group
$s_0$
under the action of the Weyl group
![]() $W_{236}$
, which is
$W_{236}$
, which is
![]() $\langle R_{\beta_0},R_{\beta_2},...,R_{\beta_9}\rangle$
for the
$\langle R_{\beta_0},R_{\beta_2},...,R_{\beta_9}\rangle$
for the
![]() $T_{236}$
subgraph of Graph (1.1). In this context, these reflections act on
$T_{236}$
subgraph of Graph (1.1). In this context, these reflections act on
![]() ${\mathbb{R}}^9$
. The hyperplane
${\mathbb{R}}^9$
. The hyperplane
![]() $H_{\beta_i}$
(the plane in
$H_{\beta_i}$
(the plane in
![]() ${\mathbb{R}}^9$
perpendicular to
${\mathbb{R}}^9$
perpendicular to
![]() $\beta_i\in H\subset {\mathbb{R}}^9$
) is perpendicular to
$\beta_i\in H\subset {\mathbb{R}}^9$
) is perpendicular to
![]() $s_0$
for
$s_0$
for
![]() $i\neq 9$
, and hence also perpendicular to
$i\neq 9$
, and hence also perpendicular to
![]() $\sigma$
. (We ignore
$\sigma$
. (We ignore
![]() $i=1$
in this discussion.) Note that
$i=1$
in this discussion.) Note that
![]() $H_{\beta_9}$
is tangent to
$H_{\beta_9}$
is tangent to
![]() $s_0$
. Let
$s_0$
. Let
![]() $s_1=R_{\beta_9}\!(s_0)$
, giving us the cross section shown in Figure 5. We note that
$s_1=R_{\beta_9}\!(s_0)$
, giving us the cross section shown in Figure 5. We note that
![]() $\sigma$
and
$\sigma$
and
![]() $\beta_9$
are at an angle of
$\beta_9$
are at an angle of
![]() $2\pi/3$
. We note that h is perpendicular to
$2\pi/3$
. We note that h is perpendicular to
![]() $\beta_i$
for all i, and h and
$\beta_i$
for all i, and h and
![]() $\sigma$
intersect at an angle of
$\sigma$
intersect at an angle of
![]() $2\pi/3$
. Finally, let
$2\pi/3$
. Finally, let
![]() $\nu$
represent the plane tangent to
$\nu$
represent the plane tangent to
![]() $s_0$
at A. Then
$s_0$
at A. Then
![]() $\nu$
is parallel to h, perpendicular to
$\nu$
is parallel to h, perpendicular to
![]() $\sigma$
, and perpendicular to
$\sigma$
, and perpendicular to
![]() $\beta_i$
for all i. This gives us the Coxeter graph
$\beta_i$
for all i. This gives us the Coxeter graph

as desired, where
![]() $\nu$
is the weight at the node h. Maxwell verifies that this packing is maximal (see the discussion after Theorem 3.3 in [Reference Maxwell16]).
$\nu$
is the weight at the node h. Maxwell verifies that this packing is maximal (see the discussion after Theorem 3.3 in [Reference Maxwell16]).

Figure 5. A cross section perpendicular to H,
![]() $s_0$
, and
$s_0$
, and
![]() $s_1$
.
$s_1$
.
Remark 9. Maxwell also presents the packing with Coxeter graph

which generates the same packing. Maxwell identifies an invariant of packings of lattice type and notes that these two packings have the same invariant, but presumably could not show equivalence.
Acknowledgments
The author is grateful to zbMath for the fortuitous request that he review Allcock’s paper and to Daniel Allcock who was kind and patient enough to explain details in that paper. The author is also grateful to David Boyd for the many conversations through the years and to Alex Kontorovich and Daniel Lautzenheiser for some useful conversations. The author is very grateful to the anonymous referee whose careful reading of the original draft led to this much improved version. This material is based upon work supported by the National Science Foundation under Grant No. DMS-1439786 and the Alfred P. Sloan Foundation award G-2019-11406, while the author was in residence at the Institute for Computational and Experimental Research in Mathematics in Providence, RI, during the illustrating Mathematics program. Finally, the author wishes to thank his home institution, UNLV, for its sabbatical assistance during the Fall of 2019.