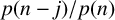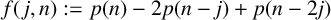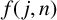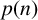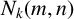THE SECOND SHIFTED DIFFERENCE OF PARTITIONS AND ITS APPLICATIONS

Abstract

A number of recent papers have estimated ratios of the partition function $p(n-j)/p(n)$ , which appear in many applications. Here, we prove an easy-to-use effective bound on these ratios. Using this, we then study the second shifted difference of partitions, $f(\,j,n) := p(n) -2p(n-j) +p(n-2j)$ , and give another easy-to-use estimate of $f(\,j,n)$ . As applications of these, we prove a shifted convexity property of $p(n)$ , as well as giving new estimates of the k-rank partition function $N_k(m,n)$ and non-k-ary partitions along with their differences.

1 Introduction and statement of results

The study of the values of the partition function $p(n)$ , which counts the number of partitions of a positive integer n, has a long history. A partition $\lambda $ of n is a nonincreasing list $(\lambda _1, \lambda _2, \ldots ,\lambda _s)$ such that $\sum _{j=1}^{s} \lambda _j = n$ . In their famed collaboration a century ago, Hardy and Ramanujan [8] proved the asymptotic formula

(1.1) $$ \begin{align} p(n) \sim \frac{1}{4\sqrt{3}n} e^{\pi \sqrt{{2n}/{3}}} \quad\mbox{as}\ n\to \infty. \end{align} $$

Their proof gave birth to the Circle Method, which is an extremely important tool used throughout analytic number theory today. Following their discovery, Rademacher [18] improved Hardy and Ramanujan’s application of the Circle Method to prove an exact formula for $p(n)$ . Over the past 100 years, there have been a plethora of investigations into estimates and asymptotics for partitions and their extensions in the literature.

Here, we will study differences of partition values in detail. To this end, let $\Delta $ be the backward difference operator defined on sequences $f(n)$ by

$$ \begin{align*} \Delta(f(n)) := f(n) - f(n-1), \end{align*} $$

and its recursive counterpart

$$ \begin{align*} \Delta^k (f(n)) := \Delta ( \Delta^{k-1} (f(n)) ). \end{align*} $$

One of the simplest properties of $p(n)$ is that it is convex for $n \geq 2$ (see, for example, [7]), that is,

$$ \begin{align*} p(n) + p(n-2) \geq 2p(n-1). \end{align*} $$

Recast using the operator $\Delta $ , this is the same as proving that

$$ \begin{align*} \Delta^2(p(n)) \geq 0 \end{align*} $$

for all $n \geq 2$ . Gupta [7] investigated higher powers of $\Delta $ applied to p, proving that there exist constants $n_r$ for all $r>0$ such that $\Delta ^r(p(n)) \geq 0$ for all $n \geq n_r$ . Odlyzko [17] considered a further conjecture of Gupta, proving that for each r, there is a fixed $n_0(r)$ such that $(-1)^n\Delta ^r(p(n))> 0$ for all $n < n_0(r)$ and $\Delta ^r(p(n)) \geq 0$ for all $n \geq n_0(r)$ , as well as giving a beautiful philosophical discussion of why this phenomenon arises. Similar differences of objects related to $p(n)$ and its extensions have been studied by many other authors (see [3, 4, 10, 11, 16] among many others).

We initiate the investigation of what we call j-shifted differences, defined for $1\leq j < n$ on sequences $f(n)$ by

$$ \begin{align*} \Delta_j (f(n)) := f(n) - f(n-j). \end{align*} $$

In analogy to Gupta, it is clear using (1.1) that there exist constants $n_{j}$ such that for all $n \geq n_j$ , one has that $\Delta _j^2(p(n))\geq 0$ . Let $N := n-{1}/{24}$ . Our methods rely on a careful study of the value of the function

$$ \begin{align*} f(\,j,n) := \Delta_j^2(p(n)) = p(n) - 2p(n-j) + p(n-2j), \end{align*} $$

and in Theorem 2.2, we prove a precise estimation of $f(\,j,n)$ with $j \leq {\!\sqrt {N}}/{4}$ , in particular providing a strict error term allowing us to closely control the precision of the formula by taking N large enough. In doing so, we provide an easy-to-use estimate for the ratio of partition numbers. Throughout, we use the notation $f(x)= O_{\leq }(g(x))$ to mean that $\lvert f(x) \rvert \leq g(x)$ for x in the appropriate domain.

Theorem 1.1. Let $n \geq 14$ and $j <{\!\sqrt {N}}/{2}$ . Then

$$ \begin{align*} \frac{p(n-j)}{p(n)} &= e^{{\pi j}/{\sqrt{6N}}} \bigg(1+\frac jN-\frac{\pi j^2}{4\sqrt{6}N}-\frac{\sqrt{3}}{\sqrt{2\pi}\sqrt{N}} + O_{\leq}\bigg( \frac{2.71}{N}\bigg) \bigg) \\ &\quad \times \bigg( 1+ \frac{\sqrt{3}}{\sqrt{2N}\pi} + O_{\leq} \bigg( \frac{1350}{N} \bigg) \bigg). \end{align*} $$

Theorems of a similar flavour to Theorem 1.1 are abundant in the literature. Lehmer [14, 13] used Rademacher’s exact formula for $p(n)$ [18] to provide bounds on the value of $p(n)$ that have seen many applications. More recently, estimates for the ratio of partition values have played a prominent role in proving that the associated Jensen polynomial is eventually hyperbolic [6, 12], a problem intricately linked with variants of the Riemann hypothesis.

Theorem 1.1 thus applies to many interesting situations. In the remainder of the introduction, we will highlight a few of particular interest. Our first main result using Theorem 2.2 gives an explicit formula for $n_j$ for ranges of j.

Theorem 1.2. Let $n \geq 2$ and $j \leq {\!\sqrt {N}}/{4}$ . Then $\Delta _j^2(p(n)) \geq 0$ . Equivalently, $p(n)$ satisfies the extended convexity result $p(n) + p(n-2j) \geq 2p(n-j)$ .

Remark 1.3. The methods here should extend to finding formulae for $n_{r,j}$ such that for all $n \geq n_{r,j}$ , one has $\Delta _j^r(p(n)) \geq 0$ ; however, this would quickly become very lengthy and so we do not pursue it here. The referee has kindly pointed out more elementary methods for proving Theorem 1.2 which we elucidate at the end of the paper.

Our results also apply outside of proving new properties of the partition function itself. We consider the k-rank function $N_k(m,n)$ which counts the number of partitions of n into at least $(k-1)$ successive Durfee squares with k-rank equal to m [5]. When $k =1$ , we recover the number of partitions of n whose Andrews–Garvan crank equals m, and when $k=2$ , we recover Dyson’s partition rank function. Then for $m> {n}/{2}$ (see, for example, [15, page 6]),

$$ \begin{align*} &N_k(m,n) = p(n-k-m+1) - p(n-k-m), \\ &\ N_k(m,n) - N_k(m+1,n) = f(1,n-k-m). \end{align*} $$

We give precise formulae both for $N_k(m,n)$ and for the differences of k-ranks in certain ranges of m in the following theorems, improving on [15, Theorem 1.4] in this range. The proof follows from a direct application of Theorem 1.1.

Theorem 1.4. Let $m> {n}/{2}$ and $\ell := n-k-m+ {23}/{24}>16$ . Then

$$ \begin{align*} \frac{N_k(m,n)}{p(n-k-m+1)} = 1-e^{{\pi}/{\sqrt{6\ell}}} \bigg(1- \frac{\sqrt{3}}{\sqrt{2\pi \ell}} + O_{\leq}\bigg( \frac{4.04}{\ell}\bigg) \bigg) \bigg( 1+ \frac{\sqrt{3}}{\sqrt{2\ell}\pi} + O_{\leq} \bigg( \frac{1350}{\ell} \bigg) \bigg). \end{align*} $$

We then turn to obtaining a precise estimate for the differences of k-ranks, with the proof following from a direct application of Theorem 2.2.

Theorem 1.5. Let $m> {n}/{2}$ and $\ell = n-k-m+{23}/{24}> 16$ . Then

$$ \begin{align*} \frac{ N_k(m,n) - N_k(m+1,n)}{p(n-k-m+1)} &= 1+ e^{{\sqrt{2}\pi}/{\sqrt{3\ell}}} \bigg( 1+ \bigg( \frac{\sqrt{3}}{\sqrt{2}\pi} - \frac{\sqrt{3}}{\sqrt{2 \pi}} \bigg) \frac{1}{\sqrt{\ell}} + O_{\leq} \bigg( \frac{2079}{\ell} \bigg)\bigg)\\ &\quad - e^{{\pi}/{\sqrt{6\ell}}} \bigg( 2 + \bigg( \frac{2\sqrt{3}}{\sqrt{2}\pi} - \frac{2\sqrt{3}}{\sqrt{2 \pi}} \bigg) \frac{1}{\sqrt{\ell}} + O_{\leq} \bigg( \frac{3929}{\ell} \bigg) \bigg). \end{align*} $$

As a direct implication, we recover positivity of the differences of k-ranks in these cases, as in [15, Corollary 1.5].

Our final application is to so-called non-k-ary partitions ( $k \in \mathbb {N}$ ), recently defined by Schneider [19] as partitions of n with no parts equal to k. (While [19] uses the terminology ‘k-nuclear’, Schneider has recommended the authors use the term non-k-ary based on advice of Andrews to better fit the case of $k=1$ , classically called the non-unitary partitions.) Letting $\nu _k(n)$ be the number of non-k-ary partitions of n, it is clear that $\nu _k(n) = p(n) -p(n-k)$ . By Theorem 1.1, we immediately obtain an effective estimate for the ratio $\nu _k(n)/p(n)$ , improving on [1, Theorem 1]. We also have

$$ \begin{align*} \nu_k(n) - \nu_k(n-k) = f(k,n), \end{align*} $$

and so we also obtain precise estimates for differences of non-k-ary partitions using Theorem 2.2 for $k < {\!\sqrt {N}}/{4}$ , with a direct implication being the following theorem.

Theorem 1.6. For $n \geq 2$ and $k \leq {\!\sqrt {N}}{/4}$ , we have $\nu _k(n) - \nu _k(n-k)> 0$ .

2 The proofs

In this section, we prove the main results of the paper. We begin by proving a technical estimate for the value of $p(n-j)$ , using Rademacher’s exact formula for the partition function.

Proposition 2.1. Let $N := n-{1}/{24}$ and $j \in \mathbb {N}_0$ . Then

$$ \begin{align*} &p(n-j) = \frac{e^{\pi\sqrt{{2(N-j)}/{3}}}}{4\sqrt{3}(N-j)}\\ &\qquad\times \bigg(1-\frac{\sqrt{3}}{\sqrt{2}\pi\sqrt{N-j}} + O_\le\bigg(\frac{2\pi^2(N-j)e^{-\pi\sqrt{{2(N-j)}/{3}}}}{3} + {2^3}{\pi} \sqrt{\frac{N-j}{3}} e^{-(\pi/2)\sqrt{{(N-j)}/{2}}} \bigg)\bigg). \end{align*} $$

Proof. We first recall the following result from [9, Theorem 1.1] with $\alpha = 1$ , which is simply Rademacher’s exact formula for the partition function [18],

(2.1) $$ \begin{align} p(n) = \frac{\pi}{2^{ 5/4} 3^{ 3/4} N^{ 3/4}}\sum\limits_{k=1}^\infty \frac{A_k(n)}{k}I_{ 3/2}\bigg( \frac{\pi}{k} \sqrt{\frac{2N}{3}} \bigg), \end{align} $$

where $I_{\nu }$ is the usual I-Bessel function and

$$ \begin{align*} A_k(n):= \sum\limits_{\substack{0 \le h < k \\ \gcd(h,k) = 1}}e^{\pi i s(h,k) - {2\pi i n h}/{k} } \end{align*} $$

is a Kloosterman sum with $s(h,k)$ the usual Dedekind sum. By [20, page 172],

(2.2) $$ \begin{align} I_{3/2}(x) = \frac{x^{3/2}}{2\sqrt{2\pi}} \int\nolimits_{-1}^1 (1-t^2)e^{xt}\,dt. \end{align} $$

We now bound the integrand for $-1\le t\le 0$ by $1$ and find that

(2.3) $$ \begin{align} \int\nolimits_{-1}^0 (1-t^2)e^{xt}\,dt = O_\le(1). \end{align} $$

Here, the notation $f(x)=O_\le (g(x))$ means that $|f(x)|\leq g(x)$ , that is, there is no implied constant in the big-O estimate.

Next we compute the integral for $0 \le t \le 1$ . To do so, we make the change of variables $u=1-t$ to find that

$$ \begin{align*} \int\nolimits_0^1 (1-t^2)e^{xt}\,dt &= e^x \bigg(2\int\nolimits_0^1 u^2e^{-xu}\,\frac{du}{u} - \int\nolimits_0^1 u^3e^{-xu}\,\frac{du}{u}\bigg). \end{align*} $$

Under the change of variables $w =ux$ , it is easy to show that this is equal to

$$ \begin{align*} \frac{2e^x}{x^2}\bigg(1-\frac1x-\Gamma(2,x)+\frac{\Gamma(3,x)}{2x}\bigg), \end{align*} $$

where $\Gamma (a,b)$ is the usual incomplete $\Gamma $ -function. Since $\Gamma (2,x) = (x+1)e^{-x}$ and $\Gamma (3,x) = (x^2+2x+2)e^{-x}$ , we find that

(2.4) $$ \begin{align} \int\nolimits_0^1 (1-t^2)e^{xt} \,dt = \frac{2e^x}{x^2} \bigg(1-\frac1x-\frac{x+1}{e^x}+\frac{x^2+2x+2}{2xe^x}\bigg). \end{align} $$

Substituting (2.3) and (2.4) into (2.2), we obtain

$$ \begin{align*} I_{3/2}(x) &= \frac{x^{3/2}}{2\sqrt{2\pi}} \bigg(\frac{2e^x}{x^2} \bigg(1-\frac1x-\frac{x+1}{e^x}+\frac{x^2+2x+2}{2xe^x}\bigg) + O_\le(1)\bigg)\\ &= \frac{e^x}{\sqrt{2\pi x}} \bigg(1-\frac1x+\bigg(\frac1x-\frac x2\bigg) e^{-x}+O_\le\bigg(\frac{x^2}{2e^x}\bigg)\bigg). \end{align*} $$

Noting that $|1/x- x/2|\le {x^2}/{2}$ for $x\ge 1$ , we have

$$ \begin{align*} I_{{3}/{2}}(x) = \frac{e^x}{\sqrt{2\pi x}}\bigg(1 - \frac{1}{x} + O_\le (x^2 e^{-x})\bigg) \end{align*} $$

for $x \ge 1$ . In particular,

(2.5) $$ \begin{align} I_{3/2}\bigg(\pi\sqrt{\frac{2N}{3}}\bigg) = \frac{3^{1/4}e^{\pi \sqrt{{2N}/{3}}}}{2^{3/4}\pi N^{1/4}} \bigg(1-\frac{\sqrt{3}}{\sqrt{2}\pi} \frac{1}{\sqrt{N}} + O_\le\bigg(\frac{2\pi^2Ne^{-\pi\sqrt{{2N}{/3}}}}{3}\bigg)\bigg) \end{align} $$

for $n\ge 1$ . This corresponds to the term $k=1$ in the sum in (2.1) and we need to bound the remaining terms of the sum. Note that $|A_k(n)| \le k$ , so we may bound the remaining terms in the sum by

$$ \begin{align*} \bigg|\sum\limits_{k=2}^\infty \frac{A_k(n)}{k} I_{ 3/2}\bigg( \frac{\pi}{k}\sqrt{\frac{2N}{3}}\bigg) \bigg| \le \sum\limits_{k=2}^\infty I_{ 3/2}\bigg( \frac{\pi}{k}\sqrt{\frac{2N}{3}}\bigg). \end{align*} $$

We now emulate [2, (3.20)]. By [2, (3.18)],

$$ \begin{align*} \sum_{2\le k\le\lfloor X\rfloor} I_{3/2} \bigg(\frac Xk\bigg) \le 2\sqrt{\frac X\pi} e^{ X/2}. \end{align*} $$

The remaining terms are

$$ \begin{align*} \sum_{k \geq \lfloor X \rfloor +1} I_{{3}/{2}} \bigg(\frac{X}{k}\bigg) \leq \frac{X^{{3}/{2}}}{\Gamma ({5}{/2}) \sqrt{2}} \sum_{k \geq \lfloor X \rfloor + 1} \frac{1}{k^{{3}/{2}}}, \end{align*} $$

where we use [2, Lemma 2.2(3)]. We thus have the bound

$$ \begin{align*} \sum_{k \geq 2} I_{{3}/{2}} \bigg(\frac{X}{k}\bigg) \leq 2 \sqrt{\frac{X}{\pi}} e^{{X}/{2}} + \frac{2X^{{3}/{2}}}{\Gamma({5}/{2}) \sqrt{2}}. \end{align*} $$

It remains to bound the final sum with basic calculus by $2\sqrt { X/\pi }e^{ X/2}$ , yielding

$$ \begin{align*} \sum_{k \geq 2} I_{{3}/{2}} \bigg(\frac{X}{k}\bigg) \leq 4 \sqrt{\frac{X}{\pi}} e^{{X}/{2}}. \end{align*} $$

In our application, this yields

(2.6) $$ \begin{align} \sum_{k=2}^\infty I_{3/2}\bigg(\frac\pi k\sqrt{\frac{2N}{3}}\bigg) \le 4\sqrt[4]{\frac{2N}{3}}e^{\pi/2\sqrt{{2N}/{3}}} = \frac{2^{9/4}N^{1/4}}{3^{1/4}} e^{\pi/2\sqrt{{2N}/{3}}}. \end{align} $$

Substituting (2.5) and (2.6) in (2.1), we find that

$$ \begin{align*} p(n) &= \frac{\pi}{2^{5/4}3^{3/4}N^{3/4}} \bigg(\frac{3^{1/4}e^{\pi\sqrt{{2N}/{3}}}}{2^{3/4}\pi N^{1/4}} \bigg(1-\frac{\sqrt{3}}{\sqrt{2}\pi\sqrt{N}} + O_\le\bigg(\frac{2\pi^2Ne^{-\pi\sqrt{{2N}/{3}}}}{3}\bigg)\bigg) \\ &\quad+ O_\le\bigg(\frac{2^{9/4}N^{1/4}}{3^{1/4}} e^{\pi/2\sqrt{{2N}/{3}}}\bigg)\bigg)\\ &= \frac{e^{\pi\sqrt{{2N}/{3}}}}{4\sqrt{3}N} \bigg(1-\frac{\sqrt{3}}{\sqrt{2}\pi\sqrt{N}} + O_\le\bigg(\frac{2\pi^2Ne^{-\pi\sqrt{{2N}/{3}}}}{3} + 2^33^{-1/2} \pi N^{1/2} e^{-\pi/2\sqrt{ N/2}}\bigg)\bigg). \end{align*} $$

Note that $N=N(n)$ is implicitly a function of n and $N(n-j) = N(n) - j$ and so the claim follows.

Next we want to estimate the functions $f(\,j,n)$ . The first step is to obtain estimates of ${p(n-j)}/{p(n)}$ analogous to those of [2], proving Theorem 1.1 en route.

Theorem 2.2. Let $j<{\!\sqrt {N}}/{4}$ and $n\geq 14$ . Then

$$ \begin{align*} \frac{f(\,j,n)}{p(n)} &= 1 + e^{{\sqrt{2}\pi j}/{\sqrt{3N}}} \bigg( 1+ \bigg( \frac{\sqrt{3}}{\sqrt{2}\pi} - \frac{\sqrt{3}}{\sqrt{2 \pi}} \bigg) \frac{1}{\sqrt{N}} + \frac{2j}{N} - \frac{\pi j^2}{\sqrt{6} N^{3/2}} + O_{\leq} \bigg( \frac{2075}{N} \bigg) \bigg)\\ &\quad - e^{{\pi j}/{\sqrt{6N}}} \bigg( 2 + \bigg( \frac{2\sqrt{3}}{\sqrt{2}\pi} - \frac{2\sqrt{3}}{\sqrt{2 \pi}} \bigg) \frac{1}{\sqrt{N}} + \frac{2j}{N} - \frac{\pi j^2}{2\sqrt{6}N^{3/2}} + O_{\leq} \bigg( \frac{3926}{N} \bigg) \bigg). \end{align*} $$

Proof. Recall that

$$ \begin{align*} \frac{f(\,j,n)}{p(n)} = 1-2\frac{p(n-j)}{p(n)}+\frac{p(n-2j)}{p(n)}. \end{align*} $$

We first bound ${1}/{p(n)}$ . By Proposition 2.1,

$$ \begin{align*} p(n) = \frac{e^{\pi\sqrt{{2N}/{3}}}}{4\sqrt{3}N} \bigg(1-\frac{\sqrt{3}}{\sqrt{2}\pi\sqrt{N}}+g(N)\bigg), \end{align*} $$

where

$$ \begin{align*} |g(N)| \le \frac{2\pi^2Ne^{-\pi\sqrt{{2N}/{3}}}}{3} + 2^3\cdot3^{-1/2}\pi N^{1/2} e^{-(\pi/2)\sqrt{ N/2}} =: h(N). \end{align*} $$

Now we want to approximate $1/p(n)$ . For $N>1$ ,

$$ \begin{align*} \bigg|\frac{\sqrt{3}}{\sqrt{2}\pi\sqrt{N}}-g(N)\bigg| < \frac{\sqrt{3}}{\sqrt{2}\pi \sqrt{N}} + |g(N)| \le \frac{\sqrt{3}}{\sqrt{2}\pi \sqrt{N}} + h(N) < 0.99, \end{align*} $$

which can be seen by taking Taylor series. We claim that for $0<|z|<0.99$ ,

$$ \begin{align*} \frac{1}{1-z} = 1+z+O_{\leq}(100|z|^2). \end{align*} $$

To see this, we bound

$$ \begin{align*} \bigg|\frac{1}{1-z}-1-z\bigg| = \bigg|\frac{1-(1+z)(1-z)}{1-z}\bigg| = \frac{|z|^2}{|1-z|} \le \frac{|z|^2}{1-|z|} < \frac{1}{0.01}|z|^2 = 100|z|^2. \end{align*} $$

Thus,

$$ \begin{align*} \frac{1}{p(n)} &= \frac{4\sqrt{3}Ne^{-\pi\sqrt{{2N}/{3}}}}{1-\frac{\sqrt{3}}{\sqrt{2}\pi\sqrt{N}}+g(N)}\\ &= 4\sqrt{3}Ne^{-\pi\sqrt{{2N}/{3}}}\bigg(1+\frac{\sqrt{3}}{\sqrt{2}\pi\sqrt{N}}-g(N) + O_\le\bigg(100\bigg|\frac{\sqrt{3}}{\sqrt{2}\pi\sqrt{N}}-g(N)\bigg|^2\bigg)\bigg)\\ &= 4\sqrt{3}Ne^{-\pi\sqrt{{2N}/{3}}}\bigg(1+\frac{\sqrt{3}}{\sqrt{2}\pi\sqrt{N}} + O_\le\bigg(|g(N)|+100\bigg|\frac{\sqrt{3}}{\sqrt{2}\pi\sqrt{N}}-g(N)\bigg|^2\bigg)\bigg). \end{align*} $$

Now the error may be bounded against

$$ \begin{align*} h(N)+100\bigg(\frac{\sqrt{3}}{\sqrt{2}\pi\sqrt{N}}+h(N)\bigg)^2 = O_\le\bigg(\frac{1350}{N}\bigg) \end{align*} $$

again by basic calculus. Thus,

$$ \begin{align*} \frac{1}{p(n)}=4\sqrt{3}Ne^{-\pi \sqrt{{2N}/{3}}} \bigg( 1+\frac{\sqrt{3}}{\sqrt{2}\pi \sqrt{N}}+O_{\leq}\bigg( \frac{1350}{N} \bigg) \bigg). \end{align*} $$

Consider $p(n-J), J\in \{\,j,2j\}.$ By Proposition 2.1,

(2.7) $$ \begin{align} p(N-J)=\frac{e^{\pi \sqrt{2/3}\sqrt{N-J}}}{4\sqrt{3}(N-J)} \bigg( 1-\frac{\sqrt{3}}{\sqrt{2}\pi \sqrt{N-J}}+O_{\leq} ( h(N-J) ) \bigg). \end{align} $$

First note that $j<{\!\sqrt {N}}/{4}$ implies that (note that $N\ge 14-{1}/{24}$ )

$$ \begin{align*} N-J \ge N-2j \ge N-\frac{\sqrt{N}}{2} \ge 12. \end{align*} $$

Moreover, since $1\le j\le {\!\sqrt {N}}/{4}$ ,

$$ \begin{align*} \frac JN \le \frac{2j}{N} \le \frac{\sqrt{N}}{2N} = \frac{1}{2\sqrt{N}} \le \frac{1}{2\sqrt{14-\frac{1}{24}}} < 0.2. \end{align*} $$

We now approximate the exponential in (2.7). We claim that

$$ \begin{align*} e^{\pi \sqrt{2/3}\sqrt{N-J}} =e^{\pi \sqrt{2/3}\sqrt{N}-{\pi J}/{\sqrt{6N}}} \bigg( 1-\frac{\pi J^2}{4\sqrt{6}N^{3/2}}+O_{\leq} \bigg( \frac{0.1}{N} \bigg) \bigg). \end{align*} $$

To see this, define

$$ \begin{align*} f(x):=\sqrt{1-x}-1+\frac x2 +\frac{x^2}{8}. \end{align*} $$

It is straightforward to show that for $0\leq x <0.2$ , we have

$$ \begin{align*} |f(x)|\leq 0.1x^3. \end{align*} $$

We use this to write

$$ \begin{align*} \sqrt{N-J}=\!\sqrt{N}\sqrt{1-\frac JN}=\sqrt{N} \bigg( f\bigg( \frac JN\bigg) +1- \frac{J}{2N} -\frac18 \bigg(\frac JN\bigg)^2 \bigg) \end{align*} $$

and obtain

$$ \begin{align*} e^{\pi \sqrt{2/3} \sqrt{N-J}-\pi \sqrt{2/3}\sqrt{N}+{\pi J}/{\sqrt{6N}}} =e^{-\pi \sqrt{2/3}\sqrt{N}(-f( J/N)+ {J^2}/{8N^2})}. \end{align*} $$

Note that

$$ \begin{align*} -f(x)+\frac{x^2}{8} =1-\frac x2-\sqrt{1-x}=\frac{x^2}{8}+\cdots>0. \end{align*} $$

Also note that for $x>0$ ,

$$ \begin{align*} e^{-x}-1+x=\sum_{n\geq 2} \frac{(-1)^nx^n}{n!}\leq \frac{x^2}{2} \end{align*} $$

by Leibnitz’s criterion. Thus,

$$ \begin{align*} &e^{-\pi\sqrt{2/3}\sqrt{N}(-f( J/N)+ {J^2}/{8N^2})} \\[-6pt] &\quad=1-\pi\sqrt{2/3}\sqrt{N}\bigg(-f\bigg( \frac JN\bigg)+ \frac{J^2}{8N^2}\bigg) +O_{\leq} \bigg( \frac12 \bigg( \sqrt{\frac23} \sqrt{N} \bigg(-f \bigg( \frac JN\bigg)+\frac{J^2}{8N^2}\bigg)\bigg)^2\bigg) \\ &\quad=1-\frac{\pi J^2}{\sqrt{6} N^{3/2}}+O_{\leq} \bigg( \pi \sqrt{\frac23} \sqrt{N} \bigg| f \bigg( \frac JN\bigg) \bigg| +\frac12 \bigg( \pi\sqrt{\frac23}\sqrt{N}\bigg(\bigg| f\bigg( \frac JN\bigg)\bigg|+ \frac{J^2}{8N^2}\bigg)\bigg)^2 \bigg). \end{align*} $$

We now bound the error against

$$ \begin{align*} &\pi\sqrt{\frac23} \sqrt{N}\cdot 0.1 \bigg( \frac JN\bigg)^3 +\frac{\pi^2}{3}N \bigg( 0.1 \bigg( \frac JN\bigg)^3+ \frac{J^2}{8N^2} \bigg)^2 \\ &\quad\leq \pi\sqrt{\frac23} \cdot 0.1 \frac{1}{2^3 N}+\frac{\pi^2}{3}N \bigg( 0.1 \bigg( \frac{1}{2\sqrt{N}}\bigg)^3+\frac18 \bigg( \frac{1}{2\sqrt{N}} \bigg)^2 \bigg)^2 \\ &\quad=\frac{0.1\pi}{4\sqrt{6}} \frac1N + \frac{\pi^2}{24} \frac1N \bigg( \frac{0.1}{\sqrt{N}}+1/4 \bigg)^2 =\bigg( \frac{0.1\pi}{4\sqrt{6}}+\frac{\pi^2}{24}\bigg( \frac{0.1}{\sqrt{N}}+1/4\bigg)^2\bigg) \frac1N \leq \frac{0.1}{N}, \end{align*} $$

where in the final inequality, we used $N\ge 14-{1}/{24}$ . This gives the claim.

Next we claim that for $x<0.2$ ,

$$ \begin{align*} \frac{1}{1-x} = 1+x+O_\le(1.25 x^2). \end{align*} $$

To see this, we bound

$$ \begin{align*} \bigg|\frac{1}{1-x}-1-x\bigg| = \frac{x^2}{|1-x|} \le \frac{x^2}{1-|x|} \le \frac{x^2}{0.8}. \end{align*} $$

We use this for

$$ \begin{align*} \frac{1}{N-J} = \frac1N \frac{1}{1- J/N} = \frac1N\bigg(1+\frac{J}{N}+O_\le\bigg(1.25\bigg(\frac JN\bigg)^2\bigg)\bigg)=\frac1N \bigg( 1+\frac{J}{N}+O_{\leq} \bigg( \frac{0.4}{N} \bigg) \bigg). \end{align*} $$

Next, for $0\le x<0.2$ ,

$$ \begin{align*} \frac{1}{\sqrt{1-x}}-1 \le 0.6x. \end{align*} $$

Thus,

$$ \begin{align*} \frac{1}{\sqrt{N-J}} = \frac{1}{\sqrt{N}}\frac{1}{\sqrt{1- J/N}} = \frac{1}{\sqrt{N}}\bigg(1+O_\le\bigg(0.6\frac JN\bigg)\bigg) = \frac{1}{\sqrt{N}}+O_\le\bigg(0.6\frac{J}{N^ {3/2}}\bigg) =\frac{1}{\sqrt{N}}+O_{\leq} \bigg( \frac{0.3}{N}\bigg). \end{align*} $$

Finally, by basic calculus, we find the bound

$$ \begin{align*} \frac{2\pi^2xe^{-\pi\sqrt{{2x}/{3}}}}{3} + 2^33^{-1/2}\pi x^{1/2} e^{-(\pi/2)\sqrt{ x/2}} \le 15x^{1/2} e^{-(\pi/2)\sqrt{ x/2}} \end{align*} $$

for $x\ge 12$ . Thus,

$$ \begin{align*} |f(N-J)|\leq 15(N-J)^{1/2} e^{-({\pi}/{2\sqrt{2})}\sqrt{N-J}}. \end{align*} $$

Now note that $ x^{1/2}e^{-(\pi /2)\sqrt { x/2}} $ is decreasing for $x\ge 1$ . We then use the bound

$$ \begin{align*} N-J \ge N-\frac{\sqrt{N}}{2} \end{align*} $$

and thus

$$ \begin{align*} (N-J)^{1/2} e^{-(\pi/2)\sqrt{{(N-J)}/{2}}} \le \bigg(N-\frac{\sqrt{N}}{2}\bigg)^{1/2} e^{-(\pi/2)\sqrt{({N-{\sqrt{N}}/{2}})/{2}}} = O_\le\bigg(\frac{1.1}{N}\bigg). \end{align*} $$

Thus,

$$ \begin{align*} p(n-J) &= \frac{1}{4\sqrt{3}}e^{\pi\sqrt{{2N}/{3}}-{\pi J}/{\sqrt{6N}}} \bigg(1-\frac{\pi J^2}{4\sqrt{6}N^3/2} +O_\le\bigg(\frac{0.1}{N}\bigg)\bigg) \frac1N\bigg(1+\frac{J}{N}+O_\le\bigg(\frac{0.4}{N} \bigg)\bigg)\\ &\quad\times \bigg(1-\frac{\sqrt{3}}{\sqrt{2\pi}}\bigg(\frac{1}{\sqrt{N}} + O_\le\bigg(\frac{0.3}{N}\bigg)\bigg) + O_\le\bigg(\frac{1.1}{N}\bigg)\bigg). \end{align*} $$

We combine

$$ \begin{align*} &\bigg(1-\frac{\pi J^2}{4\sqrt{6}N^3/2}+O_\le\bigg(\frac{0.1}{N}\bigg)\bigg) \bigg(1+\frac JN+O_\le\bigg(\frac{0.4}{N}\bigg)\bigg)\\ &\quad= 1+\frac JN-\frac{\pi J^2}{4\sqrt{6}N^3/2}\\ &\qquad + O_\le\bigg(\frac{0.4}{N}+\frac{\pi J^3}{4\sqrt{6}N^{5/2}}+\frac{0.4\pi J^2}{4\sqrt{6}N^{5/2}} +\frac{0.1}{N}+0.1\frac{J}{N^2}+0.1\cdot \frac{0.4}{N^2}\bigg). \end{align*} $$

The error may be bounded against ${0.56}/{N}$ .

Next, we estimate

$$ \begin{align*} 1-\frac{\sqrt{3}}{\sqrt{2\pi}} \bigg(\frac{1}{\sqrt{N}}+O_\le\bigg(\frac{0.3}{N}\bigg)+O_\le\bigg(\frac{1.1}{N}\bigg)\bigg) = 1-\frac{\sqrt{3}}{\sqrt{2\pi}\sqrt{N}} + O_\le \bigg( \frac{1.31}{N} \bigg). \end{align*} $$

Thus,

$$ \begin{align*} &4\sqrt{3}Ne^{-\pi\sqrt{{2N}/{3}}+{\pi J}/{\sqrt{6N}}} p(n-J)\\ &\quad= \bigg(1+\frac JN-\frac{\pi J^2}{4\sqrt{6}N^3/2}+O_\le\bigg(\frac{0.56}{N}\bigg)\bigg) \bigg(1-\frac{\sqrt{3}}{\sqrt{2\pi}\sqrt{N}}+O_\le\bigg(\frac{1.31}{N}\bigg)\bigg)\\ &\quad= 1+\frac JN - \frac{\pi J^2}{4\sqrt{6}N^3/2}-\frac{\sqrt{3}}{\sqrt{2\pi}\sqrt{N}} + O_\le\bigg( \frac{2.71}{N} \bigg). \end{align*} $$

Note that this calculation also proves Theorem 1.1. Thus, overall, we obtain

(2.8) $$ \begin{align} \frac{f(n,j)}{p(n)} & = 1+\frac{1}{p(n)}(p(n-2j)-2p(n-j)) \notag\\ & = 1+4\sqrt{3}Ne^{-\pi\sqrt{{2N}/{3}}} \bigg(1+\frac{\sqrt{3}}{\sqrt{2}\pi\sqrt{N}}+O_\le\bigg(\frac{1350}{N}\bigg)\bigg) \frac{e^{\pi\sqrt{{2N}/{3}}}}{4\sqrt{3}N} \notag\\ &\quad \times \bigg(e^{{\sqrt{2}\pi j}/{\sqrt{3N}}} \bigg(1+\frac{2j}{N}-\frac{\pi j^2}{\sqrt{6}N^3/2}-\frac{\sqrt{3}}{\sqrt{2\pi}\sqrt{N}} +O_{\leq}\bigg(\frac{2.71}{N}\bigg)\bigg) \notag\\ & \quad - 2e^{{\pi j}/{\sqrt{6N}}} \bigg(1+\frac jN-\frac{\pi j^2}{4\sqrt{6}N^{3/2}}-\frac{\sqrt{3}}{\sqrt{2\pi}\sqrt{N}} +O_{\leq}\bigg(\frac{2.71}{N}\bigg) \bigg)\bigg). \end{align} $$

Since $j \leq {\!\sqrt {N}}/{4}$ and $n \geq 14$ , a straightforward calculation gives

$$ \begin{align*} &\bigg(1+\frac{\sqrt{3}}{\sqrt{2}\pi\sqrt{N}}+O_\le\bigg(\frac{1350}{N}\bigg) \bigg) \bigg(1+\frac{2j}{N}-\frac{\pi j^2}{\sqrt{6}N^{3/2}}-\frac{\sqrt{3}}{\sqrt{2\pi}\sqrt{N}} +O_{\leq}\bigg(\frac{2.71}{N}\bigg)\bigg) \\ &\quad=1 + \bigg( \frac{\sqrt{3}}{\sqrt{2}\pi} - \frac{\sqrt{3}}{\sqrt{2 \pi}} \bigg) \frac{1}{\sqrt{N}} + \frac{2j}{N} - \frac{\pi j^2}{\sqrt{6} N^{3/2}} + O_{\leq} \bigg( \frac{2075}{N} \bigg). \end{align*} $$

We turn to the final product in (2.8) given by

$$ \begin{align*} & 2\bigg(1+\frac{\sqrt{3}}{\sqrt{2}\pi\sqrt{N}}+O_\le\bigg(\frac{1350}{N}\bigg)\bigg) \bigg(1+\frac jN-\frac{\pi j^2}{4\sqrt{6}N^{3/2}}-\frac{\sqrt{3}}{\sqrt{2\pi}\sqrt{N}} +O_{\leq}\bigg(\frac{2.71}{N}\bigg) \bigg). \end{align*} $$

Again using $j \leq {\!\sqrt {N}}/{4}$ and $n \geq 14$ , it is not hard to show that this is equal to

$$ \begin{align*} 2 + \bigg( \frac{2\sqrt{3}}{\sqrt{2}\pi} - \frac{2\sqrt{3}}{\sqrt{2 \pi}} \bigg) \frac{1}{\sqrt{N}} + \frac{2j}{N} - \frac{\pi j^2}{2\sqrt{6}N^{3/2}} + O_{\leq} \bigg( \frac{3926}{N} \bigg). \end{align*} $$

Combining everything together, we obtain the statement of the theorem.

We end by proving the eventual positivity of the ratio ${f(\,j,n)}/{p(n)}$ , which is crucial to the applications in the introduction.

Theorem 2.3. Let $j \leq {\!\sqrt {N}}/{4}$ . Then we have that ${f(\,j,n)}/{p(n)}> 0$ for all $n \geq 2$ .

Proof. Let $X = e^{{\sqrt {2}\pi j}/{\sqrt {3N}}} - 2 e^{{\pi j }/{\sqrt {6N}}}$ . By Theorem 2.2, the result follows if

(2.9) $$ \begin{align} \frac{f(\,j,n)}{p(n)} - 1 &= \bigg( 1 + \bigg( \frac{\sqrt{3}}{\sqrt{2}\pi} - \frac{\sqrt{3}}{\sqrt{2\pi}} \bigg)\frac{1}{\sqrt{N}} + \frac{j}{N} - \frac{\pi j^2}{4 \sqrt{6} N^{3/2}} + \frac{3926}{N} \bigg) X \notag \\ &\quad+ e^{{\sqrt{2}\pi j}/{\sqrt{3N}}} \bigg( \frac{j}{N} - \frac{3 \pi j^2}{4 \sqrt{6} N^{3/2}} \bigg)> -1 \end{align} $$

for all $n \geq 14$ , with a finite computer check taking care of the remaining cases.

We first observe using $j \leq {\!\sqrt {N}}/{4}$ that

$$ \begin{align*} \frac{3 \pi j^2}{4 \sqrt{6} N^{3/2}} < \frac{j}{N}, \end{align*} $$

implying that the final term in (2.9) is positive. Thus, the claim follows if

$$ \begin{align*} \bigg( 1+ \bigg( \frac{\sqrt{3}}{\sqrt{2}\pi} - \frac{\sqrt{3}}{\sqrt{2\pi}} \bigg)\frac{1}{\sqrt{N}} + \frac{j}{N} - \frac{\pi j^2}{4 \sqrt{6} N^{3/2}} + \frac{3926}{N} \bigg) X> -1. \end{align*} $$

Since $-1 < X < 0$ for all $n \geq 4$ , this follows if

$$ \begin{align*} \bigg( \frac{\sqrt{3}}{\sqrt{2}\pi} - \frac{\sqrt{3}}{\sqrt{2\pi}} \bigg)\frac{1}{\sqrt{N}} + \frac{j}{N} - \frac{\pi j^2}{4 \sqrt{6} N^{3/2}} + \frac{3926}{N} < 0. \end{align*} $$

It is simple to check that this is always satisfied for $n \geq 14$ , and the theorem follows. We note that this also proves Theorem 1.2.

We are grateful to the referee for pointing out the following more elementary approaches to proving Theorem 1.2, and in fact a wider class of inequalities for $p(n)$ . Let $V_j(n)$ be the set of non-j-ary partitions. For any $\ell \geq 0$ , we may construct a map

$$ \begin{align*} \pi : V_j(n-\ell) &\to V_j(n) \\ (\lambda_1,\ldots,\lambda_s) &\mapsto (\lambda_1+\ell, \lambda_2,\ldots,\lambda_s). \end{align*} $$

Since this map is clearly injective, we immediately obtain

$$ \begin{align*} p(n-\ell) - p(n-\ell-j) \leq p(n) - p(n-j) \end{align*} $$

for all $\ell \geq 0$ . Choosing $\ell = j$ , we recover Theorem 1.2. One may also write this in terms of coefficients of q-series, as in [17, (2.4)]:

$$ \begin{align*} \Delta^r_j(p(n)) = [q^n] (1-q^j)^r \prod_{k \geq 1} (1-q^k)^{-1}. \end{align*} $$

When $r=2$ , it is readily checked (using the q-binomial theorem) that the q-series has nonnegative coefficients, giving Theorem 1.2. However, if one fixes j and asks about the behaviour as $r \to \infty $ , it is less clear whether the q-series has nonnegative coefficients. For $j=1$ , this is Gupta’s conjecture [7]. Moreover, in [17], it is shown that $\Delta _1^r(p(n))$ alternates in sign before eventually becoming nonnegative. Does a similar phenomenon hold for $\Delta _j^r(p(n))$ ?

We remark that these more elementary approaches rely on the combinatorial structure and the infinite product representations that occur for $p(n)$ . For other objects with similar asymptotic behaviour to $p(n)$ , our analytical techniques provide a pathway to similar inequalities where one may not have a combinatorial interpretation or infinite product representation.