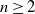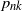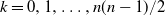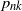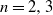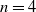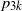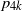1. Introduction
The problem of finding relations between probabilistic and geometric characteristics of a convex domain that remain invariant under rigid motions goes far beyond theoretical interest. The field has been significantly developed during recent decades, when an increasing number of real-life applications required rigorous mathematical foundations (see [Reference Schneider and Weil9]). For example, the reconstruction of a convex body by its random sections is the central problem of geometric tomography (introduced in [Reference Gardner5]). Some recent results on finding the chord length distribution or the distance distribution between two random points in a convex domain can be viewed in [Reference Aharonyan and Khalatyan1], [Reference Aharonyan and Ohanyan2], [Reference Harutyunyan and Ohanyan6], and [Reference Ohanyan and Martirosyan7].
The main results of this work concern the intersection probabilities of four random lines meeting a planar convex domain. This is a classical object in stochastic geometry, with a dominant geometric flavour. For a bounded open convex domain
![]() $D\subset \mathbb{R}^2$
we consider
$D\subset \mathbb{R}^2$
we consider
![]() $N_n$
, the number of intersection points of n random lines in D, given that all n lines meet D. We will assume that D contains the origin of the Cartesian plane, and for a line
$N_n$
, the number of intersection points of n random lines in D, given that all n lines meet D. We will assume that D contains the origin of the Cartesian plane, and for a line
![]() $g\subset \mathbb{R}^2$
, we let
$g\subset \mathbb{R}^2$
, we let
![]() $(p, \varphi)$
denote the polar coordinates of the foot of the perpendicular from the origin onto g.
$(p, \varphi)$
denote the polar coordinates of the foot of the perpendicular from the origin onto g.
Let
![]() $p_{nk}=\mathbb{P}(N_n=k)$
. It is easy to check that
$p_{nk}=\mathbb{P}(N_n=k)$
. It is easy to check that
![]() $p_{21}={2\pi F}/{L^2}$
, where F and L are the area and the perimeter of D, respectively. Computation of
$p_{21}={2\pi F}/{L^2}$
, where F and L are the area and the perimeter of D, respectively. Computation of
![]() $p_{3k}$
requires more invariants of D besides the area and the perimeter. These are suggested in [Reference Santaló8, Chapter 4] to be
$p_{3k}$
requires more invariants of D besides the area and the perimeter. These are suggested in [Reference Santaló8, Chapter 4] to be
where
![]() $\chi(g)=g\cap D$
is the chord in D produced by the line g,
$\chi(g)=g\cap D$
is the chord in D produced by the line g,
![]() $|\chi(g)|$
is the length of
$|\chi(g)|$
is the length of
![]() $\chi(g)$
, and
$\chi(g)$
, and
![]() $u(g_1, g_2)$
denotes the perimeter of the convex quadrilateral whose vertices are at the points of intersections of the lines
$u(g_1, g_2)$
denotes the perimeter of the convex quadrilateral whose vertices are at the points of intersections of the lines
![]() $g_1$
and
$g_1$
and
![]() $g_2$
with the boundary
$g_2$
with the boundary
![]() $\partial D$
. The measure element
$\partial D$
. The measure element
![]() $\mathrm{d} g$
is interpreted as
$\mathrm{d} g$
is interpreted as
![]() $\mathrm{d} g=\mathrm{d} p \,\mathrm{d} \varphi$
, where
$\mathrm{d} g=\mathrm{d} p \,\mathrm{d} \varphi$
, where
![]() $\mathrm{d} p$
is the one-dimensional Lebesgue measure and
$\mathrm{d} p$
is the one-dimensional Lebesgue measure and
![]() $\mathrm{d} \varphi$
is the uniform measure on the unit circle.
$\mathrm{d} \varphi$
is the uniform measure on the unit circle.
The formulas for intersection probabilities
![]() $p_{3k}$
, suggested in [Reference Santaló8, Chapter 4], contain an error. The correct formulas are
$p_{3k}$
, suggested in [Reference Santaló8, Chapter 4], contain an error. The correct formulas are
established earlier by R. Sulanke in [Reference Sulanke10]. These formulas imply
In this paper we obtain explicit formulas for probabilities
![]() $p_{4k}$
,
$p_{4k}$
,
![]() $k=1,2, \ldots, 6$
in terms of new invariants of D and find an analogue of (1.2) for those invariants. After the main results, in the final section we provide exact computations of all the new invariants for a disc of radius r. The simplest expressions in terms of r are reached. The exact values of intersection probabilities
$k=1,2, \ldots, 6$
in terms of new invariants of D and find an analogue of (1.2) for those invariants. After the main results, in the final section we provide exact computations of all the new invariants for a disc of radius r. The simplest expressions in terms of r are reached. The exact values of intersection probabilities
![]() $p_{3k}$
,
$p_{3k}$
,
![]() $0\leq k \leq 3$
and
$0\leq k \leq 3$
and
![]() $p_{4k}$
,
$p_{4k}$
,
![]() $ 0\leq k \leq 6$
are found.
$ 0\leq k \leq 6$
are found.
Our computations are based on Ambartzumian’s combinatorial algorithm (see [Reference Ambartzumian3, Chapter 5]). Before passing on to the main results, the algorithm is adapted to the new situation in Section 2.
2. The combinatorial algorithm
Let
![]() $\mathbb{G}$
be the space of all lines g in
$\mathbb{G}$
be the space of all lines g in
![]() $\mathbb{R}^2$
. We equip
$\mathbb{R}^2$
. We equip
![]() $\mathbb{G}$
with a measure
$\mathbb{G}$
with a measure
![]() $\mu$
invariant under Euclidean motions in
$\mu$
invariant under Euclidean motions in
![]() $\mathbb{R}^2$
. Then, up to a constant factor,
$\mathbb{R}^2$
. Then, up to a constant factor,
for the measurable subsets
![]() $X\subset \mathbb{G}$
(see [Reference Ambartzumian3]).
$X\subset \mathbb{G}$
(see [Reference Ambartzumian3]).
Let
![]() $\mathcal{P}=\{P_i\}_{i=1}^n$
be a finite set of points in the plane. For any line
$\mathcal{P}=\{P_i\}_{i=1}^n$
be a finite set of points in the plane. For any line
![]() $g\in\mathbb{G}$
we consider
$g\in\mathbb{G}$
we consider
![]() $\Pi_1(g)$
and
$\Pi_1(g)$
and
![]() $\Pi_2(g)$
, the two open half-planes generated by g. We call two lines
$\Pi_2(g)$
, the two open half-planes generated by g. We call two lines
![]() $g_1$
,
$g_1$
,
![]() $ g_2$
equivalent if
$ g_2$
equivalent if
![]() $\{\mathcal{P}\cap\Pi_1(g_1),\mathcal{P}\cap\Pi_2(g_1)\}=\{\mathcal{P}\cap\Pi_1(g_2),\mathcal{P}\cap\Pi_2(g_2)\}$
.
$\{\mathcal{P}\cap\Pi_1(g_1),\mathcal{P}\cap\Pi_2(g_1)\}=\{\mathcal{P}\cap\Pi_1(g_2),\mathcal{P}\cap\Pi_2(g_2)\}$
.
![]() $\mathbb{G}$
is decomposed into subsets of equivalent lines, which we call atoms. We let
$\mathbb{G}$
is decomposed into subsets of equivalent lines, which we call atoms. We let
![]() $r(\mathcal{P})$
denote the minimal ring containing all bounded atoms.
$r(\mathcal{P})$
denote the minimal ring containing all bounded atoms.
If
![]() $g\cap \mathcal{P}=\varnothing$
and neither of the sets
$g\cap \mathcal{P}=\varnothing$
and neither of the sets
![]() $\mathcal{P}\cap\Pi_1(g)$
and
$\mathcal{P}\cap\Pi_1(g)$
and
![]() $\mathcal{P}\cap\Pi_2(g)$
are empty, then consider the atom B such that
$\mathcal{P}\cap\Pi_2(g)$
are empty, then consider the atom B such that
![]() $g\in B$
. We will say that the atom B separates the points
$g\in B$
. We will say that the atom B separates the points
![]() $\mathcal{P}\cap\Pi_1(g)$
from
$\mathcal{P}\cap\Pi_1(g)$
from
![]() $\mathcal{P}\cap\Pi_2(g)$
.
$\mathcal{P}\cap\Pi_2(g)$
.
Let
![]() $\rho_{ij}$
be the Euclidean distance between points
$\rho_{ij}$
be the Euclidean distance between points
![]() $P_i$
and
$P_i$
and
![]() $P_j$
. The combinatorial algorithm below aims to express the
$P_j$
. The combinatorial algorithm below aims to express the
![]() $\mu$
-measure of any set
$\mu$
-measure of any set
![]() $B\in r(\mathcal{P})$
by linear combinations of
$B\in r(\mathcal{P})$
by linear combinations of
![]() $\rho_{ij}$
with integer coefficients belonging to
$\rho_{ij}$
with integer coefficients belonging to
![]() $\{0, \pm 1, \pm 2\}$
. The algorithm is introduced [Reference Ambartzumian3] for the case where any three points from
$\{0, \pm 1, \pm 2\}$
. The algorithm is introduced [Reference Ambartzumian3] for the case where any three points from
![]() $\mathcal{P}$
are not collinear. If there are collinear triads, then (see [Reference Ambartzumian4]) the linear combinations should be taken over those indices (i, j),
$\mathcal{P}$
are not collinear. If there are collinear triads, then (see [Reference Ambartzumian4]) the linear combinations should be taken over those indices (i, j),
![]() $ i<j$
, for which the segment
$ i<j$
, for which the segment
![]() $P_iP_j$
contains no other points from
$P_iP_j$
contains no other points from
![]() $\mathcal{P}$
. We call such points
$\mathcal{P}$
. We call such points
![]() $P_i$
and
$P_i$
and
![]() $P_j$
neighbour points.
$P_j$
neighbour points.
Let
![]() $g_{ij}$
be the line passing through the neighbour points
$g_{ij}$
be the line passing through the neighbour points
![]() $P_i$
and
$P_i$
and
![]() $P_j$
. For sufficiently small positive numbers
$P_j$
. For sufficiently small positive numbers
![]() $\delta$
and
$\delta$
and
![]() $\theta$
, we define two types of displacements for
$\theta$
, we define two types of displacements for
![]() $g_{ij}$
.
$g_{ij}$
.
![]() $\delta$
-translation. This is a set of two lines which are parallel to
$\delta$
-translation. This is a set of two lines which are parallel to
![]() $g_{ij}$
and distant from
$g_{ij}$
and distant from
![]() $g_{ij}$
by
$g_{ij}$
by
![]() $\delta$
. The set is denoted by
$\delta$
. The set is denoted by
![]() $T_{\delta}(g_{ij})$
.
$T_{\delta}(g_{ij})$
.
θ-rotation. This is a set of two lines each passing through the midpoint of
![]() $P_iP_j$
and making angle
$P_iP_j$
and making angle
![]() $\theta$
with
$\theta$
with
![]() $g_{ij}$
. The set is denoted by
$g_{ij}$
. The set is denoted by
![]() $R_{\theta}(g_{ij})$
.
$R_{\theta}(g_{ij})$
.
If
![]() $B\in r(\mathcal{P})$
, then let us define the numbers
$B\in r(\mathcal{P})$
, then let us define the numbers
where
![]() $\#$
stands for the cardinality of a set.
$\#$
stands for the cardinality of a set.
Obviously
![]() $R_{ij}(B)$
,
$R_{ij}(B)$
,
![]() $T_{ij}(B)\in \{0, 1, 2\}$
. Ambartzumian’s combinatorial algorithm/formula can now be reformulated as follows.
$T_{ij}(B)\in \{0, 1, 2\}$
. Ambartzumian’s combinatorial algorithm/formula can now be reformulated as follows.
Theorem 2.1. Let
![]() $\mathcal{P}=\{P_i\}_{i=1}^n$
be a finite set of points in the plane and
$\mathcal{P}=\{P_i\}_{i=1}^n$
be a finite set of points in the plane and
![]() $B\in r(\mathcal{P})$
. Then
$B\in r(\mathcal{P})$
. Then
where I is the set of pairs (i, j) for all neighbour points
![]() $P_i$
and
$P_i$
and
![]() $P_j$
,
$P_j$
,
![]() $i<j$
.
$i<j$
.
As an application, one can easily re-obtain the formulas for
![]() $p_{nk}$
, where
$p_{nk}$
, where
![]() $n=2,3$
. For example, let us prove the second formula in (1.1).
$n=2,3$
. For example, let us prove the second formula in (1.1).
Here and in the next sections, for any set
![]() $X\subset \mathbb{R}^2$
we let [X] denote the set of all lines
$X\subset \mathbb{R}^2$
we let [X] denote the set of all lines
![]() $g\in \mathbb{G}$
such that
$g\in \mathbb{G}$
such that
![]() $g\cap X\neq\varnothing$
. Two intersection points can occur when two of the lines
$g\cap X\neq\varnothing$
. Two intersection points can occur when two of the lines
![]() $g_1, g_2, g_3$
have no intersection inside D and the third one intersects each of them inside D. The three events where either of
$g_1, g_2, g_3$
have no intersection inside D and the third one intersects each of them inside D. The three events where either of
![]() $g_i$
is the third line are equally probable, and therefore
$g_i$
is the third line are equally probable, and therefore
where
![]() $B=[\chi(g_1)]\cap [\chi(g_2)]^c$
(the complement is taken over the sample space [D]). One can check that among
$B=[\chi(g_1)]\cap [\chi(g_2)]^c$
(the complement is taken over the sample space [D]). One can check that among
![]() $T_{ij}(B)$
and
$T_{ij}(B)$
and
![]() $R_{ij}(B)$
the only non-zero coefficients are
$R_{ij}(B)$
the only non-zero coefficients are
![]() $T_{24}(B)=2$
and
$T_{24}(B)=2$
and
![]() $R_{12}(B)=R_{23}(B)=R_{34}(B)=R_{14}(B)=1$
. Then (2.1) yields
$R_{12}(B)=R_{23}(B)=R_{34}(B)=R_{14}(B)=1$
. Then (2.1) yields
It remains to notice that
3. Introduction of new invariants: computation of
 $\textbf{p}_{4\textbf{k}}$
for
$\textbf{p}_{4\textbf{k}}$
for
 $\textbf{k}=6, 5$
$\textbf{k}=6, 5$
Definition 3.1. For any
![]() $g_1\cap g_2\in D$
, we define
$g_1\cap g_2\in D$
, we define
 \begin{gather*} d(g_1, g_2)=|\chi(g_1)|+|\chi(g_2)|, \quad c(g_1, g_2)=\mu ([\chi(g_1)]\cap[\chi(g_2)]),\\[5pt] u(g_1, g_2)=\biggl|\partial\biggl(\mathrm{conv}\biggl(\bigcup_{i=1}^2g_i\cap D\biggr)\biggr)\biggr|, \end{gather*}
\begin{gather*} d(g_1, g_2)=|\chi(g_1)|+|\chi(g_2)|, \quad c(g_1, g_2)=\mu ([\chi(g_1)]\cap[\chi(g_2)]),\\[5pt] u(g_1, g_2)=\biggl|\partial\biggl(\mathrm{conv}\biggl(\bigcup_{i=1}^2g_i\cap D\biggr)\biggr)\biggr|, \end{gather*}
and for any three lines
![]() $g_1, g_2, g_3$
such that
$g_1, g_2, g_3$
such that
![]() $g_i\cap g_j\in D$
,
$g_i\cap g_j\in D$
,
![]() $1\leq i<j\leq 3$
, we define
$1\leq i<j\leq 3$
, we define
 \begin{equation*}v(g_1, g_2, g_3)=\biggl|\partial\biggl(\mathrm{conv}\biggl(\bigcup_{i=1}^3g_i\cap D\biggr)\biggr)\biggr|,\end{equation*}
\begin{equation*}v(g_1, g_2, g_3)=\biggl|\partial\biggl(\mathrm{conv}\biggl(\bigcup_{i=1}^3g_i\cap D\biggr)\biggr)\biggr|,\end{equation*}
where
![]() $\mathrm{conv}(X)$
denotes the convex hull of
$\mathrm{conv}(X)$
denotes the convex hull of
![]() $X\subset\mathbb{R}^2$
, and
$X\subset\mathbb{R}^2$
, and
![]() $|\partial Y|$
denotes the perimeter of a convex domain Y.
$|\partial Y|$
denotes the perimeter of a convex domain Y.
The new definition of
![]() $u(g_1, g_2)$
coincides with the one we have used so far. Also, by (2.1), we have
$u(g_1, g_2)$
coincides with the one we have used so far. Also, by (2.1), we have
![]() $c(g_1, g_2)=2d(g_1, g_2)-u(g_1, g_2)$
.
$c(g_1, g_2)=2d(g_1, g_2)-u(g_1, g_2)$
.
Along with the well-known invariants
![]() $I_k=\int_{[D]}|\chi(g)|^k\,\mathrm{d} g$
,
$I_k=\int_{[D]}|\chi(g)|^k\,\mathrm{d} g$
,
![]() $k=0, 1, 2, \ldots,$
let us consider the following moments of the functions introduced in Definition 3.1:
$k=0, 1, 2, \ldots,$
let us consider the following moments of the functions introduced in Definition 3.1:
 \begin{alignat*}{3} D_k &=\int_{g_1\cap g_2 \in D}d^k(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2,\quad & C_k&=\int_{g_1\cap g_2 \in D}c^k(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2, \\[5pt] U_k &=\int_{g_1\cap g_2 \in D}u^k(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2,\quad & V_k &=\int_{g_i\cap g_j \in D,\,1\leq i<j\leq3}v^k(g_1, g_2, g_3)\,\mathrm{d} g_1\,\mathrm{d} g_2\,\mathrm{d} g_3. \end{alignat*}
\begin{alignat*}{3} D_k &=\int_{g_1\cap g_2 \in D}d^k(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2,\quad & C_k&=\int_{g_1\cap g_2 \in D}c^k(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2, \\[5pt] U_k &=\int_{g_1\cap g_2 \in D}u^k(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2,\quad & V_k &=\int_{g_i\cap g_j \in D,\,1\leq i<j\leq3}v^k(g_1, g_2, g_3)\,\mathrm{d} g_1\,\mathrm{d} g_2\,\mathrm{d} g_3. \end{alignat*}
It is easy to verify that
and
In this section we aim to express the probabilities
![]() $p_{46}$
and
$p_{46}$
and
![]() $p_{45}$
in terms of the new invariants. In this way we first obtain expressions for two useful integrals.
$p_{45}$
in terms of the new invariants. In this way we first obtain expressions for two useful integrals.
Proposition 3.1. We have
 \begin{align*} \int_{g_1\cap g_2\in D}|\chi(g_1)||\chi(g_2)|\,\mathrm{d} g_1\,\mathrm{d} g_2 & =\dfrac{D_2-4I_3}{2},\\[5pt] \int_{g_1\cap g_2\in D}|\chi(g_1)|u(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2 & =\dfrac{4D_2+U_2-C_2}{8}.\end{align*}
\begin{align*} \int_{g_1\cap g_2\in D}|\chi(g_1)||\chi(g_2)|\,\mathrm{d} g_1\,\mathrm{d} g_2 & =\dfrac{D_2-4I_3}{2},\\[5pt] \int_{g_1\cap g_2\in D}|\chi(g_1)|u(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2 & =\dfrac{4D_2+U_2-C_2}{8}.\end{align*}
Proof. Direct computation of
![]() $D_2$
leads to
$D_2$
leads to
 \begin{align*}D_2 & =\int_{g_1\cap g_2\in D}(|\chi(g_1)|^2+|\chi(g_2)|^2)\,\mathrm{d} g_1\,\mathrm{d} g_2+2\int_{g_1\cap g_2\in D}|\chi(g_1)||\chi(g_2)|\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt]&=2\int_{[D]}|\chi(g_1)|^2\int_{[\chi(g_1)]}\,\mathrm{d} g_2\,\mathrm{d} g_1+2\int_{g_1\cap g_2\in D}|\chi(g_1)||\chi(g_2)|\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt]&=4\int_{[D]}|\chi(g_1)|^3\,\mathrm{d} g_1+2\int_{g_1\cap g_2\in D}|\chi(g_1)||\chi(g_2)|\,\mathrm{d} g_1\,\mathrm{d} g_2,\end{align*}
\begin{align*}D_2 & =\int_{g_1\cap g_2\in D}(|\chi(g_1)|^2+|\chi(g_2)|^2)\,\mathrm{d} g_1\,\mathrm{d} g_2+2\int_{g_1\cap g_2\in D}|\chi(g_1)||\chi(g_2)|\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt]&=2\int_{[D]}|\chi(g_1)|^2\int_{[\chi(g_1)]}\,\mathrm{d} g_2\,\mathrm{d} g_1+2\int_{g_1\cap g_2\in D}|\chi(g_1)||\chi(g_2)|\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt]&=4\int_{[D]}|\chi(g_1)|^3\,\mathrm{d} g_1+2\int_{g_1\cap g_2\in D}|\chi(g_1)||\chi(g_2)|\,\mathrm{d} g_1\,\mathrm{d} g_2,\end{align*}
which is equivalent to the first identity.
To prove the second identity we expand the integrand of
![]() $C_2$
and obtain
$C_2$
and obtain
It remains to notice that the last two integrals coincide due to symmetry.
Definition 3.2. For
![]() $g_1, g_2, \dots , g_n\in [D]$
, let
$g_1, g_2, \dots , g_n\in [D]$
, let
![]() $\langle g_1, g_2, \dots, g_n \rangle$
be the set of all chords
$\langle g_1, g_2, \dots, g_n \rangle$
be the set of all chords
![]() $\chi_{12}$
that join an endpoint of
$\chi_{12}$
that join an endpoint of
![]() $\chi(g_i)$
to an endpoint of
$\chi(g_i)$
to an endpoint of
![]() $\chi(g_j)$
,
$\chi(g_j)$
,
![]() $1 \leq i<j \leq n$
. Then, for any integer k,
$1 \leq i<j \leq n$
. Then, for any integer k,
![]() $0\leq k \leq n-2$
, we define the function
$0\leq k \leq n-2$
, we define the function
![]() $I_k\colon \langle g_1, g_2, \dots, g_n \rangle \rightarrow{\{0, 1\}}$
by
$I_k\colon \langle g_1, g_2, \dots, g_n \rangle \rightarrow{\{0, 1\}}$
by
 \begin{equation*}I_k(\chi_{12}) = \begin{cases} 1 & \text{if $\# \bigl(\chi_{12}\cap \bigl(\bigcup_{i=1}^n\overline{\chi(g_i)}\bigr)\bigr)=k$,} \\[5pt] 0 & \text{otherwise,} \end{cases}\end{equation*}
\begin{equation*}I_k(\chi_{12}) = \begin{cases} 1 & \text{if $\# \bigl(\chi_{12}\cap \bigl(\bigcup_{i=1}^n\overline{\chi(g_i)}\bigr)\bigr)=k$,} \\[5pt] 0 & \text{otherwise,} \end{cases}\end{equation*}
where
![]() $\overline{\chi(g_i)}$
is the closure of
$\overline{\chi(g_i)}$
is the closure of
![]() $\chi(g_i)$
in
$\chi(g_i)$
in
![]() $\mathbb{R}^2$
.
$\mathbb{R}^2$
.
The following two integrals are essential for our further work.
Lemma 3.1. We have
Proof. The left-hand side of (3.2) is equal to
 \begin{align*}& \int_{g_1\cap g_2\in D}|\chi(g_1)|(2d(g_1, g_2)-u(g_1, g_2))\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt]&\quad =2\int_{g_1\cap g_2\in D}|\chi(g_1)|^2\,\mathrm{d} g_1\,\mathrm{d} g_2+2\int_{g_1\cap g_2\in D}|\chi(g_1)||\chi(g_2)|\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt]&\quad\quad -\int_{g_1\cap g_2\in D}|\chi(g_1)|u(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt] &\quad =4I_3+(D_2-4I_3)-\dfrac{4D_2+U_2-C_2}{8},\end{align*}
\begin{align*}& \int_{g_1\cap g_2\in D}|\chi(g_1)|(2d(g_1, g_2)-u(g_1, g_2))\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt]&\quad =2\int_{g_1\cap g_2\in D}|\chi(g_1)|^2\,\mathrm{d} g_1\,\mathrm{d} g_2+2\int_{g_1\cap g_2\in D}|\chi(g_1)||\chi(g_2)|\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt]&\quad\quad -\int_{g_1\cap g_2\in D}|\chi(g_1)|u(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt] &\quad =4I_3+(D_2-4I_3)-\dfrac{4D_2+U_2-C_2}{8},\end{align*}
which coincides with the right-hand side of (3.2). To prove (3.3) we first notice that
Consequently, due to symmetry, the left-hand side of (3.3) becomes equal to
 \begin{align*}& 3\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{[\chi(g_1)]\cap [\chi(g_2)]}u(g_1, g_2)\,\mathrm{d} g_3-V_1\\[5pt]&\quad =3\int_{g_1\cap g_2\in D}u(g_1, g_2)(2d(g_1, g_2)-u(g_1, g_2))\,\mathrm{d} g_1\,\mathrm{d} g_2-V_1\\[5pt] &\quad =12\int_{g_1\cap g_2\in D}|\chi(g_1)|u(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2-3U_2-V_1\\[5pt] &\quad =\dfrac{12(4D_2+U_2-C_2)}{8}-3U_2-V_1, \end{align*}
\begin{align*}& 3\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{[\chi(g_1)]\cap [\chi(g_2)]}u(g_1, g_2)\,\mathrm{d} g_3-V_1\\[5pt]&\quad =3\int_{g_1\cap g_2\in D}u(g_1, g_2)(2d(g_1, g_2)-u(g_1, g_2))\,\mathrm{d} g_1\,\mathrm{d} g_2-V_1\\[5pt] &\quad =12\int_{g_1\cap g_2\in D}|\chi(g_1)|u(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2-3U_2-V_1\\[5pt] &\quad =\dfrac{12(4D_2+U_2-C_2)}{8}-3U_2-V_1, \end{align*}
which coincides with the right-hand side of (3.3).
We are now ready to compute
![]() $p_{46}$
and
$p_{46}$
and
![]() $p_{45}$
.
$p_{45}$
.
Theorem 3.1. We have
Proof. Four lines
![]() $g_i\in[D]$
,
$g_i\in[D]$
,
![]() $i=1, 2, 3, 4$
generate six intersection points inside D if and only if
$i=1, 2, 3, 4$
generate six intersection points inside D if and only if
![]() $g_1, g_2, g_3$
generate three intersections and
$g_1, g_2, g_3$
generate three intersections and
![]() $g_4\in \bigcap_{i=1}^3 [\chi(g_i)]$
. Therefore
$g_4\in \bigcap_{i=1}^3 [\chi(g_i)]$
. Therefore
where
![]() $B_6=\bigcap_{i=1}^3 [\chi(g_i)]$
.
$B_6=\bigcap_{i=1}^3 [\chi(g_i)]$
.
Let us fix
![]() $g_1, g_2, g_3$
and consider the set of points
$g_1, g_2, g_3$
and consider the set of points
![]() $\mathcal{P}=(g_1\cup g_2\cup g_3)\cap \partial D$
. Without loss of generality one can assume that
$\mathcal{P}=(g_1\cup g_2\cup g_3)\cap \partial D$
. Without loss of generality one can assume that
![]() $g_1\cap \partial D=\{P_1, P_4\}$
,
$g_1\cap \partial D=\{P_1, P_4\}$
,
![]() $g_2\cap \partial D=\{P_2, P_5\}$
, and
$g_2\cap \partial D=\{P_2, P_5\}$
, and
![]() $g_3\cap \partial D=\{P_3, P_6\}$
, where the points
$g_3\cap \partial D=\{P_3, P_6\}$
, where the points
![]() $P_i$
are consecutively distributed over the boundary
$P_i$
are consecutively distributed over the boundary
![]() $\partial D$
.
$\partial D$
.
The set
![]() $B_6$
belongs to the ring
$B_6$
belongs to the ring
![]() $r(\mathcal{P})$
and can be written as a union of three atoms
$r(\mathcal{P})$
and can be written as a union of three atoms
![]() $B_{61}, B_{62},$
and
$B_{61}, B_{62},$
and
![]() $B_{63}$
, where
$B_{63}$
, where
![]() $B_{6i}$
separates the points
$B_{6i}$
separates the points
![]() $P_i, P_{i+1}, P_{i+2}$
from the other points of
$P_i, P_{i+1}, P_{i+2}$
from the other points of
![]() $\mathcal{P}$
. By Theorem 2.1,
$\mathcal{P}$
. By Theorem 2.1,
where we notice that
![]() $\rho_{14}=|\chi(g_1)|$
,
$\rho_{14}=|\chi(g_1)|$
,
![]() $\rho_{25}=|\chi(g_2)|$
,
$\rho_{25}=|\chi(g_2)|$
,
![]() $\rho_{36}=|\chi(g_3)|$
, and the six subtracted terms represent the lengths of all chords
$\rho_{36}=|\chi(g_3)|$
, and the six subtracted terms represent the lengths of all chords
![]() $\chi_{12}\in \langle g_1, g_2, g_2\rangle$
that meet exactly one of the closed chords
$\chi_{12}\in \langle g_1, g_2, g_2\rangle$
that meet exactly one of the closed chords
![]() $\overline{\chi(g_i)}$
,
$\overline{\chi(g_i)}$
,
![]() $i=1, 2, 3$
. Thus
$i=1, 2, 3$
. Thus
 \begin{equation} \mu(B_6)=\sum_{i=1}^3 \mu(B_{6i})=2\sum_{i=1}^3|\chi(g_i)|-\sum_{\chi_{12}\in \langle g_1, g_2, g_3\rangle}|\chi_{12}|I_1(\chi_{12}).\end{equation}
\begin{equation} \mu(B_6)=\sum_{i=1}^3 \mu(B_{6i})=2\sum_{i=1}^3|\chi(g_i)|-\sum_{\chi_{12}\in \langle g_1, g_2, g_3\rangle}|\chi_{12}|I_1(\chi_{12}).\end{equation}
Now (3.6), (3.7), and Lemma 3.1 imply
Five intersection points may occur when three lines, e.g.
![]() $g_1, g_1, g_3$
, produce three intersections, and the fourth line,
$g_1, g_1, g_3$
, produce three intersections, and the fourth line,
![]() $g_4$
, intersects only
$g_4$
, intersects only
![]() $g_1$
and
$g_1$
and
![]() $g_2$
inside D. In this scenario, the roles of
$g_2$
inside D. In this scenario, the roles of
![]() $g_3$
and
$g_3$
and
![]() $g_4$
are interchangeable. Therefore the probability
$g_4$
are interchangeable. Therefore the probability
![]() $p_{45}$
can be written as
$p_{45}$
can be written as
where
![]() $B_5=([\chi(g_1)]\kern1pt\cap\kern1pt[\chi(g_2)]\cap[\chi(g_3)]^c) \kern1pt\cup\kern1pt ([\chi(g_1)]\cap[\chi(g_2)]^c\cap[\chi(g_3)]) \kern1pt\cup\kern1pt ([\chi(g_1)]^c\cap[\chi (g_2)] \cap[\chi(g_3)])$
.
$B_5=([\chi(g_1)]\kern1pt\cap\kern1pt[\chi(g_2)]\cap[\chi(g_3)]^c) \kern1pt\cup\kern1pt ([\chi(g_1)]\cap[\chi(g_2)]^c\cap[\chi(g_3)]) \kern1pt\cup\kern1pt ([\chi(g_1)]^c\cap[\chi (g_2)] \cap[\chi(g_3)])$
.
Using the same set
![]() $\mathcal{P}$
as in the case of six intersection points, one can represent
$\mathcal{P}$
as in the case of six intersection points, one can represent
![]() $B_5$
as a union of six atoms
$B_5$
as a union of six atoms
![]() $B_{5i}\in r(\mathcal{P})$
,
$B_{5i}\in r(\mathcal{P})$
,
![]() $i=1,\dots, 6$
, where
$i=1,\dots, 6$
, where
![]() $B_{5i}$
separates
$B_{5i}$
separates
![]() $\{P_i, P_{i+1}\}$
from the other points of
$\{P_i, P_{i+1}\}$
from the other points of
![]() $\mathcal{P}$
(when
$\mathcal{P}$
(when
![]() $i=6$
we replace
$i=6$
we replace
![]() $i+1$
with 1).
$i+1$
with 1).
By Theorem 2.1,
 \begin{alignat*}{3} \mu(B_{51})&=\rho_{13}+\rho_{26}-\rho_{12}-\rho_{36},\quad & \mu(B_{52}) &=\rho_{24}+\rho_{31}-\rho_{23}-\rho_{41}, \\[5pt] \mu(B_{53})&=\rho_{35}+\rho_{42}-\rho_{34}-\rho_{52}, \quad & \mu(B_{54}) &=\rho_{46}+\rho_{53}-\rho_{45}-\rho_{63},\\[5pt] \mu(B_{55})&=\rho_{51}+\rho_{64}-\rho_{56}-\rho_{14},\quad & \mu(B_{56}) &=\rho_{62}+\rho_{15}-\rho_{61}-\rho_{25}. \end{alignat*}
\begin{alignat*}{3} \mu(B_{51})&=\rho_{13}+\rho_{26}-\rho_{12}-\rho_{36},\quad & \mu(B_{52}) &=\rho_{24}+\rho_{31}-\rho_{23}-\rho_{41}, \\[5pt] \mu(B_{53})&=\rho_{35}+\rho_{42}-\rho_{34}-\rho_{52}, \quad & \mu(B_{54}) &=\rho_{46}+\rho_{53}-\rho_{45}-\rho_{63},\\[5pt] \mu(B_{55})&=\rho_{51}+\rho_{64}-\rho_{56}-\rho_{14},\quad & \mu(B_{56}) &=\rho_{62}+\rho_{15}-\rho_{61}-\rho_{25}. \end{alignat*}
Taking into account that
![]() $\rho_{ji}=\rho_{ij}$
and recognizing the type of each
$\rho_{ji}=\rho_{ij}$
and recognizing the type of each
![]() $\rho_{ij}$
participating in the above formulas, we come up with
$\rho_{ij}$
participating in the above formulas, we come up with
 \begin{equation} \mu(B_5)=\sum_{i=1}^6 \mu(B_{5i})=2\cdot \sum_{\chi_{12}\in \langle g_1, g_2, g_3\rangle}|\chi_{12}|I_1(\chi_{12})-2\sum_{i=1}^3|\chi(g_i)|-v(g_1,g_2,g_3).\end{equation}
\begin{equation} \mu(B_5)=\sum_{i=1}^6 \mu(B_{5i})=2\cdot \sum_{\chi_{12}\in \langle g_1, g_2, g_3\rangle}|\chi_{12}|I_1(\chi_{12})-2\sum_{i=1}^3|\chi(g_i)|-v(g_1,g_2,g_3).\end{equation}
 \begin{align*} p_{45}& =\dfrac{4}{L^4}\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{[\chi(g_1)]\cap [\chi(g_2)]} \sum_{\chi_{12}\in \langle g_1, g_2, g_3\rangle}|\chi_{12}|I_1(\chi_{12})\,\mathrm{d} g_3\\[5pt]&\quad -\dfrac{12}{L^4}\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{[\chi(g_1)]\cap [\chi(g_2)]}|\chi_(g_1)|\,\mathrm{d} g_3-\dfrac{2V_1}{L^4}. \end{align*}
\begin{align*} p_{45}& =\dfrac{4}{L^4}\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{[\chi(g_1)]\cap [\chi(g_2)]} \sum_{\chi_{12}\in \langle g_1, g_2, g_3\rangle}|\chi_{12}|I_1(\chi_{12})\,\mathrm{d} g_3\\[5pt]&\quad -\dfrac{12}{L^4}\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{[\chi(g_1)]\cap [\chi(g_2)]}|\chi_(g_1)|\,\mathrm{d} g_3-\dfrac{2V_1}{L^4}. \end{align*}
It remains to apply Lemma 3.1 and establish (3.5) by combining the like terms.
4. Computation of
 $\textbf{p}_{4\textbf{k}}$
for
$\textbf{p}_{4\textbf{k}}$
for
 $\textbf{k}=4, 3, 2, 1, 0$
$\textbf{k}=4, 3, 2, 1, 0$
We will use further notation in this section to make relevant calculations in all the scenarios that may occur when four lines meet inside D at less than five points.
Given
![]() $g_1\cap g_2 \in D$
, we let
$g_1\cap g_2 \in D$
, we let
![]() $\rho_1,\rho_2, \rho_3, \rho_4$
denote the lengths of four consecutive sides of the quadrilateral
$\rho_1,\rho_2, \rho_3, \rho_4$
denote the lengths of four consecutive sides of the quadrilateral
![]() $\mathrm{conv}((g_1\cup g_2)\cap \partial D)$
. To avoid ambiguity, we will always assume that the first two sides lie in different half-planes with respect to
$\mathrm{conv}((g_1\cup g_2)\cap \partial D)$
. To avoid ambiguity, we will always assume that the first two sides lie in different half-planes with respect to
![]() $g_1$
. If two lines, e.g.
$g_1$
. If two lines, e.g.
![]() $g_2$
and
$g_2$
and
![]() $g_3$
, are from [D] but do not meet inside D, then
$g_3$
, are from [D] but do not meet inside D, then
![]() $d_1, d_2$
will stand for the lengths of the diagonals of
$d_1, d_2$
will stand for the lengths of the diagonals of
![]() $\mathrm{conv}((g_2\cup g_3)\cap \partial D)$
, and
$\mathrm{conv}((g_2\cup g_3)\cap \partial D)$
, and
![]() $s_1, s_2$
will represent the lengths of the sides of the quadrilateral which are different from
$s_1, s_2$
will represent the lengths of the sides of the quadrilateral which are different from
![]() $\chi(g_2), \chi(g_3)$
.
$\chi(g_2), \chi(g_3)$
.
The new notation is illustrated in Figure 1. These are used to define the following new invariants of D:
 \begin{align*} R & =\int_{g_1\cap g_2 \in D}((\rho_1+\rho_2)(\rho_3+\rho_4)+(\rho_2+\rho_3)(\rho_4+\rho_1))\,\mathrm{d} g_1\,\mathrm{d} g_2,\\[5pt]Q_s &=\int_{g_2\cap g_3 \not\in D}(s_1+s_2)(d_1+d_2-s_1-s_2)\,\mathrm{d} g_2\,\mathrm{d} g_3,\\[5pt]Q_d &=\int_{g_2\cap g_3 \not\in D}(d_1+d_2)(d_1+d_2-s_1-s_2)\,\mathrm{d} g_2\,\mathrm{d} g_3.\end{align*}
\begin{align*} R & =\int_{g_1\cap g_2 \in D}((\rho_1+\rho_2)(\rho_3+\rho_4)+(\rho_2+\rho_3)(\rho_4+\rho_1))\,\mathrm{d} g_1\,\mathrm{d} g_2,\\[5pt]Q_s &=\int_{g_2\cap g_3 \not\in D}(s_1+s_2)(d_1+d_2-s_1-s_2)\,\mathrm{d} g_2\,\mathrm{d} g_3,\\[5pt]Q_d &=\int_{g_2\cap g_3 \not\in D}(d_1+d_2)(d_1+d_2-s_1-s_2)\,\mathrm{d} g_2\,\mathrm{d} g_3.\end{align*}

Figure 1. Scenarios of two lines intersecting D. (a) The case
![]() $g_{1} \cap g_{2} \in D$
. (b) The case
$g_{1} \cap g_{2} \in D$
. (b) The case
![]() $g_{2} \cap g_{3} \not\in D$
.
$g_{2} \cap g_{3} \not\in D$
.
To make upcoming formulas shorter, for the given pair of lines
![]() $g_1\cap g_2\in D$
we will use
$g_1\cap g_2\in D$
we will use
![]() $\mathcal{S}$
to denote the symmetric difference of
$\mathcal{S}$
to denote the symmetric difference of
![]() $[\chi(g_1)]$
and
$[\chi(g_1)]$
and
![]() $[\chi(g_2)]$
.
$[\chi(g_2)]$
.
![]() $\mathcal{S}_1$
and
$\mathcal{S}_1$
and
![]() $\mathcal{S}_2$
will stand for
$\mathcal{S}_2$
will stand for
![]() $[\chi(g_1)]\cap[\chi(g_2)]^c$
and
$[\chi(g_1)]\cap[\chi(g_2)]^c$
and
![]() $[\chi(g_1)]^c\cap[\chi(g_2)]$
, respectively. Use of parentheses in integrands will be avoided if it does not lead to misreading.
$[\chi(g_1)]^c\cap[\chi(g_2)]$
, respectively. Use of parentheses in integrands will be avoided if it does not lead to misreading.
Lemma 4.1. Let
![]() $I_{\mathcal{S}_1}$
and
$I_{\mathcal{S}_1}$
and
![]() $I_{\mathcal{S}_2}$
be the indicator functions of
$I_{\mathcal{S}_2}$
be the indicator functions of
![]() $\mathcal{S}_1$
and
$\mathcal{S}_1$
and
![]() $\mathcal{S}_2$
, respectively. Then the following six identities hold:
$\mathcal{S}_2$
, respectively. Then the following six identities hold:
Proof. Since
![]() $\mathcal{S}=\mathcal{S}_1\cup \mathcal{S}_2$
and
$\mathcal{S}=\mathcal{S}_1\cup \mathcal{S}_2$
and
![]() $\mathcal{S}_1\cap \mathcal{S}_2=\varnothing$
,
$\mathcal{S}_1\cap \mathcal{S}_2=\varnothing$
,
Using the technique developed in the previous two sections, one can check that
![]() $\mu(\mathcal{S}_1)=u(g_1, g_2)-2|\chi(g_2)|$
,
$\mu(\mathcal{S}_1)=u(g_1, g_2)-2|\chi(g_2)|$
,
![]() $\mu(\mathcal{S}_2)=u(g_1, g_2)-2|\chi(g_1)|$
, and consequently the left-hand side of (4.1) becomes equal to
$\mu(\mathcal{S}_2)=u(g_1, g_2)-2|\chi(g_1)|$
, and consequently the left-hand side of (4.1) becomes equal to
 \begin{align*} & 2\int_{g_1\cap g_2 \in D}|\chi(g_1)|u(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2-4\int_{g_1\cap g_2 \in D}|\chi(g_1)||\chi(g_2)|\,\mathrm{d} g_1\,\mathrm{d} g_2 \\[5pt] &\quad =\dfrac{4D_2+U_2-C_2}{4}-2D_2+8I_3=\dfrac{U_2-C_2-4D_2}{4}+8I_3. \end{align*}
\begin{align*} & 2\int_{g_1\cap g_2 \in D}|\chi(g_1)|u(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2-4\int_{g_1\cap g_2 \in D}|\chi(g_1)||\chi(g_2)|\,\mathrm{d} g_1\,\mathrm{d} g_2 \\[5pt] &\quad =\dfrac{4D_2+U_2-C_2}{4}-2D_2+8I_3=\dfrac{U_2-C_2-4D_2}{4}+8I_3. \end{align*}
To prove (4.2), we change the order of integration. The left-hand side of (4.2) becomes equal to
 \begin{align*}&\int_{g_2\cap g_3\not\in D}\,\mathrm{d} g_2\,\mathrm{d} g_3\int_{[\chi(g_2)]\cap[\chi(g_3)]}\sum_{\langle g_2, g_3\rangle}|\chi_{12}|I_0(\chi_{12})\,\mathrm{d} g_1 \\[5pt]&\quad\quad +\int_{g_1\cap g_3\not\in D}\,\mathrm{d} g_1\,\mathrm{d} g_3\int_{[\chi(g_1)]\cap[\chi(g_3)]}\sum_{\langle g_1, g_3\rangle}|\chi_{12}|I_0(\chi_{12})\,\mathrm{d} g_2\\[5pt] & \quad = 2\int_{g_2\cap g_3\not\in D}\sum_{\langle g_2, g_3\rangle}|\chi_{12}|I_0(\chi_{12})\mu([\chi(g_2)]\cap[\chi(g_3)])\,\mathrm{d} g_2\,\mathrm{d} g_3\\[5pt] &\quad =2Q_s,\end{align*}
\begin{align*}&\int_{g_2\cap g_3\not\in D}\,\mathrm{d} g_2\,\mathrm{d} g_3\int_{[\chi(g_2)]\cap[\chi(g_3)]}\sum_{\langle g_2, g_3\rangle}|\chi_{12}|I_0(\chi_{12})\,\mathrm{d} g_1 \\[5pt]&\quad\quad +\int_{g_1\cap g_3\not\in D}\,\mathrm{d} g_1\,\mathrm{d} g_3\int_{[\chi(g_1)]\cap[\chi(g_3)]}\sum_{\langle g_1, g_3\rangle}|\chi_{12}|I_0(\chi_{12})\,\mathrm{d} g_2\\[5pt] & \quad = 2\int_{g_2\cap g_3\not\in D}\sum_{\langle g_2, g_3\rangle}|\chi_{12}|I_0(\chi_{12})\mu([\chi(g_2)]\cap[\chi(g_3)])\,\mathrm{d} g_2\,\mathrm{d} g_3\\[5pt] &\quad =2Q_s,\end{align*}
where the last equality holds due to
![]() $\sum_{\langle g_2, g_3\rangle}|\chi_{12}|I_0(\chi_{12})=s_1+s_2$
and
$\sum_{\langle g_2, g_3\rangle}|\chi_{12}|I_0(\chi_{12})=s_1+s_2$
and
![]() $\mu([\chi(g_2)]\cap[\chi(g_3)])=d_1+d_2-s_1-s_2$
(see Figure 1(b)).
$\mu([\chi(g_2)]\cap[\chi(g_3)])=d_1+d_2-s_1-s_2$
(see Figure 1(b)).
Let us prove (4.3). The inner integral in (4.3) can be written in the form of the sum
The integrand of the first integral in (4.7) is piecewise constant over the set of lines
![]() $g_3\in \mathcal{S}_1$
. Indeed, look at Figure 1(a). The function is equal to
$g_3\in \mathcal{S}_1$
. Indeed, look at Figure 1(a). The function is equal to
![]() $\rho_3+\rho_4$
over the atom
$\rho_3+\rho_4$
over the atom
![]() $B^+\in r(\mathcal{P})$
that separates the point
$B^+\in r(\mathcal{P})$
that separates the point
![]() $P_3$
from the other points of
$P_3$
from the other points of
![]() $\mathcal{P}=\{P_1, P_2, P_3, P_4\}$
. On the other hand, it is equal to
$\mathcal{P}=\{P_1, P_2, P_3, P_4\}$
. On the other hand, it is equal to
![]() $\rho_1+\rho_2$
over
$\rho_1+\rho_2$
over
![]() $B^-$
, the atom that separates
$B^-$
, the atom that separates
![]() $P_1$
from
$P_1$
from
![]() $\mathcal{P}\setminus P_1$
. Taking into account that
$\mathcal{P}\setminus P_1$
. Taking into account that
![]() $\mathcal{S}_1=B^+\cup B^-$
, we obtain
$\mathcal{S}_1=B^+\cup B^-$
, we obtain
By our main computational engine (2.1), it is easy to verify that
![]() $\mu(B^+)=\rho_3+\rho_4-|\chi(g_2)|$
and
$\mu(B^+)=\rho_3+\rho_4-|\chi(g_2)|$
and
![]() $\mu(B^-)=\rho_1+\rho_2-|\chi(g_2)|$
. Substitution of these values in the right-hand side of the last formula yields
$\mu(B^-)=\rho_1+\rho_2-|\chi(g_2)|$
. Substitution of these values in the right-hand side of the last formula yields
which is equivalent to
The second integral in (4.7) can be obtained from (4.8) by interchanging
![]() $g_1$
and
$g_1$
and
![]() $g_2$
:
$g_2$
:
Based on (4.7), (4.8), (4.9), and Proposition 3.1, we conclude that
which is equal to the right-hand side of (4.3). The proofs of (4.4), (4.5), and (4.6) are very similar to the ones provided for (4.3), (4.2), and (4.1) respectively, and are thus omitted.
Theorem 4.1. Let
![]() $p_{44}^{(1)}$
be the probability that
$p_{44}^{(1)}$
be the probability that
![]() $g_1, g_2, g_3, g_4\in [D]$
produce four intersection points inside D and three of them intersect each other inside D. Then
$g_1, g_2, g_3, g_4\in [D]$
produce four intersection points inside D and three of them intersect each other inside D. Then
where
Proof. There are two scenarios where four lines
![]() $g_i\in[D]$
,
$g_i\in[D]$
,
![]() $i=1, 2, 3, 4$
can generate four intersection points inside D. In the first scenario we require three of the lines to make three intersection points inside D (enclose a triangle inside D) and the fourth to cut exactly one of those three inside D. Otherwise, in the second scenario, we require any three of the four lines to make exactly two intersections inside D (the four lines enclose a convex quadrilateral inside D). We denote the two mutually exclusive events by
$i=1, 2, 3, 4$
can generate four intersection points inside D. In the first scenario we require three of the lines to make three intersection points inside D (enclose a triangle inside D) and the fourth to cut exactly one of those three inside D. Otherwise, in the second scenario, we require any three of the four lines to make exactly two intersections inside D (the four lines enclose a convex quadrilateral inside D). We denote the two mutually exclusive events by
![]() $E_1$
and
$E_1$
and
![]() $E_2$
, respectively, and need to prove that
$E_2$
, respectively, and need to prove that
In the first scenario there are four choices to select three out of four lines to enclose a triangle inside D. Let those three be
![]() $g_1, g_2, g_3$
. Consider the set of points
$g_1, g_2, g_3$
. Consider the set of points
![]() $\mathcal{P}=(g_1\cup g_2\cup g_3)\cap \partial D$
. Again, without loss of generality one can assume that
$\mathcal{P}=(g_1\cup g_2\cup g_3)\cap \partial D$
. Again, without loss of generality one can assume that
![]() $g_1\cap \partial D=\{P_1, P_4\}$
,
$g_1\cap \partial D=\{P_1, P_4\}$
,
![]() $g_2\cap \partial D=\{P_2, P_5\}$
, and
$g_2\cap \partial D=\{P_2, P_5\}$
, and
![]() $g_3\cap \partial D=\{P_3, P_6\}$
, where the points
$g_3\cap \partial D=\{P_3, P_6\}$
, where the points
![]() $P_i$
are consecutively distributed over the boundary
$P_i$
are consecutively distributed over the boundary
![]() $\partial D$
. Consider the set
$\partial D$
. Consider the set
![]() $B_4^{(1)}\in r(\mathcal{P})$
comprising six atoms
$B_4^{(1)}\in r(\mathcal{P})$
comprising six atoms
![]() $B_{4i}^{(1)}, i=1,2,\dots, 6$
, where
$B_{4i}^{(1)}, i=1,2,\dots, 6$
, where
![]() $B_{4i}^{(1)}$
separates the point
$B_{4i}^{(1)}$
separates the point
![]() $P_i$
from the other five points of
$P_i$
from the other five points of
![]() $\mathcal{P}$
. Then
$\mathcal{P}$
. Then
The measure of each of the six atoms is computed below by Theorem 2.1:
 \begin{alignat*}{3} \mu\bigl(B_{41}^{(1)}\bigr) & = \rho_{12}+\rho_{16}-\rho_{26},\quad & \mu\bigl(B_{42}^{(1)}\bigr) &=\rho_{23}+\rho_{21}-\rho_{31}, \\[5pt] \mu\bigl(B_{43}^{(1)}\bigr) & = \rho_{34}+\rho_{32}-\rho_{42}, \quad & \mu\bigl(B_{44}^{(1)}\bigr) &=\rho_{45}+\rho_{43}-\rho_{53},\\[5pt] \mu\bigl(B_{45}^{(1)}\bigr) & = \rho_{56}+\rho_{54}-\rho_{64},\quad & \mu\bigl(B_{46}^{(1)}\bigr) &=\rho_{61}+\rho_{65}-\rho_{15}. \end{alignat*}
\begin{alignat*}{3} \mu\bigl(B_{41}^{(1)}\bigr) & = \rho_{12}+\rho_{16}-\rho_{26},\quad & \mu\bigl(B_{42}^{(1)}\bigr) &=\rho_{23}+\rho_{21}-\rho_{31}, \\[5pt] \mu\bigl(B_{43}^{(1)}\bigr) & = \rho_{34}+\rho_{32}-\rho_{42}, \quad & \mu\bigl(B_{44}^{(1)}\bigr) &=\rho_{45}+\rho_{43}-\rho_{53},\\[5pt] \mu\bigl(B_{45}^{(1)}\bigr) & = \rho_{56}+\rho_{54}-\rho_{64},\quad & \mu\bigl(B_{46}^{(1)}\bigr) &=\rho_{61}+\rho_{65}-\rho_{15}. \end{alignat*}
As a result, we obtain
 \begin{align*} p(E_1)&=\dfrac{4}{L^4}\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{[\chi(g_1)]\cap [\chi(g_2)]}\sum_{i=1}^6\mu\bigl(B_{4i}^{(1)}\bigr)\,\mathrm{d} g_3\\[5pt] &=\dfrac{4}{L^4}\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{[\chi(g_1)]\cap [\chi(g_2)]}2v(g_1,g_2,g_3) -\sum_{ \langle g_1, g_2, g_3\rangle}|\chi_{12}|I_1(\chi_{12})\,\mathrm{d} g_3.\end{align*}
\begin{align*} p(E_1)&=\dfrac{4}{L^4}\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{[\chi(g_1)]\cap [\chi(g_2)]}\sum_{i=1}^6\mu\bigl(B_{4i}^{(1)}\bigr)\,\mathrm{d} g_3\\[5pt] &=\dfrac{4}{L^4}\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{[\chi(g_1)]\cap [\chi(g_2)]}2v(g_1,g_2,g_3) -\sum_{ \langle g_1, g_2, g_3\rangle}|\chi_{12}|I_1(\chi_{12})\,\mathrm{d} g_3.\end{align*}
Finally, using Lemma 3.1, we arrive at
In the second scenario we have
where
 \begin{equation*}B_4^{(2)} = \begin{cases} \mathcal{S}_2\cap [\chi(g_3)] & \text{if $g_3\in \mathcal{S}_1$,} \\[5pt] \mathcal{S}_1\cap [\chi(g_3)] & \text{if $g_3\in \mathcal{S}_2$.} \end{cases}\end{equation*}
\begin{equation*}B_4^{(2)} = \begin{cases} \mathcal{S}_2\cap [\chi(g_3)] & \text{if $g_3\in \mathcal{S}_1$,} \\[5pt] \mathcal{S}_1\cap [\chi(g_3)] & \text{if $g_3\in \mathcal{S}_2$.} \end{cases}\end{equation*}
The measure
![]() $\mu\bigl(B_4^{(2)}\bigr)$
can be computed by Theorem 2.1 with reference to Figure 2.
$\mu\bigl(B_4^{(2)}\bigr)$
can be computed by Theorem 2.1 with reference to Figure 2.
The formula (2.1) implies
and

Figure 2. The distribution of signs over the chords participating in the combinatorial decomposition of
![]() $\mu\bigl(B_{4}^{(2)}\bigr).$
(a) The case
$\mu\bigl(B_{4}^{(2)}\bigr).$
(a) The case
![]() $g_{1} \cap g_{2} \in D$
and
$g_{1} \cap g_{2} \in D$
and
![]() $g_{3}$
meets
$g_{3}$
meets
![]() $\chi(g_1)$
but not
$\chi(g_1)$
but not
![]() $\chi(g_2)$
. (b) The case
$\chi(g_2)$
. (b) The case
![]() $g_{1} \cap g_{2} \in D$
and
$g_{1} \cap g_{2} \in D$
and
![]() $g_{3}$
meets
$g_{3}$
meets
![]() $\chi(g_2)$
but not
$\chi(g_2)$
but not
![]() $\chi(g_1)$
.
$\chi(g_1)$
.
By incorporating the indicator functions
![]() $I_{\mathcal{S}_i}$
, we plug the obtained expressions into (4.12):
$I_{\mathcal{S}_i}$
, we plug the obtained expressions into (4.12):
 \begin{align*} p(E_2)& =\dfrac{3}{2L^4}\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{\mathcal{S}}2\cdot \sum_{\langle g_1, g_2\rangle}|\chi_{12}|I_1(\chi_{12})\,\mathrm{d} g_3 \\[5pt] &\quad -\dfrac{3}{2L^4}\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{\mathcal{S}}I_{\mathcal{S}_1}\sum_{\langle g_2, g_3\rangle}|\chi_{12}|I_0(\chi_{12}) +I_{\mathcal{S}_2}\sum_{\langle g_1, g_3\rangle}|\chi_{12}|I_0(\chi_{12}) \,\mathrm{d} g_3\\[5pt] &\quad -\dfrac{3}{2L^4}\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{\mathcal{S}}2\cdot I_{\mathcal{S}_1}|\chi(g_1)|+2\cdot I_{\mathcal{S}_2}|\chi(g_2)|\,\mathrm{d} g_3.\end{align*}
\begin{align*} p(E_2)& =\dfrac{3}{2L^4}\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{\mathcal{S}}2\cdot \sum_{\langle g_1, g_2\rangle}|\chi_{12}|I_1(\chi_{12})\,\mathrm{d} g_3 \\[5pt] &\quad -\dfrac{3}{2L^4}\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{\mathcal{S}}I_{\mathcal{S}_1}\sum_{\langle g_2, g_3\rangle}|\chi_{12}|I_0(\chi_{12}) +I_{\mathcal{S}_2}\sum_{\langle g_1, g_3\rangle}|\chi_{12}|I_0(\chi_{12}) \,\mathrm{d} g_3\\[5pt] &\quad -\dfrac{3}{2L^4}\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{\mathcal{S}}2\cdot I_{\mathcal{S}_1}|\chi(g_1)|+2\cdot I_{\mathcal{S}_2}|\chi(g_2)|\,\mathrm{d} g_3.\end{align*}
Finally, due to Lemma 4.1 (the first three identities), we come up with
 \begin{align*} p(E_2)&=\dfrac{3}{2L^4}\biggl(2\cdot\biggl(\dfrac{7U_2-4D_2+C_2}{4}-2R\biggr)-2Q_s-2\cdot\biggl(\dfrac{U_2-C_2-4D_2}{4}+8I_3\biggr) \biggr)\\[5pt] &=\dfrac{3}{L^4}\biggl(\dfrac{3U_2+C_2}{2}-8I_3-2R-Q_s\biggr). \end{align*}
\begin{align*} p(E_2)&=\dfrac{3}{2L^4}\biggl(2\cdot\biggl(\dfrac{7U_2-4D_2+C_2}{4}-2R\biggr)-2Q_s-2\cdot\biggl(\dfrac{U_2-C_2-4D_2}{4}+8I_3\biggr) \biggr)\\[5pt] &=\dfrac{3}{L^4}\biggl(\dfrac{3U_2+C_2}{2}-8I_3-2R-Q_s\biggr). \end{align*}
The proof is thus complete.
Three intersection points made by four lines from [D] can occur in three ways.
Event 1. The lines produce three chords each possessing two intersection points, and one containing no intersection point.
Event 2. The lines produce two chords each possessing two intersection points, and the other two each possessing one intersection point.
Event 3. The lines produce three chords each possessing one intersection point, and one possessing three intersection points.
We let
![]() $p_{43}^{(1)}$
,
$p_{43}^{(1)}$
,
![]() $p_{43}^{(2)}$
, and
$p_{43}^{(2)}$
, and
![]() $p_{43}^{(3)}$
denote the probabilities of Event 1, Event 2, and Event 3, respectively.
$p_{43}^{(3)}$
denote the probabilities of Event 1, Event 2, and Event 3, respectively.
Theorem 4.2. We have
where
Proof. Events 1, 2, and 3 are mutually exclusive and cover all the cases of three intersections inside D.
Let us now define an undirected graph T with the vertex set
![]() $\{1, 2, 3, 4\}$
, where the vertices i and j are adjacent if and only if
$\{1, 2, 3, 4\}$
, where the vertices i and j are adjacent if and only if
![]() $g_i\cap g_j\in D$
. If
$g_i\cap g_j\in D$
. If
![]() $g_1, g_2, g_3, g_4$
are placed as described in Event 1, then there are four possibilities to make a graph T (three vertices of degree 2, and one vertex of degree 0). Thus
$g_1, g_2, g_3, g_4$
are placed as described in Event 1, then there are four possibilities to make a graph T (three vertices of degree 2, and one vertex of degree 0). Thus
where
![]() $B_3^{(1)}=[\chi(g_1)]^c\cap[\chi(g_2)]^c\cap[\chi(g_3)]^c.$
$B_3^{(1)}=[\chi(g_1)]^c\cap[\chi(g_2)]^c\cap[\chi(g_3)]^c.$
Since
![]() $\mu\bigl(B_3^{(1)}\bigr)=L-v(g_1, g_2, g_3)$
, we obtain
$\mu\bigl(B_3^{(1)}\bigr)=L-v(g_1, g_2, g_3)$
, we obtain
As by (3.1),
![]() $p_{33}={C_1}/{L^3}$
, we establish (4.13).
$p_{33}={C_1}/{L^3}$
, we establish (4.13).
If
![]() $g_1, g_2, g_3, g_4$
are placed as described in Event 2, then the number of possible graphs T (with two vertices of degree 2 and two vertices of degree 1) is 12. This number will be reduced to 4 if we also require vertices 1 and 2 to be adjacent, and vertex 3 to be adjacent to either 1 or 2 but not both (see Figure 3). Hence we acquire
$g_1, g_2, g_3, g_4$
are placed as described in Event 2, then the number of possible graphs T (with two vertices of degree 2 and two vertices of degree 1) is 12. This number will be reduced to 4 if we also require vertices 1 and 2 to be adjacent, and vertex 3 to be adjacent to either 1 or 2 but not both (see Figure 3). Hence we acquire
where
 \begin{equation*}B_3^{(2)} = \begin{cases} [\chi(g_1)]^c\cap \bigl([\chi(g_2)]\Delta [\chi(g_3)]\bigr) & \text{if $g_3\in \mathcal{S}_1$,} \\[5pt] [\chi(g_2)]^c\cap \bigl([\chi(g_1)]\Delta [\chi(g_3)]\bigr) & \text{if $g_3\in \mathcal{S}_2$,} \end{cases}\end{equation*}
\begin{equation*}B_3^{(2)} = \begin{cases} [\chi(g_1)]^c\cap \bigl([\chi(g_2)]\Delta [\chi(g_3)]\bigr) & \text{if $g_3\in \mathcal{S}_1$,} \\[5pt] [\chi(g_2)]^c\cap \bigl([\chi(g_1)]\Delta [\chi(g_3)]\bigr) & \text{if $g_3\in \mathcal{S}_2$,} \end{cases}\end{equation*}
and
![]() $\Delta$
stands for the symmetric difference operation.
$\Delta$
stands for the symmetric difference operation.
In the last scenario, if
![]() $g_1, g_2, g_3, g_4$
are placed as described in Event 3, then there are only four graphs T (three vertices of degree 1 and one vertex of degree 3). An extra restriction requiring vertices 1 and 2 to be adjacent, and vertex 3 to be adjacent to either 1 or 2 but not both, allows us to construct only two graphs T. These are displayed in Figure 4. Consequently
$g_1, g_2, g_3, g_4$
are placed as described in Event 3, then there are only four graphs T (three vertices of degree 1 and one vertex of degree 3). An extra restriction requiring vertices 1 and 2 to be adjacent, and vertex 3 to be adjacent to either 1 or 2 but not both, allows us to construct only two graphs T. These are displayed in Figure 4. Consequently
where
 \begin{equation*}B_3^{(3)} = \begin{cases} [\chi(g_1)]\cap [\chi(g_2)]^c\cap [\chi(g_3)]^c & \text{if $g_3\in \mathcal{S}_1$,} \\[5pt] [\chi(g_1)]^c\cap [\chi(g_2)]\cap [\chi(g_3)]^c & \text{if $g_3\in \mathcal{S}_2$.} \end{cases}\end{equation*}
\begin{equation*}B_3^{(3)} = \begin{cases} [\chi(g_1)]\cap [\chi(g_2)]^c\cap [\chi(g_3)]^c & \text{if $g_3\in \mathcal{S}_1$,} \\[5pt] [\chi(g_1)]^c\cap [\chi(g_2)]\cap [\chi(g_3)]^c & \text{if $g_3\in \mathcal{S}_2$.} \end{cases}\end{equation*}

Figure 3. Versions of T where 1 is adjacent to 2, and 3 is adjacent to either 2 or 1 but not both (Event 2).

Figure 4. Versions of T where 1 is adjacent to 2, and 3 is adjacent to either 2 or 1 but not both (Event 3).
It remains to calculate
![]() $\mu\bigl(B_3^{(2)}\bigr)$
and
$\mu\bigl(B_3^{(2)}\bigr)$
and
![]() $\mu\bigl(B_3^{(3)}\bigr)$
and then the integrals (4.16) and (4.17) accordingly. For the measures, we apply the combinatorial formula (2.1), while the integrals need the Lemma 4.1 to be used. Computation is similar to that used for proving (4.11) and is therefore omitted.
$\mu\bigl(B_3^{(3)}\bigr)$
and then the integrals (4.16) and (4.17) accordingly. For the measures, we apply the combinatorial formula (2.1), while the integrals need the Lemma 4.1 to be used. Computation is similar to that used for proving (4.11) and is therefore omitted.
Two intersection points generated by four lines are possible in two scenarios.
Event 1. One chord possesses two intersection points, two of the chords possess one intersection point each, and one chord does not possess any intersection point.
Event 2. Each chord of the four lines possesses exactly one intersection point.
Let the probabilities of the above-mentioned events be
![]() $p_{42}^{(1)}$
and
$p_{42}^{(1)}$
and
![]() $p_{42}^{(2)}$
respectively.
$p_{42}^{(2)}$
respectively.
Theorem 4.3. We have
where
Proof. Events 1 and 2 are mutually exclusive, so it remains to verify (4.18) and (4.19). We first notice that
where
![]() $B_2^{(1)}=[\chi(g_1)]^c\cap[\chi(g_2)]^c\cap[\chi(g_3)]^c$
. Since
$B_2^{(1)}=[\chi(g_1)]^c\cap[\chi(g_2)]^c\cap[\chi(g_3)]^c$
. Since
![]() $\mu\bigl(B_2^{(1)}\bigr)=L-v(g_1, g_2, g_3)$
, we obtain
$\mu\bigl(B_2^{(1)}\bigr)=L-v(g_1, g_2, g_3)$
, we obtain
We recognize that the first term above is equal to
![]() $6\cdot \frac{2}{3}p_{32}=4p_{32}$
. Evaluation of the second term is based on (4.4) and (4.2). Indeed
$6\cdot \frac{2}{3}p_{32}=4p_{32}$
. Evaluation of the second term is based on (4.4) and (4.2). Indeed
 \begin{align*}&\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{\mathcal{S}}\sum_{\langle g_1, g_2, g_3\rangle}|\chi_{12}|I_0(\chi_{12}) \,\mathrm{d} g_3\\[5pt]&\quad = \int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{\mathcal{S}}I_{\mathcal{S}_1}\sum_{\langle g_1, g_2\rangle \cup \langle g_1, g_3\rangle }|\chi_{12}|I_0(\chi_{12}) +I_{\mathcal{S}_2}\sum_{\langle g_1, g_2\rangle \cup \langle g_2, g_3\rangle }|\chi_{12}|I_0(\chi_{12})\\[5pt] &\quad\quad + I_{\mathcal{S}_1}\sum_{\langle g_2, g_3\rangle}|\chi_{12}|I_0(\chi_{12}) +I_{\mathcal{S}_2}\sum_{\langle g_1, g_3\rangle}|\chi_{12}|I_0(\chi_{12}) \,\mathrm{d} g_3\\[5pt]&\quad = \int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{\mathcal{S}} 2\sum_{\langle g_1, g_2\rangle}|\chi_{12}|I_0(\chi_{12}) + I_{\mathcal{S}_1}\sum_{\langle g_2, g_3\rangle}|\chi_{12}|I_0(\chi_{12})\\[5pt]&\quad\quad + I_{\mathcal{S}_2}\sum_{\langle g_1, g_3\rangle}|\chi_{12}|I_0(\chi_{12})\,\mathrm{d} g_3=\dfrac{C_2-4D_2-U_2}{2}+4R+2Q_s,\end{align*}
\begin{align*}&\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{\mathcal{S}}\sum_{\langle g_1, g_2, g_3\rangle}|\chi_{12}|I_0(\chi_{12}) \,\mathrm{d} g_3\\[5pt]&\quad = \int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{\mathcal{S}}I_{\mathcal{S}_1}\sum_{\langle g_1, g_2\rangle \cup \langle g_1, g_3\rangle }|\chi_{12}|I_0(\chi_{12}) +I_{\mathcal{S}_2}\sum_{\langle g_1, g_2\rangle \cup \langle g_2, g_3\rangle }|\chi_{12}|I_0(\chi_{12})\\[5pt] &\quad\quad + I_{\mathcal{S}_1}\sum_{\langle g_2, g_3\rangle}|\chi_{12}|I_0(\chi_{12}) +I_{\mathcal{S}_2}\sum_{\langle g_1, g_3\rangle}|\chi_{12}|I_0(\chi_{12}) \,\mathrm{d} g_3\\[5pt]&\quad = \int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{\mathcal{S}} 2\sum_{\langle g_1, g_2\rangle}|\chi_{12}|I_0(\chi_{12}) + I_{\mathcal{S}_1}\sum_{\langle g_2, g_3\rangle}|\chi_{12}|I_0(\chi_{12})\\[5pt]&\quad\quad + I_{\mathcal{S}_2}\sum_{\langle g_1, g_3\rangle}|\chi_{12}|I_0(\chi_{12})\,\mathrm{d} g_3=\dfrac{C_2-4D_2-U_2}{2}+4R+2Q_s,\end{align*}
and (4.18) is proved.
The other ‘partial’ probability can be expressed by the following integral:
where
![]() $B_2^{(2)}=[\chi(g_3)]\cap[\chi(g_2)]^c\cap[\chi(g_1))]^c.$
Then
$B_2^{(2)}=[\chi(g_3)]\cap[\chi(g_2)]^c\cap[\chi(g_1))]^c.$
Then
 \begin{equation} \mu\bigl(B_2^{(2)}\bigr)=2|\chi(g_3)|-\mu \biggl(\bigcap_{i=1}^3 [\chi(g_i)]\biggr)-\mu(([\chi(g_1)]\Delta [\chi(g_2)])\cap[\chi(g_3)]).\end{equation}
\begin{equation} \mu\bigl(B_2^{(2)}\bigr)=2|\chi(g_3)|-\mu \biggl(\bigcap_{i=1}^3 [\chi(g_i)]\biggr)-\mu(([\chi(g_1)]\Delta [\chi(g_2)])\cap[\chi(g_3)]).\end{equation}
Since
 \begin{equation*} \dfrac{1}{L^4}\int_{g_1\cap g_3\not\in D}\,\mathrm{d} g_1\,\mathrm{d} g_3\int_{[\chi(g_1)]\cap[\chi(g_3)]^c}\mu\biggl(\bigcap_{i=1}^3 [\chi(g_i)]\biggr)\,\mathrm{d} g_2=\dfrac{1}{12}p_{44}^{(1)}\end{equation*}
\begin{equation*} \dfrac{1}{L^4}\int_{g_1\cap g_3\not\in D}\,\mathrm{d} g_1\,\mathrm{d} g_3\int_{[\chi(g_1)]\cap[\chi(g_3)]^c}\mu\biggl(\bigcap_{i=1}^3 [\chi(g_i)]\biggr)\,\mathrm{d} g_2=\dfrac{1}{12}p_{44}^{(1)}\end{equation*}
and
then due to (4.20) the proof will be finished if we show that
By the combinatorial formula,
Then the integral in (4.22) is equal to
The first term in (4.23) is equal to
while the second term is equal to
 \begin{align*}&\int_{g_1\cap g_3\not\in D}|\chi(g_3)|\,\mathrm{d} g_1\,\mathrm{d} g_3\int_{[\chi(g_1)]\cap [\chi(g_3)]}\,\mathrm{d} g_2\\[5pt] &\quad = \dfrac{1}{2}\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{\mathcal{S}}I_{\mathcal{S}_1}|\chi(g_2)|+I_{\mathcal{S}_2}|\chi(g_1)|\,\mathrm{d} g_3\\[5pt] &\quad =\dfrac{U_2-C_2+4D_2}{8}-4I_3,\end{align*}
\begin{align*}&\int_{g_1\cap g_3\not\in D}|\chi(g_3)|\,\mathrm{d} g_1\,\mathrm{d} g_3\int_{[\chi(g_1)]\cap [\chi(g_3)]}\,\mathrm{d} g_2\\[5pt] &\quad = \dfrac{1}{2}\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{\mathcal{S}}I_{\mathcal{S}_1}|\chi(g_2)|+I_{\mathcal{S}_2}|\chi(g_1)|\,\mathrm{d} g_3\\[5pt] &\quad =\dfrac{U_2-C_2+4D_2}{8}-4I_3,\end{align*}
where the last equality holds due to (4.6).
To complete the proof, it remains to subtract the last expression from
![]() $2\pi^2F^2-D_2+4I_3$
and check that it is equal to the right-hand side of (4.22).
$2\pi^2F^2-D_2+4I_3$
and check that it is equal to the right-hand side of (4.22).
Theorem 4.4. We have
Proof. The only possible way to generate one intersection point inside D is having two chords possessing one intersection point each, and two more chords possessing no intersection points. The model yields
where
![]() $B_1=[\chi(g_3)]^c\cap[\chi(g_2)]^c\cap[\chi(g_1))]^c.$
We deliver the computation of
$B_1=[\chi(g_3)]^c\cap[\chi(g_2)]^c\cap[\chi(g_1))]^c.$
We deliver the computation of
![]() $\mu(B_1)$
by the combinatorial algorithm through Figure 5.
$\mu(B_1)$
by the combinatorial algorithm through Figure 5.

Figure 5. The distribution of signs over the chords participating in the combinatorial decomposition of
![]() $\mu(B_{1})$
.
$\mu(B_{1})$
.
Let us fix
![]() $g_1, g_2, g_3\in [D]$
such that the first two intersect each other inside D, and
$g_1, g_2, g_3\in [D]$
such that the first two intersect each other inside D, and
![]() $g_3$
intersects none of the chords
$g_3$
intersects none of the chords
![]() $\chi(g_1),\,\chi(g_2)$
. Consider the set of points
$\chi(g_1),\,\chi(g_2)$
. Consider the set of points
![]() $\mathcal{P}=(g_1\cup g_2\cup g_3)\cap \partial D$
. Without loss of generality, we assume that
$\mathcal{P}=(g_1\cup g_2\cup g_3)\cap \partial D$
. Without loss of generality, we assume that
![]() $g_1\cap \partial D=\{P_1, P_5\}$
,
$g_1\cap \partial D=\{P_1, P_5\}$
,
![]() $g_2\cap \partial D=\{P_2, P_6\}$
, and
$g_2\cap \partial D=\{P_2, P_6\}$
, and
![]() $g_3\cap \partial D=\{P_3, P_4\}$
, where the points
$g_3\cap \partial D=\{P_3, P_4\}$
, where the points
![]() $P_i$
are consecutively distributed over the boundary
$P_i$
are consecutively distributed over the boundary
![]() $\partial D$
. As usual, we let
$\partial D$
. As usual, we let
![]() $\rho_{ij}$
denote the Euclidean distance between points
$\rho_{ij}$
denote the Euclidean distance between points
![]() $P_i$
and
$P_i$
and
![]() $P_j$
. Then
$P_j$
. Then
![]() $B_1$
consists of the lines that lie in the complement of the convex hull of
$B_1$
consists of the lines that lie in the complement of the convex hull of
![]() $\mathcal{P}$
and the atom
$\mathcal{P}$
and the atom
![]() $A\in r(\mathcal{P})$
that separates the points
$A\in r(\mathcal{P})$
that separates the points
![]() $P_3,P_4$
from the other four. Hence
$P_3,P_4$
from the other four. Hence
![]() $\mu(B_1)=L-\rho_{12}-\rho_{23}-\dots-\rho_{61}+\mu(A).$
Since
$\mu(B_1)=L-\rho_{12}-\rho_{23}-\dots-\rho_{61}+\mu(A).$
Since
![]() $\mu(A)=\rho_{24}+\rho_{35}-|\chi(g_3)|-\rho_{25},$
we obtain
$\mu(A)=\rho_{24}+\rho_{35}-|\chi(g_3)|-\rho_{25},$
we obtain
On the other hand,
![]() $\rho_{24}+\rho_{35}-\rho_{23}-\rho_{45}$
can be interpreted as the measure of the set of lines that cut
$\rho_{24}+\rho_{35}-\rho_{23}-\rho_{45}$
can be interpreted as the measure of the set of lines that cut
![]() $\chi(g_3)$
and meet at least one of the chords
$\chi(g_3)$
and meet at least one of the chords
![]() $\chi(g_1)$
,
$\chi(g_1)$
,
![]() $\chi(g_2)$
. From (4.21), that measure is equal to
$\chi(g_2)$
. From (4.21), that measure is equal to
![]() $2|\chi(g_3)|-\mu\bigl(B_2^{(2)}\bigr)$
, and therefore we establish
$2|\chi(g_3)|-\mu\bigl(B_2^{(2)}\bigr)$
, and therefore we establish
It is easy to verify that
and
Integration of
![]() $u(g_1, g_2)$
requires a change of order:
$u(g_1, g_2)$
requires a change of order:
 \begin{align*}&\dfrac{1}{L^4}\int_{g_1\cap g_3\not\in D}\,\mathrm{d} g_1\,\mathrm{d} g_3\int_{[\chi(g_1)]\cap[\chi(g_3)]^c}u(g_1,g_2)\,\mathrm{d} g_2\\[5pt]&\quad = \dfrac{1}{L^4}\int_{g_1\cap g_2\in D}u(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{[\chi(g_1)]^c\cap[\chi(g_2)]^c}\,\mathrm{d} g_3\\[5pt] &\quad = \dfrac{1}{L^4}\int_{g_1\cap g_2\in D}u(g_1, g_2)(L-u(g_1, g_2))\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt] &\quad =\dfrac{U_1}{L^3}-\dfrac{U_2}{L^4}.\end{align*}
\begin{align*}&\dfrac{1}{L^4}\int_{g_1\cap g_3\not\in D}\,\mathrm{d} g_1\,\mathrm{d} g_3\int_{[\chi(g_1)]\cap[\chi(g_3)]^c}u(g_1,g_2)\,\mathrm{d} g_2\\[5pt]&\quad = \dfrac{1}{L^4}\int_{g_1\cap g_2\in D}u(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{[\chi(g_1)]^c\cap[\chi(g_2)]^c}\,\mathrm{d} g_3\\[5pt] &\quad = \dfrac{1}{L^4}\int_{g_1\cap g_2\in D}u(g_1, g_2)(L-u(g_1, g_2))\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt] &\quad =\dfrac{U_1}{L^3}-\dfrac{U_2}{L^4}.\end{align*}
Now from (4.24) we conclude that
Finally, the probability of having no intersection points inside D is
![]() $p_{40}=1 - \sum_{k=1}^6 p_{4k}$
.
$p_{40}=1 - \sum_{k=1}^6 p_{4k}$
.
5. Representation of
 $I_3$
and
$I_3$
and
 $V_1$
by intersection probabilities
$V_1$
by intersection probabilities
In this section we first aim to express the invariants
![]() $V_1$
and
$V_1$
and
![]() $I_3$
by intersection probabilities to establish an analogue of (1.2). Looking through the formulas of
$I_3$
by intersection probabilities to establish an analogue of (1.2). Looking through the formulas of
![]() $p_{4k}$
obtained in the previous two sections, we notice that the family of new invariants can be reduced to
$p_{4k}$
obtained in the previous two sections, we notice that the family of new invariants can be reduced to
![]() $U_2$
,
$U_2$
,
![]() $C_2$
,
$C_2$
,
![]() $D_2$
,
$D_2$
,
![]() $K_d$
,
$K_d$
,
![]() $K_s$
,
$K_s$
,
![]() $V_1$
, and
$V_1$
, and
![]() $I_3$
, where
$I_3$
, where
![]() $K_s=Q_s+2R$
and
$K_s=Q_s+2R$
and
![]() $K_d=Q_d+2R$
.
$K_d=Q_d+2R$
.
![]() $I_3$
is known (by Crofton; see e.g. [Reference Santaló8]) to be equal to
$I_3$
is known (by Crofton; see e.g. [Reference Santaló8]) to be equal to
![]() $3F^2$
, but we will not be using this result below.
$3F^2$
, but we will not be using this result below.
Theorem 5.1. The following identities hold:
Proof. Equation (5.1) immediately follows from (3.1) and (4.13).
Let us compute the mean number of the intersection points generated by four lines inside D. We directly use the formulas for intersection probabilities
![]() $p_{4k}$
,
$p_{4k}$
,
![]() $k=6,5,\dots, 1$
obtained in the previous two sections. By combining the like terms accurately, we obtain
$k=6,5,\dots, 1$
obtained in the previous two sections. By combining the like terms accurately, we obtain
 \begin{equation} \sum_{k=1}^6kp_{4k}=\dfrac{12\pi F}{L^2} +\dfrac{3}{L^4}(\!-\!3U_2+3C_2-12D_2+4V_1+4K_d+32I_3).\end{equation}
\begin{equation} \sum_{k=1}^6kp_{4k}=\dfrac{12\pi F}{L^2} +\dfrac{3}{L^4}(\!-\!3U_2+3C_2-12D_2+4V_1+4K_d+32I_3).\end{equation}
On the other hand, the mean number of intersection points generated by n lines inside D is known (see [Reference Santaló8]) to be equal to
![]() ${n(n-1)\pi F}/{L^2}$
. Thus, from (5.3), we obtain
${n(n-1)\pi F}/{L^2}$
. Thus, from (5.3), we obtain
Based on (4.15), the last identity can be rewritten as
![]() $p_{43}^{(3)}\cdot L^4+4V_1-32I_3=0$
, that is,
$p_{43}^{(3)}\cdot L^4+4V_1-32I_3=0$
, that is,
Below we check the results against the second moment of the number of intersection points generated by n lines inside D (for the formula below, see [Reference Santaló8]):
We start with the direct substitution of the obtained probabilities into the second moment formula.
 \begin{align*}\sum_{k=1}^6k^2p_{4k} & =2p_{31}+16p_{32}-\dfrac{1}{2}p_{44}^{(1)}-p_{43}^{(2)}+\dfrac{1}{L^4}(\!-\!36U_2+30C_2-120D_2 \\[5pt]&\quad +42V_1+288I_3+12K_s+36K_d+36LC_1+24\pi^2 F^2 -6LU_1).\end{align*}
\begin{align*}\sum_{k=1}^6k^2p_{4k} & =2p_{31}+16p_{32}-\dfrac{1}{2}p_{44}^{(1)}-p_{43}^{(2)}+\dfrac{1}{L^4}(\!-\!36U_2+30C_2-120D_2 \\[5pt]&\quad +42V_1+288I_3+12K_s+36K_d+36LC_1+24\pi^2 F^2 -6LU_1).\end{align*}
Further substitution of the known expressions for
![]() $p_{31}$
,
$p_{31}$
,
![]() $p_{32}$
,
$p_{32}$
,
![]() $p_{44}^{(1)}$
, and
$p_{44}^{(1)}$
, and
![]() $p_{43}^{(2)}$
results in
$p_{43}^{(2)}$
results in
 \begin{align}\sum_{k=1}^6k^2p_{4k} & =\dfrac{12\pi F}{L^2}+\dfrac{24\pi^2 F^2}{L^4}+\dfrac{36(U_1+C_1)-192I_2}{L^3} \notag \\[5pt]&\quad +\dfrac{1}{L^4}(27C_2-27U_2-108D_2+36K_d+288I_3+36V_1).\end{align}
\begin{align}\sum_{k=1}^6k^2p_{4k} & =\dfrac{12\pi F}{L^2}+\dfrac{24\pi^2 F^2}{L^4}+\dfrac{36(U_1+C_1)-192I_2}{L^3} \notag \\[5pt]&\quad +\dfrac{1}{L^4}(27C_2-27U_2-108D_2+36K_d+288I_3+36V_1).\end{align}
Since
![]() $36(U_1+C_1)=72D_1=288I_2$
and, from (4.15),
$36(U_1+C_1)=72D_1=288I_2$
and, from (4.15),
(5.6) implies
 \begin{equation*}\sum_{k=1}^6k^2p_{4k} =\dfrac{12\pi F}{L^2}+\dfrac{24\pi^2 F^2}{L^4}+\dfrac{96I_2}{L^3}+\dfrac{9}{L^4}\bigl(p_{43}^{(3)}\cdot L^4+4V_1-32I_3\bigr).\end{equation*}
\begin{equation*}\sum_{k=1}^6k^2p_{4k} =\dfrac{12\pi F}{L^2}+\dfrac{24\pi^2 F^2}{L^4}+\dfrac{96I_2}{L^3}+\dfrac{9}{L^4}\bigl(p_{43}^{(3)}\cdot L^4+4V_1-32I_3\bigr).\end{equation*}
Due to (5.4), the last expression in the parentheses is equal to zero. This means that we have reached the right-hand side of (5.5) for
![]() $n=4$
.
$n=4$
.
6. Computation of intersection probabilities for a disc with radius r
The formulas obtained for intersection probabilities motivated us to compute invariants of D through simulations. For example, we used Python 3.8.8 software to approximate the values of
![]() $I_2$
,
$I_2$
,
![]() $U_1$
,
$U_1$
,
![]() $I_3$
, and
$I_3$
, and
![]() $V_1$
for the unit disc. The code for the simulations can be found here: http://rb.gy/1wei7h. Expressions of all the new invariants in terms of r for a disc of radius r are established in the current section.
$V_1$
for the unit disc. The code for the simulations can be found here: http://rb.gy/1wei7h. Expressions of all the new invariants in terms of r for a disc of radius r are established in the current section.
Let D be the disc of radius r centred at the origin. For
![]() $g_1\cap g_2 \in D$
, we consider
$g_1\cap g_2 \in D$
, we consider
![]() $g_1$
to be the horizontal line
$g_1$
to be the horizontal line
![]() $y=-r\sin a$
(
$y=-r\sin a$
(
![]() $0 < a < {\pi}/{2}$
) in the Cartesian plane, and
$0 < a < {\pi}/{2}$
) in the Cartesian plane, and
![]() $g_2$
the line that passes through the points
$g_2$
the line that passes through the points
![]() $(r\cos w_1, r\sin w_1)$
and
$(r\cos w_1, r\sin w_1)$
and
![]() $(r\cos w_2, r\sin w_2)$
, where
$(r\cos w_2, r\sin w_2)$
, where
![]() $-a < w_1 < \pi +a < w_2 < 2\pi-a$
(see Figure 6).
$-a < w_1 < \pi +a < w_2 < 2\pi-a$
(see Figure 6).

Figure 6. The model of two random lines
![]() $g_1$
and
$g_1$
and
![]() $g_2$
intersecting each other inside
$g_2$
intersecting each other inside
![]() $D = \{(x,y)\colon x^2 + y^2 < r^2\}$
.
$D = \{(x,y)\colon x^2 + y^2 < r^2\}$
.
Then
and therefore
Lemma 6.1. If D is a disc with radius r then
Proof. It is easy to verify that
Then by (6.1) we obtain
 \begin{align*} U_1&=2\pi r^3 \int_0^{{\pi}/{2}}\cos a \,\mathrm{d} a \int_{-a}^{\pi+a}\,\mathrm{d} w_1\int_{\pi+a}^{2\pi-a} \biggl(\cos\dfrac{w_1-a}{2}-\cos\dfrac{w_2-a}{2}\notag \\[5pt]&\quad + \sin\dfrac{w_1+a}{2}+\sin\dfrac{w_2+a}{2}\biggr) \sin\dfrac{w_2-w_1}{2}\,\mathrm{d} w_2,\end{align*}
\begin{align*} U_1&=2\pi r^3 \int_0^{{\pi}/{2}}\cos a \,\mathrm{d} a \int_{-a}^{\pi+a}\,\mathrm{d} w_1\int_{\pi+a}^{2\pi-a} \biggl(\cos\dfrac{w_1-a}{2}-\cos\dfrac{w_2-a}{2}\notag \\[5pt]&\quad + \sin\dfrac{w_1+a}{2}+\sin\dfrac{w_2+a}{2}\biggr) \sin\dfrac{w_2-w_1}{2}\,\mathrm{d} w_2,\end{align*}
and reduce it to
thus completing the proof.
Corollary 6.1. If D is a disc with radius r then
Proof. The proof immediately follows from (1.1), the identity
![]() $ I_2=\frac{16}{3}\pi r^3$
(see [Reference Santaló8]), and Lemma 6.1.
$ I_2=\frac{16}{3}\pi r^3$
(see [Reference Santaló8]), and Lemma 6.1.
The above technique can be applied to reveal the exact numerical values of further invariants of D.
Lemma 6.2. If D is a disc with radius r then
Proof. For
![]() $g_1\cap g_2\in D$
, the lengths of intersecting chords are
$g_1\cap g_2\in D$
, the lengths of intersecting chords are
Since
then due to (6.1), we obtain (hereafter, long intermediate steps of integration are omitted)
 \begin{align*} D_2 & = 12\pi^2r^4+8\pi r^4 \int_0^{{\pi}/{2}}\cos^2 a \,\mathrm{d} a \int_{-a}^{\pi+a}\,\mathrm{d} w_1\int_{\pi+a}^{2\pi-a} \sin^2\dfrac{w_2-w_1}{2}\,\mathrm{d} w_2\\[5pt] &=\biggl(\dfrac{2}{3}\pi^4+17\pi^2\biggr)r^4. \end{align*}
\begin{align*} D_2 & = 12\pi^2r^4+8\pi r^4 \int_0^{{\pi}/{2}}\cos^2 a \,\mathrm{d} a \int_{-a}^{\pi+a}\,\mathrm{d} w_1\int_{\pi+a}^{2\pi-a} \sin^2\dfrac{w_2-w_1}{2}\,\mathrm{d} w_2\\[5pt] &=\biggl(\dfrac{2}{3}\pi^4+17\pi^2\biggr)r^4. \end{align*}
Evaluation of
![]() $U_2$
is provided by
$U_2$
is provided by
 \begin{align*}U_2&=4\pi r^4 \int_0^{{\pi}/{2}}\cos a \,\mathrm{d} a \int_{-a}^{\pi+a}\,\mathrm{d} w_1\int_{\pi+a}^{2\pi-a} \biggl(\cos\dfrac{w_1-a}{2}-\cos\dfrac{w_2-a}{2}\\[5pt]&\quad + \sin\dfrac{w_1+a}{2}+\sin\dfrac{w_2+a}{2}\biggr)^2 \sin\dfrac{w_2-w_1}{2}\,\mathrm{d} w_2\\[5pt]&=\biggl(\dfrac{2}{3}\pi^4+41\pi^2\biggr)r^4.\end{align*}
\begin{align*}U_2&=4\pi r^4 \int_0^{{\pi}/{2}}\cos a \,\mathrm{d} a \int_{-a}^{\pi+a}\,\mathrm{d} w_1\int_{\pi+a}^{2\pi-a} \biggl(\cos\dfrac{w_1-a}{2}-\cos\dfrac{w_2-a}{2}\\[5pt]&\quad + \sin\dfrac{w_1+a}{2}+\sin\dfrac{w_2+a}{2}\biggr)^2 \sin\dfrac{w_2-w_1}{2}\,\mathrm{d} w_2\\[5pt]&=\biggl(\dfrac{2}{3}\pi^4+41\pi^2\biggr)r^4.\end{align*}
Now (6.5) follows from (6.3), (6.4), the identity
and (see (6.2))
 \begin{align*} \int_{g_1\cap g_2\in D}|\chi(g_1)|u(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2 & =16r^4\biggl(\pi^2\int_0^{{\pi}/{2}}\cos^3a \,\mathrm{d} a + 2\pi\int_0^{{\pi}/{2}}\cos^4 a \,\mathrm{d} a\biggr)\\[5pt] &=\dfrac{50}{3}\pi^2r^4. \end{align*}
\begin{align*} \int_{g_1\cap g_2\in D}|\chi(g_1)|u(g_1, g_2)\,\mathrm{d} g_1\,\mathrm{d} g_2 & =16r^4\biggl(\pi^2\int_0^{{\pi}/{2}}\cos^3a \,\mathrm{d} a + 2\pi\int_0^{{\pi}/{2}}\cos^4 a \,\mathrm{d} a\biggr)\\[5pt] &=\dfrac{50}{3}\pi^2r^4. \end{align*}
![]() $V_1$
is an integral over three lines that produce three intersection points inside D. To compute
$V_1$
is an integral over three lines that produce three intersection points inside D. To compute
![]() $V_1$
with the technique already developed, we need to represent it by an integral over
$V_1$
with the technique already developed, we need to represent it by an integral over
![]() $g_1\cap g_2$
. We complete this task in two steps. First we apply the combinatorial algorithm to suggest an alternative expression for the left-hand side of (3.3):
$g_1\cap g_2$
. We complete this task in two steps. First we apply the combinatorial algorithm to suggest an alternative expression for the left-hand side of (3.3):
 \begin{align*}&\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{[\chi(g_1)]\cap [\chi(g_2)]}\sum_{\chi_{12}\in \langle g_1, g_2, g_3\rangle}|\chi_{12}|I_1(\chi_{12}) \,\mathrm{d} g_3\\[5pt]& \quad = 3 \int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{[\chi(g_1)]\cap [\chi(g_2)]}\sum_{\chi_{12}\in \langle g_1, g_2\rangle}|\chi_{12}|I_1(\chi_{12}) \,\mathrm{d} g_3\\[5pt]& \quad = 3 \int_{g_1\cap g_2\in D}\{(\rho_1+\rho_3)[|\chi(g_1)|+|\chi(g_2)|-\rho_2-\rho_4]+(\rho_2+\rho_4) \\[5pt] & \quad \quad \times [|\chi(g_1)|+|\chi(g_2)|-\rho_1-\rho_3]\}\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt] & \quad=6\int_{g_1\cap g_2\in D}\{|\chi(g_1)|u(g_1, g_2) - (\rho_1+\rho_3)(\rho_2+\rho_4)\}\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt] & \quad=100\pi^2r^4-6\int_{g_1\cap g_2\in D} (\rho_1+\rho_3)(\rho_2+\rho_4)\,\mathrm{d} g_1\,\mathrm{d} g_2.\end{align*}
\begin{align*}&\int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{[\chi(g_1)]\cap [\chi(g_2)]}\sum_{\chi_{12}\in \langle g_1, g_2, g_3\rangle}|\chi_{12}|I_1(\chi_{12}) \,\mathrm{d} g_3\\[5pt]& \quad = 3 \int_{g_1\cap g_2\in D}\,\mathrm{d} g_1\,\mathrm{d} g_2\int_{[\chi(g_1)]\cap [\chi(g_2)]}\sum_{\chi_{12}\in \langle g_1, g_2\rangle}|\chi_{12}|I_1(\chi_{12}) \,\mathrm{d} g_3\\[5pt]& \quad = 3 \int_{g_1\cap g_2\in D}\{(\rho_1+\rho_3)[|\chi(g_1)|+|\chi(g_2)|-\rho_2-\rho_4]+(\rho_2+\rho_4) \\[5pt] & \quad \quad \times [|\chi(g_1)|+|\chi(g_2)|-\rho_1-\rho_3]\}\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt] & \quad=6\int_{g_1\cap g_2\in D}\{|\chi(g_1)|u(g_1, g_2) - (\rho_1+\rho_3)(\rho_2+\rho_4)\}\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt] & \quad=100\pi^2r^4-6\int_{g_1\cap g_2\in D} (\rho_1+\rho_3)(\rho_2+\rho_4)\,\mathrm{d} g_1\,\mathrm{d} g_2.\end{align*}
In the second step we make the obtained expression equal to the right-hand side of (3.3), substitute
![]() $C_2$
,
$C_2$
,
![]() $D_2$
, and
$D_2$
, and
![]() $U_2$
with their known values, and calculate
$U_2$
with their known values, and calculate
The pairs of the lengths of the opposite sides in the quadrilateral
![]() $\mathrm{conv}((g_1\cup g_2)\cap \partial D)$
are
$\mathrm{conv}((g_1\cup g_2)\cap \partial D)$
are
This enables us to compute the integral in (6.10):
 \begin{align*} &\int_{g_1\cap g_2\in D} (\rho_1+\rho_3)(\rho_2+\rho_4)\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt] &\quad =4\pi r^4 \int_0^{{\pi}/{2}}\cos a \,\mathrm{d} a \int_{-a}^{\pi+a}\,\mathrm{d} w_1 \\[5pt]&\quad\quad \times \int_{\pi+a}^{2\pi-a} \biggl(\cos\dfrac{w_1-a}{2}+\sin\dfrac{w_2+a}{2}\biggr)\biggl(\sin\dfrac{w_1+a}{2}-\cos\dfrac{w_2-a}{2}\biggr) \sin\dfrac{w_2-w_1}{2}\,\mathrm{d} w_2\\[5pt] &\quad= 4\pi r^4\int_0^{{\pi}/{2}}\biggl(\dfrac{16}{3}\cos^2a+2\pi\cos^3 a\biggr) \,\mathrm{d} a \\[5pt] &\quad= \dfrac{32}{3}\pi^2 r^4.\end{align*}
\begin{align*} &\int_{g_1\cap g_2\in D} (\rho_1+\rho_3)(\rho_2+\rho_4)\,\mathrm{d} g_1\,\mathrm{d} g_2\\[5pt] &\quad =4\pi r^4 \int_0^{{\pi}/{2}}\cos a \,\mathrm{d} a \int_{-a}^{\pi+a}\,\mathrm{d} w_1 \\[5pt]&\quad\quad \times \int_{\pi+a}^{2\pi-a} \biggl(\cos\dfrac{w_1-a}{2}+\sin\dfrac{w_2+a}{2}\biggr)\biggl(\sin\dfrac{w_1+a}{2}-\cos\dfrac{w_2-a}{2}\biggr) \sin\dfrac{w_2-w_1}{2}\,\mathrm{d} w_2\\[5pt] &\quad= 4\pi r^4\int_0^{{\pi}/{2}}\biggl(\dfrac{16}{3}\cos^2a+2\pi\cos^3 a\biggr) \,\mathrm{d} a \\[5pt] &\quad= \dfrac{32}{3}\pi^2 r^4.\end{align*}
Now (6.6) follows from (6.10). We omit the proof of (6.7) since we have already established the expressions of
![]() $\rho_i$
in terms of parameters a,
$\rho_i$
in terms of parameters a,
![]() $w_1$
,
$w_1$
,
![]() $ w_2$
.
$ w_2$
.
The proofs for (6.8) and (6.9) are similar. Let us prove the first. To model the case
![]() $g_1\cap g_2 \not\in D$
, we simply need to adjust the position of parameters
$g_1\cap g_2 \not\in D$
, we simply need to adjust the position of parameters
![]() $w_1$
and
$w_1$
and
![]() $w_2$
. They must now satisfy either
$w_2$
. They must now satisfy either
![]() $-a < w_1 < w_2 < \pi +a,$
or
$-a < w_1 < w_2 < \pi +a,$
or
![]() $\pi+a < w_1 < w_2 < 2\pi - a.$
$\pi+a < w_1 < w_2 < 2\pi - a.$
If
![]() $-a < w_1 < w_2 < \pi +a$
, then
$-a < w_1 < w_2 < \pi +a$
, then
If
![]() $\pi+a < w_1 < w_2 < 2\pi - a$
, then
$\pi+a < w_1 < w_2 < 2\pi - a$
, then
As a result,
 \begin{align*}Q_s & =4\pi r^4 \int_0^{{\pi}/{2}}\cos a \,\mathrm{d} a \int_{-a}^{\pi+a}\,\mathrm{d} w_1\int_{w_1}^{\pi+a} \biggl(\sin\dfrac{w_1+a}{2}+\cos\dfrac{w_2-a}{2}\biggr) \\[5pt]& \quad \times \biggl(\cos\dfrac{w_1-a}{2}+\sin\dfrac{w_2+a}{2}-\sin\dfrac{w_1+a}{2}-\cos\dfrac{w_2-a}{2}\biggr) \sin\dfrac{w_2-w_1}{2}\,\mathrm{d} w_2\\[5pt]& \quad + 4\pi r^4 \int_0^{{\pi}/{2}}\cos a \,\mathrm{d} a \int_{\pi+a}^{2\pi-a}\,\mathrm{d} w_1\int_{w_1}^{2\pi-a} \biggl(\sin\dfrac{w_2+a}{2}-\cos\dfrac{w_1-a}{2}\biggr) \\[5pt]&\quad \times \biggl(\sin\dfrac{w_1+a}{2}-\cos\dfrac{w_2-a}{2}-\sin\dfrac{w_2+a}{2}+\cos\dfrac{w_1-a}{2}\biggr) \sin\dfrac{w_2-w_1}{2}\,\mathrm{d} w_2\\[5pt]& =\biggl(\dfrac{2}{3}\pi^4-2\pi^2\biggr)r^4.\end{align*}
\begin{align*}Q_s & =4\pi r^4 \int_0^{{\pi}/{2}}\cos a \,\mathrm{d} a \int_{-a}^{\pi+a}\,\mathrm{d} w_1\int_{w_1}^{\pi+a} \biggl(\sin\dfrac{w_1+a}{2}+\cos\dfrac{w_2-a}{2}\biggr) \\[5pt]& \quad \times \biggl(\cos\dfrac{w_1-a}{2}+\sin\dfrac{w_2+a}{2}-\sin\dfrac{w_1+a}{2}-\cos\dfrac{w_2-a}{2}\biggr) \sin\dfrac{w_2-w_1}{2}\,\mathrm{d} w_2\\[5pt]& \quad + 4\pi r^4 \int_0^{{\pi}/{2}}\cos a \,\mathrm{d} a \int_{\pi+a}^{2\pi-a}\,\mathrm{d} w_1\int_{w_1}^{2\pi-a} \biggl(\sin\dfrac{w_2+a}{2}-\cos\dfrac{w_1-a}{2}\biggr) \\[5pt]&\quad \times \biggl(\sin\dfrac{w_1+a}{2}-\cos\dfrac{w_2-a}{2}-\sin\dfrac{w_2+a}{2}+\cos\dfrac{w_1-a}{2}\biggr) \sin\dfrac{w_2-w_1}{2}\,\mathrm{d} w_2\\[5pt]& =\biggl(\dfrac{2}{3}\pi^4-2\pi^2\biggr)r^4.\end{align*}
The following results directly follow from the last two lemmas and the theorems proved in Sections 3 and 4.
Theorem 6.1. If D is a disc with radius r, then
 \begin{gather*} p_{46}=\dfrac{1}{4}-\dfrac{17}{\pi^2},\quad p_{45}=\dfrac{29}{8\pi^2} -\dfrac{1}{4},\\[5pt]p_{44}=\dfrac{43}{4\pi^2} -\dfrac{7}{8}, \quad p_{44}^{(1)}=\dfrac{23}{2\pi^2} -1,\quad p_{44}^{(2)}=\dfrac{1}{8}-\dfrac{3}{4\pi^2},\\[5pt]p_{43}=1-\dfrac{29}{4\pi^2},\quad p_{43}^{(1)}=\dfrac{23}{4\pi^2} -\dfrac{1}{2},\quad p_{43}^{(2)}=1-\dfrac{35}{4\pi^2}, \quad p_{43}^{(3)}=\dfrac{1}{2}-\dfrac{17}{4\pi^2},\\[5pt]p_{42}=\dfrac{7}{4}-\dfrac{121}{8\pi^2}, \quad p_{42}^{(1)}=\dfrac{3}{2} -\dfrac{13}{\pi^2},\quad p_{42}^{(2)}=\dfrac{1}{4}-\dfrac{17}{8\pi^2},\\[5pt]p_{41}=\dfrac{29}{8\pi^2}-\dfrac{1}{4},\quad p_{40}=\dfrac{13}{2\pi^2} -\dfrac{5}{8}.\end{gather*}
\begin{gather*} p_{46}=\dfrac{1}{4}-\dfrac{17}{\pi^2},\quad p_{45}=\dfrac{29}{8\pi^2} -\dfrac{1}{4},\\[5pt]p_{44}=\dfrac{43}{4\pi^2} -\dfrac{7}{8}, \quad p_{44}^{(1)}=\dfrac{23}{2\pi^2} -1,\quad p_{44}^{(2)}=\dfrac{1}{8}-\dfrac{3}{4\pi^2},\\[5pt]p_{43}=1-\dfrac{29}{4\pi^2},\quad p_{43}^{(1)}=\dfrac{23}{4\pi^2} -\dfrac{1}{2},\quad p_{43}^{(2)}=1-\dfrac{35}{4\pi^2}, \quad p_{43}^{(3)}=\dfrac{1}{2}-\dfrac{17}{4\pi^2},\\[5pt]p_{42}=\dfrac{7}{4}-\dfrac{121}{8\pi^2}, \quad p_{42}^{(1)}=\dfrac{3}{2} -\dfrac{13}{\pi^2},\quad p_{42}^{(2)}=\dfrac{1}{4}-\dfrac{17}{8\pi^2},\\[5pt]p_{41}=\dfrac{29}{8\pi^2}-\dfrac{1}{4},\quad p_{40}=\dfrac{13}{2\pi^2} -\dfrac{5}{8}.\end{gather*}
Acknowledgements
We are grateful for the careful reading and helpful comments of anonymous referees.
Funding information
The research of the first author is supported by the Science Committee of the Ministry of Science, Education, Culture and Sports RA: grant 21AA-1A024. The research of the second author is partially supported by the Mathematical Studies Center at Yerevan State University.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.