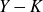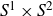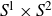1. Introduction
Given a null-homologous knot K in a 3–manifold Y and a slope
![]() $p/q\in\mathbb Q\cup\{\infty\}$
, let
$p/q\in\mathbb Q\cup\{\infty\}$
, let
![]() $Y_{p/q}(K)$
be the
$Y_{p/q}(K)$
be the
![]() $p/q$
–surgery on K. Gabai’s famous Property R Theorem [
Reference Gabai6
] asserts, among others, that if K is a nontrivial knot in
$p/q$
–surgery on K. Gabai’s famous Property R Theorem [
Reference Gabai6
] asserts, among others, that if K is a nontrivial knot in
![]() $S^3$
, then
$S^3$
, then
![]() $S^3_0(K)$
is irreducible. In particular,
$S^3_0(K)$
is irreducible. In particular,
![]() $S^3_0(K)$
does not have an
$S^3_0(K)$
does not have an
![]() $S^1\times S^2$
summand.
$S^1\times S^2$
summand.
In recently years, many generalisations of this theorem have been proved using Heegaard Floer homology. See, for example, the overview in [
Reference Ni14
]. Hom and Lidman [
Reference Hom and Lidman9
] proved two generalisations of Property R. One result they proved is, if K is a nontrivial null-homotopic knot in an irreducible rational homology sphere Y, then
![]() $Y_0(K)$
does not have an
$Y_0(K)$
does not have an
![]() $S^1\times S^2$
summand. The aim of this paper to remove the restrictions on the ambient manifold.
$S^1\times S^2$
summand. The aim of this paper to remove the restrictions on the ambient manifold.
Theorem 1·1.
Let Y be a closed, oriented, connected 3–manifold, and
![]() $K\subset Y$
be a nontrivial null-homotopic knot such that
$K\subset Y$
be a nontrivial null-homotopic knot such that
![]() $Y-K$
does not have an
$Y-K$
does not have an
![]() $S^1\times S^2$
summand, then
$S^1\times S^2$
summand, then
![]() $Y_0(K)$
does not have an
$Y_0(K)$
does not have an
![]() $S^1\times S^2$
summand.
$S^1\times S^2$
summand.
In Gabai’s work [
Reference Gabai6
], it is proved that
![]() $S^3_0(K)$
remembers the information of K about the genus and fiberedness. Motivated by this result, a concept “Property G” was introduced in [
Reference Ni13
] as a generalisation of Property R. Known results on Property G are summarised in [
Reference Ni14
]. We will not give the complete definition of Property G here. Instead, we just state the explicit result for genus–1 null-homotopic knot.
$S^3_0(K)$
remembers the information of K about the genus and fiberedness. Motivated by this result, a concept “Property G” was introduced in [
Reference Ni13
] as a generalisation of Property R. Known results on Property G are summarised in [
Reference Ni14
]. We will not give the complete definition of Property G here. Instead, we just state the explicit result for genus–1 null-homotopic knot.
Corollary 1·2. Let
![]() $K\subset Y$
be a genus–1 null-homotopic knot, then K has Property G. That is, if F is a genus–1 Seifert surface bounded by K, and
$K\subset Y$
be a genus–1 null-homotopic knot, then K has Property G. That is, if F is a genus–1 Seifert surface bounded by K, and
![]() $\widehat{F}\subset Y_0(K)$
is the torus obtained by capping off
$\widehat{F}\subset Y_0(K)$
is the torus obtained by capping off
![]() $\partial F$
with a disk, then
$\partial F$
with a disk, then
![]() $[\widehat F]\in H_2(Y_0(K))$
is not represented by a sphere. Moreover, if
$[\widehat F]\in H_2(Y_0(K))$
is not represented by a sphere. Moreover, if
![]() $Y_0(K)$
is a torus bundle over
$Y_0(K)$
is a torus bundle over
![]() $S^1$
with fiber
$S^1$
with fiber
![]() $\widehat{F}$
, then K is a fibered knot with fiber F.
$\widehat{F}$
, then K is a fibered knot with fiber F.
Corollary 1·2 answers the genus–1 case of a question of Boileau [ Reference Kirby10 , problem 1·80C]. There are easy counterexamples to the original question of Boileau, so one should modify the question to add the condition on the fiber of the zero surgery. See [ Reference Ni12 ] for more details.
The strategy of the proof of Theorem 1·1 is as follows. If
![]() $b_1(Y)>0$
, the theorem easily follows from a result of Lackenby [
Reference Lackenby11
] and Gabai [
Reference Gabai5
]. If
$b_1(Y)>0$
, the theorem easily follows from a result of Lackenby [
Reference Lackenby11
] and Gabai [
Reference Gabai5
]. If
![]() $b_1(Y)=0$
, we use results about degree-one maps and a result in [
Reference Daemi, Lidman, Vela–Vick and Wong4
] to show that if
$b_1(Y)=0$
, we use results about degree-one maps and a result in [
Reference Daemi, Lidman, Vela–Vick and Wong4
] to show that if
![]() $Y_0(K)=Z\#(S^1\times S^2)$
then
$Y_0(K)=Z\#(S^1\times S^2)$
then
![]() $\pi_1(Z)\cong\pi_1(Y)$
. Theorem 1·1 then follows from work of Hom and Lidman [
Reference Hom and Lidman9
].
$\pi_1(Z)\cong\pi_1(Y)$
. Theorem 1·1 then follows from work of Hom and Lidman [
Reference Hom and Lidman9
].
We will use the following notation. If N is a submanifold of a manifold M, let
![]() $\nu(N)$
be a closed tubular neighbourhood of N, and let
$\nu(N)$
be a closed tubular neighbourhood of N, and let
![]() $\nu^{\circ}(N)$
be the interior of
$\nu^{\circ}(N)$
be the interior of
![]() $\nu(N)$
. If X, Y are two spaces,
$\nu(N)$
. If X, Y are two spaces,
![]() $f\,{:}\,X\to Y$
is a continuous map, let
$f\,{:}\,X\to Y$
is a continuous map, let
![]() $f_*\,{:}\,\pi_1(X)\to \pi_1(Y)$
be the induced map. We will always suppress the base point in the notation when we talk about fundamental groups.
$f_*\,{:}\,\pi_1(X)\to \pi_1(Y)$
be the induced map. We will always suppress the base point in the notation when we talk about fundamental groups.
This paper is organised as follows. In Section 2, we prove general results about degree-one maps with certain properties on the induced homomorphisms on
![]() $\pi_1$
. In Section 3, we prove that if the zero surgery on a knot in Y is
$\pi_1$
. In Section 3, we prove that if the zero surgery on a knot in Y is
![]() $Z\#(S^1\times S^2)$
, then
$Z\#(S^1\times S^2)$
, then
![]() $\pi_1(Z)\cong\pi_1(Y)$
. In Section 4, we use work of Lackenby [
Reference Lackenby11
] and Hom–Lidman [
Reference Hom and Lidman9
] to prove Theorem 1·1. Corollary 1·2 is also proved as an application of this theorem.
$\pi_1(Z)\cong\pi_1(Y)$
. In Section 4, we use work of Lackenby [
Reference Lackenby11
] and Hom–Lidman [
Reference Hom and Lidman9
] to prove Theorem 1·1. Corollary 1·2 is also proved as an application of this theorem.
2. Degree-one maps which induce surface-group injective homomorphisms
In this section, we will prove results about degree-one maps which induce surface-group injective homomorphisms on
![]() $\pi_1$
.
$\pi_1$
.
A group
![]() $\Gamma$
is a surface group if it is isomorphic to the fundamental group of a closed orientable surface. Let
$\Gamma$
is a surface group if it is isomorphic to the fundamental group of a closed orientable surface. Let
![]() $\varphi\,{:}\, G\to H$
be a group homomorphism. We say
$\varphi\,{:}\, G\to H$
be a group homomorphism. We say
![]() $\varphi$
is surface-group injective, if the restriction of
$\varphi$
is surface-group injective, if the restriction of
![]() $\varphi$
to every surface subgroup of G is injective.
$\varphi$
to every surface subgroup of G is injective.
Lemma 2·1. Let
![]() $\varphi\,{:}\, G_1*G_2\to H$
be a group homomorphism. If both
$\varphi\,{:}\, G_1*G_2\to H$
be a group homomorphism. If both
![]() $\varphi|_{G_1}$
and
$\varphi|_{G_1}$
and
![]() $\varphi|_{G_2}$
are surface-group injective, then
$\varphi|_{G_2}$
are surface-group injective, then
![]() $\varphi$
is also surface-group injective.
$\varphi$
is also surface-group injective.
Proof. Let
![]() $\Gamma$
be a surface subgroup of
$\Gamma$
be a surface subgroup of
![]() $G_1*G_2$
. By the Kurosh Subgroup Theorem [
Reference Hempel8
, theorem 8·3],
$G_1*G_2$
. By the Kurosh Subgroup Theorem [
Reference Hempel8
, theorem 8·3],
![]() $\Gamma$
is the free product of a free group and conjugates of subgroups of
$\Gamma$
is the free product of a free group and conjugates of subgroups of
![]() $G_i$
,
$G_i$
,
![]() $i=1,2$
. Since
$i=1,2$
. Since
![]() $\Gamma$
is not a nontrivial free product, it is conjugated to a subgroup of
$\Gamma$
is not a nontrivial free product, it is conjugated to a subgroup of
![]() $G_i$
for some i. Since
$G_i$
for some i. Since
![]() $\varphi|_{G_i}$
is surface-group injective,
$\varphi|_{G_i}$
is surface-group injective,
![]() $\varphi$
is also injective on
$\varphi$
is also injective on
![]() $\Gamma$
.
$\Gamma$
.
The importance of the concept of surface-group injective maps is illustrated by the next lemma.
Lemma 2·2. Let X, Y be closed, oriented, connected 3–manifolds,
![]() $f\,{:}\,X\to Y$
be a surjective map such that
$f\,{:}\,X\to Y$
be a surjective map such that
![]() $f_*$
is surface-group injective. Let
$f_*$
is surface-group injective. Let
![]() $S\subset Y$
be a separating 2–sphere, and assume that
$S\subset Y$
be a separating 2–sphere, and assume that
![]() $R=f^{-1}(S)$
is a closed, oriented, connected surface. Then there exists a separating 2–sphere
$R=f^{-1}(S)$
is a closed, oriented, connected surface. Then there exists a separating 2–sphere
![]() $E\subset X$
so that R is obtained by adding tubes to E.
$E\subset X$
so that R is obtained by adding tubes to E.
Proof. Let
![]() $\iota\,{:}\, R\to X$
be the inclusion map. Since
$\iota\,{:}\, R\to X$
be the inclusion map. Since
![]() $f(R)=S$
is a sphere,
$f(R)=S$
is a sphere,
If R is not a sphere, since
![]() $f_*$
is surface-group injective, R must be compressible. Let R
$f_*$
is surface-group injective, R must be compressible. Let R
![]() $^{\prime}$
be the surface obtained by compressing R, then R can be obtained from R
$^{\prime}$
be the surface obtained by compressing R, then R can be obtained from R
![]() $^{\prime}$
by adding a tube. Let
$^{\prime}$
by adding a tube. Let
![]() $R_1^{\prime}$
be a component of R
$R_1^{\prime}$
be a component of R
![]() $^{\prime}$
, let
$^{\prime}$
, let
![]() $\iota'\,{:}\, R_1^{\prime}\to X$
be the inclusion map, then
$\iota'\,{:}\, R_1^{\prime}\to X$
be the inclusion map, then
If R
![]() $^{\prime}$
does not consist of spheres, since
$^{\prime}$
does not consist of spheres, since
![]() $f_*$
is surface-group injective, R
$f_*$
is surface-group injective, R
![]() $^{\prime}$
must be compressible. So R
$^{\prime}$
must be compressible. So R
![]() $^{\prime}$
can be obtained from another surface R
$^{\prime}$
can be obtained from another surface R
![]() $^{\prime\prime}$
by adding a tube.
$^{\prime\prime}$
by adding a tube.
Continue with the above process, we conclude that R can be obtained from some spheres by adding tubes. We can rearrange the order of the tubes, so that some tubes connecting different spheres are added first to get a single sphere E, then R is obtained by adding other tubes to E.
Let
![]() $y_1,y_2\in Y$
be two points separated by S. Since f is surjective, both
$y_1,y_2\in Y$
be two points separated by S. Since f is surjective, both
![]() $f^{-1}(y_1)$
and
$f^{-1}(y_1)$
and
![]() $f^{-1}(y_2)$
are non-empty. These two sets are clearly separated by R, so R is separating. The process of compressing a surface does not change the homology class of the surface, hence E is also separating.
$f^{-1}(y_2)$
are non-empty. These two sets are clearly separated by R, so R is separating. The process of compressing a surface does not change the homology class of the surface, hence E is also separating.
In the rest of this section, let Y be a 3–manifold which has no
![]() $S^1\times S^2$
summand,
$S^1\times S^2$
summand,
![]() $S_1,S_2,\dots,S_n$
be a collection of disjoint 2–spheres in Y satisfying the following conditions:
$S_1,S_2,\dots,S_n$
be a collection of disjoint 2–spheres in Y satisfying the following conditions:
![]() $Y\setminus (\cup_{i=1}^n S_i)$
has
$Y\setminus (\cup_{i=1}^n S_i)$
has
![]() $n+1$
components whose closures are
$n+1$
components whose closures are
![]() $\check Y_1,\check Y_2,\dots,\check Y_n,\check Y_{n+1}$
, where
$\check Y_1,\check Y_2,\dots,\check Y_n,\check Y_{n+1}$
, where
![]() $\check Y_{n+1}$
is
$\check Y_{n+1}$
is
![]() $S^3$
with n open balls removed, and a closed irreducible manifold
$S^3$
with n open balls removed, and a closed irreducible manifold
![]() $Y_i\ne S^3$
can be obtained from
$Y_i\ne S^3$
can be obtained from
![]() $\check Y_i$
by capping off
$\check Y_i$
by capping off
![]() $\partial\check Y_i=S_i$
with a ball
$\partial\check Y_i=S_i$
with a ball
![]() $B_i$
,
$B_i$
,
![]() $1\le i\le n$
. Then
$1\le i\le n$
. Then
When Y is irreducible, it is understood that
![]() $n=0$
.
$n=0$
.
Proposition 2·3. Let X be a closed, oriented, connected 3–manifold, and
![]() $f\,{:}\,X\to Y$
be a degree-one map such that
$f\,{:}\,X\to Y$
be a degree-one map such that
![]() $f_*$
is surface-group injective. Then there exists a degree-one map
$f_*$
is surface-group injective. Then there exists a degree-one map
![]() $g\,{:}\, X\to Y$
satisfying
$g\,{:}\, X\to Y$
satisfying
![]() $g_*=f_*$
, and each
$g_*=f_*$
, and each
![]() $E_i=g^{-1}(S_i)$
is a 2–sphere.
$E_i=g^{-1}(S_i)$
is a 2–sphere.
Proof. We induct on n. When
![]() $n=0$
, there is nothing to prove. So we assume
$n=0$
, there is nothing to prove. So we assume
![]() $n>0$
and the result is proved for
$n>0$
and the result is proved for
![]() $n-1$
.
$n-1$
.
Using [
Reference Rong and Wang17
, theorem 1·1], we may assume
![]() $R_1=f^{-1}(S_1)$
is a connected surface. Let
$R_1=f^{-1}(S_1)$
is a connected surface. Let
![]() $\check Y_0=\overline{Y\setminus\check Y_1}$
, and let
$\check Y_0=\overline{Y\setminus\check Y_1}$
, and let
![]() $Y_0$
be obtained by capping off
$Y_0$
be obtained by capping off
![]() $\partial \check Y_0$
with a ball
$\partial \check Y_0$
with a ball
![]() $B_0$
. Let
$B_0$
. Let
![]() $U_i=f^{-1}(\check Y_i)$
,
$U_i=f^{-1}(\check Y_i)$
,
![]() $i=0,1$
. Then
$i=0,1$
. Then
![]() $\partial U_1=\partial U_0=R_1$
.
$\partial U_1=\partial U_0=R_1$
.
By Lemma 2·2, there exists a separating 2–sphere
![]() $E_1\subset X$
, so that
$E_1\subset X$
, so that
![]() $R_1$
is obtained by adding tubes to
$R_1$
is obtained by adding tubes to
![]() $E_1$
. Now
$E_1$
. Now
![]() $E_1$
splits X into two parts
$E_1$
splits X into two parts
![]() $\check X_1,\check X_0$
, so that
$\check X_1,\check X_0$
, so that
![]() $\check X_i$
can be obtained from
$\check X_i$
can be obtained from
![]() $U_i$
by adding 1–handles and digging tunnels,
$U_i$
by adding 1–handles and digging tunnels,
![]() $i=0,1$
. Let
$i=0,1$
. Let
![]() $X_i$
be the closed manifold obtained by capping off
$X_i$
be the closed manifold obtained by capping off
![]() $\partial\check X_i$
with a ball,
$\partial\check X_i$
with a ball,
![]() $i=0,1$
.
$i=0,1$
.
We claim that each map
![]() $f|_{U_i}\,{:}\,U_i\to \check Y_i$
can be extended to a degree-one map
$f|_{U_i}\,{:}\,U_i\to \check Y_i$
can be extended to a degree-one map
![]() $f_i\,{:}\, X_i\to Y_i$
. In fact, the manifold
$f_i\,{:}\, X_i\to Y_i$
. In fact, the manifold
![]() $X_i$
can be obtained from
$X_i$
can be obtained from
![]() $U_i$
by gluing a 3–manifold
$U_i$
by gluing a 3–manifold
![]() $V_i$
which is obtained from
$V_i$
which is obtained from
![]() $B^3$
by digging tunnels and adding 1–handles. Since
$B^3$
by digging tunnels and adding 1–handles. Since
![]() $B_i$
is a ball which is contractible, we can extend
$B_i$
is a ball which is contractible, we can extend
![]() $f|_{U_i}\,{:}\,U_i\to \check Y_i$
to a map
$f|_{U_i}\,{:}\,U_i\to \check Y_i$
to a map
![]() $f_i\,{:}\, X_i\to Y_i$
by sending
$f_i\,{:}\, X_i\to Y_i$
by sending
![]() $V_i$
to
$V_i$
to
![]() $B_i$
. The degree of
$B_i$
. The degree of
![]() $f_i$
is 1 since the degree of
$f_i$
is 1 since the degree of
![]() $f|_{U_i}$
is 1.
$f|_{U_i}$
is 1.
Since
![]() $\deg f_i=1$
, after a homotopy supported in
$\deg f_i=1$
, after a homotopy supported in
![]() $V_i$
, we may assume there exists a ball
$V_i$
, we may assume there exists a ball
![]() $B^{\prime}_i\subset\mathrm{int}(B_i)$
, such that
$B^{\prime}_i\subset\mathrm{int}(B_i)$
, such that
![]() $f_i$
sends
$f_i$
sends
![]() $B^{\star}_i=f_i^{-1}(B^{\prime}_i)$
homeomorphically onto
$B^{\star}_i=f_i^{-1}(B^{\prime}_i)$
homeomorphically onto
![]() $B_i^{\prime}$
. Now we can glue
$B_i^{\prime}$
. Now we can glue
![]() $X_i\setminus\mathrm{int}(B_i^{\star})$
,
$X_i\setminus\mathrm{int}(B_i^{\star})$
,
![]() $i=0,1$
, together along their boundary, to get back
$i=0,1$
, together along their boundary, to get back
and define a map
by gluing the restrictions of
![]() $f_0,f_1$
. We rename
$f_0,f_1$
. We rename
then
![]() $E_1=(f_0\#f_1)^{-1}(S_1)$
.
$E_1=(f_0\#f_1)^{-1}(S_1)$
.
We claim that
![]() $(f_0\#f_1)_*=f_*$
. Let
$(f_0\#f_1)_*=f_*$
. Let
![]() $D\subset E_1$
be a disk such that all tubes in
$D\subset E_1$
be a disk such that all tubes in
![]() $S_1$
are added to the interior of D, and let
$S_1$
are added to the interior of D, and let
![]() $D^c=\overline{E_1\setminus D}$
. Let
$D^c=\overline{E_1\setminus D}$
. Let
![]() $V\subset X$
be the handlebody obtained by adding the 1–handles bounded by the tubes to
$V\subset X$
be the handlebody obtained by adding the 1–handles bounded by the tubes to
![]() $\nu(D)$
. Since
$\nu(D)$
. Since
![]() $\pi_1(V)$
is a quotient of
$\pi_1(V)$
is a quotient of
![]() $\pi_1(\partial V)$
, the map
$\pi_1(\partial V)$
, the map
![]() $X\setminus V\to X$
induces a surjective map on
$X\setminus V\to X$
induces a surjective map on
![]() $\pi_1$
. To prove
$\pi_1$
. To prove
![]() $(f_0\#f_1)_*=f_*$
, we only need to prove that
$(f_0\#f_1)_*=f_*$
, we only need to prove that
![]() $(f_0\#f_1)_*(\alpha)=f_*(\alpha)$
when
$(f_0\#f_1)_*(\alpha)=f_*(\alpha)$
when
![]() $\alpha$
is a homotopy class represented by a loop in
$\alpha$
is a homotopy class represented by a loop in
![]() $X\setminus V$
. We observe that
$X\setminus V$
. We observe that
![]() $f_0\#f_1=f$
on
$f_0\#f_1=f$
on
![]() $X\setminus(V\cup\nu(D^c))$
, and
$X\setminus(V\cup\nu(D^c))$
, and
![]() $\pi_1(X\setminus V)$
is the free product of the
$\pi_1(X\setminus V)$
is the free product of the
![]() $\pi_1$
of the two components of
$\pi_1$
of the two components of
![]() $X\setminus(V\cup\nu(D^c))$
, so
$X\setminus(V\cup\nu(D^c))$
, so
![]() $(f_0\#f_1)_*(\alpha)=f_*(\alpha)$
.
$(f_0\#f_1)_*(\alpha)=f_*(\alpha)$
.
By the induction hypothesis, there exists a map
![]() $g_0\,{:}\,X_0\to Y_0$
, such that
$g_0\,{:}\,X_0\to Y_0$
, such that
![]() $g_1^{-1}(S_i)$
is a sphere for
$g_1^{-1}(S_i)$
is a sphere for
![]() $2\le i\le n$
, and
$2\le i\le n$
, and
![]() $(g_1)_*=(f_0)_*$
. We can define a map
$(g_1)_*=(f_0)_*$
. We can define a map
![]() $g=g_0\#f_1$
in a similar way as
$g=g_0\#f_1$
in a similar way as
![]() $f_0\#f_1$
, then
$f_0\#f_1$
, then
![]() $g^{-1}(S_i)$
is a sphere for
$g^{-1}(S_i)$
is a sphere for
![]() $1\le i\le n$
, and
$1\le i\le n$
, and
This finishes the induction step.
3. Zero surgery on a null-homotopic knot
The aim of this section is to prove the following proposition.
Proposition 3·1. Let Y be a closed, connected, oriented 3–manifold which does not have an
![]() $S^1\times S^2$
summand, and
$S^1\times S^2$
summand, and
![]() $K\subset Y$
be a null-homotopic knot. If
$K\subset Y$
be a null-homotopic knot. If
![]() $Y_0(K)=Z\#(S^1\times S^2)$
, then
$Y_0(K)=Z\#(S^1\times S^2)$
, then
![]() $\pi_1(Z)\cong\pi_1(Y)$
.
$\pi_1(Z)\cong\pi_1(Y)$
.
We first prove a general result about surgery on null-homotopic knots.
Lemma 3·2. Let Y be a closed, oriented, connected 3–manifold, and
![]() $K\subset Y$
be a null-homotopic knot. Let V be the 2–handle cobordism from Y to
$K\subset Y$
be a null-homotopic knot. Let V be the 2–handle cobordism from Y to
![]() $Y_m(K)$
for some integer m. Then there exists a retraction
$Y_m(K)$
for some integer m. Then there exists a retraction
![]() $p\,{:}\,V\to Y$
, so that
$p\,{:}\,V\to Y$
, so that
![]() $p|_{Y_m(K)}\,{:}\,Y_m(K)\to Y$
is a degree-one map.
$p|_{Y_m(K)}\,{:}\,Y_m(K)\to Y$
is a degree-one map.
Proof. The cobordism V deformation retracts to the space V
![]() $^{\prime}$
obtained from Y by adding a 2–cell
$^{\prime}$
obtained from Y by adding a 2–cell
![]() $e^2$
along K. Since K is null-homotopic, the identity map on Y can be extended over
$e^2$
along K. Since K is null-homotopic, the identity map on Y can be extended over
![]() $e^2$
. Hence we have a retraction
$e^2$
. Hence we have a retraction
![]() $V'\to Y$
, which implies the existence of the retraction
$V'\to Y$
, which implies the existence of the retraction
![]() $p\,{:}\,V\to Y$
. The degree of the restriction
$p\,{:}\,V\to Y$
. The degree of the restriction
![]() $p|_{Y_m(K)}\,{:}\,Y_m(K)\to Y$
is 1 since it induces an isomorphism on
$p|_{Y_m(K)}\,{:}\,Y_m(K)\to Y$
is 1 since it induces an isomorphism on
![]() $H_3$
.
$H_3$
.
The existence of the above degree-one map is a well-known result. See [ Reference Boileau and Wang3 , Proposition 3·2] and [ Reference Gadgil7 ].
In the rest of this section, let V be the 2–handle cobordism from Y to
![]() $X=Y_0(K)$
,
$X=Y_0(K)$
,
![]() $p\,{:}\,V\to Y$
be the retraction in Lemma 3·2, and
$p\,{:}\,V\to Y$
be the retraction in Lemma 3·2, and
![]() $f=p|_{Y_0(K)}$
. Moreover, we assume
$f=p|_{Y_0(K)}$
. Moreover, we assume
![]() $Y_0(K)=Z\#(S^1\times S^2)$
. Let
$Y_0(K)=Z\#(S^1\times S^2)$
. Let
![]() $\check Z$
be the submanifold of
$\check Z$
be the submanifold of
![]() $Y_0(K)$
which is Z with a ball removed. Since
$Y_0(K)$
which is Z with a ball removed. Since
![]() $Y_0(K)=Z\#(S^1\times S^2)$
, we can add a 3–handle to V to get a cobordism
$Y_0(K)=Z\#(S^1\times S^2)$
, we can add a 3–handle to V to get a cobordism
![]() $W\,{:}\,Y\to Z$
.
$W\,{:}\,Y\to Z$
.
Lemma 3·3. The restriction of
![]() $f_*$
to
$f_*$
to
![]() $\pi_1(\check Z)$
is injective.
$\pi_1(\check Z)$
is injective.
Proof. Consider the following commutative diagram, where all maps except p are inclusions:

Then
![]() $f=p\circ\iota_0$
.
$f=p\circ\iota_0$
.
Since the 2–handle in V is added along the null-homotopic knot K, the inclusion
![]() $\iota_Y\,{:}\,Y\to V$
induces an isomorphism on
$\iota_Y\,{:}\,Y\to V$
induces an isomorphism on
![]() $\pi_1$
. Since
$\pi_1$
. Since
![]() $p\circ\iota_Y=\mathrm{id}_Y$
,
$p\circ\iota_Y=\mathrm{id}_Y$
,
![]() $p_*$
is an isomorphism.
$p_*$
is an isomorphism.
Since W is obtained from V by adding a 3–handle, the inclusion
![]() $V\subset W$
induces an isomorphism on
$V\subset W$
induces an isomorphism on
![]() $\pi_1$
. We have the commutative diagram
$\pi_1$
. We have the commutative diagram

The manifold W (after being turned up-side-down) can be obtained from
![]() $Z\times I$
by adding a 1–handle and a 2–handle, and the 2–handle cobordism is exactly V being turned up-side-down. By [
Reference Daemi, Lidman, Vela–Vick and Wong4
, Proposition 2·1],
$Z\times I$
by adding a 1–handle and a 2–handle, and the 2–handle cobordism is exactly V being turned up-side-down. By [
Reference Daemi, Lidman, Vela–Vick and Wong4
, Proposition 2·1],
![]() $(\iota_Z)_*$
is injective, so
$(\iota_Z)_*$
is injective, so
![]() $(\iota_{\check Z})_*$
is also injective.
$(\iota_{\check Z})_*$
is also injective.
Now consider the commutative diagram

The restriction of
![]() $f_*$
to
$f_*$
to
![]() $\pi_1(\check Z)$
is just
$\pi_1(\check Z)$
is just
![]() $p_*\circ(\iota_{\check Z})_*$
, which is injective since
$p_*\circ(\iota_{\check Z})_*$
, which is injective since
![]() $(\iota_{\check Z})_*$
is injective and
$(\iota_{\check Z})_*$
is injective and
![]() $p_*$
is an isomorphism.
$p_*$
is an isomorphism.
Corollary 3·4. The induced map
![]() $f_*\,{:}\,\pi_1(Y_0(K))\to \pi_1(Y)$
is surface-group injective.
$f_*\,{:}\,\pi_1(Y_0(K))\to \pi_1(Y)$
is surface-group injective.
Proof. This follows from Lemmas 2·1 and 3·3.
Proof of Proposition 3·1. We will use the notations in Section 2. Since
![]() $f_*$
is surface-group injective, we can apply Proposition 2·3 to get a degree-one map
$f_*$
is surface-group injective, we can apply Proposition 2·3 to get a degree-one map
![]() $g\,{:}\,X=Y_0(K)\to Y$
so that
$g\,{:}\,X=Y_0(K)\to Y$
so that
![]() $g_*=f_*$
and
$g_*=f_*$
and
![]() $g^{-1}(S_i)=E_i$
is a separating sphere whenever
$g^{-1}(S_i)=E_i$
is a separating sphere whenever
![]() $1\le i\le n$
.
$1\le i\le n$
.
Since X has an
![]() $S^1\times S^2$
summand, by the uniqueness part of the Kneser–Milnor theorem, one component of
$S^1\times S^2$
summand, by the uniqueness part of the Kneser–Milnor theorem, one component of
![]() $X\setminus(\cup_{i=1}^n E_i)$
has an
$X\setminus(\cup_{i=1}^n E_i)$
has an
![]() $S^1\times S^2$
summand.
$S^1\times S^2$
summand.
If the
![]() $S^1\times S^2$
summand is in
$S^1\times S^2$
summand is in
![]() $g^{-1}(\check Y_{n+1})$
, then
$g^{-1}(\check Y_{n+1})$
, then
![]() $g_*(S^1\times\{point\})$
is null-homotopic. It follows that
$g_*(S^1\times\{point\})$
is null-homotopic. It follows that
Since
![]() $\deg g=1$
,
$\deg g=1$
,
![]() $g_*$
is surjective. So
$g_*$
is surjective. So
![]() $g_*|_{\pi_1(Z)}$
is surjective. Our result follows from Lemma 3·3 since
$g_*|_{\pi_1(Z)}$
is surjective. Our result follows from Lemma 3·3 since
![]() $g_*=f_*$
.
$g_*=f_*$
.
If
![]() $\check X_i=g^{-1}(\check Y_i)$
has an
$\check X_i=g^{-1}(\check Y_i)$
has an
![]() $S^1\times S^2$
summand for some i satisfying
$S^1\times S^2$
summand for some i satisfying
![]() $1\le i\le n$
, without loss of generality, we may assume
$1\le i\le n$
, without loss of generality, we may assume
![]() $i=1$
. The map
$i=1$
. The map
![]() $g|_{\check X_1}$
extends to a map
$g|_{\check X_1}$
extends to a map
![]() $g_1\,{:}\,X_1\to Y_1$
. Suppose that
$g_1\,{:}\,X_1\to Y_1$
. Suppose that
![]() $X_1=Z_1\#(S^1\times S^2)$
, let
$X_1=Z_1\#(S^1\times S^2)$
, let
![]() $P\subset X_1$
be
$P\subset X_1$
be
![]() $\{\mathrm{point}\}\times S^2$
. Then
$\{\mathrm{point}\}\times S^2$
. Then
![]() $X_{1}\setminus \nu^{\circ}(P)$
is homeomorphic to
$X_{1}\setminus \nu^{\circ}(P)$
is homeomorphic to
![]() $Z_1$
with two open balls removed. Since
$Z_1$
with two open balls removed. Since
![]() $\pi_2(Y_1)=0$
,
$\pi_2(Y_1)=0$
,
![]() $(g_1)|_P$
is null-homotopic in
$(g_1)|_P$
is null-homotopic in
![]() $Y_1$
. We can then extend
$Y_1$
. We can then extend
![]() $g_1|_{X_1\setminus \nu^{\circ}(P)}$
to a map
$g_1|_{X_1\setminus \nu^{\circ}(P)}$
to a map
![]() $h_1\,{:}\, Z_1\to Y_1$
. The new map
$h_1\,{:}\, Z_1\to Y_1$
. The new map
![]() $h_1$
is again a degree-one map, so
$h_1$
is again a degree-one map, so
![]() $(h_1)_*$
is surjective.
$(h_1)_*$
is surjective.
Using Lemma 3·3, we see that
![]() $g_*$
is injective on
$g_*$
is injective on
![]() $\pi_1(X_0\#Z_1)$
. (Recall that
$\pi_1(X_0\#Z_1)$
. (Recall that
![]() $X_0$
is obtained from X by replacing
$X_0$
is obtained from X by replacing
![]() $\check X_1$
with a ball.) In particular,
$\check X_1$
with a ball.) In particular,
![]() $(h_1)_*$
is injective, so
$(h_1)_*$
is injective, so
We also get that
![]() $g_*$
is injective on
$g_*$
is injective on
![]() $\pi_1(X_0)$
. Since
$\pi_1(X_0)$
. Since
![]() $g|_{\check X_0}\,{:}\,\check X_0\to\check Y_0$
is a degree-one proper map,
$g|_{\check X_0}\,{:}\,\check X_0\to\check Y_0$
is a degree-one proper map,
![]() $(g|_{\check X_0})*$
is surjective. So
$(g|_{\check X_0})*$
is surjective. So
Since
![]() $Z\cong X_0\#Z_1$
,
$Z\cong X_0\#Z_1$
,
![]() $Y=Y_0\#Y_1$
, we have
$Y=Y_0\#Y_1$
, we have
4. Proof of the main theorem
In this section, we will prove Theorem 1·1 and Corollary 1·2.
Proof of Theorem 1·1. when
![]() $b_1(Y)>0$
Without loss of generality, we may assume
$b_1(Y)>0$
Without loss of generality, we may assume
![]() $M=Y\setminus\nu^{\circ}(K)$
is irreducible. Since
$M=Y\setminus\nu^{\circ}(K)$
is irreducible. Since
![]() $b_1(Y)>0$
, there exists a closed, oriented, connected surface S in the interior of M, so that S is taut in M. Notice that for the
$b_1(Y)>0$
, there exists a closed, oriented, connected surface S in the interior of M, so that S is taut in M. Notice that for the
![]() $\infty$
slope on K, the core of the surgery solid torus, which is K, is null-homotopic. Using [
Reference Lackenby11
, theorem A.21], which is a stronger version of the main result in [
Reference Gabai5
], we conclude that each 2–sphere in
$\infty$
slope on K, the core of the surgery solid torus, which is K, is null-homotopic. Using [
Reference Lackenby11
, theorem A.21], which is a stronger version of the main result in [
Reference Gabai5
], we conclude that each 2–sphere in
![]() $Y_0(K)$
bounds a rational homology ball. Hence
$Y_0(K)$
bounds a rational homology ball. Hence
![]() $Y_0(K)$
does not have an
$Y_0(K)$
does not have an
![]() $S^1\times S^2$
summand.
$S^1\times S^2$
summand.
Proposition 4·1. Let
![]() $Y_1,Y_2$
be two closed, oriented, connected 3–manifolds. If
$Y_1,Y_2$
be two closed, oriented, connected 3–manifolds. If
![]() $\pi_1(Y_1)\cong\pi_2(Y_2)$
, then
$\pi_1(Y_1)\cong\pi_2(Y_2)$
, then
Proof. This is a well-known consequence of the Geometrisation Theorem. As in [
Reference Aschenbrenner, Friedl and Wilton2
, theorem 2·1·3], if
![]() $\pi_1(Y_1)\cong\pi_2(Y_2)$
, then there is a one-to-one correspondence between the summands of
$\pi_1(Y_1)\cong\pi_2(Y_2)$
, then there is a one-to-one correspondence between the summands of
![]() $Y_1$
and the summands of
$Y_1$
and the summands of
![]() $Y_2$
, such that any pair of summands in the correspondence consists of either homeomorphic manifolds, (the homemorphism does not necessarily preserve the orientation), or lens spaces with the same
$Y_2$
, such that any pair of summands in the correspondence consists of either homeomorphic manifolds, (the homemorphism does not necessarily preserve the orientation), or lens spaces with the same
![]() $H_1$
. Our result then follows from basic properties of Heegaard Floer homology [
Reference Ozsváth and Szabó15, Reference Ozsváth and Szabó16
].
$H_1$
. Our result then follows from basic properties of Heegaard Floer homology [
Reference Ozsváth and Szabó15, Reference Ozsváth and Szabó16
].
Proof of Theorem 1·1. when
![]() $b_1(Y)=0$
Without loss of generality, we may assume
$b_1(Y)=0$
Without loss of generality, we may assume
![]() $Y\setminus K$
is irreducible. Assume that
$Y\setminus K$
is irreducible. Assume that
![]() $Y_0(K)=Z\#(S^1\times S^2)$
. By Proposition 3·1,
$Y_0(K)=Z\#(S^1\times S^2)$
. By Proposition 3·1,
![]() $\pi_1(Y)\cong\pi_1(Z)$
. Using Proposition 4·1, we get
$\pi_1(Y)\cong\pi_1(Z)$
. Using Proposition 4·1, we get
![]() $\mathrm{rank}\widehat{HF}(Y)=\mathrm{rank}\widehat{HF}(Z)$
. Our conclusion follows from [
Reference Hom and Lidman9
, theorem 1·1].
$\mathrm{rank}\widehat{HF}(Y)=\mathrm{rank}\widehat{HF}(Z)$
. Our conclusion follows from [
Reference Hom and Lidman9
, theorem 1·1].
Proof of Corollary 1·2. The first statement follows from Theorem 1·1. We only need to prove the second statement. In this case,
![]() $Y_0(K)$
is a torus bundle over
$Y_0(K)$
is a torus bundle over
![]() $S^1$
. By Lemma 3·2, there exists a degree-one map
$S^1$
. By Lemma 3·2, there exists a degree-one map
![]() $f\,{:}\,Y_0(K)\to Y$
. Then
$f\,{:}\,Y_0(K)\to Y$
. Then
![]() $f_*$
is surjective. We claim that Y is
$f_*$
is surjective. We claim that Y is
![]() $S^1\times S^2,\mathbb RP^3\#\mathbb RP^3$
or a spherical manifold. Then our conclusion follows from [
Reference Ai and Ni1
].
$S^1\times S^2,\mathbb RP^3\#\mathbb RP^3$
or a spherical manifold. Then our conclusion follows from [
Reference Ai and Ni1
].
If Y is reducible, then either
![]() $Y=S^1\times S^2$
or Y is a nontrivial connected sum. If
$Y=S^1\times S^2$
or Y is a nontrivial connected sum. If
![]() $Y=S^1\times S^2$
, we are done. Now we assume Y is a nontrivial connected sum, so
$Y=S^1\times S^2$
, we are done. Now we assume Y is a nontrivial connected sum, so
![]() $\pi_1(Y)\cong A*B$
with A, B nontrivial. Let T be a fiber of
$\pi_1(Y)\cong A*B$
with A, B nontrivial. Let T be a fiber of
![]() $Y_0(K)$
, then
$Y_0(K)$
, then
![]() $f_*(\pi_1(T))$
is an abelian normal subgroup of
$f_*(\pi_1(T))$
is an abelian normal subgroup of
![]() $\pi_1(Y)=f_*(\pi_1(Y_0(K)))$
. By the Kurosh Subgroup Theorem [
Reference Hempel8
, theorem 8·3],
$\pi_1(Y)=f_*(\pi_1(Y_0(K)))$
. By the Kurosh Subgroup Theorem [
Reference Hempel8
, theorem 8·3],
![]() $f_*(\pi_1(T))$
is also a free product of free groups and conjugates of subgroups of A, B. Since
$f_*(\pi_1(T))$
is also a free product of free groups and conjugates of subgroups of A, B. Since
![]() $f_*(\pi_1(T))$
is abelian, it must be either a subgroup of
$f_*(\pi_1(T))$
is abelian, it must be either a subgroup of
![]() $\mathbb Z$
or the conjugate of a subgroup of A or B. Since
$\mathbb Z$
or the conjugate of a subgroup of A or B. Since
![]() $f_*(\pi_1(T))$
is a normal subgroup of
$f_*(\pi_1(T))$
is a normal subgroup of
![]() $\pi_1(Y)\cong A*B$
, the latter case cannot happen.
$\pi_1(Y)\cong A*B$
, the latter case cannot happen.
Now
![]() $f_*(\pi_1(T))$
is a subgroup of
$f_*(\pi_1(T))$
is a subgroup of
![]() $\mathbb Z$
. Since
$\mathbb Z$
. Since
![]() $f_*$
is surjective,
$f_*$
is surjective,
![]() $\pi_1(Y)/f_*(\pi_1(T))$
is a cyclic group. If
$\pi_1(Y)/f_*(\pi_1(T))$
is a cyclic group. If
![]() $f_*(\pi_1(T))=\{1\}$
, then
$f_*(\pi_1(T))=\{1\}$
, then
![]() $\pi_1(Y)$
is cyclic, a contradiction to
$\pi_1(Y)$
is cyclic, a contradiction to
![]() $\pi_1(Y)\cong A*B$
. So
$\pi_1(Y)\cong A*B$
. So
![]() $f_*(\pi_1(T))\cong\mathbb Z$
.
$f_*(\pi_1(T))\cong\mathbb Z$
.
If
![]() $\pi_1(Y)/f_*(\pi_1(T))\cong\mathbb Z$
, then
$\pi_1(Y)/f_*(\pi_1(T))\cong\mathbb Z$
, then
![]() $\pi_1(Y)$
contains
$\pi_1(Y)$
contains
![]() $\mathbb Z^2$
as a finite index subgroup, which is not possible since
$\mathbb Z^2$
as a finite index subgroup, which is not possible since
![]() $\mathbb Z^2$
is not the fundamental group of any closed 3–manifold. If
$\mathbb Z^2$
is not the fundamental group of any closed 3–manifold. If
![]() $\pi_1(Y)/f_*(\pi_1(T))$
is finite, then
$\pi_1(Y)/f_*(\pi_1(T))$
is finite, then
![]() $\pi_1(Y)$
contains
$\pi_1(Y)$
contains
![]() $\mathbb Z$
as a finite index subgroup. It follows that Y is finitely covered by
$\mathbb Z$
as a finite index subgroup. It follows that Y is finitely covered by
![]() $S^1\times S^2$
, thus it must be
$S^1\times S^2$
, thus it must be
![]() $S^1\times S^2$
or
$S^1\times S^2$
or
![]() $\mathbb RP^3\#\mathbb RP^3$
.
$\mathbb RP^3\#\mathbb RP^3$
.
Now we consider the case Y is irreducible. If Y is a spherical manifold, we are done. If Y is irreducible and not a spherical manifold, then
![]() $f_*$
is injective by [
Reference Wang18
, theorem 4]. So
$f_*$
is injective by [
Reference Wang18
, theorem 4]. So
![]() $f_*$
is an isomorphism, a contradiction to the fact that
$f_*$
is an isomorphism, a contradiction to the fact that
![]() $b_1(Y_0(K))>b_1(Y)$
.
$b_1(Y_0(K))>b_1(Y)$
.
Acknowledgements
This research was funded by NSF grant numbers DMS-1252992 and DMS-1811900. We are grateful to Tye Lidman for very helpful comments on an earlier draft of this paper.