Let F ⊂ G be closed and A(F) = A(G)/IF. If F is a Helson set then A(F)** is an amenable (semisimple) Banach algebra. Our main result implies the following theorem: Let G be a locally compact group, F ⊂ G closed, a ∈ G. Assume either (a) For some non-discrete closed subgroup H, the interior of F ∩ aH in aH is non-empty, or (b) R ⊂ G, S ⊂ R is a symmetric set and aS ⊂ F. Then A(F)** is a non-amenable non-semisimple Banach algebra. This raises the question: How ‘thin’ can F be for A(F)** to remain a non-amenable Banach algebra?

Let G be a connected Lie group with Lie algebra g and a1, …, ad an algebraic basis of g. Further let Ai denote the generators of left translations, acting on the Lp-spaces Lp(G; dg) formed with left Haar measure dg, in the directions ai. We consider second-order operators 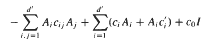in divergence form corresponding to a quadratic form with complex coefficients, bounded Hölder continuous principal coefficients cij and lower order coefficients ci, c′ii, c0 ∈ L∞ such that the matrix C= (cij) of principal coefficients satisfies the subellipticity condition 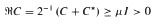uniformly over G.

We discuss the hierarchy relating smoothness properties of the coefficients of H with smoothness of the kernel and smoothness of the domain of powers of H on the Lρ-spaces. Moreover, we present Gaussian type bounds for the kernel and its derivatives.

Similar theorems are proved for strongly elliptic operators 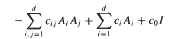in non-divergence form for which the principal coefficients are at least once differentiable.

We study the Cesàro operator on the classical group G and give a necessary and sufficient condition on the index α = α(G) for which the operator is convergent to f(U) for any continuous function f as N → ∞. The result in this paper solves a question posed by Gong in the book Harmonic analysis on classical groups.

It has been known that mixed automorphic forms arise naturally as holomorphic forms on elliptic varieties and that they include classical automorphic forms as a special case. In this paper, we show how to construct mixed automorphic forms of type (k, l) from elliptic modular forms to give nontrivial examples of mixed automorphic forms.

Crittenden and Vanden Eynden conjectured that if n arithmetic progressions, each having modulus at least k, include all the integers from 1 to k2n-k+1, then they include all the integers. They proved this for the cases k = 1 and k = 2. We give various necessary conditions for a counterexample to the conjecture; in particular we show that if a counterexample exists for some value of k, then one exists for that k and a value of n less than an explicit function of k.