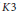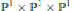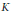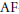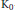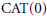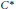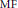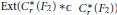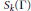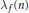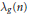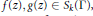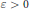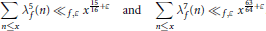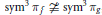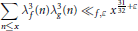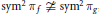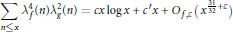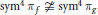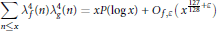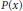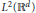Let 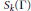 ${{S}_{k}}(\Gamma )$ be the space of holomorphic cusp forms of even integral weight
${{S}_{k}}(\Gamma )$ be the space of holomorphic cusp forms of even integral weight  $k$ for the full modular group. Let
$k$ for the full modular group. Let 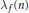 ${{\lambda }_{f}}(n)$ and
${{\lambda }_{f}}(n)$ and 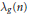 ${{\lambda }_{g}}(n)$ be the
${{\lambda }_{g}}(n)$ be the  $n$-th normalized Fourier coefficients of two holomorphic Hecke eigencuspforms
$n$-th normalized Fourier coefficients of two holomorphic Hecke eigencuspforms 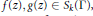 $f(z),\,g(z)\,\in \,{{S}_{k}}(\Gamma )$, respectively. In this paper we are able to show the following results about higher moments of Fourier coefficients of holomorphic cusp forms.
$f(z),\,g(z)\,\in \,{{S}_{k}}(\Gamma )$, respectively. In this paper we are able to show the following results about higher moments of Fourier coefficients of holomorphic cusp forms.
(i)For any 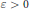 $\varepsilon \,>\,0$, we have
$\varepsilon \,>\,0$, we have
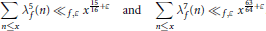 $$\sum\limits_{n\le x}{\lambda _{f}^{5}(n){{\ll }_{f,\varepsilon }}}{{x}^{\frac{15}{16}+\varepsilon }}\text{and}\sum\limits_{n\le x}{\lambda _{f}^{7}(n){{\ll }_{f,\varepsilon }}}{{x}^{\frac{63}{64}+\varepsilon }}.$$
$$\sum\limits_{n\le x}{\lambda _{f}^{5}(n){{\ll }_{f,\varepsilon }}}{{x}^{\frac{15}{16}+\varepsilon }}\text{and}\sum\limits_{n\le x}{\lambda _{f}^{7}(n){{\ll }_{f,\varepsilon }}}{{x}^{\frac{63}{64}+\varepsilon }}.$$
(ii)If 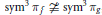 $\text{sy}{{\text{m}}^{3\,}}{{\pi }_{f}}\,\ncong \,\text{sy}{{\text{m}}^{3\,}}{{\pi }_{g}}\,$, then for any
$\text{sy}{{\text{m}}^{3\,}}{{\pi }_{f}}\,\ncong \,\text{sy}{{\text{m}}^{3\,}}{{\pi }_{g}}\,$, then for any 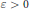 $\varepsilon \,>\,0$, we have
$\varepsilon \,>\,0$, we have
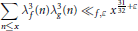 $$\sum\limits_{n\le x}{\lambda _{f}^{3}(n)\lambda _{g}^{3}(n){{\ll }_{f,\varepsilon }}}{{x}^{\frac{31}{32}+\varepsilon }};$$
$$\sum\limits_{n\le x}{\lambda _{f}^{3}(n)\lambda _{g}^{3}(n){{\ll }_{f,\varepsilon }}}{{x}^{\frac{31}{32}+\varepsilon }};$$
If 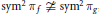 $\text{sy}{{\text{m}}^{2}}\,{{\pi }_{f}}\,\ncong \,\text{sy}{{\text{m}}^{2}}\,{{\pi }_{g}}$, then for any
$\text{sy}{{\text{m}}^{2}}\,{{\pi }_{f}}\,\ncong \,\text{sy}{{\text{m}}^{2}}\,{{\pi }_{g}}$, then for any 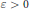 $\varepsilon \,>\,0$, we have
$\varepsilon \,>\,0$, we have
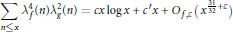 $$\sum\limits_{n\le x}{\lambda _{f}^{4}(n)\lambda _{g}^{2}(n)}=cx\log x+{c}'x+{{O}_{f,\varepsilon }}({{x}^{\frac{31}{32}+\varepsilon }});$$
$$\sum\limits_{n\le x}{\lambda _{f}^{4}(n)\lambda _{g}^{2}(n)}=cx\log x+{c}'x+{{O}_{f,\varepsilon }}({{x}^{\frac{31}{32}+\varepsilon }});$$
If 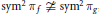 $\text{sy}{{\text{m}}^{2}}\,{{\pi }_{f}}\,\ncong \,\text{sy}{{\text{m}}^{2}}\,{{\pi }_{g}}$ and
$\text{sy}{{\text{m}}^{2}}\,{{\pi }_{f}}\,\ncong \,\text{sy}{{\text{m}}^{2}}\,{{\pi }_{g}}$ and 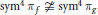 $\text{sy}{{\text{m}}^{4}}{{\pi }_{f}}\,\ncong \,\text{sy}{{\text{m}}^{4}}{{\pi }_{g}}$, then for any
$\text{sy}{{\text{m}}^{4}}{{\pi }_{f}}\,\ncong \,\text{sy}{{\text{m}}^{4}}{{\pi }_{g}}$, then for any 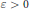 $\varepsilon \,>\,0$, we have
$\varepsilon \,>\,0$, we have
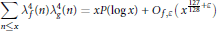 $$\sum\limits_{n\le x}{\lambda _{f}^{4}(n)\lambda _{g}^{4}(n)}=xP(\log x)+{{O}_{f,\varepsilon }}({{x}^{\frac{127}{128}+\varepsilon }}),$$
$$\sum\limits_{n\le x}{\lambda _{f}^{4}(n)\lambda _{g}^{4}(n)}=xP(\log x)+{{O}_{f,\varepsilon }}({{x}^{\frac{127}{128}+\varepsilon }}),$$
where 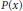 $P\left( x \right)$ is a polynomial of degree 3.
$P\left( x \right)$ is a polynomial of degree 3.