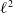1. Introduction
Let k be the function field of an irreducible projective smooth curve C defined over a finite field
![]() $\mathbb{F}_q$
. Let S be a finite non-empty set of (closed) points of C. Let
$\mathbb{F}_q$
. Let S be a finite non-empty set of (closed) points of C. Let
![]() ${\mathcal{O}}_S$
be the ring of rational functions whose poles lie in S. For each
${\mathcal{O}}_S$
be the ring of rational functions whose poles lie in S. For each
![]() $p\in S,$
there is a discrete valuation
$p\in S,$
there is a discrete valuation
![]() $\nu_x$
of k such that
$\nu_x$
of k such that
![]() $\nu_p(f)$
is the order of vanishing of f at p. The valuation ring
$\nu_p(f)$
is the order of vanishing of f at p. The valuation ring
![]() ${\mathcal{O}}_p$
is the ring of functions that do not have a pole at p, that is
${\mathcal{O}}_p$
is the ring of functions that do not have a pole at p, that is
Let
![]() $\bar{k}$
denote the algebraic closure of k. Let
$\bar{k}$
denote the algebraic closure of k. Let
![]() $\mathbf{G}$
be an affine group scheme defined over
$\mathbf{G}$
be an affine group scheme defined over
![]() $\bar{k}$
such that
$\bar{k}$
such that
![]() $\mathbf{G}(\bar{k})$
is almost simple. For each
$\mathbf{G}(\bar{k})$
is almost simple. For each
![]() $p\in S,$
there is a completion
$p\in S,$
there is a completion
![]() $k_p$
of k and the group
$k_p$
of k and the group
![]() $\mathbf{G}(k_p)$
acts on the Bruhat–Tits building
$\mathbf{G}(k_p)$
acts on the Bruhat–Tits building
![]() $X_p$
. Thus, we may embed
$X_p$
. Thus, we may embed
![]() $\mathbf{G}({\mathcal{O}}_S)$
diagonally into the product
$\mathbf{G}({\mathcal{O}}_S)$
diagonally into the product
![]() $\prod_{p\in S}\mathbf{G}(k_p)$
as an arithmetic lattice.
$\prod_{p\in S}\mathbf{G}(k_p)$
as an arithmetic lattice.
The rational cohomological dimension of a group
![]() $\Gamma$
is defined to be
$\Gamma$
is defined to be
the rational homological dimension is defined completely analogously as
In [Reference Gandini5], it is shown that
![]() $\textrm{cd}_\mathbb{Q}(\mathbf{G}({\mathcal{O}}_S))=\prod_{p\in S}\dim (X_p)$
. In light of this, Ian Leary asked the author what is
$\textrm{cd}_\mathbb{Q}(\mathbf{G}({\mathcal{O}}_S))=\prod_{p\in S}\dim (X_p)$
. In light of this, Ian Leary asked the author what is
![]() $\textrm{hd}_\mathbb{Q}(\mathbf{G}({\mathcal{O}}_S))$
?
$\textrm{hd}_\mathbb{Q}(\mathbf{G}({\mathcal{O}}_S))$
?
Theorem A. Let
![]() $\mathbf{G}$
be a simple simply connected Chevalley group. Let k and
$\mathbf{G}$
be a simple simply connected Chevalley group. Let k and
![]() ${\mathcal{O}}_S$
be as above. Then
${\mathcal{O}}_S$
be as above. Then
More generally, we obtain the following.
Corollary B. Let
![]() $\Gamma$
be a lattice in a product of simple simply connected Chevalley groups over global function fields with associated Bruhat–Tits building X. Then
$\Gamma$
be a lattice in a product of simple simply connected Chevalley groups over global function fields with associated Bruhat–Tits building X. Then
![]() $\textrm{hd}_\mathbb{Q}(\Gamma)=\textrm{cd}_\mathbb{Q}(\Gamma)=\dim (X)$
.
$\textrm{hd}_\mathbb{Q}(\Gamma)=\textrm{cd}_\mathbb{Q}(\Gamma)=\dim (X)$
.
The author expects these results are well-known; however, they do not appear in the literature so we take the opportunity to record them here.
2.
 $\ell^2$
–homology and measure equivalence
$\ell^2$
–homology and measure equivalence
Let
![]() $\Gamma$
be a group. Both
$\Gamma$
be a group. Both
![]() $\Gamma$
and the complex group algebra
$\Gamma$
and the complex group algebra
![]() $\mathbb{C} \Gamma$
act by left multiplication on the Hilbert space
$\mathbb{C} \Gamma$
act by left multiplication on the Hilbert space
![]() $\ell^2\Gamma$
of square-summable sequences. The group von Neumann algebra
$\ell^2\Gamma$
of square-summable sequences. The group von Neumann algebra
![]() ${\mathcal{N}} \Gamma$
is the ring of
${\mathcal{N}} \Gamma$
is the ring of
![]() $\Gamma$
-equivariant bounded operators on
$\Gamma$
-equivariant bounded operators on
![]() $\ell^2G$
. The non-zero divisors of
$\ell^2G$
. The non-zero divisors of
![]() ${\mathcal{N}} G$
form an Ore set and the Ore localization of
${\mathcal{N}} G$
form an Ore set and the Ore localization of
![]() ${\mathcal{N}} \Gamma$
can be identified with the ring of affiliated operators
${\mathcal{N}} \Gamma$
can be identified with the ring of affiliated operators
![]() ${\mathcal{U}} \Gamma$
.
${\mathcal{U}} \Gamma$
.
There are inclusions
![]() $\mathbb{Q}\Gamma\subseteq {\mathcal{N}} \Gamma\subseteq\ell^2\Gamma\subseteq{\mathcal{U}} \Gamma,$
and it is also known that
$\mathbb{Q}\Gamma\subseteq {\mathcal{N}} \Gamma\subseteq\ell^2\Gamma\subseteq{\mathcal{U}} \Gamma,$
and it is also known that
![]() ${\mathcal{U}} \Gamma$
is a self-injective ring which is flat over
${\mathcal{U}} \Gamma$
is a self-injective ring which is flat over
![]() ${\mathcal{N}} \Gamma$
. For more details concerning these constructions, we refer the reader to [Reference Lück12] and especially to Theorem 8.22 of Section 8.2.3 therein. The von Neumann dimension and the basic properties we need can be found in [Reference Lück12, Section 8.3].
${\mathcal{N}} \Gamma$
. For more details concerning these constructions, we refer the reader to [Reference Lück12] and especially to Theorem 8.22 of Section 8.2.3 therein. The von Neumann dimension and the basic properties we need can be found in [Reference Lück12, Section 8.3].
The
![]() $\ell^2$
-Betti numbers of a group
$\ell^2$
-Betti numbers of a group
![]() $\Gamma$
, denoted
$\Gamma$
, denoted
![]() $b_i^{(2)}(\Gamma)$
, are then defined to be the von-Neumann dimensions of the homology groups
$b_i^{(2)}(\Gamma)$
, are then defined to be the von-Neumann dimensions of the homology groups
![]() $H_i(\Gamma;\ {\mathcal{U}}\Gamma)$
. The following lemma is a triviality.
$H_i(\Gamma;\ {\mathcal{U}}\Gamma)$
. The following lemma is a triviality.
Lemma 2.1. Let
![]() $\Gamma$
be a discrete group and suppose that
$\Gamma$
be a discrete group and suppose that
![]() $b^{(2)}_i(\Gamma)>0$
. Then the homology group
$b^{(2)}_i(\Gamma)>0$
. Then the homology group
![]() $H_i(\Gamma;\ {\mathcal{U}}\Gamma)$
is non-trivial.
$H_i(\Gamma;\ {\mathcal{U}}\Gamma)$
is non-trivial.
Two countable groups
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Lambda$
are said to be measure equivalent if there exist commuting, measure-preserving, free actions of
$\Lambda$
are said to be measure equivalent if there exist commuting, measure-preserving, free actions of
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Lambda$
on some infinite Lebesgue measure space
$\Lambda$
on some infinite Lebesgue measure space
![]() $(\Omega,m)$
, such that the action of each of the groups
$(\Omega,m)$
, such that the action of each of the groups
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Lambda$
admits a finite measure fundamental domain. The key examples of measure equivalent groups are lattices in the same locally compact group [Reference Gromov6]. The relevance of this for us is the following deep theorem of Gaboriau.
$\Lambda$
admits a finite measure fundamental domain. The key examples of measure equivalent groups are lattices in the same locally compact group [Reference Gromov6]. The relevance of this for us is the following deep theorem of Gaboriau.
Theorem 2.2. (Gaboriau’s Theorem [Reference Gaboriau4]) Suppose a discrete group
![]() $\Gamma$
is measure equivalent to a discrete group
$\Gamma$
is measure equivalent to a discrete group
![]() $\Lambda$
. Then
$\Lambda$
. Then
![]() $b_p(\Gamma)=0$
if and only if
$b_p(\Gamma)=0$
if and only if
![]() $b_p(\Lambda)=0$
.
$b_p(\Lambda)=0$
.
3. Proofs
Proof of Theorem A. We first note that the group
![]() $\Gamma:=\mathbf{G}({\mathcal{O}}_S)$
is measure equivalent to the product
$\Gamma:=\mathbf{G}({\mathcal{O}}_S)$
is measure equivalent to the product
![]() $\Lambda:=\prod_{p\in S}\mathbf{G}(\mathbb{F}_q[t_p])$
for some suitably chosen
$\Lambda:=\prod_{p\in S}\mathbf{G}(\mathbb{F}_q[t_p])$
for some suitably chosen
![]() $t_p\in {\mathcal{O}}_p$
. By [Reference Petersen, Sauer and Thom13, Theorem 1.6] (see also [Reference Dymara2,Reference Dymara3,Reference Davis1]), the group
$t_p\in {\mathcal{O}}_p$
. By [Reference Petersen, Sauer and Thom13, Theorem 1.6] (see also [Reference Dymara2,Reference Dymara3,Reference Davis1]), the group
![]() $\mathbf{G}(\mathbb{F}_q[t_p])$
has one non-vanishing
$\mathbf{G}(\mathbb{F}_q[t_p])$
has one non-vanishing
![]() $\ell^2$
-Betti number in dimension
$\ell^2$
-Betti number in dimension
![]() $\dim(X_p)$
. Hence, by the Künneth formula
$\dim(X_p)$
. Hence, by the Künneth formula
![]() $\Lambda$
has one non-vanishing
$\Lambda$
has one non-vanishing
![]() $\ell^2$
-Betti number in dimension
$\ell^2$
-Betti number in dimension
![]() $d=\prod_{p\in S}\dim (X_p).$
Thus, by Gaboriau’s Theorem, the group
$d=\prod_{p\in S}\dim (X_p).$
Thus, by Gaboriau’s Theorem, the group
![]() $\Gamma$
has exactly one non-vanishing
$\Gamma$
has exactly one non-vanishing
![]() $\ell^2$
-Betti number in dimension d. It follows from Lemma 2.1 that
$\ell^2$
-Betti number in dimension d. It follows from Lemma 2.1 that
![]() $\textrm{hd}_\mathbb{Q}(\Gamma)\geq d$
. The reverse inequality follows from the fact that
$\textrm{hd}_\mathbb{Q}(\Gamma)\geq d$
. The reverse inequality follows from the fact that
![]() $\Gamma$
acts properly on the d-dimensional space
$\Gamma$
acts properly on the d-dimensional space
![]() $\prod_{p\in S}\dim (X_p)$
.
$\prod_{p\in S}\dim (X_p)$
.
Proof of Corollary B. The proof of the corollary is entirely analogous. First, we split
![]() $\mathbf{G}$
into a product of simple groups
$\mathbf{G}$
into a product of simple groups
![]() $\prod_{i=1}^n\mathbf{G}_i$
corresponding to the decomposition of the Bruhat–Tits building
$\prod_{i=1}^n\mathbf{G}_i$
corresponding to the decomposition of the Bruhat–Tits building
![]() $X=\prod_{i=1}^nX_i$
. Let
$X=\prod_{i=1}^nX_i$
. Let
![]() $\Lambda_i$
be a lattice in
$\Lambda_i$
be a lattice in
![]() $\mathbf{G}_i$
and let
$\mathbf{G}_i$
and let
![]() $\Lambda=\prod_{i=1}^n\Lambda_i$
. Each
$\Lambda=\prod_{i=1}^n\Lambda_i$
. Each
![]() $\Lambda_i$
has a non-vanishing
$\Lambda_i$
has a non-vanishing
![]() $\ell^2$
-Betti number in dimension
$\ell^2$
-Betti number in dimension
![]() $\dim (X_i)$
. In particular,
$\dim (X_i)$
. In particular,
![]() $\Lambda$
has a non-vanishing
$\Lambda$
has a non-vanishing
![]() $\ell^2$
-Betti number in dimension
$\ell^2$
-Betti number in dimension
![]() $\dim (X)=\prod_{i=1}^n\dim (X_i)$
. By Gaboriau’s Theorem,
$\dim (X)=\prod_{i=1}^n\dim (X_i)$
. By Gaboriau’s Theorem,
![]() $\Gamma$
also has non-vanishing
$\Gamma$
also has non-vanishing
![]() $\ell^2$
-Betti number in dimension
$\ell^2$
-Betti number in dimension
![]() $\dim (X)$
. It follows from Lemma 2.1 that
$\dim (X)$
. It follows from Lemma 2.1 that
![]() $\textrm{hd}_\mathbb{Q}(\Gamma)\geq d$
. The reverse inequality follows from the fact that
$\textrm{hd}_\mathbb{Q}(\Gamma)\geq d$
. The reverse inequality follows from the fact that
![]() $\Gamma$
acts properly on the d-dimensional space
$\Gamma$
acts properly on the d-dimensional space
![]() $\prod_{p\in S} X_p$
.
$\prod_{p\in S} X_p$
.
Remark 3.1. A similar argument can be applied to lattices in products of simple simply connected algebraic groups over locally compact p-adic fields. One obtains the analogous result for such a lattice
![]() $\Gamma$
that
$\Gamma$
that
![]() $\textrm{cd}_\mathbb{Q} (\Gamma)=\textrm{hd}_\mathbb{Q} (\Gamma)=\dim (X)$
, where X is the associated Bruhat–Tits building.
$\textrm{cd}_\mathbb{Q} (\Gamma)=\textrm{hd}_\mathbb{Q} (\Gamma)=\dim (X)$
, where X is the associated Bruhat–Tits building.
Acknowledgements
The author would like to thank his PhD supervisor Professor Ian Leary for his guidance, support, and suggesting of the question. This note contains material from the author’s PhD thesis [Reference Hughes7] and was originally part of [Reference Hughes8], but was split off into a number of companion papers [Reference Hughes9,Reference Hughes10] (see also [Reference Hughes and Valiunas11]) at the request of the referee. This work was supported by the Engineering and Physical Sciences Research Council grant number 2127970. The author would like to thank the referee for a number of helpful comments.
Competing interests
The author declares none.