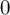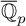Introduction
Let p be a prime number. For any perfect field F, we shall write
![]() $\overline {F}$
for the algebraic closure (determined up to isomorphisms) of F. We shall write
$\overline {F}$
for the algebraic closure (determined up to isomorphisms) of F. We shall write
![]() $\mathbb {Q}_{p}$
for the field of p-adic numbers;
$\mathbb {Q}_{p}$
for the field of p-adic numbers;
![]() $\mathbb {C}_{p}$
for the p-adic completion of
$\mathbb {C}_{p}$
for the p-adic completion of
![]() $\overline {\mathbb {Q}}_p$
. One of the central subjects/results in anabelian geometry is the Grothendieck Conjecture (cf. [Reference Mochizuki7], Theorem A; [Reference Tamagawa12], Theorem 0.4). The Grothendieck Conjecture-type results assert that ‘anabelian’ varieties over ‘sufficiently arithmetic’ fields (for instance, hyperbolic curves over number fields, p-adic local fields or finite fields) may be reconstructed from their étale fundamental groups. On the other hand, we note that the group structure of the étale fundamental groups of hyperbolic curves over algebraically closed fields of characteristic
$\overline {\mathbb {Q}}_p$
. One of the central subjects/results in anabelian geometry is the Grothendieck Conjecture (cf. [Reference Mochizuki7], Theorem A; [Reference Tamagawa12], Theorem 0.4). The Grothendieck Conjecture-type results assert that ‘anabelian’ varieties over ‘sufficiently arithmetic’ fields (for instance, hyperbolic curves over number fields, p-adic local fields or finite fields) may be reconstructed from their étale fundamental groups. On the other hand, we note that the group structure of the étale fundamental groups of hyperbolic curves over algebraically closed fields of characteristic
![]() $0$
(i.e. fields far from ‘sufficiently arithmetic’) may be completely determined by the genus and the number of cusps of the hyperbolic curves. In particular, the moduli of hyperbolic curves over algebraically closed fields of characteristic
$0$
(i.e. fields far from ‘sufficiently arithmetic’) may be completely determined by the genus and the number of cusps of the hyperbolic curves. In particular, the moduli of hyperbolic curves over algebraically closed fields of characteristic
![]() $0$
may not be determined by their étale fundamental groups.
$0$
may not be determined by their étale fundamental groups.
Next, let us recall the tempered fundamental groups of smooth algebraic varieties (i.e. smooth, separated, of finite type and geometrically integral schemes) over non-Archimedean complete valuation fields introduced by André, which may be regarded as a p-adic analogue of the usual topological fundamental groups of complex manifolds (cf. [Reference André1], [Reference André2]). Let Z be a smooth algebraic variety over a non-Archimedean complete valuation field;
![]() $\widetilde {Z} \rightarrow Z$
a pro-universal étale covering (determined up to isomorphisms). Then the tempered fundamental group
$\widetilde {Z} \rightarrow Z$
a pro-universal étale covering (determined up to isomorphisms). Then the tempered fundamental group
![]() $\Pi ^{\mathrm {tp}}_Z$
of Z (relative to a suitable choice of basepoint) may be defined as
$\Pi ^{\mathrm {tp}}_Z$
of Z (relative to a suitable choice of basepoint) may be defined as
where
![]() $Z' \rightarrow Z$
ranges over the finite étale Galois subcoverings of the fixed pro-universal étale covering
$Z' \rightarrow Z$
ranges over the finite étale Galois subcoverings of the fixed pro-universal étale covering
![]() $\widetilde {Z} \rightarrow Z$
;
$\widetilde {Z} \rightarrow Z$
;
![]() $(-)^{\mathrm {an}}$
denotes the Berkovich analytification of
$(-)^{\mathrm {an}}$
denotes the Berkovich analytification of
![]() $(-)$
;
$(-)$
;
![]() $(-)^{\mathrm {top}}$
denotes the topological universal covering of
$(-)^{\mathrm {top}}$
denotes the topological universal covering of
![]() $(-)$
. Here, each group
$(-)$
. Here, each group
![]() $\mathrm {Aut}(({Z'}^{\mathrm {an}})^{\mathrm {top}}/Z^{\mathrm {an}})$
may be regarded as a topological group endowed with the discrete topology and
$\mathrm {Aut}(({Z'}^{\mathrm {an}})^{\mathrm {top}}/Z^{\mathrm {an}})$
may be regarded as a topological group endowed with the discrete topology and
![]() $\Pi ^{\mathrm {tp}}_Z$
may be regarded as a topological group endowed with the subspace topology of the product topology on
$\Pi ^{\mathrm {tp}}_Z$
may be regarded as a topological group endowed with the subspace topology of the product topology on
![]() $\prod _{Z' \rightarrow Z} \ \mathrm {Aut}(({Z'}^{\mathrm {an}})^{\mathrm {top}}/Z^{\mathrm {an}})$
. Note that the calculation of topological fundamental groups of the Berkovich spaces associated to smooth algebraic varieties is already difficult in general. Thus, the determination of the topological group structure of the tempered fundamental group
$\prod _{Z' \rightarrow Z} \ \mathrm {Aut}(({Z'}^{\mathrm {an}})^{\mathrm {top}}/Z^{\mathrm {an}})$
. Note that the calculation of topological fundamental groups of the Berkovich spaces associated to smooth algebraic varieties is already difficult in general. Thus, the determination of the topological group structure of the tempered fundamental group
![]() $\Pi ^{\mathrm {tp}}_Z$
may be a highly nontrivial problem. Moreover, one may expect that, in general, the topological group structure of the tempered fundamental group
$\Pi ^{\mathrm {tp}}_Z$
may be a highly nontrivial problem. Moreover, one may expect that, in general, the topological group structure of the tempered fundamental group
![]() $\Pi ^{\mathrm {tp}}_Z$
tends to become so complicated and depends heavily on the geometric structure of Z, even if the base fields are algebraically closed fields of characteristic
$\Pi ^{\mathrm {tp}}_Z$
tends to become so complicated and depends heavily on the geometric structure of Z, even if the base fields are algebraically closed fields of characteristic
![]() $0$
. So, it is natural to pose the following anabelian geometric question:
$0$
. So, it is natural to pose the following anabelian geometric question:
Question 1. What geometric information does the tempered fundamental group carry?
In the remainder, for a smooth algebraic variety S over
![]() $\overline {\mathbb {Q}}_p$
, we shall write
$\overline {\mathbb {Q}}_p$
, we shall write
![]() $\Pi ^{\mathrm {tp}}_{S}$
for the tempered fundamental group of
$\Pi ^{\mathrm {tp}}_{S}$
for the tempered fundamental group of
![]() $S \times _{\overline {\mathbb {Q}}_p} \mathbb {C}_{p}$
, relative to a suitable choice of basepoint. With regard to Question 1, the following theorems have been obtained by Mochizuki and Lepage so far:
$S \times _{\overline {\mathbb {Q}}_p} \mathbb {C}_{p}$
, relative to a suitable choice of basepoint. With regard to Question 1, the following theorems have been obtained by Mochizuki and Lepage so far:
Theorem 0.1 [Reference Mochizuki9], Corollary 3.11
Let X, Y be hyperbolic curves over
![]() $\overline {\mathbb {Q}}_p$
;
$\overline {\mathbb {Q}}_p$
;
an isomorphism of topological groups. Write
![]() $\mathcal {G}_X$
,
$\mathcal {G}_X$
,
![]() $\mathcal {G}_Y$
for the semi-graphs of anabelioids associated to the special fibres of the stable models of X, Y, respectively. Then
$\mathcal {G}_Y$
for the semi-graphs of anabelioids associated to the special fibres of the stable models of X, Y, respectively. Then
![]() $\alpha $
induces an isomorphism of semi-graphs of anabelioids
$\alpha $
induces an isomorphism of semi-graphs of anabelioids
in a fashion that is functorial with respect to
![]() $\alpha $
. In particular, the following hold:
$\alpha $
. In particular, the following hold:
-
• The isomorphism
 $\alpha $
maps the cuspidal inertia subgroups of
$\alpha $
maps the cuspidal inertia subgroups of
 $\Pi ^{\mathrm {tp}}_X$
to the cuspidal inertia subgroups of
$\Pi ^{\mathrm {tp}}_X$
to the cuspidal inertia subgroups of
 $\Pi ^{\mathrm {tp}}_Y$
(cf. Notations and conventions, Fundamental groups).
$\Pi ^{\mathrm {tp}}_Y$
(cf. Notations and conventions, Fundamental groups). -
• Write
 $\Gamma _X$
,
$\Gamma _X$
,
 $\Gamma _Y$
for the underlying semi-graphs of
$\Gamma _Y$
for the underlying semi-graphs of
 $\mathcal {G}_X$
,
$\mathcal {G}_X$
,
 $\mathcal {G}_Y$
(i.e. dual semi-graphs associated to the special fibres of the stable models of X, Y), respectively. Then
$\mathcal {G}_Y$
(i.e. dual semi-graphs associated to the special fibres of the stable models of X, Y), respectively. Then
 $\alpha $
induces an isomorphism of semi-graphs in a fashion that is functorial with respect to
$\alpha $
induces an isomorphism of semi-graphs in a fashion that is functorial with respect to $$ \begin{align*}\alpha_{\Gamma} : \Gamma_X \overset{\sim}{\rightarrow} \Gamma_Y \end{align*} $$
$$ \begin{align*}\alpha_{\Gamma} : \Gamma_X \overset{\sim}{\rightarrow} \Gamma_Y \end{align*} $$
 $\alpha $
.
$\alpha $
.
Theorem 0.2 [Reference Lepage4], Theorem 4.13; [Reference Lepage5], Theorem 0.2
In the notation of Theorem 0.1, suppose that X and Y are hyperbolic Mumford curves over
![]() $\overline {\mathbb {Q}}_p$
. Then the following hold:
$\overline {\mathbb {Q}}_p$
. Then the following hold:
-
(i) The isomorphism
 $\alpha _{\Gamma }$
(cf. Theorem 0.1) is an isomorphism of metric semi-graphs.
$\alpha _{\Gamma }$
(cf. Theorem 0.1) is an isomorphism of metric semi-graphs. -
(ii) There exists a canonical homeomorphism between the underlying topological spaces of the Berkovich spaces
 $(X \times _{\overline {\mathbb {Q}}_p} \mathbb {C}_{p})^{\mathrm {an}}$
and
$(X \times _{\overline {\mathbb {Q}}_p} \mathbb {C}_{p})^{\mathrm {an}}$
and
 $(Y \times _{\overline {\mathbb {Q}}_p} \mathbb {C}_{p})^{\mathrm {an}}$
.
$(Y \times _{\overline {\mathbb {Q}}_p} \mathbb {C}_{p})^{\mathrm {an}}$
.
Theorem 0.3 [Reference Lepage5], Theorem 0.3
Let
![]() $E_1$
,
$E_1$
,
![]() $E_2$
be once-punctured Tate elliptic curves over
$E_2$
be once-punctured Tate elliptic curves over
![]() $\overline {\mathbb {Q}}_p$
. Write
$\overline {\mathbb {Q}}_p$
. Write
![]() $q_1$
,
$q_1$
,
![]() $q_2$
for the q-parameters of
$q_2$
for the q-parameters of
![]() $E_1$
,
$E_1$
,
![]() $E_2$
, respectively. Suppose that there exists an isomorphism of topological groups
$E_2$
, respectively. Suppose that there exists an isomorphism of topological groups
Then there exists an element
![]() $\sigma \in \mathrm {Gal}(\overline {\mathbb {Q}}_p/\mathbb {Q}_{p})$
such that
$\sigma \in \mathrm {Gal}(\overline {\mathbb {Q}}_p/\mathbb {Q}_{p})$
such that
![]() $q_2 = \sigma (q_1)$
.
$q_2 = \sigma (q_1)$
.
In particular, the above theorems imply that the tempered fundamental groups of hyperbolic curves carry sufficiently rich scheme-theoretic (or, geometric) information even if the base fields are algebraically closed fields of characteristic
![]() $0$
.
$0$
.
In the present paper, inspired by the above theorems, we consider Question 1 for hyperbolic curves of genus
![]() $0$
over
$0$
over
![]() $\overline {\mathbb {Q}}_p$
and prove that their tempered fundamental groups completely determine their moduli:
$\overline {\mathbb {Q}}_p$
and prove that their tempered fundamental groups completely determine their moduli:
Theorem A. Let n be an integer such that
![]() $n \geq 3$
. Suppose that there exists an isomorphism of topological groups
$n \geq 3$
. Suppose that there exists an isomorphism of topological groups
Note that
![]() $\alpha $
induces a bijection
$\alpha $
induces a bijection
(cf. Theorem 0.1; Notations and conventions, Fundamental groups). Then there exists an isomorphism of schemes
such that the bijection
![]() $\{x_1, x_2, \dots , x_n\} \overset {\sim }{\rightarrow } \{x_{1}', x_{2}', \dots , x_{n}'\}$
induced by the isomorphism
$\{x_1, x_2, \dots , x_n\} \overset {\sim }{\rightarrow } \{x_{1}', x_{2}', \dots , x_{n}'\}$
induced by the isomorphism
![]() ${\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_1, x_2, \dots , x_n\} \overset {\sim }{\rightarrow } {\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_{1}', x_{2}', \dots , x_{n}'\}$
coincides with the bijection
${\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_1, x_2, \dots , x_n\} \overset {\sim }{\rightarrow } {\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_{1}', x_{2}', \dots , x_{n}'\}$
coincides with the bijection
![]() $\alpha _{\mathrm {cusp}}$
.
$\alpha _{\mathrm {cusp}}$
.
We will apply Theorems 0.1 and 0.3, together with some complicated calculations concerning certain Belyi maps (cf. Lemma 1.1, (i), (ii)), to prove Theorem A. Note that Theorem A is related with the partial reconstruction result of hyperbolic curves obtained in an author’s previous work (cf. [Reference Tsujimura17], Theorem C), whose proof is a direct application of Theorem 0.1 (cf. [Reference Mochizuki9], Corollary 3.11), together with the theory of resolution of nonsingularities (cf. [Reference Lepage5], [Reference Tamagawa15]). On the other hand, in light of Theorems 0.3; A, it is natural to pose the following question:
Question 2. Let
![]() $E_1$
,
$E_1$
,
![]() $E_2$
be hyperbolic curves of genus
$E_2$
be hyperbolic curves of genus
![]() $1$
over
$1$
over
![]() $\overline {\mathbb {Q}}_p$
. Suppose that there exists an isomorphism of topological groups
$\overline {\mathbb {Q}}_p$
. Suppose that there exists an isomorphism of topological groups
Then does there exist an isomorphism of schemes
![]() $E_1 \overset {\sim }{\rightarrow } E_2$
?
$E_1 \overset {\sim }{\rightarrow } E_2$
?
However, at the time of writing of the present paper, the author does not know whether Question 2 is affirmative or not (even if we assume that
![]() $E_1$
and
$E_1$
and
![]() $E_2$
are once-punctured). Furthermore, interestingly, one may regard Theorem A as an analogous result in characteristic
$E_2$
are once-punctured). Furthermore, interestingly, one may regard Theorem A as an analogous result in characteristic
![]() $0$
of the corresponding result for hyperbolic curves of genus
$0$
of the corresponding result for hyperbolic curves of genus
![]() $0$
over
$0$
over
![]() $\overline {\mathbb {F}}_p$
proved by Tamagawa (cf. [Reference Tamagawa13], Theorem 0.2). So, it would also be interesting to investigate the extent to which the analogous results in characteristic
$\overline {\mathbb {F}}_p$
proved by Tamagawa (cf. [Reference Tamagawa13], Theorem 0.2). So, it would also be interesting to investigate the extent to which the analogous results in characteristic
![]() $0$
of the various results for hyperbolic/stable curves over
$0$
of the various results for hyperbolic/stable curves over
![]() $\overline {\mathbb {F}}_p$
(cf. for instance, [Reference Sarashina11], [Reference Tamagawa and Schneps14], [Reference Tamagawa16], [Reference Yang18]) hold.
$\overline {\mathbb {F}}_p$
(cf. for instance, [Reference Sarashina11], [Reference Tamagawa and Schneps14], [Reference Tamagawa16], [Reference Yang18]) hold.
The present paper is organised as follows. In §1, we observe that the open subgroups of
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
associated to certain Belyi maps are preserved (up to composition with an inner automorphism) via any automorphism of
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
associated to certain Belyi maps are preserved (up to composition with an inner automorphism) via any automorphism of
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
. In §2, we execute some elementary computations concerning the Belyi maps that appear in §1. In §3, we apply the results obtained in the previous sections, together with Lepage’s reconstruction result for the once-punctured Tate elliptic curves over
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
. In §2, we execute some elementary computations concerning the Belyi maps that appear in §1. In §3, we apply the results obtained in the previous sections, together with Lepage’s reconstruction result for the once-punctured Tate elliptic curves over
![]() $\overline {\mathbb {Q}}_p$
, to prove Theorem A.
$\overline {\mathbb {Q}}_p$
, to prove Theorem A.
Notations and conventions
Numbers: The notation
![]() $\mathbb {Q}$
will be used to denote the field of rational numbers. If p is a prime number, then the notation
$\mathbb {Q}$
will be used to denote the field of rational numbers. If p is a prime number, then the notation
![]() $\mathbb {Q}_{p}$
will be used to denote the p-adic completion of
$\mathbb {Q}_{p}$
will be used to denote the p-adic completion of
![]() $\mathbb {Q}$
. The notation
$\mathbb {Q}$
. The notation
![]() $\overline {\mathbb {Q}}_p$
will be used to denote an algebraic closure of
$\overline {\mathbb {Q}}_p$
will be used to denote an algebraic closure of
![]() $\mathbb {Q}_{p}$
. For each positive integer r, we fix a primitive
$\mathbb {Q}_{p}$
. For each positive integer r, we fix a primitive
![]() $p^r$
-th root of unity
$p^r$
-th root of unity
![]() $\zeta _{p^r} \in \overline {\mathbb {Q}}_p$
. The notation
$\zeta _{p^r} \in \overline {\mathbb {Q}}_p$
. The notation
![]() $\mathbb {C}_{p}$
will be used to denote the p-adic completion of
$\mathbb {C}_{p}$
will be used to denote the p-adic completion of
![]() $\overline {\mathbb {Q}}_p$
. It is well-known that
$\overline {\mathbb {Q}}_p$
. It is well-known that
![]() $\mathbb {C}_{p}$
is an algebraically closed field.
$\mathbb {C}_{p}$
is an algebraically closed field.
Valuations: We shall write
![]() $v_p$
for the additive valuation on
$v_p$
for the additive valuation on
![]() $\overline {\mathbb {Q}}_p$
normalised by
$\overline {\mathbb {Q}}_p$
normalised by
![]() $v_p(p) = 1$
.
$v_p(p) = 1$
.
Topological groups: Let G be a topological group. Then we shall write
![]() $\mathrm {Aut}(G)$
for the group of continuous automorphisms of G.
$\mathrm {Aut}(G)$
for the group of continuous automorphisms of G.
Curves: Let k be an algebraically closed field; X a
![]() $1$
-dimensional, connected, smooth, separated, of finite type scheme over k. Then we shall write
$1$
-dimensional, connected, smooth, separated, of finite type scheme over k. Then we shall write
![]() $X(k)$
for the set of k-valued points of X;
$X(k)$
for the set of k-valued points of X;
![]() $\overline {X}$
for the smooth compactification of X over k. We shall refer to an element
$\overline {X}$
for the smooth compactification of X over k. We shall refer to an element
![]() $\in \overline {X}\setminus X$
as a cusp of X. Let
$\in \overline {X}\setminus X$
as a cusp of X. Let
![]() $(g, n)$
be a pair of nonnegative integers. Then we shall say that X is of type
$(g, n)$
be a pair of nonnegative integers. Then we shall say that X is of type
![]() $(g, n)$
if X has genus g and the cardinality of the set of cusps of X is n. Suppose that X is of type
$(g, n)$
if X has genus g and the cardinality of the set of cusps of X is n. Suppose that X is of type
![]() $(g, n)$
. Then we shall say that X is a hyperbolic curve if
$(g, n)$
. Then we shall say that X is a hyperbolic curve if
![]() $2g-2+n>0$
(so if
$2g-2+n>0$
(so if
![]() $g=0$
, then
$g=0$
, then
![]() $n \geq 3$
). We shall write
$n \geq 3$
). We shall write
![]() ${\mathbb P}^1_{\overline {\mathbb {Q}}_p}$
for the projective line over
${\mathbb P}^1_{\overline {\mathbb {Q}}_p}$
for the projective line over
![]() $\overline {\mathbb {Q}}_p$
. We shall use t for the standard coordinate of
$\overline {\mathbb {Q}}_p$
. We shall use t for the standard coordinate of
![]() ${\mathbb P}^1_{\overline {\mathbb {Q}}_p}$
. We shall identify
${\mathbb P}^1_{\overline {\mathbb {Q}}_p}$
. We shall identify
![]() $\overline {\mathbb {Q}}_p$
with
$\overline {\mathbb {Q}}_p$
with
![]() ${\mathbb P}^1_{\overline {\mathbb {Q}}_p}(\overline {\mathbb {Q}}_p)\setminus \{\infty \}$
.
${\mathbb P}^1_{\overline {\mathbb {Q}}_p}(\overline {\mathbb {Q}}_p)\setminus \{\infty \}$
.
Fundamental groups: Let X be a hyperbolic curve over
![]() $\overline {\mathbb {Q}}_p$
. Then we shall write
$\overline {\mathbb {Q}}_p$
. Then we shall write
![]() $\Pi ^{\mathrm {tp}}_{X}$
for the tempered fundamental group of
$\Pi ^{\mathrm {tp}}_{X}$
for the tempered fundamental group of
![]() $X \times _{\overline {\mathbb {Q}}_p} \mathbb {C}_{p}$
, relative to a suitable choice of basepoint (cf. [Reference André1], [Reference André2]). Note that the projection morphism
$X \times _{\overline {\mathbb {Q}}_p} \mathbb {C}_{p}$
, relative to a suitable choice of basepoint (cf. [Reference André1], [Reference André2]). Note that the projection morphism
![]() $X \times _{\overline {\mathbb {Q}}_p} \mathbb {C}_{p} \rightarrow X$
induces a bijection between the respective sets of cusps. Let x be a cusp of X (so x determines a cusp
$X \times _{\overline {\mathbb {Q}}_p} \mathbb {C}_{p} \rightarrow X$
induces a bijection between the respective sets of cusps. Let x be a cusp of X (so x determines a cusp
![]() $x_{\mathbb {C}_{p}}$
of
$x_{\mathbb {C}_{p}}$
of
![]() $X \times _{\overline {\mathbb {Q}}_p} \mathbb {C}_{p}$
). Then we shall refer to the stabiliser subgroup of
$X \times _{\overline {\mathbb {Q}}_p} \mathbb {C}_{p}$
). Then we shall refer to the stabiliser subgroup of
![]() $\Pi ^{\mathrm {tp}}_{X}$
associated to some pro-cusp of the pro-universal tempered covering of
$\Pi ^{\mathrm {tp}}_{X}$
associated to some pro-cusp of the pro-universal tempered covering of
![]() $X \times _{\overline {\mathbb {Q}}_p} \mathbb {C}_{p}$
that lies over
$X \times _{\overline {\mathbb {Q}}_p} \mathbb {C}_{p}$
that lies over
![]() $x_{\mathbb {C}_{p}}$
as a cuspidal inertia subgroup of
$x_{\mathbb {C}_{p}}$
as a cuspidal inertia subgroup of
![]() $\Pi ^{\mathrm {tp}}_{X}$
associated to x. Note that it follows immediately from the various definitions involved that the cuspidal inertia subgroups of
$\Pi ^{\mathrm {tp}}_{X}$
associated to x. Note that it follows immediately from the various definitions involved that the cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm {tp}}_{X}$
associated to x are conjugate. Note also that, if we write
$\Pi ^{\mathrm {tp}}_{X}$
associated to x are conjugate. Note also that, if we write
![]() $I_X$
for the set of the conjugacy classes of cuspidal inertia subgroups of
$I_X$
for the set of the conjugacy classes of cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm {tp}}_{X}$
, then the natural map
$\Pi ^{\mathrm {tp}}_{X}$
, then the natural map
![]() $\overline {X}\setminus X \rightarrow I_X$
is bijective. (Indeed, the surjectivity follows immediately from the various definitions involved, and the injectivity follows immediately from the well-known structure of (the abelianisations of) the étale fundamental groups of hyperbolic curves over algebraically closed fields of characteristic
$\overline {X}\setminus X \rightarrow I_X$
is bijective. (Indeed, the surjectivity follows immediately from the various definitions involved, and the injectivity follows immediately from the well-known structure of (the abelianisations of) the étale fundamental groups of hyperbolic curves over algebraically closed fields of characteristic
![]() $0$
, together with [Reference André2], Proposition 4.4.1.). We shall identify
$0$
, together with [Reference André2], Proposition 4.4.1.). We shall identify
![]() $\overline {X}\setminus X$
with
$\overline {X}\setminus X$
with
![]() $I_X$
via this natural bijection.
$I_X$
via this natural bijection.
1 Numerical characterisations of certain Belyi maps
In the present section, we observe that the open subgroups associated to certain Belyi maps (which will be of use in the proof of our main theorem in §3) are preserved (up to composition with an inner automorphism) via any automorphism of the geometric tempered fundamental group of projective line minus three points (cf. Lemma 1.3).
Let p be a prime number.
Lemma 1.1. The following hold:
-
(i) Let r be a positive integer. Write
for the Belyi map determined by the assignment $$ \begin{align*} \phi_{p^r} : {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \big\{0, \zeta_{p^r}^{i} \ (0 \leq i \leq p^{r}-1), \infty \big\} \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{0, 1, \infty \} \end{align*} $$
Then the connected finite étale covering
$$ \begin{align*} \phi_{p^r} : {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \big\{0, \zeta_{p^r}^{i} \ (0 \leq i \leq p^{r}-1), \infty \big\} \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{0, 1, \infty \} \end{align*} $$
Then the connected finite étale covering $$ \begin{align*} t \mapsto t^{p^r}. \end{align*} $$
$$ \begin{align*} t \mapsto t^{p^r}. \end{align*} $$
 $\phi _{p^r}$
may be uniquely characterised (up to isomorphisms of connected finite étale coverings) as the connected finite étale covering
$\phi _{p^r}$
may be uniquely characterised (up to isomorphisms of connected finite étale coverings) as the connected finite étale covering $$ \begin{align*}g : X \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{0, 1, \infty \}, \end{align*} $$
$$ \begin{align*}g : X \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{0, 1, \infty \}, \end{align*} $$
satisfying the following conditions:
-
•
 $\mathrm {deg}(g) = p^r$
;
$\mathrm {deg}(g) = p^r$
; -
• g is unramified over
 $1$
;
$1$
; -
• g is totally ramified over
 $0$
and
$0$
and
 $\infty $
.
$\infty $
.
-
-
(ii) Let
 $(m, n)$
be a pair of positive integers. Write for the Belyi map determined by the assignment
$(m, n)$
be a pair of positive integers. Write for the Belyi map determined by the assignment $$ \begin{align*} \psi_{m,n} : {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{m}{m+n}, \dots, \infty \bigg\} \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{0, 1, \infty \} \end{align*} $$
Then the connected finite étale covering
$$ \begin{align*} \psi_{m,n} : {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{m}{m+n}, \dots, \infty \bigg\} \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{0, 1, \infty \} \end{align*} $$
Then the connected finite étale covering $$ \begin{align*} t \mapsto \frac{(m+n)^{m+n}}{m^m n^n}t^{m}(1-t)^{n}. \end{align*} $$
$$ \begin{align*} t \mapsto \frac{(m+n)^{m+n}}{m^m n^n}t^{m}(1-t)^{n}. \end{align*} $$
 $\psi _{m,n}$
may be uniquely characterised (up to isomorphisms of connected finite étale coverings) as the connected finite étale covering satisfying the following conditions:
$\psi _{m,n}$
may be uniquely characterised (up to isomorphisms of connected finite étale coverings) as the connected finite étale covering satisfying the following conditions: $$ \begin{align*} g : X \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{0, 1, \infty\}, \end{align*} $$
$$ \begin{align*} g : X \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{0, 1, \infty\}, \end{align*} $$
-
•
 $\mathrm {deg}(g) = m+n$
.
$\mathrm {deg}(g) = m+n$
. -
• The genus of X is
 $0$
.
$0$
. -
• Write
 $\overline {g} : \overline {X} \rightarrow {\mathbb P}^1_{\overline {\mathbb {Q}}_p}$
for the finite morphism induced by g (cf. Notations and conventions, Curves). Then
$\overline {g} : \overline {X} \rightarrow {\mathbb P}^1_{\overline {\mathbb {Q}}_p}$
for the finite morphism induced by g (cf. Notations and conventions, Curves). Then
 $\overline {g}^{-1}(0)$
consists of two closed points of
$\overline {g}^{-1}(0)$
consists of two closed points of
 $\overline {X}$
, and
$\overline {X}$
, and
 $\overline {g}^{-1}(1)$
consists of
$\overline {g}^{-1}(1)$
consists of
 $m+n-1$
closed points of
$m+n-1$
closed points of
 $\overline {X}$
.
$\overline {X}$
. -
• The ramification index of
 $\overline {g}$
at a closed point over
$\overline {g}$
at a closed point over
 $0$
coincides with m, and the ramification index of
$0$
coincides with m, and the ramification index of
 $\overline {g}$
at another closed point over
$\overline {g}$
at another closed point over
 $0$
coincides with n.
$0$
coincides with n. -
• g is totally ramified over
 $\infty $
.
$\infty $
.
-
Proof. Assertion (i) follows immediately from the well-known calculation of the étale fundamental group of the multiplicative group
![]() $\mathbb {G}_m$
. Next, we verify assertion (ii). Write
$\mathbb {G}_m$
. Next, we verify assertion (ii). Write
![]() $\overline {g}^{-1}(0) \overset {\mathrm {def}}{=} \{a, b\}$
. Then it follows immediately from the various definitions involved that we may assume without loss of generality that the ramification index of
$\overline {g}^{-1}(0) \overset {\mathrm {def}}{=} \{a, b\}$
. Then it follows immediately from the various definitions involved that we may assume without loss of generality that the ramification index of
![]() $\overline {g}$
at a coincides with m, and the ramification index of
$\overline {g}$
at a coincides with m, and the ramification index of
![]() $\overline {g}$
at b coincides with n. Note that since the genus of X is
$\overline {g}$
at b coincides with n. Note that since the genus of X is
![]() $0$
, there exists a(n) (unique) isomorphism
$0$
, there exists a(n) (unique) isomorphism
over
![]() $\overline {\mathbb {Q}}_p$
that map a, b, the unique point
$\overline {\mathbb {Q}}_p$
that map a, b, the unique point
![]() $\in \overline {g}^{-1}(\infty )$
to
$\in \overline {g}^{-1}(\infty )$
to
![]() $0$
,
$0$
,
![]() $1$
,
$1$
,
![]() $\infty $
, respectively. In particular, we may also assume without loss of generality that
$\infty $
, respectively. In particular, we may also assume without loss of generality that
-
• X is an open subscheme of
 ${\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}$
;
${\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}$
; -
•
 $\overline {X} = {\mathbb P}^1_{\overline {\mathbb {Q}}_p}$
;
$\overline {X} = {\mathbb P}^1_{\overline {\mathbb {Q}}_p}$
; -
•
 $a = 0$
,
$a = 0$
,
 $b =1$
, and
$b =1$
, and
 $\overline {g}(\infty ) = \infty $
.
$\overline {g}(\infty ) = \infty $
.
Next, since g is totally ramified over
![]() $\infty $
, it holds that g is defined by a polynomial
$\infty $
, it holds that g is defined by a polynomial
![]() $h(t) \in \overline {\mathbb {Q}}_{p}[t]$
. Observe that
$h(t) \in \overline {\mathbb {Q}}_{p}[t]$
. Observe that
![]() $0$
,
$0$
,
![]() $1$
are roots of
$1$
are roots of
![]() $h(t)$
with multiplicity m, n, respectively. Thus, since
$h(t)$
with multiplicity m, n, respectively. Thus, since
![]() $\mathrm {deg}(h(t)) = \mathrm {deg}(g) = m+n$
, there exists an element
$\mathrm {deg}(h(t)) = \mathrm {deg}(g) = m+n$
, there exists an element
![]() $c \in \overline {\mathbb {Q}}_p$
such that
$c \in \overline {\mathbb {Q}}_p$
such that
Then it holds that
On the other hand, since
![]() $\overline {g}^{-1}(1)$
consists of
$\overline {g}^{-1}(1)$
consists of
![]() $m+n-1$
closed points, and
$m+n-1$
closed points, and
![]() $0 < \frac {m}{m+n} < 1$
, it holds that
$0 < \frac {m}{m+n} < 1$
, it holds that
![]() $\overline {g}$
ramifies over
$\overline {g}$
ramifies over
![]() $1$
. Thus, we conclude that
$1$
. Thus, we conclude that
![]() $h(\frac {m}{m+n}) = 1$
, hence that
$h(\frac {m}{m+n}) = 1$
, hence that
![]() $c = \frac {(m+n)^{m+n}}{m^m n^n}$
. This completes the proof of Lemma 1.1.
$c = \frac {(m+n)^{m+n}}{m^m n^n}$
. This completes the proof of Lemma 1.1.
Remark 1.1.1. In the remainder of the present paper, for each positive integer m, we shall write
![]() $\psi _m$
for
$\psi _m$
for
![]() $\psi _{m,1}$
.
$\psi _{m,1}$
.
Remark 1.1.2. Note that
![]() $\psi _{m,n}$
is a connected finite étale covering that appears in the proof of the well-known Belyi’s theorem (cf. [Reference Belyi3], [Reference Mochizuki8]).
$\psi _{m,n}$
is a connected finite étale covering that appears in the proof of the well-known Belyi’s theorem (cf. [Reference Belyi3], [Reference Mochizuki8]).
Definition 1.2. We shall write
for the open subgroups (determined up to
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
-conjugate) of finite index determined by the connected finite étale coverings
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
-conjugate) of finite index determined by the connected finite étale coverings
![]() $\phi _{p^r}$
,
$\phi _{p^r}$
,
![]() $\psi _{m,n}$
, respectively (cf. Lemma 1.1, (i), (ii)).
$\psi _{m,n}$
, respectively (cf. Lemma 1.1, (i), (ii)).
Lemma 1.3. Let
![]() $\alpha \in \mathrm {Aut}(\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}})$
be an automorphism of topological groups. Recall that
$\alpha \in \mathrm {Aut}(\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}})$
be an automorphism of topological groups. Recall that
![]() $\alpha $
induces a bijection on the set of the conjugacy classes of cuspidal inertia subgroups of
$\alpha $
induces a bijection on the set of the conjugacy classes of cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
(cf. [Reference Mochizuki9], Corollary 3.11) that determines a bijection
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
(cf. [Reference Mochizuki9], Corollary 3.11) that determines a bijection
![]() $\alpha _{\mathrm {cusp}} : \{0, 1, \infty \} \overset {\sim }{\rightarrow } \{0, 1, \infty \}$
. Suppose that
$\alpha _{\mathrm {cusp}} : \{0, 1, \infty \} \overset {\sim }{\rightarrow } \{0, 1, \infty \}$
. Suppose that
Then there exists an inner automorphism
![]() $\iota $
of
$\iota $
of
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
, such that the composite
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
, such that the composite
![]() $\alpha \circ \iota \in \mathrm {Aut}(\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}})$
induces an automorphism of
$\alpha \circ \iota \in \mathrm {Aut}(\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}})$
induces an automorphism of
![]() $\Pi ^{\mathrm {tp}}_{\phi _{p^r}}$
(respectively,
$\Pi ^{\mathrm {tp}}_{\phi _{p^r}}$
(respectively,
![]() $\Pi ^{\mathrm {tp}}_{\psi _{m,n}}$
) via the inclusion
$\Pi ^{\mathrm {tp}}_{\psi _{m,n}}$
) via the inclusion
![]() $\Pi ^{\mathrm {tp}}_{\phi _{p^r}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
(respectively,
$\Pi ^{\mathrm {tp}}_{\phi _{p^r}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
(respectively,
![]() $\Pi ^{\mathrm {tp}}_{\psi _{m,n}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
) (cf. Definition 1.2) that maps the cuspidal inertia subgroups of
$\Pi ^{\mathrm {tp}}_{\psi _{m,n}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
) (cf. Definition 1.2) that maps the cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm {tp}}_{\phi _{p^r}}$
(respectively,
$\Pi ^{\mathrm {tp}}_{\phi _{p^r}}$
(respectively,
![]() $\Pi ^{\mathrm {tp}}_{\psi _{m,n}}$
) associated to
$\Pi ^{\mathrm {tp}}_{\psi _{m,n}}$
) associated to
![]() $\ast $
to the cuspidal inertia subgroups of
$\ast $
to the cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm {tp}}_{\phi _{p^r}}$
(respectively,
$\Pi ^{\mathrm {tp}}_{\phi _{p^r}}$
(respectively,
![]() $\Pi ^{\mathrm {tp}}_{\psi _{m,n}}$
) associated to
$\Pi ^{\mathrm {tp}}_{\psi _{m,n}}$
) associated to
![]() $\ast $
, where
$\ast $
, where
![]() $\ast \in \{0, 1, \infty \}$
.
$\ast \in \{0, 1, \infty \}$
.
Proof. Note that since
![]() $\Pi ^{\mathrm {tp}}_{\phi _{p^r}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
(respectively,
$\Pi ^{\mathrm {tp}}_{\phi _{p^r}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
(respectively,
![]() $\Pi ^{\mathrm {tp}}_{\psi _{m,n}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
) is an open subgroup of finite index, it holds that
$\Pi ^{\mathrm {tp}}_{\psi _{m,n}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
) is an open subgroup of finite index, it holds that
![]() $\alpha (\Pi ^{\mathrm {tp}}_{\phi _{p^r}}) \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
(respectively,
$\alpha (\Pi ^{\mathrm {tp}}_{\phi _{p^r}}) \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
(respectively,
![]() $\alpha (\Pi ^{\mathrm {tp}}_{\psi _{m,n}}) \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
) is also an open subgroup of finite index. Thus, the inclusion
$\alpha (\Pi ^{\mathrm {tp}}_{\psi _{m,n}}) \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
) is also an open subgroup of finite index. Thus, the inclusion
![]() $\alpha (\Pi ^{\mathrm {tp}}_{\phi _{p^r}}) \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
(respectively,
$\alpha (\Pi ^{\mathrm {tp}}_{\phi _{p^r}}) \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
(respectively,
![]() $\alpha (\Pi ^{\mathrm {tp}}_{\psi _{m,n}}) \subseteq \Pi ^{\mathrm { tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
) determines a connected finite étale covering
$\alpha (\Pi ^{\mathrm {tp}}_{\psi _{m,n}}) \subseteq \Pi ^{\mathrm { tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
) determines a connected finite étale covering
Next, observe that the numerical information that appears in the conditions in Lemma 1.1, (i) (respectively, Lemma 1.1, (ii)) may be reconstructed from the set of cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
(cf. Notations and conventions, Fundamental groups). In particular, since
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
(cf. Notations and conventions, Fundamental groups). In particular, since
![]() $\alpha _{\mathrm {cusp}}$
is the identity automorphism, it follows immediately from [Reference Mochizuki9], Corollary 3.11, that
$\alpha _{\mathrm {cusp}}$
is the identity automorphism, it follows immediately from [Reference Mochizuki9], Corollary 3.11, that
![]() $g_1$
(respectively,
$g_1$
(respectively,
![]() $g_2$
) satisfies the conditions in Lemma 1.1, (i) (respectively, Lemma 1.1, (ii)). Therefore, by replacing
$g_2$
) satisfies the conditions in Lemma 1.1, (i) (respectively, Lemma 1.1, (ii)). Therefore, by replacing
![]() $\alpha $
by the composite of
$\alpha $
by the composite of
![]() $\alpha $
with a suitable inner automorphism of
$\alpha $
with a suitable inner automorphism of
![]() $\Pi ^{\mathrm { tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
, we may assume without loss of generality that
$\Pi ^{\mathrm { tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
, we may assume without loss of generality that
(cf. Lemma 1.1, (i) (respectively, Lemma 1.1, (ii))). Write
![]() $\alpha _{p^r}$
(respectively,
$\alpha _{p^r}$
(respectively,
![]() $\alpha _{m, n}$
) for the automorphism of
$\alpha _{m, n}$
) for the automorphism of
![]() $\Pi ^{\mathrm {tp}}_{\phi _{p^r}}$
(respectively,
$\Pi ^{\mathrm {tp}}_{\phi _{p^r}}$
(respectively,
![]() $\Pi ^{\mathrm { tp}}_{\psi _{m,n}}$
) induced by
$\Pi ^{\mathrm { tp}}_{\psi _{m,n}}$
) induced by
![]() $\alpha $
via the inclusion
$\alpha $
via the inclusion
![]() $\Pi ^{\mathrm {tp}}_{\phi _{p^r}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
(respectively,
$\Pi ^{\mathrm {tp}}_{\phi _{p^r}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
(respectively,
![]() $\Pi ^{\mathrm {tp}}_{\psi _{m,n}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
). Recall that
$\Pi ^{\mathrm {tp}}_{\psi _{m,n}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
). Recall that
![]() $\alpha _{\mathrm {cusp}}$
is the identity automorphism. Thus, by replacing
$\alpha _{\mathrm {cusp}}$
is the identity automorphism. Thus, by replacing
![]() $\alpha $
by the composite of
$\alpha $
by the composite of
![]() $\alpha $
with a suitable inner automorphism of
$\alpha $
with a suitable inner automorphism of
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
, again, if necessary, we conclude from the conditions in Lemma 1.1, (i) (respectively, Lemma 1.1, (ii)) that
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}}$
, again, if necessary, we conclude from the conditions in Lemma 1.1, (i) (respectively, Lemma 1.1, (ii)) that
![]() $\alpha _{p^r}$
(respectively,
$\alpha _{p^r}$
(respectively,
![]() $\alpha _{m, n}$
) maps the cuspidal inertia subgroups of
$\alpha _{m, n}$
) maps the cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm {tp}}_{\phi _{p^r}}$
(respectively,
$\Pi ^{\mathrm {tp}}_{\phi _{p^r}}$
(respectively,
![]() $\Pi ^{\mathrm { tp}}_{\psi _{m,n}}$
) associated to
$\Pi ^{\mathrm { tp}}_{\psi _{m,n}}$
) associated to
![]() $\ast $
to the cuspidal inertia subgroups of
$\ast $
to the cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm {tp}}_{\phi _{p^r}}$
(respectively,
$\Pi ^{\mathrm {tp}}_{\phi _{p^r}}$
(respectively,
![]() $\Pi ^{\mathrm { tp}}_{\psi _{m,n}}$
) associated to
$\Pi ^{\mathrm { tp}}_{\psi _{m,n}}$
) associated to
![]() $\ast $
, where
$\ast $
, where
![]() $\ast \in \{0, 1, \infty \}$
. This completes the proof of Lemma 1.3.
$\ast \in \{0, 1, \infty \}$
. This completes the proof of Lemma 1.3.
2 Elementary lemmas
Let p be a prime number. In the present section, we discuss elementary calculations concerning the Belyi maps that appear in §1 and the p-adic valuation
![]() $v_p$
on
$v_p$
on
![]() $\overline {\mathbb {Q}}_p$
, which will be of use in the proof of our main theorem in the next section.
$\overline {\mathbb {Q}}_p$
, which will be of use in the proof of our main theorem in the next section.
Lemma 2.1. In the notation of Lemma 1.1, (i), let
![]() $x, y \in \overline {\mathbb {Q}}_p$
be such that
$x, y \in \overline {\mathbb {Q}}_p$
be such that
![]() $v_{p}(y) = 0$
. Then it holds that
$v_{p}(y) = 0$
. Then it holds that
 $$ \begin{align*} \max_{x_{r} \in \phi_{p^r}^{-1}(x), \ y_r \in \phi_{p^r}^{-1}(y)} v_{p}(x_r - y_r) \ \leq \ \max \bigg\{\frac{1}{p-1}, \ v_{p}(x-y)- r\bigg\}. \end{align*} $$
$$ \begin{align*} \max_{x_{r} \in \phi_{p^r}^{-1}(x), \ y_r \in \phi_{p^r}^{-1}(y)} v_{p}(x_r - y_r) \ \leq \ \max \bigg\{\frac{1}{p-1}, \ v_{p}(x-y)- r\bigg\}. \end{align*} $$
Proof. Fix elements
![]() $x_{r} \in \phi _{p^r}^{-1}(x)$
,
$x_{r} \in \phi _{p^r}^{-1}(x)$
,
![]() $y_r \in \phi _{p^r}^{-1}(y)$
. Note that it follows immediately from the definition of
$y_r \in \phi _{p^r}^{-1}(y)$
. Note that it follows immediately from the definition of
![]() $\phi _{p^r}$
that, for each element
$\phi _{p^r}$
that, for each element
![]() $y_{r}' \in \phi _{p^r}^{-1}(y)$
, there exists a nonnegative integer j such that
$y_{r}' \in \phi _{p^r}^{-1}(y)$
, there exists a nonnegative integer j such that
![]() $y_{r}' = \zeta _{p^r}^j\cdot y_r$
. Next, observe that
$y_{r}' = \zeta _{p^r}^j\cdot y_r$
. Next, observe that
Suppose that there exists an integer i such that
(cf. [Reference Neukirch10], Chapter I, Lemma 10.1). Then it follows immediately from our assumption that
![]() $v_{p}(y) = 0$
[so
$v_{p}(y) = 0$
[so
![]() $v_{p}(y_r) = 0$
] that, for each
$v_{p}(y_r) = 0$
] that, for each
![]() $j =0, \dots , i-1, i+1, \dots , p^r-1$
, it holds that
$j =0, \dots , i-1, i+1, \dots , p^r-1$
, it holds that
On the other hand, observe (cf., e.g. the second display in the proof of [Reference Neukirch10], Chapter I, Lemma 10.1) that
 $$ \begin{align*} \sum_{\substack{0 \leq j \leq p^r-1\\ j\neq i}} v_{p}(1-\zeta_{p^r}^{j-i}) = v_{p}(p^r) = r. \end{align*} $$
$$ \begin{align*} \sum_{\substack{0 \leq j \leq p^r-1\\ j\neq i}} v_{p}(1-\zeta_{p^r}^{j-i}) = v_{p}(p^r) = r. \end{align*} $$
Thus, since
we conclude that
This completes the proof of Lemma 2.1.
Lemma 2.2. Let
![]() $x \in \overline {\mathbb {Q}}_p \setminus \{0, 1\}$
be such that
$x \in \overline {\mathbb {Q}}_p \setminus \{0, 1\}$
be such that
![]() $v_p(x)> -p$
; r a positive integer. Then, in the notation of Lemma 1.1, (ii) (cf. Remark 1.1.1), there exists a(n) [unique] element
$v_p(x)> -p$
; r a positive integer. Then, in the notation of Lemma 1.1, (ii) (cf. Remark 1.1.1), there exists a(n) [unique] element
![]() $x_1 \in \psi _{p^r}^{-1}(x)$
such that
$x_1 \in \psi _{p^r}^{-1}(x)$
such that
-
•
 $v_p(1-x_1) = rp^r+v_{p}(x) \ (> 0)$
, and
$v_p(1-x_1) = rp^r+v_{p}(x) \ (> 0)$
, and -
• for each
 $y \in \psi _{p^r}^{-1}(x) \setminus \{x_1\}$
, it holds that
$y \in \psi _{p^r}^{-1}(x) \setminus \{x_1\}$
, it holds that
 $v_{p}(y) = \frac {rp^r+v_{p}(x)}{p^r} \ (> 0)$
.
$v_{p}(y) = \frac {rp^r+v_{p}(x)}{p^r} \ (> 0)$
.
Proof. For each
![]() $y \in \psi _{p^r}^{-1}(x)$
, it holds that
$y \in \psi _{p^r}^{-1}(x)$
, it holds that
Thus, by using the Newton polygon (cf. [Reference Neukirch10], Chapter II, Proposition 6.3), we obtain the desired conclusion. This completes the proof of Lemma 2.2.
Lemma 2.3. In the notation of Lemma 2.2, suppose that
Let
be such that
![]() $v_{p}(s) = 2$
. Write
$v_{p}(s) = 2$
. Write
![]() $\mathcal {C}_{s} \subseteq \overline {\mathbb {Q}}_p$
,
$\mathcal {C}_{s} \subseteq \overline {\mathbb {Q}}_p$
,
![]() $\mathcal {C}_{x} \subseteq \overline {\mathbb {Q}}_p$
for the subsets of the Galois-conjugates of
$\mathcal {C}_{x} \subseteq \overline {\mathbb {Q}}_p$
for the subsets of the Galois-conjugates of
![]() $s \in \overline {\mathbb {Q}}_p$
,
$s \in \overline {\mathbb {Q}}_p$
,
![]() $x \in \overline {\mathbb {Q}}_p$
, respectively. Suppose, moreover, that
$x \in \overline {\mathbb {Q}}_p$
, respectively. Suppose, moreover, that
Then it holds that
Proof. First, it follows immediately from the definition of
![]() $\psi _{p^2}$
that
$\psi _{p^2}$
that
 $$ \begin{align*} \frac{(p^2+1)^{p^2+1}}{(p^2)^{p^2}}(s^{p^2} - s^{p^2+1}) = x. \end{align*} $$
$$ \begin{align*} \frac{(p^2+1)^{p^2+1}}{(p^2)^{p^2}}(s^{p^2} - s^{p^2+1}) = x. \end{align*} $$
Next, let
![]() $w \in \mathcal {C}_{s} \setminus \{s\}$
be an element. Then since w is a Galois-conjugate of s, there exists a Galois-conjugate
$w \in \mathcal {C}_{s} \setminus \{s\}$
be an element. Then since w is a Galois-conjugate of s, there exists a Galois-conjugate
![]() $w_{x}$
of x such that
$w_{x}$
of x such that
 $$ \begin{align*} \frac{(p^2+1)^{p^2+1}}{(p^2)^{p^2}}(w^{p^2} - w^{p^2+1}) = w_{x}. \end{align*} $$
$$ \begin{align*} \frac{(p^2+1)^{p^2+1}}{(p^2)^{p^2}}(w^{p^2} - w^{p^2+1}) = w_{x}. \end{align*} $$
Thus, by taking the difference of the above equalities, we obtain an equality
 $$ \begin{align*} \frac{(p^2+1)^{p^2+1}}{(p^2)^{p^2}}(s -w)\bigg(\bigg(\sum_{0 \leq l \leq p^2-1} s^{l}w^{p^2-1-l}\bigg)-\bigg(\sum_{0 \leq l \leq p^2} s^{l}w^{p^2-l}\bigg)\bigg) = x -w_{x}. \end{align*} $$
$$ \begin{align*} \frac{(p^2+1)^{p^2+1}}{(p^2)^{p^2}}(s -w)\bigg(\bigg(\sum_{0 \leq l \leq p^2-1} s^{l}w^{p^2-1-l}\bigg)-\bigg(\sum_{0 \leq l \leq p^2} s^{l}w^{p^2-l}\bigg)\bigg) = x -w_{x}. \end{align*} $$
On the other hand, since
![]() $v_{p}(s)=v_{p}(w)=2$
, it holds that
$v_{p}(s)=v_{p}(w)=2$
, it holds that
 $$ \begin{align*} v_{p}\bigg(\bigg(\sum_{0 \leq l \leq p^2-1} s^{l}w^{p^2-1-l}\bigg)-\bigg(\sum_{0 \leq l \leq p^2} s^{l}w^{p^2-l}\bigg)\bigg) \geq 2p^2-2. \end{align*} $$
$$ \begin{align*} v_{p}\bigg(\bigg(\sum_{0 \leq l \leq p^2-1} s^{l}w^{p^2-1-l}\bigg)-\bigg(\sum_{0 \leq l \leq p^2} s^{l}w^{p^2-l}\bigg)\bigg) \geq 2p^2-2. \end{align*} $$
Thus, in the case where
![]() $x \neq w_{x}$
, it follows immediately from our assumption that
$x \neq w_{x}$
, it follows immediately from our assumption that
![]() $v_{p}(x - w_{x}) \leq 1$
that
$v_{p}(x - w_{x}) \leq 1$
that
![]() $v_{p}(s- w) \leq 3 < 4$
. In particular, we may assume without loss of generality that
$v_{p}(s- w) \leq 3 < 4$
. In particular, we may assume without loss of generality that
Then since
![]() $s -w \neq 0$
, it holds that
$s -w \neq 0$
, it holds that
 $$ \begin{align*} \bigg(\sum_{0 \leq l \leq p^2-1} s^{l}(s+(w-s))^{p^2-1-l} =\bigg) \quad \sum_{0 \leq l \leq p^2-1} s^{l}w^{p^2-1-l} \end{align*} $$
$$ \begin{align*} \bigg(\sum_{0 \leq l \leq p^2-1} s^{l}(s+(w-s))^{p^2-1-l} =\bigg) \quad \sum_{0 \leq l \leq p^2-1} s^{l}w^{p^2-1-l} \end{align*} $$
 $$ \begin{align*} = \sum_{0 \leq l \leq p^2} s^{l}w^{p^2-l} \quad \bigg(=\sum_{0 \leq l \leq p^2} s^{l}(s+(w-s))^{p^2-l}\bigg). \end{align*} $$
$$ \begin{align*} = \sum_{0 \leq l \leq p^2} s^{l}w^{p^2-l} \quad \bigg(=\sum_{0 \leq l \leq p^2} s^{l}(s+(w-s))^{p^2-l}\bigg). \end{align*} $$
Observe that
 $$ \begin{align*} \sum_{0 \leq l \leq p^2-1} s^{l}(s+(w-s))^{p^2-1-l} = \sum_{0 \leq h \leq p^2-1} c_{h}\cdot s^{p^2-1-h}(w-s)^h; \end{align*} $$
$$ \begin{align*} \sum_{0 \leq l \leq p^2-1} s^{l}(s+(w-s))^{p^2-1-l} = \sum_{0 \leq h \leq p^2-1} c_{h}\cdot s^{p^2-1-h}(w-s)^h; \end{align*} $$
 $$ \begin{align*} \sum_{0 \leq l \leq p^2} s^{l}(s+(w-s))^{p^2-l} = \sum_{0 \leq h \leq p^2} d_{h}\cdot s^{p^2-h}(w-s)^h, \end{align*} $$
$$ \begin{align*} \sum_{0 \leq l \leq p^2} s^{l}(s+(w-s))^{p^2-l} = \sum_{0 \leq h \leq p^2} d_{h}\cdot s^{p^2-h}(w-s)^h, \end{align*} $$
where
 $$ \begin{align*} c_{h} \overset{\mathrm{def}}{=} \sum_{0 \leq l \leq p^2-1-h} \binom{p^2-1-l}{h}, \quad d_{h} \overset{\mathrm{def}}{=} \sum_{0 \leq l \leq p^2-h} \binom{p^2-l}{h}. \end{align*} $$
$$ \begin{align*} c_{h} \overset{\mathrm{def}}{=} \sum_{0 \leq l \leq p^2-1-h} \binom{p^2-1-l}{h}, \quad d_{h} \overset{\mathrm{def}}{=} \sum_{0 \leq l \leq p^2-h} \binom{p^2-l}{h}. \end{align*} $$
Here, we note that
Next, suppose that
![]() $v_{p}(s - w) \geq 4$
. Then since
$v_{p}(s - w) \geq 4$
. Then since
![]() $v_{p}(s)=2$
, it holds that, for each
$v_{p}(s)=2$
, it holds that, for each
![]() $h \geq 1$
,
$h \geq 1$
,
Thus, in summary, we conclude from the above discussion that
hence that
 $$ \begin{align*} v_{p}\bigg(\frac{p^2}{p^2+1} - s\bigg) \geq 3. \end{align*} $$
$$ \begin{align*} v_{p}\bigg(\frac{p^2}{p^2+1} - s\bigg) \geq 3. \end{align*} $$
Write
 $$ \begin{align*} s' \overset{\mathrm{def}}{=} s - \frac{p^2}{p^2+1}, \quad a_{0} \overset{\mathrm{def}}{=} (p^2)^{p^2}(1-x), \quad a_{p^2+1} \overset{\mathrm{def}}{=} -(p^2+1)^{p^2+1}. \end{align*} $$
$$ \begin{align*} s' \overset{\mathrm{def}}{=} s - \frac{p^2}{p^2+1}, \quad a_{0} \overset{\mathrm{def}}{=} (p^2)^{p^2}(1-x), \quad a_{p^2+1} \overset{\mathrm{def}}{=} -(p^2+1)^{p^2+1}. \end{align*} $$
For each
![]() $l = 1, \dots , p^2$
, write
$l = 1, \dots , p^2$
, write
 $$ \begin{align*} a_{l} = (p^2)^{p^2-l}\cdot(p^2+1)^{l}\cdot \bigg(\binom{p^2}{l}-p^2\cdot \binom{p^2}{l-1}\bigg). \end{align*} $$
$$ \begin{align*} a_{l} = (p^2)^{p^2-l}\cdot(p^2+1)^{l}\cdot \bigg(\binom{p^2}{l}-p^2\cdot \binom{p^2}{l-1}\bigg). \end{align*} $$
Then it follows immediately from the equality in the first display of the present proof that
 $$ \begin{align*} \sum_{0 \leq l \leq p^2+1} a_{l} \cdot (s')^{l} = (p^2+1)^{p^2+1}\bigg(s' + \frac{p^2}{p^2+1}\bigg)^{p^2}\bigg(\frac{1}{p^2+1} - s'\bigg)-(p^2)^{p^2}x = 0. \end{align*} $$
$$ \begin{align*} \sum_{0 \leq l \leq p^2+1} a_{l} \cdot (s')^{l} = (p^2+1)^{p^2+1}\bigg(s' + \frac{p^2}{p^2+1}\bigg)^{p^2}\bigg(\frac{1}{p^2+1} - s'\bigg)-(p^2)^{p^2}x = 0. \end{align*} $$
On the other hand, since
![]() $0 \leq v_{p}(1-x) \leq 1$
, and
$0 \leq v_{p}(1-x) \leq 1$
, and
![]() $a_1 = 0$
, it follows immediately from the various definitions involved that
$a_1 = 0$
, it follows immediately from the various definitions involved that
 $$ \begin{align*} v_{p}(a_{l}) = 2p^2 - 2l + v_{p}\bigg(\binom{p^2}{l}\bigg) \quad (l = 2, \dots, p^2). \end{align*} $$
$$ \begin{align*} v_{p}(a_{l}) = 2p^2 - 2l + v_{p}\bigg(\binom{p^2}{l}\bigg) \quad (l = 2, \dots, p^2). \end{align*} $$
Moreover, for each
![]() $l = 2, \dots , p^2$
, it holds that
$l = 2, \dots , p^2$
, it holds that
 $$ \begin{align*} 1-\frac{l}{p^2} \leq v_{p}\bigg(\binom{p^2}{l}\bigg), \end{align*} $$
$$ \begin{align*} 1-\frac{l}{p^2} \leq v_{p}\bigg(\binom{p^2}{l}\bigg), \end{align*} $$
hence that
 $$ \begin{align*} -\frac{v_{p}(a_0)}{p^2}l + v_{p}(a_0) \leq -\frac{2p^2 + 1}{p^2}l + 2p^2+1 \leq 2p^2 - 2l + v_{p}\bigg(\binom{p^2}{l}\bigg) = v_{p}(a_{l}). \end{align*} $$
$$ \begin{align*} -\frac{v_{p}(a_0)}{p^2}l + v_{p}(a_0) \leq -\frac{2p^2 + 1}{p^2}l + 2p^2+1 \leq 2p^2 - 2l + v_{p}\bigg(\binom{p^2}{l}\bigg) = v_{p}(a_{l}). \end{align*} $$
Then, by using the Newton polygon, we observe that
 $$ \begin{align*} \bigg(v_{p}\bigg(s-\frac{p^2}{p^2+1}\bigg) =\bigg) \quad v_{p}(s') = \frac{v_{p}(a_0)}{p^2} \quad \bigg(\leq \frac{2p^2+1}{p^2} < 3\bigg). \end{align*} $$
$$ \begin{align*} \bigg(v_{p}\bigg(s-\frac{p^2}{p^2+1}\bigg) =\bigg) \quad v_{p}(s') = \frac{v_{p}(a_0)}{p^2} \quad \bigg(\leq \frac{2p^2+1}{p^2} < 3\bigg). \end{align*} $$
This contradicts the inequality
![]() $v_{p}(\frac {p^2}{p^2+1} - s) \geq 3$
. Thus, we conclude that
$v_{p}(\frac {p^2}{p^2+1} - s) \geq 3$
. Thus, we conclude that
![]() $v_{p}(s - w) < 4$
. This completes the proof of Lemma 2.3.
$v_{p}(s - w) < 4$
. This completes the proof of Lemma 2.3.
3 Reconstruction of moduli of hyperbolic curves of genus
 $0$
from their geometric tempered fundamental groups
$0$
from their geometric tempered fundamental groups
Let p be a prime number. In the present section, we apply the results obtained in the previous sections, together with Lepage’s reconstruction result for the Tate elliptic curves, to prove that the tempered fundamental groups of hyperbolic curves of genus
![]() $0$
over
$0$
over
![]() $\overline {\mathbb {Q}}_p$
completely determine their moduli.
$\overline {\mathbb {Q}}_p$
completely determine their moduli.
First, we begin by recalling Lepage’s result:
Theorem 3.1 [Reference Lepage5], Theorem 4.1
Let
![]() $q_1, q_2 \in \overline {\mathbb {Q}}_p$
be such that
$q_1, q_2 \in \overline {\mathbb {Q}}_p$
be such that
![]() $v_{p}(q_1)> 0$
, and
$v_{p}(q_1)> 0$
, and
![]() $v_{p}(q_2)>0$
. Write
$v_{p}(q_2)>0$
. Write
(i.e. Tate elliptic curves). Suppose that there exists an isomorphism of topological groups
Then there exists an element
![]() $\sigma \in \mathrm {Gal}(\overline {\mathbb {Q}}_p/\mathbb {Q}_{p})$
such that
$\sigma \in \mathrm {Gal}(\overline {\mathbb {Q}}_p/\mathbb {Q}_{p})$
such that
![]() $q_2 = \sigma (q_1)$
.
$q_2 = \sigma (q_1)$
.
Remark 3.1.1. In the notation of Theorem 3.1, write
![]() $j_1$
,
$j_1$
,
![]() $j_2$
for the j-invariants of the Tate elliptic curves
$j_2$
for the j-invariants of the Tate elliptic curves
![]() $E_{q_1}$
,
$E_{q_1}$
,
![]() $E_{q_2}$
, respectively. Then it follows immediately from [Reference Lütkebohmert6], Theorem 2.1.1, that
$E_{q_2}$
, respectively. Then it follows immediately from [Reference Lütkebohmert6], Theorem 2.1.1, that
Next, we apply Lemmas 1.3, 2.2; Theorem 3.1, to prove that the moduli of hyperbolic curves of type
![]() $(0, 4)$
over
$(0, 4)$
over
![]() $\overline {\mathbb {Q}}_p$
may be completely determined by their tempered fundamental groups.
$\overline {\mathbb {Q}}_p$
may be completely determined by their tempered fundamental groups.
Proposition 3.2. Let
![]() $x, x' \in \overline {\mathbb {Q}}_p \setminus \{0, 1\}$
be elements. Suppose that there exists an isomorphism of topological groups
$x, x' \in \overline {\mathbb {Q}}_p \setminus \{0, 1\}$
be elements. Suppose that there exists an isomorphism of topological groups
Note that
![]() $\alpha $
induces a bijection
$\alpha $
induces a bijection
(cf. [Reference Mochizuki9], Corollary 3.11). Suppose that
Then there exists an element
![]() $\sigma \in \mathrm {Gal}(\overline {\mathbb {Q}}_p/\mathbb {Q}_{p})$
such that
$\sigma \in \mathrm {Gal}(\overline {\mathbb {Q}}_p/\mathbb {Q}_{p})$
such that
![]() $x' = \sigma (x)$
. In particular, there exists an isomorphism of schemes
$x' = \sigma (x)$
. In particular, there exists an isomorphism of schemes
such that the bijection
![]() $\{0, 1, \infty , x\} \overset {\sim }{\rightarrow } \{0, 1, \infty , x'\}$
induced by the isomorphism
$\{0, 1, \infty , x\} \overset {\sim }{\rightarrow } \{0, 1, \infty , x'\}$
induced by the isomorphism
![]() ${\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \} \overset {\sim }{\rightarrow } {\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}$
coincides with the bijection
${\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \} \overset {\sim }{\rightarrow } {\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}$
coincides with the bijection
![]() $\alpha _{\mathrm {cusp}}$
.
$\alpha _{\mathrm {cusp}}$
.
Proof. First, we verify the following assertion:
Claim 3.2.A: We may assume without loss of generality that
![]() $v_{p}(1-x)> 0$
.
$v_{p}(1-x)> 0$
.
Indeed, suppose that Proposition 3.2 in the case where
![]() $v_{p}(1-x)> 0$
holds. First, by using suitable geometric automorphisms of
$v_{p}(1-x)> 0$
holds. First, by using suitable geometric automorphisms of
![]() ${\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}$
over
${\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty \}$
over
![]() $\overline {\mathbb {Q}}_p$
, we may assume without loss of generality that
$\overline {\mathbb {Q}}_p$
, we may assume without loss of generality that
![]() $v_{p}(x) = 0$
. Next, write
$v_{p}(x) = 0$
. Next, write
 $$ \begin{align*} \psi_{p, x} : {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{p}{p+1}, \dots, \infty\bigg\} \cup \psi_{p}^{-1}(x) \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{0, 1, \infty, x \}, \end{align*} $$
$$ \begin{align*} \psi_{p, x} : {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{p}{p+1}, \dots, \infty\bigg\} \cup \psi_{p}^{-1}(x) \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{0, 1, \infty, x \}, \end{align*} $$
 $$ \begin{align*} \psi_{p, x'} : {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{p}{p+1}, \dots, \infty\bigg\} \cup \psi_{p}^{-1}(x') \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{0, 1, \infty, x' \} \end{align*} $$
$$ \begin{align*} \psi_{p, x'} : {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{p}{p+1}, \dots, \infty\bigg\} \cup \psi_{p}^{-1}(x') \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{0, 1, \infty, x' \} \end{align*} $$
for the connected finite étale coverings induced by
![]() $\psi _p$
(cf. Lemma 1.1, (ii); Remark 1.1.1);
$\psi _p$
(cf. Lemma 1.1, (ii); Remark 1.1.1);
for the open subgroups (determined up to
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \}}$
-conjugate,
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \}}$
-conjugate,
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}}$
-conjugate, respectively) determined by
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}}$
-conjugate, respectively) determined by
![]() $\psi _{p, x}$
,
$\psi _{p, x}$
,
![]() $\psi _{p, x'}$
, respectively. Then since
$\psi _{p, x'}$
, respectively. Then since
![]() $\alpha _{\mathrm {cusp}}(0) = 0$
,
$\alpha _{\mathrm {cusp}}(0) = 0$
,
![]() $\alpha _{\mathrm {cusp}}(1) = 1$
, and
$\alpha _{\mathrm {cusp}}(1) = 1$
, and
![]() $\alpha _{\mathrm {cusp}}(\infty ) = \infty $
, it follows immediately from Lemma 1.3 that there exists an inner automorphism
$\alpha _{\mathrm {cusp}}(\infty ) = \infty $
, it follows immediately from Lemma 1.3 that there exists an inner automorphism
![]() $\iota $
of
$\iota $
of
![]() $\Pi ^{\mathrm { tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}}$
satisfying the following conditions:
$\Pi ^{\mathrm { tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}}$
satisfying the following conditions:
-
• The composite
 $\iota \circ \alpha $
induces an isomorphism of topological groupsvia the inclusions
$\iota \circ \alpha $
induces an isomorphism of topological groupsvia the inclusions $$ \begin{align*} \beta : \Pi^{\mathrm{tp}}_{\psi_{p, x}} \overset{\sim}{\rightarrow} \Pi^{\mathrm{tp}}_{\psi_{p, x'}} \end{align*} $$
$$ \begin{align*} \beta : \Pi^{\mathrm{tp}}_{\psi_{p, x}} \overset{\sim}{\rightarrow} \Pi^{\mathrm{tp}}_{\psi_{p, x'}} \end{align*} $$
 $\Pi ^{\mathrm {tp}}_{\psi _{p, x}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \}}$
and
$\Pi ^{\mathrm {tp}}_{\psi _{p, x}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \}}$
and
 $\Pi ^{\mathrm {tp}}_{\psi _{p, x'}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}}$
.
$\Pi ^{\mathrm {tp}}_{\psi _{p, x'}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}}$
.
-
• Write
for the bijection induced by $$ \begin{align*} \beta_{\mathrm{cusp}} : \bigg\{0, 1, \frac{p}{p+1}, \dots, \infty\bigg\} \cup \psi_{p}^{-1}(x) \ \overset{\sim}{\rightarrow} \ \bigg\{0, 1, \frac{p}{p+1}, \dots, \infty\bigg\} \cup \psi_{p}^{-1}(x') \end{align*} $$
$$ \begin{align*} \beta_{\mathrm{cusp}} : \bigg\{0, 1, \frac{p}{p+1}, \dots, \infty\bigg\} \cup \psi_{p}^{-1}(x) \ \overset{\sim}{\rightarrow} \ \bigg\{0, 1, \frac{p}{p+1}, \dots, \infty\bigg\} \cup \psi_{p}^{-1}(x') \end{align*} $$
 $\beta $
(cf. [Reference Mochizuki9], Corollary 3.11). Then it holds that
$\beta $
(cf. [Reference Mochizuki9], Corollary 3.11). Then it holds that $$ \begin{align*} \beta_{\mathrm{cusp}}(0) = 0, \quad \beta_{\mathrm{cusp}}(1) = 1, \quad \beta_{\mathrm{cusp}}(\infty) = \infty. \end{align*} $$
$$ \begin{align*} \beta_{\mathrm{cusp}}(0) = 0, \quad \beta_{\mathrm{cusp}}(1) = 1, \quad \beta_{\mathrm{cusp}}(\infty) = \infty. \end{align*} $$
Let
![]() $x_1 \in \psi _{p}^{-1}(x)$
be such that
$x_1 \in \psi _{p}^{-1}(x)$
be such that
![]() $v_{p}(1-x_1)> 0$
(cf. Lemma 2.2). Write
$v_{p}(1-x_1)> 0$
(cf. Lemma 2.2). Write
![]() $x_{1}' \overset {\mathrm {def}}{=} \beta _{\mathrm {cusp}}(x_1)$
. Note that the kernels of the natural surjections
$x_{1}' \overset {\mathrm {def}}{=} \beta _{\mathrm {cusp}}(x_1)$
. Note that the kernels of the natural surjections
(induced by the natural open immersions of hyperbolic curves over
![]() $\overline {\mathbb {Q}}_p$
) are topologically generated by cuspidal inertia subgroups of
$\overline {\mathbb {Q}}_p$
) are topologically generated by cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm {tp}}_{\psi _p, x}$
,
$\Pi ^{\mathrm {tp}}_{\psi _p, x}$
,
![]() $\Pi ^{\mathrm {tp}}_{\psi _p, x'}$
associated to the cusps
$\Pi ^{\mathrm {tp}}_{\psi _p, x'}$
associated to the cusps
![]() $\not \in \{0, 1, \infty , x_1\}$
, the cusps
$\not \in \{0, 1, \infty , x_1\}$
, the cusps
![]() $\not \in \{0, 1, \infty , x_{1}'\}$
, respectively. Then
$\not \in \{0, 1, \infty , x_{1}'\}$
, respectively. Then
![]() $\beta : \Pi ^{\mathrm {tp}}_{\psi _p, x} \overset {\sim }{\rightarrow } \Pi ^{\mathrm {tp}}_{\psi _p, x'}$
induces an isomorphism of topological groups
$\beta : \Pi ^{\mathrm {tp}}_{\psi _p, x} \overset {\sim }{\rightarrow } \Pi ^{\mathrm {tp}}_{\psi _p, x'}$
induces an isomorphism of topological groups
via the above surjections. Moreover, for each
![]() $\ast \in \{0, 1, \infty \}$
, it holds that
$\ast \in \{0, 1, \infty \}$
, it holds that
![]() $\alpha _1$
maps the cuspidal inertia subgroups of
$\alpha _1$
maps the cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm { tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x_1 \}}$
associated to
$\Pi ^{\mathrm { tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x_1 \}}$
associated to
![]() $\ast $
to the cuspidal inertia subgroups of
$\ast $
to the cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm { tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x_{1}' \}}$
associated to
$\Pi ^{\mathrm { tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x_{1}' \}}$
associated to
![]() $\ast $
. Then since
$\ast $
. Then since
![]() $v_{p}(1-x_1)> 0$
, it follows from our assumption (that Proposition 3.2 in the case where
$v_{p}(1-x_1)> 0$
, it follows from our assumption (that Proposition 3.2 in the case where
![]() $v_{p}(1-x)> 0$
holds) that there exists an element
$v_{p}(1-x)> 0$
holds) that there exists an element
![]() $\sigma \in \mathrm { Gal}(\overline {\mathbb {Q}}_p/\mathbb {Q}_{p})$
such that
$\sigma \in \mathrm { Gal}(\overline {\mathbb {Q}}_p/\mathbb {Q}_{p})$
such that
![]() $x_{1}' = \sigma (x_1)$
. Thus, since
$x_{1}' = \sigma (x_1)$
. Thus, since
![]() $\psi _p$
is defined over
$\psi _p$
is defined over
![]() $\mathbb {Q}_{p}$
, it holds that
$\mathbb {Q}_{p}$
, it holds that
![]() $x' = \sigma (x)$
. This completes the proof of Claim 3.2.A.
$x' = \sigma (x)$
. This completes the proof of Claim 3.2.A.
Next, we verify the following assertion:
Claim 3.2.B: Suppose that
![]() $v_{p}(1-x)> 0$
. Then it holds that
$v_{p}(1-x)> 0$
. Then it holds that
Indeed, it follows immediately from [Reference Mochizuki9], Corollary 3.11, that
![]() $v_{p}(1-x')> 0$
. Write
$v_{p}(1-x')> 0$
. Write
for the finite étale Galois coverings of degree
![]() $2$
that ramify over every cusp of
$2$
that ramify over every cusp of
![]() ${\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \}$
,
${\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \}$
,
![]() ${\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}$
, respectively;
${\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}$
, respectively;
for the normal open subgroups of index
![]() $2$
determined by the above finite étale Galois coverings of degree
$2$
determined by the above finite étale Galois coverings of degree
![]() $2$
. Observe that the normal open subgroup
$2$
. Observe that the normal open subgroup
![]() $\Pi ^{\mathrm {tp}}_{E} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \}}$
coincides with the kernel of the unique surjection
$\Pi ^{\mathrm {tp}}_{E} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \}}$
coincides with the kernel of the unique surjection
such that the image of every cuspidal inertia subgroup of
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \}}$
is nontrivial. The normal open subgroup
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \}}$
is nontrivial. The normal open subgroup
![]() $\Pi ^{\mathrm {tp}}_{E'} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}}$
admits a similar characterisation. Thus, since
$\Pi ^{\mathrm {tp}}_{E'} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}}$
admits a similar characterisation. Thus, since
![]() $\alpha $
maps the cuspidal inertia subgroups of
$\alpha $
maps the cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \}}$
to the cuspidal inertia subgroups of
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \}}$
to the cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}}$
, the isomorphism
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}}$
, the isomorphism
![]() $\alpha $
induces an isomorphism of topological groups
$\alpha $
induces an isomorphism of topological groups
via the inclusions
![]() $\Pi ^{\mathrm {tp}}_{E} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \}}$
and
$\Pi ^{\mathrm {tp}}_{E} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \}}$
and
![]() $\Pi ^{\mathrm {tp}}_{E'} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}}$
. On the other hand, since
$\Pi ^{\mathrm {tp}}_{E'} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}}$
. On the other hand, since
![]() $v_{p}(1-x)> 0$
, and
$v_{p}(1-x)> 0$
, and
![]() $v_{p}(1-x')> 0$
, the hyperbolic curves E,
$v_{p}(1-x')> 0$
, the hyperbolic curves E,
![]() $E'$
(of type
$E'$
(of type
![]() $(1, 4)$
) may be regarded as open subschemes of once-punctured Tate elliptic curves
$(1, 4)$
) may be regarded as open subschemes of once-punctured Tate elliptic curves
![]() $E_1$
,
$E_1$
,
![]() $E_{1}'$
over
$E_{1}'$
over
![]() $\overline {\mathbb {Q}}_p$
, where the cusps of
$\overline {\mathbb {Q}}_p$
, where the cusps of
![]() $E_1$
,
$E_1$
,
![]() $E_{1}'$
are the origins and correspond to the cusps of E,
$E_{1}'$
are the origins and correspond to the cusps of E,
![]() $E'$
that lie over
$E'$
that lie over
![]() $\infty $
via the finite étale Galois coverings
$\infty $
via the finite étale Galois coverings
![]() $E \rightarrow {\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \}$
,
$E \rightarrow {\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \}$
,
![]() $E' \rightarrow {\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}$
, respectively. In particular, since
$E' \rightarrow {\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}$
, respectively. In particular, since
![]() $\alpha _{\mathrm {cusp}}(\infty ) = \infty $
, the isomorphism
$\alpha _{\mathrm {cusp}}(\infty ) = \infty $
, the isomorphism
![]() $\Pi ^{\mathrm {tp}}_{E} \overset {\sim }{\rightarrow } \Pi ^{\mathrm { tp}}_{E'}$
induces an isomorphism
$\Pi ^{\mathrm {tp}}_{E} \overset {\sim }{\rightarrow } \Pi ^{\mathrm { tp}}_{E'}$
induces an isomorphism
Write
![]() $j(E_{1})$
,
$j(E_{1})$
,
![]() $j(E_{1}')$
for the j-invariants of
$j(E_{1}')$
for the j-invariants of
![]() $E_1$
,
$E_1$
,
![]() $E_{1}'$
, respectively. Then it follows immediately from Theorem 3.1, together with Remark 3.1.1, that there exists an element
$E_{1}'$
, respectively. Then it follows immediately from Theorem 3.1, together with Remark 3.1.1, that there exists an element
![]() $\sigma \in \mathrm { Gal}(\overline {\mathbb {Q}}_p/\mathbb {Q}_{p})$
such that
$\sigma \in \mathrm { Gal}(\overline {\mathbb {Q}}_p/\mathbb {Q}_{p})$
such that
Therefore, it holds that
 $$ \begin{align*} \sigma(x) \in \bigg\{x', \frac{1}{1-x'}, \frac{x'-1}{x'}, \frac{1}{x'}, \frac{x'}{x'-1}, 1-x'\bigg\}. \end{align*} $$
$$ \begin{align*} \sigma(x) \in \bigg\{x', \frac{1}{1-x'}, \frac{x'-1}{x'}, \frac{1}{x'}, \frac{x'}{x'-1}, 1-x'\bigg\}. \end{align*} $$
Moreover, since
![]() $v_{p}(1-x)> 0$
, and
$v_{p}(1-x)> 0$
, and
![]() $v_{p}(1-x')> 0$
, we conclude that
$v_{p}(1-x')> 0$
, we conclude that
This completes the proof of Claim 3.2.B.
To complete the proof of Proposition 3.2, by applying Claims 3.2.A and 3.2.B, we may assume without loss of generality that
Write
 $$ \begin{align*} X_{x} \overset{\mathrm{def}}{=} {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{1}{2}, \infty, \frac{1+{\sqrt{1-x}}}{2}, \frac{1-{\sqrt{1-x}}}{2} \bigg\}; \end{align*} $$
$$ \begin{align*} X_{x} \overset{\mathrm{def}}{=} {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{1}{2}, \infty, \frac{1+{\sqrt{1-x}}}{2}, \frac{1-{\sqrt{1-x}}}{2} \bigg\}; \end{align*} $$
 $$ \begin{align*} X_{x'} \overset{\mathrm{def}}{=} {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{1}{2}, \infty, \frac{1+{\sqrt{1-x'}}}{2}, \frac{1-{\sqrt{1-x'}}}{2} \bigg\}; \end{align*} $$
$$ \begin{align*} X_{x'} \overset{\mathrm{def}}{=} {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{1}{2}, \infty, \frac{1+{\sqrt{1-x'}}}{2}, \frac{1-{\sqrt{1-x'}}}{2} \bigg\}; \end{align*} $$
for the finite étale Galois coverings of degree
![]() $2$
defined by the assignment
$2$
defined by the assignment
![]() $t \mapsto 4t(1-t)$
. Then
$t \mapsto 4t(1-t)$
. Then
![]() $\alpha $
induces an isomorphism of topological groups
$\alpha $
induces an isomorphism of topological groups
(cf. Lemma 1.3). By replacing
![]() $\alpha $
by a suitable composite of
$\alpha $
by a suitable composite of
![]() $\alpha $
with an inner automorphism of
$\alpha $
with an inner automorphism of
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}}$
, we may assume without loss of generality that
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}}$
, we may assume without loss of generality that
![]() $\gamma $
maps the cuspidal inertia subgroups of
$\gamma $
maps the cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm { tp}}_{X_{x}}$
associated to
$\Pi ^{\mathrm { tp}}_{X_{x}}$
associated to
![]() $1$
to the cuspidal inertia subgroups of
$1$
to the cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm {tp}}_{X_{x'}}$
associated to
$\Pi ^{\mathrm {tp}}_{X_{x'}}$
associated to
![]() $1$
. Write
$1$
. Write
Then
![]() $\gamma $
induces, via the respective quotients of
$\gamma $
induces, via the respective quotients of
![]() $\Pi ^{\mathrm {tp}}_{X_{x}}$
,
$\Pi ^{\mathrm {tp}}_{X_{x}}$
,
![]() $\Pi ^{\mathrm {tp}}_{X_{x'}}$
by the normal closed subgroups topologically generated by the cuspidal inertia subgroups associated to
$\Pi ^{\mathrm {tp}}_{X_{x'}}$
by the normal closed subgroups topologically generated by the cuspidal inertia subgroups associated to
![]() $1$
, an isomorphism of topological groups
$1$
, an isomorphism of topological groups
Write
for the bijection induced by
![]() $\delta $
(cf. [Reference Mochizuki9], Corollary 3.11);
$\delta $
(cf. [Reference Mochizuki9], Corollary 3.11);
Observe that
Then since
![]() $v_{p}(1-x_{1}) = v_{p}(\sqrt {1-x}) = \frac {v_{p}(1-x)}{2}> 0$
, it follows from Claim 3.2.B that there exists an element
$v_{p}(1-x_{1}) = v_{p}(\sqrt {1-x}) = \frac {v_{p}(1-x)}{2}> 0$
, it follows from Claim 3.2.B that there exists an element
![]() $\sigma _{1} \in \mathrm {Gal}(\overline {\mathbb {Q}}_p/\mathbb {Q}_{p})$
such that
$\sigma _{1} \in \mathrm {Gal}(\overline {\mathbb {Q}}_p/\mathbb {Q}_{p})$
such that
Note that
![]() $\psi _{1,x}$
and
$\psi _{1,x}$
and
![]() $\psi _{1,x'}$
are defined over
$\psi _{1,x'}$
are defined over
![]() $\mathbb {Q}_{p}$
. Therefore, if
$\mathbb {Q}_{p}$
. Therefore, if
![]() $x_{1}' = \sigma _{1}(x_1)$
, then
$x_{1}' = \sigma _{1}(x_1)$
, then
![]() $x' = \sigma _{1}(x)$
. In particular, it suffices to consider the case where
$x' = \sigma _{1}(x)$
. In particular, it suffices to consider the case where
In this case, it holds that
where
![]() $P(t) \overset {\mathrm {def}}{=} t(2-t) \in \overline {\mathbb {Q}}_{p}[t]$
. Moreover, it holds that
$P(t) \overset {\mathrm {def}}{=} t(2-t) \in \overline {\mathbb {Q}}_{p}[t]$
. Moreover, it holds that
This implies that one of the following assertions holds:
-
(a)
 $x_{1}'$
and
$x_{1}'$
and
 $(x_{1}')^{-1}$
are Galois-conjugate.
$(x_{1}')^{-1}$
are Galois-conjugate. -
(b)
 $x_{1}'$
is contained in the Galois closure of
$x_{1}'$
is contained in the Galois closure of
 $\mathbb {Q}_{p}(x')$
over
$\mathbb {Q}_{p}(x')$
over
 $\mathbb {Q}_{p}$
.
$\mathbb {Q}_{p}$
.
Note that since
![]() $x_{1}' \in \big \{1+{\sqrt {1-x'}}, 1-{\sqrt {1-x'}} \big \}$
, it holds that
$x_{1}' \in \big \{1+{\sqrt {1-x'}}, 1-{\sqrt {1-x'}} \big \}$
, it holds that
Note also that the p-adic valuation on the Galois closure of
![]() $\mathbb {Q}_{p}(x')$
over
$\mathbb {Q}_{p}(x')$
over
![]() $\mathbb {Q}_{p}$
is discrete. Then, by applying the above discussion repeatedly, we may assume without loss of generality that assertion (b) does not hold. In particular, assertion (a) holds. Thus, since
$\mathbb {Q}_{p}$
is discrete. Then, by applying the above discussion repeatedly, we may assume without loss of generality that assertion (b) does not hold. In particular, assertion (a) holds. Thus, since
![]() $(x_{1}')^{-1} = \sigma _{1}(x_1)$
, we conclude that
$(x_{1}')^{-1} = \sigma _{1}(x_1)$
, we conclude that
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{1}'$
are Galois-conjugate, hence that x and
$x_{1}'$
are Galois-conjugate, hence that x and
![]() $x'$
are Galois-conjugate. This completes the proof of Proposition 3.2.
$x'$
are Galois-conjugate. This completes the proof of Proposition 3.2.
Remark 3.2.1. At the time of writing of the present paper, the author does not know
whether the given isomorphism
![]() $\alpha $
arises from some isomorphism of schemes
$\alpha $
arises from some isomorphism of schemes
![]() ${\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \} \overset {\sim }{\rightarrow } {\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}$
or not.
${\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x \} \overset {\sim }{\rightarrow } {\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}$
or not.
Finally, we apply Lemmas 2.1, 2.3, and Proposition 3.2, to prove our main theorem (i.e. the tempered fundamental groups of hyperbolic curves of genus
![]() $0$
over
$0$
over
![]() $\overline {\mathbb {Q}}_p$
completely determine their moduli):
$\overline {\mathbb {Q}}_p$
completely determine their moduli):
Theorem 3.3. Let n be an integer such that
![]() $n \geq 3$
. Suppose that there exists an isomorphism of topological groups
$n \geq 3$
. Suppose that there exists an isomorphism of topological groups
Note that
![]() $\alpha $
induces a bijection
$\alpha $
induces a bijection
(cf. [Reference Mochizuki9], Corollary 3.11). Then there exists an isomorphism of schemes
such that the bijection
![]() $\{x_1, x_2, \dots , x_n\} \overset {\sim }{\rightarrow } \{x_{1}', x_{2}', \dots , x_{n}'\}$
induced by the isomorphism
$\{x_1, x_2, \dots , x_n\} \overset {\sim }{\rightarrow } \{x_{1}', x_{2}', \dots , x_{n}'\}$
induced by the isomorphism
![]() ${\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_1, x_2, \dots , x_n\} \overset {\sim }{\rightarrow } {\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_{1}', x_{2}', \dots , x_{n}'\}$
coincides with the bijection
${\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_1, x_2, \dots , x_n\} \overset {\sim }{\rightarrow } {\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_{1}', x_{2}', \dots , x_{n}'\}$
coincides with the bijection
![]() $\alpha _{\mathrm {cusp}}$
.
$\alpha _{\mathrm {cusp}}$
.
Proof. First, if
![]() $n = 3$
, then the desired assertion follows immediately from the well-known structure of the automorphism group of
$n = 3$
, then the desired assertion follows immediately from the well-known structure of the automorphism group of
![]() ${\mathbb P}^1_{\overline {\mathbb {Q}}_p}$
. Thus, we may assume without loss of generality that
${\mathbb P}^1_{\overline {\mathbb {Q}}_p}$
. Thus, we may assume without loss of generality that
Moreover, by replacing
![]() $\alpha $
by the composite of
$\alpha $
by the composite of
![]() $\alpha $
with the outer isomorphisms arising from suitable geometric automorphisms of
$\alpha $
with the outer isomorphisms arising from suitable geometric automorphisms of
![]() ${\mathbb P}^1_{\overline {\mathbb {Q}}_p}$
, together with the various definitions involved, we may also assume without loss of generality that
${\mathbb P}^1_{\overline {\mathbb {Q}}_p}$
, together with the various definitions involved, we may also assume without loss of generality that
-
•
 $x_1 = x_{1}' = 0$
;
$x_1 = x_{1}' = 0$
;
 $x_2 = x_{2}' = 1$
;
$x_2 = x_{2}' = 1$
;
 $x_3 = x_{3}' = \infty $
;
$x_3 = x_{3}' = \infty $
; -
•
 $\alpha _{\mathrm {cusp}}(x_i) = x_{i}'$
, for each
$\alpha _{\mathrm {cusp}}(x_i) = x_{i}'$
, for each
 $i = 1, \dots , n$
.
$i = 1, \dots , n$
.
Then our goal is to prove that
-
(* n ) there exists an element
 $\sigma \in \mathrm {Gal}(\overline {\mathbb {Q}}_p/\mathbb {Q}_{p})$
such that
$\sigma \in \mathrm {Gal}(\overline {\mathbb {Q}}_p/\mathbb {Q}_{p})$
such that
 $x_{i}' = \sigma (x_{i})$
, for each
$x_{i}' = \sigma (x_{i})$
, for each
 $i = 4, \dots , n$
.
$i = 4, \dots , n$
.
Next, we verify the following assertion:
Claim 3.3.A: We may assume without loss of generality that
for each
![]() $i = 4, \dots , n$
.
$i = 4, \dots , n$
.
Indeed, let r be a positive integer such that, for each
![]() $i = 4, \dots , m$
, it holds that
$i = 4, \dots , m$
, it holds that
![]() $v_{p}(y_i)> -p$
, where
$v_{p}(y_i)> -p$
, where
![]() $y_i$
denotes a
$y_i$
denotes a
![]() $p^r$
-th root of
$p^r$
-th root of
![]() $x_i$
. Write
$x_i$
. Write
for the finite étale Galois coverings of degree
![]() $p^r$
determined by the assignment
$p^r$
determined by the assignment
![]() $t \mapsto t^{p^r}$
(cf. Lemma 1.1, (i)), where
$t \mapsto t^{p^r}$
(cf. Lemma 1.1, (i)), where
![]() $y_2 \overset {\mathrm {def}}{=} 1$
;
$y_2 \overset {\mathrm {def}}{=} 1$
;
![]() $y_{2}' \overset {\mathrm {def}}{=} 1$
;
$y_{2}' \overset {\mathrm {def}}{=} 1$
;
![]() $y_{i}'$
denotes a
$y_{i}'$
denotes a
![]() $p^r$
-th root of
$p^r$
-th root of
![]() $x_{i}'$
. Then
$x_{i}'$
. Then
![]() $\alpha $
induces an isomorphism of topological groups
$\alpha $
induces an isomorphism of topological groups
(cf. Lemma 1.3). By replacing
![]() $\alpha $
by the composite of
$\alpha $
by the composite of
![]() $\alpha $
with a suitable inner automorphism of
$\alpha $
with a suitable inner automorphism of
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}}$
, we may assume without loss of generality that
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x' \}}$
, we may assume without loss of generality that
![]() $\epsilon $
maps the cuspidal inertia subgroups of
$\epsilon $
maps the cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm { tp}}_{Y}$
associated to
$\Pi ^{\mathrm { tp}}_{Y}$
associated to
![]() $y_2 = 1$
to the cuspidal inertia subgroups of
$y_2 = 1$
to the cuspidal inertia subgroups of
![]() $\Pi ^{\mathrm {tp}}_{Y'}$
associated to
$\Pi ^{\mathrm {tp}}_{Y'}$
associated to
![]() $y_{2}' = 1$
. Moreover, by replacing
$y_{2}' = 1$
. Moreover, by replacing
![]() $y_{i}'$
by a suitable
$y_{i}'$
by a suitable
![]() $p^r$
-th root of
$p^r$
-th root of
![]() $x_{i}'$
, if necessary, we may assume without loss of generality that
$x_{i}'$
, if necessary, we may assume without loss of generality that
![]() $\epsilon $
maps the cuspidal inertia subgroups associated to
$\epsilon $
maps the cuspidal inertia subgroups associated to
![]() $y_{i}$
to the cuspidal inertia subgroups associated to
$y_{i}$
to the cuspidal inertia subgroups associated to
![]() $y_{i}'$
for each
$y_{i}'$
for each
![]() $i = 4, \dots , n$
. Then
$i = 4, \dots , n$
. Then
![]() $\epsilon $
induces, via the quotients of
$\epsilon $
induces, via the quotients of
![]() $\Pi ^{\mathrm {tp}}_{Y}$
,
$\Pi ^{\mathrm {tp}}_{Y}$
,
![]() $\Pi ^{\mathrm {tp}}_{Y'}$
by the normal closed subgroups topologically generated by cuspidal inertia subgroups associated to the cusps
$\Pi ^{\mathrm {tp}}_{Y'}$
by the normal closed subgroups topologically generated by cuspidal inertia subgroups associated to the cusps
![]() $\not \in \{0, 1, \infty , y_i \ (i=4, \dots , n)\}$
, the cusps
$\not \in \{0, 1, \infty , y_i \ (i=4, \dots , n)\}$
, the cusps
![]() $\not \in \{0, 1, \infty , y_{i}' \ (i=4, \dots , n)\}$
, respectively, an isomorphism of topological groups
$\not \in \{0, 1, \infty , y_{i}' \ (i=4, \dots , n)\}$
, respectively, an isomorphism of topological groups
Since
![]() $\phi _{p^{r},x}$
and
$\phi _{p^{r},x}$
and
![]() $\phi _{p^{r},x'}$
are defined over
$\phi _{p^{r},x'}$
are defined over
![]() $\mathbb {Q}_{p}$
, by replacing
$\mathbb {Q}_{p}$
, by replacing
![]() $y_i$
,
$y_i$
,
![]() $y_{i}'$
by
$y_{i}'$
by
![]() $x_i$
,
$x_i$
,
![]() $x_{i}'$
, respectively, we may assume without loss of generality that
$x_{i}'$
, respectively, we may assume without loss of generality that
![]() $v_{p}(x_i)> -p$
.
$v_{p}(x_i)> -p$
.
Next, we consider the connected finite étale covering
 $$ \begin{align*} \psi_{p} : {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{p}{p+1}, \dots, \infty \bigg\} \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{0, 1, \infty \} \end{align*} $$
$$ \begin{align*} \psi_{p} : {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{p}{p+1}, \dots, \infty \bigg\} \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{0, 1, \infty \} \end{align*} $$
(cf. Lemma 1.1, (ii)). For each
![]() $i = 4, \dots , n$
, let
$i = 4, \dots , n$
, let
![]() $z_i \in \psi _{p}^{-1}(x_i)$
be such that
$z_i \in \psi _{p}^{-1}(x_i)$
be such that
![]() $v_{p}(1-z_i)> 0$
(cf. Lemma 2.2). Recall that
$v_{p}(1-z_i)> 0$
(cf. Lemma 2.2). Recall that
![]() $\psi _{p}$
is also defined over
$\psi _{p}$
is also defined over
![]() $\mathbb {Q}_{p}$
. Thus, in light of Lemmas 1.3 and 2.2, it follows from a similar argument to the above argument that, by replacing
$\mathbb {Q}_{p}$
. Thus, in light of Lemmas 1.3 and 2.2, it follows from a similar argument to the above argument that, by replacing
![]() $z_i$
by
$z_i$
by
![]() $x_i$
, we may assume without loss of generality that
$x_i$
, we may assume without loss of generality that
![]() $v_{p}(x_i) = 0$
for each
$v_{p}(x_i) = 0$
for each
![]() $i = 4, \dots , n$
. This completes the proof of Claim 3.3.A.
$i = 4, \dots , n$
. This completes the proof of Claim 3.3.A.
Write
for the set of the Galois-conjugates of
![]() $x_i$
. Next, we verify the following assertion:
$x_i$
. Next, we verify the following assertion:
Claim 3.3.B: We may assume without loss of generality that
for each
![]() $i = 4, \dots , n$
.
$i = 4, \dots , n$
.
Indeed, by applying Claim 3.3.A, we may assume without loss of generality that
![]() $v_{p}(x_i) = 0$
for each
$v_{p}(x_i) = 0$
for each
![]() $i = 4, \dots , m$
. Then, in light of Lemma 2.1, one may apply a similar argument to the argument applied in the proof of Claim 3.3.A, together with the use of the connected finite étale covering
$i = 4, \dots , m$
. Then, in light of Lemma 2.1, one may apply a similar argument to the argument applied in the proof of Claim 3.3.A, together with the use of the connected finite étale covering
(cf. Lemma 1.1, (i)) for sufficiently large r, to obtain the desired conclusion. This completes the proof of Claim 3.3.B.
In the remainder, we prove
![]() $(\ast _n)$
by induction on n. We already observed that
$(\ast _n)$
by induction on n. We already observed that
![]() $(\ast _4)$
holds (cf. Proposition 3.2). Let m be a positive integer such that
$(\ast _4)$
holds (cf. Proposition 3.2). Let m be a positive integer such that
![]() $m \geq 4$
. Suppose that
$m \geq 4$
. Suppose that
![]() $(\ast _n)$
in the case where
$(\ast _n)$
in the case where
![]() $n \leq m$
holds. Then our goal is to prove that
$n \leq m$
holds. Then our goal is to prove that
![]() $(\ast _{m+1})$
holds.
$(\ast _{m+1})$
holds.
Next, we verify the following assertion:
Claim 3.3.C: Suppose that
-
•
 $v_{p}(x_4) \geq v_{p}(x_{m+1})$
;
$v_{p}(x_4) \geq v_{p}(x_{m+1})$
; -
•
 $\max _{w \in \mathcal {C}_{i} \setminus \{x_i\}} \ v_{p}(x_i -w) < 2$
, for each
$\max _{w \in \mathcal {C}_{i} \setminus \{x_i\}} \ v_{p}(x_i -w) < 2$
, for each
 $i = 4, \dots , m$
;
$i = 4, \dots , m$
; -
•
 $v_{p}(1-x_{m+1}) \geq 2$
.
$v_{p}(1-x_{m+1}) \geq 2$
.
Then
![]() $(\ast _{m+1})$
holds.
$(\ast _{m+1})$
holds.
First, we note that since
![]() $\alpha _{\mathrm {cusp}}(x_{m+1}) = x_{m+1}'$
, the isomorphism
$\alpha _{\mathrm {cusp}}(x_{m+1}) = x_{m+1}'$
, the isomorphism
![]() $\alpha $
induces an isomorphism of topological groups
$\alpha $
induces an isomorphism of topological groups
Then, by applying the induction hypothesis, we may assume without loss of generality that
for each
![]() $i = 4, \dots , m$
. Next, write
$i = 4, \dots , m$
. Next, write
for the isomorphisms of topological groups (determined up to
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x_4, \dots , \frac {x_{4}}{x_{m+1}} \}}$
-conjugate,
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x_4, \dots , \frac {x_{4}}{x_{m+1}} \}}$
-conjugate,
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x_4, \dots , \frac {x_{4}}{x_{m+1}'} \}}$
-conjugate, respectively) induced by the isomorphism of schemes defined by the assignment
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{0, 1, \infty , x_4, \dots , \frac {x_{4}}{x_{m+1}'} \}}$
-conjugate, respectively) induced by the isomorphism of schemes defined by the assignment
![]() $t \mapsto \frac {x_4}{t}$
. Then we obtain an isomorphism of topological groups
$t \mapsto \frac {x_4}{t}$
. Then we obtain an isomorphism of topological groups
Next, write
 $$ \begin{align*}\eta_{\mathrm{cusp}} : \bigg\{0, 1, \infty, x_4, \dots, \frac{x_{4}}{x_{m+1}} \bigg\} \overset{\sim}{\rightarrow} \bigg\{0, 1, \infty, x_4, \dots, \frac{x_{4}}{x_{m+1}'} \bigg\} \end{align*} $$
$$ \begin{align*}\eta_{\mathrm{cusp}} : \bigg\{0, 1, \infty, x_4, \dots, \frac{x_{4}}{x_{m+1}} \bigg\} \overset{\sim}{\rightarrow} \bigg\{0, 1, \infty, x_4, \dots, \frac{x_{4}}{x_{m+1}'} \bigg\} \end{align*} $$
for the bijection induced by
![]() $\eta $
. Recall that
$\eta $
. Recall that
![]() $\alpha _{\mathrm {cusp}}(x_i) = x_{i}'$
, for each
$\alpha _{\mathrm {cusp}}(x_i) = x_{i}'$
, for each
![]() $i = 1, \dots , n$
. Then it follows immediately from the definition of
$i = 1, \dots , n$
. Then it follows immediately from the definition of
![]() $\eta _{\mathrm {cusp}}$
that
$\eta _{\mathrm {cusp}}$
that
 $$ \begin{align*}\eta_{\mathrm{cusp}}\bigg(\frac{x_{4}}{x_{j}}\bigg) = \frac{x_{4}}{x_{j}'}, \end{align*} $$
$$ \begin{align*}\eta_{\mathrm{cusp}}\bigg(\frac{x_{4}}{x_{j}}\bigg) = \frac{x_{4}}{x_{j}'}, \end{align*} $$
for each
![]() $j = 5, \dots , m+1$
. In particular,
$j = 5, \dots , m+1$
. In particular,
![]() $\eta $
induces an isomorphism of topological groups
$\eta $
induces an isomorphism of topological groups
Thus, by applying the induction hypothesis, we obtain an element
![]() $\tau \in \mathrm {Gal}(\overline {\mathbb {Q}}_p/\mathbb {Q}_{p})$
such that
$\tau \in \mathrm {Gal}(\overline {\mathbb {Q}}_p/\mathbb {Q}_{p})$
such that
 $$ \begin{align*}\frac{x_{4}}{x_{j}'} = \tau\bigg(\frac{x_{4}}{x_{j}}\bigg), \end{align*} $$
$$ \begin{align*}\frac{x_{4}}{x_{j}'} = \tau\bigg(\frac{x_{4}}{x_{j}}\bigg), \end{align*} $$
for each
![]() $j = 5, \dots , m+1$
. Next, observe that
$j = 5, \dots , m+1$
. Next, observe that
-
•
 $v_{p}(x_{m+1}) = v_{p}(x_{m+1}')$
(cf. [Reference Lepage4], Theorem 4.6);
$v_{p}(x_{m+1}) = v_{p}(x_{m+1}')$
(cf. [Reference Lepage4], Theorem 4.6); -
•
 $v_{p}(1-x_{m+1}) = v_{p}(1-x_{m+1}')$
(cf. [Reference Lepage4], Theorem 4.6);
$v_{p}(1-x_{m+1}) = v_{p}(1-x_{m+1}')$
(cf. [Reference Lepage4], Theorem 4.6); -
•
 $v_{p}(x_4 - \frac {x_{4}}{x_{m+1}'}) = v_{p}(x_4 -\tau (x_4) + \tau (x_4) - \tau (\frac {x_{4}}{x_{m+1}}))$
;
$v_{p}(x_4 - \frac {x_{4}}{x_{m+1}'}) = v_{p}(x_4 -\tau (x_4) + \tau (x_4) - \tau (\frac {x_{4}}{x_{m+1}}))$
; -
•
 $v_{p}(x_4 - \frac {x_{4}}{x_{m+1}}) = v_{p}(\tau (x_4) - \tau (\frac {x_{4}}{x_{m+1}}))$
.
$v_{p}(x_4 - \frac {x_{4}}{x_{m+1}}) = v_{p}(\tau (x_4) - \tau (\frac {x_{4}}{x_{m+1}}))$
.
Note that the first, second and forth equalities imply that
 $$ \begin{align*}v_{p}\bigg(x_4 - \frac{x_{4}}{x_{m+1}'}\bigg) = v_{p}\bigg(\tau(x_4) - \tau\bigg(\frac{x_{4}}{x_{m+1}}\bigg)\bigg). \end{align*} $$
$$ \begin{align*}v_{p}\bigg(x_4 - \frac{x_{4}}{x_{m+1}'}\bigg) = v_{p}\bigg(\tau(x_4) - \tau\bigg(\frac{x_{4}}{x_{m+1}}\bigg)\bigg). \end{align*} $$
Thus, it follows immediately from the third equality that
 $$ \begin{align*}v_{p}(x_4 -\tau(x_4)) \geq v_{p}\bigg(x_4 - \frac{x_{4}}{x_{m+1}'}\bigg). \end{align*} $$
$$ \begin{align*}v_{p}(x_4 -\tau(x_4)) \geq v_{p}\bigg(x_4 - \frac{x_{4}}{x_{m+1}'}\bigg). \end{align*} $$
On the other hand, since
it holds that
 $$ \begin{align*}v_{p}\bigg(x_4 - \frac{x_{4}}{x_{m+1}'}\bigg) \geq 2. \end{align*} $$
$$ \begin{align*}v_{p}\bigg(x_4 - \frac{x_{4}}{x_{m+1}'}\bigg) \geq 2. \end{align*} $$
Then we obtain an inequality
Thus, by applying our assumption that
![]() $\max _{w \in \mathcal {C}_{4} \setminus \{x_4\}} v_{p}(x_4 -w) < 2$
, we conclude that
$\max _{w \in \mathcal {C}_{4} \setminus \{x_4\}} v_{p}(x_4 -w) < 2$
, we conclude that
Therefore, by combining with the equality
![]() $\frac {x_{4}}{x_{j}'} = \tau (\frac {x_{4}}{x_{j}})$
, we also conclude that
$\frac {x_{4}}{x_{j}'} = \tau (\frac {x_{4}}{x_{j}})$
, we also conclude that
for each
![]() $j = 5, \dots , m+1$
. This completes the proof of Claim 3.3.C.
$j = 5, \dots , m+1$
. This completes the proof of Claim 3.3.C.
Next, we verify the following assertion:
Claim 3.3.D: Suppose that, for each
![]() $i = 4, \dots , m+1$
, it holds that
$i = 4, \dots , m+1$
, it holds that
-
•
 $v_{p}(x_i) = 0$
,
$v_{p}(x_i) = 0$
, -
•
 $v_{p}(1-x_i) \leq 1$
, and
$v_{p}(1-x_i) \leq 1$
, and -
•
 $\max _{w \in \mathcal {C}_{i} \setminus \{x_i\}} \ v_{p}(x_i -w) \leq 1$
.
$\max _{w \in \mathcal {C}_{i} \setminus \{x_i\}} \ v_{p}(x_i -w) \leq 1$
.
For each
![]() $i = 4, \dots , m$
, let
$i = 4, \dots , m$
, let
![]() $s_i \in \psi _{p^2}^{-1}(x_i)$
be, such that
$s_i \in \psi _{p^2}^{-1}(x_i)$
be, such that
![]() $v_{p}(s_i) = 2$
(cf. Lemma 2.2). Let
$v_{p}(s_i) = 2$
(cf. Lemma 2.2). Let
![]() $s_{m+1} \in \psi _{p^2}^{-1}(x_{m+1})$
be such that
$s_{m+1} \in \psi _{p^2}^{-1}(x_{m+1})$
be such that
![]() $v_{p}(1-s_{m+1})> 0$
(cf. Lemma 2.2). For each
$v_{p}(1-s_{m+1})> 0$
(cf. Lemma 2.2). For each
![]() $i = 4, \dots , m+1$
, write
$i = 4, \dots , m+1$
, write
![]() $u_i \overset {\mathrm {def}}{=} 1-\frac {p^2}{(p^2+1)s_{i}}$
;
$u_i \overset {\mathrm {def}}{=} 1-\frac {p^2}{(p^2+1)s_{i}}$
;
![]() $\mathcal {C}_{u_i}$
for the set of the Galois-conjugates of
$\mathcal {C}_{u_i}$
for the set of the Galois-conjugates of
![]() $u_i$
. Then it holds that
$u_i$
. Then it holds that
for each
![]() $i = 4, \dots , m$
.
$i = 4, \dots , m$
.
The assertions in the first display follow immediately from the facts that
![]() $v_{p}(s_4) = 2$
, and
$v_{p}(s_4) = 2$
, and
![]() $v_{p}(s_{m+1}) = 0$
. Next, we verify the assertion in the second display. For each
$v_{p}(s_{m+1}) = 0$
. Next, we verify the assertion in the second display. For each
![]() $i = 4, \dots , m$
, write
$i = 4, \dots , m$
, write
![]() $\mathcal {C}_{s_i}$
for the set of the Galois-conjugates of
$\mathcal {C}_{s_i}$
for the set of the Galois-conjugates of
![]() $s_i$
. Let
$s_i$
. Let
![]() $w_{i} \in \mathcal {C}_{s_i} \setminus \{s_i\}$
be an element. Then since
$w_{i} \in \mathcal {C}_{s_i} \setminus \{s_i\}$
be an element. Then since
![]() $v_{p}(s_i) = v_{p}(w_i) = 2$
, it suffices to prove that
$v_{p}(s_i) = v_{p}(w_i) = 2$
, it suffices to prove that
However, this inequality follows from Lemma 2.3. This completes the proof of Claim 3.3.D.
Finally, we complete the proof of the assertion
![]() $(\ast _{m+1})$
. By applying Claim 3.3.B, we may assume without loss of generality that
$(\ast _{m+1})$
. By applying Claim 3.3.B, we may assume without loss of generality that
for each
![]() $i = 4, \dots , m+1$
. Write
$i = 4, \dots , m+1$
. Write
 $$ \begin{align*}\psi_{p^{2}, x} : {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{p^2}{p^2 +1}, \dots, \infty\bigg\} \cup \psi_{p^2}^{-1}(T) \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{x_1, x_2, \dots, x_n\}, \end{align*} $$
$$ \begin{align*}\psi_{p^{2}, x} : {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{p^2}{p^2 +1}, \dots, \infty\bigg\} \cup \psi_{p^2}^{-1}(T) \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{x_1, x_2, \dots, x_n\}, \end{align*} $$
 $$ \begin{align*}\psi_{p^{2}, x'} : {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{p^2}{p^2 +1}, \dots, \infty\bigg\} \cup \psi_{p^2}^{-1}(T') \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{x_{1}', x_{2}', \dots, x_{n}'\} \end{align*} $$
$$ \begin{align*}\psi_{p^{2}, x'} : {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{p^2}{p^2 +1}, \dots, \infty\bigg\} \cup \psi_{p^2}^{-1}(T') \longrightarrow {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \{x_{1}', x_{2}', \dots, x_{n}'\} \end{align*} $$
for the connected finite étale coverings induced by
![]() $\psi _{p^2}$
(cf. Lemma 1.1, (ii); Remark 1.1.1);
$\psi _{p^2}$
(cf. Lemma 1.1, (ii); Remark 1.1.1);
for the open subgroups of finite index (determined up to
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_1, x_2, \dots , x_n\}}$
-conjugate,
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_1, x_2, \dots , x_n\}}$
-conjugate,
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_{1}', x_{2}', \dots , x_{n}'\}}$
-conjugate, respectively) determined by
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_{1}', x_{2}', \dots , x_{n}'\}}$
-conjugate, respectively) determined by
![]() $\psi _{p^{2}, x}$
,
$\psi _{p^{2}, x}$
,
![]() $\psi _{p^{2}, x'}$
, respectively. Here, we note that
$\psi _{p^{2}, x'}$
, respectively. Here, we note that
![]() $\frac {p^2}{p^2 +1}$
is a unique cusp
$\frac {p^2}{p^2 +1}$
is a unique cusp
![]() $\ast $
such that
$\ast $
such that
![]() $\psi _{p^{2}}$
ramifies at
$\psi _{p^{2}}$
ramifies at
![]() $\ast $
, and
$\ast $
, and
![]() $\ast $
lies over
$\ast $
lies over
![]() $1$
via
$1$
via
![]() $\psi _{p^{2}}$
(cf. Lemma 1.1, (ii)). Then since
$\psi _{p^{2}}$
(cf. Lemma 1.1, (ii)). Then since
![]() $\alpha _{\mathrm {cusp}}(0) = 0$
,
$\alpha _{\mathrm {cusp}}(0) = 0$
,
![]() $\alpha _{\mathrm {cusp}}(1) = 1$
,
$\alpha _{\mathrm {cusp}}(1) = 1$
,
![]() $\alpha _{\mathrm {cusp}}(\infty ) = \infty $
, and
$\alpha _{\mathrm {cusp}}(\infty ) = \infty $
, and
![]() $\alpha _{\mathrm {cusp}}(x_i) = x_{i}'$
, for each
$\alpha _{\mathrm {cusp}}(x_i) = x_{i}'$
, for each
![]() $i = 4, \dots , n$
, it follows immediately from Lemma 1.3 that there exists an inner automorphism
$i = 4, \dots , n$
, it follows immediately from Lemma 1.3 that there exists an inner automorphism
![]() $\iota $
of
$\iota $
of
![]() $\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_{1}', x_{2}', \dots , x_{n}'\}}$
satisfying the following conditions:
$\Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_{1}', x_{2}', \dots , x_{n}'\}}$
satisfying the following conditions:
-
• The composite morphism
 $\iota \circ \alpha $
induces an isomorphism of topological groups via the inclusions
$\iota \circ \alpha $
induces an isomorphism of topological groups via the inclusions $$ \begin{align*}\theta : \Pi^{\mathrm{tp}}_{\psi_{p^{2}, x}} \overset{\sim}{\rightarrow} \Pi^{\mathrm{tp}}_{\psi_{p^{2}, x'}} \end{align*} $$
$$ \begin{align*}\theta : \Pi^{\mathrm{tp}}_{\psi_{p^{2}, x}} \overset{\sim}{\rightarrow} \Pi^{\mathrm{tp}}_{\psi_{p^{2}, x'}} \end{align*} $$
 $\Pi ^{\mathrm {tp}}_{\psi _{p^{2}, x}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_1, x_2, \dots , x_n\}}$
and
$\Pi ^{\mathrm {tp}}_{\psi _{p^{2}, x}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_1, x_2, \dots , x_n\}}$
and
 $\Pi ^{\mathrm {tp}}_{\psi _{p^{2}, x'}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_{1}', x_{2}', \dots , x_{n}'\}}$
.
$\Pi ^{\mathrm {tp}}_{\psi _{p^{2}, x'}} \subseteq \Pi ^{\mathrm {tp}}_{{\mathbb P}^1_{\overline {\mathbb {Q}}_p} \backslash \{x_{1}', x_{2}', \dots , x_{n}'\}}$
.
-
• Write
for the bijection induced by $$ \begin{align*}\theta_{\mathrm{cusp}} : \bigg\{0, 1, \frac{p^2}{p^2 +1}, \dots, \infty\bigg\} \cup \psi_{p^2}^{-1}(T) \ \overset{\sim}{\rightarrow} \ \bigg\{0, 1, \frac{p^2}{p^2 +1}, \dots, \infty\bigg\} \cup \psi_{p^2}^{-1}(T') \end{align*} $$
$$ \begin{align*}\theta_{\mathrm{cusp}} : \bigg\{0, 1, \frac{p^2}{p^2 +1}, \dots, \infty\bigg\} \cup \psi_{p^2}^{-1}(T) \ \overset{\sim}{\rightarrow} \ \bigg\{0, 1, \frac{p^2}{p^2 +1}, \dots, \infty\bigg\} \cup \psi_{p^2}^{-1}(T') \end{align*} $$
 $\theta $
(cf. [Reference Mochizuki9], Corollary 3.11). Then it holds that
$\theta $
(cf. [Reference Mochizuki9], Corollary 3.11). Then it holds that $$ \begin{align*}\theta_{\mathrm{cusp}}(0) = 0, \quad \theta_{\mathrm{cusp}}(1) = 1, \quad \theta_{\mathrm{cusp}}(\infty) = \infty, \quad \theta_{\mathrm{cusp}}\bigg(\frac{p^2}{p^2 +1}\bigg) = \frac{p^2}{p^2 +1}. \end{align*} $$
$$ \begin{align*}\theta_{\mathrm{cusp}}(0) = 0, \quad \theta_{\mathrm{cusp}}(1) = 1, \quad \theta_{\mathrm{cusp}}(\infty) = \infty, \quad \theta_{\mathrm{cusp}}\bigg(\frac{p^2}{p^2 +1}\bigg) = \frac{p^2}{p^2 +1}. \end{align*} $$
For each
![]() $i = 4, \dots , m+1$
, write
$i = 4, \dots , m+1$
, write
![]() $s_{i}' \overset {\mathrm {def}}{=} \theta _{\mathrm {cusp}}(s_i)$
(cf. Claim 3.3.D). Then the isomorphism
$s_{i}' \overset {\mathrm {def}}{=} \theta _{\mathrm {cusp}}(s_i)$
(cf. Claim 3.3.D). Then the isomorphism
![]() $\theta $
induces an isomorphism of topological groups
$\theta $
induces an isomorphism of topological groups
Write
 $$ \begin{align*}\omega : {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{\infty, \frac{1}{p^2+1}, 0, \dots, 1 \bigg\} \overset{\sim}{\rightarrow} {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{p^2}{p^2+1}, \dots, \infty \bigg\} \end{align*} $$
$$ \begin{align*}\omega : {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{\infty, \frac{1}{p^2+1}, 0, \dots, 1 \bigg\} \overset{\sim}{\rightarrow} {\mathbb P}^1_{\overline{\mathbb{Q}}_p} \backslash \bigg\{0, 1, \frac{p^2}{p^2+1}, \dots, \infty \bigg\} \end{align*} $$
for the inverse of the isomorphism determined by the assignment
![]() $t \mapsto 1-\frac {p^2}{(p^2+1)t}$
. For each
$t \mapsto 1-\frac {p^2}{(p^2+1)t}$
. For each
![]() $i = 4, \dots , m+1$
, write
$i = 4, \dots , m+1$
, write
![]() $u_{i}' \overset {\mathrm {def}}{=} 1-\frac {p^2}{(p^2+1)s_{i}'}$
. Then
$u_{i}' \overset {\mathrm {def}}{=} 1-\frac {p^2}{(p^2+1)s_{i}'}$
. Then
![]() $\xi $
and
$\xi $
and
![]() $\omega $
induce, in a similar way to the construction of
$\omega $
induce, in a similar way to the construction of
![]() $\eta $
, an isomorphism of topological groups
$\eta $
, an isomorphism of topological groups
Note that, if we write
for the bijection induced by the above isomorphism, then it holds that
for each
![]() $i = 4, \dots , m+1$
. On the other hand, observe that the composite morphism
$i = 4, \dots , m+1$
. On the other hand, observe that the composite morphism
![]() $\psi _{p^2} \circ \omega $
is defined over
$\psi _{p^2} \circ \omega $
is defined over
![]() $\mathbb {Q}_{p}$
. Then, by replacing
$\mathbb {Q}_{p}$
. Then, by replacing
![]() $u_{i}$
by
$u_{i}$
by
![]() $x_i$
, together with Claim 3.3.D, we may assume without loss of generality that
$x_i$
, together with Claim 3.3.D, we may assume without loss of generality that
Thus, we conclude from Claim 3.3.C that
![]() $(\ast _{m+1})$
holds. This completes the proof of Theorem 3.3.
$(\ast _{m+1})$
holds. This completes the proof of Theorem 3.3.
Acknowledgements
The author would like to express deep gratitude to Professor Yu Yang for his interest, stimulating discussions and helpful comments concerning the contents of the present paper. The author also would like to thank Professor Yuichiro Hoshi for helpful discussions concerning the contents of the present paper. Finally, the author also would like to thank Professor Emmanuel Lepage for stimulating comments concerning the contents of the present paper during his stay at Kyoto University in 2019. The author was supported by Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Number 18J10260. This research was also supported by the Research Institute for Mathematical Sciences, an International Joint Usage/Research Center located in Kyoto University.
Conflicts of Interest
The author declares none.