We propose a new method, probabilistic divide-and-conquer, for improving the success probability in rejection sampling. For the example of integer partitions, there is an ideal recursive scheme which improves the rejection cost from asymptotically order n3/4 to a constant. We show other examples for which a non-recursive, one-time application of probabilistic divide-and-conquer removes a substantial fraction of the rejection sampling cost.

We also present a variation of probabilistic divide-and-conquer for generating i.i.d. samples that exploits features of the coupon collector's problem, in order to obtain a cost that is sublinear in the number of samples.

In this note we establish a uniform bound for the distribution of a sum Sn=X1+···+Xn of independent non-homogeneous Bernoulli trials. Specifically, we prove that σn(Sn = j) ≤ η, where σn denotes the standard deviation of Sn, and η is a universal constant. We compute the best possible constant η ~ 0.4688 and we show that the bound also holds for limits of sums and differences of Bernoullis, including the Poisson laws which constitute the worst case and attain the bound. We also investigate the optimal bounds for n and j fixed. An application to estimate the rate of convergence of Mann's fixed-point iterations is presented.

The discrete Green's function (without boundary) 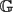$\mathbb{G}$ is a pseudo-inverse of the combinatorial Laplace operator of a graph G = (V, E). We reveal the intimate connection between Green's function and the theory of exact stopping rules for random walks on graphs. We give an elementary formula for Green's function in terms of state-to-state hitting times of the underlying graph. Namely,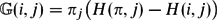$\mathbb{G}(i,j) = \pi_j \bigl( H(\pi,j) - H(i,j) \bigr),$ where πi is the stationary distribution at vertex i, H(i, j) is the expected hitting time for a random walk starting from vertex i to first reach vertex j, and H(π, j) = ∑k∈V πkH(k, j). This formula also holds for the digraph Laplace operator.

The most important characteristics of a stopping rule are its exit frequencies, which are the expected number of exits of a given vertex before the rule halts the walk. We show that Green's function is, in fact, a matrix of exit frequencies plus a rank one matrix. In the undirected case, we derive spectral formulas for Green's function and for some mixing measures arising from stopping rules. Finally, we further explore the exit frequency matrix point of view, and discuss a natural generalization of Green's function for any distribution τ defined on the vertex set of the graph.

In 1981 Beck and Fiala proved an upper bound for the discrepancy of a set system of degree d that is independent of the size of the ground set. In the intervening years the bound has been decreased from 2d − 2 to 2d − 4. We improve the bound to 2d − log*d.

A family of sets is called union-closed if whenever A and B are sets of the family, so is A ∪ B. The long-standing union-closed conjecture states that if a family of subsets of [n] is union-closed, some element appears in at least half the sets of the family. A natural weakening is that the union-closed conjecture holds for large families, that is, families consisting of at least p02n sets for some constant p0. The first result in this direction appears in a recent paper of Balla, Bollobás and Eccles [1], who showed that union-closed families of at least $\tfrac{2}{3}$2n sets satisfy the conjecture; they proved this by determining the minimum possible average size of a set in a union-closed family of given size. However, the methods used in that paper cannot prove a better constant than $\tfrac{2}{3}$. Here, we provide a stability result for the main theorem of [1], and as a consequence we prove the union-closed conjecture for families of at least ($\tfrac{2}{3}$ − c)2n sets, for a positive constant c.

Let G be an additive abelian group, let n ⩾ 1 be an integer, let S be a sequence over G of length |S| ⩾ n + 1, and let ${\mathsf h}$(S) denote the maximum multiplicity of a term in S. Let Σn(S) denote the set consisting of all elements in G which can be expressed as the sum of terms from a subsequence of S having length n. In this paper, we prove that either ng ∈ Σn(S) for every term g in S whose multiplicity is at least ${\mathsf h}$(S) − 1 or |Σn(S)| ⩾ min{n + 1, |S| − n + | supp (S)| − 1}, where |supp(S)| denotes the number of distinct terms that occur in S. When G is finite cyclic and n = |G|, this confirms a conjecture of Y. O. Hamidoune from 2003.

We consider large random graphs with prescribed degrees, as generated by the configuration model. In the regime where the empirical degree distribution approaches a limit μ with finite mean, we establish the systematic convergence of a broad class of graph parameters that includes the independence number, the maximum cut size, the logarithm of the Tutte polynomial, and the free energy of the anti-ferromagnetic Ising and Potts models. Contrary to previous works, our results are not a priori limited to the free energy of some prescribed graphical model. They apply more generally to any additive, Lipschitz and concave graph parameter. In addition, the corresponding limits are shown to be Lipschitz and concave in the degree distribution μ. This considerably extends the applicability of the celebrated interpolation method, introduced in the context of spin glasses, and recently related to the challenging question of right-convergence of sparse graphs.

We give an easy method for constructing containers for simple hypergraphs. The method also has consequences for non-simple hypergraphs. Some applications are given; in particular, a very transparent calculation is offered for the number of H-free hypergraphs, where H is some fixed uniform hypergraph.

We show that for any coprime integers λ1, . . ., λk and any finite A ⊂ $\mathbb{Z}$, one has

|\lambda_1 \cdot A + \cdots + \lambda_k \cdot A| \geq (|\lambda_1| + \cdots + |\lambda_k|)|A|- C,

In a recent paper, Baxter and Zeilberger showed that the two most important Mahonian statistics, the inversion number and the major index, are asymptotically independently normally distributed on permutations. In another recent paper, Canfield, Janson and Zeilberger proved the result, already known to statisticians, that the Mahonian distribution is asymptotically normal on words. This leaves one question unanswered: What, asymptotically, is the joint distribution of the inversion number and the major index on words? We answer this question by establishing convergence to a bivariate normal distribution.

In my recent paper [1] there is a mistake in the proof of Corollary 3. The first line of the displayed equation in that proof asserts that

\[\int_G|\langle u,\pi^g v\rangle_V|^2\,\rm{d} g = \int_G\langle u\otimes u,(\pi^g\otimes \pi^g)(v\otimes v)\rangle_{V\otimes V}\, \rm{d} g.\]