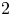1. Introduction
An important fact in the characterization of a finite permutation group $G$![]() on a finite set $\Omega$
on a finite set $\Omega$![]() is that all $2$
is that all $2$![]() -transitive groups are primitive. However, there is a large gap between primitivity and $2$
-transitive groups are primitive. However, there is a large gap between primitivity and $2$![]() -transitivity, in the sense that relatively few primitive groups are $2$
-transitivity, in the sense that relatively few primitive groups are $2$![]() -transitive. In [Reference Araújo, Cameron and Steinberg1], Araújo, Cameron and Steinberg introduced a hierarchy of classes of permutation groups that provides a finer characterization. These classes include spreading groups, defined in terms of sets and multisets of elements of $\Omega$
-transitive. In [Reference Araújo, Cameron and Steinberg1], Araújo, Cameron and Steinberg introduced a hierarchy of classes of permutation groups that provides a finer characterization. These classes include spreading groups, defined in terms of sets and multisets of elements of $\Omega$![]() (see § 2 for a precise definition); separating groups, defined in terms of subsets of $\Omega$
(see § 2 for a precise definition); separating groups, defined in terms of subsets of $\Omega$![]() , or graphs on $\Omega$
, or graphs on $\Omega$![]() preserved by $G$
preserved by $G$![]() ; and synchronizing groups, originally defined in [Reference Arnold and Steinberg2] in terms of transformation semigroups on $\Omega$
; and synchronizing groups, originally defined in [Reference Arnold and Steinberg2] in terms of transformation semigroups on $\Omega$![]() containing $G$
containing $G$![]() . (See also [Reference Bamberg and Lansdown6] for equivalent definitions of these properties in terms of $G$
. (See also [Reference Bamberg and Lansdown6] for equivalent definitions of these properties in terms of $G$![]() -modules.) In particular, these members of the hierarchy are related as follows (see [Reference Araújo, Cameron and Steinberg1, p. 151]):
-modules.) In particular, these members of the hierarchy are related as follows (see [Reference Araújo, Cameron and Steinberg1, p. 151]):
Moreover, the finite primitive groups can be divided into five types via the O'Nan–Scott Theorem, and by [Reference Araújo, Cameron and Steinberg1, Thereom 2.11 & Proposition 3.7], each synchronizing group is one of three types: almost simple, affine or diagonal (the relevant diagonal type groups will be defined in § 2). It is also well-known that each finite $2$![]() -transitive group is almost simple or affine.
-transitive group is almost simple or affine.
Now, [Reference Araújo, Cameron and Steinberg1, § 6–7] classifies the affine spreading groups, and provides examples of almost simple groups that are spreading but not $2$![]() -transitive, separating but not spreading, or synchronizing but not separating, while [Reference Bamberg, Giudici, Lansdown and Royle5] describes affine synchronizing groups that are not spreading. In addition, [Reference Bray, Cai, Cameron, Spiga and Zhang8, Theorem 1.4] states that a primitive group that is not almost simple is synchronizing if and only if it is separating. The first (and so far only) known examples of synchronizing groups of diagonal type were presented in [Reference Bamberg, Giudici, Lansdown and Royle4]: the groups $\operatorname {{\mathrm {PSL}}}_2(q) \times \operatorname {{\mathrm {PSL}}}_2(q)$
-transitive, separating but not spreading, or synchronizing but not separating, while [Reference Bamberg, Giudici, Lansdown and Royle5] describes affine synchronizing groups that are not spreading. In addition, [Reference Bray, Cai, Cameron, Spiga and Zhang8, Theorem 1.4] states that a primitive group that is not almost simple is synchronizing if and only if it is separating. The first (and so far only) known examples of synchronizing groups of diagonal type were presented in [Reference Bamberg, Giudici, Lansdown and Royle4]: the groups $\operatorname {{\mathrm {PSL}}}_2(q) \times \operatorname {{\mathrm {PSL}}}_2(q)$![]() acting diagonally on $\operatorname {{\mathrm {PSL}}}_2(q)$
acting diagonally on $\operatorname {{\mathrm {PSL}}}_2(q)$![]() , with $q = 13$
, with $q = 13$![]() and $q = 17$
and $q = 17$![]() .
.
Many open questions involving this hierarchy of permutation groups remain, and in this paper, we work towards solving Problem 12.4 of [Reference Araújo, Cameron and Steinberg1], the classification of spreading groups (of almost simple or diagonal type). Specifically, we completely resolve the diagonal case, with the aid of the following theorem.
Theorem 1.1 [Reference Bray, Cai, Cameron, Spiga and Zhang8, Theorem 1.5]
Let $G$![]() be a synchronizing primitive group of diagonal type. Then $G$
be a synchronizing primitive group of diagonal type. Then $G$![]() has socle $T \times T$
has socle $T \times T$![]() , where $T$
, where $T$![]() is a non-abelian finite simple group.
is a non-abelian finite simple group.
In addition, it is shown in [Reference Bamberg, Giudici, Lansdown and Royle4, Theorem 2] that the diagonal type group $\operatorname {{\mathrm {PSL}}}_2(q) \times \operatorname {{\mathrm {PSL}}}_2(q)$![]() is non-spreading for every prime power $q$
is non-spreading for every prime power $q$![]() . We generalize this result to all groups of diagonal type, as follows.
. We generalize this result to all groups of diagonal type, as follows.
Theorem 1.2 Each primitive group of diagonal type is non-spreading.
Therefore, the types of spreading groups are precisely the types of finite $2$![]() -transitive groups: almost simple and affine.
-transitive groups: almost simple and affine.
For all but six possible socles $T \times T$![]() , we will prove Theorem 1.2 as a consequence of the following result, which may be of general interest, and which distinguishes six sporadic simple groups from all other non-abelian finite simple groups. For the six remaining socles, we employ elementary character theory.
, we will prove Theorem 1.2 as a consequence of the following result, which may be of general interest, and which distinguishes six sporadic simple groups from all other non-abelian finite simple groups. For the six remaining socles, we employ elementary character theory.
Theorem 1.3 Let $T$![]() be a non-abelian finite simple group. Then the following are equivalent.
be a non-abelian finite simple group. Then the following are equivalent.
(i) There exists a proper subgroup $A$
 of $T$
of $T$ and a proper normal subgroup $B$
and a proper normal subgroup $B$ of $A$
of $A$ such that $A = B(A \cap A^\tau )$
such that $A = B(A \cap A^\tau )$ for all $\tau \in \operatorname {{\mathrm {Aut}}}(T)$
for all $\tau \in \operatorname {{\mathrm {Aut}}}(T)$ .
.(ii) There exists a proper subgroup $A$
 of $T$
of $T$ and a proper normal subgroup $B$
and a proper normal subgroup $B$ of $A$
of $A$ such that $A = B(A \cap A^t)$
such that $A = B(A \cap A^t)$ for all $t \in T$
for all $t \in T$ .
.(iii) The group $T$
 does not lie in the set $\{\mathrm {J}_1,\, \mathrm {M}_{22},\, \mathrm {J}_3,\, \mathrm {McL},\, \mathrm {Th},\, \mathbb {M}\}$
does not lie in the set $\{\mathrm {J}_1,\, \mathrm {M}_{22},\, \mathrm {J}_3,\, \mathrm {McL},\, \mathrm {Th},\, \mathbb {M}\}$ of sporadic groups.
of sporadic groups.
Property (ii) of this theorem implies that, in the transitive action of $T$![]() on the set of right cosets of $A$
on the set of right cosets of $A$![]() , the proper normal subgroup $B$
, the proper normal subgroup $B$![]() of the point stabilizer $A$
of the point stabilizer $A$![]() is supplemented by all corresponding two-point stabilizers. This is a stronger property than all two-point stabilizers being nontrivial, which is equivalent to the action having base size at least three.
is supplemented by all corresponding two-point stabilizers. This is a stronger property than all two-point stabilizers being nontrivial, which is equivalent to the action having base size at least three.
2. Background
In this section, we provide the background on spreading permutation groups, and on primitive groups of diagonal type, that will be necessary to prove Theorems 1.2 and 1.3.
Given a set $\Omega$![]() , a multiset (or set) $J$
, a multiset (or set) $J$![]() of elements of $\Omega$
of elements of $\Omega$![]() and a point $\omega \in \Omega$
and a point $\omega \in \Omega$![]() , we write $\mu _J(\omega )$
, we write $\mu _J(\omega )$![]() to denote the multiplicity of $\omega$
to denote the multiplicity of $\omega$![]() in $J$
in $J$![]() . We say that $J$
. We say that $J$![]() is trivial if either $\mu _J$
is trivial if either $\mu _J$![]() is constant on $\Omega$
is constant on $\Omega$![]() , or there exists a unique point $\omega \in \Omega$
, or there exists a unique point $\omega \in \Omega$![]() such that $\mu _J(\omega ) \ne 0$
such that $\mu _J(\omega ) \ne 0$![]() . Additionally, a sum $J+K$
. Additionally, a sum $J+K$![]() of multisets is defined so that $\mu _{J+K}(\omega ) = \mu _J(\omega ) + \mu _K(\omega )$
of multisets is defined so that $\mu _{J+K}(\omega ) = \mu _J(\omega ) + \mu _K(\omega )$![]() for all $\omega$
for all $\omega$![]() , and similarly for scalar products of multisets. As usual, the cardinality of $J$
, and similarly for scalar products of multisets. As usual, the cardinality of $J$![]() is $|J| := \sum _{\omega \in \Omega } \mu _J(\omega )$
is $|J| := \sum _{\omega \in \Omega } \mu _J(\omega )$![]() .
.
We are now able to define spreading permutation groups.
Definition 2.1 [Reference Araújo, Cameron and Steinberg1, § 5.5]
A transitive permutation group $G$![]() on $\Omega$
on $\Omega$![]() is non-spreading if there exist a nontrivial subset $X$
is non-spreading if there exist a nontrivial subset $X$![]() of $\Omega$
of $\Omega$![]() and a nontrivial multiset $J$
and a nontrivial multiset $J$![]() of elements of $\Omega$
of elements of $\Omega$![]() , such that $|J|$
, such that $|J|$![]() divides $|\Omega |$
divides $|\Omega |$![]() and $\sum _{x \in X^g} \mu _J(x)$
and $\sum _{x \in X^g} \mu _J(x)$![]() is constant for all $g \in G$
is constant for all $g \in G$![]() . Otherwise, $G$
. Otherwise, $G$![]() is spreading.
is spreading.
We shall call a pair $(X,\,J)$![]() satisfying the above properties a witness to $G$
satisfying the above properties a witness to $G$![]() being non-spreading. Recall from § 1 that each imprimitive group is non-spreading. It is also immediate from Definition 2.1 that if $G$
being non-spreading. Recall from § 1 that each imprimitive group is non-spreading. It is also immediate from Definition 2.1 that if $G$![]() is non-spreading, then so is each transitive subgroup of $G$
is non-spreading, then so is each transitive subgroup of $G$![]() . The following theorem provides a useful method for finding a witness to a group being non-spreading.
. The following theorem provides a useful method for finding a witness to a group being non-spreading.
Theorem 2.2 [Reference Bamberg, Giudici, Lansdown and Royle3]
Let $G$![]() be a finite group acting transitively on a finite set $\Omega$
be a finite group acting transitively on a finite set $\Omega$![]() , let $A$
, let $A$![]() be a subgroup of $G$
be a subgroup of $G$![]() , and let $B$
, and let $B$![]() a proper normal subgroup of $A$
a proper normal subgroup of $A$![]() . Additionally, let $\omega _1,\, \ldots,\, \omega _k \in \Omega$
. Additionally, let $\omega _1,\, \ldots,\, \omega _k \in \Omega$![]() with $k\geqslant 2$
with $k\geqslant 2$![]() , such that $\omega _i^B \neq \omega _j^B$
, such that $\omega _i^B \neq \omega _j^B$![]() for
$i \neq j$
for
$i \neq j$![]() , and
, and
Finally, let $\Delta := \{Y \in X^G \mid Y \cap \omega _1^A \neq \varnothing \}$![]() for some non-empty $X \subsetneq \Omega$
for some non-empty $X \subsetneq \Omega$![]() . If $B$
. If $B$![]() is transitive on each $A$
is transitive on each $A$![]() -orbit of $\Delta$
-orbit of $\Delta$![]() , then $(X,\,\Omega + k\omega _1^B - \omega _1^A)$
, then $(X,\,\Omega + k\omega _1^B - \omega _1^A)$![]() is a witness to $G$
is a witness to $G$![]() being non-spreading.
being non-spreading.
Now, let $T$![]() be a non-abelian finite simple group. In the remainder of this section, we shall consider the primitive groups of diagonal type with socle $T \times T$
be a non-abelian finite simple group. In the remainder of this section, we shall consider the primitive groups of diagonal type with socle $T \times T$![]() . To define these groups, let $T \times T$
. To define these groups, let $T \times T$![]() act on the set $\Omega :=T$
act on the set $\Omega :=T$![]() by $x^{(t_1,t_2)}:=t_1^{-1}xt_2$
by $x^{(t_1,t_2)}:=t_1^{-1}xt_2$![]() . In addition, let $\rho _1:T\times T \to \operatorname {{\mathrm {Sym}}}(\Omega )$
. In addition, let $\rho _1:T\times T \to \operatorname {{\mathrm {Sym}}}(\Omega )$![]() be the corresponding permutation representation, and let $\rho _2:\operatorname {{\mathrm {Aut}}}(T) \to \operatorname {{\mathrm {Sym}}}(\Omega )$
be the corresponding permutation representation, and let $\rho _2:\operatorname {{\mathrm {Aut}}}(T) \to \operatorname {{\mathrm {Sym}}}(\Omega )$![]() be the natural permutation representation of $\operatorname {{\mathrm {Aut}}}(T)$
be the natural permutation representation of $\operatorname {{\mathrm {Aut}}}(T)$![]() on $\Omega$
on $\Omega$![]() . Then $\rho _2(\operatorname {{\mathrm {Inn}}}(T))=\rho _1(\{(t,\,t)\mid t\in T\})$
. Then $\rho _2(\operatorname {{\mathrm {Inn}}}(T))=\rho _1(\{(t,\,t)\mid t\in T\})$![]() . Finally, let $\sigma \in \operatorname {{\mathrm {Sym}}}(\Omega )$
. Finally, let $\sigma \in \operatorname {{\mathrm {Sym}}}(\Omega )$![]() such that $x^\sigma =x^{-1}$
such that $x^\sigma =x^{-1}$![]() for all $x\in T$
for all $x\in T$![]() . Define $W(T):=\langle \rho _1(T\times T),\,\rho _2(\operatorname {{\mathrm {Aut}}}(T)),\,\sigma \rangle \leqslant \operatorname {{\mathrm {Sym}}}(\Omega )$
. Define $W(T):=\langle \rho _1(T\times T),\,\rho _2(\operatorname {{\mathrm {Aut}}}(T)),\,\sigma \rangle \leqslant \operatorname {{\mathrm {Sym}}}(\Omega )$![]() , and note that $W(T)\cong (T\times T).(\operatorname {{\mathrm {Out}}}(T) \times C_2)$
, and note that $W(T)\cong (T\times T).(\operatorname {{\mathrm {Out}}}(T) \times C_2)$![]() . The groups of diagonal type with socle $T \times T$
. The groups of diagonal type with socle $T \times T$![]() are precisely the subgroups of $W(T)$
are precisely the subgroups of $W(T)$![]() containing $\rho _1(T\times T)$
containing $\rho _1(T\times T)$![]() (see, for example, [Reference Liebeck, Praeger and Saxl17, § 1]). We will often drop the use of $\rho _1$
(see, for example, [Reference Liebeck, Praeger and Saxl17, § 1]). We will often drop the use of $\rho _1$![]() and $\rho _2$
and $\rho _2$![]() , and allow elements (and subgroups) of $T\times T$
, and allow elements (and subgroups) of $T\times T$![]() and $\operatorname {{\mathrm {Aut}}}(T)$
and $\operatorname {{\mathrm {Aut}}}(T)$![]() to denote permutations (and subgroups) of $\operatorname {{\mathrm {Sym}}}(\Omega )$
to denote permutations (and subgroups) of $\operatorname {{\mathrm {Sym}}}(\Omega )$![]() .
.
In order to derive Theorem 1.2 from Theorem 1.3 (for most non-abelian finite simple groups), we require the following corollary of Theorem 2.2. Throughout the remainder of this section, we will use the elementary fact that if $G$![]() is a transitive permutation group on a set $\Sigma$
is a transitive permutation group on a set $\Sigma$![]() and $H\leqslant G$
and $H\leqslant G$![]() , then $H$
, then $H$![]() acts transitively on $\Sigma$
acts transitively on $\Sigma$![]() if and only if $G=HG_\alpha$
if and only if $G=HG_\alpha$![]() for each $\alpha \in \Sigma$
for each $\alpha \in \Sigma$![]() .
.
Corollary 2.3 Let $T$![]() be a non-abelian finite simple group, and suppose that there exists a proper subgroup $A$
be a non-abelian finite simple group, and suppose that there exists a proper subgroup $A$![]() of $T$
of $T$![]() and a proper normal subgroup $B$
and a proper normal subgroup $B$![]() of $A$
of $A$![]() such that $A = B(A \cap A^\tau )$
such that $A = B(A \cap A^\tau )$![]() for all $\tau \in \operatorname {{\mathrm {Aut}}}(T)$
for all $\tau \in \operatorname {{\mathrm {Aut}}}(T)$![]() . Then $(A,\,\Omega +|A:B|B-A)$
. Then $(A,\,\Omega +|A:B|B-A)$![]() is a witness to the diagonal type group $W(T)$
is a witness to the diagonal type group $W(T)$![]() being non-spreading in its action on $\Omega = T$
being non-spreading in its action on $\Omega = T$![]() .
.
Proof. Let $G:=W(T)$![]() , $M:=\rho _1(1\times T)$
, $M:=\rho _1(1\times T)$![]() , $\omega _1:=1_T$
, $\omega _1:=1_T$![]() , and $D:=G_{\omega _1} = \langle \rho _2(\operatorname {{\mathrm {Aut}}}(T)), \sigma \rangle \cong \operatorname {{\mathrm {Aut}}}(T)\times C_2$
, and $D:=G_{\omega _1} = \langle \rho _2(\operatorname {{\mathrm {Aut}}}(T)), \sigma \rangle \cong \operatorname {{\mathrm {Aut}}}(T)\times C_2$![]() . Note that $G=DM$
. Note that $G=DM$![]() , as $M$
, as $M$![]() acts transitively on $\Omega$
acts transitively on $\Omega$![]() . Let $X:=A\subsetneq \Omega$
. Let $X:=A\subsetneq \Omega$![]() . Then $\omega _1^{1 \times B} = B < A = \omega _1^{1 \times A}$
. Then $\omega _1^{1 \times B} = B < A = \omega _1^{1 \times A}$![]() , and $X^{G}=X^{DM}=\{A^\tau t\mid \tau \in \operatorname {{\mathrm {Aut}}}(T), t\in T\}$
, and $X^{G}=X^{DM}=\{A^\tau t\mid \tau \in \operatorname {{\mathrm {Aut}}}(T), t\in T\}$![]() . Next, define $\Delta :={\{Y\in X^G\mid Y\cap \omega _1^{1\times A}\neq \varnothing \}}$
. Next, define $\Delta :={\{Y\in X^G\mid Y\cap \omega _1^{1\times A}\neq \varnothing \}}$![]() , and observe that $\Delta = \{A^\tau a\mid \tau \in \operatorname {{\mathrm {Aut}}}(T),\,a\in A\}$
, and observe that $\Delta = \{A^\tau a\mid \tau \in \operatorname {{\mathrm {Aut}}}(T),\,a\in A\}$![]() . Thus the orbits of $1 \times A$
. Thus the orbits of $1 \times A$![]() on $\Delta$
on $\Delta$![]() are $\Delta _\tau =\{A^\tau a\mid a\in A\}$
are $\Delta _\tau =\{A^\tau a\mid a\in A\}$![]() for each $\tau \in \operatorname {{\mathrm {Aut}}}(T)$
for each $\tau \in \operatorname {{\mathrm {Aut}}}(T)$![]() . Additionally, the stabilizer in $1\times A$
. Additionally, the stabilizer in $1\times A$![]() of $A^\tau \in \Delta _\tau$
of $A^\tau \in \Delta _\tau$![]() is $1\times (A\cap A^\tau )$
is $1\times (A\cap A^\tau )$![]() . As $A=B(A\cap A^\tau )$
. As $A=B(A\cap A^\tau )$![]() , we observe that $1\times B$
, we observe that $1\times B$![]() is transitive on $\Delta _\tau$
is transitive on $\Delta _\tau$![]() . The result now follows from Theorem 2.2, applied to the groups $G$
. The result now follows from Theorem 2.2, applied to the groups $G$![]() , $1 \times A$
, $1 \times A$![]() and $1 \times B$
and $1 \times B$![]() .
.
Our next lemma translates Property (i) of Theorem 1.3 into the language of coset actions.
Lemma 2.4 Let $T$![]() be a non-abelian finite simple group, $R \in \{T,\,\operatorname {{\mathrm {Aut}}}(T)\}$
be a non-abelian finite simple group, $R \in \{T,\,\operatorname {{\mathrm {Aut}}}(T)\}$![]() , and $A$
, and $A$![]() a proper subgroup of $T$
a proper subgroup of $T$![]() . Suppose also that $A$
. Suppose also that $A$![]() has a proper normal subgroup $B$
has a proper normal subgroup $B$![]() that acts transitively on each orbit of $A$
that acts transitively on each orbit of $A$![]() in its action on the right cosets of $A$
in its action on the right cosets of $A$![]() in $R$
in $R$![]() . If $R = \operatorname {{\mathrm {Aut}}}(T)$
. If $R = \operatorname {{\mathrm {Aut}}}(T)$![]() , or if all $\operatorname {{\mathrm {Aut}}}(T)$
, or if all $\operatorname {{\mathrm {Aut}}}(T)$![]() -conjugates of $A$
-conjugates of $A$![]() are conjugate in $T$
are conjugate in $T$![]() , then $A = B(A \cap A^\tau )$
, then $A = B(A \cap A^\tau )$![]() for all $\tau \in \operatorname {{\mathrm {Aut}}}(T)$
for all $\tau \in \operatorname {{\mathrm {Aut}}}(T)$![]() .
.
Proof. Let $\Sigma$![]() be the set of right cosets of $A$
be the set of right cosets of $A$![]() in $R$
in $R$![]() . Then the point stabilizers in the action of $A$
. Then the point stabilizers in the action of $A$![]() on $\Sigma$
on $\Sigma$![]() are precisely the subgroups $A \cap A^t$
are precisely the subgroups $A \cap A^t$![]() with $t \in R$
with $t \in R$![]() . As $B$
. As $B$![]() is transitive on each orbit in this action, it follows that $A = B(A \cap A^t)$
is transitive on each orbit in this action, it follows that $A = B(A \cap A^t)$![]() for all $t \in R$
for all $t \in R$![]() . Hence we are done if $R = \operatorname {{\mathrm {Aut}}}(T)$
. Hence we are done if $R = \operatorname {{\mathrm {Aut}}}(T)$![]() . Assume therefore that all $\operatorname {{\mathrm {Aut}}}(T)$
. Assume therefore that all $\operatorname {{\mathrm {Aut}}}(T)$![]() -conjugates of $A$
-conjugates of $A$![]() are conjugate in $T$
are conjugate in $T$![]() . Then for each $\tau \in \operatorname {{\mathrm {Aut}}}(T)$
. Then for each $\tau \in \operatorname {{\mathrm {Aut}}}(T)$![]() , there exists $t \in T$
, there exists $t \in T$![]() such that $A^\tau = A^t$
such that $A^\tau = A^t$![]() , and so $B(A \cap A^\tau ) = B(A \cap A^t) = A$
, and so $B(A \cap A^\tau ) = B(A \cap A^t) = A$![]() .
.
In the case where $T$![]() is one of the six sporadic groups listed in Property (iii) of Theorem 1.3, we will show that $W(T)$
is one of the six sporadic groups listed in Property (iii) of Theorem 1.3, we will show that $W(T)$![]() is non-spreading using the following lemma, which involves elementary character theory. The multiset in the witness here is similar to that of Theorem 2.2.
is non-spreading using the following lemma, which involves elementary character theory. The multiset in the witness here is similar to that of Theorem 2.2.
Lemma 2.5 Let $T$![]() be a non-abelian finite simple group, and let $\mathrm {Irr}(T)$
be a non-abelian finite simple group, and let $\mathrm {Irr}(T)$![]() be the set of irreducible complex characters of $T$
be the set of irreducible complex characters of $T$![]() . Suppose also that there exist pairwise non-conjugate elements $r$
. Suppose also that there exist pairwise non-conjugate elements $r$![]() , $s_1$
, $s_1$![]() and $s_2$
and $s_2$![]() of $T$
of $T$![]() , such that:
, such that:
(i) $|s_1^T| = |s_2^T|$
 ; and
; and(ii) $\chi (r^\tau ) = 0$
 for all $\tau \in \operatorname {{\mathrm {Aut}}}(T)$
for all $\tau \in \operatorname {{\mathrm {Aut}}}(T)$ and all $\chi \in \mathrm {Irr}(T)$
and all $\chi \in \mathrm {Irr}(T)$ with $\chi (s_1) \ne \chi (s_2)$
with $\chi (s_1) \ne \chi (s_2)$ .
.
Then $(r^T,\,\Omega +s_1^T-s_2^T)$![]() is a witness to the diagonal type group $W(T)$
is a witness to the diagonal type group $W(T)$![]() being non-spreading in its action on $\Omega = T$
being non-spreading in its action on $\Omega = T$![]() .
.
Proof. The set $X:=r^T$![]() and the multiset $J:=\Omega +s_1^T-s_2^T$
and the multiset $J:=\Omega +s_1^T-s_2^T$![]() are clearly nontrivial, and (i) implies that $|J| = |\Omega |$
are clearly nontrivial, and (i) implies that $|J| = |\Omega |$![]() . Thus by Definition 2.1, it remains to prove that $\sum _{x \in X^g} \mu _J(x)$
. Thus by Definition 2.1, it remains to prove that $\sum _{x \in X^g} \mu _J(x)$![]() is constant for all $g \in G:=W(T)$
is constant for all $g \in G:=W(T)$![]() . In fact, we will show that $|X^g \cap s_1^T| = |X^g \cap s_2^T|$
. In fact, we will show that $|X^g \cap s_1^T| = |X^g \cap s_2^T|$![]() for all $g$
for all $g$![]() , and it will follow immediately that $\sum _{x \in X^g} \mu _J(x) = |X|$
, and it will follow immediately that $\sum _{x \in X^g} \mu _J(x) = |X|$![]() for all $g$
for all $g$![]() .
.
As above, $G_{1_T} = \langle \rho _2(\operatorname {{\mathrm {Aut}}}(T)),\,\sigma \rangle$![]() , and the transitivity of $M:=\rho _1(1 \times T)$
, and the transitivity of $M:=\rho _1(1 \times T)$![]() on $\Omega$
on $\Omega$![]() implies that $G = G_{1_T}M$
implies that $G = G_{1_T}M$![]() . Hence for each $g \in G$
. Hence for each $g \in G$![]() , there exist $\tau \in \operatorname {{\mathrm {Aut}}}(T)$
, there exist $\tau \in \operatorname {{\mathrm {Aut}}}(T)$![]() , $\varepsilon = \pm 1$
, $\varepsilon = \pm 1$![]() and $t \in T$
and $t \in T$![]() such that $X^g = ((r^\tau )^{\varepsilon })^Tt$
such that $X^g = ((r^\tau )^{\varepsilon })^Tt$![]() . Letting $m:=(r^\tau )^\varepsilon$
. Letting $m:=(r^\tau )^\varepsilon$![]() , $i \in \{1,\,2\}$
, $i \in \{1,\,2\}$![]() and $h \in s_i^T$
and $h \in s_i^T$![]() , we observe from [Reference Isaacs16, Problem 3.9] that the set $\{(x,\,y) \mid x \in m^T,\, y \in t^T,\, xy = h\}$
, we observe from [Reference Isaacs16, Problem 3.9] that the set $\{(x,\,y) \mid x \in m^T,\, y \in t^T,\, xy = h\}$![]() has size
has size

where $\overline {\chi (s_i)}$![]() is the complex conjugate of $\chi (s_i)$
is the complex conjugate of $\chi (s_i)$![]() . Since $a_{g,i}$
. Since $a_{g,i}$![]() is constant for all $h \in s_i^T$
is constant for all $h \in s_i^T$![]() , and $|m^Tt^u \cap s_i^T|$
, and $|m^Tt^u \cap s_i^T|$![]() is constant for all $u \in T$
is constant for all $u \in T$![]() , it follows that $|X^g \cap s_i^T| = a_{g,i}|s_i^T|/|t^T|$
, it follows that $|X^g \cap s_i^T| = a_{g,i}|s_i^T|/|t^T|$![]() . As $\chi ((r^\tau )^{-1})\,{=}\, \overline {\chi (r^\tau )}$
. As $\chi ((r^\tau )^{-1})\,{=}\, \overline {\chi (r^\tau )}$![]() for each character $\chi$
for each character $\chi$![]() of $T$
of $T$![]() , (i) and (ii) yield $|X^g \,{\cap}\, s_1^T| \,{=}\, |X^g \,{\cap}\, s_2^T|$
, (i) and (ii) yield $|X^g \,{\cap}\, s_1^T| \,{=}\, |X^g \,{\cap}\, s_2^T|$![]() for all $g \in G$
for all $g \in G$![]() , as required.
, as required.
Remark 2.6 For many small non-abelian finite simple groups $T$![]() , it is possible to choose an element $r \in T$
, it is possible to choose an element $r \in T$![]() satisfying Property (ii) of Lemma 2.5 when $s_1$
satisfying Property (ii) of Lemma 2.5 when $s_1$![]() and $s_2$
and $s_2$![]() are non-conjugate elements of $T$
are non-conjugate elements of $T$![]() such that $s_1^{-1} = s_2$
such that $s_1^{-1} = s_2$![]() , or more generally, such that $\langle s_1 \rangle = \langle s_2 \rangle$
, or more generally, such that $\langle s_1 \rangle = \langle s_2 \rangle$![]() . The non-abelian finite simple groups with all elements conjugate to their inverses are classified in [Reference Tiep and Zalesski18, Theorem 1.2], and [Reference Feit and Seitz14, Corollary B.1] shows that $\operatorname {{\mathrm {PSp}}}_6(2)$
. The non-abelian finite simple groups with all elements conjugate to their inverses are classified in [Reference Tiep and Zalesski18, Theorem 1.2], and [Reference Feit and Seitz14, Corollary B.1] shows that $\operatorname {{\mathrm {PSp}}}_6(2)$![]() and $\operatorname {{\mathrm {P}\Omega }}^+_8(2)$
and $\operatorname {{\mathrm {P}\Omega }}^+_8(2)$![]() are the only such groups where $u,\,v \in T$
are the only such groups where $u,\,v \in T$![]() are conjugate whenever $\langle u \rangle = \langle v \rangle$
are conjugate whenever $\langle u \rangle = \langle v \rangle$![]() . Denoting conjugacy classes as in the Atlas [Reference Conway, Curtis, Norton, Parker and Wilson13], we observe by inspecting the Atlas character tables of these two groups that we can choose $r \in \mathrm {7A}$
. Denoting conjugacy classes as in the Atlas [Reference Conway, Curtis, Norton, Parker and Wilson13], we observe by inspecting the Atlas character tables of these two groups that we can choose $r \in \mathrm {7A}$![]() , $s_1 \in \mathrm {6A}$
, $s_1 \in \mathrm {6A}$![]() and $s_2 \in \mathrm {6B}$
and $s_2 \in \mathrm {6B}$![]() when $T = \operatorname {{\mathrm {PSp}}}_6(2)$
when $T = \operatorname {{\mathrm {PSp}}}_6(2)$![]() , and $r \in \mathrm {7A}$
, and $r \in \mathrm {7A}$![]() , $s_1 \in \mathrm {15A}$
, $s_1 \in \mathrm {15A}$![]() and $s_2 \in \mathrm {15B}$
and $s_2 \in \mathrm {15B}$![]() when $T = \operatorname {{\mathrm {P}\Omega }}^+_8(2)$
when $T = \operatorname {{\mathrm {P}\Omega }}^+_8(2)$![]() . We leave open the problem of determining which non-abelian finite simple groups, if any, do not contain pairwise non-conjugate elements $r$
. We leave open the problem of determining which non-abelian finite simple groups, if any, do not contain pairwise non-conjugate elements $r$![]() , $s_1$
, $s_1$![]() and $s_2$
and $s_2$![]() satisfying Properties (i) and (ii) of Lemma 2.5.
satisfying Properties (i) and (ii) of Lemma 2.5.
3. Non-abelian finite simple groups and groups of diagonal type
In this section, we show that Property (i) of Theorem 1.3 holds for all non-abelian finite simple groups other than the sporadic groups $\mathrm {J}_1$![]() , $\mathrm {M}_{22}$
, $\mathrm {M}_{22}$![]() , $\mathrm {J}_3$
, $\mathrm {J}_3$![]() , $\mathrm {McL}$
, $\mathrm {McL}$![]() , $\mathrm {Th}$
, $\mathrm {Th}$![]() and $\mathbb {M}$
and $\mathbb {M}$![]() , and then prove Theorems 1.3 and 1.2. Note that we address the Tits group ${}^2F_{4}(2)'$
, and then prove Theorems 1.3 and 1.2. Note that we address the Tits group ${}^2F_{4}(2)'$![]() together with the sporadic groups. Throughout, we use Atlas [Reference Conway, Curtis, Norton, Parker and Wilson13] notation for the structures of groups.
together with the sporadic groups. Throughout, we use Atlas [Reference Conway, Curtis, Norton, Parker and Wilson13] notation for the structures of groups.
We first consider the finite simple groups of Lie type, beginning with the Chevalley groups (i.e. the untwisted groups of Lie type) defined over fields of size $q \ge 3$![]() , then the twisted groups of Lie type, and finally the Chevalley groups with $q = 2$
, then the twisted groups of Lie type, and finally the Chevalley groups with $q = 2$![]() .
.
Proposition 3.1 Let $T$![]() be a finite simple Chevalley group $X_\ell (q)$
be a finite simple Chevalley group $X_\ell (q)$![]() , with $q \ge 3$
, with $q \ge 3$![]() . Then Property (i) of Theorem 1.3 holds for $T$
. Then Property (i) of Theorem 1.3 holds for $T$![]() .
.
Proof. Let $p$![]() be the prime dividing $q$
be the prime dividing $q$![]() , and let $U$
, and let $U$![]() be a Sylow $p$
be a Sylow $p$![]() -subgroup of $T$
-subgroup of $T$![]() . Then $T$
. Then $T$![]() contains a subgroup $N$
contains a subgroup $N$![]() such that $A:=N_T(U)$
such that $A:=N_T(U)$![]() and $N$
and $N$![]() form a $(B,\,N)$
form a $(B,\,N)$![]() -pair, and the normal subgroup $H:=A \cap N$
-pair, and the normal subgroup $H:=A \cap N$![]() of $N$
of $N$![]() complements $U$
complements $U$![]() in $A$
in $A$![]() (see [Reference Carter12, Ch. 7.2–9.4]). Since $q \ge 3$
(see [Reference Carter12, Ch. 7.2–9.4]). Since $q \ge 3$![]() (and since $T$
(and since $T$![]() is not the soluble group $A_1(3) = \operatorname {{\mathrm {PSL}}}_2(3)$
is not the soluble group $A_1(3) = \operatorname {{\mathrm {PSL}}}_2(3)$![]() ), we observe from [Reference Carter12, pp. 121–122] that $|H| > 1$
), we observe from [Reference Carter12, pp. 121–122] that $|H| > 1$![]() , and so $U$
, and so $U$![]() is a proper subgroup of $A$
is a proper subgroup of $A$![]() . Furthermore, as $A$
. Furthermore, as $A$![]() is the normalizer in $T$
is the normalizer in $T$![]() of the Sylow subgroup $U$
of the Sylow subgroup $U$![]() , all $\operatorname {{\mathrm {Aut}}}(T)$
, all $\operatorname {{\mathrm {Aut}}}(T)$![]() -conjugates of $A$
-conjugates of $A$![]() are conjugate in $T$
are conjugate in $T$![]() .
.
By Lemma 2.4, it suffices to show that $A$![]() and $U$
and $U$![]() have the same orbits in the action of $T$
have the same orbits in the action of $T$![]() on the set of right cosets of $A$
on the set of right cosets of $A$![]() . For each element $w$
. For each element $w$![]() of the Weyl group $W:=N/H$
of the Weyl group $W:=N/H$![]() , fix a preimage $n_w \in N$
, fix a preimage $n_w \in N$![]() of $w$
of $w$![]() under the natural homomorphism from $N$
under the natural homomorphism from $N$![]() to $W$
to $W$![]() . In addition, let $x$
. In addition, let $x$![]() and $y$
and $y$![]() be elements of $T$
be elements of $T$![]() so that $Ax$
so that $Ax$![]() and $Ay$
and $Ay$![]() lie in a common $A$
lie in a common $A$![]() -orbit. Then the double cosets $AxA$
-orbit. Then the double cosets $AxA$![]() and $AyA$
and $AyA$![]() are equal. By [Reference Carter12, Theorem 8.4.3], there exist $a_x,\,a_y \in A$
are equal. By [Reference Carter12, Theorem 8.4.3], there exist $a_x,\,a_y \in A$![]() , $w_x,\,w_y \in W$
, $w_x,\,w_y \in W$![]() and $u_x,\,u_y \in U < A$
and $u_x,\,u_y \in U < A$![]() such that $x = a_x n_{w_x} u_x$
such that $x = a_x n_{w_x} u_x$![]() and $y = a_y n_{w_y} u_y$
and $y = a_y n_{w_y} u_y$![]() . It follows that $A n_{w_x} A = A n_{w_y} A$
. It follows that $A n_{w_x} A = A n_{w_y} A$![]() . As $A$
. As $A$![]() and $N$
and $N$![]() form a $(B,\,N)$
form a $(B,\,N)$![]() -pair, [Reference Carter12, Proposition 8.2.3] yields $n_{w_x} = n_{w_y}$
-pair, [Reference Carter12, Proposition 8.2.3] yields $n_{w_x} = n_{w_y}$![]() . Thus $AxU = An_{w_x}U = An_{w_y}U = AyU$
. Thus $AxU = An_{w_x}U = An_{w_y}U = AyU$![]() , i.e. $Ax$
, i.e. $Ax$![]() and $Ay$
and $Ay$![]() lie in the same $U$
lie in the same $U$![]() -orbit, as required.
-orbit, as required.
Proposition 3.2 Let $T$![]() be a finite simple twisted group of Lie type ${}^tX_\ell (q)$
be a finite simple twisted group of Lie type ${}^tX_\ell (q)$![]() . Then Property (i) of Theorem 1.3 holds for $T$
. Then Property (i) of Theorem 1.3 holds for $T$![]() .
.
Proof. Note that $T \not \cong {}^2F_4(2)'$![]() . As above, let $p$
. As above, let $p$![]() be the prime dividing $q$
be the prime dividing $q$![]() , and let $U$
, and let $U$![]() be a Sylow $p$
be a Sylow $p$![]() -subgroup of $T$
-subgroup of $T$![]() . By [Reference Carter12, Ch. 13–14], $T$
. By [Reference Carter12, Ch. 13–14], $T$![]() contains subgroups $N$
contains subgroups $N$![]() , $H$
, $H$![]() and $W$
and $W$![]() analogous to those in the proof of Proposition 3.1, so that $A:=U \mkern 3mu{:}\mkern 3mu H$
analogous to those in the proof of Proposition 3.1, so that $A:=U \mkern 3mu{:}\mkern 3mu H$![]() and $N$
and $N$![]() form a $(B,\,N)$
form a $(B,\,N)$![]() -pair, and $W = N/H$
-pair, and $W = N/H$![]() . Furthermore, $H$
. Furthermore, $H$![]() is nontrivial for all $q$
is nontrivial for all $q$![]() , as $T$
, as $T$![]() is not isomorphic to ${}^2A_2(2) = \operatorname {{\mathrm {PSU}}}_3(2)$
is not isomorphic to ${}^2A_2(2) = \operatorname {{\mathrm {PSU}}}_3(2)$![]() , ${}^2B_2(2) = \mathrm {Sz}(2)$
, ${}^2B_2(2) = \mathrm {Sz}(2)$![]() or ${}^2F_4(2)$
or ${}^2F_4(2)$![]() . Although [Reference Carter12] directly states only that $A \le N_T(U)$
. Although [Reference Carter12] directly states only that $A \le N_T(U)$![]() , we can show that $A = N_T(U)$
, we can show that $A = N_T(U)$![]() . Indeed, if this were not the case, then some preimage $n_w \in N$
. Indeed, if this were not the case, then some preimage $n_w \in N$![]() of a fundamental reflection $w \in W$
of a fundamental reflection $w \in W$![]() would normalise $U$
would normalise $U$![]() (see [Reference Carter12, Proposition 8.2.2 & Theorem 8.3.2]). However, we deduce from Proposition 13.6.1 and the proof of Theorem 13.5.4 in [Reference Carter12] that no such $w$
(see [Reference Carter12, Proposition 8.2.2 & Theorem 8.3.2]). However, we deduce from Proposition 13.6.1 and the proof of Theorem 13.5.4 in [Reference Carter12] that no such $w$![]() exists, and so $A = N_T(U)$
exists, and so $A = N_T(U)$![]() . We now proceed exactly as in the proof of Proposition 3.1, this time using Proposition 13.5.3 of [Reference Carter12] instead of Theorem 8.4.3.
. We now proceed exactly as in the proof of Proposition 3.1, this time using Proposition 13.5.3 of [Reference Carter12] instead of Theorem 8.4.3.
Proposition 3.3 Let $T$![]() be a finite simple Chevalley group $X_\ell (2)$
be a finite simple Chevalley group $X_\ell (2)$![]() . Then Property (i) of Theorem 1.3 holds for $T$
. Then Property (i) of Theorem 1.3 holds for $T$![]() .
.
Proof. Since $A_2(2) = \operatorname {{\mathrm {PSL}}}_3(2) \cong \operatorname {{\mathrm {PSL}}}_2(7)$![]() is addressed by Proposition 3.1, and since the remaining groups $X_\ell (2)$
is addressed by Proposition 3.1, and since the remaining groups $X_\ell (2)$![]() with $\ell \le 2$
with $\ell \le 2$![]() are not simple, we shall assume that $\ell \ge 3$
are not simple, we shall assume that $\ell \ge 3$![]() . Let $\Phi \subseteq \mathbb {R}^\ell$
. Let $\Phi \subseteq \mathbb {R}^\ell$![]() be a root system for $T$
be a root system for $T$![]() , with $\Phi ^+ \subseteq \Phi$
, with $\Phi ^+ \subseteq \Phi$![]() a system of positive roots and $\Pi \subseteq \Phi ^+$
a system of positive roots and $\Pi \subseteq \Phi ^+$![]() a system of simple roots (see, for example, [Reference Carter12, Ch. 2]). Then $\Phi$
a system of simple roots (see, for example, [Reference Carter12, Ch. 2]). Then $\Phi$![]() is the disjoint union of $\Phi ^+$
is the disjoint union of $\Phi ^+$![]() and $-\Phi ^+$
and $-\Phi ^+$![]() , and each node in the Dynkin diagram $D$
, and each node in the Dynkin diagram $D$![]() corresponding to $T$
corresponding to $T$![]() is associated with a unique root in $\Pi$
is associated with a unique root in $\Pi$![]() (and vice versa). Hence each diagram automorphism of $D$
(and vice versa). Hence each diagram automorphism of $D$![]() induces a permutation of $\Pi$
induces a permutation of $\Pi$![]() . Let $r$
. Let $r$![]() and $s$
and $s$![]() be the simple roots associated with a leaf in $D$
be the simple roots associated with a leaf in $D$![]() and the adjacent node, respectively. Additionally, let $S$
and the adjacent node, respectively. Additionally, let $S$![]() be the closure of the set $\{s\}$
be the closure of the set $\{s\}$![]() under the group of diagram automorphisms of $D$
under the group of diagram automorphisms of $D$![]() , so that $|S| \in \{1,\,2\}$
, so that $|S| \in \{1,\,2\}$![]() .
.
Next, let $U$![]() , $N$
, $N$![]() and $W$
and $W$![]() be as in the proof of Proposition 3.1. In this case, the group $H$
be as in the proof of Proposition 3.1. In this case, the group $H$![]() from that proof is trivial, and so $N_T(U) = U$
from that proof is trivial, and so $N_T(U) = U$![]() and $W \cong N$
and $W \cong N$![]() . By [Reference Carter12, Proposition 2.1.8, p. 68 & p. 93], $T$
. By [Reference Carter12, Proposition 2.1.8, p. 68 & p. 93], $T$![]() is generated by a set $\{x_u \mid u \in \Phi \}$
is generated by a set $\{x_u \mid u \in \Phi \}$![]() of involutions ($x_u$
of involutions ($x_u$![]() is written as $x_u(1)$
is written as $x_u(1)$![]() in [Reference Carter12]), with $U = \langle x_u \mid u \in \Phi ^+ \rangle$
in [Reference Carter12]), with $U = \langle x_u \mid u \in \Phi ^+ \rangle$![]() , and $N$
, and $N$![]() is generated by a set $\{n_v \mid v \in \Pi \}$
is generated by a set $\{n_v \mid v \in \Pi \}$![]() of involutions. Let $A := \langle U,\, n_v \mid v \in \Pi \setminus S\rangle$
of involutions. Let $A := \langle U,\, n_v \mid v \in \Pi \setminus S\rangle$![]() be the parabolic subgroup of $T$
be the parabolic subgroup of $T$![]() corresponding to the subset $\Pi \setminus S$
corresponding to the subset $\Pi \setminus S$![]() of $\Pi$
of $\Pi$![]() . Then by [Reference Carter12, Ch. 8.5] and the well-known structure of parabolic subgroups of Chevalley groups, $A$
. Then by [Reference Carter12, Ch. 8.5] and the well-known structure of parabolic subgroups of Chevalley groups, $A$![]() has shape $[2^m]:(L_{\{r\}} \times L_{\Pi \setminus (\{r\} \cup S)})$
has shape $[2^m]:(L_{\{r\}} \times L_{\Pi \setminus (\{r\} \cup S)})$![]() for some positive integer $m$
for some positive integer $m$![]() , where $L_{\{r\}} \cong A_1(2) \cong S_3$
, where $L_{\{r\}} \cong A_1(2) \cong S_3$![]() and $L_{\Pi \setminus (\{r\} \cup S)}$
and $L_{\Pi \setminus (\{r\} \cup S)}$![]() are Levi subgroups. Since $q = 2$
are Levi subgroups. Since $q = 2$![]() , all automorphisms of $T$
, all automorphisms of $T$![]() are products of inner and graph automorphisms. Moreover, $\Pi \setminus S$
are products of inner and graph automorphisms. Moreover, $\Pi \setminus S$![]() is fixed setwise by all diagram automorphisms of $D$
is fixed setwise by all diagram automorphisms of $D$![]() , which correspond to the graph automorphisms of $T$
, which correspond to the graph automorphisms of $T$![]() , and so all $\operatorname {{\mathrm {Aut}}}(T)$
, and so all $\operatorname {{\mathrm {Aut}}}(T)$![]() -conjugates of $A$
-conjugates of $A$![]() are conjugate in $T$
are conjugate in $T$![]() . In addition, $A$
. In addition, $A$![]() contains an index two subgroup $B$
contains an index two subgroup $B$![]() of shape $[2^m]:(F \times L_{\Pi \setminus (\{r\} \cup S)})$
of shape $[2^m]:(F \times L_{\Pi \setminus (\{r\} \cup S)})$![]() , where $F := L_{\{r\}}' \cong C_3$
, where $F := L_{\{r\}}' \cong C_3$![]() . We will show that $AtA = AtB$
. We will show that $AtA = AtB$![]() for all $t \in T$
for all $t \in T$![]() , and the result will follow from Lemma 2.4.
, and the result will follow from Lemma 2.4.
Since $N_T(U) = U \le A$![]() , we deduce as in the proof of Proposition 3.1 that, for each $t \in T$
, we deduce as in the proof of Proposition 3.1 that, for each $t \in T$![]() , there exists $n \in N$
, there exists $n \in N$![]() such that $AtA = AnA$
such that $AtA = AnA$![]() . Thus it suffices to prove that $AnA = AnB$
. Thus it suffices to prove that $AnA = AnB$![]() for all $n \in N$
for all $n \in N$![]() (it will immediately follow that $AnB = AtB$
(it will immediately follow that $AnB = AtB$![]() for the corresponding $t \in T$
for the corresponding $t \in T$![]() ). We also observe using [Reference Carter12, Ch. 8.5] (and the fact that $F$
). We also observe using [Reference Carter12, Ch. 8.5] (and the fact that $F$![]() has index two in $L_{\{r\}}$
has index two in $L_{\{r\}}$![]() ) that $x_r \in A \setminus B$
) that $x_r \in A \setminus B$![]() and $x_{-r} x_r \in B$
and $x_{-r} x_r \in B$![]() . The former containment implies that $AnA = AnB \cup Anx_rB$
. The former containment implies that $AnA = AnB \cup Anx_rB$![]() . To complete the proof, we will show that $Anx_rB = AnB$
. To complete the proof, we will show that $Anx_rB = AnB$![]() .
.
The Weyl group $W$![]() acts linearly on $\mathbb {R}^\ell$
acts linearly on $\mathbb {R}^\ell$![]() and fixes $\Phi$
and fixes $\Phi$![]() . Let $w$
. Let $w$![]() be the element of $W$
be the element of $W$![]() corresponding to $n$
corresponding to $n$![]() . By [Reference Carter12, Lemma 7.2.1(i)], $nx_r = x_{w(r)} n$
. By [Reference Carter12, Lemma 7.2.1(i)], $nx_r = x_{w(r)} n$![]() and $x_{-w(r)} n = x_{w(-r)} n = nx_{-r}$
and $x_{-w(r)} n = x_{w(-r)} n = nx_{-r}$![]() . If $w(r) \in \Phi ^+$
. If $w(r) \in \Phi ^+$![]() , then $x_{w(r)} \in \langle x_u \mid u \in \Phi ^+ \rangle = U \le A$
, then $x_{w(r)} \in \langle x_u \mid u \in \Phi ^+ \rangle = U \le A$![]() , and so $Anx_r = An$
, and so $Anx_r = An$![]() . Otherwise, $-w(r) \in \Phi ^+$
. Otherwise, $-w(r) \in \Phi ^+$![]() and $x_{-w(r)} \in A$
and $x_{-w(r)} \in A$![]() , yielding $An = An x_{-r}$
, yielding $An = An x_{-r}$![]() and hence $Anx_r = An x_{-r} x_r$
and hence $Anx_r = An x_{-r} x_r$![]() , which lies in $AnB$
, which lies in $AnB$![]() by the previous paragraph. In either case, we see that $Anx_rB = AnB$
by the previous paragraph. In either case, we see that $Anx_rB = AnB$![]() , as required.
, as required.
Next, we consider the alternating groups, followed by the sporadic groups and the Tits group.
Proposition 3.4 Let $T$![]() be a finite simple alternating group $A_n$
be a finite simple alternating group $A_n$![]() . Then Property (i) of Theorem 1.3 holds for $T$
. Then Property (i) of Theorem 1.3 holds for $T$![]() .
.
Proof. Since $A_5 \cong \operatorname {{\mathrm {PSL}}}_2(4) = A_1(4)$![]() and $A_6 \cong \operatorname {{\mathrm {PSL}}}_2(9) = A_1(9)$
and $A_6 \cong \operatorname {{\mathrm {PSL}}}_2(9) = A_1(9)$![]() are addressed by Proposition 3.1, we shall assume that $n \ge 7$
are addressed by Proposition 3.1, we shall assume that $n \ge 7$![]() . Let $\Sigma$
. Let $\Sigma$![]() be the set of $3$
be the set of $3$![]() -subsets of a set of size $n$
-subsets of a set of size $n$![]() , and let $\alpha \in \Sigma$
, and let $\alpha \in \Sigma$![]() . Then $A:=T_\alpha =(S_3\times S_{n-3})\cap T$
. Then $A:=T_\alpha =(S_3\times S_{n-3})\cap T$![]() , and all $\operatorname {{\mathrm {Aut}}}(T)$
, and all $\operatorname {{\mathrm {Aut}}}(T)$![]() -conjugates of $A$
-conjugates of $A$![]() are conjugate in $T$
are conjugate in $T$![]() . Additionally, $A$
. Additionally, $A$![]() has four orbits on $\Sigma$
has four orbits on $\Sigma$![]() , namely $\{\alpha \}$
, namely $\{\alpha \}$![]() and $\{\beta \in \Sigma \mid |\beta \cap \alpha |=i\}$
and $\{\beta \in \Sigma \mid |\beta \cap \alpha |=i\}$![]() for $i \in \{0,\,1,\,2\}$
for $i \in \{0,\,1,\,2\}$![]() . Since the index two subgroup $B:=A_3 \times A_{n-3}$
. Since the index two subgroup $B:=A_3 \times A_{n-3}$![]() of $A$
of $A$![]() acts transitively on each of these orbits, and since the action of $T$
acts transitively on each of these orbits, and since the action of $T$![]() on $\Sigma$
on $\Sigma$![]() is equivalent to its action on the right cosets of $A$
is equivalent to its action on the right cosets of $A$![]() , the result follows from Lemma 2.4.
, the result follows from Lemma 2.4.
Proposition 3.5 Let $T$![]() be the Tits group ${}^2F_{4}(2)'$
be the Tits group ${}^2F_{4}(2)'$![]() , or a sporadic simple group that does not lie in $\{\mathrm {J}_1,\, \mathrm {M}_{22},\, \mathrm {J}_3,\, \mathrm {McL},\, \mathrm {Th},\, \mathbb {M}\}$
, or a sporadic simple group that does not lie in $\{\mathrm {J}_1,\, \mathrm {M}_{22},\, \mathrm {J}_3,\, \mathrm {McL},\, \mathrm {Th},\, \mathbb {M}\}$![]() . Then Property (i) of Theorem 1.3 holds for $T$
. Then Property (i) of Theorem 1.3 holds for $T$![]() .
.
Proof. We observe from the Atlas [Reference Conway, Curtis, Norton, Parker and Wilson13] that $T$![]() has a maximal subgroup $A$
has a maximal subgroup $A$![]() , as specified in Table 1, such that either $T = \mathrm {O'N}$
, as specified in Table 1, such that either $T = \mathrm {O'N}$![]() or all $\operatorname {{\mathrm {Aut}}}(T)$
or all $\operatorname {{\mathrm {Aut}}}(T)$![]() -conjugates of $T_\alpha$
-conjugates of $T_\alpha$![]() are conjugate in $T$
are conjugate in $T$![]() . It is also clear that the group $B$
. It is also clear that the group $B$![]() in the table is a proper normal subgroup of $A$
in the table is a proper normal subgroup of $A$![]() . Note that if $T = \mathrm {M}_{12}$
. Note that if $T = \mathrm {M}_{12}$![]() , then $A$
, then $A$![]() has two normal subgroups isomorphic to $S_5$
has two normal subgroups isomorphic to $S_5$![]() ; in what follows, $B$
; in what follows, $B$![]() may be chosen as either.
may be chosen as either.
Table 1. A maximal subgroup $A$![]() of a group $T$
of a group $T$![]() from Proposition 3.5, with $B$
from Proposition 3.5, with $B$![]() a proper normal subgroup of $A$
a proper normal subgroup of $A$![]()

.
Now, let $R:=\operatorname {{\mathrm {Aut}}}(T)$![]() if $T = \mathrm {O'N}$
if $T = \mathrm {O'N}$![]() , and $R:=T$
, and $R:=T$![]() otherwise. Additionally, let $\chi$
otherwise. Additionally, let $\chi$![]() be the permutation character corresponding to the action of $R$
be the permutation character corresponding to the action of $R$![]() on the set $\Sigma$
on the set $\Sigma$![]() of right cosets of $A$
of right cosets of $A$![]() in $R$
in $R$![]() . Then for each $t \in R$
. Then for each $t \in R$![]() , the number of points in $\Sigma$
, the number of points in $\Sigma$![]() fixed by $t$
fixed by $t$![]() is equal to $\chi (t)$
is equal to $\chi (t)$![]() . By the Cauchy–Frobenius Lemma, $A$
. By the Cauchy–Frobenius Lemma, $A$![]() and $B$
and $B$![]() have $c_A:={1}/{|A|}\sum _{a \in A} \chi (a)$
have $c_A:={1}/{|A|}\sum _{a \in A} \chi (a)$![]() and $c_B:={1}/{|B|}\sum _{b \in B} \chi (b)$
and $c_B:={1}/{|B|}\sum _{b \in B} \chi (b)$![]() orbits on $\Sigma$
orbits on $\Sigma$![]() , respectively. It is straightforward to compute $c_A$
, respectively. It is straightforward to compute $c_A$![]() and $c_B$
and $c_B$![]() in GAP [15] using the Character Table Library [Reference Breuer9] ($c_A$
in GAP [15] using the Character Table Library [Reference Breuer9] ($c_A$![]() is most readily calculated as the inner product $[\chi,\,\chi ]$
is most readily calculated as the inner product $[\chi,\,\chi ]$![]() ), and in each case we obtain $c_A = c_B$
), and in each case we obtain $c_A = c_B$![]() . Thus Lemma 2.4 yields the result.
. Thus Lemma 2.4 yields the result.
We are now able to prove Theorem 1.3. Given a group $G$![]() and a non-trivial (core-free) subgroup $H$
and a non-trivial (core-free) subgroup $H$![]() of $G$
of $G$![]() , we will write $b(G,\,H)$
, we will write $b(G,\,H)$![]() to denote the base size of $G$
to denote the base size of $G$![]() in its action on the set $\Sigma$
in its action on the set $\Sigma$![]() of right cosets of $H$
of right cosets of $H$![]() , i.e., the minimum size of a subset $\Delta$
, i.e., the minimum size of a subset $\Delta$![]() of $\Sigma$
of $\Sigma$![]() such that the pointwise stabilizer $G_{(\Delta )}$
such that the pointwise stabilizer $G_{(\Delta )}$![]() is trivial. Notice that $b(G,\,H) \ge 2$
is trivial. Notice that $b(G,\,H) \ge 2$![]() , as $H$
, as $H$![]() is a point stabilizer in this action.
is a point stabilizer in this action.
Proof of Theorem 1.3 Propositions 3.1–3.5 show that (iii) implies (i), which clearly implies (ii). To complete the proof, we will show that if (iii) does not hold, then neither does (ii). If $T \in \{\mathrm {J}_1,\, \mathrm {M}_{22},\, \mathrm {J}_3,\, \mathrm {McL}\}$![]() , then we construct $T$
, then we construct $T$![]() in Magma [Reference Bosma, Cannon and Playoust7] via the AutomorphismGroupSimpleGroup and Socle functions, and show that (ii) does not hold via fast, direct computations.
in Magma [Reference Bosma, Cannon and Playoust7] via the AutomorphismGroupSimpleGroup and Socle functions, and show that (ii) does not hold via fast, direct computations.
Suppose next that $T = \mathrm {Th}$![]() , let $C$
, let $C$![]() be a proper subgroup of $T$
be a proper subgroup of $T$![]() , and let $A$
, and let $A$![]() be a subgroup of $C$
be a subgroup of $C$![]() . Observe that if $b(T,\,C) = 2$
. Observe that if $b(T,\,C) = 2$![]() , then (as discussed below the statement of Theorem 1.3) the two-point stabilizer $C \cap C^t$
, then (as discussed below the statement of Theorem 1.3) the two-point stabilizer $C \cap C^t$![]() is trivial for some $t$
is trivial for some $t$![]() . Hence $A \,{\cap}\, A^t \,{=}\, 1$
. Hence $A \,{\cap}\, A^t \,{=}\, 1$![]() , and so $A$
, and so $A$![]() does not satisfy (ii). In general, $b(T,\,A) \le b(T,\,C)$
does not satisfy (ii). In general, $b(T,\,A) \le b(T,\,C)$![]() . By [Reference Burness, O'Brien and Wilson11, Theorem 1], $T$
. By [Reference Burness, O'Brien and Wilson11, Theorem 1], $T$![]() has only two maximal subgroups (up to conjugacy) with corresponding base size greater than two, namely $M_1:={}^3D_4(2) \mkern 3mu{:}\mkern 3mu 3$
has only two maximal subgroups (up to conjugacy) with corresponding base size greater than two, namely $M_1:={}^3D_4(2) \mkern 3mu{:}\mkern 3mu 3$![]() and $M_2:=2^5.\operatorname {{\mathrm {PSL}}}_5(2)$
and $M_2:=2^5.\operatorname {{\mathrm {PSL}}}_5(2)$![]() , and $b(T,\,M_1) = b(T,\,M_2) = 3$
, and $b(T,\,M_1) = b(T,\,M_2) = 3$![]() . Hence any proper subgroup $A$
. Hence any proper subgroup $A$![]() of $T$
of $T$![]() satisfying (ii) is a non-simple subgroup of $M_1$
satisfying (ii) is a non-simple subgroup of $M_1$![]() or $M_2$
or $M_2$![]() with $b(T,\,A) = 3$
with $b(T,\,A) = 3$![]() .
.
Now, let $\Sigma$![]() be the set of right cosets in $T$
be the set of right cosets in $T$![]() of a proper subgroup $A$
of a proper subgroup $A$![]() , and let $c$
, and let $c$![]() be the number of orbits of $A$
be the number of orbits of $A$![]() on $\Sigma$
on $\Sigma$![]() . If $b(T,\,A) \ge 3$
. If $b(T,\,A) \ge 3$![]() , then $|A \cap A^t| \ge 2$
, then $|A \cap A^t| \ge 2$![]() for all $t \in T$
for all $t \in T$![]() , and it follows from the Orbit-Stabiliser Theorem that $c|A|/2 \ge |\Sigma |$
, and it follows from the Orbit-Stabiliser Theorem that $c|A|/2 \ge |\Sigma |$![]() . If $A$
. If $A$![]() is a maximal subgroup of either $M_1$
is a maximal subgroup of either $M_1$![]() or $M_1' \cong {}^3D_4(2)$
or $M_1' \cong {}^3D_4(2)$![]() , then the character table of $A$
, then the character table of $A$![]() is included in The GAP Character Table Library. Thus for every such $A \ne M_1'$
is included in The GAP Character Table Library. Thus for every such $A \ne M_1'$![]() , we can compute $c$
, we can compute $c$![]() as in the proof of Proposition 3.5, and we see that in fact $c|A|/2 < |\Sigma |$
as in the proof of Proposition 3.5, and we see that in fact $c|A|/2 < |\Sigma |$![]() , and hence $b(T,\,A) = 2$
, and hence $b(T,\,A) = 2$![]() . To show that $b(T,\,A) = 2$
. To show that $b(T,\,A) = 2$![]() for each maximal subgroup $A$
for each maximal subgroup $A$![]() of $M_2$
of $M_2$![]() , we construct $T$
, we construct $T$![]() and $M_2$
and $M_2$![]() in Magma as subgroups of $\operatorname {{\mathrm {GL}}}_{248}(2)$
in Magma as subgroups of $\operatorname {{\mathrm {GL}}}_{248}(2)$![]() using the respective generating pairs $\{x,\,y\}$
using the respective generating pairs $\{x,\,y\}$![]() and $\{w_1,\,w_2\}$
and $\{w_1,\,w_2\}$![]() given in [Reference Wilson, Walsh, Tripp, Suleiman, Parker, Norton, Nickerson, Linton, Bray and Abbott19]. Magma calculations (with a runtime of less than 10 minutes and a memory usage of 1.5 GB) then show that $A \cap A^y = 1$
given in [Reference Wilson, Walsh, Tripp, Suleiman, Parker, Norton, Nickerson, Linton, Bray and Abbott19]. Magma calculations (with a runtime of less than 10 minutes and a memory usage of 1.5 GB) then show that $A \cap A^y = 1$![]() for all representatives $A$
for all representatives $A$![]() of the conjugacy classes of maximal subgroups of $M_2$
of the conjugacy classes of maximal subgroups of $M_2$![]() returned by the MaximalSubgroups function. Therefore, $M_1$
returned by the MaximalSubgroups function. Therefore, $M_1$![]() and $M_2$
and $M_2$![]() are the only non-simple subgroups of $T$
are the only non-simple subgroups of $T$![]() with corresponding base size at least three. Further character table computations in GAP show that if $A \in \{M_1,\,M_2\}$
with corresponding base size at least three. Further character table computations in GAP show that if $A \in \{M_1,\,M_2\}$![]() , then for each proper normal subgroup $B$
, then for each proper normal subgroup $B$![]() of $A$
of $A$![]() , the number of $B$
, the number of $B$![]() -orbits on $\Sigma$
-orbits on $\Sigma$![]() is greater than the number of $A$
is greater than the number of $A$![]() -orbits. An additional application of the Orbit-Stabiliser Theorem yields $B(A \cap A^t) < A$
-orbits. An additional application of the Orbit-Stabiliser Theorem yields $B(A \cap A^t) < A$![]() for some $t \in T$
for some $t \in T$![]() . Therefore, (ii) does not hold.
. Therefore, (ii) does not hold.
Finally, suppose that $T = \mathbb {M}$![]() . As above, any proper subgroup $A$
. As above, any proper subgroup $A$![]() of $T$
of $T$![]() satisfying (ii) also satisfies $b(T,\,A) \ge 3$
satisfying (ii) also satisfies $b(T,\,A) \ge 3$![]() . By [Reference Burness10, Theorem 3.1], the unique (up to conjugacy) proper subgroup $A$
. By [Reference Burness10, Theorem 3.1], the unique (up to conjugacy) proper subgroup $A$![]() of $T$
of $T$![]() with $b(T,\,A) \ge 3$
with $b(T,\,A) \ge 3$![]() is the maximal subgroup $K:=2.\mathbb {B}$
is the maximal subgroup $K:=2.\mathbb {B}$![]() , with $b(T,\,K) = 3$
, with $b(T,\,K) = 3$![]() . Since $K$
. Since $K$![]() is quasisimple, its centre $Z$
is quasisimple, its centre $Z$![]() of order two is its unique nontrivial proper normal subgroup, and $Z$
of order two is its unique nontrivial proper normal subgroup, and $Z$![]() lies in each maximal subgroup of $K$
lies in each maximal subgroup of $K$![]() . Hence $Z(K \cap K^t) < K$
. Hence $Z(K \cap K^t) < K$![]() for all $t \in T \setminus K$
for all $t \in T \setminus K$![]() , and so (ii) does not hold.
, and so (ii) does not hold.
We now prove our main theorem.
Proof of Theorem 1.2 As each spreading primitive group is synchronizing, Theorem 1.1 implies that a spreading primitive group of diagonal type has socle $T \times T$![]() , for some non-abelian finite simple group $T$
, for some non-abelian finite simple group $T$![]() . For each $T$
. For each $T$![]() , let $\Omega := T$
, let $\Omega := T$![]() , and let $W(T)$
, and let $W(T)$![]() be the subgroup of $\operatorname {{\mathrm {Sym}}}(\Omega )$
be the subgroup of $\operatorname {{\mathrm {Sym}}}(\Omega )$![]() defined in § 2. Recall also that each subgroup of a non-spreading group is non-spreading. Thus it suffices to show that $W(T)$
defined in § 2. Recall also that each subgroup of a non-spreading group is non-spreading. Thus it suffices to show that $W(T)$![]() is non-spreading for each $T$
is non-spreading for each $T$![]() . If $T \notin \{\mathrm {J}_1,\,\mathrm {M}_{22},\, \mathrm {J}_3,\, \mathrm {McL},\,\mathrm {Th},\,\mathbb {M}\}$
. If $T \notin \{\mathrm {J}_1,\,\mathrm {M}_{22},\, \mathrm {J}_3,\, \mathrm {McL},\,\mathrm {Th},\,\mathbb {M}\}$![]() , then this is an immediate consequence of Theorem 1.3 and Corollary 2.3.
, then this is an immediate consequence of Theorem 1.3 and Corollary 2.3.
For each of the six remaining groups $T$![]() , let $r$
, let $r$![]() , $s_1$
, $s_1$![]() and $s_2$
and $s_2$![]() be members of the conjugacy classes of $T$
be members of the conjugacy classes of $T$![]() given in Table 2. By inspecting the character table for $T$
given in Table 2. By inspecting the character table for $T$![]() in [Reference Conway, Curtis, Norton, Parker and Wilson13], we observe that these elements satisfy Properties (i) and (ii) of Lemma 2.5. Therefore, that lemma shows that $W(T)$
in [Reference Conway, Curtis, Norton, Parker and Wilson13], we observe that these elements satisfy Properties (i) and (ii) of Lemma 2.5. Therefore, that lemma shows that $W(T)$![]() is non-spreading.
is non-spreading.
Table 2. Elements $r$![]() , $s_1$
, $s_1$![]() and $s_2$
and $s_2$![]() that satisfy Properties (i) and (ii) of Lemma 2.5, for each of six sporadic groups $T$
that satisfy Properties (i) and (ii) of Lemma 2.5, for each of six sporadic groups $T$![]()

Each element is specified by its corresponding conjugacy class, labelled as in the Atlas [Reference Conway, Curtis, Norton, Parker and Wilson13].
Acknowledgements
This work forms part of an Australian Research Council Discovery Project DP200101951. We thank Tim Burness for drawing our attention to the result [Reference Burness10, Theorem 3.1], which helped us to resolve the $\mathbb {M}$![]() case of Theorem 1.3. We also thank the referee for some helpful suggestions.
case of Theorem 1.3. We also thank the referee for some helpful suggestions.