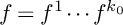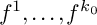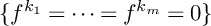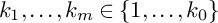1 Introduction
Let
![]() $f(\mathbf {z})$
and
$f(\mathbf {z})$
and
![]() $g(\mathbf {z})$
be two nonconstant polynomial functions of n complex variables
$g(\mathbf {z})$
be two nonconstant polynomial functions of n complex variables
![]() $\mathbf {z}=(z_1,\ldots ,z_n)$
such that
$\mathbf {z}=(z_1,\ldots ,z_n)$
such that
![]() $f(\mathbf {0})=g(\mathbf {0})=0$
. (Here, f and g may have a nonisolated singularity at
$f(\mathbf {0})=g(\mathbf {0})=0$
. (Here, f and g may have a nonisolated singularity at
![]() $\mathbf {0}$
.) The goal of this paper is to find easy-to-check conditions on the functions f and g that guarantee that their Milnor fibrations at
$\mathbf {0}$
.) The goal of this paper is to find easy-to-check conditions on the functions f and g that guarantee that their Milnor fibrations at
![]() $\mathbf {0}$
are isomorphic (i.e., there is a fiber-preserving diffeomorphism from the total space of the Milnor fibration of f onto that of g). In [Reference Oka9], the second named author proved that if f and g are (Newton) nondegenerate and have the same Newton boundary, then necessarily they have isomorphic Milnor fibrations (the special cases where, in addition, f is weighted homogeneous or has an isolated singularity at
$\mathbf {0}$
are isomorphic (i.e., there is a fiber-preserving diffeomorphism from the total space of the Milnor fibration of f onto that of g). In [Reference Oka9], the second named author proved that if f and g are (Newton) nondegenerate and have the same Newton boundary, then necessarily they have isomorphic Milnor fibrations (the special cases where, in addition, f is weighted homogeneous or has an isolated singularity at
![]() $\mathbf {0}$
were first proved in [Reference Oka8] and [Reference Oka7], respectively). The crucial step in the proof of this result is a similar assertion, also proved in [Reference Oka9], for one-parameter families of functions. It says that if
$\mathbf {0}$
were first proved in [Reference Oka8] and [Reference Oka7], respectively). The crucial step in the proof of this result is a similar assertion, also proved in [Reference Oka9], for one-parameter families of functions. It says that if
![]() $\tau _0>0$
and if
$\tau _0>0$
and if
![]() $\{f_t\}_{\vert t\vert \leq \tau _0}$
is a family of nondegenerate polynomial functions with the same Newton boundary, then the Milnor fibrations of
$\{f_t\}_{\vert t\vert \leq \tau _0}$
is a family of nondegenerate polynomial functions with the same Newton boundary, then the Milnor fibrations of
![]() $f_t$
and
$f_t$
and
![]() $f_0$
at
$f_0$
at
![]() $\mathbf {0}$
are isomorphic for any t,
$\mathbf {0}$
are isomorphic for any t,
![]() $\vert t\vert \leq \tau _0$
. This theorem, in turn, is a consequence of another important result, still proved in [Reference Oka9], which asserts that any family
$\vert t\vert \leq \tau _0$
. This theorem, in turn, is a consequence of another important result, still proved in [Reference Oka9], which asserts that any family
![]() $\{f_t\}_{\vert t\vert \leq \tau _0}$
satisfying the above conditions has a so-called uniform stable radius for the Milnor fibrations of its elements
$\{f_t\}_{\vert t\vert \leq \tau _0}$
satisfying the above conditions has a so-called uniform stable radius for the Milnor fibrations of its elements
![]() $f_t$
.
$f_t$
.
Although the scope of the abovementioned theorems is relatively wide, it does not include, for instance, the following quite common situation. Suppose that
![]() $f(\mathbf {z})$
is the product of
$f(\mathbf {z})$
is the product of
![]() $k_0\geq 2$
polynomial functions
$k_0\geq 2$
polynomial functions
![]() $f^1(\mathbf {z}),\ldots ,f^{k_0}(\mathbf {z})$
on
$f^1(\mathbf {z}),\ldots ,f^{k_0}(\mathbf {z})$
on
![]() $\mathbb {C}^n$
with
$\mathbb {C}^n$
with
![]() $n\geq 3$
(so, in particular, we have
$n\geq 3$
(so, in particular, we have
![]() $\dim _{\mathbf {0}}(V(f^k)\cap V(f^{k'}))\geq n-2\geq 1$
, where, as usual,
$\dim _{\mathbf {0}}(V(f^k)\cap V(f^{k'}))\geq n-2\geq 1$
, where, as usual,
![]() $V(f^k)$
and
$V(f^k)$
and
![]() $V(f^{k'})$
denote the hypersurfaces defined by
$V(f^{k'})$
denote the hypersurfaces defined by
![]() $f^k$
and
$f^k$
and
![]() $f^{k'}$
, respectively; here, the upper index denotes an index, not a power). Then we claim that f is never nondegenerate (and hence the results of [Reference Oka9] do not apply to this situation). If f is convenient (i.e., if its Newton boundary intersects each coordinate axis), then our claim is an immediate consequence of a theorem of Kouchnirenko [Reference Kouchnirenko5], which asserts that a convenient nondegenerate function always has an isolated singularity at the origin. In the above situation, since for
$f^{k'}$
, respectively; here, the upper index denotes an index, not a power). Then we claim that f is never nondegenerate (and hence the results of [Reference Oka9] do not apply to this situation). If f is convenient (i.e., if its Newton boundary intersects each coordinate axis), then our claim is an immediate consequence of a theorem of Kouchnirenko [Reference Kouchnirenko5], which asserts that a convenient nondegenerate function always has an isolated singularity at the origin. In the above situation, since for
![]() $k\not =k'$
the intersection
$k\not =k'$
the intersection
![]() $V(f^k)\cap V(f^{k'})$
is contained in the singular locus of
$V(f^k)\cap V(f^{k'})$
is contained in the singular locus of
![]() $V(f)$
, if the function f is convenient, then Kouchnirenko’s theorem implies that it must be degenerate (i.e., not nondegenerate). In the case where f is not a convenient function, our claim follows from a theorem of Bernstein [Reference Bernstein1] and Proposition 2.3 in Chapter 4 of [Reference Oka10], which imply that for
$V(f)$
, if the function f is convenient, then Kouchnirenko’s theorem implies that it must be degenerate (i.e., not nondegenerate). In the case where f is not a convenient function, our claim follows from a theorem of Bernstein [Reference Bernstein1] and Proposition 2.3 in Chapter 4 of [Reference Oka10], which imply that for
![]() $k\not =k'$
the intersection
$k\not =k'$
the intersection
![]() $V(f^k_{\mathbf {w}})\cap V(f^{k'}_{\mathbf {w}})\cap \mathbb {C}^{*n}$
is nonempty whenever
$V(f^k_{\mathbf {w}})\cap V(f^{k'}_{\mathbf {w}})\cap \mathbb {C}^{*n}$
is nonempty whenever
![]() $\mathbf {w}\in \mathbb {N}^{*n}$
is such that
$\mathbf {w}\in \mathbb {N}^{*n}$
is such that
![]() $f^{k}_{\mathbf {w}}$
and
$f^{k}_{\mathbf {w}}$
and
![]() $f^{k'}_{\mathbf {w}}$
are not monomials and the dimension of the Minkowski sum
$f^{k'}_{\mathbf {w}}$
are not monomials and the dimension of the Minkowski sum
![]() $\Delta (\mathbf {w};f^k)+\Delta (\mathbf {w};f^{k'})$
is
$\Delta (\mathbf {w};f^k)+\Delta (\mathbf {w};f^{k'})$
is
![]() $\geq 2$
. Here,
$\geq 2$
. Here,
![]() $\Delta (\mathbf {w};f^k)$
(resp.
$\Delta (\mathbf {w};f^k)$
(resp.
![]() $f^k_{\mathbf {w}}$
) denotes the face of the Newton polyhedron of
$f^k_{\mathbf {w}}$
) denotes the face of the Newton polyhedron of
![]() $f^k$
(resp. the face function of
$f^k$
(resp. the face function of
![]() $f^k$
) with respect to
$f^k$
) with respect to
![]() $\mathbf {w}$
; similarly for the function
$\mathbf {w}$
; similarly for the function
![]() $f^{k'}$
(see §2 for the definitions). Of course, this implies that the face function
$f^{k'}$
(see §2 for the definitions). Of course, this implies that the face function
![]() $f_{\mathbf {w}}$
of f with respect to
$f_{\mathbf {w}}$
of f with respect to
![]() $\mathbf {w}$
has a critical point in
$\mathbf {w}$
has a critical point in
![]() $V(f_{\mathbf {w}})\cap \mathbb {C}^{*n}$
, that is, f is degenerate.
$V(f_{\mathbf {w}})\cap \mathbb {C}^{*n}$
, that is, f is degenerate.
In the present paper, we generalize the results of [Reference Oka9] to a class of polynomial functions that includes the “degenerate” examples mentioned above. A first class of such functions was already given by the authors in [Reference Eyral and Oka2] in the case of one-parameter families of functions of the form
![]() $f_t(\mathbf {z})=f_t^1(\mathbf {z})\cdots f_t^{k_0}(\mathbf {z})$
under a condition called Newton-admissibility. This condition says that the Newton boundaries of the functions
$f_t(\mathbf {z})=f_t^1(\mathbf {z})\cdots f_t^{k_0}(\mathbf {z})$
under a condition called Newton-admissibility. This condition says that the Newton boundaries of the functions
![]() $f^k_t$
which appear in the product must be independent of t and the (germs at
$f^k_t$
which appear in the product must be independent of t and the (germs at
![]() $\mathbf {0}$
of the) varieties
$\mathbf {0}$
of the) varieties
![]() $V(f^{k_1}_t,\ldots ,f^{k_m}_t):=\{f^{k_1}_t=\cdots =f^{k_m}_t\,{=}\,0\}$
must be nondegenerate, uniformly locally tame, complete intersection varieties for any
$V(f^{k_1}_t,\ldots ,f^{k_m}_t):=\{f^{k_1}_t=\cdots =f^{k_m}_t\,{=}\,0\}$
must be nondegenerate, uniformly locally tame, complete intersection varieties for any
![]() $k_1,\ldots ,k_m\in \{1,\ldots ,k_0\}$
. The uniform local tameness is a nondegeneracy-type condition with respect to the variables corresponding to the “compact directions” of the noncompact faces of the Newton polyhedron, the variables corresponding to the “noncompact directions” being fixed in a small ball independent of t (for a precise definition, see [Reference Eyral and Oka2]).
$k_1,\ldots ,k_m\in \{1,\ldots ,k_0\}$
. The uniform local tameness is a nondegeneracy-type condition with respect to the variables corresponding to the “compact directions” of the noncompact faces of the Newton polyhedron, the variables corresponding to the “noncompact directions” being fixed in a small ball independent of t (for a precise definition, see [Reference Eyral and Oka2]).
In fact, under the Newton-admissibility condition, we proved in [Reference Eyral and Oka2] a much stronger result on the local geometry of the family of hypersurfaces
![]() $V(f_t)$
: we showed that any Newton-admissible family is Whitney equisingular and satisfies Thom’s condition. Then, as a consequence of these two results, we easily obtained that the Milnor fibrations of
$V(f_t)$
: we showed that any Newton-admissible family is Whitney equisingular and satisfies Thom’s condition. Then, as a consequence of these two results, we easily obtained that the Milnor fibrations of
![]() $f_t$
and
$f_t$
and
![]() $f_0$
at the origin are isomorphic for all small t. Note that in the case of nonisolated singularities, the Newton-admissibility condition is a crucial assumption when we want to study geometric properties like Whitney equisingularity or Thom’s condition. However, if our goal is only to investigate the Milnor fibrations of the family members
$f_0$
at the origin are isomorphic for all small t. Note that in the case of nonisolated singularities, the Newton-admissibility condition is a crucial assumption when we want to study geometric properties like Whitney equisingularity or Thom’s condition. However, if our goal is only to investigate the Milnor fibrations of the family members
![]() $f_t$
, then, as we are going to show it in the present work, the uniform local tameness condition (which appears through the Newton-admissibility condition) can be completely dropped.
$f_t$
, then, as we are going to show it in the present work, the uniform local tameness condition (which appears through the Newton-admissibility condition) can be completely dropped.
Our first main theorem here says that if the Newton boundaries of the functions
![]() $f^k_t (1\leq k\leq k_0)$
are independent of t and if the varieties
$f^k_t (1\leq k\leq k_0)$
are independent of t and if the varieties
![]() $V(f^{k_1}_t,\ldots ,f^{k_m}_t)$
are nondegenerate complete intersection varieties for any
$V(f^{k_1}_t,\ldots ,f^{k_m}_t)$
are nondegenerate complete intersection varieties for any
![]() $k_1,\ldots ,k_m\in \{1,\ldots ,k_0\}$
, then the Milnor fibrations of
$k_1,\ldots ,k_m\in \{1,\ldots ,k_0\}$
, then the Milnor fibrations of
![]() $f_t$
and
$f_t$
and
![]() $f_0$
at
$f_0$
at
![]() $\mathbf {0}$
are isomorphic for all small t (see Theorem 4.5). The main step to prove this theorem is the following assertion, which is interesting itself. It says that, under the same assumptions, the family
$\mathbf {0}$
are isomorphic for all small t (see Theorem 4.5). The main step to prove this theorem is the following assertion, which is interesting itself. It says that, under the same assumptions, the family
![]() $\{f_t\}$
has a uniform stable radius (see Theorem 4.3 and Corollary 4.4). In the course of the proof of this assertion, we also show how a stable radius for the Milnor fibration of a function of the form
$\{f_t\}$
has a uniform stable radius (see Theorem 4.3 and Corollary 4.4). In the course of the proof of this assertion, we also show how a stable radius for the Milnor fibration of a function of the form
![]() $f(\mathbf {z})=f^1(\mathbf {z})\cdots f^{k_0}(\mathbf {z})$
can be obtained when the corresponding varieties
$f(\mathbf {z})=f^1(\mathbf {z})\cdots f^{k_0}(\mathbf {z})$
can be obtained when the corresponding varieties
![]() $V(f^{k_1},\ldots ,f^{k_m})$
are nondegenerate complete intersection varieties for any
$V(f^{k_1},\ldots ,f^{k_m})$
are nondegenerate complete intersection varieties for any
![]() $k_1,\ldots ,k_m\in \{1,\ldots ,k_0\}$
(see Theorem 3.5).
$k_1,\ldots ,k_m\in \{1,\ldots ,k_0\}$
(see Theorem 3.5).
Our second main theorem, which is deduced from the first one, asserts that given two polynomial functions
![]() $f(\mathbf {z})=f^1(\mathbf {z})\cdots f^{k_0}(\mathbf {z})$
and
$f(\mathbf {z})=f^1(\mathbf {z})\cdots f^{k_0}(\mathbf {z})$
and
![]() $g(\mathbf {z})=g^1(\mathbf {z})\cdots g^{k_0}(\mathbf {z})$
, if
$g(\mathbf {z})=g^1(\mathbf {z})\cdots g^{k_0}(\mathbf {z})$
, if
![]() $V(f^{k_1},\ldots ,f^{k_m})$
and
$V(f^{k_1},\ldots ,f^{k_m})$
and
![]() $V(g^{k_1},\ldots ,g^{k_m})$
are nondegenerate complete intersection varieties for any
$V(g^{k_1},\ldots ,g^{k_m})$
are nondegenerate complete intersection varieties for any
![]() $k_1,\ldots ,k_m\in \{1,\ldots ,k_0\}$
, and if for each
$k_1,\ldots ,k_m\in \{1,\ldots ,k_0\}$
, and if for each
![]() $1\leq k\leq k_0$
, the Newton boundaries of
$1\leq k\leq k_0$
, the Newton boundaries of
![]() $f^k$
and
$f^k$
and
![]() $g^k$
coincide, then the Milnor fibrations of f and g at
$g^k$
coincide, then the Milnor fibrations of f and g at
![]() $\mathbf {0}$
are isomorphic (see Theorem 5.2).
$\mathbf {0}$
are isomorphic (see Theorem 5.2).
Note that in the special case where
![]() $k_0=1$
(for which the functions under consideration are necessarily nondegenerate), we recover all the results of [Reference Oka9]—a paper from which the present work is inspired.
$k_0=1$
(for which the functions under consideration are necessarily nondegenerate), we recover all the results of [Reference Oka9]—a paper from which the present work is inspired.
2 Nondegenerate complete intersection varieties
Let
![]() $\mathbf {z}:=(z_1,\ldots , z_n)$
be coordinates for
$\mathbf {z}:=(z_1,\ldots , z_n)$
be coordinates for
![]() $\mathbb {C}^n$
, and let
$\mathbb {C}^n$
, and let
![]() $f(\mathbf {z})=\sum _\alpha c_\alpha \, \mathbf {z}^\alpha $
be a nonconstant polynomial function which vanishes at the origin. Here,
$f(\mathbf {z})=\sum _\alpha c_\alpha \, \mathbf {z}^\alpha $
be a nonconstant polynomial function which vanishes at the origin. Here,
![]() $\alpha :=(\alpha _1,\ldots ,\alpha _n)\in \mathbb {N}^n$
,
$\alpha :=(\alpha _1,\ldots ,\alpha _n)\in \mathbb {N}^n$
,
![]() $c_\alpha \in \mathbb {C}$
, and
$c_\alpha \in \mathbb {C}$
, and
![]() $\mathbf {z}^{\alpha }$
is a notation for the monomial
$\mathbf {z}^{\alpha }$
is a notation for the monomial
![]() $z_1^{\alpha _1}\cdots z_n^{\alpha _n}$
. For any
$z_1^{\alpha _1}\cdots z_n^{\alpha _n}$
. For any
![]() $I\subseteq \{1,\ldots , n\}$
, we denote by
$I\subseteq \{1,\ldots , n\}$
, we denote by
![]() $\mathbb {C}^I$
(resp.
$\mathbb {C}^I$
(resp.
![]() $\mathbb {C}^{*I}$
) the set of points
$\mathbb {C}^{*I}$
) the set of points
![]() $(z_1,\ldots , z_n)\in \mathbb {C}^n$
such that
$(z_1,\ldots , z_n)\in \mathbb {C}^n$
such that
![]() $z_i=0$
if
$z_i=0$
if
![]() $i\notin I$
(resp.
$i\notin I$
(resp.
![]() $z_i=0$
if and only if
$z_i=0$
if and only if
![]() $i\notin I$
). In particular, we have
$i\notin I$
). In particular, we have
![]() $\mathbb {C}^{\emptyset }=\mathbb {C}^{*\emptyset }=\{\mathbf {0}\}$
and
$\mathbb {C}^{\emptyset }=\mathbb {C}^{*\emptyset }=\{\mathbf {0}\}$
and
![]() $\mathbb {C}^{*\{1,\ldots ,n\}}=\mathbb {C}^{*n}$
, where
$\mathbb {C}^{*\{1,\ldots ,n\}}=\mathbb {C}^{*n}$
, where
![]() $\mathbb {C}^*:=\mathbb {C}\setminus \{\mathbf {0}\}$
. Throughout this paper, we are only interested in a local situation, that is, in (arbitrarily small representatives of) germs at the origin.
$\mathbb {C}^*:=\mathbb {C}\setminus \{\mathbf {0}\}$
. Throughout this paper, we are only interested in a local situation, that is, in (arbitrarily small representatives of) germs at the origin.
To start with, let us recall the definition of a nondegenerate complete intersection variety, which is a key notion in this paper. (A standard reference for this is [Reference Oka10].)
The Newton polyhedron
![]() $\Gamma _{\! +}(f)$
of the germ of f at the origin
$\Gamma _{\! +}(f)$
of the germ of f at the origin
![]() $\mathbf {0}\in \mathbb {C}^n$
(with respect to the coordinates
$\mathbf {0}\in \mathbb {C}^n$
(with respect to the coordinates
![]() $\mathbf {z}=(z_1,\ldots , z_n)$
) is the convex hull in
$\mathbf {z}=(z_1,\ldots , z_n)$
) is the convex hull in
![]() $\mathbb {R}_+^n$
of the set
$\mathbb {R}_+^n$
of the set
 $$ \begin{align*} \bigcup_{c_\alpha\not=0} (\alpha+\mathbb{R}_+^n). \end{align*} $$
$$ \begin{align*} \bigcup_{c_\alpha\not=0} (\alpha+\mathbb{R}_+^n). \end{align*} $$
The Newton boundary of f (denoted by
![]() $\Gamma (f)$
) is the union of the compact faces of
$\Gamma (f)$
) is the union of the compact faces of
![]() $\Gamma _{\! +}(f)$
. For any weight vector
$\Gamma _{\! +}(f)$
. For any weight vector
![]() $\mathbf {w}:=(w_1,\ldots ,w_n)\in \mathbb {N}^n$
, let
$\mathbf {w}:=(w_1,\ldots ,w_n)\in \mathbb {N}^n$
, let
![]() $d(\mathbf {w};f)$
be the minimal value of the restriction to
$d(\mathbf {w};f)$
be the minimal value of the restriction to
![]() $\Gamma _{+}(f)$
of the linear map
$\Gamma _{+}(f)$
of the linear map
 $$ \begin{align*} \mathbf{x}=(x_1,\ldots,x_n)\in \mathbb{R}^n\mapsto\sum_{i=1}^n x_i w_i \in \mathbb{R}, \end{align*} $$
$$ \begin{align*} \mathbf{x}=(x_1,\ldots,x_n)\in \mathbb{R}^n\mapsto\sum_{i=1}^n x_i w_i \in \mathbb{R}, \end{align*} $$
and let
![]() $\Delta (\mathbf {w};f)$
be the (possibly noncompact) face of
$\Delta (\mathbf {w};f)$
be the (possibly noncompact) face of
![]() $\Gamma _{+}(f)$
defined as
$\Gamma _{+}(f)$
defined as
 $$ \begin{align*} \Delta(\mathbf{w};f)=\bigg\{\mathbf{x}\in \Gamma_{+}(f)\,; \, \sum_{i=1}^n x_i w_i = d(\mathbf{w};f)\bigg\}. \end{align*} $$
$$ \begin{align*} \Delta(\mathbf{w};f)=\bigg\{\mathbf{x}\in \Gamma_{+}(f)\,; \, \sum_{i=1}^n x_i w_i = d(\mathbf{w};f)\bigg\}. \end{align*} $$
Note that if all the
![]() $w_i$
’s are positive, then
$w_i$
’s are positive, then
![]() $\Delta (\mathbf {w};f)$
is a (compact) face of
$\Delta (\mathbf {w};f)$
is a (compact) face of
![]() $\Gamma (f)$
, and if
$\Gamma (f)$
, and if
![]() $\mathbf {w}=\mathbf {0}$
, then
$\mathbf {w}=\mathbf {0}$
, then
![]() $\Delta (\mathbf {w};f)=\Gamma _{+}(f)$
. The face function of f with respect to
$\Delta (\mathbf {w};f)=\Gamma _{+}(f)$
. The face function of f with respect to
![]() $\mathbf {w}$
is the function
$\mathbf {w}$
is the function
 $$ \begin{align*} \mathbf{z}\in\mathbb{C}^n \mapsto \sum_{\alpha\in \Delta(\mathbf{w};f)} c_\alpha\, \mathbf{z}^\alpha\in\mathbb{C}. \end{align*} $$
$$ \begin{align*} \mathbf{z}\in\mathbb{C}^n \mapsto \sum_{\alpha\in \Delta(\mathbf{w};f)} c_\alpha\, \mathbf{z}^\alpha\in\mathbb{C}. \end{align*} $$
Hereafter, this function will be denoted by
![]() $f_{\mathbf {w}}$
or
$f_{\mathbf {w}}$
or
![]() $f_{\Delta (\mathbf {w};f)}$
.
$f_{\Delta (\mathbf {w};f)}$
.
Now, consider the set
![]() $\mathcal {I}(f)$
consisting of all subsets
$\mathcal {I}(f)$
consisting of all subsets
![]() $I\subseteq \{1,\ldots ,n\}$
such that the restriction of f to
$I\subseteq \{1,\ldots ,n\}$
such that the restriction of f to
![]() $\mathbb {C}^I$
(denoted by
$\mathbb {C}^I$
(denoted by
![]() $f^I$
) does not identically vanishes. Clearly,
$f^I$
) does not identically vanishes. Clearly,
![]() $I\in \mathcal {I}(f)$
if and only if
$I\in \mathcal {I}(f)$
if and only if
![]() $\Gamma (f^I)=\Gamma (f)\cap \mathbb {R}^I$
is not empty, where
$\Gamma (f^I)=\Gamma (f)\cap \mathbb {R}^I$
is not empty, where
![]() $\mathbb {R}^I$
is defined in a similar way as
$\mathbb {R}^I$
is defined in a similar way as
![]() $\mathbb {C}^I$
. Hereafter, for any weight vector
$\mathbb {C}^I$
. Hereafter, for any weight vector
![]() $\mathbf {w}\in \mathbb {N}^I$
, we shall use the simplified following notation:
$\mathbf {w}\in \mathbb {N}^I$
, we shall use the simplified following notation:
(Of course,
![]() $\mathbb {N}^I$
is defined in a similar way as
$\mathbb {N}^I$
is defined in a similar way as
![]() $\mathbb {C}^I$
and
$\mathbb {C}^I$
and
![]() $\mathbb {R}^I$
.) Note that for all
$\mathbb {R}^I$
.) Note that for all
![]() $\mathbf {w}\in \mathbb {N}^I$
, we have
$\mathbf {w}\in \mathbb {N}^I$
, we have
Definition 2.1 (See [Reference Kouchnirenko5]).
The germ at
![]() $\mathbf {0}$
of the hypersurface
$\mathbf {0}$
of the hypersurface
![]() $V(f):=f^{-1}(0)\subseteq \mathbb {C}^n$
is called nondegenerate if for any “positive” weight vector
$V(f):=f^{-1}(0)\subseteq \mathbb {C}^n$
is called nondegenerate if for any “positive” weight vector
![]() $\mathbf {w}\in \mathbb {N}^{*n}$
(i.e.,
$\mathbf {w}\in \mathbb {N}^{*n}$
(i.e.,
![]() $w_i>0$
for all i), the hypersurface
$w_i>0$
for all i), the hypersurface
is a reduced, nonsingular hypersurface in the complex torus
![]() $\mathbb {C}^{*n}$
. This means that
$\mathbb {C}^{*n}$
. This means that
![]() $f_{\mathbf {w}}$
has no critical point in
$f_{\mathbf {w}}$
has no critical point in
![]() $V^*(f_{\mathbf {w}})$
, that is, the
$V^*(f_{\mathbf {w}})$
, that is, the
![]() $1$
-form
$1$
-form
![]() $df_{\mathbf {w}}$
is nowhere vanishing in
$df_{\mathbf {w}}$
is nowhere vanishing in
![]() $V^*(f_{\mathbf {w}})$
. We emphasize that
$V^*(f_{\mathbf {w}})$
. We emphasize that
![]() $V^*(f_{\mathbf {w}})$
is globally defined in
$V^*(f_{\mathbf {w}})$
is globally defined in
![]() $\mathbb {C}^{*n}$
.
$\mathbb {C}^{*n}$
.
Now, consider
![]() $k_0$
nonconstant polynomial functions
$k_0$
nonconstant polynomial functions
![]() $f^1(\mathbf {z}),\ldots , f^{k_0}(\mathbf {z})$
which all vanish at the origin.
$f^1(\mathbf {z}),\ldots , f^{k_0}(\mathbf {z})$
which all vanish at the origin.
Definition 2.2 (See [Reference Oka10]).
We say that the germ at
![]() $\mathbf {0}$
of the variety
$\mathbf {0}$
of the variety
is a germ of a nondegenerate complete intersection variety if for any positive weight vector
![]() $\mathbf {w}\in \mathbb {N}^{*n}$
, the variety
$\mathbf {w}\in \mathbb {N}^{*n}$
, the variety
is a reduced, nonsingular, complete intersection variety in
![]() $\mathbb {C}^{*n}$
, that is, the
$\mathbb {C}^{*n}$
, that is, the
![]() $k_0$
-form
$k_0$
-form
is nowhere vanishing in
![]() $V^*(f^1_{\mathbf {w}},\ldots ,f^{k_0}_{\mathbf {w}})$
. Again, we emphasize that
$V^*(f^1_{\mathbf {w}},\ldots ,f^{k_0}_{\mathbf {w}})$
. Again, we emphasize that
![]() $V^*(f^1_{\mathbf {w}},\ldots ,f^{k_0}_{\mathbf {w}})$
is globally defined in
$V^*(f^1_{\mathbf {w}},\ldots ,f^{k_0}_{\mathbf {w}})$
is globally defined in
![]() $\mathbb {C}^{*n}$
.
$\mathbb {C}^{*n}$
.
Remark 2.3. If
![]() $V(f^1,\ldots ,f^{k_0})$
is a germ of a nondegenerate complete intersection variety, then, by [Reference Oka10, Chap. III, Lem. 2.2], for any
$V(f^1,\ldots ,f^{k_0})$
is a germ of a nondegenerate complete intersection variety, then, by [Reference Oka10, Chap. III, Lem. 2.2], for any
![]() $I\in \mathcal {I}(f^1)\cap \cdots \cap \mathcal {I}(f^{k_0})$
, the germ at
$I\in \mathcal {I}(f^1)\cap \cdots \cap \mathcal {I}(f^{k_0})$
, the germ at
![]() $\mathbf {0}$
of the variety
$\mathbf {0}$
of the variety
is a germ of a nondegenerate complete intersection variety too. In other words, for any
![]() $\mathbf {w}\in \mathbb {N}^{*I}$
, the
$\mathbf {w}\in \mathbb {N}^{*I}$
, the
![]() $k_0$
-form
$k_0$
-form
![]() $ df^{1,I}_{\mathbf {w}}\wedge \cdots \wedge df^{k_0,I}_{\mathbf {w}} $
is nowhere vanishing in
$ df^{1,I}_{\mathbf {w}}\wedge \cdots \wedge df^{k_0,I}_{\mathbf {w}} $
is nowhere vanishing in
(As usual,
![]() $f^{k,I}$
is the restriction of
$f^{k,I}$
is the restriction of
![]() $f^k$
to
$f^k$
to
![]() $\mathbb {C}^I$
and
$\mathbb {C}^I$
and
![]() $f^{k,I}_{\mathbf {w}}$
is the face function
$f^{k,I}_{\mathbf {w}}$
is the face function
![]() $(f^{k,I})_{\mathbf {w}}\equiv (f^{k,I})_{\Delta (\mathbf {w};f^{k,I})}$
.)
$(f^{k,I})_{\mathbf {w}}\equiv (f^{k,I})_{\Delta (\mathbf {w};f^{k,I})}$
.)
3 Stable radius for the Milnor fibration
Let again
![]() $f^1(\mathbf {z}),\ldots , f^{k_0}(\mathbf {z})$
be nonconstant polynomial functions of n complex variables
$f^1(\mathbf {z}),\ldots , f^{k_0}(\mathbf {z})$
be nonconstant polynomial functions of n complex variables
![]() $\mathbf {z}=(z_1,\ldots ,z_n)$
such that
$\mathbf {z}=(z_1,\ldots ,z_n)$
such that
![]() $f^k(\mathbf {0})=0$
for all
$f^k(\mathbf {0})=0$
for all
![]() $1\leq k\leq k_0$
.
$1\leq k\leq k_0$
.
Assumptions 3.1. Throughout this section, we assume that for any
![]() $k_1,\ldots , k_m\in \{1,\ldots , k_0\}$
, the germ of the variety
$k_1,\ldots , k_m\in \{1,\ldots , k_0\}$
, the germ of the variety
![]() $V(f^{k_1},\ldots ,f^{k_m})$
at
$V(f^{k_1},\ldots ,f^{k_m})$
at
![]() $\mathbf {0}$
is the germ of a nondegenerate complete intersection variety.
$\mathbf {0}$
is the germ of a nondegenerate complete intersection variety.
Remark 3.2. Note that, by Remark 2.3, Assumptions 3.1 imply that for any
![]() $k_1,\ldots , k_m\in \{1,\ldots , k_0\}$
, any
$k_1,\ldots , k_m\in \{1,\ldots , k_0\}$
, any
![]() $I\in \mathcal {I}(f^{k_1})\cap \cdots \cap \mathcal {I}(f^{k_m})$
, and any
$I\in \mathcal {I}(f^{k_1})\cap \cdots \cap \mathcal {I}(f^{k_m})$
, and any
![]() $\mathbf {w}\in \mathbb {N}^{*I}$
, the following inclusion holds true:
$\mathbf {w}\in \mathbb {N}^{*I}$
, the following inclusion holds true:
 $$ \begin{align*} \Sigma^I(f_{\mathbf{w}}^{k_1},\ldots,f_{\mathbf{w}}^{k_m}) \cap V^I(f_{\mathbf{w}}^{k_1},\ldots,f_{\mathbf{w}}^{k_m}) \subseteq \bigg\{ \mathbf{z}\in\mathbb{C}^I \, ;\, \prod_{i\in I} z_i=0 \bigg\}, \end{align*} $$
$$ \begin{align*} \Sigma^I(f_{\mathbf{w}}^{k_1},\ldots,f_{\mathbf{w}}^{k_m}) \cap V^I(f_{\mathbf{w}}^{k_1},\ldots,f_{\mathbf{w}}^{k_m}) \subseteq \bigg\{ \mathbf{z}\in\mathbb{C}^I \, ;\, \prod_{i\in I} z_i=0 \bigg\}, \end{align*} $$
where
![]() $\Sigma ^I(f_{\mathbf {w}}^{k_1},\ldots ,f_{\mathbf {w}}^{k_m})$
is the critical set of the restriction to
$\Sigma ^I(f_{\mathbf {w}}^{k_1},\ldots ,f_{\mathbf {w}}^{k_m})$
is the critical set of the restriction to
![]() $\mathbb {C}^I$
of the mapping
$\mathbb {C}^I$
of the mapping
We start with the following lemma which is crucial for the paper. Note that in the special case where
![]() $k_0=1$
, the function
$k_0=1$
, the function
![]() $f^1$
(or the hypersurface
$f^1$
(or the hypersurface
![]() $V(f^1)$
) is nondegenerate, and the lemma below coincides with Lemma 1 of [Reference Oka9].
$V(f^1)$
) is nondegenerate, and the lemma below coincides with Lemma 1 of [Reference Oka9].
Lemma 3.3. Under Assumptions 3.1, there exists
![]() $\varepsilon>0$
such that for any
$\varepsilon>0$
such that for any
![]() $k_1,\ldots , k_m\in \{1,\ldots , k_0\}$
, any
$k_1,\ldots , k_m\in \{1,\ldots , k_0\}$
, any
![]() $I\subseteq \{1,\ldots ,n\}\,$
with
$I\subseteq \{1,\ldots ,n\}\,$
with
![]() $I\in \mathcal {I}(f^{k_1})\cap \cdots \cap \mathcal {I}(f^{k_m})$
, any weight vector
$I\in \mathcal {I}(f^{k_1})\cap \cdots \cap \mathcal {I}(f^{k_m})$
, any weight vector
![]() ${\mathbf {w}=(w_1,\ldots ,w_n)\in \mathbb {N}^{I}}$
, and any (possibly zero)
${\mathbf {w}=(w_1,\ldots ,w_n)\in \mathbb {N}^{I}}$
, and any (possibly zero)
![]() $\lambda \in \mathbb {C}$
, if
$\lambda \in \mathbb {C}$
, if
![]() $\mathbf {a}=(a_1,\ldots ,a_n)$
is a point in
$\mathbf {a}=(a_1,\ldots ,a_n)$
is a point in
![]() $\mathbb {C}^{I}$
satisfying the following two conditions:
$\mathbb {C}^{I}$
satisfying the following two conditions:
-
(1)
 $f_{\mathbf {w}}^{k_1,I}(\mathbf {a})=\cdots =f_{\mathbf {w}}^{k_m,I}(\mathbf {a})=0$
;
$f_{\mathbf {w}}^{k_1,I}(\mathbf {a})=\cdots =f_{\mathbf {w}}^{k_m,I}(\mathbf {a})=0$
; -
(2) there exists an m-tuple
 $(\mu _{k_1},\ldots ,\mu _{k_m})\in \mathbb {C}^m\setminus \{\mathbf {0}\}$
such that for all
$(\mu _{k_1},\ldots ,\mu _{k_m})\in \mathbb {C}^m\setminus \{\mathbf {0}\}$
such that for all
 $i\in I$
:
$i\in I$
:  $$ \begin{align*} \sum_{j=1}^m \mu_{k_j}\frac{\partial f_{\mathbf{w}}^{k_j,I}}{\partial z_{i}}(\mathbf{a})= \left\{ \begin{aligned} & \lambda\bar a_{i}, &&\mbox{if} && i\in I\cap I(\mathbf{w}),\\ & 0, &&\mbox{if} && i\in I\setminus I(\mathbf{w}), \end{aligned} \right. \end{align*} $$
$$ \begin{align*} \sum_{j=1}^m \mu_{k_j}\frac{\partial f_{\mathbf{w}}^{k_j,I}}{\partial z_{i}}(\mathbf{a})= \left\{ \begin{aligned} & \lambda\bar a_{i}, &&\mbox{if} && i\in I\cap I(\mathbf{w}),\\ & 0, &&\mbox{if} && i\in I\setminus I(\mathbf{w}), \end{aligned} \right. \end{align*} $$
where
 $\bar a_i$
is the complex conjugate of
$\bar a_i$
is the complex conjugate of
 $a_i$
and
$a_i$
and
 $I(\mathbf {w}):=\{i\in \{1,\ldots ,n\};\, w_i=0\}$
;
$I(\mathbf {w}):=\{i\in \{1,\ldots ,n\};\, w_i=0\}$
;
then we must have
 $$ \begin{align*} \mathbf{a}\notin\bigg\{\mathbf{z}\in \mathbb{C}^{*I}\, ;\, \sum_{i\in I\cap I(\mathbf{w})}|z_i|^2\leq \varepsilon^2\bigg\}. \end{align*} $$
$$ \begin{align*} \mathbf{a}\notin\bigg\{\mathbf{z}\in \mathbb{C}^{*I}\, ;\, \sum_{i\in I\cap I(\mathbf{w})}|z_i|^2\leq \varepsilon^2\bigg\}. \end{align*} $$
Remark 3.4. Lemma 3.3 amounts to saying that, under Assumptions 3.1, there exists
![]() $\varepsilon>0$
such that for any
$\varepsilon>0$
such that for any
![]() $k_1,\ldots , k_m\in \{1,\ldots , k_0\}$
, any
$k_1,\ldots , k_m\in \{1,\ldots , k_0\}$
, any
![]() $I\in \mathcal {I}(f^{k_1})\cap \cdots \cap \mathcal {I}(f^{k_m})$
, and any
$I\in \mathcal {I}(f^{k_1})\cap \cdots \cap \mathcal {I}(f^{k_m})$
, and any
![]() $\mathbf {w}\in \mathbb {N}^{I}$
, the intersection
$\mathbf {w}\in \mathbb {N}^{I}$
, the intersection
is contained in the set
![]() $\{ \mathbf {z}\in \mathbb {C}^I \, ;\, \prod _{i\in I} z_i=0 \}$
, where
$\{ \mathbf {z}\in \mathbb {C}^I \, ;\, \prod _{i\in I} z_i=0 \}$
, where
 $$ \begin{align*} \varrho_{\mathbf{w}}(\mathbf{z}):=\sum_{i\in I\cap I(\mathbf{w})}|z_i|^2 \end{align*} $$
$$ \begin{align*} \varrho_{\mathbf{w}}(\mathbf{z}):=\sum_{i\in I\cap I(\mathbf{w})}|z_i|^2 \end{align*} $$
and
![]() $\Sigma ^I(f_{\mathbf {w}}^{k_1},\ldots ,f_{\mathbf {w}}^{k_m},\varrho _{\mathbf {w}})$
is the critical set of the restriction to
$\Sigma ^I(f_{\mathbf {w}}^{k_1},\ldots ,f_{\mathbf {w}}^{k_m},\varrho _{\mathbf {w}})$
is the critical set of the restriction to
![]() $\mathbb {C}^I$
of the mapping
$\mathbb {C}^I$
of the mapping
We shall prove Lemma 3.3 at the end of this section. First, let us use it in order to prove the following first important theorem.
Theorem 3.5. Under Assumptions 3.1, if
![]() $f(\mathbf {z}):=f^1(\mathbf {z})\cdots f^{k_0}(\mathbf {z})$
, then the number
$f(\mathbf {z}):=f^1(\mathbf {z})\cdots f^{k_0}(\mathbf {z})$
, then the number
![]() $\varepsilon $
which appears in Lemma 3.3 is a stable radius for the Milnor fibration of f.
$\varepsilon $
which appears in Lemma 3.3 is a stable radius for the Milnor fibration of f.
We recall that
![]() $\varepsilon $
is called a stable radius for the Milnor fibration of f if for any
$\varepsilon $
is called a stable radius for the Milnor fibration of f if for any
![]() $0<\varepsilon _1\leq \varepsilon _2<\varepsilon $
, there exists
$0<\varepsilon _1\leq \varepsilon _2<\varepsilon $
, there exists
![]() $\delta (\varepsilon _1,\varepsilon _2)>0$
such that for any
$\delta (\varepsilon _1,\varepsilon _2)>0$
such that for any
![]() $\eta \in \mathbb {C}$
with
$\eta \in \mathbb {C}$
with
![]() $0<|\eta |\leq \delta (\varepsilon _1,\varepsilon _2)$
, the hypersurface
$0<|\eta |\leq \delta (\varepsilon _1,\varepsilon _2)$
, the hypersurface
![]() $f^{-1}(\eta )\subseteq \mathbb {C}^n$
is nonsingular in
$f^{-1}(\eta )\subseteq \mathbb {C}^n$
is nonsingular in
![]() $\mathring {B}_{\varepsilon }:=\{\mathbf {z}\in \mathbb {C}^n\, ;\, \Vert \mathbf {z} \Vert <\varepsilon \}$
and transversely intersects the spheres
$\mathring {B}_{\varepsilon }:=\{\mathbf {z}\in \mathbb {C}^n\, ;\, \Vert \mathbf {z} \Vert <\varepsilon \}$
and transversely intersects the spheres
![]() $S_{\varepsilon _{12}}:=\{\mathbf {z}\in \mathbb {C}^n\, ;\, \Vert \mathbf {z} \Vert =\varepsilon _{12}\}$
for any
$S_{\varepsilon _{12}}:=\{\mathbf {z}\in \mathbb {C}^n\, ;\, \Vert \mathbf {z} \Vert =\varepsilon _{12}\}$
for any
![]() $\varepsilon _1\leq \varepsilon _{12}\leq \varepsilon _2$
. (Equivalently,
$\varepsilon _1\leq \varepsilon _{12}\leq \varepsilon _2$
. (Equivalently,
![]() $\Sigma (f,\varrho )\cap (B_{\varepsilon _2}\setminus \mathring {B}_{\varepsilon _1})\subseteq V(f)$
for any
$\Sigma (f,\varrho )\cap (B_{\varepsilon _2}\setminus \mathring {B}_{\varepsilon _1})\subseteq V(f)$
for any
![]() $0<\varepsilon _1\leq \varepsilon _2<\varepsilon $
, where
$0<\varepsilon _1\leq \varepsilon _2<\varepsilon $
, where
![]() $\varrho (\mathbf {z}):=\sum _{i=1}^n |z_i|^2$
,
$\varrho (\mathbf {z}):=\sum _{i=1}^n |z_i|^2$
,
![]() $\Sigma (f,\varrho )$
is the critical set of the mapping
$\Sigma (f,\varrho )$
is the critical set of the mapping
![]() $(f,\varrho ) \colon \mathbb {C}^n\to \mathbb {C}\times \mathbb {R}$
, and
$(f,\varrho ) \colon \mathbb {C}^n\to \mathbb {C}\times \mathbb {R}$
, and
![]() $B_{\varepsilon _2}:=\{\mathbf {z}\in \mathbb {C}^n\, ;\, \Vert \mathbf {z} \Vert \leq \varepsilon _2\}$
.) The existence of such a radius was proved by Hamm and Lê in [Reference Hamm and Lê4, Lem. 2.1.4].
$B_{\varepsilon _2}:=\{\mathbf {z}\in \mathbb {C}^n\, ;\, \Vert \mathbf {z} \Vert \leq \varepsilon _2\}$
.) The existence of such a radius was proved by Hamm and Lê in [Reference Hamm and Lê4, Lem. 2.1.4].
Note that Theorem 3.5 includes Theorem 1 of [Reference Oka9], which is obtained by taking
![]() $k_0=1$
.
$k_0=1$
.
Proof of Theorem 3.5
We argue by contradiction. By [Reference Milnor6, Cor. 2.8], for
![]() $\delta>0$
small enough, the fibers
$\delta>0$
small enough, the fibers
![]() $f^{-1}(\eta )\cap \mathring {B}_\varepsilon $
are nonsingular for any
$f^{-1}(\eta )\cap \mathring {B}_\varepsilon $
are nonsingular for any
![]() $\eta $
,
$\eta $
,
![]() $0<|\eta |\leq \delta $
. It follows that if the assertion in Theorem 3.5 is not true, then, by the Curve Selection Lemma (see [Reference Hamm3], [Reference Milnor6]), there exist a real analytic curve
$0<|\eta |\leq \delta $
. It follows that if the assertion in Theorem 3.5 is not true, then, by the Curve Selection Lemma (see [Reference Hamm3], [Reference Milnor6]), there exist a real analytic curve
![]() $\mathbf {z}(s)=(z_1(s),\ldots ,z_n(s))$
in
$\mathbf {z}(s)=(z_1(s),\ldots ,z_n(s))$
in
![]() $\mathbb {C}^n$
,
$\mathbb {C}^n$
,
![]() $0\leq s\leq 1$
, and a family of complex numbers
$0\leq s\leq 1$
, and a family of complex numbers
![]() $\lambda (s)$
,
$\lambda (s)$
,
![]() $0<s\leq 1$
, satisfying the following three conditions:
$0<s\leq 1$
, satisfying the following three conditions:
-
(i)
 $\frac {\partial f}{\partial z_i}(\mathbf {z}(s)) = \lambda (s) \bar z_i(s)$
for
$\frac {\partial f}{\partial z_i}(\mathbf {z}(s)) = \lambda (s) \bar z_i(s)$
for
 $1\leq i\leq n$
and
$1\leq i\leq n$
and
 $s\not =0$
.
$s\not =0$
. -
(ii)
 $f(\mathbf {z}(0))=0$
, but
$f(\mathbf {z}(0))=0$
, but
 $f(\mathbf {z}(s))$
is not constantly zero.
$f(\mathbf {z}(s))$
is not constantly zero. -
(iii) There exists
 $\varepsilon '>0$
such that
$\varepsilon '>0$
such that
 $\varepsilon '\leq \Vert \mathbf {z}(s)\Vert \leq \varepsilon $
.
$\varepsilon '\leq \Vert \mathbf {z}(s)\Vert \leq \varepsilon $
.
Note that, by (i) and (ii),
![]() $\lambda (s)\not \equiv 0$
and we can express it in a Laurent series
$\lambda (s)\not \equiv 0$
and we can express it in a Laurent series
where
![]() $\lambda _0\in \mathbb {C}^*$
. Throughout, the dots “
$\lambda _0\in \mathbb {C}^*$
. Throughout, the dots “
![]() $\cdots $
” stand for the higher-order terms. Let
$\cdots $
” stand for the higher-order terms. Let
![]() $I:=\{i\, ;\, z_i(s)\not \equiv 0\}$
. By (ii),
$I:=\{i\, ;\, z_i(s)\not \equiv 0\}$
. By (ii),
![]() $I\in \mathcal {I}(f)$
, and hence
$I\in \mathcal {I}(f)$
, and hence
![]() $I\in \mathcal {I}(f^{1})\cap \cdots \cap \mathcal {I}(f^{k_0})$
. For each
$I\in \mathcal {I}(f^{1})\cap \cdots \cap \mathcal {I}(f^{k_0})$
. For each
![]() $i\in I$
, consider the Taylor expansion
$i\in I$
, consider the Taylor expansion
where
![]() $a_i\in \mathbb {C}^*$
and
$a_i\in \mathbb {C}^*$
and
![]() $w_i\in \mathbb {N}$
.
$w_i\in \mathbb {N}$
.
Claim 3.6. There exists
![]() $1\leq k\leq k_0$
such that
$1\leq k\leq k_0$
such that
![]() $f^{k,I}_{\mathbf {w}}(\mathbf {a})\equiv (f^{k,I})_{\mathbf {w}}(\mathbf {a})=0$
, where
$f^{k,I}_{\mathbf {w}}(\mathbf {a})\equiv (f^{k,I})_{\mathbf {w}}(\mathbf {a})=0$
, where
![]() $\mathbf {a}$
and
$\mathbf {a}$
and
![]() $\mathbf {w}$
are the points in
$\mathbf {w}$
are the points in
![]() $\mathbb {C}^{*I}$
and
$\mathbb {C}^{*I}$
and
![]() $\mathbb {N}^{I}$
, respectively, whose ith coordinates (
$\mathbb {N}^{I}$
, respectively, whose ith coordinates (
![]() $i\in I$
) are
$i\in I$
) are
![]() $a_{i}$
and
$a_{i}$
and
![]() $w_{i}$
, respectively.
$w_{i}$
, respectively.
Hereafter, to simplify the notation, we shall assume that
![]() $I=\{1,\ldots ,n\}$
, so that the function
$I=\{1,\ldots ,n\}$
, so that the function
![]() $f^{k,I}$
is simply written as
$f^{k,I}$
is simply written as
![]() $f^k$
, the intersection
$f^k$
, the intersection
![]() $I\cap I(\mathbf {w})$
is written as
$I\cap I(\mathbf {w})$
is written as
![]() $I(\mathbf {w})$
(where, as in Lemma 3.3,
$I(\mathbf {w})$
(where, as in Lemma 3.3,
![]() $I(\mathbf {w})$
is the set of all indexes
$I(\mathbf {w})$
is the set of all indexes
![]() $i\in \{1,\ldots ,n\}$
for which
$i\in \{1,\ldots ,n\}$
for which
![]() $w_i=0$
), and so on. The argument for a general I is completely similar.
$w_i=0$
), and so on. The argument for a general I is completely similar.
Before proving Claim 3.6, let us first complete the proof of Theorem 3.5. For that purpose, we look at the set consisting of all integers k for which
![]() $f^{k}_{\mathbf {w}}(\mathbf {a})=0$
, which is not empty by Claim 3.6. For simplicity again, we shall assume
$f^{k}_{\mathbf {w}}(\mathbf {a})=0$
, which is not empty by Claim 3.6. For simplicity again, we shall assume
 $$ \begin{align*} \begin{aligned} & f^{k}_{\mathbf{w}}(\mathbf{a})=0 &&\mbox{ for } && 1\leq k\leq k_0'\leq k_0;\\ & f^{k}_{\mathbf{w}}(\mathbf{a})\not=0 &&\mbox{ for } && k^{\prime}_0+1\leq k\leq k_0. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & f^{k}_{\mathbf{w}}(\mathbf{a})=0 &&\mbox{ for } && 1\leq k\leq k_0'\leq k_0;\\ & f^{k}_{\mathbf{w}}(\mathbf{a})\not=0 &&\mbox{ for } && k^{\prime}_0+1\leq k\leq k_0. \end{aligned} \end{align*} $$
Write
![]() $f=f^1\cdots f^{k_0'}\cdot h$
, where
$f=f^1\cdots f^{k_0'}\cdot h$
, where
![]() $h:=f^{k_0'+1}\cdots f^{k_0}$
if
$h:=f^{k_0'+1}\cdots f^{k_0}$
if
![]() $k_0'\leq k_0-1$
and
$k_0'\leq k_0-1$
and
![]() $h:=1$
if
$h:=1$
if
![]() $k_0'=k_0$
. Then, for all
$k_0'=k_0$
. Then, for all
![]() $1\leq i\leq n$
, we have
$1\leq i\leq n$
, we have
 $$ \begin{align} \frac{\partial f}{\partial z_i}(\mathbf{z}(s)) = \sum_{k=1}^{k_0'} \bigg( \frac{\partial f^{k}}{\partial z_i}(\mathbf{z}(s))\cdot h(\mathbf{z}(s))\cdot\prod_{\genfrac{}{}{0pt}{}{1\leq \ell\leq k_0'}{\ell\not=k}} f^{\ell}(\mathbf{z}(s))\bigg) +\frac{\partial h}{\partial z_i}(\mathbf{z}(s))\cdot\prod_{1\leq k\leq k_0'} f^{k}(\mathbf{z}(s)). \end{align} $$
$$ \begin{align} \frac{\partial f}{\partial z_i}(\mathbf{z}(s)) = \sum_{k=1}^{k_0'} \bigg( \frac{\partial f^{k}}{\partial z_i}(\mathbf{z}(s))\cdot h(\mathbf{z}(s))\cdot\prod_{\genfrac{}{}{0pt}{}{1\leq \ell\leq k_0'}{\ell\not=k}} f^{\ell}(\mathbf{z}(s))\bigg) +\frac{\partial h}{\partial z_i}(\mathbf{z}(s))\cdot\prod_{1\leq k\leq k_0'} f^{k}(\mathbf{z}(s)). \end{align} $$
For each
![]() $1\leq k\leq k_0'$
, if
$1\leq k\leq k_0'$
, if
![]() $o_k\equiv \mbox {ord}\, f^{k}(\mathbf {z}(s))$
denotes the order (in s) of
$o_k\equiv \mbox {ord}\, f^{k}(\mathbf {z}(s))$
denotes the order (in s) of
![]() $f^{k}(\mathbf {z}(s))$
and if
$f^{k}(\mathbf {z}(s))$
and if
![]() $e_k:=d(\mathbf {w};f^{k})-o_k+\sum _{\ell =1}^{k_0'} o_{\ell }$
, then
$e_k:=d(\mathbf {w};f^{k})-o_k+\sum _{\ell =1}^{k_0'} o_{\ell }$
, then
 $$ \begin{align} \mbox{ord}\bigg( \frac{\partial f^{k}}{\partial z_i}(\mathbf{z}(s))\cdot h(\mathbf{z}(s))\cdot\prod_{\genfrac{}{}{0pt}{}{1\leq \ell\leq k_0'}{\ell\not=k}} f^{\ell}(\mathbf{z}(s))\bigg)\geq d(\mathbf{w};h)-w_i+e_k, \end{align} $$
$$ \begin{align} \mbox{ord}\bigg( \frac{\partial f^{k}}{\partial z_i}(\mathbf{z}(s))\cdot h(\mathbf{z}(s))\cdot\prod_{\genfrac{}{}{0pt}{}{1\leq \ell\leq k_0'}{\ell\not=k}} f^{\ell}(\mathbf{z}(s))\bigg)\geq d(\mathbf{w};h)-w_i+e_k, \end{align} $$
and the equality holds if and only if
![]() $\frac {\partial f^{k}_{\mathbf {w}}}{\partial z_i}(\mathbf {a})\not =0$
. Since
$\frac {\partial f^{k}_{\mathbf {w}}}{\partial z_i}(\mathbf {a})\not =0$
. Since
![]() $o_k>d(\mathbf {w};f^{k})$
for
$o_k>d(\mathbf {w};f^{k})$
for
![]() $1\leq k\leq k^{\prime }_0$
, we also have
$1\leq k\leq k^{\prime }_0$
, we also have
 $$ \begin{align} \mbox{ord}\bigg(\frac{\partial h}{\partial z_i}(\mathbf{z}(s))\cdot\prod_{\ell=1}^{k_0'} f^{\ell}(\mathbf{z}(s))\bigg) \geq d(\mathbf{w};h)-w_i+\sum_{\ell=1}^{k_0'} o_{\ell}> d(\mathbf{w};h)-w_i+e_k \end{align} $$
$$ \begin{align} \mbox{ord}\bigg(\frac{\partial h}{\partial z_i}(\mathbf{z}(s))\cdot\prod_{\ell=1}^{k_0'} f^{\ell}(\mathbf{z}(s))\bigg) \geq d(\mathbf{w};h)-w_i+\sum_{\ell=1}^{k_0'} o_{\ell}> d(\mathbf{w};h)-w_i+e_k \end{align} $$
for all
![]() $1\leq k\leq k_0'$
. Still for simplicity, let us assume that
$1\leq k\leq k_0'$
. Still for simplicity, let us assume that
The relations (3.1)–(3.3) show that there exist
![]() $\mu _1,\ldots ,\mu _{k^{\prime \prime }_0}\in \mathbb {C}^*$
such that for any
$\mu _1,\ldots ,\mu _{k^{\prime \prime }_0}\in \mathbb {C}^*$
such that for any
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
 $$ \begin{align*} \frac{\partial f}{\partial z_{i}}(\mathbf{z}(s))=\sum_{k=1}^{k^{\prime\prime}_0}\frac{\partial {f^{k}_{\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\cdot \mu_k\cdot s^{d(\mathbf{w};h)-w_{i}+e_{\text{min}}}+\cdots, \end{align*} $$
$$ \begin{align*} \frac{\partial f}{\partial z_{i}}(\mathbf{z}(s))=\sum_{k=1}^{k^{\prime\prime}_0}\frac{\partial {f^{k}_{\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\cdot \mu_k\cdot s^{d(\mathbf{w};h)-w_{i}+e_{\text{min}}}+\cdots, \end{align*} $$
and hence, by multiplying both sides of the relation (i) by
![]() $s^{w_i}$
,
$s^{w_i}$
,
 $$ \begin{align} \sum_{k=1}^{k^{\prime\prime}_0}\frac{\partial {f^{k}_{\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\cdot \mu_k\cdot s^{d(\mathbf{w};h)+e_{\text{min}}}+\cdots = \lambda_0 \bar a_{i}s^{c+2w_{i}}+\cdots. \end{align} $$
$$ \begin{align} \sum_{k=1}^{k^{\prime\prime}_0}\frac{\partial {f^{k}_{\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\cdot \mu_k\cdot s^{d(\mathbf{w};h)+e_{\text{min}}}+\cdots = \lambda_0 \bar a_{i}s^{c+2w_{i}}+\cdots. \end{align} $$
Note that the coefficient
![]() $\lambda _0 \bar a_i$
of
$\lambda _0 \bar a_i$
of
![]() $s^{c+2w_i}$
on the right-hand side of (3.4) being nonzero, we must have
$s^{c+2w_i}$
on the right-hand side of (3.4) being nonzero, we must have
![]() $d(\mathbf {w};h)+e_{\text {min}}\leq c+2w_i$
for any
$d(\mathbf {w};h)+e_{\text {min}}\leq c+2w_i$
for any
![]() $1\leq i\leq n$
, and since
$1\leq i\leq n$
, and since
![]() $I(\mathbf {w})\not =\emptyset $
(by (iii)), in fact, we have
$I(\mathbf {w})\not =\emptyset $
(by (iii)), in fact, we have
![]() $d(\mathbf {w};h)+e_{\text {min}}\leq c$
. It follows that for any
$d(\mathbf {w};h)+e_{\text {min}}\leq c$
. It follows that for any
![]() $i\notin I(\mathbf {w})$
, the sum
$i\notin I(\mathbf {w})$
, the sum
 $$ \begin{align*} S_i:=\sum_{k=1}^{k^{\prime\prime}_0} \mu_k \frac{\partial {f^{k}_{\mathbf{w}}}}{\partial z_{i}} (\mathbf{a}) \end{align*} $$
$$ \begin{align*} S_i:=\sum_{k=1}^{k^{\prime\prime}_0} \mu_k \frac{\partial {f^{k}_{\mathbf{w}}}}{\partial z_{i}} (\mathbf{a}) \end{align*} $$
vanishes. (Indeed, if there exists
![]() $i_0\notin I(\mathbf {w})$
such that
$i_0\notin I(\mathbf {w})$
such that
![]() $S_{i_0}\not =0$
, then
$S_{i_0}\not =0$
, then
![]() $ c+2w_{i_0}=d(\mathbf {w};h)+e_{\text {min}}\leq c, $
which is a contradiction.) Now, if we also have
$ c+2w_{i_0}=d(\mathbf {w};h)+e_{\text {min}}\leq c, $
which is a contradiction.) Now, if we also have
![]() $S_i=0$
for all
$S_i=0$
for all
![]() $i\in I(\mathbf {w})$
, then the condition (2) of Lemma 3.3 is satisfied. (Note that the complex number denoted by
$i\in I(\mathbf {w})$
, then the condition (2) of Lemma 3.3 is satisfied. (Note that the complex number denoted by
![]() $\lambda $
in Lemma 3.3 may vanish.) However, the relation (iii) implies
$\lambda $
in Lemma 3.3 may vanish.) However, the relation (iii) implies
 $$ \begin{align} \mathbf{a}\in\bigg\{\mathbf{z}\in \mathbb{C}^{*n};\sum_{i\in I(\mathbf{w})}|z_i|^2\leq \varepsilon^2\bigg\}, \end{align} $$
$$ \begin{align} \mathbf{a}\in\bigg\{\mathbf{z}\in \mathbb{C}^{*n};\sum_{i\in I(\mathbf{w})}|z_i|^2\leq \varepsilon^2\bigg\}, \end{align} $$
which contradicts the conclusion of this lemma. If there exists
![]() $i_0\in I(\mathbf {w})$
such that
$i_0\in I(\mathbf {w})$
such that
![]() $S_{i_0}\not =0$
, then it follows that
$S_{i_0}\not =0$
, then it follows that
![]() $S_i\not =0$
for any
$S_i\not =0$
for any
![]() $i\in I(\mathbf {w})$
, so that for all such i’s,
$i\in I(\mathbf {w})$
, so that for all such i’s,
 $$ \begin{align*} S_i\equiv\sum_{k=1}^{k^{\prime\prime}_0} \mu_k \frac{\partial {f^{k}_{\mathbf{w}}}}{\partial z_i} (\mathbf{a}) = \lambda_0 \bar a_i. \end{align*} $$
$$ \begin{align*} S_i\equiv\sum_{k=1}^{k^{\prime\prime}_0} \mu_k \frac{\partial {f^{k}_{\mathbf{w}}}}{\partial z_i} (\mathbf{a}) = \lambda_0 \bar a_i. \end{align*} $$
Thus, the condition (2) of Lemma 3.3 is satisfied in this case too, and again the relation (iii) (which implies (3.5)) leads to a contradiction with the conclusion of the lemma. So, up to Claim 3.6, the theorem is proved.
To complete the proof of the theorem, it remains to prove Claim 3.6.
Proof of Claim 3.6
Again, to simplify, we assume
![]() $I=\{1,\ldots ,n\}$
, so that
$I=\{1,\ldots ,n\}$
, so that
![]() $f^{k,I}=f^k$
,
$f^{k,I}=f^k$
,
![]() $I\cap I(\mathbf {w})=I(\mathbf {w})$
, and so on. We argue by contradiction. Suppose
$I\cap I(\mathbf {w})=I(\mathbf {w})$
, and so on. We argue by contradiction. Suppose
![]() $f^{k}_{\mathbf {w}}(\mathbf {a})\not =0$
for all
$f^{k}_{\mathbf {w}}(\mathbf {a})\not =0$
for all
![]() $1\leq k\leq k_0$
. Then
$1\leq k\leq k_0$
. Then
![]() $d(\mathbf {w};f^{k})=o_k$
for all
$d(\mathbf {w};f^{k})=o_k$
for all
![]() $1\leq k\leq k_0$
, where
$1\leq k\leq k_0$
, where
![]() $o_k$
is the order of
$o_k$
is the order of
![]() $f^{k}(\mathbf {z}(s))$
. Furthermore, note that, by (ii), there exists
$f^{k}(\mathbf {z}(s))$
. Furthermore, note that, by (ii), there exists
![]() $1\leq k_1\leq k_0$
such that
$1\leq k_1\leq k_0$
such that
![]() $f^{k_1}(\mathbf {z}(0))=0$
. If
$f^{k_1}(\mathbf {z}(0))=0$
. If
![]() $I(\mathbf {w})=\{1,\ldots ,n\}$
, then
$I(\mathbf {w})=\{1,\ldots ,n\}$
, then
![]() $d(\mathbf {w};f^{k_1})=0$
and
$d(\mathbf {w};f^{k_1})=0$
and
and therefore
![]() $0=f^{k_1}(\mathbf {z}(0))=f^{k_1}_{\mathbf {w}}(\mathbf {a})$
, which is a contradiction. So, from now on, suppose that
$0=f^{k_1}(\mathbf {z}(0))=f^{k_1}_{\mathbf {w}}(\mathbf {a})$
, which is a contradiction. So, from now on, suppose that
![]() $I(\mathbf {w})$
is a proper subset of
$I(\mathbf {w})$
is a proper subset of
![]() $\{1,\ldots ,n\}$
and
$\{1,\ldots ,n\}$
and
![]() $d(\mathbf {w};f^{k_1})\not =0$
. Put
$d(\mathbf {w};f^{k_1})\not =0$
. Put
![]() $e:=\sum _{k=1}^{k_0} o_{k}$
. Then, as above, there exist nonzero complex numbers
$e:=\sum _{k=1}^{k_0} o_{k}$
. Then, as above, there exist nonzero complex numbers
![]() $\mu _1,\ldots ,\mu _{k_0}$
(actually, here, for each k,
$\mu _1,\ldots ,\mu _{k_0}$
(actually, here, for each k,
![]() $\mu _k=\prod _{\ell \not = k}f^{\ell }_{\mathbf {w}}(\mathbf {a})$
) such that for any
$\mu _k=\prod _{\ell \not = k}f^{\ell }_{\mathbf {w}}(\mathbf {a})$
) such that for any
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
 $$ \begin{align*} \frac{\partial f}{\partial z_{i}}(\mathbf{z}(s))=\sum_{k=1}^{k_0}\frac{\partial {f^{k}_{\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\cdot \mu_k\cdot s^{-w_{i}+e}+\cdots, \end{align*} $$
$$ \begin{align*} \frac{\partial f}{\partial z_{i}}(\mathbf{z}(s))=\sum_{k=1}^{k_0}\frac{\partial {f^{k}_{\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\cdot \mu_k\cdot s^{-w_{i}+e}+\cdots, \end{align*} $$
and hence, by multiplying both sides of the relation (i) by
![]() $s^{w_i}$
,
$s^{w_i}$
,
 $$ \begin{align*} \sum_{k=1}^{k_0}\frac{\partial {f^{k}_{\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\cdot \mu_k\cdot s^{e}+\cdots = \lambda_0 \bar a_{i}s^{c+2w_{i}}+\cdots. \end{align*} $$
$$ \begin{align*} \sum_{k=1}^{k_0}\frac{\partial {f^{k}_{\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\cdot \mu_k\cdot s^{e}+\cdots = \lambda_0 \bar a_{i}s^{c+2w_{i}}+\cdots. \end{align*} $$
Again, since
![]() $\lambda _0 \bar a_i\not =0$
and
$\lambda _0 \bar a_i\not =0$
and
![]() $I(\mathbf {w})\not =\emptyset $
, we have
$I(\mathbf {w})\not =\emptyset $
, we have
![]() $e\leq c$
and the sum
$e\leq c$
and the sum
![]() $\sum _{k=1}^{k_0}\mu _k\frac {\partial {f^{k}_{\mathbf {w}}}}{\partial z_{i}} (\mathbf {a})$
vanishes for all
$\sum _{k=1}^{k_0}\mu _k\frac {\partial {f^{k}_{\mathbf {w}}}}{\partial z_{i}} (\mathbf {a})$
vanishes for all
![]() $i\in I(\mathbf {w})^c:=\{1,\ldots ,n\}\setminus I(\mathbf {w})$
. As
$i\in I(\mathbf {w})^c:=\{1,\ldots ,n\}\setminus I(\mathbf {w})$
. As
![]() $f^{k}_{\mathbf {w}}$
is weighted homogeneous, this, together with the Euler identity, implies that
$f^{k}_{\mathbf {w}}$
is weighted homogeneous, this, together with the Euler identity, implies that
 $$ \begin{align*} 0 & = \sum_{i\in I(\mathbf{w})^c}a_i w_i\bigg(\underbrace{\sum_{k=1}^{k_0}\frac{\partial {f^{k}_{\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\cdot \mu_k}_{=0}\bigg) = \sum_{k=1}^{k_0}\bigg(\prod_{\genfrac{}{}{0pt}{}{1\leq \ell\leq k_0}{\ell\not=k}}f^{\ell}_{\mathbf{w}}(\mathbf{a})\cdot \sum_{i\in I(\mathbf{w})^c}a_i w_i \frac{\partial {f^{k}_{\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\bigg)\\ & = \sum_{k=1}^{k_0}\bigg(\prod_{\genfrac{}{}{0pt}{}{1\leq \ell\leq k_0}{\ell\not=k}}f^{\ell}_{\mathbf{w}}(\mathbf{a})\bigg)\cdot d(\mathbf{w};f^{k})\cdot f^{k}_{\mathbf{w}}(\mathbf{a}) = \bigg(\prod_{\ell=1}^{k_0}f^{\ell}_{\mathbf{w}}(\mathbf{a})\bigg)\cdot\sum_{k=1}^{k_0} d(\mathbf{w};f^{k})\not=0, \end{align*} $$
$$ \begin{align*} 0 & = \sum_{i\in I(\mathbf{w})^c}a_i w_i\bigg(\underbrace{\sum_{k=1}^{k_0}\frac{\partial {f^{k}_{\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\cdot \mu_k}_{=0}\bigg) = \sum_{k=1}^{k_0}\bigg(\prod_{\genfrac{}{}{0pt}{}{1\leq \ell\leq k_0}{\ell\not=k}}f^{\ell}_{\mathbf{w}}(\mathbf{a})\cdot \sum_{i\in I(\mathbf{w})^c}a_i w_i \frac{\partial {f^{k}_{\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\bigg)\\ & = \sum_{k=1}^{k_0}\bigg(\prod_{\genfrac{}{}{0pt}{}{1\leq \ell\leq k_0}{\ell\not=k}}f^{\ell}_{\mathbf{w}}(\mathbf{a})\bigg)\cdot d(\mathbf{w};f^{k})\cdot f^{k}_{\mathbf{w}}(\mathbf{a}) = \bigg(\prod_{\ell=1}^{k_0}f^{\ell}_{\mathbf{w}}(\mathbf{a})\bigg)\cdot\sum_{k=1}^{k_0} d(\mathbf{w};f^{k})\not=0, \end{align*} $$
which is a contradiction too.
Now, let us prove Lemma 3.3.
Proof of Lemma 3.3
First, observe that if the assertion fails for some
![]() $k_1,\dots ,k_m$
, I, and
$k_1,\dots ,k_m$
, I, and
![]() $\Delta (\mathbf {w};f^{k_1}),\ldots ,\Delta (\mathbf {w};f^{k_m})$
such that
$\Delta (\mathbf {w};f^{k_1}),\ldots ,\Delta (\mathbf {w};f^{k_m})$
such that
![]() $I\cap I(\mathbf {w})=\emptyset $
, then for any
$I\cap I(\mathbf {w})=\emptyset $
, then for any
![]() $\varepsilon>0$
, the set
$\varepsilon>0$
, the set
 $$ \begin{align*} \bigg\{\mathbf{z}\in \mathbb{C}^{*I}\, ;\, \sum_{i\in I\cap I(\mathbf{w})=\emptyset}|z_i|^2\leq \varepsilon^2\bigg\} \end{align*} $$
$$ \begin{align*} \bigg\{\mathbf{z}\in \mathbb{C}^{*I}\, ;\, \sum_{i\in I\cap I(\mathbf{w})=\emptyset}|z_i|^2\leq \varepsilon^2\bigg\} \end{align*} $$
is nothing but
![]() $\mathbb {C}^{*I}$
and there exists a point
$\mathbb {C}^{*I}$
and there exists a point
![]() $\mathbf {a}$
in it that satisfies the conditions (1) and (2) of the lemma; in particular,
$\mathbf {a}$
in it that satisfies the conditions (1) and (2) of the lemma; in particular,
![]() $\mathbf {a}\in V^{*I}(f^{k_1}_{\mathbf {w}},\ldots ,f^{k_m}_{\mathbf {w}})$
and the vectors
$\mathbf {a}\in V^{*I}(f^{k_1}_{\mathbf {w}},\ldots ,f^{k_m}_{\mathbf {w}})$
and the vectors
![]() $\mathbf {z}^{k_{1}}(\mathbf {a}),\ldots ,\mathbf {z}^{k_{m}}(\mathbf {a})\in \mathbb {C}^I$
whose ith coordinates (
$\mathbf {z}^{k_{1}}(\mathbf {a}),\ldots ,\mathbf {z}^{k_{m}}(\mathbf {a})\in \mathbb {C}^I$
whose ith coordinates (
![]() $i\in I$
) are
$i\in I$
) are
 $$ \begin{align*} \frac{\partial f_{\mathbf{w}}^{k_{1},I}}{\partial z_{i}}(\mathbf{a}),\ldots,\frac{\partial f_{\mathbf{w}}^{k_{m},I}}{\partial z_{i}}(\mathbf{a}), \end{align*} $$
$$ \begin{align*} \frac{\partial f_{\mathbf{w}}^{k_{1},I}}{\partial z_{i}}(\mathbf{a}),\ldots,\frac{\partial f_{\mathbf{w}}^{k_{m},I}}{\partial z_{i}}(\mathbf{a}), \end{align*} $$
respectively, are linearly dependent, that is,
However, since
![]() $I\in \mathcal {I}(f^{k_1})\cap \cdots \cap \mathcal {I}(f^{k_m})$
and
$I\in \mathcal {I}(f^{k_1})\cap \cdots \cap \mathcal {I}(f^{k_m})$
and
![]() $I\cap I(\mathbf {w})=\emptyset $
, this contradicts Assumptions 3.1, which imply that
$I\cap I(\mathbf {w})=\emptyset $
, this contradicts Assumptions 3.1, which imply that
for any
![]() $\mathbf {p}\in V^{*I}(f^{k_1}_{\mathbf {w}},\ldots ,f^{k_m}_{\mathbf {w}})$
(see Remark 2.3).
$\mathbf {p}\in V^{*I}(f^{k_1}_{\mathbf {w}},\ldots ,f^{k_m}_{\mathbf {w}})$
(see Remark 2.3).
Now, assume that the assertion in Lemma 3.3 fails for some
![]() $k_1,\dots ,k_m$
, I and
$k_1,\dots ,k_m$
, I and
![]() $\Delta (\mathbf {w};f^{k_1}),\ldots , \Delta (\mathbf {w};f^{k_m})$
such that
$\Delta (\mathbf {w};f^{k_1}),\ldots , \Delta (\mathbf {w};f^{k_m})$
such that
![]() $I\cap I(\mathbf {w})\not =\emptyset $
. Again, without loss of generality, and in order to simplify the notation, we assume that
$I\cap I(\mathbf {w})\not =\emptyset $
. Again, without loss of generality, and in order to simplify the notation, we assume that
![]() $I=\{1,\ldots ,n\}$
, so that
$I=\{1,\ldots ,n\}$
, so that
![]() $f^{k,I}_{\mathbf {w}}=f^{k}_{\mathbf {w}}$
,
$f^{k,I}_{\mathbf {w}}=f^{k}_{\mathbf {w}}$
,
![]() $I\cap I(\mathbf {w})=I(\mathbf {w})$
,
$I\cap I(\mathbf {w})=I(\mathbf {w})$
,
![]() $\mathbb {C}^{*I}=\mathbb {C}^{*n}$
, and so on. Then there is a sequence
$\mathbb {C}^{*I}=\mathbb {C}^{*n}$
, and so on. Then there is a sequence
![]() $\{\mathbf {p}_q\}_{q\in \mathbb {N}}$
of points in
$\{\mathbf {p}_q\}_{q\in \mathbb {N}}$
of points in
![]() $\mathbb {C}^{*n}$
and a sequence
$\mathbb {C}^{*n}$
and a sequence
![]() $\{\lambda _q\}_{q\in \mathbb {N}}$
of complex numbers such that:
$\{\lambda _q\}_{q\in \mathbb {N}}$
of complex numbers such that:
-
(1)
 $f_{\mathbf {w}}^{k_1}(\mathbf {p}_q)=\cdots =f_{\mathbf {w}}^{k_m}(\mathbf {p}_q)=0$
for all
$f_{\mathbf {w}}^{k_1}(\mathbf {p}_q)=\cdots =f_{\mathbf {w}}^{k_m}(\mathbf {p}_q)=0$
for all
 $q\in \mathbb {N}$
.
$q\in \mathbb {N}$
. -
(2) There exists a sequence
 $\{(\mu _{k_1,q},\ldots ,\mu _{k_m,q})\}_{q\in \mathbb {N}}$
of points in
$\{(\mu _{k_1,q},\ldots ,\mu _{k_m,q})\}_{q\in \mathbb {N}}$
of points in
 $\mathbb {C}^m\setminus \{\mathbf {0}\}$
such that for all
$\mathbb {C}^m\setminus \{\mathbf {0}\}$
such that for all
 $q\in \mathbb {N}$
and all
$q\in \mathbb {N}$
and all
 $1\leq i\leq n$
,
$1\leq i\leq n$
,  $$ \begin{align*} \sum_{j=1}^m \mu_{k_j,q}\frac{\partial f_{\mathbf{w}}^{k_j}}{\partial z_i}(\mathbf{p}_q)=\left\{ \begin{aligned} & \lambda_q \, \bar p_{q,i}, &&\mbox{if} && i\in I(\mathbf{w}),\\ & 0, &&\mbox{if} && i\notin I(\mathbf{w}), \end{aligned} \right. \end{align*} $$
$$ \begin{align*} \sum_{j=1}^m \mu_{k_j,q}\frac{\partial f_{\mathbf{w}}^{k_j}}{\partial z_i}(\mathbf{p}_q)=\left\{ \begin{aligned} & \lambda_q \, \bar p_{q,i}, &&\mbox{if} && i\in I(\mathbf{w}),\\ & 0, &&\mbox{if} && i\notin I(\mathbf{w}), \end{aligned} \right. \end{align*} $$
where, for each
 $1\leq i\leq n$
,
$1\leq i\leq n$
,
 $\bar p_{q,i}$
denotes the conjugate of the ith coordinate
$\bar p_{q,i}$
denotes the conjugate of the ith coordinate
 $p_{q,i}$
of
$p_{q,i}$
of
 $\mathbf {p}_q$
.
$\mathbf {p}_q$
. -
(3)
 $\sum _{i\in I(\mathbf {w})} |p_{q,i}|^2\to 0$
as
$\sum _{i\in I(\mathbf {w})} |p_{q,i}|^2\to 0$
as
 $q\to \infty $
.
$q\to \infty $
.
For any
![]() $\zeta \in \mathbb {C}$
and any
$\zeta \in \mathbb {C}$
and any
![]() $\mathbf {z}\in \mathbb {C}^n$
, let
$\mathbf {z}\in \mathbb {C}^n$
, let
![]() $\zeta *\mathbf {z}=((\zeta *\mathbf {z})_1,\ldots ,(\zeta *\mathbf {z})_n)$
be the point of
$\zeta *\mathbf {z}=((\zeta *\mathbf {z})_1,\ldots ,(\zeta *\mathbf {z})_n)$
be the point of
![]() $\mathbb {C}^n$
defined by
$\mathbb {C}^n$
defined by
 $$ \begin{align*} (\zeta*\mathbf{z})_i:= \zeta^{w_i}z_i= \left\{ \begin{aligned} &z_i, &&\mbox{for} && i\in I(\mathbf{w}),\\ & \zeta^{w_i}z_i, &&\mbox{for} && i\notin I(\mathbf{w}).\\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*} (\zeta*\mathbf{z})_i:= \zeta^{w_i}z_i= \left\{ \begin{aligned} &z_i, &&\mbox{for} && i\in I(\mathbf{w}),\\ & \zeta^{w_i}z_i, &&\mbox{for} && i\notin I(\mathbf{w}).\\ \end{aligned} \right. \end{align*} $$
Then pick a sequence
![]() $\{\zeta _q\}_{q\in \mathbb {N}}$
of points in
$\{\zeta _q\}_{q\in \mathbb {N}}$
of points in
![]() $\mathbb {C}^{*}$
that converges to zero sufficiently fast so that the sequence
$\mathbb {C}^{*}$
that converges to zero sufficiently fast so that the sequence
![]() $\{\zeta _q*\mathbf {p}_q\}_{q\in \mathbb {N}}$
converges to the origin of
$\{\zeta _q*\mathbf {p}_q\}_{q\in \mathbb {N}}$
converges to the origin of
![]() $\mathbb {C}^{n}$
. Clearly,
$\mathbb {C}^{n}$
. Clearly,
![]() $\{\zeta _q*\mathbf {p}_q\}_{q\in \mathbb {N}}$
also satisfies the above properties (1)–(3). Indeed, for any
$\{\zeta _q*\mathbf {p}_q\}_{q\in \mathbb {N}}$
also satisfies the above properties (1)–(3). Indeed, for any
![]() $1\leq j\leq m$
, we have
$1\leq j\leq m$
, we have
so
![]() $\{\zeta _q*\mathbf {p}_q\}_{q\in \mathbb {N}}$
satisfies (1). For each
$\{\zeta _q*\mathbf {p}_q\}_{q\in \mathbb {N}}$
satisfies (1). For each
![]() $1\leq i\leq n$
, we also have
$1\leq i\leq n$
, we also have
 $$ \begin{align*} \frac{\partial f_{\mathbf{w}}^{k_j}}{\partial z_i}(\zeta_q*\mathbf{p}_q)= \zeta_q^{d(\mathbf{w};f^{k_j})-w_i} \, \frac{\partial f_{\mathbf{w}}^{k_j}}{\partial z_i}(\mathbf{p}_q), \end{align*} $$
$$ \begin{align*} \frac{\partial f_{\mathbf{w}}^{k_j}}{\partial z_i}(\zeta_q*\mathbf{p}_q)= \zeta_q^{d(\mathbf{w};f^{k_j})-w_i} \, \frac{\partial f_{\mathbf{w}}^{k_j}}{\partial z_i}(\mathbf{p}_q), \end{align*} $$
and since
![]() $\zeta _q^{w_i}=1$
for all
$\zeta _q^{w_i}=1$
for all
![]() $i\in I(\mathbf {w})$
and
$i\in I(\mathbf {w})$
and
![]() $\zeta _q^{w_i}$
(which is nonzero) is independent of the index j (
$\zeta _q^{w_i}$
(which is nonzero) is independent of the index j (
![]() $1\leq j\leq m$
) for all
$1\leq j\leq m$
) for all
![]() $i\notin I(\mathbf {w})$
, it follows that
$i\notin I(\mathbf {w})$
, it follows that
 $$ \begin{align*} \sum_{j=1}^m \frac{\mu_{k_j,q}}{\zeta_q^{d(\mathbf{w};f^{k_j})}} \frac{\partial f_{\mathbf{w}}^{k_j}}{\partial z_i}(\zeta_q*\mathbf{p}_q)=\left\{ \begin{aligned} & \lambda_q \, \bar p_{q,i}, &&\mbox{for} && i\in I(\mathbf{w}),\\ & 0, &&\mbox{for} && i\notin I(\mathbf{w}), \end{aligned} \right. \end{align*} $$
$$ \begin{align*} \sum_{j=1}^m \frac{\mu_{k_j,q}}{\zeta_q^{d(\mathbf{w};f^{k_j})}} \frac{\partial f_{\mathbf{w}}^{k_j}}{\partial z_i}(\zeta_q*\mathbf{p}_q)=\left\{ \begin{aligned} & \lambda_q \, \bar p_{q,i}, &&\mbox{for} && i\in I(\mathbf{w}),\\ & 0, &&\mbox{for} && i\notin I(\mathbf{w}), \end{aligned} \right. \end{align*} $$
so that the sequence
![]() $\{\zeta _q*\mathbf {p}_q\}_{q\in \mathbb {N}}$
satisfies (2) with the complex numbers
$\{\zeta _q*\mathbf {p}_q\}_{q\in \mathbb {N}}$
satisfies (2) with the complex numbers
![]() $\mu _{k_j,q} / \zeta _q^{d(\mathbf {w};f^{k_j})}$
(
$\mu _{k_j,q} / \zeta _q^{d(\mathbf {w};f^{k_j})}$
(
![]() $1\leq j\leq m$
). Finally,
$1\leq j\leq m$
). Finally,
 $$ \begin{align*} \sum_{i\in I(\mathbf{w})} |(\zeta_q*\mathbf{p}_q)_i|^2 = \sum_{i\in I(\mathbf{w})} |p_{q,i}|^2\to 0, \end{align*} $$
$$ \begin{align*} \sum_{i\in I(\mathbf{w})} |(\zeta_q*\mathbf{p}_q)_i|^2 = \sum_{i\in I(\mathbf{w})} |p_{q,i}|^2\to 0, \end{align*} $$
as
![]() $q\to \infty $
, so
$q\to \infty $
, so
![]() $\{\zeta _q*\mathbf {p}_q\}_{q\in \mathbb {N}}$
also satisfies (3). Altogether,
$\{\zeta _q*\mathbf {p}_q\}_{q\in \mathbb {N}}$
also satisfies (3). Altogether,
![]() $\{\zeta _q*\mathbf {p}_q\}_{q\in \mathbb {N}}$
satisfies the properties (1)–(3). Therefore, we can apply the Curve Selection Lemma to this situation in order to find a real analytic curve
$\{\zeta _q*\mathbf {p}_q\}_{q\in \mathbb {N}}$
satisfies the properties (1)–(3). Therefore, we can apply the Curve Selection Lemma to this situation in order to find a real analytic curve
![]() $\mathbf {a}(s)=(a_1(s),\ldots ,a_n(s))$
in
$\mathbf {a}(s)=(a_1(s),\ldots ,a_n(s))$
in
![]() $\mathbb {C}^n$
,
$\mathbb {C}^n$
,
![]() $0\leq s\leq 1$
, and a family of complex numbers
$0\leq s\leq 1$
, and a family of complex numbers
![]() $\lambda (s)$
,
$\lambda (s)$
,
![]() $0<s\leq 1$
, such that:
$0<s\leq 1$
, such that:
-
(1′)
 $f_{\mathbf {w}}^{k_1}(\mathbf {a}(s))=\cdots =f_{\mathbf {w}}^{k_m}(\mathbf {a}(s))=0$
for all
$f_{\mathbf {w}}^{k_1}(\mathbf {a}(s))=\cdots =f_{\mathbf {w}}^{k_m}(\mathbf {a}(s))=0$
for all
 $s\not =0$
.
$s\not =0$
. -
(2′) There exists a real analytic curve
 $(\mu _{k_1}(s),\ldots ,\mu _{k_m}(s))$
in
$(\mu _{k_1}(s),\ldots ,\mu _{k_m}(s))$
in
 $\mathbb {C}^m\setminus \{\mathbf {0}\}$
,
$\mathbb {C}^m\setminus \{\mathbf {0}\}$
,
 $0< s\leq 1$
, such that for all
$0< s\leq 1$
, such that for all
 $s\not =0$
and all
$s\not =0$
and all
 $1\leq i\leq n$
,
$1\leq i\leq n$
,  $$ \begin{align*} \sum_{j=1}^m \mu_{k_j}(s)\, \frac{\partial f_{\mathbf{w}}^{k_j}}{\partial z_i}(\mathbf{a}(s))=\left\{ \begin{aligned} & \lambda(s)\, \bar a_{i}(s), &&\mbox{if} &&i\in I(\mathbf{w}),\\ & 0, &&\mbox{if} &&i\notin I(\mathbf{w}). \end{aligned} \right. \end{align*} $$
$$ \begin{align*} \sum_{j=1}^m \mu_{k_j}(s)\, \frac{\partial f_{\mathbf{w}}^{k_j}}{\partial z_i}(\mathbf{a}(s))=\left\{ \begin{aligned} & \lambda(s)\, \bar a_{i}(s), &&\mbox{if} &&i\in I(\mathbf{w}),\\ & 0, &&\mbox{if} &&i\notin I(\mathbf{w}). \end{aligned} \right. \end{align*} $$
-
(3′)
 $\mathbf {a}(0)=\mathbf {0}$
and
$\mathbf {a}(0)=\mathbf {0}$
and
 $\mathbf {a}(s)\in \mathbb {C}^{*n}$
for
$\mathbf {a}(s)\in \mathbb {C}^{*n}$
for
 $s\not =0$
.
$s\not =0$
.
For each
![]() $1\leq i\leq n$
, consider the Taylor expansion
$1\leq i\leq n$
, consider the Taylor expansion
where
![]() $b_i\in \mathbb {C}^*$
and
$b_i\in \mathbb {C}^*$
and
![]() $v_i\in \mathbb {N}^*$
. Since the
$v_i\in \mathbb {N}^*$
. Since the
![]() $v_i$
’s are all positive, for each
$v_i$
’s are all positive, for each
![]() $1\leq j\leq m$
, the face
$1\leq j\leq m$
, the face
![]() $\Delta \big (\mathbf {v};f_{\mathbf {w}}^{k_j}\big )$
is a compact face of
$\Delta \big (\mathbf {v};f_{\mathbf {w}}^{k_j}\big )$
is a compact face of
![]() $\Delta (\mathbf {w};f^{k_j})$
, and hence
$\Delta (\mathbf {w};f^{k_j})$
, and hence
![]() $\Delta \big (\mathbf {v};f_{\mathbf {w}}^{k_j}\big )$
is a face of
$\Delta \big (\mathbf {v};f_{\mathbf {w}}^{k_j}\big )$
is a face of
![]() $\Gamma (f^{k_j})$
, where
$\Gamma (f^{k_j})$
, where
![]() $\mathbf {v}$
is the point of
$\mathbf {v}$
is the point of
![]() $\mathbb {N}^{*n}$
whose ith coordinate is
$\mathbb {N}^{*n}$
whose ith coordinate is
![]() $v_i$
. Furthermore, note that for each j, we have
$v_i$
. Furthermore, note that for each j, we have
![]() $d\big (\mathbf {v};f_{\mathbf {w}}^{k_j}\big )>0$
, and since
$d\big (\mathbf {v};f_{\mathbf {w}}^{k_j}\big )>0$
, and since
for all
![]() $s\not =0$
, we also have
$s\not =0$
, we also have
![]() $\big (f_{\mathbf {w}}^{k_j}\big )_{\mathbf {v}}(\mathbf {b})=0$
, where
$\big (f_{\mathbf {w}}^{k_j}\big )_{\mathbf {v}}(\mathbf {b})=0$
, where
![]() $\mathbf {b}$
is the point of
$\mathbf {b}$
is the point of
![]() $\mathbb {C}^{*n}$
whose ith coordinate is
$\mathbb {C}^{*n}$
whose ith coordinate is
![]() $b_i$
. (As usual,
$b_i$
. (As usual,
![]() $\big (f_{\mathbf {w}}^{k_j}\big )_{\mathbf {v}}$
is the face function of
$\big (f_{\mathbf {w}}^{k_j}\big )_{\mathbf {v}}$
is the face function of
![]() $f_{\mathbf {w}}^{k_j}$
with respect to
$f_{\mathbf {w}}^{k_j}$
with respect to
![]() $\mathbf {v}$
.)
$\mathbf {v}$
.)
Write
![]() $\mu _{k_j}(s)=\mu _{k_j} s^{g_j}+\cdots $
, where
$\mu _{k_j}(s)=\mu _{k_j} s^{g_j}+\cdots $
, where
![]() $\mu _{k_j}\not =0$
. If
$\mu _{k_j}\not =0$
. If
![]() $\mu _{k_j}(s)\equiv 0$
, then
$\mu _{k_j}(s)\equiv 0$
, then
![]() $g_j=\infty $
. Let
$g_j=\infty $
. Let
and put
 $$ \begin{align*} \tilde\mu_{k_j} = \left\{ \begin{aligned} & \mu_{k_j}, &&\mbox{if} && d\big(\mathbf{v};f_{\mathbf{w}}^{k_j}\big)+g_j=\delta,\\ & 0, &&\mbox{if} && d\big(\mathbf{v};f_{\mathbf{w}}^{k_j}\big)+g_j>\delta. \end{aligned} \right. \end{align*} $$
$$ \begin{align*} \tilde\mu_{k_j} = \left\{ \begin{aligned} & \mu_{k_j}, &&\mbox{if} && d\big(\mathbf{v};f_{\mathbf{w}}^{k_j}\big)+g_j=\delta,\\ & 0, &&\mbox{if} && d\big(\mathbf{v};f_{\mathbf{w}}^{k_j}\big)+g_j>\delta. \end{aligned} \right. \end{align*} $$
Claim 3.7. There exists
![]() $i_0\in I(\mathbf {w})$
such that
$i_0\in I(\mathbf {w})$
such that
 $ \sum _{j=1}^m \tilde \mu _{k_j} \frac {\partial \big (f_{\mathbf {w}}^{k_j}\big )_{\mathbf {v}}}{\partial z_{i_0}}(\mathbf {b})\not =0. $
(We recall that
$ \sum _{j=1}^m \tilde \mu _{k_j} \frac {\partial \big (f_{\mathbf {w}}^{k_j}\big )_{\mathbf {v}}}{\partial z_{i_0}}(\mathbf {b})\not =0. $
(We recall that
![]() $\mu _{k_j}(s)\not \equiv 0$
for at least an index j.)
$\mu _{k_j}(s)\not \equiv 0$
for at least an index j.)
Proof. First, observe that for all
![]() $1\leq j\leq m$
and all
$1\leq j\leq m$
and all
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
 $$ \begin{align*} \frac{\partial f_{\mathbf{w}}^{k_j}}{\partial z_{i}}(\mathbf{a}(s)) = \frac{\partial \big(f_{\mathbf{w}}^{k_j}\big)_{\mathbf{v}}}{\partial z_{i}}(\mathbf{b})\, s^{d\big(\mathbf{v};f_{\mathbf{w}}^{k_j}\big)-v_i} + \cdots. \end{align*} $$
$$ \begin{align*} \frac{\partial f_{\mathbf{w}}^{k_j}}{\partial z_{i}}(\mathbf{a}(s)) = \frac{\partial \big(f_{\mathbf{w}}^{k_j}\big)_{\mathbf{v}}}{\partial z_{i}}(\mathbf{b})\, s^{d\big(\mathbf{v};f_{\mathbf{w}}^{k_j}\big)-v_i} + \cdots. \end{align*} $$
Thus, if the assertion in Claim 3.7 fails, then the sum
 $$ \begin{align*} \sum_{j=1}^m \tilde\mu_{k_j} \frac{\partial \big(f_{\mathbf{w}}^{k_j}\big)_{\mathbf{v}}}{\partial z_{i}}(\mathbf{b}) \end{align*} $$
$$ \begin{align*} \sum_{j=1}^m \tilde\mu_{k_j} \frac{\partial \big(f_{\mathbf{w}}^{k_j}\big)_{\mathbf{v}}}{\partial z_{i}}(\mathbf{b}) \end{align*} $$
vanishes for all
![]() $i\in I(\mathbf {w})$
, and so, by (
$i\in I(\mathbf {w})$
, and so, by (
![]() $2'$
), it vanishes for all
$2'$
), it vanishes for all
![]() $1\leq i\leq n$
. In other words, if
$1\leq i\leq n$
. In other words, if
![]() $k_{j_1},\ldots ,k_{j_p}$
are the elements of the set
$k_{j_1},\ldots ,k_{j_p}$
are the elements of the set
![]() $\{k_1,\ldots ,k_m\}$
for which
$\{k_1,\ldots ,k_m\}$
for which
![]() $d\big (\mathbf {v};f_{\mathbf {w}}^{k_{j_\ell }}\big )+g_{j_\ell }=\delta $
,
$d\big (\mathbf {v};f_{\mathbf {w}}^{k_{j_\ell }}\big )+g_{j_\ell }=\delta $
,
![]() $1\leq \ell \leq p$
, then the vectors
$1\leq \ell \leq p$
, then the vectors
 $$ \begin{align*} \bigg(\frac{\partial \big(f_{\mathbf{w}}^{k_{j_1}}\big)_{\mathbf{v}}}{\partial z_{1}}(\mathbf{b}),\ldots,\frac{\partial \big(f_{\mathbf{w}}^{k_{j_1}}\big)_{\mathbf{v}}}{\partial z_{n}}(\mathbf{b})\bigg) ,\ldots, \bigg(\frac{\partial \big(f_{\mathbf{w}}^{k_{j_p}}\big)_{\mathbf{v}}}{\partial z_{1}}(\mathbf{b}),\ldots,\frac{\partial \big(f_{\mathbf{w}}^{k_{j_p}}\big)_{\mathbf{v}}}{\partial z_{n}}(\mathbf{b})\bigg) \end{align*} $$
$$ \begin{align*} \bigg(\frac{\partial \big(f_{\mathbf{w}}^{k_{j_1}}\big)_{\mathbf{v}}}{\partial z_{1}}(\mathbf{b}),\ldots,\frac{\partial \big(f_{\mathbf{w}}^{k_{j_1}}\big)_{\mathbf{v}}}{\partial z_{n}}(\mathbf{b})\bigg) ,\ldots, \bigg(\frac{\partial \big(f_{\mathbf{w}}^{k_{j_p}}\big)_{\mathbf{v}}}{\partial z_{1}}(\mathbf{b}),\ldots,\frac{\partial \big(f_{\mathbf{w}}^{k_{j_p}}\big)_{\mathbf{v}}}{\partial z_{n}}(\mathbf{b})\bigg) \end{align*} $$
of
![]() $\mathbb {C}^n$
are linearly dependent, that is,
$\mathbb {C}^n$
are linearly dependent, that is,
As
![]() $\big (f_{\mathbf {w}}^{k_{j_\ell }}\big )_{\mathbf {v}} = f_{\mathbf {v}+\nu \mathbf {w}}^{k_{j_\ell }}$
for any sufficiently large integer
$\big (f_{\mathbf {w}}^{k_{j_\ell }}\big )_{\mathbf {v}} = f_{\mathbf {v}+\nu \mathbf {w}}^{k_{j_\ell }}$
for any sufficiently large integer
![]() $\nu \in \mathbb {N}$
(so that
$\nu \in \mathbb {N}$
(so that
![]() $\big (f_{\mathbf {w}}^{k_{j_\ell }}\big )_{\mathbf {v}}$
is the face function of
$\big (f_{\mathbf {w}}^{k_{j_\ell }}\big )_{\mathbf {v}}$
is the face function of
![]() $f^{k_{j_\ell }}$
with respect to the weight vector
$f^{k_{j_\ell }}$
with respect to the weight vector
![]() $\mathbf {v}+\nu \mathbf {w}$
) and
$\mathbf {v}+\nu \mathbf {w}$
) and
![]() $\big (f_{\mathbf {w}}^{k_{j_\ell }}\big )_{\mathbf {v}}(\mathbf {b})=0$
for
$\big (f_{\mathbf {w}}^{k_{j_\ell }}\big )_{\mathbf {v}}(\mathbf {b})=0$
for
![]() $1\leq \ell \leq p$
, this contradicts the nondegeneracy of
$1\leq \ell \leq p$
, this contradicts the nondegeneracy of
![]() $V(f^{k_{j_1}},\ldots ,f^{k_{j_p}})$
(see Assumptions 3.1).
$V(f^{k_{j_1}},\ldots ,f^{k_{j_p}})$
(see Assumptions 3.1).
Combined with (
![]() $2'$
) again, Claim 3.7 implies that
$2'$
) again, Claim 3.7 implies that
![]() $\lambda (s)$
is not constantly zero. Write it as a Laurent series
$\lambda (s)$
is not constantly zero. Write it as a Laurent series
![]() $\lambda (s)=\lambda _0 s^c+\cdots $
, where
$\lambda (s)=\lambda _0 s^c+\cdots $
, where
![]() $\lambda _0\not =0$
. Then, still from (
$\lambda _0\not =0$
. Then, still from (
![]() $2'$
), we deduce that for all
$2'$
), we deduce that for all
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
 $$ \begin{align} \sum_{j=1}^m \tilde\mu_{k_j} \frac{\partial \big(f_{\mathbf{w}}^{k_j}\big)_{\mathbf{v}}}{\partial z_i}(\mathbf{b})\, s^{\delta} + \cdots = \left\{ \begin{aligned} & \lambda_0 \bar b_i\, s^{c+2v_i}+\cdots, &&\mbox{if} &&i\in I(\mathbf{w}),\\ & 0, &&\mbox{if} &&i\notin I(\mathbf{w}). \end{aligned} \right. \end{align} $$
$$ \begin{align} \sum_{j=1}^m \tilde\mu_{k_j} \frac{\partial \big(f_{\mathbf{w}}^{k_j}\big)_{\mathbf{v}}}{\partial z_i}(\mathbf{b})\, s^{\delta} + \cdots = \left\{ \begin{aligned} & \lambda_0 \bar b_i\, s^{c+2v_i}+\cdots, &&\mbox{if} &&i\in I(\mathbf{w}),\\ & 0, &&\mbox{if} &&i\notin I(\mathbf{w}). \end{aligned} \right. \end{align} $$
Put
![]() $S_i:=\sum _{j=1}^m \tilde \mu _{k_j} \frac {\partial \big (f_{\mathbf {w}}^{k_j}\big )_{\mathbf {v}}}{\partial z_i}(\mathbf {b})$
, and define
$S_i:=\sum _{j=1}^m \tilde \mu _{k_j} \frac {\partial \big (f_{\mathbf {w}}^{k_j}\big )_{\mathbf {v}}}{\partial z_i}(\mathbf {b})$
, and define
Since the coefficient
![]() $\lambda _0\bar b_i$
on the right-hand side of (3.6) is nonzero and the set of indexes
$\lambda _0\bar b_i$
on the right-hand side of (3.6) is nonzero and the set of indexes
![]() $i\in I(\mathbf {w})$
such that
$i\in I(\mathbf {w})$
such that
![]() $S_i\not =0$
is not empty (see Claim 3.7), we have
$S_i\not =0$
is not empty (see Claim 3.7), we have
![]() $\delta =c+2v_0$
and
$\delta =c+2v_0$
and
![]() $S_i\not =0$
for any
$S_i\not =0$
for any
![]() $i\in I_0$
. In fact, for any
$i\in I_0$
. In fact, for any
![]() $1\leq i\leq n$
, the following equality holds:
$1\leq i\leq n$
, the following equality holds:
 $$ \begin{align} S_i\equiv\sum_{j=1}^m \tilde\mu_{k_j} \frac{\partial \big(f_{\mathbf{w}}^{k_j}\big)_{\mathbf{v}}}{\partial z_i}(\mathbf{b})= \left\{ \begin{aligned} & \lambda_0 \bar b_i, && \mbox{if} && i\in I_0,\\ & 0, && \mbox{if} && i\notin I_0. \end{aligned} \right. \end{align} $$
$$ \begin{align} S_i\equiv\sum_{j=1}^m \tilde\mu_{k_j} \frac{\partial \big(f_{\mathbf{w}}^{k_j}\big)_{\mathbf{v}}}{\partial z_i}(\mathbf{b})= \left\{ \begin{aligned} & \lambda_0 \bar b_i, && \mbox{if} && i\in I_0,\\ & 0, && \mbox{if} && i\notin I_0. \end{aligned} \right. \end{align} $$
Since
![]() $I_0\not =\emptyset $
and
$I_0\not =\emptyset $
and
![]() $\big (f_{\mathbf {w}}^{k_j}\big )_{\mathbf {v}}(\mathbf {b})=0$
(
$\big (f_{\mathbf {w}}^{k_j}\big )_{\mathbf {v}}(\mathbf {b})=0$
(
![]() $1\leq j\leq m$
), combined with the Euler identity, the relation (3.8) implies
$1\leq j\leq m$
), combined with the Euler identity, the relation (3.8) implies
 $$ \begin{align*} 0 & = \sum_{j=1}^{m}\tilde\mu_{k_j}\cdot d\big(\mathbf{v};f_{\mathbf{w}}^{k_j}\big) \cdot \big(f_{\mathbf{w}}^{k_j}\big)_{\mathbf{v}}(\mathbf{b}) = \sum_{j=1}^{m}\tilde\mu_{k_j}\bigg(\sum_{i=1}^n v_i b_i \frac{\partial \big(f_{\mathbf{w}}^{k_j}\big)_{\mathbf{v}}}{\partial z_i}(\mathbf{b})\bigg) \\ & = \sum_{i\in I_0}v_i b_i\bigg( \sum_{j=1}^{m}\tilde\mu_{k_j} \frac{\partial \big(f_{\mathbf{w}}^{k_j}\big)_{\mathbf{v}}}{\partial z_i}(\mathbf{b}) \bigg) =\lambda_0\cdot\sum_{i\in I_0} v_i |b_i|^2\not=0, \end{align*} $$
$$ \begin{align*} 0 & = \sum_{j=1}^{m}\tilde\mu_{k_j}\cdot d\big(\mathbf{v};f_{\mathbf{w}}^{k_j}\big) \cdot \big(f_{\mathbf{w}}^{k_j}\big)_{\mathbf{v}}(\mathbf{b}) = \sum_{j=1}^{m}\tilde\mu_{k_j}\bigg(\sum_{i=1}^n v_i b_i \frac{\partial \big(f_{\mathbf{w}}^{k_j}\big)_{\mathbf{v}}}{\partial z_i}(\mathbf{b})\bigg) \\ & = \sum_{i\in I_0}v_i b_i\bigg( \sum_{j=1}^{m}\tilde\mu_{k_j} \frac{\partial \big(f_{\mathbf{w}}^{k_j}\big)_{\mathbf{v}}}{\partial z_i}(\mathbf{b}) \bigg) =\lambda_0\cdot\sum_{i\in I_0} v_i |b_i|^2\not=0, \end{align*} $$
which is a contradiction. This completes the proof of Lemma 3.3.
4 Uniformly stable family and uniform stable radius
Now, let
![]() $f^1(t,\mathbf {z}),\ldots , f^{k_0}(t,\mathbf {z})$
be nonconstant polynomial functions of
$f^1(t,\mathbf {z}),\ldots , f^{k_0}(t,\mathbf {z})$
be nonconstant polynomial functions of
![]() $n+1$
complex variables
$n+1$
complex variables
![]() $(t,\mathbf {z})=(t,z_1,\ldots ,z_n)$
such that
$(t,\mathbf {z})=(t,z_1,\ldots ,z_n)$
such that
![]() $f^k(t,\mathbf {0})=0$
for all
$f^k(t,\mathbf {0})=0$
for all
![]() $t\in \mathbb {C}$
and all
$t\in \mathbb {C}$
and all
![]() $1\leq k\leq k_0$
. As usual, for any
$1\leq k\leq k_0$
. As usual, for any
![]() $t\in \mathbb {C}$
, we write
$t\in \mathbb {C}$
, we write
![]() $f^k_t(\mathbf {z}):=f^k(t,\mathbf {z})$
.
$f^k_t(\mathbf {z}):=f^k(t,\mathbf {z})$
.
Assumptions 4.1. Throughout this section, we suppose that for any sufficiently small t (say,
![]() $|t|\leq \tau _0$
for some
$|t|\leq \tau _0$
for some
![]() $\tau _0>0$
), the following two conditions hold true:
$\tau _0>0$
), the following two conditions hold true:
-
(1) For any
 $1\leq k\leq k_0$
, the Newton boundary
$1\leq k\leq k_0$
, the Newton boundary
 $\Gamma (f^k_t)$
is independent of t. (We may still have
$\Gamma (f^k_t)$
is independent of t. (We may still have
 $\Gamma (f_t^{k})\not =\Gamma (f_t^{k'})$
for
$\Gamma (f_t^{k})\not =\Gamma (f_t^{k'})$
for
 $k\not =k'$
.).
$k\not =k'$
.). -
(2) For any
 $k_1,\ldots ,k_m\in \{k_1,\ldots ,k_0\}$
, the germ at
$k_1,\ldots ,k_m\in \{k_1,\ldots ,k_0\}$
, the germ at
 $\mathbf {0}$
of the variety
$\mathbf {0}$
of the variety
 $V(f^{k_1}_t,\ldots ,f^{k_m}_t)$
is the germ of a nondegenerate complete intersection variety.
$V(f^{k_1}_t,\ldots ,f^{k_m}_t)$
is the germ of a nondegenerate complete intersection variety.
Note that (1) implies that the set
![]() $\mathcal {I}(f^k_t)$
is independent of t.
$\mathcal {I}(f^k_t)$
is independent of t.
4.1 Statements of the results of §4
By Lemma 3.3, we know that under Assumptions 4.1, there exists
![]() $\varepsilon _0>0$
such that for any
$\varepsilon _0>0$
such that for any
![]() $k_1,\ldots , k_m\in \{1,\ldots , k_0\}$
, any
$k_1,\ldots , k_m\in \{1,\ldots , k_0\}$
, any
![]() $I\subseteq \{1,\ldots ,n\}$
with
$I\subseteq \{1,\ldots ,n\}$
with
![]() $I\in \mathcal {I}(f_0^{k_1})\cap \cdots \cap \mathcal {I}(f_0^{k_m})$
, any weight vector
$I\in \mathcal {I}(f_0^{k_1})\cap \cdots \cap \mathcal {I}(f_0^{k_m})$
, any weight vector
![]() $\mathbf {w}\in \mathbb {N}^{I}$
, and any
$\mathbf {w}\in \mathbb {N}^{I}$
, and any
![]() $\lambda \in \mathbb {C}$
, if
$\lambda \in \mathbb {C}$
, if
![]() $\mathbf {a}\in \mathbb {C}^{I}$
satisfies the conditions (1) and (2) of this lemma for the functions
$\mathbf {a}\in \mathbb {C}^{I}$
satisfies the conditions (1) and (2) of this lemma for the functions
![]() $f_{0,\mathbf {w}}^{k_1,I},\ldots ,f_{0,\mathbf {w}}^{k_m,I}$
, then
$f_{0,\mathbf {w}}^{k_1,I},\ldots ,f_{0,\mathbf {w}}^{k_m,I}$
, then
 $$ \begin{align*} \mathbf{a}\notin\bigg\{\mathbf{z}\in \mathbb{C}^{*I}\, ;\, \sum_{i\in I\cap I(\mathbf{w})}|z_i|^2\leq \varepsilon_0^2\bigg\}. \end{align*} $$
$$ \begin{align*} \mathbf{a}\notin\bigg\{\mathbf{z}\in \mathbb{C}^{*I}\, ;\, \sum_{i\in I\cap I(\mathbf{w})}|z_i|^2\leq \varepsilon_0^2\bigg\}. \end{align*} $$
(Here,
![]() $f_{0,\mathbf {w}}^{k,I}$
denotes the face function
$f_{0,\mathbf {w}}^{k,I}$
denotes the face function
![]() $(f_{0}^{k,I})_{\mathbf {w}}\equiv (f_{0}^{k,I})_{\Delta (\mathbf {w};f_{0}^{k,I})}$
of
$(f_{0}^{k,I})_{\mathbf {w}}\equiv (f_{0}^{k,I})_{\Delta (\mathbf {w};f_{0}^{k,I})}$
of
![]() $f_{0}^{k,I}$
with respect to
$f_{0}^{k,I}$
with respect to
![]() $\mathbf {w}$
.)
$\mathbf {w}$
.)
Once for all, let us fix such a number
![]() $\varepsilon _0$
. Then we have the following result which asserts that if t is small enough, then Lemma 3.3 also holds for the functions
$\varepsilon _0$
. Then we have the following result which asserts that if t is small enough, then Lemma 3.3 also holds for the functions
![]() $f_{t,\mathbf {w}}^{k_1,I},\ldots ,f_{t,\mathbf {w}}^{k_m,I}$
with the same number
$f_{t,\mathbf {w}}^{k_1,I},\ldots ,f_{t,\mathbf {w}}^{k_m,I}$
with the same number
![]() $\varepsilon _0$
.
$\varepsilon _0$
.
Lemma 4.2. Under Assumptions 4.1, there exists
![]() $\tau $
with
$\tau $
with
![]() $0<\tau \leq \tau _0$
such that for any
$0<\tau \leq \tau _0$
such that for any
![]() $t\in D_\tau :=\{t\in \mathbb {C}\, ;\, |t|\leq \tau \}$
, any
$t\in D_\tau :=\{t\in \mathbb {C}\, ;\, |t|\leq \tau \}$
, any
![]() $k_1,\ldots , k_m\in \{1,\ldots , k_0\}$
, any
$k_1,\ldots , k_m\in \{1,\ldots , k_0\}$
, any
![]() $I\subseteq \{1,\ldots ,n\}$
with
$I\subseteq \{1,\ldots ,n\}$
with
![]() $I\in \mathcal {I}(f_t^{k_1})\cap \cdots \cap \mathcal {I}(f_t^{k_m})$
, any weight vector
$I\in \mathcal {I}(f_t^{k_1})\cap \cdots \cap \mathcal {I}(f_t^{k_m})$
, any weight vector
![]() $\mathbf {w}\in \mathbb {N}^{I}$
, and any
$\mathbf {w}\in \mathbb {N}^{I}$
, and any
![]() $\lambda \in \mathbb {C}$
, if
$\lambda \in \mathbb {C}$
, if
![]() $\mathbf {a}=(a_1,\ldots ,a_n)\in \mathbb {C}^{I}$
satisfies the conditions (1) and (2) of Lemma 3.3 for the functions
$\mathbf {a}=(a_1,\ldots ,a_n)\in \mathbb {C}^{I}$
satisfies the conditions (1) and (2) of Lemma 3.3 for the functions
![]() $f_{t,\mathbf {w}}^{k_1,I},\ldots ,f_{t,\mathbf {w}}^{k_m,I}$
, that is, if:
$f_{t,\mathbf {w}}^{k_1,I},\ldots ,f_{t,\mathbf {w}}^{k_m,I}$
, that is, if:
-
(1)
 $f_{t,\mathbf {w}}^{k_1,I}(\mathbf {a})=\cdots =f_{t,\mathbf {w}}^{k_m,I}(\mathbf {a})=0$
;
$f_{t,\mathbf {w}}^{k_1,I}(\mathbf {a})=\cdots =f_{t,\mathbf {w}}^{k_m,I}(\mathbf {a})=0$
; -
(2) there exists an m-tuple
 $(\mu _{k_1},\ldots ,\mu _{k_m})\in \mathbb {C}^m\setminus \{\mathbf {0}\}$
such that for all
$(\mu _{k_1},\ldots ,\mu _{k_m})\in \mathbb {C}^m\setminus \{\mathbf {0}\}$
such that for all
 $i\in I$
,
$i\in I$
,  $$ \begin{align*} \sum_{j=1}^m \mu_{k_j}\frac{\partial f_{t,\mathbf{w}}^{k_j,I}}{\partial z_{i}}(\mathbf{a})= \left\{ \begin{aligned} & \lambda\bar a_{i}, &&\mbox{if} && i\in I\cap I(\mathbf{w}),\\ & 0, &&\mbox{if} && i\in I\setminus I(\mathbf{w}), \end{aligned} \right. \end{align*} $$
$$ \begin{align*} \sum_{j=1}^m \mu_{k_j}\frac{\partial f_{t,\mathbf{w}}^{k_j,I}}{\partial z_{i}}(\mathbf{a})= \left\{ \begin{aligned} & \lambda\bar a_{i}, &&\mbox{if} && i\in I\cap I(\mathbf{w}),\\ & 0, &&\mbox{if} && i\in I\setminus I(\mathbf{w}), \end{aligned} \right. \end{align*} $$
where again
 $\bar a_i$
is the complex conjugate of
$\bar a_i$
is the complex conjugate of
 $a_i$
and
$a_i$
and
 $I(\mathbf {w}):=\{i\in \{1,\ldots ,n\};\, w_i=0\}$
;
$I(\mathbf {w}):=\{i\in \{1,\ldots ,n\};\, w_i=0\}$
;
then we must have
 $$ \begin{align*} \mathbf{a}\notin\bigg\{\mathbf{z}\in \mathbb{C}^{*I}\, ;\, \sum_{i\in I\cap I(\mathbf{w})}|z_i|^2\leq \varepsilon_0^2\bigg\}, \end{align*} $$
$$ \begin{align*} \mathbf{a}\notin\bigg\{\mathbf{z}\in \mathbb{C}^{*I}\, ;\, \sum_{i\in I\cap I(\mathbf{w})}|z_i|^2\leq \varepsilon_0^2\bigg\}, \end{align*} $$
where
![]() $\varepsilon _0$
is the number set above.
$\varepsilon _0$
is the number set above.
We shall prove Lemma 4.2 in §4.3. Note that it generalizes Lemma 3 of [Reference Oka9] (obtained by taking
![]() $k_0=1$
). Using Lemma 4.2, we shall prove the following second important theorem, which recovers Theorem 2 of [Reference Oka9] (obtained for
$k_0=1$
). Using Lemma 4.2, we shall prove the following second important theorem, which recovers Theorem 2 of [Reference Oka9] (obtained for
![]() $k_0=1$
).
$k_0=1$
).
Put
![]() $f(t,\mathbf {z}):=f^1(t,\mathbf {z})\cdots f^{k_0}(t,\mathbf {z})$
, and as usual, write
$f(t,\mathbf {z}):=f^1(t,\mathbf {z})\cdots f^{k_0}(t,\mathbf {z})$
, and as usual, write
![]() $f_t(\mathbf {z}):=f(t,\mathbf {z})$
.
$f_t(\mathbf {z}):=f(t,\mathbf {z})$
.
Theorem 4.3. Under Assumptions 4.1, the family
![]() $\{f_t\}_{t\in D_\tau }$
is a uniformly stable family with uniform stable radius
$\{f_t\}_{t\in D_\tau }$
is a uniformly stable family with uniform stable radius
![]() $\varepsilon _0$
. (Here,
$\varepsilon _0$
. (Here,
![]() $\tau $
is the number that appears in Lemma 4.2 and
$\tau $
is the number that appears in Lemma 4.2 and
![]() $\varepsilon _0$
is the number that we have fixed just before the statement of this lemma.)
$\varepsilon _0$
is the number that we have fixed just before the statement of this lemma.)
We recall that the family
![]() $\{f_t\}_{t\in D_\tau }$
is said to be uniformly stable with uniform stable radius
$\{f_t\}_{t\in D_\tau }$
is said to be uniformly stable with uniform stable radius
![]() $\varepsilon _0$
if for any
$\varepsilon _0$
if for any
![]() $0<\varepsilon _1\leq \varepsilon _2< \varepsilon _0$
, there exists
$0<\varepsilon _1\leq \varepsilon _2< \varepsilon _0$
, there exists
![]() $\delta (\varepsilon _1,\varepsilon _2)>0$
such that for any
$\delta (\varepsilon _1,\varepsilon _2)>0$
such that for any
![]() $\eta \in \mathbb {C}$
with
$\eta \in \mathbb {C}$
with
![]() $0<\vert \eta \vert \leq \delta (\varepsilon _1,\varepsilon _2)$
, the hypersurface
$0<\vert \eta \vert \leq \delta (\varepsilon _1,\varepsilon _2)$
, the hypersurface
![]() $f_t^{-1}(\eta )$
is nonsingular in
$f_t^{-1}(\eta )$
is nonsingular in
![]() $\mathring {B}_{\varepsilon _0}:=\{\mathbf {z}\in \mathbb {C}^n\, ;\, \Vert \mathbf {z} \Vert <\varepsilon _0\}$
and transversely intersects the sphere
$\mathring {B}_{\varepsilon _0}:=\{\mathbf {z}\in \mathbb {C}^n\, ;\, \Vert \mathbf {z} \Vert <\varepsilon _0\}$
and transversely intersects the sphere
![]() $S_{\varepsilon _{12}}:=\{\mathbf {z}\in \mathbb {C}^n\, ;\, \Vert \mathbf {z} \Vert =\varepsilon _{12}\}$
for any
$S_{\varepsilon _{12}}:=\{\mathbf {z}\in \mathbb {C}^n\, ;\, \Vert \mathbf {z} \Vert =\varepsilon _{12}\}$
for any
![]() $\varepsilon _1\leq \varepsilon _{12}\leq \varepsilon _2$
and any
$\varepsilon _1\leq \varepsilon _{12}\leq \varepsilon _2$
and any
![]() $t\in D_\tau $
.
$t\in D_\tau $
.
We shall prove Theorem 4.3 in §4.2, but before giving the proof, let us state the first main theorem of this paper (Theorem 4.5). For that purpose, we first observe that Theorem 4.3 has the following corollary, which generalizes Corollary 1 of [Reference Oka9] (obtained by taking
![]() $k_0=1$
).
$k_0=1$
).
Corollary 4.4. Under Assumptions 4.1, the family
![]() $\{f_t\}_{t\in D_{\tau _0}}$
is a uniformly stable family.
$\{f_t\}_{t\in D_{\tau _0}}$
is a uniformly stable family.
Proof. By Lemma 3.3, for any
![]() $t_0\in D_{\tau _0}$
, there exists
$t_0\in D_{\tau _0}$
, there exists
![]() $\varepsilon (t_0)>0$
such that for any
$\varepsilon (t_0)>0$
such that for any
![]() $k_1,\ldots , k_m\in \{1,\ldots , k_0\}$
, any
$k_1,\ldots , k_m\in \{1,\ldots , k_0\}$
, any
![]() $I\subseteq \{1,\ldots ,n\}$
with
$I\subseteq \{1,\ldots ,n\}$
with
![]() $I\in \mathcal {I}(f_{t_0}^{k_1})\cap \cdots \cap \mathcal {I}(f_{t_0}^{k_m})$
, any weight vector
$I\in \mathcal {I}(f_{t_0}^{k_1})\cap \cdots \cap \mathcal {I}(f_{t_0}^{k_m})$
, any weight vector
![]() $\mathbf {w}\in \mathbb {N}^{I}$
, and any
$\mathbf {w}\in \mathbb {N}^{I}$
, and any
![]() $\lambda \in \mathbb {C}$
, if
$\lambda \in \mathbb {C}$
, if
![]() $\mathbf {a}\in \mathbb {C}^{I}$
satisfies the conditions (1) and (2) of this lemma for the functions
$\mathbf {a}\in \mathbb {C}^{I}$
satisfies the conditions (1) and (2) of this lemma for the functions
![]() $f_{t_0,\mathbf {w}}^{k_1,I},\ldots ,f_{t_0,\mathbf {w}}^{k_m,I}$
, then
$f_{t_0,\mathbf {w}}^{k_1,I},\ldots ,f_{t_0,\mathbf {w}}^{k_m,I}$
, then
![]() $\mathbf {a}$
does not belong to the set
$\mathbf {a}$
does not belong to the set
 $$ \begin{align} \bigg\{\mathbf{z}\in \mathbb{C}^{*I}\, ;\, \sum_{i\in I\cap I(\mathbf{w})}|z_i|^2\leq \varepsilon(t_0)^2\bigg\}. \end{align} $$
$$ \begin{align} \bigg\{\mathbf{z}\in \mathbb{C}^{*I}\, ;\, \sum_{i\in I\cap I(\mathbf{w})}|z_i|^2\leq \varepsilon(t_0)^2\bigg\}. \end{align} $$
Then, by (the corresponding version of) Lemma 4.2, there exists
![]() $\tau (t_0)>0$
such that for any
$\tau (t_0)>0$
such that for any
![]() $t\in D_{\tau (t_0)}(t_0):=\{t\in \mathbb {C}\, ;\, |t-t_0|\leq \tau (t_0)\}$
, any
$t\in D_{\tau (t_0)}(t_0):=\{t\in \mathbb {C}\, ;\, |t-t_0|\leq \tau (t_0)\}$
, any
![]() $k_1,\ldots , k_m\in \{1,\ldots , k_0\}$
, any
$k_1,\ldots , k_m\in \{1,\ldots , k_0\}$
, any
![]() $I\subseteq \{1,\ldots ,n\}$
with
$I\subseteq \{1,\ldots ,n\}$
with
![]() $I\in \mathcal {I}(f_t^{k_1})\cap \cdots \cap \mathcal {I}(f_t^{k_m})$
, any weight vector
$I\in \mathcal {I}(f_t^{k_1})\cap \cdots \cap \mathcal {I}(f_t^{k_m})$
, any weight vector
![]() $\mathbf {w}\in \mathbb {N}^{I}$
, and any
$\mathbf {w}\in \mathbb {N}^{I}$
, and any
![]() $\lambda \in \mathbb {C}$
, if
$\lambda \in \mathbb {C}$
, if
![]() $\mathbf {a}\in \mathbb {C}^{I}$
satisfies the conditions (1) and (2) of Lemma 3.3 for the functions
$\mathbf {a}\in \mathbb {C}^{I}$
satisfies the conditions (1) and (2) of Lemma 3.3 for the functions
![]() $f_{t,\mathbf {w}}^{k_1,I},\ldots ,f_{t,\mathbf {w}}^{k_m,I}$
, then
$f_{t,\mathbf {w}}^{k_1,I},\ldots ,f_{t,\mathbf {w}}^{k_m,I}$
, then
![]() $\mathbf {a}$
does not belong to the set (4.1). Now, applying (the corresponding version of) Theorem 4.3 shows that the family
$\mathbf {a}$
does not belong to the set (4.1). Now, applying (the corresponding version of) Theorem 4.3 shows that the family
![]() $\{f_t\}_{t\in D_{\tau (t_0)}}$
is a uniformly stable family with uniform stable radius
$\{f_t\}_{t\in D_{\tau (t_0)}}$
is a uniformly stable family with uniform stable radius
![]() $\varepsilon (t_0)$
. Corollary 4.4 then follows from the compactness of the disk
$\varepsilon (t_0)$
. Corollary 4.4 then follows from the compactness of the disk
![]() $D_{\tau _0}$
.
$D_{\tau _0}$
.
Now, by [Reference Oka9, Lem. 2], we know that if
![]() $\{f_t\}_{t\in D_{\tau _0}}$
is a uniformly stable family—say, with uniform stable radius
$\{f_t\}_{t\in D_{\tau _0}}$
is a uniformly stable family—say, with uniform stable radius
![]() $\varepsilon $
—then the Milnor fibrations of
$\varepsilon $
—then the Milnor fibrations of
![]() $f_t$
and
$f_t$
and
![]() $f_0$
at
$f_0$
at
![]() $\mathbf {0}$
are isomorphic for all
$\mathbf {0}$
are isomorphic for all
![]() $t\in D_{\tau _0}$
, that is, for all such t’s, there exists a fiber-preserving diffeomorphism
$t\in D_{\tau _0}$
, that is, for all such t’s, there exists a fiber-preserving diffeomorphism
where
![]() $\delta (\varepsilon ,\frac {\varepsilon }{2})$
is the number that appears in the definition of a uniform stable family given just after the statement of Theorem 4.3, and where
$\delta (\varepsilon ,\frac {\varepsilon }{2})$
is the number that appears in the definition of a uniform stable family given just after the statement of Theorem 4.3, and where
![]() $S_{\delta (\varepsilon ,\frac {\varepsilon }{2})}:=\{z\in \mathbb {C}\, ;\, \vert z\vert =\delta (\varepsilon ,\frac {\varepsilon }{2})\}$
. Combining this result with Corollary 4.4 gives our first main theorem, the statement of which is as follows. Again, the special case
$S_{\delta (\varepsilon ,\frac {\varepsilon }{2})}:=\{z\in \mathbb {C}\, ;\, \vert z\vert =\delta (\varepsilon ,\frac {\varepsilon }{2})\}$
. Combining this result with Corollary 4.4 gives our first main theorem, the statement of which is as follows. Again, the special case
![]() $k_0=1$
(for which the functions
$k_0=1$
(for which the functions
![]() $f_t$
are necessarily nondegenerate) is already contained in [Reference Oka9].
$f_t$
are necessarily nondegenerate) is already contained in [Reference Oka9].
Theorem 4.5. Under Assumptions 4.1, the Milnor fibrations of
![]() $f_t$
and
$f_t$
and
![]() $f_0$
at
$f_0$
at
![]() $\mathbf {0}$
are isomorphic for all
$\mathbf {0}$
are isomorphic for all
![]() $t\in D_{\tau _0}$
.
$t\in D_{\tau _0}$
.
The following two subsections (§§4.2 and 4.3) are devoted to the proofs of Theorem 4.3 and Lemma 4.2, respectively.
4.2 Proof of Theorem 4.3
It is along the same lines as the proof of Theorem 3.5. We start with the following claim, which plays a role similar to that of [Reference Milnor6, Cor. 2.8] in the proof of Theorem 3.5.
Claim 4.6. There exists
![]() $\delta>0$
such that for any
$\delta>0$
such that for any
![]() $\eta \in \mathbb {C}$
with
$\eta \in \mathbb {C}$
with
![]() $0<|\eta |\leq \delta $
, the hypersurface
$0<|\eta |\leq \delta $
, the hypersurface
![]() $f_t^{-1}(\eta )$
is nonsingular in
$f_t^{-1}(\eta )$
is nonsingular in
![]() $\mathring {B}_{\varepsilon _0}$
for any
$\mathring {B}_{\varepsilon _0}$
for any
![]() $t\in D_{\tau }$
. (Of course, we work under Assumptions 4.1.)
$t\in D_{\tau }$
. (Of course, we work under Assumptions 4.1.)
We postpone the proof of this claim at the end of §4.2, and we first complete the proof of Theorem 4.3. We argue by contradiction. By Claim 4.6, if the assertion in Theorem 4.3 is false, then it follows from the Curve Selection Lemma that there exist a real analytic curve
![]() $(t(s),\mathbf {z}(s))=(t(s),z_1(s),\ldots ,z_n(s))$
in
$(t(s),\mathbf {z}(s))=(t(s),z_1(s),\ldots ,z_n(s))$
in
![]() $D_\tau \times \mathring {B}_{\varepsilon _0}$
,
$D_\tau \times \mathring {B}_{\varepsilon _0}$
,
![]() $0\leq s\leq 1$
, and a family of complex numbers
$0\leq s\leq 1$
, and a family of complex numbers
![]() $\lambda (s)$
,
$\lambda (s)$
,
![]() $0< s\leq 1$
, such that the following three conditions hold:
$0< s\leq 1$
, such that the following three conditions hold:
-
(i)
 $\frac {\partial f_{t(s)}}{\partial z_i}(\mathbf {z}(s)) = \lambda (s) \bar z_i(s)$
for
$\frac {\partial f_{t(s)}}{\partial z_i}(\mathbf {z}(s)) = \lambda (s) \bar z_i(s)$
for
 $1\leq i\leq n$
and
$1\leq i\leq n$
and
 $s\not =0$
.
$s\not =0$
. -
(ii)
 $f_{t(0)}(\mathbf {z}(0))=0$
, but
$f_{t(0)}(\mathbf {z}(0))=0$
, but
 $f_{t(s)}(\mathbf {z}(s))\not =0$
for
$f_{t(s)}(\mathbf {z}(s))\not =0$
for
 $s\not =0$
.
$s\not =0$
. -
(iii) There exists
 $\varepsilon>0$
such that
$\varepsilon>0$
such that
 $\varepsilon \leq \Vert \mathbf {z}(s)\Vert \leq \varepsilon _0$
.
$\varepsilon \leq \Vert \mathbf {z}(s)\Vert \leq \varepsilon _0$
.
By (i) and (ii),
![]() $\lambda (s)\not \equiv 0$
, and we can express it as a Laurent series
$\lambda (s)\not \equiv 0$
, and we can express it as a Laurent series
where
![]() $\lambda _0\in \mathbb {C}^*$
. Let
$\lambda _0\in \mathbb {C}^*$
. Let
![]() $I:=\{i\, ;\, z_i(s)\not \equiv 0\}$
. By (ii),
$I:=\{i\, ;\, z_i(s)\not \equiv 0\}$
. By (ii),
![]() $I\in \mathcal {I}(f_{t(s)})$
, and hence
$I\in \mathcal {I}(f_{t(s)})$
, and hence
![]() $I\in \mathcal {I}(f^{1}_{t(s)})\cap \cdots \cap \mathcal {I}(f^{k_0}_{t(s)})$
. For each
$I\in \mathcal {I}(f^{1}_{t(s)})\cap \cdots \cap \mathcal {I}(f^{k_0}_{t(s)})$
. For each
![]() $i\in I$
, consider the Taylor expansion
$i\in I$
, consider the Taylor expansion
where
![]() $a_i\in \mathbb {C}^*$
and
$a_i\in \mathbb {C}^*$
and
![]() $w_i\in \mathbb {N}$
. The following is the counterpart of Claim 3.6.
$w_i\in \mathbb {N}$
. The following is the counterpart of Claim 3.6.
Claim 4.7. There exists
![]() $1\leq k\leq k_0$
such that
$1\leq k\leq k_0$
such that
![]() $f^{k,I}_{t(0),\mathbf {w}}(\mathbf {a})=0$
, where again
$f^{k,I}_{t(0),\mathbf {w}}(\mathbf {a})=0$
, where again
![]() $\mathbf {a}$
and
$\mathbf {a}$
and
![]() $\mathbf {w}$
are the points in
$\mathbf {w}$
are the points in
![]() $\mathbb {C}^{*I}$
and
$\mathbb {C}^{*I}$
and
![]() $\mathbb {N}^{I}$
, respectively, whose ith coordinates (
$\mathbb {N}^{I}$
, respectively, whose ith coordinates (
![]() $i\in I$
) are
$i\in I$
) are
![]() $a_{i}$
and
$a_{i}$
and
![]() $w_{i}$
, respectively.
$w_{i}$
, respectively.
Again, we shall prove this claim later. First, we complete the proof of the theorem. Once more, hereafter, to simplify the notation, we shall assume that
![]() $I=\{1,\ldots ,n\}$
, so that the function
$I=\{1,\ldots ,n\}$
, so that the function
![]() $f_t^{k,I}$
is simply written as
$f_t^{k,I}$
is simply written as
![]() $f_t^k$
, the intersection
$f_t^k$
, the intersection
![]() $I\cap I(\mathbf {w})$
is written as
$I\cap I(\mathbf {w})$
is written as
![]() $I(\mathbf {w})$
(where, as in Lemma 4.2,
$I(\mathbf {w})$
(where, as in Lemma 4.2,
![]() $I(\mathbf {w})$
is the set of all indexes
$I(\mathbf {w})$
is the set of all indexes
![]() $i\in \{1,\ldots ,n\}$
for which
$i\in \{1,\ldots ,n\}$
for which
![]() $w_i=0$
), and so on.
$w_i=0$
), and so on.
Look at the set consisting of all integers k for which
![]() $f^{k}_{t(0),\mathbf {w}}(\mathbf {a})=0$
. By Claim 4.7, this set is not empty. As in the proof of Theorem 3.5, we assume that
$f^{k}_{t(0),\mathbf {w}}(\mathbf {a})=0$
. By Claim 4.7, this set is not empty. As in the proof of Theorem 3.5, we assume that
![]() $f^{k}_{t(0),\mathbf {w}}(\mathbf {a})$
vanishes for
$f^{k}_{t(0),\mathbf {w}}(\mathbf {a})$
vanishes for
![]() $1\leq k\leq k_0'$
and does not vanish for
$1\leq k\leq k_0'$
and does not vanish for
![]() $k^{\prime }_0+1\leq k\leq k_0$
, and we write
$k^{\prime }_0+1\leq k\leq k_0$
, and we write
![]() $f=f^1\cdots f^{k_0'}\cdot h$
where
$f=f^1\cdots f^{k_0'}\cdot h$
where
![]() $h:=f^{k_0'+1}\cdots f^{k_0}$
if
$h:=f^{k_0'+1}\cdots f^{k_0}$
if
![]() $k_0'\leq k_0-1$
and
$k_0'\leq k_0-1$
and
![]() $h:=1$
if
$h:=1$
if
![]() $k_0'=k_0$
; finally, for each
$k_0'=k_0$
; finally, for each
![]() $1\leq k\leq k^{\prime }_0$
, we put
$1\leq k\leq k^{\prime }_0$
, we put
 $$ \begin{align*} e_k:=d\big(\mathbf{w};f_{t(0)}^{k}\big)-\mbox{ord}\, f_{t(s)}^{k}(\mathbf{z}(s))+\sum_{\ell=1}^{k_0'} \mbox{ord}\, f_{t(s)}^{\ell}(\mathbf{z}(s)) \end{align*} $$
$$ \begin{align*} e_k:=d\big(\mathbf{w};f_{t(0)}^{k}\big)-\mbox{ord}\, f_{t(s)}^{k}(\mathbf{z}(s))+\sum_{\ell=1}^{k_0'} \mbox{ord}\, f_{t(s)}^{\ell}(\mathbf{z}(s)) \end{align*} $$
(where, as usual,
![]() $\mbox {ord} f_{t(s)}^{\ell }(\mathbf {z}(s))$
means the order, in s, of the expression
$\mbox {ord} f_{t(s)}^{\ell }(\mathbf {z}(s))$
means the order, in s, of the expression
![]() $f_{t(s)}^{\ell }(\mathbf {z}(s))\equiv f^{\ell }(t(s),\mathbf {z}(s))$
), and we suppose that
$f_{t(s)}^{\ell }(\mathbf {z}(s))\equiv f^{\ell }(t(s),\mathbf {z}(s))$
), and we suppose that
Note that the equality
![]() $\Gamma _+\big (f^{k}_{t(s)}\big )=\Gamma _+\big (f^{k}_{t(0)}\big )$
implies
$\Gamma _+\big (f^{k}_{t(s)}\big )=\Gamma _+\big (f^{k}_{t(0)}\big )$
implies
![]() $\Delta \big (\mathbf {w};f^{k}_{t(s)}\big )=\Delta \big (\mathbf {w};f^{k}_{t(0)}\big )$
and
$\Delta \big (\mathbf {w};f^{k}_{t(s)}\big )=\Delta \big (\mathbf {w};f^{k}_{t(0)}\big )$
and
![]() $d\big (\mathbf {w};f^{k}_{t(s)}\big )=d\big (\mathbf {w};f^{k}_{t(0)}\big )=d(\hat {\mathbf {w}};f^k)$
for all s, where
$d\big (\mathbf {w};f^{k}_{t(s)}\big )=d\big (\mathbf {w};f^{k}_{t(0)}\big )=d(\hat {\mathbf {w}};f^k)$
for all s, where
![]() $\hat {\mathbf {w}}=(w_0,\mathbf {w})$
with
$\hat {\mathbf {w}}=(w_0,\mathbf {w})$
with
![]() $w_0$
defined by the Taylor expansion
$w_0$
defined by the Taylor expansion
![]() $t(s):=t_0s^{w_0}+\cdots $
,
$t(s):=t_0s^{w_0}+\cdots $
,
![]() $t_0\not =0$
. Still as in the proof of Theorem 3.5 (see (3.1)–(3.4)), it follows from the relation (i) that there exist nonzero complex numbers
$t_0\not =0$
. Still as in the proof of Theorem 3.5 (see (3.1)–(3.4)), it follows from the relation (i) that there exist nonzero complex numbers
![]() $\mu _1,\ldots ,\mu _{k^{\prime \prime }_0}$
such that for any
$\mu _1,\ldots ,\mu _{k^{\prime \prime }_0}$
such that for any
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
 $$ \begin{align*} \sum_{k=1}^{k^{\prime\prime}_0}\frac{\partial {f^{k}_{t(0),\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\cdot \mu_k\cdot s^{d(\hat{\mathbf{w}};h)+e_{\text{min}}}+\cdots = \lambda_0 \bar a_{i}s^{c+2w_{i}}+\cdots, \end{align*} $$
$$ \begin{align*} \sum_{k=1}^{k^{\prime\prime}_0}\frac{\partial {f^{k}_{t(0),\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\cdot \mu_k\cdot s^{d(\hat{\mathbf{w}};h)+e_{\text{min}}}+\cdots = \lambda_0 \bar a_{i}s^{c+2w_{i}}+\cdots, \end{align*} $$
and since
![]() $\lambda _0 \bar a_{i}\not =0$
and
$\lambda _0 \bar a_{i}\not =0$
and
![]() $I(\mathbf {w})\not =\emptyset $
(by (iii)), by the same argument as the one given after (3.4), we deduce that the sum
$I(\mathbf {w})\not =\emptyset $
(by (iii)), by the same argument as the one given after (3.4), we deduce that the sum
 $$ \begin{align*} S_i:=\sum_{k=1}^{k^{\prime\prime}_0} \mu_k \frac{\partial {f^{k}_{t(0),\mathbf{w}}}}{\partial z_{i}} (\mathbf{a}) \end{align*} $$
$$ \begin{align*} S_i:=\sum_{k=1}^{k^{\prime\prime}_0} \mu_k \frac{\partial {f^{k}_{t(0),\mathbf{w}}}}{\partial z_{i}} (\mathbf{a}) \end{align*} $$
vanishes for all
![]() $i\notin I(\mathbf {w})$
. If it also vanishes for all
$i\notin I(\mathbf {w})$
. If it also vanishes for all
![]() $i\in I(\mathbf {w})$
, then we get a contradiction with Lemma 4.2 because
$i\in I(\mathbf {w})$
, then we get a contradiction with Lemma 4.2 because
![]() $\mathbf {z}(s)\in \mathring {B}_{\varepsilon _0}$
, and hence
$\mathbf {z}(s)\in \mathring {B}_{\varepsilon _0}$
, and hence
 $$ \begin{align} \sum_{i\in I(\mathbf{w})}\vert a_i \vert^2= \Vert \mathbf{z}(0)\Vert^2\leq \varepsilon_0^2. \end{align} $$
$$ \begin{align} \sum_{i\in I(\mathbf{w})}\vert a_i \vert^2= \Vert \mathbf{z}(0)\Vert^2\leq \varepsilon_0^2. \end{align} $$
If there is an index
![]() $i_0\in I(\mathbf {w})$
such that
$i_0\in I(\mathbf {w})$
such that
![]() $S_{i_0}\not =0$
, then
$S_{i_0}\not =0$
, then
 $$ \begin{align*} S_i=\sum_{k=1}^{k^{\prime\prime}_0} \mu_k \frac{\partial {f^{k}_{t(0),\mathbf{w}}}}{\partial z_{i}} (\mathbf{a}) =\left\{ \begin{aligned} & \lambda_0 \bar a_i, &&\mbox{for}&& i\in I(\mathbf{w}),\\ & 0, &&\mbox{for}&& i\notin I(\mathbf{w}), \end{aligned} \right. \end{align*} $$
$$ \begin{align*} S_i=\sum_{k=1}^{k^{\prime\prime}_0} \mu_k \frac{\partial {f^{k}_{t(0),\mathbf{w}}}}{\partial z_{i}} (\mathbf{a}) =\left\{ \begin{aligned} & \lambda_0 \bar a_i, &&\mbox{for}&& i\in I(\mathbf{w}),\\ & 0, &&\mbox{for}&& i\notin I(\mathbf{w}), \end{aligned} \right. \end{align*} $$
and still by (4.2), we get a new contradiction with Lemma 4.2.
To complete the proof of Theorem 4.3, it remains to prove Claims 4.6 and 4.7. We start with the proof of Claim 4.7.
Proof of Claim 4.7
It is similar to the proof of Claim 3.6. Again, we assume
![]() $I=\{1,\ldots ,n\}$
, so that
$I=\{1,\ldots ,n\}$
, so that
![]() $f^{k,I}_{t(0),\mathbf {w}}=f^{k}_{t(0),\mathbf {w}}$
. We argue by contradiction. Suppose that
$f^{k,I}_{t(0),\mathbf {w}}=f^{k}_{t(0),\mathbf {w}}$
. We argue by contradiction. Suppose that
![]() $f^{k}_{t(0),\mathbf {w}}(\mathbf {a})\not =0$
for all
$f^{k}_{t(0),\mathbf {w}}(\mathbf {a})\not =0$
for all
![]() $1\leq k\leq k_0$
. Then
$1\leq k\leq k_0$
. Then
![]() $f^k_{\hat {\mathbf {w}}}(t_0,\mathbf {a})=f^k_{t(0),\mathbf {w}}(\mathbf {a})\not =0$
and
$f^k_{\hat {\mathbf {w}}}(t_0,\mathbf {a})=f^k_{t(0),\mathbf {w}}(\mathbf {a})\not =0$
and
![]() $d\big (\mathbf {w};f_{t(0)}^{k}\big )=d(\hat {\mathbf {w}};f^k)=\mbox {ord}\, f_{t(s)}^{k}(\mathbf {z}(s))$
for all
$d\big (\mathbf {w};f_{t(0)}^{k}\big )=d(\hat {\mathbf {w}};f^k)=\mbox {ord}\, f_{t(s)}^{k}(\mathbf {z}(s))$
for all
![]() $1\leq k\leq k_0$
(where
$1\leq k\leq k_0$
(where
![]() $\hat {\mathbf {w}}$
and
$\hat {\mathbf {w}}$
and
![]() $t_0$
are defined as above), and by (ii), there exists
$t_0$
are defined as above), and by (ii), there exists
![]() $1\leq k_1\leq k_0$
such that
$1\leq k_1\leq k_0$
such that
![]() $f_{t(0)}^{k_1}(\mathbf {z}(0))=0$
. If
$f_{t(0)}^{k_1}(\mathbf {z}(0))=0$
. If
![]() $I(\mathbf {w})=\{1,\ldots ,n\}$
, then
$I(\mathbf {w})=\{1,\ldots ,n\}$
, then
![]() $d\big (\mathbf {w};f_{t(0)}^{k_1}\big )=0$
and
$d\big (\mathbf {w};f_{t(0)}^{k_1}\big )=0$
and
so that
![]() $0=f_{t(0)}^{k_1}(\mathbf {z}(0))=f^{k_1}_{t(0),\mathbf {w}}(\mathbf {a})$
, which is a contradiction. If
$0=f_{t(0)}^{k_1}(\mathbf {z}(0))=f^{k_1}_{t(0),\mathbf {w}}(\mathbf {a})$
, which is a contradiction. If
![]() $I(\mathbf {w})$
is a proper subset of
$I(\mathbf {w})$
is a proper subset of
![]() $\{1,\ldots ,n\}$
and
$\{1,\ldots ,n\}$
and
![]() $d\big (\mathbf {w};f_{t(0)}^{k_1}\big )\not =0$
, then, exactly as in the proof of Claim 3.6, if
$d\big (\mathbf {w};f_{t(0)}^{k_1}\big )\not =0$
, then, exactly as in the proof of Claim 3.6, if
![]() $e:=\sum _{k=1}^{k_0} \mbox {ord}\, f_{t(s)}^{k}(\mathbf {z}(s))$
, then for any
$e:=\sum _{k=1}^{k_0} \mbox {ord}\, f_{t(s)}^{k}(\mathbf {z}(s))$
, then for any
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
 $$ \begin{align} \sum_{k=1}^{k_0} \bigg(\prod_{\genfrac{}{}{0pt}{}{1\leq \ell\leq k_0}{\ell\not=k}}f^{\ell}_{t(0),\mathbf{w}}(\mathbf{a})\bigg)\cdot\frac{\partial {f^{k}_{t(0),\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\cdot s^{e}+\cdots = \lambda_0 \bar a_{i}s^{c+2w_{i}}+\cdots. \end{align} $$
$$ \begin{align} \sum_{k=1}^{k_0} \bigg(\prod_{\genfrac{}{}{0pt}{}{1\leq \ell\leq k_0}{\ell\not=k}}f^{\ell}_{t(0),\mathbf{w}}(\mathbf{a})\bigg)\cdot\frac{\partial {f^{k}_{t(0),\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\cdot s^{e}+\cdots = \lambda_0 \bar a_{i}s^{c+2w_{i}}+\cdots. \end{align} $$
As above, since
![]() $\lambda _0 \bar a_{i}\not =0$
and
$\lambda _0 \bar a_{i}\not =0$
and
![]() $I(\mathbf {w})\not =\emptyset $
, this implies that the sum
$I(\mathbf {w})\not =\emptyset $
, this implies that the sum
 $$ \begin{align*} \sum_{k=1}^{k_0} \bigg(\prod_{\genfrac{}{}{0pt}{}{1\leq \ell\leq k_0}{\ell\not=k}}f^{\ell}_{t(0),\mathbf{w}}(\mathbf{a})\bigg)\cdot\frac{\partial {f^{k}_{t(0),\mathbf{w}}}}{\partial z_{i}} (\mathbf{a}) \end{align*} $$
$$ \begin{align*} \sum_{k=1}^{k_0} \bigg(\prod_{\genfrac{}{}{0pt}{}{1\leq \ell\leq k_0}{\ell\not=k}}f^{\ell}_{t(0),\mathbf{w}}(\mathbf{a})\bigg)\cdot\frac{\partial {f^{k}_{t(0),\mathbf{w}}}}{\partial z_{i}} (\mathbf{a}) \end{align*} $$
vanishes for all
![]() $i\notin I(\mathbf {w})$
, and using the Euler identity, we get exactly the same contradiction as in the proof of Claim 3.6.
$i\notin I(\mathbf {w})$
, and using the Euler identity, we get exactly the same contradiction as in the proof of Claim 3.6.
Now, we prove Claim 4.6.
Proof of Claim 3.6
The argument is very similar to that given in the proof of Theorem 4.3. We argue by contradiction. If the assertion in the claim is false, then, by the Curve Selection Lemma, there exists a real analytic curve
![]() $(t(s),\mathbf {z}(s))=(t(s),z_1(s),\ldots ,z_n(s))$
in
$(t(s),\mathbf {z}(s))=(t(s),z_1(s),\ldots ,z_n(s))$
in
![]() $D_\tau \times \mathring {B}_{\varepsilon _0}$
,
$D_\tau \times \mathring {B}_{\varepsilon _0}$
,
![]() $0\leq s\leq 1$
, such that the following two conditions hold:
$0\leq s\leq 1$
, such that the following two conditions hold:
-
(i)
 $\frac {\partial f_{t(s)}}{\partial z_i}(\mathbf {z}(s)) = 0$
for
$\frac {\partial f_{t(s)}}{\partial z_i}(\mathbf {z}(s)) = 0$
for
 $1\leq i\leq n$
.
$1\leq i\leq n$
. -
(ii)
 $f_{t(0)}(\mathbf {z}(0))=0$
, but
$f_{t(0)}(\mathbf {z}(0))=0$
, but
 $f_{t(s)}(\mathbf {z}(s))\not =0$
for
$f_{t(s)}(\mathbf {z}(s))\not =0$
for
 $s\not =0$
.
$s\not =0$
.
Let
![]() $I:=\{i\, ;\, z_i(s)\not \equiv 0\}$
. By (ii),
$I:=\{i\, ;\, z_i(s)\not \equiv 0\}$
. By (ii),
![]() $I\in \mathcal {I}(f^{1}_{t(s)})\cap \cdots \cap \mathcal {I}(f^{k_0}_{t(s)})$
. For each
$I\in \mathcal {I}(f^{1}_{t(s)})\cap \cdots \cap \mathcal {I}(f^{k_0}_{t(s)})$
. For each
![]() $i\in I$
, consider the Taylor expansion
$i\in I$
, consider the Taylor expansion
where
![]() $a_i\in \mathbb {C}^*$
and
$a_i\in \mathbb {C}^*$
and
![]() $w_i\in \mathbb {N}$
.
$w_i\in \mathbb {N}$
.
Claim 4.8. There exists
![]() $1\leq k\leq k_0$
such that
$1\leq k\leq k_0$
such that
![]() $f^{k,I}_{t(0),\mathbf {w}}(\mathbf {a})=0$
, where again
$f^{k,I}_{t(0),\mathbf {w}}(\mathbf {a})=0$
, where again
![]() $\mathbf {a}$
and
$\mathbf {a}$
and
![]() $\mathbf {w}$
are the points in
$\mathbf {w}$
are the points in
![]() $\mathbb {C}^{*I}$
and
$\mathbb {C}^{*I}$
and
![]() $\mathbb {N}^{I}$
, respectively, whose ith coordinates (
$\mathbb {N}^{I}$
, respectively, whose ith coordinates (
![]() $i\in I$
) are
$i\in I$
) are
![]() $a_{i}$
and
$a_{i}$
and
![]() $w_{i}$
, respectively.
$w_{i}$
, respectively.
The proof of Claim 4.8 is completely similar to that of Claim 4.7. The only difference is that the right-hand side of the equality (4.3) is now zero. However, this does not change anything in the argument.
Once more, we assume
![]() $I=\{1,\ldots ,n\}$
, so that
$I=\{1,\ldots ,n\}$
, so that
![]() $f_{t(0),\mathbf {w}}^{k,I}=f_{t(0),\mathbf {w}}^k$
, and we look at the set consisting of all integers k for which
$f_{t(0),\mathbf {w}}^{k,I}=f_{t(0),\mathbf {w}}^k$
, and we look at the set consisting of all integers k for which
![]() $f^{k}_{t(0),\mathbf {w}}(\mathbf {a})=0$
. By Claim 4.8, this set is not empty. As in the proof of Theorem 3.5 or 4.3, we assume that
$f^{k}_{t(0),\mathbf {w}}(\mathbf {a})=0$
. By Claim 4.8, this set is not empty. As in the proof of Theorem 3.5 or 4.3, we assume that
![]() $f^{k}_{t(0),\mathbf {w}}(\mathbf {a})$
vanishes for
$f^{k}_{t(0),\mathbf {w}}(\mathbf {a})$
vanishes for
![]() $1\leq k\leq k_0'$
and does not vanish for
$1\leq k\leq k_0'$
and does not vanish for
![]() $k^{\prime }_0+1\leq k\leq k_0$
, and we write
$k^{\prime }_0+1\leq k\leq k_0$
, and we write
![]() $f=f^1\cdots f^{k_0'}\cdot h$
where
$f=f^1\cdots f^{k_0'}\cdot h$
where
![]() $h:=f^{k_0'+1}\cdots f^{k_0}$
if
$h:=f^{k_0'+1}\cdots f^{k_0}$
if
![]() $k_0'\leq k_0-1$
and
$k_0'\leq k_0-1$
and
![]() $h:=1$
if
$h:=1$
if
![]() $k_0'=k_0$
; finally, for each
$k_0'=k_0$
; finally, for each
![]() $1\leq k\leq k^{\prime }_0$
, we put
$1\leq k\leq k^{\prime }_0$
, we put
 $$ \begin{align*} e_k:=d\big(\mathbf{w};f_{t(0)}^{k}\big)-\mbox{ord}\, f_{t(s)}^{k}(\mathbf{z}(s))+\sum_{\ell=1}^{k_0'} \mbox{ord}\, f_{t(s)}^{\ell}(\mathbf{z}(s)), \end{align*} $$
$$ \begin{align*} e_k:=d\big(\mathbf{w};f_{t(0)}^{k}\big)-\mbox{ord}\, f_{t(s)}^{k}(\mathbf{z}(s))+\sum_{\ell=1}^{k_0'} \mbox{ord}\, f_{t(s)}^{\ell}(\mathbf{z}(s)), \end{align*} $$
and we suppose that
Still as in the proof of Theorem 3.5 or 4.3, it follows from the relation (i) that there exist nonzero complex numbers
![]() $\mu _1,\ldots ,\mu _{k^{\prime \prime }_0}$
such that for any
$\mu _1,\ldots ,\mu _{k^{\prime \prime }_0}$
such that for any
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
 $$ \begin{align*} \sum_{k=1}^{k^{\prime\prime}_0}\frac{\partial {f^{k}_{t(0),\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\cdot \mu_k\cdot s^{d(\hat{\mathbf{w}};h)+e_{\text{min}}}+\cdots = 0, \end{align*} $$
$$ \begin{align*} \sum_{k=1}^{k^{\prime\prime}_0}\frac{\partial {f^{k}_{t(0),\mathbf{w}}}}{\partial z_{i}} (\mathbf{a})\cdot \mu_k\cdot s^{d(\hat{\mathbf{w}};h)+e_{\text{min}}}+\cdots = 0, \end{align*} $$
and hence
![]() $ \sum _{k=1}^{k^{\prime \prime }_0} \mu _k \frac {\partial {f^{k}_{t(0),\mathbf {w}}}}{\partial z_{i}} (\mathbf {a})=0. $
In other words, the vectors
$ \sum _{k=1}^{k^{\prime \prime }_0} \mu _k \frac {\partial {f^{k}_{t(0),\mathbf {w}}}}{\partial z_{i}} (\mathbf {a})=0. $
In other words, the vectors
 $$ \begin{align*} \bigg(\frac{\partial {f^{1}_{t(0),\mathbf{w}}}}{\partial z_{1}} (\mathbf{a}),\ldots, \frac{\partial {f^{1}_{t(0),\mathbf{w}}}}{\partial z_{n}} (\mathbf{a})\bigg) ,\ldots, \bigg(\frac{\partial {f^{k_0"}_{t(0),\mathbf{w}}}}{\partial z_{1}} (\mathbf{a}),\ldots, \frac{\partial {f^{k_0"}_{t(0),\mathbf{w}}}}{\partial z_{n}} (\mathbf{a})\bigg) \end{align*} $$
$$ \begin{align*} \bigg(\frac{\partial {f^{1}_{t(0),\mathbf{w}}}}{\partial z_{1}} (\mathbf{a}),\ldots, \frac{\partial {f^{1}_{t(0),\mathbf{w}}}}{\partial z_{n}} (\mathbf{a})\bigg) ,\ldots, \bigg(\frac{\partial {f^{k_0"}_{t(0),\mathbf{w}}}}{\partial z_{1}} (\mathbf{a}),\ldots, \frac{\partial {f^{k_0"}_{t(0),\mathbf{w}}}}{\partial z_{n}} (\mathbf{a})\bigg) \end{align*} $$
of
![]() $\mathbb {C}^n$
are linearly dependent, that is,
$\mathbb {C}^n$
are linearly dependent, that is,
which contradicts the nondegeneracy of
![]() $V\big (f^{1}_{t(0)},\ldots ,f^{k_0"}_{t(0)}\big )$
if
$V\big (f^{1}_{t(0)},\ldots ,f^{k_0"}_{t(0)}\big )$
if
![]() $I(\mathbf {w})=\emptyset $
. In the case where
$I(\mathbf {w})=\emptyset $
. In the case where
![]() $I(\mathbf {w})\not =\emptyset $
, we cannot proceed like that. However, in this case, Lemma 4.2 (applied with
$I(\mathbf {w})\not =\emptyset $
, we cannot proceed like that. However, in this case, Lemma 4.2 (applied with
![]() $\lambda =0$
) implies
$\lambda =0$
) implies
 $$ \begin{align*} \mathbf{a}\notin\bigg\{\mathbf{z}\in \mathbb{C}^{*n}\, ;\, \sum_{i\in I(\mathbf{w})}|z_i|^2\leq \varepsilon_0^2\bigg\}, \end{align*} $$
$$ \begin{align*} \mathbf{a}\notin\bigg\{\mathbf{z}\in \mathbb{C}^{*n}\, ;\, \sum_{i\in I(\mathbf{w})}|z_i|^2\leq \varepsilon_0^2\bigg\}, \end{align*} $$
and since
![]() $\mathbf {z}(s)\in \mathring {B}_{\varepsilon _0}$
, we also have
$\mathbf {z}(s)\in \mathring {B}_{\varepsilon _0}$
, we also have
 $$ \begin{align*} \sum_{i\in I(\mathbf{w})}|a_i|^2\leq\sum_{i=1}^n |z_i(0)|^2=\Vert\mathbf{z}(0)\Vert^2<\varepsilon_0^2, \end{align*} $$
$$ \begin{align*} \sum_{i\in I(\mathbf{w})}|a_i|^2\leq\sum_{i=1}^n |z_i(0)|^2=\Vert\mathbf{z}(0)\Vert^2<\varepsilon_0^2, \end{align*} $$
which is a contradiction.
4.3 Proof of Lemma 4.2
If the assertion of this lemma fails for some
![]() $k_1,\dots ,k_m$
, I and
$k_1,\dots ,k_m$
, I and
![]() $\Delta (\mathbf {w};f_0^{k_1}),\ldots ,\Delta (\mathbf {w};f_0^{k_m})$
such that
$\Delta (\mathbf {w};f_0^{k_1}),\ldots ,\Delta (\mathbf {w};f_0^{k_m})$
such that
![]() $I\cap I(\mathbf {w})=\emptyset $
, then, as in the proof of Lemma 3.3, we get a contradiction with the nondegeneracy condition (see Assumptions 4.1 and Remark 2.3).
$I\cap I(\mathbf {w})=\emptyset $
, then, as in the proof of Lemma 3.3, we get a contradiction with the nondegeneracy condition (see Assumptions 4.1 and Remark 2.3).
Now, assume that the assertion fails for some
![]() $k_1,\dots ,k_m$
, I and
$k_1,\dots ,k_m$
, I and
![]() $\Delta (\mathbf {w};f_0^{k_1}),\ldots ,\Delta (\mathbf {w};f_0^{k_m})$
such that
$\Delta (\mathbf {w};f_0^{k_1}),\ldots ,\Delta (\mathbf {w};f_0^{k_m})$
such that
![]() $I\cap I(\mathbf {w})\not =\emptyset $
. Again, without loss of generality, and in order to simplify the notation, we assume that
$I\cap I(\mathbf {w})\not =\emptyset $
. Again, without loss of generality, and in order to simplify the notation, we assume that
![]() $I=\{1,\ldots ,n\}$
, so that
$I=\{1,\ldots ,n\}$
, so that
![]() $f^{k,I}_{t,\mathbf {w}}=f^{k}_{t,\mathbf {w}}$
,
$f^{k,I}_{t,\mathbf {w}}=f^{k}_{t,\mathbf {w}}$
,
![]() $I\cap I(\mathbf {w})=I(\mathbf {w})$
,
$I\cap I(\mathbf {w})=I(\mathbf {w})$
,
![]() $\mathbb {C}^{*I}=\mathbb {C}^{*n}$
, and so on. Then there exist sequences
$\mathbb {C}^{*I}=\mathbb {C}^{*n}$
, and so on. Then there exist sequences
![]() $\{\mathbf {p}_q\}_{q\in \mathbb {N}}$
,
$\{\mathbf {p}_q\}_{q\in \mathbb {N}}$
,
![]() $\{\lambda _q\}_{q\in \mathbb {N}}$
and
$\{\lambda _q\}_{q\in \mathbb {N}}$
and
![]() $\{t_q\}_{q\in \mathbb {N}}$
of points in
$\{t_q\}_{q\in \mathbb {N}}$
of points in
![]() $\mathbb {C}^{*n}$
,
$\mathbb {C}^{*n}$
,
![]() $\mathbb {C}$
, and
$\mathbb {C}$
, and
![]() $\mathbb {C}^*$
, respectively, such that:
$\mathbb {C}^*$
, respectively, such that:
-
(1)
 $f_{t_q,\mathbf {w}}^{k_1}(\mathbf {p}_q)=\cdots =f_{t_q,\mathbf {w}}^{k_m}(\mathbf {p}_q)=0$
for all
$f_{t_q,\mathbf {w}}^{k_1}(\mathbf {p}_q)=\cdots =f_{t_q,\mathbf {w}}^{k_m}(\mathbf {p}_q)=0$
for all
 $q\in \mathbb {N}$
.
$q\in \mathbb {N}$
. -
(2) There exists a sequence
 $\{(\mu _{k_1,q},\ldots ,\mu _{k_m,q})\}_{q\in \mathbb {N}}$
of points in
$\{(\mu _{k_1,q},\ldots ,\mu _{k_m,q})\}_{q\in \mathbb {N}}$
of points in
 $\mathbb {C}^m\setminus \{\mathbf {0}\}$
such that for all
$\mathbb {C}^m\setminus \{\mathbf {0}\}$
such that for all
 $q\in \mathbb {N}$
and all
$q\in \mathbb {N}$
and all
 $1\leq i\leq n$
,
$1\leq i\leq n$
,  $$ \begin{align*} \sum_{j=1}^m \mu_{k_j,q}\, \frac{\partial f_{t_q,\mathbf{w}}^{k_j}}{\partial z_i}(\mathbf{p}_q)=\left\{ \begin{aligned} & \lambda_q \, \bar p_{q,i}, &&\mbox{if} && i\in I(\mathbf{w}),\\ & 0, &&\mbox{if} && i\notin I(\mathbf{w}), \end{aligned} \right. \end{align*} $$
$$ \begin{align*} \sum_{j=1}^m \mu_{k_j,q}\, \frac{\partial f_{t_q,\mathbf{w}}^{k_j}}{\partial z_i}(\mathbf{p}_q)=\left\{ \begin{aligned} & \lambda_q \, \bar p_{q,i}, &&\mbox{if} && i\in I(\mathbf{w}),\\ & 0, &&\mbox{if} && i\notin I(\mathbf{w}), \end{aligned} \right. \end{align*} $$
where, for each
 $1\leq i\leq n$
,
$1\leq i\leq n$
,
 $\bar p_{q,i}$
denotes the conjugate of the ith coordinate
$\bar p_{q,i}$
denotes the conjugate of the ith coordinate
 $p_{q,i}$
of
$p_{q,i}$
of
 $\mathbf {p}_q$
.
$\mathbf {p}_q$
. -
(3)
 $\sum _{i\in I(\mathbf {w})} |p_{q,i}|^2\leq \varepsilon _0^2$
and
$\sum _{i\in I(\mathbf {w})} |p_{q,i}|^2\leq \varepsilon _0^2$
and
 $t_q\to 0$
as
$t_q\to 0$
as
 $q\to \infty $
.
$q\to \infty $
.
(Again,
![]() $f_{t_q,\mathbf {w}}^{k_j}$
denotes the face function
$f_{t_q,\mathbf {w}}^{k_j}$
denotes the face function
![]() $(f_{t_q}^{k_j})_{\mathbf {w}}\equiv (f_{t_q}^{k_j})_{\Delta \big (\mathbf {w};f_{t_q}^{k_j}\big )}$
of
$(f_{t_q}^{k_j})_{\mathbf {w}}\equiv (f_{t_q}^{k_j})_{\Delta \big (\mathbf {w};f_{t_q}^{k_j}\big )}$
of
![]() $f_{t_q}^{k_j}$
with respect to
$f_{t_q}^{k_j}$
with respect to
![]() $\mathbf {w}$
.) By an argument similar to that used in the proof of Lemma 3.3, we can assume that the sequences
$\mathbf {w}$
.) By an argument similar to that used in the proof of Lemma 3.3, we can assume that the sequences
![]() $\{p_{q,i}\}_{q\in \mathbb {N}}$
converge to
$\{p_{q,i}\}_{q\in \mathbb {N}}$
converge to
![]() $0$
for all
$0$
for all
![]() $i\notin I(\mathbf {w})$
, so that, once again, we can apply the Curve Selection Lemma to get a real analytic curve
$i\notin I(\mathbf {w})$
, so that, once again, we can apply the Curve Selection Lemma to get a real analytic curve
![]() $ (t(s),\mathbf {a}(s))=(t(s),a_1(s),\ldots ,a_n(s)) $
in
$ (t(s),\mathbf {a}(s))=(t(s),a_1(s),\ldots ,a_n(s)) $
in
![]() $\mathbb {C}\times \mathbb {C}^{n}$
,
$\mathbb {C}\times \mathbb {C}^{n}$
,
![]() $0\leq s\leq 1$
, and a family of complex numbers
$0\leq s\leq 1$
, and a family of complex numbers
![]() $\lambda (s)$
,
$\lambda (s)$
,
![]() $0<s\leq 1$
, such that:
$0<s\leq 1$
, such that:
-
(1′)
 $f_{t(s),\mathbf {w}}^{k_1}(\mathbf {a}(s))=\cdots =f_{t(s),\mathbf {w}}^{k_m}(\mathbf {a}(s))=0$
for all
$f_{t(s),\mathbf {w}}^{k_1}(\mathbf {a}(s))=\cdots =f_{t(s),\mathbf {w}}^{k_m}(\mathbf {a}(s))=0$
for all
 $s\not =0$
.
$s\not =0$
. -
(2′) There exists a real analytic curve
 $(\mu _{k_1}(s),\ldots ,\mu _{k_m}(s))$
in
$(\mu _{k_1}(s),\ldots ,\mu _{k_m}(s))$
in
 $\mathbb {C}^m\setminus \{\mathbf {0}\}$
,
$\mathbb {C}^m\setminus \{\mathbf {0}\}$
,
 $0< s\leq 1$
, such that for all
$0< s\leq 1$
, such that for all
 $s\not =0$
and all
$s\not =0$
and all
 $1\leq i\leq n$
,
$1\leq i\leq n$
,  $$ \begin{align*} \sum_{j=1}^m \mu_{k_j}(s)\, \frac{\partial f_{t(s),\mathbf{w}}^{k_j}}{\partial z_i}(\mathbf{a}(s))=\left\{ \begin{aligned} & \lambda(s)\, \bar a_{i}(s), &&\mbox{if} &&i\in I(\mathbf{w}),\\ & 0, &&\mbox{if} &&i\notin I(\mathbf{w}). \end{aligned} \right. \end{align*} $$
$$ \begin{align*} \sum_{j=1}^m \mu_{k_j}(s)\, \frac{\partial f_{t(s),\mathbf{w}}^{k_j}}{\partial z_i}(\mathbf{a}(s))=\left\{ \begin{aligned} & \lambda(s)\, \bar a_{i}(s), &&\mbox{if} &&i\in I(\mathbf{w}),\\ & 0, &&\mbox{if} &&i\notin I(\mathbf{w}). \end{aligned} \right. \end{align*} $$
-
(3′)
 $\sum _{i\in I(\mathbf {w})} |a_i(s)|^2\leq \varepsilon _0^2$
,
$\sum _{i\in I(\mathbf {w})} |a_i(s)|^2\leq \varepsilon _0^2$
,
 $t(0)=0$
,
$t(0)=0$
,
 $a_i(0)=0$
for
$a_i(0)=0$
for
 $i\notin I(\mathbf {w})$
, and
$i\notin I(\mathbf {w})$
, and
 $\mathbf {a}(s)\in \mathbb {C}^{*n}$
for
$\mathbf {a}(s)\in \mathbb {C}^{*n}$
for
 $s\not =0$
.
$s\not =0$
.
For each
![]() $1\leq i\leq n$
, consider the Taylor expansion
$1\leq i\leq n$
, consider the Taylor expansion
where
![]() $b_i\in \mathbb {C}^*$
and
$b_i\in \mathbb {C}^*$
and
![]() $v_i\in \mathbb {N}$
, and put
$v_i\in \mathbb {N}$
, and put
![]() $v_{\text {min}}:=\mbox {min}\{v_1,\ldots ,v_n\}$
. Then we divide the proof into two cases depending on whether
$v_{\text {min}}:=\mbox {min}\{v_1,\ldots ,v_n\}$
. Then we divide the proof into two cases depending on whether
![]() $v_{\text {min}}=0$
or
$v_{\text {min}}=0$
or
![]() $v_{\text {min}}>0$
. Let us first assume
$v_{\text {min}}>0$
. Let us first assume
![]() $v_{\text {min}}>0$
. In this case, the proof is similar to that of Lemma 3.3. Indeed, exactly as in this proof, for each
$v_{\text {min}}>0$
. In this case, the proof is similar to that of Lemma 3.3. Indeed, exactly as in this proof, for each
![]() $1\leq j\leq m$
, the face
$1\leq j\leq m$
, the face
![]() $\Delta \big (\mathbf {v};f_{0,\mathbf {w}}^{k_j}\big )$
is a (compact) face of
$\Delta \big (\mathbf {v};f_{0,\mathbf {w}}^{k_j}\big )$
is a (compact) face of
![]() $\Gamma \big (f_{0}^{k_j}\big )$
and
$\Gamma \big (f_{0}^{k_j}\big )$
and
![]() $d\big (\mathbf {v};f_{0,\mathbf {w}}^{k_j}\big )>0$
. Since
$d\big (\mathbf {v};f_{0,\mathbf {w}}^{k_j}\big )>0$
. Since
![]() $\Gamma _+\big (f^{k_j}_t\big )$
—and hence
$\Gamma _+\big (f^{k_j}_t\big )$
—and hence
![]() $\Delta \big (\mathbf {w};f^{k_j}_t\big )$
—is independent of t, we have
$\Delta \big (\mathbf {w};f^{k_j}_t\big )$
—is independent of t, we have
for all
![]() $s\not =0$
, and hence
$s\not =0$
, and hence
![]() $f_{0,\mathbf {w},\mathbf {v}}^{k_j}(\mathbf {b})=0$
, where
$f_{0,\mathbf {w},\mathbf {v}}^{k_j}(\mathbf {b})=0$
, where
![]() $\mathbf {v}$
and
$\mathbf {v}$
and
![]() $\mathbf {b}$
are the points of
$\mathbf {b}$
are the points of
![]() $\mathbb {N}^{*n}$
and
$\mathbb {N}^{*n}$
and
![]() $\mathbb {C}^{*n}$
, respectively, whose ith coordinates are
$\mathbb {C}^{*n}$
, respectively, whose ith coordinates are
![]() $v_i$
and
$v_i$
and
![]() $b_i$
, respectively. Here, according to our notation, by
$b_i$
, respectively. Here, according to our notation, by
![]() $f_{0,\mathbf {w},\mathbf {v}}^{k_j}$
, we mean the face function
$f_{0,\mathbf {w},\mathbf {v}}^{k_j}$
, we mean the face function
![]() $\big (\big (f_{0}^{k_j}\big )_{\mathbf {w}}\big )_{\mathbf {v}}$
of
$\big (\big (f_{0}^{k_j}\big )_{\mathbf {w}}\big )_{\mathbf {v}}$
of
![]() $f_{0,\mathbf {w}}^{k_j}\equiv \big (f_{0}^{k_j}\big )_{\mathbf {w}}$
with respect to
$f_{0,\mathbf {w}}^{k_j}\equiv \big (f_{0}^{k_j}\big )_{\mathbf {w}}$
with respect to
![]() $\mathbf {v}$
.
$\mathbf {v}$
.
Write
![]() $\mu _{k_j}(s)=\mu _{k_j} s^{g_j}+\cdots $
, where
$\mu _{k_j}(s)=\mu _{k_j} s^{g_j}+\cdots $
, where
![]() $\mu _{k_j}\not =0$
. Again, if
$\mu _{k_j}\not =0$
. Again, if
![]() $\mu _{k_j}(s)\equiv 0$
, then
$\mu _{k_j}(s)\equiv 0$
, then
![]() $g_j=\infty $
. Put
$g_j=\infty $
. Put
and define
![]() $\tilde \mu _{k_j}$
to be equal to
$\tilde \mu _{k_j}$
to be equal to
![]() $\mu _{k_j}$
or
$\mu _{k_j}$
or
![]() $0$
depending on whether
$0$
depending on whether
![]() $d\big (\mathbf {v};f_{0,\mathbf {w}}^{k_j}\big )+g_j$
is equal to
$d\big (\mathbf {v};f_{0,\mathbf {w}}^{k_j}\big )+g_j$
is equal to
![]() $\delta $
or not, respectively.
$\delta $
or not, respectively.
Claim 4.9. There exists
![]() $i_0\in I(\mathbf {w})$
such that
$i_0\in I(\mathbf {w})$
such that
![]() $ \sum _{j=1}^m \tilde \mu _{k_j} \frac {\partial f_{0,\mathbf {w},\mathbf {v}}^{k_j}}{\partial z_{i_0}}(\mathbf {b})\not =0. $
$ \sum _{j=1}^m \tilde \mu _{k_j} \frac {\partial f_{0,\mathbf {w},\mathbf {v}}^{k_j}}{\partial z_{i_0}}(\mathbf {b})\not =0. $
Proof. It is along the same lines as the proof of Claim 3.7. More precisely, since
![]() $\Gamma _+\big (f^{k_j}_t\big )$
is independent of t, we have
$\Gamma _+\big (f^{k_j}_t\big )$
is independent of t, we have
 $$ \begin{align*} \frac{\partial f_{t(s),\mathbf{w}}^{k_j}}{\partial z_i}(\mathbf{a}(s)) = \frac{\partial f_{0,\mathbf{w},\mathbf{v}}^{k_j}}{\partial z_i}(\mathbf{b})\, s^{d\big(\mathbf{v};f_{0,\mathbf{w}}^{k_j}\big)-v_i}+\cdots \end{align*} $$
$$ \begin{align*} \frac{\partial f_{t(s),\mathbf{w}}^{k_j}}{\partial z_i}(\mathbf{a}(s)) = \frac{\partial f_{0,\mathbf{w},\mathbf{v}}^{k_j}}{\partial z_i}(\mathbf{b})\, s^{d\big(\mathbf{v};f_{0,\mathbf{w}}^{k_j}\big)-v_i}+\cdots \end{align*} $$
for all
![]() $1\leq j\leq m$
and all
$1\leq j\leq m$
and all
![]() $1\leq i\leq n$
. Thus, if the assertion in Claim 4.9 fails, then the sum
$1\leq i\leq n$
. Thus, if the assertion in Claim 4.9 fails, then the sum
 $$ \begin{align*} \sum_{j=1}^m \tilde\mu_{k_j} \frac{\partial f_{0,\mathbf{w},\mathbf{v}}^{k_j}}{\partial z_{i}}(\mathbf{b}) \end{align*} $$
$$ \begin{align*} \sum_{j=1}^m \tilde\mu_{k_j} \frac{\partial f_{0,\mathbf{w},\mathbf{v}}^{k_j}}{\partial z_{i}}(\mathbf{b}) \end{align*} $$
vanishes for all
![]() $i\in I(\mathbf {w})$
, and so, by (
$i\in I(\mathbf {w})$
, and so, by (
![]() $2'$
), it vanishes for all
$2'$
), it vanishes for all
![]() $1\leq i\leq n$
. As in the proof of Claim 3.7, this implies that
$1\leq i\leq n$
. As in the proof of Claim 3.7, this implies that
where the
![]() $k_{j_\ell }$
’s (
$k_{j_\ell }$
’s (
![]() $1\leq \ell \leq p$
) are the elements of
$1\leq \ell \leq p$
) are the elements of
![]() $\{k_1,\ldots ,k_m\}$
for which
$\{k_1,\ldots ,k_m\}$
for which
![]() $d\big (\mathbf {v};f_{0,\mathbf {w}}^{k_{j_\ell }}\big )+g_{j_\ell }=\delta $
. Since
$d\big (\mathbf {v};f_{0,\mathbf {w}}^{k_{j_\ell }}\big )+g_{j_\ell }=\delta $
. Since
![]() $f_{0,\mathbf {w},\mathbf {v}}^{k_{j_\ell }} = f_{0,\mathbf {v}+\nu \mathbf {w}}^{k_{j_\ell }}$
for any sufficiently large integer
$f_{0,\mathbf {w},\mathbf {v}}^{k_{j_\ell }} = f_{0,\mathbf {v}+\nu \mathbf {w}}^{k_{j_\ell }}$
for any sufficiently large integer
![]() $\nu \in \mathbb {N}$
(so that
$\nu \in \mathbb {N}$
(so that
![]() $f_{0,\mathbf {w},\mathbf {v}}^{k_{j_\ell }}$
is the face function of
$f_{0,\mathbf {w},\mathbf {v}}^{k_{j_\ell }}$
is the face function of
![]() $f_{0}^{k_{j_\ell }}$
with respect to the weight vector
$f_{0}^{k_{j_\ell }}$
with respect to the weight vector
![]() $\mathbf {v}+\nu \mathbf {w}$
) and
$\mathbf {v}+\nu \mathbf {w}$
) and
![]() $f_{0,\mathbf {w},\mathbf {v}}^{k_{j_\ell }}(\mathbf {b})=0$
for
$f_{0,\mathbf {w},\mathbf {v}}^{k_{j_\ell }}(\mathbf {b})=0$
for
![]() $1\leq \ell \leq p$
, and since
$1\leq \ell \leq p$
, and since
![]() $v_i+\nu w_i>0$
for all
$v_i+\nu w_i>0$
for all
![]() $1\leq i\leq n$
, this contradicts the nondegeneracy of
$1\leq i\leq n$
, this contradicts the nondegeneracy of
![]() $V\big (f_0^{k_{j_1}},\ldots ,f_0^{k_{j_p}}\big )$
(see Assumptions 4.1).
$V\big (f_0^{k_{j_1}},\ldots ,f_0^{k_{j_p}}\big )$
(see Assumptions 4.1).
Combined with (
![]() $2'$
) again, Claim 4.9 implies that
$2'$
) again, Claim 4.9 implies that
![]() $\lambda (s)$
is not constantly zero. Write it as a Laurent series
$\lambda (s)$
is not constantly zero. Write it as a Laurent series
![]() $\lambda (s)=\lambda _0 s^c+\cdots $
, where
$\lambda (s)=\lambda _0 s^c+\cdots $
, where
![]() $\lambda _0\not =0$
. Then, still from (
$\lambda _0\not =0$
. Then, still from (
![]() $2'$
), we deduce that for all
$2'$
), we deduce that for all
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
 $$ \begin{align*} \sum_{j=1}^m \tilde\mu_{k_j} \frac{\partial f_{0,\mathbf{w},\mathbf{v}}^{k_j}}{\partial z_i}(\mathbf{b})\, s^{\delta} + \cdots = \left\{ \begin{aligned} & \lambda_0 \bar b_i\, s^{c+2v_i}+\cdots, &&\mbox{if} &&i\in I(\mathbf{w}),\\ & 0, &&\mbox{if} &&i\notin I(\mathbf{w}). \end{aligned} \right. \end{align*} $$
$$ \begin{align*} \sum_{j=1}^m \tilde\mu_{k_j} \frac{\partial f_{0,\mathbf{w},\mathbf{v}}^{k_j}}{\partial z_i}(\mathbf{b})\, s^{\delta} + \cdots = \left\{ \begin{aligned} & \lambda_0 \bar b_i\, s^{c+2v_i}+\cdots, &&\mbox{if} &&i\in I(\mathbf{w}),\\ & 0, &&\mbox{if} &&i\notin I(\mathbf{w}). \end{aligned} \right. \end{align*} $$
Now, put
![]() $S_i:=\sum _{j=1}^m \tilde \mu _{k_j} \frac {\partial f_{0,\mathbf {w},\mathbf {v}}^{k_j}}{\partial z_i}(\mathbf {b})$
and define
$S_i:=\sum _{j=1}^m \tilde \mu _{k_j} \frac {\partial f_{0,\mathbf {w},\mathbf {v}}^{k_j}}{\partial z_i}(\mathbf {b})$
and define
![]() $v_0\in \mathbb {N}$
and
$v_0\in \mathbb {N}$
and
![]() $I_0\subseteq \{1,\ldots ,n\}$
as in (3.7), that is,
$I_0\subseteq \{1,\ldots ,n\}$
as in (3.7), that is,
![]() $v_0:=\mbox {min}\{v_i\, ;\, i\in I(\mathbf {w})\}$
and
$v_0:=\mbox {min}\{v_i\, ;\, i\in I(\mathbf {w})\}$
and
![]() $I_0:=\{i\in I(\mathbf {w})\, ;\, v_i=v_0\}$
. (Note that, in general,
$I_0:=\{i\in I(\mathbf {w})\, ;\, v_i=v_0\}$
. (Note that, in general,
![]() $v_0\geq v_{\text {min}}$
.) Then, as in the proof of Lemma 3.3, since
$v_0\geq v_{\text {min}}$
.) Then, as in the proof of Lemma 3.3, since
![]() $\lambda _0 \bar b_i\not =0$
and the set
$\lambda _0 \bar b_i\not =0$
and the set
![]() $\{i\in I(\mathbf {w})\, ;\, S_i\not =0\}$
is not empty (see Claim 4.9), we have
$\{i\in I(\mathbf {w})\, ;\, S_i\not =0\}$
is not empty (see Claim 4.9), we have
![]() $\delta =c+2v_0$
and
$\delta =c+2v_0$
and
![]() $S_i\not =0$
for any
$S_i\not =0$
for any
![]() $i\in I_0$
. In fact, for any
$i\in I_0$
. In fact, for any
![]() $1\leq i\leq n$
, the following holds:
$1\leq i\leq n$
, the following holds:
 $$ \begin{align} S_i\equiv\sum_{j=1}^m \tilde\mu_{k_j} \frac{\partial f_{0,\mathbf{w},\mathbf{v}}^{k_j}}{\partial z_i}(\mathbf{b})= \left\{ \begin{aligned} & \lambda_0 \bar b_i, && \mbox{if} && i\in I_0,\\ & 0, && \mbox{if} && i\notin I_0. \end{aligned} \right. \end{align} $$
$$ \begin{align} S_i\equiv\sum_{j=1}^m \tilde\mu_{k_j} \frac{\partial f_{0,\mathbf{w},\mathbf{v}}^{k_j}}{\partial z_i}(\mathbf{b})= \left\{ \begin{aligned} & \lambda_0 \bar b_i, && \mbox{if} && i\in I_0,\\ & 0, && \mbox{if} && i\notin I_0. \end{aligned} \right. \end{align} $$
Since
![]() $I_0\not =\emptyset $
and
$I_0\not =\emptyset $
and
![]() $f_{0,\mathbf {w},\mathbf {v}}^{k_j}(\mathbf {b})=0$
(
$f_{0,\mathbf {w},\mathbf {v}}^{k_j}(\mathbf {b})=0$
(
![]() $1\leq j\leq m$
), the relation (4.4) together with the Euler identity imply
$1\leq j\leq m$
), the relation (4.4) together with the Euler identity imply
 $$ \begin{align} \begin{aligned} 0 & = \sum_{j=1}^{m}\tilde\mu_{k_j}\cdot d\big(\mathbf{v};f_{0,\mathbf{w}}^{k_j}\big) \cdot f_{0,\mathbf{w},\mathbf{v}}^{k_j}(\mathbf{b}) = \sum_{j=1}^{m}\tilde\mu_{k_j}\bigg(\sum_{i=1}^n v_i b_i \frac{\partial f_{0,\mathbf{w},\mathbf{v}}^{k_j}}{\partial z_i}(\mathbf{b})\bigg) \\ & = \sum_{i\in I_0}v_i b_i\bigg( \sum_{j=1}^{m}\tilde\mu_{k_j} \frac{\partial f_{0,\mathbf{w},\mathbf{v}}^{k_j}}{\partial z_i}(\mathbf{b}) \bigg) =\lambda_0\cdot\sum_{i\in I_0} v_i |b_i|^2\not=0, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} 0 & = \sum_{j=1}^{m}\tilde\mu_{k_j}\cdot d\big(\mathbf{v};f_{0,\mathbf{w}}^{k_j}\big) \cdot f_{0,\mathbf{w},\mathbf{v}}^{k_j}(\mathbf{b}) = \sum_{j=1}^{m}\tilde\mu_{k_j}\bigg(\sum_{i=1}^n v_i b_i \frac{\partial f_{0,\mathbf{w},\mathbf{v}}^{k_j}}{\partial z_i}(\mathbf{b})\bigg) \\ & = \sum_{i\in I_0}v_i b_i\bigg( \sum_{j=1}^{m}\tilde\mu_{k_j} \frac{\partial f_{0,\mathbf{w},\mathbf{v}}^{k_j}}{\partial z_i}(\mathbf{b}) \bigg) =\lambda_0\cdot\sum_{i\in I_0} v_i |b_i|^2\not=0, \end{aligned} \end{align} $$
which is a contradiction. This completes the proof of Lemma 4.2 in the case
![]() $v_{\text {min}}>0$
.
$v_{\text {min}}>0$
.
Let us now assume
![]() $v_{\text {min}}=0$
. Clearly, we still have
$v_{\text {min}}=0$
. Clearly, we still have
![]() $f_{0,\mathbf {w},\mathbf {v}}^{k_j}(\mathbf {b})=0$
for
$f_{0,\mathbf {w},\mathbf {v}}^{k_j}(\mathbf {b})=0$
for
![]() $1\leq j\leq m$
.
$1\leq j\leq m$
.
Claim 4.10. Even when
![]() $v_{\text {{min}}}=0$
, there exists
$v_{\text {{min}}}=0$
, there exists
![]() $i_0\in I(\mathbf {w})$
such that
$i_0\in I(\mathbf {w})$
such that
![]() $ \sum _{j=1}^m \tilde \mu _{k_j} \frac {\partial f_{0,\mathbf {w},\mathbf {v}}^{k_j}}{\partial z_{i_0}}(\mathbf {b})\not = 0. $
$ \sum _{j=1}^m \tilde \mu _{k_j} \frac {\partial f_{0,\mathbf {w},\mathbf {v}}^{k_j}}{\partial z_{i_0}}(\mathbf {b})\not = 0. $
Proof. When
![]() $v_{\text {min}}=0$
, the argument given in the proof of Claim 4.9 does not apply. In fact, in this case, Claim 4.10 directly follows from Lemma 3.3 and our choice of
$v_{\text {min}}=0$
, the argument given in the proof of Claim 4.9 does not apply. In fact, in this case, Claim 4.10 directly follows from Lemma 3.3 and our choice of
![]() $\varepsilon _0$
. More precisely, we know that
$\varepsilon _0$
. More precisely, we know that
![]() $\mathbf {b}\in \mathbb {C}^{*n}$
,
$\mathbf {b}\in \mathbb {C}^{*n}$
,
![]() $f_{0,\mathbf {w},\mathbf {v}}^{k_j}(\mathbf {b})=0$
(
$f_{0,\mathbf {w},\mathbf {v}}^{k_j}(\mathbf {b})=0$
(
![]() $1\leq j\leq m$
), and
$1\leq j\leq m$
), and
![]() $f_{0,\mathbf {w},\mathbf {v}}^{k_j}=f_{0,\mathbf {v}+\nu \mathbf {w}}^{k_j}$
for
$f_{0,\mathbf {w},\mathbf {v}}^{k_j}=f_{0,\mathbf {v}+\nu \mathbf {w}}^{k_j}$
for
![]() $\nu \in \mathbb {N}$
large enough. Therefore, arguing by contradiction, if
$\nu \in \mathbb {N}$
large enough. Therefore, arguing by contradiction, if
 $$ \begin{align*} \sum_{j=1}^m \tilde\mu_{k_j} \frac{\partial f_{0,\mathbf{w},\mathbf{v}}^{k_j}}{\partial z_{i}}(\mathbf{b})=0 \end{align*} $$
$$ \begin{align*} \sum_{j=1}^m \tilde\mu_{k_j} \frac{\partial f_{0,\mathbf{w},\mathbf{v}}^{k_j}}{\partial z_{i}}(\mathbf{b})=0 \end{align*} $$
for all
![]() $i\in I(\mathbf {w})$
(and hence, by (
$i\in I(\mathbf {w})$
(and hence, by (
![]() $2'$
), for all
$2'$
), for all
![]() $1\leq i\leq n$
), then Lemma 3.3 and our choice of
$1\leq i\leq n$
), then Lemma 3.3 and our choice of
![]() $\varepsilon _0$
show that
$\varepsilon _0$
show that
 $$ \begin{align*} \mathbf{b}\notin\bigg\{\mathbf{z}\in \mathbb{C}^{*n}\, ;\, \sum_{i\in I(\mathbf{v}+\nu\mathbf{w})}|z_i|^2\leq \varepsilon_0^2\bigg\}. \end{align*} $$
$$ \begin{align*} \mathbf{b}\notin\bigg\{\mathbf{z}\in \mathbb{C}^{*n}\, ;\, \sum_{i\in I(\mathbf{v}+\nu\mathbf{w})}|z_i|^2\leq \varepsilon_0^2\bigg\}. \end{align*} $$
However, since
![]() $I(\mathbf {v+\nu \mathbf {w}})\subseteq I(\mathbf {v})$
, we have
$I(\mathbf {v+\nu \mathbf {w}})\subseteq I(\mathbf {v})$
, we have
 $$ \begin{align*} \sum_{i\in I(\mathbf{v}+\nu\mathbf{w})}|b_i|^2 \leq \sum_{i\in I(\mathbf{v})}|b_i|^2 = \sum_{i\in I(\mathbf{v})}|a_i(0)|^2 \leq \underbrace{\sum_{i\in I(\mathbf{w})}|a_i(0)|^2}_{\leq \varepsilon_0^2} + \underbrace{\sum_{i\in I(\mathbf{w})^c}|a_i(0)|^2}_{=0} \leq \varepsilon_0^2, \end{align*} $$
$$ \begin{align*} \sum_{i\in I(\mathbf{v}+\nu\mathbf{w})}|b_i|^2 \leq \sum_{i\in I(\mathbf{v})}|b_i|^2 = \sum_{i\in I(\mathbf{v})}|a_i(0)|^2 \leq \underbrace{\sum_{i\in I(\mathbf{w})}|a_i(0)|^2}_{\leq \varepsilon_0^2} + \underbrace{\sum_{i\in I(\mathbf{w})^c}|a_i(0)|^2}_{=0} \leq \varepsilon_0^2, \end{align*} $$
which is a contradiction. (Here,
![]() $I(\mathbf {w})^c:=\{1,\ldots ,n\}\setminus I(\mathbf {w})$
.)
$I(\mathbf {w})^c:=\{1,\ldots ,n\}\setminus I(\mathbf {w})$
.)
Combined with (
![]() $2'$
), Claim 4.10 shows that
$2'$
), Claim 4.10 shows that
![]() $\lambda (s)$
is not constantly zero, and exactly as above we deduce that the relation (4.4) holds true for
$\lambda (s)$
is not constantly zero, and exactly as above we deduce that the relation (4.4) holds true for
![]() $v_{\text {min}}=0$
too. (The subset
$v_{\text {min}}=0$
too. (The subset
![]() $I_0$
and the number
$I_0$
and the number
![]() $v_0$
are defined as before; we also use the same Laurent expansion
$v_0$
are defined as before; we also use the same Laurent expansion
![]() $\lambda (s)=\lambda _0 s^c+\cdots $
.) If
$\lambda (s)=\lambda _0 s^c+\cdots $
.) If
![]() $v_0=0$
, then
$v_0=0$
, then
![]() $I_0=I(\mathbf {w})\cap I(\mathbf {v})=I(\mathbf {v}+\nu \mathbf {w})$
, and since
$I_0=I(\mathbf {w})\cap I(\mathbf {v})=I(\mathbf {v}+\nu \mathbf {w})$
, and since
![]() $\sum _{i\in I(\mathbf {v}+\nu \mathbf {w})}|b_i|^2\leq \varepsilon _0^2$
, then, once again, we get a contradiction with Lemma 3.3 and our choice of
$\sum _{i\in I(\mathbf {v}+\nu \mathbf {w})}|b_i|^2\leq \varepsilon _0^2$
, then, once again, we get a contradiction with Lemma 3.3 and our choice of
![]() $\varepsilon _0$
. If
$\varepsilon _0$
. If
![]() $v_0\not =0$
, then we get a contradiction exactly as in (4.5). This completes the proof of Lemma 4.2 in the case
$v_0\not =0$
, then we get a contradiction exactly as in (4.5). This completes the proof of Lemma 4.2 in the case
![]() $v_{\text {min}}=0$
.
$v_{\text {min}}=0$
.
5 The “nonfamily” case
In the previous section, we have studied the case of families of functions. Hereafter, we investigate the “nonfamily” case. For that purpose, we consider
![]() $2k_0$
nonconstant polynomial functions
$2k_0$
nonconstant polynomial functions
![]() $f^1(\mathbf {z}),\ldots , f^{k_0}(\mathbf {z})$
and
$f^1(\mathbf {z}),\ldots , f^{k_0}(\mathbf {z})$
and
![]() $g^1(\mathbf {z}),\ldots , g^{k_0}(\mathbf {z})$
, each of them in n complex variables
$g^1(\mathbf {z}),\ldots , g^{k_0}(\mathbf {z})$
, each of them in n complex variables
![]() $\mathbf {z}=(z_1,\ldots ,z_n)$
, and as usual we assume that
$\mathbf {z}=(z_1,\ldots ,z_n)$
, and as usual we assume that
![]() $f^k(\mathbf {0})=g^k(\mathbf {0})=0$
for all
$f^k(\mathbf {0})=g^k(\mathbf {0})=0$
for all
![]() $1\leq k\leq k_0$
.
$1\leq k\leq k_0$
.
Assumptions 5.1. Throughout this section, we suppose that the following two conditions hold true:
-
(1) For any
 $1\leq k\leq k_0$
, the Newton boundaries
$1\leq k\leq k_0$
, the Newton boundaries
 $\Gamma (f^k)$
and
$\Gamma (f^k)$
and
 $\Gamma (g^k)$
coincide.
$\Gamma (g^k)$
coincide. -
(2) For any
 $k_1,\ldots ,k_m\in \{k_1,\ldots ,k_0\}$
, the germs at
$k_1,\ldots ,k_m\in \{k_1,\ldots ,k_0\}$
, the germs at
 $\mathbf {0}$
of the varieties
$\mathbf {0}$
of the varieties
 $V(f^{k_1},\ldots ,f^{k_m})$
and
$V(f^{k_1},\ldots ,f^{k_m})$
and
 $V(g^{k_1},\ldots ,g^{k_m})$
are the germs of nondegenerate complete intersection varieties.
$V(g^{k_1},\ldots ,g^{k_m})$
are the germs of nondegenerate complete intersection varieties.
Put
![]() $f(\mathbf {z}):=f^1(\mathbf {z})\cdots f^{k_0}(\mathbf {z})$
and
$f(\mathbf {z}):=f^1(\mathbf {z})\cdots f^{k_0}(\mathbf {z})$
and
![]() $g(\mathbf {z}):=g^1(\mathbf {z})\cdots g^{k_0}(\mathbf {z})$
. The second main theorem of this paper is stated as follows. Once more, note that when
$g(\mathbf {z}):=g^1(\mathbf {z})\cdots g^{k_0}(\mathbf {z})$
. The second main theorem of this paper is stated as follows. Once more, note that when
![]() $k_0=1$
, the functions f and g are nondegenerate, and then we recover Theorem 3 of [Reference Oka9].
$k_0=1$
, the functions f and g are nondegenerate, and then we recover Theorem 3 of [Reference Oka9].
Theorem 5.2. Under Assumptions 5.1, the Milnor fibrations of f and g at
![]() $\mathbf {0}$
are isomorphic.
$\mathbf {0}$
are isomorphic.
Proof. For any
![]() $1\leq k\leq k_0$
and any
$1\leq k\leq k_0$
and any
![]() $t\in D_1:=\{t\in \mathbb {C}\, ;\, \vert t\vert \leq 1\}$
, we consider the polynomial functions
$t\in D_1:=\{t\in \mathbb {C}\, ;\, \vert t\vert \leq 1\}$
, we consider the polynomial functions
where
 $$ \begin{align*} F^k(\mathbf{z}):=\sum_{\alpha\in\Gamma(f^k)}c_\alpha\, \mathbf{z}^\alpha \quad\mbox{and}\quad G^k(\mathbf{z}):=\sum_{\alpha\in\Gamma(g^k)}c^{\prime}_\alpha\, \mathbf{z}^\alpha \end{align*} $$
$$ \begin{align*} F^k(\mathbf{z}):=\sum_{\alpha\in\Gamma(f^k)}c_\alpha\, \mathbf{z}^\alpha \quad\mbox{and}\quad G^k(\mathbf{z}):=\sum_{\alpha\in\Gamma(g^k)}c^{\prime}_\alpha\, \mathbf{z}^\alpha \end{align*} $$
are the Newton principal parts of
 $$ \begin{align*} f^k(\mathbf{z}):=\sum_{\alpha\in\mathbb{N}^n}c_\alpha\, \mathbf{z}^\alpha \quad\mbox{and}\quad g^k(\mathbf{z}):=\sum_{\alpha\in\mathbb{N}^n}c^{\prime}_\alpha\, \mathbf{z}^\alpha, \end{align*} $$
$$ \begin{align*} f^k(\mathbf{z}):=\sum_{\alpha\in\mathbb{N}^n}c_\alpha\, \mathbf{z}^\alpha \quad\mbox{and}\quad g^k(\mathbf{z}):=\sum_{\alpha\in\mathbb{N}^n}c^{\prime}_\alpha\, \mathbf{z}^\alpha, \end{align*} $$
respectively.
Claim 5.3. The Milnor fibrations of
![]() $f^1\cdots f^{k_0}$
and
$f^1\cdots f^{k_0}$
and
![]() $F^1\cdots F^{k_0}$
(resp. of
$F^1\cdots F^{k_0}$
(resp. of
![]() $g^1\cdots g^{k_0}$
and
$g^1\cdots g^{k_0}$
and
![]() $G^1\cdots G^{k_0}$
) at
$G^1\cdots G^{k_0}$
) at
![]() $\mathbf {0}$
are isomorphic.
$\mathbf {0}$
are isomorphic.
Proof. First, observe that for any
![]() $1\leq k\leq k_0$
and any positive weight vector
$1\leq k\leq k_0$
and any positive weight vector
![]() $\mathbf {w}$
, we have
$\mathbf {w}$
, we have
From this observation and Assumptions 5.1, we deduce that
![]() $V(f_t^{k_1},\ldots ,f_t^{k_m})$
is a nondegenerate complete intersection variety for any
$V(f_t^{k_1},\ldots ,f_t^{k_m})$
is a nondegenerate complete intersection variety for any
![]() $t\in D_1$
, and since
$t\in D_1$
, and since
![]() $\Gamma (f^k_t)=\Gamma (f^k)$
, it follows from Theorem 4.8 that the functions
$\Gamma (f^k_t)=\Gamma (f^k)$
, it follows from Theorem 4.8 that the functions
![]() $f_t(\mathbf {z}):=f_t^1(\mathbf {z})\cdots f_t^{k_0}(\mathbf {z})$
and
$f_t(\mathbf {z}):=f_t^1(\mathbf {z})\cdots f_t^{k_0}(\mathbf {z})$
and
![]() $f_0(\mathbf {z}):=f_0^1(\mathbf {z})\cdots f_0^{k_0}(\mathbf {z})=f^1(\mathbf {z})\cdots f^{k_0}(\mathbf {z})$
have isomorphic Milnor fibrations for any
$f_0(\mathbf {z}):=f_0^1(\mathbf {z})\cdots f_0^{k_0}(\mathbf {z})=f^1(\mathbf {z})\cdots f^{k_0}(\mathbf {z})$
have isomorphic Milnor fibrations for any
![]() $t\in D_1$
. In particular, taking
$t\in D_1$
. In particular, taking
![]() $t=1$
gives that
$t=1$
gives that
![]() $F^1\cdots F^{k_0}$
and
$F^1\cdots F^{k_0}$
and
![]() $f^1\cdots f^{k_0}$
have isomorphic Milnor fibrations as announced.
$f^1\cdots f^{k_0}$
have isomorphic Milnor fibrations as announced.
Claim 5.4. The Milnor fibrations of
![]() $F^1\cdots F^{k_0}$
and
$F^1\cdots F^{k_0}$
and
![]() $G^1\cdots G^{k_0}$
at
$G^1\cdots G^{k_0}$
at
![]() $\mathbf {0}$
are isomorphic.
$\mathbf {0}$
are isomorphic.
The proof of this claim is given below. Of course, Theorem 5.2 follows from Claims 5.3 and 5.4.
Now, let us prove Claim 5.4.
Proof of Claim 5.4
For each
![]() $1\leq k\leq k_0$
, let
$1\leq k\leq k_0$
, let
![]() $\nu _{k,1},\ldots ,\nu _{k,n_k}$
be the integral points of
$\nu _{k,1},\ldots ,\nu _{k,n_k}$
be the integral points of
![]() $\Gamma (f^k)=\Gamma (F^k)$
, and for any
$\Gamma (f^k)=\Gamma (F^k)$
, and for any
![]() $\mathbf {c}_k=(c_{k,1},\ldots ,c_{k,n_k})\in \mathbb {C}^{n_k}$
, put
$\mathbf {c}_k=(c_{k,1},\ldots ,c_{k,n_k})\in \mathbb {C}^{n_k}$
, put
 $$ \begin{align*} h^k_{\mathbf{c}_k}(\mathbf{z}):=\sum_{j=1}^{n_k} c_{k,j}\, \mathbf{z}^{\nu_{k,j}}. \end{align*} $$
$$ \begin{align*} h^k_{\mathbf{c}_k}(\mathbf{z}):=\sum_{j=1}^{n_k} c_{k,j}\, \mathbf{z}^{\nu_{k,j}}. \end{align*} $$
Now, consider the set U of points
![]() $(\mathbf {c}_1,\ldots ,\mathbf {c}_{k_0})$
in
$(\mathbf {c}_1,\ldots ,\mathbf {c}_{k_0})$
in
![]() $\mathbb {C}^{n_1}\times \cdots \times \mathbb {C}^{n_{k_0}}$
such that:
$\mathbb {C}^{n_1}\times \cdots \times \mathbb {C}^{n_{k_0}}$
such that:
-
(1)
 $\Gamma (h^k_{\mathbf {c}_k})=\Gamma (f^k)$
for any
$\Gamma (h^k_{\mathbf {c}_k})=\Gamma (f^k)$
for any
 $1\leq k\leq k_0$
.
$1\leq k\leq k_0$
. -
(2) For any
 $1\leq k_1,\ldots ,k_m\leq k_0$
, the variety
$1\leq k_1,\ldots ,k_m\leq k_0$
, the variety
 $V(h^{k_1}_{\mathbf {c}_{k_1}},\ldots ,h^{k_m}_{\mathbf {c}_{k_m}})$
is a nondegenerate complete intersection variety.
$V(h^{k_1}_{\mathbf {c}_{k_1}},\ldots ,h^{k_m}_{\mathbf {c}_{k_m}})$
is a nondegenerate complete intersection variety.
Claim 5.5. The set U is a Zariski open subset of
![]() $\mathbb {C}^{n_1}\times \cdots \times \mathbb {C}^{n_{k_0}}$
; in particular, it is path-connected.
$\mathbb {C}^{n_1}\times \cdots \times \mathbb {C}^{n_{k_0}}$
; in particular, it is path-connected.
The special case
![]() $k_0=1$
in Claim 5.5 is treated in the Appendix of [Reference Oka7]. Before proving this claim in the general case, we complete the proof of Claim 5.4.
$k_0=1$
in Claim 5.5 is treated in the Appendix of [Reference Oka7]. Before proving this claim in the general case, we complete the proof of Claim 5.4.
For each
![]() $1\leq k\leq k_0$
, let
$1\leq k\leq k_0$
, let
be the points defined by
 $$ \begin{align*} F^k(\mathbf{z}):=h^k_{\mathbf{c}_{k}(F^k)}(\mathbf{z}) :=\sum_{j=1}^{n_k} c_{k,j}(F^k)\, \mathbf{z}^{\nu_{k,j}} \quad\mbox{and}\quad G^k(\mathbf{z}):=h^k_{\mathbf{c}_{k}(G^k)}(\mathbf{z}) :=\sum_{j=1}^{n_k} c_{k,j}(G^k)\, \mathbf{z}^{\nu_{k,j}}. \end{align*} $$
$$ \begin{align*} F^k(\mathbf{z}):=h^k_{\mathbf{c}_{k}(F^k)}(\mathbf{z}) :=\sum_{j=1}^{n_k} c_{k,j}(F^k)\, \mathbf{z}^{\nu_{k,j}} \quad\mbox{and}\quad G^k(\mathbf{z}):=h^k_{\mathbf{c}_{k}(G^k)}(\mathbf{z}) :=\sum_{j=1}^{n_k} c_{k,j}(G^k)\, \mathbf{z}^{\nu_{k,j}}. \end{align*} $$
By Claim 5.5, we can choose a finite sequence of (say,
![]() $p_0$
)
$p_0$
)
![]() $k_0$
-tuples
$k_0$
-tuples
in U, starting at
![]() $(\mathbf {c}_1(F^1),\ldots ,\mathbf {c}_{k_0}(F^{k_0}))$
and ending at
$(\mathbf {c}_1(F^1),\ldots ,\mathbf {c}_{k_0}(F^{k_0}))$
and ending at
![]() $(\mathbf {c}_1(G^1),\ldots ,\mathbf {c}_{k_0}(G^{k_0}))$
, such that for each
$(\mathbf {c}_1(G^1),\ldots ,\mathbf {c}_{k_0}(G^{k_0}))$
, such that for each
![]() $1\leq p\leq p_0-1$
, the straight-line segment
$1\leq p\leq p_0-1$
, the straight-line segment
(
![]() $1\leq t\leq 1$
) is contained in U. For each
$1\leq t\leq 1$
) is contained in U. For each
![]() $1\leq p\leq p_0-1$
, we consider the family
$1\leq p\leq p_0-1$
, we consider the family
![]() $\big \{h_{\ell _{p}(t)}\big \}_{0\leq t\leq 1}$
of polynomial functions defined by
$\big \{h_{\ell _{p}(t)}\big \}_{0\leq t\leq 1}$
of polynomial functions defined by
where
![]() $\ell ^{k}_{p}(t):=(1-t)\mathbf {c}_{k}(p)+t\mathbf {c}_{k}(p+1)$
is the kth coordinate of
$\ell ^{k}_{p}(t):=(1-t)\mathbf {c}_{k}(p)+t\mathbf {c}_{k}(p+1)$
is the kth coordinate of
![]() $\ell _{p}(t)$
. By Theorem 4.8, the Milnor fibrations of
$\ell _{p}(t)$
. By Theorem 4.8, the Milnor fibrations of
![]() $h_{\ell _{p}(0)}$
and
$h_{\ell _{p}(0)}$
and
![]() $h_{\ell _{p}(1)}$
at
$h_{\ell _{p}(1)}$
at
![]() $\mathbf {0}$
are isomorphic. Claim 5.4 then follows from the equalities
$\mathbf {0}$
are isomorphic. Claim 5.4 then follows from the equalities
Now, let us prove Claim 5.5.
Proof of Claim 5.5
For any
![]() $1\leq k\leq k_0$
and any positive weight vector
$1\leq k\leq k_0$
and any positive weight vector
![]() $\mathbf {w}$
defining a (compact) face
$\mathbf {w}$
defining a (compact) face
![]() $\Delta (\mathbf {w};f^k)$
of
$\Delta (\mathbf {w};f^k)$
of
![]() $\Gamma (f^k)$
with maximal dimension, let us denote by
$\Gamma (f^k)$
with maximal dimension, let us denote by
![]() $\theta _{k,1},\ldots ,\theta _{k,q_k}$
the integral points of
$\theta _{k,1},\ldots ,\theta _{k,q_k}$
the integral points of
![]() $\Delta (\mathbf {w};f^k)$
. Then, for any
$\Delta (\mathbf {w};f^k)$
. Then, for any
![]() $\mathbf {a}_k=(a_{k,1},\ldots ,a_{k,q_k})\in \mathbb {C}^{q_k}$
, put
$\mathbf {a}_k=(a_{k,1},\ldots ,a_{k,q_k})\in \mathbb {C}^{q_k}$
, put
 $$ \begin{align*} \phi^k_{\mathbf{a}_k}(\mathbf{z}):=\sum_{j=1}^{q_k} a_{k,j}\, \mathbf{z}^{\theta_{k,j}}. \end{align*} $$
$$ \begin{align*} \phi^k_{\mathbf{a}_k}(\mathbf{z}):=\sum_{j=1}^{q_k} a_{k,j}\, \mathbf{z}^{\theta_{k,j}}. \end{align*} $$
Note that
![]() $\phi ^k_{\mathbf {a}_k}$
is weighted homogeneous with respect to
$\phi ^k_{\mathbf {a}_k}$
is weighted homogeneous with respect to
![]() $\mathbf {w}$
. Now, consider the set
$\mathbf {w}$
. Now, consider the set
![]() $U_{\mathbf {w}}$
consisting of the points
$U_{\mathbf {w}}$
consisting of the points
![]() $(\mathbf {a}_1,\ldots ,\mathbf {a}_{k_0})$
in
$(\mathbf {a}_1,\ldots ,\mathbf {a}_{k_0})$
in
![]() $\mathbb {C}^{q_1}\times \cdots \times \mathbb {C}^{q_{k_0}}$
satisfying the following two properties:
$\mathbb {C}^{q_1}\times \cdots \times \mathbb {C}^{q_{k_0}}$
satisfying the following two properties:
-
(1)
 $\Gamma (\phi ^k_{\mathbf {a}_k})=\Delta (\mathbf {w};f^k)$
for any
$\Gamma (\phi ^k_{\mathbf {a}_k})=\Delta (\mathbf {w};f^k)$
for any
 $1\leq k\leq k_0$
.
$1\leq k\leq k_0$
. -
(2) For any
 $1\leq k_1,\ldots ,k_m\leq k_0$
, the variety
$1\leq k_1,\ldots ,k_m\leq k_0$
, the variety
 $V(\phi ^{k_1}_{\mathbf {a}_{k_1}},\ldots ,\phi ^{k_m}_{\mathbf {a}_{k_m}})$
is a nondegenerate complete intersection variety.
$V(\phi ^{k_1}_{\mathbf {a}_{k_1}},\ldots ,\phi ^{k_m}_{\mathbf {a}_{k_m}})$
is a nondegenerate complete intersection variety.
To prove Claim 5.5, it suffices to show that
![]() $U_{\mathbf {w}}$
is a Zariski open set. To do that, we first observe that since
$U_{\mathbf {w}}$
is a Zariski open set. To do that, we first observe that since
![]() $\phi ^{k_j}_{\mathbf {a}_{k_j}}$
(
$\phi ^{k_j}_{\mathbf {a}_{k_j}}$
(
![]() $1\leq j\leq m$
) is weighted homogeneous, there exist
$1\leq j\leq m$
) is weighted homogeneous, there exist
![]() $\lambda _1,\ldots ,\lambda _n\in \mathbb {N}^*$
such that the polynomial
$\lambda _1,\ldots ,\lambda _n\in \mathbb {N}^*$
such that the polynomial
is homogeneous. Then, since
![]() $V(\phi ^{k_1}_{\mathbf {a}_{k_1}},\ldots ,\phi ^{k_m}_{\mathbf {a}_{k_m}})$
is nondegenerate if and only if
$V(\phi ^{k_1}_{\mathbf {a}_{k_1}},\ldots ,\phi ^{k_m}_{\mathbf {a}_{k_m}})$
is nondegenerate if and only if
![]() $V(\Phi ^{k_1}_{\mathbf {a}_{k_1}},\ldots ,\Phi ^{k_m}_{\mathbf {a}_{k_m}})$
is nondegenerate, we may assume that
$V(\Phi ^{k_1}_{\mathbf {a}_{k_1}},\ldots ,\Phi ^{k_m}_{\mathbf {a}_{k_m}})$
is nondegenerate, we may assume that
![]() $\phi ^{k_j}_{\mathbf {a}_{k_j}}$
is homogeneous for any
$\phi ^{k_j}_{\mathbf {a}_{k_j}}$
is homogeneous for any
![]() $1\leq j\leq m$
. Now, observe that for any positive weight vector
$1\leq j\leq m$
. Now, observe that for any positive weight vector
![]() $\mathbf {w}'$
, the set
$\mathbf {w}'$
, the set
![]() $\Delta (\mathbf {w}';f^k_{\mathbf {w}})$
is a (compact) face of
$\Delta (\mathbf {w}';f^k_{\mathbf {w}})$
is a (compact) face of
![]() $\Delta (\mathbf {w};f^k)$
, and then consider the set
$\Delta (\mathbf {w};f^k)$
, and then consider the set
![]() $V_{\mathbf {w}}(\mathbf {w}')$
made up of all the points
$V_{\mathbf {w}}(\mathbf {w}')$
made up of all the points
![]() $(\mathbf {a}_1,\ldots ,\mathbf {a}_{k_0},\mathbf {z})$
in
$(\mathbf {a}_1,\ldots ,\mathbf {a}_{k_0},\mathbf {z})$
in
![]() $\mathbb {P}^{q_1-1}\times \cdots \times \mathbb {P}^{q_{k_0}-1}\times \mathbb {P}^{n-1}$
for which there exists a subset
$\mathbb {P}^{q_1-1}\times \cdots \times \mathbb {P}^{q_{k_0}-1}\times \mathbb {P}^{n-1}$
for which there exists a subset
![]() $K\subseteq \{1,\ldots , k_0\}$
such that
$K\subseteq \{1,\ldots , k_0\}$
such that
 $$ \begin{align*} \forall k\in K,\ \phi^{k}_{\mathbf{a}_{k},\mathbf{w}'}(\mathbf{z})=0 \quad\mbox{and}\quad \bigwedge_{k\in K} d\phi^{k}_{\mathbf{a}_{k},\mathbf{w}'}(\mathbf{z})=0, \end{align*} $$
$$ \begin{align*} \forall k\in K,\ \phi^{k}_{\mathbf{a}_{k},\mathbf{w}'}(\mathbf{z})=0 \quad\mbox{and}\quad \bigwedge_{k\in K} d\phi^{k}_{\mathbf{a}_{k},\mathbf{w}'}(\mathbf{z})=0, \end{align*} $$
where we still denote by
![]() $\mathbf {a}_1,\ldots ,\mathbf {a}_{k_0}$
and
$\mathbf {a}_1,\ldots ,\mathbf {a}_{k_0}$
and
![]() $\mathbf {z}$
the classes of
$\mathbf {z}$
the classes of
![]() $\mathbf {a}_1,\ldots ,\mathbf {a}_{k_0}$
and
$\mathbf {a}_1,\ldots ,\mathbf {a}_{k_0}$
and
![]() $\mathbf {z}$
in the projective spaces
$\mathbf {z}$
in the projective spaces
![]() $\mathbb {P}^{q_1-1},\ldots ,\mathbb {P}^{q_{k_0}-1}$
and
$\mathbb {P}^{q_1-1},\ldots ,\mathbb {P}^{q_{k_0}-1}$
and
![]() $\mathbb {P}^{n-1}$
, respectively. (Once more, let us recall that
$\mathbb {P}^{n-1}$
, respectively. (Once more, let us recall that
![]() $\phi ^{k}_{\mathbf {a}_{k},\mathbf {w}'}\equiv (\phi ^{k}_{\mathbf {a}_{k}})_{\mathbf {w}'}$
denotes the face function of
$\phi ^{k}_{\mathbf {a}_{k},\mathbf {w}'}\equiv (\phi ^{k}_{\mathbf {a}_{k}})_{\mathbf {w}'}$
denotes the face function of
![]() $\phi ^{k}_{\mathbf {a}_{k}}$
with respect to the weight vector
$\phi ^{k}_{\mathbf {a}_{k}}$
with respect to the weight vector
![]() $\mathbf {w}'$
.) Let
$\mathbf {w}'$
.) Let
![]() $\bar V_{\mathbf {w}}(\mathbf {w}')$
be the closure of
$\bar V_{\mathbf {w}}(\mathbf {w}')$
be the closure of
![]() $V_{\mathbf {w}}^*(\mathbf {w}'):=V_{\mathbf {w}}(\mathbf {w}')\cap \{z_1\cdots z_n\not =0\}$
in
$V_{\mathbf {w}}^*(\mathbf {w}'):=V_{\mathbf {w}}(\mathbf {w}')\cap \{z_1\cdots z_n\not =0\}$
in
![]() $\mathbb {P}^{q_1-1}\times \cdots \times \mathbb {P}^{q_{k_0}-1}\times \mathbb {P}^{n-1}$
. Then
$\mathbb {P}^{q_1-1}\times \cdots \times \mathbb {P}^{q_{k_0}-1}\times \mathbb {P}^{n-1}$
. Then
![]() $\bar V_{\mathbf {w}}(\mathbf {w}')$
is an algebraic set of dimension
$\bar V_{\mathbf {w}}(\mathbf {w}')$
is an algebraic set of dimension
![]() $\dim V^*(\mathbf {w}')$
(see [Reference Whitney12, Lem. 3.9]). Let
$\dim V^*(\mathbf {w}')$
(see [Reference Whitney12, Lem. 3.9]). Let
be the standard projection, and let
where
 $$ \begin{align*} V_{\mathbf{w}}^*:=\bigcup_{\mathbf{w}'\in\mathbb{N}^{*n}} V_{\mathbf{w}}^*(\mathbf{w}') \quad\mbox{and}\quad \bar V_{\mathbf{w}}:=\bigcup_{\mathbf{w}'\in\mathbb{N}^{*n}} \bar V_{\mathbf{w}}(\mathbf{w}'). \end{align*} $$
$$ \begin{align*} V_{\mathbf{w}}^*:=\bigcup_{\mathbf{w}'\in\mathbb{N}^{*n}} V_{\mathbf{w}}^*(\mathbf{w}') \quad\mbox{and}\quad \bar V_{\mathbf{w}}:=\bigcup_{\mathbf{w}'\in\mathbb{N}^{*n}} \bar V_{\mathbf{w}}(\mathbf{w}'). \end{align*} $$
Clearly,
![]() $U_{\mathbf {w}}$
is the complement of
$U_{\mathbf {w}}$
is the complement of
![]() $(p_1\times \cdots \times p_{k_0})^{-1}(W_{\mathbf {w}}^*)\cup \{\mathbf {0}\}$
, where
$(p_1\times \cdots \times p_{k_0})^{-1}(W_{\mathbf {w}}^*)\cup \{\mathbf {0}\}$
, where
![]() $p_k\colon \mathbb {C}^{q_k}\setminus \{\mathbf {0}\}\to \mathbb {P}^{q_k-1}$
is the standard canonical map. By the proper mapping theorem (see [Reference Remmert11, Satz 23]),
$p_k\colon \mathbb {C}^{q_k}\setminus \{\mathbf {0}\}\to \mathbb {P}^{q_k-1}$
is the standard canonical map. By the proper mapping theorem (see [Reference Remmert11, Satz 23]),
![]() $\bar W_{\mathbf {w}}$
is an algebraic set containing
$\bar W_{\mathbf {w}}$
is an algebraic set containing
![]() $W_{\mathbf {w}}^*$
. In fact, we are going to prove that
$W_{\mathbf {w}}^*$
. In fact, we are going to prove that
![]() $W_{\mathbf {w}}^*=\bar W_{\mathbf {w}}$
, which implies that
$W_{\mathbf {w}}^*=\bar W_{\mathbf {w}}$
, which implies that
![]() $U_{\mathbf {w}}$
is a Zariski open set. To show the equality
$U_{\mathbf {w}}$
is a Zariski open set. To show the equality
![]() $W_{\mathbf {w}}^*=\bar W_{\mathbf {w}}$
, we argue by contradiction. Suppose that
$W_{\mathbf {w}}^*=\bar W_{\mathbf {w}}$
, we argue by contradiction. Suppose that
![]() $W_{\mathbf {w}}^*\subsetneq \bar W_{\mathbf {w}}$
. Then there exists
$W_{\mathbf {w}}^*\subsetneq \bar W_{\mathbf {w}}$
. Then there exists
![]() $(\mathbf {a}_1,\ldots ,\mathbf {a}_{k_0},\mathbf {z})\in \bar V_{\mathbf {w}}$
such that
$(\mathbf {a}_1,\ldots ,\mathbf {a}_{k_0},\mathbf {z})\in \bar V_{\mathbf {w}}$
such that
![]() $(\mathbf {a}_1,\ldots ,\mathbf {a}_{k_0})\in \bar W_{\mathbf {w}}\setminus W_{\mathbf {w}}^*$
. By the Curve Selection Lemma, there exist a real analytic curve
$(\mathbf {a}_1,\ldots ,\mathbf {a}_{k_0})\in \bar W_{\mathbf {w}}\setminus W_{\mathbf {w}}^*$
. By the Curve Selection Lemma, there exist a real analytic curve
![]() $0\leq s\leq 1$
, and a positive weight vector
$0\leq s\leq 1$
, and a positive weight vector
![]() $\mathbf {w}'\in \mathbb {N}^{*n}$
such that
$\mathbf {w}'\in \mathbb {N}^{*n}$
such that
![]() $\rho (s)\in V^*_{\mathbf {w}}(\mathbf {w}')$
for
$\rho (s)\in V^*_{\mathbf {w}}(\mathbf {w}')$
for
![]() $s>0$
and
$s>0$
and
![]() $\rho (0)=(\mathbf {a}_1,\ldots ,\mathbf {a}_{k_0},\mathbf {z})$
. For each
$\rho (0)=(\mathbf {a}_1,\ldots ,\mathbf {a}_{k_0},\mathbf {z})$
. For each
![]() $1\leq k\leq k_0$
, write
$1\leq k\leq k_0$
, write
By the assumption,
![]() $b_i\in \mathbb {C}^*$
,
$b_i\in \mathbb {C}^*$
,
![]() $w^{\prime \prime }_i\in \mathbb {N}$
(
$w^{\prime \prime }_i\in \mathbb {N}$
(
![]() $1\leq i\leq n$
) and
$1\leq i\leq n$
) and
![]() $\mbox {max}\{w^{\prime \prime }_i\, ;\, 1\leq i\leq n\}>0$
. Moreover, for any
$\mbox {max}\{w^{\prime \prime }_i\, ;\, 1\leq i\leq n\}>0$
. Moreover, for any
![]() $s\not =0$
, there exists
$s\not =0$
, there exists
![]() $K(s)\subseteq \{1,\ldots ,k_0\}$
such that
$K(s)\subseteq \{1,\ldots ,k_0\}$
such that
 $$ \begin{align*} \forall k\in K(s),\ \phi^{k}_{\mathbf{a}_{k}(s),\mathbf{w}'}(\mathbf{z}(s))=0 \quad\mbox{and}\quad \bigwedge_{k\in K(s)} d\phi^{k}_{\mathbf{a}_{k}(s),\mathbf{w}'}(\mathbf{z}(s))=0. \end{align*} $$
$$ \begin{align*} \forall k\in K(s),\ \phi^{k}_{\mathbf{a}_{k}(s),\mathbf{w}'}(\mathbf{z}(s))=0 \quad\mbox{and}\quad \bigwedge_{k\in K(s)} d\phi^{k}_{\mathbf{a}_{k}(s),\mathbf{w}'}(\mathbf{z}(s))=0. \end{align*} $$
By looking at the leading terms (with respect to s) in the above expressions, it follows that there exists a subset
![]() $K(0)\subseteq \{1,\ldots ,k_0\}$
such that
$K(0)\subseteq \{1,\ldots ,k_0\}$
such that
 $$ \begin{align} \forall k\in K(0),\ \big(\phi^{k}_{\mathbf{a}_{k},\mathbf{w}'}\big)_{\Delta}(\mathbf{b})=0 \quad\mbox{and}\quad \bigwedge_{k\in K(0)} d\big(\phi^{k}_{\mathbf{a}_{k},\mathbf{w}'}\big)_{\Delta}(\mathbf{b})=0, \end{align} $$
$$ \begin{align} \forall k\in K(0),\ \big(\phi^{k}_{\mathbf{a}_{k},\mathbf{w}'}\big)_{\Delta}(\mathbf{b})=0 \quad\mbox{and}\quad \bigwedge_{k\in K(0)} d\big(\phi^{k}_{\mathbf{a}_{k},\mathbf{w}'}\big)_{\Delta}(\mathbf{b})=0, \end{align} $$
where
![]() $\mathbf {b}:=(b_1,\ldots ,b_n)$
,
$\mathbf {b}:=(b_1,\ldots ,b_n)$
,
![]() $\Delta $
is the (compact) face of
$\Delta $
is the (compact) face of
![]() $\Delta (\mathbf {w}';f^k_{\mathbf {w}})$
on which the linear form
$\Delta (\mathbf {w}';f^k_{\mathbf {w}})$
on which the linear form
 $$ \begin{align*} \alpha\in\Delta(\mathbf{w}';f^k_{\mathbf{w}})\mapsto \sum_{i=1}^n \alpha_i w_i"\in\mathbb{R} \end{align*} $$
$$ \begin{align*} \alpha\in\Delta(\mathbf{w}';f^k_{\mathbf{w}})\mapsto \sum_{i=1}^n \alpha_i w_i"\in\mathbb{R} \end{align*} $$
takes its minimal value, and
![]() $\big (\phi ^{k}_{\mathbf {a}_{k},\mathbf {w}'}\big )_{\Delta }$
is the corresponding face function. However, since
$\big (\phi ^{k}_{\mathbf {a}_{k},\mathbf {w}'}\big )_{\Delta }$
is the corresponding face function. However, since
![]() $b_i\in \mathbb {C}^*$
for all
$b_i\in \mathbb {C}^*$
for all
![]() $1\leq i\leq n$
, the relations (5.1) imply
$1\leq i\leq n$
, the relations (5.1) imply
![]() $(\mathbf {a}_1,\ldots ,\mathbf {a}_{k_0})\in W^*_{\mathbf {w}}$
, which is a contradiction.
$(\mathbf {a}_1,\ldots ,\mathbf {a}_{k_0})\in W^*_{\mathbf {w}}$
, which is a contradiction.
Acknowledgment
We thank the referee for his/her comments and suggestions.