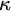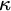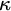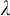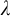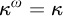1. Introduction
As we know that there are many combinatorial notions of largeness in a semigroup S that are studied extensively. In [Reference Carlson, Hindman, McLeod and Strauss1], Carlson et al. investigated partition problems of some notions of largeness. Based on the fact that any central set in
![]() $(\mathbb {N}, +)$
can be partitioned into infinitely many pairwise disjoint central sets, they extended this result to a large class of semigroups. To be precise, they showed that if S is a very weakly cancellative semigroup with size
$(\mathbb {N}, +)$
can be partitioned into infinitely many pairwise disjoint central sets, they extended this result to a large class of semigroups. To be precise, they showed that if S is a very weakly cancellative semigroup with size
![]() $\kappa $
,
$\kappa $
,
![]() $\kappa \geq \omega $
, then every central set in S contains
$\kappa \geq \omega $
, then every central set in S contains
![]() $\kappa $
disjoint central sets. Furthermore, if
$\kappa $
disjoint central sets. Furthermore, if
![]() $\kappa $
contains
$\kappa $
contains
![]() $\lambda $
almost disjoint sets, then every central set in S contains
$\lambda $
almost disjoint sets, then every central set in S contains
![]() $\lambda $
almost disjoint central sets. They also observed that the same statement holds for thick sets. And if the semigroup is left cancellative, the conclusion applies for piecewise syndetic sets; if the size
$\lambda $
almost disjoint central sets. They also observed that the same statement holds for thick sets. And if the semigroup is left cancellative, the conclusion applies for piecewise syndetic sets; if the size
![]() $\kappa $
of the semigroup is regular, then the conclusion holds for very thick sets. They also considered syndetic sets, but this situation is more complicated (see [Reference Carlson, Hindman, McLeod and Strauss1] for more details).
$\kappa $
of the semigroup is regular, then the conclusion holds for very thick sets. They also considered syndetic sets, but this situation is more complicated (see [Reference Carlson, Hindman, McLeod and Strauss1] for more details).
Besides these notions of largeness, there are many other notions whose properties of partition are not known yet. So in this article, we will focus on this question and investigate three notions of largeness: quasi-central sets, C-sets, and J-sets. And we obtain that the same conclusion holds for quasi-central sets (Corollary 2.4) as for central sets. If the semigroup is also commutative, then the conclusion holds for C-sets (Corollary 3.3). Moreover, if the size
![]() $\kappa $
of the semigroup satisfies
$\kappa $
of the semigroup satisfies
![]() $\kappa ^\omega = \kappa $
, then the conclusion holds for J-sets (Theorem 3.4).
$\kappa ^\omega = \kappa $
, then the conclusion holds for J-sets (Theorem 3.4).
Now let us introduce some notions, notations and basic facts that we will refer to. Most of this information can be found in [Reference Hindman and Strauss3]. Given a discrete semigroup
![]() $(S, \cdot )$
,
$(S, \cdot )$
,
![]() $\beta S$
is the Stone–Čech compactification of S and there is a natural extension of
$\beta S$
is the Stone–Čech compactification of S and there is a natural extension of
![]() $\cdot $
to
$\cdot $
to
![]() $\beta S$
making
$\beta S$
making
![]() $\beta S$
a compact right topological semigroup. For each
$\beta S$
a compact right topological semigroup. For each
![]() $p \in \beta S$
, the function
$p \in \beta S$
, the function
![]() $\rho _p: \beta \rightarrow \beta S$
, defined by
$\rho _p: \beta \rightarrow \beta S$
, defined by
![]() $\rho _p(q) = q \cdot p$
, is continuous, and for each
$\rho _p(q) = q \cdot p$
, is continuous, and for each
![]() $x \in S$
,
$x \in S$
,
![]() $\lambda _x: \beta \rightarrow \beta S$
, defined by
$\lambda _x: \beta \rightarrow \beta S$
, defined by
![]() $\lambda _x(p) = x \cdot p$
, is also continuous. The topological basis of
$\lambda _x(p) = x \cdot p$
, is also continuous. The topological basis of
![]() $\beta S$
is
$\beta S$
is
![]() $\{U_A: \emptyset \neq A \subseteq S \}$
, where
$\{U_A: \emptyset \neq A \subseteq S \}$
, where
![]() $U_A = \{p \in \beta S: A \in p \}$
. Given a compact right topological semigroup S, it has a smallest ideal
$U_A = \{p \in \beta S: A \in p \}$
. Given a compact right topological semigroup S, it has a smallest ideal
![]() $K(S)$
, which is the union of all minimal left ideals of S and also the union of all minimal right ideals of S. An idempotent in
$K(S)$
, which is the union of all minimal left ideals of S and also the union of all minimal right ideals of S. An idempotent in
![]() $K(S)$
is called minimal.
$K(S)$
is called minimal.
Let
![]() $(S, +)$
be a semigroup,
$(S, +)$
be a semigroup,
![]() $\langle x_n \rangle _{n=1}^\infty $
be a sequence in S, write
$\langle x_n \rangle _{n=1}^\infty $
be a sequence in S, write
![]() $\mathrm {FS}(\langle x_n \rangle _{n=1}^\infty ) = \{\sum _{n \in H}x_n: H \in \mathcal {P}_f(\mathbb {N}) \}$
, where
$\mathrm {FS}(\langle x_n \rangle _{n=1}^\infty ) = \{\sum _{n \in H}x_n: H \in \mathcal {P}_f(\mathbb {N}) \}$
, where
![]() $\mathcal {P}_f(\mathbb {N})$
is the set of nonempty finite subsets of
$\mathcal {P}_f(\mathbb {N})$
is the set of nonempty finite subsets of
![]() $\mathbb {N}$
and
$\mathbb {N}$
and
![]() $\sum _{n \in H}x_n$
is the sum in increasing order of indices. Given a subset A of S, we call A a quasi-central set [Reference Hindman, Maleki and Strauss2] if there is an idempotent
$\sum _{n \in H}x_n$
is the sum in increasing order of indices. Given a subset A of S, we call A a quasi-central set [Reference Hindman, Maleki and Strauss2] if there is an idempotent
![]() $p \in \beta S$
such that
$p \in \beta S$
such that
![]() $A \in p \in cl K(\beta S)$
, where
$A \in p \in cl K(\beta S)$
, where
![]() $cl X$
is the topological closure of X. To introduce J-sets, we denote
$cl X$
is the topological closure of X. To introduce J-sets, we denote
![]() $S_L(a, H) = \{a + \sum _{t \in H}f(t): f \in L \}$
, where
$S_L(a, H) = \{a + \sum _{t \in H}f(t): f \in L \}$
, where
![]() $a \in S$
,
$a \in S$
,
![]() $H \in \mathcal {P}_f(\mathbb {N})$
and
$H \in \mathcal {P}_f(\mathbb {N})$
and
![]() $L \in \mathcal {P}_f({^{\mathbb {N}}S})$
. Then given a commutative semigroup
$L \in \mathcal {P}_f({^{\mathbb {N}}S})$
. Then given a commutative semigroup
![]() $(S, +)$
,
$(S, +)$
,
![]() $A \subseteq S$
is a J-set in S if for any
$A \subseteq S$
is a J-set in S if for any
![]() $L \in \mathcal {P}_f({^{\mathbb {N}}S})$
, there exist
$L \in \mathcal {P}_f({^{\mathbb {N}}S})$
, there exist
![]() $a \in S$
and
$a \in S$
and
![]() $H \in \mathcal {P}_f(\mathbb {N})$
such that
$H \in \mathcal {P}_f(\mathbb {N})$
such that
![]() $S_L(a, H) \subseteq A$
.
$S_L(a, H) \subseteq A$
.
![]() $A \subseteq S$
is a C-set if there exist functions
$A \subseteq S$
is a C-set if there exist functions
![]() $\alpha : \mathcal {P}_f({^{\mathbb {N}}S}) \rightarrow S$
and
$\alpha : \mathcal {P}_f({^{\mathbb {N}}S}) \rightarrow S$
and
![]() $H: \mathcal {P}_f({^{\mathbb {N}}S}) \rightarrow \mathcal {P}_f(\mathbb {N})$
such that
$H: \mathcal {P}_f({^{\mathbb {N}}S}) \rightarrow \mathcal {P}_f(\mathbb {N})$
such that
![]() $\max H(F) < \min H(G)$
for every
$\max H(F) < \min H(G)$
for every
![]() $F, G \in \mathcal {P}_f({^{\mathbb {N}}S})$
satisfying
$F, G \in \mathcal {P}_f({^{\mathbb {N}}S})$
satisfying
![]() $F \subsetneq G$
, and
$F \subsetneq G$
, and
![]() $\sum _{i=1}^{m}(\alpha (G_i) + \sum _{t \in H(G_i)}f_i(t)) \in A$
whenever
$\sum _{i=1}^{m}(\alpha (G_i) + \sum _{t \in H(G_i)}f_i(t)) \in A$
whenever
![]() $m \in \mathbb {N}$
,
$m \in \mathbb {N}$
,
![]() $G_1, \ldots , G_m \in \mathcal {P}_f({^{\mathbb {N}}S})$
,
$G_1, \ldots , G_m \in \mathcal {P}_f({^{\mathbb {N}}S})$
,
![]() $G_1 \subsetneq \dots \subsetneq G_m$
and
$G_1 \subsetneq \dots \subsetneq G_m$
and
![]() $f_i \in G_i$
for each
$f_i \in G_i$
for each
![]() $i \in \{ 1, \ldots , m \}$
.
$i \in \{ 1, \ldots , m \}$
.
![]() $J(S) = \{p \in \beta S: \forall A \in p (A$
is a J-set in
$J(S) = \{p \in \beta S: \forall A \in p (A$
is a J-set in
![]() $S ) \}$
.
$S ) \}$
.
![]() $J(S)$
is a compact ideal of
$J(S)$
is a compact ideal of
![]() $\beta S$
, and A is a C-set if and only if there is an idempotent
$\beta S$
, and A is a C-set if and only if there is an idempotent
![]() $p \in J(S)$
such that
$p \in J(S)$
such that
![]() $A \in p$
.
$A \in p$
.
Let
![]() $(S, \cdot )$
be a semigroup. A subset A of S is called a left solution set of S (respectively, a right solution set of S) if there are
$(S, \cdot )$
be a semigroup. A subset A of S is called a left solution set of S (respectively, a right solution set of S) if there are
![]() $a, b \in S$
such that
$a, b \in S$
such that
![]() $A = \{x \in S: ax = b \}$
(respectively,
$A = \{x \in S: ax = b \}$
(respectively,
![]() $A = \{x \in S: xa = b \}$
). Let S be an infinite semigroup with size
$A = \{x \in S: xa = b \}$
). Let S be an infinite semigroup with size
![]() $\kappa $
. We say S is very weakly left cancellative (respectively, very weakly right cancellative) if the union of less than
$\kappa $
. We say S is very weakly left cancellative (respectively, very weakly right cancellative) if the union of less than
![]() $\kappa $
left solution sets of S (respectively, right solution sets of S) has size less than
$\kappa $
left solution sets of S (respectively, right solution sets of S) has size less than
![]() $\kappa $
. We say S is very weakly cancellative if it is both very weakly left cancellative and very weakly right cancellative. Let S be a nonempty set, an ultrafilter p on S is called uniform if for any
$\kappa $
. We say S is very weakly cancellative if it is both very weakly left cancellative and very weakly right cancellative. Let S be a nonempty set, an ultrafilter p on S is called uniform if for any
![]() $X \in p$
,
$X \in p$
,
![]() $|X| = |S|$
. Given a semigroup S, we denote the set of uniform ultrafilters on S by U. If S is infinite very weakly cancellative, then U is an ideal of
$|X| = |S|$
. Given a semigroup S, we denote the set of uniform ultrafilters on S by U. If S is infinite very weakly cancellative, then U is an ideal of
![]() $\beta S$
[Reference Carlson, Hindman, McLeod and Strauss1].
$\beta S$
[Reference Carlson, Hindman, McLeod and Strauss1].
2. Disjoint quasi-central sets
In this section, we establish the existence of almost disjoint families of quasi-central subsets of a given quasi-central set in an infinite very weakly cancellative semigroup. Let X be an infinite set. We call
![]() $\mathcal {A}$
a set of almost disjoint subsets of X if for any
$\mathcal {A}$
a set of almost disjoint subsets of X if for any
![]() $A \in \mathcal {A}$
,
$A \in \mathcal {A}$
,
![]() $A \subseteq X$
and
$A \subseteq X$
and
![]() $|A| = |X|$
, and for distinct
$|A| = |X|$
, and for distinct
![]() $A, B \in \mathcal {A}$
,
$A, B \in \mathcal {A}$
,
![]() $|A \cap B| < |X|$
. Then there is the following fact:
$|A \cap B| < |X|$
. Then there is the following fact:
Lemma 2.1 [Reference Carlson, Hindman, McLeod and Strauss1, Lemma 2.1]
Let
![]() $\kappa $
be an infinite cardinal.
$\kappa $
be an infinite cardinal.
-
(i) If there is a family
 $\{ A_\alpha : \alpha < \delta \}$
of almost disjoint subsets of
$\{ A_\alpha : \alpha < \delta \}$
of almost disjoint subsets of
 $\kappa $
, then there is a family
$\kappa $
, then there is a family
 $\{ \mathcal {A}_\alpha : \alpha < \delta \}$
of almost disjoint subsets of
$\{ \mathcal {A}_\alpha : \alpha < \delta \}$
of almost disjoint subsets of
 $\mathcal {P}_f(\kappa )$
such that for any
$\mathcal {P}_f(\kappa )$
such that for any
 $F \in \mathcal {P}_f(\kappa )$
and any
$F \in \mathcal {P}_f(\kappa )$
and any
 $\alpha < \delta $
there is some
$\alpha < \delta $
there is some
 $G \in \mathcal {A}_\alpha $
such that
$G \in \mathcal {A}_\alpha $
such that
 $F \subseteq G$
.
$F \subseteq G$
. -
(ii) There is a family
 $\{ \mathcal {B}_\alpha : \alpha < \kappa \}$
of pairwise disjoint subsets of
$\{ \mathcal {B}_\alpha : \alpha < \kappa \}$
of pairwise disjoint subsets of
 $\mathcal {P}_f(\kappa )$
, each with size
$\mathcal {P}_f(\kappa )$
, each with size
 $\kappa $
, such that for any
$\kappa $
, such that for any
 $F \in \mathcal {P}_f(\kappa )$
and any
$F \in \mathcal {P}_f(\kappa )$
and any
 $\alpha < \delta $
there is some
$\alpha < \delta $
there is some
 $G \in \mathcal {B}_\alpha $
such that
$G \in \mathcal {B}_\alpha $
such that
 $F \subseteq G$
.
$F \subseteq G$
.
Lemma 2.2 [Reference Carlson, Hindman, McLeod and Strauss1, Lemma 3.1]
If S is very weakly left cancellative, U is a left ideal of
![]() $\beta S$
. If S is very weakly cancellative, U is an ideal of
$\beta S$
. If S is very weakly cancellative, U is an ideal of
![]() $\beta S$
.
$\beta S$
.
If
![]() $(S, \cdot )$
is a semigroup, I is an ideal of
$(S, \cdot )$
is a semigroup, I is an ideal of
![]() $\beta S$
, and
$\beta S$
, and
![]() $A \subseteq S$
, recall that
$A \subseteq S$
, recall that
![]() $U_A = \{p \in \beta S: A \in p \}$
. For convenience, we call A an I-large subset of S if there is an idempotent
$U_A = \{p \in \beta S: A \in p \}$
. For convenience, we call A an I-large subset of S if there is an idempotent
![]() $p \in I\cap U_A$
; and we call A a uniform I-large subset of S if there is a uniform idempotent
$p \in I\cap U_A$
; and we call A a uniform I-large subset of S if there is a uniform idempotent
![]() $p \in I\cap U_A$
. Then we have the following facts, the argument of which is similar to that of [Reference Carlson, Hindman, McLeod and Strauss1, Theorem 3.3], but more general.
$p \in I\cap U_A$
. Then we have the following facts, the argument of which is similar to that of [Reference Carlson, Hindman, McLeod and Strauss1, Theorem 3.3], but more general.
Theorem 2.3. Suppose
![]() $\kappa $
is an infinite cardinal, S is a very weakly left cancellative semigroup with size
$\kappa $
is an infinite cardinal, S is a very weakly left cancellative semigroup with size
![]() $\kappa $
, I is an ideal of
$\kappa $
, I is an ideal of
![]() $\beta S$
, and C is uniform I-large in S.
$\beta S$
, and C is uniform I-large in S.
-
(i) If there is a family of
 $\delta $
almost disjoint subsets of
$\delta $
almost disjoint subsets of
 $\kappa $
, then C contains
$\kappa $
, then C contains
 $\delta $
almost disjoint uniform I-large sets.
$\delta $
almost disjoint uniform I-large sets. -
(ii) C contains
 $\kappa $
disjoint uniform I-large sets.
$\kappa $
disjoint uniform I-large sets.
Proof The proof of (ii) is the same as (i). So here we only prove (i). Since C is uniform I-large, we pick a uniform idempotent
![]() $p \in I\cap U_C$
. Define
$p \in I\cap U_C$
. Define
![]() ${C^\star = \{s \in C: s^{-1}C \in p \}}$
, so by [Reference Hindman and Strauss3, Lemma 4.14], for any
${C^\star = \{s \in C: s^{-1}C \in p \}}$
, so by [Reference Hindman and Strauss3, Lemma 4.14], for any
![]() $s \in C^\star $
,
$s \in C^\star $
,
![]() $s^{-1}C^\star \in p$
. For each
$s^{-1}C^\star \in p$
. For each
![]() $F \in \mathcal {P}_f(C^\star )$
, define
$F \in \mathcal {P}_f(C^\star )$
, define
![]() $S_F = C^\star \cap \bigcap _{s \in F}s^{-1}C^\star $
. So
$S_F = C^\star \cap \bigcap _{s \in F}s^{-1}C^\star $
. So
![]() $S_F \in p$
.
$S_F \in p$
.
Let
![]() $V = \bigcap _{F \in \mathcal {P}_f(C^\star )}U_{S_F}$
. So
$V = \bigcap _{F \in \mathcal {P}_f(C^\star )}U_{S_F}$
. So
![]() $p \in V$
. Now let us show that V is a semigroup of
$p \in V$
. Now let us show that V is a semigroup of
![]() $\beta S$
. Observe that for each
$\beta S$
. Observe that for each
![]() $F \in \mathcal {P}_f(C^\star )$
and each
$F \in \mathcal {P}_f(C^\star )$
and each
![]() $s \in S_F$
, if
$s \in S_F$
, if
![]() $H = \{ s \} \cup Fs$
, then
$H = \{ s \} \cup Fs$
, then
![]() $sS_H \subseteq S_F$
. Since for each
$sS_H \subseteq S_F$
. Since for each
![]() $t \in S_H$
, we have
$t \in S_H$
, we have
![]() $st \in C^\star $
, and since for each
$st \in C^\star $
, and since for each
![]() $r \in F$
,
$r \in F$
,
![]() $rs \in H$
, so
$rs \in H$
, so
![]() $rst \in C^\star $
. Hence
$rst \in C^\star $
. Hence
![]() $st \in S_F$
, which means
$st \in S_F$
, which means
![]() $sS_H \subseteq S_F$
. Then by [Reference Hindman and Strauss3, Theorem 4.20], V is a semigroup of
$sS_H \subseteq S_F$
. Then by [Reference Hindman and Strauss3, Theorem 4.20], V is a semigroup of
![]() $\beta S$
.
$\beta S$
.
Now well order
![]() $\mathcal {P}_f(C^\star )$
by
$\mathcal {P}_f(C^\star )$
by
![]() $<$
as a
$<$
as a
![]() $\kappa $
-sequence. Now we define
$\kappa $
-sequence. Now we define
![]() $x_F$
for each
$x_F$
for each
![]() ${F \in \mathcal {P}_f(C^\star )}$
such that
${F \in \mathcal {P}_f(C^\star )}$
such that
![]() $Fx_F \cap Hx_H = \emptyset $
and
$Fx_F \cap Hx_H = \emptyset $
and
![]() $x_F \neq x_H$
whenever F and H are distinct elements of
$x_F \neq x_H$
whenever F and H are distinct elements of
![]() $\mathcal {P}_f(C^\star )$
. Assume we have obtained
$\mathcal {P}_f(C^\star )$
. Assume we have obtained
![]() $\{x_F: F < H \}$
. Since S is very weakly left cancellative,
$\{x_F: F < H \}$
. Since S is very weakly left cancellative,
![]() $|\{y \in S: Hy \cap \bigcup _{F < H}Fx_F \neq \emptyset \}| < \kappa $
, while
$|\{y \in S: Hy \cap \bigcup _{F < H}Fx_F \neq \emptyset \}| < \kappa $
, while
![]() $S_H \in p$
so
$S_H \in p$
so
![]() $S_H$
has size
$S_H$
has size
![]() $\kappa $
. Then we pick
$\kappa $
. Then we pick
![]() $x_H \in S_H \setminus (\{y \in S: Hy \cap \bigcup _{F < H}Fx_F \neq \emptyset \} \cup \{x_F: F < H \})$
.
$x_H \in S_H \setminus (\{y \in S: Hy \cap \bigcup _{F < H}Fx_F \neq \emptyset \} \cup \{x_F: F < H \})$
.
By Lemma 2.1(i), there is a family
![]() $\{ \mathcal {A}_\alpha : \alpha < \delta \}$
of almost disjoint subsets of
$\{ \mathcal {A}_\alpha : \alpha < \delta \}$
of almost disjoint subsets of
![]() $\mathcal {P}_f(C^\star )$
such that for any
$\mathcal {P}_f(C^\star )$
such that for any
![]() $F \in \mathcal {P}_f(C^\star )$
and any
$F \in \mathcal {P}_f(C^\star )$
and any
![]() $\alpha < \delta $
there is some
$\alpha < \delta $
there is some
![]() $G \in \mathcal {A}_\alpha $
such that
$G \in \mathcal {A}_\alpha $
such that
![]() $F \subseteq G$
. Let
$F \subseteq G$
. Let
![]() $A_\alpha = \bigcup _{F \in \mathcal {A}_\alpha }Fx_F$
for each
$A_\alpha = \bigcup _{F \in \mathcal {A}_\alpha }Fx_F$
for each
![]() $\alpha \in \delta $
. Notice that
$\alpha \in \delta $
. Notice that
![]() $\{A_\alpha : \alpha < \delta \}$
is an almost disjoint family of subsets of C. Now let us show each
$\{A_\alpha : \alpha < \delta \}$
is an almost disjoint family of subsets of C. Now let us show each
![]() $A_\alpha $
is uniform I-large.
$A_\alpha $
is uniform I-large.
Fix some
![]() $\alpha < \delta $
. Observe that
$\alpha < \delta $
. Observe that
![]() $\{H: H \in \mathcal {A}_\alpha \wedge F \subseteq H \}$
has size
$\{H: H \in \mathcal {A}_\alpha \wedge F \subseteq H \}$
has size
![]() $\kappa $
for each
$\kappa $
for each
![]() $F \in \mathcal {P}_f(C^\star )$
, so
$F \in \mathcal {P}_f(C^\star )$
, so
![]() $X_F = \{x_H: H \in \mathcal {A}_\alpha \wedge F \subseteq H \}$
has size
$X_F = \{x_H: H \in \mathcal {A}_\alpha \wedge F \subseteq H \}$
has size
![]() $\kappa $
and
$\kappa $
and
![]() $\{X_F: F \in \mathcal {P}_f(C^\star ) \}$
has the
$\{X_F: F \in \mathcal {P}_f(C^\star ) \}$
has the
![]() $\kappa $
-uniform finite intersection property [Reference Hindman and Strauss3, Definition 3.60]. Then by [Reference Hindman and Strauss3, Theorem 3.62], we take a uniform ultrafilter
$\kappa $
-uniform finite intersection property [Reference Hindman and Strauss3, Definition 3.60]. Then by [Reference Hindman and Strauss3, Theorem 3.62], we take a uniform ultrafilter
![]() $q \in \beta S$
such that
$q \in \beta S$
such that
![]() $\{X_F: F \in \mathcal {P}_f(C^\star ) \} \subseteq q$
. For any
$\{X_F: F \in \mathcal {P}_f(C^\star ) \} \subseteq q$
. For any
![]() $F \in \mathcal {P}_f(C^\star )$
, if
$F \in \mathcal {P}_f(C^\star )$
, if
![]() $x_H \in X_F$
, then
$x_H \in X_F$
, then
![]() $H \in \mathcal {A}_\alpha $
and
$H \in \mathcal {A}_\alpha $
and
![]() $F \subseteq H$
, so
$F \subseteq H$
, so
![]() $S_H \subseteq S_F$
, while
$S_H \subseteq S_F$
, while
![]() $x_H \in S_H$
, hence
$x_H \in S_H$
, hence
![]() $X_F \subseteq S_F$
, which implies that
$X_F \subseteq S_F$
, which implies that
![]() $q \in V$
.
$q \in V$
.
For each
![]() $s \in C^\star $
, and each
$s \in C^\star $
, and each
![]() $H \in \mathcal {A}_\alpha $
satisfying
$H \in \mathcal {A}_\alpha $
satisfying
![]() $s \in H$
, we have
$s \in H$
, we have
![]() $sx_H \in Hx_H \subseteq A_\alpha $
, so
$sx_H \in Hx_H \subseteq A_\alpha $
, so
![]() $X_{\{ s \}} \subseteq s^{-1}A_\alpha $
. Hence
$X_{\{ s \}} \subseteq s^{-1}A_\alpha $
. Hence
![]() $s^{-1}A_\alpha \in q$
, which means
$s^{-1}A_\alpha \in q$
, which means
![]() $sq \in U_{A_\alpha }$
. Since s is arbitrary in
$sq \in U_{A_\alpha }$
. Since s is arbitrary in
![]() $C^\star $
, we have
$C^\star $
, we have
![]() $C^\star q \subseteq U_{A_\alpha }$
, so
$C^\star q \subseteq U_{A_\alpha }$
, so
![]() $cl C^\star q \subseteq U_{A_\alpha }$
. Note that
$cl C^\star q \subseteq U_{A_\alpha }$
. Note that
![]() $V \subseteq U_{C^\star } = cl C^\star $
, so
$V \subseteq U_{C^\star } = cl C^\star $
, so
![]() ${Vq \subseteq U_{A_\alpha }}$
. Also note that
${Vq \subseteq U_{A_\alpha }}$
. Also note that
![]() $Vq$
is a left ideal of V, so we can pick an idempotent
$Vq$
is a left ideal of V, so we can pick an idempotent
![]() $r \in Vq$
which is minimal in V, hence
$r \in Vq$
which is minimal in V, hence
![]() $r \in U_{A_\alpha } \cap K(V)$
. Observe that
$r \in U_{A_\alpha } \cap K(V)$
. Observe that
![]() $V \cap I \neq \emptyset $
since
$V \cap I \neq \emptyset $
since
![]() $p \in V \cap I$
, so
$p \in V \cap I$
, so
![]() $V \cap I$
is an ideal of V, and thus
$V \cap I$
is an ideal of V, and thus
![]() $K(V) \subseteq V \cap I \subseteq I$
, so
$K(V) \subseteq V \cap I \subseteq I$
, so
![]() $r \in U_{A_\alpha } \cap I$
. By Lemma 2.2, U is a left ideal of
$r \in U_{A_\alpha } \cap I$
. By Lemma 2.2, U is a left ideal of
![]() $\beta S$
, then
$\beta S$
, then
![]() $r \in Vq \subseteq \beta S q \subseteq \beta S U \subseteq U$
, so r is uniform, therefore
$r \in Vq \subseteq \beta S q \subseteq \beta S U \subseteq U$
, so r is uniform, therefore
![]() $A_\alpha $
is uniform I-large.
$A_\alpha $
is uniform I-large.
If S is a semigroup, recall that
![]() $cl K(\beta S)$
is an ideal of
$cl K(\beta S)$
is an ideal of
![]() $\beta S$
, and quasi-central sets in S are exactly
$\beta S$
, and quasi-central sets in S are exactly
![]() $cl K(\beta S)$
-large sets. Then we have the following corollary of Theorem 2.3.
$cl K(\beta S)$
-large sets. Then we have the following corollary of Theorem 2.3.
Corollary 2.4. Suppose
![]() $\kappa $
is an infinite cardinal and S is a very weakly cancellative semigroup with size
$\kappa $
is an infinite cardinal and S is a very weakly cancellative semigroup with size
![]() $\kappa $
.
$\kappa $
.
-
1. If
 $\kappa $
contains
$\kappa $
contains
 $\delta $
almost disjoint subsets, then every quasi-central set in S contains
$\delta $
almost disjoint subsets, then every quasi-central set in S contains
 $\delta $
almost disjoint quasi-central subsets.
$\delta $
almost disjoint quasi-central subsets. -
2. Every quasi-central set in S contains
 $\kappa $
disjoint quasi-central subsets.
$\kappa $
disjoint quasi-central subsets.
Proof Take a quasi-central set A in S. Then there is some idempotent
![]() ${p \in cl K(\beta S) \cap U_A}$
. Note that U is a closed ideal of
${p \in cl K(\beta S) \cap U_A}$
. Note that U is a closed ideal of
![]() $\beta S$
, so
$\beta S$
, so
![]() $cl K(\beta S) \subseteq U$
, which implies that p is uniform, so A is uniform
$cl K(\beta S) \subseteq U$
, which implies that p is uniform, so A is uniform
![]() $cl K(\beta S)$
-large. Then we can apply Theorem 2.3 to obtain the result.
$cl K(\beta S)$
-large. Then we can apply Theorem 2.3 to obtain the result.
3. Disjoint C-sets and J-sets
In this section, we investigate two other kinds of large sets: J-sets and C-sets. Recall that given a commutative semigroup
![]() $(S, +)$
,
$(S, +)$
,
![]() $L \in \mathcal {P}_f({^{\mathbb {N}}S})$
,
$L \in \mathcal {P}_f({^{\mathbb {N}}S})$
,
![]() $a \in S$
and
$a \in S$
and
![]() $H \in \mathcal {P}_f(\mathbb {N})$
, we have defined
$H \in \mathcal {P}_f(\mathbb {N})$
, we have defined
![]() $S_L(a, H) = \{a + \sum _{t \in H}f(t): f \in L \}$
.
$S_L(a, H) = \{a + \sum _{t \in H}f(t): f \in L \}$
.
Lemma 3.1. Let
![]() $(S, +)$
be a commutative semigroup and let
$(S, +)$
be a commutative semigroup and let
![]() $A \subseteq S$
. Then A is a J-set in S if and only if for each
$A \subseteq S$
. Then A is a J-set in S if and only if for each
![]() $L \in \mathcal {P}_f({^{\mathbb {N}}S})$
, there exist
$L \in \mathcal {P}_f({^{\mathbb {N}}S})$
, there exist
![]() $a \in A$
and
$a \in A$
and
![]() $H \in \mathcal {P}_f(\mathbb {N})$
such that
$H \in \mathcal {P}_f(\mathbb {N})$
such that
![]() $S_L(a, H) \subseteq A$
.
$S_L(a, H) \subseteq A$
.
Proof The sufficiency is immediate. For the necessity, let
![]() $L \in \mathcal {P}_f({^{\mathbb {N}}S})$
and pick
$L \in \mathcal {P}_f({^{\mathbb {N}}S})$
and pick
![]() $g \in L$
. Let
$g \in L$
. Let
![]() $L^\prime = \{ g \} \cup \{ g + f: f \in L \}$
, pick
$L^\prime = \{ g \} \cup \{ g + f: f \in L \}$
, pick
![]() $b \in S$
and
$b \in S$
and
![]() $H \in \mathcal {P}_f(\mathbb {N})$
such that
$H \in \mathcal {P}_f(\mathbb {N})$
such that
![]() $S_{L^\prime }(b, H) \subseteq A$
, and let
$S_{L^\prime }(b, H) \subseteq A$
, and let
![]() $a = b + \sum _{t \in H}g(t)$
. Then
$a = b + \sum _{t \in H}g(t)$
. Then
![]() $a \in A$
and
$a \in A$
and
![]() $S_L(a, H) \subseteq A$
.
$S_L(a, H) \subseteq A$
.
Theorem 3.2. Suppose
![]() $(S, +)$
is an infinite commutative very weakly cancellative semigroup with size
$(S, +)$
is an infinite commutative very weakly cancellative semigroup with size
![]() $\kappa $
. Then every J-set in S has size
$\kappa $
. Then every J-set in S has size
![]() $\kappa $
.
$\kappa $
.
Proof Assume that there is a J-set A such that
![]() $|A| < \kappa $
. Let us construct an injective sequence in A of length
$|A| < \kappa $
. Let us construct an injective sequence in A of length
![]() $\kappa $
, so that a contradiction appears.
$\kappa $
, so that a contradiction appears.
Assume we have already obtained
![]() $\langle a_\xi \rangle _{\xi < \delta }$
for some
$\langle a_\xi \rangle _{\xi < \delta }$
for some
![]() $\delta < \kappa $
, which is an injective sequence in A, let us define
$\delta < \kappa $
, which is an injective sequence in A, let us define
![]() $a_{\delta }$
. For each
$a_{\delta }$
. For each
![]() $(a, \xi ) \in A \times \delta $
, let
$(a, \xi ) \in A \times \delta $
, let
![]() $B_{a, \xi } = \{x \in S: a + x = a_\xi \}$
, which is a left solution set. Then let
$B_{a, \xi } = \{x \in S: a + x = a_\xi \}$
, which is a left solution set. Then let
![]() $B = \bigcup _{(a, \xi ) \in A \times \delta }B_{a, \xi }$
. Since S is very weakly cancellative,
$B = \bigcup _{(a, \xi ) \in A \times \delta }B_{a, \xi }$
. Since S is very weakly cancellative,
![]() $|B| < \kappa $
. Now we need to build a sequence
$|B| < \kappa $
. Now we need to build a sequence
![]() $\langle b_n \rangle _{n=1}^\infty $
which satisfies
$\langle b_n \rangle _{n=1}^\infty $
which satisfies
![]() $\mathrm {FS}(\langle b_n \rangle _{n=1}^\infty ) \subseteq S \setminus B$
, and which will be used to define
$\mathrm {FS}(\langle b_n \rangle _{n=1}^\infty ) \subseteq S \setminus B$
, and which will be used to define
![]() $a_\delta $
. First take
$a_\delta $
. First take
![]() $b_1 \in S \setminus B$
. Assume we have obtained
$b_1 \in S \setminus B$
. Assume we have obtained
![]() $\langle b_i \rangle _{i=1}^n$
for some
$\langle b_i \rangle _{i=1}^n$
for some
![]() $n \in \mathbb {N}$
such that
$n \in \mathbb {N}$
such that
![]() $\mathrm {FS}(\langle b_i \rangle _{i=1}^n) \subseteq S \setminus B$
. For each
$\mathrm {FS}(\langle b_i \rangle _{i=1}^n) \subseteq S \setminus B$
. For each
![]() $y \in \mathrm {FS}(\langle b_i \rangle _{i=1}^n)$
, let
$y \in \mathrm {FS}(\langle b_i \rangle _{i=1}^n)$
, let
![]() $B_y = \bigcup _{(a, \xi ) \in A \times \delta }B_{y, a, \xi }$
, where
$B_y = \bigcup _{(a, \xi ) \in A \times \delta }B_{y, a, \xi }$
, where
![]() $B_{y, a, \xi } = \{x \in S: a + y + x = a_\xi \}$
. Hence each
$B_{y, a, \xi } = \{x \in S: a + y + x = a_\xi \}$
. Hence each
![]() $B_y$
has size less than
$B_y$
has size less than
![]() $\kappa $
, so
$\kappa $
, so
![]() $|\bigcup _{y \in \mathrm {FS}(\langle b_i \rangle _{i=1}^n)}B_y| < \kappa $
. Then take
$|\bigcup _{y \in \mathrm {FS}(\langle b_i \rangle _{i=1}^n)}B_y| < \kappa $
. Then take
![]() $b_{n + 1} \in S \setminus (B \cup (\bigcup _{y \in \mathrm {FS}(\langle b_i \rangle _{i=1}^n)}B_y))$
.
$b_{n + 1} \in S \setminus (B \cup (\bigcup _{y \in \mathrm {FS}(\langle b_i \rangle _{i=1}^n)}B_y))$
.
Then for any
![]() $z = b_{i_1} + \dots + b_{i_m} \in \mathrm {FS}(\langle b_i \rangle _{i=1}^{n+1})$
, if
$z = b_{i_1} + \dots + b_{i_m} \in \mathrm {FS}(\langle b_i \rangle _{i=1}^{n+1})$
, if
![]() $i_m \neq n + 1$
, then
$i_m \neq n + 1$
, then
![]() $z \in \mathrm {FS}(\langle b_i \rangle _{i=1}^n)$
so by hypothesis
$z \in \mathrm {FS}(\langle b_i \rangle _{i=1}^n)$
so by hypothesis
![]() $z \in S \setminus B$
. Otherwise,
$z \in S \setminus B$
. Otherwise,
![]() $i_m = n + 1$
. If
$i_m = n + 1$
. If
![]() $m = 1$
, then
$m = 1$
, then
![]() $z = b_{n + 1} \in S \setminus B$
. Otherwise,
$z = b_{n + 1} \in S \setminus B$
. Otherwise,
![]() $z = y + b_{n+1}$
for some
$z = y + b_{n+1}$
for some
![]() $y \in \mathrm {FS}(\langle b_i \rangle _{i=1}^n)$
. Note that
$y \in \mathrm {FS}(\langle b_i \rangle _{i=1}^n)$
. Note that
![]() $b_{n+1} \notin B_y$
, so there is no
$b_{n+1} \notin B_y$
, so there is no
![]() $(a, \xi ) \in A \times \delta $
such that
$(a, \xi ) \in A \times \delta $
such that
![]() $a + y + b_{n+1} = a_\xi $
. That is,
$a + y + b_{n+1} = a_\xi $
. That is,
![]() $z \notin B$
. Therefore,
$z \notin B$
. Therefore,
![]() $\mathrm {FS}(\langle b_i \rangle _{i=1}^{n+1}) \subseteq S \setminus B$
.
$\mathrm {FS}(\langle b_i \rangle _{i=1}^{n+1}) \subseteq S \setminus B$
.
Finally, we obtain
![]() $\langle b_n \rangle _{n=1}^\infty $
such that
$\langle b_n \rangle _{n=1}^\infty $
such that
![]() $\mathrm {FS}(\langle b_n \rangle _{n=1}^\infty ) \subseteq S \setminus B$
. Since A is a J-set, for
$\mathrm {FS}(\langle b_n \rangle _{n=1}^\infty ) \subseteq S \setminus B$
. Since A is a J-set, for
![]() $\langle b_n \rangle _{n=1}^\infty $
, by Lemma 3.1, there is some
$\langle b_n \rangle _{n=1}^\infty $
, by Lemma 3.1, there is some
![]() $a \in A$
and
$a \in A$
and
![]() $H \in \mathcal {P}_f(\mathbb {N})$
such that
$H \in \mathcal {P}_f(\mathbb {N})$
such that
![]() ${a + \sum _{i \in H}b_i \in A}$
. Now let
${a + \sum _{i \in H}b_i \in A}$
. Now let
![]() $z = \sum _{i \in H}b_i$
and
$z = \sum _{i \in H}b_i$
and
![]() $a_\delta = a + z$
, so
$a_\delta = a + z$
, so
![]() $a_\delta \in A$
and
$a_\delta \in A$
and
![]() $a_\delta $
is not equal to any
$a_\delta $
is not equal to any
![]() $a_\xi $
,
$a_\xi $
,
![]() $\xi < \delta $
. (If there is some
$\xi < \delta $
. (If there is some
![]() $\xi < \delta $
such that
$\xi < \delta $
such that
![]() $a_\delta = a_\xi $
, then
$a_\delta = a_\xi $
, then
![]() $a + z = a_\xi $
, so
$a + z = a_\xi $
, so
![]() $z \in B$
while
$z \in B$
while
![]() $z \in \mathrm {FS} (\langle b_n \rangle _{n=1}^\infty ) \subseteq S \setminus B$
, which is a contradiction.) Hence
$z \in \mathrm {FS} (\langle b_n \rangle _{n=1}^\infty ) \subseteq S \setminus B$
, which is a contradiction.) Hence
![]() $\langle a_\xi \rangle _{\xi < \delta + 1}$
is an injective sequence in A.
$\langle a_\xi \rangle _{\xi < \delta + 1}$
is an injective sequence in A.
By induction, we obtain an injective
![]() $\kappa $
-sequence in A; this is a contradiction.
$\kappa $
-sequence in A; this is a contradiction.
Therefore, by Theorem 3.2, we know that in any infinite commutative very weakly cancellative semigroup S,
![]() $J(S) \subseteq U$
. Then we have the following result.
$J(S) \subseteq U$
. Then we have the following result.
Corollary 3.3. Suppose
![]() $\kappa $
is an infinite cardinal and S is a commutative very weakly cancellative semigroup with size
$\kappa $
is an infinite cardinal and S is a commutative very weakly cancellative semigroup with size
![]() $\kappa $
.
$\kappa $
.
-
1. If
 $\kappa $
contains
$\kappa $
contains
 $\delta $
almost disjoint subsets, then every C-set in S contains
$\delta $
almost disjoint subsets, then every C-set in S contains
 $\delta $
almost disjoint C-sets.
$\delta $
almost disjoint C-sets. -
2. Every C-set in S contains
 $\kappa $
disjoint C-sets.
$\kappa $
disjoint C-sets.
Proof Since S is commutative very weakly cancellative, every C-set is uniform
![]() $J(S)$
-large. Then by Theorem 2.3 we deduce the result.
$J(S)$
-large. Then by Theorem 2.3 we deduce the result.
As for J-sets, we also have a similar result.
Theorem 3.4. Suppose
![]() $\kappa $
is an infinite cardinal satisfying
$\kappa $
is an infinite cardinal satisfying
![]() $\kappa ^\omega = \kappa $
and S is a commutative very weakly cancellative semigroup with size
$\kappa ^\omega = \kappa $
and S is a commutative very weakly cancellative semigroup with size
![]() $\kappa $
.
$\kappa $
.
-
1. If
 $\kappa $
contains
$\kappa $
contains
 $\delta $
almost disjoint subsets, then every J-set in S contains
$\delta $
almost disjoint subsets, then every J-set in S contains
 $\delta $
almost disjoint J-sets.
$\delta $
almost disjoint J-sets. -
2. Every J-set in S contains
 $\kappa $
disjoint J-sets.
$\kappa $
disjoint J-sets.
Proof Since the proofs of the two items are essentially the same, here we only provide the proof of the first item. Let A be a J-set. Since
![]() $\kappa ^\omega = \kappa $
,
$\kappa ^\omega = \kappa $
,
![]() $|\mathcal {P}_f({^{\mathbb {N}}S})| = \kappa $
. Enumerate
$|\mathcal {P}_f({^{\mathbb {N}}S})| = \kappa $
. Enumerate
![]() $\mathcal {P}_f({^{\mathbb {N}}S})$
as
$\mathcal {P}_f({^{\mathbb {N}}S})$
as
![]() $\langle L_\sigma \rangle _{\sigma < \kappa }$
. We will inductively build two
$\langle L_\sigma \rangle _{\sigma < \kappa }$
. We will inductively build two
![]() $\kappa $
-sequences
$\kappa $
-sequences
![]() $\langle a_\sigma \rangle _{\sigma < \kappa }$
and
$\langle a_\sigma \rangle _{\sigma < \kappa }$
and
![]() $\langle H_\sigma \rangle _{\sigma < \kappa }$
such that for each
$\langle H_\sigma \rangle _{\sigma < \kappa }$
such that for each
![]() $\sigma < \kappa $
,
$\sigma < \kappa $
,
![]() $a_\sigma \in S$
,
$a_\sigma \in S$
,
![]() $H_\sigma \in \mathcal {P}_f(\mathbb {N})$
,
$H_\sigma \in \mathcal {P}_f(\mathbb {N})$
,
![]() $S_{L_\sigma }(a_\sigma , H_\sigma ) \subseteq A$
, and for
$S_{L_\sigma }(a_\sigma , H_\sigma ) \subseteq A$
, and for
![]() $\alpha < \sigma < \kappa $
,
$\alpha < \sigma < \kappa $
,
![]() $S_{L_\alpha }(a_\alpha , H_\alpha ) \cap S_{L_\sigma }(a_\sigma , H_\sigma ) = \emptyset $
.
$S_{L_\alpha }(a_\alpha , H_\alpha ) \cap S_{L_\sigma }(a_\sigma , H_\sigma ) = \emptyset $
.
Since A is a J-set, pick
![]() $a_0 \in S$
and
$a_0 \in S$
and
![]() $H_0 \in \mathcal {P}_f(\mathbb {N})$
such that
$H_0 \in \mathcal {P}_f(\mathbb {N})$
such that
![]() $S_{L_0}(a_0, H_0) \subseteq A$
. Let
$S_{L_0}(a_0, H_0) \subseteq A$
. Let
![]() $0 < \sigma < \kappa $
and assume that
$0 < \sigma < \kappa $
and assume that
![]() $\langle a_\alpha \rangle _{\alpha < \sigma }$
and
$\langle a_\alpha \rangle _{\alpha < \sigma }$
and
![]() $\langle H_\alpha \rangle _{\alpha < \sigma }$
have been chosen. Let
$\langle H_\alpha \rangle _{\alpha < \sigma }$
have been chosen. Let
![]() $S_\sigma = \bigcup _{\alpha < \sigma }S_{L_\alpha }(a_\alpha , H_\alpha )$
and note that
$S_\sigma = \bigcup _{\alpha < \sigma }S_{L_\alpha }(a_\alpha , H_\alpha )$
and note that
![]() $|S_\sigma | < \kappa $
.
$|S_\sigma | < \kappa $
.
Claim 1. Let
![]() $C = \{(a, H): a \in S, H \in \mathcal {P}_f(\mathbb {N})$
and
$C = \{(a, H): a \in S, H \in \mathcal {P}_f(\mathbb {N})$
and
![]() $S_{L_\sigma }(a, H) \cap S_\sigma \neq \emptyset \}$
. Then
$S_{L_\sigma }(a, H) \cap S_\sigma \neq \emptyset \}$
. Then
![]() $|C| < \kappa $
.
$|C| < \kappa $
.
Proof Note that, since
![]() $\kappa = \kappa ^\omega $
and
$\kappa = \kappa ^\omega $
and
![]() $\kappa < \kappa ^{\mathrm {cf}(\kappa )}$
, we have that
$\kappa < \kappa ^{\mathrm {cf}(\kappa )}$
, we have that
![]() $\mathrm {cf}(\kappa )> \omega $
. For
$\mathrm {cf}(\kappa )> \omega $
. For
![]() ${H \in \mathcal {P}_f(\mathbb {N})}$
let
${H \in \mathcal {P}_f(\mathbb {N})}$
let
![]() $D_H = \{a \in S: S_{L_\sigma }(a, H) \cap S_\sigma \neq \emptyset \}$
. Then
$D_H = \{a \in S: S_{L_\sigma }(a, H) \cap S_\sigma \neq \emptyset \}$
. Then
![]() $C = \bigcup \{D_H \times \{ H \}: H \in \mathcal {P}_f(\mathbb {N}) \}$
so
$C = \bigcup \{D_H \times \{ H \}: H \in \mathcal {P}_f(\mathbb {N}) \}$
so
![]() $|C| \leq \sum _{H \in \mathcal {P}_f(\mathbb {N})}|D_H|$
. Given
$|C| \leq \sum _{H \in \mathcal {P}_f(\mathbb {N})}|D_H|$
. Given
![]() $H \in \mathcal {P}_f(\mathbb {N})$
,
$H \in \mathcal {P}_f(\mathbb {N})$
,
![]() $D_H \subseteq \bigcup _{x \in S_\sigma }\bigcup _{f \in L_\sigma }\{a \in S: x = a + \sum _{t \in H}f(t) \}$
and each
$D_H \subseteq \bigcup _{x \in S_\sigma }\bigcup _{f \in L_\sigma }\{a \in S: x = a + \sum _{t \in H}f(t) \}$
and each
![]() $\{a \in S: x = a + \sum _{t \in H}f(t) \}$
is a right solution set, so we have
$\{a \in S: x = a + \sum _{t \in H}f(t) \}$
is a right solution set, so we have
![]() $|D_H| < \kappa $
. Therefore, since
$|D_H| < \kappa $
. Therefore, since
![]() $|\mathcal {P}_f(\mathbb {N})| = \omega $
and
$|\mathcal {P}_f(\mathbb {N})| = \omega $
and
![]() $\mathrm {cf}(\kappa )> \omega $
, we have
$\mathrm {cf}(\kappa )> \omega $
, we have
![]() $|C| < \kappa $
as claimed.
$|C| < \kappa $
as claimed.
Claim 2. Let
![]() $D = \{(a, H): a \in S, H \in \mathcal {P}_f(\mathbb {N})$
and
$D = \{(a, H): a \in S, H \in \mathcal {P}_f(\mathbb {N})$
and
![]() $S_{L_\sigma }(a, H) \subseteq A \}$
. Then
$S_{L_\sigma }(a, H) \subseteq A \}$
. Then
![]() ${|D| = \kappa }$
.
${|D| = \kappa }$
.
Proof Since
![]() $|D| \geq |\{ a \in S: (\exists H \in \mathcal {P}_f(\mathbb {N}))(S_{L_\sigma }(a, H) \subseteq A) \}|$
, it suffices by Theorem 3.2 to show that
$|D| \geq |\{ a \in S: (\exists H \in \mathcal {P}_f(\mathbb {N}))(S_{L_\sigma }(a, H) \subseteq A) \}|$
, it suffices by Theorem 3.2 to show that
is a J-set.
So let
![]() $L \in \mathcal {P}_f({^{\mathbb {N}}S})$
and let
$L \in \mathcal {P}_f({^{\mathbb {N}}S})$
and let
![]() $L^\prime = \{ f + g: f \in L$
and
$L^\prime = \{ f + g: f \in L$
and
![]() $g \in L_\sigma \}$
. Since A is a J-set, pick
$g \in L_\sigma \}$
. Since A is a J-set, pick
![]() $b \in S$
and
$b \in S$
and
![]() $K \in \mathcal {P}_f(\mathbb {N})$
such that
$K \in \mathcal {P}_f(\mathbb {N})$
such that
Then
![]() $S_L(b ,K) \subseteq \{ a \in S: (\exists H \in \mathcal {P}_f(\mathbb {N}))(S_{L_\sigma }(a, H) \subseteq A) \}$
.
$S_L(b ,K) \subseteq \{ a \in S: (\exists H \in \mathcal {P}_f(\mathbb {N}))(S_{L_\sigma }(a, H) \subseteq A) \}$
.
Then we take
![]() $(a_\sigma , H_\sigma ) \in D \setminus C$
, which is as desired.
$(a_\sigma , H_\sigma ) \in D \setminus C$
, which is as desired.
By Lemma 2.1(i), we obtain a family
![]() $\{ \mathcal {A}_\alpha : \alpha < \delta \}$
of almost disjoint subsets of
$\{ \mathcal {A}_\alpha : \alpha < \delta \}$
of almost disjoint subsets of
![]() $\mathcal {P}_f(\kappa )$
such that for any
$\mathcal {P}_f(\kappa )$
such that for any
![]() $F \in \mathcal {P}_f(\kappa )$
and any
$F \in \mathcal {P}_f(\kappa )$
and any
![]() $\alpha < \delta $
there is some
$\alpha < \delta $
there is some
![]() $G \in \mathcal {A}_\alpha $
such that
$G \in \mathcal {A}_\alpha $
such that
![]() $F \subseteq G$
. For any
$F \subseteq G$
. For any
![]() $\xi < \delta $
, let
$\xi < \delta $
, let
![]() $D_\xi = \bigcup \{S_{L_\sigma }(a_\sigma , H_\sigma ): \sigma < \kappa $
and
$D_\xi = \bigcup \{S_{L_\sigma }(a_\sigma , H_\sigma ): \sigma < \kappa $
and
![]() $L_\sigma \in \mathcal {A}_\xi \}$
; since
$L_\sigma \in \mathcal {A}_\xi \}$
; since
![]() $|\mathcal {A}_\xi | = \kappa $
,
$|\mathcal {A}_\xi | = \kappa $
,
![]() $|D_\xi | = \kappa $
. For any
$|D_\xi | = \kappa $
. For any
![]() $\alpha < \beta < \delta $
,
$\alpha < \beta < \delta $
,
![]() $D_\alpha \cap D_\beta = \bigcup \{S_{L_\sigma }(a_\sigma , H_\sigma ): \sigma < \kappa $
and
$D_\alpha \cap D_\beta = \bigcup \{S_{L_\sigma }(a_\sigma , H_\sigma ): \sigma < \kappa $
and
![]() $L_\sigma \in \mathcal {A}_\alpha \cap \mathcal {A}_\beta \}$
so
$L_\sigma \in \mathcal {A}_\alpha \cap \mathcal {A}_\beta \}$
so
![]() $|D_\alpha \cap D_\beta | < \kappa $
. Finally we let
$|D_\alpha \cap D_\beta | < \kappa $
. Finally we let
![]() $\xi < \delta $
and show that
$\xi < \delta $
and show that
![]() $D_\xi $
is a J-set. Let
$D_\xi $
is a J-set. Let
![]() $L \in \mathcal {P}_f({^{\mathbb {N}}S})$
and pick
$L \in \mathcal {P}_f({^{\mathbb {N}}S})$
and pick
![]() $M \in \mathcal {P}_f({^{\mathbb {N}}S})$
such that
$M \in \mathcal {P}_f({^{\mathbb {N}}S})$
such that
![]() $M \in \mathcal {A}_\xi $
and
$M \in \mathcal {A}_\xi $
and
![]() $L \subseteq M$
. Then
$L \subseteq M$
. Then
![]() $M = L_\beta $
for some
$M = L_\beta $
for some
![]() $\beta < \kappa $
so
$\beta < \kappa $
so
![]() $S_L(a_\beta , H_\beta ) \subseteq S_{L_\beta }(a_\beta , H_\beta ) \subseteq D_\xi $
.
$S_L(a_\beta , H_\beta ) \subseteq S_{L_\beta }(a_\beta , H_\beta ) \subseteq D_\xi $
.
Acknowledgements
I acknowledge support received from the Scientific Research Foundation via grant F701108N03. I would like to thank my institution Zhejiang University of Science and Technology for approving this foundation. And I am very thankful to the referee, who gave me a lot of help, including the improvement of proof details and professional advice on paper format and writing.