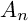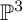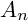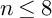1. Introduction
We work with projective varieties over
![]() $\mathbb C$
. Classification of algebraic varieties is one of the fundamental goals in algebraic geometry. The Minimal Model Program says that every variety is birational to either a minimal model or a Mori fiber space. Two Mori fiber spaces are birational if they are connected by a sequence of Sarkisov links (see [Reference Corti17], [Reference Hacon and McKernan26]). In the extreme case, the Mori fiber space is birationally rigid, meaning that it is essentially the unique Mori fiber space in its birational class.
$\mathbb C$
. Classification of algebraic varieties is one of the fundamental goals in algebraic geometry. The Minimal Model Program says that every variety is birational to either a minimal model or a Mori fiber space. Two Mori fiber spaces are birational if they are connected by a sequence of Sarkisov links (see [Reference Corti17], [Reference Hacon and McKernan26]). In the extreme case, the Mori fiber space is birationally rigid, meaning that it is essentially the unique Mori fiber space in its birational class.
Examples of Mori fiber spaces include Fano varieties. The first birational rigidity result was in the seminal paper by Iskovskikh and Manin [Reference Iskovskih and Manin28] for smooth quartic 3-folds in
![]() $\mathbb P^4$
. A wealth of examples of birationally rigid varieties was given in [Reference Cheltsov and Park15], [Reference Corti, Pukhlikov and Reid19], by showing that every quasismooth member of the 95 families of Fano 3-folds that are hypersurfaces in weighted projective spaces is birationally rigid. One major consequence of birational rigidity is nonrationality. Birational rigidity remains an active area of research (see [Reference Ahmadinezhad and Okada3], [Reference Cheltsov and Grinenko13], [Reference Cheltsov and Shramov16], [Reference de Fernex22], [Reference Eckl and Pukhlikov23], [Reference Krylov38], [Reference Prokhorov45]).
$\mathbb P^4$
. A wealth of examples of birationally rigid varieties was given in [Reference Cheltsov and Park15], [Reference Corti, Pukhlikov and Reid19], by showing that every quasismooth member of the 95 families of Fano 3-folds that are hypersurfaces in weighted projective spaces is birationally rigid. One major consequence of birational rigidity is nonrationality. Birational rigidity remains an active area of research (see [Reference Ahmadinezhad and Okada3], [Reference Cheltsov and Grinenko13], [Reference Cheltsov and Shramov16], [Reference de Fernex22], [Reference Eckl and Pukhlikov23], [Reference Krylov38], [Reference Prokhorov45]).
Among smooth Fano 3-folds, the projective space has the highest degree (
![]() $64$
), and sextic double solids, double covers of
$64$
), and sextic double solids, double covers of
![]() $\mathbb P^3$
branched along a sextic surface, have the least degree (
$\mathbb P^3$
branched along a sextic surface, have the least degree (
![]() $2$
). In [Reference Iskovskikh29], it is proved that smooth sextic double solids are birationally rigid. It is interesting to see how this changes as we impose singularities on the variety. The paper [Reference Pukhlikov46] proved that sextic double solids stay birationally rigid if we impose an ordinary double point, meaning the 3-fold
$2$
). In [Reference Iskovskikh29], it is proved that smooth sextic double solids are birationally rigid. It is interesting to see how this changes as we impose singularities on the variety. The paper [Reference Pukhlikov46] proved that sextic double solids stay birationally rigid if we impose an ordinary double point, meaning the 3-fold
![]() $A_1$
singularity
$A_1$
singularity
![]() $x_1^2 + x_2^2 + x_3^2 + x_4^2$
. A sextic double solid can have up to 65 singular points (see [Reference Basset6], [Reference Jaffe and Ruberman31], [Reference Wahl51]), and for each
$x_1^2 + x_2^2 + x_3^2 + x_4^2$
. A sextic double solid can have up to 65 singular points (see [Reference Basset6], [Reference Jaffe and Ruberman31], [Reference Wahl51]), and for each
![]() $n \leq 65$
, there exists a sextic double solid with exactly n ordinary double points and smooth otherwise (see [Reference Barth5], [Reference Catanese and Ceresa12]). A sextic double solid with only ordinary double points is birationally rigid if and only if it is factorial, which is true, for example, if it has at most 14 ordinary double points (see [Reference Cheltsov, Park, Bogomolov and Tschinkel14, Th. B]).
$n \leq 65$
, there exists a sextic double solid with exactly n ordinary double points and smooth otherwise (see [Reference Barth5], [Reference Catanese and Ceresa12]). A sextic double solid with only ordinary double points is birationally rigid if and only if it is factorial, which is true, for example, if it has at most 14 ordinary double points (see [Reference Cheltsov, Park, Bogomolov and Tschinkel14, Th. B]).
The next natural question is to consider more complicated singularities in the Mori category. We study sextic double solids with an isolated compound
![]() $A_n$
singularity, also called a
$A_n$
singularity, also called a
![]() $cA_n$
singularity, meaning that the general section through the point is the Du Val
$cA_n$
singularity, meaning that the general section through the point is the Du Val
![]() $A_n$
singularity
$A_n$
singularity
![]() $x_1 x_2 + x_3^{n+1}$
. A
$x_1 x_2 + x_3^{n+1}$
. A
![]() $cA_n$
singularity is locally analytically given by
$cA_n$
singularity is locally analytically given by
![]() $x_1 x_2 + h(x_3, x_4)$
where the least degree among monomials in h is
$x_1 x_2 + h(x_3, x_4)$
where the least degree among monomials in h is
![]() $n+1$
. The first main result of the paper is describing sextic double solids with an isolated
$n+1$
. The first main result of the paper is describing sextic double solids with an isolated
![]() $cA_n$
singularity.
$cA_n$
singularity.
Theorem (see Theorem A)
If a sextic double solid has an isolated
![]() $cA_n$
point, then
$cA_n$
point, then
![]() $n \leq 8$
.
$n \leq 8$
.
Moreover, in Theorem A, we explicitly parametrize all sextic double solids with an isolated
![]() $cA_n$
singularity for every
$cA_n$
singularity for every
![]() $n \leq 8$
. These form
$n \leq 8$
. These form
![]() $11$
families, as there are four families for
$11$
families, as there are four families for
![]() $cA_7$
. Every family except for family 7.4 contains members that are Mori fiber spaces over a point.
$cA_7$
. Every family except for family 7.4 contains members that are Mori fiber spaces over a point.
We say a few words on bounding the number of
![]() $cA_n$
singularities. It is clear that an isolated
$cA_n$
singularities. It is clear that an isolated
![]() $cA_n$
singularity has Milnor number at least
$cA_n$
singularity has Milnor number at least
![]() $n^2$
. Since the third Betti number of a smooth sextic double solid is
$n^2$
. Since the third Betti number of a smooth sextic double solid is
![]() $104$
(see [Reference Iskovskikh and Prokhorov30, Table 12.2]), an argument similar to [Reference Ahmadinezhad and Kaloghiros2, §3.2] shows that the total Milnor number of a sextic double solid which is a Mori fiber space is at most
$104$
(see [Reference Iskovskikh and Prokhorov30, Table 12.2]), an argument similar to [Reference Ahmadinezhad and Kaloghiros2, §3.2] shows that the total Milnor number of a sextic double solid which is a Mori fiber space is at most
![]() $104$
. This gives the bounds that a Mori fiber space sextic double solid can have up to 1
$104$
. This gives the bounds that a Mori fiber space sextic double solid can have up to 1
![]() $cA_8$
singularity, or up to 2
$cA_8$
singularity, or up to 2
![]() $cA_7$
singularities, or up to 2
$cA_7$
singularities, or up to 2
![]() $cA_6$
singularities, …, or up to 26
$cA_6$
singularities, …, or up to 26
![]() $cA_2$
singularities. We do not expect these bounds to be sharp, as already for ordinary double points it gives an upper bound of 104, far from the actual 65. Using Theorem A, it is possible to construct sextic double solids with a
$cA_2$
singularities. We do not expect these bounds to be sharp, as already for ordinary double points it gives an upper bound of 104, far from the actual 65. Using Theorem A, it is possible to construct sextic double solids with a
![]() $cA_8$
point, a
$cA_8$
point, a
![]() $cA_3$
point, and two ordinary double points with both total Milnor and total Tjurina number at least 66.
$cA_3$
point, and two ordinary double points with both total Milnor and total Tjurina number at least 66.
The second main result is the following theorem.
Theorem (see Theorem B and Proposition 5.6)
A general sextic double solid which is a Mori fiber space with an isolated
![]() $cA_n$
singularity where
$cA_n$
singularity where
![]() $n \geq 4$
is not birationally rigid.
$n \geq 4$
is not birationally rigid.
Birational nonrigidity for a sextic double solid X is proved by describing a birational model, meaning a Mori fiber space
![]() $T \to S$
such that X and T are birational. We find the birational models by explicitly constructing a Sarkisov link for each family of sextic double solids, under the generality conditions described in Definition 5.1. Table 1 gives an overview of the Sarkisov links
$T \to S$
such that X and T are birational. We find the birational models by explicitly constructing a Sarkisov link for each family of sextic double solids, under the generality conditions described in Definition 5.1. Table 1 gives an overview of the Sarkisov links
![]() $X \gets Y_0 \dashrightarrow Y_2 \to Z$
and the birational models, which are either fibrations
$X \gets Y_0 \dashrightarrow Y_2 \to Z$
and the birational models, which are either fibrations
![]() $Y_2 \to Z$
or Fano varieties Z. In the latter case,
$Y_2 \to Z$
or Fano varieties Z. In the latter case,
![]() $Y_2 \to Z$
is a divisorial contraction to the given singular point. The morphism
$Y_2 \to Z$
is a divisorial contraction to the given singular point. The morphism
![]() $Y_0 \to X$
is a divisorial contraction with center the
$Y_0 \to X$
is a divisorial contraction with center the
![]() $cA_n$
point. The birational maps
$cA_n$
point. The birational maps
![]() $Y_0 \dashrightarrow Y_2$
are isomorphisms in codimension 1.
$Y_0 \dashrightarrow Y_2$
are isomorphisms in codimension 1.
Table 1 Birational models for general sextic double solids that are Mori fiber spaces with an isolated
![]() $cA_n$
singularity
$cA_n$
singularity


Note that when we say that a birational map
![]() $Y_0 \dashrightarrow Y_1$
is k Atiyah flops, then we mean that algebraically it is one flop, contracting k curves to k points and extracting k curves, and locally analytically around each of those points, it is an Atiyah flop. Similarly for flips. Also note that the Sarkisov link to a sextic double solid with a
$Y_0 \dashrightarrow Y_1$
is k Atiyah flops, then we mean that algebraically it is one flop, contracting k curves to k points and extracting k curves, and locally analytically around each of those points, it is an Atiyah flop. Similarly for flips. Also note that the Sarkisov link to a sextic double solid with a
![]() $cA_4$
singularity was already described in [Reference Okada43, §9, No. 9], starting from a general quasismooth complete intersection
$cA_4$
singularity was already described in [Reference Okada43, §9, No. 9], starting from a general quasismooth complete intersection
![]() $X_{5, 6} \subseteq \mathbb P(1, 1, 1, 2, 3, 4)$
.
$X_{5, 6} \subseteq \mathbb P(1, 1, 1, 2, 3, 4)$
.
We briefly describe the proof. The first step in the Sarkisov link starting from a Fano variety X is a divisorial contraction
![]() $Y \to X$
. Kawakita described divisorial contractions to
$Y \to X$
. Kawakita described divisorial contractions to
![]() $cA_n$
points locally analytically, showing that they are certain weighted blowups. To construct Sarkisov links, we need a global description. In Proposition 4.6 and Lemma 4.9, we show how to construct divisorial contractions to
$cA_n$
points locally analytically, showing that they are certain weighted blowups. To construct Sarkisov links, we need a global description. In Proposition 4.6 and Lemma 4.9, we show how to construct divisorial contractions to
![]() $cA_n$
points algebraically on affine hypersurfaces, and use this in Section 5 to construct divisorial contractions
$cA_n$
points algebraically on affine hypersurfaces, and use this in Section 5 to construct divisorial contractions
![]() $Y \to X$
for (projective) sextic double solids X. Using unprojection techniques (see [Reference Papadakis and Reid44] for a general theory of unprojection), we find an embedding of Y inside a toric variety T, such that the 2-ray link of T restricts to a Sarkisov link for X (following [Reference Ahmadinezhad and Zucconi4], [Reference Brown and Zucconi10]).
$Y \to X$
for (projective) sextic double solids X. Using unprojection techniques (see [Reference Papadakis and Reid44] for a general theory of unprojection), we find an embedding of Y inside a toric variety T, such that the 2-ray link of T restricts to a Sarkisov link for X (following [Reference Ahmadinezhad and Zucconi4], [Reference Brown and Zucconi10]).
If we try the same methods as in the proof of Theorem B on sextic double solids with a
![]() $cA_n$
singularity where
$cA_n$
singularity where
![]() $n \leq 3$
, then we do not find any new birational models. More precisely, a
$n \leq 3$
, then we do not find any new birational models. More precisely, a
![]() $(3, 1, 1, 1)$
-Kawakita blowup of a
$(3, 1, 1, 1)$
-Kawakita blowup of a
![]() $cA_3$
singularity on a general Mori fiber space sextic double solid initiates a Sarkisov link to itself
$cA_3$
singularity on a general Mori fiber space sextic double solid initiates a Sarkisov link to itself
![]() $X \dashrightarrow X$
. A
$X \dashrightarrow X$
. A
![]() $(2, 2, 1, 1)$
-Kawakita blowup for a
$(2, 2, 1, 1)$
-Kawakita blowup for a
![]() $cA_3$
singularity, a
$cA_3$
singularity, a
![]() $(2, 1, 1, 1)$
-Kawakita blowup for an
$(2, 1, 1, 1)$
-Kawakita blowup for an
![]() $x_1 x_2 + x_3^3 + x_4^3$
singularity, and the (usual) blowup for an ordinary double point on a general Mori fiber space sextic double solid initiate bad links, which end in either a nonterminal 3-fold or a K3-fibration. These are 2-ray links which are not Sarkisov links, where in the last step of the 2-ray game only K-trivial curves are contracted, leaving the Mori category. We expect that general Mori fiber space sextic double solids with a
$x_1 x_2 + x_3^3 + x_4^3$
singularity, and the (usual) blowup for an ordinary double point on a general Mori fiber space sextic double solid initiate bad links, which end in either a nonterminal 3-fold or a K3-fibration. These are 2-ray links which are not Sarkisov links, where in the last step of the 2-ray game only K-trivial curves are contracted, leaving the Mori category. We expect that general Mori fiber space sextic double solids with a
![]() $cA_3$
singularity are birationally rigid, and with certain
$cA_3$
singularity are birationally rigid, and with certain
![]() $cA_2$
or
$cA_2$
or
![]() $cA_1$
singularities are birationally superrigid.
$cA_1$
singularities are birationally superrigid.
Organization of the paper
In Sections 2.1, 2.3, and 2.5, we give known results that we use, respectively, in Sections 3–5. In Section 3, we construct a parameter space of sextic double solids in Theorem A with an isolated
![]() $cA_n$
singularity. In Section 4, we explain the relationship between algebraic and local analytic weighted blowups, and in Proposition 4.6 and the technical Lemma 4.9, we show how to construct divisorial contractions to
$cA_n$
singularity. In Section 4, we explain the relationship between algebraic and local analytic weighted blowups, and in Proposition 4.6 and the technical Lemma 4.9, we show how to construct divisorial contractions to
![]() $cA_n$
points algebraically on affine hypersurfaces. In Section 5, we construct birational models for general sextic double solids which are Mori fiber spaces with an isolated
$cA_n$
points algebraically on affine hypersurfaces. In Section 5, we construct birational models for general sextic double solids which are Mori fiber spaces with an isolated
![]() $cA_n$
singularity where
$cA_n$
singularity where
![]() $n \geq 4$
, thereby showing that they are not birationally rigid. We treat the seven families separately.
$n \geq 4$
, thereby showing that they are not birationally rigid. We treat the seven families separately.
2. Preliminaries
An algebraic variety is an integral separated scheme of finite type over the complex numbers
![]() $\mathbb C$
. When we say morphism, we mean a morphism over
$\mathbb C$
. When we say morphism, we mean a morphism over
![]() $\mathbb C$
.
$\mathbb C$
.
We study sextic double solids, which are double covers of the projective
![]() $3$
-space branched along a sextic surface. We use the following equivalent characterization.
$3$
-space branched along a sextic surface. We use the following equivalent characterization.
Definition 2.1. A sextic double solid is the variety given by the zero locus of an irreducible polynomial
![]() $w^2 + g$
in the weighted projective space
$w^2 + g$
in the weighted projective space
![]() $\mathbb P(1, 1, 1, 1, 3)$
with variables
$\mathbb P(1, 1, 1, 1, 3)$
with variables
![]() $x, y, z, t, w$
, where
$x, y, z, t, w$
, where
![]() $g \in \mathbb C[x, y, z, t]$
is homogeneous of degree 6.
$g \in \mathbb C[x, y, z, t]$
is homogeneous of degree 6.
2.1. Singularity theory
We recall some results from the singularity theory of complex analytic spaces and terminal singularities.
We denote the variables on
![]() $\mathbb C^n$
by
$\mathbb C^n$
by
![]() $\boldsymbol {x} = (x_1, \ldots , x_n)$
, where n is a positive integer. Let
$\boldsymbol {x} = (x_1, \ldots , x_n)$
, where n is a positive integer. Let
![]() $\mathbb C\{\boldsymbol {x}\}$
denote the convergent power series ring. The zero set of an ideal
$\mathbb C\{\boldsymbol {x}\}$
denote the convergent power series ring. The zero set of an ideal
![]() $I \subseteq \mathbb C\{\boldsymbol {x}\}$
is denoted by
$I \subseteq \mathbb C\{\boldsymbol {x}\}$
is denoted by
![]() $\mathbb V(I)$
, where I is either an ideal of regular functions or holomorphic functions, depending on the context. Given a point
$\mathbb V(I)$
, where I is either an ideal of regular functions or holomorphic functions, depending on the context. Given a point
![]() $P \in \mathbb V(I)$
, the pair
$P \in \mathbb V(I)$
, the pair
![]() $(\mathbb V(I), P)$
denotes the (possibly reducible or non-reduced) complex space subgerm of
$(\mathbb V(I), P)$
denotes the (possibly reducible or non-reduced) complex space subgerm of
![]() $(\mathbb C^n, P)$
given by I. Given a regular or holomorphic function f on a variety or a complex space X, denote the nonzero locus of f by
$(\mathbb C^n, P)$
given by I. Given a regular or holomorphic function f on a variety or a complex space X, denote the nonzero locus of f by
![]() $X_f$
. Given positive integer weights
$X_f$
. Given positive integer weights
![]() $\boldsymbol {w} = (w_1, \ldots , w_n)$
for
$\boldsymbol {w} = (w_1, \ldots , w_n)$
for
![]() $\boldsymbol {x}$
, we can write a nonzero polynomial or power series f as a sum of its weighted homogeneous parts
$\boldsymbol {x}$
, we can write a nonzero polynomial or power series f as a sum of its weighted homogeneous parts
![]() $f_i$
. Then, the weight of f, denoted
$f_i$
. Then, the weight of f, denoted
![]() $\operatorname {wt}(f)$
, is the least nonnegative integer d such that
$\operatorname {wt}(f)$
, is the least nonnegative integer d such that
![]() $f_d \neq 0$
. We define
$f_d \neq 0$
. We define
![]() $\operatorname {wt}(0) = \infty $
. If
$\operatorname {wt}(0) = \infty $
. If
![]() $\boldsymbol {w} = (1, \ldots , 1)$
, then d is called the multiplicity, denoted
$\boldsymbol {w} = (1, \ldots , 1)$
, then d is called the multiplicity, denoted
![]() $\operatorname {mult}(f)$
. A hypersurface singularity is a complex analytic space germ (not necessarily irreducible or reduced) that is isomorphic to
$\operatorname {mult}(f)$
. A hypersurface singularity is a complex analytic space germ (not necessarily irreducible or reduced) that is isomorphic to
![]() $(\mathbb V(f), \boldsymbol {0})$
for some
$(\mathbb V(f), \boldsymbol {0})$
for some
![]() $f \in \mathbb C\{\boldsymbol {x}\}$
. A singularity is isolated if it has a smooth analytic punctured neighborhood.
$f \in \mathbb C\{\boldsymbol {x}\}$
. A singularity is isolated if it has a smooth analytic punctured neighborhood.
Definition 2.2 [Reference Greuel, Lossen and Shustin25, Def. 2.9]
Let
![]() $f, g \in \mathbb C\{\boldsymbol {x}\}$
.
$f, g \in \mathbb C\{\boldsymbol {x}\}$
.
-
(a) We say f and g are right equivalent if there exists a biholomorphic map germ
 $\varphi \colon (\mathbb C^n, \boldsymbol {0}) \to (\mathbb C^n, \boldsymbol {0})$
such that
$\varphi \colon (\mathbb C^n, \boldsymbol {0}) \to (\mathbb C^n, \boldsymbol {0})$
such that
 $g = f \circ \varphi $
.
$g = f \circ \varphi $
. -
(b) We say f and g are contact equivalent if there exist a biholomorphic map germ
 $\varphi \colon (\mathbb C^n, \boldsymbol {0}) \to (\mathbb C^n, \boldsymbol {0})$
and a unit
$\varphi \colon (\mathbb C^n, \boldsymbol {0}) \to (\mathbb C^n, \boldsymbol {0})$
and a unit
 $u \in \mathbb C\{x_1, \ldots , x_n\}$
such that
$u \in \mathbb C\{x_1, \ldots , x_n\}$
such that
 $g = u(f \circ \varphi )$
.
$g = u(f \circ \varphi )$
.
Remark 2.3 [Reference Greuel, Lossen and Shustin25, Rem. 2.9.1(3)]
Two convergent power series
![]() $f, g \in \mathbb C\{\boldsymbol {x}\}$
are contact equivalent if and only if the complex analytic space germs
$f, g \in \mathbb C\{\boldsymbol {x}\}$
are contact equivalent if and only if the complex analytic space germs
![]() $(\mathbb V(f), \boldsymbol {0})$
and
$(\mathbb V(f), \boldsymbol {0})$
and
![]() $(\mathbb V(g), \boldsymbol {0})$
are isomorphic.
$(\mathbb V(g), \boldsymbol {0})$
are isomorphic.
We use the following proposition in Section 3 to parametrize sextic double solids with a
![]() $cA_1$
singularity.
$cA_1$
singularity.
Proposition 2.4 [Reference Greuel, Lossen and Shustin25, Rem. 2.50.1]
Let
![]() $f, g \in \mathbb C\{x_1, \ldots , x_n\}$
be two contact equivalent power series with zero constant term. Then their multiplicity m (as defined above) is the same and, furthermore,
$f, g \in \mathbb C\{x_1, \ldots , x_n\}$
be two contact equivalent power series with zero constant term. Then their multiplicity m (as defined above) is the same and, furthermore,
![]() $f_m$
and
$f_m$
and
![]() $g_m$
are the same up to an invertible linear change of coordinates.
$g_m$
are the same up to an invertible linear change of coordinates.
We use the following proposition in Section 3 to construct sextic double solids with a
![]() $cA_n$
singularity where
$cA_n$
singularity where
![]() $n \geq 2$
, as well as in Section 4 to describe weighted blowups of
$n \geq 2$
, as well as in Section 4 to describe weighted blowups of
![]() $cA_n$
points.
$cA_n$
points.
Proposition 2.5. Let
![]() $F = x_1^2 + \cdots + x_k^2 + f$
and
$F = x_1^2 + \cdots + x_k^2 + f$
and
![]() $G = x_1^2 + \cdots + x_k^2 + g$
, where f and g are convergent power series in
$G = x_1^2 + \cdots + x_k^2 + g$
, where f and g are convergent power series in
![]() $\mathbb C\{x_{k+1}, \ldots , x_n\}$
with zero constant term. Then F and G are contact (resp. right) equivalent if and only if f and g are contact (resp. right) equivalent.
$\mathbb C\{x_{k+1}, \ldots , x_n\}$
with zero constant term. Then F and G are contact (resp. right) equivalent if and only if f and g are contact (resp. right) equivalent.
Proof. By a result of Mather and Yau [Reference Mather and Yau40] (see also [Reference Greuel, Lossen and Shustin25, Th. 2.26]), f and g are contact equivalent if and only if the Tjurina algebras
![]() $T_f$
and
$T_f$
and
![]() $T_g$
are isomorphic. A simple computation shows that
$T_g$
are isomorphic. A simple computation shows that
![]() $T_f \cong T_F$
and
$T_f \cong T_F$
and
![]() $T_g \cong T_G$
, which proves the proposition for contact equivalence.
$T_g \cong T_G$
, which proves the proposition for contact equivalence.
The proof for right equivalence is similar. Namely, we use a statement analogous to [Reference Mather and Yau40]: two elements
![]() $h, k \in \mathbb C\{\boldsymbol {x}\}$
with zero constant term are right equivalent if and only if the Milnor algebras
$h, k \in \mathbb C\{\boldsymbol {x}\}$
with zero constant term are right equivalent if and only if the Milnor algebras
![]() $M_h$
and
$M_h$
and
![]() $M_k$
are isomorphic as algebras over the ring
$M_k$
are isomorphic as algebras over the ring
![]() $\mathbb C\{t\}$
, where t acts on
$\mathbb C\{t\}$
, where t acts on
![]() $M_h$
(resp.
$M_h$
(resp.
![]() $M_k$
) by multiplying by h (resp. k) (see [Reference Greuel, Lossen and Shustin25, Th. 2.28]).
$M_k$
) by multiplying by h (resp. k) (see [Reference Greuel, Lossen and Shustin25, Th. 2.28]).
Reid defined in [Reference Reid47, Def. 2.1] that a compound Du Val singularity is a three-dimensional singularity where a hypersurface section is a Du Val singularity, also called a surface ADE singularity. The singularity is denoted
![]() $cA_n$
,
$cA_n$
,
![]() $cD_n$
, or
$cD_n$
, or
![]() $ce:n$
, respectively, if the general hyperplane section is an
$ce:n$
, respectively, if the general hyperplane section is an
![]() $A_n$
,
$A_n$
,
![]() $D_n$
, or
$D_n$
, or
![]() $E_n$
singularity, respectively. Reid showed in [Reference Reid48, Th. 0.6] that a three-dimensional hypersurface singularity is terminal if and only if it is an isolated compound Du Val singularity.
$E_n$
singularity, respectively. Reid showed in [Reference Reid48, Th. 0.6] that a three-dimensional hypersurface singularity is terminal if and only if it is an isolated compound Du Val singularity.
In this paper, we focus on the most general class of compound Du Val singularities, namely
![]() $cA_n$
singularities. Since a surface
$cA_n$
singularities. Since a surface
![]() $A_n$
singularity is given by
$A_n$
singularity is given by
![]() $x^2 + y^2 + z^{n+1}$
, we have the following corollary.
$x^2 + y^2 + z^{n+1}$
, we have the following corollary.
Corollary 2.6. Let n be a positive integer. A singularity is of type
![]() $cA_n$
if and only if it is isomorphic to the complex analytic space subgerm
$cA_n$
if and only if it is isomorphic to the complex analytic space subgerm
![]() $(\mathbb V(x_1^2 + x_2^2 + g), \boldsymbol {0})$
of
$(\mathbb V(x_1^2 + x_2^2 + g), \boldsymbol {0})$
of
![]() $(\mathbb C^4, \boldsymbol {0})$
with variables
$(\mathbb C^4, \boldsymbol {0})$
with variables
![]() $x_1, x_2, x_3, x_4$
for some convergent power series
$x_1, x_2, x_3, x_4$
for some convergent power series
![]() $g \in \mathbb C\{x_3, x_4\}$
of multiplicity
$g \in \mathbb C\{x_3, x_4\}$
of multiplicity
![]() $n+1$
.
$n+1$
.
For a proof of Corollary 2.6, see [Reference Kollár35, Th. 2.8].
The simplest example of a
![]() $cA_1$
singularity is the ordinary double point, given by
$cA_1$
singularity is the ordinary double point, given by
![]() $x^2 + y^2 + z^2 + t^2$
.
$x^2 + y^2 + z^2 + t^2$
.
Remark 2.7. Terminal sextic double solids have only isolated hypersurface singularities, therefore only
![]() $cA_n$
,
$cA_n$
,
![]() $cD_n$
, and
$cD_n$
, and
![]() $ce:n$
singularities. Sextic double solids are Gorenstein, since by [Reference Eisenbud24, Cor. 21.19] every variety with local complete intersection singularities is Gorenstein.
$ce:n$
singularities. Sextic double solids are Gorenstein, since by [Reference Eisenbud24, Cor. 21.19] every variety with local complete intersection singularities is Gorenstein.
2.2.
 $\mathbb Q$
-factoriality
$\mathbb Q$
-factoriality
Definition 2.8. A Weil divisor D on a normal algebraic variety is
![]() $\mathbb Q$
-Cartier if a positive integer multiple of D is Cartier. A normal algebraic variety X is factorial (resp.
$\mathbb Q$
-Cartier if a positive integer multiple of D is Cartier. A normal algebraic variety X is factorial (resp.
![]() $\mathbb Q$
-factorial), if every Weil divisor on X is Cartier (resp.
$\mathbb Q$
-factorial), if every Weil divisor on X is Cartier (resp.
![]() $\mathbb Q$
-Cartier).
$\mathbb Q$
-Cartier).
Definition 2.9. A Fano variety is a normal projective algebraic variety with an ample
![]() $\mathbb Q$
-Cartier anti-canonical divisor.
$\mathbb Q$
-Cartier anti-canonical divisor.
To prove factoriality of certain singular sextic double solids, we use the following proposition by Namikawa.
Proposition 2.10 [Reference Namikawa42, Prop. 2]
Let X be a Fano 3-fold with Gorenstein terminal singularities and D its general effective anti-canonical divisor. Then, the natural homomorphism
![]() $\operatorname {Pic}(X) \to \operatorname {Pic}(D)$
is an injection.
$\operatorname {Pic}(X) \to \operatorname {Pic}(D)$
is an injection.
Remark 2.11. The proof of [Reference Namikawa42, Prop. 2] contains a few typos that do not affect the result:
-
(1) The sentence “Since
 $\operatorname {Pic}(X) \cong \operatorname {Pic}(U)$
, we have shown that…” should be replaced with “Since
$\operatorname {Pic}(X) \cong \operatorname {Pic}(U)$
, we have shown that…” should be replaced with “Since
 $\operatorname {Pic}(X)$
injects into
$\operatorname {Pic}(X)$
injects into
 $\operatorname {Pic}(U)$
, we have shown that….” The isomorphism of
$\operatorname {Pic}(U)$
, we have shown that….” The isomorphism of
 $\operatorname {Pic}(X)$
and
$\operatorname {Pic}(X)$
and
 $\operatorname {Pic}(U)$
would imply that every X that is smooth along D is factorial, which is not true. To see that
$\operatorname {Pic}(U)$
would imply that every X that is smooth along D is factorial, which is not true. To see that
 $\operatorname {Pic}(X)$
injects into
$\operatorname {Pic}(X)$
injects into
 $\operatorname {Pic}(U)$
for every Zariski open set U containing D, note that since the complement of U in X is of codimension at least
$\operatorname {Pic}(U)$
for every Zariski open set U containing D, note that since the complement of U in X is of codimension at least
 $2$
, the class groups
$2$
, the class groups
 $\operatorname {Cl}(X)$
and
$\operatorname {Cl}(X)$
and
 $\operatorname {Cl}(U)$
are isomorphic. We have a map
$\operatorname {Cl}(U)$
are isomorphic. We have a map
 $\operatorname {Pic}(X) \to \operatorname {Pic}(U)$
, since every Weil divisor which is Cartier on X is Cartier on U. The map
$\operatorname {Pic}(X) \to \operatorname {Pic}(U)$
, since every Weil divisor which is Cartier on X is Cartier on U. The map
 $\operatorname {Pic}(X) \to \operatorname {Pic}(U)$
is injective.
$\operatorname {Pic}(X) \to \operatorname {Pic}(U)$
is injective. -
(2) The sentence “Thus, the complement
 $X - U$
is of codimension
$X - U$
is of codimension
 $2$
in X” should be replaced with “Thus, the complement
$2$
in X” should be replaced with “Thus, the complement
 $X - U$
is of codimension at least
$X - U$
is of codimension at least
 $2$
in X.”
$2$
in X.” -
(3) The sentence “There is a Zariski open subset U of W…” should be replaced with “There is a Zariski open subset U of X….”
We remind that a terminal variety is log terminal (see [Reference Kollár and Mori37, Def. 2.34]). The Picard number of log terminal sextic double solids is
![]() $1$
by the following proposition.
$1$
by the following proposition.
Proposition 2.12. Let X be a log terminal complete intersection Fano variety of dimension
![]() $n \geq 3$
in a weighted projective space
$n \geq 3$
in a weighted projective space
![]() $\mathbb P$
. Then the Picard number of
$\mathbb P$
. Then the Picard number of
![]() $X$
is 1.
$X$
is 1.
Proof. By [Reference Iskovskikh and Prokhorov30, Prop. 2.1.2], we have natural isomorphisms
![]() $\operatorname {Pic}(\mathbb P) \cong H^2(\mathbb P^{\mathrm {an}}_{\mathrm{top}}, {\mathbb Z})$
and
$\operatorname {Pic}(\mathbb P) \cong H^2(\mathbb P^{\mathrm {an}}_{\mathrm{top}}, {\mathbb Z})$
and
![]() $\operatorname {Pic}(X) \cong H^2(X^{\mathrm {an}}_{\mathrm{top}}, {\mathbb Z})$
, where
$\operatorname {Pic}(X) \cong H^2(X^{\mathrm {an}}_{\mathrm{top}}, {\mathbb Z})$
, where
![]() $\mathbb{P}^{\mathrm {an}}_{\mathrm{top}}$
, respectively
$\mathbb{P}^{\mathrm {an}}_{\mathrm{top}}$
, respectively
![]() $X^{\mathrm {an}}_{\mathrm{top}}$
denotes the underlying topological space of the analytification of
$X^{\mathrm {an}}_{\mathrm{top}}$
denotes the underlying topological space of the analytification of
![]() $\mathbb{P}$
, respectively
$\mathbb{P}$
, respectively
![]() $X$
. By [Reference Mavlyutov41, Proposition 1.4], the restriction map
$X$
. By [Reference Mavlyutov41, Proposition 1.4], the restriction map
![]() $H^{i}(\mathbb{P}^{\mathrm{an}}_{\mathrm{top}}, \mathbb{C}) \rightarrow H^{i}(X^{\mathrm{an}}_{\mathrm{top}}, \mathbb{C})$
is an isomorphism for is an isomorphism for
$H^{i}(\mathbb{P}^{\mathrm{an}}_{\mathrm{top}}, \mathbb{C}) \rightarrow H^{i}(X^{\mathrm{an}}_{\mathrm{top}}, \mathbb{C})$
is an isomorphism for is an isomorphism for
![]() $i < n$
. By [Reference Zhang53, Corollary 1],
$i < n$
. By [Reference Zhang53, Corollary 1],
![]() $X$
and
$X$
and
![]() $\mathbb{P}$
are simply connected. The proposition now follows from universal coefficienttheorems.
$\mathbb{P}$
are simply connected. The proposition now follows from universal coefficienttheorems.
To show that some sextic double solids are not
![]() $\mathbb Q$
-factorial, we use the lemma below.
$\mathbb Q$
-factorial, we use the lemma below.
Lemma 2.13. Let X be a projective variety of Picard number one. Let
![]() $D$
be a non-zero effective
$D$
be a non-zero effective
![]() $\mathbb{Q}$
-Cartier divisor and
$\mathbb{Q}$
-Cartier divisor and
![]() $C$
a closed curve in
$C$
a closed curve in
![]() $X$
. Then
$X$
. Then
![]() $D\cdot C > 0$
.
$D\cdot C > 0$
.
Proof. Replacing
![]() $D$
by a suitable multiple, it suffices to consider the case where
$D$
by a suitable multiple, it suffices to consider the case where
![]() $D$
isCartier. There are no non-zero effective principal divisors on a normal projective variety.Therefore, since
$D$
isCartier. There are no non-zero effective principal divisors on a normal projective variety.Therefore, since
![]() $X$
has Picard number one, either
$X$
has Picard number one, either
![]() $D$
or
$D$
or
![]() $-D$
is ample. Since
$-D$
is ample. Since
![]() $D$
intersectssome closed integral curve positively,
$D$
intersectssome closed integral curve positively,
![]() $D$
is ample by Kleiman’s criterion. Again byKleiman’s criterion,
$D$
is ample by Kleiman’s criterion. Again byKleiman’s criterion,
![]() $D$
intersects
$D$
intersects
![]() $C$
positively.
$C$
positively.
2.3. Weighted blowups
We remind the definition of weighted blowups, Definition 2.15.
Definition 2.14. Let
![]() $\varphi \colon Y \to X$
and
$\varphi \colon Y \to X$
and
![]() $\varphi '\colon Y' \to X'$
be birational morphisms of varieties (or bimeromorphic holomorphisms of complex analytic spaces). We say that an isomorphism
$\varphi '\colon Y' \to X'$
be birational morphisms of varieties (or bimeromorphic holomorphisms of complex analytic spaces). We say that an isomorphism
![]() $X \to X'$
lifts if there exists an isomorphism
$X \to X'$
lifts if there exists an isomorphism
![]() $Y \cong Y'$
such that the diagram
$Y \cong Y'$
such that the diagram

commutes. We say that
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi '$
are equivalent if there exists an isomorphism
$\varphi '$
are equivalent if there exists an isomorphism
![]() $X \cong X'$
that lifts. We say
$X \cong X'$
that lifts. We say
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi '$
are locally equivalent if there exist isomorphic open subsets
$\varphi '$
are locally equivalent if there exist isomorphic open subsets
![]() $U \subseteq X$
and
$U \subseteq X$
and
![]() $U' \subseteq X'$
containing the centers of the morphisms
$U' \subseteq X'$
containing the centers of the morphisms
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi '$
such that the restrictions
$\varphi '$
such that the restrictions
![]() $\varphi |_{\varphi ^{-1}U}\colon \varphi ^{-1}U \to U$
and
$\varphi |_{\varphi ^{-1}U}\colon \varphi ^{-1}U \to U$
and
![]() $\varphi '|_{\varphi ^{\prime -1}U'}\colon \varphi ^{\prime -1}U' \to U'$
are equivalent.
$\varphi '|_{\varphi ^{\prime -1}U'}\colon \varphi ^{\prime -1}U' \to U'$
are equivalent.
If we consider the complex analytic space corresponding to a variety or when we wish to emphasize that we are working in the category of complex analytic spaces, we sometimes say analytically equivalent or locally analytically equivalent.
Definition 2.15. Let n be a positive integer, and let
![]() $\boldsymbol {w} = (w_1, \ldots , w_n)$
be positive integers, called the weights of the blowup. Define a
$\boldsymbol {w} = (w_1, \ldots , w_n)$
be positive integers, called the weights of the blowup. Define a
![]() $\mathbb C^*$
-action on
$\mathbb C^*$
-action on
![]() $\mathbb C^{n+1}$
by
$\mathbb C^{n+1}$
by
![]() $\lambda \cdot (u, x_1, \ldots , x_n) = (\lambda ^{-1} u, \lambda ^{w_1} x_1, \ldots , \lambda ^{w_n} x_n)$
and define T by the geometric quotient
$\lambda \cdot (u, x_1, \ldots , x_n) = (\lambda ^{-1} u, \lambda ^{w_1} x_1, \ldots , \lambda ^{w_n} x_n)$
and define T by the geometric quotient
![]() $(\mathbb C^{n+1} \setminus \mathbb V(x_1, \ldots , x_n)) / \mathbb C^*$
(or its analytification). Then the map
$(\mathbb C^{n+1} \setminus \mathbb V(x_1, \ldots , x_n)) / \mathbb C^*$
(or its analytification). Then the map
![]() $\varphi \colon T \to \mathbb C^n$
,
$\varphi \colon T \to \mathbb C^n$
,
![]() $[u, x_1, \ldots , x_n] \mapsto (u^{w_1} x_1, \ldots , u^{w_n} x_n)$
is called the
$[u, x_1, \ldots , x_n] \mapsto (u^{w_1} x_1, \ldots , u^{w_n} x_n)$
is called the
![]() $\boldsymbol {w}$
-blowup of
$\boldsymbol {w}$
-blowup of
![]() $\mathbb C^n$
. If
$\mathbb C^n$
. If
![]() $Z \subseteq \mathbb C^n$
is a closed subvariety (or a closed complex subspace
$Z \subseteq \mathbb C^n$
is a closed subvariety (or a closed complex subspace
![]() $Z \subseteq D$
where
$Z \subseteq D$
where
![]() $D \subseteq \mathbb C^n$
is open) and
$D \subseteq \mathbb C^n$
is open) and
![]() $\tilde Z$
is the closure of
$\tilde Z$
is the closure of
![]() $\varphi ^{-1}(Z \setminus \{\boldsymbol {0}\})$
in T (in
$\varphi ^{-1}(Z \setminus \{\boldsymbol {0}\})$
in T (in
![]() $\varphi ^{-1} D$
), then the restriction
$\varphi ^{-1} D$
), then the restriction
![]() $\varphi |_{\tilde Z}\colon \tilde Z \to Z$
is called the
$\varphi |_{\tilde Z}\colon \tilde Z \to Z$
is called the
![]() $\boldsymbol {w}$
-blowup of Z. Let
$\boldsymbol {w}$
-blowup of Z. Let
![]() $\rho \colon Y \to X$
be a surjective birational morphism of varieties (or a surjective bimeromorphic holomorphism of complex spaces). Given an open subset
$\rho \colon Y \to X$
be a surjective birational morphism of varieties (or a surjective bimeromorphic holomorphism of complex spaces). Given an open subset
![]() $U \subseteq X$
containing the center of
$U \subseteq X$
containing the center of
![]() $\rho $
and an isomorphism
$\rho $
and an isomorphism
![]() $U \cong Z \subseteq \mathbb C^n$
taking a point
$U \cong Z \subseteq \mathbb C^n$
taking a point
![]() $P \in X$
to the origin
$P \in X$
to the origin
![]() $\boldsymbol {0}$
, the map
$\boldsymbol {0}$
, the map
![]() $\rho $
is called the
$\rho $
is called the
![]() $\boldsymbol {w}$
-blowup of X at P if the isomorphism
$\boldsymbol {w}$
-blowup of X at P if the isomorphism
![]() $U \cong Z$
lifts to
$U \cong Z$
lifts to
![]() $\rho ^{-1}U \to \tilde Z$
.
$\rho ^{-1}U \to \tilde Z$
.
Remark 2.16.
-
(a) A weighted blowup crucially depends on both the isomorphism
 $U \cong X'$
and a choice of coordinates
$U \cong X'$
and a choice of coordinates
 $x_1, \ldots , x_n$
, even though it is not explicit in the notation.
$x_1, \ldots , x_n$
, even though it is not explicit in the notation. -
(b) Replacing
 $\boldsymbol {w}$
by
$\boldsymbol {w}$
by
 $(w_1/g, \ldots , w_n/g)$
in Definition 2.15, where g is the greatest common divisor of
$(w_1/g, \ldots , w_n/g)$
in Definition 2.15, where g is the greatest common divisor of
 $w_1, \ldots , w_n$
, gives an isomorphic blowup over X.
$w_1, \ldots , w_n$
, gives an isomorphic blowup over X. -
(c) By [Reference Cox, Little and Schenck21, Th. 5.1.11], the weighted blowup of an affine space in Definition 2.15 coincides with the toric description of subdividing a cone in [Reference Kollár and Mori36, Prop.–Def. 10.3].
We give alternative definitions of weighted blowup in Definitions 2.17 and 2.18 that we use in Corollary 4.4.
Definition 2.17. Let
![]() $n \in \mathbb Z_{\geq 1}$
and
$n \in \mathbb Z_{\geq 1}$
and
![]() $\boldsymbol {w} \in \mathbb Z_{\geq 1}^n$
. Let
$\boldsymbol {w} \in \mathbb Z_{\geq 1}^n$
. Let
![]() $X = \operatorname {Spec} \mathbb C[\boldsymbol {x}]/I$
be an affine variety. Define the
$X = \operatorname {Spec} \mathbb C[\boldsymbol {x}]/I$
be an affine variety. Define the
![]() $\mathbb Z_{\geq 0}$
-graded
$\mathbb Z_{\geq 0}$
-graded
![]() $\mathbb C$
-algebra
$\mathbb C$
-algebra
where t denotes the grading and
![]() $\bar x_i \in \mathbb C[\boldsymbol {x}]/I$
denotes the image of
$\bar x_i \in \mathbb C[\boldsymbol {x}]/I$
denotes the image of
![]() $x_i \in \mathbb C[\boldsymbol {x}]$
. Define the morphism
$x_i \in \mathbb C[\boldsymbol {x}]$
. Define the morphism
![]() $\operatorname {Proj} R_X \to X$
.
$\operatorname {Proj} R_X \to X$
.
Definition 2.18. Let
![]() $n \in \mathbb Z_{\geq 1}$
and
$n \in \mathbb Z_{\geq 1}$
and
![]() $\boldsymbol {w} \in \mathbb Z_{\geq 1}^n$
. Let
$\boldsymbol {w} \in \mathbb Z_{\geq 1}^n$
. Let
![]() $D \subseteq \mathbb C^n$
be an open subset. Let
$D \subseteq \mathbb C^n$
be an open subset. Let
![]() $X \subseteq D$
be a closed complex analytic space. For every open
$X \subseteq D$
be a closed complex analytic space. For every open
![]() $V \subseteq D$
, we denote the image of
$V \subseteq D$
, we denote the image of
![]() $f \in \mathcal O_{\mathbb C^n}(V)$
in
$f \in \mathcal O_{\mathbb C^n}(V)$
in
![]() $\mathcal O_X(X \cap V)$
by
$\mathcal O_X(X \cap V)$
by
![]() $\bar f$
. Define the finitely presented
$\bar f$
. Define the finitely presented
![]() $\mathbb Z_{\geq 0}$
-graded
$\mathbb Z_{\geq 0}$
-graded
![]() $\mathcal O_X$
-algebra
$\mathcal O_X$
-algebra
![]() $\mathcal B_X$
to be the sheafification of the presheaf
$\mathcal B_X$
to be the sheafification of the presheaf
![]() $\mathcal A_X$
given by
$\mathcal A_X$
given by
where
![]() $U \subseteq X$
is open and t denotes the grading. By [Reference Campana, Dethloff, Grauert, Petemell and Remmert11, Prop. II.3.19], we have a morphism
$U \subseteq X$
is open and t denotes the grading. By [Reference Campana, Dethloff, Grauert, Petemell and Remmert11, Prop. II.3.19], we have a morphism
![]() $\operatorname {Projan} \mathcal B_X \to X$
, where
$\operatorname {Projan} \mathcal B_X \to X$
, where
![]() $\operatorname {Projan}$
is the analytic homogeneous spectrum.
$\operatorname {Projan}$
is the analytic homogeneous spectrum.
Proof. First, we show that Definition 2.17 is the
![]() $\boldsymbol {w}$
-blowup when X is the affine space
$\boldsymbol {w}$
-blowup when X is the affine space
![]() $\mathbb A^n = \operatorname {Spec} \mathbb C[x_1, \ldots , x_n]$
. Let
$\mathbb A^n = \operatorname {Spec} \mathbb C[x_1, \ldots , x_n]$
. Let
![]() $S = \mathbb C[u, \boldsymbol {x}]$
be the
$S = \mathbb C[u, \boldsymbol {x}]$
be the
![]() $\mathbb Z$
-graded
$\mathbb Z$
-graded
![]() $\mathbb C$
-algebra with grading
$\mathbb C$
-algebra with grading
![]() $(-1, \operatorname {wt} x_1, \ldots , \operatorname {wt} x_n)$
for
$(-1, \operatorname {wt} x_1, \ldots , \operatorname {wt} x_n)$
for
![]() $u, \boldsymbol {x}$
. Let
$u, \boldsymbol {x}$
. Let
![]() $S_{\geq 0}$
be the nonnegatively graded part of S. By definition of the geometric quotient, the weighted blowup of
$S_{\geq 0}$
be the nonnegatively graded part of S. By definition of the geometric quotient, the weighted blowup of
![]() $\mathbb A^n$
is given by
$\mathbb A^n$
is given by
![]() $\operatorname {Proj} S_{\geq 0} \to \mathbb A^n$
. The
$\operatorname {Proj} S_{\geq 0} \to \mathbb A^n$
. The
![]() $\mathbb Z_{\geq 0}$
-graded
$\mathbb Z_{\geq 0}$
-graded
![]() $\mathbb C$
-algebra isomorphism
$\mathbb C$
-algebra isomorphism
 $$\begin{align*}\begin{gathered} S_{\geq0} \to R_{\mathbb A^n}\\ u \mapsto t^{-1}, \quad x_i \mapsto t^{\operatorname{wt} x_i} x_i \end{gathered} \end{align*}$$
$$\begin{align*}\begin{gathered} S_{\geq0} \to R_{\mathbb A^n}\\ u \mapsto t^{-1}, \quad x_i \mapsto t^{\operatorname{wt} x_i} x_i \end{gathered} \end{align*}$$
induces an isomorphism
![]() $\operatorname {Proj} R \to \operatorname {Proj} S_{\geq 0}$
over
$\operatorname {Proj} R \to \operatorname {Proj} S_{\geq 0}$
over
![]() $\mathbb A^n$
.
$\mathbb A^n$
.
We show that Definition 2.17 is the
![]() $\boldsymbol {w}$
-blowup for any X. Define
$\boldsymbol {w}$
-blowup for any X. Define
![]() $N = n \cdot \operatorname {lcm}(w_1, \ldots , w_n)$
. If
$N = n \cdot \operatorname {lcm}(w_1, \ldots , w_n)$
. If
![]() $M = x_1^{a_1} \cdot \ldots \cdot x_n^{a_n}$
is any monomial such that
$M = x_1^{a_1} \cdot \ldots \cdot x_n^{a_n}$
is any monomial such that
![]() $\sum a_i w_i> N$
, then M is divisible by
$\sum a_i w_i> N$
, then M is divisible by
![]() $x_k^{N / (n w_k)}$
for some k. It follows that the Nth Veronese subring
$x_k^{N / (n w_k)}$
for some k. It follows that the Nth Veronese subring
![]() $R_X^{(N)}$
of
$R_X^{(N)}$
of
![]() $R_X$
is generated by its degree
$R_X$
is generated by its degree
![]() $1$
part
$1$
part
![]() $(R_X)_N$
. Therefore,
$(R_X)_N$
. Therefore,
![]() $\operatorname {Proj} R_X$
is isomorphic over X to
$\operatorname {Proj} R_X$
is isomorphic over X to
![]() $\operatorname {Bl}_{(R_X)_N} X$
, where
$\operatorname {Bl}_{(R_X)_N} X$
, where
![]() $\operatorname {Bl}_{(R_X)_N} X \to X$
is blowup of X along
$\operatorname {Bl}_{(R_X)_N} X \to X$
is blowup of X along
![]() $(R_X)_N$
. Since the intersection of
$(R_X)_N$
. Since the intersection of
![]() $\operatorname {Spec} (R_{\mathbb A^n})_N$
and X is
$\operatorname {Spec} (R_{\mathbb A^n})_N$
and X is
![]() $\operatorname {Spec} (R_X)_N$
, we find that
$\operatorname {Spec} (R_X)_N$
, we find that
![]() $\operatorname {Bl}_{(R_X)_N} X$
is the strict transform of X under the blowup of
$\operatorname {Bl}_{(R_X)_N} X$
is the strict transform of X under the blowup of
![]() $\mathbb A^n$
along
$\mathbb A^n$
along
![]() $(R_{\mathbb A^n})_N$
, which coincides with the closure of the inverse image of
$(R_{\mathbb A^n})_N$
, which coincides with the closure of the inverse image of
![]() $X \setminus \mathbb V(x_1, \ldots , x_n)$
in
$X \setminus \mathbb V(x_1, \ldots , x_n)$
in
![]() $\operatorname {Bl}_{(R_{\mathbb A^n})_N} \mathbb A^n$
.
$\operatorname {Bl}_{(R_{\mathbb A^n})_N} \mathbb A^n$
.
We show that Definition 2.18 is the
![]() $\boldsymbol {w}$
-blowup. We similarly prove that
$\boldsymbol {w}$
-blowup. We similarly prove that
![]() $\operatorname {Projan} \mathcal B_X$
is the closure of the inverse image of
$\operatorname {Projan} \mathcal B_X$
is the closure of the inverse image of
![]() $X \setminus \{\boldsymbol {0}\}$
in
$X \setminus \{\boldsymbol {0}\}$
in
![]() $\operatorname {Projan} \mathcal B_D$
. Now, it suffices to note that the analytification of
$\operatorname {Projan} \mathcal B_D$
. Now, it suffices to note that the analytification of
![]() $\operatorname {Proj} R_{\mathbb A^n} \to \mathbb A^n$
is
$\operatorname {Proj} R_{\mathbb A^n} \to \mathbb A^n$
is
![]() $\operatorname {Projan} \mathcal B_{\mathbb C^n} \to \mathbb C^n$
.
$\operatorname {Projan} \mathcal B_{\mathbb C^n} \to \mathbb C^n$
.
In Corollary 4.4, we give a simple criterion for a local biholomorphism to lift to weighted blowups.
2.4. Divisorial contractions
The first step in a Sarkisov link from a Fano variety is a divisorial contraction.
Definition 2.20. A divisorial contraction is a proper birational morphism
![]() $\varphi \colon Y \to X$
between normal varieties with terminal singularities such that
$\varphi \colon Y \to X$
between normal varieties with terminal singularities such that
-
(1) the exceptional locus of
 $\varphi $
is a prime divisor and
$\varphi $
is a prime divisor and -
(2)
 $-K_Y$
is
$-K_Y$
is
 $\varphi $
-ample.
$\varphi $
-ample.
Kawakita [Reference Kawakita32] described divisorial contractions with center a
![]() $cA_n$
point by weighted blowups. Notational differences from [Reference Kawakita32, Th. 1.13] are that below we have left out the description for
$cA_n$
point by weighted blowups. Notational differences from [Reference Kawakita32, Th. 1.13] are that below we have left out the description for
![]() $cA_1$
singularities and an exceptional case for
$cA_1$
singularities and an exceptional case for
![]() $cA_2$
. Also, we have written out the converse statement more explicitly (that being a Kawakita blowup implies that it is a divisorial contraction).
$cA_2$
. Also, we have written out the converse statement more explicitly (that being a Kawakita blowup implies that it is a divisorial contraction).
Theorem 2.21 [Reference Kawakita32, Th. 1.13]
Let P be a
![]() $cA_n$
point where
$cA_n$
point where
![]() $n \geq 3$
of a variety X with terminal singularities. Let
$n \geq 3$
of a variety X with terminal singularities. Let
![]() $\varphi \colon Y \to X$
be a morphism of varieties such that the restriction
$\varphi \colon Y \to X$
be a morphism of varieties such that the restriction
![]() $\varphi |_{Y \setminus E}\colon Y \setminus E \to X \setminus \{P\}$
is an isomorphism, where the closed subvariety E is given by
$\varphi |_{Y \setminus E}\colon Y \setminus E \to X \setminus \{P\}$
is an isomorphism, where the closed subvariety E is given by
![]() $\varphi ^{-1}\{P\}$
. If
$\varphi ^{-1}\{P\}$
. If
![]() $\varphi $
is a divisorial contraction, then
$\varphi $
is a divisorial contraction, then
![]() $\varphi $
is locally analytically equivalent to the
$\varphi $
is locally analytically equivalent to the
![]() $(r_1, r_2, a, 1)$
-blowup of
$(r_1, r_2, a, 1)$
-blowup of
![]() $\mathbb V(x_1 x_2 + g(x_3, x_4)) \subseteq \mathbb C^4$
at
$\mathbb V(x_1 x_2 + g(x_3, x_4)) \subseteq \mathbb C^4$
at
![]() $\boldsymbol {0}$
with variables
$\boldsymbol {0}$
with variables
![]() $x_1, x_2, x_3, x_4$
where
$x_1, x_2, x_3, x_4$
where
-
(1) a divides
 $r_1 + r_2$
and is coprime to both
$r_1 + r_2$
and is coprime to both
 $r_1$
and
$r_1$
and
 $r_2$
,
$r_2$
, -
(2) g has weight
 $r_1 + r_2$
, and
$r_1 + r_2$
, and -
(3) the monomial
 $x_3^{(r_1 + r_2)/a}$
appears in g with nonzero coefficient.
$x_3^{(r_1 + r_2)/a}$
appears in g with nonzero coefficient.
Moreover, any
![]() $\varphi $
which is locally analytically equivalent to a weighted blowup as above is a divisorial contraction, even for
$\varphi $
which is locally analytically equivalent to a weighted blowup as above is a divisorial contraction, even for
![]() $n = 2$
.
$n = 2$
.
Any weighted blowup that is locally analytically equivalent to
![]() $\varphi $
in Theorem 2.21 for
$\varphi $
in Theorem 2.21 for
![]() $n \geq 2$
is called a
$n \geq 2$
is called a
![]() $(r_1, r_2, a, 1)$
-Kawakita blowup, or simply a Kawakita blowup.
$(r_1, r_2, a, 1)$
-Kawakita blowup, or simply a Kawakita blowup.
2.5. Sarkisov links
One of the possible outcomes of the minimal model program is a Mori fiber space.
Definition 2.22. A Mori fiber space is a morphism of normal projective varieties
![]() $\varphi \colon X \to S$
with connected fibers such that
$\varphi \colon X \to S$
with connected fibers such that
-
(1) X is
 $\mathbb Q$
-factorial and has terminal singularities,
$\mathbb Q$
-factorial and has terminal singularities, -
(2) the anti-canonical class
 $-K_X$
is
$-K_X$
is
 $\varphi $
-ample,
$\varphi $
-ample, -
(3)
 $X/S$
has relative Picard number 1, and
$X/S$
has relative Picard number 1, and -
(4)
 $\dim S < \dim X$
.
$\dim S < \dim X$
.
If
![]() $\dim S> 0$
, then we say
$\dim S> 0$
, then we say
![]() $\varphi $
is a strict Mori fiber space.
$\varphi $
is a strict Mori fiber space.
The main examples of Mori fiber spaces we see in this paper are Fano 3-folds that are projective,
![]() $\mathbb Q$
-factorial, with terminal singularities and Picard number 1, considered as a morphism over a point.
$\mathbb Q$
-factorial, with terminal singularities and Picard number 1, considered as a morphism over a point.
Any birational map between two Mori fiber spaces is a composition of Sarkisov links (see [Reference Corti17] or [Reference Hacon and McKernan26]). Below, we describe the two possible types of Sarkisov links starting from a Fano variety.
Definition 2.23. A Sarkisov link of type I (resp. II) between a Fano variety X and a strict Mori fiber space
![]() $Y_k \to Z$
(resp. Fano variety Z) is a diagram of the form
$Y_k \to Z$
(resp. Fano variety Z) is a diagram of the form

where X,
![]() $Y_0$
, …,
$Y_0$
, …,
![]() $Y_k$
, Z are normal, projective, and
$Y_k$
, Z are normal, projective, and
![]() $\mathbb Q$
-factorial, the varieties X,
$\mathbb Q$
-factorial, the varieties X,
![]() $Y_0$
, …,
$Y_0$
, …,
![]() $Y_k$
have terminal singularities, Z has terminal singularities if it three-dimensional, X has Picard number 1,
$Y_k$
have terminal singularities, Z has terminal singularities if it three-dimensional, X has Picard number 1,
![]() $\varphi \colon Y_0 \to X$
is a divisorial contraction,
$\varphi \colon Y_0 \to X$
is a divisorial contraction,
![]() $Y_0 \dashrightarrow \cdots \dashrightarrow Y_k$
is a sequence of anti-flips, flops, and flips, and
$Y_0 \dashrightarrow \cdots \dashrightarrow Y_k$
is a sequence of anti-flips, flops, and flips, and
![]() $\psi \colon Y_k \to Z$
is a strict Mori fiber space (resp. divisorial contraction). If we do not require the varieties
$\psi \colon Y_k \to Z$
is a strict Mori fiber space (resp. divisorial contraction). If we do not require the varieties
![]() $X, Y_0, \ldots Y_k$
(resp.
$X, Y_0, \ldots Y_k$
(resp.
![]() $X, Y_0, \ldots Y_k, Z$
) to be terminal and we do not require
$X, Y_0, \ldots Y_k, Z$
) to be terminal and we do not require
![]() $-K_{Y_0}$
to be
$-K_{Y_0}$
to be
![]() $\varphi $
-ample and we do not require
$\varphi $
-ample and we do not require
![]() $-K_{Y_k}$
to be
$-K_{Y_k}$
to be
![]() $\psi $
-ample but all the other properties hold, then the diagram above is called a 2-ray link [Reference Brown and Zucconi10, Def. 2.1].
$\psi $
-ample but all the other properties hold, then the diagram above is called a 2-ray link [Reference Brown and Zucconi10, Def. 2.1].
Definition 2.24. A Fano 3-fold X that is a Mori fiber space is birationally rigid if for any Mori fiber space
![]() $Y \to S$
such that X and Y are birational, we have that S is a point and X and Y are isomorphic.
$Y \to S$
such that X and Y are birational, we have that S is a point and X and Y are isomorphic.
In Section 5, we show that a general sextic double solid X with a
![]() $cA_n$
singularity with
$cA_n$
singularity with
![]() $n \geq 4$
which is a Mori fiber space is not birationally rigid. We show this by explicitly constructing a Sarkisov link between X and another Mori fiber space. We find the Sarkisov link by restricting from a toric 2-ray link, as described in Construction 2.25.
$n \geq 4$
which is a Mori fiber space is not birationally rigid. We show this by explicitly constructing a Sarkisov link between X and another Mori fiber space. We find the Sarkisov link by restricting from a toric 2-ray link, as described in Construction 2.25.
See [Reference Cox20] for the definition of Cox rings for toric varieties (where it is called the homogeneous coordinate ring) and [Reference Hu and Keel27, Def. 2.6] for the definition of Cox rings for Mori dream spaces. Note that isomorphic varieties can have different Cox rings. By [Reference Cox20, Th. 3.7], closed subschemes of a toric variety T with only cyclic quotient singularities are given by homogeneous ideals in the Cox ring
![]() $\operatorname {Cox} T$
, which is a polynomial ring.
$\operatorname {Cox} T$
, which is a polynomial ring.
Construction 2.25. Let X be a Fano variety embedded in a weighted projective space
![]() $\mathbb P$
, where X is a Mori fiber space, and let
$\mathbb P$
, where X is a Mori fiber space, and let
![]() $Y_0 \to X$
be a divisorial contraction from a projective
$Y_0 \to X$
be a divisorial contraction from a projective
![]() $\mathbb Q$
-factorial variety Y. By [Reference Ahmadinezhad and Kaloghiros2, Lem. 2.9], the divisorial contraction
$\mathbb Q$
-factorial variety Y. By [Reference Ahmadinezhad and Kaloghiros2, Lem. 2.9], the divisorial contraction
![]() $Y_0 \to X$
can be part of a Sarkisov link only if
$Y_0 \to X$
can be part of a Sarkisov link only if
![]() $Y_0$
is a Mori dream space.
$Y_0$
is a Mori dream space.
By [Reference Hu and Keel27, Prop. 2.11], we can embed a Mori dream space
![]() $Y_0$
into a projective toric variety
$Y_0$
into a projective toric variety
![]() $T_0$
with cyclic quotient singularities such that the Mori chambers of
$T_0$
with cyclic quotient singularities such that the Mori chambers of
![]() $Y_0$
are unions of finitely many Mori chambers of
$Y_0$
are unions of finitely many Mori chambers of
![]() $T_0$
. Moreover, we can embed
$T_0$
. Moreover, we can embed
![]() $Y_0$
in such a way that
$Y_0$
in such a way that
![]() $Y_0$
is given by a homogeneous ideal
$Y_0$
is given by a homogeneous ideal
![]() $I_Y$
in
$I_Y$
in
![]() $\operatorname {Cox} T_0$
, and the toric 2-ray link
$\operatorname {Cox} T_0$
, and the toric 2-ray link

restricts to a 2-ray link

where each
![]() $Y_i \subseteq T_i$
is given by the same ideal
$Y_i \subseteq T_i$
is given by the same ideal
![]() $I_Y \subseteq \operatorname {Cox} T_0 = \cdots = \operatorname {Cox} T_r$
, and
$I_Y \subseteq \operatorname {Cox} T_0 = \cdots = \operatorname {Cox} T_r$
, and
![]() $W_i \subseteq \mathcal W_i$
is given by the ideal
$W_i \subseteq \mathcal W_i$
is given by the ideal
![]() $I_Y \cap \mathbb C[\nu _0, \ldots , \nu _s]$
, where
$I_Y \cap \mathbb C[\nu _0, \ldots , \nu _s]$
, where
![]() $\mathcal W_i$
is given by
$\mathcal W_i$
is given by
![]() $\operatorname {Proj} \mathbb C[\nu _0, \ldots , \nu _s]$
for some polynomials
$\operatorname {Proj} \mathbb C[\nu _0, \ldots , \nu _s]$
for some polynomials
![]() $\nu _j \in \operatorname {Cox} T_0$
that depend on i (see [Reference Ahmadinezhad and Zucconi4, Rem. 4]). In this case,
$\nu _j \in \operatorname {Cox} T_0$
that depend on i (see [Reference Ahmadinezhad and Zucconi4, Rem. 4]). In this case,
![]() $\operatorname {Cox}(T_0) / I_Y$
is a Cox ring for
$\operatorname {Cox}(T_0) / I_Y$
is a Cox ring for
![]() $Y_0$
and we say that
$Y_0$
and we say that
![]() $I_Y$
2-ray follows
$I_Y$
2-ray follows
![]() $T_0$
. In contrast to [Reference Ahmadinezhad and Zucconi4, Def. 3.5], we emphasize the ideal
$T_0$
. In contrast to [Reference Ahmadinezhad and Zucconi4, Def. 3.5], we emphasize the ideal
![]() $I_Y$
, since there could be other ideals I satisfying
$I_Y$
, since there could be other ideals I satisfying
![]() $\mathbb V(I_Y) = \mathbb V(I)$
such that the toric 2-ray link restricts to a 2-ray link for
$\mathbb V(I_Y) = \mathbb V(I)$
such that the toric 2-ray link restricts to a 2-ray link for
![]() $I_Y$
but not for I.
$I_Y$
but not for I.
Note that some of the small birational maps
![]() $T_i \dashrightarrow T_{i+1}$
may restrict to isomorphisms
$T_i \dashrightarrow T_{i+1}$
may restrict to isomorphisms
![]() $Y_i \to Y_{i+1}$
. If all the varieties
$Y_i \to Y_{i+1}$
. If all the varieties
![]() $Y_i$
are terminal and the anti-canonical divisor
$Y_i$
are terminal and the anti-canonical divisor
![]() $-K_{Y_0}$
of
$-K_{Y_0}$
of
![]() $Y_0$
is inside the interior
$Y_0$
is inside the interior
![]() $\operatorname {int} (\operatorname {Mov} Y_0)$
of the movable cone, then the 2-ray link for
$\operatorname {int} (\operatorname {Mov} Y_0)$
of the movable cone, then the 2-ray link for
![]() $Y_0$
is a Sarkisov link (see [Reference Ahmadinezhad and Kaloghiros2, Lem. 2.9]), otherwise it is called a bad link.
$Y_0$
is a Sarkisov link (see [Reference Ahmadinezhad and Kaloghiros2, Lem. 2.9]), otherwise it is called a bad link.
In Section 5, where X is a sextic double solid and the center of
![]() $Y_0 \to X$
is a
$Y_0 \to X$
is a
![]() $cA_n$
point, we use a projective version of Corollary 4.10 to construct the divisorial contraction
$cA_n$
point, we use a projective version of Corollary 4.10 to construct the divisorial contraction
![]() $Y_0 \to X$
, which is the restriction of a toric weighted blowup
$Y_0 \to X$
, which is the restriction of a toric weighted blowup
![]() $\bar T_0 \to \mathbb P$
. This gives us an embedding
$\bar T_0 \to \mathbb P$
. This gives us an embedding
![]() $Y_0 \to \mathbb V(I_{\bar Y}) \subseteq \bar T_0$
where
$Y_0 \to \mathbb V(I_{\bar Y}) \subseteq \bar T_0$
where
![]() $I_{\bar Y}$
might not 2-ray follow
$I_{\bar Y}$
might not 2-ray follow
![]() $\bar T_0$
. We use unprojection to modify
$\bar T_0$
. We use unprojection to modify
![]() $\bar T_0$
to find an embedding
$\bar T_0$
to find an embedding
![]() $Y_0 \to \mathbb V(I_Y) \subseteq T_0$
such that
$Y_0 \to \mathbb V(I_Y) \subseteq T_0$
such that
![]() $I_Y$
2-ray follows
$I_Y$
2-ray follows
![]() $T_0$
. See [Reference Reid49, §2.1] for a simple example of unprojection, and §§5.2, 5.5, 5.6, and 5.8 for applications of unprojection.
$T_0$
. See [Reference Reid49, §2.1] for a simple example of unprojection, and §§5.2, 5.5, 5.6, and 5.8 for applications of unprojection.
To explain the notation we use for 2-ray links, we do an example in detail, namely the 2-ray link for the ambient space of the sextic double solid with a
![]() $cA_4$
singularity in Section 5.2.
$cA_4$
singularity in Section 5.2.
Example 2.26 (2-ray link for
 $\mathbb P(1, 1, 1, 1, 3, 5)$
)
$\mathbb P(1, 1, 1, 1, 3, 5)$
)
Denote the variables on
![]() $\mathbb P(1, 1, 1, 1, 3, 5)$
by
$\mathbb P(1, 1, 1, 1, 3, 5)$
by
![]() $x, y, z, t, \alpha , \xi $
. We perform the weighted blowup
$x, y, z, t, \alpha , \xi $
. We perform the weighted blowup
![]() $T_0 \to \mathbb P(1, 1, 1, 1, 3, 5)$
with weights
$T_0 \to \mathbb P(1, 1, 1, 1, 3, 5)$
with weights
![]() $(1, 1, 2, 3, 6)$
for variables
$(1, 1, 2, 3, 6)$
for variables
![]() $y, z, t, \alpha , \xi $
, where the center is the point
$y, z, t, \alpha , \xi $
, where the center is the point
![]() $P_x = [1, 0, 0, 0, 0, 0]$
.
$P_x = [1, 0, 0, 0, 0, 0]$
.
We define
![]() $T_0$
as a geometric quotient. By a slight abuse of notation, we denote the variables on
$T_0$
as a geometric quotient. By a slight abuse of notation, we denote the variables on
![]() $\mathbb C^7$
by
$\mathbb C^7$
by
![]() $u, x, y, z, \alpha , \xi , t$
, repeating the symbols for
$u, x, y, z, \alpha , \xi , t$
, repeating the symbols for
![]() $\mathbb P(1, 1, 1, 1, 3, 5)$
. Define a
$\mathbb P(1, 1, 1, 1, 3, 5)$
. Define a
![]() $(\mathbb C^*)^2$
-action on
$(\mathbb C^*)^2$
-action on
![]() $\mathbb C^7$
for all
$\mathbb C^7$
for all
![]() $(\lambda , \mu ) \in (\mathbb C^*)^2$
by
$(\lambda , \mu ) \in (\mathbb C^*)^2$
by
Define the irrelevant ideal
![]() $I_0 = (u, x) \cap (y, z, \alpha , \xi , t)$
, and define
$I_0 = (u, x) \cap (y, z, \alpha , \xi , t)$
, and define
![]() $T_0$
by the geometric quotient
$T_0$
by the geometric quotient
![]() $\mathbb C^7 \setminus \mathbb V(I_0) / (\mathbb C^*)^2$
. We use the notation
$\mathbb C^7 \setminus \mathbb V(I_0) / (\mathbb C^*)^2$
. We use the notation

to describe this construction of
![]() $T_0$
. Note that we order the variables
$T_0$
. Note that we order the variables
![]() $u, x, \ldots , t$
such that the corresponding rays
$u, x, \ldots , t$
such that the corresponding rays
![]() $\left (\begin {smallmatrix}0\\-1\end {smallmatrix}\right )$
,
$\left (\begin {smallmatrix}0\\-1\end {smallmatrix}\right )$
,
![]() ${\left (\begin {smallmatrix}1\\0\end {smallmatrix}\right )}$
, …,
${\left (\begin {smallmatrix}1\\0\end {smallmatrix}\right )}$
, …,
![]() ${\left (\begin {smallmatrix}1\\2\end {smallmatrix}\right )}$
are ordered anticlockwise around the origin. The vertical bar indicates that the irrelevant ideal is
${\left (\begin {smallmatrix}1\\2\end {smallmatrix}\right )}$
are ordered anticlockwise around the origin. The vertical bar indicates that the irrelevant ideal is
![]() $(u, x) \cap (y, z, \alpha , \xi , t)$
. The Cox ring of
$(u, x) \cap (y, z, \alpha , \xi , t)$
. The Cox ring of
![]() $T_0$
is given by
$T_0$
is given by
![]() $\operatorname {Cox} T_0 = \mathbb C[u, x, y, z, \alpha , \xi , t]$
. The weighted blowup
$\operatorname {Cox} T_0 = \mathbb C[u, x, y, z, \alpha , \xi , t]$
. The weighted blowup
![]() $T_0 \to \mathbb P(1, 1, 1, 1, 3, 5)$
is given by
$T_0 \to \mathbb P(1, 1, 1, 1, 3, 5)$
is given by
We describe the cones of the toric variety
![]() $T_0$
(Figure 1). By [Reference Hu and Keel27],
$T_0$
(Figure 1). By [Reference Hu and Keel27],
![]() $T_0$
is a Mori dream space. The Picard group of
$T_0$
is a Mori dream space. The Picard group of
![]() $T_0$
is generated by
$T_0$
is generated by
![]() $\mathbb V(u)$
, the reduced exceptional divisor, and
$\mathbb V(u)$
, the reduced exceptional divisor, and
![]() $\mathbb V(x)$
, the strict transform of a plane not passing through
$\mathbb V(x)$
, the strict transform of a plane not passing through
![]() $P_x$
, which have bidegree
$P_x$
, which have bidegree
![]() ${\left (\begin {smallmatrix}0\\-1\end {smallmatrix}\right )}$
and
${\left (\begin {smallmatrix}0\\-1\end {smallmatrix}\right )}$
and
![]() ${\left (\begin {smallmatrix}1\\0\end {smallmatrix}\right )}$
, respectively. The variety
${\left (\begin {smallmatrix}1\\0\end {smallmatrix}\right )}$
, respectively. The variety
![]() $T_0$
is
$T_0$
is
![]() $\mathbb Q$
-factorial, and any two divisors with the same bidegree are linearly equivalent. As in [Reference Brown and Zucconi10, §4.1.3], the effective cone
$\mathbb Q$
-factorial, and any two divisors with the same bidegree are linearly equivalent. As in [Reference Brown and Zucconi10, §4.1.3], the effective cone
![]() $\operatorname {Eff}(T_0)$
is given by
$\operatorname {Eff}(T_0)$
is given by
![]() $\langle \mathbb V(u), \mathbb V(x)\rangle $
, a cone in the group
$\langle \mathbb V(u), \mathbb V(x)\rangle $
, a cone in the group
![]() $N^1(T_0)$
of divisors of
$N^1(T_0)$
of divisors of
![]() $T_0$
up to numerical equivalence with coefficients in
$T_0$
up to numerical equivalence with coefficients in
![]() $\mathbb R$
. As in [Reference Ahmadinezhad and Zucconi4, §3.2], the movable cone
$\mathbb R$
. As in [Reference Ahmadinezhad and Zucconi4, §3.2], the movable cone
![]() $\operatorname {Mov(T_0)}$
is
$\operatorname {Mov(T_0)}$
is
![]() $\langle \mathbb V(x), \mathbb V(\xi )\rangle $
, and it is divided into the nef cone
$\langle \mathbb V(x), \mathbb V(\xi )\rangle $
, and it is divided into the nef cone
![]() $\operatorname {Nef}(T_0) = \langle \mathbb V(x), \mathbb V(y)\rangle $
of
$\operatorname {Nef}(T_0) = \langle \mathbb V(x), \mathbb V(y)\rangle $
of
![]() $T_0$
and
$T_0$
and
![]() $\langle \mathbb V(y), \mathbb V(\xi )\rangle $
, which is the pullback of the nef cone of the small
$\langle \mathbb V(y), \mathbb V(\xi )\rangle $
, which is the pullback of the nef cone of the small
![]() $\mathbb Q$
-factorial modification
$\mathbb Q$
-factorial modification
![]() $T_1$
of
$T_1$
of
![]() $T_0$
. The cones
$T_0$
. The cones
![]() $\langle \mathbb V(x), \mathbb V(y)\rangle $
and
$\langle \mathbb V(x), \mathbb V(y)\rangle $
and
![]() $\langle \mathbb V(y), \mathbb V(\xi )\rangle $
are called Mori chambers. The variety
$\langle \mathbb V(y), \mathbb V(\xi )\rangle $
are called Mori chambers. The variety
![]() $T_1$
is defined by
$T_1$
is defined by

Here,
![]() $T_1$
is the geometric quotient
$T_1$
is the geometric quotient
![]() $(\mathbb C^7 \setminus I_1) / (\mathbb C^*)^2$
, where the irrelevant ideal
$(\mathbb C^7 \setminus I_1) / (\mathbb C^*)^2$
, where the irrelevant ideal
![]() $I_1$
is given by
$I_1$
is given by
![]() $(u, x, y, z, \alpha ) \cap (\xi , t)$
, which is indicated by the position of the vertical bar in the action matrix. The Cox ring of
$(u, x, y, z, \alpha ) \cap (\xi , t)$
, which is indicated by the position of the vertical bar in the action matrix. The Cox ring of
![]() $T_1$
is equal to the Cox ring of
$T_1$
is equal to the Cox ring of
![]() $T_0$
, namely
$T_0$
, namely
![]() $\operatorname {Cox} T_1 = \mathbb C[u, x, y, z, \alpha , \xi , t]$
.
$\operatorname {Cox} T_1 = \mathbb C[u, x, y, z, \alpha , \xi , t]$
.

Figure 1 Cones of
![]() $T_0$
.
$T_0$
.
The weighted blowup morphism
![]() $T_0 \to \mathbb P(1, 1, 1, 1, 3, 5)$
can be read off from the action-matrix of
$T_0 \to \mathbb P(1, 1, 1, 1, 3, 5)$
can be read off from the action-matrix of
![]() $T_0$
. Consider the ray given by
$T_0$
. Consider the ray given by
![]() $\mathbb V(x)$
in
$\mathbb V(x)$
in
![]() $N^1(T_0)$
. The union of the linear systems
$N^1(T_0)$
. The union of the linear systems
![]() ${\left \lvert \left (\begin {smallmatrix}n\\0\end {smallmatrix}\right ) \right \rvert }$
where
${\left \lvert \left (\begin {smallmatrix}n\\0\end {smallmatrix}\right ) \right \rvert }$
where
![]() $n \geq 0$
has a
$n \geq 0$
has a
![]() $\mathbb C$
-algebra basis
$\mathbb C$
-algebra basis
![]() $x, uy, uz, u^2t, u^3\alpha , u^6\xi $
. So, the ample model (see [Reference Birkar, Cascini, Hacon and McKernan7, Def. 3.6.5]) of the divisor class
$x, uy, uz, u^2t, u^3\alpha , u^6\xi $
. So, the ample model (see [Reference Birkar, Cascini, Hacon and McKernan7, Def. 3.6.5]) of the divisor class
![]() $\mathbb V(x)$
is the morphism
$\mathbb V(x)$
is the morphism
 $$\begin{align*}T_0 \to \operatorname{Proj} \bigoplus_{n \geq 0} H^0(T_0, \mathcal O_{T_0}(n {\left(\begin{smallmatrix}1\\0\end{smallmatrix}\right)})) = \operatorname{Proj} \mathbb C[x, uy, uz, u^2t, u^3\alpha, u^6\xi] = \mathbb P(1, 1, 1, 1, 3, 5) \end{align*}$$
$$\begin{align*}T_0 \to \operatorname{Proj} \bigoplus_{n \geq 0} H^0(T_0, \mathcal O_{T_0}(n {\left(\begin{smallmatrix}1\\0\end{smallmatrix}\right)})) = \operatorname{Proj} \mathbb C[x, uy, uz, u^2t, u^3\alpha, u^6\xi] = \mathbb P(1, 1, 1, 1, 3, 5) \end{align*}$$
given by
which is precisely the weighted blowup
![]() $T_0 \to \mathbb P(1, 1, 1, 1, 3, 5)$
given in Equation (2.1).
$T_0 \to \mathbb P(1, 1, 1, 1, 3, 5)$
given in Equation (2.1).
As in [Reference Brown and Zucconi10, §2.1], there are two projective morphisms of relative Picard number 1 from
![]() $T_0$
up to isomorphisms, corresponding to the ample models of divisors in the two edges of the nef cone of
$T_0$
up to isomorphisms, corresponding to the ample models of divisors in the two edges of the nef cone of
![]() $T_0$
. The ample model of any divisor in the interior of the nef cone of
$T_0$
. The ample model of any divisor in the interior of the nef cone of
![]() $T_0$
gives an embedding of
$T_0$
gives an embedding of
![]() $T_0$
into a weighted projective space. The ample model of
$T_0$
into a weighted projective space. The ample model of
![]() $\mathbb V(y) \in N^1(T_0)$
is given by
$\mathbb V(y) \in N^1(T_0)$
is given by
 $$\begin{align*}\begin{aligned} T_0 & \to \operatorname{Proj} \mathbb C[y, z, \alpha, u\xi, ut, x\xi, xt] \subseteq \mathbb P(1, 1, 3, 5, 1, 6, 2)\\ [u, x, y, z, \alpha, \xi, t] & \mapsto [y, z, \alpha, u\xi, ut, x\xi, xt]. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} T_0 & \to \operatorname{Proj} \mathbb C[y, z, \alpha, u\xi, ut, x\xi, xt] \subseteq \mathbb P(1, 1, 3, 5, 1, 6, 2)\\ [u, x, y, z, \alpha, \xi, t] & \mapsto [y, z, \alpha, u\xi, ut, x\xi, xt]. \end{aligned} \end{align*}$$
Denoting
![]() $\mathcal W_0 = \operatorname {Proj} \mathbb C[y, z, \alpha , u\xi , ut, x\xi , xt]$
, we see that the morphism
$\mathcal W_0 = \operatorname {Proj} \mathbb C[y, z, \alpha , u\xi , ut, x\xi , xt]$
, we see that the morphism
![]() $T_0 \to \mathcal W_0$
contracts
$T_0 \to \mathcal W_0$
contracts
![]() $\mathbb V(\xi , t)$
to the surface
$\mathbb V(\xi , t)$
to the surface
![]() $\mathbb P(1, 1, 3) \subseteq \mathcal W_0$
and is an isomorphism elsewhere. The ample model of
$\mathbb P(1, 1, 3) \subseteq \mathcal W_0$
and is an isomorphism elsewhere. The ample model of
![]() $\mathbb V(y) \in N^1(T_1)$
is given similarly by
$\mathbb V(y) \in N^1(T_1)$
is given similarly by
contracting
![]() $\mathbb V(u, x)$
to
$\mathbb V(u, x)$
to
![]() $\mathbb P(1, 1, 3)$
. This induces a birational map
$\mathbb P(1, 1, 3)$
. This induces a birational map
![]() $T_0 \dashrightarrow T_1$
, a small
$T_0 \dashrightarrow T_1$
, a small
![]() $\mathbb Q$
-factorial modification, given by
$\mathbb Q$
-factorial modification, given by
Note that this is the identity map on the affine space
![]() $\mathbb A^7$
, but it is not an isomorphism between
$\mathbb A^7$
, but it is not an isomorphism between
![]() $T_0$
and
$T_0$
and
![]() $T_1$
since the irrelevant ideals are different. The diagram
$T_1$
since the irrelevant ideals are different. The diagram
![]() $T_0 \to \mathcal W_0 \gets T_1$
is a flop.
$T_0 \to \mathcal W_0 \gets T_1$
is a flop.
Note that multiplying the action matrix of
![]() $T_0$
or
$T_0$
or
![]() $T_1$
with a matrix in
$T_1$
with a matrix in
![]() $\operatorname {GL}(2, \mathbb Q)$
is equivalent to choosing a different basis for the group
$\operatorname {GL}(2, \mathbb Q)$
is equivalent to choosing a different basis for the group
![]() $(\mathbb C^*)^2$
, so the geometric quotients
$(\mathbb C^*)^2$
, so the geometric quotients
![]() $T_0$
and
$T_0$
and
![]() $T_1$
stay the same (see [Reference Ahmadinezhad1, Lem. 2.4]). If we multiply with a matrix with negative determinant, then we change the order of the rays in
$T_1$
stay the same (see [Reference Ahmadinezhad1, Lem. 2.4]). If we multiply with a matrix with negative determinant, then we change the order of the rays in
![]() $N^1(T_0)$
from anticlockwise to clockwise.
$N^1(T_0)$
from anticlockwise to clockwise.
Similarly, there are only two projective morphisms of relative Picard number 1 from
![]() $T_1$
: the contraction
$T_1$
: the contraction
![]() $T_1 \to \mathcal W_0$
and the ample model of
$T_1 \to \mathcal W_0$
and the ample model of
![]() $\mathbb V(\xi )$
. We multiply the action matrix of
$\mathbb V(\xi )$
. We multiply the action matrix of
![]() $T_1$
by the matrix
$T_1$
by the matrix
![]() ${\left (\begin {smallmatrix}6 & -5\\2 & -1\end {smallmatrix}\right )}$
with determinant
${\left (\begin {smallmatrix}6 & -5\\2 & -1\end {smallmatrix}\right )}$
with determinant
![]() $4$
to find
$4$
to find

The ample model of
![]() $\mathbb V(\xi )$
is given by
$\mathbb V(\xi )$
is given by
 $$\begin{align*}\begin{aligned} T_1 & \to \mathbb P(1, 1, 1, 2, 3, 4)\\ [u, x, y, z, \alpha, \xi, t] & \mapsto \left[ t^{\frac54} u, t^{\frac14} y, t^{\frac14} z, t^{\frac32} x, t^{\frac34} \alpha, \xi \right]. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} T_1 & \to \mathbb P(1, 1, 1, 2, 3, 4)\\ [u, x, y, z, \alpha, \xi, t] & \mapsto \left[ t^{\frac54} u, t^{\frac14} y, t^{\frac14} z, t^{\frac32} x, t^{\frac34} \alpha, \xi \right]. \end{aligned} \end{align*}$$
Note that this is a morphism of varieties despite having fractional powers (see [Reference Brown and Buczyński9]).
The 2-ray link that we have found for
![]() $\mathbb P(1, 1, 1, 1, 3, 5)$
is summarized by the diagram below.
$\mathbb P(1, 1, 1, 1, 3, 5)$
is summarized by the diagram below.

For more examples on toric 2-ray links, see [Reference Brown and Zucconi10, §4].
3. Constructing sextic double solids with a
 $cA_n$
singularity
$cA_n$
singularity
In this section, we give a bound
![]() $n \leq 8$
for an isolated
$n \leq 8$
for an isolated
![]() $cA_n$
singularity on a sextic double solid, and we explicitly describe all sextic double solids that contain an isolated
$cA_n$
singularity on a sextic double solid, and we explicitly describe all sextic double solids that contain an isolated
![]() $cA_n$
singularity where
$cA_n$
singularity where
![]() $n \leq 8$
. The main tool we use for this is the splitting lemma from singularity theory, first introduced in [Reference Thom50], which is used for separating the quadratic terms and the higher-order terms of a power series.
$n \leq 8$
. The main tool we use for this is the splitting lemma from singularity theory, first introduced in [Reference Thom50], which is used for separating the quadratic terms and the higher-order terms of a power series.
3.1. Splitting lemma from singularity theory
The splitting lemma below is taken from [Reference Greuel, Lossen and Shustin25, Th. 2.47], with a slight modification in notation. Specifically, we write
![]() $v(x+p)$
instead of
$v(x+p)$
instead of
![]() $x + g$
, where v is a unit in the power series ring and p does not depend on x, as we use this form in Section 5 for constructing birational models.
$x + g$
, where v is a unit in the power series ring and p does not depend on x, as we use this form in Section 5 for constructing birational models.
Theorem 3.1 (Splitting lemma)
Let m be a positive integer, and let
![]() $\boldsymbol {y}$
denote variables
$\boldsymbol {y}$
denote variables
![]() $(y_1, \ldots , y_m)$
. Let
$(y_1, \ldots , y_m)$
. Let
![]() $f \in \mathbb C\{x, \boldsymbol {y}\}$
be a convergent power series of multiplicity 2, with degree two part of the form
$f \in \mathbb C\{x, \boldsymbol {y}\}$
be a convergent power series of multiplicity 2, with degree two part of the form
![]() $x^2 + \textit {(terms in }\boldsymbol {y})$
. Then, there exist unique
$x^2 + \textit {(terms in }\boldsymbol {y})$
. Then, there exist unique
![]() $v \in \mathbb C[[x, \boldsymbol {y}]]$
and
$v \in \mathbb C[[x, \boldsymbol {y}]]$
and
![]() $p, h \in \mathbb C[[\boldsymbol {y}]]$
, where v is a unit and the multiplicity of p is at least 2, such that
$p, h \in \mathbb C[[\boldsymbol {y}]]$
, where v is a unit and the multiplicity of p is at least 2, such that
Moreover, the power series
![]() $h, p$
, and v are absolutely convergent around the origin, and the multiplicity of h is at least 2. It follows immediately that f is right equivalent to
$h, p$
, and v are absolutely convergent around the origin, and the multiplicity of h is at least 2. It follows immediately that f is right equivalent to
![]() $x^2 + h$
.
$x^2 + h$
.
Proof. It is proved in [Reference Greuel, Lossen and Shustin25, Th. 2.47] that there exist unique
![]() $g \in \mathbb C[[x, \boldsymbol {y}]]$
and
$g \in \mathbb C[[x, \boldsymbol {y}]]$
and
![]() $h \in \mathbb C[[\boldsymbol {y}]]$
, where the multiplicity of g is at least 2, such that
$h \in \mathbb C[[\boldsymbol {y}]]$
, where the multiplicity of g is at least 2, such that
![]() $f = (x + g)^2 + h$
. Moreover, it is proved that the power series g and h are absolutely convergent around the origin, and the multiplicity of h is at least 2.
$f = (x + g)^2 + h$
. Moreover, it is proved that the power series g and h are absolutely convergent around the origin, and the multiplicity of h is at least 2.
By the Weierstrass preparation theorem (see [Reference Greuel, Lossen and Shustin25, Th. 1.6]), there exist a unique unit
![]() $v \in \mathbb C\{x, \boldsymbol {y}\}$
and a unique
$v \in \mathbb C\{x, \boldsymbol {y}\}$
and a unique
![]() $p \in \mathbb C\{\boldsymbol {y}\}$
such that
$p \in \mathbb C\{\boldsymbol {y}\}$
such that
![]() $x + g = v(x + p)$
.
$x + g = v(x + p)$
.
Below, we give explicit recurrent formulas for
![]() $g, h, p, v$
of the splitting lemma in terms of the coefficients of f.
$g, h, p, v$
of the splitting lemma in terms of the coefficients of f.
Proposition 3.2 (Explicit splitting lemma)
Below, we use the same notation as in the splitting lemma Theorem 3.1 and its proof. Denote
 $$\begin{align*}f = \sum_{i, d \geq 0} x^i f_{i, d}, \qquad g = \sum_{i, d \geq 0} x^i g_{i, d}, \qquad h = \sum_{d \geq 0} h_{d}, \qquad p = \sum_{d \geq 0} p_{d}, \qquad v = \sum_{i, d \geq 0} x^i v_{i, d}, \end{align*}$$
$$\begin{align*}f = \sum_{i, d \geq 0} x^i f_{i, d}, \qquad g = \sum_{i, d \geq 0} x^i g_{i, d}, \qquad h = \sum_{d \geq 0} h_{d}, \qquad p = \sum_{d \geq 0} p_{d}, \qquad v = \sum_{i, d \geq 0} x^i v_{i, d}, \end{align*}$$
where
![]() $f_{i, d}, g_{i, d}, h_d, p_d, v_{i, d} \in \mathbb C[\boldsymbol {y}]$
are homogeneous of degree d. Then,
$f_{i, d}, g_{i, d}, h_d, p_d, v_{i, d} \in \mathbb C[\boldsymbol {y}]$
are homogeneous of degree d. Then,
 $$ \begin{align} g_{1, 0} & = 0, \nonumber \\g_{i, d} & = \frac{1}{2} \left(f_{i+1, d} - \sum_{k=0}^{d} \sum_{j = \max(0, 2-k)}^{\min(i+1, i+d-k-1)} g_{j, k} g_{i+1-j, d-k} \right), \quad \text{if }(i, d) \neq (1, 0), \end{align} $$
$$ \begin{align} g_{1, 0} & = 0, \nonumber \\g_{i, d} & = \frac{1}{2} \left(f_{i+1, d} - \sum_{k=0}^{d} \sum_{j = \max(0, 2-k)}^{\min(i+1, i+d-k-1)} g_{j, k} g_{i+1-j, d-k} \right), \quad \text{if }(i, d) \neq (1, 0), \end{align} $$
 $$ \begin{align} h_{d} & = f_{0, d} - \sum_{j=2}^{d-2} g_{0, j} g_{0, d-j}, \end{align} $$
$$ \begin{align} h_{d} & = f_{0, d} - \sum_{j=2}^{d-2} g_{0, j} g_{0, d-j}, \end{align} $$
 $$ \begin{align} p_d & = g_{0, d} - \sum_{j=2}^{d-1} v_{0, d-j} p_j, \end{align} $$
$$ \begin{align} p_d & = g_{0, d} - \sum_{j=2}^{d-1} v_{0, d-j} p_j, \end{align} $$
 $$ \begin{align} v_{0, 0} & = 1, \nonumber\\ v_{i, d} & = g_{i+1, d} - \sum_{j=2}^{d} \left( v_{i+1, d-j} p_j \right), \quad \text{if }(i, d) \neq (0, 0). \end{align} $$
$$ \begin{align} v_{0, 0} & = 1, \nonumber\\ v_{i, d} & = g_{i+1, d} - \sum_{j=2}^{d} \left( v_{i+1, d-j} p_j \right), \quad \text{if }(i, d) \neq (0, 0). \end{align} $$
Proof. Taking the degree d part of the coefficient of
![]() $x^{i+1}$
in
$x^{i+1}$
in
![]() $f = (x + g)^2 + h$
where
$f = (x + g)^2 + h$
where
![]() $i \geq 0$
, we find Equation (3.1). Taking all degree d terms of
$i \geq 0$
, we find Equation (3.1). Taking all degree d terms of
![]() $f = (x + g)^2 + h$
that are not divisible by x, we find Equation (3.2). Taking the degree d part of the coefficient of
$f = (x + g)^2 + h$
that are not divisible by x, we find Equation (3.2). Taking the degree d part of the coefficient of
![]() $x^{i+1}$
in
$x^{i+1}$
in
![]() $x + g = v(x + p)$
where
$x + g = v(x + p)$
where
![]() $i \geq 0$
, we find Equation (3.4), and taking all degree d terms not divisible by x, we find Equation (3.3).
$i \geq 0$
, we find Equation (3.4), and taking all degree d terms not divisible by x, we find Equation (3.3).
Example 3.3. Using the notation of Proposition 3.2, the first few homogeneous parts of h are given in terms of coefficients of f by
 $$ \begin{align*} h_2 & = f_{0, 2},\\ h_3 & = f_{0, 3},\\ h_4 & = f_{0, 4} - \frac{f_{1, 2}^2}{4},\\ h_5 & = f_{0, 5} - \frac{f_{1, 2}^2 f_{2, 1}}{4} - \frac{f_{1, 2} f_{1, 3}}{2},\\ h_6 & = f_{0, 6} - \frac{f_{1, 2}^3 f_{3, 0}}{8} + \frac{f_{1, 2}^2 f_{2, 2}}{4} - \frac{f_{1, 2}^2 f_{2, 1}^2}{4} + \frac{f_{1, 2} f_{1, 3} f_{2, 1}}{2} - \frac{f_{1, 2} f_{1, 4}}{2} - \frac{f_{1, 3}^2}{4}. \end{align*} $$
$$ \begin{align*} h_2 & = f_{0, 2},\\ h_3 & = f_{0, 3},\\ h_4 & = f_{0, 4} - \frac{f_{1, 2}^2}{4},\\ h_5 & = f_{0, 5} - \frac{f_{1, 2}^2 f_{2, 1}}{4} - \frac{f_{1, 2} f_{1, 3}}{2},\\ h_6 & = f_{0, 6} - \frac{f_{1, 2}^3 f_{3, 0}}{8} + \frac{f_{1, 2}^2 f_{2, 2}}{4} - \frac{f_{1, 2}^2 f_{2, 1}^2}{4} + \frac{f_{1, 2} f_{1, 3} f_{2, 1}}{2} - \frac{f_{1, 2} f_{1, 4}}{2} - \frac{f_{1, 3}^2}{4}. \end{align*} $$
3.2. Parameter spaces of sextic double solids
We apply the explicit splitting lemma (Proposition 3.2) to describe the equation of a sextic double solid
![]() $X \subseteq \mathbb P(1, 1, 1, 1, 3)$
that has a singular point at
$X \subseteq \mathbb P(1, 1, 1, 1, 3)$
that has a singular point at
![]() $P_x = [1, 0, 0, 0, 0]$
.
$P_x = [1, 0, 0, 0, 0]$
.
Notation 3.4. Let X be the subscheme of
![]() $\mathbb P(1, 1, 1, 1, 3)$
, with variables
$\mathbb P(1, 1, 1, 1, 3)$
, with variables
![]() $x, y, z, t, w$
, defined by f, where
$x, y, z, t, w$
, defined by f, where
 $$ \begin{align} \begin{aligned} f & = -w^2 + x^4 (t^2 + Q_2) \\ &\quad + x^3(4t^3a_0 + 4t^2a_1 + 2ta_2 + a_3) \\ &\quad + x^2(2t^4b_0 + 2t^3b_1 + 2t^2b_2 + 2tb_3 + b_4) \\ &\quad + x(2t^5c_0 + 2t^4c_1 + 2t^3c_2 + 2t^2c_3 + 2tc_4 + c_5) \\ &\quad + t^6d_0 + 2t^5d_1 + t^4d_2 + 2t^3d_3 + t^2d_4 + 2td_5 + d_6, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} f & = -w^2 + x^4 (t^2 + Q_2) \\ &\quad + x^3(4t^3a_0 + 4t^2a_1 + 2ta_2 + a_3) \\ &\quad + x^2(2t^4b_0 + 2t^3b_1 + 2t^2b_2 + 2tb_3 + b_4) \\ &\quad + x(2t^5c_0 + 2t^4c_1 + 2t^3c_2 + 2t^2c_3 + 2tc_4 + c_5) \\ &\quad + t^6d_0 + 2t^5d_1 + t^4d_2 + 2t^3d_3 + t^2d_4 + 2td_5 + d_6, \end{aligned} \end{align} $$
where the polynomials
![]() $a_j, b_j, c_j, d_j \in \mathbb C[y, z]$
and
$a_j, b_j, c_j, d_j \in \mathbb C[y, z]$
and
![]() $Q_j \in \mathbb C[y, z, t]$
are homogeneous of degree j.
$Q_j \in \mathbb C[y, z, t]$
are homogeneous of degree j.
We define the following
![]() $11$
technical conditions, where
$11$
technical conditions, where
![]() $i \in \{1, 2, 3, 4\}$
:
$i \in \{1, 2, 3, 4\}$
:
-
(1) (This condition is always true).
-
(2)
 $Q_2 = 0$
.
$Q_2 = 0$
. -
(3) Condition (2) holds and
 $a_3 = 0$
.
$a_3 = 0$
. -
(4) Condition (3) holds and
 $b_4 = a_2^2$
.
$b_4 = a_2^2$
. -
(5) Condition (4) holds and
 $c_5 = 2a_2b_3 - 4a_1a_2^2$
.
$c_5 = 2a_2b_3 - 4a_1a_2^2$
. -
(6) Condition (5) holds and
 $d_6 = 2a_2c_4 + b_3^2 - 8a_1a_2b_3 - 2a_2^2b_2 + 4a_0a_2^3 + 16a_1^2a_2^2$
.
$d_6 = 2a_2c_4 + b_3^2 - 8a_1a_2b_3 - 2a_2^2b_2 + 4a_0a_2^3 + 16a_1^2a_2^2$
. -
(7.i) Condition (6) holds and there exist polynomials
 $q, r, s, e \in \mathbb C[y, z]$
that are, respectively, homogeneous of degrees
$q, r, s, e \in \mathbb C[y, z]$
that are, respectively, homogeneous of degrees
 $i-1$
,
$i-1$
,
 $3-i$
,
$3-i$
,
 $4-i$
,
$4-i$
,
 $i+1$
, where
$i+1$
, where
 $0$
is considered to be the only polynomial homogeneous of degree
$0$
is considered to be the only polynomial homogeneous of degree
 $-1$
, such that
$-1$
, such that  $$\begin{align*}\begin{aligned} a_2 & = qr,\\ b_3 & = qs + 4a_1qr,\\ c_4 & = 2a_1qs - 6a_0q^2r^2 + 8a_1^2qr + er,\\ d_5 & = 2b_2qs - 8a_1^2qs - es - b_1q^2r^2 + c_3qr. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} a_2 & = qr,\\ b_3 & = qs + 4a_1qr,\\ c_4 & = 2a_1qs - 6a_0q^2r^2 + 8a_1^2qr + er,\\ d_5 & = 2b_2qs - 8a_1^2qs - es - b_1q^2r^2 + c_3qr. \end{aligned} \end{align*}$$
-
(8) Condition (7.1) holds and there exist a constant
 $A_0 \in \mathbb C$
and a polynomial
$A_0 \in \mathbb C$
and a polynomial
 $B_1 \in \mathbb C[y, z]$
homogeneous of degree
$B_1 \in \mathbb C[y, z]$
homogeneous of degree
 $1$
such that
$1$
such that  $$\begin{align*}\begin{aligned} e_2 & = 4A_0r_2 + b_2 - 6a_1^2,\\ c_3 & = 6a_0s_3 - 4A_0s_3 + 4a_0a_1r_2 - 8A_0a_1r_2 + B_1r_2 + 2a_1b_2 - 4a_1^3,\\ d_4 & = -2s_3B_1 + 16r_2^2A_0^2 - 8b_2r_2A_0 + 16a_1^2r_2A_0 + 4b_1s_3\\ &\quad - 8a_0a_1s_3 - 2b_0r_2^2 + 2c_2r_2 + b_2^2 - 4a_1^2b_2 + 4a_1^4. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} e_2 & = 4A_0r_2 + b_2 - 6a_1^2,\\ c_3 & = 6a_0s_3 - 4A_0s_3 + 4a_0a_1r_2 - 8A_0a_1r_2 + B_1r_2 + 2a_1b_2 - 4a_1^3,\\ d_4 & = -2s_3B_1 + 16r_2^2A_0^2 - 8b_2r_2A_0 + 16a_1^2r_2A_0 + 4b_1s_3\\ &\quad - 8a_0a_1s_3 - 2b_0r_2^2 + 2c_2r_2 + b_2^2 - 4a_1^2b_2 + 4a_1^4. \end{aligned} \end{align*}$$
Note that zero is homogeneous of every nonnegative degree, so, for example, in Condition (7.1), the term e can be zero.
Next, define the set of
![]() $11$
rational indices
$11$
rational indices
Let
![]() $\lfloor k\rfloor $
denote the greatest integer not greater than k. For every
$\lfloor k\rfloor $
denote the greatest integer not greater than k. For every
![]() $k \in \mathrm {Inds}$
, let
$k \in \mathrm {Inds}$
, let
![]() $R_k$
denote the
$R_k$
denote the
![]() $\mathbb C$
-algebra freely generated by the coefficients of the polynomials
$\mathbb C$
-algebra freely generated by the coefficients of the polynomials
-
•
 $Q_2, a_i, b_i, c_i, d_i$
if
$Q_2, a_i, b_i, c_i, d_i$
if
 $k \leq 6$
,
$k \leq 6$
, -
•
 $a_i, b_i, c_i, d_i, q, r, s, e$
if
$a_i, b_i, c_i, d_i, q, r, s, e$
if
 $k \in \{7.1,\, 7.2,\, 7.3,\, 7.4\}$
, and
$k \in \{7.1,\, 7.2,\, 7.3,\, 7.4\}$
, and -
•
 $a_i, b_i, c_i, d_i, q, r, s, e, A_0, B_1$
if
$a_i, b_i, c_i, d_i, q, r, s, e, A_0, B_1$
if
 $k = 8$
,
$k = 8$
,
where we consider the coefficients to be variables satisfying Condition
![]() $(k)$
. Define
$(k)$
. Define
where
![]() $f \in R_k[x, y, z, t, w]$
is the polynomial in Equation (3.5). Let family k denote the set of fibers of
$f \in R_k[x, y, z, t, w]$
is the polynomial in Equation (3.5). Let family k denote the set of fibers of
![]() $F_k \to \operatorname {Spec} R_k$
over closed points. We say that a general sextic double solid in family k satisfies a property if the property is satisfied by all the fibers of
$F_k \to \operatorname {Spec} R_k$
over closed points. We say that a general sextic double solid in family k satisfies a property if the property is satisfied by all the fibers of
![]() $F_k \to \operatorname {Spec} R_k$
over the closed points of some Zariski open dense set in
$F_k \to \operatorname {Spec} R_k$
over the closed points of some Zariski open dense set in
![]() $\operatorname {Spec} R_k$
. We say that an analytically very general sextic double solid in family k satisfies a property if there is a Zariski open dense subset U of
$\operatorname {Spec} R_k$
. We say that an analytically very general sextic double solid in family k satisfies a property if there is a Zariski open dense subset U of
![]() $\operatorname {Spec} R_k$
such that the property is satisfied by all the fibers of
$\operatorname {Spec} R_k$
such that the property is satisfied by all the fibers of
![]() $F_k \to \operatorname {Spec} R_k$
over the closed points of U that are in the complement of some countable union of closed analytic proper subsets.
$F_k \to \operatorname {Spec} R_k$
over the closed points of U that are in the complement of some countable union of closed analytic proper subsets.
Table 2 Dimension of the space of sextic double solids with an isolated
![]() $cA_{\lfloor k\rfloor }$
$cA_{\lfloor k\rfloor }$

Remark 3.5.
-
(a) The following are equivalent in Notation 3.4:
-
(i) X is a sextic double solid,
-
(ii) X is a variety,
-
(iii) f is irreducible, and
-
(iv)
 $f + w^2$
is not the square of a polynomial in
$f + w^2$
is not the square of a polynomial in
 $\mathbb C[x, y, z, t]$
.
$\mathbb C[x, y, z, t]$
.
Note that if
 $(\mathbb V(f), \boldsymbol {0})$
is a
$(\mathbb V(f), \boldsymbol {0})$
is a
 $cA_n$
singularity for some n, then f is irreducible.
$cA_n$
singularity for some n, then f is irreducible. -
-
(b) Every closed point of
 $\operatorname {Spec} R_k$
bijectively corresponds to a choice of complex coefficients of
$\operatorname {Spec} R_k$
bijectively corresponds to a choice of complex coefficients of-
•
 $Q_2, a_i, b_i, c_i, d_i$
if
$Q_2, a_i, b_i, c_i, d_i$
if
 $k \leq 6$
,
$k \leq 6$
, -
•
 $a_i, b_i, c_i, d_i, q, r, s, e$
if
$a_i, b_i, c_i, d_i, q, r, s, e$
if
 $k \in \{7.1,\, 7.2,\, 7.3,\, 7.4\}$
, and
$k \in \{7.1,\, 7.2,\, 7.3,\, 7.4\}$
, and -
•
 $a_i, b_i, c_i, d_i, q, r, s, e, A_0, B_1$
if
$a_i, b_i, c_i, d_i, q, r, s, e, A_0, B_1$
if
 $k = 8$
,
$k = 8$
,
so determines a unique polynomial
 $f \in \mathbb C[x, y, z, t, w]$
. For every closed point
$f \in \mathbb C[x, y, z, t, w]$
. For every closed point
 ${P \in \operatorname {Spec} R_k}$
such that f is irreducible, the fiber of
${P \in \operatorname {Spec} R_k}$
such that f is irreducible, the fiber of
 $F_k \to \operatorname {Spec} R_k$
over P is a sextic double solid.
$F_k \to \operatorname {Spec} R_k$
over P is a sextic double solid. -
-
(c) The varieties
 $\operatorname {Spec} R_k$
are affine spaces, and their dimensions are given in Table 2. The affine spaces
$\operatorname {Spec} R_k$
are affine spaces, and their dimensions are given in Table 2. The affine spaces
 $\operatorname {Spec} R_{7.1}$
,
$\operatorname {Spec} R_{7.1}$
,
 $\operatorname {Spec} R_{7.2}$
,
$\operatorname {Spec} R_{7.2}$
,
 $\operatorname {Spec} R_{7.3}$
, and
$\operatorname {Spec} R_{7.3}$
, and
 $\operatorname {Spec} R_{7.4}$
all have the same dimension.
$\operatorname {Spec} R_{7.4}$
all have the same dimension. -
(d) Let
 $k \in \mathrm {Inds}$
, and let
$k \in \mathrm {Inds}$
, and let
 $f \in \mathbb C[x, y, z, t, w]$
in Notation 3.4 satisfy Condition (k). The graded
$f \in \mathbb C[x, y, z, t, w]$
in Notation 3.4 satisfy Condition (k). The graded
 $\mathbb C$
-algebra automorphisms
$\mathbb C$
-algebra automorphisms
 $\sigma $
of
$\sigma $
of
 $\mathbb C[x, y, z, t, w]$
, which fix the point
$\mathbb C[x, y, z, t, w]$
, which fix the point
 $P_x = [1, 0, 0, 0, 0]$
and take f to another polynomial
$P_x = [1, 0, 0, 0, 0]$
and take f to another polynomial
 $\sigma (f)$
of the form in Notation 3.4 satisfying Condition (k), are given by when
$\sigma (f)$
of the form in Notation 3.4 satisfying Condition (k), are given by when $$\begin{align*}\begin{pmatrix} x\\y\\z\\t\\w \end{pmatrix} \mapsto \begin{pmatrix}\alpha & R_3 &\\ & M_3 &\\ & & \pm 1\end{pmatrix} \begin{pmatrix}x\\y\\z\\t\\w\end{pmatrix} \end{align*}$$
$$\begin{align*}\begin{pmatrix} x\\y\\z\\t\\w \end{pmatrix} \mapsto \begin{pmatrix}\alpha & R_3 &\\ & M_3 &\\ & & \pm 1\end{pmatrix} \begin{pmatrix}x\\y\\z\\t\\w\end{pmatrix} \end{align*}$$
 $k = 1$
, and given by when
$k = 1$
, and given by when $$\begin{align*}\begin{pmatrix} x\\ y\\ z\\ t\\ w \end{pmatrix} \mapsto \begin{pmatrix}\alpha & R_2 & \beta\\ & M_2 & C_2 &\\ & & \alpha^{-2} &\\ & & & \pm 1\end{pmatrix} \begin{pmatrix} x\\ y\\ z\\ t\\ w\end{pmatrix} \end{align*}$$
$$\begin{align*}\begin{pmatrix} x\\ y\\ z\\ t\\ w \end{pmatrix} \mapsto \begin{pmatrix}\alpha & R_2 & \beta\\ & M_2 & C_2 &\\ & & \alpha^{-2} &\\ & & & \pm 1\end{pmatrix} \begin{pmatrix} x\\ y\\ z\\ t\\ w\end{pmatrix} \end{align*}$$
 $k \geq 2$
, where
$k \geq 2$
, where
 $M_i \in \operatorname {GL}(i, \mathbb C)$
are matrices,
$M_i \in \operatorname {GL}(i, \mathbb C)$
are matrices,
 $R_i \in \mathbb C^i$
are row vectors,
$R_i \in \mathbb C^i$
are row vectors,
 $C_2 \in \mathbb C^2$
is a column vector, and
$C_2 \in \mathbb C^2$
is a column vector, and
 $\alpha \in \mathbb C^*, \beta \in \mathbb C$
are scalars. These automorphisms form an algebraic group which is of dimension
$\alpha \in \mathbb C^*, \beta \in \mathbb C$
are scalars. These automorphisms form an algebraic group which is of dimension
 $13$
if
$13$
if
 $k = 1$
and of dimension
$k = 1$
and of dimension
 $10$
if
$10$
if
 $k \geq 2$
.
$k \geq 2$
.
If
 $k> 7$
, then we also have the
$k> 7$
, then we also have the
 $\mathbb C^*$
-action which leaves f invariant.
$\mathbb C^*$
-action which leaves f invariant. $$\begin{align*}\lambda \cdot q := \lambda q, \quad \lambda \cdot r := \lambda^{-1}r, \quad \lambda \cdot s := \lambda^{-1}s, \quad \lambda \cdot e := \lambda e, \end{align*}$$
$$\begin{align*}\lambda \cdot q := \lambda q, \quad \lambda \cdot r := \lambda^{-1}r, \quad \lambda \cdot s := \lambda^{-1}s, \quad \lambda \cdot e := \lambda e, \end{align*}$$
If a coarse moduli space of sextic double solids with an isolated
 $cA_{\lfloor k\rfloor }$
singularity exists, then we expect its dimension to differ from
$cA_{\lfloor k\rfloor }$
singularity exists, then we expect its dimension to differ from
 $\dim \operatorname {Spec} R_k$
by
$\dim \operatorname {Spec} R_k$
by
 $13$
if
$13$
if
 $k = 1$
, by
$k = 1$
, by
 $10$
if
$10$
if
 $2 \leq k \leq 6$
, and by
$2 \leq k \leq 6$
, and by
 $11$
if
$11$
if
 $k> 7$
. The moduli space of smooth sextic double solids has dimension 68. Table 2 shows the expected moduli space dimensions.
$k> 7$
. The moduli space of smooth sextic double solids has dimension 68. Table 2 shows the expected moduli space dimensions. -
(e) If X has an isolated singularity at
 $P_x$
, then by using the
$P_x$
, then by using the
 $\mathbb C^*$
-action described in (d) for
$\mathbb C^*$
-action described in (d) for
 $k> 7$
and Proposition 3.8, we can set
$k> 7$
and Proposition 3.8, we can set
 $q = 1$
,
$q = 1$
,
 $r = 1$
, and
$r = 1$
, and
 $s = 1$
, respectively, for families 7.1, 7.3, and 7.4.
$s = 1$
, respectively, for families 7.1, 7.3, and 7.4.
We state the main theorem of this section, describing sextic double solids with an isolated
![]() $cA_n$
singularity.
$cA_n$
singularity.
Theorem A. For every positive integer n, both of the following hold:
-
(a) If a sextic double solid has an isolated
 $cA_n$
singularity, then
$cA_n$
singularity, then
 $n \leq 8$
.
$n \leq 8$
. -
(b) Every sextic double solid with an isolated
 $cA_n$
singularity P is isomorphic to a variety X in Notation 3.4 satisfying Condition
$cA_n$
singularity P is isomorphic to a variety X in Notation 3.4 satisfying Condition
 $(l)$
for some
$(l)$
for some
 $l \in \mathrm {Inds}$
such that
$l \in \mathrm {Inds}$
such that
 $\lfloor l\rfloor = n$
, with the isomorphism sending P to
$\lfloor l\rfloor = n$
, with the isomorphism sending P to
 $P_x = [1, 0, 0, 0, 0]$
.
$P_x = [1, 0, 0, 0, 0]$
.
Furthermore, for every
![]() $k \in \mathrm {Inds}$
, all of the following hold:
$k \in \mathrm {Inds}$
, all of the following hold:
-
(c) If
 $k \geq 2$
, then every scheme X in Notation 3.4 satisfying Condition
$k \geq 2$
, then every scheme X in Notation 3.4 satisfying Condition
 $(k)$
has either a (possibly non-isolated)
$(k)$
has either a (possibly non-isolated)
 $cA_m$
singularity or the singularity
$cA_m$
singularity or the singularity
 $(\mathbb V(x_1^2 + x_2^2), \boldsymbol {0}) \subseteq (\mathbb C^4, \boldsymbol {0})$
at
$(\mathbb V(x_1^2 + x_2^2), \boldsymbol {0}) \subseteq (\mathbb C^4, \boldsymbol {0})$
at
 $P_x$
, where
$P_x$
, where
 $m \geq \lfloor k\rfloor $
and
$m \geq \lfloor k\rfloor $
and
 $\mathbb C^4$
has variables
$\mathbb C^4$
has variables
 $x_1, x_2, x_3, x_4$
.
$x_1, x_2, x_3, x_4$
. -
(d) A general sextic double solid in family k is smooth outside a
 $cA_{\lfloor k\rfloor }$
singularity at
$cA_{\lfloor k\rfloor }$
singularity at
 $P_x$
.
$P_x$
. -
(e) An analytically very general sextic double solid in family k is factorial, except for
 ${k = 7.4}$
. No terminal variety in family
${k = 7.4}$
. No terminal variety in family
 $7.4$
is
$7.4$
is
 $\mathbb Q$
-factorial.
$\mathbb Q$
-factorial.
Remark 3.6.
-
(a) By Proposition 2.12, all log terminal sextic double solids have Picard number
 $1$
. Therefore, by Theorem A(d) and (e), an analytically very general sextic double solid in each family
$1$
. Therefore, by Theorem A(d) and (e), an analytically very general sextic double solid in each family
 $k \in \mathrm {Inds} \setminus \{7.4\}$
is a Mori fiber space over a point.
$k \in \mathrm {Inds} \setminus \{7.4\}$
is a Mori fiber space over a point. -
(b) Let
 $k \in \mathrm {Inds} \setminus \{1, 8\}$
. Let X satisfy Condition
$k \in \mathrm {Inds} \setminus \{1, 8\}$
. Let X satisfy Condition
 $(k)$
but not Condition
$(k)$
but not Condition
 $(l)$
for any
$(l)$
for any
 $l \in \mathrm {Inds}$
satisfying
$l \in \mathrm {Inds}$
satisfying
 $\lfloor l\rfloor = \lfloor k\rfloor + 1$
. The proof of Theorem A(b) implies that if one of the following holds:
$\lfloor l\rfloor = \lfloor k\rfloor + 1$
. The proof of Theorem A(b) implies that if one of the following holds:-
•
 $k < 6$
,
$k < 6$
, -
•
 $P_x$
is an isolated singularity, or
$P_x$
is an isolated singularity, or -
•
 $\lfloor k\rfloor = 7$
, r and s are coprime, and q and e are coprime,
$\lfloor k\rfloor = 7$
, r and s are coprime, and q and e are coprime,
then X has a
 $cA_{\lfloor k\rfloor }$
singularity at
$cA_{\lfloor k\rfloor }$
singularity at
 $P_x$
.
$P_x$
. -
3.3. Bound
 $n \leq 8$
for an isolated
$n \leq 8$
for an isolated
 $cA_n$
singularity
$cA_n$
singularity
In this section, we prove Theorem A(a) and (c), showing that the parameter spaces in Notation 3.4 describe sextic double solids with a
![]() $cA_n$
singularity. In addition, we prove Theorem A(b), namely the bound
$cA_n$
singularity. In addition, we prove Theorem A(b), namely the bound
![]() $n \leq 8$
for an isolated
$n \leq 8$
for an isolated
![]() $cA_n$
singularity. The bound
$cA_n$
singularity. The bound
![]() $n \leq 8$
for an isolated
$n \leq 8$
for an isolated
![]() $cA_n$
singularity is proved by explicitly describing a curve of singularities for
$cA_n$
singularity is proved by explicitly describing a curve of singularities for
![]() $n> 9$
.
$n> 9$
.
First, we state a few lemmas needed for the proof.
Lemma 3.7. If X in Notation 3.4 satisfies Condition
![]() $(6)$
and
$(6)$
and
![]() $P_x$
is an isolated singularity of X, then
$P_x$
is an isolated singularity of X, then
![]() $a_2 \neq 0$
or
$a_2 \neq 0$
or
![]() $b_3 \neq 0$
.
$b_3 \neq 0$
.
Proof. If Condition
![]() $(6)$
holds and
$(6)$
holds and
![]() $a_2 = b_3 = 0$
, then
$a_2 = b_3 = 0$
, then
![]() $a_3 = b_4 = c_5 = d_6 = 0$
. Let C be the curve defined by the ideal
$a_3 = b_4 = c_5 = d_6 = 0$
. Let C be the curve defined by the ideal
![]() $(t, w, 2xc_4 + 2d_5)$
. Note that C contains
$(t, w, 2xc_4 + 2d_5)$
. Note that C contains
![]() $P_x$
. Taking partial derivatives, we see that every point of C is a singular point of X.
$P_x$
. Taking partial derivatives, we see that every point of C is a singular point of X.
The following proposition is useful when using Notation 3.4.
Proposition 3.8. If X in Notation 3.4 satisfies Condition
![]() $(k)$
and
$(k)$
and
![]() $P_x$
is an isolated singularity of X where
$P_x$
is an isolated singularity of X where
![]() $k> 7$
, then q and e are coprime and r and s are coprime as polynomials in
$k> 7$
, then q and e are coprime and r and s are coprime as polynomials in
![]() $\mathbb C[y, z]$
.
$\mathbb C[y, z]$
.
Proof. Let
![]() $D \in \mathbb C[y, z]$
be a common prime divisor of r and s or a common prime divisor of q and e. Then D divides
$D \in \mathbb C[y, z]$
be a common prime divisor of r and s or a common prime divisor of q and e. Then D divides
![]() $a_2, b_3, c_4, d_5$
, and
$a_2, b_3, c_4, d_5$
, and
![]() $D^2$
divides
$D^2$
divides
![]() $a_3, b_4, c_5, d_6$
. Let C be the curve defined by the ideal
$a_3, b_4, c_5, d_6$
. Let C be the curve defined by the ideal
![]() $(D, t, w)$
. Note that C contains
$(D, t, w)$
. Note that C contains
![]() $P_x$
. Taking partial derivatives, we see that X is singular at every point of C
$P_x$
. Taking partial derivatives, we see that X is singular at every point of C
Lemma 3.9. Let
![]() $r, s \in \mathbb C[y, z]$
have no common prime divisors, and let
$r, s \in \mathbb C[y, z]$
have no common prime divisors, and let
![]() $q \in \mathbb C[y, z]$
be nonzero. Let
$q \in \mathbb C[y, z]$
be nonzero. Let
![]() $h_n \in \mathbb C[y, z]$
be of the form
$h_n \in \mathbb C[y, z]$
be of the form
![]() $h_n = q^\alpha (r^\beta C_r - s^\gamma C_s)$
where
$h_n = q^\alpha (r^\beta C_r - s^\gamma C_s)$
where
![]() $C_r, C_s \in \mathbb C[y, z]$
and
$C_r, C_s \in \mathbb C[y, z]$
and
![]() $\alpha , \beta , \gamma $
are nonnegative integers. Then
$\alpha , \beta , \gamma $
are nonnegative integers. Then
Proof. Obvious.
Proof of Theorem A(b)
First, we prove that every sextic double solid
![]() $Y \subseteq \mathbb P(1, 1, 1, 1, 3)$
with a singular point P (not necessarily of type
$Y \subseteq \mathbb P(1, 1, 1, 1, 3)$
with a singular point P (not necessarily of type
![]() $cA_n$
) is isomorphic to some X in Notation 3.4, with the isomorphism sending P to
$cA_n$
) is isomorphic to some X in Notation 3.4, with the isomorphism sending P to
![]() $P_x = [1, 0, 0, 0, 0]$
. For this, it suffices to note that Notation 3.4 describes all sextic double solids with a singular point at
$P_x = [1, 0, 0, 0, 0]$
. For this, it suffices to note that Notation 3.4 describes all sextic double solids with a singular point at
![]() $P_x$
, and that we can move any point of Y to
$P_x$
, and that we can move any point of Y to
![]() $P_x$
using an automorphism of
$P_x$
using an automorphism of
![]() $\mathbb P(1, 1, 1, 1, 3)$
. This proves the case
$\mathbb P(1, 1, 1, 1, 3)$
. This proves the case
![]() $n = 1$
. For the rest of the proof, X is given by some f in Notation 3.4 with a (not necessarily isolated)
$n = 1$
. For the rest of the proof, X is given by some f in Notation 3.4 with a (not necessarily isolated)
![]() $cA_n$
singularity at
$cA_n$
singularity at
![]() $P_x$
and n is at least
$P_x$
and n is at least
![]() $2$
.
$2$
.
Let
![]() $X^{\mathrm {an}}$
denote the analytification of X. By Propositions 2.4 and 2.5 and Corollary 2.6, after applying a suitable linear invertible coordinate change on
$X^{\mathrm {an}}$
denote the analytification of X. By Propositions 2.4 and 2.5 and Corollary 2.6, after applying a suitable linear invertible coordinate change on
![]() $y, z, t$
, Condition (2) holds. This proves the case
$y, z, t$
, Condition (2) holds. This proves the case
![]() $n = 2$
. For the rest of the proof, Condition (2) holds and n is at least
$n = 2$
. For the rest of the proof, Condition (2) holds and n is at least
![]() $3$
.
$3$
.
Let
denote the affine open of X given by inverting x. Let
![]() $g \in \mathbb C\{y, z, t\}$
and
$g \in \mathbb C\{y, z, t\}$
and
![]() $h \in \mathbb C\{y, z\}$
be the unique convergent power series of multiplicity at least 2 such that
$h \in \mathbb C\{y, z\}$
be the unique convergent power series of multiplicity at least 2 such that
Since by assumption
![]() $(X^{\mathrm {an}}, P_x)$
is a
$(X^{\mathrm {an}}, P_x)$
is a
![]() $cA_n$
singularity, Propositions 2.4 and 2.5 and Corollary 2.6 imply that
$cA_n$
singularity, Propositions 2.4 and 2.5 and Corollary 2.6 imply that
![]() $h_2 = \cdots = h_n = 0$
, where
$h_2 = \cdots = h_n = 0$
, where
![]() $h_j \in \mathbb C[x_3, x_4]$
is the homogeneous degree j part of h.
$h_j \in \mathbb C[x_3, x_4]$
is the homogeneous degree j part of h.
Using the explicit splitting lemma (Proposition 3.2), it is straightforward to compute that
![]() $h_2 = \cdots = h_n = 0$
is equivalent to satisfying Condition
$h_2 = \cdots = h_n = 0$
is equivalent to satisfying Condition
![]() $(n)$
when
$(n)$
when
![]() $n \leq 6$
, even if
$n \leq 6$
, even if
![]() $P_x$
is not an isolated singularity. This proves the cases
$P_x$
is not an isolated singularity. This proves the cases
![]() $n \in \{3, \ldots , 6\}$
. For the rest of the proof, Condition (6) holds,
$n \in \{3, \ldots , 6\}$
. For the rest of the proof, Condition (6) holds,
![]() $(X^{\mathrm {an}}, P_x)$
is an isolated
$(X^{\mathrm {an}}, P_x)$
is an isolated
![]() $cA_n$
singularity, and n is at least
$cA_n$
singularity, and n is at least
![]() $7$
.
$7$
.
By Lemma 3.7,
![]() $a_2 \neq 0$
or
$a_2 \neq 0$
or
![]() $b_3 \neq 0$
. Define q to be a homogeneous greatest common divisor of
$b_3 \neq 0$
. Define q to be a homogeneous greatest common divisor of
![]() $a_2$
and
$a_2$
and
![]() $b_3$
. Define r and
$b_3$
. Define r and
![]() $s \in \mathbb C[y, z]$
to be the unique homogeneous polynomials such that
$s \in \mathbb C[y, z]$
to be the unique homogeneous polynomials such that
 $$\begin{align*}\begin{aligned} a_2 & = qr,\\ b_3 & = qs + 4a_1qr. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} a_2 & = qr,\\ b_3 & = qs + 4a_1qr. \end{aligned} \end{align*}$$
Then r and s are coprime. Using the explicit splitting lemma (Proposition 3.2), we compute that
Using Lemma 3.9, the equations
![]() $h_2 = \cdots = h_7 = 0$
imply the existence of a polynomial
$h_2 = \cdots = h_7 = 0$
imply the existence of a polynomial
![]() $e \in \mathbb C[y, z]$
such that
$e \in \mathbb C[y, z]$
such that
 $$\begin{align*}\begin{aligned} c_4 & = 2a_1qs - 6a_0q^2r^2 + 8a_1^2qr + er,\\ d_5 & = 2b_2qs - 8a_1^2qs - es - b_1q^2r^2 + c_3qr. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} c_4 & = 2a_1qs - 6a_0q^2r^2 + 8a_1^2qr + er,\\ d_5 & = 2b_2qs - 8a_1^2qs - es - b_1q^2r^2 + c_3qr. \end{aligned} \end{align*}$$
Therefore,
![]() $h_2 = \cdots = h_7 = 0$
implies Condition
$h_2 = \cdots = h_7 = 0$
implies Condition
![]() $(7.i)$
, where i is defined by
$(7.i)$
, where i is defined by
where
![]() $\deg \gcd (a_2, b_3)$
is the degree of a greatest common divisor of
$\deg \gcd (a_2, b_3)$
is the degree of a greatest common divisor of
![]() $a_2 \in \mathbb C[y, z]$
and
$a_2 \in \mathbb C[y, z]$
and
![]() $b_3 \in \mathbb C[y, z]$
. This proves
$b_3 \in \mathbb C[y, z]$
. This proves
![]() $n = 7$
.
$n = 7$
.
Next, we show that if
![]() $h_2 = \cdots = h_8 = 0$
and one of Conditions
$h_2 = \cdots = h_8 = 0$
and one of Conditions
![]() $(7.2)$
–
$(7.2)$
–
![]() $(7.4)$
holds, then r and s have a common prime divisor or q and e have a common prime divisor, which contradicts Proposition 3.8. In Condition
$(7.4)$
holds, then r and s have a common prime divisor or q and e have a common prime divisor, which contradicts Proposition 3.8. In Condition
![]() $(7.2)$
, we calculate that
$(7.2)$
, we calculate that
![]() $h_8 + e^2r^2$
is divisible by q, giving
$h_8 + e^2r^2$
is divisible by q, giving
![]() $r = Cq$
for some
$r = Cq$
for some
![]() $C \in \mathbb C$
. Substituting into
$C \in \mathbb C$
. Substituting into
![]() $h_8$
, we compute that
$h_8$
, we compute that
![]() $h_8 - 2qes^2$
is divisible by
$h_8 - 2qes^2$
is divisible by
![]() $q^2$
. Therefore, q and s have a common prime divisor, giving that r and s have a common prime divisor, a contradiction. Conditions
$q^2$
. Therefore, q and s have a common prime divisor, giving that r and s have a common prime divisor, a contradiction. Conditions
![]() $(7.3)$
and
$(7.3)$
and
![]() $(7.4)$
are similar.
$(7.4)$
are similar.
Hence, if
![]() $h_2 = \cdots = h_8 = 0$
, then Condition
$h_2 = \cdots = h_8 = 0$
, then Condition
![]() $(7.1)$
holds. Using the explicit splitting lemma, we calculate
$(7.1)$
holds. Using the explicit splitting lemma, we calculate
![]() $h_8$
, and using Lemma 3.9, we can show that
$h_8$
, and using Lemma 3.9, we can show that
![]() $h_2 = \cdots = h_8 = 0$
implies Condition
$h_2 = \cdots = h_8 = 0$
implies Condition
![]() $(8)$
.
$(8)$
.
Proof of Theorem A(a)
Assume that X is a sextic double solid with an isolated
![]() $cA_n$
singularity where
$cA_n$
singularity where
![]() $n \geq 9$
. Using the notation in the proof of Theorem A(b), we find that Condition (8) holds and
$n \geq 9$
. Using the notation in the proof of Theorem A(b), we find that Condition (8) holds and
![]() $h_2 = \cdots = h_9 = 0$
. Using the explicit splitting lemma, we compute
$h_2 = \cdots = h_9 = 0$
. Using the explicit splitting lemma, we compute
![]() $h_9$
, and using Lemma 3.9, we find that there exists
$h_9$
, and using Lemma 3.9, we find that there exists
![]() $B_0 \in \mathbb C$
such that
$B_0 \in \mathbb C$
such that
 $$\begin{align*}\begin{aligned} A_0 & = a_0,\\ B_1 & = b_1,\\ d_3 & = -s_3B_0 + 2b_0s_3 - 2a_0^2s_3 + c_1r_2 - 4a_0b_1r_2 \\ &\quad + 16a_0^2a_1r_2 + b_1b_2 - 4a_0a_1b_2 - 2a_1^2b_1 + 8a_0a_1^3,\\ c_2 & = r_2B_0 - 6a_0^2r_2 + 2a_0b_2 + 2a_1b_1 - 12a_0a_1^2. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} A_0 & = a_0,\\ B_1 & = b_1,\\ d_3 & = -s_3B_0 + 2b_0s_3 - 2a_0^2s_3 + c_1r_2 - 4a_0b_1r_2 \\ &\quad + 16a_0^2a_1r_2 + b_1b_2 - 4a_0a_1b_2 - 2a_1^2b_1 + 8a_0a_1^3,\\ c_2 & = r_2B_0 - 6a_0^2r_2 + 2a_0b_2 + 2a_1b_1 - 12a_0a_1^2. \end{aligned} \end{align*}$$
Substituting into f gives
 $$\begin{align*}\begin{aligned} x^3a_3 + x^2b_4 + xc_5 + d_6 & = (s_3 + 2a_1r_2 + xr_2)^2,\\ x^3a_2 + x^2b_3 + xc_4 + d_5 & = (s_3 + 2a_1r_2 + xr_2)(-2a_0r_2 + b_2 - 2a_1^2 + 2xa_1 + x^2). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} x^3a_3 + x^2b_4 + xc_5 + d_6 & = (s_3 + 2a_1r_2 + xr_2)^2,\\ x^3a_2 + x^2b_3 + xc_4 + d_5 & = (s_3 + 2a_1r_2 + xr_2)(-2a_0r_2 + b_2 - 2a_1^2 + 2xa_1 + x^2). \end{aligned} \end{align*}$$
Define the curve C by the ideal
![]() $(w, t, s_3 + 2a_1r_2 + xr_2)$
. Taking partial derivatives, we find that X is singular at every point of C, a contradiction.
$(w, t, s_3 + 2a_1r_2 + xr_2)$
. Taking partial derivatives, we find that X is singular at every point of C, a contradiction.
Proof of Theorem A(c)
Let
![]() $X^{\mathrm {an}}$
denote the analytification of X. Using the explicit splitting lemma (Proposition 3.2), we can compute that the complex space germ
$X^{\mathrm {an}}$
denote the analytification of X. Using the explicit splitting lemma (Proposition 3.2), we can compute that the complex space germ
![]() $(X^{\mathrm {an}}, P_x)$
is isomorphic to
$(X^{\mathrm {an}}, P_x)$
is isomorphic to
![]() $(\mathbb V(-w^2 + t^2 + h))$
, where
$(\mathbb V(-w^2 + t^2 + h))$
, where
![]() $h \in \mathbb C[y, z]$
is zero or has multiplicity at least
$h \in \mathbb C[y, z]$
is zero or has multiplicity at least
![]() $\lfloor k\rfloor + 1$
. By Propositions 2.4 and 2.5 and Corollary 2.6, X has either a (possibly non-isolated)
$\lfloor k\rfloor + 1$
. By Propositions 2.4 and 2.5 and Corollary 2.6, X has either a (possibly non-isolated)
![]() $cA_m$
singularity or the singularity
$cA_m$
singularity or the singularity
![]() $(\mathbb V(x_1^2 + x_2^2), \boldsymbol {0}) \subseteq (\mathbb C^4, \boldsymbol {0})$
at
$(\mathbb V(x_1^2 + x_2^2), \boldsymbol {0}) \subseteq (\mathbb C^4, \boldsymbol {0})$
at
![]() $P_x$
, where
$P_x$
, where
![]() $m \geq \lfloor k\rfloor $
and
$m \geq \lfloor k\rfloor $
and
![]() $\mathbb C^4$
has variables
$\mathbb C^4$
has variables
![]() $x_1, x_2, x_3, x_4$
.
$x_1, x_2, x_3, x_4$
.
3.4. Smoothness outside the isolated
 $cA_n$
point
$cA_n$
point
In this section, we prove Theorem A(d) using dimension count arguments, showing that a general sextic double solid with an isolated
![]() $cA_n$
singularity is smooth outside the
$cA_n$
singularity is smooth outside the
![]() $cA_n$
point.
$cA_n$
point.
Lemma 3.10. For every
![]() $k \in \mathrm {Inds}$
, a general member of family k in Notation 3.4 is smooth at every point with t-coordinate nonzero.
$k \in \mathrm {Inds}$
, a general member of family k in Notation 3.4 is smooth at every point with t-coordinate nonzero.
Proof. Let
![]() $\widehat {\mathcal A}_k$
denote the set of closed points Q of
$\widehat {\mathcal A}_k$
denote the set of closed points Q of
![]() $\operatorname {Spec} R_k$
such that the fiber of
$\operatorname {Spec} R_k$
such that the fiber of
![]() $F_k \to \operatorname {Spec} R_k$
over Q has a singular point at
$F_k \to \operatorname {Spec} R_k$
over Q has a singular point at
![]() $P_t = [0, 0, 0, 1, 0]$
. We find
$P_t = [0, 0, 0, 1, 0]$
. We find
 $$\begin{align*}f(P_t) = d_0, \quad \frac{\partial f}{\partial x}(P_t) = 2c_0, \quad \frac{\partial f}{\partial y}(P_t) = 2\frac{\partial d_1}{\partial y}, \quad \frac{\partial f}{\partial z}(P_t) = 2\frac{\partial d_1}{\partial z}, \quad \frac{\partial f}{\partial t}(P_t) = 6d_0. \end{align*}$$
$$\begin{align*}f(P_t) = d_0, \quad \frac{\partial f}{\partial x}(P_t) = 2c_0, \quad \frac{\partial f}{\partial y}(P_t) = 2\frac{\partial d_1}{\partial y}, \quad \frac{\partial f}{\partial z}(P_t) = 2\frac{\partial d_1}{\partial z}, \quad \frac{\partial f}{\partial t}(P_t) = 6d_0. \end{align*}$$
By the Jacobian criterion ([Reference Liu39, Exer. 4.2.10]),
![]() $\widehat {\mathcal A}_k$
is the set of closed points of
$\widehat {\mathcal A}_k$
is the set of closed points of
 $$\begin{align*}\mathcal A_k = \mathbb V_{\operatorname{Spec} R_k}\left(d_0, c_0, \frac{\partial d_1}{\partial y}, \frac{\partial d_1}{\partial z}\right). \end{align*}$$
$$\begin{align*}\mathcal A_k = \mathbb V_{\operatorname{Spec} R_k}\left(d_0, c_0, \frac{\partial d_1}{\partial y}, \frac{\partial d_1}{\partial z}\right). \end{align*}$$
We see that
![]() $\dim \mathcal A_k = \dim \operatorname {Spec} R_k - 4$
.
$\dim \mathcal A_k = \dim \operatorname {Spec} R_k - 4$
.
The
![]() $\mathbb C$
-algebra automorphism
$\mathbb C$
-algebra automorphism
![]() $x \mapsto x + \alpha _x t$
,
$x \mapsto x + \alpha _x t$
,
![]() $y \mapsto y + \alpha _y t$
,
$y \mapsto y + \alpha _y t$
,
![]() $z \mapsto z + \alpha _z t$
of
$z \mapsto z + \alpha _z t$
of
![]() $\mathbb C[x, y, z, t, w]$
defines a morphism
$\mathbb C[x, y, z, t, w]$
defines a morphism
with closed image. The set of closed points Q of
![]() $\operatorname {Spec} R_k$
, where the fiber of
$\operatorname {Spec} R_k$
, where the fiber of
![]() $F_k \to \operatorname {Spec} R_k$
over Q has a singular point with t-coordinate nonzero, is precisely the set of closed points of the image of
$F_k \to \operatorname {Spec} R_k$
over Q has a singular point with t-coordinate nonzero, is precisely the set of closed points of the image of
![]() $\pi _{\mathcal A_k}$
. The image of
$\pi _{\mathcal A_k}$
. The image of
![]() $\pi _{\mathcal A_k}$
has codimension at least
$\pi _{\mathcal A_k}$
has codimension at least
![]() $1$
.
$1$
.
Lemma 3.11. For every
![]() $k \in \mathrm {Inds}$
, a general member of family k in Notation 3.4 is smooth at every point different from
$k \in \mathrm {Inds}$
, a general member of family k in Notation 3.4 is smooth at every point different from
![]() $P_x$
that has t-coordinate zero.
$P_x$
that has t-coordinate zero.
Proof. Let
![]() $P = [0, \beta , \gamma , 0, 0] \in \mathbb P(1, 1, 1, 1, 3)$
, where
$P = [0, \beta , \gamma , 0, 0] \in \mathbb P(1, 1, 1, 1, 3)$
, where
![]() $(\beta , \gamma ) \in \mathbb C^2 \setminus \{(0, 0)\}$
. We find
$(\beta , \gamma ) \in \mathbb C^2 \setminus \{(0, 0)\}$
. We find
 $$\begin{align*}f(P) = d_6(P),\ \frac{\partial f}{\partial x}(P) = c_5(P),\ \frac{\partial f}{\partial y}(P) = \frac{\partial d_6}{\partial y}(P),\ \frac{\partial f}{\partial z}(P) = \frac{\partial d_6}{\partial z}(P),\ \frac{\partial f}{\partial t}(P) = 2d_5(P). \end{align*}$$
$$\begin{align*}f(P) = d_6(P),\ \frac{\partial f}{\partial x}(P) = c_5(P),\ \frac{\partial f}{\partial y}(P) = \frac{\partial d_6}{\partial y}(P),\ \frac{\partial f}{\partial z}(P) = \frac{\partial d_6}{\partial z}(P),\ \frac{\partial f}{\partial t}(P) = 2d_5(P). \end{align*}$$
Define the linear polynomial
![]() $l = \gamma y - \beta z$
. By the Jacobian criterion ([Reference Liu39, Exer. 4.2.10]), P is a singular point of X if and only if the following divisibility constraint is satisfied:
$l = \gamma y - \beta z$
. By the Jacobian criterion ([Reference Liu39, Exer. 4.2.10]), P is a singular point of X if and only if the following divisibility constraint is satisfied:
The set of closed points
![]() $Q \in \operatorname {Spec} R_k$
, where the fiber of
$Q \in \operatorname {Spec} R_k$
, where the fiber of
![]() $F_k \to \operatorname {Spec} R_k$
over Q is singular at P for some
$F_k \to \operatorname {Spec} R_k$
over Q is singular at P for some
![]() $(\beta , \gamma ) \in \mathbb C^2 \setminus \{(0, 0)\}$
, coincides with the set of closed points of a closed subset
$(\beta , \gamma ) \in \mathbb C^2 \setminus \{(0, 0)\}$
, coincides with the set of closed points of a closed subset
![]() $\mathcal B_k$
of
$\mathcal B_k$
of
![]() $\operatorname {Spec} R_k$
. We show that
$\operatorname {Spec} R_k$
. We show that
![]() $\dim \mathcal B_k$
is at most
$\dim \mathcal B_k$
is at most
![]() $\dim \operatorname {Spec} R_k - 2$
.
$\dim \operatorname {Spec} R_k - 2$
.
-
• If
 $k \leq 4$
, then the
$k \leq 4$
, then the
 $19$
coefficients of
$19$
coefficients of
 $c_5, d_5$
, and
$c_5, d_5$
, and
 $d_6$
are algebraically independent in
$d_6$
are algebraically independent in
 $R_k$
. By the divisibility constraint (3.6),
$R_k$
. By the divisibility constraint (3.6),
 $\dim \mathcal B_k = \dim \operatorname {Spec} R_k - 3$
.
$\dim \mathcal B_k = \dim \operatorname {Spec} R_k - 3$
. -
• If
 $k = 5$
, then the
$k = 5$
, then the
 $20$
coefficients of
$20$
coefficients of
 $a_2, b_3, d_5$
, and
$a_2, b_3, d_5$
, and
 $d_6$
are algebraically independent in
$d_6$
are algebraically independent in
 $R_k$
. We have
$R_k$
. We have
 $c_5 = a_2(2b_3 - 4a_1a_2)$
. If l divides
$c_5 = a_2(2b_3 - 4a_1a_2)$
. If l divides
 $c_5$
, then l divides
$c_5$
, then l divides
 $a_2$
or l divides
$a_2$
or l divides
 $b_3 - 2a_1a_2$
. By the divisibility constraint (3.6), in both cases we have three less degrees of freedom. More formally,
$b_3 - 2a_1a_2$
. By the divisibility constraint (3.6), in both cases we have three less degrees of freedom. More formally,
 $\mathcal B_k$
is the union of the images of two morphisms, both having codimension exactly
$\mathcal B_k$
is the union of the images of two morphisms, both having codimension exactly
 $3$
in
$3$
in
 $\operatorname {Spec} R_k$
. Therefore,
$\operatorname {Spec} R_k$
. Therefore,
 $\dim \mathcal B_k = \dim \operatorname {Spec} R_k - 3$
.
$\dim \mathcal B_k = \dim \operatorname {Spec} R_k - 3$
. -
• If
 $k = 6$
, then the
$k = 6$
, then the
 $23$
coefficients of
$23$
coefficients of
 $a_2, b_3, c_4, d_5$
are algebraically independent in
$a_2, b_3, c_4, d_5$
are algebraically independent in
 $R_k$
. We have
$R_k$
. We have
 $c_5 = a_2(2b_3 - 4a_1a_2)$
and
$c_5 = a_2(2b_3 - 4a_1a_2)$
and
 $d_6 = a_2 \cdot (2 c_4 + G) + b_3^2$
for a polynomial
$d_6 = a_2 \cdot (2 c_4 + G) + b_3^2$
for a polynomial
 $G \in \mathbb C[y, z]$
homogeneous of degree
$G \in \mathbb C[y, z]$
homogeneous of degree
 $4$
which does not contain
$4$
which does not contain
 $c_4$
.
$c_4$
.If l divides
 $a_2$
, then using the divisibility constraint (3.6), we find that l divides
$a_2$
, then using the divisibility constraint (3.6), we find that l divides
 $b_3$
. Now,
$b_3$
. Now,
 $l^2$
divides
$l^2$
divides
 $a_2$
or l divides
$a_2$
or l divides
 $2 c_4 + G$
. So, there are three less degrees of freedom in choosing
$2 c_4 + G$
. So, there are three less degrees of freedom in choosing
 $a_2$
,
$a_2$
,
 $b_3$
,
$b_3$
,
 $c_4$
, and
$c_4$
, and
 $d_5$
.
$d_5$
.If l does not divide
 $a_2$
, then l divides
$a_2$
, then l divides
 $b_3 - 2a_1a_2$
, so
$b_3 - 2a_1a_2$
, so
 $b_3 = 2a_1a_2 + Ql$
for some homogeneous quadratic form
$b_3 = 2a_1a_2 + Ql$
for some homogeneous quadratic form
 $Q \in \mathbb C[y, z]$
. From
$Q \in \mathbb C[y, z]$
. From
 $l \mid d_6$
, we find that l divides
$l \mid d_6$
, we find that l divides
 $c_4 - a_2b_2 + 2a_0a_2^2 + 2a_1^2a_2$
, so
$c_4 - a_2b_2 + 2a_0a_2^2 + 2a_1^2a_2$
, so
 $c_4 = Cl + a_2b_2 - 2a_0a_2^2 - 2a_1^2a_2$
for some homogeneous cubic form
$c_4 = Cl + a_2b_2 - 2a_0a_2^2 - 2a_1^2a_2$
for some homogeneous cubic form
 $C \in \mathbb C[y, z]$
. From
$C \in \mathbb C[y, z]$
. From
 $l^2 \mid d_6$
, we find that l divides
$l^2 \mid d_6$
, we find that l divides
 $C - 4Qa_1$
. Therefore, after fixing
$C - 4Qa_1$
. Therefore, after fixing
 $a_0, a_1, a_2$
, and
$a_0, a_1, a_2$
, and
 $b_2$
, there are at least two less degrees of freedom in choosing
$b_2$
, there are at least two less degrees of freedom in choosing
 $b_3$
,
$b_3$
,
 $c_4$
, and
$c_4$
, and
 $d_5$
.
$d_5$
.In both cases, we see that
 $\dim \mathcal B_k \leq \dim \operatorname {Spec} R_k - 2$
.
$\dim \mathcal B_k \leq \dim \operatorname {Spec} R_k - 2$
. -
• If
 $\lfloor k\rfloor = 7$
, then Let us consider f for a closed point in
$\lfloor k\rfloor = 7$
, then Let us consider f for a closed point in $$\begin{align*}\begin{aligned} c_5 & = 4q^2r(2s + a_1r),\\ d_5 & = -es + q(2b_2s - a_1^2s - 4b_1qr^2 + c_3r),\\ d_6 & = 4q(er^2 + q(s^2 + a_1rs - 8a_0qr^3 - b_2r^2 + a_1^2r^2)). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} c_5 & = 4q^2r(2s + a_1r),\\ d_5 & = -es + q(2b_2s - a_1^2s - 4b_1qr^2 + c_3r),\\ d_6 & = 4q(er^2 + q(s^2 + a_1rs - 8a_0qr^3 - b_2r^2 + a_1^2r^2)). \end{aligned} \end{align*}$$
 $\mathcal B_k$
. If
$\mathcal B_k$
. If
 $l \mid q$
, then since q and e are coprime, we have
$l \mid q$
, then since q and e are coprime, we have
 $l \mid r$
and
$l \mid r$
and
 $l \mid s$
, a contradiction. If
$l \mid s$
, a contradiction. If
 $l \mid r$
, then since
$l \mid r$
, then since
 $l \mid d_6$
, we find
$l \mid d_6$
, we find
 $l \mid s$
, a contradiction. Therefore, l divides neither q nor r.
$l \mid s$
, a contradiction. Therefore, l divides neither q nor r.
So, l divides
 $2s + a_1r$
. Using
$2s + a_1r$
. Using
 $l^2 \mid d_6$
, we see that
$l^2 \mid d_6$
, we see that
 $l^2$
divides
$l^2$
divides
 $-32a_0q^2r - 4b_2q + 3a_1^2q + 4e$
. After fixing
$-32a_0q^2r - 4b_2q + 3a_1^2q + 4e$
. After fixing
 $a_0, a_1, b_2, q$
, and r, we see that there are at least two less degrees of freedom in choosing s and e. So, we have
$a_0, a_1, b_2, q$
, and r, we see that there are at least two less degrees of freedom in choosing s and e. So, we have
 $\dim \mathcal B_k \leq \dim \operatorname {Spec} R_k - 2$
.
$\dim \mathcal B_k \leq \dim \operatorname {Spec} R_k - 2$
. -
• If
 $k = 8$
, then We consider f for a closed point in
$k = 8$
, then We consider f for a closed point in $$\begin{align*}\begin{aligned} c_5 & = 2r_2(s_3 + 2a_1r_2),\\ d_5 & = r_2(r_2B_1 - 8s_3A_0 - 8a_1r_2A_0 + 6a_0s_3 - b_1r_2 + 4a_0a_1r_2 + 2a_1b_2 - 4a_1^3) \\ &\quad + s_3(b_2 - 2a_1^2),\\ d_6 & = r_2(8r_2^2A_0 + 4a_1s_3 - 8a_0r_2^2 + 4a_1^2r_2) + s_3^2. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} c_5 & = 2r_2(s_3 + 2a_1r_2),\\ d_5 & = r_2(r_2B_1 - 8s_3A_0 - 8a_1r_2A_0 + 6a_0s_3 - b_1r_2 + 4a_0a_1r_2 + 2a_1b_2 - 4a_1^3) \\ &\quad + s_3(b_2 - 2a_1^2),\\ d_6 & = r_2(8r_2^2A_0 + 4a_1s_3 - 8a_0r_2^2 + 4a_1^2r_2) + s_3^2. \end{aligned} \end{align*}$$
 $\mathcal B_k$
. If
$\mathcal B_k$
. If
 $l \mid r_2$
, then
$l \mid r_2$
, then
 $l \mid s_3$
, a contradiction. So, l divides
$l \mid s_3$
, a contradiction. So, l divides
 $s_3 + 2a_1r_2$
. Since l divides
$s_3 + 2a_1r_2$
. Since l divides
 $d_6$
, we have
$d_6$
, we have
 $l \mid r_2^3(A_0 - a_0)$
. So,
$l \mid r_2^3(A_0 - a_0)$
. So,
 $A_0 = a_0$
. Since l divides
$A_0 = a_0$
. Since l divides
 $d_5$
, we see that
$d_5$
, we see that
 $l \mid r_2^2(B_1 - b_1)$
. We find that the coefficients of f have at least two less degrees of freedom, namely
$l \mid r_2^2(B_1 - b_1)$
. We find that the coefficients of f have at least two less degrees of freedom, namely
 $A_0 = a_0$
, and the polynomials
$A_0 = a_0$
, and the polynomials
 $B_1 - b_1$
and
$B_1 - b_1$
and
 $s_3 + 2a_1r_2$
have a common prime divisor. So, we have
$s_3 + 2a_1r_2$
have a common prime divisor. So, we have
 $\dim \mathcal B_k \leq \dim \operatorname {Spec} R_k - 2$
.
$\dim \mathcal B_k \leq \dim \operatorname {Spec} R_k - 2$
.
The
![]() $\mathbb C$
-algebra automorphism
$\mathbb C$
-algebra automorphism
![]() $x \mapsto x + \alpha y$
of
$x \mapsto x + \alpha y$
of
![]() $\mathbb C[x, y, z, t, w]$
defines a morphism
$\mathbb C[x, y, z, t, w]$
defines a morphism
and the
![]() $\mathbb C$
-algebra automorphism
$\mathbb C$
-algebra automorphism
![]() $x \mapsto x + \alpha z$
of
$x \mapsto x + \alpha z$
of
![]() $\mathbb C[x, y, z, t, w]$
defines a morphism
$\mathbb C[x, y, z, t, w]$
defines a morphism
Every closed point Q of
![]() $\operatorname {Spec} R_k$
, where the fiber of
$\operatorname {Spec} R_k$
, where the fiber of
![]() $F_k \to \operatorname {Spec} R_k$
over Q has a singular point different from
$F_k \to \operatorname {Spec} R_k$
over Q has a singular point different from
![]() $P_x$
with t-coordinate zero, belongs to the image of
$P_x$
with t-coordinate zero, belongs to the image of
![]() $\pi _{\mathcal B_k, 1}$
or
$\pi _{\mathcal B_k, 1}$
or
![]() $\pi _{\mathcal B_k, 2}$
. The union of the images of
$\pi _{\mathcal B_k, 2}$
. The union of the images of
![]() $\pi _{\mathcal B_k, 1}$
and
$\pi _{\mathcal B_k, 1}$
and
![]() $\pi _{\mathcal B_k, 2}$
has codimension at least
$\pi _{\mathcal B_k, 2}$
has codimension at least
![]() $1$
.
$1$
.
Proof of Theorem A(d)
It follows from Lemmas 3.10 and 3.11 that a general sextic double solid in family k has exactly one singular point, namely the point
![]() $P_x$
. The singularity of X at
$P_x$
. The singularity of X at
![]() $P_x$
is of type
$P_x$
is of type
![]() $cA_{\lfloor k\rfloor }$
if the homogeneous part
$cA_{\lfloor k\rfloor }$
if the homogeneous part
![]() $h_{\lfloor k\rfloor + 1} \in \mathbb C[y, z]$
of h is nonzero, where h is as in the proof of Theorem A(b). Since this is an open condition, a general sextic double solid in family k has a
$h_{\lfloor k\rfloor + 1} \in \mathbb C[y, z]$
of h is nonzero, where h is as in the proof of Theorem A(b). Since this is an open condition, a general sextic double solid in family k has a
![]() $cA_{\lfloor k\rfloor }$
singularity at
$cA_{\lfloor k\rfloor }$
singularity at
![]() $P_x$
.
$P_x$
.
3.5. Factoriality
Lemma 3.12 [Reference Kawamata33, Lemma 5.1]
A terminal Gorenstein Fano 3-fold is factorial if and only if it is
![]() $\mathbb Q$
-factorial.
$\mathbb Q$
-factorial.
Lemma 3.13. There are no
![]() $\mathbb Q$
-factorial log terminal sextic double solids in family
$\mathbb Q$
-factorial log terminal sextic double solids in family
![]() $7.4$
.
$7.4$
.
Proof. Let X be a log terminal variety in family 7.4. The Cartier divisor
![]() $\mathbb V_X(t)$
is the sum of the two prime divisors
$\mathbb V_X(t)$
is the sum of the two prime divisors
![]() $D_1 = \mathbb V(t, q - w)$
and
$D_1 = \mathbb V(t, q - w)$
and
![]() $D_2 = \mathbb V(t, q + w)$
. Let
$D_2 = \mathbb V(t, q + w)$
. Let
![]() $l \varepsilon \mathbb{C}[y,z]$
be a non-zero linear form that does not divide
$l \varepsilon \mathbb{C}[y,z]$
be a non-zero linear form that does not divide
![]() $q$
. Define the curve
$q$
. Define the curve
![]() $C = V(q+w, x, l)$
. If
$C = V(q+w, x, l)$
. If
![]() $D_1$
is
$D_1$
is
![]() $\mathbb{Q}$
-Cartier, then
$\mathbb{Q}$
-Cartier, then
![]() $D_1\cdot C=0$
, which contradicts Proposition 2.12 and lemma 2.13. Therefore, neither
$D_1\cdot C=0$
, which contradicts Proposition 2.12 and lemma 2.13. Therefore, neither
![]() $D_1$
nor
$D_1$
nor
![]() $D_2$
is
$D_2$
is
![]() $\mathbb{Q}$
-Cartier.
$\mathbb{Q}$
-Cartier.
Our proof of factoriality relies on the following corollary of Proposition 2.10.
Corollary 3.14. Let X be a Gorenstein terminal Fano 3-fold which is smooth along its general effective anti-canonical divisor D. Then the natural homomorphism
![]() $\operatorname {Cl}(X) \to \operatorname {Pic}(D)$
from the class group of X is injective.
$\operatorname {Cl}(X) \to \operatorname {Pic}(D)$
from the class group of X is injective.
Proof. Let U be any Zariski open set in the smooth locus of X that contains D. By Remark 2.11(1), we have an isomorphism of class groups
![]() $\operatorname {Cl}(X) \cong \operatorname {Cl}(U)$
. Since U is smooth, we have an isomorphism
$\operatorname {Cl}(X) \cong \operatorname {Cl}(U)$
. Since U is smooth, we have an isomorphism
![]() $\operatorname {Cl}(U) \cong \operatorname {Pic}(U)$
. It follows from the proof of [Reference Namikawa42, Prop. 2] that we can choose a small enough U such that
$\operatorname {Cl}(U) \cong \operatorname {Pic}(U)$
. It follows from the proof of [Reference Namikawa42, Prop. 2] that we can choose a small enough U such that
![]() $\operatorname {Pic}(U)$
injects into
$\operatorname {Pic}(U)$
injects into
![]() $\operatorname {Pic}(D)$
.
$\operatorname {Pic}(D)$
.
Corollary 3.15. Let X be a terminal Gorenstein Fano 3-fold and D a smooth effective anti-canonical divisor such that X is smooth along D and D has Picard number
![]() $1$
. Then X is factorial.
$1$
. Then X is factorial.
Proof. By adjunction, every smooth anti-canonical divisor of a Fano variety is a K3 surface. A very general projective K3 surface has Picard number
![]() $1$
. Therefore, X is smooth along an analytically very general anti-canonical divisor with Picard number
$1$
. Therefore, X is smooth along an analytically very general anti-canonical divisor with Picard number
![]() $1$
. By Corollary 3.14, X is
$1$
. By Corollary 3.14, X is
![]() $\mathbb Q$
-factorial. By Lemma 3.12, X is factorial.
$\mathbb Q$
-factorial. By Lemma 3.12, X is factorial.
Lemma 3.16. For every
![]() $k \in \mathrm {Inds} \setminus \{7.4\}$
and for an analytically very general sextic double solid X in family k, the subvariety
$k \in \mathrm {Inds} \setminus \{7.4\}$
and for an analytically very general sextic double solid X in family k, the subvariety
![]() $\mathbb V_X(x)$
is smooth and has Picard number
$\mathbb V_X(x)$
is smooth and has Picard number
![]() $1$
.
$1$
.
Proof. Let
![]() $S_k$
be the
$S_k$
be the
![]() $\mathbb C$
-algebra freely generated by the
$\mathbb C$
-algebra freely generated by the
![]() $28$
coefficients, considered as variables, of polynomials
$28$
coefficients, considered as variables, of polynomials
![]() $g \in \mathbb C[y, z, t]$
homogeneous of degree
$g \in \mathbb C[y, z, t]$
homogeneous of degree
![]() $6$
. By Remark 3.5(b), closed points P of
$6$
. By Remark 3.5(b), closed points P of
![]() $\operatorname {Spec} R_k$
bijectively correspond to polynomials
$\operatorname {Spec} R_k$
bijectively correspond to polynomials
![]() $f_P \in \mathbb C[x, y, z, t, w]$
in Notation 3.4. Let
$f_P \in \mathbb C[x, y, z, t, w]$
in Notation 3.4. Let
![]() $\theta \colon \mathbb C[x, y, z, t, w] \to \mathbb C[y, z, t]$
be the homomorphism
$\theta \colon \mathbb C[x, y, z, t, w] \to \mathbb C[y, z, t]$
be the homomorphism
![]() $x \mapsto 0$
,
$x \mapsto 0$
,
![]() $w \mapsto 0$
. Let
$w \mapsto 0$
. Let
![]() $\pi _k\colon \operatorname {Spec} R_k \to \operatorname {Spec} S_k$
be the morphism of affine spaces given on closed points by
$\pi _k\colon \operatorname {Spec} R_k \to \operatorname {Spec} S_k$
be the morphism of affine spaces given on closed points by
![]() $f_P \mapsto \theta (f_P)$
. The
$f_P \mapsto \theta (f_P)$
. The
![]() $\mathbb C$
-algebra automorphisms
$\mathbb C$
-algebra automorphisms
![]() $t \mapsto \alpha y + \beta z + t$
of
$t \mapsto \alpha y + \beta z + t$
of
![]() $\mathbb C[y, z, t]$
induce a morphism
$\mathbb C[y, z, t]$
induce a morphism ![]() . Define
. Define
![]() $\rho _k$
to be the composition
$\rho _k$
to be the composition
We can compute that the rank of the Jacobian matrix of
![]() $\rho _k$
at some specified point is
$\rho _k$
at some specified point is
![]() $28$
for all
$28$
for all
![]() $k \in \mathrm {Inds} \setminus \{7.4\}$
. It follows that
$k \in \mathrm {Inds} \setminus \{7.4\}$
. It follows that
![]() $\rho _k$
is a dominant morphism of affine spaces for all
$\rho _k$
is a dominant morphism of affine spaces for all
![]() $k \in \mathrm {Inds} \setminus \{7.4\}$
.
$k \in \mathrm {Inds} \setminus \{7.4\}$
.
The closed points Q of
![]() $\operatorname {Spec} S_k$
bijectively correspond to polynomials
$\operatorname {Spec} S_k$
bijectively correspond to polynomials
![]() $g_Q \in \mathbb C[y, z, t]$
homogeneous of degree
$g_Q \in \mathbb C[y, z, t]$
homogeneous of degree
![]() $6$
, and therefore also to subschemes
$6$
, and therefore also to subschemes
![]() $Z_Q$
of
$Z_Q$
of
![]() $\mathbb P(1, 1, 1, 3)$
with variables
$\mathbb P(1, 1, 1, 3)$
with variables
![]() $y, z, t, w$
given by
$y, z, t, w$
given by
![]() $-w^2 + g_Q$
. Smooth schemes
$-w^2 + g_Q$
. Smooth schemes
![]() $Z_Q \subseteq \mathbb P(1, 1, 1, 3)$
are K3 surfaces that are called sextic double planes. It is known that a very general projective K3 surface has Picard number
$Z_Q \subseteq \mathbb P(1, 1, 1, 3)$
are K3 surfaces that are called sextic double planes. It is known that a very general projective K3 surface has Picard number
![]() $1$
. It follows that an analytically very general sextic double solid X in family
$1$
. It follows that an analytically very general sextic double solid X in family
![]() $k \in \mathrm {Inds} \setminus \{7.4\}$
satisfies that
$k \in \mathrm {Inds} \setminus \{7.4\}$
satisfies that
![]() $\mathbb V_X(x)$
has Picard number
$\mathbb V_X(x)$
has Picard number
![]() $1$
.
$1$
.
Proof of Theorem A(e)
By Theorem A(d), a general sextic double solid in family k is terminal and is smooth along the anti-canonical divisor
![]() $\mathbb V(x)$
. By Corollary 3.15 and Lemma 3.16, an analytically very general sextic double solid in family
$\mathbb V(x)$
. By Corollary 3.15 and Lemma 3.16, an analytically very general sextic double solid in family
![]() $k \neq 7.4$
is factorial.
$k \neq 7.4$
is factorial.
Remark 3.17. In some cases, we can prove that it suffices if the sextic double solid is only general in Theorem A(e) as opposed to analytically very general:
-
(a) A general sextic double solid in family
 $1$
has only one singularity and that singularity is an ordinary double point. Every sextic double solid which is smooth outside an ordinary double point is factorial and has Picard number
$1$
has only one singularity and that singularity is an ordinary double point. Every sextic double solid which is smooth outside an ordinary double point is factorial and has Picard number
 $1$
(see [Reference Cheltsov, Park, Bogomolov and Tschinkel14, Th. B]).
$1$
(see [Reference Cheltsov, Park, Bogomolov and Tschinkel14, Th. B]). -
(b) A general sextic double solid in family
 $4$
is factorial, since in Section 5.2 we construct a Sarkisov link to a complete intersection
$4$
is factorial, since in Section 5.2 we construct a Sarkisov link to a complete intersection
 $Z_{5, 6} \subseteq \mathbb P(1, 1, 1, 2, 3, 4)$
which is
$Z_{5, 6} \subseteq \mathbb P(1, 1, 1, 2, 3, 4)$
which is
 $\mathbb Q$
-factorial if it is general.
$\mathbb Q$
-factorial if it is general.
3.6. Other
 $cA_n$
singularities
$cA_n$
singularities
Although the primary interest is in isolated
![]() $cA_n$
singularities since these are terminal, it is also possible to study non-isolated singularities with the same methods.
$cA_n$
singularities since these are terminal, it is also possible to study non-isolated singularities with the same methods.
We describe uncountably many examples of sextic double solids with a non-isolated
![]() $cA_n$
singularity for all
$cA_n$
singularity for all
![]() $9 \leq n \leq 11$
.
$9 \leq n \leq 11$
.
Proposition 3.18. Let
![]() $8 \leq n \leq 11$
. Let
$8 \leq n \leq 11$
. Let
![]() $r_2$
and
$r_2$
and
![]() $s_3$
be coprime, and let
$s_3$
be coprime, and let
![]() $q_0$
be nonzero. Let X in Notation 3.4 satisfy Condition
$q_0$
be nonzero. Let X in Notation 3.4 satisfy Condition
![]() $(n)$
but not satisfy Condition
$(n)$
but not satisfy Condition
![]() $(n+1)$
, where Conditions (9)–(12) are defined below:
$(n+1)$
, where Conditions (9)–(12) are defined below:
-
(9) Condition
 $(8)$
of Notation 3.4 is satisfied, and there exists
$(8)$
of Notation 3.4 is satisfied, and there exists
 $B_0 \in \mathbb C$
such that
$B_0 \in \mathbb C$
such that  $$\begin{align*}\begin{aligned} A_0 & = a_0,\\ B_1 & = b_1,\\ d_3 & = -s_3B_0 + 2b_0s_3 - 2a_0^2s_3 + c_1r_2 - 4a_0b_1r_2 \\ & \quad + 16a_0^2a_1r_2 + b_1b_2 - 4a_0a_1b_2 - 2a_1^2b_1 + 8a_0a_1^3,\\ c_2 & = r_2B_0 - 6a_0^2r_2 + 2a_0b_2 + 2a_1b_1 - 12a_0a_1^2. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} A_0 & = a_0,\\ B_1 & = b_1,\\ d_3 & = -s_3B_0 + 2b_0s_3 - 2a_0^2s_3 + c_1r_2 - 4a_0b_1r_2 \\ & \quad + 16a_0^2a_1r_2 + b_1b_2 - 4a_0a_1b_2 - 2a_1^2b_1 + 8a_0a_1^3,\\ c_2 & = r_2B_0 - 6a_0^2r_2 + 2a_0b_2 + 2a_1b_1 - 12a_0a_1^2. \end{aligned} \end{align*}$$
-
(10) Condition
 $(9)$
is satisfied and
$(9)$
is satisfied and  $$\begin{align*}\begin{aligned} B_0 & = b_0,\\ d_2 & = 2c_0r_2 - 8a_0b_0r_2 + 16a_0^3r_2 + 2b_0b_2 - 4a_0^2b_2 + b_1^2 - 8a_0a_1b_1 - 4a_1^2b_0 + 24a_0^2a_1^2,\\ c_1 & = 2a_0b_1 + 2a_1b_0 - 12a_0^2a_1, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} B_0 & = b_0,\\ d_2 & = 2c_0r_2 - 8a_0b_0r_2 + 16a_0^3r_2 + 2b_0b_2 - 4a_0^2b_2 + b_1^2 - 8a_0a_1b_1 - 4a_1^2b_0 + 24a_0^2a_1^2,\\ c_1 & = 2a_0b_1 + 2a_1b_0 - 12a_0^2a_1, \end{aligned} \end{align*}$$
-
(11) Condition
 $(10)$
is satisfied and
$(10)$
is satisfied and  $$\begin{align*}\begin{aligned} c_0 & = 2a_0b_0 - 4a_0^3,\\ d_1 & = b_0b_1 - 2a_0^2b_1 - 4a_0a_1b_0 + 8a_0^3a_1, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} c_0 & = 2a_0b_0 - 4a_0^3,\\ d_1 & = b_0b_1 - 2a_0^2b_1 - 4a_0a_1b_0 + 8a_0^3a_1, \end{aligned} \end{align*}$$
-
(12) Condition
 $(11)$
is satisfied and
$(11)$
is satisfied and
 $\begin {aligned}[t] d_0 = b_0^2 - 4a_0^2b_0 + 4a_0^4.\end {aligned}$
$\begin {aligned}[t] d_0 = b_0^2 - 4a_0^2b_0 + 4a_0^4.\end {aligned}$
Then
![]() $P_x$
is a
$P_x$
is a
![]() $cA_n$
singularity of X. Moreover, if
$cA_n$
singularity of X. Moreover, if
![]() $n \geq 9$
, then the singularity is non-isolated.
$n \geq 9$
, then the singularity is non-isolated.
Proof. Use the explicit splitting lemma (Proposition 3.2) and repeatedly apply Lemma 3.9 similarly to the proof of Theorem A(b).
Remark 3.19.
-
(1) By the proof of Theorem A(a), if X in Proposition 3.18 satisfies Condition
 $(9)$
, then X is singular along the curve
$(9)$
, then X is singular along the curve
 $C\colon \mathbb V(t, w, s_3 + 2a_1r_2 + xr_2)$
passing through
$C\colon \mathbb V(t, w, s_3 + 2a_1r_2 + xr_2)$
passing through
 $P_x$
. We can compute that at a general point of C, the singularity is locally analytically
$P_x$
. We can compute that at a general point of C, the singularity is locally analytically
 $\mathbb C^1 \times \operatorname {ODP}$
, that is, it is isomorphic to the germ
$\mathbb C^1 \times \operatorname {ODP}$
, that is, it is isomorphic to the germ
 $(Z, \boldsymbol {0})$
where Z is
$(Z, \boldsymbol {0})$
where Z is
 $\mathbb V(x_1^2 + x_2^2 + x_3^2) \subseteq \mathbb C^4$
with variables
$\mathbb V(x_1^2 + x_2^2 + x_3^2) \subseteq \mathbb C^4$
with variables
 $x_1, x_2, x_3, x_4$
.
$x_1, x_2, x_3, x_4$
. -
(2) Translating the point
 $P_t = [0, 0, 0, 1, 0]$
to
$P_t = [0, 0, 0, 1, 0]$
to
 $[1, 0, 0, 0, 0]$
, we can find conditions similar to Notation 3.4 for having a
$[1, 0, 0, 0, 0]$
, we can find conditions similar to Notation 3.4 for having a
 $cA_n$
singularity at
$cA_n$
singularity at
 $P_t \in X$
, which can be used to construct general sextic double solids with two
$P_t \in X$
, which can be used to construct general sextic double solids with two
 $cA_n$
singularities. The following is a simple example with
$cA_n$
singularities. The following is a simple example with
 $cA_5$
singularities at
$cA_5$
singularities at
 $P_x$
and at
$P_x$
and at
 $P_t$
:
$P_t$
:  $$\begin{align*}\mathbb V(-w^2 + x^4t^2 + x^2t^4 + y^6 + z^6) \subseteq \mathbb P(1, 1, 1, 1, 3). \end{align*}$$
$$\begin{align*}\mathbb V(-w^2 + x^4t^2 + x^2t^4 + y^6 + z^6) \subseteq \mathbb P(1, 1, 1, 1, 3). \end{align*}$$
4. Divisorial contractions with center a
 $cA_n$
point
$cA_n$
point
In this section, we discuss weighted blowups from both algebraic and local analytic points of view. In Proposition 4.6, we show that to check whether a weighted blowup is a Kawakita blowup (see Theorem 2.21), it suffices to compute the weight of the defining power series. Using this, in the technical Lemma 4.9, we show how to algebraically construct Kawakita blowups of
![]() $cA_n$
points on affine hypersurfaces.
$cA_n$
points on affine hypersurfaces.
4.1. Weight-respecting maps
Let n and m be positive integers. Let
![]() $\boldsymbol {x} = (x_1, \ldots , x_n)$
and
$\boldsymbol {x} = (x_1, \ldots , x_n)$
and
![]() $\boldsymbol {y} = (y_1, \ldots , y_m)$
denote the coordinates on
$\boldsymbol {y} = (y_1, \ldots , y_m)$
denote the coordinates on
![]() $\mathbb C^n$
and
$\mathbb C^n$
and
![]() $\mathbb C^m$
, respectively. Choose positive integer weights for
$\mathbb C^m$
, respectively. Choose positive integer weights for
![]() $\boldsymbol {x}$
and
$\boldsymbol {x}$
and
![]() $\boldsymbol {y}$
.
$\boldsymbol {y}$
.
Definition 4.1. Let
![]() $X \subseteq \mathbb C^n$
and
$X \subseteq \mathbb C^n$
and
![]() $X' \subseteq \mathbb C^m$
be complex analytic spaces. We say that a biholomorphic map
$X' \subseteq \mathbb C^m$
be complex analytic spaces. We say that a biholomorphic map
![]() $\psi \colon X \to X'$
taking
$\psi \colon X \to X'$
taking
![]() $\boldsymbol {0}$
to
$\boldsymbol {0}$
to
![]() $\boldsymbol {0}$
is weight-respecting if denoting its inverse by
$\boldsymbol {0}$
is weight-respecting if denoting its inverse by
![]() $\theta $
, we can locally analytically around the origins write
$\theta $
, we can locally analytically around the origins write
![]() $\psi = (\psi _1, \ldots , \psi _m)$
and
$\psi = (\psi _1, \ldots , \psi _m)$
and
![]() $\theta = (\theta _1, \ldots , \theta _n)$
where for all i and j, the power series
$\theta = (\theta _1, \ldots , \theta _n)$
where for all i and j, the power series
![]() $\psi _j \in \mathbb C\{\boldsymbol {x}\}$
and
$\psi _j \in \mathbb C\{\boldsymbol {x}\}$
and
![]() $\theta _i \in \mathbb C\{\boldsymbol {y}\}$
satisfy
$\theta _i \in \mathbb C\{\boldsymbol {y}\}$
satisfy
![]() $\operatorname {wt}(\psi _j) \geq \operatorname {wt}(y_j)$
and
$\operatorname {wt}(\psi _j) \geq \operatorname {wt}(y_j)$
and
![]() $\operatorname {wt}(\theta _i) \geq \operatorname {wt}(x_i)$
.
$\operatorname {wt}(\theta _i) \geq \operatorname {wt}(x_i)$
.
It is known that a biholomorphic map taking the origin to the origin lifts to a unique biholomorphic map of the blown-up spaces under the usual weights
![]() $(1, \ldots , 1)$
(see, e.g., [Reference Greuel, Lossen and Shustin25, Rem. 3.17.1(4)]). It is easy to come up with examples where a biholomorphic map does not lift under weighted blowups. We give one example below.
$(1, \ldots , 1)$
(see, e.g., [Reference Greuel, Lossen and Shustin25, Rem. 3.17.1(4)]). It is easy to come up with examples where a biholomorphic map does not lift under weighted blowups. We give one example below.
Example 4.2. Let
![]() $X \subseteq \mathbb C^3$
be the complex analytic space given by
$X \subseteq \mathbb C^3$
be the complex analytic space given by
![]() $\mathbb V(f)$
where
$\mathbb V(f)$
where
for some
![]() $a, b \in \mathbb C^*$
. Define
$a, b \in \mathbb C^*$
. Define
![]() $X' \subseteq \mathbb C^3$
by
$X' \subseteq \mathbb C^3$
by
![]() $\mathbb V(f')$
where
$\mathbb V(f')$
where
![]() $f' = f(x_1, x_2, -x_2 + x_3)$
. Choose weights
$f' = f(x_1, x_2, -x_2 + x_3)$
. Choose weights
![]() $(1, 1, 2)$
for
$(1, 1, 2)$
for
![]() $(x_1, x_2, x_3)$
. Then, X and
$(x_1, x_2, x_3)$
. Then, X and
![]() $X'$
are biholomorphic and
$X'$
are biholomorphic and
![]() $\operatorname {wt} f = \operatorname {wt} f'$
, but the weighted blowups of X and
$\operatorname {wt} f = \operatorname {wt} f'$
, but the weighted blowups of X and
![]() $X'$
are not locally analytically equivalent.
$X'$
are not locally analytically equivalent.
Proof. Let
![]() $\psi \colon X \to X'$
be any local biholomorphism taking the origin to the origin. Composing with a suitable weight-respecting biholomorphic map and using Corollary 4.4, it suffices to consider the case where
$\psi \colon X \to X'$
be any local biholomorphism taking the origin to the origin. Composing with a suitable weight-respecting biholomorphic map and using Corollary 4.4, it suffices to consider the case where
![]() $\psi $
is a linear biholomorphism. Since the elliptic curve defined by f in
$\psi $
is a linear biholomorphism. Since the elliptic curve defined by f in
![]() $\mathbb P^2$
with variables
$\mathbb P^2$
with variables
![]() $x_1, x_2, x_3$
has only two automorphisms, there are only four possibilities for a linear biholomorphism
$x_1, x_2, x_3$
has only two automorphisms, there are only four possibilities for a linear biholomorphism
![]() $X \to X'$
, namely
$X \to X'$
, namely
![]() $(x_1, x_2, x_3) \mapsto (x_1, \pm x_2, \pm x_2 + x_3)$
.
$(x_1, x_2, x_3) \mapsto (x_1, \pm x_2, \pm x_2 + x_3)$
.
Let
![]() $Y \to X$
and
$Y \to X$
and
![]() $Y' \to X'$
be the
$Y' \to X'$
be the
![]() $(1, 1, 2)$
-blowups of X and
$(1, 1, 2)$
-blowups of X and
![]() $X'$
, respectively. Then Y is given by
$X'$
, respectively. Then Y is given by
![]() $\mathbb V(g)$
where
$\mathbb V(g)$
where
Denoting the points of Y and
![]() $Y'$
by
$Y'$
by
![]() $[u, x_1, x_2, x_3]$
, the lifted map
$[u, x_1, x_2, x_3]$
, the lifted map
![]() $\psi _Y\colon Y \to Y'$
is given by
$\psi _Y\colon Y \to Y'$
is given by
![]() $[u, x_1, x_2, x_3] \mapsto [u, x_1, \pm x_2, \pm x_2/u + x_3]$
, which is not holomorphic on the exceptional locus
$[u, x_1, x_2, x_3] \mapsto [u, x_1, \pm x_2, \pm x_2/u + x_3]$
, which is not holomorphic on the exceptional locus
![]() $\mathbb V(u)$
.
$\mathbb V(u)$
.
On the other hand, a weight-respecting coordinate change does lift to weighted blowups (see Corollary 4.4).
Lemma 4.3. Let
![]() $X \subseteq \mathbb C^n$
and
$X \subseteq \mathbb C^n$
and
![]() $X' \subseteq \mathbb C^m$
be complex analytic spaces strictly containing the origins and
$X' \subseteq \mathbb C^m$
be complex analytic spaces strictly containing the origins and
![]() $\psi \colon X \to X'$
a biholomorphism. Then
$\psi \colon X \to X'$
a biholomorphism. Then
![]() $\psi $
is weight-respecting if and only if
$\psi $
is weight-respecting if and only if
![]() $\psi $
induces an isomorphism of the
$\psi $
induces an isomorphism of the
![]() $\mathbb Z_{\geq 0}$
-graded
$\mathbb Z_{\geq 0}$
-graded
![]() $\mathcal O_{X'}$
-algebras
$\mathcal O_{X'}$
-algebras
![]() $\mathcal B_{X'}$
and
$\mathcal B_{X'}$
and
![]() $\psi _* \mathcal B_X$
of Definition 2.18.
$\psi _* \mathcal B_X$
of Definition 2.18.
Proof. “
![]() $\Longrightarrow $
.” The induced morphism
$\Longrightarrow $
.” The induced morphism
![]() $\mathcal B_{X'} \to \psi _* \mathcal B_X$
is given by
$\mathcal B_{X'} \to \psi _* \mathcal B_X$
is given by
 $$\begin{align*}\begin{aligned} \mathcal B_{X'}(U) & \to \mathcal B_X(\psi^{-1} U)\\ t^d \bar y_j & \mapsto t^d \bar{\psi}_j, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \mathcal B_{X'}(U) & \to \mathcal B_X(\psi^{-1} U)\\ t^d \bar y_j & \mapsto t^d \bar{\psi}_j, \end{aligned} \end{align*}$$
where
![]() $U \subseteq X'$
is open. Since
$U \subseteq X'$
is open. Since
![]() $\operatorname {wt} \psi _j \geq \operatorname {wt} y_j$
, the morphism
$\operatorname {wt} \psi _j \geq \operatorname {wt} y_j$
, the morphism
![]() $\mathcal B_{X'} \to \psi _* \mathcal B_X$
is well-defined. Similarly, we define a morphism
$\mathcal B_{X'} \to \psi _* \mathcal B_X$
is well-defined. Similarly, we define a morphism
![]() $\mathcal B_{X'} \gets \psi _* \mathcal B_X$
, which is its inverse.
$\mathcal B_{X'} \gets \psi _* \mathcal B_X$
, which is its inverse.
“
![]() $\Longleftarrow $
.” Let
$\Longleftarrow $
.” Let
![]() $t^{\operatorname {wt} y_j} \Psi _j$
be the image of
$t^{\operatorname {wt} y_j} \Psi _j$
be the image of
![]() $t^{\operatorname {wt} y_j} y_j$
under
$t^{\operatorname {wt} y_j} y_j$
under
![]() $\mathcal B_{X'}(X') \to \psi _* \mathcal B_X(X)$
. There exists
$\mathcal B_{X'}(X') \to \psi _* \mathcal B_X(X)$
. There exists
![]() $\psi _j \in \mathbb C\{\boldsymbol {x}\}$
such that
$\psi _j \in \mathbb C\{\boldsymbol {x}\}$
such that
![]() $\operatorname {wt} \psi _j \geq \operatorname {wt} y_j$
and
$\operatorname {wt} \psi _j \geq \operatorname {wt} y_j$
and
![]() $\bar {\psi }_j = \Psi _j$
. Similarly, we can find
$\bar {\psi }_j = \Psi _j$
. Similarly, we can find
![]() $\theta _i$
, showing that
$\theta _i$
, showing that
![]() $\psi $
is weight-respecting.
$\psi $
is weight-respecting.
Corollary 4.4. A weight-respecting biholomorphism
![]() $\psi $
from
$\psi $
from
![]() $X \subseteq \mathbb C^n$
to
$X \subseteq \mathbb C^n$
to
![]() $X' \subseteq \mathbb C^m$
lifts to the weighted blown-up spaces.
$X' \subseteq \mathbb C^m$
lifts to the weighted blown-up spaces.
4.2. Kawakita blowup in analytic neighborhoods
In the following, we focus on Kawakita blowups (see Theorem 2.21). Unlike Example 4.2, for
![]() $cA_n$
singularities, having the correct weight for the defining power series is enough for the local analytic equivalence of weighted blowups.
$cA_n$
singularities, having the correct weight for the defining power series is enough for the local analytic equivalence of weighted blowups.
Notation 4.5. We choose positive integer weights
![]() $\boldsymbol {w} = (r_1, r_2, a, 1)$
for variables
$\boldsymbol {w} = (r_1, r_2, a, 1)$
for variables
![]() $\boldsymbol {x} = (x_1, x_2, x_3, x_4)$
on
$\boldsymbol {x} = (x_1, x_2, x_3, x_4)$
on
![]() $\mathbb C^4$
and define
$\mathbb C^4$
and define
![]() $n = (r_1 + r_2)/a - 1$
such that
$n = (r_1 + r_2)/a - 1$
such that
-
• a divides
 $r_1 + r_2$
and is coprime to both
$r_1 + r_2$
and is coprime to both
 $r_1$
and
$r_1$
and
 $r_2$
,
$r_2$
, -
•
 $r_1 \geq r_2$
, and
$r_1 \geq r_2$
, and -
•
 $n \geq 2$
.
$n \geq 2$
.
Proposition 4.6. Using Notation 4.5, let
![]() $f \in \mathbb C\{\boldsymbol {x}\}$
be such that
$f \in \mathbb C\{\boldsymbol {x}\}$
be such that
![]() $\mathbb V(f)$
has an isolated
$\mathbb V(f)$
has an isolated
![]() $cA_n$
singularity at the origin and f has weight
$cA_n$
singularity at the origin and f has weight
![]() $r_1 + r_2$
. Then, the
$r_1 + r_2$
. Then, the
![]() $\boldsymbol {w}$
-blowup of
$\boldsymbol {w}$
-blowup of
![]() $\mathbb V(f) \subseteq \mathbb C^4$
is a
$\mathbb V(f) \subseteq \mathbb C^4$
is a
![]() $\boldsymbol {w}$
-Kawakita blowup.
$\boldsymbol {w}$
-Kawakita blowup.
Proof. First, we remind that the terms homogeneous, degree, and multiplicity are with respect to the standard weights
![]() $(1, \ldots , 1)$
. Let the quadratic part of f denote the homogeneous part of f of degree
$(1, \ldots , 1)$
. Let the quadratic part of f denote the homogeneous part of f of degree
![]() $2$
. After a suitable invertible linear weight-respecting coordinate change, the quadratic part of f is
$2$
. After a suitable invertible linear weight-respecting coordinate change, the quadratic part of f is
![]() $x_1 x_2$
.
$x_1 x_2$
.
We find that
![]() $f = x_1 x_2 + x_1 G + H$
, where
$f = x_1 x_2 + x_1 G + H$
, where
![]() $G \in \mathbb C\{x_1, \ldots , x_4\}$
has weight at least
$G \in \mathbb C\{x_1, \ldots , x_4\}$
has weight at least
![]() $r_2$
and multiplicity
$r_2$
and multiplicity
![]() $m \geq 2$
, and
$m \geq 2$
, and
![]() $H \in \mathbb C\{x_2, x_3, x_4\}$
. The coordinate change
$H \in \mathbb C\{x_2, x_3, x_4\}$
. The coordinate change
![]() $x_2 \mapsto x_2 - G_m$
, where
$x_2 \mapsto x_2 - G_m$
, where
![]() $G_m$
is the homogeneous degree m part of G, takes f to
$G_m$
is the homogeneous degree m part of G, takes f to
![]() $x_1 x_2 + x_1 G' + H'$
, where
$x_1 x_2 + x_1 G' + H'$
, where
![]() $G'$
has multiplicity at least
$G'$
has multiplicity at least
![]() $m + 1$
. By induction, this defines the unique formal power series
$m + 1$
. By induction, this defines the unique formal power series
![]() $K \in \mathbb C[[x_1, \ldots , x_4]]$
of multiplicity at least
$K \in \mathbb C[[x_1, \ldots , x_4]]$
of multiplicity at least
![]() $2$
and weight at least
$2$
and weight at least
![]() $r_2$
such that the transformation
$r_2$
such that the transformation
![]() $x_2 \mapsto x_2 + K$
takes f to the form
$x_2 \mapsto x_2 + K$
takes f to the form
![]() $x_1 x_2 + H"$
where
$x_1 x_2 + H"$
where
![]() $H" \in \mathbb C[[x_2, x_3, x_4]]$
. Similarly, we transform f into
$H" \in \mathbb C[[x_2, x_3, x_4]]$
. Similarly, we transform f into
![]() $x_1 x_2 + h$
where
$x_1 x_2 + h$
where
![]() $h \in \mathbb C[[x_3, x_4]]$
, using
$h \in \mathbb C[[x_3, x_4]]$
, using
![]() $x_1 \mapsto x_1 + L$
where
$x_1 \mapsto x_1 + L$
where
![]() $L \in \mathbb C[[x_2, x_3, x_4]]$
.
$L \in \mathbb C[[x_2, x_3, x_4]]$
.
We show how to find a convergent weight-respecting coordinate change which changes f to
![]() $x_1 x_2 + h$
. Instead of the coordinate changes
$x_1 x_2 + h$
. Instead of the coordinate changes
![]() $x_2 \mapsto x_2 + K$
,
$x_2 \mapsto x_2 + K$
,
![]() $x_1 \mapsto x_1 + L$
, which might not be convergent, we do a coordinate change
$x_1 \mapsto x_1 + L$
, which might not be convergent, we do a coordinate change
![]() $\Theta _N$
with truncated power series
$\Theta _N$
with truncated power series
![]() $K_{\leq N}$
and
$K_{\leq N}$
and
![]() $L_{\leq N}$
of homogeneous parts of K and L of degree at most N. The coordinate change
$L_{\leq N}$
of homogeneous parts of K and L of degree at most N. The coordinate change
![]() $\Psi \colon x_1 \mapsto x_1 + i x_2$
,
$\Psi \colon x_1 \mapsto x_1 + i x_2$
,
![]() $x_2 \mapsto x_1 - i x_2$
takes
$x_2 \mapsto x_1 - i x_2$
takes
![]() $x_1 x_2$
into
$x_1 x_2$
into
![]() $x_1^2 + x_2^2$
. Now we use the splitting lemma, which gives a convergent coordinate change
$x_1^2 + x_2^2$
. Now we use the splitting lemma, which gives a convergent coordinate change
![]() $\Phi _N$
which respects the weighting when N is large enough, to give f the form
$\Phi _N$
which respects the weighting when N is large enough, to give f the form
![]() $x_1^2 + x_2^2 + h(x_3, x_4)$
where h converges. Applying
$x_1^2 + x_2^2 + h(x_3, x_4)$
where h converges. Applying
![]() $\Psi ^{-1}$
, we get
$\Psi ^{-1}$
, we get
![]() $x_1 x_2 + h$
. Note that the coordinate changes
$x_1 x_2 + h$
. Note that the coordinate changes
![]() $\Psi $
and
$\Psi $
and
![]() $\Psi ^{-1}$
might not respect the weighting
$\Psi ^{-1}$
might not respect the weighting
![]() $\boldsymbol {w}$
, but the total coordinate change
$\boldsymbol {w}$
, but the total coordinate change
![]() $\Psi ^{-1} \circ \Phi _N \circ \Psi \circ \Theta _N$
is weight-respecting if N is large enough.
$\Psi ^{-1} \circ \Phi _N \circ \Psi \circ \Theta _N$
is weight-respecting if N is large enough.
Since the singularity is
![]() $cA_n$
where
$cA_n$
where
![]() $n = (r_1 + r_2)/a - 1$
, h must contain a monomial of degree
$n = (r_1 + r_2)/a - 1$
, h must contain a monomial of degree
![]() $(r_1 + r_2)/a$
. Since
$(r_1 + r_2)/a$
. Since
![]() $x_1 x_2 + h$
has weight
$x_1 x_2 + h$
has weight
![]() $r_1 + r_2$
, if
$r_1 + r_2$
, if
![]() $a> 1$
, then the coefficient of
$a> 1$
, then the coefficient of
![]() $x_3^{(r_1 + r_2)/a}$
in h is nonzero. If
$x_3^{(r_1 + r_2)/a}$
in h is nonzero. If
![]() $a = 1$
, then after a suitable invertible linear coordinate change on
$a = 1$
, then after a suitable invertible linear coordinate change on
![]() $\mathbb C\{x_3, x_4\}$
, the coefficient of
$\mathbb C\{x_3, x_4\}$
, the coefficient of
![]() $x_3^{(r_1 + r_2)/a}$
in h is nonzero.
$x_3^{(r_1 + r_2)/a}$
in h is nonzero.
We found that we can transform f into the form
![]() $x_1 x_2 + h$
where the coefficient of
$x_1 x_2 + h$
where the coefficient of
![]() $x_3^{(r_1 + r_2)/a}$
in h is nonzero, by using only weight-respecting coordinate changes. By Corollary 4.4, the weighted blowup of f is locally analytically equivalent to the weighted blowup of
$x_3^{(r_1 + r_2)/a}$
in h is nonzero, by using only weight-respecting coordinate changes. By Corollary 4.4, the weighted blowup of f is locally analytically equivalent to the weighted blowup of
![]() $x_1 x_2 + h$
, which is precisely a Kawakita blowup.
$x_1 x_2 + h$
, which is precisely a Kawakita blowup.
Given a variety X with an isolated
![]() $cA_n$
point P, we show that any two
$cA_n$
point P, we show that any two
![]() $\boldsymbol {w}$
-Kawakita blowups
$\boldsymbol {w}$
-Kawakita blowups
![]() $Y \to X$
and
$Y \to X$
and
![]() $Y' \to X$
of the point P are locally analytically equivalent. Note that they need not be globally algebraically equivalent. For example, [Reference Corti and Mella18, Rem. 2.4] describes two different
$Y' \to X$
of the point P are locally analytically equivalent. Note that they need not be globally algebraically equivalent. For example, [Reference Corti and Mella18, Rem. 2.4] describes two different
![]() $(2, 1, 1, 1)$
-Kawakita blowups of a
$(2, 1, 1, 1)$
-Kawakita blowups of a
![]() $cA_2$
singularity on a quartic 3-fold.
$cA_2$
singularity on a quartic 3-fold.
Proposition 4.7. Any two
![]() $\boldsymbol {w}$
-Kawakita blowups of locally biholomorphic singularities are locally analytically equivalent.
$\boldsymbol {w}$
-Kawakita blowups of locally biholomorphic singularities are locally analytically equivalent.
Proof. Let
![]() $f = x_1 x_2 + g(x_3, x_4)$
and
$f = x_1 x_2 + g(x_3, x_4)$
and
![]() $f' = x_1 x_2 + g'(x_3, x_4)$
be contact equivalent, where
$f' = x_1 x_2 + g'(x_3, x_4)$
be contact equivalent, where
![]() $g, g' \in \mathbb C\{x_3, x_4\}$
have weight
$g, g' \in \mathbb C\{x_3, x_4\}$
have weight
![]() $r_1 + r_2$
and
$r_1 + r_2$
and
![]() $x_3^{(r_1 + r_2)/a}$
appears in both g and in
$x_3^{(r_1 + r_2)/a}$
appears in both g and in
![]() $g'$
with nonzero coefficient. It suffices to show that there exist a weight-respecting map from
$g'$
with nonzero coefficient. It suffices to show that there exist a weight-respecting map from
![]() $\mathbb V(f)$
to
$\mathbb V(f)$
to
![]() $\mathbb V(f')$
.
$\mathbb V(f')$
.
Since f and
![]() $f'$
are contact equivalent, there exist a unit
$f'$
are contact equivalent, there exist a unit
![]() $u \in \mathbb C\{\boldsymbol {x}\}$
and a local biholomorphism
$u \in \mathbb C\{\boldsymbol {x}\}$
and a local biholomorphism
![]() $\psi \colon (\mathbb C^4, \boldsymbol {0}) \to (\mathbb C^4, \boldsymbol {0})$
such that
$\psi \colon (\mathbb C^4, \boldsymbol {0}) \to (\mathbb C^4, \boldsymbol {0})$
such that
![]() $f' = u(f \circ \psi )$
. Note that
$f' = u(f \circ \psi )$
. Note that
![]() $f'$
and
$f'$
and
![]() $f \circ \psi $
have the same weight
$f \circ \psi $
have the same weight
![]() $r_1 + r_2$
, and
$r_1 + r_2$
, and
![]() $x_3^{(r_1 + r_2)/a}$
appears in
$x_3^{(r_1 + r_2)/a}$
appears in
![]() $f \circ \psi $
with nonzero coefficient. It suffices to show that there exist a weight-respecting map from
$f \circ \psi $
with nonzero coefficient. It suffices to show that there exist a weight-respecting map from
![]() $\mathbb V(f)$
to
$\mathbb V(f)$
to
![]() $\mathbb V(f \circ \psi )$
.
$\mathbb V(f \circ \psi )$
.
Using arguments similar to the proof of Proposition 4.6, we can find a weight-respecting biholomorphic map germ
![]() $\theta \colon (\mathbb C^4, \boldsymbol {0}) \to (\mathbb C^4, \boldsymbol {0})$
such that
$\theta \colon (\mathbb C^4, \boldsymbol {0}) \to (\mathbb C^4, \boldsymbol {0})$
such that
![]() $f \circ \psi \circ \theta $
is of the form
$f \circ \psi \circ \theta $
is of the form
![]() $x_1 x_2 + g"$
where
$x_1 x_2 + g"$
where
![]() $g" \in \mathbb C\{x_3, x_4\}$
contains
$g" \in \mathbb C\{x_3, x_4\}$
contains
![]() $x^{(r_1 + r_2)/a}$
and has weight
$x^{(r_1 + r_2)/a}$
and has weight
![]() $r_1 + r_2$
. It suffices to show that there exist a weight-respecting map from
$r_1 + r_2$
. It suffices to show that there exist a weight-respecting map from
![]() $\mathbb V(f)$
to
$\mathbb V(f)$
to
![]() $\mathbb V(f \circ \psi \circ \theta )$
.
$\mathbb V(f \circ \psi \circ \theta )$
.
By Proposition 2.5, g and
![]() $g"$
are right equivalent, meaning there exists an automorphism
$g"$
are right equivalent, meaning there exists an automorphism
![]() $\Phi $
of
$\Phi $
of
![]() $\mathbb C\{x_3, x_4\}$
such that
$\mathbb C\{x_3, x_4\}$
such that
![]() $\Phi (g) = g"$
. Since
$\Phi (g) = g"$
. Since
![]() $x_3^{(r_1 + r_2)/a}$
has nonzero coefficient in both g and
$x_3^{(r_1 + r_2)/a}$
has nonzero coefficient in both g and
![]() $g"$
, and both g and
$g"$
, and both g and
![]() $g"$
have weight
$g"$
have weight
![]() $r_1 + r_2$
, the image of
$r_1 + r_2$
, the image of
![]() $x_3$
has weight a under both
$x_3$
has weight a under both
![]() $\Phi $
and
$\Phi $
and
![]() $\Phi ^{-1}$
. Define the biholomorphic map germ
$\Phi ^{-1}$
. Define the biholomorphic map germ
![]() $\varphi \colon (\mathbb V(f \circ \psi \circ \theta ), \boldsymbol {0}) \to (\mathbb V(f), \boldsymbol {0})$
by
$\varphi \colon (\mathbb V(f \circ \psi \circ \theta ), \boldsymbol {0}) \to (\mathbb V(f), \boldsymbol {0})$
by
![]() $\boldsymbol {x} \mapsto (x_1, x_2, \Phi (x_3), \Phi (x_4))$
. By Corollary 4.4, the
$\boldsymbol {x} \mapsto (x_1, x_2, \Phi (x_3), \Phi (x_4))$
. By Corollary 4.4, the
![]() $\boldsymbol {w}$
-blowups of
$\boldsymbol {w}$
-blowups of
![]() $\mathbb V(f \circ \psi \circ \theta ) \subseteq \mathbb C^4$
and
$\mathbb V(f \circ \psi \circ \theta ) \subseteq \mathbb C^4$
and
![]() $\mathbb V(f) \subseteq \mathbb C^4$
are locally analytically equivalent.
$\mathbb V(f) \subseteq \mathbb C^4$
are locally analytically equivalent.
4.3. Kawakita blowups on affine hypersurfaces
In this section, we see how to construct weighted blowups for affine hypersurfaces with a
![]() $cA_n$
singularity where
$cA_n$
singularity where
![]() $n \geq 2$
such that locally analytically they are Kawakita blowups.
$n \geq 2$
such that locally analytically they are Kawakita blowups.
Most
![]() $cA_n$
singularities do not admit
$cA_n$
singularities do not admit
![]() $(r_1, r_2, a, 1)$
-Kawakita blowups where
$(r_1, r_2, a, 1)$
-Kawakita blowups where
![]() $a \geq 2$
. Below, we define the type of an isolated
$a \geq 2$
. Below, we define the type of an isolated
![]() $cA_n$
singularity, which for
$cA_n$
singularity, which for
![]() $n \geq 2$
is equal to the highest integer a such that it admits some
$n \geq 2$
is equal to the highest integer a such that it admits some
![]() $(r_1, r_2, a, 1)$
-Kawakita blowup locally analytically. General sextic double solids with an isolated
$(r_1, r_2, a, 1)$
-Kawakita blowup locally analytically. General sextic double solids with an isolated
![]() $cA_n$
singularity have a type
$cA_n$
singularity have a type
![]() $1 cA_n$
singularity.
$1 cA_n$
singularity.
Definition 4.8. Let
![]() $(X, P)$
be the complex analytic space germ of an isolated
$(X, P)$
be the complex analytic space germ of an isolated
![]() $cA_n$
singularity. Let a be the largest integer such that
$cA_n$
singularity. Let a be the largest integer such that
![]() $(X, P)$
is isomorphic to some germ
$(X, P)$
is isomorphic to some germ
![]() $(\mathbb V(x_1 x_2 + g), \boldsymbol {0})$
where
$(\mathbb V(x_1 x_2 + g), \boldsymbol {0})$
where
![]() $g \in \mathbb C\{x_3, x_4\}$
has weight
$g \in \mathbb C\{x_3, x_4\}$
has weight
![]() $a(n+1)$
under the weighting
$a(n+1)$
under the weighting
![]() $(a, 1)$
for
$(a, 1)$
for
![]() $(x_3, x_4)$
. Then, we say that the
$(x_3, x_4)$
. Then, we say that the
![]() $cA_n$
singularity is of type a.
$cA_n$
singularity is of type a.
It is not obvious how to globally algebraically construct a Kawakita blowup for a variety with a
![]() $cA_n$
singularity. We show this for affine hypersurfaces in the technical Lemma 4.9. We use a projectivization of Corollary 4.10 in Section 5 for constructing Kawakita blowups of sextic double solids.
$cA_n$
singularity. We show this for affine hypersurfaces in the technical Lemma 4.9. We use a projectivization of Corollary 4.10 in Section 5 for constructing Kawakita blowups of sextic double solids.
We describe the notation for Lemma 4.9. Choose positive integers
![]() $n, r_1, r_2$
, and a as in Notation 4.5. Let
$n, r_1, r_2$
, and a as in Notation 4.5. Let
![]() $F \in \mathbb C[x_1, x_2, x_3, x_4]$
have multiplicity at least
$F \in \mathbb C[x_1, x_2, x_3, x_4]$
have multiplicity at least
![]() $3$
, and let
$3$
, and let
be such that
![]() $\mathbb V(f) \subseteq \mathbb C^4$
has terminal singularities and has a
$\mathbb V(f) \subseteq \mathbb C^4$
has terminal singularities and has a
![]() $cA_n$
singularity of type at least a at the origin. Let
$cA_n$
singularity of type at least a at the origin. Let
![]() $q, w$
be the power series when splitting with respect to
$q, w$
be the power series when splitting with respect to
![]() $x_1$
(Theorem 3.1), and
$x_1$
(Theorem 3.1), and
![]() $p, v$
be the power series when splitting with respect to
$p, v$
be the power series when splitting with respect to
![]() $x_2$
, that is,
$x_2$
, that is,
where
![]() $q \in \mathbb C\{x_2, x_3, x_4\}$
and
$q \in \mathbb C\{x_2, x_3, x_4\}$
and
![]() $p \in \mathbb C\{x_3, x_4\}$
both have multiplicity at least 2, and
$p \in \mathbb C\{x_3, x_4\}$
both have multiplicity at least 2, and
![]() $w \in \mathbb C\{x_1, x_2, x_3, x_4\}$
and
$w \in \mathbb C\{x_1, x_2, x_3, x_4\}$
and
![]() $v \in \mathbb C\{x_2, x_3, x_4\}$
are units, and
$v \in \mathbb C\{x_2, x_3, x_4\}$
are units, and
![]() $h \in \mathbb C\{x_3, x_4\}$
has multiplicity at least 3. If
$h \in \mathbb C\{x_3, x_4\}$
has multiplicity at least 3. If
![]() $a> 1$
, then perform a coordinate change on
$a> 1$
, then perform a coordinate change on
![]() $x_3, x_4$
for f such that h has weight
$x_3, x_4$
for f such that h has weight
![]() $r_1 + r_2$
.
$r_1 + r_2$
.
Now choose weights
for the variables
![]() $\alpha , \beta , x_3, x_4$
on
$\alpha , \beta , x_3, x_4$
on
![]() $\mathbb C^4$
and
$\mathbb C^4$
and
for the variables
![]() $\alpha , \beta , x_1, x_2, x_3, x_4$
on
$\alpha , \beta , x_1, x_2, x_3, x_4$
on
![]() $\mathbb C^6$
, where
$\mathbb C^6$
, where
![]() $m = \min (r_2, \operatorname {mult} q)$
. Writing a power series
$m = \min (r_2, \operatorname {mult} q)$
. Writing a power series
![]() $s \in \mathbb C\{x_1, x_2, x_3, x_4\}$
as a sum of its
$s \in \mathbb C\{x_1, x_2, x_3, x_4\}$
as a sum of its
![]() $\boldsymbol {w}'$
-weighted homogeneous parts
$\boldsymbol {w}'$
-weighted homogeneous parts
![]() $s = \sum _{i=0}^\infty s_i$
, let
$s = \sum _{i=0}^\infty s_i$
, let
![]() $s_{<k}$
denote
$s_{<k}$
denote
![]() $\sum _{i<k} s_i$
and
$\sum _{i<k} s_i$
and
![]() $s_{\geq k}$
denote
$s_{\geq k}$
denote
![]() $\sum _{i\geq k} s_i$
. Define the ideal
$\sum _{i\geq k} s_i$
. Define the ideal
of
![]() $\mathbb C[\alpha , \beta , x_1, x_2, x_3, x_4]$
, where
$\mathbb C[\alpha , \beta , x_1, x_2, x_3, x_4]$
, where
![]() $v_{<r_1-r_2}$
is defined to be
$v_{<r_1-r_2}$
is defined to be
![]() $1$
when
$1$
when
![]() $r_1 = r_2$
and where
$r_1 = r_2$
and where
![]() $w_{<r_1-m}$
is defined to be
$w_{<r_1-m}$
is defined to be
![]() $1$
when
$1$
when
![]() $r_1 = m$
. Note that the affine varieties
$r_1 = m$
. Note that the affine varieties
![]() $\mathbb V(f) \subseteq \mathbb C^4$
and
$\mathbb V(f) \subseteq \mathbb C^4$
and
![]() $\mathbb V(I) \subseteq \mathbb C^6$
are isomorphic.
$\mathbb V(I) \subseteq \mathbb C^6$
are isomorphic.
Lemma 4.9. Using the notation above, the
![]() $\boldsymbol {w}'$
-blowup of
$\boldsymbol {w}'$
-blowup of
![]() $\mathbb V(I)$
is a
$\mathbb V(I)$
is a
![]() $\boldsymbol {w}$
-Kawakita blowup.
$\boldsymbol {w}$
-Kawakita blowup.
Proof. The morphism
 $$\begin{align*}\begin{aligned} \varphi\colon \mathbb C^4 & \to \mathbb C^4\\ (x_1, x_2, x_3, x_4) & \mapsto ((x_1 + q_{<r_1})w_{<r_1-m} + (x_2 + p_{<r_1})v_{<r_1-r_2},\ x_2 + p_{<r_2},\ x_3,\ x_4) \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \varphi\colon \mathbb C^4 & \to \mathbb C^4\\ (x_1, x_2, x_3, x_4) & \mapsto ((x_1 + q_{<r_1})w_{<r_1-m} + (x_2 + p_{<r_1})v_{<r_1-r_2},\ x_2 + p_{<r_2},\ x_3,\ x_4) \end{aligned} \end{align*}$$
has a local analytic inverse
![]() $\varphi ^{-1}$
, given by
$\varphi ^{-1}$
, given by
 $$\begin{align*}\begin{aligned} \varphi^{-1}\colon (\mathbb C^4, \boldsymbol{0}) & \to (\mathbb C^4, \boldsymbol{0})\\ (\alpha, \beta, x_3, x_4) & \mapsto ((\alpha - (\beta - p_{<r_2} + p_{<r_1})v')u - q',\ \beta - p_{<r_2},\ x_3,\ x_4), \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \varphi^{-1}\colon (\mathbb C^4, \boldsymbol{0}) & \to (\mathbb C^4, \boldsymbol{0})\\ (\alpha, \beta, x_3, x_4) & \mapsto ((\alpha - (\beta - p_{<r_2} + p_{<r_1})v')u - q',\ \beta - p_{<r_2},\ x_3,\ x_4), \end{aligned} \end{align*}$$
where
![]() $u \in \mathbb C\{\alpha , \beta , x_3, x_4\}$
is a unit,
$u \in \mathbb C\{\alpha , \beta , x_3, x_4\}$
is a unit,
![]() $v' = v_{<r_1-r_2}(\beta - p_{<r_2}, x_3, x_4)$
and
$v' = v_{<r_1-r_2}(\beta - p_{<r_2}, x_3, x_4)$
and
![]() $q' = q_{<r_1}(\beta - p_{<r_2}, x_3, x_4)$
. Define the map germ
$q' = q_{<r_1}(\beta - p_{<r_2}, x_3, x_4)$
. Define the map germ
 $$\begin{align*}\begin{aligned} \psi\colon (\mathbb C^4, \boldsymbol{0}) & \to (\mathbb C^6, \boldsymbol{0})\\ (\alpha, \beta, x_3, x_4) & \mapsto (\alpha, \beta, \varphi^{-1}(\alpha, \beta, x_3, x_4)). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \psi\colon (\mathbb C^4, \boldsymbol{0}) & \to (\mathbb C^6, \boldsymbol{0})\\ (\alpha, \beta, x_3, x_4) & \mapsto (\alpha, \beta, \varphi^{-1}(\alpha, \beta, x_3, x_4)). \end{aligned} \end{align*}$$
The restriction of
![]() $\psi $
to
$\psi $
to
![]() $\mathbb V(I) \to \mathbb V(f \circ \psi )$
is a weight-respecting local biholomorphism, whose inverse is a projection. Therefore, the
$\mathbb V(I) \to \mathbb V(f \circ \psi )$
is a weight-respecting local biholomorphism, whose inverse is a projection. Therefore, the
![]() $\boldsymbol {w}$
-blowup of
$\boldsymbol {w}$
-blowup of
![]() $\mathbb V(f \circ \psi )$
is equivalent to the
$\mathbb V(f \circ \psi )$
is equivalent to the
![]() $\boldsymbol {w}'$
-blowup of
$\boldsymbol {w}'$
-blowup of
![]() $\mathbb V(I)$
. If the
$\mathbb V(I)$
. If the
![]() $\boldsymbol {w}$
-weight of
$\boldsymbol {w}$
-weight of
![]() $f \circ \psi $
is
$f \circ \psi $
is
![]() $r_1 + r_2$
, then by Proposition 4.6, the
$r_1 + r_2$
, then by Proposition 4.6, the
![]() $\boldsymbol {w}$
-blowup of
$\boldsymbol {w}$
-blowup of
![]() $\mathbb V(f \circ \psi )$
is the
$\mathbb V(f \circ \psi )$
is the
![]() $\boldsymbol {w}$
-Kawakita blowup map germ. Using Equation (4.1), it suffices to show that
$\boldsymbol {w}$
-Kawakita blowup map germ. Using Equation (4.1), it suffices to show that
Since
![]() $\psi $
is weight-respecting, we have
$\psi $
is weight-respecting, we have
 $$ \begin{align*} \operatorname{wt}[(x_1 + q)w_{\geq r_1-m} \circ \psi)] & \geq r_1,\\ \operatorname{wt}[q_{\geq r_1}w_{<r_1-m} \circ \psi)] & \geq r_1,\\ \operatorname{wt}[(x_2 + p)v_{\geq r_1-r_2} \circ \psi] & \geq r_1,\\ \operatorname{wt}[p_{\geq r_1} v_{<r_1-r_2} \circ \psi] & \geq r_1. \end{align*} $$
$$ \begin{align*} \operatorname{wt}[(x_1 + q)w_{\geq r_1-m} \circ \psi)] & \geq r_1,\\ \operatorname{wt}[q_{\geq r_1}w_{<r_1-m} \circ \psi)] & \geq r_1,\\ \operatorname{wt}[(x_2 + p)v_{\geq r_1-r_2} \circ \psi] & \geq r_1,\\ \operatorname{wt}[p_{\geq r_1} v_{<r_1-r_2} \circ \psi] & \geq r_1. \end{align*} $$
Since
![]() $((x_1 + q_{<r_1})w_{<r_1-m} + (x_2 + p_{<r_1})v_{<r_1-r_2}) \circ \psi = \alpha $
, this proves Equation (4.2). Using, in addition, that
$((x_1 + q_{<r_1})w_{<r_1-m} + (x_2 + p_{<r_1})v_{<r_1-r_2}) \circ \psi = \alpha $
, this proves Equation (4.2). Using, in addition, that
![]() $\operatorname {wt}[(x_2 + p_{<r_1})v_{<r_1-r_2} \circ \psi ] = r_2$
, Equation (4.3) follows.
$\operatorname {wt}[(x_2 + p_{<r_1})v_{<r_1-r_2} \circ \psi ] = r_2$
, Equation (4.3) follows.
Corollary 4.10. Using the notation above, if
![]() $F \in \mathbb C[x_2, x_3, x_4]$
, or equivalently, if
$F \in \mathbb C[x_2, x_3, x_4]$
, or equivalently, if
![]() $q = 0$
and
$q = 0$
and
![]() $w = 1$
, then define the ideal
$w = 1$
, then define the ideal
![]() $J \subseteq \mathbb C[\alpha , \beta , x_2, x_3, x_4]$
by
$J \subseteq \mathbb C[\alpha , \beta , x_2, x_3, x_4]$
by
where
![]() $v_{<r_1-r_2}$
is defined to be
$v_{<r_1-r_2}$
is defined to be
![]() $1$
if
$1$
if
![]() $r_1 = r_2$
. Then,
$r_1 = r_2$
. Then,
![]() $\mathbb V(J)$
and
$\mathbb V(J)$
and
![]() $\mathbb V(f)$
are isomorphic affine varieties, and the
$\mathbb V(f)$
are isomorphic affine varieties, and the
![]() $(r_1, r_2, \min (r_2, \operatorname {mult} p), a, 1)$
-blowup of
$(r_1, r_2, \min (r_2, \operatorname {mult} p), a, 1)$
-blowup of
![]() $\mathbb V(J)$
is a
$\mathbb V(J)$
is a
![]() $\boldsymbol {w}$
-Kawakita blowup. If in addition
$\boldsymbol {w}$
-Kawakita blowup. If in addition
![]() $r_1 = r_2$
, then define the ideal
$r_1 = r_2$
, then define the ideal
![]() $J' \subseteq \mathbb C[x_1, \beta , x_2, x_3, x_4]$
by
$J' \subseteq \mathbb C[x_1, \beta , x_2, x_3, x_4]$
by
Then,
![]() $\mathbb V(J')$
and
$\mathbb V(J')$
and
![]() $\mathbb V(f)$
are isomorphic affine varieties, and the
$\mathbb V(f)$
are isomorphic affine varieties, and the
![]() $(r_1, r_2, \min (r_2, \operatorname {mult} p), a, 1)$
-blowup of
$(r_1, r_2, \min (r_2, \operatorname {mult} p), a, 1)$
-blowup of
![]() $\mathbb V(J')$
is a
$\mathbb V(J')$
is a
![]() $\boldsymbol {w}$
-Kawakita blowup.
$\boldsymbol {w}$
-Kawakita blowup.
Proof. The isomorphism between
![]() $\mathbb V(I)$
and
$\mathbb V(I)$
and
![]() $\mathbb V(J)$
is a projection, with inverse given by
$\mathbb V(J)$
is a projection, with inverse given by
![]() $x_1 \mapsto \alpha - (\beta - p_{<r_2} + p_{<r_1})v_{<r_1-r_2}$
, which is weight-respecting. If
$x_1 \mapsto \alpha - (\beta - p_{<r_2} + p_{<r_1})v_{<r_1-r_2}$
, which is weight-respecting. If
![]() $r_1 = r_2$
, the isomorphism between
$r_1 = r_2$
, the isomorphism between
![]() $\mathbb V(J)$
and
$\mathbb V(J)$
and
![]() $\mathbb V(J')$
is given by
$\mathbb V(J')$
is given by
![]() $x_1 \mapsto \alpha - \beta $
, which is weight-respecting.
$x_1 \mapsto \alpha - \beta $
, which is weight-respecting.
The power series p, v, q, w can be expressed in terms of the coefficients of F using the explicit splitting lemma, Proposition 3.2.
5. Birational models of sextic double solids
In this section, we prove Theorem B on birational nonrigidity of certain sextic double solids. First, we give the generality conditions that we use.
Definition 5.1. Let X be a sextic double solid in Notation 3.4. Let
![]() $\mathbb P(1, 1, 3)$
have variables
$\mathbb P(1, 1, 3)$
have variables
![]() $y, z, w$
, and let
$y, z, w$
, and let
![]() $\mathbb P^1$
have variables
$\mathbb P^1$
have variables
![]() $y, z$
. Define the following generality conditions, depending on the family that X lies in:
$y, z$
. Define the following generality conditions, depending on the family that X lies in:
-
(4)
 $\mathbb V(2wa_2 + c_5, w^2 - d_6) \subseteq \mathbb P(1, 1, 3)$
is
$\mathbb V(2wa_2 + c_5, w^2 - d_6) \subseteq \mathbb P(1, 1, 3)$
is
 $10$
distinct points,
$10$
distinct points, -
(5)
 $\mathbb V(a_2, -w^2 + d_6) \subseteq \mathbb P(1, 1, 3)$
is
$\mathbb V(a_2, -w^2 + d_6) \subseteq \mathbb P(1, 1, 3)$
is
 $4$
distinct points,
$4$
distinct points, -
(6)
 ${c_4 - 2a_1b_3 - a_2b_2 + 2a_0a_2^2 + 6a_1^2a_2} \in \mathbb C[y, z]$
is nonzero, and
${c_4 - 2a_1b_3 - a_2b_2 + 2a_0a_2^2 + 6a_1^2a_2} \in \mathbb C[y, z]$
is nonzero, and
 $\mathbb V(a_2) \subseteq \mathbb P^1$
is two distinct points, and for both of these points P, one of
$\mathbb V(a_2) \subseteq \mathbb P^1$
is two distinct points, and for both of these points P, one of
 $b_3(P)$
,
$b_3(P)$
,
 $c_4(P)$
or
$c_4(P)$
or
 $d_5(P)$
is nonzero,
$d_5(P)$
is nonzero, -
(7.1)
 $\mathbb V({-e_2 + 4a_0r_2 + b_2 - 6a_1^2}) \subseteq \mathbb P^1$
is two distinct points,
$\mathbb V({-e_2 + 4a_0r_2 + b_2 - 6a_1^2}) \subseteq \mathbb P^1$
is two distinct points, -
(7.2)
 $r_1$
and
$r_1$
and
 $q_1$
are coprime in
$q_1$
are coprime in
 $\mathbb C[y, z]$
,
$\mathbb C[y, z]$
, -
(7.3)
 $q_2 \in \mathbb C[y, z]$
is not a square,
$q_2 \in \mathbb C[y, z]$
is not a square, -
(8)
 $a_0 \neq A_0$
.
$a_0 \neq A_0$
.
Theorem B. Every terminal
![]() $\mathbb Q$
-factorial sextic double solid with a
$\mathbb Q$
-factorial sextic double solid with a
![]() $cA_n$
singularity with
$cA_n$
singularity with
![]() $n \geq 4$
that satisfies the generality conditions in Definition 5.1 has a Sarkisov link starting with a weighted blowup with center the
$n \geq 4$
that satisfies the generality conditions in Definition 5.1 has a Sarkisov link starting with a weighted blowup with center the
![]() $cA_n$
point.
$cA_n$
point.
We treat each of the seven families separately. We use the notation in Construction 2.25 and Example 2.26 for the 2-ray links. We write the
![]() $cA_4$
case in more detail. Below, when we say that a birational map is m Atiyah flops, then we mean that the base of the flop is m points, above each we are contracting a curve and extracting a curve, and locally analytically above each of the points it is an Atiyah flop. Similarly for flips. Below, for a morphism
$cA_4$
case in more detail. Below, when we say that a birational map is m Atiyah flops, then we mean that the base of the flop is m points, above each we are contracting a curve and extracting a curve, and locally analytically above each of the points it is an Atiyah flop. Similarly for flips. Below, for a morphism
![]() $\Phi \colon T_0 \to \mathbb P$
, we let
$\Phi \colon T_0 \to \mathbb P$
, we let
![]() $\Phi ^*\colon \operatorname {Cox} \mathbb P \to \operatorname {Cox} T_0$
denote a corresponding
$\Phi ^*\colon \operatorname {Cox} \mathbb P \to \operatorname {Cox} T_0$
denote a corresponding
![]() $\mathbb C$
-algebra homomorphism of Cox rings (this is described explicitly in the proof of Proposition 5.4).
$\mathbb C$
-algebra homomorphism of Cox rings (this is described explicitly in the proof of Proposition 5.4).
5.1. Singularities after divisorial contraction
The non-Gorenstein singularities on Y for an ordinary type divisorial contraction
![]() $Y \to X$
with center a
$Y \to X$
with center a
![]() $cA_n$
singularity can be easily found using the result by Kawakita, Theorem 2.21. On the other hand, the structure or the number of Gorenstein singularities is unclear. We show in Proposition 5.3 that if X in one of the 11 families is general, then Y has no Gorenstein singularities. We do not give the generality conditions of Proposition 5.3 explicitly. We do not need Proposition 5.3 for proving Theorem B.
$cA_n$
singularity can be easily found using the result by Kawakita, Theorem 2.21. On the other hand, the structure or the number of Gorenstein singularities is unclear. We show in Proposition 5.3 that if X in one of the 11 families is general, then Y has no Gorenstein singularities. We do not give the generality conditions of Proposition 5.3 explicitly. We do not need Proposition 5.3 for proving Theorem B.
Lemma 5.2. Let
![]() $a, b \in \mathbb C[y, z]$
be nonzero homogeneous polynomials with
$a, b \in \mathbb C[y, z]$
be nonzero homogeneous polynomials with
![]() $\deg a \geq \deg b$
such that for every homogeneous polynomial
$\deg a \geq \deg b$
such that for every homogeneous polynomial
![]() $c \in \mathbb C[y, z]$
of degree
$c \in \mathbb C[y, z]$
of degree
![]() $\deg a - \deg b$
, the polynomial
$\deg a - \deg b$
, the polynomial
![]() $a + bc$
is divisible by the square of a linear form. Then a and b are both divisible by the square of the same linear form.
$a + bc$
is divisible by the square of a linear form. Then a and b are both divisible by the square of the same linear form.
Proof. Suffices to prove that for polynomials
![]() $f, g \in \mathbb C[x]$
, if
$f, g \in \mathbb C[x]$
, if
![]() $f + \lambda g$
has a repeated root for infinitely
$f + \lambda g$
has a repeated root for infinitely
![]() $\lambda \in \mathbb C$
, then f and g have a common repeated root. Dividing f and g by suitable linear polynomials, it suffices to consider the case where every common root of f and g is a common repeated root of f and g.
$\lambda \in \mathbb C$
, then f and g have a common repeated root. Dividing f and g by suitable linear polynomials, it suffices to consider the case where every common root of f and g is a common repeated root of f and g.
If the set
is finite, then there exist
![]() $\alpha \in \mathbb C$
and
$\alpha \in \mathbb C$
and
![]() $\lambda _1 \neq \lambda _2$
such that
$\lambda _1 \neq \lambda _2$
such that
![]() $\alpha $
is a repeated root of both
$\alpha $
is a repeated root of both
![]() $f + \lambda _1 g$
and
$f + \lambda _1 g$
and
![]() $f + \lambda _2 g$
. It follows that
$f + \lambda _2 g$
. It follows that
![]() $\alpha $
is a repeated root of both f and g.
$\alpha $
is a repeated root of both f and g.
Without loss of generality, both f and g are nonconstant. Subtracting
![]() $g \cdot \dfrac {\mathrm d (f + \lambda g)}{\mathrm d x}$
from
$g \cdot \dfrac {\mathrm d (f + \lambda g)}{\mathrm d x}$
from
![]() $\dfrac {\mathrm d g}{\mathrm d x} \cdot (f + \lambda g)$
, we find that a repeated root of
$\dfrac {\mathrm d g}{\mathrm d x} \cdot (f + \lambda g)$
, we find that a repeated root of
![]() $f + \lambda g$
is necessarily a root of
$f + \lambda g$
is necessarily a root of
![]() $f \dfrac {\mathrm d g}{\mathrm d x} - g \dfrac {\mathrm d f}{\mathrm d x}$
. If
$f \dfrac {\mathrm d g}{\mathrm d x} - g \dfrac {\mathrm d f}{\mathrm d x}$
. If
![]() $f \dfrac {\mathrm d g}{\mathrm d x} = g \dfrac {\mathrm d f}{\mathrm d x}$
, then a prime factor of g is a prime factor of f. If
$f \dfrac {\mathrm d g}{\mathrm d x} = g \dfrac {\mathrm d f}{\mathrm d x}$
, then a prime factor of g is a prime factor of f. If
![]() $f \dfrac {\mathrm d g}{\mathrm d x} \neq g \dfrac {\mathrm d f}{\mathrm d x}$
, then the set A is finite. In both cases, f and g have a common repeated root.
$f \dfrac {\mathrm d g}{\mathrm d x} \neq g \dfrac {\mathrm d f}{\mathrm d x}$
, then the set A is finite. In both cases, f and g have a common repeated root.
Proposition 5.3. Let X be a member of family
![]() $k \in \mathrm {Inds}$
of Notation 3.4 which is smooth outside a
$k \in \mathrm {Inds}$
of Notation 3.4 which is smooth outside a
![]() $cA_{\lfloor k\rfloor }$
singularity at
$cA_{\lfloor k\rfloor }$
singularity at
![]() $P_x = [1, 0, 0, 0, 0]$
. Let
$P_x = [1, 0, 0, 0, 0]$
. Let
![]() $Y \to X$
be a divisorial contraction with center
$Y \to X$
be a divisorial contraction with center
![]() $P_x$
, which is an
$P_x$
, which is an
![]() $(r_1, r_2, 1, 1)$
-Kawakita blowup. If X is general, then Y has a quotient singularity
$(r_1, r_2, 1, 1)$
-Kawakita blowup. If X is general, then Y has a quotient singularity
![]() $1/r_1(1, 1, r_1 - 1)$
if
$1/r_1(1, 1, r_1 - 1)$
if
![]() $r_1> 1$
and a quotient singularity
$r_1> 1$
and a quotient singularity
![]() $1/r_2(1, 1, r_2 - 1)$
if
$1/r_2(1, 1, r_2 - 1)$
if
![]() $r_2> 1$
and is smooth elsewhere.
$r_2> 1$
and is smooth elsewhere.
Proof. We show that Y has only up to two quotient singularities on the exceptional divisor and is smooth elsewhere. Since
![]() $Y \to X$
is an
$Y \to X$
is an
![]() $(r_1, r_2, 1, 1)$
-Kawakita blowup, we can consider the local analytic coordinate system around
$(r_1, r_2, 1, 1)$
-Kawakita blowup, we can consider the local analytic coordinate system around
![]() $P_x$
where X is given by
$P_x$
where X is given by
![]() $wt + h(y, z)$
where
$wt + h(y, z)$
where
![]() $h \in \mathbb C\{y, z\}$
has multiplicity
$h \in \mathbb C\{y, z\}$
has multiplicity
![]() $n+1$
. The variety Y is locally analytically around the exceptional divisor given by
$n+1$
. The variety Y is locally analytically around the exceptional divisor given by
![]() $wt + \frac {1}{u^{n+1}}h(uy, uz)$
inside the geometric quotient
$wt + \frac {1}{u^{n+1}}h(uy, uz)$
inside the geometric quotient
![]() $(\mathbb C^5 \setminus \mathbb V(w, t, y, z))/\mathbb C^*$
where the
$(\mathbb C^5 \setminus \mathbb V(w, t, y, z))/\mathbb C^*$
where the
![]() $\mathbb C^*$
-action is given by
$\mathbb C^*$
-action is given by
![]() $\lambda \cdot (u, w, t, y, z) = (\lambda ^{-1} u, \lambda ^{r_1} w, \lambda ^{r_2} t, \lambda y, \lambda z)$
. The singular locus of Y is given by
$\lambda \cdot (u, w, t, y, z) = (\lambda ^{-1} u, \lambda ^{r_1} w, \lambda ^{r_2} t, \lambda y, \lambda z)$
. The singular locus of Y is given by
 $$\begin{align*}\operatorname{Sing} Y = \mathbb V\left( u, w, t, h_{n+1}, \frac{\partial h_{n+1}}{\partial y}, \frac{\partial h_{n+1}}{\partial z}, h_{n+2} \right) \cup \{P_w\}_{\text{if }r_1> 1} \cup \{P_t\}_{\text{if }r_2 > 1}, \end{align*}$$
$$\begin{align*}\operatorname{Sing} Y = \mathbb V\left( u, w, t, h_{n+1}, \frac{\partial h_{n+1}}{\partial y}, \frac{\partial h_{n+1}}{\partial z}, h_{n+2} \right) \cup \{P_w\}_{\text{if }r_1> 1} \cup \{P_t\}_{\text{if }r_2 > 1}, \end{align*}$$
where
![]() $h_i$
denotes the homogeneous degree i part of h, and
$h_i$
denotes the homogeneous degree i part of h, and
![]() $P_w$
and
$P_w$
and
![]() $P_t$
are the points
$P_t$
are the points
![]() $[0, 1, 0, 0, 0]$
and
$[0, 1, 0, 0, 0]$
and
![]() $[0, 0, 1, 0, 0]$
, respectively. We see that Y is singular outside of
$[0, 0, 1, 0, 0]$
, respectively. We see that Y is singular outside of
![]() $P_w$
and
$P_w$
and
![]() $P_t$
if and only if there exists a homogeneous linear form
$P_t$
if and only if there exists a homogeneous linear form
![]() $L \in \mathbb C[y, z]$
such that
$L \in \mathbb C[y, z]$
such that
![]() $L^2$
divides
$L^2$
divides
![]() $h_{n+1}$
and L divides
$h_{n+1}$
and L divides
![]() $h_{n+2}$
. For all
$h_{n+2}$
. For all
![]() $k \in \mathrm {Inds}$
, exactly one of the following holds:
$k \in \mathrm {Inds}$
, exactly one of the following holds:
-
•
 $Y \setminus \{P_w, P_t\}$
is smooth for a general X in family k, or
$Y \setminus \{P_w, P_t\}$
is smooth for a general X in family k, or -
• for all X in family k, there exists a homogeneous linear form
 $L \in \mathbb C[y, z]$
such that
$L \in \mathbb C[y, z]$
such that
 $L^2$
divides
$L^2$
divides
 $h_{n+1}$
and L divides
$h_{n+1}$
and L divides
 $h_{n+2}$
.
$h_{n+2}$
.
We write the proof for family 8 in detail, the proofs for the other 10 families are similar. Using the explicit splitting lemma (Proposition 3.2), we compute that
where
![]() $Q, R \in \mathbb C[y, z]$
are homogeneous of degrees
$Q, R \in \mathbb C[y, z]$
are homogeneous of degrees
![]() $9$
and
$9$
and
![]() $7$
, respectively, and Q does not contain the polynomial
$7$
, respectively, and Q does not contain the polynomial
![]() $d_3$
. Assume that for all X in family 8, there exists L such that
$d_3$
. Assume that for all X in family 8, there exists L such that
![]() $L^2$
divides
$L^2$
divides
![]() $h_9$
. Using Lemma 5.2 with
$h_9$
. Using Lemma 5.2 with
![]() $(a, b, c) = (Q,\, r_2^3,\, -2d_3)$
, we find that a prime divisor of
$(a, b, c) = (Q,\, r_2^3,\, -2d_3)$
, we find that a prime divisor of
![]() $r_2$
divides
$r_2$
divides
![]() $h_9$
. Therefore, a general member X of family 8 satisfies that
$h_9$
. Therefore, a general member X of family 8 satisfies that
![]() $r_2$
and
$r_2$
and
![]() $s_3$
have a common prime divisor, contradicting Theorem A(d) and Proposition 3.8. So, for a general X in family 8,
$s_3$
have a common prime divisor, contradicting Theorem A(d) and Proposition 3.8. So, for a general X in family 8,
![]() $Y \setminus \{P_w, P_t\}$
is smooth.
$Y \setminus \{P_w, P_t\}$
is smooth.
5.2.
 $cA_4$
model
$cA_4$
model
Note that Okada described a Sarkisov link starting from a general complete intersection
![]() $Z_{5, 6} \subseteq \mathbb P(1, 1, 1, 2, 3, 4)$
to a sextic double solid (see entry No. 9 of the table in [Reference Okada43, §9]). We show the converse:
$Z_{5, 6} \subseteq \mathbb P(1, 1, 1, 2, 3, 4)$
to a sextic double solid (see entry No. 9 of the table in [Reference Okada43, §9]). We show the converse:
Proposition 5.4. A sextic double solid with a
![]() $cA_4$
singularity satisfying Definition 5.1 has a Sarkisov link to a complete intersection
$cA_4$
singularity satisfying Definition 5.1 has a Sarkisov link to a complete intersection
![]() $Z_{5, 6} \subseteq \mathbb P(1, 1, 1, 2, 3, 4)$
, starting with a
$Z_{5, 6} \subseteq \mathbb P(1, 1, 1, 2, 3, 4)$
, starting with a
![]() $(3, 2, 1, 1)$
-blowup of the
$(3, 2, 1, 1)$
-blowup of the
![]() $cA_4$
point, then
$cA_4$
point, then
![]() $10$
Atiyah flops, and finally a Kawamata divisorial contraction (see [Reference Kawamata34]) to a terminal quotient
$10$
Atiyah flops, and finally a Kawamata divisorial contraction (see [Reference Kawamata34]) to a terminal quotient
![]() $1/4(1, 1, 3)$
point. Under further generality conditions (Proposition 5.3), Z is quasismooth.
$1/4(1, 1, 3)$
point. Under further generality conditions (Proposition 5.3), Z is quasismooth.
Proof. We exhibit the diagram below.

The corresponding diagram for the ambient toric spaces is given in detail in Example 2.26.
By Theorem A, every sextic double solid
![]() $\hat X$
with an isolated
$\hat X$
with an isolated
![]() $cA_4$
singularity can be given by
$cA_4$
singularity can be given by
with variables
![]() $x, y, z, t, w$
where
$x, y, z, t, w$
where
where
![]() $a_2 \in \mathbb C[y, z]$
is homogeneous of degree
$a_2 \in \mathbb C[y, z]$
is homogeneous of degree
![]() $2$
, and
$2$
, and
![]() $A_i, B_i, C_i, D_i \in \mathbb C[y, z, t]$
are homogeneous of degree i.
$A_i, B_i, C_i, D_i \in \mathbb C[y, z, t]$
are homogeneous of degree i.
Below, we perform the following constructions:
-
(1) We define a weighted projective space
 $\mathbb P = \mathbb P(1, 1, 1, 1, 3, 5)$
.
$\mathbb P = \mathbb P(1, 1, 1, 1, 3, 5)$
. -
(2) We define a subvariety X of
 $\mathbb P$
by explicitly describing a homogeneous ideal.
$\mathbb P$
by explicitly describing a homogeneous ideal. -
(3) We show that X and
 $\hat X$
are isomorphic by constructing an explicit isomorphism.
$\hat X$
are isomorphic by constructing an explicit isomorphism. -
(4) We construct a toric variety
 $T_0$
.
$T_0$
. -
(5) We define a morphism
 $\Phi \colon T_0 \to \mathbb P$
.
$\Phi \colon T_0 \to \mathbb P$
. -
(6) We construct a subvariety
 $Y_0$
of
$Y_0$
of
 $T_0$
by explicitly describing a bihomogeneous ideal
$T_0$
by explicitly describing a bihomogeneous ideal
 $I_Y$
of the Cox ring of
$I_Y$
of the Cox ring of
 $T_0$
.
$T_0$
. -
(7) We restrict the morphism
 $\Phi $
to
$\Phi $
to
 $Y_0$
and check that its image is X.
$Y_0$
and check that its image is X.
Although computational, the above steps are completely elementary. The reason for these constructions is that, as we prove below, the morphism
![]() $Y_0 \to X$
is the
$Y_0 \to X$
is the
![]() $(3, 2, 1, 1)$
-Kawakita blowup and
$(3, 2, 1, 1)$
-Kawakita blowup and
![]() $I_Y$
2-ray follows
$I_Y$
2-ray follows
![]() $T_0$
.
$T_0$
.
The reader might have the philosophical question of how the author found the varieties
![]() $\mathbb P, X, T_0$
and
$\mathbb P, X, T_0$
and
![]() $Y_0$
, described below, and why they are defined exactly as they are. In Remark 5.5, we describe the methods we used to arrive at the construction of
$Y_0$
, described below, and why they are defined exactly as they are. In Remark 5.5, we describe the methods we used to arrive at the construction of
![]() $\mathbb P, X, T_0$
and
$\mathbb P, X, T_0$
and
![]() $Y_0$
. Note that the choices involved in (1), (2), (4), and (6) above are somewhat arbitrary. Namely, there exist other varieties
$Y_0$
. Note that the choices involved in (1), (2), (4), and (6) above are somewhat arbitrary. Namely, there exist other varieties
![]() $\mathbb P, X, T_0$
and
$\mathbb P, X, T_0$
and
![]() $Y_0$
such that
$Y_0$
such that
![]() $Y_0 \to X$
is the
$Y_0 \to X$
is the
![]() $(3, 2, 1, 1)$
-Kawakita blowup and
$(3, 2, 1, 1)$
-Kawakita blowup and
![]() $I_Y$
2-ray follows
$I_Y$
2-ray follows
![]() $T_0$
.
$T_0$
.
We start by constructing X. Define the bidegree
![]() $(5, 6)$
complete intersection X, isomorphic to
$(5, 6)$
complete intersection X, isomorphic to
![]() $\hat X$
, by
$\hat X$
, by
with variables
![]() $x, y, z, t, \alpha , \xi $
, where
$x, y, z, t, \alpha , \xi $
, where
The isomorphism is given by
 $$\begin{align*}\begin{aligned} \hat X & \to X\\ [x, y, z, t, w] & \mapsto \left[ {x, y, z, t, \alpha', 2\alpha'a_2 + 2\alpha'xt + x^2t^2A_1 + xtB_3 + C_5} \right], \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \hat X & \to X\\ [x, y, z, t, w] & \mapsto \left[ {x, y, z, t, \alpha', 2\alpha'a_2 + 2\alpha'xt + x^2t^2A_1 + xtB_3 + C_5} \right], \end{aligned} \end{align*}$$
where
![]() $\alpha ' = w + x^2t + xa_2$
, with inverse
$\alpha ' = w + x^2t + xa_2$
, with inverse
We describe the divisorial contraction
![]() $\varphi \colon Y_0 \to X$
. Define the toric variety
$\varphi \colon Y_0 \to X$
. Define the toric variety

as in Example 2.26. Let
![]() $\Phi $
be the ample model of
$\Phi $
be the ample model of
![]() $\mathbb V(x)$
, that is,
$\mathbb V(x)$
, that is,
 $$\begin{align*}\begin{aligned} \Phi\colon T_0 & \to \mathbb P(1, 1, 1, 1, 3, 5)\\ [u, x, y, z, \alpha, \xi, t] & \mapsto [x, uy, uz, u^2t, u^3\alpha, u^6\xi]. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \Phi\colon T_0 & \to \mathbb P(1, 1, 1, 1, 3, 5)\\ [u, x, y, z, \alpha, \xi, t] & \mapsto [x, uy, uz, u^2t, u^3\alpha, u^6\xi]. \end{aligned} \end{align*}$$
Let
![]() $Y_0$
be the strict transform of X. Let
$Y_0$
be the strict transform of X. Let
![]() $\Phi ^*$
denote the corresponding
$\Phi ^*$
denote the corresponding
![]() $\mathbb C$
-algebra homomorphism, namely
$\mathbb C$
-algebra homomorphism, namely
 $$ \begin{gather*} \Phi^*\colon \mathbb C[x, y, z, t, \alpha, \xi] \to \mathbb C[u, x, y, z, \alpha, \xi, t]\\ \Phi^*\colon x \mapsto x,\ y \mapsto uy,\ z \mapsto uz,\ t \mapsto u^2 t,\ \alpha \mapsto u^3 \alpha,\ \xi \mapsto u^6 \xi. \end{gather*} $$
$$ \begin{gather*} \Phi^*\colon \mathbb C[x, y, z, t, \alpha, \xi] \to \mathbb C[u, x, y, z, \alpha, \xi, t]\\ \Phi^*\colon x \mapsto x,\ y \mapsto uy,\ z \mapsto uz,\ t \mapsto u^2 t,\ \alpha \mapsto u^3 \alpha,\ \xi \mapsto u^6 \xi. \end{gather*} $$
Define
and define the polynomial
![]() $g = \Phi ^*f / u^5$
, that is,
$g = \Phi ^*f / u^5$
, that is,
Then,
![]() $Y_0$
is given by
$Y_0$
is given by
We will see later that
![]() $I_Y$
2-ray follows
$I_Y$
2-ray follows
![]() $T_0$
. Note that there exist other ideals that define the same variety
$T_0$
. Note that there exist other ideals that define the same variety
![]() $Y_0 \subseteq T_0$
(see [Reference Cox20, Cor. 3.9]), but where the ideal might not 2-ray follow
$Y_0 \subseteq T_0$
(see [Reference Cox20, Cor. 3.9]), but where the ideal might not 2-ray follow
![]() $T_0$
. Also note that we have not (and do not need to) prove that the ideal
$T_0$
. Also note that we have not (and do not need to) prove that the ideal
![]() $I_Y$
is saturated with respect to u, although in general, saturating might help in finding the ideal that 2-ray follows
$I_Y$
is saturated with respect to u, although in general, saturating might help in finding the ideal that 2-ray follows
![]() $T_0$
. The morphism
$T_0$
. The morphism
![]() $Y_0 \to X$
is the restriction of
$Y_0 \to X$
is the restriction of
![]() $T_0 \to \mathbb P(1, 1, 1, 1, 3, 5)$
. Locally,
$T_0 \to \mathbb P(1, 1, 1, 1, 3, 5)$
. Locally,
![]() $(Y_0)_x \to X_x$
is the
$(Y_0)_x \to X_x$
is the
![]() $(3, 2, 1, 1)$
-blowup of
$(3, 2, 1, 1)$
-blowup of
![]() $\mathbb V(f') \subseteq \mathbb C^4$
with variables
$\mathbb V(f') \subseteq \mathbb C^4$
with variables
![]() $\alpha , t, y, z$
, where
$\alpha , t, y, z$
, where
Since
![]() $\operatorname {wt} f' = 5$
, by Proposition 4.6,
$\operatorname {wt} f' = 5$
, by Proposition 4.6,
![]() $(Y_0)_x \to X_x$
is a
$(Y_0)_x \to X_x$
is a
![]() $(3, 2, 1, 1)$
-Kawakita blowup.
$(3, 2, 1, 1)$
-Kawakita blowup.
The first diagram in the 2-ray game for
![]() $Y_0$
is
$Y_0$
is
![]() $10$
Atiyah flops, under Definition 5.1. We describe the diagram
$10$
Atiyah flops, under Definition 5.1. We describe the diagram
![]() $Y_0 \to W_0 \gets Y_1$
globally. Multiplying the action matrix of
$Y_0 \to W_0 \gets Y_1$
globally. Multiplying the action matrix of
![]() $T_0$
by the matrix
$T_0$
by the matrix
![]() ${\left (\begin {smallmatrix}1 & 0\\-1 & 1\end {smallmatrix}\right )}$
, define
${\left (\begin {smallmatrix}1 & 0\\-1 & 1\end {smallmatrix}\right )}$
, define

Define
![]() $Y_1$
by
$Y_1$
by
![]() $\mathbb V(I_Y) \subseteq T_1$
. Define the morphisms
$\mathbb V(I_Y) \subseteq T_1$
. Define the morphisms
![]() $Y_0 \to W_0$
and
$Y_0 \to W_0$
and
![]() $Y_1 \to W_0$
as the ample models of
$Y_1 \to W_0$
as the ample models of
![]() $\mathbb V(y)$
. The exceptional locus of
$\mathbb V(y)$
. The exceptional locus of
![]() $Y_0 \to W_0$
is
$Y_0 \to W_0$
is
![]() $E_0^- = \mathbb V(\xi , t) \subseteq Y_0$
, the exceptional locus of
$E_0^- = \mathbb V(\xi , t) \subseteq Y_0$
, the exceptional locus of
![]() $Y_1 \to W_0$
is
$Y_1 \to W_0$
is
![]() $E_1^+ = \mathbb V(u, x) \subseteq Y_1$
, and the base of the flop is
$E_1^+ = \mathbb V(u, x) \subseteq Y_1$
, and the base of the flop is
where
![]() $\mathbb P(1, 1, 3)$
has variables
$\mathbb P(1, 1, 3)$
has variables
![]() $y, z, \alpha $
. If
$y, z, \alpha $
. If
![]() $a_2$
,
$a_2$
,
![]() $C_5(y, z, 0)$
and
$C_5(y, z, 0)$
and
![]() $D_5(y, z, 0)$
are general enough, that is, if Definition 5.1 is satisfied, then the base of the flop is
$D_5(y, z, 0)$
are general enough, that is, if Definition 5.1 is satisfied, then the base of the flop is
![]() $10$
points
$10$
points
![]() $\{P_i\}_{1\leq i\leq 10}$
, and both
$\{P_i\}_{1\leq i\leq 10}$
, and both
![]() $E_0^-$
and
$E_0^-$
and
![]() $E_1^+$
are
$E_1^+$
are
![]() $10$
disjoint curves mapping to
$10$
disjoint curves mapping to
![]() $\{P_i\}_{1\leq i\leq 10}$
.
$\{P_i\}_{1\leq i\leq 10}$
.
We show that locally analytically, the diagram
![]() $Y_0 \to W_0 \gets Y_1$
is
$Y_0 \to W_0 \gets Y_1$
is
![]() $10$
Atiyah flops. Let
$10$
Atiyah flops. Let
![]() $P \in W_0$
be any point in the base of the flop. Then, P has y or z coordinate nonzero. We consider the case where the y-coordinate is nonzero, the other case is similar. Since the base of the flop is
$P \in W_0$
be any point in the base of the flop. Then, P has y or z coordinate nonzero. We consider the case where the y-coordinate is nonzero, the other case is similar. Since the base of the flop is
![]() $10$
points, the point P is smooth in
$10$
points, the point P is smooth in
![]() $\mathbb P(1, 1, 3)$
. By the implicit function theorem, we can locally analytically equivariantly express
$\mathbb P(1, 1, 3)$
. By the implicit function theorem, we can locally analytically equivariantly express
![]() $\alpha $
and z in terms of the variables
$\alpha $
and z in terms of the variables
![]() $u, x, \xi , t$
on the patches
$u, x, \xi , t$
on the patches
![]() $(Y_0)_y$
,
$(Y_0)_y$
,
![]() $(W_0)_y$
, and
$(W_0)_y$
, and
![]() $(Y_1)_y$
. So, the flop
$(Y_1)_y$
. So, the flop
![]() $Y_0 \to W_0 \gets Y_1$
is locally analytically a
$Y_0 \to W_0 \gets Y_1$
is locally analytically a
![]() $(1, 1, -1, -1)$
-flop, the so-called Atiyah flop, around P.
$(1, 1, -1, -1)$
-flop, the so-called Atiyah flop, around P.
The last morphism
![]() $Y_1 \to Z$
in the link for X is a divisorial contraction. Multiplying the action matrix of
$Y_1 \to Z$
in the link for X is a divisorial contraction. Multiplying the action matrix of
![]() $T_0$
by the matrix
$T_0$
by the matrix
![]() ${\left (\begin {smallmatrix}6 & -5\\2 & -1\end {smallmatrix}\right )}$
with determinant
${\left (\begin {smallmatrix}6 & -5\\2 & -1\end {smallmatrix}\right )}$
with determinant
![]() $4$
, we see that
$4$
, we see that

Let
![]() $Y_1 \to Z$
be the ample model of
$Y_1 \to Z$
be the ample model of
![]() $\frac 14 \mathbb V(\xi )$
, that is,
$\frac 14 \mathbb V(\xi )$
, that is,
 $$\begin{align*}\begin{aligned} Y_1 & \to Z\\ [u, x, y, z, \alpha, \xi, t] & \mapsto \left[ t^{\frac54} u, t^{\frac14} y, t^{\frac14} z, t^{\frac32} x, t^{\frac34} \alpha, \xi \right]. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} Y_1 & \to Z\\ [u, x, y, z, \alpha, \xi, t] & \mapsto \left[ t^{\frac54} u, t^{\frac14} y, t^{\frac14} z, t^{\frac32} x, t^{\frac34} \alpha, \xi \right]. \end{aligned} \end{align*}$$
Then Z is the bidegree
![]() $(5, 6)$
complete intersection
$(5, 6)$
complete intersection
with variables
![]() $u, y, z, x, \alpha , \xi $
, where the h is given by applying the
$u, y, z, x, \alpha , \xi $
, where the h is given by applying the
![]() $\mathbb C$
-algebra homomorphism
$\mathbb C$
-algebra homomorphism
![]() $t \mapsto 1$
to g. The morphism
$t \mapsto 1$
to g. The morphism
![]() $Y_1 \to Z$
contracts the exceptional divisor
$Y_1 \to Z$
contracts the exceptional divisor
![]() $\mathbb V(t) \subseteq Y_1$
to the point
$\mathbb V(t) \subseteq Y_1$
to the point
![]() $P_\xi = [0, 0, 0, 0, 0, 1]$
. On the quasiprojective patch
$P_\xi = [0, 0, 0, 0, 0, 1]$
. On the quasiprojective patch
![]() $(Y_1)_\xi $
, we can express u and x locally analytically equivariantly in terms of
$(Y_1)_\xi $
, we can express u and x locally analytically equivariantly in terms of
![]() $y, z, \alpha , t$
. So, the morphism
$y, z, \alpha , t$
. So, the morphism
![]() $Y_1 \to Z$
is locally analytically the Kawamata weighted blowdown (see [Reference Kawamata34]) to the terminal quotient singular point
$Y_1 \to Z$
is locally analytically the Kawamata weighted blowdown (see [Reference Kawamata34]) to the terminal quotient singular point
![]() $P_\xi $
of type
$P_\xi $
of type
![]() $1/4(1, 1, 3)$
.
$1/4(1, 1, 3)$
.
Remark 5.5. We explain below how we found the variety X used in Proposition 5.4. We start with the variety
![]() $\hat X$
, given by Theorem A. Note that it is not possible to assign weights to the coordinates of
$\hat X$
, given by Theorem A. Note that it is not possible to assign weights to the coordinates of
![]() $\mathbb P(1, 1, 1, 1, 3)$
such that the corresponding weighted blowup of
$\mathbb P(1, 1, 1, 1, 3)$
such that the corresponding weighted blowup of
![]() $\hat X$
would be a
$\hat X$
would be a
![]() $(3, 2, 1, 1)$
-Kawakita blowup. To amend this, we first replace the variety
$(3, 2, 1, 1)$
-Kawakita blowup. To amend this, we first replace the variety
![]() $\hat X$
by a variety
$\hat X$
by a variety
![]() $\bar X$
such that choosing the weights appropriately, the weighted blowup of
$\bar X$
such that choosing the weights appropriately, the weighted blowup of
![]() $\bar X$
is the
$\bar X$
is the
![]() $(3, 2, 1, 1)$
-Kawakita blowup. So far the process is algorithmic. Unfortunately, as we see below, the constructed ideal
$(3, 2, 1, 1)$
-Kawakita blowup. So far the process is algorithmic. Unfortunately, as we see below, the constructed ideal
![]() $I_{\bar Y}$
does not 2-ray follow the ambient toric variety
$I_{\bar Y}$
does not 2-ray follow the ambient toric variety
![]() $\bar T_0$
. Using the technique known as unprojection, we construct another toric variety
$\bar T_0$
. Using the technique known as unprojection, we construct another toric variety
![]() $T_0$
and a subvariety
$T_0$
and a subvariety
![]() $Y_0$
given by an ideal
$Y_0$
given by an ideal
![]() $I_Y$
. This time we are lucky, since as the proof of Proposition 5.4 shows, the ideal
$I_Y$
. This time we are lucky, since as the proof of Proposition 5.4 shows, the ideal
![]() $I_Y$
2-ray follows
$I_Y$
2-ray follows
![]() $T_0$
. Note that the variety
$T_0$
. Note that the variety
![]() $Y_0$
has higher codimension in
$Y_0$
has higher codimension in
![]() $T_0$
than
$T_0$
than
![]() $\bar Y_0$
had in
$\bar Y_0$
had in
![]() $\bar T_0$
. We give details below.
$\bar T_0$
. We give details below.
We perform the coordinate change
![]() $\hat X \to \bar X$
given in Equation (4.4) of Corollary 4.10, with
$\hat X \to \bar X$
given in Equation (4.4) of Corollary 4.10, with
![]() $(r_1, r_2, a, 1) = (3, 2, 1, 1)$
,
$(r_1, r_2, a, 1) = (3, 2, 1, 1)$
,
![]() $p_2 = a_2$
and
$p_2 = a_2$
and
![]() $v_0 = 1$
. We see that
$v_0 = 1$
. We see that
![]() $\hat X$
is isomorphic to
$\hat X$
is isomorphic to
with variables
![]() $x, y, z, t, \alpha $
, where
$x, y, z, t, \alpha $
, where
We construct a
![]() $(3, 2, 1, 1)$
-Kawakita blowup
$(3, 2, 1, 1)$
-Kawakita blowup
![]() $\bar Y_0 \to \bar X$
. Define the toric variety
$\bar Y_0 \to \bar X$
. Define the toric variety
![]() $\bar T_0$
by
$\bar T_0$
by

In other words,
![]() $\bar T_0$
is given by the geometric quotient
$\bar T_0$
is given by the geometric quotient
 $$\begin{align*}\bar T_0 = \frac{\mathbb C^6 \setminus \mathbb V((u, x) \cap (y, z, \alpha, t))}{(\mathbb C^*)^2}. \end{align*}$$
$$\begin{align*}\bar T_0 = \frac{\mathbb C^6 \setminus \mathbb V((u, x) \cap (y, z, \alpha, t))}{(\mathbb C^*)^2}. \end{align*}$$
Let
![]() $\bar {\Phi }$
be the ample model of
$\bar {\Phi }$
be the ample model of
![]() $\mathbb V(x)$
, and let
$\mathbb V(x)$
, and let
![]() $\bar Y_0 \subseteq \bar T_0$
be the strict transform of
$\bar Y_0 \subseteq \bar T_0$
be the strict transform of
![]() $\bar X$
. By Corollary 4.10,
$\bar X$
. By Corollary 4.10,
![]() $\bar Y_0 \to \bar X$
is a
$\bar Y_0 \to \bar X$
is a
![]() $(3, 2, 1, 1)$
-Kawakita blowup. Alternatively, define
$(3, 2, 1, 1)$
-Kawakita blowup. Alternatively, define
![]() $\bar Y_0$
by
$\bar Y_0$
by
![]() $\mathbb V(\bar g) \subseteq T_0$
where
$\mathbb V(\bar g) \subseteq T_0$
where
and use Proposition 4.6 on the patch
![]() $(\bar Y_0)_x \to \bar X_x$
to show that
$(\bar Y_0)_x \to \bar X_x$
to show that
![]() $\bar Y_0 \to \bar X$
is a
$\bar Y_0 \to \bar X$
is a
![]() $(3, 2, 1, 1)$
-Kawakita blowup, similarly to Proposition 5.4.
$(3, 2, 1, 1)$
-Kawakita blowup, similarly to Proposition 5.4.
We show that
![]() $I_{\bar Y}$
does not 2-ray follow
$I_{\bar Y}$
does not 2-ray follow
![]() $\bar T_0$
. We describe the next (and the final) map in the 2-ray game for
$\bar T_0$
. We describe the next (and the final) map in the 2-ray game for
![]() $\bar T_0$
. Acting by the matrix
$\bar T_0$
. Acting by the matrix
![]() ${\left (\begin {smallmatrix}1 & -1\\2 & -1\end {smallmatrix}\right )}$
, we can write
${\left (\begin {smallmatrix}1 & -1\\2 & -1\end {smallmatrix}\right )}$
, we can write
![]() $\bar T_0$
by
$\bar T_0$
by

The ample model of the divisor
![]() $\mathbb V(y)$
is the weighted blowup
$\mathbb V(y)$
is the weighted blowup
 $$\begin{align*}\begin{aligned} \bar T_0 & \to \mathbb P(1, 1, 1, 2, 3)\\ [u, x, y, z, \alpha, t] & \mapsto [y, z, ut, xt, \alpha], \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \bar T_0 & \to \mathbb P(1, 1, 1, 2, 3)\\ [u, x, y, z, \alpha, t] & \mapsto [y, z, ut, xt, \alpha], \end{aligned} \end{align*}$$
where the center is the surface
![]() $\mathbb P(1, 1, 3)$
given by
$\mathbb P(1, 1, 3)$
given by
![]() $\mathbb V(u, x) \subseteq \mathbb P(1, 1, 1, 2, 3)$
with variables
$\mathbb V(u, x) \subseteq \mathbb P(1, 1, 1, 2, 3)$
with variables
![]() $y, z, u, x, \alpha $
. Above every point in
$y, z, u, x, \alpha $
. Above every point in
![]() $\mathbb P(1, 1, 3)$
, the fiber is
$\mathbb P(1, 1, 3)$
, the fiber is
![]() $\mathbb P^1$
. Define
$\mathbb P^1$
. Define
where
where
We show that when restricting the weighted blowup to
![]() $\bar Y_0 \to \bar Z$
, the exceptional locus is one-dimensional. After restricting to
$\bar Y_0 \to \bar Z$
, the exceptional locus is one-dimensional. After restricting to
![]() $\bar Y_0$
, the exceptional divisor
$\bar Y_0$
, the exceptional divisor
![]() $\mathbb V(t)$
becomes
$\mathbb V(t)$
becomes
![]() $\mathbb V(t, x(2\alpha a_2 + C_5(y, z, 0)) + u(-\alpha ^2 + D_6(y, z, 0)))$
. By Definition 5.1, there are exactly
$\mathbb V(t, x(2\alpha a_2 + C_5(y, z, 0)) + u(-\alpha ^2 + D_6(y, z, 0)))$
. By Definition 5.1, there are exactly
![]() $10$
points
$10$
points
![]() $P_1, \ldots , P_{10} \in \mathbb P(1, 1, 3) \subseteq \bar Z$
such that
$P_1, \ldots , P_{10} \in \mathbb P(1, 1, 3) \subseteq \bar Z$
such that
![]() $2\alpha a_2 + C_5(y, z, 0)$
and
$2\alpha a_2 + C_5(y, z, 0)$
and
![]() $-\alpha ^2 + D_6(y, z, 0)$
have a common solution. Above each of those points, the fiber is
$-\alpha ^2 + D_6(y, z, 0)$
have a common solution. Above each of those points, the fiber is
![]() $\mathbb P^1$
. Above any other point, the fiber is just one point. Therefore, the morphism
$\mathbb P^1$
. Above any other point, the fiber is just one point. Therefore, the morphism
![]() $\bar Y_0 \to \bar Z$
contracts 10 curves onto 10 points, and is an isomorphism elsewhere. This shows that
$\bar Y_0 \to \bar Z$
contracts 10 curves onto 10 points, and is an isomorphism elsewhere. This shows that
![]() $\bar Y_0$
does not 2-ray follow
$\bar Y_0$
does not 2-ray follow
![]() $\bar T_0$
, since
$\bar T_0$
, since
![]() $\bar Z$
is not
$\bar Z$
is not
![]() $\mathbb Q$
-factorial and a 2-ray link ends with either a fibration or a divisorial contraction.
$\mathbb Q$
-factorial and a 2-ray link ends with either a fibration or a divisorial contraction.
The problem with the previous embedding was that
![]() $\bar g$
belonged to the irrelevant ideal
$\bar g$
belonged to the irrelevant ideal
![]() $(u, x)$
. We unproject the divisor
$(u, x)$
. We unproject the divisor
![]() $\mathbb V(u, x)$
, to embed
$\mathbb V(u, x)$
, to embed
![]() $\bar Y_0$
into a toric variety
$\bar Y_0$
into a toric variety
![]() $T_0$
such that
$T_0$
such that
![]() $Y_0$
2-ray follows
$Y_0$
2-ray follows
![]() $T_0$
. The varieties
$T_0$
. The varieties
![]() $Y_0 \subseteq T_0$
are defined as in the proof of Proposition 5.4. We see that
$Y_0 \subseteq T_0$
are defined as in the proof of Proposition 5.4. We see that
![]() $\bar Y_0$
is isomorphic to
$\bar Y_0$
is isomorphic to
![]() $Y_0$
through the map
$Y_0$
through the map
 $$\begin{align*}[u, x, y, z, \alpha, t] \mapsto \left[ u, x, y, z, \alpha, \frac{\alpha^2 - D_Y}{x}, t \right]. \end{align*}$$
$$\begin{align*}[u, x, y, z, \alpha, t] \mapsto \left[ u, x, y, z, \alpha, \frac{\alpha^2 - D_Y}{x}, t \right]. \end{align*}$$
The map is a morphism, since we have the equality
 $$\begin{align*}\frac{\alpha^2 - D_Y}{x} = \frac{2\alpha a_2 + 2\alpha xt + x^2t^2A_Y + xtB_Y + C_Y}{u} \end{align*}$$
$$\begin{align*}\frac{\alpha^2 - D_Y}{x} = \frac{2\alpha a_2 + 2\alpha xt + x^2t^2A_Y + xtB_Y + C_Y}{u} \end{align*}$$
in the field of fractions of
![]() $\mathbb C[u, x, y, z, \alpha , t]$
, and x or u is nonzero at every point of
$\mathbb C[u, x, y, z, \alpha , t]$
, and x or u is nonzero at every point of
![]() $T_0$
. For more details on this kind of unprojection, see [Reference Reid49, §2] or [Reference Papadakis and Reid44, §2.3].
$T_0$
. For more details on this kind of unprojection, see [Reference Reid49, §2] or [Reference Papadakis and Reid44, §2.3].
The coordinate change
![]() $\bar Y_0 \to Y_0$
induces a coordinate change
$\bar Y_0 \to Y_0$
induces a coordinate change
![]() $\bar X \to X$
, where X is defined as in the proof of Proposition 5.4.
$\bar X \to X$
, where X is defined as in the proof of Proposition 5.4.
5.3.
 $cA_5$
model
$cA_5$
model
Proposition 5.6. A sextic double solid X which is a Mori fiber space with a
![]() $cA_5$
singularity satisfying Definition 5.1 has a Sarkisov link to a sextic double solid Z with a
$cA_5$
singularity satisfying Definition 5.1 has a Sarkisov link to a sextic double solid Z with a
![]() $cA_5$
singularity, starting with a
$cA_5$
singularity, starting with a
![]() $(3, 3, 1, 1)$
-blowup of the
$(3, 3, 1, 1)$
-blowup of the
![]() $cA_5$
point in X, then four Atiyah flops, and finally a
$cA_5$
point in X, then four Atiyah flops, and finally a
![]() $(3, 3, 1, 1)$
-blowdown to a
$(3, 3, 1, 1)$
-blowdown to a
![]() $cA_5$
point. If in addition
$cA_5$
point. If in addition
![]() $c_4$
is general after fixing
$c_4$
is general after fixing
![]() $a_i$
,
$a_i$
,
![]() $b_i$
, and
$b_i$
, and
![]() $d_6$
in Notation 3.4, then X and Z are not isomorphic. Under further generality conditions (Proposition 5.3), both X and Z are smooth outside the
$d_6$
in Notation 3.4, then X and Z are not isomorphic. Under further generality conditions (Proposition 5.3), both X and Z are smooth outside the
![]() $cA_5$
point.
$cA_5$
point.
Proof. We exhibit the diagram below.

We construct X and a
![]() $(3, 3, 1, 1)$
-Kawakita blowup
$(3, 3, 1, 1)$
-Kawakita blowup
![]() $Y_0 \to X$
. Using Theorem A, and performing the coordinate change in Equation (4.5) of Corollary 4.10 (with
$Y_0 \to X$
. Using Theorem A, and performing the coordinate change in Equation (4.5) of Corollary 4.10 (with
![]() $p_2 = a_2$
), we can write a sextic double solid X with a
$p_2 = a_2$
), we can write a sextic double solid X with a
![]() $cA_5$
singularity by
$cA_5$
singularity by
with variables
![]() $x, y, z, t, \beta , w$
where
$x, y, z, t, \beta , w$
where
where
![]() $B_i$
,
$B_i$
,
![]() $C_i$
,
$C_i$
,
![]() $D_i \in \mathbb C[y, z, t]$
are homogeneous of degrees i. Define
$D_i \in \mathbb C[y, z, t]$
are homogeneous of degrees i. Define
![]() $T_0$
by
$T_0$
by

Let
![]() $\Phi \colon T_0 \to \mathbb P(1, 1, 1, 1, 2, 3)$
be the ample model of
$\Phi \colon T_0 \to \mathbb P(1, 1, 1, 1, 2, 3)$
be the ample model of
![]() $\mathbb V(x)$
,
$\mathbb V(x)$
,
![]() $Y_0 \subseteq T_0$
the strict transform of X, and
$Y_0 \subseteq T_0$
the strict transform of X, and
![]() $Y_0 \to X$
the restriction of
$Y_0 \to X$
the restriction of
![]() $\Phi $
. Then,
$\Phi $
. Then,
![]() $Y_0$
is given by
$Y_0$
is given by
and
![]() $Y_0 \to X$
is a
$Y_0 \to X$
is a
![]() $(3, 3, 1, 1)$
-Kawakita blowup.
$(3, 3, 1, 1)$
-Kawakita blowup.
We show that the first map in the 2-ray game for
![]() $Y_0$
is a flop, locally analytically
$Y_0$
is a flop, locally analytically
![]() $4$
Atiyah flops, under Definition 5.1. Acting by the matrix
$4$
Atiyah flops, under Definition 5.1. Acting by the matrix
![]() ${\left (\begin {smallmatrix}1 & 0\\ -1 & 1\end {smallmatrix}\right )}$
, we find
${\left (\begin {smallmatrix}1 & 0\\ -1 & 1\end {smallmatrix}\right )}$
, we find

The base of the flop in
![]() $\mathbb P(1, 1, 3) \subseteq W_0$
is given by
$\mathbb P(1, 1, 3) \subseteq W_0$
is given by
![]() $\mathbb V(a_2, -w^2 + D_6(y, z, 0)) \subseteq \mathbb P(1, 1, 3)$
. If
$\mathbb V(a_2, -w^2 + D_6(y, z, 0)) \subseteq \mathbb P(1, 1, 3)$
. If
![]() $a_2$
and
$a_2$
and
![]() $D_6(y, z, 0)$
are general, that is, Definition 5.1 is satisfied, then this is exactly four points. In this case, any such point P is a smooth point in
$D_6(y, z, 0)$
are general, that is, Definition 5.1 is satisfied, then this is exactly four points. In this case, any such point P is a smooth point in
![]() $\mathbb P(1, 1, 3)$
. Consider the case where the y-coordinate of P is nonzero, the case where z is nonzero is similar. Locally analytically equivariantly, we can express z and w in terms of
$\mathbb P(1, 1, 3)$
. Consider the case where the y-coordinate of P is nonzero, the case where z is nonzero is similar. Locally analytically equivariantly, we can express z and w in terms of
![]() $u, x, \beta , t$
in
$u, x, \beta , t$
in
![]() $Y_0$
,
$Y_0$
,
![]() $W_0$
, and
$W_0$
, and
![]() $Y_1$
. So, the diagram
$Y_1$
. So, the diagram
![]() $Y_0 \to W_0 \gets Y_1$
is locally analytically four Atiyah flops.
$Y_0 \to W_0 \gets Y_1$
is locally analytically four Atiyah flops.
The last map in the 2-ray game of
![]() $Y_0$
is a weighted blowdown
$Y_0$
is a weighted blowdown
![]() $Y_1 \to Z$
. After acting by
$Y_1 \to Z$
. After acting by
![]() ${\left (\begin {smallmatrix}3 & -2\\2 & -1\end {smallmatrix}\right )}$
on the initial matrix of
${\left (\begin {smallmatrix}3 & -2\\2 & -1\end {smallmatrix}\right )}$
on the initial matrix of
![]() $T_0$
, we find that
$T_0$
, we find that
![]() $T_1$
is given by
$T_1$
is given by

We see that
![]() $Z \subseteq \mathbb P(1, 1, 1, 1, 2, 3)$
with variables
$Z \subseteq \mathbb P(1, 1, 1, 1, 2, 3)$
with variables
![]() $\beta , u, y, z, x, w$
is given by the ideal
$\beta , u, y, z, x, w$
is given by the ideal
where h is given by sending t to
![]() $1$
in
$1$
in
![]() $\Phi ^*f / u^6$
, namely
$\Phi ^*f / u^6$
, namely
and
Substituting
![]() $x = u\beta - a_2$
into h, we find that Z is a sextic double solid. Applying the explicit splitting lemma (Proposition 3.2), we find that the complex analytic space germ
$x = u\beta - a_2$
into h, we find that Z is a sextic double solid. Applying the explicit splitting lemma (Proposition 3.2), we find that the complex analytic space germ
![]() $(Z, P_\beta )$
is isomorphic to
$(Z, P_\beta )$
is isomorphic to
![]() $(\mathbb V(h_{\operatorname {ana}}), \boldsymbol {0}) \subseteq (\mathbb C^4, \boldsymbol {0})$
with variables
$(\mathbb V(h_{\operatorname {ana}}), \boldsymbol {0}) \subseteq (\mathbb C^4, \boldsymbol {0})$
with variables
![]() $w, u, y, z$
, where
$w, u, y, z$
, where
where (h.o.t in
![]() $y, z)$
stands for higher-order terms in the variables
$y, z)$
stands for higher-order terms in the variables
![]() $y, z$
. So,
$y, z$
. So,
![]() $P_\beta \in Z$
is a
$P_\beta \in Z$
is a
![]() $cA_5$
singularity. On the patch where
$cA_5$
singularity. On the patch where
![]() $\beta $
is nonzero, we can substitute
$\beta $
is nonzero, we can substitute
![]() $u = xt + a_2$
, so the morphism
$u = xt + a_2$
, so the morphism
![]() $(Y_1)_\beta \to Z_\beta $
is a weighted blowup of a hypersurface given by a weight
$(Y_1)_\beta \to Z_\beta $
is a weighted blowup of a hypersurface given by a weight
![]() $6$
polynomial. By Proposition 4.6,
$6$
polynomial. By Proposition 4.6,
![]() $Y_1 \to Z$
is a
$Y_1 \to Z$
is a
![]() $(3, 3, 1, 1)$
-Kawakita blowup.
$(3, 3, 1, 1)$
-Kawakita blowup.
We show that X and Z are not isomorphic when
![]() $a_2 \neq 0$
and
$a_2 \neq 0$
and
![]() $c_4$
is general, using a dimension counting argument similar to [Reference Greuel, Lossen and Shustin25, Th. 2.55]. Using the explicit splitting lemma, we find that the complex analytic space germ
$c_4$
is general, using a dimension counting argument similar to [Reference Greuel, Lossen and Shustin25, Th. 2.55]. Using the explicit splitting lemma, we find that the complex analytic space germ
![]() $(X, P_x)$
is isomorphic to
$(X, P_x)$
is isomorphic to
![]() $(\mathbb V(f_{\operatorname {ana}}), \boldsymbol {0}) \subseteq (\mathbb C^4, \boldsymbol {0})$
with variables
$(\mathbb V(f_{\operatorname {ana}}), \boldsymbol {0}) \subseteq (\mathbb C^4, \boldsymbol {0})$
with variables
![]() $w, t, y, z$
where
$w, t, y, z$
where
If X and Z are isomorphic, then this implies that the complex analytic space germs
![]() $(X, P_x)$
and
$(X, P_x)$
and
![]() $(Z, P_\beta )$
are isomorphic, implying by Propositions 2.4 and 2.5 that the degree
$(Z, P_\beta )$
are isomorphic, implying by Propositions 2.4 and 2.5 that the degree
![]() $6$
parts of
$6$
parts of
![]() $f_{\operatorname {ana}}(0, 0, y, z)$
and
$f_{\operatorname {ana}}(0, 0, y, z)$
and
![]() $h_{\operatorname {ana}}(0, 0, y, z)$
are the same up to an invertible linear coordinate change on
$h_{\operatorname {ana}}(0, 0, y, z)$
are the same up to an invertible linear coordinate change on
![]() $y, z$
. Fixing
$y, z$
. Fixing
![]() $a_0$
,
$a_0$
,
![]() $a_1$
,
$a_1$
,
![]() $a_2$
,
$a_2$
,
![]() $b_2$
,
$b_2$
,
![]() $b_3$
, and
$b_3$
, and
![]() $d_6$
, we see that
$d_6$
, we see that
![]() $h_{\operatorname {ana}}(0, 0, y, z)$
is fixed, but
$h_{\operatorname {ana}}(0, 0, y, z)$
is fixed, but
![]() $f_{\operatorname {ana}}(0, 0, y, z)$
has
$f_{\operatorname {ana}}(0, 0, y, z)$
has
![]() $5$
degrees of freedom. Since there are only
$5$
degrees of freedom. Since there are only
![]() $4$
degrees of freedom in picking an element of
$4$
degrees of freedom in picking an element of
![]() $\operatorname {GL}(2, \mathbb C)$
, the polynomials
$\operatorname {GL}(2, \mathbb C)$
, the polynomials
![]() $f_{\operatorname {ana}}(0, 0, y, z)$
and
$f_{\operatorname {ana}}(0, 0, y, z)$
and
![]() $h_{\operatorname {ana}}(0, 0, y, z)$
are not related by an invertible linear coordinate change when
$h_{\operatorname {ana}}(0, 0, y, z)$
are not related by an invertible linear coordinate change when
![]() $c_4$
is general. This shows that if X is general, then the varieties X and Z are not isomorphic.
$c_4$
is general. This shows that if X is general, then the varieties X and Z are not isomorphic.
5.4.
 $cA_6$
model
$cA_6$
model
Proposition 5.7. A sextic double solid that is a Mori space with a
![]() $cA_6$
singularity satisfying Definition 5.1 has a Sarkisov link to a hypersurface
$cA_6$
singularity satisfying Definition 5.1 has a Sarkisov link to a hypersurface
![]() $Z_5 \subseteq \mathbb P(1, 1, 1, 1, 2)$
with a
$Z_5 \subseteq \mathbb P(1, 1, 1, 1, 2)$
with a
![]() $cA_3$
singularity, starting with a
$cA_3$
singularity, starting with a
![]() $(4, 3, 1, 1)$
-blowup of the
$(4, 3, 1, 1)$
-blowup of the
![]() $cA_6$
point, then two
$cA_6$
point, then two
![]() $(1, 1, -1, -1)$
-flops, then a
$(1, 1, -1, -1)$
-flops, then a
![]() $(4, 1, 1, -2, -1; 2)$
-flip, and finally a
$(4, 1, 1, -2, -1; 2)$
-flip, and finally a
![]() $(2, 2, 1, 1)$
-blowdown to a
$(2, 2, 1, 1)$
-blowdown to a
![]() $cA_3$
point. Under further generality conditions, the singular locus of Z consists of three points, namely the
$cA_3$
point. Under further generality conditions, the singular locus of Z consists of three points, namely the
![]() $cA_3$
point, the
$cA_3$
point, the
![]() $1/2(1, 1, 1)$
quotient singularity, and an ordinary double point.
$1/2(1, 1, 1)$
quotient singularity, and an ordinary double point.
Proof. We exhibit the diagram below.

We construct X and a
![]() $(4, 3, 1, 1)$
-Kawakita blowup
$(4, 3, 1, 1)$
-Kawakita blowup
![]() $Y_0 \to X$
. Using Theorem A and Corollary 4.10 with
$Y_0 \to X$
. Using Theorem A and Corollary 4.10 with
![]() $p_2 = a_2$
and
$p_2 = a_2$
and
![]() $p_3 = b_3 - 4a_1a_2$
, we can write a sextic double solid X with a
$p_3 = b_3 - 4a_1a_2$
, we can write a sextic double solid X with a
![]() $cA_6$
singularity by
$cA_6$
singularity by
with variables
![]() $x, y, z, t, \beta , w$
where
$x, y, z, t, \beta , w$
where
 $$\begin{align*}\begin{aligned} f & = \alpha(-\alpha + 2(b_3 - 4\beta a_1 + 4xta_1 + x\beta)) \\& \quad + 2\beta(c_4 - \beta b_2 + 2xtb_2 + 2x\beta a_1 + 2\beta^2a_0 - 6xt\beta a_0 + 6x^2t^2a_0) \\& \quad + x^2t^3B_1 + xt^2C_3 + tD_5, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} f & = \alpha(-\alpha + 2(b_3 - 4\beta a_1 + 4xta_1 + x\beta)) \\& \quad + 2\beta(c_4 - \beta b_2 + 2xtb_2 + 2x\beta a_1 + 2\beta^2a_0 - 6xt\beta a_0 + 6x^2t^2a_0) \\& \quad + x^2t^3B_1 + xt^2C_3 + tD_5, \end{aligned} \end{align*}$$
where
![]() $B_i$
,
$B_i$
,
![]() $C_i$
,
$C_i$
,
![]() $D_i \in \mathbb C[y, z, t]$
are homogeneous of degree i. Define
$D_i \in \mathbb C[y, z, t]$
are homogeneous of degree i. Define
![]() $T_0$
by
$T_0$
by

Let
![]() $\Phi \colon T_0 \to \mathbb P(1, 1, 1, 1, 2, 3)$
be the ample model of
$\Phi \colon T_0 \to \mathbb P(1, 1, 1, 1, 2, 3)$
be the ample model of
![]() $\mathbb V(x)$
,
$\mathbb V(x)$
,
![]() $Y_0 \subseteq T_0$
the strict transform of X, and
$Y_0 \subseteq T_0$
the strict transform of X, and
![]() $Y_0 \to X$
the restriction of
$Y_0 \to X$
the restriction of
![]() $\Phi $
. Then,
$\Phi $
. Then,
![]() $Y_0$
is given by
$Y_0$
is given by
and
![]() $Y_0 \to X$
is a
$Y_0 \to X$
is a
![]() $(4, 3, 1, 1)$
-Kawakita blowup.
$(4, 3, 1, 1)$
-Kawakita blowup.
We show that the first diagram
![]() $Y_0 \to W_0 \gets Y_1$
in the 2-ray game for
$Y_0 \to W_0 \gets Y_1$
in the 2-ray game for
![]() $Y_0$
is locally analytically two Atiyah flops under Definition 5.1, namely that
$Y_0$
is locally analytically two Atiyah flops under Definition 5.1, namely that
![]() $\mathbb V(a_2) \subseteq \mathbb P^1$
with variables
$\mathbb V(a_2) \subseteq \mathbb P^1$
with variables
![]() $y, z$
consists of exactly two points, and for both of the points P, one of
$y, z$
consists of exactly two points, and for both of the points P, one of
![]() $b_3(P)$
,
$b_3(P)$
,
![]() $c_4(P)$
or
$c_4(P)$
or
![]() $d_5(P)$
is nonzero, where
$d_5(P)$
is nonzero, where
![]() $D_5 = t^5d_0 + 2t^4d_1 + t^3d_2 + 2t^2d_3 + td_4 + 2d_5$
. Acting by the matrix
$D_5 = t^5d_0 + 2t^4d_1 + t^3d_2 + 2t^2d_3 + td_4 + 2d_5$
. Acting by the matrix
![]() ${\left (\begin {smallmatrix}4 & -3\\-1 & 1\end {smallmatrix}\right )}$
, we find
${\left (\begin {smallmatrix}4 & -3\\-1 & 1\end {smallmatrix}\right )}$
, we find

Under the above condition, after a suitable linear change of coordinates on
![]() $y, z$
, we find that
$y, z$
, we find that
![]() $a_2 = yz$
. Let
$a_2 = yz$
. Let
![]() $P = \mathbb V(z) \in \mathbb P^1 \subseteq W_0$
, the case where
$P = \mathbb V(z) \in \mathbb P^1 \subseteq W_0$
, the case where
![]() $P = \mathbb V(y)$
is similar. On the patch where y is nonzero, we can substitute
$P = \mathbb V(y)$
is similar. On the patch where y is nonzero, we can substitute
![]() $z = u\beta - xt$
. The contracted locus is
$z = u\beta - xt$
. The contracted locus is
![]() $\mathbb P^1 \cong \mathbb V(\alpha , \beta , t) \subseteq (Y_0)_y$
, and the extracted locus is
$\mathbb P^1 \cong \mathbb V(\alpha , \beta , t) \subseteq (Y_0)_y$
, and the extracted locus is
![]() $\mathbb V(u, x) = \mathbb V(u, x, \alpha b_3(1, 0) + \beta c_4(1, 0) + td_5(1, 0)) \subseteq (Y_1)_y$
. By Definition 5.1, we can express one of
$\mathbb V(u, x) = \mathbb V(u, x, \alpha b_3(1, 0) + \beta c_4(1, 0) + td_5(1, 0)) \subseteq (Y_1)_y$
. By Definition 5.1, we can express one of
![]() $\alpha , \beta , t$
equivariantly locally analytically in the other variables. So, the flop diagram
$\alpha , \beta , t$
equivariantly locally analytically in the other variables. So, the flop diagram
![]() $Y_0 \to W_0 \gets Y_1$
is locally analytically a
$Y_0 \to W_0 \gets Y_1$
is locally analytically a
![]() $(1, 1, -1, -1)$
-flop above both of the points.
$(1, 1, -1, -1)$
-flop above both of the points.
We show that the next diagram in the 2-ray game of
![]() $Y_0$
is a
$Y_0$
is a
![]() $(4, 1, 1, -2, -1; 2)$
-flip (this is case (1) in [Reference Brown8, Th. 8]). The toric variety
$(4, 1, 1, -2, -1; 2)$
-flip (this is case (1) in [Reference Brown8, Th. 8]). The toric variety
![]() $T_1$
is given by
$T_1$
is given by

The base of the flip is
![]() $P_\alpha = [0, 0, 0, 0, 1, 0, 0]$
. On the patch where
$P_\alpha = [0, 0, 0, 0, 1, 0, 0]$
. On the patch where
![]() $\alpha $
is nonzero, we can express u locally analytically and equivariantly in terms of
$\alpha $
is nonzero, we can express u locally analytically and equivariantly in terms of
![]() $x, y, z, \beta , t$
. After substitution, the ideal is principal, with generator
$x, y, z, \beta , t$
. After substitution, the ideal is principal, with generator
![]() $f' = -\beta \cdot (2x + \cdots ) + xt + a_2$
. Under Definition 5.1,
$f' = -\beta \cdot (2x + \cdots ) + xt + a_2$
. Under Definition 5.1,
![]() $a_2$
has a nonzero coefficient in
$a_2$
has a nonzero coefficient in
![]() $f'$
, so the flip diagram corresponds to case (1) in [Reference Brown8, Th. 8]. The flips contracts a curve containing a
$f'$
, so the flip diagram corresponds to case (1) in [Reference Brown8, Th. 8]. The flips contracts a curve containing a
![]() $1/4(1, 1, 3)$
singularity and extracts a curve containing a
$1/4(1, 1, 3)$
singularity and extracts a curve containing a
![]() $1/2(1, 1, 1)$
singularity and an ordinary double point. The ordinary double point on
$1/2(1, 1, 1)$
singularity and an ordinary double point. The ordinary double point on
![]() $Y_2$
is at
$Y_2$
is at
![]() $[u_0, 0, 0, 0, 2, 1, 1]$
for some
$[u_0, 0, 0, 0, 2, 1, 1]$
for some
![]() $u_0 \in \mathbb C$
.
$u_0 \in \mathbb C$
.
We show that the last map in the 2-ray game of
![]() $Y_0$
is a weighted blowup
$Y_0$
is a weighted blowup
![]() $Y_2 \to Z$
, where Z is isomorphic to a hypersurface
$Y_2 \to Z$
, where Z is isomorphic to a hypersurface
![]() $Z_5 \subseteq \mathbb P(1, 1, 1, 1, 2)$
with variables
$Z_5 \subseteq \mathbb P(1, 1, 1, 1, 2)$
with variables
![]() $u, y, z, \beta , \alpha $
. Acting by the matrix
$u, y, z, \beta , \alpha $
. Acting by the matrix
![]() ${\left (\begin {smallmatrix}3 & -2\\2 & -1\end {smallmatrix}\right )}$
on the initial action-matrix of
${\left (\begin {smallmatrix}3 & -2\\2 & -1\end {smallmatrix}\right )}$
on the initial action-matrix of
![]() $T_0$
, we find that
$T_0$
, we find that
![]() $T_2$
is given by
$T_2$
is given by

Define the bidegree
![]() $(5, 2)$
complete intersection
$(5, 2)$
complete intersection
![]() $Z\colon \mathbb V(h, a_2 - u\beta + x) \subseteq \mathbb P(1, 1, 1, 1, 2, 2)$
with variables
$Z\colon \mathbb V(h, a_2 - u\beta + x) \subseteq \mathbb P(1, 1, 1, 1, 2, 2)$
with variables
![]() $u, y, z, \beta , x, \alpha $
, where
$u, y, z, \beta , x, \alpha $
, where
 $$\begin{align*}\begin{aligned} h & = \alpha(-u\alpha + 2(b_3 - 4u\beta a_1 + 4xa_1 + x\beta)) \\ & \quad + 2\beta(c_4 - u\beta b_2 + 2xb_2 + 2x\beta a_1 + 2u^2\beta^2a_0 - 6ux\beta a_0 + 6x^2a_0) \\ & \quad + x^2B_Z + xC_Z + D_Z, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} h & = \alpha(-u\alpha + 2(b_3 - 4u\beta a_1 + 4xa_1 + x\beta)) \\ & \quad + 2\beta(c_4 - u\beta b_2 + 2xb_2 + 2x\beta a_1 + 2u^2\beta^2a_0 - 6ux\beta a_0 + 6x^2a_0) \\ & \quad + x^2B_Z + xC_Z + D_Z, \end{aligned} \end{align*}$$
where
The morphism
![]() $Y_2 \to Z$
given by the ample model of
$Y_2 \to Z$
given by the ample model of
![]() $\mathbb V(\beta )$
is a weighted blowdown with center
$\mathbb V(\beta )$
is a weighted blowdown with center
![]() $P_\beta $
and exceptional locus
$P_\beta $
and exceptional locus
![]() $\mathbb V(t)$
. Substituting
$\mathbb V(t)$
. Substituting
into h, we find that Z is isomorphic to a hypersurface
![]() $Z_5 \subseteq \mathbb P(1, 1, 1, 1, 2)$
with variables
$Z_5 \subseteq \mathbb P(1, 1, 1, 1, 2)$
with variables
![]() $u, y, z, \beta , \alpha $
. The substitution (5.1) does not lift onto
$u, y, z, \beta , \alpha $
. The substitution (5.1) does not lift onto
![]() $Y_2$
. Instead, on the patch
$Y_2$
. Instead, on the patch
![]() $Z_\beta $
, we can substitute
$Z_\beta $
, we can substitute
![]() $u = (a_2 + x)/\beta $
. This substitution lifts to
$u = (a_2 + x)/\beta $
. This substitution lifts to
![]() $(Y_2)_\beta $
. By Definition 5.1,
$(Y_2)_\beta $
. By Definition 5.1,
![]() $P_\beta \in Z$
is a
$P_\beta \in Z$
is a
![]() $cA_3$
singularity and the hypersurface
$cA_3$
singularity and the hypersurface
![]() $Z_\beta $
is given by a weight 4 polynomial. By Proposition 4.6,
$Z_\beta $
is given by a weight 4 polynomial. By Proposition 4.6,
![]() $(Y_2)_\beta \to Z_\beta $
is a
$(Y_2)_\beta \to Z_\beta $
is a
![]() $(3, 1, 1, 1)$
-Kawakita blowup.
$(3, 1, 1, 1)$
-Kawakita blowup.
Note that Z has an ordinary double point at
![]() $[u_0, 0, 0, 1, 2]$
for some
$[u_0, 0, 0, 1, 2]$
for some
![]() $u_0 \in \mathbb C$
.
$u_0 \in \mathbb C$
.
5.5.
 $cA_7$
family 7.1 model
$cA_7$
family 7.1 model
Proposition 5.8. A Mori fiber space sextic double solid with a
![]() $cA_7$
singularity in family 7.1 satisfying Definition 5.1 has a Sarkisov link to
$cA_7$
singularity in family 7.1 satisfying Definition 5.1 has a Sarkisov link to
![]() $Z_{3, 4} \subseteq \mathbb P(1, 1, 1, 1, 2, 2)$
with an ordinary double point, starting with a
$Z_{3, 4} \subseteq \mathbb P(1, 1, 1, 1, 2, 2)$
with an ordinary double point, starting with a
![]() $(4, 4, 1, 1)$
-blowup of the
$(4, 4, 1, 1)$
-blowup of the
![]() $cA_7$
point, then two
$cA_7$
point, then two
![]() $(4, 1, 1, -2, -1; 2)$
-flips, and finally a blowdown (with standard weights
$(4, 1, 1, -2, -1; 2)$
-flips, and finally a blowdown (with standard weights
![]() $(1, 1, 1, 1)$
) to an ordinary double point. Under further generality conditions, Z has exactly five singular points, namely two
$(1, 1, 1, 1)$
) to an ordinary double point. Under further generality conditions, Z has exactly five singular points, namely two
![]() $1/2(1, 1, 1)$
singularities and three ordinary double points.
$1/2(1, 1, 1)$
singularities and three ordinary double points.
Proof. We exhibit the diagram below.

We construct X and a
![]() $(4, 4, 1, 1)$
-Kawakita blowup
$(4, 4, 1, 1)$
-Kawakita blowup
![]() $Y_0 \to X$
. We can write a sextic double solid X with an isolated
$Y_0 \to X$
. We can write a sextic double solid X with an isolated
![]() $cA_7$
singularity in family 7.1 by
$cA_7$
singularity in family 7.1 by
with variables
![]() $x, y, z, t, \beta , \gamma , w$
, where
$x, y, z, t, \beta , \gamma , w$
, where
 $$\begin{align*}\begin{aligned} f & = -w^2 + \gamma^2 - 2 t \gamma e_2 + 2 \beta^2 e_2 + 2 t \beta c_3 + 4 t \gamma b_2 - 2 \beta^2 b_2 - 2 t \beta^2 b_1 + 4 x t^2 \beta b_1 \\ & \quad + 2 x^2 t^4 b_0 - 16 t \gamma a_1^2 + 16 \beta^2 a_1^2 + 4 \beta \gamma a_1 - 8 \beta^3 a_0 + 12 x t \beta^2 a_0 + x t^3 C_2 + t^2 D_4, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} f & = -w^2 + \gamma^2 - 2 t \gamma e_2 + 2 \beta^2 e_2 + 2 t \beta c_3 + 4 t \gamma b_2 - 2 \beta^2 b_2 - 2 t \beta^2 b_1 + 4 x t^2 \beta b_1 \\ & \quad + 2 x^2 t^4 b_0 - 16 t \gamma a_1^2 + 16 \beta^2 a_1^2 + 4 \beta \gamma a_1 - 8 \beta^3 a_0 + 12 x t \beta^2 a_0 + x t^3 C_2 + t^2 D_4, \end{aligned} \end{align*}$$
where
![]() $C_i$
,
$C_i$
,
![]() $D_i \in \mathbb C[y, z, t]$
are homogeneous of degree i. Define
$D_i \in \mathbb C[y, z, t]$
are homogeneous of degree i. Define
![]() $T_0$
by
$T_0$
by

Define
![]() $Y_0$
by
$Y_0$
by
The ample model of
![]() $\mathbb V(x) \subseteq Y_0$
is a
$\mathbb V(x) \subseteq Y_0$
is a
![]() $(4, 4, 1, 1)$
-Kawakita blowup
$(4, 4, 1, 1)$
-Kawakita blowup
![]() $Y_0 \to X$
.
$Y_0 \to X$
.
We show that the diagram
![]() $Y_0 \to W_0 \gets Y_1$
induces an isomorphism
$Y_0 \to W_0 \gets Y_1$
induces an isomorphism
![]() $Y_0 \to Y_1$
. Acting by the matrix
$Y_0 \to Y_1$
. Acting by the matrix
![]() ${\left (\begin {smallmatrix}4 & -3\\-1 & 1\end {smallmatrix}\right )}$
, we find
${\left (\begin {smallmatrix}4 & -3\\-1 & 1\end {smallmatrix}\right )}$
, we find

Define
![]() $T_1$
(resp.
$T_1$
(resp.
![]() $T_2$
) with the same action as
$T_2$
) with the same action as
![]() $T_0$
but with irrelevant ideal
$T_0$
but with irrelevant ideal
![]() $(u, x, y, z) \cap (w, \gamma , \beta , t)$
(resp.
$(u, x, y, z) \cap (w, \gamma , \beta , t)$
(resp.
![]() $(u, x, y, z, w, \gamma ) \cap (\beta , t)$
). Define
$(u, x, y, z, w, \gamma ) \cap (\beta , t)$
). Define
![]() $Y_1 \subseteq T_1$
and
$Y_1 \subseteq T_1$
and
![]() $Y_2 \subseteq T_2$
by the same ideal
$Y_2 \subseteq T_2$
by the same ideal
![]() $I_Y$
. The base of the flop
$I_Y$
. The base of the flop
![]() $T_0 \to \mathcal W_0 \gets T_1$
restricts to
$T_0 \to \mathcal W_0 \gets T_1$
restricts to
![]() $\mathbb V(r_2, s_3) \subseteq \mathbb P^1 \subseteq W_0$
, which is empty. Therefore,
$\mathbb V(r_2, s_3) \subseteq \mathbb P^1 \subseteq W_0$
, which is empty. Therefore,
![]() $Y_0 \to W_0$
and
$Y_0 \to W_0$
and
![]() $W_0 \gets Y_1$
are isomorphisms.
$W_0 \gets Y_1$
are isomorphisms.
We show that the next diagram
![]() $Y_1 \to W_1 \gets Y_2$
in the 2-ray game of
$Y_1 \to W_1 \gets Y_2$
in the 2-ray game of
![]() $Y_0$
is locally analytically two
$Y_0$
is locally analytically two
![]() $(4, 1, 1, -2, -1; 2)$
-flips. The only monomials in
$(4, 1, 1, -2, -1; 2)$
-flips. The only monomials in
![]() $\Phi ^*f / u^8$
that are not in
$\Phi ^*f / u^8$
that are not in
![]() $(u, x, y, z, \beta , t)$
are
$(u, x, y, z, \beta , t)$
are
![]() $-w^2$
and
$-w^2$
and
![]() $\gamma ^2$
. Therefore, the base of the flip is two points,
$\gamma ^2$
. Therefore, the base of the flip is two points,
![]() $[1, 1]$
and
$[1, 1]$
and
![]() $[-1, 1] \in \mathbb P^1$
with variables w and
$[-1, 1] \in \mathbb P^1$
with variables w and
![]() $\gamma $
inside
$\gamma $
inside
![]() $W_1$
. We make a change of coordinates
$W_1$
. We make a change of coordinates
![]() $w' = w - \gamma $
, respectively
$w' = w - \gamma $
, respectively
![]() $w' = w + \gamma $
, for the flip above
$w' = w + \gamma $
, for the flip above
![]() $[1, 1]$
, respectively
$[1, 1]$
, respectively
![]() $[-1, 1]$
. On the patch where
$[-1, 1]$
. On the patch where
![]() $\gamma $
is nonzero, we can substitute
$\gamma $
is nonzero, we can substitute
![]() $u = s_3 + x \beta $
in
$u = s_3 + x \beta $
in
![]() $\Phi ^*f / u^8$
, and express
$\Phi ^*f / u^8$
, and express
![]() $w'$
locally analytically and equivariantly above
$w'$
locally analytically and equivariantly above
![]() $[1, 1]$
, respectively
$[1, 1]$
, respectively
![]() $[-1, 1]$
, in terms of
$[-1, 1]$
, in terms of
![]() $x, y, z, \beta , t$
. After projecting away the variables u and
$x, y, z, \beta , t$
. After projecting away the variables u and
![]() $w'$
, we are left with the principal ideal
$w'$
, we are left with the principal ideal
![]() $(\beta s_3 - r_2 + x \beta ^2 - x t)$
. Since it contains both
$(\beta s_3 - r_2 + x \beta ^2 - x t)$
. Since it contains both
![]() $r_2$
and
$r_2$
and
![]() $xt$
, by case (1) in [Reference Brown8, Th. 8], it is a terminal
$xt$
, by case (1) in [Reference Brown8, Th. 8], it is a terminal
![]() $(4, 1, 1, -2, -1; 2)$
-flip above both
$(4, 1, 1, -2, -1; 2)$
-flip above both
![]() $[1, 1]$
and
$[1, 1]$
and
![]() $[-1, 1]$
. The flip contracts two curves, both containing a
$[-1, 1]$
. The flip contracts two curves, both containing a
![]() $1/4(1, 1, 3)$
singularity, and extracts two curves, both containing a
$1/4(1, 1, 3)$
singularity, and extracts two curves, both containing a
![]() $1/2(1, 1, 1)$
singularity and a
$1/2(1, 1, 1)$
singularity and a
![]() $cA_1$
singularity. The
$cA_1$
singularity. The
![]() $cA_1$
points are both ordinary double points if
$cA_1$
points are both ordinary double points if
![]() $r_2$
is not a square of a linear form, and are both 3-fold
$r_2$
is not a square of a linear form, and are both 3-fold
![]() $A_2$
singularities (given by
$A_2$
singularities (given by
![]() $x_1^2 + x_2^2 + x_3^2 + x_4^3$
) otherwise. On
$x_1^2 + x_2^2 + x_3^2 + x_4^3$
) otherwise. On
![]() $Y_2$
, the
$Y_2$
, the
![]() $cA_1$
singularities are at
$cA_1$
singularities are at
![]() $[0, 0, 0, 0, 1, 1, 1, 1]$
and
$[0, 0, 0, 0, 1, 1, 1, 1]$
and
![]() $[0, 0, 0, 0, -1, 1, 1, 1]$
.
$[0, 0, 0, 0, -1, 1, 1, 1]$
.
We show that the last map in the link for X is a divisorial contraction
![]() $Y_2 \to Z'$
. Acting by the matrix
$Y_2 \to Z'$
. Acting by the matrix
![]() ${\left (\begin {smallmatrix}3 & -2\\2 & -1\end {smallmatrix}\right )}$
on the initial action-matrix of
${\left (\begin {smallmatrix}3 & -2\\2 & -1\end {smallmatrix}\right )}$
on the initial action-matrix of
![]() $T_0$
, we see that
$T_0$
, we see that

Define
![]() $Z' \subseteq \mathbb P(1, 1, 1, 1, 2, 2, 2)$
with variables
$Z' \subseteq \mathbb P(1, 1, 1, 1, 2, 2, 2)$
with variables
![]() $u, y, z, \beta , w, \gamma , x$
by the ideal
$u, y, z, \beta , w, \gamma , x$
by the ideal
![]() $I_{Z'}$
, where
$I_{Z'}$
, where
![]() $I_{Z'}$
is the image of the ideal
$I_{Z'}$
is the image of the ideal
![]() $I_Y$
under the homomorphism
$I_Y$
under the homomorphism
![]() $t \mapsto 1$
. Let
$t \mapsto 1$
. Let
![]() $Y_2 \to Z'$
be the ample model of
$Y_2 \to Z'$
be the ample model of
![]() $\mathbb V(\beta )$
. On the affine patch
$\mathbb V(\beta )$
. On the affine patch
![]() $Z^{\prime }_\beta $
, we can express u and x locally analytically and equivariantly in terms of
$Z^{\prime }_\beta $
, we can express u and x locally analytically and equivariantly in terms of
![]() $y, z, w, \gamma , \beta , t$
. This coordinate change lifts to
$y, z, w, \gamma , \beta , t$
. This coordinate change lifts to
![]() $Y_2$
. By Definition 5.1, we can compute that
$Y_2$
. By Definition 5.1, we can compute that
![]() $P_\beta \in Z'$
is an ordinary double point, and
$P_\beta \in Z'$
is an ordinary double point, and
![]() $Y_2 \to Z'$
is locally analytically the (usual) blowup with center
$Y_2 \to Z'$
is locally analytically the (usual) blowup with center
![]() $P_\beta $
.
$P_\beta $
.
The variety
![]() $Z'$
is isomorphic to a complete intersection
$Z'$
is isomorphic to a complete intersection
![]() $Z_{3, 4} \subseteq \mathbb P(1^4, 2^2)$
, by projecting away from x. The variety Z is given by
$Z_{3, 4} \subseteq \mathbb P(1^4, 2^2)$
, by projecting away from x. The variety Z is given by
with variables
![]() $u, y, z, \beta , w, \gamma $
, where
$u, y, z, \beta , w, \gamma $
, where
 $$\begin{align*}\begin{aligned} h & = -w^2 + \gamma^2 + 2 b_0 r_2^2 - 4 \beta b_1 r_2 - 4 u \beta b_0 r_2 - 12 \beta^2 a_0 r_2 - 2 \gamma e_2 + 2 \beta^2 e_2 + 2 \beta c_3 + 4 \gamma b_2 \\ & \quad - 2 \beta^2 b_2 + 2 u \beta^2 b_1 + 2 u^2 \beta^2 b_0 - 16 \gamma a_1^2 + 16 \beta^2 a_1^2 + 4 \beta \gamma a_1 + 4 u \beta^3 a_0 + (u \beta - r_2) C_Z + D_Z, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} h & = -w^2 + \gamma^2 + 2 b_0 r_2^2 - 4 \beta b_1 r_2 - 4 u \beta b_0 r_2 - 12 \beta^2 a_0 r_2 - 2 \gamma e_2 + 2 \beta^2 e_2 + 2 \beta c_3 + 4 \gamma b_2 \\ & \quad - 2 \beta^2 b_2 + 2 u \beta^2 b_1 + 2 u^2 \beta^2 b_0 - 16 \gamma a_1^2 + 16 \beta^2 a_1^2 + 4 \beta \gamma a_1 + 4 u \beta^3 a_0 + (u \beta - r_2) C_Z + D_Z, \end{aligned} \end{align*}$$
where
![]() $C_Z = C_2(y, z, u)$
and
$C_Z = C_2(y, z, u)$
and
![]() $D_Z = D_4(y, z, u)$
. The variety Z has two
$D_Z = D_4(y, z, u)$
. The variety Z has two
![]() $cA_1$
singularities at
$cA_1$
singularities at
![]() $[0, 0, 0, 1, 1, 1]$
and
$[0, 0, 0, 1, 1, 1]$
and
![]() $[0, 0, 0, 1, -1, 1]$
.
$[0, 0, 0, 1, -1, 1]$
.
Remark 5.9. We explain how we found the variety X. Using
![]() $p_2 = r_2$
and
$p_2 = r_2$
and
![]() $p_3 = s_3$
, we can write a sextic double solid with an isolated
$p_3 = s_3$
, we can write a sextic double solid with an isolated
![]() $cA_7$
in family 7.1 by
$cA_7$
in family 7.1 by
![]() $\bar X\colon \mathbb V(\bar f, x^2 t + x r_2 + s_3 - \bar {\gamma })$
inside
$\bar X\colon \mathbb V(\bar f, x^2 t + x r_2 + s_3 - \bar {\gamma })$
inside
![]() $\mathbb P(1, 1, 1, 1, 3, 3)$
with variables
$\mathbb P(1, 1, 1, 1, 3, 3)$
with variables
![]() $x, y, z, t, w, \bar {\gamma }$
, where
$x, y, z, t, w, \bar {\gamma }$
, where
![]() $\bar f$
is given as in Theorem A. The
$\bar f$
is given as in Theorem A. The
![]() $(1, 1, 4, 4, 2)$
-blowup
$(1, 1, 4, 4, 2)$
-blowup
![]() $\bar Y_0 \to \bar X$
for variables
$\bar Y_0 \to \bar X$
for variables
![]() $y, z, w, \bar {\gamma }, t$
is a
$y, z, w, \bar {\gamma }, t$
is a
![]() $(4, 4, 1, 1)$
-Kawakita blowup, but the 2-ray game of
$(4, 4, 1, 1)$
-Kawakita blowup, but the 2-ray game of
![]() $\bar Y_0$
does not follow the ambient toric variety
$\bar Y_0$
does not follow the ambient toric variety
![]() $\bar T_0$
. Namely, the toric anti-flip
$\bar T_0$
. Namely, the toric anti-flip
![]() $\bar T_0 \to \bar {\mathcal W}_0 \gets \bar T_1$
restricts to
$\bar T_0 \to \bar {\mathcal W}_0 \gets \bar T_1$
restricts to
![]() $\bar Y_0 \to \bar {W}_0 \gets \bar Y_1$
, where
$\bar Y_0 \to \bar {W}_0 \gets \bar Y_1$
, where
![]() $\bar Y_0 \to \bar {W}_0$
is an isomorphism and
$\bar Y_0 \to \bar {W}_0$
is an isomorphism and
![]() $\bar {W}_0 \gets \bar Y_1$
extracts
$\bar {W}_0 \gets \bar Y_1$
extracts
![]() $\mathbb P^2$
, a divisor on
$\mathbb P^2$
, a divisor on
![]() $\bar Y_1$
. The reason why
$\bar Y_1$
. The reason why
![]() $\bar Y_0$
was not the correct variety is that one of the generators of the ideal of
$\bar Y_0$
was not the correct variety is that one of the generators of the ideal of
![]() $\bar Y_0$
is
$\bar Y_0$
is
![]() $\bar g_1 = x^2 t + x r_2 + u s_3 - u \bar {\gamma }$
, which is inside the irrelevant ideal
$\bar g_1 = x^2 t + x r_2 + u s_3 - u \bar {\gamma }$
, which is inside the irrelevant ideal
![]() $(u, x)$
. We find the correct variety
$(u, x)$
. We find the correct variety
![]() $Y_0$
by unprojecting
$Y_0$
by unprojecting
![]() $\bar g_1 = 0$
with respect to
$\bar g_1 = 0$
with respect to
![]() $u, x$
. By unprojection, we mean the coordinate change
$u, x$
. By unprojection, we mean the coordinate change
![]() $\bar Y_0 \to Y_0$
, an isomorphism. See [Reference Reid49, §2] or [Reference Papadakis and Reid44, §2.3] for more details on this type of unprojection. This coordinate change induces the coordinate change
$\bar Y_0 \to Y_0$
, an isomorphism. See [Reference Reid49, §2] or [Reference Papadakis and Reid44, §2.3] for more details on this type of unprojection. This coordinate change induces the coordinate change
![]() $\bar X \to X$
, where X is given as in the proof of Proposition 5.8.
$\bar X \to X$
, where X is given as in the proof of Proposition 5.8.
5.6.
 $cA_7$
family 7.2 model
$cA_7$
family 7.2 model
Proposition 5.10. A Mori fiber space sextic double solid with a
![]() $cA_7$
singularity in family 7.2 satisfying Definition 5.1 has a Sarkisov link to a complete intersection
$cA_7$
singularity in family 7.2 satisfying Definition 5.1 has a Sarkisov link to a complete intersection
![]() $Z_{2, 4} \subseteq \mathbb P(1, 1, 1, 1, 1, 2)$
with a
$Z_{2, 4} \subseteq \mathbb P(1, 1, 1, 1, 1, 2)$
with a
![]() $cA_2$
singularity, starting with a
$cA_2$
singularity, starting with a
![]() $(4, 4, 1, 1)$
-blowup of the
$(4, 4, 1, 1)$
-blowup of the
![]() $cA_7$
point, followed by one Atiyah flop, then two
$cA_7$
point, followed by one Atiyah flop, then two
![]() $(4, 1, -1, -3)$
-flips, and finally a
$(4, 1, -1, -3)$
-flips, and finally a
![]() $(3, 3, 2, 1)$
-blowdown to a
$(3, 3, 2, 1)$
-blowdown to a
![]() $cA_2$
point. Under further generality conditions, the variety Z is smooth outside the
$cA_2$
point. Under further generality conditions, the variety Z is smooth outside the
![]() $cA_2$
point.
$cA_2$
point.
Proof. We exhibit the diagram below.

We describe the sextic double solid X. Define
![]() $X \subseteq \mathbb P(1, 1, 1, 1, 2, 3, 3, 3)$
with variables x, y, z, t,
$X \subseteq \mathbb P(1, 1, 1, 1, 2, 3, 3, 3)$
with variables x, y, z, t,
![]() $\beta $
, w,
$\beta $
, w,
![]() $\gamma $
,
$\gamma $
,
![]() $\xi $
by the ideal
$\xi $
by the ideal
where
 $$\begin{align*}\begin{aligned} f & = -w^2 + \gamma^2 + 2 t \beta c_3 + 4 t \gamma b_2 - 2 \beta^2 b_2 - 2 t \beta^2 b_1 + 4 x t^2 \beta b_1 + 2 x^2 t^4 b_0 \\ & \quad - 16 t \gamma a_1^2 + 16 \beta^2 a_1^2 + 4 \beta \gamma a_1 - 8 \beta^3 a_0 + 12 x t \beta^2 a_0 + x t^3 C_2 + t^2 D_4, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} f & = -w^2 + \gamma^2 + 2 t \beta c_3 + 4 t \gamma b_2 - 2 \beta^2 b_2 - 2 t \beta^2 b_1 + 4 x t^2 \beta b_1 + 2 x^2 t^4 b_0 \\ & \quad - 16 t \gamma a_1^2 + 16 \beta^2 a_1^2 + 4 \beta \gamma a_1 - 8 \beta^3 a_0 + 12 x t \beta^2 a_0 + x t^3 C_2 + t^2 D_4, \end{aligned} \end{align*}$$
where
![]() $C_i$
,
$C_i$
,
![]() $D_i \in \mathbb C[y, z, t]$
are homogeneous of degree i.
$D_i \in \mathbb C[y, z, t]$
are homogeneous of degree i.
We describe the weighted blowup
![]() $Y_0 \to X$
, restriction of
$Y_0 \to X$
, restriction of
![]() $\Phi \colon T_0 \to \mathbb P(1, 1, 1, 1, 2, 3, 3, 3)$
. Define
$\Phi \colon T_0 \to \mathbb P(1, 1, 1, 1, 2, 3, 3, 3)$
. Define
![]() $T_0$
by
$T_0$
by

Define
![]() $Y_0 \subseteq T_0$
by the ideal
$Y_0 \subseteq T_0$
by the ideal
![]() $I_Y$
with the six generators
$I_Y$
with the six generators
 $$\begin{align*}\begin{aligned} g - 2 e_3 \xi, && u \beta - q_1 r_1 - x t, && u \gamma - q_1 s_2 - x \beta,\\ -u \xi + t s_2 - \beta r_1, && -x \xi + \beta s_2 - \gamma r_1, && -q_1 \xi + t \gamma - \beta^2, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} g - 2 e_3 \xi, && u \beta - q_1 r_1 - x t, && u \gamma - q_1 s_2 - x \beta,\\ -u \xi + t s_2 - \beta r_1, && -x \xi + \beta s_2 - \gamma r_1, && -q_1 \xi + t \gamma - \beta^2, \end{aligned} \end{align*}$$
where
![]() $g = \Phi ^*f / u^8$
. On the affine patch
$g = \Phi ^*f / u^8$
. On the affine patch
![]() $X_x$
, we can express
$X_x$
, we can express
![]() $\beta , t$
, and
$\beta , t$
, and
![]() $\xi $
in terms of
$\xi $
in terms of
![]() $w, \gamma , y, z$
, to get a hypersurface in
$w, \gamma , y, z$
, to get a hypersurface in
![]() $\mathbb C^4$
given by
$\mathbb C^4$
given by
![]() $f_{\operatorname {hyp}} \in \mathbb C[w, \gamma , y, z]$
. Note that these coordinate changes lift to
$f_{\operatorname {hyp}} \in \mathbb C[w, \gamma , y, z]$
. Note that these coordinate changes lift to
![]() $(Y_0)_x$
. Since
$(Y_0)_x$
. Since
![]() $f_{\operatorname {hyp}}$
has weight
$f_{\operatorname {hyp}}$
has weight
![]() $8$
, by Proposition 4.6,
$8$
, by Proposition 4.6,
![]() $Y_0 \to X$
is a
$Y_0 \to X$
is a
![]() $(4, 4, 1, 1)$
-Kawakita blowup.
$(4, 4, 1, 1)$
-Kawakita blowup.
We show that the first diagram
![]() $Y_0 \to W_0 \gets Y_1$
in the 2-ray game of
$Y_0 \to W_0 \gets Y_1$
in the 2-ray game of
![]() $Y_0$
is an Atiyah flop, provided that
$Y_0$
is an Atiyah flop, provided that
![]() $r_1$
and
$r_1$
and
![]() $q_1$
are coprime in
$q_1$
are coprime in
![]() $\mathbb C[y, z]$
. Acting by the matrix
$\mathbb C[y, z]$
. Acting by the matrix
![]() ${\left (\begin {smallmatrix}4 & -3\\-1 & 1\end {smallmatrix}\right )}$
on the action-matrix of
${\left (\begin {smallmatrix}4 & -3\\-1 & 1\end {smallmatrix}\right )}$
on the action-matrix of
![]() $T_0$
, define
$T_0$
, define
![]() $T_1$
by
$T_1$
by

Define
![]() $Y_1 \subseteq T_1$
by the ideal
$Y_1 \subseteq T_1$
by the ideal
![]() $I_Y$
. The base of the flop is
$I_Y$
. The base of the flop is
![]() $\mathbb V(q_1) \subseteq \mathbb P^1$
with variables
$\mathbb V(q_1) \subseteq \mathbb P^1$
with variables
![]() $y, z$
, which is one point. Perform a suitable invertible linear coordinate change on
$y, z$
, which is one point. Perform a suitable invertible linear coordinate change on
![]() $y, z$
such that
$y, z$
such that
![]() $q_1 = z$
and
$q_1 = z$
and
![]() $r_1 = y$
. Since
$r_1 = y$
. Since
![]() $u \beta - q_1 r_1 - x t$
is in
$u \beta - q_1 r_1 - x t$
is in
![]() $I_Y$
, we can substitute
$I_Y$
, we can substitute
![]() $z = u \beta - x t$
on the patch where y is nonzero. The coefficients of
$z = u \beta - x t$
on the patch where y is nonzero. The coefficients of
![]() $\beta $
in
$\beta $
in
![]() $-u \xi + t s_2 - \beta y \in I_Y$
and
$-u \xi + t s_2 - \beta y \in I_Y$
and
![]() $\gamma $
in
$\gamma $
in
![]() $-x \xi + \beta s_2 - \gamma y \in I_Y$
are nonzero on the patch where y is nonzero. Therefore, we can locally analytically equivariantly express
$-x \xi + \beta s_2 - \gamma y \in I_Y$
are nonzero on the patch where y is nonzero. Therefore, we can locally analytically equivariantly express
![]() $\beta $
and
$\beta $
and
![]() $\gamma $
in terms of
$\gamma $
in terms of
![]() $u, x, w, t$
. After substituting
$u, x, w, t$
. After substituting
![]() $z, \beta , \gamma $
, we find that the diagram
$z, \beta , \gamma $
, we find that the diagram
![]() $Y_0 \to W_0 \gets Y_1$
is locally analytically the Atiyah flop.
$Y_0 \to W_0 \gets Y_1$
is locally analytically the Atiyah flop.
The next diagram in the 2-ray game of
![]() $Y_0$
is the flip
$Y_0$
is the flip
![]() $Y_1 \to W_1 \gets Y_2$
. The base of the flip is
$Y_1 \to W_1 \gets Y_2$
. The base of the flip is
![]() $\mathbb V(\gamma ^2 - w^2) \subseteq \mathbb P^1$
with variables
$\mathbb V(\gamma ^2 - w^2) \subseteq \mathbb P^1$
with variables
![]() $w, \gamma $
, which is two points
$w, \gamma $
, which is two points
![]() $[1, 1]$
and
$[1, 1]$
and
![]() $[-1, 1]$
. We consider the point
$[-1, 1]$
. We consider the point
![]() $P = [1, 1]$
, the flip for the other point is similar. Perform a coordinate change
$P = [1, 1]$
, the flip for the other point is similar. Perform a coordinate change
![]() $w' = w - \gamma $
. On the patch where
$w' = w - \gamma $
. On the patch where
![]() $\gamma $
is nonzero, we find
$\gamma $
is nonzero, we find
![]() $u = q_1 s_2 + x \beta $
and
$u = q_1 s_2 + x \beta $
and
![]() $t = q_1 \xi + \beta ^2$
. Writing
$t = q_1 \xi + \beta ^2$
. Writing
![]() $q_1 = z$
and
$q_1 = z$
and
![]() $r_1 = y$
as before, we find
$r_1 = y$
as before, we find
![]() $y = -x \xi + \beta s_2$
. We are left with the principal ideal in
$y = -x \xi + \beta s_2$
. We are left with the principal ideal in
![]() $\mathbb C[x, z, w', \beta , \xi ]$
generated by
$\mathbb C[x, z, w', \beta , \xi ]$
generated by
![]() $-w'(2 + w') + {}$
terms not involving
$-w'(2 + w') + {}$
terms not involving
![]() $w'$
. So, we can locally analytically equivariantly express
$w'$
. So, we can locally analytically equivariantly express
![]() $w'$
in terms of
$w'$
in terms of
![]() $x, z, \beta , \xi $
. So, the diagram
$x, z, \beta , \xi $
. So, the diagram
![]() $Y_1 \to W_1 \gets Y_2$
is locally analytically two
$Y_1 \to W_1 \gets Y_2$
is locally analytically two
![]() $(-4, -1, 1, 3)$
-flips.
$(-4, -1, 1, 3)$
-flips.
The next diagram in the toric 2-ray game
![]() $T_2 \to \mathcal W_2 \gets T_3$
restricts to isomorphisms
$T_2 \to \mathcal W_2 \gets T_3$
restricts to isomorphisms
![]() $Y_2 \to W_2 \gets Y_3$
. The reason is that the base of the toric flip
$Y_2 \to W_2 \gets Y_3$
. The reason is that the base of the toric flip
![]() $P_\beta $
restricts to an empty set in
$P_\beta $
restricts to an empty set in
![]() $W_2$
, since
$W_2$
, since
![]() $I_Y$
contains the polynomial
$I_Y$
contains the polynomial
![]() $t \gamma - \beta ^2 - q \xi $
.
$t \gamma - \beta ^2 - q \xi $
.
We show that the last diagram in the 2-ray game of
![]() $Y_0$
is a divisorial contraction
$Y_0$
is a divisorial contraction
![]() $Y_3 \to Z$
. Multiplying the action-matrix of
$Y_3 \to Z$
. Multiplying the action-matrix of
![]() $T_1$
by
$T_1$
by
![]() ${\left (\begin {smallmatrix}2 & 3\\1 & 2\end {smallmatrix}\right )}$
, we see that
${\left (\begin {smallmatrix}2 & 3\\1 & 2\end {smallmatrix}\right )}$
, we see that
![]() $T_3$
is given by
$T_3$
is given by

Consider the variety
![]() $Z \subseteq \mathbb P(1, 1, 1, 1, 1, 2, 2, 2)$
with variables
$Z \subseteq \mathbb P(1, 1, 1, 1, 1, 2, 2, 2)$
with variables
![]() $\xi , u, y, z, \beta , x, w, \gamma $
where
$\xi , u, y, z, \beta , x, w, \gamma $
where
![]() $Y_3 \to Z$
is the ample model of
$Y_3 \to Z$
is the ample model of
![]() $\mathbb V(\xi )$
. On the patch
$\mathbb V(\xi )$
. On the patch
![]() $Z_\xi $
, we can substitute
$Z_\xi $
, we can substitute
![]() $u = s_2 - \beta r_1$
,
$u = s_2 - \beta r_1$
,
![]() $x = \beta s_2 - \gamma r_1$
and
$x = \beta s_2 - \gamma r_1$
and
![]() $z = \gamma - \beta ^2$
, and compute that
$z = \gamma - \beta ^2$
, and compute that
![]() $Z_\xi $
is a hypersurface given by a weight
$Z_\xi $
is a hypersurface given by a weight
![]() $6$
polynomial, with a
$6$
polynomial, with a
![]() $cA_2$
singularity at
$cA_2$
singularity at
![]() $P_\xi \in Z_\xi $
, of type at least
$P_\xi \in Z_\xi $
, of type at least
![]() $2$
(see Definition 4.8). These substitutions lift to
$2$
(see Definition 4.8). These substitutions lift to
![]() $(Y_3)_\xi $
, showing that
$(Y_3)_\xi $
, showing that
![]() $Y_3 \to Z$
is a
$Y_3 \to Z$
is a
![]() $(3, 3, 2, 1)$
-Kawakita blowup with center
$(3, 3, 2, 1)$
-Kawakita blowup with center
![]() $P_\xi $
. If the coefficients are general, namely when
$P_\xi $
. If the coefficients are general, namely when
is not a full square, where
![]() $r_\beta = r_1(y, -\beta ^2)$
,
$r_\beta = r_1(y, -\beta ^2)$
,
![]() $e_\beta = e_3(y, -\beta ^2)$
,
$e_\beta = e_3(y, -\beta ^2)$
,
![]() $a_\beta = a_1(y, -\beta ^2)$
, and
$a_\beta = a_1(y, -\beta ^2)$
, and
![]() $b_\beta = b_2(y, -\beta ^2)$
, then the point
$b_\beta = b_2(y, -\beta ^2)$
, then the point
![]() $P_\xi $
is exactly of type
$P_\xi $
is exactly of type
![]() $2$
.
$2$
.
The variety Z is isomorphic to a complete intersection
![]() $Z_{2, 4} \subseteq \mathbb P(1, 1, 1, 1, 1, 2)$
with variables
$Z_{2, 4} \subseteq \mathbb P(1, 1, 1, 1, 1, 2)$
with variables
![]() $u, y, z, \beta , \xi , w$
. We see this by substituting
$u, y, z, \beta , \xi , w$
. We see this by substituting
![]() $x = u \beta - q_1 r_1$
and
$x = u \beta - q_1 r_1$
and
![]() $\gamma = q_1 \xi + \beta ^2$
. We find that Z is isomorphic to
$\gamma = q_1 \xi + \beta ^2$
. We find that Z is isomorphic to
![]() $Z_{2, 4}\colon \mathbb V(-u \xi + s_2 - \beta r_1,\, h)$
, where
$Z_{2, 4}\colon \mathbb V(-u \xi + s_2 - \beta r_1,\, h)$
, where
 $$\begin{align*}\begin{aligned} h & = -w^2 + \xi^2 q_1^2 - 2 e_3 \xi + \beta^4 + 2 b_0 q_1^2 r_1^2 - 4 \beta b_1 q_1 r_1 - 4 u \beta b_0 q_1 r_1 - 12 \beta^2 a_0 q_1 r_1 + 4 \xi b_2 q_1 \\&\quad - 16 \xi a_1^2 q_1 + 4 \beta \xi a_1 q_1 + 2 \beta^2 \xi q_1 + 2 \beta c_3 + 2 \beta^2 b_2 + 2 u \beta^2 b_1 + 2 u^2 \beta^2 b_0 + 4 \beta^3 a_1 + 4 u \beta^3 a_0 \\&\quad + (u \beta - q_1 r_1) C_Z + D_Z, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} h & = -w^2 + \xi^2 q_1^2 - 2 e_3 \xi + \beta^4 + 2 b_0 q_1^2 r_1^2 - 4 \beta b_1 q_1 r_1 - 4 u \beta b_0 q_1 r_1 - 12 \beta^2 a_0 q_1 r_1 + 4 \xi b_2 q_1 \\&\quad - 16 \xi a_1^2 q_1 + 4 \beta \xi a_1 q_1 + 2 \beta^2 \xi q_1 + 2 \beta c_3 + 2 \beta^2 b_2 + 2 u \beta^2 b_1 + 2 u^2 \beta^2 b_0 + 4 \beta^3 a_1 + 4 u \beta^3 a_0 \\&\quad + (u \beta - q_1 r_1) C_Z + D_Z, \end{aligned} \end{align*}$$
where
![]() $C_Z = C_2(y, z, u)$
and
$C_Z = C_2(y, z, u)$
and
![]() $D_Z = D_4(y, z, u)$
.
$D_Z = D_4(y, z, u)$
.
Remark 5.11. We explain below how we found the embedding of X. Using Theorem A and the coordinate change in
![]() $cA_7$
family 7.1, we can write a sextic double solid
$cA_7$
family 7.1, we can write a sextic double solid
![]() $\bar X$
with an isolated
$\bar X$
with an isolated
![]() $cA_7$
in family 7.2 by
$cA_7$
in family 7.2 by
with variables
![]() $x, y, z, t, \beta , \gamma , w$
.
$x, y, z, t, \beta , \gamma , w$
.
We construct a
![]() $(4, 4, 1, 1)$
-Kawakita blowup
$(4, 4, 1, 1)$
-Kawakita blowup
![]() $\bar Y_0 \to \bar X$
. Define
$\bar Y_0 \to \bar X$
. Define
![]() $\bar T_0$
by
$\bar T_0$
by

Let
![]() $T_0 \to \mathbb P(1, 1, 1, 1, 2, 3, 3)$
be the ample model of
$T_0 \to \mathbb P(1, 1, 1, 1, 2, 3, 3)$
be the ample model of
![]() $\mathbb V(x)$
and
$\mathbb V(x)$
and
![]() $Y_0 \subseteq T_0$
the strict transform of X. Then
$Y_0 \subseteq T_0$
the strict transform of X. Then
![]() $\bar Y_0$
is given by the ideal
$\bar Y_0$
is given by the ideal
![]() $I_{\bar Y} = (\bar g_1, \ldots , \bar g_5)$
, where
$I_{\bar Y} = (\bar g_1, \ldots , \bar g_5)$
, where
 $$\begin{align*}\begin{aligned} \bar g_1 & = u g + 2 e_3 (\beta r_1 - t s_2), & \bar g_2 & = u \beta - q_1 r_1 - x t, & \bar g_3 & = u \gamma - q_1 s_2 - x \beta,\\ \bar g_4 & = x g + 2 e_3 (\gamma r_1 - \beta s_2), & \bar g_5 & = q_1 g + 2 e_3 (\beta^2 - t \gamma)). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \bar g_1 & = u g + 2 e_3 (\beta r_1 - t s_2), & \bar g_2 & = u \beta - q_1 r_1 - x t, & \bar g_3 & = u \gamma - q_1 s_2 - x \beta,\\ \bar g_4 & = x g + 2 e_3 (\gamma r_1 - \beta s_2), & \bar g_5 & = q_1 g + 2 e_3 (\beta^2 - t \gamma)). \end{aligned} \end{align*}$$
The morphism
![]() $\bar Y_0 \to \bar X$
is a
$\bar Y_0 \to \bar X$
is a
![]() $(4, 4, 1, 1)$
-Kawakita blowup, as can be checked on the patch
$(4, 4, 1, 1)$
-Kawakita blowup, as can be checked on the patch
![]() $(\bar Y_0)_x \to \bar X_x$
.
$(\bar Y_0)_x \to \bar X_x$
.
Note that we do not prove that
![]() $I_{\bar Y}$
is saturated with respect to u. In fact, the saturation will not be
$I_{\bar Y}$
is saturated with respect to u. In fact, the saturation will not be
![]() $I_Y$
if we do not use assume some generality conditions, similarly to
$I_Y$
if we do not use assume some generality conditions, similarly to
![]() $cA_6$
and
$cA_6$
and
![]() $cA_7$
family 7.1. As a heuristic argument to see why
$cA_7$
family 7.1. As a heuristic argument to see why
![]() $I_{\bar Y}$
might be saturated in the general case (general meaning a Zariski open dense set of the parameter space), we can use computer algebra software, pretend that
$I_{\bar Y}$
might be saturated in the general case (general meaning a Zariski open dense set of the parameter space), we can use computer algebra software, pretend that
![]() $a_i$
,
$a_i$
,
![]() $b_i$
,
$b_i$
,
![]() $c_i$
,
$c_i$
,
![]() $d_i$
,
$d_i$
,
![]() $q_1$
,
$q_1$
,
![]() $r_1$
,
$r_1$
,
![]() $s_2$
,
$s_2$
,
![]() $e_3$
are algebraically independent variables of a polynomial ring over
$e_3$
are algebraically independent variables of a polynomial ring over
![]() $\mathbb Q$
or
$\mathbb Q$
or
![]() $\mathbb Z_p$
for a large prime p, and calculate that the saturation in that case indeed equals the ideal
$\mathbb Z_p$
for a large prime p, and calculate that the saturation in that case indeed equals the ideal
![]() $I_{\bar Y}$
.
$I_{\bar Y}$
.
Similarly to the diagram
![]() $Y_0 \to W_0 \gets Y_1$
in the proof of Proposition 5.10, the diagram
$Y_0 \to W_0 \gets Y_1$
in the proof of Proposition 5.10, the diagram
![]() $\bar Y_0 \to \bar {W}_0 \gets \bar Y_1$
is an Atiyah flop, provided
$\bar Y_0 \to \bar {W}_0 \gets \bar Y_1$
is an Atiyah flop, provided
![]() $r_1$
and
$r_1$
and
![]() $q_1$
are coprime.
$q_1$
are coprime.
We show that
![]() $I_{\bar Y}$
does not 2-ray follow
$I_{\bar Y}$
does not 2-ray follow
![]() $\bar T_0$
, namely that the diagram
$\bar T_0$
, namely that the diagram
![]() $\bar Y_1 \to \bar {W}_1 \gets Y_2$
contracts a curve and extracts a divisor. Acting by the matrix
$\bar Y_1 \to \bar {W}_1 \gets Y_2$
contracts a curve and extracts a divisor. Acting by the matrix
![]() ${\left (\begin {smallmatrix}4 & -3\\-1 & 1\end {smallmatrix}\right )}$
on the action matrix of
${\left (\begin {smallmatrix}4 & -3\\-1 & 1\end {smallmatrix}\right )}$
on the action matrix of
![]() $\bar T_0$
, define
$\bar T_0$
, define
![]() $\bar T_1$
by
$\bar T_1$
by

and define
![]() $\bar Y_1 \subseteq \bar T_1$
by the zeros of
$\bar Y_1 \subseteq \bar T_1$
by the zeros of
![]() $I_{\bar Y}$
. We consider the toric flip
$I_{\bar Y}$
. We consider the toric flip
![]() $\bar T_1 \to \bar {\mathcal W}_1 \gets \bar T_2$
and restrict it to
$\bar T_1 \to \bar {\mathcal W}_1 \gets \bar T_2$
and restrict it to
![]() $\bar Y_1 \to \bar {W}_1 \gets \bar Y_2$
. Since
$\bar Y_1 \to \bar {W}_1 \gets \bar Y_2$
. Since
![]() $I_{\bar Y}$
is the zero ideal when restricting to
$I_{\bar Y}$
is the zero ideal when restricting to
![]() $\mathbb V(u, x, y, z, \beta , t)$
, the base
$\mathbb V(u, x, y, z, \beta , t)$
, the base
of the toric flip restricts to
![]() $\mathbb P^1 \subseteq \bar {W}_1$
with variables
$\mathbb P^1 \subseteq \bar {W}_1$
with variables
![]() $w, \gamma $
. The morphism
$w, \gamma $
. The morphism
![]() $\bar Y_1 \to \bar {W}_1$
contracts a curve
$\bar Y_1 \to \bar {W}_1$
contracts a curve
![]() $\mathbb P^1$
to both of the points
$\mathbb P^1$
to both of the points
![]() $[1, 1]$
and
$[1, 1]$
and
![]() $[1, -1]$
in the base
$[1, -1]$
in the base
![]() $\mathbb P^1 \subseteq \bar {W}_1$
and is an isomorphism elsewhere. The morphism
$\mathbb P^1 \subseteq \bar {W}_1$
and is an isomorphism elsewhere. The morphism
![]() $\bar {W}_1 \gets \bar Y_2$
extracts a curve
$\bar {W}_1 \gets \bar Y_2$
extracts a curve
![]() $\mathbb P^1$
for every point in the base
$\mathbb P^1$
for every point in the base
![]() $\mathbb P^1 \subseteq \bar {W}_1$
, so extracts a divisor on
$\mathbb P^1 \subseteq \bar {W}_1$
, so extracts a divisor on
![]() $\bar Y_2$
. The diagram
$\bar Y_2$
. The diagram
![]() $\bar Y_1 \to \bar {W}_1 \gets \bar Y_2$
is not a step in the 2-ray game of
$\bar Y_1 \to \bar {W}_1 \gets \bar Y_2$
is not a step in the 2-ray game of
![]() $\bar Y_0$
, so
$\bar Y_0$
, so
![]() $I_{\bar Y}$
does not 2-ray follow
$I_{\bar Y}$
does not 2-ray follow
![]() $\bar T_0$
. The reason for this was that the ideal
$\bar T_0$
. The reason for this was that the ideal
![]() $I_{\bar Y}$
is contained in
$I_{\bar Y}$
is contained in
![]() $(u, x, y, z)$
, so the surface
$(u, x, y, z)$
, so the surface
![]() $\mathbb V(u, x, y, z) \subseteq \bar T_2$
exists on
$\mathbb V(u, x, y, z) \subseteq \bar T_2$
exists on
![]() $\bar Y_2$
, but does not exist on
$\bar Y_2$
, but does not exist on
![]() $\bar T_1$
.
$\bar T_1$
.
We unproject
![]() $\bar g_1 = \bar g_4 = \bar g_5 = 0$
with respect to
$\bar g_1 = \bar g_4 = \bar g_5 = 0$
with respect to
![]() $u, x, y, z$
in
$u, x, y, z$
in
![]() $\bar Y_1 \subseteq \bar T_1$
, to find a variety
$\bar Y_1 \subseteq \bar T_1$
, to find a variety
![]() $Y_1 \subseteq T_1$
. We explain below what we mean by this. We can write the system of equations
$Y_1 \subseteq T_1$
. We explain below what we mean by this. We can write the system of equations
![]() $\bar g_1 = \bar g_4 = \bar g_5 = 0$
in the matrix form
$\bar g_1 = \bar g_4 = \bar g_5 = 0$
in the matrix form
 $$\begin{align*}\begin{pmatrix} g & 0 & 0 & \beta r_1 - t s_2\\ 0 & g & 0 & \gamma r_1 - \beta s_2\\ 0 & 0 & g & \beta^2 - t \gamma \end{pmatrix} \begin{pmatrix} u\\x\\q_1\\2 e_3 \end{pmatrix} = \boldsymbol{0}. \end{align*}$$
$$\begin{align*}\begin{pmatrix} g & 0 & 0 & \beta r_1 - t s_2\\ 0 & g & 0 & \gamma r_1 - \beta s_2\\ 0 & 0 & g & \beta^2 - t \gamma \end{pmatrix} \begin{pmatrix} u\\x\\q_1\\2 e_3 \end{pmatrix} = \boldsymbol{0}. \end{align*}$$
If the above equations hold, then we have
 $$\begin{align*}\frac{\left\lvert \begin{pmatrix} 0 & 0 & \beta r_1 - t s_2\\ g & 0 & \gamma r_1 - \beta s_2\\ 0 & g & \beta^2 - t \gamma \end{pmatrix} \right\rvert}{u} = \frac{\left\lvert \begin{pmatrix} g & 0 & \beta r_1 - t s_2\\ 0 & 0 & \gamma r_1 - \beta s_2\\ 0 & g & \beta^2 - t \gamma \end{pmatrix} \right\rvert}{-x} = \frac{\left\lvert \begin{pmatrix} g & 0 & \beta r_1 - t s_2\\ 0 & g & \gamma r_1 - \beta s_2\\ 0 & 0 & \beta^2 - t \gamma \end{pmatrix} \right\rvert}{q_1} = \frac{\left\lvert \begin{pmatrix} g & 0 & 0\\ 0 & g & 0\\ 0 & 0 & g \end{pmatrix} \right\rvert}{{-2 e_3}}. \end{align*}$$
$$\begin{align*}\frac{\left\lvert \begin{pmatrix} 0 & 0 & \beta r_1 - t s_2\\ g & 0 & \gamma r_1 - \beta s_2\\ 0 & g & \beta^2 - t \gamma \end{pmatrix} \right\rvert}{u} = \frac{\left\lvert \begin{pmatrix} g & 0 & \beta r_1 - t s_2\\ 0 & 0 & \gamma r_1 - \beta s_2\\ 0 & g & \beta^2 - t \gamma \end{pmatrix} \right\rvert}{-x} = \frac{\left\lvert \begin{pmatrix} g & 0 & \beta r_1 - t s_2\\ 0 & g & \gamma r_1 - \beta s_2\\ 0 & 0 & \beta^2 - t \gamma \end{pmatrix} \right\rvert}{q_1} = \frac{\left\lvert \begin{pmatrix} g & 0 & 0\\ 0 & g & 0\\ 0 & 0 & g \end{pmatrix} \right\rvert}{{-2 e_3}}. \end{align*}$$
Calculating the determinants and dividing by
![]() $-g^2$
, we find the equalities
$-g^2$
, we find the equalities
 $$ \begin{align} \frac{{t s_2 - \beta r_1}}{u} = \frac{{\beta s_2 - \gamma r_1}}{x} = \frac{{t \gamma - \beta^2}}{q_1} = \frac{g}{{2 e_3}}, \end{align} $$
$$ \begin{align} \frac{{t s_2 - \beta r_1}}{u} = \frac{{\beta s_2 - \gamma r_1}}{x} = \frac{{t \gamma - \beta^2}}{q_1} = \frac{g}{{2 e_3}}, \end{align} $$
between elements of the field of fractions of
![]() $\mathbb C[u, x, y, z, w, \gamma , \beta , t] / I_{\bar Y}$
. Using Equation (5.3), we see that the morphism
$\mathbb C[u, x, y, z, w, \gamma , \beta , t] / I_{\bar Y}$
. Using Equation (5.3), we see that the morphism
![]() $\bar Y_1 \to Y_1$
given by
$\bar Y_1 \to Y_1$
given by
is an isomorphism, where
![]() $Y_1$
is described in the proof of Proposition 5.10.
$Y_1$
is described in the proof of Proposition 5.10.
The coordinate change
![]() $\bar Y_1 \to Y_1$
induces an isomorphism
$\bar Y_1 \to Y_1$
induces an isomorphism
![]() $\bar X \to X$
, giving the variety X.
$\bar X \to X$
, giving the variety X.
5.7.
 $cA_7$
family 7.3 model
$cA_7$
family 7.3 model
Proposition 5.12. A Mori fiber space sextic double solid with a
![]() $cA_7$
singularity in family 7.3 satisfying Definition 5.1 has a Sarkisov link to a degree
$cA_7$
singularity in family 7.3 satisfying Definition 5.1 has a Sarkisov link to a degree
![]() $2$
del Pezzo fibration, starting with a
$2$
del Pezzo fibration, starting with a
![]() $(4, 4, 1, 1)$
-blowup of the
$(4, 4, 1, 1)$
-blowup of the
![]() $cA_7$
point and followed by two Atiyah flops.
$cA_7$
point and followed by two Atiyah flops.
Proof. We exhibit the diagram below.

First, we define X and a
![]() $(4, 4, 1, 1)$
-Kawakita blowup
$(4, 4, 1, 1)$
-Kawakita blowup
![]() $Y_0 \to X$
. Any sextic double solid with an isolated
$Y_0 \to X$
. Any sextic double solid with an isolated
![]() $cA_7$
family 7.3 can be given by a bidegree
$cA_7$
family 7.3 can be given by a bidegree
![]() $(6, 2)$
complete intersection
$(6, 2)$
complete intersection
with variables
![]() $x, y, z, t, \xi , w$
, where
$x, y, z, t, \xi , w$
, where
 $$\begin{align*}\begin{aligned} f & = -w^2 + x^2 \xi^2 - 2 \xi e_4 + \xi^2 (s_1^2 + 4 a_1 s_1 + 2 x s_1 - 2 b_2 + 16 a_1^2 + 4 x a_1 + 8 \xi a_0) \\& \quad + t (t s_1^4 + 4 t a_1 s_1^3 - 8 t^2 a_0 s_1^3 - 2 \xi s_1^3 + 2 t b_2 s_1^2 - 2 t^2 b_1 s_1^2 - 8 \xi a_1 s_1^2 + 24 t \xi a_0 s_1^2 \\& \quad + 12 x t^2 a_0 s_1^2 - 2 x \xi s_1^2 + 2 t c_3 s_1 + 4 t \xi b_1 s_1 + 4 x t^2 b_1 s_1 - 16 \xi a_1^2 s_1 - 4 x \xi a_1 s_1 \\& \quad - 24 \xi^2 a_0 s_1 - 24 x t \xi a_0 s_1 - 2 \xi c_3 - 4 x \xi b_2 - 2 \xi^2 b_1 - 4 x t \xi b_1 + 2 x^2 t^3 b_0 + 16 x \xi a_1^2 \\& \quad + 12 x \xi^2 a_0 + x t^2 C_2 + t D_4), \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} f & = -w^2 + x^2 \xi^2 - 2 \xi e_4 + \xi^2 (s_1^2 + 4 a_1 s_1 + 2 x s_1 - 2 b_2 + 16 a_1^2 + 4 x a_1 + 8 \xi a_0) \\& \quad + t (t s_1^4 + 4 t a_1 s_1^3 - 8 t^2 a_0 s_1^3 - 2 \xi s_1^3 + 2 t b_2 s_1^2 - 2 t^2 b_1 s_1^2 - 8 \xi a_1 s_1^2 + 24 t \xi a_0 s_1^2 \\& \quad + 12 x t^2 a_0 s_1^2 - 2 x \xi s_1^2 + 2 t c_3 s_1 + 4 t \xi b_1 s_1 + 4 x t^2 b_1 s_1 - 16 \xi a_1^2 s_1 - 4 x \xi a_1 s_1 \\& \quad - 24 \xi^2 a_0 s_1 - 24 x t \xi a_0 s_1 - 2 \xi c_3 - 4 x \xi b_2 - 2 \xi^2 b_1 - 4 x t \xi b_1 + 2 x^2 t^3 b_0 + 16 x \xi a_1^2 \\& \quad + 12 x \xi^2 a_0 + x t^2 C_2 + t D_4), \end{aligned} \end{align*}$$
where
![]() $C_i$
,
$C_i$
,
![]() $D_i \in \mathbb C[y, z, t]$
are homogeneous of degree i. Define
$D_i \in \mathbb C[y, z, t]$
are homogeneous of degree i. Define

Define
![]() $\Phi \colon T_0 \to \mathbb P(1, 1, 1, 1, 2, 3)$
by the ample model of
$\Phi \colon T_0 \to \mathbb P(1, 1, 1, 1, 2, 3)$
by the ample model of
![]() $\mathbb V(x)$
, and define
$\mathbb V(x)$
, and define
![]() $Y_0$
as the strict transform of X. Then,
$Y_0$
as the strict transform of X. Then,
![]() $Y_0$
is given by
$Y_0$
is given by
Using Proposition 4.6, we see that
![]() $Y_0 \to X$
is a
$Y_0 \to X$
is a
![]() $(4, 4, 1, 1)$
-Kawakita blowup.
$(4, 4, 1, 1)$
-Kawakita blowup.
We describe the flop
![]() $Y_0 \to W_0 \gets Y_1$
. Multiplying the action matrix of
$Y_0 \to W_0 \gets Y_1$
. Multiplying the action matrix of
![]() $T_0$
by
$T_0$
by
![]() ${\left (\begin {smallmatrix}1 & -1\\0 & 1\end {smallmatrix}\right )}$
, we find
${\left (\begin {smallmatrix}1 & -1\\0 & 1\end {smallmatrix}\right )}$
, we find

The base of the flop is given by
![]() $\mathbb V(q_2) \subseteq \mathbb P^1 \subseteq W_0$
. After a suitable coordinate change on
$\mathbb V(q_2) \subseteq \mathbb P^1 \subseteq W_0$
. After a suitable coordinate change on
![]() $y, z$
, we find
$y, z$
, we find
![]() $q_2 = yz$
. Consider the flop over
$q_2 = yz$
. Consider the flop over
![]() $\mathbb V(y)$
, the flop over the other point is similar. Since
$\mathbb V(y)$
, the flop over the other point is similar. Since
![]() $q_2$
and
$q_2$
and
![]() $e_4$
have no common divisor, on the patch where z is nonzero, we can express y and
$e_4$
have no common divisor, on the patch where z is nonzero, we can express y and
![]() $\xi $
locally analytically equivariantly in terms of
$\xi $
locally analytically equivariantly in terms of
![]() $u, x, t, w$
. So,
$u, x, t, w$
. So,
![]() $Y_0 \to W_0 \gets Y_1$
is locally analytically two Atiyah flops.
$Y_0 \to W_0 \gets Y_1$
is locally analytically two Atiyah flops.
The morphisms
![]() $Y_1 \to W_1 \gets Y_2$
are isomorphisms, since
$Y_1 \to W_1 \gets Y_2$
are isomorphisms, since
![]() $w^2$
has a nonzero coefficient in
$w^2$
has a nonzero coefficient in
![]() $\Phi ^*f / u^8$
.
$\Phi ^*f / u^8$
.
We show that
![]() $Y_2$
is a degree
$Y_2$
is a degree
![]() $2$
del Pezzo fibration. Multiplying the original action matrix of
$2$
del Pezzo fibration. Multiplying the original action matrix of
![]() $T_0$
by the matrix
$T_0$
by the matrix
![]() ${\left (\begin {smallmatrix}1 & 0\\2 & -1\end {smallmatrix}\right )}$
with determinant
${\left (\begin {smallmatrix}1 & 0\\2 & -1\end {smallmatrix}\right )}$
with determinant
![]() $-1$
, we find
$-1$
, we find

The ample model of
![]() $\mathbb V(t)$
is
$\mathbb V(t)$
is
 $$\begin{align*}\begin{aligned} Y_2 & \to \mathbb P(2, 1)\\ [u, x, y, z, w, \xi, t] & \mapsto [\xi, t]. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} Y_2 & \to \mathbb P(2, 1)\\ [u, x, y, z, w, \xi, t] & \mapsto [\xi, t]. \end{aligned} \end{align*}$$
Since
![]() $\mathbb P(2, 1)$
is isomorphic to
$\mathbb P(2, 1)$
is isomorphic to
![]() $\mathbb P^1$
, we see that
$\mathbb P^1$
, we see that
![]() $Y_2$
is a fibration onto
$Y_2$
is a fibration onto
![]() $\mathbb P^1$
. On the patch
$\mathbb P^1$
. On the patch
![]() $(Y_2)_t$
, we can substitute
$(Y_2)_t$
, we can substitute
![]() ${x = u s_1 - q_2 - u^2 \xi }$
, to find that the general fiber is a weighted degree
${x = u s_1 - q_2 - u^2 \xi }$
, to find that the general fiber is a weighted degree
![]() $4$
hypersurface in
$4$
hypersurface in
![]() $\mathbb P(1, 1, 1, 2)$
, so a degree
$\mathbb P(1, 1, 1, 2)$
, so a degree
![]() $2$
del Pezzo surface.
$2$
del Pezzo surface.
5.8.
 $cA_8$
model
$cA_8$
model
Proposition 5.13. A Mori fiber space sextic double solid with a
![]() $cA_8$
singularity satisfying Definition 5.1 has a Sarkisov link to a complete intersection
$cA_8$
singularity satisfying Definition 5.1 has a Sarkisov link to a complete intersection
![]() $Z_{3, 3} \subseteq \mathbb P(1, 1, 1, 1, 1, 2)$
with a
$Z_{3, 3} \subseteq \mathbb P(1, 1, 1, 1, 1, 2)$
with a
![]() $cD_4$
singularity, starting with a
$cD_4$
singularity, starting with a
![]() $(5, 4, 1, 1)$
-blowup of the
$(5, 4, 1, 1)$
-blowup of the
![]() $cA_8$
point, followed by a
$cA_8$
point, followed by a
![]() $(4, 1, 1, -1, -2; 2)$
-flip, and finally a
$(4, 1, 1, -1, -2; 2)$
-flip, and finally a
![]() $(3, 2, 2, 1, 5)$
-blowdown to the
$(3, 2, 2, 1, 5)$
-blowdown to the
![]() $cD_4$
singularity. Under further generality conditions, the singular locus of Z consists of three points, namely the
$cD_4$
singularity. Under further generality conditions, the singular locus of Z consists of three points, namely the
![]() $cD_4$
point, the
$cD_4$
point, the
![]() $1/2(1, 1, 1)$
singularity, and an ordinary double point.
$1/2(1, 1, 1)$
singularity, and an ordinary double point.
Proof. We exhibit the diagram below.

First, we describe X and the weighted blowup
![]() $Y_0 \to X$
. A sextic double solid with a
$Y_0 \to X$
. A sextic double solid with a
![]() $cA_8$
singularity can be given by a multidegree
$cA_8$
singularity can be given by a multidegree
![]() $(6, 2, 3)$
complete intersection
$(6, 2, 3)$
complete intersection
with variables
![]() $x, y, z, t, \beta , \gamma , \xi $
where
$x, y, z, t, \beta , \gamma , \xi $
where
 $$\begin{align*}{ \begin{aligned} f & = 8 \beta^3 (A_0 - a_0) + \xi (-\xi + 2 \gamma - 8 t A_0 r_2 + 2 t b_2 - 4 t a_1^2 + 4 \beta a_1) \\& \quad + t (-16 t \beta A_0^2 r_2 + 2 t \beta c_2 + 4 t \gamma b_1 - 2 \beta^2 b_1 - 2 t \beta^2 b_0 + 4 x t^2 \beta b_0 - 8 t \gamma a_0 a_1 + 8 \beta^2 a_0 a_1 \\& \quad + 12 \beta \gamma a_0 - 2 t \gamma B_1 + 2 \beta^2 B_1 + 16 t \beta^2 A_0^2 - 16 x t^2 \beta A_0^2 - 8 \beta \gamma A_0 + x t^3 C_1 + t^2 D_3), \end{aligned} } \end{align*}$$
$$\begin{align*}{ \begin{aligned} f & = 8 \beta^3 (A_0 - a_0) + \xi (-\xi + 2 \gamma - 8 t A_0 r_2 + 2 t b_2 - 4 t a_1^2 + 4 \beta a_1) \\& \quad + t (-16 t \beta A_0^2 r_2 + 2 t \beta c_2 + 4 t \gamma b_1 - 2 \beta^2 b_1 - 2 t \beta^2 b_0 + 4 x t^2 \beta b_0 - 8 t \gamma a_0 a_1 + 8 \beta^2 a_0 a_1 \\& \quad + 12 \beta \gamma a_0 - 2 t \gamma B_1 + 2 \beta^2 B_1 + 16 t \beta^2 A_0^2 - 16 x t^2 \beta A_0^2 - 8 \beta \gamma A_0 + x t^3 C_1 + t^2 D_3), \end{aligned} } \end{align*}$$
where
![]() $C_i$
,
$C_i$
,
![]() $D_i \in \mathbb C[y, z, t]$
are homogeneous of degree i. Note that
$D_i \in \mathbb C[y, z, t]$
are homogeneous of degree i. Note that
![]() $B_1 \in \mathbb C[y, z]$
. Define
$B_1 \in \mathbb C[y, z]$
. Define

Let
![]() $\Phi \colon T_0 \to \mathbb P(1, 1, 1, 1, 2, 3, 3)$
be the ample model of
$\Phi \colon T_0 \to \mathbb P(1, 1, 1, 1, 2, 3, 3)$
be the ample model of
![]() $\mathbb V(x)$
, and let
$\mathbb V(x)$
, and let
![]() $Y_0 \subseteq T_0$
be the strict transform of X. Then
$Y_0 \subseteq T_0$
be the strict transform of X. Then
![]() $Y_0$
is given by
$Y_0$
is given by
and
![]() $Y_0 \to X$
is a
$Y_0 \to X$
is a
![]() $(5, 4, 1, 1)$
-Kawakita blowup.
$(5, 4, 1, 1)$
-Kawakita blowup.
The first diagram in the 2-ray game of
![]() $T_0$
restricts to a isomorphisms
$T_0$
restricts to a isomorphisms
![]() $Y_0 \to W_0 \gets Y_1$
, since
$Y_0 \to W_0 \gets Y_1$
, since
![]() $r_2$
and
$r_2$
and
![]() $s_3$
are coprime.
$s_3$
are coprime.
The second diagram in the 2-ray game of
![]() $T_0$
restricts to a
$T_0$
restricts to a
![]() $(4, 1, 1, -1, -2; 2)$
-flip
$(4, 1, 1, -1, -2; 2)$
-flip
![]() $Y_1 \to W_1 \gets Y_2$
. Define the toric variety
$Y_1 \to W_1 \gets Y_2$
. Define the toric variety
![]() $T_1$
by multiplying the action matrix of
$T_1$
by multiplying the action matrix of
![]() $T_0$
by the matrix
$T_0$
by the matrix
![]() ${\left (\begin {smallmatrix}4 & -3\\3 & -2\end {smallmatrix}\right )}$
,
${\left (\begin {smallmatrix}4 & -3\\3 & -2\end {smallmatrix}\right )}$
,

On the patch where
![]() $\gamma $
is nonzero, we have
$\gamma $
is nonzero, we have
![]() ${u = x \beta + s_3}$
and we can write
${u = x \beta + s_3}$
and we can write
![]() $\xi $
locally analytically equivariantly in terms of
$\xi $
locally analytically equivariantly in terms of
![]() $x, y, z, \beta , t$
. We are left with the hypersurface given by
$x, y, z, \beta , t$
. We are left with the hypersurface given by
![]() ${x \beta ^2 + \beta s_3 - x t - r_2}$
in
${x \beta ^2 + \beta s_3 - x t - r_2}$
in
![]() $\mathbb C^5$
with variables
$\mathbb C^5$
with variables
![]() $x, y, z, \beta , t$
with weights
$x, y, z, \beta , t$
with weights
![]() $(4, 1, 1, -1, -2)$
. The polynomial contains
$(4, 1, 1, -1, -2)$
. The polynomial contains
![]() $xt$
and
$xt$
and
![]() $r_2$
, so this corresponds to case (1) in [Reference Brown8, Th. 8], a
$r_2$
, so this corresponds to case (1) in [Reference Brown8, Th. 8], a
![]() $(4, 1, 1, -1, -2; 2)$
-flip. Similarly to Proposition 5.8, the flip contracts a curve containing a
$(4, 1, 1, -1, -2; 2)$
-flip. Similarly to Proposition 5.8, the flip contracts a curve containing a
![]() $1/4(1, 1, 3)$
singularity, and extracts a curve containing a
$1/4(1, 1, 3)$
singularity, and extracts a curve containing a
![]() $1/2(1, 1, 1)$
singularity and a
$1/2(1, 1, 1)$
singularity and a
![]() $cA_1$
singularity, which is an ordinary double point if
$cA_1$
singularity, which is an ordinary double point if
![]() $r_2$
is not a square and is a 3-fold
$r_2$
is not a square and is a 3-fold
![]() $A_2$
singularity otherwise. The
$A_2$
singularity otherwise. The
![]() $cA_1$
singularity on
$cA_1$
singularity on
![]() $Y_2$
is at
$Y_2$
is at
![]() ${[0, 0, 0, 0, 1, 1, -2 a_0, 1]}$
.
${[0, 0, 0, 0, 1, 1, -2 a_0, 1]}$
.
The third diagram in the 2-ray game of
![]() $T_0$
restricts to isomorphisms
$T_0$
restricts to isomorphisms
![]() $Y_2 \to W_2 \gets Y_3$
, under Definition 5.1, namely that
$Y_2 \to W_2 \gets Y_3$
, under Definition 5.1, namely that
![]() $a_0 \neq A_0$
. On the patch where
$a_0 \neq A_0$
. On the patch where
![]() $\beta $
is nonzero, the base of the toric flip restricts to
$\beta $
is nonzero, the base of the toric flip restricts to
![]() $\mathbb V(A_0 - a_0, u, x, y, z, \gamma , \xi , t) \subseteq W_2$
.
$\mathbb V(A_0 - a_0, u, x, y, z, \gamma , \xi , t) \subseteq W_2$
.
We describe the weighted blowdown
![]() $Y_3 \to Z$
. Multiplying the action matrix of
$Y_3 \to Z$
. Multiplying the action matrix of
![]() $T_0$
by the matrix
$T_0$
by the matrix
![]() ${\left (\begin {smallmatrix}5 & -3\\2 & -1\end {smallmatrix}\right )}$
, the toric variety
${\left (\begin {smallmatrix}5 & -3\\2 & -1\end {smallmatrix}\right )}$
, the toric variety
![]() $T_3$
is given by
$T_3$
is given by

The ample model of
![]() $\mathbb V(\xi )$
is
$\mathbb V(\xi )$
is
![]() $Y_3 \to Z$
where Z is the tridegree
$Y_3 \to Z$
where Z is the tridegree
![]() $(3, 2, 3)$
complete intersection
$(3, 2, 3)$
complete intersection
with variables
![]() $u, y, z, \beta , \xi , x, \gamma $
, where
$u, y, z, \beta , \xi , x, \gamma $
, where
 $$\begin{align*}\begin{aligned} h & = 8 \beta^3 (A_0 - a_0) + \xi (-u \xi + 2 \gamma - 8 A_0 r_2 + 2 b_2 - 4 a_1^2 + 4 \beta a_1) \\&\quad - 16 \beta A_0^2 r_2 + 2 \beta c_2 + 4 \gamma b_1 - 2 \beta^2 b_1 - 2 u \beta^2 b_0 + 4 x \beta b_0 - 8 \gamma a_0 a_1 + 8 \beta^2 a_0 a_1 \\&\quad + 12 \beta \gamma a_0 - 2 \gamma B_1 + 2 \beta^2 B_1 + 16 u \beta^2 A_0^2 - 16 x \beta A_0^2 - 8 \beta \gamma A_0 + x C_Z + D_Z, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} h & = 8 \beta^3 (A_0 - a_0) + \xi (-u \xi + 2 \gamma - 8 A_0 r_2 + 2 b_2 - 4 a_1^2 + 4 \beta a_1) \\&\quad - 16 \beta A_0^2 r_2 + 2 \beta c_2 + 4 \gamma b_1 - 2 \beta^2 b_1 - 2 u \beta^2 b_0 + 4 x \beta b_0 - 8 \gamma a_0 a_1 + 8 \beta^2 a_0 a_1 \\&\quad + 12 \beta \gamma a_0 - 2 \gamma B_1 + 2 \beta^2 B_1 + 16 u \beta^2 A_0^2 - 16 x \beta A_0^2 - 8 \beta \gamma A_0 + x C_Z + D_Z, \end{aligned} \end{align*}$$
where
![]() $C_Z = C_1(y, z, u)$
and
$C_Z = C_1(y, z, u)$
and
![]() $D_Z = D_3(y, z, u)$
. Substituting
$D_Z = D_3(y, z, u)$
. Substituting
![]() ${x = u \beta - r_2}$
, we see that Z is isomorphic to a complete intersection of bidegree
${x = u \beta - r_2}$
, we see that Z is isomorphic to a complete intersection of bidegree
![]() $(3, 3)$
in
$(3, 3)$
in
![]() $\mathbb P(1^5, 2)$
with variables
$\mathbb P(1^5, 2)$
with variables
![]() $u, y, z, \beta , \xi , \gamma $
. The variety Z has a
$u, y, z, \beta , \xi , \gamma $
. The variety Z has a
![]() $cA_1$
singularity at
$cA_1$
singularity at
![]() ${[0, 0, 0, 1, -2 a_0, 1]}$
. We can compute that the point
${[0, 0, 0, 1, -2 a_0, 1]}$
. We can compute that the point
![]() $P_\xi \in Z$
is a
$P_\xi \in Z$
is a
![]() $cD_4$
point, by showing the complex analytic space germ
$cD_4$
point, by showing the complex analytic space germ
![]() $(Z, P_\xi )$
is isomorphic to
$(Z, P_\xi )$
is isomorphic to
![]() $({\mathbb V(u^2 + 2 \beta r_2 - s_3 + \mathrm {h.o.t})}, \boldsymbol {0}) \subseteq (\mathbb C^4, \boldsymbol {0})$
with variables
$({\mathbb V(u^2 + 2 \beta r_2 - s_3 + \mathrm {h.o.t})}, \boldsymbol {0}) \subseteq (\mathbb C^4, \boldsymbol {0})$
with variables
![]() $u, \beta , y, z$
, where
$u, \beta , y, z$
, where
![]() $\mathrm {h.o.t}$
are higher-order terms in
$\mathrm {h.o.t}$
are higher-order terms in
![]() $y, z, \beta $
. We can compute that
$y, z, \beta $
. We can compute that
![]() $Y_3 \to Z$
is the divisorial contraction to a
$Y_3 \to Z$
is the divisorial contraction to a
![]() $cD_4$
point described in [Reference Yamamoto52, Th. 2.3].
$cD_4$
point described in [Reference Yamamoto52, Th. 2.3].
Acknowledgment
The author would like to thank Jihun Park for discussions on factoriality.