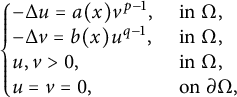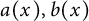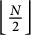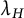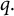1 Introduction
The main purpose of the paper is to study the existence and multiplicity of positive solutions for the following system of supercritical nonlinear elliptic equations:
 $$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta u = a(x)v^{p-1}, \quad &\text{ in } \Omega,\\ -\Delta v = b(x)u^{q-1}, \quad &\text{ in } \Omega,\\ u,v>0, \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial\Omega, \end{array} \right. \end{align} $$
$$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta u = a(x)v^{p-1}, \quad &\text{ in } \Omega,\\ -\Delta v = b(x)u^{q-1}, \quad &\text{ in } \Omega,\\ u,v>0, \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial\Omega, \end{array} \right. \end{align} $$
where
![]() $\Omega $
is a bounded annular domain (not necessarily an annulus) in
$\Omega $
is a bounded annular domain (not necessarily an annulus) in
![]() $\mathbb{R} ^N, (N \geq 3), q\geq p> 2,$
and
$\mathbb{R} ^N, (N \geq 3), q\geq p> 2,$
and
![]() $a,b \in C(\bar \Omega )$
with
$a,b \in C(\bar \Omega )$
with
![]() $a(x)\geq a_0>0$
and
$a(x)\geq a_0>0$
and
![]() $b(x)\geq b_0>0,$
where
$b(x)\geq b_0>0,$
where
![]() $a_0$
and
$a_0$
and
![]() $b_0$
are constants. In addition, for the case when
$b_0$
are constants. In addition, for the case when
![]() $a(x)=b(x)=1$
and
$a(x)=b(x)=1$
and
![]() $\Omega $
is an annulus defined as
$\Omega $
is an annulus defined as
we shall address the symmetry breaking of the solutions by proving the existence and multiplicity of positive non-radial solutions provided that
![]() $R_1$
and
$R_1$
and
![]() $R_2$
satisfy certain conditions. Symmetry considerations dominate modern fundamental physics, both in quantum theory and in relativity. Such symmetry breaking is responsible for the existence of magnetism in which rotational invariance is broken.
$R_2$
satisfy certain conditions. Symmetry considerations dominate modern fundamental physics, both in quantum theory and in relativity. Such symmetry breaking is responsible for the existence of magnetism in which rotational invariance is broken.
Introduced independently by Mitidieri [Reference Mitidieri21] and Van der Vorst [Reference Van der Vorst31], the Sobolev critical hyperbola
plays a crucial role in the analysis of (1). Our main contribution is to prove existence and multiplicity of positive solutions for the supercritical case by means of the Sobolev critical hyperbola
![]() $1/p+1/q=1-2/N$
.
$1/p+1/q=1-2/N$
.
Over the past 30 years, Hamiltonian systems have been widely studied with results including, but not limited to, existence, multiplicity, concentration phenomena, positivity, symmetry, and Liouville theorems. We redirect the interested reader to the surveys [Reference Bonheure, Moreira dos Santos and Tavares3, Reference de Figueiredo13, Reference Ruf25] for an overview of the topic and to the works [Reference Bonheure, Moreira dos Santos, Ramos and Tavares2, Reference Cardoso, do and Medeiros6, Reference Cassani and Zhang7, Reference Lange Ferreira Melo and Moreira dos Santos16] for some recent results. One of the first mathematical works studying systems of Hardy–Hénon-type equations were done by Calanchi and Ruf in [Reference Calanchi and Ruf5]. The system of Hardy–Hénon-type equations is given by
 $$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta u = |x|^\beta v^{q-1}, \quad &\text{ in } \Omega,\\ -\Delta v = |x|^\alpha u^{p-1}, \quad &\text{ in } \Omega,\\ u,v>0, \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial \Omega, \end{array} \right. \end{align} $$
$$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta u = |x|^\beta v^{q-1}, \quad &\text{ in } \Omega,\\ -\Delta v = |x|^\alpha u^{p-1}, \quad &\text{ in } \Omega,\\ u,v>0, \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial \Omega, \end{array} \right. \end{align} $$
where
![]() $\Omega $
is a bounded domain in
$\Omega $
is a bounded domain in
![]() $\mathbb{R} ^N, (N\geq 3),$
with
$\mathbb{R} ^N, (N\geq 3),$
with
![]() $0 \in \Omega , p,q>2,$
and
$0 \in \Omega , p,q>2,$
and
![]() ${\alpha , \beta> -N.}$
The authors in [Reference Calanchi and Ruf5] presented existence and nonexistence of positive solutions along with symmetry breaking results for ground states when
${\alpha , \beta> -N.}$
The authors in [Reference Calanchi and Ruf5] presented existence and nonexistence of positive solutions along with symmetry breaking results for ground states when
![]() $\Omega $
is the unit ball in
$\Omega $
is the unit ball in
![]() $\mathbb{R} ^N.$
Calanchi and Ruf remarked that systems of type (3) are closely related to the double weighted Hardy–Littlewood–Sobolev inequality (see [Reference Lieb18, Reference Stein and Weiss29] for instance). Later on, the authors Bonheure, Moreira dos Santos, and Ramos in [Reference Bonheure, Moreira dos Santos and Ramos1] presented qualitative properties of ground state solutions corresponding to the following system of equations:
$\mathbb{R} ^N.$
Calanchi and Ruf remarked that systems of type (3) are closely related to the double weighted Hardy–Littlewood–Sobolev inequality (see [Reference Lieb18, Reference Stein and Weiss29] for instance). Later on, the authors Bonheure, Moreira dos Santos, and Ramos in [Reference Bonheure, Moreira dos Santos and Ramos1] presented qualitative properties of ground state solutions corresponding to the following system of equations:
 $$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta u = |x|^\beta|v|^{q-2}v, \quad &\text{ in } B,\\ -\Delta v = |x|^\alpha |u|^{p-2}u, \quad &\text{ in } B,\\ u=v=0, \quad &\text{ on } \partial B, \end{array} \right. \end{align} $$
$$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta u = |x|^\beta|v|^{q-2}v, \quad &\text{ in } B,\\ -\Delta v = |x|^\alpha |u|^{p-2}u, \quad &\text{ in } B,\\ u=v=0, \quad &\text{ on } \partial B, \end{array} \right. \end{align} $$
where B denotes the open unit ball in
![]() $\mathbb{R} ^N, N\geq 1, \alpha , \beta \geq 0,$
and
$\mathbb{R} ^N, N\geq 1, \alpha , \beta \geq 0,$
and
![]() $p,q>1.$
Here, the authors describe the system (4) as a Lane–Emden system with Hénon-type weights. Consider the following Hénon equation:
$p,q>1.$
Here, the authors describe the system (4) as a Lane–Emden system with Hénon-type weights. Consider the following Hénon equation:
 $$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta u = |x|^\alpha |u|^{p-2}u, \quad &\text{ in } B, \\ u=0, \quad &\text{ on } \partial B, \end{array} \right. \end{align*} $$
$$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta u = |x|^\alpha |u|^{p-2}u, \quad &\text{ in } B, \\ u=0, \quad &\text{ on } \partial B, \end{array} \right. \end{align*} $$
where
![]() $\alpha>0,$
and
$\alpha>0,$
and
![]() $p>2.$
As
$p>2.$
As
![]() $|x|^\alpha $
increases with respect to
$|x|^\alpha $
increases with respect to
![]() $|x|,$
we observe that reflection and symmetric arguments are inapplicable to prove radial symmetry of either positive or ground state solutions to the Hénon equation. According to [Reference Smets, Su and Willem26], the authors Smets, Su, and Willem proved that the radial symmetry holds for small values of
$|x|,$
we observe that reflection and symmetric arguments are inapplicable to prove radial symmetry of either positive or ground state solutions to the Hénon equation. According to [Reference Smets, Su and Willem26], the authors Smets, Su, and Willem proved that the radial symmetry holds for small values of
![]() $\alpha $
whereas the symmetry breaks for sufficiently large values of
$\alpha $
whereas the symmetry breaks for sufficiently large values of
![]() $\alpha .$
However, in [Reference Pacella23, Reference Smets and Willem27], the authors showed that the ground state solutions still possess a residual symmetry, namely, the foliated Schwarz symmetry.
$\alpha .$
However, in [Reference Pacella23, Reference Smets and Willem27], the authors showed that the ground state solutions still possess a residual symmetry, namely, the foliated Schwarz symmetry.
We would like to remark that in the Hardy–Hénon system, one gets improved compactness due to the presence of the terms
![]() $|x|^\alpha $
and
$|x|^\alpha $
and
![]() $|x|^\beta .$
In this paper, we assume that the functions a and b in (1) are strictly positive and away from zero. As a result, no improved compactness is induced from these functions.
$|x|^\beta .$
In this paper, we assume that the functions a and b in (1) are strictly positive and away from zero. As a result, no improved compactness is induced from these functions.
As we are dealing with Hamiltonian systems, we highlight some further contributions on problems of type (4) presented in [Reference de Figueiredo, Peral and Rossi14, Reference Liu and Yang19]. As for nonexistence of solutions, we refer the interested reader to the works of [Reference de Figueiredo, Peral and Rossi14, Reference Liu and Yang19] and in particular, Theorem 2(a) in [Reference Calanchi and Ruf5]. Specifically speaking, Theorem 2(a) states that the problem (4) possesses no positive solutions,
![]() $u, v$
in the open unit ball B in
$u, v$
in the open unit ball B in
![]() $\mathbb{R} ^N$
for the case
$\mathbb{R} ^N$
for the case
As a result, this is a consequence of a suitable Pohoz̆aev-type identity. The authors in [Reference Bonheure, Moreira dos Santos and Ramos1] presented that the hyperbola
is in fact, the exact threshold for the existence of positive solutions associated with (4).
Prior to introducing the main results of this paper, we conclude with some works pertaining to the Dirichlet problem for the generalized Hénon equation
 $$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta u + \kappa u = |x|^\alpha |u|^{p-2}u, \quad &\text{ in } \Omega,\\ u=0, \quad &\text{ on } \partial\Omega, \end{array} \right. \end{align} $$
$$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta u + \kappa u = |x|^\alpha |u|^{p-2}u, \quad &\text{ in } \Omega,\\ u=0, \quad &\text{ on } \partial\Omega, \end{array} \right. \end{align} $$
and its corresponding problem for a Hénon–Schrödinger system
 $$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta u + \kappa_1 u = |x|^{\alpha} \partial_{u} F(u,v), \quad &\text{ in } \Omega,\\ -\Delta v + \kappa_2 v = |x|^{\alpha} \partial_{v} F(u,v), \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial{\Omega}, \end{array} \right. \end{align} $$
$$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta u + \kappa_1 u = |x|^{\alpha} \partial_{u} F(u,v), \quad &\text{ in } \Omega,\\ -\Delta v + \kappa_2 v = |x|^{\alpha} \partial_{v} F(u,v), \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial{\Omega}, \end{array} \right. \end{align} $$
where
![]() $\Omega $
is the unit ball in
$\Omega $
is the unit ball in
![]() $\mathbb{R} ^N, N\geq 2, \kappa , \kappa _1, \kappa _2\geq 0, p>2, \alpha >-1$
and where
$\mathbb{R} ^N, N\geq 2, \kappa , \kappa _1, \kappa _2\geq 0, p>2, \alpha >-1$
and where
![]() ${F:\mathbb{R} ^2\to \mathbb{R}} $
is homogeneous of degree
${F:\mathbb{R} ^2\to \mathbb{R}} $
is homogeneous of degree
![]() $p>2.$
$p>2.$
We remark that problem (5) is called the Hénon equation when
![]() $\kappa \equiv 0.$
In [Reference Lou, Weth and Zhang20], Lou, Weth, and Zhang observed that the Morse index of nontrivial radial solutions corresponding to (6) (positive or sign-changing) tends to infinity as
$\kappa \equiv 0.$
In [Reference Lou, Weth and Zhang20], Lou, Weth, and Zhang observed that the Morse index of nontrivial radial solutions corresponding to (6) (positive or sign-changing) tends to infinity as
![]() $\alpha $
tends to infinity. Moreover in [Reference Clapp and Soares9], Clapp and Soares studied a related problem
$\alpha $
tends to infinity. Moreover in [Reference Clapp and Soares9], Clapp and Soares studied a related problem
 $$ \begin{align*} -\Delta u_i + u_{i} =\sum_{j=1}^l \beta_{ij}|u_j|^{p}|u_i|^{p-2}u_i, \quad u_i\in H^1(\mathbb{R}^{N}), \quad i=1,\dots, l, \end{align*} $$
$$ \begin{align*} -\Delta u_i + u_{i} =\sum_{j=1}^l \beta_{ij}|u_j|^{p}|u_i|^{p-2}u_i, \quad u_i\in H^1(\mathbb{R}^{N}), \quad i=1,\dots, l, \end{align*} $$
where
![]() $N\geq 4, 1<p<N/(N-2),$
and
$N\geq 4, 1<p<N/(N-2),$
and
![]() $(\beta _{ij})$
represents a symmetric matrix admitting a block decomposition with entries either positive or zero within each block and negative for all remaining entries. The authors resulted in the existence of fully nontrivial solutions, that is, nontrivial solutions component-wise, provided certain conditions are satisfied for the symmetric matrix
$(\beta _{ij})$
represents a symmetric matrix admitting a block decomposition with entries either positive or zero within each block and negative for all remaining entries. The authors resulted in the existence of fully nontrivial solutions, that is, nontrivial solutions component-wise, provided certain conditions are satisfied for the symmetric matrix
![]() $(\beta _{ij}).$
Furthermore, the authors derived the existence of solutions with positive and non-radial sign-changing components to the system of singularly perturbed elliptic equations
$(\beta _{ij}).$
Furthermore, the authors derived the existence of solutions with positive and non-radial sign-changing components to the system of singularly perturbed elliptic equations
 $$ \begin{align*} -\epsilon^2 \Delta u_i + u_i = \sum_{j=1}^l\beta_{ij}|u_j|^p|u_i|^{p-2}u_i, \quad u_i \in H_0^1(B_1(0)), \quad i=1,\dots, l, \end{align*} $$
$$ \begin{align*} -\epsilon^2 \Delta u_i + u_i = \sum_{j=1}^l\beta_{ij}|u_j|^p|u_i|^{p-2}u_i, \quad u_i \in H_0^1(B_1(0)), \quad i=1,\dots, l, \end{align*} $$
where
![]() $B_1(0)$
is the unit ball exhibiting two different kinds of asymptotic behavior—the first being solutions whose components decouple as
$B_1(0)$
is the unit ball exhibiting two different kinds of asymptotic behavior—the first being solutions whose components decouple as
![]() $\epsilon \to 0,$
while the second behavior being solutions whose components remain coupled up to their limit.
$\epsilon \to 0,$
while the second behavior being solutions whose components remain coupled up to their limit.
In this work, we are concerned with domains
![]() $\Omega \subset \mathbb{R} ^N$
that are invariant by the group action
$\Omega \subset \mathbb{R} ^N$
that are invariant by the group action
![]() $O(m)\times O(n)$
for
$O(m)\times O(n)$
for
![]() $N=m+n$
and
$N=m+n$
and
![]() $m,n\geq 1$
. We refer to Section 2 for the official definitions and further details. Here, we briefly introduce this class of domains in order to be able to state our main results in this paper. Inspired by the work [Reference Cabré and Ros-Oton4], for each
$m,n\geq 1$
. We refer to Section 2 for the official definitions and further details. Here, we briefly introduce this class of domains in order to be able to state our main results in this paper. Inspired by the work [Reference Cabré and Ros-Oton4], for each
![]() $x=(x_1, x_2,\dots ,x_N)\in \Omega \subset \mathbb{R} ^N=\mathbb{R} ^m \times \mathbb{R} ^n, $
we shall consider the change of variable
$x=(x_1, x_2,\dots ,x_N)\in \Omega \subset \mathbb{R} ^N=\mathbb{R} ^m \times \mathbb{R} ^n, $
we shall consider the change of variable
Thus the domain
![]() $\Omega $
can be represented in the
$\Omega $
can be represented in the
![]() $(s,t)$
variable as follows:
$(s,t)$
variable as follows:
for some appropriate domain
![]() $U \in \mathbb{R} ^2$
. Using polar coordinates, we can set
$U \in \mathbb{R} ^2$
. Using polar coordinates, we can set
![]() $s=r\cos (\theta ), t=r\sin (\theta ),$
where
$s=r\cos (\theta ), t=r\sin (\theta ),$
where
![]() $r=|x|=|(s,t)|$
and
$r=|x|=|(s,t)|$
and
![]() $\theta $
the usual polar angle in the
$\theta $
the usual polar angle in the
![]() $(s,t)$
-plane. To describe the domains in terms of the above polar coordinates, we write
$(s,t)$
-plane. To describe the domains in terms of the above polar coordinates, we write
We say that
![]() $\Omega $
is an annular domain if its associated domain given by
$\Omega $
is an annular domain if its associated domain given by
![]() $\widehat \Omega $
in the
$\widehat \Omega $
in the
![]() $(s,t)$
-plane in
$(s,t)$
-plane in
![]() $\mathbb{R} ^2$
is of the form
$\mathbb{R} ^2$
is of the form
in polar coordinates. Here,
![]() $g_i>0$
is smooth on
$g_i>0$
is smooth on
![]() $\left [0,\frac {\pi }{2}\right ]$
with
$\left [0,\frac {\pi }{2}\right ]$
with
![]() $g_i'(0)=g_i'(\frac {\pi }{2})=0$
and
$g_i'(0)=g_i'(\frac {\pi }{2})=0$
and
![]() $g_2(\theta )>g_1(\theta )$
on
$g_2(\theta )>g_1(\theta )$
on
![]() $\left [0,\frac {\pi }{2}\right ].$
Moreover, we say that
$\left [0,\frac {\pi }{2}\right ].$
Moreover, we say that
![]() $\Omega $
is an annular domain with monotonicity if
$\Omega $
is an annular domain with monotonicity if
![]() $g_1$
is increasing and
$g_1$
is increasing and
![]() $g_2$
is decreasing on
$g_2$
is decreasing on
![]() $\left (0,\frac {\pi }{2}\right ).$
The class of annular domains with monotonicity is indeed quite rich. For instance, a regular annulus
$\left (0,\frac {\pi }{2}\right ).$
The class of annular domains with monotonicity is indeed quite rich. For instance, a regular annulus
is an annular domain with monotonicity. We can also consider a slightly more general version where the inner and outer boundaries are replaced with ellipsoids instead of balls. Take
![]() $ \Omega $
to have outer boundary given by the ellipsoid
$ \Omega $
to have outer boundary given by the ellipsoid
 $$ \begin{align*} \sum_{k=1}^{m} \frac{x_k^2}{A^2}+ \sum_{k=m+1}^{N} \frac{x_k^2}{B^2} =1,\end{align*} $$
$$ \begin{align*} \sum_{k=1}^{m} \frac{x_k^2}{A^2}+ \sum_{k=m+1}^{N} \frac{x_k^2}{B^2} =1,\end{align*} $$
and the inner boundary given by
 $$ \begin{align*}\sum_{k=1}^{m} \frac{x_k^2}{C^2}+ \sum_{k=m+1}^{N} \frac{x_k^2}{D^2} =1,\end{align*} $$
$$ \begin{align*}\sum_{k=1}^{m} \frac{x_k^2}{C^2}+ \sum_{k=m+1}^{N} \frac{x_k^2}{D^2} =1,\end{align*} $$
where
![]() $ A,B,C,D>0$
are chosen such that the resulting domain is an annular region.
$ A,B,C,D>0$
are chosen such that the resulting domain is an annular region.
We also assume that the function a (resp. b) is a continuous and strictly positive function of
![]() $(s,t)$
that is
$(s,t)$
that is
![]() $a(x)=a(s,t).$
Moreover, we say that a (resp. b) satisfies (
$a(x)=a(s,t).$
Moreover, we say that a (resp. b) satisfies (
![]() $\mathcal {A}$
) if a (resp. b) is a continuously differentiable function with respect to
$\mathcal {A}$
) if a (resp. b) is a continuously differentiable function with respect to
![]() $(s,t)$
and
$(s,t)$
and
![]() $sa_{t}-ta_s \leq 0$
(resp.
$sa_{t}-ta_s \leq 0$
(resp.
![]() $sb_{t}-tb_s \leq 0$
) in
$sb_{t}-tb_s \leq 0$
) in
![]() $\widehat \Omega .$
$\widehat \Omega .$
As observed in [Reference Clapp and Pistoia8], for problems having the
![]() $O(m)\times O(n)$
symmetry (with
$O(m)\times O(n)$
symmetry (with
![]() ${N=m+n}$
) on an annular domain that is also invariant by
${N=m+n}$
) on an annular domain that is also invariant by
![]() $O(m)\times O(n)$
, the hyperbola
$O(m)\times O(n)$
, the hyperbola
is no longer the critical hyperbola, as one has the required compactness for the following improved inequality:
Our main contribution in this paper is to go well beyond the latter inequality for the lower bound of
![]() $1/p+1/q$
and to prove the existence for
$1/p+1/q$
and to prove the existence for
We begin with the statement of the first main result arising in this paper.
Theorem 1.1 Suppose
![]() $\Omega $
is an annular domain with monotonicity in
$\Omega $
is an annular domain with monotonicity in
![]() $\mathbb{R} ^N$
for
$\mathbb{R} ^N$
for
![]() $N\geq 3.$
Let
$N\geq 3.$
Let
![]() $N=m+n$
for
$N=m+n$
for
![]() $1\leq n\leq m.$
In addition, assume that a and b satisfy
$1\leq n\leq m.$
In addition, assume that a and b satisfy
![]() $(\mathcal {A}).$
Let
$(\mathcal {A}).$
Let
![]() $q\geq p> 2.$
If
$q\geq p> 2.$
If
then equation (1) has a positive weak solution
![]() $(u,v)$
that is invariant under the group action
$(u,v)$
that is invariant under the group action
![]() $O(m)\times O(n)$
.
$O(m)\times O(n)$
.
We would like to remark that in Theorem 1.1, we are not imposing any lower bound condition on
![]() $1/p+1/q$
for the case where
$1/p+1/q$
for the case where
![]() $n\leq (p+1)/(p-1).$
We would also like to remind the reader that the functions a and b do not add any compactness to the problem. In addition, we note that the same proof in Theorem 1.1 is valid for the case when
$n\leq (p+1)/(p-1).$
We would also like to remind the reader that the functions a and b do not add any compactness to the problem. In addition, we note that the same proof in Theorem 1.1 is valid for the case when
![]() $a=b=1.$
Similar results have been proved in an influential paper by Y. Y. Li [Reference Li17] in the scalar version.
$a=b=1.$
Similar results have been proved in an influential paper by Y. Y. Li [Reference Li17] in the scalar version.
As for our remaining results, we consider a specific problem of (1) given by
 $$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta u = v^{p-1}, \quad &\text{ in } \Omega,\\ -\Delta v = u^{q-1}, \quad &\text{ in } \Omega,\\ u,v>0, \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial\Omega, \end{array} \right. \end{align} $$
$$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta u = v^{p-1}, \quad &\text{ in } \Omega,\\ -\Delta v = u^{q-1}, \quad &\text{ in } \Omega,\\ u,v>0, \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial\Omega, \end{array} \right. \end{align} $$
where the conditions in problem (1) are carried over to problem (8) with the exception that
![]() $a=b=1$
and
$a=b=1$
and
![]() $\Omega $
is an annulus defined as
$\Omega $
is an annulus defined as
where the radii
![]() $R_1$
and
$R_1$
and
![]() $R_2$
satisfy certain conditions. We shall see in the following theorem that the solution obtained from Theorem 1.1 is non-radial.
$R_2$
satisfy certain conditions. We shall see in the following theorem that the solution obtained from Theorem 1.1 is non-radial.
Theorem 1.2 Let
![]() $m,n \geq 1$
with
$m,n \geq 1$
with
![]() $N=m+n,$
and
$N=m+n,$
and
![]() $q\geq p> 2$
. Suppose
$q\geq p> 2$
. Suppose
![]() $(u,v)$
is the solution of (8) obtained in Theorem 1.1 that is invariant under the group action
$(u,v)$
is the solution of (8) obtained in Theorem 1.1 that is invariant under the group action
![]() $O(m)\times O(n)$
. Define
$O(m)\times O(n)$
. Define
 $$ \begin{align*}\lambda_H := \inf_{0\neq \eta \in H_0^1(\Omega)} \frac{\int_\Omega |\nabla \eta|^2}{\int_\Omega \frac{|\eta|^2}{|x|^2}}dx.\end{align*} $$
$$ \begin{align*}\lambda_H := \inf_{0\neq \eta \in H_0^1(\Omega)} \frac{\int_\Omega |\nabla \eta|^2}{\int_\Omega \frac{|\eta|^2}{|x|^2}}dx.\end{align*} $$
If
 $$ \begin{align*}(p-1)(q-1)> \Big(1+\frac{2N}{\lambda_H}\Big)^2\left(\frac{q}{p}\right),\end{align*} $$
$$ \begin{align*}(p-1)(q-1)> \Big(1+\frac{2N}{\lambda_H}\Big)^2\left(\frac{q}{p}\right),\end{align*} $$
then
![]() $(u,v)$
is non-radial.
$(u,v)$
is non-radial.
We remark that
![]() $\lambda _H$
is the optimal constant in the classical Hardy inequality on
$\lambda _H$
is the optimal constant in the classical Hardy inequality on
![]() $\Omega ,$
and is independent of the choices of p and
$\Omega ,$
and is independent of the choices of p and
![]() $q.$
Indeed,
$q.$
Indeed,
![]() $\lambda _H$
is the characteristic of the domain
$\lambda _H$
is the characteristic of the domain
![]() $\Omega $
and not the supercritical nonlinearities in the system of equations (1). The following theorem addresses the multiplicity of positive solutions corresponding to problem (8).
$\Omega $
and not the supercritical nonlinearities in the system of equations (1). The following theorem addresses the multiplicity of positive solutions corresponding to problem (8).
Theorem 1.3 For each
![]() $1 \leq k \leq \lfloor \frac {N}{2}\rfloor ,$
where
$1 \leq k \leq \lfloor \frac {N}{2}\rfloor ,$
where
![]() $\lfloor x\rfloor $
is the floor function of
$\lfloor x\rfloor $
is the floor function of
![]() $x,$
and
$x,$
and
![]() $q\geq p> 2,$
the equation (8) has k distinct positive non-radial solutions if
$q\geq p> 2,$
the equation (8) has k distinct positive non-radial solutions if
 $$ \begin{align*}(p-1)(q-1)>\Big(1+\frac{2N}{\lambda_H}\Big)^2\left(\frac{q}{p}\right)\end{align*} $$
$$ \begin{align*}(p-1)(q-1)>\Big(1+\frac{2N}{\lambda_H}\Big)^2\left(\frac{q}{p}\right)\end{align*} $$
and either of the following two conditions hold:
-
1.
 $k>(p+1)/(p-1)$
and or;
$k>(p+1)/(p-1)$
and or; $$ \begin{align*}\frac{1}{p}+\frac{1}{ q}> 1-\frac{2}{k+1}\end{align*} $$
$$ \begin{align*}\frac{1}{p}+\frac{1}{ q}> 1-\frac{2}{k+1}\end{align*} $$
-
2.
 $k\leq (p+1)/(p-1)$
and no lower bound condition imposed for
$k\leq (p+1)/(p-1)$
and no lower bound condition imposed for
 $1/p+1/q.$
$1/p+1/q.$
The following corollary states that under certain conditions on the radii, we conclude that there is a range of p and q for which
![]() $\lambda _H$
becomes sufficiently large. We intend to use Theorem 1.3 to validate this corollary.
$\lambda _H$
becomes sufficiently large. We intend to use Theorem 1.3 to validate this corollary.
Corollary 1.4 The following assertions hold:
-
1. For
 $0<R_1<R_2 <\infty $
and sufficiently large
$0<R_1<R_2 <\infty $
and sufficiently large
 $(p-1)(q-1)(p/q),$
there are at least
$(p-1)(q-1)(p/q),$
there are at least
 $\lfloor \frac {p+1}{p-1}\rfloor $
distinct positive non-radial solutions of (8).
$\lfloor \frac {p+1}{p-1}\rfloor $
distinct positive non-radial solutions of (8). -
2. For fixed
and $$ \begin{align*}\frac{1}{p}+\frac{1}{q}> 1-\frac{2}{\lfloor \frac{N}{2}\rfloor+1}\end{align*} $$
with
$$ \begin{align*}\frac{1}{p}+\frac{1}{q}> 1-\frac{2}{\lfloor \frac{N}{2}\rfloor+1}\end{align*} $$
with $$ \begin{align*}(p-1)(q-1)> \frac{q}{p}\end{align*} $$
$$ \begin{align*}(p-1)(q-1)> \frac{q}{p}\end{align*} $$
 $\lambda _H$
sufficiently large, there are
$\lambda _H$
sufficiently large, there are
 $\lfloor \frac {N}{2}\rfloor $
distinct positive non-radial solutions of (8). For instance, under either of the following conditions,
$\lfloor \frac {N}{2}\rfloor $
distinct positive non-radial solutions of (8). For instance, under either of the following conditions,
 $\lambda _H$
can be sufficiently large and therefore there are
$\lambda _H$
can be sufficiently large and therefore there are
 $\lfloor \frac {N}{2}\rfloor $
distinct positive non-radial solutions of (8):
$\lfloor \frac {N}{2}\rfloor $
distinct positive non-radial solutions of (8):
-
2.(a): Let
 $R_1=R$
and
$R_1=R$
and
 $R_2=R+1.$
Then
$R_2=R+1.$
Then
 $\lambda _H$
is sufficiently large for large values of
$\lambda _H$
is sufficiently large for large values of
 $R.$
Note by scaling, we can take
$R.$
Note by scaling, we can take
 $R_1=1$
and
$R_1=1$
and
 $R_2= 1+\frac {1}{R}$
and obtain the same result for large
$R_2= 1+\frac {1}{R}$
and obtain the same result for large
 $R.$
$R.$
-
2.(b): Let
 $R < \gamma (R)$
with
$R < \gamma (R)$
with
 $\frac {\gamma (R)}{R} \to 1$
as
$\frac {\gamma (R)}{R} \to 1$
as
 $R\to \infty .$
With
$R\to \infty .$
With
 $\Omega _R = \{x\in \mathbb{R} ^N: R<|x|<\gamma (R) \},$
we have that for R large enough, the
$\Omega _R = \{x\in \mathbb{R} ^N: R<|x|<\gamma (R) \},$
we have that for R large enough, the
 $\lambda _H$
corresponding to
$\lambda _H$
corresponding to
 $\Omega _R$
is sufficiently large.
$\Omega _R$
is sufficiently large.
-
The structure of the paper is presented as follows. In Section 2, we present some fundamental background on domains of double revolution along with some important definitions and results arising from convex analysis and minimax principles for lower semi-continuous functions. Afterward in Section 3, we use a variational formulation on convex closed subsets of an appropriate Sobolev space that plays a detrimental role in proving our main results of the paper. We conclude the paper with Section 4 on the proofs of the remaining results which deal with multiplicity results of positive non-radial solutions when
![]() $\Omega $
is an annulus.
$\Omega $
is an annulus.
2 Preliminaries
2.1 Domains of double revolution
We dedicate this section to introduce some fundamental background on domains of double revolution. Unless otherwise stated, we assume that our domain is of double revolution. We begin with some notations. Let
![]() $\mathbb{R} ^N = \mathbb{R} ^m \times \mathbb{R} ^n,$
where
$\mathbb{R} ^N = \mathbb{R} ^m \times \mathbb{R} ^n,$
where
![]() $m,n \geq 1$
and
$m,n \geq 1$
and
![]() $m+n = N.$
For each
$m+n = N.$
For each
![]() $x=(x_1, x_2,\dots ,x_N)\in \Omega \subset \mathbb{R} ^N, $
we shall consider the change of variables in terms of s and t as
$x=(x_1, x_2,\dots ,x_N)\in \Omega \subset \mathbb{R} ^N, $
we shall consider the change of variables in terms of s and t as
Definition 2.1 We say that
![]() $\Omega \subset \mathbb{R} ^N$
is a domain of double revolution if it is invariant under rotations of the first m variables and invariant under rotations of the last n variables. Equivalently,
$\Omega \subset \mathbb{R} ^N$
is a domain of double revolution if it is invariant under rotations of the first m variables and invariant under rotations of the last n variables. Equivalently,
![]() $\Omega $
is of the form
$\Omega $
is of the form
![]() $\Omega = \{x \in \mathbb{R} ^N: (s,t)\in U\}$
, where U is a domain in
$\Omega = \{x \in \mathbb{R} ^N: (s,t)\in U\}$
, where U is a domain in
![]() $\mathbb{R} ^2$
which is symmetric with respect to the two coordinate axes. In fact,
$\mathbb{R} ^2$
which is symmetric with respect to the two coordinate axes. In fact,
is the intersection of
![]() $\Omega $
with the
$\Omega $
with the
![]() $(x_1, x_{m+1})$
-plane.
$(x_1, x_{m+1})$
-plane.
We remark that U is smooth if and only if
![]() $\Omega $
is smooth. Next, we denote
$\Omega $
is smooth. Next, we denote
![]() $\widehat \Omega $
to be the intersection of U with the first quadrant of
$\widehat \Omega $
to be the intersection of U with the first quadrant of
![]() $\mathbb{R} ^2,$
in other words,
$\mathbb{R} ^2,$
in other words,
Using polar coordinates, we can set
![]() ${s=r\cos (\theta ), t=r\sin (\theta )}$
where
${s=r\cos (\theta ), t=r\sin (\theta )}$
where
![]() $r=|x|=|(s,t)|$
and
$r=|x|=|(s,t)|$
and
![]() $\theta $
the usual polar angle in the
$\theta $
the usual polar angle in the
![]() $(s,t)$
-plane.
$(s,t)$
-plane.
In this paper, we consider domains to be annular with a certain monotonicity (or convexity) assumption with respect to the polar angle. In addition, all domains under consideration will be bounded in
![]() $\mathbb{R} ^N$
with smooth boundary unless explicitly stated. We describe the domains in terms of the above polar coordinates by
$\mathbb{R} ^N$
with smooth boundary unless explicitly stated. We describe the domains in terms of the above polar coordinates by
Now, we can formally define an annular domain stated as follows.
Definition 2.2 Let
![]() $\Omega \subset \mathbb{R} ^N$
be a domain of double revolution in
$\Omega \subset \mathbb{R} ^N$
be a domain of double revolution in
![]() $\mathbb{R} ^N$
with
$\mathbb{R} ^N$
with
![]() $N=m+n$
for
$N=m+n$
for
![]() $m,n\geq 1.$
We say that
$m,n\geq 1.$
We say that
![]() $\Omega $
is an annular domain if its associated domain given by
$\Omega $
is an annular domain if its associated domain given by
![]() $\widehat \Omega $
in the
$\widehat \Omega $
in the
![]() $(s,t)$
-plane in
$(s,t)$
-plane in
![]() $\mathbb{R} ^2$
is of the form
$\mathbb{R} ^2$
is of the form
in polar coordinates. Here,
![]() $g_i>0$
is smooth on
$g_i>0$
is smooth on
![]() $\left [0,\frac {\pi }{2}\right ]$
with
$\left [0,\frac {\pi }{2}\right ]$
with
![]() $g_i'(0)=g_i'(\frac {\pi }{2})=0$
and
$g_i'(0)=g_i'(\frac {\pi }{2})=0$
and
![]() $g_2(\theta )>g_1(\theta )$
on
$g_2(\theta )>g_1(\theta )$
on
![]() $\left [0,\frac {\pi }{2}\right ].$
Moreover, we say that
$\left [0,\frac {\pi }{2}\right ].$
Moreover, we say that
![]() $\Omega $
is an annular domain with monotonicity if
$\Omega $
is an annular domain with monotonicity if
![]() $g_1$
is increasing and
$g_1$
is increasing and
![]() $g_2$
is decreasing on
$g_2$
is decreasing on
![]() $\left (0,\frac {\pi }{2}\right ).$
$\left (0,\frac {\pi }{2}\right ).$
We refer the interested reader to the paper [Reference Cowan and Moameni11] and [Reference Cowan and Moameni12] for further explicit examples of annular domains. Now, we provide some assumptions on the functions a and b in which we encounter later in the paper.
Definition 2.3 We assume that a and b are continuous and strictly positive functions of
![]() $(s,t)$
that is
$(s,t)$
that is
![]() $a(x)=a(s,t)$
(resp.
$a(x)=a(s,t)$
(resp.
![]() $b(x)=b(s,t)$
). Moreover, we say that a (resp. b) satisfies (
$b(x)=b(s,t)$
). Moreover, we say that a (resp. b) satisfies (
![]() $\mathcal {A}$
) if a (resp. b) is a continuously differentiable function with respect to
$\mathcal {A}$
) if a (resp. b) is a continuously differentiable function with respect to
![]() $(s,t)$
and
$(s,t)$
and
![]() $sa_{t}-ta_s \leq 0$
(resp.
$sa_{t}-ta_s \leq 0$
(resp.
![]() $sb_{t}-tb_s \leq 0$
) in
$sb_{t}-tb_s \leq 0$
) in
![]() $\widehat \Omega .$
$\widehat \Omega .$
2.2 Convex analysis and minimax principles for lower semi-continuous functions
In this section, we lay out some important definitions and fundamental results from convex analysis and minimax principles for lower semi-continuous functions. Consider V to be a real Banach space,
![]() $V^*$
to be its topological dual, and we denote the pairing of V and
$V^*$
to be its topological dual, and we denote the pairing of V and
![]() $V^*$
by
$V^*$
by
![]() $\langle \cdot , \cdot \rangle .$
We denote the weak topology on V induced by the pairing
$\langle \cdot , \cdot \rangle .$
We denote the weak topology on V induced by the pairing
![]() $\langle \cdot , \cdot \rangle $
to be
$\langle \cdot , \cdot \rangle $
to be
![]() $\sigma (V, V^*).$
We say a function
$\sigma (V, V^*).$
We say a function
![]() $\Psi : V\to \mathbb{R} $
is weakly lower semi-continuous if for each
$\Psi : V\to \mathbb{R} $
is weakly lower semi-continuous if for each
![]() $u \in V$
and for any sequence
$u \in V$
and for any sequence
![]() $\{u_n\}_{n=1}^\infty $
approaching u in the weak topology
$\{u_n\}_{n=1}^\infty $
approaching u in the weak topology
![]() $\sigma (V, V^*),$
$\sigma (V, V^*),$
Consider
![]() $\Phi : V\to \mathbb{R} \cup \{\infty \}$
to be a proper convex function. We define the subdifferential
$\Phi : V\to \mathbb{R} \cup \{\infty \}$
to be a proper convex function. We define the subdifferential
![]() $\partial \Psi $
of
$\partial \Psi $
of
![]() $\Psi $
to be the following set-valued operator: if
$\Psi $
to be the following set-valued operator: if
![]() $u\in Dom(\Psi )=\{v\in V: \Psi (v) < \infty \},$
then we set
$u\in Dom(\Psi )=\{v\in V: \Psi (v) < \infty \},$
then we set
and if
![]() $u \notin Dom(\Psi ),$
we set
$u \notin Dom(\Psi ),$
we set
![]() $\partial \Psi (u)=\emptyset .$
If
$\partial \Psi (u)=\emptyset .$
If
![]() $\Psi $
is Gâteaux differentiable at
$\Psi $
is Gâteaux differentiable at
![]() $u,$
then we denote the derivative of
$u,$
then we denote the derivative of
![]() $\Psi $
at u by
$\Psi $
at u by
![]() $D\Psi (u).$
In this case,
$D\Psi (u).$
In this case,
![]() $\partial \Psi (u) = \{D\Psi (u)\}.$
$\partial \Psi (u) = \{D\Psi (u)\}.$
Now, we arrive to the topic on minimax principles for lower semi-continuous functions. We begin with the definition of a critical point arising in Szulkin [Reference Szulkin30].
Definition 2.4 Let V be a real Banach space,
![]() $\Phi \in C^1(V,\mathbb{R} ),$
and
$\Phi \in C^1(V,\mathbb{R} ),$
and
![]() $\Psi : V \to (-\infty , \infty ]$
be a proper (i.e.,
$\Psi : V \to (-\infty , \infty ]$
be a proper (i.e.,
![]() $Dom(\Psi ) \neq \emptyset $
), convex and lower semi-continuous function. A point
$Dom(\Psi ) \neq \emptyset $
), convex and lower semi-continuous function. A point
![]() $u\in V$
is said to be a critical point of
$u\in V$
is said to be a critical point of
if
![]() $u\in Dom(\Psi )$
and if it satisfies the inequality
$u\in Dom(\Psi )$
and if it satisfies the inequality
We utilize the following important property of uniformly convex spaces.
Proposition 2.1 Suppose that V is a uniformly convex Banach space. Let
![]() $\{u_n\}_{n=1}^\infty $
be a sequence in V such that
$\{u_n\}_{n=1}^\infty $
be a sequence in V such that
![]() $u_n \rightharpoonup u$
weakly
$u_n \rightharpoonup u$
weakly
![]() $\sigma (V, V^*)$
and
$\sigma (V, V^*)$
and
Then
![]() $u_n \to u$
strongly.
$u_n \to u$
strongly.
The following definition leads to the mountain pass theorem in which we primarily use to prove our first main result.
Definition 2.5 We say that I satisfies the Palais–Smale compactness condition (PS) if for every sequence
![]() $\{u_n\}_{n=1}^\infty $
such that:
$\{u_n\}_{n=1}^\infty $
such that:
-
(i)
 $I(u_n) \to c \in \mathbb{R} ,$
$I(u_n) \to c \in \mathbb{R} ,$
-
(ii)
 $\langle D\Phi (u_n), u_n-v\rangle + \Psi (v)-\Psi (u_n) \geq -\epsilon _n \|v-u_n\|, \quad \forall v \in V,$
$\langle D\Phi (u_n), u_n-v\rangle + \Psi (v)-\Psi (u_n) \geq -\epsilon _n \|v-u_n\|, \quad \forall v \in V,$
where
![]() $\epsilon _n \to 0,$
we have
$\epsilon _n \to 0,$
we have
![]() $\{u_n\}_{n=1}^\infty $
possessing a convergent subsequence.
$\{u_n\}_{n=1}^\infty $
possessing a convergent subsequence.
Now, we present the mountain pass theorem provided by Szulkin [Reference Szulkin30].
Theorem 2.6 (Mountain Pass Theorem)
Let
![]() $I: V\to (-\infty , \infty ]$
be of the form
$I: V\to (-\infty , \infty ]$
be of the form
where
![]() $\Psi : V \to (-\infty , \infty ]$
is a proper convex and lower semi-continuous function and
$\Psi : V \to (-\infty , \infty ]$
is a proper convex and lower semi-continuous function and
![]() $\Phi \in C^1(V,\mathbb{R} ).$
Suppose that I satisfies the Palais–Smale condition and the mountain pass geometry (MPG):
$\Phi \in C^1(V,\mathbb{R} ).$
Suppose that I satisfies the Palais–Smale condition and the mountain pass geometry (MPG):
-
(i)
 $I(0)=0,$
$I(0)=0,$
-
(ii) there exists
 $e \in V$
such that
$e \in V$
such that
 $I(e) \leq 0,$
$I(e) \leq 0,$
-
(iii) there exists some
 $\rho $
such that
$\rho $
such that
 $0< \rho < \|e\|$
and for every
$0< \rho < \|e\|$
and for every
 $u\in V$
with
$u\in V$
with
 $\|u\| = \rho $
one has
$\|u\| = \rho $
one has
 $I(u)> 0.$
$I(u)> 0.$
Then I has a critical value
![]() $c>0$
which is characterized by
$c>0$
which is characterized by
where
![]() $\Gamma = \{\gamma \in C([0,1], V): \gamma (0)=0, \gamma (1)=e\}.$
$\Gamma = \{\gamma \in C([0,1], V): \gamma (0)=0, \gamma (1)=e\}.$
3 A variational formulation and the proof of Theorem 1.1
Our interest in this paper lies within solving the following system:
 $$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta u = a(x)v^{p-1}, \quad &\text{ in } \Omega,\\ -\Delta v = b(x)u^{q-1}, \quad &\text{ in } \Omega,\\ u,v>0, \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial\Omega, \end{array} \right. \end{align} $$
$$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta u = a(x)v^{p-1}, \quad &\text{ in } \Omega,\\ -\Delta v = b(x)u^{q-1}, \quad &\text{ in } \Omega,\\ u,v>0, \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial\Omega, \end{array} \right. \end{align} $$
where
![]() $\Omega $
is a bounded annular domain (not necessarily an annulus) in
$\Omega $
is a bounded annular domain (not necessarily an annulus) in
![]() $\mathbb{R} ^N, (N \geq 3), q\geq p> 2,$
and
$\mathbb{R} ^N, (N \geq 3), q\geq p> 2,$
and
![]() $a,b \in C(\bar \Omega )$
with
$a,b \in C(\bar \Omega )$
with
![]() $a(x)\geq a_0>0$
and
$a(x)\geq a_0>0$
and
![]() $b(x)\geq b_0>0$
where
$b(x)\geq b_0>0$
where
![]() $a_0$
and
$a_0$
and
![]() $b_0$
are constants. Let
$b_0$
are constants. Let
![]() $p'=p/(p-1)$
and consider the Banach space
$p'=p/(p-1)$
and consider the Banach space
![]() $V=W^{2,p'}(\Omega ) \cap W_0^{1, p'}(\Omega ) \cap L^q(\Omega )$
equipped with the following norm:
$V=W^{2,p'}(\Omega ) \cap W_0^{1, p'}(\Omega ) \cap L^q(\Omega )$
equipped with the following norm:
Recall the duality pairing between V and its dual space
![]() $V^*$
is defined by
$V^*$
is defined by
Following for instance the work by Wang [Reference Wang32], one can get from (11) that
Inserting this equation into the second equation of (11) results in the following scalar equation corresponding to the u-component:
Considering the fact that
![]() $p'-1=1/(p-1)$
we arrive at
$p'-1=1/(p-1)$
we arrive at
Formally, the Euler–Lagrange functional associated with problem (12) is given by
 $$ \begin{align*}I(u) := \frac{1}{p'}\int_\Omega \frac{|-\Delta u|^{p'}}{a(x)^{p'-1}} dx - \frac{1}{q}\int_\Omega b(x)|u|^q dx.\end{align*} $$
$$ \begin{align*}I(u) := \frac{1}{p'}\int_\Omega \frac{|-\Delta u|^{p'}}{a(x)^{p'-1}} dx - \frac{1}{q}\int_\Omega b(x)|u|^q dx.\end{align*} $$
We define
![]() $\Psi : V \to \mathbb{R} $
and
$\Psi : V \to \mathbb{R} $
and
![]() $\Phi : V \to \mathbb{R} $
by
$\Phi : V \to \mathbb{R} $
by
 $$ \begin{align*}\Psi(u) = \frac{1}{p'}\int_\Omega \frac{|-\Delta u|^{p'}}{a(x)^{p'-1}} dx\end{align*} $$
$$ \begin{align*}\Psi(u) = \frac{1}{p'}\int_\Omega \frac{|-\Delta u|^{p'}}{a(x)^{p'-1}} dx\end{align*} $$
and
respectively. Let K be a convex subset of
![]() $V.$
Finally, we introduce the functional
$V.$
Finally, we introduce the functional
![]() ${I_K: V \to (-\infty , \infty ]}$
to be defined by
${I_K: V \to (-\infty , \infty ]}$
to be defined by
where the restriction of
![]() $\Psi $
on K at
$\Psi $
on K at
![]() $u,$
denoted by
$u,$
denoted by
![]() $\Psi _K(u)$
is defined by
$\Psi _K(u)$
is defined by
 $$ \begin{align*}\Psi_K(u)=\left\{ \begin{array}{@{}cc} \frac{1}{p'}\int_\Omega \frac{|-\Delta u|^{p'}}{a(x)^{p'-1}} dx,& \quad u \in K,\\ +\infty, & \quad u \not \in K. \end{array} \right. \end{align*} $$
$$ \begin{align*}\Psi_K(u)=\left\{ \begin{array}{@{}cc} \frac{1}{p'}\int_\Omega \frac{|-\Delta u|^{p'}}{a(x)^{p'-1}} dx,& \quad u \in K,\\ +\infty, & \quad u \not \in K. \end{array} \right. \end{align*} $$
We denote the functional
![]() $I_K$
the Euler–Lagrange functional corresponding to (12) restricted on
$I_K$
the Euler–Lagrange functional corresponding to (12) restricted on
![]() $K.$
$K.$
The following proposition states the existence of a critical point for the functional
![]() $I_K$
and we use Theorem 2.6 to prove the proposition.
$I_K$
and we use Theorem 2.6 to prove the proposition.
Proposition 3.1 Let
![]() $\Omega $
be a domain in
$\Omega $
be a domain in
![]() $\mathbb{R} ^N$
, and let
$\mathbb{R} ^N$
, and let
![]() $q\geq p> 2.$
Let
$q\geq p> 2.$
Let
![]() $a,b \in C(\bar \Omega )$
with
$a,b \in C(\bar \Omega )$
with
![]() $a(x)\geq a_0>0$
and
$a(x)\geq a_0>0$
and
![]() $b(x)\geq b_0>0$
where
$b(x)\geq b_0>0$
where
![]() $a_0$
and
$a_0$
and
![]() $b_0$
are constants. Consider the Euler–Lagrange functional
$b_0$
are constants. Consider the Euler–Lagrange functional
![]() $I: V \to \mathbb{R} $
associated with problem (12)
$I: V \to \mathbb{R} $
associated with problem (12)
 $$ \begin{align*}I(u) := \frac{1}{p'}\int_\Omega \frac{|-\Delta u|^{p'}}{a(x)^{p'-1}} dx - \frac{1}{q}\int_\Omega b(x)|u|^q dx.\end{align*} $$
$$ \begin{align*}I(u) := \frac{1}{p'}\int_\Omega \frac{|-\Delta u|^{p'}}{a(x)^{p'-1}} dx - \frac{1}{q}\int_\Omega b(x)|u|^q dx.\end{align*} $$
Let K be a weakly closed convex subset of
![]() $W^{2,p'}(\Omega )\cap W_0^{1, p'}(\Omega ) $
which is compactly embedded in
$W^{2,p'}(\Omega )\cap W_0^{1, p'}(\Omega ) $
which is compactly embedded in
![]() $L^q(\Omega ).$
Then the functional I has a critical point
$L^q(\Omega ).$
Then the functional I has a critical point
![]() $\bar u$
on K by means of Definition 2.4.
$\bar u$
on K by means of Definition 2.4.
Proof Note that the function a is bounded from above, and is also away from zero. Thus, an equivalent norm on
![]() $W^{2,p'}(\Omega )\cap W_0^{1, p'}(\Omega ) $
can be defined by
$W^{2,p'}(\Omega )\cap W_0^{1, p'}(\Omega ) $
can be defined by
 $$ \begin{align*}\|u\|_{W^{2,p'}(\Omega)}^{p'} = \int_\Omega \frac{|-\Delta u|^{p'}}{a(x)^{p'-1}} dx, \qquad \forall u \in W^{2,p'}(\Omega)\cap W_0^{1, p'}(\Omega).\end{align*} $$
$$ \begin{align*}\|u\|_{W^{2,p'}(\Omega)}^{p'} = \int_\Omega \frac{|-\Delta u|^{p'}}{a(x)^{p'-1}} dx, \qquad \forall u \in W^{2,p'}(\Omega)\cap W_0^{1, p'}(\Omega).\end{align*} $$
By assumption, K is compactly embedded in
![]() $L^q(\Omega ).$
So there exists a constant
$L^q(\Omega ).$
So there exists a constant
![]() $C>0$
such that
$C>0$
such that
In order to satisfy the mountain pass theorem, we must satisfy the (PS)-compactness condition and the mountain pass geometry. We begin by verifying the (PS)-compactness condition. Suppose that
![]() $\{u_n\}_{n=1}^\infty $
is a sequence in K such that
$\{u_n\}_{n=1}^\infty $
is a sequence in K such that
![]() $I(u_n) \to c \in \mathbb{R} , \epsilon _n \to 0,$
and
$I(u_n) \to c \in \mathbb{R} , \epsilon _n \to 0,$
and
We want to prove that
![]() $\{u_n\}_{n=1}^\infty $
has a converging subsequence in
$\{u_n\}_{n=1}^\infty $
has a converging subsequence in
![]() $V.$
First, we prove that
$V.$
First, we prove that
![]() $\{u_n\}_{n=1}^\infty $
is bounded in
$\{u_n\}_{n=1}^\infty $
is bounded in
![]() $W^{2,p'}(\Omega ).$
Since
$W^{2,p'}(\Omega ).$
Since
![]() $I(u_n) \to c,$
it follows that for large values of
$I(u_n) \to c,$
it follows that for large values of
![]() $n,$
we obtain
$n,$
we obtain
 $$ \begin{align} I(u_n) &= \frac{1}{p'}\int_\Omega \frac{|-\Delta u_n|^{p'}}{a(x)^{p'-1}} dx - \frac{1}{q}\int_\Omega b(x)|u_n|^q dx \nonumber\\ &= \frac{1}{p'}\|u_n\|_{W^{2,p'}(\Omega)}^{p'} - \frac{1}{q}\int_\Omega b(x)|u_n|^q dx \nonumber\\ &\leq c+1. \end{align} $$
$$ \begin{align} I(u_n) &= \frac{1}{p'}\int_\Omega \frac{|-\Delta u_n|^{p'}}{a(x)^{p'-1}} dx - \frac{1}{q}\int_\Omega b(x)|u_n|^q dx \nonumber\\ &= \frac{1}{p'}\|u_n\|_{W^{2,p'}(\Omega)}^{p'} - \frac{1}{q}\int_\Omega b(x)|u_n|^q dx \nonumber\\ &\leq c+1. \end{align} $$
Note that
Since
![]() $q>2>p',$
there exists
$q>2>p',$
there exists
![]() $\delta>0$
such that
$\delta>0$
such that
Setting
![]() $v=ru_n$
in (15) with
$v=ru_n$
in (15) with
![]() $r=1+\delta /q,$
we get
$r=1+\delta /q,$
we get
 $$ \begin{align} &\frac{1}{p'}\int_\Omega \frac{|-\Delta ru_n|^{p'}}{a(x)^{p'-1}} dx - \frac{1}{p'}\int_\Omega \frac{|-\Delta u_n|^{p'}}{a(x)^{p'-1}} dx \nonumber\\&\quad+ \int_\Omega b(x)|u_n|^{q-2}u_n\cdot (u_n-ru_n) dx \geq -\epsilon_n \|ru_n-u_n\|_V \nonumber\\ \implies &\frac{r^{p'}}{p'}\int_\Omega \frac{|-\Delta u_n|^{p'}}{a(x)^{p'-1}} dx - \frac{1}{p'}\int_\Omega \frac{|-\Delta u_n|^{p'}}{a(x)^{p'-1}} dx\nonumber\\&\quad + \int_\Omega b(x)|u_n|^{q-2}u_n\cdot (u_n-ru_n) dx \geq -(r-1)\epsilon_n \|u_n\|_V \nonumber\\\implies &\frac{r^{p'}-1}{p'}\|u_n\|_{W^{2,p'}(\Omega)}^{p'} + (1-r)\int_\Omega b(x)|u_n|^q dx \geq -(r-1)\epsilon_n \|u_n\|_V \nonumber \\ \implies &\frac{1-r^{p'}}{p'}\|u_n\|_{W^{2,p'}(\Omega)}^{p'} + (r-1)\int_\Omega b(x)|u_n|^q dx \leq (r-1)\epsilon_n \|u_n\|_V. \end{align} $$
$$ \begin{align} &\frac{1}{p'}\int_\Omega \frac{|-\Delta ru_n|^{p'}}{a(x)^{p'-1}} dx - \frac{1}{p'}\int_\Omega \frac{|-\Delta u_n|^{p'}}{a(x)^{p'-1}} dx \nonumber\\&\quad+ \int_\Omega b(x)|u_n|^{q-2}u_n\cdot (u_n-ru_n) dx \geq -\epsilon_n \|ru_n-u_n\|_V \nonumber\\ \implies &\frac{r^{p'}}{p'}\int_\Omega \frac{|-\Delta u_n|^{p'}}{a(x)^{p'-1}} dx - \frac{1}{p'}\int_\Omega \frac{|-\Delta u_n|^{p'}}{a(x)^{p'-1}} dx\nonumber\\&\quad + \int_\Omega b(x)|u_n|^{q-2}u_n\cdot (u_n-ru_n) dx \geq -(r-1)\epsilon_n \|u_n\|_V \nonumber\\\implies &\frac{r^{p'}-1}{p'}\|u_n\|_{W^{2,p'}(\Omega)}^{p'} + (1-r)\int_\Omega b(x)|u_n|^q dx \geq -(r-1)\epsilon_n \|u_n\|_V \nonumber \\ \implies &\frac{1-r^{p'}}{p'}\|u_n\|_{W^{2,p'}(\Omega)}^{p'} + (r-1)\int_\Omega b(x)|u_n|^q dx \leq (r-1)\epsilon_n \|u_n\|_V. \end{align} $$
Multiplying (16) by
![]() $\delta $
and adding the result by (17) yield that
$\delta $
and adding the result by (17) yield that
 $$ \begin{align*} \Big(\frac{\delta}{p'}+\frac{1-r^{p'}}{p'}\Big)\|u_n\|_{W^{2,p'}(\Omega)}^{p'} \leq \delta c + \delta+ \frac{\epsilon_n \delta }{q}\|u_n\|_V. \end{align*} $$
$$ \begin{align*} \Big(\frac{\delta}{p'}+\frac{1-r^{p'}}{p'}\Big)\|u_n\|_{W^{2,p'}(\Omega)}^{p'} \leq \delta c + \delta+ \frac{\epsilon_n \delta }{q}\|u_n\|_V. \end{align*} $$
Note that for n large enough, by applying (14), we obtain
 $$ \begin{align*} \|u_n\|_{W^{2,p'}(\Omega)}^{p'} &< C_0(1+\|u_n\|_V) \\ &\leq C_0\Big(1+C\|u_n\|_{W^{2,p'}(\Omega)}\Big), \end{align*} $$
$$ \begin{align*} \|u_n\|_{W^{2,p'}(\Omega)}^{p'} &< C_0(1+\|u_n\|_V) \\ &\leq C_0\Big(1+C\|u_n\|_{W^{2,p'}(\Omega)}\Big), \end{align*} $$
for a constant
![]() $C_0.$
Thus, we conclude that
$C_0.$
Thus, we conclude that
![]() $\{u_n\}_{n=1}^\infty $
is bounded in
$\{u_n\}_{n=1}^\infty $
is bounded in
![]() $W^{2,p'}(\Omega ).$
Since
$W^{2,p'}(\Omega ).$
Since
![]() $\{u_n\}_{n=1}^\infty $
is bounded in
$\{u_n\}_{n=1}^\infty $
is bounded in
![]() $W^{2,p'}(\Omega ),$
it follows that, up to a subsequence, there exists
$W^{2,p'}(\Omega ),$
it follows that, up to a subsequence, there exists
![]() ${\bar u \in W^{2,p'}(\Omega )}$
such that
${\bar u \in W^{2,p'}(\Omega )}$
such that
![]() $u_n \rightharpoonup \bar u$
weakly in
$u_n \rightharpoonup \bar u$
weakly in
![]() $W^{2,p'}(\Omega )$
and
$W^{2,p'}(\Omega )$
and
![]() $u_n \to \bar u$
a.e.. By assumption that K is compactly embedded in
$u_n \to \bar u$
a.e.. By assumption that K is compactly embedded in
![]() $L^q(\Omega ),$
we can deduce from boundedness of
$L^q(\Omega ),$
we can deduce from boundedness of
![]() $\{u_n\}_{n=1}^\infty \subset K$
in
$\{u_n\}_{n=1}^\infty \subset K$
in
![]() $W^{2,p'}(\Omega )$
strong convergence of
$W^{2,p'}(\Omega )$
strong convergence of
![]() $u_n$
to
$u_n$
to
![]() $\bar u$
in
$\bar u$
in
![]() $L^q(\Omega ).$
Setting
$L^q(\Omega ).$
Setting
![]() $v=\bar u$
in (15), we get
$v=\bar u$
in (15), we get
Taking
![]() $\limsup _{n\to \infty }$
on both sides of (18), we obtain
$\limsup _{n\to \infty }$
on both sides of (18), we obtain
By Proposition 2.1, we have
and therefore, we conclude that
![]() $u_n \to \bar u$
strongly in
$u_n \to \bar u$
strongly in
![]() $V,$
as desired. Now, we verify the mountain pass geometry for the functional
$V,$
as desired. Now, we verify the mountain pass geometry for the functional
![]() $I_K.$
Clearly,
$I_K.$
Clearly,
![]() $I_K(0)=0$
which satisfies condition
$I_K(0)=0$
which satisfies condition
![]() $(i).$
For condition
$(i).$
For condition
![]() $(ii),$
let
$(ii),$
let
![]() $u\in K.$
Then for
$u\in K.$
Then for
![]() $t\geq 0,$
$t\geq 0,$
 $$ \begin{align*} I_K(tu) &= \frac{1}{p'}\int_\Omega \frac{|-\Delta tu|^{p'}}{a(x)^{p'-1}} dx - \frac{1}{q}\int_\Omega b(x)|tu|^q dx \\ &=\frac{t^{p'}}{p'}\int_\Omega \frac{|-\Delta u|^{p'}}{a(x)^{p'-1}} dx - \frac{t^q}{q}\int_\Omega b(x)|u|^q dx. \end{align*} $$
$$ \begin{align*} I_K(tu) &= \frac{1}{p'}\int_\Omega \frac{|-\Delta tu|^{p'}}{a(x)^{p'-1}} dx - \frac{1}{q}\int_\Omega b(x)|tu|^q dx \\ &=\frac{t^{p'}}{p'}\int_\Omega \frac{|-\Delta u|^{p'}}{a(x)^{p'-1}} dx - \frac{t^q}{q}\int_\Omega b(x)|u|^q dx. \end{align*} $$
Since
![]() $q> 2>p',$
it follows that for t large enough, we obtain
$q> 2>p',$
it follows that for t large enough, we obtain
![]() $I_K(tu) < 0$
and setting
$I_K(tu) < 0$
and setting
![]() $e:= tu,$
condition
$e:= tu,$
condition
![]() $(ii)$
holds. To satisfy condition
$(ii)$
holds. To satisfy condition
![]() $(iii),$
take
$(iii),$
take
![]() $u\in K$
with
$u\in K$
with
![]() $\|u\|_V = \rho>0.$
Then
$\|u\|_V = \rho>0.$
Then
By (14), there exists a constant
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $u\in K,$
we have
$u\in K,$
we have
In addition, we have
for some constant
![]() $C_1>0.$
So,
$C_1>0.$
So,
 $$ \begin{align*} I_K(u) &= \frac{1}{p'}\|u\|_{W^{2,p'}(\Omega)}^{p'} - \frac{1}{q}\int_\Omega b(x)|u|^q dx\\ &\geq \frac{1}{p'}\|u\|_{W^{2,p'}(\Omega)}^{p'} - \frac{C_1}{q}\|u\|_V^q \\ &\geq \frac{1}{{p'}C^{p'}}\|u\|_V^{p'} - \frac{C_1}{q}\|u\|_V^q \\ &= \frac{1}{{p'}C^{p'}}\rho^{p'} - \frac{C_1}{q}\rho^q>0, \end{align*} $$
$$ \begin{align*} I_K(u) &= \frac{1}{p'}\|u\|_{W^{2,p'}(\Omega)}^{p'} - \frac{1}{q}\int_\Omega b(x)|u|^q dx\\ &\geq \frac{1}{p'}\|u\|_{W^{2,p'}(\Omega)}^{p'} - \frac{C_1}{q}\|u\|_V^q \\ &\geq \frac{1}{{p'}C^{p'}}\|u\|_V^{p'} - \frac{C_1}{q}\|u\|_V^q \\ &= \frac{1}{{p'}C^{p'}}\rho^{p'} - \frac{C_1}{q}\rho^q>0, \end{align*} $$
provided
![]() $\rho $
is small enough as
$\rho $
is small enough as
![]() $q> 2>p'.$
Note that if
$q> 2>p'.$
Note that if
![]() $u\not \in K,$
then
$u\not \in K,$
then
![]() $I_K(u)>0$
by definition of
$I_K(u)>0$
by definition of
![]() $\Psi _K(u).$
Thus, the mountain pass geometry holds for the functional
$\Psi _K(u).$
Thus, the mountain pass geometry holds for the functional
![]() $I_K.$
By the mountain pass theorem,
$I_K.$
By the mountain pass theorem,
![]() $I_K$
has a critical point
$I_K$
has a critical point
![]() $\bar u \in K$
with
$\bar u \in K$
with
![]() $I_K(\bar u) = c,$
where
$I_K(\bar u) = c,$
where
![]() $c>0$
is the critical value characterized by
$c>0$
is the critical value characterized by
where
![]() $\Gamma = \{\gamma \in C([0,1], V): \gamma (0)=0, \gamma (1)=e, I_K(\gamma (1))\leq 0\}.$
$\Gamma = \{\gamma \in C([0,1], V): \gamma (0)=0, \gamma (1)=e, I_K(\gamma (1))\leq 0\}.$
Lemma 3.1 Let V be a reflexive Banach space, and let
![]() $f: V \to \mathbb{R} $
be a convex and differentiable functional. If
$f: V \to \mathbb{R} $
be a convex and differentiable functional. If
then
![]() $Df(u)=Df(\bar u), $
where
$Df(u)=Df(\bar u), $
where
![]() $\langle .,.\rangle $
is the duality pairing between V and
$\langle .,.\rangle $
is the duality pairing between V and
![]() $V^*.$
In particular, if f is strictly convex, then
$V^*.$
In particular, if f is strictly convex, then
![]() $u=\bar u.$
$u=\bar u.$
Proof By the convexity of
![]() $f,$
$f,$
So, (20) and (21) implies that
Note that for all
![]() $v\in V,$
$v\in V,$
Equivalently,
 $$ \begin{align*} f(v) \geq f(u) + \langle Df(u), v-u\rangle &\implies f(v) \geq f(u) + \langle Df(u), v \rangle - \langle Df(u), u\rangle \\ &\implies f(v) - \langle Df(u), v\rangle \geq f(u) - \langle Df(u), u\rangle. \end{align*} $$
$$ \begin{align*} f(v) \geq f(u) + \langle Df(u), v-u\rangle &\implies f(v) \geq f(u) + \langle Df(u), v \rangle - \langle Df(u), u\rangle \\ &\implies f(v) - \langle Df(u), v\rangle \geq f(u) - \langle Df(u), u\rangle. \end{align*} $$
Let
![]() $G(v) = f(v) -\langle Df(u), v\rangle .$
Then for all
$G(v) = f(v) -\langle Df(u), v\rangle .$
Then for all
![]() $v \in V,$
$v \in V,$
and when
![]() $v=\bar u,$
$v=\bar u,$
So G attains its minimum at
![]() $v =\bar u,$
i.e.,
$v =\bar u,$
i.e.,
![]() $DG(\bar u)=0.$
Thus,
$DG(\bar u)=0.$
Thus,
Now, we show that
![]() $u=\bar u$
provided that f is strictly convex. Indeed, it follows that
$u=\bar u$
provided that f is strictly convex. Indeed, it follows that
from which we obtain the desired result.
Inspired by an argument in [Reference Moameni22], the following proposition links the critical points of
![]() $I_K$
to the solutions of the system (11).
$I_K$
to the solutions of the system (11).
Proposition 3.2 Let
![]() $\bar u$
be a critical point of the functional
$\bar u$
be a critical point of the functional
![]() $I_K.$
If there exists
$I_K.$
If there exists
![]() $\tilde u\in K$
and
$\tilde u\in K$
and
![]() $\tilde v\in W^{2,q'}(\Omega )\cap W_0^{1, q'}(\Omega ),$
where
$\tilde v\in W^{2,q'}(\Omega )\cap W_0^{1, q'}(\Omega ),$
where
![]() $1/q + 1/q' = 1$
such that
$1/q + 1/q' = 1$
such that
 $$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta \tilde u = a(x)|\tilde v|^{p-2}\tilde v,\\ -\Delta \tilde v = b(x)|\bar u|^{q-2}\bar u, \end{array} \right. \end{align} $$
$$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta \tilde u = a(x)|\tilde v|^{p-2}\tilde v,\\ -\Delta \tilde v = b(x)|\bar u|^{q-2}\bar u, \end{array} \right. \end{align} $$
then
![]() $\bar u=\tilde u$
, and
$\bar u=\tilde u$
, and
![]() $(\tilde u,\tilde v)$
is a solution of
$(\tilde u,\tilde v)$
is a solution of
 $$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta u = a(x)|v|^{p-2}v,\\ -\Delta v = b(x)|u|^{q-2}u. \end{array} \right. \end{align*} $$
$$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta u = a(x)|v|^{p-2}v,\\ -\Delta v = b(x)|u|^{q-2}u. \end{array} \right. \end{align*} $$
Proof Define the functional
![]() $F: W^{2,p'}(\Omega )\cap W_0^{1, p'}(\Omega ) \to \mathbb{R} $
by
$F: W^{2,p'}(\Omega )\cap W_0^{1, p'}(\Omega ) \to \mathbb{R} $
by
 $$ \begin{align*}F(w) = \frac{1}{p'}\int_\Omega \frac{|-\Delta w|^{p'}}{a(x)^{p'-1}} dx - \int_\Omega b(x)|\bar u|^{q-2}\bar u wdx.\end{align*} $$
$$ \begin{align*}F(w) = \frac{1}{p'}\int_\Omega \frac{|-\Delta w|^{p'}}{a(x)^{p'-1}} dx - \int_\Omega b(x)|\bar u|^{q-2}\bar u wdx.\end{align*} $$
We first show that
![]() $\tilde u$
is a critical point of
$\tilde u$
is a critical point of
![]() $F.$
By (22), we have that
$F.$
By (22), we have that
 $$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta \tilde u = a(x)|\tilde v|^{p-2}\tilde v,\\ -\Delta \tilde v = b(x)|\bar u|^{q-2}\bar u. \end{array} \right. \end{align*} $$
$$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta \tilde u = a(x)|\tilde v|^{p-2}\tilde v,\\ -\Delta \tilde v = b(x)|\bar u|^{q-2}\bar u. \end{array} \right. \end{align*} $$
Therefore,
 $$ \begin{align}\left\{ \begin{array}{@{}ll} \tilde v = \frac{1}{a(x)^{p'-1}}|-\Delta \tilde u|^{p'-2}(-\Delta \tilde u),\\ \bar u = \frac{1}{b(x)^{q'-1}}|-\Delta \tilde v|^{q'-2}(-\Delta \tilde v). \end{array} \right. \end{align} $$
$$ \begin{align}\left\{ \begin{array}{@{}ll} \tilde v = \frac{1}{a(x)^{p'-1}}|-\Delta \tilde u|^{p'-2}(-\Delta \tilde u),\\ \bar u = \frac{1}{b(x)^{q'-1}}|-\Delta \tilde v|^{q'-2}(-\Delta \tilde v). \end{array} \right. \end{align} $$
Now, take
![]() $\eta \in W^{2,p'}(\Omega ) \cap W_0^{1,p'}(\Omega ).$
It follows that
$\eta \in W^{2,p'}(\Omega ) \cap W_0^{1,p'}(\Omega ).$
It follows that
 $$ \begin{align*} \langle F'(\tilde u),\eta\rangle &= \int_\Omega \frac{1}{a(x)^{p'-1}}|-\Delta \tilde u|^{p'-2}(-\Delta \tilde u)(-\Delta \eta) dx - \int_\Omega b(x)|\bar u|^{q-2}\bar u \eta dx\\ &= \int_\Omega \tilde v (-\Delta \eta)dx - \int_\Omega b(x)|\bar u|^{q-2} \bar u \eta dx, \qquad (\text{as a result of } (23))\\&= \int_\Omega (-\Delta \tilde v)\eta dx - \int_\Omega b(x)|\bar u|^{q-2}\bar u \eta dx\\ &= \int_\Omega b(x)|\bar u|^{q-2}\bar u \eta dx - \int_\Omega b(x)|\bar u|^{q-2}\bar u \eta dx, \qquad (\text{as a result of } (22))\\&=0. \end{align*} $$
$$ \begin{align*} \langle F'(\tilde u),\eta\rangle &= \int_\Omega \frac{1}{a(x)^{p'-1}}|-\Delta \tilde u|^{p'-2}(-\Delta \tilde u)(-\Delta \eta) dx - \int_\Omega b(x)|\bar u|^{q-2}\bar u \eta dx\\ &= \int_\Omega \tilde v (-\Delta \eta)dx - \int_\Omega b(x)|\bar u|^{q-2} \bar u \eta dx, \qquad (\text{as a result of } (23))\\&= \int_\Omega (-\Delta \tilde v)\eta dx - \int_\Omega b(x)|\bar u|^{q-2}\bar u \eta dx\\ &= \int_\Omega b(x)|\bar u|^{q-2}\bar u \eta dx - \int_\Omega b(x)|\bar u|^{q-2}\bar u \eta dx, \qquad (\text{as a result of } (22))\\&=0. \end{align*} $$
Thus,
![]() $\tilde u$
is a critical point of F. It then follows that
$\tilde u$
is a critical point of F. It then follows that
 $$ \begin{align*} 0&=\langle F'(\tilde u), \tilde u-\bar u\rangle \\&\quad= \int_\Omega \frac{1}{a(x)^{p'-1}}|-\Delta \tilde u|^{p'-2}(-\Delta \tilde u)(-\Delta (\tilde u-\bar u)) dx - \int_\Omega b(x)|\bar u|^{q-2}\bar u (\tilde u-\bar u) dx, \end{align*} $$
$$ \begin{align*} 0&=\langle F'(\tilde u), \tilde u-\bar u\rangle \\&\quad= \int_\Omega \frac{1}{a(x)^{p'-1}}|-\Delta \tilde u|^{p'-2}(-\Delta \tilde u)(-\Delta (\tilde u-\bar u)) dx - \int_\Omega b(x)|\bar u|^{q-2}\bar u (\tilde u-\bar u) dx, \end{align*} $$
from which we obtain
Since
![]() $\bar u$
is a critical point on
$\bar u$
is a critical point on
![]() $I_K,$
by definition of a critical point, we have
$I_K,$
by definition of a critical point, we have
 $$ \begin{align} \frac{1}{p'}\int_\Omega \frac{|-\Delta w|^{p'}}{a(x)^{p'-1}} dx - \frac{1}{p'} \int_\Omega \frac{|-\Delta \bar u|^{p'}}{a(x)^{p'-1}} dx \geq \langle b(x)|\bar u|^{q-2}\bar u, w-\bar u\rangle, \quad \forall w\in K. \end{align} $$
$$ \begin{align} \frac{1}{p'}\int_\Omega \frac{|-\Delta w|^{p'}}{a(x)^{p'-1}} dx - \frac{1}{p'} \int_\Omega \frac{|-\Delta \bar u|^{p'}}{a(x)^{p'-1}} dx \geq \langle b(x)|\bar u|^{q-2}\bar u, w-\bar u\rangle, \quad \forall w\in K. \end{align} $$
Plugging (24) into (25) for
![]() $w = \tilde u,$
we get
$w = \tilde u,$
we get
 $$ \begin{align*}\frac{1}{p'}\int_\Omega \frac{|-\Delta \tilde u|^{p'}}{a(x)^{p'-1}} dx - \frac{1}{p'} \int_\Omega \frac{|-\Delta \bar u|^{p'}}{a(x)^{p'-1}} dx \geq \int_\Omega \frac{1}{a(x)^{p'-1}}|-\Delta \tilde u|^{p'-2}(-\Delta \tilde u)(-\Delta (\tilde u-\bar u)) dx.\end{align*} $$
$$ \begin{align*}\frac{1}{p'}\int_\Omega \frac{|-\Delta \tilde u|^{p'}}{a(x)^{p'-1}} dx - \frac{1}{p'} \int_\Omega \frac{|-\Delta \bar u|^{p'}}{a(x)^{p'-1}} dx \geq \int_\Omega \frac{1}{a(x)^{p'-1}}|-\Delta \tilde u|^{p'-2}(-\Delta \tilde u)(-\Delta (\tilde u-\bar u)) dx.\end{align*} $$
Thus, by Lemma 3.1, we obtain
The result now follows from (22) considering
![]() $\tilde u = \bar u.$
$\tilde u = \bar u.$
So far, we have considered K to be a weakly closed convex subset of
![]() $W^{2, p'}(\Omega )$
which is compactly embedded in
$W^{2, p'}(\Omega )$
which is compactly embedded in
![]() $L^q(\Omega ).$
Now, we explicitly define our convex set K to be given by
$L^q(\Omega ).$
Now, we explicitly define our convex set K to be given by
where
![]() $W_G^{2,p'}(\Omega ) :=\{u \in W^{2, p'}(\Omega ): gu = u, \quad \forall g \in G\}$
where
$W_G^{2,p'}(\Omega ) :=\{u \in W^{2, p'}(\Omega ): gu = u, \quad \forall g \in G\}$
where
![]() $G:= O(m) \times O(n).$
Here,
$G:= O(m) \times O(n).$
Here,
![]() $O(k)$
is the orthogonal group in
$O(k)$
is the orthogonal group in
![]() $\mathbb{R} ^k$
with
$\mathbb{R} ^k$
with
![]() $gu(x):=u(g^{-1}x).$
We remind the reader that we can express K as functions u such that if we write
$gu(x):=u(g^{-1}x).$
We remind the reader that we can express K as functions u such that if we write
![]() $(s,t)$
in terms of polar coordinates, we have
$(s,t)$
in terms of polar coordinates, we have
![]() $u_\theta \leq 0$
on
$u_\theta \leq 0$
on
![]() $\widetilde \Omega $
defined in (10). Before we introduce the embedding theorem for annular domains, for the convenience of the reader, we recall the following standard embedding theorem for which we make frequent use in this paper.
$\widetilde \Omega $
defined in (10). Before we introduce the embedding theorem for annular domains, for the convenience of the reader, we recall the following standard embedding theorem for which we make frequent use in this paper.
Theorem 3.2 Let
![]() $\mathcal {O}$
be a bounded domain in
$\mathcal {O}$
be a bounded domain in
![]() $\mathbb{R} ^k.$
Let
$\mathbb{R} ^k.$
Let
![]() $j \geq 1$
be an integer, and let
$j \geq 1$
be an integer, and let
![]() ${1\leq \mathcal {P} < \infty .}$
Suppose
${1\leq \mathcal {P} < \infty .}$
Suppose
![]() $\mathcal {O}$
satisfies the cone condition. Then the following embeddings are compact:
$\mathcal {O}$
satisfies the cone condition. Then the following embeddings are compact:
-
(i) If
 $j \mathcal {P}< k,$
then
$j \mathcal {P}< k,$
then  $$ \begin{align*}W^{j,\mathcal{P}}(\mathcal{O}) \hookrightarrow L^d(\mathcal{O}), \quad \text{ for } 1\leq d < \mathcal{P}^*=k\mathcal{P}/(k-j\mathcal{P}).\end{align*} $$
$$ \begin{align*}W^{j,\mathcal{P}}(\mathcal{O}) \hookrightarrow L^d(\mathcal{O}), \quad \text{ for } 1\leq d < \mathcal{P}^*=k\mathcal{P}/(k-j\mathcal{P}).\end{align*} $$
-
(ii) If
 $j\mathcal {P} \geq k,$
then
$j\mathcal {P} \geq k,$
then  $$ \begin{align*}W^{j,\mathcal{P}}(\mathcal{O}) \hookrightarrow L^d(\mathcal{O}), \quad \text{ for } 1\leq d< \infty.\end{align*} $$
$$ \begin{align*}W^{j,\mathcal{P}}(\mathcal{O}) \hookrightarrow L^d(\mathcal{O}), \quad \text{ for } 1\leq d< \infty.\end{align*} $$
Theorem 3.3 Let
![]() $\Omega \subset \mathbb{R} ^N=\mathbb{R} ^{m+n}$
be an annular domain of double revolution.
$\Omega \subset \mathbb{R} ^N=\mathbb{R} ^{m+n}$
be an annular domain of double revolution.
-
(i) (Embedding without monotonicity). Let
 $\mathcal {P}>1.$
Suppose
$\mathcal {P}>1.$
Suppose
 $\Omega $
has no monotonicity and Then the embedding
$\Omega $
has no monotonicity and Then the embedding $$ \begin{align*}1 \leq d < \min\left\{\frac{(m+1)\mathcal{P}}{(m+1)-2\mathcal{P}},\frac{(n+1)\mathcal{P}}{(n+1)-2\mathcal{P}}\right\}.\end{align*} $$
$$ \begin{align*}1 \leq d < \min\left\{\frac{(m+1)\mathcal{P}}{(m+1)-2\mathcal{P}},\frac{(n+1)\mathcal{P}}{(n+1)-2\mathcal{P}}\right\}.\end{align*} $$
 $W_{G}^{2,\mathcal {P}}(\Omega ) \hookrightarrow L^d(\Omega )$
is compact with the obvious interpretation if
$W_{G}^{2,\mathcal {P}}(\Omega ) \hookrightarrow L^d(\Omega )$
is compact with the obvious interpretation if
 $(m+1)-2\mathcal {P} \leq 0$
and
$(m+1)-2\mathcal {P} \leq 0$
and
 $(n+1)-2\mathcal {P} \leq 0.$
$(n+1)-2\mathcal {P} \leq 0.$
-
(ii) (Embedding with monotonicity). Let
 $p'>1$
and suppose
$p'>1$
and suppose
 $\Omega $
is a domain of double revolution with monotonicity,
$\Omega $
is a domain of double revolution with monotonicity,
 $n\leq m$
and In addition, let
$n\leq m$
and In addition, let $$ \begin{align*}1 \leq d < \frac{(n+1)p'}{(n+1)-2p'} = \max\left\{\frac{(m+1)p'}{(m+1)-2p'},\frac{(n+1)p'}{(n+1)-2p'}\right\}.\end{align*} $$
Then the embedding
$$ \begin{align*}1 \leq d < \frac{(n+1)p'}{(n+1)-2p'} = \max\left\{\frac{(m+1)p'}{(m+1)-2p'},\frac{(n+1)p'}{(n+1)-2p'}\right\}.\end{align*} $$
Then the embedding $$ \begin{align*}K:=\left\{0\leq u=u(s,t) \in W_{G}^{2,p'}(\Omega)\cap W_0^{1,p'}(\Omega): su_t - tu_s \leq 0 \text{ a.e. in } \widehat \Omega\right\}.\end{align*} $$
$$ \begin{align*}K:=\left\{0\leq u=u(s,t) \in W_{G}^{2,p'}(\Omega)\cap W_0^{1,p'}(\Omega): su_t - tu_s \leq 0 \text{ a.e. in } \widehat \Omega\right\}.\end{align*} $$
 $K \hookrightarrow L^d(\Omega )$
is compact with the obvious interpretation if
$K \hookrightarrow L^d(\Omega )$
is compact with the obvious interpretation if
 $(n+1)-2p' \leq 0.$
$(n+1)-2p' \leq 0.$
Proof We begin by proving
![]() $(i).$
Assume that
$(i).$
Assume that
![]() $N=m+n.$
Then, expressing in terms of s and
$N=m+n.$
Then, expressing in terms of s and
![]() $t,$
i.e.,
$t,$
i.e.,
![]() $u(x) = u(s,t),$
we obtain
$u(x) = u(s,t),$
we obtain
Take
![]() $\delta $
small enough so that
$\delta $
small enough so that
![]() $t\geq \delta $
if and only if
$t\geq \delta $
if and only if
![]() $s \leq \delta .$
So
$s \leq \delta .$
So
 $$ \begin{align}&\int_{\widehat \Omega}|u(s,t)|^d s^{m-1}t^{n-1} dsdt \\&\quad= \int_{\{\widehat \Omega, t\geq \delta\}} |u(s,t)|^d s^{m-1}t^{n-1} dsdt + \int_{\{\widehat \Omega, s\geq \delta\}} |u(s,t)|^d s^{m-1}t^{n-1} dsdt.\nonumber\end{align} $$
$$ \begin{align}&\int_{\widehat \Omega}|u(s,t)|^d s^{m-1}t^{n-1} dsdt \\&\quad= \int_{\{\widehat \Omega, t\geq \delta\}} |u(s,t)|^d s^{m-1}t^{n-1} dsdt + \int_{\{\widehat \Omega, s\geq \delta\}} |u(s,t)|^d s^{m-1}t^{n-1} dsdt.\nonumber\end{align} $$
Looking at the first term on the right-hand side of (27),
Let
![]() $u(s,t) = u(y,z),$
where
$u(s,t) = u(y,z),$
where
![]() $s=|y|$
and
$s=|y|$
and
![]() $t=|z|.$
Then by change of variables,
$t=|z|.$
Then by change of variables,
where
![]() $\Omega _1 =\{(y,t): (|y|,t)\in \widehat \Omega \}\in \mathbb{R} ^m \times \mathbb{R} .$
Note that
$\Omega _1 =\{(y,t): (|y|,t)\in \widehat \Omega \}\in \mathbb{R} ^m \times \mathbb{R} .$
Note that
![]() $\Omega _1 \subset \mathbb{R} ^{m+1}.$
If
$\Omega _1 \subset \mathbb{R} ^{m+1}.$
If
 $$ \begin{align*}d < \frac{(m+1)\mathcal{P}}{(m+1)-2\mathcal{P}},\end{align*} $$
$$ \begin{align*}d < \frac{(m+1)\mathcal{P}}{(m+1)-2\mathcal{P}},\end{align*} $$
then by Theorem 3.2,
 $$ \begin{align*} \Big(\int_{\Omega_1} |u(y,t)|^d dydt\Big)^{\mathcal{P}/d} &\leq c_2 \|u\|^{\mathcal{P}}_{W^{2,\mathcal{P}}(\Omega_1)}\\ &\leq c_3 \int_{\Omega_1} \Big(|D^2 u(y,t)|^{\mathcal{P}}+|\nabla u(y,t)|^{\mathcal{P}} + |u(y,t)|^{\mathcal{P}}\Big)t^{n-1}dydt\\ &\leq c_4 \int_\Omega \Big(|D^2 u(y,z)|^{\mathcal{P}}+|\nabla u(y,z)|^{\mathcal{P}} + |u(y,z)|^{\mathcal{P}}\Big) dydz\\ &= c_4 \|u\|_{W^{2,\mathcal{P}}(\Omega)}^{\mathcal{P}}. \end{align*} $$
$$ \begin{align*} \Big(\int_{\Omega_1} |u(y,t)|^d dydt\Big)^{\mathcal{P}/d} &\leq c_2 \|u\|^{\mathcal{P}}_{W^{2,\mathcal{P}}(\Omega_1)}\\ &\leq c_3 \int_{\Omega_1} \Big(|D^2 u(y,t)|^{\mathcal{P}}+|\nabla u(y,t)|^{\mathcal{P}} + |u(y,t)|^{\mathcal{P}}\Big)t^{n-1}dydt\\ &\leq c_4 \int_\Omega \Big(|D^2 u(y,z)|^{\mathcal{P}}+|\nabla u(y,z)|^{\mathcal{P}} + |u(y,z)|^{\mathcal{P}}\Big) dydz\\ &= c_4 \|u\|_{W^{2,\mathcal{P}}(\Omega)}^{\mathcal{P}}. \end{align*} $$
So we have the compact embedding
![]() $W_{G}^{2,\mathcal {P}}(\Omega ) \hookrightarrow L^d(\Omega )$
for
$W_{G}^{2,\mathcal {P}}(\Omega ) \hookrightarrow L^d(\Omega )$
for
 $$ \begin{align*}d< \frac{(m+1)\mathcal{P}}{(m+1)-2\mathcal{P}}.\end{align*} $$
$$ \begin{align*}d< \frac{(m+1)\mathcal{P}}{(m+1)-2\mathcal{P}}.\end{align*} $$
For the second term on the right-hand side of (27), we have that
 $$ \begin{align*} \int_{\{\widehat \Omega, s\geq \delta\}} |u(s,t)|^d s^{m-1}t^{n-1} dsdt &\leq c'_1 \int_{\widehat \Omega} |u(s,t)|^dt^{n-1} dsdt\\ &=c_1^{"}\int_{\Omega_2}|u(s,z)|^d dsdz, \end{align*} $$
$$ \begin{align*} \int_{\{\widehat \Omega, s\geq \delta\}} |u(s,t)|^d s^{m-1}t^{n-1} dsdt &\leq c'_1 \int_{\widehat \Omega} |u(s,t)|^dt^{n-1} dsdt\\ &=c_1^{"}\int_{\Omega_2}|u(s,z)|^d dsdz, \end{align*} $$
where
![]() $\Omega _2 = \{(s,z): (s,|z|)\in \widehat \Omega \} \in \mathbb{R} ^n \times \mathbb{R} .$
Note that
$\Omega _2 = \{(s,z): (s,|z|)\in \widehat \Omega \} \in \mathbb{R} ^n \times \mathbb{R} .$
Note that
![]() $\Omega _2 \subset \mathbb{R} ^{n+1}.$
If
$\Omega _2 \subset \mathbb{R} ^{n+1}.$
If
 $$ \begin{align*}d< \frac{(n+1)\mathcal{P}}{(n+1)-2\mathcal{P}},\end{align*} $$
$$ \begin{align*}d< \frac{(n+1)\mathcal{P}}{(n+1)-2\mathcal{P}},\end{align*} $$
then by Theorem 3.2,
 $$ \begin{align*} \Big(\int_{\Omega_2} |u(s,z)|^d dsdz\Big)^{\mathcal{P}/d} &\leq c'_2 \|u\|^{\mathcal{P}}_{W^{2,\mathcal{P}}(\Omega_2)} \\ &\leq c'_3 \int_{\Omega_2}\Big(|D^2 u(s,z)|^{\mathcal{P}}+|\nabla u(s,z)|^{\mathcal{P}} + |u(s,z)|^{\mathcal{P}}\Big)s^{m-1}dsdz\\ &\leq c'_4 \int_\Omega \Big(|D^2u(y,z)|^{\mathcal{P}}+|\nabla u(y,z)|^{\mathcal{P}} + |u(y,z)|^{\mathcal{P}}\Big) dydz\\ &= c'_4 \|u\|_{W^{2,\mathcal{P}}(\Omega)}^{\mathcal{P}}. \end{align*} $$
$$ \begin{align*} \Big(\int_{\Omega_2} |u(s,z)|^d dsdz\Big)^{\mathcal{P}/d} &\leq c'_2 \|u\|^{\mathcal{P}}_{W^{2,\mathcal{P}}(\Omega_2)} \\ &\leq c'_3 \int_{\Omega_2}\Big(|D^2 u(s,z)|^{\mathcal{P}}+|\nabla u(s,z)|^{\mathcal{P}} + |u(s,z)|^{\mathcal{P}}\Big)s^{m-1}dsdz\\ &\leq c'_4 \int_\Omega \Big(|D^2u(y,z)|^{\mathcal{P}}+|\nabla u(y,z)|^{\mathcal{P}} + |u(y,z)|^{\mathcal{P}}\Big) dydz\\ &= c'_4 \|u\|_{W^{2,\mathcal{P}}(\Omega)}^{\mathcal{P}}. \end{align*} $$
So we have the embedding
![]() $W_G^{2,\mathcal {P}}(\Omega ) \hookrightarrow L^d(\Omega )$
is compact for
$W_G^{2,\mathcal {P}}(\Omega ) \hookrightarrow L^d(\Omega )$
is compact for
 $$ \begin{align*}d< \frac{(n+1)\mathcal{P}}{(n+1)-2\mathcal{P}}.\end{align*} $$
$$ \begin{align*}d< \frac{(n+1)\mathcal{P}}{(n+1)-2\mathcal{P}}.\end{align*} $$
Taking
 $$ \begin{align*}\min\left\{\frac{(m+1)\mathcal{P}}{(m+1)-2\mathcal{P}},\frac{(n+1)\mathcal{P}}{(n+1)-2\mathcal{P}}\right\},\end{align*} $$
$$ \begin{align*}\min\left\{\frac{(m+1)\mathcal{P}}{(m+1)-2\mathcal{P}},\frac{(n+1)\mathcal{P}}{(n+1)-2\mathcal{P}}\right\},\end{align*} $$
we obtain the desired result in part (i). Now, we proceed with proving part
![]() $(ii).$
Let
$(ii).$
Let
![]() $1\leq n \leq m$
and
$1\leq n \leq m$
and
 $$ \begin{align*}d < \frac{(n+1)p'}{(n+1)-2p'}.\end{align*} $$
$$ \begin{align*}d < \frac{(n+1)p'}{(n+1)-2p'}.\end{align*} $$
Using polar coordinates with
![]() $s=r\cos (\theta )$
and
$s=r\cos (\theta )$
and
![]() $t=r\sin (\theta ),$
we obtain
$t=r\sin (\theta ),$
we obtain
 $$ \begin{align*}\int_{\widehat \Omega} u(s,t)^d s^{m-1}t^{n-1} dsdt = \int_0^{\pi/2}\int_{g_1}^{g_2} r^{m-1}\cos^{m-1}(\theta)r^{n-1}\sin^{n-1}(\theta)u(r,\theta)^drdrd\theta.\end{align*} $$
$$ \begin{align*}\int_{\widehat \Omega} u(s,t)^d s^{m-1}t^{n-1} dsdt = \int_0^{\pi/2}\int_{g_1}^{g_2} r^{m-1}\cos^{m-1}(\theta)r^{n-1}\sin^{n-1}(\theta)u(r,\theta)^drdrd\theta.\end{align*} $$
For
![]() $\theta \in [\pi /3, \pi /2]$
, we have that
$\theta \in [\pi /3, \pi /2]$
, we have that
![]() $\sin (\theta ) \leq c\sin (\theta -\pi /4)$
for some constant
$\sin (\theta ) \leq c\sin (\theta -\pi /4)$
for some constant
![]() $c>0.$
According to the monotonicity properties of
$c>0.$
According to the monotonicity properties of
![]() $g_1, g_2$
and
$g_1, g_2$
and
![]() $\theta \mapsto u(r,\theta ),$
we obtain that
$\theta \mapsto u(r,\theta ),$
we obtain that
 $$ \begin{align*} &\int_{\pi/3}^{\pi/2}\int_{g_1(\theta)}^{g_2(\theta)} r^{m-1}\cos^{m-1}(\theta)r^{n-1}\sin^{n-1}u(r,\theta)^d rdrd\theta\\ &\leq c^{n-1} \int_{\pi/3}^{\pi/2}\int_{g_1(\theta-\pi/4)}^{g_2(\theta-\pi/4)}r^{m-1}\cos^{m-1}(\theta-\pi/4)r^{n-1}\sin^{n-1}(\theta-\pi/4)u(r,\theta-\pi/4)^drdrd\theta\\ &=c^{n-1}\int_{\pi/12}^{\pi/4}\int_{g_1(\theta)}^{g_2(\theta)} r^{m-1}\cos^{m-1}(\theta)r^{n-1}\sin^{n-1}(\theta)u(r,\theta)^drdrd\theta. \end{align*} $$
$$ \begin{align*} &\int_{\pi/3}^{\pi/2}\int_{g_1(\theta)}^{g_2(\theta)} r^{m-1}\cos^{m-1}(\theta)r^{n-1}\sin^{n-1}u(r,\theta)^d rdrd\theta\\ &\leq c^{n-1} \int_{\pi/3}^{\pi/2}\int_{g_1(\theta-\pi/4)}^{g_2(\theta-\pi/4)}r^{m-1}\cos^{m-1}(\theta-\pi/4)r^{n-1}\sin^{n-1}(\theta-\pi/4)u(r,\theta-\pi/4)^drdrd\theta\\ &=c^{n-1}\int_{\pi/12}^{\pi/4}\int_{g_1(\theta)}^{g_2(\theta)} r^{m-1}\cos^{m-1}(\theta)r^{n-1}\sin^{n-1}(\theta)u(r,\theta)^drdrd\theta. \end{align*} $$
Thus, there is a constant
![]() $C_1>0$
such that
$C_1>0$
such that
 $$ \begin{align*}&\int_0^{\pi/2}\int_{g_1}^{g_2}r^{m-1}\cos^{m-1}(\theta)r^{n-1}\sin^{n-1}(\theta)u(r,\theta)^drdrd\theta \\&\quad\leq C_1\int_0^{\pi/3}\int_{g_1}^{g_2}r^{m-1}\cos^{m-1}(\theta)r^{n-1}\sin^{n-1}(\theta)u(r,\theta)^drdrd\theta.\end{align*} $$
$$ \begin{align*}&\int_0^{\pi/2}\int_{g_1}^{g_2}r^{m-1}\cos^{m-1}(\theta)r^{n-1}\sin^{n-1}(\theta)u(r,\theta)^drdrd\theta \\&\quad\leq C_1\int_0^{\pi/3}\int_{g_1}^{g_2}r^{m-1}\cos^{m-1}(\theta)r^{n-1}\sin^{n-1}(\theta)u(r,\theta)^drdrd\theta.\end{align*} $$
On the other hand,
 $$ \begin{align*}\int_0^{\pi/3}\int_{g_1}^{g_2}r^{m-1}\cos^{m-1}(\theta)r^{n-1}\sin^{n-1}(\theta)u(r,\theta)^drdrd\theta = \int_{\{\widehat \Omega, s\geq \beta\}}u(s,t)^ds^{m-1}t^{n-1}dsdt\end{align*} $$
$$ \begin{align*}\int_0^{\pi/3}\int_{g_1}^{g_2}r^{m-1}\cos^{m-1}(\theta)r^{n-1}\sin^{n-1}(\theta)u(r,\theta)^drdrd\theta = \int_{\{\widehat \Omega, s\geq \beta\}}u(s,t)^ds^{m-1}t^{n-1}dsdt\end{align*} $$
for some positive constant
![]() $\beta .$
Hence,
$\beta .$
Hence,
 $$ \begin{align*}\Big(\int_{\{\widehat \Omega, s\geq \beta\}}u(s,t)^ds^{m-1}t^{n-1}dsdt\Big)^{p'/d} \leq C_2 \Big(\int_{\{\widehat \Omega, s\geq \beta\}}u(s,t)^dt^{n-1}dsdt\Big)^{p'/d}.\end{align*} $$
$$ \begin{align*}\Big(\int_{\{\widehat \Omega, s\geq \beta\}}u(s,t)^ds^{m-1}t^{n-1}dsdt\Big)^{p'/d} \leq C_2 \Big(\int_{\{\widehat \Omega, s\geq \beta\}}u(s,t)^dt^{n-1}dsdt\Big)^{p'/d}.\end{align*} $$
Thus, by part
![]() $(i),$
we have
$(i),$
we have
 $$ \begin{align*} &\Big(\int_{\{\widehat \Omega, s\geq \beta\}}u(s,t)^dt^{n-1}dsdt\Big)^{p'/d} \\&\quad\leq C_3\int_{\{\widehat \Omega, s\geq \beta\}}\Big(|D^2 u(s,t)|^{p'}+|\nabla u(s,t)|^{p'} + |u(s,t)|^{p'}\Big)t^{n-1}dsdt\\ &\quad\leq C_4 \int_{\{\widehat \Omega, s\geq \beta\}}\Big(|D^2 u(s,t)|^{p'}+|\nabla u(s,t)|^{p'} + |u(s,t)|^{p'}\Big)t^{n-1}s^{m-1}dsdt\\ &\quad\leq C_5\int_{\widehat \Omega}\Big(|D^2 u(s,t)|^{p'}+|\nabla u(s,t)|^{p'} + |u(s,t)|^{p'}\Big)t^{n-1}s^{m-1}dsdt\\ &\quad= C_6 \int_\Omega \Big(|D^2 u|^{p'}+|\nabla u|^{p'} + |u|^{p'}\Big) dx \\ &\quad= C_6 \|u\|_{W^{2,{p'}}(\Omega)}^{p'}. \end{align*} $$
$$ \begin{align*} &\Big(\int_{\{\widehat \Omega, s\geq \beta\}}u(s,t)^dt^{n-1}dsdt\Big)^{p'/d} \\&\quad\leq C_3\int_{\{\widehat \Omega, s\geq \beta\}}\Big(|D^2 u(s,t)|^{p'}+|\nabla u(s,t)|^{p'} + |u(s,t)|^{p'}\Big)t^{n-1}dsdt\\ &\quad\leq C_4 \int_{\{\widehat \Omega, s\geq \beta\}}\Big(|D^2 u(s,t)|^{p'}+|\nabla u(s,t)|^{p'} + |u(s,t)|^{p'}\Big)t^{n-1}s^{m-1}dsdt\\ &\quad\leq C_5\int_{\widehat \Omega}\Big(|D^2 u(s,t)|^{p'}+|\nabla u(s,t)|^{p'} + |u(s,t)|^{p'}\Big)t^{n-1}s^{m-1}dsdt\\ &\quad= C_6 \int_\Omega \Big(|D^2 u|^{p'}+|\nabla u|^{p'} + |u|^{p'}\Big) dx \\ &\quad= C_6 \|u\|_{W^{2,{p'}}(\Omega)}^{p'}. \end{align*} $$
This completes the proof.
Remark 3.4 Let
![]() $p>1$
, and let
$p>1$
, and let
![]() $p'$
be the conjugate of
$p'$
be the conjugate of
![]() $p,$
that is,
$p,$
that is,
Suppose
![]() $\Omega $
is an annular domain with monotonicity, and
$\Omega $
is an annular domain with monotonicity, and
![]() $n\leq m.$
We can rewrite the condition in Theorem 3.3(ii) given by
$n\leq m.$
We can rewrite the condition in Theorem 3.3(ii) given by
 $$ \begin{align*} 1\leq d < \frac{(n+1)p'}{(n+1)-2p'} = \max\left\{\frac{(m+1)p'}{(m+1)-2p'}, \frac{(n+1)p'}{(n+1)-2p'}\right\}, \quad &\text{ for } n>2p'-1,\\ 1\leq d < \infty, \quad &\text{ for } n\leq 2p'-1, \end{align*} $$
$$ \begin{align*} 1\leq d < \frac{(n+1)p'}{(n+1)-2p'} = \max\left\{\frac{(m+1)p'}{(m+1)-2p'}, \frac{(n+1)p'}{(n+1)-2p'}\right\}, \quad &\text{ for } n>2p'-1,\\ 1\leq d < \infty, \quad &\text{ for } n\leq 2p'-1, \end{align*} $$
as follows:
 $$ \begin{align*} \frac{1}{p}+\frac{1}{d}> 1-\frac{2}{n+1}=\min\left\{1-\frac{2}{m+1}, 1-\frac{2}{n+1}\right\}, \quad &\text{ for } n>\frac{p+1}{p-1},\\ \text{no lower bound condition imposed on } \frac{1}{p}+\frac{1}{d}, \quad &\text{ for } n\leq \frac{p+1}{p-1}. \end{align*} $$
$$ \begin{align*} \frac{1}{p}+\frac{1}{d}> 1-\frac{2}{n+1}=\min\left\{1-\frac{2}{m+1}, 1-\frac{2}{n+1}\right\}, \quad &\text{ for } n>\frac{p+1}{p-1},\\ \text{no lower bound condition imposed on } \frac{1}{p}+\frac{1}{d}, \quad &\text{ for } n\leq \frac{p+1}{p-1}. \end{align*} $$
Proof By Theorem 3.3
![]() $(ii)$
, we have compactness when
$(ii)$
, we have compactness when
 $$ \begin{align*}1\leq d < \frac{(n+1)p'}{(n+1)-2p'} = \max\left\{\frac{(m+1)p'}{(m+1)-2p'},\frac{(n+1)p'}{(n+1)-2p'}\right\}, \quad \text{ for } n+1-2p'>0,\end{align*} $$
$$ \begin{align*}1\leq d < \frac{(n+1)p'}{(n+1)-2p'} = \max\left\{\frac{(m+1)p'}{(m+1)-2p'},\frac{(n+1)p'}{(n+1)-2p'}\right\}, \quad \text{ for } n+1-2p'>0,\end{align*} $$
and
Equivalently,
 $$ \begin{align*}1\leq d < \frac{(n+1)p}{(n+1)(p-1)-2p}, \quad \text{ for } (n+1)(p-1)-2p>0,\end{align*} $$
$$ \begin{align*}1\leq d < \frac{(n+1)p}{(n+1)(p-1)-2p}, \quad \text{ for } (n+1)(p-1)-2p>0,\end{align*} $$
and
Simplifying, we obtain
and with no lower bound condition on
![]() $1/p+1/d$
for
$1/p+1/d$
for
![]() $(n+1)(p-1)-2p \leq 0.$
On the other hand,
$(n+1)(p-1)-2p \leq 0.$
On the other hand,
Therefore, we conclude that
 $$ \begin{align*} \frac{1}{p}+\frac{1}{d}> 1-\frac{2}{n+1}=\min\left\{1-\frac{2}{m+1},1-\frac{2}{n+1}\right\}, \quad &\text{ for } n > \frac{p+1}{p-1},\\ \text{ no lower bound condition imposed on } \frac{1}{p}+\frac{1}{d}, \quad &\text{ for } n\leq \frac{p+1}{p-1}. \\[-40pt]\end{align*} $$
$$ \begin{align*} \frac{1}{p}+\frac{1}{d}> 1-\frac{2}{n+1}=\min\left\{1-\frac{2}{m+1},1-\frac{2}{n+1}\right\}, \quad &\text{ for } n > \frac{p+1}{p-1},\\ \text{ no lower bound condition imposed on } \frac{1}{p}+\frac{1}{d}, \quad &\text{ for } n\leq \frac{p+1}{p-1}. \\[-40pt]\end{align*} $$
We require the following proposition arising from Cowan and Moameni in [Reference Cowan and Moameni11].
Proposition 3.3 Suppose
![]() $\Omega \subset \mathbb{R} ^m \times \mathbb{R} ^n$
is an annular domain with monotonicity (see Definition 2.2), and assume that
$\Omega \subset \mathbb{R} ^m \times \mathbb{R} ^n$
is an annular domain with monotonicity (see Definition 2.2), and assume that
![]() $\kappa (x)$
satisfies (
$\kappa (x)$
satisfies (
![]() $\mathcal {A}$
) as in Definition 2.3. Let
$\mathcal {A}$
) as in Definition 2.3. Let
![]() $0 \leq \tilde u\in H_{0,G}^1(\Omega )\cap L^{\mathcal {P}}(\Omega )$
with
$0 \leq \tilde u\in H_{0,G}^1(\Omega )\cap L^{\mathcal {P}}(\Omega )$
with
![]() $s\tilde u_t - t\tilde u_s \leq 0$
a.e. on
$s\tilde u_t - t\tilde u_s \leq 0$
a.e. on
![]() $\widehat \Omega $
where
$\widehat \Omega $
where
![]() $\mathcal {P}>2,$
and
$\mathcal {P}>2,$
and
Suppose that
![]() $\tilde v$
is the solution of
$\tilde v$
is the solution of
 $$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta \tilde v = \kappa(x) \tilde u^{\mathcal{P}-1}, &\quad \text{ in } \Omega,\\ \tilde v = 0, &\quad \text { on } \partial \Omega. \end{array} \right. \end{align*} $$
$$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta \tilde v = \kappa(x) \tilde u^{\mathcal{P}-1}, &\quad \text{ in } \Omega,\\ \tilde v = 0, &\quad \text { on } \partial \Omega. \end{array} \right. \end{align*} $$
Then
![]() $0\leq \tilde v\in H_{0,G}^1(\Omega )\cap L^{\mathcal {P}}(\Omega )$
with
$0\leq \tilde v\in H_{0,G}^1(\Omega )\cap L^{\mathcal {P}}(\Omega )$
with
![]() $s\tilde v_t - t\tilde v_s \leq 0$
a.e. on
$s\tilde v_t - t\tilde v_s \leq 0$
a.e. on
![]() $\widehat \Omega .$
$\widehat \Omega .$
Now, we can prove the first main result of the paper.
Proof of Theorem 1.1.
First, we recall the convex cone
![]() $K:=K(m,n)$
as in (26), namely,
$K:=K(m,n)$
as in (26), namely,
where
![]() $W_G^{2,p'}(\Omega ) :=\{u \in W^{2, p'}(\Omega ): gu = u, \quad \forall g \in G\},$
where
$W_G^{2,p'}(\Omega ) :=\{u \in W^{2, p'}(\Omega ): gu = u, \quad \forall g \in G\},$
where
![]() $G:= O(m) \times O(n)$
, and where
$G:= O(m) \times O(n)$
, and where
![]() $O(k)$
is the orthogonal group in
$O(k)$
is the orthogonal group in
![]() $\mathbb{R} ^k$
with
$\mathbb{R} ^k$
with
![]() $gu(x):=u(g^{-1}x).$
By Theorem 3.3
$gu(x):=u(g^{-1}x).$
By Theorem 3.3
![]() $(ii)$
, we have that the embedding
$(ii)$
, we have that the embedding
![]() $K\hookrightarrow L^q(\Omega )$
is compact for
$K\hookrightarrow L^q(\Omega )$
is compact for
 $$ \begin{align*} 1\leq q < \frac{(n+1)-p'}{(n+1)-2p'}, \quad &\text{ if } (n+1)-2p'>0,\\ 1\leq q < \infty, \quad &\text{ if } (n+1)-2p' \leq 0. \end{align*} $$
$$ \begin{align*} 1\leq q < \frac{(n+1)-p'}{(n+1)-2p'}, \quad &\text{ if } (n+1)-2p'>0,\\ 1\leq q < \infty, \quad &\text{ if } (n+1)-2p' \leq 0. \end{align*} $$
By Remark 3.4, this can be rewritten as
with no condition on the lower bound of
It follows from Proposition 3.1 that
![]() $I_K$
has a critical point
$I_K$
has a critical point
![]() $\bar u$
in K with
$\bar u$
in K with
![]() $I_K(\bar u)=c,$
where
$I_K(\bar u)=c,$
where
![]() $c>0$
is the critical value characterized by
$c>0$
is the critical value characterized by
where
![]() $\Gamma = \{\gamma \in C([0,1], V): \gamma (0) = 0, \gamma (1) = e, I_K(\gamma (1))\leq 0.\}$
Since
$\Gamma = \{\gamma \in C([0,1], V): \gamma (0) = 0, \gamma (1) = e, I_K(\gamma (1))\leq 0.\}$
Since
![]() $I_K(\bar u)>0,$
it follows that
$I_K(\bar u)>0,$
it follows that
![]() $\bar u$
is nonzero. Now, we want to show that there exists
$\bar u$
is nonzero. Now, we want to show that there exists
![]() $\tilde u\in K$
and
$\tilde u\in K$
and
![]() $\tilde v \in W^{2,q'}(\Omega )\cap W_0^{1,q}(\Omega )$
satisfying
$\tilde v \in W^{2,q'}(\Omega )\cap W_0^{1,q}(\Omega )$
satisfying
 $$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta \tilde u = a(x)|\tilde v|^{p-2}\tilde v,\\ -\Delta \tilde v = b(x)|\bar u|^{q-2}\bar u, \end{array} \right. \end{align*} $$
$$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta \tilde u = a(x)|\tilde v|^{p-2}\tilde v,\\ -\Delta \tilde v = b(x)|\bar u|^{q-2}\bar u, \end{array} \right. \end{align*} $$
so that we can conclude by Proposition 3.2 that
![]() $(\tilde u, \tilde v)$
is a solution of
$(\tilde u, \tilde v)$
is a solution of
 $$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta u = a(x)|v|^{p-2}v,\\ -\Delta v = b(x)|u|^{q-2}u. \end{array} \right. \end{align*} $$
$$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta u = a(x)|v|^{p-2}v,\\ -\Delta v = b(x)|u|^{q-2}u. \end{array} \right. \end{align*} $$
Indeed, it follows from Proposition 3.3 that there exists
![]() $\tilde v \in K$
such that
$\tilde v \in K$
such that
Applying Proposition 3.3 once again, there exists
![]() $\tilde u \in K$
satisfying
$\tilde u \in K$
satisfying
Thus,
![]() $(\tilde u, \tilde v)$
satisfies the equation
$(\tilde u, \tilde v)$
satisfies the equation
 $$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta \tilde u = a(x)|\tilde v|^{p-2}\tilde v,\\ -\Delta \tilde v = b(x)|\bar u|^{q-2}\bar u, \end{array} \right. \end{align*} $$
$$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta \tilde u = a(x)|\tilde v|^{p-2}\tilde v,\\ -\Delta \tilde v = b(x)|\bar u|^{q-2}\bar u, \end{array} \right. \end{align*} $$
and by Proposition 3.2, we conclude that
![]() $(\tilde u, \tilde v)$
is a solution of
$(\tilde u, \tilde v)$
is a solution of
 $$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta u = a(x)|v|^{p-2}v,\\ -\Delta v = b(x)|u|^{q-2}u. \end{array} \right. \end{align*} $$
$$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta u = a(x)|v|^{p-2}v,\\ -\Delta v = b(x)|u|^{q-2}u. \end{array} \right. \end{align*} $$
Note that both
![]() $\tilde u $
and
$\tilde u $
and
![]() $\tilde v $
are nonzero and nonnegative. It now follows from the strong maximum principle [Reference Gilbarg and Trudinger15, Theorem 8.19] that both
$\tilde v $
are nonzero and nonnegative. It now follows from the strong maximum principle [Reference Gilbarg and Trudinger15, Theorem 8.19] that both
![]() $\tilde u$
and
$\tilde u$
and
![]() $\tilde v$
are strictly positive.
$\tilde v$
are strictly positive.
4 Non-radial solutions when
 $\Omega $
is an annulus
$\Omega $
is an annulus
In this section, we discuss the case when
![]() $a(x)=b(x)=1$
, and
$a(x)=b(x)=1$
, and
![]() $\Omega $
is an annulus, that is,
$\Omega $
is an annulus, that is,
![]() $\Omega =\{x:\, R_1< |x|<R_2\}, $
$\Omega =\{x:\, R_1< |x|<R_2\}, $
 $$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta u = v^{p-1}, \quad &\text{ in } \Omega,\\ -\Delta v = u^{q-1}, \quad &\text{ in } \Omega,\\ u,v>0, \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial\Omega. \end{array} \right. \end{align} $$
$$ \begin{align}\left\{ \begin{array}{@{}ll} -\Delta u = v^{p-1}, \quad &\text{ in } \Omega,\\ -\Delta v = u^{q-1}, \quad &\text{ in } \Omega,\\ u,v>0, \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial\Omega. \end{array} \right. \end{align} $$
We shall prove that the solution obtained in Theorem 1.1 is non-radial when radii
![]() $R_1, R_2$
satisfy certain conditions. We first begin with the following general result for positive solutions of (28).
$R_1, R_2$
satisfy certain conditions. We first begin with the following general result for positive solutions of (28).
Theorem 4.1 Let
![]() $q\geq p\geq 2.$
Assume that
$q\geq p\geq 2.$
Assume that
![]() $(u,v)$
is a positive solution of (28). The following assertion hold:
$(u,v)$
is a positive solution of (28). The following assertion hold:
 $$ \begin{align} \inf_{0 \neq \eta \in H^1_0(\Omega)} \frac{\int_{\Omega} |\nabla \eta|^2\, dx }{\int_\Omega \eta^2 v(x)^{\frac{p-2}{2}}u(x)^{\frac{q-2}{2}}\, dx }\leq \sqrt{\frac{q}{p}}. \end{align} $$
$$ \begin{align} \inf_{0 \neq \eta \in H^1_0(\Omega)} \frac{\int_{\Omega} |\nabla \eta|^2\, dx }{\int_\Omega \eta^2 v(x)^{\frac{p-2}{2}}u(x)^{\frac{q-2}{2}}\, dx }\leq \sqrt{\frac{q}{p}}. \end{align} $$
Proof We first prove that
Let
![]() $\sigma =p/q \in (0,1]$
and
$\sigma =p/q \in (0,1]$
and
![]() $e=\sigma ^{-\frac {1}{q}}.$
Define
$e=\sigma ^{-\frac {1}{q}}.$
Define
![]() $z(x)=u(x)-e v(x)^\sigma .$
It follows that
$z(x)=u(x)-e v(x)^\sigma .$
It follows that
 $$ \begin{align*} \Delta z & = \Delta u-e\sigma v^{\sigma-1}\Delta v-e \sigma (\sigma-1)v^{\sigma-2}|\nabla v|^2\\ &\geq \Delta u-e\sigma v^{\sigma-1}\Delta v\\ &= v^{\sigma-1}\left(\frac{u^{q-1}}{e^{q-1}}-v^{\sigma (q-1)} \right), \end{align*} $$
$$ \begin{align*} \Delta z & = \Delta u-e\sigma v^{\sigma-1}\Delta v-e \sigma (\sigma-1)v^{\sigma-2}|\nabla v|^2\\ &\geq \Delta u-e\sigma v^{\sigma-1}\Delta v\\ &= v^{\sigma-1}\left(\frac{u^{q-1}}{e^{q-1}}-v^{\sigma (q-1)} \right), \end{align*} $$
from which we obtain that
![]() $\Delta z\geq 0$
on the set
$\Delta z\geq 0$
on the set
Take
![]() $\epsilon>0.$
It follows that
$\epsilon>0.$
It follows that
and therefore
This implies that
![]() $z \leq \epsilon ,$
and since
$z \leq \epsilon ,$
and since
![]() $\epsilon $
is arbitrary the inequality (30) follows.
$\epsilon $
is arbitrary the inequality (30) follows.
We shall now prove inequality (29). It follows from inequality (30) that
 $$ \begin{align*} v \geq \left(\frac{p}{q}\right)^{\frac{1}{p}}u ^{\frac{q}{p}}.\end{align*} $$
$$ \begin{align*} v \geq \left(\frac{p}{q}\right)^{\frac{1}{p}}u ^{\frac{q}{p}}.\end{align*} $$
Therefore,
 $$ \begin{align*}v^{\frac{p-2}{2}}u^{\frac{q-2}{2}} v^2=u^{\frac{q-2}{2}} v^{\frac{p}{2}}v \geq \sqrt{\frac{p}{q}}u^{\frac{q-2}{2}} u^{\frac{q}{2}}v= \sqrt{\frac{p}{q}}u^{q-1}v.\end{align*} $$
$$ \begin{align*}v^{\frac{p-2}{2}}u^{\frac{q-2}{2}} v^2=u^{\frac{q-2}{2}} v^{\frac{p}{2}}v \geq \sqrt{\frac{p}{q}}u^{\frac{q-2}{2}} u^{\frac{q}{2}}v= \sqrt{\frac{p}{q}}u^{q-1}v.\end{align*} $$
It then follows that
 $$ \begin{align*} \inf_{0 \neq \eta \in H^1_0(\Omega)} \frac{\int_{\Omega} |\nabla \eta|^2\, dx }{\int_\Omega \eta^2 v(x)^{\frac{p-2}{2}}u(x)^{\frac{q-2}{2}}\, dx }\leq \frac{\int_{\Omega} |\nabla v|^2\, dx }{\int_\Omega v^2 v(x)^{\frac{p-2}{2}}u(x)^{\frac{q-2}{2}}\, dx } \leq \frac{\int_{\Omega} u^{q-1}v\, dx }{\int_\Omega\sqrt{\frac{p}{q}}u^{q-1}v\, dx }=\sqrt{\frac{q}{p}.} \end{align*} $$
$$ \begin{align*} \inf_{0 \neq \eta \in H^1_0(\Omega)} \frac{\int_{\Omega} |\nabla \eta|^2\, dx }{\int_\Omega \eta^2 v(x)^{\frac{p-2}{2}}u(x)^{\frac{q-2}{2}}\, dx }\leq \frac{\int_{\Omega} |\nabla v|^2\, dx }{\int_\Omega v^2 v(x)^{\frac{p-2}{2}}u(x)^{\frac{q-2}{2}}\, dx } \leq \frac{\int_{\Omega} u^{q-1}v\, dx }{\int_\Omega\sqrt{\frac{p}{q}}u^{q-1}v\, dx }=\sqrt{\frac{q}{p}.} \end{align*} $$
Remark 4.2 We would like to remark that inequalities of the type (30) were first developed to study Liouville-type theorems for stable Lane–Emden systems and Hardy–Hénon elliptic systems on
![]() $\mathbb{R} ^N$
. We refer the interested reader to [Reference Cowan10, Reference Phan24, Reference Souplet28].
$\mathbb{R} ^N$
. We refer the interested reader to [Reference Cowan10, Reference Phan24, Reference Souplet28].
Let
![]() $w(x)=w(s,t)$
be a function of
$w(x)=w(s,t)$
be a function of
![]() $(s, t).$
If we write w in terms of polar coordinates (recall we have
$(s, t).$
If we write w in terms of polar coordinates (recall we have
![]() $ s=r\cos (\theta ), t = r \sin (\theta )$
), we obtain that
$ s=r\cos (\theta ), t = r \sin (\theta )$
), we obtain that
![]() $w(x)=w(r, \theta )$
. Writing the Laplace operator in polar coordinates gives
$w(x)=w(r, \theta )$
. Writing the Laplace operator in polar coordinates gives
where
 $$ \begin{align} h(\theta)= (m-1) \tan(\theta) - \frac{(n-1)}{\tan(\theta)}. \end{align} $$
$$ \begin{align} h(\theta)= (m-1) \tan(\theta) - \frac{(n-1)}{\tan(\theta)}. \end{align} $$
Let
![]() $ (\mu _1,\psi _1)$
be the second eigenpair of the following eigenvalue problem:
$ (\mu _1,\psi _1)$
be the second eigenpair of the following eigenvalue problem:
 $$ \begin{align} \left\{\begin{array}{@{}ll} -\psi_1"(\theta) + \psi_1'(\theta)h(\theta)= \mu_1 \psi_1(\theta),& \text{ in } (0, \frac{\pi}{2}), \\ \psi'(\theta)>0, & \text{ in } (0, \frac{\pi}{2}), \\ \psi_1'(0)= \psi_1'(\frac{\pi}{2})=0, & \end {array} \right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{@{}ll} -\psi_1"(\theta) + \psi_1'(\theta)h(\theta)= \mu_1 \psi_1(\theta),& \text{ in } (0, \frac{\pi}{2}), \\ \psi'(\theta)>0, & \text{ in } (0, \frac{\pi}{2}), \\ \psi_1'(0)= \psi_1'(\frac{\pi}{2})=0, & \end {array} \right. \end{align} $$
and note that the first eigenpair is given by
![]() $ (\mu _0,\psi _0)=(0,1)$
. Note in this problem, one can find an explicit solution given by
$ (\mu _0,\psi _0)=(0,1)$
. Note in this problem, one can find an explicit solution given by
and note we can apply Sturm–Liouville theory and count the number of zeros of
![]() $ \psi _1$
to see it is in fact the second pair.
$ \psi _1$
to see it is in fact the second pair.
Proof of Theorem 1.2.
Let us assume the solution
![]() $(u,v)$
of (28) obtained in Theorem 1.1 is radial. Let
$(u,v)$
of (28) obtained in Theorem 1.1 is radial. Let
![]() $(\lambda _1, \varphi ) $
be the first eigenpair of the following eigenvalue problem:
$(\lambda _1, \varphi ) $
be the first eigenpair of the following eigenvalue problem:
 $$ \begin{align*} \left\{\begin{array}{@{}ll} -\varphi"(r)-\frac{(N-1)\varphi'(r)}{r}+\frac{2N \varphi(r)}{r^2}=\lambda_1v(r)^{\frac{p-2}{2}}u(r)^{\frac{q-2}{2}}\varphi(r),& r \in (R_1,R_2), \\ \varphi(r)=0, & r \in \{R_1, R_2\}. \end {array} \right. \end{align*} $$
$$ \begin{align*} \left\{\begin{array}{@{}ll} -\varphi"(r)-\frac{(N-1)\varphi'(r)}{r}+\frac{2N \varphi(r)}{r^2}=\lambda_1v(r)^{\frac{p-2}{2}}u(r)^{\frac{q-2}{2}}\varphi(r),& r \in (R_1,R_2), \\ \varphi(r)=0, & r \in \{R_1, R_2\}. \end {array} \right. \end{align*} $$
Set
![]() $w(x)=\varphi (r)\psi _1(\theta )$
and note that
$w(x)=\varphi (r)\psi _1(\theta )$
and note that
 $$ \begin{align*} -\Delta w(x)&= -w_{rr} -\frac{(N-1) w_r}{r}- \frac{w_{\theta \theta}}{r^2} + \frac{w_\theta}{r^2} h(\theta)\\ &= -\varphi_{rr}(r)\psi_1(\theta) -\frac{(N-1) \varphi_r(r)\psi_1(\theta)}{r}- \frac{\varphi(r)\psi_1"( \theta)}{r^2} + \frac{\varphi(r)\psi_1'(\theta)}{r^2} h(\theta)\\ &=-\varphi_{rr}(r)\psi_1(\theta) -\frac{(N-1) \varphi_r(r)\psi_1(\theta)}{r}+\frac{2N\varphi(r)\psi_1( \theta)}{r^2}\\ &= \lambda_1v(|x|)^{\frac{p-2}{2}}u(|x|)^{\frac{q-2}{2}}w(x). \end{align*} $$
$$ \begin{align*} -\Delta w(x)&= -w_{rr} -\frac{(N-1) w_r}{r}- \frac{w_{\theta \theta}}{r^2} + \frac{w_\theta}{r^2} h(\theta)\\ &= -\varphi_{rr}(r)\psi_1(\theta) -\frac{(N-1) \varphi_r(r)\psi_1(\theta)}{r}- \frac{\varphi(r)\psi_1"( \theta)}{r^2} + \frac{\varphi(r)\psi_1'(\theta)}{r^2} h(\theta)\\ &=-\varphi_{rr}(r)\psi_1(\theta) -\frac{(N-1) \varphi_r(r)\psi_1(\theta)}{r}+\frac{2N\varphi(r)\psi_1( \theta)}{r^2}\\ &= \lambda_1v(|x|)^{\frac{p-2}{2}}u(|x|)^{\frac{q-2}{2}}w(x). \end{align*} $$
Recall that
![]() $I_K(u)= c>0,$
where the critical value c is characterized by
$I_K(u)= c>0,$
where the critical value c is characterized by
where
For the sake of simplifying the notations, we use I instead of
![]() $I_K$
in the rest of the proof.
$I_K$
in the rest of the proof.
Set
![]() $\gamma _\sigma (\tau )= \tau ({u}+ \sigma w)l$
, where
$\gamma _\sigma (\tau )= \tau ({u}+ \sigma w)l$
, where
![]() $l>0$
is chosen in such a way that
$l>0$
is chosen in such a way that
![]() $I\big ( ({u}+ \sigma w)l\big )\leq 0$
for all
$I\big ( ({u}+ \sigma w)l\big )\leq 0$
for all
![]() $|\sigma |\leq 1$
. Note that
$|\sigma |\leq 1$
. Note that
![]() $\gamma _{\sigma }\in \Gamma $
. We shall show that there exists
$\gamma _{\sigma }\in \Gamma $
. We shall show that there exists
![]() $\sigma>0$
such that for every
$\sigma>0$
such that for every
![]() $\tau \in [0,1]$
one has
$\tau \in [0,1]$
one has
![]() $I(\gamma _\sigma (\tau ))< I({u})$
, and therefore,
$I(\gamma _\sigma (\tau ))< I({u})$
, and therefore,
which leads to a contradiction since
![]() $I(u)=c.$
Note first that there exists a unique twice differentiable real function g on a small neighborhood of zero with
$I(u)=c.$
Note first that there exists a unique twice differentiable real function g on a small neighborhood of zero with
![]() $g'(0)=0$
and
$g'(0)=0$
and
![]() $g(0)=1/l$
such that
$g(0)=1/l$
such that
![]() $\max _{\tau \in [0,1]} I(\gamma _\sigma (\tau ))=I\big (g(\sigma )({u}+ \sigma w)l\big ).$
We now define
$\max _{\tau \in [0,1]} I(\gamma _\sigma (\tau ))=I\big (g(\sigma )({u}+ \sigma w)l\big ).$
We now define
![]() $h: \mathbb{R} \to \mathbb{R} $
by
$h: \mathbb{R} \to \mathbb{R} $
by
Clearly, we have
![]() $h(0)=0$
. Note also that
$h(0)=0$
. Note also that
![]() $h'(0)=0$
due to the fact that
$h'(0)=0$
due to the fact that
![]() $I'(u)=0$
. We now show that
$I'(u)=0$
. We now show that
![]() $h"(0)<0$
. Indeed,
$h"(0)<0$
. Indeed,
 $$ \begin{align*} h"(0)&=(p'-1)\int_\Omega |\Delta u|^{p'-2}(-\Delta w)^2\, dx-(q-1)\int_\Omega | u|^{q-2}(w)^2\, dx\\ &=(p'-1)\lambda_1^2\int_\Omega |\Delta u|^{p'-2} v(|x|)^{p-2}u(|x|)^{q-2} w^2(x)\, dx-(q-1)\int_\Omega | u|^{q-2}(w)^2\, dx\\ &=(p'-1)\lambda_1^2\int_\Omega \big ( v(|x|)^{p-1}\big)^{p'-2} v(|x|)^{p-2}u(|x|)^{q-2} w^2(x)\, dx-(q-1)\int_\Omega | u|^{q-2}(w)^2\, dx\\ &=(p'-1)\lambda_1^2\int_\Omega u(|x|)^{q-2} w^2(x)\, dx-(q-1)\int_\Omega | u|^{q-2}(w)^2\, dx\\ &=\Big ((p'-1)\lambda_1^2-(q-1)\Big )\int_\Omega u(|x|)^{q-2} w^2(x)\, dx. \end{align*} $$
$$ \begin{align*} h"(0)&=(p'-1)\int_\Omega |\Delta u|^{p'-2}(-\Delta w)^2\, dx-(q-1)\int_\Omega | u|^{q-2}(w)^2\, dx\\ &=(p'-1)\lambda_1^2\int_\Omega |\Delta u|^{p'-2} v(|x|)^{p-2}u(|x|)^{q-2} w^2(x)\, dx-(q-1)\int_\Omega | u|^{q-2}(w)^2\, dx\\ &=(p'-1)\lambda_1^2\int_\Omega \big ( v(|x|)^{p-1}\big)^{p'-2} v(|x|)^{p-2}u(|x|)^{q-2} w^2(x)\, dx-(q-1)\int_\Omega | u|^{q-2}(w)^2\, dx\\ &=(p'-1)\lambda_1^2\int_\Omega u(|x|)^{q-2} w^2(x)\, dx-(q-1)\int_\Omega | u|^{q-2}(w)^2\, dx\\ &=\Big ((p'-1)\lambda_1^2-(q-1)\Big )\int_\Omega u(|x|)^{q-2} w^2(x)\, dx. \end{align*} $$
Note that
Let
![]() $\lambda _H$
denote the best constant in the Hardy inequality
$\lambda _H$
denote the best constant in the Hardy inequality
 $$ \begin{align*}\lambda_H=\inf_{0 \neq \eta \in H^1_0(\Omega)}\frac{\int_{\Omega} |\nabla \eta|^2 \,dx}{\int_{\Omega} \frac{| \eta|^2 }{|x|^2}\,dx}.\end{align*} $$
$$ \begin{align*}\lambda_H=\inf_{0 \neq \eta \in H^1_0(\Omega)}\frac{\int_{\Omega} |\nabla \eta|^2 \,dx}{\int_{\Omega} \frac{| \eta|^2 }{|x|^2}\,dx}.\end{align*} $$
It follows that
 $$ \begin{align*}\lambda_1&=\inf_{0 \neq \eta \in H^1_0(\Omega)} \frac{\int_{\Omega} |\nabla \eta|^2\, dx +2N\int_{\Omega} \frac{| \eta|^2}{|x|^2}\, dx }{\int_\Omega \eta^2 v(x)^{\frac{p-2}{2}}u(x)^{\frac{q-2}{2}}\, dx } \\&\quad\leq \inf_{0 \neq \eta \in H^1_0(\Omega)} \frac{\Big(1+\frac{2N}{\lambda_H}\Big)\int_{\Omega} |\nabla \eta|^2\, dx }{\int_\Omega \eta^2 v(x)^{\frac{p-2}{2}}u(x)^{\frac{q-2}{2}}\, dx }\leq \sqrt{\frac{q}{p}}\left(1+\frac{2N}{\lambda_H}\right), \end{align*} $$
$$ \begin{align*}\lambda_1&=\inf_{0 \neq \eta \in H^1_0(\Omega)} \frac{\int_{\Omega} |\nabla \eta|^2\, dx +2N\int_{\Omega} \frac{| \eta|^2}{|x|^2}\, dx }{\int_\Omega \eta^2 v(x)^{\frac{p-2}{2}}u(x)^{\frac{q-2}{2}}\, dx } \\&\quad\leq \inf_{0 \neq \eta \in H^1_0(\Omega)} \frac{\Big(1+\frac{2N}{\lambda_H}\Big)\int_{\Omega} |\nabla \eta|^2\, dx }{\int_\Omega \eta^2 v(x)^{\frac{p-2}{2}}u(x)^{\frac{q-2}{2}}\, dx }\leq \sqrt{\frac{q}{p}}\left(1+\frac{2N}{\lambda_H}\right), \end{align*} $$
where the last inequality follows from Theorem 4.1. In particular, if
 $$ \begin{align*}\frac{q}{p}\left(1+\frac{2N}{\lambda_H}\right)^2<(p-1)(q-1),\end{align*} $$
$$ \begin{align*}\frac{q}{p}\left(1+\frac{2N}{\lambda_H}\right)^2<(p-1)(q-1),\end{align*} $$
then
![]() $(p'-1)\lambda _1^2-(q-1)<0.$
This implies that
$(p'-1)\lambda _1^2-(q-1)<0.$
This implies that
![]() $h"(0)<0.$
This in fact shows that
$h"(0)<0.$
This in fact shows that
for small
![]() $\sigma>0$
as desired.
$\sigma>0$
as desired.
Recall from (26) that
which corresponds to the decomposition
![]() $\mathbb{R} ^{m}\times \mathbb{R} ^{n}$
of the annulus
$\mathbb{R} ^{m}\times \mathbb{R} ^{n}$
of the annulus
![]() ${\Omega =\{x:\, R_1< |x|<R_2\}}$
in
${\Omega =\{x:\, R_1< |x|<R_2\}}$
in
![]() $ \mathbb{R} ^N$
with
$ \mathbb{R} ^N$
with
![]() $N=m+n.$
We have the following result regarding the distinction of solutions for different decompositions of
$N=m+n.$
We have the following result regarding the distinction of solutions for different decompositions of
![]() $ \mathbb{R} ^N$
.
$ \mathbb{R} ^N$
.
Lemma 4.3 Let
![]() $1 < n <n'\leq \lfloor \frac {N}{2}\rfloor $
and set
$1 < n <n'\leq \lfloor \frac {N}{2}\rfloor $
and set
![]() $m=N-n$
,
$m=N-n$
,
![]() $m'=N-n'.$
Let
$m'=N-n'.$
Let
![]() $u_{m,n} \in K(m,n)$
and
$u_{m,n} \in K(m,n)$
and
![]() $u_{m',n'}\in K(m',n')$
be the solutions obtained in Theorem 1.1 corresponding to the decomposition
$u_{m',n'}\in K(m',n')$
be the solutions obtained in Theorem 1.1 corresponding to the decomposition
![]() $\mathbb{R} ^{m}\times \mathbb{R} ^{n}$
and
$\mathbb{R} ^{m}\times \mathbb{R} ^{n}$
and
![]() $\mathbb{R} ^{m'}\times \mathbb{R} ^{n'}$
of
$\mathbb{R} ^{m'}\times \mathbb{R} ^{n'}$
of
![]() $\mathbb{R} ^N$
, respectively. Then
$\mathbb{R} ^N$
, respectively. Then
![]() $u_{m,n} \not = u_{m',n'}$
unless they are both radial functions.
$u_{m,n} \not = u_{m',n'}$
unless they are both radial functions.
Proof Let
![]() $u_{m,n} =u_{m',n'}=u.$
We shall show that u must be radial. It follows that
$u_{m,n} =u_{m',n'}=u.$
We shall show that u must be radial. It follows that
![]() $u(x)=f(s,t)=g(s',t')$
for two functions f and
$u(x)=f(s,t)=g(s',t')$
for two functions f and
![]() $g,$
where
$g,$
where
and
By assuming
![]() $x_i=0$
for
$x_i=0$
for
![]() $i\not = x_1, x_{m}$
, we obtain that
$i\not = x_1, x_{m}$
, we obtain that
from which we obtain that g must be a radial function. To show that f is a radial function, we assume that
![]() $x_i = 0$
for
$x_i = 0$
for
![]() $i \neq x_{m'+1}, x_N.$
Then
$i \neq x_{m'+1}, x_N.$
Then
from which we obtain that f is a radial function.
Proof of Theorem 1.3.
We begin by proving the existence of a positive solution. Afterward, we show that the positive solution is in fact, non-radial.
Part 1. It follows from Theorem 1.1 that for each
![]() $n\leq k$
and
$n\leq k$
and
![]() $q\geq p> 2,$
equation (28) has a solution of the form
$q\geq p> 2,$
equation (28) has a solution of the form
![]() $(u_{m,n}, v_{m,n}) =\left (u_{m,n}(s,t), v_{m,n}(s,t)\right )$
, where
$(u_{m,n}, v_{m,n}) =\left (u_{m,n}(s,t), v_{m,n}(s,t)\right )$
, where
provided
Since
![]() $n\leq k,$
it follows that
$n\leq k,$
it follows that
Thus, for each
![]() $n\leq k,$
we have a positive solution provided
$n\leq k,$
we have a positive solution provided
Part 2. If
![]() $k\leq (p+1)/(p-1),$
then
$k\leq (p+1)/(p-1),$
then
![]() $n\leq (p+1)/(p-1).$
So, by Theorem 1.1, there exists a positive solution of (28).
$n\leq (p+1)/(p-1).$
So, by Theorem 1.1, there exists a positive solution of (28).
Now, we proceed to prove that the solution in parts 1 and 2 are non-radial. Indeed, by Theorem 1.2, the solution
![]() $(u_{m,n},v_{m,n})$
is non-radial provided
$(u_{m,n},v_{m,n})$
is non-radial provided
 $$ \begin{align*}(p-1)(q-1)> \left(1+\frac{2N}{\lambda_H}\right)^2\left(\frac{q}{p}\right).\end{align*} $$
$$ \begin{align*}(p-1)(q-1)> \left(1+\frac{2N}{\lambda_H}\right)^2\left(\frac{q}{p}\right).\end{align*} $$
Thus, for each
![]() $n \in \{1,\dots ,k\}$
we have a non-radial solution
$n \in \{1,\dots ,k\}$
we have a non-radial solution
![]() $(u_{m,n},v_{m,n}).$
On the other hand, by Lemma 4.3, we have that
$(u_{m,n},v_{m,n}).$
On the other hand, by Lemma 4.3, we have that
![]() $u_{m,n} \not = u_{m',n'}$
for all
$u_{m,n} \not = u_{m',n'}$
for all
![]() $n\not =n'.$
Similarly, by Lemma 4.3, we obtain
$n\not =n'.$
Similarly, by Lemma 4.3, we obtain
![]() $v_{m,n} \not = v_{m',n'}$
for all
$v_{m,n} \not = v_{m',n'}$
for all
![]() $n \not = n'.$
This indeed implies that we have k distinct positive non-radial solutions.
$n \not = n'.$
This indeed implies that we have k distinct positive non-radial solutions.
Proof of Corollary 1.4.
1. For each
![]() $k\in \mathbb{N} $
with
$k\in \mathbb{N} $
with
![]() $1\leq k \leq \lfloor \frac {p+1}{p-1}\rfloor ,$
by part 2 of Theorem 1.3, there exists a solution provided
$1\leq k \leq \lfloor \frac {p+1}{p-1}\rfloor ,$
by part 2 of Theorem 1.3, there exists a solution provided
 $$ \begin{align*} (p-1)(q-1)> \left(1+\frac{2N}{\lambda_H}\right)^2\left(\frac{q}{p}\right).\end{align*} $$
$$ \begin{align*} (p-1)(q-1)> \left(1+\frac{2N}{\lambda_H}\right)^2\left(\frac{q}{p}\right).\end{align*} $$
Thus, if
 $$ \begin{align*}(p-1)(q-1)\left(\frac{p}{q}\right)> \left(1+\frac{2N}{\lambda_H}\right)^2,\end{align*} $$
$$ \begin{align*}(p-1)(q-1)\left(\frac{p}{q}\right)> \left(1+\frac{2N}{\lambda_H}\right)^2,\end{align*} $$
then we must have
![]() $\lfloor \frac {p+1}{p-1}\rfloor $
positive non-radial solutions.
$\lfloor \frac {p+1}{p-1}\rfloor $
positive non-radial solutions.
2. Assuming
![]() $k=\Big \lfloor \frac {N}{2} \Big \rfloor $
in Theorem 1.3, we obtain that there are
$k=\Big \lfloor \frac {N}{2} \Big \rfloor $
in Theorem 1.3, we obtain that there are
![]() $\Bigl \lfloor \frac {N}{2} \Bigr \rfloor $
positive non-radial solutions provided that
$\Bigl \lfloor \frac {N}{2} \Bigr \rfloor $
positive non-radial solutions provided that
 $$ \begin{align*}(p-1)(q-1)>\Big(1+\frac{2N}{\lambda_H}\Big)^2\left(\frac{q}{p}\right) \end{align*} $$
$$ \begin{align*}(p-1)(q-1)>\Big(1+\frac{2N}{\lambda_H}\Big)^2\left(\frac{q}{p}\right) \end{align*} $$
and
 $$ \begin{align*}\frac{1}{p}+\frac{1}{q}>1-\frac{2}{\Big\lfloor\frac{N}{2} \Big\rfloor+1}.\end{align*} $$
$$ \begin{align*}\frac{1}{p}+\frac{1}{q}>1-\frac{2}{\Big\lfloor\frac{N}{2} \Big\rfloor+1}.\end{align*} $$
Now, to obtain
we want to show that
![]() $\lambda _H$
can be sufficiently large under conditions
$\lambda _H$
can be sufficiently large under conditions
![]() $2(a)$
and
$2(a)$
and
![]() $2(b)$
and hence, we conclude that there are
$2(b)$
and hence, we conclude that there are
![]() $\lfloor \frac {N}{2}\rfloor $
positive non-radial solutions. As for the proof of
$\lfloor \frac {N}{2}\rfloor $
positive non-radial solutions. As for the proof of
![]() $2(a)$
and
$2(a)$
and
![]() $2(b),$
we refer the interested reader to [Reference Cowan and Moameni11].
$2(b),$
we refer the interested reader to [Reference Cowan and Moameni11].
Acknowledgments
We would like to thank the referees for carefully reading our manuscript and for giving us valuable comments that substantially improved the clarity of the original manuscript.
Data availability statement
Data sharing is not applicable to this article as no data-sets were generated or analyzed during the current study.
Competing interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.