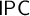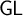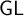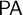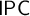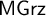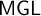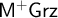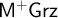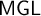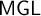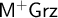1 Introduction
1.1 Propositional case
The intuitionistic point of view identifies truth with provability. This has resulted in the well-known Brouwer–Heyting–Kolmogorov interpretation (BHK-interpretation for short), which is considered as the intended, albeit informal interpretation of intuitionistic logic (see, e.g., [Reference Artemov and Beklemishev2] and the references therein). Gödel [Reference Gödel and Feferman27] took the first step in making this interpretation more formal by introducing a modal calculus of classical provability and translating the intuitionistic propositional calculus
![]() $\mathsf {IPC}$
into it. Gödel’s modal calculus turned out to be equivalent to Lewis’ well-known modal logic
$\mathsf {IPC}$
into it. Gödel’s modal calculus turned out to be equivalent to Lewis’ well-known modal logic
![]() $\mathsf {S4}$
, and the translation became known as the Gödel translation. We recall that it is defined as follows:
$\mathsf {S4}$
, and the translation became known as the Gödel translation. We recall that it is defined as follows:
-
•
 $p^t=\square p$
for a propositional letter p;
$p^t=\square p$
for a propositional letter p; -
•
 $(\varphi \vee \psi )^t = \varphi ^t\vee \psi ^t$
;
$(\varphi \vee \psi )^t = \varphi ^t\vee \psi ^t$
; -
•
 $(\varphi \wedge \psi )^t = \varphi ^t\wedge \psi ^t$
;
$(\varphi \wedge \psi )^t = \varphi ^t\wedge \psi ^t$
; -
•
 $(\varphi \rightarrow \psi )^t = \square (\varphi ^t\to \psi ^t)$
;
$(\varphi \rightarrow \psi )^t = \square (\varphi ^t\to \psi ^t)$
; -
•
 $(\neg \varphi )^t = \square (\neg \varphi ^t)$
.
$(\neg \varphi )^t = \square (\neg \varphi ^t)$
.
McKinsey and Tarski [Reference McKinsey and Tarski33] proved that this translation is full and faithful; that is,
There are many other normal extensions of
![]() $\mathsf {S4}$
, called modal companions of
$\mathsf {S4}$
, called modal companions of
![]() $\mathsf {IPC}$
, in which
$\mathsf {IPC}$
, in which
![]() $\mathsf {IPC}$
is embedded fully and faithfully. Esakia [Reference Esakia14] showed that the largest such companion is Grzegorczyk’s logic
$\mathsf {IPC}$
is embedded fully and faithfully. Esakia [Reference Esakia14] showed that the largest such companion is Grzegorczyk’s logic
![]() $\mathsf {Grz}$
, which is the normal extension of
$\mathsf {Grz}$
, which is the normal extension of
![]() $\mathsf {S4}$
with the Grzegorczyk axiom
$\mathsf {S4}$
with the Grzegorczyk axiom
Thus, we have
Goldblatt [Reference Goldblatt28], Boolos [Reference Boolos7], and Kuznetsov and Muravitsky [Reference Kuznetsov and Muravitsky32] showed that the splitting translation embeds
![]() $\mathsf {Grz}$
into the Gödel–Löb logic
$\mathsf {Grz}$
into the Gödel–Löb logic
![]() $\mathsf {GL}$
which is the normal extension of the least normal modal logic
$\mathsf {GL}$
which is the normal extension of the least normal modal logic
![]() $\mathsf {K}$
with the axiom
$\mathsf {K}$
with the axiom
We recall that the splitting translation is defined by “splitting boxes” in formulas (see, e.g., [Reference Boolos8, p. 8]); that is, for a modal formula
![]() $\varphi $
, let
$\varphi $
, let
![]() $\square ^{+}\varphi $
be the abbreviation of the formula
$\square ^{+}\varphi $
be the abbreviation of the formula
![]() $\varphi \wedge \square \varphi $
. Then the splitting translation is defined by letting
$\varphi \wedge \square \varphi $
. Then the splitting translation is defined by letting
![]() $\varphi ^s$
be the result of replacing all occurrences of
$\varphi ^s$
be the result of replacing all occurrences of
![]() $\square $
in
$\square $
in
![]() $\varphi $
by
$\varphi $
by
![]() $\square ^{+}$
. We then have
$\square ^{+}$
. We then have
Combining these results yields
Finally, by Solovay’s theorem [Reference Solovay40],
![]() $\mathsf {GL}$
can be thought of as the modal logic of the provability predicate of Peano Arithmetic
$\mathsf {GL}$
can be thought of as the modal logic of the provability predicate of Peano Arithmetic
![]() $\mathsf {PA}$
. Thus, both
$\mathsf {PA}$
. Thus, both
![]() $\mathsf {IPC}$
and
$\mathsf {IPC}$
and
![]() $\mathsf {Grz}$
admit provability interpretations. That
$\mathsf {Grz}$
admit provability interpretations. That
![]() $\mathsf {IPC}$
admits such an interpretation is especially important in relation to the BHK-interpretation.
$\mathsf {IPC}$
admits such an interpretation is especially important in relation to the BHK-interpretation.
1.2 Predicate case
The Gödel translation extends to the predicate case by setting
-
•
 $(\forall x\varphi )^t = \square \forall x (\varphi ^t),$
$(\forall x\varphi )^t = \square \forall x (\varphi ^t),$
-
•
 $(\exists x\varphi )^t = \exists x(\varphi ^t)$
.
$(\exists x\varphi )^t = \exists x(\varphi ^t)$
.
Let
![]() $\mathsf {IQC}$
be the intuitionistic predicate calculus and let
$\mathsf {IQC}$
be the intuitionistic predicate calculus and let
![]() $\mathsf {QS4}$
be the predicate
$\mathsf {QS4}$
be the predicate
![]() $\mathsf {S4}$
(the definitions of predicate intuitionistic and modal logics can, for example, be found in [Reference Gabbay, Shehtman and Skvortsov26]). Then
$\mathsf {S4}$
(the definitions of predicate intuitionistic and modal logics can, for example, be found in [Reference Gabbay, Shehtman and Skvortsov26]). Then
so the extension of the Gödel translation to the predicate case remains full and faithful (see, e.g., [Reference Rasiowa and Sikorski39]). Let
![]() $\mathsf {QGrz}$
be the predicate
$\mathsf {QGrz}$
be the predicate
![]() $\mathsf {Grz}$
and let
$\mathsf {Grz}$
and let
![]() $\mathsf {QGL}$
be the predicate
$\mathsf {QGL}$
be the predicate
![]() $\mathsf {GL}$
. In [Reference Gabbay, Shehtman and Skvortsov26, p. 157] it is attributed to Pankratyev that the Gödel translation of
$\mathsf {GL}$
. In [Reference Gabbay, Shehtman and Skvortsov26, p. 157] it is attributed to Pankratyev that the Gödel translation of
![]() $\mathsf {IQC}$
into
$\mathsf {IQC}$
into
![]() $\mathsf {QGrz}$
remains full and faithful. However, these are the only positive results in the predicate case since Montagna [Reference Montagna34] showed that Solovay’s theorem no longer holds for
$\mathsf {QGrz}$
remains full and faithful. However, these are the only positive results in the predicate case since Montagna [Reference Montagna34] showed that Solovay’s theorem no longer holds for
![]() $\mathsf {QGL}$
. Moreover, the splitting translation does not embed
$\mathsf {QGL}$
. Moreover, the splitting translation does not embed
![]() $\mathsf {QGrz}$
fully and faithfully into
$\mathsf {QGrz}$
fully and faithfully into
![]() $\mathsf {QGL}$
(see below).
$\mathsf {QGL}$
(see below).
1.3 Monadic case
In view of the above, Esakia [Reference Esakia17] suggested to study these translations for the monadic (one-variable) fragments of
![]() $\mathsf {IQC}$
,
$\mathsf {IQC}$
,
![]() $\mathsf {QGrz}$
, and
$\mathsf {QGrz}$
, and
![]() $\mathsf {QGL}$
. The monadic fragment of
$\mathsf {QGL}$
. The monadic fragment of
![]() $\mathsf {IQC}$
was introduced by Prior [Reference Prior38] under the name of
$\mathsf {IQC}$
was introduced by Prior [Reference Prior38] under the name of
![]() $\mathsf {MIPC}$
. The monadic fragment of
$\mathsf {MIPC}$
. The monadic fragment of
![]() $\mathsf {QS4}$
was studied by Fischer-Servi [Reference Fischer-Servi22], and the monadic fragments of
$\mathsf {QS4}$
was studied by Fischer-Servi [Reference Fischer-Servi22], and the monadic fragments of
![]() $\mathsf {QGrz}$
and
$\mathsf {QGrz}$
and
![]() $\mathsf {QGL}$
by Esakia [Reference Esakia17]. We denote these fragments by
$\mathsf {QGL}$
by Esakia [Reference Esakia17]. We denote these fragments by
![]() $\mathsf {MS4}$
,
$\mathsf {MS4}$
,
![]() $\mathsf {MGrz}$
, and
$\mathsf {MGrz}$
, and
![]() $\mathsf {MGL}$
, respectively.
$\mathsf {MGL}$
, respectively.
Fischer-Servi [Reference Fischer-Servi22] proved that the Gödel translation embeds
![]() $\mathsf {MIPC}$
into
$\mathsf {MIPC}$
into
![]() $\mathsf {MS4}$
fully and faithfully. As we will see, the Gödel translation also embeds
$\mathsf {MS4}$
fully and faithfully. As we will see, the Gödel translation also embeds
![]() $\mathsf {MIPC}$
fully and faithfully into
$\mathsf {MIPC}$
fully and faithfully into
![]() $\mathsf {MGrz}$
. Japaridze [Reference Japaridze30, Reference Japaridze31] proved that Solovay’s result extends to
$\mathsf {MGrz}$
. Japaridze [Reference Japaridze30, Reference Japaridze31] proved that Solovay’s result extends to
![]() $\mathsf {MGL}$
. Therefore, to complete the picture, it would be sufficient to show that the splitting translation embeds
$\mathsf {MGL}$
. Therefore, to complete the picture, it would be sufficient to show that the splitting translation embeds
![]() $\mathsf {MGrz}$
into
$\mathsf {MGrz}$
into
![]() $\mathsf {MGL}$
fully and faithfully. However, as was observed by Esakia, this is no longer true. To see this, we recall Casari’s predicate formula
$\mathsf {MGL}$
fully and faithfully. However, as was observed by Esakia, this is no longer true. To see this, we recall Casari’s predicate formula
Let
![]() $\mathsf {IQ^+C}$
be the predicate logic obtained from
$\mathsf {IQ^+C}$
be the predicate logic obtained from
![]() $\mathsf {IQC}$
by postulating Casari’s formula as a new axiom. It was pointed out by Esakia [Reference Esakia18] (see also [Reference Esakia19, Section 7]) that
$\mathsf {IQC}$
by postulating Casari’s formula as a new axiom. It was pointed out by Esakia [Reference Esakia18] (see also [Reference Esakia19, Section 7]) that
![]() $\mathsf {IQ^+C}$
is equivalent to the predicate logic obtained from
$\mathsf {IQ^+C}$
is equivalent to the predicate logic obtained from
![]() $\mathsf {IQC}$
by postulating the following modified version of universal generalization:
$\mathsf {IQC}$
by postulating the following modified version of universal generalization:
 $$ \begin{align} \frac{(P(a)\to\forall x P(x))\to P(a)}{\forall x P(x)}. \end{align} $$
$$ \begin{align} \frac{(P(a)\to\forall x P(x))\to P(a)}{\forall x P(x)}. \end{align} $$
Among other things, Esakia observed that
![]() $\mathsf {IQ^+C}$
is a conservative extension of
$\mathsf {IQ^+C}$
is a conservative extension of
![]() $\mathsf {IPC}$
and that Kuroda’s formula
$\mathsf {IPC}$
and that Kuroda’s formula
![]() $\forall x\neg \neg P(x)\to \neg \neg \forall x P(x)$
is provable in
$\forall x\neg \neg P(x)\to \neg \neg \forall x P(x)$
is provable in
![]() $\mathsf {IQ^+C}$
. In this regard it is worthwhile to point out that Heyting considered it “one of the most striking features of intuitionistic logic” that Kuroda’s formula is not derivable in
$\mathsf {IQ^+C}$
. In this regard it is worthwhile to point out that Heyting considered it “one of the most striking features of intuitionistic logic” that Kuroda’s formula is not derivable in
![]() $\mathsf {IQC}$
; see, e.g., [Reference Esakia18, p. 27].
$\mathsf {IQC}$
; see, e.g., [Reference Esakia18, p. 27].
We consider the monadic version of Casari’s formula
Using the same notation for the Gödel and splitting translations in the monadic setting, we have that
![]() $\mathsf {MGL}\vdash ((\mathsf {MCas})^t)^s$
but
$\mathsf {MGL}\vdash ((\mathsf {MCas})^t)^s$
but
![]() $\mathsf {MGrz}\not \vdash (\mathsf {MCas})^t$
(see Theorems 3.9 and 3.10). This yields that
$\mathsf {MGrz}\not \vdash (\mathsf {MCas})^t$
(see Theorems 3.9 and 3.10). This yields that
![]() $\mathsf {MGrz}$
does not embed into
$\mathsf {MGrz}$
does not embed into
![]() $\mathsf {MGL}$
faithfully.
$\mathsf {MGL}$
faithfully.
Let
be the extension of
![]() $\mathsf {{MIPC}}$
by
$\mathsf {{MIPC}}$
by
![]() $\mathsf {MCas}$
, and let
$\mathsf {MCas}$
, and let
be the extension of
![]() $\mathsf {MGrz}$
by
$\mathsf {MGrz}$
by
![]() $(\mathsf {MCas})^t$
. Esakia claimed that the translations
$(\mathsf {MCas})^t$
. Esakia claimed that the translations
are lifted to
Verifying this claim will be our main goal, which together with Japaridze’s result [Reference Japaridze30, Reference Japaridze31] on arithmetical completeness of
![]() $\mathsf {MGL}$
yields the desired provability interpretations of
$\mathsf {MGL}$
yields the desired provability interpretations of
![]() $\mathsf {M^{+}IPC}$
and
$\mathsf {M^{+}IPC}$
and
![]() $\mathsf {M^{+}Grz}$
. As we point out in Remark 5.19,
$\mathsf {M^{+}Grz}$
. As we point out in Remark 5.19,
![]() $\mathsf {M^{+}IPC}$
axiomatizes the monadic fragment of
$\mathsf {M^{+}IPC}$
axiomatizes the monadic fragment of
![]() $\mathsf {IQ^+C}$
. Thus, it is the monadic fragment of the amended intuitionistic calculus
$\mathsf {IQ^+C}$
. Thus, it is the monadic fragment of the amended intuitionistic calculus
![]() $\mathsf {IQ^+C}$
, and not of
$\mathsf {IQ^+C}$
, and not of
![]() $\mathsf {IQC}$
, that admits a provability interpretation. It would be of interest to investigate philosophical consequences of this result in connection with the BHK-interpretation.
$\mathsf {IQC}$
, that admits a provability interpretation. It would be of interest to investigate philosophical consequences of this result in connection with the BHK-interpretation.
1.4 Main contribution and organization
Our main result is the following theorem.
Theorem.
![]() $\mathsf {M^{+}IPC}\vdash \varphi $
iff
$\mathsf {M^{+}IPC}\vdash \varphi $
iff
![]() $\mathsf {M^{+}Grz}\vdash \varphi ^t$
iff
$\mathsf {M^{+}Grz}\vdash \varphi ^t$
iff
![]() $\mathsf {MGL}\vdash (\varphi ^t)^s.$
$\mathsf {MGL}\vdash (\varphi ^t)^s.$
We will prove the theorem semantically. The most challenging part of our argument is in establishing the finite model property for
![]() $\mathsf {M^{+}IPC}$
and
$\mathsf {M^{+}IPC}$
and
![]() $\mathsf {M^{+}Grz}$
(see Sections 5 and 6). That
$\mathsf {M^{+}Grz}$
(see Sections 5 and 6). That
![]() $\mathsf {{MGL}}$
also has the finite model property was proven by Japaridze [Reference Japaridze30]. In fact, our technique of proving the finite model property for
$\mathsf {{MGL}}$
also has the finite model property was proven by Japaridze [Reference Japaridze30]. In fact, our technique of proving the finite model property for
![]() $\mathsf {M^{+}Grz}$
can be adapted to provide an alternative proof of Japaridze’s result for
$\mathsf {M^{+}Grz}$
can be adapted to provide an alternative proof of Japaridze’s result for
![]() $\mathsf {{MGL}}$
(see [Reference Brantley9]). Once the finite model property of these logics is established, the standard argument yields our main result (see the proof of Theorem 4.12 for details).
$\mathsf {{MGL}}$
(see [Reference Brantley9]). Once the finite model property of these logics is established, the standard argument yields our main result (see the proof of Theorem 4.12 for details).
The paper is organized as follows. Section 2 provides a brief overview of monadic logics and their corresponding algebraic and relational semantics. Section 3 discusses the Gödel and splitting translations in the monadic setting. In Section 4 we investigate how the addition of the adapted variations of Casari’s formula affect the semantics. Finally, in Sections 5 and 6 we establish the finite model property for
![]() $\mathsf {M^{+}IPC}$
and
$\mathsf {M^{+}IPC}$
and
![]() $\mathsf {M^{+}Grz}$
, respectively, using a modified selective filtration, which allows us to conclude the main result stated above.
$\mathsf {M^{+}Grz}$
, respectively, using a modified selective filtration, which allows us to conclude the main result stated above.
We use the following as our standard references: [Reference Chagrov and Zakharyaschev12] for intuitionistic and modal propositional logics, [Reference Gabbay, Shehtman and Skvortsov26] for intuitionistic and modal predicate logics, and [Reference Gabbay, Kurucz, Wolter and Zakharyaschev25] for intuitionistic modal logics and classical bi-modal systems.
2 Monadic logics
In this section we recall the notion of monadic intuitionistic and modal logics and discuss their algebraic and frame-based semantics.
2.1 Monadic intuitionistic logic
The monadic intuitionistic propositional calculus
![]() $\mathsf {MIPC}$
was defined by Prior [Reference Prior38] and it was shown by Bull [Reference Bull11] that
$\mathsf {MIPC}$
was defined by Prior [Reference Prior38] and it was shown by Bull [Reference Bull11] that
![]() $\mathsf {MIPC}$
axiomatizes the monadic fragment of the predicate intuitionistic logic. To define
$\mathsf {MIPC}$
axiomatizes the monadic fragment of the predicate intuitionistic logic. To define
![]() $\mathsf {MIPC}$
, let
$\mathsf {MIPC}$
, let
![]() $\mathcal L$
be the language of propositional intuitionistic logic, and let
$\mathcal L$
be the language of propositional intuitionistic logic, and let
![]() $\mathcal {L}_{\forall \exists }$
be the enrichment of
$\mathcal {L}_{\forall \exists }$
be the enrichment of
![]() $\mathcal {L}$
with the quantifier modalities
$\mathcal {L}$
with the quantifier modalities
![]() $\forall $
and
$\forall $
and
![]() $\exists $
.Footnote
1
$\exists $
.Footnote
1
Definition 2.1.
![]() $\mathsf {MIPC}$
is the smallest set of
$\mathsf {MIPC}$
is the smallest set of
![]() $\mathcal {L}_{\forall \exists }$
-formulas containing
$\mathcal {L}_{\forall \exists }$
-formulas containing
-
• all axioms of
 $\mathsf {IPC}$
,
$\mathsf {IPC}$
, -
• the
 $\mathsf {S4}$
-axioms for
$\mathsf {S4}$
-axioms for
 $\forall $
,Footnote
2
$\forall $
,Footnote
2
-
• the
 $\mathsf {S5}$
-axioms for
$\mathsf {S5}$
-axioms for
 $\exists $
,Footnote
3
$\exists $
,Footnote
3
-
• the connecting axioms
 $\exists p\to \forall \exists p$
and
$\exists p\to \forall \exists p$
and
 $\exists \forall p\to \forall p$
,
$\exists \forall p\to \forall p$
,
and closed under the inference rules of substitution, modus ponens, and
![]() $\forall $
-necessitation
$\forall $
-necessitation
![]() $\frac {\varphi }{\forall \varphi }$
.
$\frac {\varphi }{\forall \varphi }$
.
Remark 2.2. The non-symmetric feature of intuitionistic quantifiers is captured in the fact that while
![]() $\exists $
is an
$\exists $
is an
![]() $\sf S5$
-modality,
$\sf S5$
-modality,
![]() $\forall $
is merely an
$\forall $
is merely an
![]() $\mathsf {S4}$
-modality, and the
$\mathsf {S4}$
-modality, and the
![]() $\forall $
-counterpart
$\forall $
-counterpart
![]() $\forall (\forall p\vee q)\leftrightarrow (\forall p\vee \forall q)$
of
$\forall (\forall p\vee q)\leftrightarrow (\forall p\vee \forall q)$
of
![]() $\exists (\exists p\wedge q)\leftrightarrow (\exists p\wedge \exists q)$
is not provable in
$\exists (\exists p\wedge q)\leftrightarrow (\exists p\wedge \exists q)$
is not provable in
![]() $\mathsf {MIPC}$
.
$\mathsf {MIPC}$
.
Algebraic semantics for
![]() $\mathsf {MIPC}$
is given by monadic Heyting algebras [Reference Bezhanishvili3, Reference Monteiro and Varsavsky35].
$\mathsf {MIPC}$
is given by monadic Heyting algebras [Reference Bezhanishvili3, Reference Monteiro and Varsavsky35].
Definition 2.3. A monadic Heyting algebra is a triple
![]() $(H,\forall ,\exists )$
where
$(H,\forall ,\exists )$
where
-
• H is a Heyting algebra,
-
•
 $\forall :H\to H$
is an
$\forall :H\to H$
is an
 $\mathsf {S4}$
-operator,Footnote
4
$\mathsf {S4}$
-operator,Footnote
4
-
•
 $\exists :H\to H$
is an
$\exists :H\to H$
is an
 $\mathsf {S5}$
-operator,Footnote
5
$\mathsf {S5}$
-operator,Footnote
5
-
•
 $\exists a\le \forall \exists a$
and
$\exists a\le \forall \exists a$
and
 $\exists \forall a\le \forall a$
.
$\exists \forall a\le \forall a$
.
Remark 2.4. This in particular implies that the fixpoints of
![]() $\forall $
and
$\forall $
and
![]() $\exists $
are equal and form a Heyting subalgebra of H. In fact, every monadic Heyting algebra can be represented as a pair
$\exists $
are equal and form a Heyting subalgebra of H. In fact, every monadic Heyting algebra can be represented as a pair
![]() $(H,H_0)$
where
$(H,H_0)$
where
![]() $H_0$
is a Heyting subalgebra of H and the inclusion has both the right (
$H_0$
is a Heyting subalgebra of H and the inclusion has both the right (
![]() $\forall $
) and left
$\forall $
) and left
![]() $(\exists )$
adjoint.
$(\exists )$
adjoint.
As usual, propositional letters of
![]() $\mathcal {L}_{\forall \exists }$
are evaluated as elements of H, the connectives as the corresponding operations of H, and the quantifier modalities as the corresponding modal operators of H. The standard Lindenbaum–Tarski construction then yields:
$\mathcal {L}_{\forall \exists }$
are evaluated as elements of H, the connectives as the corresponding operations of H, and the quantifier modalities as the corresponding modal operators of H. The standard Lindenbaum–Tarski construction then yields:
Theorem 2.5.
![]() $\mathsf {MIPC}\vdash \varphi \Leftrightarrow \mathfrak {H}\vDash \varphi $
for each monadic Heyting algebra
$\mathsf {MIPC}\vdash \varphi \Leftrightarrow \mathfrak {H}\vDash \varphi $
for each monadic Heyting algebra
![]() $\mathfrak {H}$
.
$\mathfrak {H}$
.
Kripke semantics for
![]() $\mathsf {MIPC}$
is an extension of Kripke semantics for
$\mathsf {MIPC}$
is an extension of Kripke semantics for
![]() $\mathsf {IPC}$
, and was developed in [Reference Esakia17, Reference Fischer-Servi24, Reference Ono36].
$\mathsf {IPC}$
, and was developed in [Reference Esakia17, Reference Fischer-Servi24, Reference Ono36].
Definition 2.6. An
![]() $\mathsf {MIPC}$
-frame is a triple
$\mathsf {MIPC}$
-frame is a triple
![]() $\mathfrak {F}=(W,R,E)$
where
$\mathfrak {F}=(W,R,E)$
where
![]() $(W,R)$
is an
$(W,R)$
is an
![]() $\mathsf {IPC}$
-frameFootnote
6
and E is an equivalence relation on W satisfying
$\mathsf {IPC}$
-frameFootnote
6
and E is an equivalence relation on W satisfying
that is, if
![]() $xEy$
and
$xEy$
and
![]() $yRz$
, then there is
$yRz$
, then there is
![]() $w\in W$
such that
$w\in W$
such that
![]() $xRw$
and
$xRw$
and
![]() $wEz$
:
$wEz$
:

We refer to this condition as commutativity. We will sometimes refer to R as a ‘vertical relation’, and to E as a ‘horizontal relation’, as depicted in the diagram above.
Valuations on
![]() $\mathsf {MIPC}$
-frames are defined as for
$\mathsf {MIPC}$
-frames are defined as for
![]() $\mathsf {IPC}$
-frames; that is, a valuation
$\mathsf {IPC}$
-frames; that is, a valuation
![]() $\nu $
on
$\nu $
on
![]() $\mathfrak F=(W,R,E)$
is an assignment of R-upsets of
$\mathfrak F=(W,R,E)$
is an assignment of R-upsets of
![]() $\mathfrak F$
to propositional letters.Footnote
7
As usual, the truth relation in
$\mathfrak F$
to propositional letters.Footnote
7
As usual, the truth relation in
![]() $\mathfrak F$
is defined by induction. The clauses for the connectives
$\mathfrak F$
is defined by induction. The clauses for the connectives
![]() $\wedge ,\vee ,\to ,\neg $
are the same as for
$\wedge ,\vee ,\to ,\neg $
are the same as for
![]() $\mathsf {IPC}$
-frames:
$\mathsf {IPC}$
-frames:
 $$\begin{align*}\begin{array}{lcl} w\vDash_\nu p \quad &\text{iff} & \quad w\in\nu(p); \\ w\vDash_\nu\varphi\wedge\psi \quad &\text{iff}& \quad w\vDash_\nu\varphi \text{ and } w\vDash_\nu\psi;\\ w\vDash_\nu\varphi\vee\psi \quad &\text{iff}& \quad w\vDash_\nu\varphi \text{ or } w\vDash_\nu\psi;\\ w\vDash_\nu\varphi\to\psi \quad &\text{iff}& \quad (\text{for all } v)(wRv \text{ and } v\vDash_\nu\varphi \text{ imply } v\vDash_\nu\psi);\\ w\vDash_\nu\neg\varphi\quad &\text{iff} & \quad (\text{for all } v)(wRv \text{ implies } v\not\vDash_\nu\varphi).\\ \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{lcl} w\vDash_\nu p \quad &\text{iff} & \quad w\in\nu(p); \\ w\vDash_\nu\varphi\wedge\psi \quad &\text{iff}& \quad w\vDash_\nu\varphi \text{ and } w\vDash_\nu\psi;\\ w\vDash_\nu\varphi\vee\psi \quad &\text{iff}& \quad w\vDash_\nu\varphi \text{ or } w\vDash_\nu\psi;\\ w\vDash_\nu\varphi\to\psi \quad &\text{iff}& \quad (\text{for all } v)(wRv \text{ and } v\vDash_\nu\varphi \text{ imply } v\vDash_\nu\psi);\\ w\vDash_\nu\neg\varphi\quad &\text{iff} & \quad (\text{for all } v)(wRv \text{ implies } v\not\vDash_\nu\varphi).\\ \end{array} \end{align*}$$
To extend this to the truth relation for quantifier modalities, we first define a new relation Q on W as the composition
![]() $E\circ R$
; that is,
$E\circ R$
; that is,
![]() $xQy$
iff there is
$xQy$
iff there is
![]() $z\in W$
such that
$z\in W$
such that
![]() $xRz$
and
$xRz$
and
![]() $zEy$
:
$zEy$
:

Then Q is a quasi-order (reflexive and transitive) and
![]() $\forall ,\exists $
are interpreted in
$\forall ,\exists $
are interpreted in
![]() $\mathfrak F$
as follows:
$\mathfrak F$
as follows:
Sometimes we also write
![]() $(\mathfrak F, w) \vDash _\nu \varphi $
to emphasize the underlying frame
$(\mathfrak F, w) \vDash _\nu \varphi $
to emphasize the underlying frame
![]() $\mathfrak F$
or simply
$\mathfrak F$
or simply
![]() $w \vDash \varphi $
in case
$w \vDash \varphi $
in case
![]() $\mathfrak F$
and
$\mathfrak F$
and
![]() $\nu $
are clear from the context.
$\nu $
are clear from the context.
There is a close connection between algebraic and relational semantics for
![]() $\mathsf {MIPC}$
. To see this, let
$\mathsf {MIPC}$
. To see this, let
![]() $\mathfrak F=(W,R,E)$
be an
$\mathfrak F=(W,R,E)$
be an
![]() $\mathsf {MIPC}$
-frame. For
$\mathsf {MIPC}$
-frame. For
![]() $x\in W$
, let
$x\in W$
, let
Set
![]() $\mathfrak F^+=(\mathsf {Up}(\mathfrak F),\forall ,\exists )$
where
$\mathfrak F^+=(\mathsf {Up}(\mathfrak F),\forall ,\exists )$
where
![]() $\mathsf {Up}(\mathfrak F)$
is the Heyting algebra of R-upsets of
$\mathsf {Up}(\mathfrak F)$
is the Heyting algebra of R-upsets of
![]() $\mathfrak F$
, and for
$\mathfrak F$
, and for
![]() $U\in \mathsf {Up}(\mathfrak F)$
,
$U\in \mathsf {Up}(\mathfrak F)$
,
Then
![]() $\mathfrak F^+$
is a monadic Heyting algebra, and every monadic Heyting algebra is represented as a subalgebra of such. To see this, for a monadic Heyting algebra
$\mathfrak F^+$
is a monadic Heyting algebra, and every monadic Heyting algebra is represented as a subalgebra of such. To see this, for a monadic Heyting algebra
![]() $\mathfrak H=(H,\forall ,\exists )$
, let W be the set of prime filters of H, let R be the inclusion, and let E be defined by
$\mathfrak H=(H,\forall ,\exists )$
, let W be the set of prime filters of H, let R be the inclusion, and let E be defined by
![]() $\eta E \zeta $
iff
$\eta E \zeta $
iff
![]() $\eta \cap H_0=\zeta \cap H_0$
, where we recall that
$\eta \cap H_0=\zeta \cap H_0$
, where we recall that
![]() $H_0$
is the fixpoint subalgebra of H (see Remark 2.4). Then
$H_0$
is the fixpoint subalgebra of H (see Remark 2.4). Then
![]() $\mathfrak H_+ := (W,R,E)$
is an
$\mathfrak H_+ := (W,R,E)$
is an
![]() $\mathsf {MIPC}$
-frame (where
$\mathsf {MIPC}$
-frame (where
![]() $\eta Q\zeta $
iff
$\eta Q\zeta $
iff
![]() $\eta \cap H_0\subseteq \zeta \cap H_0$
) and there is an embedding
$\eta \cap H_0\subseteq \zeta \cap H_0$
) and there is an embedding
![]() $e:\mathfrak H\to \mathfrak (\mathfrak H_+)^+$
given by
$e:\mathfrak H\to \mathfrak (\mathfrak H_+)^+$
given by
In general, the embedding e is not onto, so to recognize the e-image of H in the Heyting algebra of upsets, we introduce the concept of a descriptive
![]() $\mathsf {MIPC}$
-frame. One way to do this is to introduce topology on an
$\mathsf {MIPC}$
-frame. One way to do this is to introduce topology on an
![]() $\mathsf {MIPC}$
-frame.
$\mathsf {MIPC}$
-frame.
We recall that a topological space is a Stone space if it is compact Hausdorff and zero-dimensional.Footnote
8
A relation R on a Stone space W is continuous if (i)
![]() $R(x)$
is closed for each
$R(x)$
is closed for each
![]() $x\in W$
and (ii) U clopen implies
$x\in W$
and (ii) U clopen implies
![]() $R^{-1}(U)$
is clopen, where
$R^{-1}(U)$
is clopen, where
Definition 2.7. An
![]() $\mathsf {MIPC}$
-frame
$\mathsf {MIPC}$
-frame
![]() $\mathfrak {F}=(W,R,E)$
is a descriptive
$\mathfrak {F}=(W,R,E)$
is a descriptive
![]() $\mathsf {MIPC}$
-frame if
$\mathsf {MIPC}$
-frame if
-
• W is a Stone space,
-
• R and Q are continuous relations,
-
• if A is a clopen R-upset, then
 $E(A)$
is a clopen R-upset.
$E(A)$
is a clopen R-upset.
Remark 2.8. This does not imply that A clopen implies
![]() $E(A)$
is clopen; see [Reference Bezhanishvili4, p. 32]. However, we do have that A closed implies
$E(A)$
is clopen; see [Reference Bezhanishvili4, p. 32]. However, we do have that A closed implies
![]() $E(A)$
is closed; see [Reference Bezhanishvili4, Lemma 7].
$E(A)$
is closed; see [Reference Bezhanishvili4, Lemma 7].
As follows from Esakia’s representation of Heyting algebras [Reference Esakia13], for a Heyting algebra H, there is a Stone topology on the set W of prime filters of H generated by the basis
the inclusion relation R on W is continuous, and e is a Heyting isomorphism from H onto the Heyting algebra of clopen R-upsets of W.
By [Reference Bezhanishvili4, Theorem 13], if
![]() $\mathfrak H=(H,\forall ,\exists )$
is a monadic Heyting algebra, then
$\mathfrak H=(H,\forall ,\exists )$
is a monadic Heyting algebra, then
![]() $(W,R,E)$
is a descriptive
$(W,R,E)$
is a descriptive
![]() $\mathsf {MIPC}$
-frame, which we denote by
$\mathsf {MIPC}$
-frame, which we denote by
![]() $\mathfrak H_*$
, and e is an isomorphism from
$\mathfrak H_*$
, and e is an isomorphism from
![]() $\mathfrak H$
onto the monadic Heyting algebra
$\mathfrak H$
onto the monadic Heyting algebra
![]() $(\mathfrak H_*)^*$
of clopen R-upsets of
$(\mathfrak H_*)^*$
of clopen R-upsets of
![]() $\mathfrak H_*$
. Thus, every monadic Heyting algebra can be thought of as the algebra of clopen R-upsets of some descriptive
$\mathfrak H_*$
. Thus, every monadic Heyting algebra can be thought of as the algebra of clopen R-upsets of some descriptive
![]() $\mathsf {MIPC}$
-frame. This representation together with Theorem 2.5 yields:
$\mathsf {MIPC}$
-frame. This representation together with Theorem 2.5 yields:
Theorem 2.9.
![]() $\mathsf {MIPC}\vdash \varphi \Leftrightarrow \mathfrak {F}\vDash \varphi $
for each descriptive
$\mathsf {MIPC}\vdash \varphi \Leftrightarrow \mathfrak {F}\vDash \varphi $
for each descriptive
![]() $\mathsf {MIPC}$
-frame
$\mathsf {MIPC}$
-frame
![]() $\mathfrak {F}$
.
$\mathfrak {F}$
.
If the descriptive
![]() $\mathsf {MIPC}$
-frame is finite, then the topology is discrete, and hence finite descriptive
$\mathsf {MIPC}$
-frame is finite, then the topology is discrete, and hence finite descriptive
![]() $\mathsf {MIPC}$
-frames are simply finite
$\mathsf {MIPC}$
-frames are simply finite
![]() $\mathsf {MIPC}$
-frames. It is well known that
$\mathsf {MIPC}$
-frames. It is well known that
![]() $\mathsf {MIPC}$
has the finite model property (FMP):
$\mathsf {MIPC}$
has the finite model property (FMP):
Theorem 2.10.
![]() $\mathsf {MIPC}\vdash \varphi \Leftrightarrow \mathfrak {F}\vDash \varphi $
for each finite
$\mathsf {MIPC}\vdash \varphi \Leftrightarrow \mathfrak {F}\vDash \varphi $
for each finite
![]() $\mathsf {MIPC}$
-frame
$\mathsf {MIPC}$
-frame
![]() $\mathfrak {F}$
.
$\mathfrak {F}$
.
This was first proved by Bull [Reference Bull10] using algebraic semantics. Bull’s proof contained a gap, which was later filled by Fischer-Servi [Reference Fischer-Servi23] and Ono [Reference Ono36] independently of each other. For a more frame-theoretic proof, using the technique of selective filtration, see [Reference Gabbay, Kurucz, Wolter and Zakharyaschev25, Section 10.3].
We finish Section 2.1 by recalling an important property of descriptive
![]() $\mathsf {MIPC}$
-frames, which will be useful later on.
$\mathsf {MIPC}$
-frames, which will be useful later on.
Definition 2.11. Let
![]() $\mathfrak {F}=(W,R,E)$
be a descriptive
$\mathfrak {F}=(W,R,E)$
be a descriptive
![]() $\mathsf {MIPC}$
-frame and let
$\mathsf {MIPC}$
-frame and let
![]() $A\subseteq W$
.
$A\subseteq W$
.
-
1. We say
 $x\in A$
is R-maximal in A if
$x\in A$
is R-maximal in A if
 $xRy$
and
$xRy$
and
 $y\in A$
imply
$y\in A$
imply
 $x=y$
.
$x=y$
. -
2. The R-maximum of A is the set of all R-maximal points of A, i.e.,
 $$ \begin{align*}\max A=\{x\in A \mid xRy\text{ and } y\in A \mbox{ imply } x=y\}.\end{align*} $$
$$ \begin{align*}\max A=\{x\in A \mid xRy\text{ and } y\in A \mbox{ imply } x=y\}.\end{align*} $$
The next lemma states that every point in the E-saturation of clopen A sees a point that is maximal in the E-saturation of A. The proof follows from the result of Fine [Reference Fine21] and Esakia [Reference Esakia16, Reference Esakia20] that can be phrased as follows: If A is a closed subset of a descriptive
![]() $\mathsf {IPC}$
-frame, then for each
$\mathsf {IPC}$
-frame, then for each
![]() $x\in A$
there is
$x\in A$
there is
![]() $y\in \max A$
such that
$y\in \max A$
such that
![]() $xRy$
. Since A clopen implies that
$xRy$
. Since A clopen implies that
![]() $E(A)$
is closed (see Remark 2.8), the proof is a consequence of the Fine-Esakia lemma.
$E(A)$
is closed (see Remark 2.8), the proof is a consequence of the Fine-Esakia lemma.
Lemma 2.12. Let
![]() $\mathfrak {F}=(W,R,E)$
be a descriptive
$\mathfrak {F}=(W,R,E)$
be a descriptive
![]() $\mathsf {MIPC}$
-frame. For each clopen A and
$\mathsf {MIPC}$
-frame. For each clopen A and
![]() $x\in E(A)$
, there is
$x\in E(A)$
, there is
![]() $y\in \max E(A)$
such that
$y\in \max E(A)$
such that
![]() $xRy$
.
$xRy$
.
2.2 Monadic modal logics
Let
![]() $\mathcal {ML}$
be the basic propositional modal language (with one modality
$\mathcal {ML}$
be the basic propositional modal language (with one modality
![]() $\Box $
). As usual, the least normal modal logic will be denoted by
$\Box $
). As usual, the least normal modal logic will be denoted by
![]() $\mathsf {K}$
, and normal modal logics are normal extensions of
$\mathsf {K}$
, and normal modal logics are normal extensions of
![]() $\mathsf {K}$
.
$\mathsf {K}$
.
Let
![]() $\mathcal {ML_{\forall }}$
be the bimodal language which enriches
$\mathcal {ML_{\forall }}$
be the bimodal language which enriches
![]() $\mathcal {ML}$
with the modality
$\mathcal {ML}$
with the modality
![]() $\forall $
. We use the abbreviation
$\forall $
. We use the abbreviation
![]() $\exists \varphi $
for
$\exists \varphi $
for
![]() $\neg \forall \neg \varphi $
.
$\neg \forall \neg \varphi $
.
Definition 2.13.
-
1. The monadic
 $\mathsf {K}$
is the least set of
$\mathsf {K}$
is the least set of
 $\mathcal {ML_{\forall }}$
-formulas containing
$\mathcal {ML_{\forall }}$
-formulas containing-
• the
 $\mathsf {K}$
-axiom for
$\mathsf {K}$
-axiom for
 $\Box $
,Footnote
9
$\Box $
,Footnote
9
-
• the
 $\mathsf {S5}$
-axioms for
$\mathsf {S5}$
-axioms for
 $\forall $
,Footnote
10
$\forall $
,Footnote
10
-
• the bridge axiom
 $\square \forall p\to \forall \square p$
,
$\square \forall p\to \forall \square p$
,
and closed under
 $\forall $
-necessitation
$\forall $
-necessitation
 $\frac {\varphi }{\forall \varphi }$
as well as under the usual rules of substitution, modus ponens, and
$\frac {\varphi }{\forall \varphi }$
as well as under the usual rules of substitution, modus ponens, and
 $\square $
-necessitation. We denote the monadic
$\square $
-necessitation. We denote the monadic
 $\mathsf {K}$
by
$\mathsf {K}$
by
 $\mathsf {MK}$
.
$\mathsf {MK}$
. -
-
2. A normal extension of
 $\mathsf {MK}$
is an extension of
$\mathsf {MK}$
is an extension of
 $\mathsf {MK}$
which is closed under the above rules of inference. We call normal extensions of
$\mathsf {MK}$
which is closed under the above rules of inference. We call normal extensions of
 $\mathsf {MK}$
normal monadic modal logics or simply mm-logics.
$\mathsf {MK}$
normal monadic modal logics or simply mm-logics. -
3. Let
 $\mathsf {L}$
be a normal modal logic (in
$\mathsf {L}$
be a normal modal logic (in
 $\mathcal {ML}$
). The least monadic extension
$\mathcal {ML}$
). The least monadic extension
 $\mathsf {ML}$
of
$\mathsf {ML}$
of
 $\mathsf {L}$
is the smallest mm-logic containing
$\mathsf {L}$
is the smallest mm-logic containing
 $\mathsf {MK}\cup \mathsf {L}$
.
$\mathsf {MK}\cup \mathsf {L}$
.
Remark 2.14.
-
1. Monadic modal logics are bimodal logics in the language with two modalities
 $\square ,\forall $
, where
$\square ,\forall $
, where
 $\forall $
is an
$\forall $
is an
 $\mathsf {S5}$
-modality. They correspond to expanding relativized products discussed in [Reference Gabbay, Kurucz, Wolter and Zakharyaschev25, Section 9].
$\mathsf {S5}$
-modality. They correspond to expanding relativized products discussed in [Reference Gabbay, Kurucz, Wolter and Zakharyaschev25, Section 9]. -
2. The formula
 $\forall \square p\to \square \forall p$
, which is the converse of the bridge axiom, and is the monadic version of Barcan’s formula, is not provable in
$\forall \square p\to \square \forall p$
, which is the converse of the bridge axiom, and is the monadic version of Barcan’s formula, is not provable in
 $\mathsf {MK}$
.
$\mathsf {MK}$
.
Algebraic semantics for monadic modal logics is given by monadic modal algebras.
Definition 2.15. A monadic modal algebra or simply an mm-algebra is a triple
![]() $(B,\square ,\forall )$
where
$(B,\square ,\forall )$
where
-
•
 $(B,\square )$
is a modal algebra,Footnote
11
$(B,\square )$
is a modal algebra,Footnote
11
-
•
 $(B,\forall )$
is an
$(B,\forall )$
is an
 $\mathsf {S5}$
-algebra,Footnote
12
$\mathsf {S5}$
-algebra,Footnote
12
-
•
 $\square \forall a\le \forall \square a$
.
$\square \forall a\le \forall \square a$
.
Remark 2.16. As with monadic Heyting algebras, the
![]() $\forall $
-fixpoints of an mm-algebra
$\forall $
-fixpoints of an mm-algebra
![]() $(B,\square ,\forall )$
form a subalgebra of the modal algebra
$(B,\square ,\forall )$
form a subalgebra of the modal algebra
![]() $(B,\square )$
, and each mm-algebra is represented as a pair
$(B,\square )$
, and each mm-algebra is represented as a pair
![]() $(B,B_0)$
of modal algebras such that the embedding of
$(B,B_0)$
of modal algebras such that the embedding of
![]() $B_0$
into B has a right adjoint (
$B_0$
into B has a right adjoint (
![]() $\forall $
).
$\forall $
).
Kripke semantics for mm-logics is given by the augmented Kripke frames of Esakia [Reference Esakia17].
Definition 2.17. An augmented Kripke frame is a triple
![]() $\mathfrak {F}=(W,R,E)$
where
$\mathfrak {F}=(W,R,E)$
where
![]() $(W,R)$
is a Kripke frameFootnote
13
and E is an equivalence relation on W satisfying commutativity, i.e.,
$(W,R)$
is a Kripke frameFootnote
13
and E is an equivalence relation on W satisfying commutativity, i.e.,
![]() $(R\circ E)(x)\subseteq (E\circ R)(x)$
for all
$(R\circ E)(x)\subseteq (E\circ R)(x)$
for all
![]() $x\in W$
; that is, if
$x\in W$
; that is, if
![]() $xEy$
and
$xEy$
and
![]() $yRz$
, then there is
$yRz$
, then there is
![]() $w\in W$
such that
$w\in W$
such that
![]() $xRw$
and
$xRw$
and
![]() $wEz$
:
$wEz$
:

As with
![]() $\mathsf {MIPC}$
-frames, we may refer to R as a ‘vertical relation’, and to E as a ‘horizontal relation’, as depicted in the diagram above.
$\mathsf {MIPC}$
-frames, we may refer to R as a ‘vertical relation’, and to E as a ‘horizontal relation’, as depicted in the diagram above.
Valuations on augmented Kripke frames are defined analogously to Kripke frames; that is, a valuation
![]() $\nu $
on an augmented Kripke frame
$\nu $
on an augmented Kripke frame
![]() $\mathfrak {F}=(W,R,E)$
assigns subsets of W to propositional letters. The truth relation clauses for the connectives
$\mathfrak {F}=(W,R,E)$
assigns subsets of W to propositional letters. The truth relation clauses for the connectives
![]() $\vee , \neg $
, the modality
$\vee , \neg $
, the modality
![]() $ \Box $
, and its dual
$ \Box $
, and its dual
![]() $\Diamond $
are defined as for Kripke frames:
$\Diamond $
are defined as for Kripke frames:
 $$ \begin{align*} &x \vDash_{\nu} p \quad &\text{ iff }&\quad x\in\nu(p); \\ &x \vDash_{\nu}\psi\vee\chi \quad &\text{ iff } & \quad x \vDash_{\nu}\psi\text{ or } x \vDash_{\nu}\chi; \\ &x \vDash_{\nu}\neg\psi \quad& \text{ iff } & \quad x \not\vDash_{\nu}\psi; \\ & x \vDash_{\nu}\square\psi \quad & \text{ iff }&\quad (\text{for all } y\in W) (xRy\Rightarrow y\vDash_{\nu}\psi); \\ &x \vDash_{\nu}\lozenge\psi \quad & \text{ iff }&\quad (\text{there exists } y\in W )(xRy\text{ and } y \vDash_{\nu}\psi).\\ &&&\hspace{-100pt}\text{The modality }\forall \text{ and its dual }\exists\text{ are interpreted via the relation }E\text{ as follows:}\\ & x\vDash_{\nu}\forall\varphi\quad &\text{iff} &\quad (\text{for all } y\in W)(xEy\Rightarrow y\vDash_{\nu}\varphi);\\ & x\vDash_{\nu}\exists\varphi\quad & \text{iff} &\quad(\text{there exists } y\in W)(xEy\text{ and }y\vDash_{\nu}\varphi). \end{align*} $$
$$ \begin{align*} &x \vDash_{\nu} p \quad &\text{ iff }&\quad x\in\nu(p); \\ &x \vDash_{\nu}\psi\vee\chi \quad &\text{ iff } & \quad x \vDash_{\nu}\psi\text{ or } x \vDash_{\nu}\chi; \\ &x \vDash_{\nu}\neg\psi \quad& \text{ iff } & \quad x \not\vDash_{\nu}\psi; \\ & x \vDash_{\nu}\square\psi \quad & \text{ iff }&\quad (\text{for all } y\in W) (xRy\Rightarrow y\vDash_{\nu}\psi); \\ &x \vDash_{\nu}\lozenge\psi \quad & \text{ iff }&\quad (\text{there exists } y\in W )(xRy\text{ and } y \vDash_{\nu}\psi).\\ &&&\hspace{-100pt}\text{The modality }\forall \text{ and its dual }\exists\text{ are interpreted via the relation }E\text{ as follows:}\\ & x\vDash_{\nu}\forall\varphi\quad &\text{iff} &\quad (\text{for all } y\in W)(xEy\Rightarrow y\vDash_{\nu}\varphi);\\ & x\vDash_{\nu}\exists\varphi\quad & \text{iff} &\quad(\text{there exists } y\in W)(xEy\text{ and }y\vDash_{\nu}\varphi). \end{align*} $$
We also use the notation
![]() $(\mathfrak F, w) \vDash _\nu \varphi $
or
$(\mathfrak F, w) \vDash _\nu \varphi $
or
![]() $w \vDash \varphi $
.
$w \vDash \varphi $
.
As in the case of
![]() $\mathsf {MIPC}$
, there is a close connection between algebraic and relational semantics for mm-logics. For an augmented Kripke frame
$\mathsf {MIPC}$
, there is a close connection between algebraic and relational semantics for mm-logics. For an augmented Kripke frame
![]() $\mathfrak F=(W,R,E)$
, set
$\mathfrak F=(W,R,E)$
, set
![]() $\mathfrak F^+=(\wp (\mathfrak F),\square ,\forall )$
where
$\mathfrak F^+=(\wp (\mathfrak F),\square ,\forall )$
where
![]() $\wp (\mathfrak F)$
is the powerset of
$\wp (\mathfrak F)$
is the powerset of
![]() $\mathfrak F$
, and for
$\mathfrak F$
, and for
![]() $U\in \mathsf {Up}(\mathfrak F)$
,
$U\in \mathsf {Up}(\mathfrak F)$
,
Then
![]() $\mathfrak F^+$
is an mm-algebra, and every mm-algebra is represented as a subalgebra of such. To see this, for an mm-algebra
$\mathfrak F^+$
is an mm-algebra, and every mm-algebra is represented as a subalgebra of such. To see this, for an mm-algebra
![]() $\mathfrak B=(B,\square ,\forall )$
, let W be the set of ultrafilters of B, and let R and E be defined by
$\mathfrak B=(B,\square ,\forall )$
, let W be the set of ultrafilters of B, and let R and E be defined by
Then
![]() $\mathfrak B_+=(W,R,E)$
is an augmented Kripke frame and there is an embedding
$\mathfrak B_+=(W,R,E)$
is an augmented Kripke frame and there is an embedding
![]() $e:\mathfrak B\to \mathfrak (\mathfrak B_+)^+$
given by
$e:\mathfrak B\to \mathfrak (\mathfrak B_+)^+$
given by
In general, the embedding e is not onto, so to recognize the e-image of
![]() $\mathfrak B$
in the powerset, we introduce the concept of a descriptive augmented Kripke frame. As in the case of
$\mathfrak B$
in the powerset, we introduce the concept of a descriptive augmented Kripke frame. As in the case of
![]() $\mathsf {MIPC}$
, we do this by introducing topology on augmented Kripke frames.
$\mathsf {MIPC}$
, we do this by introducing topology on augmented Kripke frames.
Definition 2.18. An augmented Kripke frame
![]() $\mathfrak {F}=(W,R,E)$
is a descriptive augmented Kripke frame if W is a Stone space and R and E are continuous relations.
$\mathfrak {F}=(W,R,E)$
is a descriptive augmented Kripke frame if W is a Stone space and R and E are continuous relations.
As follows from the representation of modal algebras, for a modal algebra B, there is a Stone topology on the set W of ultrafilters of B generated by the basis
![]() $\{e(a)\mid a\in B\}$
, the relation R on W is continuous, and e is a modal isomorphism from B onto the modal algebra of clopen subsets of W.
$\{e(a)\mid a\in B\}$
, the relation R on W is continuous, and e is a modal isomorphism from B onto the modal algebra of clopen subsets of W.
If
![]() $\mathfrak B=(B,\square ,\forall )$
is an mm-algebra, then
$\mathfrak B=(B,\square ,\forall )$
is an mm-algebra, then
![]() $(W,R,E)$
is a descriptive augmented Kripke frame, which we denote by
$(W,R,E)$
is a descriptive augmented Kripke frame, which we denote by
![]() $\mathfrak B_*$
, and e is an isomorphism from
$\mathfrak B_*$
, and e is an isomorphism from
![]() $\mathfrak B$
onto the mm-algebra
$\mathfrak B$
onto the mm-algebra
![]() $(\mathfrak B_*)^*$
of clopen subsets of
$(\mathfrak B_*)^*$
of clopen subsets of
![]() $\mathfrak B_*$
. Thus, every mm-algebra can be thought of as the algebra of clopen subsets of some descriptive augmented Kripke frame.
$\mathfrak B_*$
. Thus, every mm-algebra can be thought of as the algebra of clopen subsets of some descriptive augmented Kripke frame.
2.3
 $\mathsf {MS4}$
,
$\mathsf {MS4}$
,
 $\mathsf {MGrz}$
, and
$\mathsf {MGrz}$
, and
 $\mathsf {MGL}$
$\mathsf {MGL}$
We next focus on the least monadic extension
![]() $\mathsf {MS4}$
of the modal logic
$\mathsf {MS4}$
of the modal logic
![]() $\mathsf {S4}$
.
$\mathsf {S4}$
.
Definition 2.19.
-
1. The monadic
 $\mathsf {S4}$
is the least monadic extension
$\mathsf {S4}$
is the least monadic extension
 $\mathsf {MS4}$
of the modal logic
$\mathsf {MS4}$
of the modal logic
 $\mathsf {S4}$
.
$\mathsf {S4}$
. -
2. An
 $\mathsf {MS4}$
-algebra is an mm-algebra
$\mathsf {MS4}$
-algebra is an mm-algebra
 $(B,\square ,\forall )$
such that
$(B,\square ,\forall )$
such that
 $(B,\square )$
is an
$(B,\square )$
is an
 $\mathsf {S4}$
-algebra.
$\mathsf {S4}$
-algebra. -
3. An
 $\mathsf {MS4}$
-frame is an augmented Kripke frame
$\mathsf {MS4}$
-frame is an augmented Kripke frame
 $\mathfrak {F}=(W,R,E)$
such that
$\mathfrak {F}=(W,R,E)$
such that
 $(W,R)$
is an
$(W,R)$
is an
 $\mathsf {S4}$
-frame.
$\mathsf {S4}$
-frame. -
4. A descriptive
 $\mathsf {MS4}$
-frame is a descriptive augmented Kripke frame
$\mathsf {MS4}$
-frame is a descriptive augmented Kripke frame
 $\mathfrak {F}=(W,R,E)$
such that
$\mathfrak {F}=(W,R,E)$
such that
 $(W,R,E)$
is an
$(W,R,E)$
is an
 $\mathsf {MS4}$
-frame.
$\mathsf {MS4}$
-frame.
As in the case of
![]() $\mathsf {MIPC}$
, we have the following standard completeness results:
$\mathsf {MIPC}$
, we have the following standard completeness results:
Theorem 2.20.
-
1.
 $\mathsf {MS4}\vdash \varphi \Leftrightarrow \mathfrak {B}\vDash \varphi $
for each
$\mathsf {MS4}\vdash \varphi \Leftrightarrow \mathfrak {B}\vDash \varphi $
for each
 $\mathsf {MS4}$
-algebra
$\mathsf {MS4}$
-algebra
 $\mathfrak {B}$
.
$\mathfrak {B}$
. -
2.
 $\mathsf {MS4}\vdash \varphi \Leftrightarrow \mathfrak {F}\vDash \varphi $
for each descriptive
$\mathsf {MS4}\vdash \varphi \Leftrightarrow \mathfrak {F}\vDash \varphi $
for each descriptive
 $\mathsf {MS4}$
-frame
$\mathsf {MS4}$
-frame
 $\mathfrak {F}$
.
$\mathfrak {F}$
.
We also have that
![]() $\mathsf {MS4}$
has the finite model property (see [Reference Bezhanishvili and Carai6] and the references therein).
$\mathsf {MS4}$
has the finite model property (see [Reference Bezhanishvili and Carai6] and the references therein).
Theorem 2.21.
![]() $\mathsf {MS4}\vdash \varphi \Leftrightarrow \mathfrak {F}\vDash \varphi $
for each finite
$\mathsf {MS4}\vdash \varphi \Leftrightarrow \mathfrak {F}\vDash \varphi $
for each finite
![]() $\mathsf {MS4}$
-frame
$\mathsf {MS4}$
-frame
![]() $\mathfrak {F}$
.
$\mathfrak {F}$
.
Let
![]() $\mathfrak {F}=(W,R,E)$
be a descriptive
$\mathfrak {F}=(W,R,E)$
be a descriptive
![]() $\mathsf {MS4}$
-frame and
$\mathsf {MS4}$
-frame and
![]() $A \subseteq W$
. The R-maximal points of A and the R-maximum of A are defined as in Definition 2.11. In the context of
$A \subseteq W$
. The R-maximal points of A and the R-maximum of A are defined as in Definition 2.11. In the context of
![]() $\mathsf {MS4}$
-frames, we also need the notion of quasi-R-maximal points.
$\mathsf {MS4}$
-frames, we also need the notion of quasi-R-maximal points.
Definition 2.22. Let
![]() $\mathfrak {F}=(W,R,E)$
be a descriptive
$\mathfrak {F}=(W,R,E)$
be a descriptive
![]() $\mathsf {MS4}$
-frame and
$\mathsf {MS4}$
-frame and
![]() $A \subseteq W$
.
$A \subseteq W$
.
-
1. We say
 $x\in A$
is quasi-R-maximal in A if
$x\in A$
is quasi-R-maximal in A if
 $xRy$
and
$xRy$
and
 $y\in A$
imply
$y\in A$
imply
 $yRx$
.
$yRx$
. -
2. The quasi-R-maximum of A is the set of all quasi-
 $R$
-maximal points of A, i.e.,
$R$
-maximal points of A, i.e.,  $$ \begin{align*}\text{q}\hspace{-.25em}\max A=\{x\in A \mid xRy\text{ and }y\in A \text{ imply } yRx\}.\end{align*} $$
$$ \begin{align*}\text{q}\hspace{-.25em}\max A=\{x\in A \mid xRy\text{ and }y\in A \text{ imply } yRx\}.\end{align*} $$
Note that
![]() $\max A\subseteq \text {q}\hspace {-.25em}\max A$
as R is reflexive, but not conversely. The following lemma is a consequence of the Fine-Esakia lemma [Reference Esakia16, Reference Esakia20, Reference Fine21] for descriptive
$\max A\subseteq \text {q}\hspace {-.25em}\max A$
as R is reflexive, but not conversely. The following lemma is a consequence of the Fine-Esakia lemma [Reference Esakia16, Reference Esakia20, Reference Fine21] for descriptive
![]() $\mathsf {S4}$
-frames.
$\mathsf {S4}$
-frames.
Lemma 2.23. Let
![]() $\mathfrak {F}=(W,R,E)$
be a descriptive
$\mathfrak {F}=(W,R,E)$
be a descriptive
![]() $\mathsf {MS4}$
-frame. For each closed
$\mathsf {MS4}$
-frame. For each closed
![]() $A \subseteq W$
we have
$A \subseteq W$
we have
![]() $A\subseteq R^{-1}\mathrm{q}\kern-2pt\max A$
.
$A\subseteq R^{-1}\mathrm{q}\kern-2pt\max A$
.
Definition 2.24.
-
1. The monadic
 $\mathsf {Grz}$
is the least monadic extension
$\mathsf {Grz}$
is the least monadic extension
 $\mathsf {MGrz}$
of Grzegorczyk’s logic
$\mathsf {MGrz}$
of Grzegorczyk’s logic
 $\mathsf {Grz}$
.
$\mathsf {Grz}$
. -
2. An
 $\mathsf {MGrz}$
-algebra is an mm-algebra
$\mathsf {MGrz}$
-algebra is an mm-algebra
 $(B,\square ,\forall )$
such that
$(B,\square ,\forall )$
such that
 $(B,\square )$
is a
$(B,\square )$
is a
 $\mathsf {Grz}$
-algebra.
$\mathsf {Grz}$
-algebra. -
3. An
 $\mathsf {MGrz}$
-frame is an augmented Kripke frame
$\mathsf {MGrz}$
-frame is an augmented Kripke frame
 $\mathfrak {F}=(W,R,E)$
such that
$\mathfrak {F}=(W,R,E)$
such that
 $(W,R)$
is a
$(W,R)$
is a
 $\mathsf {Grz}$
-frame.
$\mathsf {Grz}$
-frame. -
4. A descriptive
 $\mathsf {MGrz}$
-frame is a descriptive
$\mathsf {MGrz}$
-frame is a descriptive
 $\mathsf {S4}$
-frame
$\mathsf {S4}$
-frame
 $\mathfrak {F}=(W,R,E)$
validating Grzegorczyk’s axiom
$\mathfrak {F}=(W,R,E)$
validating Grzegorczyk’s axiom
 $\mathsf {grz}$
.
$\mathsf {grz}$
.
Again, we have the following standard completeness results:
Theorem 2.25.
-
1.
 $\mathsf {MGrz}\vdash \varphi \Leftrightarrow \mathfrak {B}\vDash \varphi $
for each
$\mathsf {MGrz}\vdash \varphi \Leftrightarrow \mathfrak {B}\vDash \varphi $
for each
 $\mathsf {MGrz}$
-algebra
$\mathsf {MGrz}$
-algebra
 $\mathfrak {B}$
.
$\mathfrak {B}$
. -
2.
 $\mathsf {MGrz}\vdash \varphi \Leftrightarrow \mathfrak {F}\vDash \varphi $
for each descriptive
$\mathsf {MGrz}\vdash \varphi \Leftrightarrow \mathfrak {F}\vDash \varphi $
for each descriptive
 $\mathsf {MGrz}$
-frame
$\mathsf {MGrz}$
-frame
 $\mathfrak {F}$
.
$\mathfrak {F}$
.
It is well known that an
![]() $\mathsf {S4}$
-frame
$\mathsf {S4}$
-frame
![]() $\mathfrak {F}=(W,R)$
is a
$\mathfrak {F}=(W,R)$
is a
![]() $\mathsf {Grz}$
-frame iff R is a Noetherian partial order; that is, a partial order with no infinite ascending chains (of distinct points). Thus, if
$\mathsf {Grz}$
-frame iff R is a Noetherian partial order; that is, a partial order with no infinite ascending chains (of distinct points). Thus, if
![]() $\mathfrak {F}$
is finite, then
$\mathfrak {F}$
is finite, then
![]() $\mathfrak {F}$
is a
$\mathfrak {F}$
is a
![]() $\mathsf {Grz}$
-frame iff R is a partial order.
$\mathsf {Grz}$
-frame iff R is a partial order.
It is a result of Esakia that a descriptive
![]() $\mathsf {S4}$
-frame
$\mathsf {S4}$
-frame
![]() $\mathfrak {F}=(W,R)$
is a descriptive
$\mathfrak {F}=(W,R)$
is a descriptive
![]() $\mathsf {Grz}$
-frame iff for each clopen
$\mathsf {Grz}$
-frame iff for each clopen
![]() $A \subseteq W$
the R-maximal and quasi-R-maximal points of A coincide. These results clearly hold for
$A \subseteq W$
the R-maximal and quasi-R-maximal points of A coincide. These results clearly hold for
![]() $\mathsf {MGrz}$
as well.
$\mathsf {MGrz}$
as well.
Lemma 2.26. [Reference Esakia15]
-
1. Let
 $\mathfrak {F}=(W,R,E)$
be a descriptive
$\mathfrak {F}=(W,R,E)$
be a descriptive
 $\mathsf {MS4}$
-frame. Then
$\mathsf {MS4}$
-frame. Then
 $\mathfrak {F}\vDash \mathsf {grz}$
iff for each clopen A we have
$\mathfrak {F}\vDash \mathsf {grz}$
iff for each clopen A we have
 $\mathrm{q}\hspace {-.25em}\max A=\max A$
.
$\mathrm{q}\hspace {-.25em}\max A=\max A$
. -
2. Let
 $\mathfrak {F}=(W,R,E)$
be a descriptive
$\mathfrak {F}=(W,R,E)$
be a descriptive
 $\mathsf {MGrz}$
-frame. For each clopen A we have
$\mathsf {MGrz}$
-frame. For each clopen A we have
 $A\subseteq R^{-1}\max A$
.
$A\subseteq R^{-1}\max A$
.
Definition 2.27.
-
1. The monadic
 $\mathsf {GL}$
is the least monadic extension
$\mathsf {GL}$
is the least monadic extension
 $\mathsf {MGL}$
of the Gödel–Löb logic
$\mathsf {MGL}$
of the Gödel–Löb logic
 $\mathsf {GL}$
.
$\mathsf {GL}$
. -
2. An
 $\mathsf {MGL}$
-algebra is an mm-algebra
$\mathsf {MGL}$
-algebra is an mm-algebra
 $(B,\square ,\forall )$
such that
$(B,\square ,\forall )$
such that
 $(B,\square )$
is a
$(B,\square )$
is a
 $\mathsf {GL}$
-algebra.
$\mathsf {GL}$
-algebra. -
3. An
 $\mathsf {MGL}$
-frame is an augmented Kripke frame
$\mathsf {MGL}$
-frame is an augmented Kripke frame
 $\mathfrak {F}=(W,R,E)$
such that
$\mathfrak {F}=(W,R,E)$
such that
 $(W,R)$
is a
$(W,R)$
is a
 $\mathsf {GL}$
-frame.
$\mathsf {GL}$
-frame. -
4. A descriptive
 $\mathsf {MGL}$
-frame is a descriptive augmented Kripke frame
$\mathsf {MGL}$
-frame is a descriptive augmented Kripke frame
 $\mathfrak {F}=(W,R,E)$
validating
$\mathfrak {F}=(W,R,E)$
validating
 $\mathsf {gl}$
.
$\mathsf {gl}$
.
As before, we have the following standard completeness results:
Theorem 2.28.
-
1.
 $\mathsf {MGL}\vdash \varphi \Leftrightarrow \mathfrak {B}\vDash \varphi $
for each
$\mathsf {MGL}\vdash \varphi \Leftrightarrow \mathfrak {B}\vDash \varphi $
for each
 $\mathsf {MGL}$
-algebra
$\mathsf {MGL}$
-algebra
 $\mathfrak {B}$
.
$\mathfrak {B}$
. -
2.
 $\mathsf {MGL}\vdash \varphi \Leftrightarrow \mathfrak {F}\vDash \varphi $
for each descriptive
$\mathsf {MGL}\vdash \varphi \Leftrightarrow \mathfrak {F}\vDash \varphi $
for each descriptive
 $\mathsf {MGL}$
-frame
$\mathsf {MGL}$
-frame
 $\mathfrak {F}$
.
$\mathfrak {F}$
.
It is well known that a Kripke frame
![]() $\mathfrak {F}=(W,R)$
is a
$\mathfrak {F}=(W,R)$
is a
![]() $\mathsf {GL}$
-frame iff R is transitive and dually well founded (no infinite ascending chains). Call R a strict partial order if R is irreflexive and transitive. If W is finite, then
$\mathsf {GL}$
-frame iff R is transitive and dually well founded (no infinite ascending chains). Call R a strict partial order if R is irreflexive and transitive. If W is finite, then
![]() $\mathfrak {F}$
is a
$\mathfrak {F}$
is a
![]() $\mathsf {GL}$
-frame iff R is a strict partial order.
$\mathsf {GL}$
-frame iff R is a strict partial order.
A characterization of descriptive
![]() $\mathsf {GL}$
-frames was originally established by Esakia and given in [Reference Abashidze1]. It generalizes directly to descriptive
$\mathsf {GL}$
-frames was originally established by Esakia and given in [Reference Abashidze1]. It generalizes directly to descriptive
![]() $\mathsf {MGL}$
-frames. For a transitive frame
$\mathsf {MGL}$
-frames. For a transitive frame
![]() $\mathfrak {F}=(W,R)$
and
$\mathfrak {F}=(W,R)$
and
![]() $A\subseteq W$
, define the irreflexive maximum of A by
$A\subseteq W$
, define the irreflexive maximum of A by
Lemma 2.29. [Reference Abashidze1]
Let
![]() $\mathfrak {F}=(W,R,E)$
be a descriptive augmented Kripke frame. Then
$\mathfrak {F}=(W,R,E)$
be a descriptive augmented Kripke frame. Then
![]() $\mathfrak {F}$
is a descriptive
$\mathfrak {F}$
is a descriptive
![]() $\mathsf {MGL}$
-frame iff
$\mathsf {MGL}$
-frame iff
![]() $\mathfrak F$
is transitive and
$\mathfrak F$
is transitive and
![]() $A\subseteq \mu (A)\cup R^{-1}\mu (A)$
for each clopen A.
$A\subseteq \mu (A)\cup R^{-1}\mu (A)$
for each clopen A.
Thus, a descriptive augmented Kripke frame is a descriptive
![]() $\mathsf {MGL}$
-frame iff it is transitive and each point in a clopen set is either in the irreflexive maximum of the clopen or sees a point in the irreflexive maximum. It was observed by Japaridze that
$\mathsf {MGL}$
-frame iff it is transitive and each point in a clopen set is either in the irreflexive maximum of the clopen or sees a point in the irreflexive maximum. It was observed by Japaridze that
![]() $\mathsf {MGL}$
has the finite model property.
$\mathsf {MGL}$
has the finite model property.
Theorem 2.30. [Reference Japaridze30]
![]() $\mathsf {MGL}\vdash \varphi \Leftrightarrow \mathfrak {F}\vDash \varphi $
for all finite
$\mathsf {MGL}\vdash \varphi \Leftrightarrow \mathfrak {F}\vDash \varphi $
for all finite
![]() $\mathsf {MGL}$
-frames
$\mathsf {MGL}$
-frames
![]() $\mathfrak {F}$
.
$\mathfrak {F}$
.
3 The Gödel and splitting translations in the monadic setting
In this section we discuss the Gödel and splitting translations in the monadic setting. While the Gödel translation embeds
![]() $\mathsf {MIPC}$
fully and faithfully into
$\mathsf {MIPC}$
fully and faithfully into
![]() $\mathsf {MGrz}$
, the splitting translation from
$\mathsf {MGrz}$
, the splitting translation from
![]() $\mathsf {MGrz}$
into
$\mathsf {MGrz}$
into
![]() $\mathsf {MGL}$
does not yield a faithful embedding.
$\mathsf {MGL}$
does not yield a faithful embedding.
3.1 Gödel translation
The Gödel translation extends to the monadic setting by defining
 $$ \begin{align*} (\forall\varphi)^t & = \square\forall \varphi^t,\\ (\exists\varphi)^t & = \exists \varphi^t. \end{align*} $$
$$ \begin{align*} (\forall\varphi)^t & = \square\forall \varphi^t,\\ (\exists\varphi)^t & = \exists \varphi^t. \end{align*} $$
Using algebraic semantics, Fisher-Servi [Reference Fischer-Servi22, Reference Fischer-Servi23] proved that this provides a full and faithful embedding of
![]() $\mathsf {MIPC}$
into
$\mathsf {MIPC}$
into
![]() $\mathsf {MS4}$
. The proof also yields a full and faithful embedding of
$\mathsf {MS4}$
. The proof also yields a full and faithful embedding of
![]() $\mathsf {MIPC}$
into
$\mathsf {MIPC}$
into
![]() $\mathsf {MGrz}$
. Below we give an alternate proof of this result, using relational semantics. The proof extends a semantical proof that
$\mathsf {MGrz}$
. Below we give an alternate proof of this result, using relational semantics. The proof extends a semantical proof that
![]() $\mathsf {IPC}\vdash \varphi $
iff
$\mathsf {IPC}\vdash \varphi $
iff
![]() $\mathsf {S4}\vdash \varphi ^t$
as given, e.g., in [Reference Chagrov and Zakharyaschev12, pp. 96–97].
$\mathsf {S4}\vdash \varphi ^t$
as given, e.g., in [Reference Chagrov and Zakharyaschev12, pp. 96–97].
For notational simplicity, we abbreviate the formula
![]() $\square \forall \psi $
as
$\square \forall \psi $
as
![]() $\blacksquare \psi $
and the formula
$\blacksquare \psi $
and the formula
![]() $\lozenge \exists \psi $
as
$\lozenge \exists \psi $
as
![]() $\blacklozenge \psi $
. Observe that this keeps the duality between box and diamond since
$\blacklozenge \psi $
. Observe that this keeps the duality between box and diamond since
![]() $\blacksquare \psi =\square \forall \psi =\neg \lozenge \neg \neg \exists \neg \psi ,$
which is provably equivalent to
$\blacksquare \psi =\square \forall \psi =\neg \lozenge \neg \neg \exists \neg \psi ,$
which is provably equivalent to
![]() $\neg \lozenge \exists \neg \psi =\neg \blacklozenge \neg \psi $
.
$\neg \lozenge \exists \neg \psi =\neg \blacklozenge \neg \psi $
.
Remark 3.1. The modalities
![]() $\blacksquare ,\blacklozenge $
are
$\blacksquare ,\blacklozenge $
are
![]() $\mathsf {S4}$
-modalities which can be modeled using the relation
$\mathsf {S4}$
-modalities which can be modeled using the relation
![]() $Q=E\circ R$
, i.e., we have
$Q=E\circ R$
, i.e., we have
 $$\begin{align*}& w \vDash\blacksquare\varphi\quad\text{iff}\quad (\text{for all } v)(wQv \text{ implies } v\vDash\varphi);\\ & w \vDash\blacklozenge\varphi\quad\text{iff}\quad (\text{there exists } v)(wQv\text{ and } v\vDash\varphi). \end{align*}$$
$$\begin{align*}& w \vDash\blacksquare\varphi\quad\text{iff}\quad (\text{for all } v)(wQv \text{ implies } v\vDash\varphi);\\ & w \vDash\blacklozenge\varphi\quad\text{iff}\quad (\text{there exists } v)(wQv\text{ and } v\vDash\varphi). \end{align*}$$
Using this notation, the
![]() $\forall $
-step in the Gödel translation is
$\forall $
-step in the Gödel translation is
For an
![]() $\mathsf {MS4}$
-frame
$\mathsf {MS4}$
-frame
![]() $\mathfrak {F}=(W, R, E)$
define an equivalence relation
$\mathfrak {F}=(W, R, E)$
define an equivalence relation
![]() $\sim $
on
$\sim $
on
![]() $\mathfrak {F}$
by
$\mathfrak {F}$
by
Let
![]() $[x]$
be the equivalence class of x, and let
$[x]$
be the equivalence class of x, and let
![]() $W_{\sim }=W/{\sim }$
be the set of all equivalence classes. Define
$W_{\sim }=W/{\sim }$
be the set of all equivalence classes. Define
![]() $R_{\sim }$
and
$R_{\sim }$
and
![]() $E_{\sim }$
on
$E_{\sim }$
on
![]() $W_{\sim }$
by
$W_{\sim }$
by
 $$ \begin{align*} [x] R_{\sim} [y] \quad &\text{iff} \quad xRy; \quad \\ [x] E_{\sim} [y] \quad &\text{iff} \quad xQy \text{ and } yQx. \end{align*} $$
$$ \begin{align*} [x] R_{\sim} [y] \quad &\text{iff} \quad xRy; \quad \\ [x] E_{\sim} [y] \quad &\text{iff} \quad xQy \text{ and } yQx. \end{align*} $$
That
![]() $E_\sim $
is well defined follows from
$E_\sim $
is well defined follows from
![]() $R \circ Q \circ R \subseteq Q$
which is true by commutativity in
$R \circ Q \circ R \subseteq Q$
which is true by commutativity in
![]() $\mathfrak F$
and transitivity of R. Let
$\mathfrak F$
and transitivity of R. Let
![]() $\mathfrak {F}_{\sim }=(W_{\sim }, R_{\sim }, E_{\sim })$
. Set
$\mathfrak {F}_{\sim }=(W_{\sim }, R_{\sim }, E_{\sim })$
. Set
![]() $Q_\sim = E_\sim \circ R_\sim $
.
$Q_\sim = E_\sim \circ R_\sim $
.
Lemma 3.2. Let
![]() $\mathfrak {F}=(W, R, E)$
be an
$\mathfrak {F}=(W, R, E)$
be an
![]() $\mathsf {MS4}$
-frame and
$\mathsf {MS4}$
-frame and
![]() $x, y \in W$
.
$x, y \in W$
.
-
1.
 $x E y$
implies
$x E y$
implies
 $[x] E_\sim [y]$
;
$[x] E_\sim [y]$
; -
2.
 $x Q y$
iff
$x Q y$
iff
 $[x] Q_\sim [y]$
.
$[x] Q_\sim [y]$
.
Proof. (1) If
![]() $x E y$
, then
$x E y$
, then
![]() $x Q y$
and
$x Q y$
and
![]() $y Q x$
, so
$y Q x$
, so
![]() $[x] E_\sim [y]$
by definition of
$[x] E_\sim [y]$
by definition of
![]() $E_\sim $
.
$E_\sim $
.
(2) Suppose that
![]() $x Q y$
. Then there is
$x Q y$
. Then there is
![]() $y'$
with
$y'$
with
![]() $x R y'$
and
$x R y'$
and
![]() $y' E y$
. Therefore,
$y' E y$
. Therefore,
![]() $[x] R_{\sim} [y']$
by definition of
$[x] R_{\sim} [y']$
by definition of
![]() $R_{\sim}$
and
$R_{\sim}$
and
![]() $[y'] E_\sim [y]$
by (1). Thus,
$[y'] E_\sim [y]$
by (1). Thus,
![]() $[x] Q_\sim [y]$
. Conversely, if
$[x] Q_\sim [y]$
. Conversely, if
![]() $[x] Q_\sim [y]$
, then there is
$[x] Q_\sim [y]$
, then there is
![]() $[y']$
with
$[y']$
with
![]() $[x] R_\sim [y']$
and
$[x] R_\sim [y']$
and
![]() $[y'] E_\sim [y]$
. By the definitions of
$[y'] E_\sim [y]$
. By the definitions of
![]() $R_\sim $
and
$R_\sim $
and
![]() $E_\sim $
, we have
$E_\sim $
, we have
![]() $x R y'$
and
$x R y'$
and
![]() $y' Q y$
. Thus,
$y' Q y$
. Thus,
![]() $x Q y$
.⊣
$x Q y$
.⊣
Lemma 3.3.
![]() $\mathfrak {F}_{\sim }$
is an
$\mathfrak {F}_{\sim }$
is an
![]() $\mathsf {MIPC}$
-frame.
$\mathsf {MIPC}$
-frame.
Proof. It is well known (and easy to verify) that
![]() $R_{\sim }$
is a partial order (see, e.g., [Reference Chagrov and Zakharyaschev12, p. 68]). Transitivity and reflexivity of
$R_{\sim }$
is a partial order (see, e.g., [Reference Chagrov and Zakharyaschev12, p. 68]). Transitivity and reflexivity of
![]() $E_\sim $
easily follow from transitivity and reflexivity of Q, and
$E_\sim $
easily follow from transitivity and reflexivity of Q, and
![]() $E_\sim $
is symmetric by definition. To see that
$E_\sim $
is symmetric by definition. To see that
![]() $\mathfrak {F}_{\sim }$
satisfies commutativity, let
$\mathfrak {F}_{\sim }$
satisfies commutativity, let
![]() $[x], [y], [z] \in W_\sim $
with
$[x], [y], [z] \in W_\sim $
with
![]() $[x] E_\sim [y]$
and
$[x] E_\sim [y]$
and
![]() $[y] R_\sim [z]$
. Then
$[y] R_\sim [z]$
. Then
![]() $xQy$
and
$xQy$
and
![]() $yRz$
, so
$yRz$
, so
![]() $xQz$
. Therefore, there is
$xQz$
. Therefore, there is
![]() $z'$
with
$z'$
with
![]() $x R z'$
and
$x R z'$
and
![]() $z' E z$
. From
$z' E z$
. From
![]() $xRz'$
it follows that
$xRz'$
it follows that
![]() $[x] R [z']$
, and
$[x] R [z']$
, and
![]() $z' E z$
implies
$z' E z$
implies
![]() $[z'] E_\sim [z]$
by Lemma 3.2(1). Thus,
$[z'] E_\sim [z]$
by Lemma 3.2(1). Thus,
![]() $\mathfrak F_\sim $
satisfies commutativity.⊣
$\mathfrak F_\sim $
satisfies commutativity.⊣
Given a valuation
![]() $\nu $
on
$\nu $
on
![]() $\mathfrak F$
, define a valuation
$\mathfrak F$
, define a valuation
![]() $\nu _{\sim }$
on
$\nu _{\sim }$
on
![]() $\mathfrak F_{\sim }$
by
$\mathfrak F_{\sim }$
by
Clearly
![]() $\nu _{\sim }(p)$
is an upset. We call
$\nu _{\sim }(p)$
is an upset. We call
![]() $\mathfrak F_{\sim }$
the skeleton of
$\mathfrak F_{\sim }$
the skeleton of
![]() $\mathfrak F$
and
$\mathfrak F$
and
![]() $(\mathfrak F_{\sim }, \nu _\sim )$
the skeleton of
$(\mathfrak F_{\sim }, \nu _\sim )$
the skeleton of
![]() $(\mathfrak F, \nu )$
.
$(\mathfrak F, \nu )$
.
Conversely, given an
![]() $\mathsf {MIPC}$
-frame
$\mathsf {MIPC}$
-frame
![]() $\mathfrak F$
, we regard it as an
$\mathfrak F$
, we regard it as an
![]() $\mathsf {MS4}$
-frame. In addition, if
$\mathsf {MS4}$
-frame. In addition, if
![]() $\mathfrak F$
is finite, then we regard it as a finite
$\mathfrak F$
is finite, then we regard it as a finite
![]() $\mathsf {MGrz}$
-frame. If
$\mathsf {MGrz}$
-frame. If
![]() $\nu $
is a valuation on the
$\nu $
is a valuation on the
![]() $\mathsf {MIPC}$
-frame
$\mathsf {MIPC}$
-frame
![]() $\mathfrak F$
, then we regard it as a valuation on the
$\mathfrak F$
, then we regard it as a valuation on the
![]() $\mathsf {MGrz}$
-frame
$\mathsf {MGrz}$
-frame
![]() $\mathfrak F$
.
$\mathfrak F$
.
The following lemma describes how the above frame transformations behave with respect to the Gödel translation. It is proved by induction on the complexity of
![]() $\varphi $
.
$\varphi $
.
Lemma 3.4. Let
![]() $\varphi $
be a formula of
$\varphi $
be a formula of
![]() $\mathcal {L}_{\forall \exists }$
.
$\mathcal {L}_{\forall \exists }$
.
-
1. For an
 $\mathsf {MIPC}$
-frame
$\mathsf {MIPC}$
-frame
 $\mathfrak {F}$
with a valuation
$\mathfrak {F}$
with a valuation
 $\nu $
and every
$\nu $
and every
 $x \in \mathfrak F$
we have
$x \in \mathfrak F$
we have  $$ \begin{align*} (\mathfrak F, x) \vDash_{\nu}\varphi \Leftrightarrow (\mathfrak F, x) \vDash_{\nu}\varphi^t. \end{align*} $$
$$ \begin{align*} (\mathfrak F, x) \vDash_{\nu}\varphi \Leftrightarrow (\mathfrak F, x) \vDash_{\nu}\varphi^t. \end{align*} $$
-
2. For an
 $\mathsf {MS4}$
-frame
$\mathsf {MS4}$
-frame
 $\mathfrak F$
with a valuation
$\mathfrak F$
with a valuation
 $\nu $
and every
$\nu $
and every
 $x \in \mathfrak F$
, we have
$x \in \mathfrak F$
, we have  $$ \begin{align*} (\mathfrak F, x) \vDash_{\nu}\varphi^t \Leftrightarrow (\mathfrak F_{\sim}, [x]) \models_{\nu_{\sim}}\varphi. \end{align*} $$
$$ \begin{align*} (\mathfrak F, x) \vDash_{\nu}\varphi^t \Leftrightarrow (\mathfrak F_{\sim}, [x]) \models_{\nu_{\sim}}\varphi. \end{align*} $$
Proof. If
![]() $\mathfrak F$
is an
$\mathfrak F$
is an
![]() $\mathsf {MIPC}$
-frame, then
$\mathsf {MIPC}$
-frame, then
![]() $\mathfrak F_\sim $
is isomorphic to
$\mathfrak F_\sim $
is isomorphic to
![]() $\mathfrak F$
. Therefore, (1) follows from (2). To prove (2), by [Reference Chagrov and Zakharyaschev12, Lemma 3.81], it is sufficient to only consider the case for the modalities
$\mathfrak F$
. Therefore, (1) follows from (2). To prove (2), by [Reference Chagrov and Zakharyaschev12, Lemma 3.81], it is sufficient to only consider the case for the modalities
![]() $\forall $
and
$\forall $
and
![]() $\exists $
. Let
$\exists $
. Let
![]() $\varphi =\forall \psi $
. Then
$\varphi =\forall \psi $
. Then
 $$\begin{align*} \quad[x] \vDash \forall\psi \quad &\Leftrightarrow\quad (\mbox{for all } [y]) ([x]Q_\sim [y] \Rightarrow [y]\vDash \psi) \\ &\Leftrightarrow\quad (\mbox{for all } [y]) ([x]Q_\sim[y] \Rightarrow y\vDash \psi^t) \quad\text{(Inductive Hypothesis)} &\\ &\Leftrightarrow\quad (\mbox{for all } y) (xQy \Rightarrow y \vDash \psi^t) \quad\text{(Lemma 3.2(2))} \\ &\Leftrightarrow\quad x\vDash \blacksquare \psi^t \\ &\Leftrightarrow\quad x\vDash (\forall\psi)^t. \end{align*}$$
$$\begin{align*} \quad[x] \vDash \forall\psi \quad &\Leftrightarrow\quad (\mbox{for all } [y]) ([x]Q_\sim [y] \Rightarrow [y]\vDash \psi) \\ &\Leftrightarrow\quad (\mbox{for all } [y]) ([x]Q_\sim[y] \Rightarrow y\vDash \psi^t) \quad\text{(Inductive Hypothesis)} &\\ &\Leftrightarrow\quad (\mbox{for all } y) (xQy \Rightarrow y \vDash \psi^t) \quad\text{(Lemma 3.2(2))} \\ &\Leftrightarrow\quad x\vDash \blacksquare \psi^t \\ &\Leftrightarrow\quad x\vDash (\forall\psi)^t. \end{align*}$$
Next let
![]() $\varphi =\exists \psi $
. If
$\varphi =\exists \psi $
. If
![]() $x \models (\exists \psi )^t $
, then there is y with
$x \models (\exists \psi )^t $
, then there is y with
![]() $x Ey $
and
$x Ey $
and
![]() $y \models \psi ^t $
. Therefore,
$y \models \psi ^t $
. Therefore,
![]() $[y] \models \psi $
by the inductive hypothesis, and
$[y] \models \psi $
by the inductive hypothesis, and
![]() $[x] E_{\sim} [y]$
by Lemma 3.2(1). Thus,
$[x] E_{\sim} [y]$
by Lemma 3.2(1). Thus,
![]() $[x] \models \exists \psi $
. Conversely, suppose that
$[x] \models \exists \psi $
. Conversely, suppose that
![]() $[x] \models \exists \psi $
. Then there is
$[x] \models \exists \psi $
. Then there is
![]() $[y]$
with
$[y]$
with
![]() $[x] E_\sim [y]$
and
$[x] E_\sim [y]$
and
![]() $[y] \models \psi $
. Therefore,
$[y] \models \psi $
. Therefore,
![]() $y Q x$
by the definition of
$y Q x$
by the definition of
![]() $E_\sim $
. Thus, there is
$E_\sim $
. Thus, there is
![]() $x'$
with
$x'$
with
![]() $y R x'$
and
$y R x'$
and
![]() $x' E x$
. By the definition of
$x' E x$
. By the definition of
![]() $R_\sim $
, we have
$R_\sim $
, we have
![]() $[y] R_\sim [x']$
. So
$[y] R_\sim [x']$
. So
![]() $[x'] \models \psi $
by persistence in
$[x'] \models \psi $
by persistence in
![]() $\mathfrak F_\sim $
. Consequently,
$\mathfrak F_\sim $
. Consequently,
![]() $x' \models \psi ^t$
by the inductive hypothesis, so
$x' \models \psi ^t$
by the inductive hypothesis, so
![]() $x\models\exists\psi^t$
, and hence
$x\models\exists\psi^t$
, and hence
![]() $x\models (\exists\psi)^t$
.⊣
$x\models (\exists\psi)^t$
.⊣
Theorem 3.5.
![]() $ \mathsf {MIPC}\vdash \varphi \text { iff } \mathsf {MS4}\vdash \varphi ^t \text { iff } \mathsf {MGrz}\vdash \varphi ^t$
.
$ \mathsf {MIPC}\vdash \varphi \text { iff } \mathsf {MS4}\vdash \varphi ^t \text { iff } \mathsf {MGrz}\vdash \varphi ^t$
.
Proof. Suppose that
![]() $\mathsf {MIPC}\not \vdash \varphi $
. Since
$\mathsf {MIPC}\not \vdash \varphi $
. Since
![]() $\mathsf {MIPC}$
has the FMP (Theorem 2.10), there exists a finite
$\mathsf {MIPC}$
has the FMP (Theorem 2.10), there exists a finite
![]() $\mathsf {MIPC}$
-frame
$\mathsf {MIPC}$
-frame
![]() $\mathfrak F$
, a valuation
$\mathfrak F$
, a valuation
![]() $\nu $
on
$\nu $
on
![]() $\mathfrak F$
, and
$\mathfrak F$
, and
![]() $x \in \mathfrak F$
such that
$x \in \mathfrak F$
such that
![]() $x \not \models _\nu \varphi $
. Viewing
$x \not \models _\nu \varphi $
. Viewing
![]() $\mathfrak F$
as an
$\mathfrak F$
as an
![]() $\mathsf {MGrz}$
-frame,
$\mathsf {MGrz}$
-frame,
![]() $x \not \models _\nu \varphi ^t$
by Lemma 3.4(1). Therefore,
$x \not \models _\nu \varphi ^t$
by Lemma 3.4(1). Therefore,
![]() $\mathsf {MGrz}\not \vdash \varphi ^t$
. Since
$\mathsf {MGrz}\not \vdash \varphi ^t$
. Since
![]() $\mathsf {MS4}\subseteq \mathsf {MGrz}$
, it follows that
$\mathsf {MS4}\subseteq \mathsf {MGrz}$
, it follows that
![]() $\mathsf {MS4}\not \vdash \varphi ^t$
.
$\mathsf {MS4}\not \vdash \varphi ^t$
.
Conversely, if
![]() $\mathsf {MGrz}\not \vdash \varphi ^t$
, then
$\mathsf {MGrz}\not \vdash \varphi ^t$
, then
![]() $\mathsf {MS4}\not \vdash \varphi ^t$
. By the FMP for
$\mathsf {MS4}\not \vdash \varphi ^t$
. By the FMP for
![]() $\mathsf {MS4}$
(see Theorem 2.21), there is a finite
$\mathsf {MS4}$
(see Theorem 2.21), there is a finite
![]() $\mathsf {MS4}$
-frame
$\mathsf {MS4}$
-frame
![]() $\mathfrak F$
, a valuation
$\mathfrak F$
, a valuation
![]() $\nu $
on
$\nu $
on
![]() $\mathfrak F$
, and
$\mathfrak F$
, and
![]() $x \in \mathfrak F$
such that
$x \in \mathfrak F$
such that
![]() $(\mathfrak F, x) \not \models _{\nu } \varphi ^t$
. By Lemma 3.4(2),
$(\mathfrak F, x) \not \models _{\nu } \varphi ^t$
. By Lemma 3.4(2),
![]() $(\mathfrak F_{\sim }, [x]) \not \models _{\nu _{\sim }}\varphi $
. Thus,
$(\mathfrak F_{\sim }, [x]) \not \models _{\nu _{\sim }}\varphi $
. Thus,
![]() $\mathsf {MIPC}\not \vdash \varphi $
.⊣
$\mathsf {MIPC}\not \vdash \varphi $
.⊣
3.2 Splitting translation
Next we discuss the splitting translation in the monadic setting. The key here is Esakia’s observation that the splitting translation does not yield a faithful embedding of
![]() $\mathsf {MGrz}$
into
$\mathsf {MGrz}$
into
![]() $\mathsf {MGL}$
. Since this result is unpublished, we give a proof of it.
$\mathsf {MGL}$
. Since this result is unpublished, we give a proof of it.
Definition 3.6. Let
![]() $\mathfrak {F}=(W,R,E)$
be an augmented Kripke frame (modal or intuitionistic), and let
$\mathfrak {F}=(W,R,E)$
be an augmented Kripke frame (modal or intuitionistic), and let
![]() $x\in W$
.
$x\in W$
.
-
1. An E-cluster (or cluster) is a subset of W of the form
(it is the equivalence class of $$ \begin{align*} E(x)=\{w\in W \mid xEw\} \end{align*} $$
$$ \begin{align*} E(x)=\{w\in W \mid xEw\} \end{align*} $$
 $x\in W$
with respect to E).
$x\in W$
with respect to E).
-
2. We say that the E-cluster
 $E(x)$
is dirty if there are
$E(x)$
is dirty if there are
 $u,v\in E(x)$
with
$u,v\in E(x)$
with
 $u\not =v$
and
$u\not =v$
and
 $uRv$
.
$uRv$
. -
3. We say that the cluster is clean otherwise; that is,
 $u,v\in E(x)$
and
$u,v\in E(x)$
and
 $uRv$
imply
$uRv$
imply
 $u=v$
:
$u=v$
:

Descriptive
![]() $\mathsf {MGL}$
-frames have the property that clusters in the irreflexive maximum of an E-saturated clopen are clean.
$\mathsf {MGL}$
-frames have the property that clusters in the irreflexive maximum of an E-saturated clopen are clean.
Lemma 3.7. Let
![]() $\mathfrak {F}=(W,R,E)$
be a descriptive
$\mathfrak {F}=(W,R,E)$
be a descriptive
![]() $\mathsf {MGL}$
-frame. For clopen A and
$\mathsf {MGL}$
-frame. For clopen A and
![]() $m\in \mu (E(A))$
we have that
$m\in \mu (E(A))$
we have that
![]() $E(m)$
is clean.
$E(m)$
is clean.
Proof. Suppose there exist clopen A and
![]() $m\in \mu (E(A))$
with
$m\in \mu (E(A))$
with
![]() $E(m)$
dirty. Then there are
$E(m)$
dirty. Then there are
![]() $x,y\in E(m)$
with
$x,y\in E(m)$
with
![]() $xRy$
,
$xRy$
,
![]() $xEy$
, and
$xEy$
, and
![]() $x\not =y$
. By commutativity, there is
$x\not =y$
. By commutativity, there is
![]() $w$
such that
$w$
such that
![]() $mRw$
and
$mRw$
and
![]() $wEy$
, as shown below:
$wEy$
, as shown below:

Since
![]() $y\in E(A)$
we have
$y\in E(A)$
we have
![]() $w\in E(A)$
. But this contradicts
$w\in E(A)$
. But this contradicts
![]() $R(m)\cap E(A)=\varnothing $
. Thus, we cannot have a dirty cluster in
$R(m)\cap E(A)=\varnothing $
. Thus, we cannot have a dirty cluster in
![]() $\mu (E(A))$
.⊣
$\mu (E(A))$
.⊣
As a consequence of Lemma 3.7, we obtain:
Lemma 3.8. Finite
![]() $\mathsf {MGL}$
-frames are finite strict partial orders in which all clusters are clean.
$\mathsf {MGL}$
-frames are finite strict partial orders in which all clusters are clean.
We next show that the splitting translation of the Gödel translation of the monadic version of Casari’s formula
is provable in
![]() $\mathsf {MGL}$
.
$\mathsf {MGL}$
.
Since
![]() $\square \forall p\leftrightarrow \square \forall \square p$
is provable in
$\square \forall p\leftrightarrow \square \forall \square p$
is provable in
![]() $\mathsf {MS4}$
, it is straightforward to check that
$\mathsf {MS4}$
, it is straightforward to check that
![]() $(\mathsf {MCas})^t$
is provably equivalent to
$(\mathsf {MCas})^t$
is provably equivalent to
![]() $\square \forall \big (\square (\square p\rightarrow \square \forall p)\rightarrow \square \forall p\big )\rightarrow \square \forall p$
. Using the notation
$\square \forall \big (\square (\square p\rightarrow \square \forall p)\rightarrow \square \forall p\big )\rightarrow \square \forall p$
. Using the notation
![]() $\blacksquare $
introduced above, we have that
$\blacksquare $
introduced above, we have that
![]() $(\mathsf {MCas})^t$
is:
$(\mathsf {MCas})^t$
is:
We use
![]() $\blacksquare ^{+}\psi $
to abbreviate
$\blacksquare ^{+}\psi $
to abbreviate
![]() $\forall \psi \wedge \square \forall \psi =\square ^{+}\forall \psi $
. Then the splitting translation of
$\forall \psi \wedge \square \forall \psi =\square ^{+}\forall \psi $
. Then the splitting translation of
![]() $\mathsf {M_\Box Cas}$
is
$\mathsf {M_\Box Cas}$
is
Theorem 3.9.
![]() $\mathsf {MGL}\vdash (\mathsf {M_\Box Cas})^s$
.
$\mathsf {MGL}\vdash (\mathsf {M_\Box Cas})^s$
.
Proof. Suppose
![]() $\mathfrak {F}=(W,R,E)$
is a descriptive
$\mathfrak {F}=(W,R,E)$
is a descriptive
![]() $\mathsf {MGL}$
-frame. We will prove that
$\mathsf {MGL}$
-frame. We will prove that
![]() $\mathfrak {F}\vDash (\mathsf {M_\Box Cas})^s$
. Let
$\mathfrak {F}\vDash (\mathsf {M_\Box Cas})^s$
. Let
![]() $\nu $
be a valuation on
$\nu $
be a valuation on
![]() $\mathfrak F$
,
$\mathfrak F$
,
![]() $x \in \mathfrak F$
, and
$x \in \mathfrak F$
, and
![]() $x\not \vDash _\nu \blacksquare ^{+}p$
. We show that
$x\not \vDash _\nu \blacksquare ^{+}p$
. We show that
![]() $x\not \vDash \blacksquare ^{+}(\square ^{+}(\square ^{+}p\rightarrow \blacksquare ^{+}p)\rightarrow \blacksquare ^{+}p)$
. Let
$x\not \vDash \blacksquare ^{+}(\square ^{+}(\square ^{+}p\rightarrow \blacksquare ^{+}p)\rightarrow \blacksquare ^{+}p)$
. Let
![]() $A=W\setminus \nu (\blacksquare ^{+}p)$
. Then
$A=W\setminus \nu (\blacksquare ^{+}p)$
. Then
![]() $x \in A$
and so by Lemma 2.29,
$x \in A$
and so by Lemma 2.29,
![]() $x\in \mu (A)\cup R^{-1}\mu (A)$
. If
$x\in \mu (A)\cup R^{-1}\mu (A)$
. If
![]() $x \in R^{-1}\mu (A)$
, then there is
$x \in R^{-1}\mu (A)$
, then there is
![]() $x' \in \mu (A)$
with
$x' \in \mu (A)$
with
![]() $x R x'$
. If
$x R x'$
. If
![]() $x \in \mu (A)$
, we let
$x \in \mu (A)$
, we let
![]() $x' = x$
. From
$x' = x$
. From
![]() $x' \in \mu (A)$
it follows that
$x' \in \mu (A)$
it follows that
![]() $x' \in A$
, so
$x' \in A$
, so
![]() $x' \not \models \blacksquare ^{+}p= \forall p \wedge \Box \forall p$
. We show that
$x' \not \models \blacksquare ^{+}p= \forall p \wedge \Box \forall p$
. We show that
![]() $x' \not \models \forall p$
. If
$x' \not \models \forall p$
. If
![]() $x' \not \models \Box \forall p$
, then there is y with
$x' \not \models \Box \forall p$
, then there is y with
![]() $x'Ry$
and
$x'Ry$
and
![]() $y \not \models \forall p$
. Therefore,
$y \not \models \forall p$
. Therefore,
![]() $y \not \models \blacksquare ^{+} p$
, so
$y \not \models \blacksquare ^{+} p$
, so
![]() $y \in A$
. But this contradicts
$y \in A$
. But this contradicts
![]() $x' \in \mu (A)$
. Thus,
$x' \in \mu (A)$
. Thus,
![]() $x' \not \models \forall p$
. So there is w with
$x' \not \models \forall p$
. So there is w with
![]() $w E x'$
and
$w E x'$
and
![]() $w \not \models p$
. We show that
$w \not \models p$
. We show that
Since
![]() $w\not \vDash p$
, we have
$w\not \vDash p$
, we have
![]() $w\not \vDash p\wedge \square p$
, so
$w\not \vDash p\wedge \square p$
, so
![]() $w\not \vDash \square ^{+} p$
, and hence
$w\not \vDash \square ^{+} p$
, and hence
![]() $w\vDash \square ^{+}p\rightarrow \blacksquare ^{+}p$
. Let
$w\vDash \square ^{+}p\rightarrow \blacksquare ^{+}p$
. Let
![]() $w R z$
. By commutativity, there is y such that
$w R z$
. By commutativity, there is y such that
![]() $x'Ry$
and
$x'Ry$
and
![]() $yEz$
. Since
$yEz$
. Since
![]() $x' \in \mu (A)$
, we have
$x' \in \mu (A)$
, we have
![]() $y \not \in A$
. Therefore,
$y \not \in A$
. Therefore,
![]() $y\vDash \blacksquare ^{+}p$
, so
$y\vDash \blacksquare ^{+}p$
, so
![]() $y\vDash \forall p$
, and hence
$y\vDash \forall p$
, and hence
![]() $z\vDash \forall p$
:
$z\vDash \forall p$
:

In fact, if
![]() $zRt$
, then
$zRt$
, then
![]() $wRt$
by transitivity, and so by the same reasoning as above we have
$wRt$
by transitivity, and so by the same reasoning as above we have
![]() $t\vDash \forall p$
. It follows that
$t\vDash \forall p$
. It follows that
![]() $z\vDash \Box \forall p$
, and so
$z\vDash \Box \forall p$
, and so
![]() $z\vDash \blacksquare ^{+}p$
. Thus,
$z\vDash \blacksquare ^{+}p$
. Thus,
![]() $z\vDash \square ^{+}p\rightarrow \blacksquare ^{+}p$
, and hence
$z\vDash \square ^{+}p\rightarrow \blacksquare ^{+}p$
, and hence
![]() $w\vDash \square (\square ^{+}p\rightarrow \blacksquare ^{+}p)$
. This together with
$w\vDash \square (\square ^{+}p\rightarrow \blacksquare ^{+}p)$
. This together with
![]() $w\vDash \square ^{+}p\rightarrow \blacksquare ^{+}p$
yields
$w\vDash \square ^{+}p\rightarrow \blacksquare ^{+}p$
yields
![]() $w\vDash \square ^{+}(\square ^{+}p\rightarrow \blacksquare ^{+} p)$
. Since
$w\vDash \square ^{+}(\square ^{+}p\rightarrow \blacksquare ^{+} p)$
. Since
![]() $w\not \vDash \blacksquare ^{+} p$
, we obtain
$w\not \vDash \blacksquare ^{+} p$
, we obtain
![]() $w \not \vDash \square ^{+}(\square ^{+}p\rightarrow \blacksquare ^{+} p) \rightarrow \blacksquare ^{+} p$
.
$w \not \vDash \square ^{+}(\square ^{+}p\rightarrow \blacksquare ^{+} p) \rightarrow \blacksquare ^{+} p$
.
If
![]() $x = x'$
, then
$x = x'$
, then
![]() $x E w$
, and so
$x E w$
, and so
![]() $x \not \vDash \forall (\square ^{+}(\square ^{+}p\rightarrow \blacksquare ^{+} p) \rightarrow \blacksquare ^{+} p)$
. Otherwise,
$x \not \vDash \forall (\square ^{+}(\square ^{+}p\rightarrow \blacksquare ^{+} p) \rightarrow \blacksquare ^{+} p)$
. Otherwise,
![]() $x R x'$
and
$x R x'$
and
![]() $x' Ew$
imply
$x' Ew$
imply
![]() $x Q w$
, so
$x Q w$
, so
![]() $x \not \models \blacksquare (\square ^{+}(\square ^{+}p\rightarrow \blacksquare ^{+} p) \rightarrow \blacksquare ^{+} p)$
. Thus, in either case,
$x \not \models \blacksquare (\square ^{+}(\square ^{+}p\rightarrow \blacksquare ^{+} p) \rightarrow \blacksquare ^{+} p)$
. Thus, in either case,
![]() $x \not \models \blacksquare ^+ (\square ^{+}(\square ^{+}p\rightarrow \blacksquare ^{+} p) \rightarrow \blacksquare ^{+} p)$
as desired. This yields
$x \not \models \blacksquare ^+ (\square ^{+}(\square ^{+}p\rightarrow \blacksquare ^{+} p) \rightarrow \blacksquare ^{+} p)$
as desired. This yields
![]() $x\vDash (\mathsf {M_\Box Cas})^s$
. Since x was arbitrary,
$x\vDash (\mathsf {M_\Box Cas})^s$
. Since x was arbitrary,
![]() $\mathfrak {F}\vDash (\mathsf {M_\Box Cas})^s$
. Because
$\mathfrak {F}\vDash (\mathsf {M_\Box Cas})^s$
. Because
![]() $\mathfrak F$
is an arbitrary descriptive
$\mathfrak F$
is an arbitrary descriptive
![]() $\mathsf {MGL}$
-frame, by Theorem 2.28(2),
$\mathsf {MGL}$
-frame, by Theorem 2.28(2),
![]() $\mathsf {MGL}\vdash (\mathsf {M_\Box Cas})^s$
.⊣
$\mathsf {MGL}\vdash (\mathsf {M_\Box Cas})^s$
.⊣
Theorem 3.10.
![]() $\mathsf {MGrz}\not \vdash \mathsf {M_\Box Cas}$
.
$\mathsf {MGrz}\not \vdash \mathsf {M_\Box Cas}$
.
Proof. Consider the
![]() $\mathsf {MGrz}$
-frame
$\mathsf {MGrz}$
-frame
![]() $\mathfrak {F}=(W,R,E)$
where
$\mathfrak {F}=(W,R,E)$
where
![]() $W=\{x,y\}$
,
$W=\{x,y\}$
,
![]() $R=\{(x,x),(y,y),(x,y)\}$
, and
$R=\{(x,x),(y,y),(x,y)\}$
, and
![]() $E=W^{2}=\{(x,x),(y,y),(x,y),(y,x)\}$
, as shown below:
$E=W^{2}=\{(x,x),(y,y),(x,y),(y,x)\}$
, as shown below:

The arrow represents the nontrivial R-relation and the circle represents that both points are in the same E-equivalence class. It is easy to see that this is an
![]() $\mathsf {MGrz}$
-frame. Let
$\mathsf {MGrz}$
-frame. Let
![]() $\nu $
be a valuation on
$\nu $
be a valuation on
![]() $\mathfrak {F}$
with
$\mathfrak {F}$
with
![]() $\nu (p)=\{y\}$
. We first show that
$\nu (p)=\{y\}$
. We first show that
Note that
![]() $x\not \vDash \blacksquare p$
and
$x\not \vDash \blacksquare p$
and
![]() $y\not \vDash \blacksquare p$
, but since
$y\not \vDash \blacksquare p$
, but since
![]() $y\vDash p$
and y only sees itself (with respect to R), we have
$y\vDash p$
and y only sees itself (with respect to R), we have
![]() $y\vDash \square p$
. Therefore,
$y\vDash \square p$
. Therefore,
![]() $y\not \vDash \square p\rightarrow \blacksquare p$
, so
$y\not \vDash \square p\rightarrow \blacksquare p$
, so
![]() $x\not \vDash \square (\square p\rightarrow \blacksquare p)$
, and hence
$x\not \vDash \square (\square p\rightarrow \blacksquare p)$
, and hence
![]() $x\vDash \square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p$
. Moreover, since
$x\vDash \square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p$
. Moreover, since
![]() $y\not \vDash \square (\square p\rightarrow \blacksquare p)$
, we have
$y\not \vDash \square (\square p\rightarrow \blacksquare p)$
, we have
![]() $y\vDash \square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p$
, and hence
$y\vDash \square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p$
, and hence
![]() $x\vDash \blacksquare (\square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p)$
. However,
$x\vDash \blacksquare (\square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p)$
. However,
![]() $x\not \vDash \blacksquare p$
as
$x\not \vDash \blacksquare p$
as
![]() $xQx$
and
$xQx$
and
![]() $x\not \vDash p$
. Thus,
$x\not \vDash p$
. Thus,
![]() $x\not \vDash \blacksquare (\square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p)\rightarrow \blacksquare p$
, so
$x\not \vDash \blacksquare (\square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p)\rightarrow \blacksquare p$
, so
![]() $\mathfrak {F}\not \vDash _{\mathsf {MGrz}}\mathsf {M_\Box Cas}$
, and hence
$\mathfrak {F}\not \vDash _{\mathsf {MGrz}}\mathsf {M_\Box Cas}$
, and hence
![]() $\mathsf {MGrz}\not \vdash \mathsf {M_\Box Cas}$
.⊣
$\mathsf {MGrz}\not \vdash \mathsf {M_\Box Cas}$
.⊣
As an immediate consequence of Theorems 3.9 and 3.10, we obtain:
Corollary 3.11 (Esakia)
The splitting translation does not embed
![]() $\mathsf {MGrz}$
into
$\mathsf {MGrz}$
into
![]() $\mathsf {MGL}$
faithfully.
$\mathsf {MGL}$
faithfully.
4 The logics
 $\mathsf {M^{+}IPC}$
and
$\mathsf {M^{+}IPC}$
and
 $\mathsf {M^+Grz}$
$\mathsf {M^+Grz}$
In the previous section we saw that the splitting translation does not embed
![]() $\mathsf {MGrz}$
into
$\mathsf {MGrz}$
into
![]() $\mathsf {MGL}$
faithfully. In fact, the Gödel translation of
$\mathsf {MGL}$
faithfully. In fact, the Gödel translation of
![]() $\mathsf {MCas}$
is not provable in
$\mathsf {MCas}$
is not provable in
![]() $\mathsf {MGrz}$
, but the splitting translation of the Gödel translation of
$\mathsf {MGrz}$
, but the splitting translation of the Gödel translation of
![]() $\mathsf {MCas}$
is provable in
$\mathsf {MCas}$
is provable in
![]() $\mathsf {MGL}$
. To repair this disbalance, Esakia suggested to strengthen
$\mathsf {MGL}$
. To repair this disbalance, Esakia suggested to strengthen
![]() $\mathsf {MIPC}$
with
$\mathsf {MIPC}$
with
![]() $\mathsf {MCas}$
and
$\mathsf {MCas}$
and
![]() $\mathsf {MGrz}$
with the Gödel translation of
$\mathsf {MGrz}$
with the Gödel translation of
![]() $\mathsf {MCas}$
. This is what we do in this section.
$\mathsf {MCas}$
. This is what we do in this section.
4.1
 $\mathsf {M^{+}IPC}$
$\mathsf {M^{+}IPC}$
Definition 4.1. The logic
![]() $\mathsf {M^{+}IPC}$
is defined as the extension of
$\mathsf {M^{+}IPC}$
is defined as the extension of
![]() $\mathsf {MIPC}$
by
$\mathsf {MIPC}$
by
![]() $\mathsf {MCas}$
:
$\mathsf {MCas}$
:
Recall from Definition 3.6 that a cluster of an
![]() $\mathsf {MIPC}$
-frame is called clean if no distinct points in the cluster are R-related. The following semantic characterization of
$\mathsf {MIPC}$
-frame is called clean if no distinct points in the cluster are R-related. The following semantic characterization of
![]() $\mathsf {M^+IPC}$
-frames was established by Esakia. For a proof see [Reference Bezhanishvili5, Lemma 38]. It states that a descriptive
$\mathsf {M^+IPC}$
-frames was established by Esakia. For a proof see [Reference Bezhanishvili5, Lemma 38]. It states that a descriptive
![]() $\mathsf {MIPC}$
-frame is a descriptive
$\mathsf {MIPC}$
-frame is a descriptive
![]() $\mathsf {M^+IPC}$
-frame iff the cluster of each point in the R-maximum of the E-saturation of a clopen set is clean.
$\mathsf {M^+IPC}$
-frame iff the cluster of each point in the R-maximum of the E-saturation of a clopen set is clean.
Lemma 4.2. [Reference Bezhanishvili5, Lemma 38]
Let
![]() $\mathfrak {F}=(W,R,E)$
be a descriptive
$\mathfrak {F}=(W,R,E)$
be a descriptive
![]() $\mathsf {MIPC}$
-frame. Then
$\mathsf {MIPC}$
-frame. Then
![]() $\mathfrak {F}\vDash \mathsf {MCas}$
iff for each clopen A, if
$\mathfrak {F}\vDash \mathsf {MCas}$
iff for each clopen A, if
![]() $m\in \max E(A)$
, then
$m\in \max E(A)$
, then
![]() $E(m)$
is clean.
$E(m)$
is clean.
Remark 4.3. The condition in [Reference Bezhanishvili5, Lemma 38] is that
![]() $\mathfrak {F}\vDash \mathsf {MCas}$
iff for each clopen A we have
$\mathfrak {F}\vDash \mathsf {MCas}$
iff for each clopen A we have
![]() $A\subseteq Q^{-1}(\max A\cap \max Q^{-1}A)$
. But, as discussed after the proof of [Reference Bezhanishvili5, Lemma 38], this statement is equivalent to the statement in Lemma 4.2.
$A\subseteq Q^{-1}(\max A\cap \max Q^{-1}A)$
. But, as discussed after the proof of [Reference Bezhanishvili5, Lemma 38], this statement is equivalent to the statement in Lemma 4.2.
As a consequence of Lemma 4.2, we obtain:
Lemma 4.4. Finite
![]() $\mathsf {M^{+}IPC}$
-frames are finite
$\mathsf {M^{+}IPC}$
-frames are finite
![]() $\mathsf {MIPC}$
-frames in which all clusters are clean.
$\mathsf {MIPC}$
-frames in which all clusters are clean.
4.2
 $\mathsf {M^{+}Grz}$
$\mathsf {M^{+}Grz}$
Definition 4.5. The logic
![]() $\mathsf {M^{+}Grz}$
is the extension of
$\mathsf {M^{+}Grz}$
is the extension of
![]() $\mathsf {MGrz}$
by
$\mathsf {MGrz}$
by
![]() $\mathsf {M_\Box Cas}$
:
$\mathsf {M_\Box Cas}$
:
Remark 4.6. As we pointed out in the previous section,
![]() $\mathsf {M_\Box Cas}$
is provably equivalent to the Gödel translation of
$\mathsf {M_\Box Cas}$
is provably equivalent to the Gödel translation of
![]() $\mathsf {MCas}$
.
$\mathsf {MCas}$
.
In order to obtain a semantic characterization of
![]() $\mathsf {M^+Grz}$
, which is an analogue of Lemma 4.2, we require the following lemma.
$\mathsf {M^+Grz}$
, which is an analogue of Lemma 4.2, we require the following lemma.
Lemma 4.7. Let
![]() $\mathfrak {F}=(W,R,E)$
be a descriptive
$\mathfrak {F}=(W,R,E)$
be a descriptive
![]() $\mathsf {MGrz}$
-frame,
$\mathsf {MGrz}$
-frame,
![]() $A \subseteq W$
clopen, and
$A \subseteq W$
clopen, and
![]() $y \in \max E(A)$
. If
$y \in \max E(A)$
. If
![]() $E(y)$
is clean, then:
$E(y)$
is clean, then:
-
1.
 $E(y) \subseteq \max E(A)$
.
$E(y) \subseteq \max E(A)$
. -
2. For all
 $z \in W$
, from
$z \in W$
, from
 $yR z$
and
$yR z$
and
 $z R y$
it follows that
$z R y$
it follows that
 $y = z$
.
$y = z$
.
Proof. (1) Let
![]() $z \in E(y)$
and
$z \in E(y)$
and
![]() $w \in E(A)$
with
$w \in E(A)$
with
![]() $ z R w$
. By commutativity, there is
$ z R w$
. By commutativity, there is
![]() $w'$
with
$w'$
with
![]() $y R w'$
and
$y R w'$
and
![]() $w' E w$
. Therefore,
$w' E w$
. Therefore,
![]() $w' \in E(A)$
. Since
$w' \in E(A)$
. Since
![]() $y \in \max E(A)$
, we have
$y \in \max E(A)$
, we have
![]() $y=w'$
. Thus,
$y=w'$
. Thus,
![]() $z, w \in E(y)$
and
$z, w \in E(y)$
and
![]() $z R w$
. As
$z R w$
. As
![]() $E(y)$
is clean,
$E(y)$
is clean,
![]() $z = w$
. This shows that
$z = w$
. This shows that
![]() $z \in \max E(A)$
.
$z \in \max E(A)$
.
(2) Suppose
![]() $yR z$
and
$yR z$
and
![]() $z R y$
. From
$z R y$
. From
![]() $y \in E (A)$
and
$y \in E (A)$
and
![]() $yRy$
, we have
$yRy$
, we have
![]() $y \in R^{-1}E(A)$
. We show that
$y \in R^{-1}E(A)$
. We show that
![]() $y \in \text {q}\hspace {-.25em}\max R^{-1}E(A)$
. Let
$y \in \text {q}\hspace {-.25em}\max R^{-1}E(A)$
. Let
![]() $yRw$
and
$yRw$
and
![]() $w\in R^{-1}E(A)$
, so
$w\in R^{-1}E(A)$
, so
![]() $wRu$
for some
$wRu$
for some
![]() $u\in E(A)$
. Then
$u\in E(A)$
. Then
![]() $yRu$
by transitivity, and
$yRu$
by transitivity, and
![]() $y\in \max E(A)$
implies
$y\in \max E(A)$
implies
![]() $y=u$
, hence
$y=u$
, hence
![]() $wRy$
, and so
$wRy$
, and so
![]() $y\in \text {q}\hspace {-.25em}\max R^{-1}E(A)$
. By Lemma 2.26(1), this means
$y\in \text {q}\hspace {-.25em}\max R^{-1}E(A)$
. By Lemma 2.26(1), this means
![]() $y\in \max R^{-1}E(A)$
. Since
$y\in \max R^{-1}E(A)$
. Since
![]() $zR y$
, we have
$zR y$
, we have
![]() $z \in R^{-1}E(A)$
, so
$z \in R^{-1}E(A)$
, so
![]() $yRz$
implies
$yRz$
implies
![]() $z=y$
. ⊣
$z=y$
. ⊣
We now have the necessary machinery to prove a semantic characterization of
![]() $\mathsf {M^+Grz}$
, which states that a descriptive
$\mathsf {M^+Grz}$
, which states that a descriptive
![]() $\mathsf {MGrz}$
-frame is a descriptive
$\mathsf {MGrz}$
-frame is a descriptive
![]() $\mathsf {M^+Grz}$
-frame iff the cluster of every point in the maximum of the E-saturation of a clopen set is clean.
$\mathsf {M^+Grz}$
-frame iff the cluster of every point in the maximum of the E-saturation of a clopen set is clean.
Lemma 4.8. Let
![]() $\mathfrak {F}=(W,R,E)$
be a descriptive
$\mathfrak {F}=(W,R,E)$
be a descriptive
![]() $\mathsf {MGrz}$
-frame. Then
$\mathsf {MGrz}$
-frame. Then
![]() ${\mathfrak {F}\vDash \mathsf {M_\Box Cas}}$
iff for each clopen A and
${\mathfrak {F}\vDash \mathsf {M_\Box Cas}}$
iff for each clopen A and
![]() $m\in \max E(A)$
we have that
$m\in \max E(A)$
we have that
![]() $E(m)$
is clean.
$E(m)$
is clean.
Proof. First suppose
![]() $\mathfrak {F}\not \vDash \mathsf {M_\Box Cas}$
. Then there is
$\mathfrak {F}\not \vDash \mathsf {M_\Box Cas}$
. Then there is
![]() $x\in W$
such that
$x\in W$
such that
and hence
![]() $x\vDash \blacksquare (\square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p)$
but
$x\vDash \blacksquare (\square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p)$
but
![]() $x\not \vDash \blacksquare p$
. Since
$x\not \vDash \blacksquare p$
. Since
![]() $x\not \vDash \blacksquare p$
, there is
$x\not \vDash \blacksquare p$
, there is
![]() $x' \in W$
such that
$x' \in W$
such that
![]() $xQx'$
and
$xQx'$
and
![]() $x'\not \vDash p$
. Let
$x'\not \vDash p$
. Let
![]() $A=\{w\in W \mid w\not \vDash p\}$
. Then
$A=\{w\in W \mid w\not \vDash p\}$
. Then
![]() $x'\in A$
, and as
$x'\in A$
, and as
![]() $x'Ex'$
, we have
$x'Ex'$
, we have
![]() $x' \in E(A)$
. Because A is clopen, so is
$x' \in E(A)$
. Because A is clopen, so is
![]() $E(A)$
. By Lemma 2.26(2), there is
$E(A)$
. By Lemma 2.26(2), there is
![]() $y \in \max E(A)$
with
$y \in \max E(A)$
with
![]() $x'R y$
. If
$x'R y$
. If
![]() $E(y)$
is dirty, then we are done. So assume that
$E(y)$
is dirty, then we are done. So assume that
![]() $E(y)$
is clean. We show that this leads to a contradiction. Since
$E(y)$
is clean. We show that this leads to a contradiction. Since
![]() $y \in E(A)$
, there is
$y \in E(A)$
, there is
![]() $y' \in A$
with
$y' \in A$
with
![]() $y E y'$
. By Lemma 4.7(1),
$y E y'$
. By Lemma 4.7(1),
![]() $y' \in \max E(A)$
. As
$y' \in \max E(A)$
. As
![]() $x Q y'$
and
$x Q y'$
and
![]() $x\vDash \blacksquare (\square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p)$
, we have
$x\vDash \blacksquare (\square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p)$
, we have
![]() $y'\vDash \square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p$
. Because
$y'\vDash \square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p$
. Because
![]() $y' \in A$
, we have
$y' \in A$
, we have
![]() $y'\not \vDash p$
and since
$y'\not \vDash p$
and since
![]() $y'Qy'$
, we have
$y'Qy'$
, we have
![]() $y'\not \vDash \blacksquare p$
, so we must have
$y'\not \vDash \blacksquare p$
, so we must have
![]() $y'\not \vDash \square (\square p\rightarrow \blacksquare p)$
. Thus, there is
$y'\not \vDash \square (\square p\rightarrow \blacksquare p)$
. Thus, there is
![]() $z\in W$
such that
$z\in W$
such that
![]() $y'Rz$
and
$y'Rz$
and
![]() $z\not \vDash \square p\rightarrow \blacksquare p$
, which means
$z\not \vDash \square p\rightarrow \blacksquare p$
, which means
![]() $z\vDash \square p$
but
$z\vDash \square p$
but
![]() $z\not \vDash \blacksquare p$
. Because
$z\not \vDash \blacksquare p$
. Because
![]() $z\not \vDash \blacksquare p$
, there exist
$z\not \vDash \blacksquare p$
, there exist
![]() $w',w\in W$
such that
$w',w\in W$
such that
![]() $zRw'Ew$
and
$zRw'Ew$
and
![]() $w\not \vDash p$
(see the diagram below):
$w\not \vDash p$
(see the diagram below):

Now, since
![]() $w\not \vDash p$
, we have
$w\not \vDash p$
, we have
![]() $w\in A$
and hence
$w\in A$
and hence
![]() $w'\in E(A)$
. Thus,
$w'\in E(A)$
. Thus,
![]() $y'Rw'$
and
$y'Rw'$
and
![]() $w'\in E(A)$
, so by R-maximality of
$w'\in E(A)$
, so by R-maximality of
![]() $y'$
in
$y'$
in
![]() $E(A)$
, we must have
$E(A)$
, we must have
![]() $y'=w'$
. But then
$y'=w'$
. But then
![]() $y'R z$
and
$y'R z$
and
![]() $z R y'$
, and so by Lemma 4.7(2),
$z R y'$
, and so by Lemma 4.7(2),
![]() $y'=z$
. This, however, is a contradiction since
$y'=z$
. This, however, is a contradiction since
![]() $z\vDash \square p$
, hence
$z\vDash \square p$
, hence
![]() $z\vDash p$
, whereas
$z\vDash p$
, whereas
![]() $y'\not \vDash p$
.
$y'\not \vDash p$
.
For the converse, suppose that A is clopen and
![]() $m\in \max E(A)$
with
$m\in \max E(A)$
with
![]() $E(m)$
dirty. First observe that since m is maximal in
$E(m)$
dirty. First observe that since m is maximal in
![]() $E(A)$
, from
$E(A)$
, from
![]() $m Q t$
it follows that
$m Q t$
it follows that
![]() $t \in E(m)$
for all
$t \in E(m)$
for all
![]() $t \in E(A)$
. Indeed, if
$t \in E(A)$
. Indeed, if
![]() $m Q t$
for
$m Q t$
for
![]() $t \in E(A)$
, then there is
$t \in E(A)$
, then there is
![]() $t'$
with
$t'$
with
![]() $m R t'$
and
$m R t'$
and
![]() $t' E t$
. Since
$t' E t$
. Since
![]() $t' \in E(A)$
, we have
$t' \in E(A)$
, we have
![]() $t' =m$
by maximality of m in
$t' =m$
by maximality of m in
![]() $E(A)$
. Thus,
$E(A)$
. Thus,
![]() $t \in E(m)$
.
$t \in E(m)$
.
Now, since
![]() $E(m)$
is dirty, there are
$E(m)$
is dirty, there are
![]() $x , x' \in E(m)$
with
$x , x' \in E(m)$
with
![]() $x R x'$
and
$x R x'$
and
![]() $x \neq x'$
. In particular,
$x \neq x'$
. In particular,
![]() $x \not \in \max E(A)$
. Since
$x \not \in \max E(A)$
. Since
![]() $E(A)$
is clopen,
$E(A)$
is clopen,
![]() $\max E(A)$
is closed (see, e.g., [Reference Esakia20, Section III.2]). Thus, we can find clopen B such that
$\max E(A)$
is closed (see, e.g., [Reference Esakia20, Section III.2]). Thus, we can find clopen B such that
![]() $x\in B$
but
$x\in B$
but
![]() $B\cap \max E(A)=\varnothing $
, as shown below:
$B\cap \max E(A)=\varnothing $
, as shown below:

Choose a valuation
![]() $\nu $
with
$\nu $
with
![]() $\nu (p)=W\setminus (B\cap E(A))$
. Note that
$\nu (p)=W\setminus (B\cap E(A))$
. Note that
![]() $\nu $
is well-defined as B and
$\nu $
is well-defined as B and
![]() $E(A)$
are clopen. We aim to show that
$E(A)$
are clopen. We aim to show that
![]() $x\vDash \blacksquare (\square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p)$
but
$x\vDash \blacksquare (\square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p)$
but
![]() $x\not \vDash \blacksquare p$
. Since
$x\not \vDash \blacksquare p$
. Since
![]() $x \in B\cap E(A)$
, we have
$x \in B\cap E(A)$
, we have
![]() $x \not \models p$
. This implies that
$x \not \models p$
. This implies that
![]() $x \not \models \blacksquare p$
because
$x \not \models \blacksquare p$
because
![]() $x Q x$
. To finish the argument it suffices to show that
$x Q x$
. To finish the argument it suffices to show that
![]() $y \models \square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p$
for all y with
$y \models \square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p$
for all y with
![]() $x Q y$
. So let
$x Q y$
. So let
![]() $x Q y$
and assume that
$x Q y$
and assume that
![]() $y\not \models \blacksquare p$
. Then there is z with
$y\not \models \blacksquare p$
. Then there is z with
![]() $yQ z$
and
$yQ z$
and
![]() $z \not \models p$
. Therefore,
$z \not \models p$
. Therefore,
![]() $z \in B\cap E(A)$
and there is
$z \in B\cap E(A)$
and there is
![]() $z'$
with
$z'$
with
![]() $y R z'$
and
$y R z'$
and
![]() $z' E z$
. Clearly
$z' E z$
. Clearly
![]() $z' \in E(A)$
. By Lemma 2.26(2), there is
$z' \in E(A)$
. By Lemma 2.26(2), there is
![]() $t \in \max E(A)$
with
$t \in \max E(A)$
with
![]() $z'R t$
:
$z'R t$
:

Since
![]() $t \in \max E(A)$
, we have
$t \in \max E(A)$
, we have
![]() $t \not \in B$
, so
$t \not \in B$
, so
![]() $t \models p$
and if
$t \models p$
and if
![]() $t R v$
for
$t R v$
for
![]() $t \neq v$
, then
$t \neq v$
, then
![]() $v \not \in E(A)$
by maximality of t, so
$v \not \in E(A)$
by maximality of t, so
![]() $v \models p$
. Thus,
$v \models p$
. Thus,
![]() $t \models \Box p$
. On the other hand,
$t \models \Box p$
. On the other hand,
![]() $x Q y$
,
$x Q y$
,
![]() $y R z' $
, and
$y R z' $
, and
![]() $z' R t$
imply
$z' R t$
imply
![]() $m Q t$
. As we saw above, this means
$m Q t$
. As we saw above, this means
![]() $t \in E(m)$
, and so
$t \in E(m)$
, and so
![]() $t Ex$
. Since
$t Ex$
. Since
![]() $x \not \models p$
, we have
$x \not \models p$
, we have
![]() $t \not \models \blacksquare p$
. This yields that
$t \not \models \blacksquare p$
. This yields that
![]() $t \not \models \square p\rightarrow \blacksquare p$
, so
$t \not \models \square p\rightarrow \blacksquare p$
, so
![]() $y \not \models \square ( \square p\rightarrow \blacksquare p )$
, and hence
$y \not \models \square ( \square p\rightarrow \blacksquare p )$
, and hence
![]() $y \models \square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p$
as desired.⊣
$y \models \square (\square p\rightarrow \blacksquare p)\rightarrow \blacksquare p$
as desired.⊣
As a consequence of Lemma 4.8, we obtain:
Lemma 4.9. Finite
![]() $\mathsf {M^{+}Grz}$
-frames are finite
$\mathsf {M^{+}Grz}$
-frames are finite
![]() $\mathsf {MGrz}$
-frames in which all clusters are clean.
$\mathsf {MGrz}$
-frames in which all clusters are clean.
4.3 The translations
 $\mathsf {M^{+}IPC}\to \mathsf {M^{+}Grz}\to \mathsf {MGL}$
$\mathsf {M^{+}IPC}\to \mathsf {M^{+}Grz}\to \mathsf {MGL}$
The remaining part of the paper establishes the finite model property for the logics
![]() $\mathsf {M^+IPC}$
and
$\mathsf {M^+IPC}$
and
![]() $\mathsf {M^+Grz}$
. We finish this section by explaining how a proof of Esakia’s claim is then obtained.
$\mathsf {M^+Grz}$
. We finish this section by explaining how a proof of Esakia’s claim is then obtained.
Let R be a binary relation. We recall that the irreflexive reduction of R, denoted
![]() $R^{i}$
, is defined by
$R^{i}$
, is defined by
and the reflexive closure of R, denoted
![]() $R^{r}$
, is defined by
$R^{r}$
, is defined by
For an augmented Kripke frame
![]() $\mathfrak {F}=( W,R, E)$
, let
$\mathfrak {F}=( W,R, E)$
, let
![]() $\mathfrak {F}^i=( W,R^i, E)$
and
$\mathfrak {F}^i=( W,R^i, E)$
and
![]() $\mathfrak {F}^{r}=( W,R^{r}, E)$
. Following the terminology of [Reference Chagrov and Zakharyaschev12, pp. 98–99], we call
$\mathfrak {F}^{r}=( W,R^{r}, E)$
. Following the terminology of [Reference Chagrov and Zakharyaschev12, pp. 98–99], we call
![]() $\mathfrak {F}^i$
the irreflexive reduction and
$\mathfrak {F}^i$
the irreflexive reduction and
![]() $\mathfrak {F}^{r}$
the reflexive closure of
$\mathfrak {F}^{r}$
the reflexive closure of
![]() $\mathfrak {F}$
.
$\mathfrak {F}$
.
Lemma 4.10.
-
1. If
 $\mathfrak F$
is a finite
$\mathfrak F$
is a finite
 $\mathsf {M^+Grz}$
-frame, then
$\mathsf {M^+Grz}$
-frame, then
 $\mathfrak {F}^i$
is a finite
$\mathfrak {F}^i$
is a finite
 $\mathsf {MGL}$
-frame.
$\mathsf {MGL}$
-frame. -
2. If
 $\mathfrak F$
is a finite
$\mathfrak F$
is a finite
 $\mathsf {MGL}$
-frame, then
$\mathsf {MGL}$
-frame, then
 $\mathfrak {F}^r$
is a finite
$\mathfrak {F}^r$
is a finite
 $\mathsf {M^+Grz}$
-frame.
$\mathsf {M^+Grz}$
-frame.
Proof. Since finite
![]() $\mathsf {M^+Grz}$
-frames are finite partial orders with clean clusters (Lemma 4.9) and finite
$\mathsf {M^+Grz}$
-frames are finite partial orders with clean clusters (Lemma 4.9) and finite
![]() $\mathsf {MGL}$
-frames are finite strict partial orders with clean clusters (Lemma 3.8), this is an immediate consequence of [Reference Chagrov and Zakharyaschev12, pp. 98–99].⊣
$\mathsf {MGL}$
-frames are finite strict partial orders with clean clusters (Lemma 3.8), this is an immediate consequence of [Reference Chagrov and Zakharyaschev12, pp. 98–99].⊣
Lemma 4.11. Let
![]() $\varphi $
be a formula of
$\varphi $
be a formula of
![]() $\mathcal {ML}_{\forall }$
.
$\mathcal {ML}_{\forall }$
.
-
1. For a finite
 $\mathsf {M^{+}Grz}$
-frame
$\mathsf {M^{+}Grz}$
-frame
 $\mathfrak {F}$
, a valuation
$\mathfrak {F}$
, a valuation
 $\nu $
on
$\nu $
on
 $\mathfrak F$
, and every
$\mathfrak F$
, and every
 $x \in \mathfrak F$
we have
$x \in \mathfrak F$
we have  $$ \begin{align*} (\mathfrak F, x) \vDash_{\nu}\varphi \Leftrightarrow (\mathfrak F^i, x) \vDash_{\nu}\varphi^s. \end{align*} $$
$$ \begin{align*} (\mathfrak F, x) \vDash_{\nu}\varphi \Leftrightarrow (\mathfrak F^i, x) \vDash_{\nu}\varphi^s. \end{align*} $$
-
2. For a finite
 $\mathsf {MGL}$
-frame
$\mathsf {MGL}$
-frame
 $\mathfrak F$
, a valuation
$\mathfrak F$
, a valuation
 $\nu $
on
$\nu $
on
 $\mathfrak F$
, and every
$\mathfrak F$
, and every
 $x \in \mathfrak F$
we have
$x \in \mathfrak F$
we have  $$ \begin{align*} (\mathfrak F, x) \vDash_{\nu}\varphi^s \Leftrightarrow (\mathfrak F^r, x) \models_{\nu}\varphi. \end{align*} $$
$$ \begin{align*} (\mathfrak F, x) \vDash_{\nu}\varphi^s \Leftrightarrow (\mathfrak F^r, x) \models_{\nu}\varphi. \end{align*} $$
Proof. The proof is an immediate consequence of [Reference Chagrov and Zakharyaschev12, pp. 98–99] since the quantifier modalities are not changed by the translation
![]() $(-)^s$
, nor is the relation E altered going from
$(-)^s$
, nor is the relation E altered going from
![]() $\mathfrak F$
to
$\mathfrak F$
to
![]() $\mathfrak F^i$
or
$\mathfrak F^i$
or
![]() $\mathfrak F^r$
.⊣
$\mathfrak F^r$
.⊣
We are ready to provide a proof of Esakia’s claim.
Theorem 4.12.
![]() $\mathsf {M^{+}IPC}\vdash \varphi \text { iff }\mathsf {M^{+}Grz}\vdash \varphi ^t \text { iff } \mathsf {MGL}\vdash (\varphi ^t)^s$
.
$\mathsf {M^{+}IPC}\vdash \varphi \text { iff }\mathsf {M^{+}Grz}\vdash \varphi ^t \text { iff } \mathsf {MGL}\vdash (\varphi ^t)^s$
.
Proof. The first equivalence is proved exactly as Theorem 3.5 using the fact that finite
![]() $\mathsf {M^+IPC}$
-frames and finite
$\mathsf {M^+IPC}$
-frames and finite
![]() $\mathsf {M^+Grz}$
-frames coincide.
$\mathsf {M^+Grz}$
-frames coincide.
For the second equivalence, suppose
![]() $\mathsf {MGL}\not \vdash (\varphi ^t)^s$
. Since
$\mathsf {MGL}\not \vdash (\varphi ^t)^s$
. Since
![]() $\mathsf {MGL}$
has the FMP, there exist a finite
$\mathsf {MGL}$
has the FMP, there exist a finite
![]() $\mathsf {MGL}$
-frame
$\mathsf {MGL}$
-frame
![]() $\mathfrak {F}$
, a valuation
$\mathfrak {F}$
, a valuation
![]() $\nu $
on
$\nu $
on
![]() $\mathfrak F$
, and
$\mathfrak F$
, and
![]() $x \in \mathfrak F$
such that
$x \in \mathfrak F$
such that
![]() $(\mathfrak F, x)\not \vDash _{\nu }(\varphi ^t)^s$
. By Lemma 4.11(2),
$(\mathfrak F, x)\not \vDash _{\nu }(\varphi ^t)^s$
. By Lemma 4.11(2),
![]() $(\mathfrak {F}^{r}, x) \not \vDash _{\nu }\varphi ^t$
. By Lemma 4.10(2),
$(\mathfrak {F}^{r}, x) \not \vDash _{\nu }\varphi ^t$
. By Lemma 4.10(2),
![]() $\mathfrak F^r$
is an
$\mathfrak F^r$
is an
![]() $\mathsf {M^+Grz}$
-frame. Thus,
$\mathsf {M^+Grz}$
-frame. Thus,
![]() $\mathsf {M^{+}Grz}\not \vdash \varphi ^t$
. For the converse, let
$\mathsf {M^{+}Grz}\not \vdash \varphi ^t$
. For the converse, let
![]() $\mathsf {M^{+}Grz}\not \vdash \varphi ^t$
. Since
$\mathsf {M^{+}Grz}\not \vdash \varphi ^t$
. Since
![]() $\mathsf {M^{+}Grz}$
has the FMP, there exist a finite
$\mathsf {M^{+}Grz}$
has the FMP, there exist a finite
![]() $\mathsf {M^{+}Grz}$
-frame
$\mathsf {M^{+}Grz}$
-frame
![]() $\mathfrak {F}$
, a valuation
$\mathfrak {F}$
, a valuation
![]() $\nu $
on
$\nu $
on
![]() $\mathfrak F$
, and
$\mathfrak F$
, and
![]() $x \in \mathfrak F$
such that
$x \in \mathfrak F$
such that
![]() $(\mathfrak {F},x)\not \models _{\nu }\varphi ^t$
. By Lemma 4.11(1),
$(\mathfrak {F},x)\not \models _{\nu }\varphi ^t$
. By Lemma 4.11(1),
![]() $(\mathfrak {F}^{i}, x) \not \vDash _{\nu }(\varphi ^t)^s$
. By Lemma 4.10(1),
$(\mathfrak {F}^{i}, x) \not \vDash _{\nu }(\varphi ^t)^s$
. By Lemma 4.10(1),
![]() $\mathfrak F^i$
is an
$\mathfrak F^i$
is an
![]() $\mathsf {MGL}$
-frame. Consequently,
$\mathsf {MGL}$
-frame. Consequently,
![]() $\mathsf {MGL}\not \vdash (\varphi ^t)^s$
.⊣
$\mathsf {MGL}\not \vdash (\varphi ^t)^s$
.⊣
This concludes lifting the original correspondences given by Goldblatt, Boolos, and Kuznetsov and Muravitsky from the propositional setting to the monadic setting, verifying Esakia’s claim. Combining this with Japaridze’s result of arithmetical completeness for
![]() $\mathsf {MGL}$
yields provability interpretations of
$\mathsf {MGL}$
yields provability interpretations of
![]() $\mathsf {M^{+}IPC}$
and
$\mathsf {M^{+}IPC}$
and
![]() $\mathsf {M^{+}Grz}$
.
$\mathsf {M^{+}Grz}$
.
5 The finite model property of
 $\mathsf {M^{+}IPC}$
$\mathsf {M^{+}IPC}$
This section is dedicated to the proof of the finite model property of
![]() $\mathsf {M^+IPC}$
. We do this by modifying the selective filtration technique originally developed by Grefe [Reference Grefe29] to prove the finite model property of Fischer Servi’s intuitionistic modal logic
$\mathsf {M^+IPC}$
. We do this by modifying the selective filtration technique originally developed by Grefe [Reference Grefe29] to prove the finite model property of Fischer Servi’s intuitionistic modal logic
![]() $\mathsf {FS}$
. In [Reference Gabbay, Kurucz, Wolter and Zakharyaschev25, Section 10.3] it was used to give an alternative proof of the finite model property of
$\mathsf {FS}$
. In [Reference Gabbay, Kurucz, Wolter and Zakharyaschev25, Section 10.3] it was used to give an alternative proof of the finite model property of
![]() $\mathsf {MIPC}$
.
$\mathsf {MIPC}$
.
We start by collecting some properties of descriptive
![]() $\mathsf {M^+IPC}$
-frames that will be useful in what follows. We first give the
$\mathsf {M^+IPC}$
-frames that will be useful in what follows. We first give the
![]() $\mathsf {M^+IPC}$
-version of Lemma 4.7(1).
$\mathsf {M^+IPC}$
-version of Lemma 4.7(1).
Lemma 5.1. Let
![]() $\mathfrak F= (W, R, E) $
be a descriptive
$\mathfrak F= (W, R, E) $
be a descriptive
![]() $\mathsf {M^+IPC}$
-frame,
$\mathsf {M^+IPC}$
-frame,
![]() $A \subseteq W$
clopen,
$A \subseteq W$
clopen,
![]() $y \in \max E(A)$
, and
$y \in \max E(A)$
, and
![]() $E(y)$
clean. Then
$E(y)$
clean. Then
![]() $E(y) \subseteq \max E(A)$
.
$E(y) \subseteq \max E(A)$
.
Proof. If
![]() $E(y) \not \subseteq \max E(A)$
, then there are distinct
$E(y) \not \subseteq \max E(A)$
, then there are distinct
![]() $t \in E(y)$
and
$t \in E(y)$
and
![]() $u \in E(A)$
with
$u \in E(A)$
with
![]() $t R u$
. By commutativity, there is
$t R u$
. By commutativity, there is
![]() $u'$
with
$u'$
with
![]() $y R u'$
and
$y R u'$
and
![]() $u' E u$
. Therefore,
$u' E u$
. Therefore,
![]() $u' \in E(A)$
, so by maximality of y in
$u' \in E(A)$
, so by maximality of y in
![]() $E(A)$
we have
$E(A)$
we have
![]() $y = u'$
. This implies that
$y = u'$
. This implies that
![]() $t E u$
, contradicting that
$t E u$
, contradicting that
![]() $E(y)$
is a clean cluster.⊣
$E(y)$
is a clean cluster.⊣
We say a point x is maximal with respect to a formula
![]() $\psi $
if
$\psi $
if
![]() $x\not \vDash \psi $
and for each y with
$x\not \vDash \psi $
and for each y with
![]() $xRy$
and
$xRy$
and
![]() $x\neq y$
we have
$x\neq y$
we have
![]() $y\vDash \psi $
(that is, x refutes
$y\vDash \psi $
(that is, x refutes
![]() $\psi $
and every point strictly above x validates
$\psi $
and every point strictly above x validates
![]() $\psi $
).
$\psi $
).
Lemma 5.2. Let
![]() $\mathfrak F= (W, R, E) $
be a descriptive
$\mathfrak F= (W, R, E) $
be a descriptive
![]() $\mathsf {M^+IPC}$
-frame,
$\mathsf {M^+IPC}$
-frame,
![]() $t \in W$
, and
$t \in W$
, and
![]() $\nu $
a valuation on
$\nu $
a valuation on
![]() $\mathfrak F$
.
$\mathfrak F$
.
-
1. Let
 $A \subseteq W$
be clopen. If
$A \subseteq W$
be clopen. If
 $t \in E(A)$
, then there is
$t \in E(A)$
, then there is
 $x \in \max E(A)$
such that
$x \in \max E(A)$
such that
 $tRx$
and
$tRx$
and
 $E(x)$
is clean.
$E(x)$
is clean. -
2. If
 $t \not \models \forall \varphi $
, then there is x such that
$t \not \models \forall \varphi $
, then there is x such that
 $t R x$
, x is maximal with respect to
$t R x$
, x is maximal with respect to
 $\forall \varphi $
, and
$\forall \varphi $
, and
 $E(x)$
is clean.
$E(x)$
is clean. -
3. Let
 $A \subseteq W$
be clopen. If
$A \subseteq W$
be clopen. If
 $t \in A$
, then there is
$t \in A$
, then there is
 $x \in A \cap \max E(A)$
such that
$x \in A \cap \max E(A)$
such that
 $tQx$
and
$tQx$
and
 $E(x)$
is clean.
$E(x)$
is clean. -
4. If
 $t \not \models \varphi $
, then there is x such that
$t \not \models \varphi $
, then there is x such that
 $t Q x $
, x is maximal with respect to
$t Q x $
, x is maximal with respect to
 $\varphi $
, and
$\varphi $
, and
 $E(x)$
is clean.
$E(x)$
is clean.
Proof. (1) Let
![]() $t \in E(A)$
. By Lemma 2.12, there is
$t \in E(A)$
. By Lemma 2.12, there is
![]() $x \in \max E(A)$
such that
$x \in \max E(A)$
such that
![]() $tRx$
. By Lemma 4.2,
$tRx$
. By Lemma 4.2,
![]() $E(x)$
is clean.
$E(x)$
is clean.
(2) Suppose that
![]() $t \not \models \forall \varphi $
. Let
$t \not \models \forall \varphi $
. Let
![]() $A = W\setminus\nu(\forall\varphi)$
. Then A is clopen,
$A = W\setminus\nu(\forall\varphi)$
. Then A is clopen,
![]() $E(A) = A$
, and
$E(A) = A$
, and
![]() $t \in E(A)$
. By (1), there is
$t \in E(A)$
. By (1), there is
![]() $x \in \max E(A)$
such that
$x \in \max E(A)$
such that
![]() $tRx$
and
$tRx$
and
![]() $E(x)$
is clean. Since
$E(x)$
is clean. Since
![]() $E(A) =A$
, it immediately follows that x is maximal with respect to
$E(A) =A$
, it immediately follows that x is maximal with respect to
![]() $\forall \varphi $
.
$\forall \varphi $
.
(3) Let
![]() $t \in A$
. Then
$t \in A$
. Then
![]() $t \in E(A)$
. By (1), there is
$t \in E(A)$
. By (1), there is
![]() $x' \in \max E(A)$
such that
$x' \in \max E(A)$
such that
![]() $tRx'$
and
$tRx'$
and
![]() $E(x')$
is clean. Since
$E(x')$
is clean. Since
![]() $x' \in E(A)$
, there is
$x' \in E(A)$
, there is
![]() $x \in A$
with
$x \in A$
with
![]() $x' E x$
. Therefore,
$x' E x$
. Therefore,
![]() $t Q x$
, and because
$t Q x$
, and because
![]() $E(x')$
is clean, we have that
$E(x')$
is clean, we have that
![]() $x \in \max E(A)$
by Lemma 5.1.
$x \in \max E(A)$
by Lemma 5.1.
(4) Suppose that
![]() $t \not \models \varphi $
. Let
$t \not \models \varphi $
. Let
![]() $A = W\setminus\nu(\varphi)$
. Then A is clopen and
$A = W\setminus\nu(\varphi)$
. Then A is clopen and
![]() $t \in A$
. By (3), there is
$t \in A$
. By (3), there is
![]() $x \in A \cap \max E(A)$
such that
$x \in A \cap \max E(A)$
such that
![]() $t Q x$
and
$t Q x$
and
![]() $E(x)$
is clean. Since
$E(x)$
is clean. Since
![]() $x \in A$
, we also have
$x \in A$
, we also have
![]() $x \in \max A$
. But the latter means that x is maximal with respect to
$x \in \max A$
. But the latter means that x is maximal with respect to
![]() $\varphi $
. Thus, x is as desired.⊣
$\varphi $
. Thus, x is as desired.⊣
5.1 The construction
We start with a formula
![]() $\varphi $
, a descriptive
$\varphi $
, a descriptive
![]() $\mathsf {M^+IPC}$
-frame
$\mathsf {M^+IPC}$
-frame
![]() $\mathfrak F=(W, R, E)$
, and a valuation
$\mathfrak F=(W, R, E)$
, and a valuation
![]() $\nu $
on
$\nu $
on
![]() $\mathfrak F$
such that
$\mathfrak F$
such that
![]() $\mathfrak F \not \models \varphi $
. By modifying the construction in [Reference Gabbay, Kurucz, Wolter and Zakharyaschev25, Section 10.3], we will construct a sequence of finite
$\mathfrak F \not \models \varphi $
. By modifying the construction in [Reference Gabbay, Kurucz, Wolter and Zakharyaschev25, Section 10.3], we will construct a sequence of finite
![]() $\mathsf {M^{+}IPC}$
-frames
$\mathsf {M^{+}IPC}$
-frames
![]() $\mathfrak {F}_{h}=(W_{h},R_{h},E_{h})$
such that
$\mathfrak {F}_{h}=(W_{h},R_{h},E_{h})$
such that
![]() $\mathfrak {F}_{h}\subseteq \mathfrak {F}_{h+1}$
for all
$\mathfrak {F}_{h}\subseteq \mathfrak {F}_{h+1}$
for all
![]() $h<\omega $
. For each point
$h<\omega $
. For each point
![]() $t\in W_{h}$
that we select, we will be creating a copy of some original point in W. We give each added point a new name, say t, and let
$t\in W_{h}$
that we select, we will be creating a copy of some original point in W. We give each added point a new name, say t, and let
![]() $\widehat {t}$
denote the original point in W that t was copied from and will behave similar to. Thus, it is possible to have two different points
$\widehat {t}$
denote the original point in W that t was copied from and will behave similar to. Thus, it is possible to have two different points
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{2}$
in our new frame, where
$x_{2}$
in our new frame, where
![]() $\widehat {x_{1}}=\widehat {x_{2}}$
. The main difference between our construction and the construction given in [Reference Gabbay, Kurucz, Wolter and Zakharyaschev25, Section 10.3] will be seen in the
$\widehat {x_{1}}=\widehat {x_{2}}$
. The main difference between our construction and the construction given in [Reference Gabbay, Kurucz, Wolter and Zakharyaschev25, Section 10.3] will be seen in the
![]() $\rightarrow $
-step, which requires a more careful selection of new points.
$\rightarrow $
-step, which requires a more careful selection of new points.
To start the construction, let
![]() $\mathfrak {F}_{0}=(W_{0},R_{0},E_{0})$
where
$\mathfrak {F}_{0}=(W_{0},R_{0},E_{0})$
where
and
![]() $\widehat {t_{0}}$
is a point in W such that
$\widehat {t_{0}}$
is a point in W such that
![]() $\widehat {t_0}$
is from a clean cluster and is maximal with respect to
$\widehat {t_0}$
is from a clean cluster and is maximal with respect to
![]() $\varphi $
. The existence of such
$\varphi $
. The existence of such
![]() $\widehat {t_0}$
follows from Lemma 5.2(4). Moreover, let
$\widehat {t_0}$
follows from Lemma 5.2(4). Moreover, let
![]() $W^{\forall H}_{-1}= \varnothing $
.
$W^{\forall H}_{-1}= \varnothing $
.
Let
![]() $\mathsf {Sub}(\varphi )$
be the set of subformulas of
$\mathsf {Sub}(\varphi )$
be the set of subformulas of
![]() $\varphi $
, and let
$\varphi $
, and let
![]() $(W', R', E')$
be any of our frames in the construction. To each
$(W', R', E')$
be any of our frames in the construction. To each
![]() $t \in W'$
we associate the following subsets of
$t \in W'$
we associate the following subsets of
![]() $\mathsf {Sub}(\varphi )$
:
$\mathsf {Sub}(\varphi )$
:
 $$\begin{align*} \Sigma^{\exists}(t) &= \{\exists\delta\in \mathsf{Sub}(\varphi) \mid \widehat{t}\ \vDash\exists\delta\text\},\\ \Sigma^{\forall H}(t) &=\{\forall\beta\in \mathsf{Sub}(\varphi) \mid \widehat{t}\text{ is maximal wrt }\forall\beta\},\\ \Sigma^{\forall V}(t) &= \{\forall\gamma\in \mathsf{Sub}(\varphi) \mid \widehat {t}\ \not\vDash\forall\gamma\text{ but is not maximal wrt }\forall\gamma\},\\ \Sigma^{\rightarrow}(t) &= \{\alpha\rightarrow\sigma\in \mathsf{Sub}(\varphi) \mid \widehat {t}\ \not\vDash\alpha\rightarrow\sigma \text{ and }\widehat{t}\not\vDash\alpha\}. \end{align*}$$
$$\begin{align*} \Sigma^{\exists}(t) &= \{\exists\delta\in \mathsf{Sub}(\varphi) \mid \widehat{t}\ \vDash\exists\delta\text\},\\ \Sigma^{\forall H}(t) &=\{\forall\beta\in \mathsf{Sub}(\varphi) \mid \widehat{t}\text{ is maximal wrt }\forall\beta\},\\ \Sigma^{\forall V}(t) &= \{\forall\gamma\in \mathsf{Sub}(\varphi) \mid \widehat {t}\ \not\vDash\forall\gamma\text{ but is not maximal wrt }\forall\gamma\},\\ \Sigma^{\rightarrow}(t) &= \{\alpha\rightarrow\sigma\in \mathsf{Sub}(\varphi) \mid \widehat {t}\ \not\vDash\alpha\rightarrow\sigma \text{ and }\widehat{t}\not\vDash\alpha\}. \end{align*}$$
These are precisely the subformulas of
![]() $\varphi $
whose truth-value at
$\varphi $
whose truth-value at
![]() $\widehat {t}$
is relevant for constructing our countermodel. Note that if
$\widehat {t}$
is relevant for constructing our countermodel. Note that if
![]() $\alpha\rightarrow\sigma\in\Sigma^\rightarrow(t)$
, then
$\alpha\rightarrow\sigma\in\Sigma^\rightarrow(t)$
, then
![]() $\widehat{t}$
is not maximal with respect to
$\widehat{t}$
is not maximal with respect to
![]() $\alpha\rightarrow\sigma$
.
$\alpha\rightarrow\sigma$
.
Suppose
![]() $\mathfrak {F}_{h-1}=(W_{h-1},R_{h-1},E_{h-1})$
has already been constructed so that
$\mathfrak {F}_{h-1}=(W_{h-1},R_{h-1},E_{h-1})$
has already been constructed so that
![]() $\mathfrak {F}_{h-1}$
is a finite
$\mathfrak {F}_{h-1}$
is a finite
![]() $\mathsf {M^+IPC}$
-frame and
$\mathsf {M^+IPC}$
-frame and
![]() $E(\,\widehat {w}\;)$
is a clean cluster for each
$E(\,\widehat {w}\;)$
is a clean cluster for each
![]() $w\in W_{h-1}$
. We construct
$w\in W_{h-1}$
. We construct
![]() $\mathfrak {F}_{h}$
by applying the four steps described below. They are designed to add the necessary witnesses required by the formulas in the sets
$\mathfrak {F}_{h}$
by applying the four steps described below. They are designed to add the necessary witnesses required by the formulas in the sets
![]() $\Sigma ^{\exists }(t)$
,
$\Sigma ^{\exists }(t)$
,
![]() $\Sigma ^{\forall H}(t)$
,
$\Sigma ^{\forall H}(t)$
,
![]() $\Sigma ^{\forall V}(t)$
, and
$\Sigma ^{\forall V}(t)$
, and
![]() $\Sigma ^{\rightarrow }(t)$
, respectively. In the
$\Sigma ^{\rightarrow }(t)$
, respectively. In the
![]() $\exists $
-step we ensure that for each formula in
$\exists $
-step we ensure that for each formula in
![]() $\Sigma ^{\exists }(t)$
the point t has an E-successor that witnesses the existential statement. In the
$\Sigma ^{\exists }(t)$
the point t has an E-successor that witnesses the existential statement. In the
![]() $\forall H$
-step we ensure that for each formula in
$\forall H$
-step we ensure that for each formula in
![]() $\Sigma ^{\forall H}(t)$
the point t has an E-successor that witnesses the refutation of the universal statement. In the vertical steps
$\Sigma ^{\forall H}(t)$
the point t has an E-successor that witnesses the refutation of the universal statement. In the vertical steps
![]() $\forall V$
and
$\forall V$
and
![]() $\rightarrow $
we make sure that t has the necessary R-successors that are maximal with respect to the formulas in
$\rightarrow $
we make sure that t has the necessary R-successors that are maximal with respect to the formulas in
![]() $\Sigma ^{\forall V}(t)$
and
$\Sigma ^{\forall V}(t)$
and
![]() $\Sigma ^{\rightarrow }(t)$
, respectively. In each step of the construction we add also points to witness commutativity. Note that the first three of the following four steps are only done once per cluster. This is enough since all points of a cluster in
$\Sigma ^{\rightarrow }(t)$
, respectively. In each step of the construction we add also points to witness commutativity. Note that the first three of the following four steps are only done once per cluster. This is enough since all points of a cluster in
![]() $\mathfrak F$
agree on refuting an
$\mathfrak F$
agree on refuting an
![]() $\forall $
- or
$\forall $
- or
![]() $\exists $
-formula and points from a clean cluster agree whether such a refutation is maximal.
$\exists $
-formula and points from a clean cluster agree whether such a refutation is maximal.
Roughly speaking, points are added to the construction in the following order: In the first round the cluster of the starting point
![]() $t_{0}$
is built by adding points for formulas in
$t_{0}$
is built by adding points for formulas in
![]() $\Sigma ^{\exists }(t_0)$
and
$\Sigma ^{\exists }(t_0)$
and
![]() $\Sigma ^{\forall H}(t_0)$
. After this, no more points are added to this cluster. We call this the ‘bottom cluster’ of our frame. The first round of the construction proceeds by adding vertical witnesses for each formula in
$\Sigma ^{\forall H}(t_0)$
. After this, no more points are added to this cluster. We call this the ‘bottom cluster’ of our frame. The first round of the construction proceeds by adding vertical witnesses for each formula in
![]() $\Sigma ^{\forall V}(t_0)$
and closing each such cluster by adding points for commutativity. The first round then finishes by adding for each point t in the ‘bottom cluster’ vertical witnesses for the formulas in
$\Sigma ^{\forall V}(t_0)$
and closing each such cluster by adding points for commutativity. The first round then finishes by adding for each point t in the ‘bottom cluster’ vertical witnesses for the formulas in
![]() $\Sigma ^{\rightarrow }(t)$
and closing under commutativity. In the next round all these newly built clusters will possibly be enlarged in the horizontal steps and then new vertical witnesses will be added in the
$\Sigma ^{\rightarrow }(t)$
and closing under commutativity. In the next round all these newly built clusters will possibly be enlarged in the horizontal steps and then new vertical witnesses will be added in the
![]() $\forall V$
- and
$\forall V$
- and
![]() $\rightarrow $
-steps.
$\rightarrow $
-steps.
![]() $\exists $
-step
$\exists $
-step
![]() $($
Horizontal
$($
Horizontal
![]() $)$
: Let
$)$
: Let
![]() $W^\exists _{h} = W_{h-1}$
,
$W^\exists _{h} = W_{h-1}$
,
![]() $R^\exists _{h} = R_{h-1}$
, and
$R^\exists _{h} = R_{h-1}$
, and
![]() $E^\exists _{h} = E_{h-1}$
. For each
$E^\exists _{h} = E_{h-1}$
. For each
![]() $E^{\exists }_{h}(t)\subseteq W^{\exists }_{h}\backslash W_{h-1}^{\forall H}$
, if
$E^{\exists }_{h}(t)\subseteq W^{\exists }_{h}\backslash W_{h-1}^{\forall H}$
, if
![]() $\exists \delta \in \Sigma ^{\exists }(t)$
but there is no
$\exists \delta \in \Sigma ^{\exists }(t)$
but there is no
![]() $s\in W^\exists _{h}$
already such that
$s\in W^\exists _{h}$
already such that
![]() $tE^{\exists }_{h}s$
and
$tE^{\exists }_{h}s$
and
![]() $\widehat {s}\ \vDash \delta $
, then we add a point s to
$\widehat {s}\ \vDash \delta $
, then we add a point s to
![]() $W^\exists _{h}$
with
$W^\exists _{h}$
with
![]() $\widehat {s} \models \delta $
and
$\widehat {s} \models \delta $
and
![]() $\widehat {t} E \widehat {s}$
. Such a point
$\widehat {t} E \widehat {s}$
. Such a point
![]() $\widehat {s}$
exists in W since
$\widehat {s}$
exists in W since
![]() $\widehat {t} \models \exists \delta $
. We then add the ordered pairs
$\widehat {t} \models \exists \delta $
. We then add the ordered pairs
![]() $(s,s)$
to
$(s,s)$
to
![]() $R^\exists _{h}$
, the ordered pairs
$R^\exists _{h}$
, the ordered pairs
![]() $(t,s)$
to
$(t,s)$
to
![]() $E^\exists _{h}$
, and generate the least equivalence relation.
$E^\exists _{h}$
, and generate the least equivalence relation.
![]() $\forall H$
-step
$\forall H$
-step
![]() $($
Horizontal
$($
Horizontal
![]() $)$
: Let
$)$
: Let
![]() $W^{\forall H}_{h} = W^\exists _{h}$
,
$W^{\forall H}_{h} = W^\exists _{h}$
,
![]() $R^{\forall H}_{h} = R^\exists _{h}$
, and
$R^{\forall H}_{h} = R^\exists _{h}$
, and
![]() $E^{\forall H}_{h} = E^\exists _{h} $
. For each
$E^{\forall H}_{h} = E^\exists _{h} $
. For each
![]() $E^{\forall H}_{h}(t)\subseteq W^{\forall H}_{h}\backslash W_{h-1}^{\forall H}$
, if
$E^{\forall H}_{h}(t)\subseteq W^{\forall H}_{h}\backslash W_{h-1}^{\forall H}$
, if
![]() $\forall \beta \in \Sigma ^{\forall H}(t)$
but there is no
$\forall \beta \in \Sigma ^{\forall H}(t)$
but there is no
![]() $s\in W_{h}^{\forall H}$
already such that
$s\in W_{h}^{\forall H}$
already such that
![]() $tE_{h}^{\forall H}s$
and
$tE_{h}^{\forall H}s$
and
![]() $\widehat {s}\ \not \vDash \beta $
, then we add a point s to
$\widehat {s}\ \not \vDash \beta $
, then we add a point s to
![]() $W_{h}^{\forall H}$
with
$W_{h}^{\forall H}$
with
![]() $\widehat {s}\ \not \models \beta $
and
$\widehat {s}\ \not \models \beta $
and
![]() $\widehat {t} E \widehat {s}$
. Such a point
$\widehat {t} E \widehat {s}$
. Such a point
![]() $\widehat {s}$
exists in W since
$\widehat {s}$
exists in W since
![]() $\widehat {t}$
is maximal with respect to
$\widehat {t}$
is maximal with respect to
![]() $\forall \beta $
. We then add the ordered pairs
$\forall \beta $
. We then add the ordered pairs
![]() $(s,s)$
to
$(s,s)$
to
![]() $R^{\forall H}_{h}$
, the ordered pairs
$R^{\forall H}_{h}$
, the ordered pairs
![]() $(t,s)$
to
$(t,s)$
to
![]() $E^{\forall H}_{h}$
, and generate the least equivalence relation.
$E^{\forall H}_{h}$
, and generate the least equivalence relation.
![]() $\forall $
V-step
$\forall $
V-step
![]() $($
Vertical
$($
Vertical
![]() $)$
: Let
$)$
: Let
![]() $W^{\forall V}_{h} = W^{\forall H}_{h} $
,
$W^{\forall V}_{h} = W^{\forall H}_{h} $
,
![]() $R^{\forall V}_{h} = R^{\forall H}_{h}$
, and
$R^{\forall V}_{h} = R^{\forall H}_{h}$
, and
![]() $E^{\forall V}_{h} = E^{\forall H}_{h}$
. For each
$E^{\forall V}_{h} = E^{\forall H}_{h}$
. For each
![]() $E^{\forall V}_{h}(t)\subseteq W^{\forall V}_{h}\backslash W_{h-1}^{\forall H}$
, consider
$E^{\forall V}_{h}(t)\subseteq W^{\forall V}_{h}\backslash W_{h-1}^{\forall H}$
, consider
![]() $\forall \gamma \in \Sigma ^{\forall V}(t)$
. Since
$\forall \gamma \in \Sigma ^{\forall V}(t)$
. Since
![]() $\widehat {t}\ \not \vDash \forall \gamma $
, we can pick a point
$\widehat {t}\ \not \vDash \forall \gamma $
, we can pick a point
![]() $\widehat {s} \in W$
as in Lemma 5.2(2). We add the point s to
$\widehat {s} \in W$
as in Lemma 5.2(2). We add the point s to
![]() $W_{h}^{\forall V}$
and
$W_{h}^{\forall V}$
and
![]() $(t,s)$
to
$(t,s)$
to
![]() $R_{h}^{\forall V}$
.
$R_{h}^{\forall V}$
.
Since W satisfies commutativity, for each
![]() $w\in E_{h}^{\forall V}(t)$
, there is
$w\in E_{h}^{\forall V}(t)$
, there is
![]() $z_{w}\in W$
such that
$z_{w}\in W$
such that
![]() $\widehat {w}Rz_{w}$
and
$\widehat {w}Rz_{w}$
and
![]() $z_{w}E \widehat {s}$
. To ensure commutativity is satisfied in our new frame, we add the points
$z_{w}E \widehat {s}$
. To ensure commutativity is satisfied in our new frame, we add the points
![]() $s_{w}$
to
$s_{w}$
to
![]() $W_{h}^{\forall V}$
where
$W_{h}^{\forall V}$
where
![]() $\widehat {s_{w}}=z_{w}$
. We then add
$\widehat {s_{w}}=z_{w}$
. We then add
![]() $(w,s_{w})$
to
$(w,s_{w})$
to
![]() $R_{h}^{\forall V}$
and take the reflexive and transitive closure. We also add
$R_{h}^{\forall V}$
and take the reflexive and transitive closure. We also add
![]() $(s_{w},s)$
to
$(s_{w},s)$
to
![]() $E_{h}^{\forall V}$
and generate the least equivalence relation.
$E_{h}^{\forall V}$
and generate the least equivalence relation.
![]() $\rightarrow $
-step
$\rightarrow $
-step
![]() $($
Vertical
$($
Vertical
![]() $)$
: Let
$)$
: Let
![]() $W^{\rightarrow }_{h} = W^{\forall V}_{h} $
,
$W^{\rightarrow }_{h} = W^{\forall V}_{h} $
,
![]() $R^{\rightarrow }_{h} = R^{\forall V}_{h}$
, and
$R^{\rightarrow }_{h} = R^{\forall V}_{h}$
, and
![]() $E^{\rightarrow }_{h} = E^{\forall V}_{h}$
. For each
$E^{\rightarrow }_{h} = E^{\forall V}_{h}$
. For each
![]() $t\in W_{h}^{\forall H} \backslash W_{h-1}^{\forall H}$
(hence including any points added in the horizontal steps above, but not in the previous vertical step), consider all
$t\in W_{h}^{\forall H} \backslash W_{h-1}^{\forall H}$
(hence including any points added in the horizontal steps above, but not in the previous vertical step), consider all
![]() $\alpha \rightarrow \sigma \in \Sigma ^{\rightarrow }(t)$
such that there is no
$\alpha \rightarrow \sigma \in \Sigma ^{\rightarrow }(t)$
such that there is no
![]() $s\in W^{\rightarrow }_{h}$
already such that
$s\in W^{\rightarrow }_{h}$
already such that
![]() $tR^{\rightarrow }_{h}s$
,
$tR^{\rightarrow }_{h}s$
,
![]() $\widehat{s}\vDash\alpha$
, and
$\widehat{s}\vDash\alpha$
, and
![]() $\widehat{s}\not\vDash\sigma$
. Consider
$\widehat{s}\not\vDash\sigma$
. Consider
 $$ \begin{align*} A=[W \setminus \nu(\alpha\rightarrow\sigma)]\cap\bigcap_{\psi\in\mathsf{Sub}(\varphi)}\{\nu(\psi):\widehat{t}\ \vDash\psi\}. \end{align*} $$
$$ \begin{align*} A=[W \setminus \nu(\alpha\rightarrow\sigma)]\cap\bigcap_{\psi\in\mathsf{Sub}(\varphi)}\{\nu(\psi):\widehat{t}\ \vDash\psi\}. \end{align*} $$
Then A is clopen and
![]() $\widehat {t} \in A$
, so by Lemma 5.2(3) there is
$\widehat {t} \in A$
, so by Lemma 5.2(3) there is
![]() $z \in A$
with
$z \in A$
with
![]() $z \in \max E(A)$
,
$z \in \max E(A)$
,
![]() $\widehat {t} Q z$
, and
$\widehat {t} Q z$
, and
![]() $E(z)$
clean. We add the point s to
$E(z)$
clean. We add the point s to
![]() $W_{h}^{ \rightarrow }$
where
$W_{h}^{ \rightarrow }$
where
![]() $\widehat {s}=z$
(s is a distinct new copy of z) and
$\widehat {s}=z$
(s is a distinct new copy of z) and
![]() $(t,s)$
to
$(t,s)$
to
![]() $R_{h}^{ \rightarrow }$
.
$R_{h}^{ \rightarrow }$
.
Remark 5.3. It is at this step that we have altered the construction given in [Reference Gabbay, Kurucz, Wolter and Zakharyaschev25, Section 10.3], in which witnesses for implications are added in the same manner as in the
![]() $\forall V$
-step. In our version, we took an original Q-relation and turned it into an R-relation. The reason for this is that we cannot guarantee the existence of an R-successor of t that is maximal with respect to
$\forall V$
-step. In our version, we took an original Q-relation and turned it into an R-relation. The reason for this is that we cannot guarantee the existence of an R-successor of t that is maximal with respect to
![]() $\alpha \rightarrow \sigma $
and at the same time belongs to a clean cluster.
$\alpha \rightarrow \sigma $
and at the same time belongs to a clean cluster.
Before wrapping up the step, we show two properties of the chosen points.
Lemma 5.4. The point
![]() $\widehat {s}=z$
, as chosen above, is maximal with respect to
$\widehat {s}=z$
, as chosen above, is maximal with respect to
![]() $\alpha \rightarrow \sigma $
.
$\alpha \rightarrow \sigma $
.
Proof. Let
![]() $zRu$
for some
$zRu$
for some
![]() $u\not \vDash \alpha \rightarrow \sigma $
. Since
$u\not \vDash \alpha \rightarrow \sigma $
. Since
![]() $zRu$
and each
$zRu$
and each
![]() $\nu (\psi )$
in
$\nu (\psi )$
in
![]() $\{\nu (\psi ):\widehat {t}\ \vDash \psi \}$
is an upset, we have
$\{\nu (\psi ):\widehat {t}\ \vDash \psi \}$
is an upset, we have
![]() $u\in A$
. Because
$u\in A$
. Because
![]() $z \in \max A$
, we obtain
$z \in \max A$
, we obtain
![]() $z =u$
. Thus, z is maximal with respect to
$z =u$
. Thus, z is maximal with respect to
![]() $\alpha \rightarrow \sigma $
.⊣
$\alpha \rightarrow \sigma $
.⊣
Lemma 5.5.
![]() $E(\,\widehat {t}\;)\neq E(\,\widehat {s}\;)$
.
$E(\,\widehat {t}\;)\neq E(\,\widehat {s}\;)$
.
Proof. If
![]() $E(\,\widehat {t}\;) = E(\,\widehat {s}\;)$
, then
$E(\,\widehat {t}\;) = E(\,\widehat {s}\;)$
, then
![]() $\widehat {t}\in \max E(A)$
by Lemma 5.1. Since
$\widehat {t}\in \max E(A)$
by Lemma 5.1. Since
![]() $\widehat {t} \in A$
, we have
$\widehat {t} \in A$
, we have
![]() $\widehat {t} \in \max A$
. Therefore, the same argument as in the proof of the previous lemma yields that
$\widehat {t} \in \max A$
. Therefore, the same argument as in the proof of the previous lemma yields that
![]() $\widehat {t}$
is maximal with respect to
$\widehat {t}$
is maximal with respect to
![]() $\alpha \rightarrow \sigma $
. This contradicts the fact that
$\alpha \rightarrow \sigma $
. This contradicts the fact that
![]() $\alpha \rightarrow \sigma \in \Sigma ^{\rightarrow }(t)$
.⊣
$\alpha \rightarrow \sigma \in \Sigma ^{\rightarrow }(t)$
.⊣
We wrap up the
![]() $\rightarrow $
-step the same way as the
$\rightarrow $
-step the same way as the
![]() $\forall V$
-step. Since W satisfies commutativity, for each
$\forall V$
-step. Since W satisfies commutativity, for each
![]() $w\in E_{h}^{\forall V}(t)$
there is
$w\in E_{h}^{\forall V}(t)$
there is
![]() $z_w\in W$
with
$z_w\in W$
with
![]() $\widehat {w}Rz_{w}$
and
$\widehat {w}Rz_{w}$
and
![]() $z_w E \widehat {s}$
. We add the points
$z_w E \widehat {s}$
. We add the points
![]() $s_{w}$
to
$s_{w}$
to
![]() $W_{h}^{\forall V}$
where
$W_{h}^{\forall V}$
where
![]() $\widehat {s_{w}}=z_{w}$
. We then add
$\widehat {s_{w}}=z_{w}$
. We then add
![]() $(w,s_{w})$
to
$(w,s_{w})$
to
![]() $R_{h}^{\rightarrow }$
and take the reflexive and transitive closure. We also add
$R_{h}^{\rightarrow }$
and take the reflexive and transitive closure. We also add
![]() $(s_{w},s)$
to
$(s_{w},s)$
to
![]() $E_{h}^{\rightarrow }$
and generate the least equivalence relation.
$E_{h}^{\rightarrow }$
and generate the least equivalence relation.
To end this stage of the construction, we let
![]() $\mathfrak {F}_{h}=(W_{h},R_{h},E_{h})$
where
$\mathfrak {F}_{h}=(W_{h},R_{h},E_{h})$
where
Lemma 5.6.
![]() $\mathfrak F_{h}$
is a finite
$\mathfrak F_{h}$
is a finite
![]() $\mathsf {M^+IPC}$
-frame.
$\mathsf {M^+IPC}$
-frame.
Proof. First we show that
![]() $R_{h}$
is a partial order. Since in the
$R_{h}$
is a partial order. Since in the
![]() $\exists $
- and
$\exists $
- and
![]() $\forall H$
-steps we only added reflexive arrows to
$\forall H$
-steps we only added reflexive arrows to
![]() $R_{h-1}$
, the relation
$R_{h-1}$
, the relation
![]() $R^{\forall H}_{h}$
is a partial order. By moving from
$R^{\forall H}_{h}$
is a partial order. By moving from
![]() $R^{\forall H}_{h}$
to
$R^{\forall H}_{h}$
to
![]() $R_{h}$
we finished by taking the reflexive and transitive closure, hence
$R_{h}$
we finished by taking the reflexive and transitive closure, hence
![]() $R_{h}$
is clearly reflexive and transitive. Antisymmetry of
$R_{h}$
is clearly reflexive and transitive. Antisymmetry of
![]() $R_{h}$
follows from the fact that every R-arrow added in the
$R_{h}$
follows from the fact that every R-arrow added in the
![]() $\forall V$
-step and
$\forall V$
-step and
![]() $\rightarrow $
-step is either reflexive or an arrow from a previously existing point into a freshly added point.
$\rightarrow $
-step is either reflexive or an arrow from a previously existing point into a freshly added point.
That
![]() $E_{h}$
is an equivalence relation is clear from the construction. Moreover, the extra points added in the
$E_{h}$
is an equivalence relation is clear from the construction. Moreover, the extra points added in the
![]() $\forall V$
-step and
$\forall V$
-step and
![]() $\rightarrow $
-step make sure that commutativity is satisfied. In fact, the added points assure commutativity for immediate successors and by transitivity this implies commutativity for the whole frame. Therefore,
$\rightarrow $
-step make sure that commutativity is satisfied. In fact, the added points assure commutativity for immediate successors and by transitivity this implies commutativity for the whole frame. Therefore,
![]() $\mathfrak F_{h}$
is an
$\mathfrak F_{h}$
is an
![]() $\mathsf {MIPC}$
-frame.
$\mathsf {MIPC}$
-frame.
It follows from the construction that
![]() $\mathfrak F_{h}$
is finite. Thus, by Lemma 4.4, it is left to show that
$\mathfrak F_{h}$
is finite. Thus, by Lemma 4.4, it is left to show that
![]() $\mathfrak F_{h}$
has clean clusters. Note that in the
$\mathfrak F_{h}$
has clean clusters. Note that in the
![]() $\exists $
-step and
$\exists $
-step and
![]() $\forall H$
-step all freshly introduced
$\forall H$
-step all freshly introduced
![]() $E_h$
-relations are of the shape
$E_h$
-relations are of the shape
![]() $(s, t)$
where either
$(s, t)$
where either
![]() $s \in W_h$
and
$s \in W_h$
and
![]() $t \in W^{\forall H}_{h} \setminus W_{h-1}$
or
$t \in W^{\forall H}_{h} \setminus W_{h-1}$
or
![]() $s, t \in W^{\forall H}_{h} $
. Since no non-reflexive
$s, t \in W^{\forall H}_{h} $
. Since no non-reflexive
![]() $R_{h}$
-arrows are introduced in these steps, no dirty cluster could have been built. We have already discussed the shape of the
$R_{h}$
-arrows are introduced in these steps, no dirty cluster could have been built. We have already discussed the shape of the
![]() $R_{h}$
arrows introduced in the
$R_{h}$
arrows introduced in the
![]() $\forall V$
-step and
$\forall V$
-step and
![]() $\rightarrow $
-step. This guarantees that no cluster in
$\rightarrow $
-step. This guarantees that no cluster in
![]() $W^{\forall H}_{h}$
is made dirty. The freshly introduced
$W^{\forall H}_{h}$
is made dirty. The freshly introduced
![]() $E_{h}$
-relations in these steps are of the shape
$E_{h}$
-relations in these steps are of the shape
![]() $(s, t)$
where
$(s, t)$
where
![]() $s, t \in W_{h} \setminus W^{\forall H}_{h}$
. Since no non-reflexive
$s, t \in W_{h} \setminus W^{\forall H}_{h}$
. Since no non-reflexive
![]() $R_{h}$
relations exist between these points, we infer that all clusters are clean.⊣
$R_{h}$
relations exist between these points, we infer that all clusters are clean.⊣
5.2 Auxiliary lemmas
To prove that our construction terminates after finitely many steps, we require several auxiliary lemmas.
Lemma 5.7. Let
![]() $x,y\in W_h$
.
$x,y\in W_h$
.
-
1. If
 $xR_{h}y$
and
$xR_{h}y$
and
 $x\neq y$
, then
$x\neq y$
, then
 $\widehat {x}Q\widehat {y}$
and
$\widehat {x}Q\widehat {y}$
and
 $E(\,\widehat {x}\;)\neq E(\,\widehat {y}\;)$
.
$E(\,\widehat {x}\;)\neq E(\,\widehat {y}\;)$
. -
2. If
 $xE_{h}y$
, then
$xE_{h}y$
, then
 $\widehat {x}E\widehat {y}$
.
$\widehat {x}E\widehat {y}$
. -
3. If
 $xQ_{h}y$
, then
$xQ_{h}y$
, then
 $\widehat {x}Q\widehat {y}$
.
$\widehat {x}Q\widehat {y}$
.
Proof. (1) Observe that in the construction each non-trivial
![]() $R_{h}$
-relation between immediate successors comes from either a non-trivial R-relation (as in the case of points added for commutativity or in the
$R_{h}$
-relation between immediate successors comes from either a non-trivial R-relation (as in the case of points added for commutativity or in the
![]() $\forall V$
-step) or a non-trivial Q-relation (as in the case of points added in the
$\forall V$
-step) or a non-trivial Q-relation (as in the case of points added in the
![]() $\rightarrow $
-step). In the former case, it is obvious that
$\rightarrow $
-step). In the former case, it is obvious that
![]() $\widehat{x}Q\widehat{y}$
and
$\widehat{x}Q\widehat{y}$
and
![]() $E(\,\widehat{x}\;)\neq E(\,\widehat{y}\;)$
. In the latter case, there is
$E(\,\widehat{x}\;)\neq E(\,\widehat{y}\;)$
. In the latter case, there is
![]() $w\in W$
with
$w\in W$
with
![]() $\widehat {x}\neq w$
,
$\widehat {x}\neq w$
,
![]() $\widehat {x}Rw$
, and
$\widehat {x}Rw$
, and
![]() $wE\widehat {y}$
. In that case we obviously have
$wE\widehat {y}$
. In that case we obviously have
![]() $\widehat {x} Q \widehat {y}$
and by Lemma 5.5,
$\widehat {x} Q \widehat {y}$
and by Lemma 5.5,
![]() $E(\,\widehat {x}\;)\neq E(\,\widehat {y}\;)$
. If the relation
$E(\,\widehat {x}\;)\neq E(\,\widehat {y}\;)$
. If the relation
![]() $x R_h y$
was added by transitivity, there is a chain
$x R_h y$
was added by transitivity, there is a chain
![]() $x = x_0 R_h x_1 R_h \cdots R_h x_n = y$
of immediate
$x = x_0 R_h x_1 R_h \cdots R_h x_n = y$
of immediate
![]() $R_h$
-successors to which the previous applies, hence
$R_h$
-successors to which the previous applies, hence
![]() $\widehat{x}Q\widehat{y}$
and
$\widehat{x}Q\widehat{y}$
and
![]() $E(\,\widehat {x}\;)\neq E(\,\widehat {y}\;)$
by induction.
$E(\,\widehat {x}\;)\neq E(\,\widehat {y}\;)$
by induction.
(2) It is obvious that each
![]() $E_{h}$
-relation in
$E_{h}$
-relation in
![]() $W_{h}$
comes from a pre-existing E-relation in W.
$W_{h}$
comes from a pre-existing E-relation in W.
(3) If
![]() $xQ_{h}y$
, then there is z with
$xQ_{h}y$
, then there is z with
![]() $xR_{h}z$
and
$xR_{h}z$
and
![]() $zE_{h}y$
. If
$zE_{h}y$
. If
![]() $x = z$
, then
$x = z$
, then
![]() $x E_h y$
, so
$x E_h y$
, so
![]() $\widehat {x} E \widehat {y}$
by (2), and hence
$\widehat {x} E \widehat {y}$
by (2), and hence
![]() $\widehat {x} Q \widehat {y}$
. If
$\widehat {x} Q \widehat {y}$
. If
![]() $x \neq z$
, then
$x \neq z$
, then
![]() $\widehat {x} Q \widehat {z}$
by (1). Also,
$\widehat {x} Q \widehat {z}$
by (1). Also,
![]() $z E_{h} y$
implies
$z E_{h} y$
implies
![]() $\widehat {z} E \widehat {y}$
by (2). Thus,
$\widehat {z} E \widehat {y}$
by (2). Thus,
![]() $\widehat {x} Q \widehat {y}$
.⊣
$\widehat {x} Q \widehat {y}$
.⊣
Lemma 5.8 (Persistence)
If
![]() $u R_h w$
, then
$u R_h w$
, then
![]() $\widehat {u}\ \vDash \psi $
implies
$\widehat {u}\ \vDash \psi $
implies
![]() $\widehat {w}\ \vDash \psi $
for all
$\widehat {w}\ \vDash \psi $
for all
![]() $\psi \in \mathsf {Sub}(\varphi )$
.
$\psi \in \mathsf {Sub}(\varphi )$
.
Proof. Suppose
![]() $uR_{h}w$
,
$uR_{h}w$
,
![]() $\psi \in \mathsf {Sub}(\varphi )$
, and
$\psi \in \mathsf {Sub}(\varphi )$
, and
![]() $\widehat {u}\ \vDash \psi $
. It suffices to show the result for an immediate
$\widehat {u}\ \vDash \psi $
. It suffices to show the result for an immediate
![]() $R_{h}$
-successor
$R_{h}$
-successor
![]() $w$
of u, the general result then follows by induction. We consider how the
$w$
of u, the general result then follows by induction. We consider how the
![]() $R_{h}$
-arrow from u to
$R_{h}$
-arrow from u to
![]() $w$
was added. By construction, either
$w$
was added. By construction, either
![]() $\widehat {u}R\widehat {w}$
or
$\widehat {u}R\widehat {w}$
or
![]() $w$
was added to witness some implication in
$w$
was added to witness some implication in
![]() $\Sigma ^{\rightarrow }(u)$
. If
$\Sigma ^{\rightarrow }(u)$
. If
![]() $\ \widehat {u}R\widehat {w}$
, then clearly
$\ \widehat {u}R\widehat {w}$
, then clearly
![]() $\widehat {u}\ \vDash \psi $
implies
$\widehat {u}\ \vDash \psi $
implies
![]() $\widehat {w}\ \vDash \psi $
. If
$\widehat {w}\ \vDash \psi $
. If
![]() $w$
was added in a
$w$
was added in a
![]() $\rightarrow $
-step, then
$\rightarrow $
-step, then
![]() $w$
is specifically chosen so that
$w$
is specifically chosen so that
![]() $\widehat {w}\in \nu (\gamma )$
for all
$\widehat {w}\in \nu (\gamma )$
for all
![]() $\gamma \in \mathsf {Sub}(\varphi )$
such that
$\gamma \in \mathsf {Sub}(\varphi )$
such that
![]() $\widehat {u}\ \vDash \gamma $
. Thus,
$\widehat {u}\ \vDash \gamma $
. Thus,
![]() $\widehat {u}\ \vDash \psi $
implies
$\widehat {u}\ \vDash \psi $
implies
![]() $\widehat {w}\ \vDash \psi $
.⊣
$\widehat {w}\ \vDash \psi $
.⊣
Lemma 5.9.
-
1. If
 $t E_h u$
, then
$t E_h u$
, then
 $\Sigma ^{\exists }(t) =\Sigma ^{\exists }(u)$
,
$\Sigma ^{\exists }(t) =\Sigma ^{\exists }(u)$
,
 $\Sigma ^{\forall H}(t) =\Sigma ^{\forall H}(u)$
, and
$\Sigma ^{\forall H}(t) =\Sigma ^{\forall H}(u)$
, and
 $\Sigma ^{\forall V }(t) = \Sigma ^{\forall V}(u)$
.
$\Sigma ^{\forall V }(t) = \Sigma ^{\forall V}(u)$
. -
2. If
 $t R_h v$
and
$t R_h v$
and
 $\exists \gamma \in \Sigma ^{\exists }(t) \cap \Sigma ^{\exists }(v)$
, then there are
$\exists \gamma \in \Sigma ^{\exists }(t) \cap \Sigma ^{\exists }(v)$
, then there are
 $u, w$
such that
$u, w$
such that
 $t E_h u$
,
$t E_h u$
,
 $u R_h w$
,
$u R_h w$
,
 $w E_h v$
,
$w E_h v$
,
 $\widehat {u} \models \gamma $
, and
$\widehat {u} \models \gamma $
, and
 $\widehat {w} \models \gamma $
.
$\widehat {w} \models \gamma $
. -
3. If
 $t R_h v$
and
$t R_h v$
and
 $t\not =v$
, then
$t\not =v$
, then
 $\Sigma ^{\forall H}(t) \cap \Sigma ^{\forall H}(v) = \varnothing $
.
$\Sigma ^{\forall H}(t) \cap \Sigma ^{\forall H}(v) = \varnothing $
. -
4. Along an
 $R_{h}$
-chain, each formula in can serve at most once as a reason to enlarge a cluster in a horizontal step.
$R_{h}$
-chain, each formula in can serve at most once as a reason to enlarge a cluster in a horizontal step. $$ \begin{align*} \{\forall \psi \mid \forall \psi \in \mathsf {Sub}(\varphi )\} \cup \{\exists \psi \mid \exists \psi \in \mathsf {Sub}(\varphi )\} \end{align*} $$
$$ \begin{align*} \{\forall \psi \mid \forall \psi \in \mathsf {Sub}(\varphi )\} \cup \{\exists \psi \mid \exists \psi \in \mathsf {Sub}(\varphi )\} \end{align*} $$
-
5. If
 $t R_h u$
, then
$t R_h u$
, then
 $\Sigma ^{\forall V }(u) \subseteq \Sigma ^{\forall V}(t)$
and if u was added as an immediate
$\Sigma ^{\forall V }(u) \subseteq \Sigma ^{\forall V}(t)$
and if u was added as an immediate
 $R_h$
-successor to t because of
$R_h$
-successor to t because of
 $\forall \alpha \in \Sigma ^{\forall V} (t)$
, then
$\forall \alpha \in \Sigma ^{\forall V} (t)$
, then
 $\Sigma ^{\forall V }(u) \subset \Sigma ^{\forall V}(t)$
.
$\Sigma ^{\forall V }(u) \subset \Sigma ^{\forall V}(t)$
. -
6. If
 $t R_h u$
, then
$t R_h u$
, then
 $\Sigma ^{\rightarrow }(u) \subseteq \Sigma ^{\rightarrow }(t)$
and if u was added as an immediate
$\Sigma ^{\rightarrow }(u) \subseteq \Sigma ^{\rightarrow }(t)$
and if u was added as an immediate
 $R_h$
-successor to t because of
$R_h$
-successor to t because of
 $\alpha \rightarrow \beta \in \Sigma ^{\rightarrow } (t)$
, then
$\alpha \rightarrow \beta \in \Sigma ^{\rightarrow } (t)$
, then
 $\Sigma ^{\rightarrow }(u) \subset \Sigma ^{\rightarrow }(t)$
.
$\Sigma ^{\rightarrow }(u) \subset \Sigma ^{\rightarrow }(t)$
.
Proof. (1) Suppose
![]() $t E_h u$
. Then
$t E_h u$
. Then
![]() $\widehat {t} E \widehat {u}$
by Lemma 5.7(2). Therefore,
$\widehat {t} E \widehat {u}$
by Lemma 5.7(2). Therefore,
![]() $E(\,\widehat {t}\;) = E(\,\widehat {u}\;)$
and
$E(\,\widehat {t}\;) = E(\,\widehat {u}\;)$
and
![]() $Q(\,\widehat {t}\;) = Q(\,\widehat {u}\;)$
. Thus,
$Q(\,\widehat {t}\;) = Q(\,\widehat {u}\;)$
. Thus,
![]() $\widehat {t}\ \vDash \exists \gamma $
iff
$\widehat {t}\ \vDash \exists \gamma $
iff
![]() $\widehat {u}\ \vDash \exists \gamma $
, and
$\widehat {u}\ \vDash \exists \gamma $
, and
![]() $\widehat {t}\ \vDash \forall \gamma $
iff
$\widehat {t}\ \vDash \forall \gamma $
iff
![]() $\widehat {u}\ \vDash \forall \gamma $
. Moreover, since
$\widehat {u}\ \vDash \forall \gamma $
. Moreover, since
![]() $E(\,\widehat {t}\;)$
is a clean cluster,
$E(\,\widehat {t}\;)$
is a clean cluster,
![]() $\widehat {t}$
is not maximal wrt
$\widehat {t}$
is not maximal wrt
![]() $\forall \gamma $
iff
$\forall \gamma $
iff
![]() $\widehat {u}$
is not maximal wrt
$\widehat {u}$
is not maximal wrt
![]() $\forall \gamma $
. Consequently,
$\forall \gamma $
. Consequently,
![]() $\Sigma ^{\exists }(t) =\Sigma ^{\exists }(u)$
,
$\Sigma ^{\exists }(t) =\Sigma ^{\exists }(u)$
,
![]() $\Sigma ^{\forall H}(t) =\Sigma ^{\forall H}(u)$
, and
$\Sigma ^{\forall H}(t) =\Sigma ^{\forall H}(u)$
, and
![]() $\Sigma ^{\forall V }(t) = \Sigma ^{\forall V}(u)$
.
$\Sigma ^{\forall V }(t) = \Sigma ^{\forall V}(u)$
.
(2) Suppose
![]() $t R_h v$
and
$t R_h v$
and
![]() $\exists \gamma \in \Sigma ^{\exists }(t) \cap \Sigma ^{\exists }(v)$
. By the construction, there is u with
$\exists \gamma \in \Sigma ^{\exists }(t) \cap \Sigma ^{\exists }(v)$
. By the construction, there is u with
![]() $t E_h u$
and
$t E_h u$
and
![]() $\widehat {u}\ \vDash \gamma $
. Since
$\widehat {u}\ \vDash \gamma $
. Since
![]() $\mathfrak F_h$
satisfies commutativity, there is
$\mathfrak F_h$
satisfies commutativity, there is
![]() $w$
with
$w$
with
![]() $u R_h w$
and
$u R_h w$
and
![]() $w E_h v$
. By Lemma 5.8,
$w E_h v$
. By Lemma 5.8,
![]() $\widehat {w}\ \vDash \gamma $
.
$\widehat {w}\ \vDash \gamma $
.
(3) Suppose
![]() $t R_h v$
and
$t R_h v$
and
![]() $t\not =v$
. Then
$t\not =v$
. Then
![]() $\widehat {t}Q\widehat {v}$
and
$\widehat {t}Q\widehat {v}$
and
![]() $E(\,\widehat {t}\;) \neq E(\,\widehat {v}\;)$
by Lemma 5.7(1), so
$E(\,\widehat {t}\;) \neq E(\,\widehat {v}\;)$
by Lemma 5.7(1), so
![]() $\widehat {t}\neq \widehat {v}$
. Thus, if
$\widehat {t}\neq \widehat {v}$
. Thus, if
![]() $\forall \psi \in \Sigma ^{\forall H}(t)$
, then
$\forall \psi \in \Sigma ^{\forall H}(t)$
, then
![]() $\widehat {v}\ \vDash \forall \psi $
by maximality of
$\widehat {v}\ \vDash \forall \psi $
by maximality of
![]() $\widehat {t}$
, so
$\widehat {t}$
, so
![]() $\forall \psi \not \in \Sigma ^{\forall H}(v)$
. Conversely, if
$\forall \psi \not \in \Sigma ^{\forall H}(v)$
. Conversely, if
![]() $\forall \psi \in \Sigma ^{\forall H}(v)$
, then
$\forall \psi \in \Sigma ^{\forall H}(v)$
, then
![]() $\widehat {t}$
cannot be maximal with respect to
$\widehat {t}$
cannot be maximal with respect to
![]() $\forall \psi $
, so
$\forall \psi $
, so
![]() $\forall \psi \not \in \Sigma ^{\forall H}(t)$
.
$\forall \psi \not \in \Sigma ^{\forall H}(t)$
.
(4) Let
![]() $\{v_i \mid i \in \mathbb N\}$
be an
$\{v_i \mid i \in \mathbb N\}$
be an
![]() $R_h$
-chain in
$R_h$
-chain in
![]() $W_h$
, i.e.,
$W_h$
, i.e.,
![]() $v_i R_h v_{i+1}$
for all
$v_i R_h v_{i+1}$
for all
![]() $i \in \mathbb N$
. Suppose
$i \in \mathbb N$
. Suppose
![]() $\exists \psi \in \mathsf {Sub}(\varphi )$
. Let k be the least stage at which the formula
$\exists \psi \in \mathsf {Sub}(\varphi )$
. Let k be the least stage at which the formula
![]() $\exists \psi $
has been used to enlarge the cluster
$\exists \psi $
has been used to enlarge the cluster
![]() $E_{h}(v_{k})$
in a horizontal step. By (2), all
$E_{h}(v_{k})$
in a horizontal step. By (2), all
![]() $E_{h}(v_{l})$
for
$E_{h}(v_{l})$
for
![]() $l>k$
already contain a witness for
$l>k$
already contain a witness for
![]() $\psi $
, so no cluster above will need to be enlarged in a horizontal step to witness the formula
$\psi $
, so no cluster above will need to be enlarged in a horizontal step to witness the formula
![]() $\exists \psi $
. Now suppose
$\exists \psi $
. Now suppose
![]() $\forall \psi \in \mathsf {Sub}(\varphi )$
. Let l be a stage at which the formula
$\forall \psi \in \mathsf {Sub}(\varphi )$
. Let l be a stage at which the formula
![]() $\forall \psi $
has been used to enlarge the cluster
$\forall \psi $
has been used to enlarge the cluster
![]() $E_{h}(v_{l})$
in a horizontal step. Then
$E_{h}(v_{l})$
in a horizontal step. Then
![]() $\forall \psi \in \Sigma ^{\forall H}(v_{l})$
. By (3),
$\forall \psi \in \Sigma ^{\forall H}(v_{l})$
. By (3),
![]() $\forall \psi \not \in \Sigma ^{\forall H}(v_{k})$
for
$\forall \psi \not \in \Sigma ^{\forall H}(v_{k})$
for
![]() $k\neq l$
. Thus,
$k\neq l$
. Thus,
![]() $\forall \psi $
is responsible for enlarging a cluster at most once in a horizontal step.
$\forall \psi $
is responsible for enlarging a cluster at most once in a horizontal step.
(5) We show the statement for immediate
![]() $R_{h}$
-successors only, the general case follows by induction. Suppose
$R_{h}$
-successors only, the general case follows by induction. Suppose
![]() $t R_h u$
and
$t R_h u$
and
![]() $\forall \psi \in \Sigma ^{\forall V }(u)$
. If
$\forall \psi \in \Sigma ^{\forall V }(u)$
. If
![]() $t=u$
, then the result is clear. Suppose
$t=u$
, then the result is clear. Suppose
![]() $t \neq u$
. Since
$t \neq u$
. Since
![]() $tR_{h}u$
, either
$tR_{h}u$
, either
![]() $\widehat {t} R \widehat {u}$
in W or u was added as a successor of t in some
$\widehat {t} R \widehat {u}$
in W or u was added as a successor of t in some
![]() $\rightarrow $
-step. If
$\rightarrow $
-step. If
![]() $\ \widehat {t} R \widehat {u}$
, then
$\ \widehat {t} R \widehat {u}$
, then
![]() $\forall \psi \in \Sigma ^{\forall V }(t)$
by persistence (see Lemma 5.8). Suppose u was added as an
$\forall \psi \in \Sigma ^{\forall V }(t)$
by persistence (see Lemma 5.8). Suppose u was added as an
![]() $R_h$
-successor to t as a witness to some implication. By the choice of u, we have
$R_h$
-successor to t as a witness to some implication. By the choice of u, we have
![]() $\widehat {u}\ \vDash \chi $
for all
$\widehat {u}\ \vDash \chi $
for all
![]() $\chi \in \mathsf {Sub}(\varphi )$
with
$\chi \in \mathsf {Sub}(\varphi )$
with
![]() $\widehat {t}\ \vDash \chi $
. Therefore, if
$\widehat {t}\ \vDash \chi $
. Therefore, if
![]() $\ \widehat {t}\ \vDash \forall \psi $
, then we would have
$\ \widehat {t}\ \vDash \forall \psi $
, then we would have
![]() $\widehat {u}\ \vDash \forall \psi $
, contradicting
$\widehat {u}\ \vDash \forall \psi $
, contradicting
![]() $\forall \psi \in \Sigma ^{\forall V}(u)$
. Thus, we must have
$\forall \psi \in \Sigma ^{\forall V}(u)$
. Thus, we must have
![]() $\widehat {t}\ \not \models \forall \psi $
. Moreover, since
$\widehat {t}\ \not \models \forall \psi $
. Moreover, since
![]() $\widehat {t}R\widehat {u}$
,
$\widehat {t}R\widehat {u}$
,
![]() $\widehat {t}\neq \widehat {u}$
, and
$\widehat {t}\neq \widehat {u}$
, and
![]() $\widehat {u}\ \not \vDash \forall \psi $
, we have that
$\widehat {u}\ \not \vDash \forall \psi $
, we have that
![]() $\widehat {t}$
is not maximal with respect to
$\widehat {t}$
is not maximal with respect to
![]() $\forall \psi $
, so
$\forall \psi $
, so
![]() $\forall \psi \in \Sigma ^{\forall V} (t)$
. Consequently, we have
$\forall \psi \in \Sigma ^{\forall V} (t)$
. Consequently, we have
![]() $\Sigma ^{\forall V }(u) \subseteq \Sigma ^{\forall V}(t)$
.
$\Sigma ^{\forall V }(u) \subseteq \Sigma ^{\forall V}(t)$
.
Suppose that u was added as an immediate
![]() $R_{h}$
-successor to t because of
$R_{h}$
-successor to t because of
![]() $\forall \alpha \in \Sigma ^{\forall V}(t)$
. Since
$\forall \alpha \in \Sigma ^{\forall V}(t)$
. Since
![]() $\forall \alpha \in \Sigma ^{\forall V}(t)$
, we have
$\forall \alpha \in \Sigma ^{\forall V}(t)$
, we have
![]() $\widehat {t}\ \not \vDash \forall \alpha $
but
$\widehat {t}\ \not \vDash \forall \alpha $
but
![]() $\widehat {t}$
is not maximal with respect to
$\widehat {t}$
is not maximal with respect to
![]() $\forall \alpha $
. Since u was added as an immediate
$\forall \alpha $
. Since u was added as an immediate
![]() $R_{h}$
-successor of t because of
$R_{h}$
-successor of t because of
![]() $\forall \alpha $
, we specifically chose u so that
$\forall \alpha $
, we specifically chose u so that
![]() $\widehat {u}\ \not \vDash \forall \alpha $
maximally, hence
$\widehat {u}\ \not \vDash \forall \alpha $
maximally, hence
![]() $\forall \alpha \not \in \Sigma ^{\forall V}(u)$
.
$\forall \alpha \not \in \Sigma ^{\forall V}(u)$
.
(6) We show the statement for immediate
![]() $R_h$
-successors only, the general case follows by induction. Suppose
$R_h$
-successors only, the general case follows by induction. Suppose
![]() $tR_{h}u$
and
$tR_{h}u$
and
![]() $\alpha \rightarrow \beta \in \Sigma ^{\rightarrow }(u)$
. Then
$\alpha \rightarrow \beta \in \Sigma ^{\rightarrow }(u)$
. Then
![]() $\widehat {u}\ \not \vDash \alpha \rightarrow \beta $
and
$\widehat {u}\ \not \vDash \alpha \rightarrow \beta $
and
![]() $\widehat {u}\ \not \vDash \alpha $
. If
$\widehat {u}\ \not \vDash \alpha $
. If
![]() $t=u$
, then the result is clear. Suppose
$t=u$
, then the result is clear. Suppose
![]() $t \neq u$
. Since
$t \neq u$
. Since
![]() $t R_h u$
, either
$t R_h u$
, either
![]() $\widehat {t} R \widehat {u}$
in W or u was added as a successor of t in some
$\widehat {t} R \widehat {u}$
in W or u was added as a successor of t in some
![]() $\rightarrow $
-step. If
$\rightarrow $
-step. If
![]() $\ \widehat {t} R \widehat {u}$
, then
$\ \widehat {t} R \widehat {u}$
, then
![]() $\alpha \rightarrow \beta \in \Sigma ^{\rightarrow }(t)$
by persistence (see Lemma 5.8). Suppose u was added as an
$\alpha \rightarrow \beta \in \Sigma ^{\rightarrow }(t)$
by persistence (see Lemma 5.8). Suppose u was added as an
![]() $R_h$
-successor to t as a witness to some implication. By the choice of u, we have
$R_h$
-successor to t as a witness to some implication. By the choice of u, we have
![]() $\widehat {u}\ \vDash \psi $
for all
$\widehat {u}\ \vDash \psi $
for all
![]() $\psi \in \mathsf {Sub}(\varphi )$
with
$\psi \in \mathsf {Sub}(\varphi )$
with
![]() $\widehat {t}\ \vDash \psi $
. Therefore, we must have
$\widehat {t}\ \vDash \psi $
. Therefore, we must have
![]() $\widehat {t}\ \not \models \alpha \rightarrow \beta $
and
$\widehat {t}\ \not \models \alpha \rightarrow \beta $
and
![]() $\widehat {t}\ \not \models \alpha $
, so
$\widehat {t}\ \not \models \alpha $
, so
![]() $\Sigma ^{\rightarrow }(u) \subseteq \Sigma ^{\rightarrow }(t)$
. Moreover, if
$\Sigma ^{\rightarrow }(u) \subseteq \Sigma ^{\rightarrow }(t)$
. Moreover, if
![]() $u$
was added as an immediate
$u$
was added as an immediate
![]() $R_h$
successor to
$R_h$
successor to
![]() $t$
because of
$t$
because of
![]() $\alpha\rightarrow\beta$
, then
$\alpha\rightarrow\beta$
, then
![]() $\widehat {u}$
refutes
$\widehat {u}$
refutes
![]() $\alpha \rightarrow \beta $
maximally (Lemma 5.4), and hence
$\alpha \rightarrow \beta $
maximally (Lemma 5.4), and hence
![]() $\widehat {u}\ \vDash \alpha $
. Thus,
$\widehat {u}\ \vDash \alpha $
. Thus,
![]() $\alpha \rightarrow \beta \not \in \Sigma ^{\rightarrow }(u)$
. ⊣
$\alpha \rightarrow \beta \not \in \Sigma ^{\rightarrow }(u)$
. ⊣
5.3 Termination of the construction
With the aid of the auxiliary lemmas of the previous section, we will now prove that the end result of our construction is a finite frame. We will do this by looking at three important parameters of our frame: cluster size, R-branching, and R-depth.
Definition 5.10.
-
1. A frame
 $\mathfrak {F}$
has bounded cluster size if there exists
$\mathfrak {F}$
has bounded cluster size if there exists
 $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
 $|E(t)|\leq k$
for all
$|E(t)|\leq k$
for all
 $t\in W$
.
$t\in W$
. -
2. A frame
 $\mathfrak {F}$
has bounded R-branching if there exists
$\mathfrak {F}$
has bounded R-branching if there exists
 $m\in \mathbb {N}$
such that t has at most m distinct immediate R-successors for all
$m\in \mathbb {N}$
such that t has at most m distinct immediate R-successors for all
 $t\in W$
.
$t\in W$
. -
3. A frame
 $\mathfrak {F}$
has bounded R-depth if there exists
$\mathfrak {F}$
has bounded R-depth if there exists
 $n\in \mathbb {N}$
such that there is no R-chain in
$n\in \mathbb {N}$
such that there is no R-chain in
 $\mathfrak {F}$
with more than n distinct elements.
$\mathfrak {F}$
with more than n distinct elements.
We call
![]() $\mathfrak{F} =(W,R,E)$
rooted if there exists
$\mathfrak{F} =(W,R,E)$
rooted if there exists
![]() $w\in W$
, called a root of
$w\in W$
, called a root of
![]() $\mathfrak F$
, such that
$\mathfrak F$
, such that
![]() $W=Q(w)$
.
$W=Q(w)$
.
Lemma 5.11. Let
![]() $\mathfrak {F}=(W,R,E)$
be a partially ordered rooted augmented Kripke frame. If
$\mathfrak {F}=(W,R,E)$
be a partially ordered rooted augmented Kripke frame. If
![]() $\mathfrak {F}$
has bounded cluster size, bounded R-branching, and bounded R-depth, then
$\mathfrak {F}$
has bounded cluster size, bounded R-branching, and bounded R-depth, then
![]() $\mathfrak F$
is finite.
$\mathfrak F$
is finite.
Proof. Suppose
![]() $\mathfrak {F}=(W,R,E)$
is a partially ordered rooted augmented Kripke frame with bounded cluster size, R-branching, and R-depth. Consider the quotient
$\mathfrak {F}=(W,R,E)$
is a partially ordered rooted augmented Kripke frame with bounded cluster size, R-branching, and R-depth. Consider the quotient
![]() $(W/{E},R_{E})$
whose worlds are the clusters
$(W/{E},R_{E})$
whose worlds are the clusters
![]() $E(x)$
where
$E(x)$
where
![]() $x\in W$
and
$x\in W$
and
![]() $E(x)R_{E}E(y)$
iff
$E(x)R_{E}E(y)$
iff
![]() $xQ y$
. To see that
$xQ y$
. To see that
![]() $R_{E}$
is well defined, suppose
$R_{E}$
is well defined, suppose
![]() $x Q y$
,
$x Q y$
,
![]() $x' \in E(x)$
, and
$x' \in E(x)$
, and
![]() $y' \in E(y)$
. Then
$y' \in E(y)$
. Then
![]() $x'ExQyEy'$
, so
$x'ExQyEy'$
, so
![]() $x'Qy'$
, and hence
$x'Qy'$
, and hence
![]() $R_E$
is well defined.
$R_E$
is well defined.
Because Q is reflexive and transitive, so is
![]() $R_E$
. Since R is a partial order and
$R_E$
. Since R is a partial order and
![]() $\mathfrak F$
has bounded R-depth, from
$\mathfrak F$
has bounded R-depth, from
![]() $x Q y $
and
$x Q y $
and
![]() $y Q x$
it follows that
$y Q x$
it follows that
![]() $x E y$
by [Reference Bezhanishvili4, Lemma 3(b)]. This shows that
$x E y$
by [Reference Bezhanishvili4, Lemma 3(b)]. This shows that
![]() $R_E$
is anti-symmetric, and hence a partial order. Clearly
$R_E$
is anti-symmetric, and hence a partial order. Clearly
![]() $(W/{E},R_{E})$
is rooted since so is
$(W/{E},R_{E})$
is rooted since so is
![]() $\mathfrak F$
. Using commutativity in
$\mathfrak F$
. Using commutativity in
![]() $\mathfrak F$
it is easy to verify that
$\mathfrak F$
it is easy to verify that
![]() $(W/{E},R_{E})$
inherits bounded depth and bounded branching from
$(W/{E},R_{E})$
inherits bounded depth and bounded branching from
![]() $\mathfrak F$
. Since every rooted partial order with these properties is finite, we have that
$\mathfrak F$
. Since every rooted partial order with these properties is finite, we have that
![]() $W/E$
is finite. Because W has bounded cluster size, we conclude that W is finite too.⊣
$W/E$
is finite. Because W has bounded cluster size, we conclude that W is finite too.⊣
Let
![]() $m_{1},m_{2},m_{3}$
be the non-negative integers
$m_{1},m_{2},m_{3}$
be the non-negative integers
 $$\begin{align*}m_{1} &= |\{\exists\psi \mid \exists\psi\in \mathsf{Sub}(\varphi)\}|,\\ m_{2} &= |\{\forall\psi \mid \forall\psi\in \mathsf{Sub}(\varphi)\}|,\\ m_{3} &= |\{\psi\rightarrow\chi \mid \psi\rightarrow\chi\in\mathsf{Sub}(\varphi)\}|. \end{align*}$$
$$\begin{align*}m_{1} &= |\{\exists\psi \mid \exists\psi\in \mathsf{Sub}(\varphi)\}|,\\ m_{2} &= |\{\forall\psi \mid \forall\psi\in \mathsf{Sub}(\varphi)\}|,\\ m_{3} &= |\{\psi\rightarrow\chi \mid \psi\rightarrow\chi\in\mathsf{Sub}(\varphi)\}|. \end{align*}$$
Lemma 5.12. For all
![]() $h<\omega $
, the cluster size of
$h<\omega $
, the cluster size of
![]() $\mathfrak {F}_{h}=(W_{h},R_{h},E_{h})$
is bounded by
$\mathfrak {F}_{h}=(W_{h},R_{h},E_{h})$
is bounded by
![]() $1+m_1+m_2$
.
$1+m_1+m_2$
.
Proof. Recall how the clusters of our frame are built. The ‘bottom cluster’ of the starting point
![]() $t_{0}$
contains points added via the horizontal
$t_{0}$
contains points added via the horizontal
![]() $\exists $
- and
$\exists $
- and
![]() $\forall H$
-steps. After this, no more points are added to this cluster.
$\forall H$
-steps. After this, no more points are added to this cluster.
All other clusters are constructed as follows. First points of a new cluster are added via the vertical
![]() $\forall V$
- or
$\forall V$
- or
![]() $\rightarrow $
-steps, and then the cluster is enlarged by the points added for commutativity. We refer to this stage as the ‘building phase’ of the cluster. In the next round of the construction, the cluster is (possibly) enlarged via the two horizontal steps. After this, no more points are added to the cluster. In the horizontal steps, we enlarge the cluster for only two different reasons:
$\rightarrow $
-steps, and then the cluster is enlarged by the points added for commutativity. We refer to this stage as the ‘building phase’ of the cluster. In the next round of the construction, the cluster is (possibly) enlarged via the two horizontal steps. After this, no more points are added to the cluster. In the horizontal steps, we enlarge the cluster for only two different reasons:
Thus, each enlargement of a cluster after its building phase is due to a formula in
![]() $ \{\forall \psi \mid \forall \psi \in \mathsf {Sub}(\varphi )\} \cup \{\exists \psi \mid \exists \psi \in \mathsf {Sub}(\varphi )\}. $
At the end of its building phase, the bottom cluster contains just one point. Observe that every cluster can be reached from the bottom cluster by an
$ \{\forall \psi \mid \forall \psi \in \mathsf {Sub}(\varphi )\} \cup \{\exists \psi \mid \exists \psi \in \mathsf {Sub}(\varphi )\}. $
At the end of its building phase, the bottom cluster contains just one point. Observe that every cluster can be reached from the bottom cluster by an
![]() $R_h$
-chain. It follows from Lemma 5.9(4) that every formula in
$R_h$
-chain. It follows from Lemma 5.9(4) that every formula in
![]() $\{\forall \psi \mid \forall \psi \in \mathsf {Sub}(\varphi )\} \cup \{\exists \psi \mid \exists \psi \in \mathsf {Sub}(\varphi )\}$
can serve at most once as a reason to enlarge a cluster after its building phase along an
$\{\forall \psi \mid \forall \psi \in \mathsf {Sub}(\varphi )\} \cup \{\exists \psi \mid \exists \psi \in \mathsf {Sub}(\varphi )\}$
can serve at most once as a reason to enlarge a cluster after its building phase along an
![]() $R_h$
-chain. This entails that every cluster has size at most
$R_h$
-chain. This entails that every cluster has size at most
![]() $1 +m_1 + m_2$
.⊣
$1 +m_1 + m_2$
.⊣
Lemma 5.13. For all
![]() $h<\omega $
, the
$h<\omega $
, the
![]() $R_{h}$
-branching of
$R_{h}$
-branching of
![]() $\mathfrak {F}_{h}=(W_{h},R_{h},E_{h})$
is bounded by
$\mathfrak {F}_{h}=(W_{h},R_{h},E_{h})$
is bounded by
![]() $m_{2} + (1+m_{1}+m_{2})\cdot m_{3}$
.
$m_{2} + (1+m_{1}+m_{2})\cdot m_{3}$
.
Proof. Immediate
![]() $R_h$
-successors are added in the
$R_h$
-successors are added in the
![]() $\forall V$
-step and
$\forall V$
-step and
![]() $\rightarrow $
-step. First observe that since we are adding points to witness commutativity, every point in a cluster has the same number of immediate
$\rightarrow $
-step. First observe that since we are adding points to witness commutativity, every point in a cluster has the same number of immediate
![]() $R_h$
-successors by the end of a stage. Thus, it is enough to count the immediate successors of a point t that we picked in the
$R_h$
-successors by the end of a stage. Thus, it is enough to count the immediate successors of a point t that we picked in the
![]() $\forall V$
-step.
$\forall V$
-step.
To such a point t we add immediate
![]() $R_h$
-successors for three different reasons:
$R_h$
-successors for three different reasons:
-
1.
 $\forall \gamma \in \Sigma ^{\forall V}(t)$
,
$\forall \gamma \in \Sigma ^{\forall V}(t)$
, -
2.
 $\alpha \rightarrow \sigma \in \Sigma ^{\rightarrow }(t)$
, or
$\alpha \rightarrow \sigma \in \Sigma ^{\rightarrow }(t)$
, or -
3.
 $\alpha \rightarrow \sigma \in \Sigma ^{\rightarrow }(y)$
for some
$\alpha \rightarrow \sigma \in \Sigma ^{\rightarrow }(y)$
for some
 $y \in E_h(t)$
with
$y \in E_h(t)$
with
 $y \neq t$
.
$y \neq t$
.
The last reason covers the case where we add an
![]() $R_h$
-successor to t to witness commutativity. Note that all reasons occur at most once for each formula in the respective sets. Therefore, reason (1) occurs at most
$R_h$
-successor to t to witness commutativity. Note that all reasons occur at most once for each formula in the respective sets. Therefore, reason (1) occurs at most
![]() $m_2$
-times and reason (2) at most
$m_2$
-times and reason (2) at most
![]() $m_3$
-times. Finally, reason (3) occurs at most
$m_3$
-times. Finally, reason (3) occurs at most
![]() $(m_{1}+m_{2})\cdot m_{3}$
times since by Lemma 5.12 there are at most
$(m_{1}+m_{2})\cdot m_{3}$
times since by Lemma 5.12 there are at most
![]() $m_1+ m_2$
points apart from t in the cluster of t. Thus, the
$m_1+ m_2$
points apart from t in the cluster of t. Thus, the
![]() $R_{h}$
-branching of
$R_{h}$
-branching of
![]() $\mathfrak F$
is bounded by
$\mathfrak F$
is bounded by
(see the diagram below):

⊣
Lemma 5.14. For all
![]() $h<\omega $
, the
$h<\omega $
, the
![]() $R_{h}$
-depth of
$R_{h}$
-depth of
![]() $\mathfrak {F}_{h}=(W_{h},R_{h},E_{h})$
is bounded by
$\mathfrak {F}_{h}=(W_{h},R_{h},E_{h})$
is bounded by
![]() $(1+m_{1}+m_{2})\cdot (m_{2}+m_{3})$
.
$(1+m_{1}+m_{2})\cdot (m_{2}+m_{3})$
.
Proof. The reason for adding an immediate successor to
![]() $t \in W_h$
via an
$t \in W_h$
via an
![]() $R_h$
-relation is due to either a formula in
$R_h$
-relation is due to either a formula in
![]() $\Sigma ^{\forall V}(t)$
or a formula in
$\Sigma ^{\forall V}(t)$
or a formula in
![]() $\Sigma ^{\rightarrow }(y)$
for some
$\Sigma ^{\rightarrow }(y)$
for some
![]() $y \in E_h(t)$
(as discussed in the proof of Lemma 5.13). Let s be a (not necessarily immediate)
$y \in E_h(t)$
(as discussed in the proof of Lemma 5.13). Let s be a (not necessarily immediate)
![]() $R_h$
-successor of t. Then s could have been added via direct formula witnessing, i.e., there is an immediate predecessor
$R_h$
-successor of t. Then s could have been added via direct formula witnessing, i.e., there is an immediate predecessor
![]() $t'$
of s with
$t'$
of s with
![]() $t R_h t' R_h s$
and s was added due to a formula in
$t R_h t' R_h s$
and s was added due to a formula in
![]() $\Sigma ^{\forall V }(t')$
or
$\Sigma ^{\forall V }(t')$
or
![]() $\Sigma ^{\rightarrow }(t')$
, or else s was added to satisfy commutativity.
$\Sigma ^{\rightarrow }(t')$
, or else s was added to satisfy commutativity.
As we saw in Lemma 5.9, moving up along an
![]() $R_{h}$
-chain, the cardinality of the sets
$R_{h}$
-chain, the cardinality of the sets
![]() $\Sigma ^{\forall V }(t)$
and
$\Sigma ^{\forall V }(t)$
and
![]() $\Sigma ^{\rightarrow }(t)$
does not increase, and it in fact decreases whenever an
$\Sigma ^{\rightarrow }(t)$
does not increase, and it in fact decreases whenever an
![]() $R_h$
-successor is added by direct formula witnessing. In particular, each point can have at most
$R_h$
-successor is added by direct formula witnessing. In particular, each point can have at most
![]() $m_{2}+m_{3}\ R_h$
-successors that have been added via direct formula witnessing and since in each cluster there are at most
$m_{2}+m_{3}\ R_h$
-successors that have been added via direct formula witnessing and since in each cluster there are at most
![]() $1+m_{1}+m_{2}$
points (Lemma 5.12), we have that the total
$1+m_{1}+m_{2}$
points (Lemma 5.12), we have that the total
![]() $R_h$
-depth cannot exceed
$R_h$
-depth cannot exceed
(see the diagram below):

Lemma 5.15. There is
![]() $h \in \mathbb N$
such that
$h \in \mathbb N$
such that
![]() $\mathfrak F_{h'} = \mathfrak F_h$
for all
$\mathfrak F_{h'} = \mathfrak F_h$
for all
![]() $h' \geq h$
.
$h' \geq h$
.
Proof. All points in the bottom cluster are added in round 1 and in each round we enlarge the
![]() $R_h$
-length of a path by at most one. Thus, in stage k of the construction, all
$R_h$
-length of a path by at most one. Thus, in stage k of the construction, all
![]() $R_h$
-chains are bounded by k. The construction continues only until vertical witnesses are required. Since, by Lemma 5.14, the
$R_h$
-chains are bounded by k. The construction continues only until vertical witnesses are required. Since, by Lemma 5.14, the
![]() $R_h$
-depth of
$R_h$
-depth of
![]() $\mathfrak F_k$
is bounded by
$\mathfrak F_k$
is bounded by
![]() $m = (1+m_{1}+m_{2})\cdot (m_{2}+m_{3})$
, we have
$m = (1+m_{1}+m_{2})\cdot (m_{2}+m_{3})$
, we have
![]() $\mathfrak F_{h'} = \mathfrak F_{m+1}$
for all
$\mathfrak F_{h'} = \mathfrak F_{m+1}$
for all
![]() $h' \geq m+1$
.⊣
$h' \geq m+1$
.⊣
Set
![]() $\mathfrak {F}'=(W',R',E')$
where
$\mathfrak {F}'=(W',R',E')$
where
and h is as in Lemma 5.15. Then
![]() $\mathfrak F'$
is a finite
$\mathfrak F'$
is a finite
![]() $\mathsf {M^+IPC}$
-frame by Lemma 5.6.
$\mathsf {M^+IPC}$
-frame by Lemma 5.6.
5.4 Truth lemma
Define a valuation
![]() $\nu '$
on
$\nu '$
on
![]() $W'$
by
$W'$
by
for
![]() $p\in \mathsf {Sub}(\varphi )$
and
$p\in \mathsf {Sub}(\varphi )$
and
![]() $\nu '(q)=\varnothing $
for variables q not occurring in
$\nu '(q)=\varnothing $
for variables q not occurring in
![]() $\varphi $
. That
$\varphi $
. That
![]() $\nu '$
is well defined follows from Lemma 5.8, which ensures that the sets
$\nu '$
is well defined follows from Lemma 5.8, which ensures that the sets
![]() $\nu '(\psi )$
are in
$\nu '(\psi )$
are in
![]() $\mathsf {Up}(\mathfrak {F'})$
for each
$\mathsf {Up}(\mathfrak {F'})$
for each
![]() $\psi \in \mathsf {Sub}(\varphi )$
.
$\psi \in \mathsf {Sub}(\varphi )$
.
Lemma 5.16 (Truth Lemma)
For all
![]() $t\in W'$
and
$t\in W'$
and
![]() $\psi \in \mathsf {Sub}(\varphi )$
, we have
$\psi \in \mathsf {Sub}(\varphi )$
, we have
![]() $t\vDash '\psi $
iff
$t\vDash '\psi $
iff
![]() $\widehat {t}\ \vDash \psi $
.
$\widehat {t}\ \vDash \psi $
.
Proof. The proof is by induction on the complexity of
![]() $\psi $
. The base cases
$\psi $
. The base cases
![]() $\psi =\bot $
and
$\psi =\bot $
and
![]() $\psi =p$
(p a propositional variable) follow from the definition, and the cases
$\psi =p$
(p a propositional variable) follow from the definition, and the cases
![]() $\psi =\psi _{1}\wedge \psi _{2}$
and
$\psi =\psi _{1}\wedge \psi _{2}$
and
![]() $\psi =\psi _{1}\vee \psi _{2}$
are easily verified. So we focus on the cases
$\psi =\psi _{1}\vee \psi _{2}$
are easily verified. So we focus on the cases
![]() $\psi =\psi _{1}\rightarrow \psi _{2}$
(and hence
$\psi =\psi _{1}\rightarrow \psi _{2}$
(and hence
![]() $\psi =\neg \psi _{1}=\psi _{1}\rightarrow \bot $
),
$\psi =\neg \psi _{1}=\psi _{1}\rightarrow \bot $
),
![]() $\psi =\exists \psi _{1}$
, and
$\psi =\exists \psi _{1}$
, and
![]() $\psi =\forall \psi _{1}$
.
$\psi =\forall \psi _{1}$
.
![]() ${\rightarrow { case}}$
: Let
${\rightarrow { case}}$
: Let
![]() $\psi =\psi _{1}\rightarrow \psi _{2}$
and
$\psi =\psi _{1}\rightarrow \psi _{2}$
and
![]() $t\in W'$
. Suppose
$t\in W'$
. Suppose
![]() $t\not \,\vDash '\psi _{1}\rightarrow \psi _{2}$
. Then
$t\not \,\vDash '\psi _{1}\rightarrow \psi _{2}$
. Then
![]() $tR's$
for some
$tR's$
for some
![]() $s\in W'$
with
$s\in W'$
with
![]() $s\vDash '\psi _{1}$
and
$s\vDash '\psi _{1}$
and
![]() $s\not \,\vDash '\psi _{2}$
. By the inductive hypothesis,
$s\not \,\vDash '\psi _{2}$
. By the inductive hypothesis,
![]() $\widehat {s}\ \vDash \psi _{1}$
and
$\widehat {s}\ \vDash \psi _{1}$
and
![]() $\widehat {s}\ \not \vDash \psi _{2}$
. Thus,
$\widehat {s}\ \not \vDash \psi _{2}$
. Thus,
![]() $\widehat {s}\ \not \vDash \psi _{1}\rightarrow \psi _{2}$
. Since
$\widehat {s}\ \not \vDash \psi _{1}\rightarrow \psi _{2}$
. Since
![]() $tR's$
, we have
$tR's$
, we have
![]() $\widehat {t}\ \not \vDash \psi _{1}\rightarrow \psi _{2}$
by persistence (Lemma 5.8).
$\widehat {t}\ \not \vDash \psi _{1}\rightarrow \psi _{2}$
by persistence (Lemma 5.8).
Conversely, suppose
![]() $\widehat {t}\ \not \vDash \psi _{1}\rightarrow \psi _{2}$
. If
$\widehat {t}\ \not \vDash \psi _{1}\rightarrow \psi _{2}$
. If
![]() $\ \widehat {t}\ \vDash \psi _{1}$
, then we have
$\ \widehat {t}\ \vDash \psi _{1}$
, then we have
![]() $\widehat {t}\ \vDash \psi _{1}$
but
$\widehat {t}\ \vDash \psi _{1}$
but
![]() $\widehat {t}\ \not \vDash \psi _{2}$
. By the inductive hypothesis,
$\widehat {t}\ \not \vDash \psi _{2}$
. By the inductive hypothesis,
![]() $t\vDash '\psi _{1}$
but
$t\vDash '\psi _{1}$
but
![]() $t\not \,\vDash '\psi _{2}$
. By construction,
$t\not \,\vDash '\psi _{2}$
. By construction,
![]() $tR't$
. Therefore,
$tR't$
. Therefore,
![]() $t\not \,\vDash '\psi _{1}\rightarrow \psi _{2}$
. If
$t\not \,\vDash '\psi _{1}\rightarrow \psi _{2}$
. If
![]() $\ \widehat {t}\ \not \vDash \psi _{1}$
, then in the
$\ \widehat {t}\ \not \vDash \psi _{1}$
, then in the
![]() $\rightarrow $
-step of the stage immediately after t is added to
$\rightarrow $
-step of the stage immediately after t is added to
![]() $W'$
, we add s to
$W'$
, we add s to
![]() $W'$
and
$W'$
and
![]() $tR's$
where
$tR's$
where
![]() $\widehat {s}\ \not \vDash \psi _{1}\rightarrow \psi _{2}$
maximally (Lemma 5.4). Thus,
$\widehat {s}\ \not \vDash \psi _{1}\rightarrow \psi _{2}$
maximally (Lemma 5.4). Thus,
![]() $\widehat {s}\ \vDash \psi _{1}$
and
$\widehat {s}\ \vDash \psi _{1}$
and
![]() $\widehat {s}\ \not \vDash \psi _{2}$
, so by the inductive hypothesis,
$\widehat {s}\ \not \vDash \psi _{2}$
, so by the inductive hypothesis,
![]() $s\vDash '\psi _{1}$
and
$s\vDash '\psi _{1}$
and
![]() $s\not \,\vDash '\psi _{2}$
. Since
$s\not \,\vDash '\psi _{2}$
. Since
![]() $tR's$
, we conclude that
$tR's$
, we conclude that
![]() $t\not \,\vDash '\psi _{1}\rightarrow \psi _{2}$
.
$t\not \,\vDash '\psi _{1}\rightarrow \psi _{2}$
.
![]() ${\exists\ { case}}$
: Let
${\exists\ { case}}$
: Let
![]() $\psi =\exists \psi _{1}$
and
$\psi =\exists \psi _{1}$
and
![]() $t\in W'$
. Suppose
$t\in W'$
. Suppose
![]() $t\vDash '\exists \psi _{1}$
. Then
$t\vDash '\exists \psi _{1}$
. Then
![]() $tE's$
for some
$tE's$
for some
![]() $s\in W'$
with
$s\in W'$
with
![]() $s\vDash '\psi _{1}$
. By the inductive hypothesis,
$s\vDash '\psi _{1}$
. By the inductive hypothesis,
![]() $\widehat {s}\ \vDash \psi _{1}$
, and
$\widehat {s}\ \vDash \psi _{1}$
, and
![]() $tE's$
implies
$tE's$
implies
![]() $\widehat {t}E\widehat {s}$
by Lemma 5.7(2). Thus,
$\widehat {t}E\widehat {s}$
by Lemma 5.7(2). Thus,
![]() $\widehat {t}\ \vDash \exists \psi _{1}$
.
$\widehat {t}\ \vDash \exists \psi _{1}$
.
Conversely, suppose
![]() $\widehat {t}\ \vDash \exists \psi _{1}$
. Then
$\widehat {t}\ \vDash \exists \psi _{1}$
. Then
![]() $\exists \psi _{1}\in \Sigma ^{\exists }(t)$
, so in the
$\exists \psi _{1}\in \Sigma ^{\exists }(t)$
, so in the
![]() $\exists $
-step of the next stage of the construction after t is added, we add s to
$\exists $
-step of the next stage of the construction after t is added, we add s to
![]() $W'$
and
$W'$
and
![]() $(t,s)$
to
$(t,s)$
to
![]() $E'$
where s is a copy of some
$E'$
where s is a copy of some
![]() $\widehat {s}\in W$
with
$\widehat {s}\in W$
with
![]() $\widehat {t}E\widehat {s}$
and
$\widehat {t}E\widehat {s}$
and
![]() $\widehat {s}\ \vDash \psi _{1}$
. By the inductive hypothesis,
$\widehat {s}\ \vDash \psi _{1}$
. By the inductive hypothesis,
![]() $s\vDash '\psi _{1}$
. Since
$s\vDash '\psi _{1}$
. Since
![]() $tE's$
, we conclude that
$tE's$
, we conclude that
![]() $t\vDash '\exists \psi _{1}$
.
$t\vDash '\exists \psi _{1}$
.
![]() ${\forall\ { case}}$
: Let
${\forall\ { case}}$
: Let
![]() $\psi =\forall \psi _{1}$
and
$\psi =\forall \psi _{1}$
and
![]() $t\in W'$
. Suppose
$t\in W'$
. Suppose
![]() $t\not \,\vDash '\forall \psi _{1}$
. Then
$t\not \,\vDash '\forall \psi _{1}$
. Then
![]() $tQ'w$
for some
$tQ'w$
for some
![]() $w\in W'$
with
$w\in W'$
with
![]() $w\not \,\vDash '\psi _{1}$
. By the inductive hypothesis,
$w\not \,\vDash '\psi _{1}$
. By the inductive hypothesis,
![]() $\widehat {w}\ \not \vDash \psi _{1}$
, and
$\widehat {w}\ \not \vDash \psi _{1}$
, and
![]() $tQ'w$
implies
$tQ'w$
implies
![]() $\widehat {t}Q\widehat {w}$
by Lemma 5.7(3). Thus,
$\widehat {t}Q\widehat {w}$
by Lemma 5.7(3). Thus,
![]() $\widehat {t}\ \not \vDash \forall \psi _{1}$
.
$\widehat {t}\ \not \vDash \forall \psi _{1}$
.
Conversely, suppose
![]() $\widehat {t}\ \not \vDash \forall \psi _{1}$
. If
$\widehat {t}\ \not \vDash \forall \psi _{1}$
. If
![]() $\ \widehat {t}$
is maximal with respect to
$\ \widehat {t}$
is maximal with respect to
![]() $\forall \psi _{1}$
, then
$\forall \psi _{1}$
, then
![]() $\forall \psi _{1}\in \Sigma ^{\forall H}(t)$
, so at some point in the construction of the next stage after t is added, we add s to
$\forall \psi _{1}\in \Sigma ^{\forall H}(t)$
, so at some point in the construction of the next stage after t is added, we add s to
![]() $W'$
and
$W'$
and
![]() $(t,s)$
to
$(t,s)$
to
![]() $E'$
where s is a copy of some
$E'$
where s is a copy of some
![]() $\widehat {s}\in W$
with
$\widehat {s}\in W$
with
![]() $\widehat {t}E\widehat {s}$
and
$\widehat {t}E\widehat {s}$
and
![]() $\widehat {s}\ \not \vDash \psi _{1}$
. By the inductive hypothesis,
$\widehat {s}\ \not \vDash \psi _{1}$
. By the inductive hypothesis,
![]() $s\not \,\vDash '\psi _{1}$
, so
$s\not \,\vDash '\psi _{1}$
, so
![]() $t\not \,\vDash '\forall \psi _{1}$
. If
$t\not \,\vDash '\forall \psi _{1}$
. If
![]() $\ \widehat {t}$
is not maximal, then we add s to
$\ \widehat {t}$
is not maximal, then we add s to
![]() $W'$
and
$W'$
and
![]() $(t,s)$
to
$(t,s)$
to
![]() $R'$
where s is a copy of some
$R'$
where s is a copy of some
![]() $\widehat {s}\in W$
and
$\widehat {s}\in W$
and
![]() $\widehat {s}$
is maximal with respect to
$\widehat {s}$
is maximal with respect to
![]() $\forall \psi _{1}$
. Therefore,
$\forall \psi _{1}$
. Therefore,
![]() $\forall \psi _{1}\in \Sigma ^{\forall H}(s)$
, and in the next stage we add
$\forall \psi _{1}\in \Sigma ^{\forall H}(s)$
, and in the next stage we add
![]() $w$
to
$w$
to
![]() $W'$
and
$W'$
and
![]() $(s,w)$
to
$(s,w)$
to
![]() $E'$
where
$E'$
where
![]() $\widehat {w}\in W$
and
$\widehat {w}\in W$
and
![]() $\widehat {w}\ \not \vDash \psi _{1}$
. But then
$\widehat {w}\ \not \vDash \psi _{1}$
. But then
![]() $tQ'w$
, and by the inductive hypothesis,
$tQ'w$
, and by the inductive hypothesis,
![]() $w\not \,\vDash '\psi _{1}$
. Thus,
$w\not \,\vDash '\psi _{1}$
. Thus,
![]() $t\not \,\vDash '\forall \psi _{1}$
.⊣
$t\not \,\vDash '\forall \psi _{1}$
.⊣
The FMP of
![]() $\mathsf {M^+IPC}$
is now an immediate consequence of the above.
$\mathsf {M^+IPC}$
is now an immediate consequence of the above.
Theorem 5.17.
![]() $\mathsf {M^+IPC}$
has the finite model property.
$\mathsf {M^+IPC}$
has the finite model property.
Proof. Suppose
![]() $\mathsf {M^+IPC} \not \vdash \varphi $
. By completeness of
$\mathsf {M^+IPC} \not \vdash \varphi $
. By completeness of
![]() $\mathsf {M^+IPC} $
with respect to descriptive frames, there are a descriptive
$\mathsf {M^+IPC} $
with respect to descriptive frames, there are a descriptive
![]() $\mathsf {M^+IPC} $
-frame
$\mathsf {M^+IPC} $
-frame
![]() $\mathfrak F$
and a valuation
$\mathfrak F$
and a valuation
![]() $\nu $
on
$\nu $
on
![]() $\mathfrak F$
such that
$\mathfrak F$
such that
![]() $(\mathfrak F, \nu ) \not \models \varphi $
. Let
$(\mathfrak F, \nu ) \not \models \varphi $
. Let
![]() $\mathfrak F'$
be the finite
$\mathfrak F'$
be the finite
![]() $\mathsf {M^+IPC}$
-frame constructed above. Since
$\mathsf {M^+IPC}$
-frame constructed above. Since
![]() $t_0$
was chosen so that
$t_0$
was chosen so that
![]() $\widehat {t_0}$
refutes
$\widehat {t_0}$
refutes
![]() $\varphi $
in
$\varphi $
in
![]() $\mathfrak F$
, by Lemma 5.16,
$\mathfrak F$
, by Lemma 5.16,
![]() $t_0$
refutes
$t_0$
refutes
![]() $\varphi $
in
$\varphi $
in
![]() $\mathfrak F'$
. We thus found a finite
$\mathfrak F'$
. We thus found a finite
![]() $\mathsf {M^+IPC}$
-frame refuting
$\mathsf {M^+IPC}$
-frame refuting
![]() $\varphi $
.⊣
$\varphi $
.⊣
Since
![]() $\mathsf {M^{+}IPC}$
is finitely axiomatizable and has the finite model property, it is decidable, meaning that there is an effective method for determining whether an arbitrary formula is a theorem of
$\mathsf {M^{+}IPC}$
is finitely axiomatizable and has the finite model property, it is decidable, meaning that there is an effective method for determining whether an arbitrary formula is a theorem of
![]() $\mathsf {M^{+}IPC}$
.
$\mathsf {M^{+}IPC}$
.
Corollary 5.18.
![]() $\mathsf {M^{+}IPC}$
is decidable.
$\mathsf {M^{+}IPC}$
is decidable.
Remark 5.19. Another consequence of Theorem 5.17 is that
![]() $\mathsf {M^{+}IPC}$
is the monadic fragment of
$\mathsf {M^{+}IPC}$
is the monadic fragment of
![]() $\mathsf {IQ^+C}$
. This can be seen by utilizing the Translation Theorem of Ono and Suzuki (see [Reference Ono and Suzuki37, Theorem 3.5]).
$\mathsf {IQ^+C}$
. This can be seen by utilizing the Translation Theorem of Ono and Suzuki (see [Reference Ono and Suzuki37, Theorem 3.5]).
6 The finite model property of
 $\mathsf {M^{+}Grz}$
$\mathsf {M^{+}Grz}$
In this section we prove that
![]() $\mathsf {M^{+}Grz}$
has the finite model property. Our proof, which consists of three steps, is a mixture of selective and standard filtration techniques. The main reasons why the same technique as for
$\mathsf {M^{+}Grz}$
has the finite model property. Our proof, which consists of three steps, is a mixture of selective and standard filtration techniques. The main reasons why the same technique as for
![]() $\mathsf {M^{+}IPC}$
does not work are the lack of persistence in
$\mathsf {M^{+}IPC}$
does not work are the lack of persistence in
![]() $\mathsf {M^{+}Grz}$
-models and the fact that witnesses for
$\mathsf {M^{+}Grz}$
-models and the fact that witnesses for
![]() $\forall $
-formulas cannot be chosen maximally wrt Q-relations. A rough structure of the proof is as follows.
$\forall $
-formulas cannot be chosen maximally wrt Q-relations. A rough structure of the proof is as follows.
Suppose that
![]() $\mathsf {M^{+}Grz}\not \vdash \varphi $
. Then there is a descriptive
$\mathsf {M^{+}Grz}\not \vdash \varphi $
. Then there is a descriptive
![]() $\mathsf {M^{+}Grz}$
-frame
$\mathsf {M^{+}Grz}$
-frame
![]() $\mathfrak {F}_{0}=(W_{0},R_{0},E_{0})$
and a valuation
$\mathfrak {F}_{0}=(W_{0},R_{0},E_{0})$
and a valuation
![]() $\nu _{0}$
on
$\nu _{0}$
on
![]() $W_{0}$
such that
$W_{0}$
such that
![]() $\mathfrak {F}_{0}\not \vDash _{0}\varphi $
. We build a finite
$\mathfrak {F}_{0}\not \vDash _{0}\varphi $
. We build a finite
![]() $\mathsf {M^{+}Grz}$
-frame from
$\mathsf {M^{+}Grz}$
-frame from
![]() $\mathfrak {F}_{0}$
in three steps:
$\mathfrak {F}_{0}$
in three steps:
-
1. First we select a (possibly infinite) partially ordered
 $\mathsf {MS4}$
-frame
$\mathsf {MS4}$
-frame
 $\mathfrak {F}_{1}=(W_1,R_1,E_1)$
from
$\mathfrak {F}_{1}=(W_1,R_1,E_1)$
from
 $\mathfrak {F}_{0}$
, in which all clusters are clean and
$\mathfrak {F}_{0}$
, in which all clusters are clean and
 $\varphi $
is refuted. An important feature of this step is that
$\varphi $
is refuted. An important feature of this step is that
 $R_1$
is not simply the restriction of
$R_1$
is not simply the restriction of
 $R_0$
to
$R_0$
to
 $W_1$
, but rather its strengthening. Its construction resembles the construction of R-relations from Q-relations in the
$W_1$
, but rather its strengthening. Its construction resembles the construction of R-relations from Q-relations in the
 $\rightarrow $
-step of the
$\rightarrow $
-step of the
 $\mathsf {M^{+}IPC}$
-construction.
$\mathsf {M^{+}IPC}$
-construction. -
2. Next we construct a (possibly infinite) partially ordered
 $\mathsf {MS4}$
-frame
$\mathsf {MS4}$
-frame
 $\mathfrak {F}_{2}$
from
$\mathfrak {F}_{2}$
from
 $\mathfrak {F}_{1}$
, in which all clusters are both clean and finite and
$\mathfrak {F}_{1}$
, in which all clusters are both clean and finite and
 $\varphi $
is refuted. In this step we use standard filtration to collapse
$\varphi $
is refuted. In this step we use standard filtration to collapse
 $E_1$
-clusters of
$E_1$
-clusters of
 $\mathfrak F_1$
so that each cluster contains only one point representing all points that satisfy the same formulas of
$\mathfrak F_1$
so that each cluster contains only one point representing all points that satisfy the same formulas of
 $\mathsf {Sub}(\varphi )$
.
$\mathsf {Sub}(\varphi )$
. -
3. Finally, as in Step 1, we use selective filtration to construct a finite partially ordered
 $\mathsf {MS4}$
-frame
$\mathsf {MS4}$
-frame
 $\mathfrak {F}_{3}$
from
$\mathfrak {F}_{3}$
from
 $\mathfrak {F}_{2}$
, in which all clusters are clean (hence
$\mathfrak {F}_{2}$
, in which all clusters are clean (hence
 $\mathfrak {F}_{3}$
is an
$\mathfrak {F}_{3}$
is an
 $\mathsf {M^{+}Grz}$
-frame) and
$\mathsf {M^{+}Grz}$
-frame) and
 $\varphi $
is refuted. This step resembles the
$\varphi $
is refuted. This step resembles the
 $\mathsf {M^{+}IPC}$
-construction, but in order for
$\mathsf {M^{+}IPC}$
-construction, but in order for
 $\mathfrak F_3$
to inherit the bounded cluster size from
$\mathfrak F_3$
to inherit the bounded cluster size from
 $\mathfrak F_2$
, we need to add only a single copy of an original point in
$\mathfrak F_2$
, we need to add only a single copy of an original point in
 $\mathfrak F_2$
to a cluster.
$\mathfrak F_2$
to a cluster.
6.1 Step 1: Ensuring all clusters are clean
Let
![]() $\mathfrak {F}_{0}=(W_{0},R_{0},E_{0})$
be as above. For
$\mathfrak {F}_{0}=(W_{0},R_{0},E_{0})$
be as above. For
![]() $x, y \in W_0$
let
$x, y \in W_0$
let
We construct
![]() $\mathfrak {F}_{1}=(W_{1},R_{1},E_{1})$
as follows:
$\mathfrak {F}_{1}=(W_{1},R_{1},E_{1})$
as follows:
-
•
 $W_{1}= \{x\in W_{0} \mid x\in \max _{R_0}E_{0}(A)\text { for some clopen } A \text { of } \mathfrak F_0\}$
.
$W_{1}= \{x\in W_{0} \mid x\in \max _{R_0}E_{0}(A)\text { for some clopen } A \text { of } \mathfrak F_0\}$
. -
•
 $xR_{1}y\Leftrightarrow x=y$
or
$xR_{1}y\Leftrightarrow x=y$
or
 and
and
 $x\vDash _{0}\square \psi \Rightarrow y\vDash _{0}\square \psi $
for all
$x\vDash _{0}\square \psi \Rightarrow y\vDash _{0}\square \psi $
for all
 $\square \psi \in \mathsf {Sub}(\varphi )$
.
$\square \psi \in \mathsf {Sub}(\varphi )$
. -
•
 $xE_{1}y\Leftrightarrow xE_{0}y$
.
$xE_{1}y\Leftrightarrow xE_{0}y$
. -
• We define a valuation
 $\nu _1$
on
$\nu _1$
on
 $\mathfrak F_1$
by
$\mathfrak F_1$
by
 $\nu _{1}(p)=\{x \mid x\in \nu _{0}(p)\}$
for all
$\nu _{1}(p)=\{x \mid x\in \nu _{0}(p)\}$
for all
 $p\in \mathsf {Sub}(\varphi )$
, and
$p\in \mathsf {Sub}(\varphi )$
, and
 $\nu _{1}(q)=\varnothing $
for all other propositional variables q.
$\nu _{1}(q)=\varnothing $
for all other propositional variables q.
We first show that there is a point in
![]() $W_{1}$
which refutes
$W_{1}$
which refutes
![]() $\varphi $
(in
$\varphi $
(in
![]() $\mathfrak F_{0}$
).
$\mathfrak F_{0}$
).
Lemma 6.1. There is
![]() $v\in W_{0}$
such that
$v\in W_{0}$
such that
![]() $v\not \vDash _{0}\varphi $
and
$v\not \vDash _{0}\varphi $
and
![]() $v\in \max _{R_0}E_{0}(\nu (\neg \varphi )) ($
hence
$v\in \max _{R_0}E_{0}(\nu (\neg \varphi )) ($
hence
![]() $E_{0}(v)$
is clean and
$E_{0}(v)$
is clean and
![]() $v\in W_{1})$
.
$v\in W_{1})$
.
Proof. Since
![]() $\mathfrak {F}_{0}\not \vDash _{0}\varphi $
, there is
$\mathfrak {F}_{0}\not \vDash _{0}\varphi $
, there is
![]() $t\in W_{0}$
such that
$t\in W_{0}$
such that
![]() $t\not \vDash _{0}\varphi $
. Then
$t\not \vDash _{0}\varphi $
. Then
![]() $t\in \nu _{0}(\neg \varphi )$
, so
$t\in \nu _{0}(\neg \varphi )$
, so
![]() $t\in E_{0}(\nu _{0}(\neg \varphi ))$
. Because
$t\in E_{0}(\nu _{0}(\neg \varphi ))$
. Because
![]() $\nu _{0}(\neg \varphi )$
is clopen,
$\nu _{0}(\neg \varphi )$
is clopen,
![]() $E_{0}(\nu _{0}(\neg \varphi ))$
is clopen. Therefore, Lemma 2.26(2) yields
$E_{0}(\nu _{0}(\neg \varphi ))$
is clopen. Therefore, Lemma 2.26(2) yields
![]() $u\in \max _{R_{0}}E_{0}(\nu _{0}(\neg \varphi ))$
with
$u\in \max _{R_{0}}E_{0}(\nu _{0}(\neg \varphi ))$
with
![]() $tR_{0}u$
. Since
$tR_{0}u$
. Since
![]() $u\in E_{0}(\nu _{0}(\neg \varphi ))$
, there is
$u\in E_{0}(\nu _{0}(\neg \varphi ))$
, there is
![]() $v\in W_{0}$
with
$v\in W_{0}$
with
![]() $uE_{0}v$
and
$uE_{0}v$
and
![]() $v\not \vDash _{0}\varphi $
. We now show that
$v\not \vDash _{0}\varphi $
. We now show that
![]() $v$
is our desired point. Because
$v$
is our desired point. Because
![]() $u\in \max _{R_{0}}E_{0}(\nu _{0}(\neg \varphi ))$
, the cluster
$u\in \max _{R_{0}}E_{0}(\nu _{0}(\neg \varphi ))$
, the cluster
![]() $E_{0}(u)=E_{0}(v)$
is clean (Lemma 4.8). Therefore,
$E_{0}(u)=E_{0}(v)$
is clean (Lemma 4.8). Therefore,
![]() $v\in \max _{R_{0}}E_{0}(\nu _{0}(\neg \varphi ))$
by Lemma 4.7(1). Now, since
$v\in \max _{R_{0}}E_{0}(\nu _{0}(\neg \varphi ))$
by Lemma 4.7(1). Now, since
![]() $v\in \max _{R_{0}}E_{0}(\nu _{0}(\neg \varphi ))$
and
$v\in \max _{R_{0}}E_{0}(\nu _{0}(\neg \varphi ))$
and
![]() $v\in \nu _{0}(\neg \varphi )$
, it is easy to see that
$v\in \nu _{0}(\neg \varphi )$
, it is easy to see that
![]() $v$
is
$v$
is
![]() $R_{0}$
-maximal with respect to
$R_{0}$
-maximal with respect to
![]() $\varphi $
, hence is our desired point.⊣
$\varphi $
, hence is our desired point.⊣
We next highlight some fundamental properties of
![]() $\mathfrak {F}_{1}$
.
$\mathfrak {F}_{1}$
.
Lemma 6.2.
-
1.
 $E_0(x) \subseteq W_0$
is a clean cluster in
$E_0(x) \subseteq W_0$
is a clean cluster in
 $\mathfrak F_0$
for all
$\mathfrak F_0$
for all
 $x \in W_1$
.
$x \in W_1$
. -
2. If
 $x\in W_{1}$
, then
$x\in W_{1}$
, then
 $E_{0}(x)\subseteq W_{1}$
.
$E_{0}(x)\subseteq W_{1}$
. -
3.
 iff
iff
 $xQ_{0}y$
but
$xQ_{0}y$
but
 $xE{\kern-2pt}\!\!\!\!\ /_{0}y$
for all
$xE{\kern-2pt}\!\!\!\!\ /_{0}y$
for all
 $x, y \in W_1$
.
$x, y \in W_1$
. -
4. The restriction of
 to
to
 $W_1$
is a strict partial order.
$W_1$
is a strict partial order. -
5.
 $R_{1}$
is a partial order.
$R_{1}$
is a partial order. -
6.
 $E_1$
is an equivalence relation.
$E_1$
is an equivalence relation. -
7.
 $R_{1}$
and
$R_{1}$
and
 $E_{1}$
satisfy commutativity.
$E_{1}$
satisfy commutativity. -
8.
 $\mathfrak F_1$
has clean clusters.
$\mathfrak F_1$
has clean clusters. -
9. For
 $x\in W_{1}$
and
$x\in W_{1}$
and
 $\square \gamma \in \mathsf {Sub}(\varphi )$
, if
$\square \gamma \in \mathsf {Sub}(\varphi )$
, if
 $x\not \vDash _{0}\square \gamma $
, then there is
$x\not \vDash _{0}\square \gamma $
, then there is
 $y\in W_{1}$
such that
$y\in W_{1}$
such that
 $xR_{1}y$
,
$xR_{1}y$
,
 $y\in A \cap \max _{R_0}E_{0}(A)$
, where and
$y\in A \cap \max _{R_0}E_{0}(A)$
, where and $$ \begin{align*} A=\nu_{0}(\neg\square\gamma)\cap\bigcap\{\nu_{0}(\square\psi) \mid \square\psi\in\mathsf{Sub}(\varphi) \text{ and } x\vDash_{0}\square\psi\}, \end{align*} $$
$$ \begin{align*} A=\nu_{0}(\neg\square\gamma)\cap\bigcap\{\nu_{0}(\square\psi) \mid \square\psi\in\mathsf{Sub}(\varphi) \text{ and } x\vDash_{0}\square\psi\}, \end{align*} $$
 $y\not \vDash _{0}\square \gamma\ R_{0}$
-maximally.
$y\not \vDash _{0}\square \gamma\ R_{0}$
-maximally.
Proof. (1) This is an immediate consequence of Lemma 4.8.
(2) Let
![]() $x \in W_1$
and
$x \in W_1$
and
![]() $y \in E_0(x)$
. Then
$y \in E_0(x)$
. Then
![]() $x \in \max _{R_0}E(A)$
for some clopen
$x \in \max _{R_0}E(A)$
for some clopen
![]() $A \subseteq W_0$
. Therefore,
$A \subseteq W_0$
. Therefore,
![]() $E_0(x)$
is clean by (1), and so
$E_0(x)$
is clean by (1), and so
![]() $y \in \max _{R_0}E(A)$
by Lemma 4.7(1). Thus,
$y \in \max _{R_0}E(A)$
by Lemma 4.7(1). Thus,
![]() $y \in W_1$
.
$y \in W_1$
.
(3) The implication from right to left is obvious. For the converse, suppose that
![]() $x, y \in W_1$
and there is
$x, y \in W_1$
and there is
![]() $w\in W_0$
such that
$w\in W_0$
such that
![]() $w\neq x,\ xR_{0}w, \text { and } wE_{0}y$
. Then clearly
$w\neq x,\ xR_{0}w, \text { and } wE_{0}y$
. Then clearly
![]() $xQ_{0}y$
. Also, since x is from a clean cluster,
$xQ_{0}y$
. Also, since x is from a clean cluster,
![]() $xE{\kern-2pt}\!\!\!\!\ /_{0}w$
. Thus,
$xE{\kern-2pt}\!\!\!\!\ /_{0}w$
. Thus,
![]() $xE{\kern-2pt}\!\!\!\!\ /_{0}y$
.
$xE{\kern-2pt}\!\!\!\!\ /_{0}y$
.
(4) Irreflexivity of
![]() on
on
![]() $W_1$
follows from the reflexivity of
$W_1$
follows from the reflexivity of
![]() $E_0$
and (3). We show that
$E_0$
and (3). We show that
![]() is transitive on
is transitive on
![]() $W_1$
. Suppose
$W_1$
. Suppose
![]() for
for
![]() $x, y, z \in W_1$
. Then there are
$x, y, z \in W_1$
. Then there are
![]() $y' \neq x$
and
$y' \neq x$
and
![]() $z' \neq y$
with
$z' \neq y$
with
![]() $x R_0 y'$
,
$x R_0 y'$
,
![]() $y' E_0 y$
and
$y' E_0 y$
and
![]() $y R_0 z'$
and
$y R_0 z'$
and
![]() $z' E_0 z$
. By commutativity, there is
$z' E_0 z$
. By commutativity, there is
![]() $z''$
with
$z''$
with
![]() $y' R_0 z''$
and
$y' R_0 z''$
and
![]() $z'' E_0 z$
. Therefore,
$z'' E_0 z$
. Therefore,
![]() $x R_0 z''$
and
$x R_0 z''$
and
![]() $z'' E_0 z$
. If we had
$z'' E_0 z$
. If we had
![]() $x = z''$
, then we would obtain
$x = z''$
, then we would obtain
![]() $x R_0 y' R_0 x$
, and so
$x R_0 y' R_0 x$
, and so
![]() $x = y'$
by Lemma 4.7(2). The latter contradicts the choice of
$x = y'$
by Lemma 4.7(2). The latter contradicts the choice of
![]() $y'$
. Thus,
$y'$
. Thus,
![]() $z'' \neq x$
and so
$z'' \neq x$
and so
![]() .
.
(5)
![]() $R_1$
is reflexive by definition. To see that
$R_1$
is reflexive by definition. To see that
![]() $R_1$
is transitive, suppose
$R_1$
is transitive, suppose
![]() $x, y, z \in W_1$
with
$x, y, z \in W_1$
with
![]() $x R_1 y R_1 z$
. Without loss of generality we may assume that
$x R_1 y R_1 z$
. Without loss of generality we may assume that
![]() $x,y,z$
are pairwise distinct. Then
$x,y,z$
are pairwise distinct. Then
![]() and
and
![]() , so
, so
![]() by (4). Moreover, if
by (4). Moreover, if
![]() $ x \models \Box \psi $
for
$ x \models \Box \psi $
for
![]() $\Box \psi \in \mathsf {Sub}(\varphi )$
, then since
$\Box \psi \in \mathsf {Sub}(\varphi )$
, then since
![]() $x R_1 y R_1 z$
, we have
$x R_1 y R_1 z$
, we have
![]() $ y \models \Box \psi $
and so
$ y \models \Box \psi $
and so
![]() $z \models \Box \psi $
. Therefore,
$z \models \Box \psi $
. Therefore,
![]() $R_1$
is transitive. Finally, if
$R_1$
is transitive. Finally, if
![]() $x R_1 y R_1 x$
and
$x R_1 y R_1 x$
and
![]() $x \neq y$
, then
$x \neq y$
, then
![]() . The latter implies
. The latter implies
![]() by transitivity of
by transitivity of
![]() , which contradicts irreflexivity of
, which contradicts irreflexivity of
![]() . Thus,
. Thus,
![]() $R_1$
is anti-symmetric.
$R_1$
is anti-symmetric.
(6) This is immediate since
![]() $E_0$
is an equivalence relation.
$E_0$
is an equivalence relation.
(7) Suppose that
![]() $xR_{1}y$
and
$xR_{1}y$
and
![]() $xE_{1}z$
. Without loss of generality we may assume that
$xE_{1}z$
. Without loss of generality we may assume that
![]() $x\neq y$
and
$x\neq y$
and
![]() $x\neq z$
. Then
$x\neq z$
. Then
![]() , so there is
, so there is
![]() $u\in W_{0}$
such that
$u\in W_{0}$
such that
![]() $x\neq u$
,
$x\neq u$
,
![]() $xR_{0}u$
, and
$xR_{0}u$
, and
![]() $uE_{0}y$
. By commutativity in
$uE_{0}y$
. By commutativity in
![]() $W_{0}$
, there is
$W_{0}$
, there is
![]() $v$
such that
$v$
such that
![]() $zR_{0}v$
and
$zR_{0}v$
and
![]() $vE_{0}u$
. We show that
$vE_{0}u$
. We show that
![]() $v$
is the required witness for commutativity in
$v$
is the required witness for commutativity in
![]() $W_{1}$
. From
$W_{1}$
. From
![]() $vE_{0}u$
and
$vE_{0}u$
and
![]() $uE_{0}y$
we have
$uE_{0}y$
we have
![]() $vE_{0}y$
, so
$vE_{0}y$
, so
![]() $v\in W_{1}$
by (2). Because
$v\in W_{1}$
by (2). Because
![]() $x\neq u$
,
$x\neq u$
,
![]() $xR_{0}u$
, and x is from a clean cluster, we have
$xR_{0}u$
, and x is from a clean cluster, we have
![]() $xE{\kern-2pt}\!\!\!\!\ /_{0} u$
. Thus,
$xE{\kern-2pt}\!\!\!\!\ /_{0} u$
. Thus,
![]() $zE{\kern-2pt}\!\!\!\!\ /_{0} v$
. In particular,
$zE{\kern-2pt}\!\!\!\!\ /_{0} v$
. In particular,
![]() $z\neq v$
, and so
$z\neq v$
, and so
![]() . Moreover,
. Moreover,
![]() $zR_{0}v$
gives that if
$zR_{0}v$
gives that if
![]() $z\vDash _{0}\square \gamma $
, then
$z\vDash _{0}\square \gamma $
, then
![]() $v\vDash _{0}\square \gamma $
, so
$v\vDash _{0}\square \gamma $
, so
![]() $zR_{1}v$
. From
$zR_{1}v$
. From
![]() $vE_{0}y$
we have
$vE_{0}y$
we have
![]() $vE_{1}y$
, yielding commutativity in
$vE_{1}y$
, yielding commutativity in
![]() $W_{1}$
.
$W_{1}$
.
(8) Suppose there are
![]() $x,y\in W_{1}$
with
$x,y\in W_{1}$
with
![]() $x\neq y$
,
$x\neq y$
,
![]() $xE_{1}y$
, and
$xE_{1}y$
, and
![]() $xR_{1}y$
. Since
$xR_{1}y$
. Since
![]() $xE_{1}y$
, we have
$xE_{1}y$
, we have
![]() $xE_{0}y$
, and because
$xE_{0}y$
, and because
![]() $xR_{1}y$
and
$xR_{1}y$
and
![]() $x\neq y$
, we have
$x\neq y$
, we have
![]() . Thus, there is
. Thus, there is
![]() $w\in W_{0}$
with
$w\in W_{0}$
with
![]() $x\neq w$
,
$x\neq w$
,
![]() $xR_{0}w$
, and
$xR_{0}w$
, and
![]() $wE_{0}y$
. From
$wE_{0}y$
. From
![]() $xE_{0}y$
and
$xE_{0}y$
and
![]() $yE_{0}w$
we have
$yE_{0}w$
we have
![]() $xE_{0}w$
. By (1), x is chosen from a clean cluster in
$xE_{0}w$
. By (1), x is chosen from a clean cluster in
![]() $W_{0}$
, so
$W_{0}$
, so
![]() $xR_{0}w$
and
$xR_{0}w$
and
![]() $xE_{0}w$
imply
$xE_{0}w$
imply
![]() $x=w$
, a contradiction.
$x=w$
, a contradiction.
(9) Suppose
![]() $x\not \vDash _{0}\square \gamma $
. Consider
$x\not \vDash _{0}\square \gamma $
. Consider
Clearly
![]() $x\in A$
, so
$x\in A$
, so
![]() $x\in E_{0}(A)$
. We have
$x\in E_{0}(A)$
. We have
![]() $x\in \max _{R_{0}}E_{0}(A)$
or
$x\in \max _{R_{0}}E_{0}(A)$
or
![]() $x\not \in \max _{R_{0}}E_{0}(A)$
.
$x\not \in \max _{R_{0}}E_{0}(A)$
.
![]() $ {{Case\ 1{:}}\ x\in \max _{R_{0}}E_{0}(A)}$
$ {{Case\ 1{:}}\ x\in \max _{R_{0}}E_{0}(A)}$
If
![]() $x\in \max _{R_{0}}E_{0}(A)$
, then from
$x\in \max _{R_{0}}E_{0}(A)$
, then from
![]() $xR_{0}w$
and
$xR_{0}w$
and
![]() $x\neq w$
it follows that
$x\neq w$
it follows that
![]() $w\not \in E_{0}(A)$
, so
$w\not \in E_{0}(A)$
, so
![]() $w\not \in A$
. But
$w\not \in A$
. But
![]() $xR_{0}w$
implies
$xR_{0}w$
implies
![]() ${w\in \bigcap \{\nu _{0}(\square \psi ) \mid \square \psi \in \mathsf {Sub}(\varphi ) \mbox { and } x\vDash _{0}\square \psi \}}$
, so we must have
${w\in \bigcap \{\nu _{0}(\square \psi ) \mid \square \psi \in \mathsf {Sub}(\varphi ) \mbox { and } x\vDash _{0}\square \psi \}}$
, so we must have
![]() $w\not \in \nu _{0}(\neg \square \gamma )$
. Therefore,
$w\not \in \nu _{0}(\neg \square \gamma )$
. Therefore,
![]() $w\vDash _{0}\square \gamma $
. Since
$w\vDash _{0}\square \gamma $
. Since
![]() $x\not \vDash _{0}\square \gamma $
but
$x\not \vDash _{0}\square \gamma $
but
![]() $w\vDash _{0}\square \gamma $
for all
$w\vDash _{0}\square \gamma $
for all
![]() $w\neq x$
with
$w\neq x$
with
![]() $xR_{0}w$
, we must have
$xR_{0}w$
, we must have
![]() $x\not \vDash _{0}\square \gamma\ R_{0}$
-maximally.
$x\not \vDash _{0}\square \gamma\ R_{0}$
-maximally.
![]() ${{Case\ 2{:}}\ x\not \in \max _{R_{0}}E_{0}(A)}$
${{Case\ 2{:}}\ x\not \in \max _{R_{0}}E_{0}(A)}$
If
![]() $x\not \in \max _{R_{0}}E_{0}(A)$
, then Lemma 2.26(2) yields
$x\not \in \max _{R_{0}}E_{0}(A)$
, then Lemma 2.26(2) yields
![]() $t\in \max _{R_{0}}E_{0}(A)$
such that
$t\in \max _{R_{0}}E_{0}(A)$
such that
![]() $x\neq t$
and
$x\neq t$
and
![]() $xR_{0}t$
. But then
$xR_{0}t$
. But then
![]() $tE_{0}y$
for some
$tE_{0}y$
for some
![]() $y\in A$
. Since
$y\in A$
. Since
![]() $t\in \max _{R_{0}}E_{0}(A)$
, we have
$t\in \max _{R_{0}}E_{0}(A)$
, we have
![]() $t\in W_{1}$
, so
$t\in W_{1}$
, so
![]() $y\in W_{1}$
by (2). From
$y\in W_{1}$
by (2). From
![]() $x\neq t$
and
$x\neq t$
and
![]() $xR_{0}t$
it follows that
$xR_{0}t$
it follows that
![]() . Since
. Since
![]() $y\in A$
, if
$y\in A$
, if
![]() $x\vDash _{0}\square \psi $
then
$x\vDash _{0}\square \psi $
then
![]() $y\vDash _{0}\square \psi $
for all
$y\vDash _{0}\square \psi $
for all
![]() $\Box \psi \in \mathsf {Sub}(\varphi )$
, so
$\Box \psi \in \mathsf {Sub}(\varphi )$
, so
![]() $xR_{1}y$
. From
$xR_{1}y$
. From
![]() $y\in A$
it follows that
$y\in A$
it follows that
![]() $y\not \vDash _{0}\square \gamma $
. We show that
$y\not \vDash _{0}\square \gamma $
. We show that
![]() $y\not \vDash _{0}\square \gamma\ R_{0}$
-maximally. Suppose
$y\not \vDash _{0}\square \gamma\ R_{0}$
-maximally. Suppose
![]() $yR_{0}z$
and
$yR_{0}z$
and
![]() $z\not \vDash _{0}\square \gamma $
. If
$z\not \vDash _{0}\square \gamma $
. If
![]() $x\vDash _{0}\square \psi $
, then
$x\vDash _{0}\square \psi $
, then
![]() $y\vDash _{0}\square \psi $
(as
$y\vDash _{0}\square \psi $
(as
![]() $y\in A$
), so
$y\in A$
), so
![]() $yR_{0}z$
implies
$yR_{0}z$
implies
![]() $z\vDash _{0}\square \psi $
. Thus,
$z\vDash _{0}\square \psi $
. Thus,
![]() $z\in A$
, hence
$z\in A$
, hence
![]() $z\in E_{0}(A)$
, and maximality of y in
$z\in E_{0}(A)$
, and maximality of y in
![]() $E_{0}(A)$
yields
$E_{0}(A)$
yields
![]() $y=z$
. Consequently, y is
$y=z$
. Consequently, y is
![]() $R_{0}$
-maximal with respect to
$R_{0}$
-maximal with respect to
![]() $\square \gamma $
.⊣
$\square \gamma $
.⊣
We conclude Step 1 by proving the truth lemma for
![]() $\mathfrak {F}_{1}$
.
$\mathfrak {F}_{1}$
.
Lemma 6.3 (Truth Lemma)
For all
![]() $x\in W_{1}$
and
$x\in W_{1}$
and
![]() $\psi \in \mathsf {Sub}(\varphi )$
,
$\psi \in \mathsf {Sub}(\varphi )$
,
Proof. The proof is by induction on the complexity of
![]() $\psi $
. The base case
$\psi $
. The base case
![]() $\psi =p$
is clear from the definition of
$\psi =p$
is clear from the definition of
![]() $\nu _{1}$
. The cases of
$\nu _{1}$
. The cases of
![]() $\psi =\psi _{1}\vee \psi _{2}$
and
$\psi =\psi _{1}\vee \psi _{2}$
and
![]() $\psi =\neg \psi _{1}$
are straightforward, so we focus on the cases
$\psi =\neg \psi _{1}$
are straightforward, so we focus on the cases
![]() $\psi =\forall \psi _{1}$
and
$\psi =\forall \psi _{1}$
and
![]() $\psi =\square \psi _{1}$
.
$\psi =\square \psi _{1}$
.
Suppose
![]() $\psi =\forall \psi _{1}$
. If
$\psi =\forall \psi _{1}$
. If
![]() $x\not \vDash _{0}\forall \psi _{1}$
, then
$x\not \vDash _{0}\forall \psi _{1}$
, then
![]() $xE_{0}y$
for some
$xE_{0}y$
for some
![]() $y\not \vDash _{0}\psi _{1}$
. By Lemma 6.2(2),
$y\not \vDash _{0}\psi _{1}$
. By Lemma 6.2(2),
![]() $y \in W_1$
, so
$y \in W_1$
, so
![]() $y\not \vDash _{1}\psi _{1}$
by the inductive hypothesis. From
$y\not \vDash _{1}\psi _{1}$
by the inductive hypothesis. From
![]() $xE_{0}y$
we have
$xE_{0}y$
we have
![]() $xE_{1}y$
by the definition of
$xE_{1}y$
by the definition of
![]() $E_1$
. Thus,
$E_1$
. Thus,
![]() $x\not \vDash _{1}\forall \psi _{1}$
. The proof of the converse implication is immediate.
$x\not \vDash _{1}\forall \psi _{1}$
. The proof of the converse implication is immediate.
Suppose
![]() $\psi =\square \psi _{1}$
. If
$\psi =\square \psi _{1}$
. If
![]() $x\not \vDash _{0}\square \psi _{1}$
, then by Lemma 6.2(9), there is
$x\not \vDash _{0}\square \psi _{1}$
, then by Lemma 6.2(9), there is
![]() $y\in W_{1}$
such that
$y\in W_{1}$
such that
![]() $xR_{1}y$
and
$xR_{1}y$
and
![]() $y\not \vDash _{0}\psi _{1}$
. By the inductive hypothesis,
$y\not \vDash _{0}\psi _{1}$
. By the inductive hypothesis,
![]() $y\not \vDash _{1}\psi _{1}$
, hence
$y\not \vDash _{1}\psi _{1}$
, hence
![]() $x\not \vDash _{1}\square \psi _{1}$
. Conversely, if
$x\not \vDash _{1}\square \psi _{1}$
. Conversely, if
![]() $x\not \vDash _{1}\square \psi _{1}$
, then there is
$x\not \vDash _{1}\square \psi _{1}$
, then there is
![]() $y\in W_{1}$
such that
$y\in W_{1}$
such that
![]() $xR_{1}y$
and
$xR_{1}y$
and
![]() $y\not \vDash _{1}\psi _{1}$
. By the inductive hypothesis,
$y\not \vDash _{1}\psi _{1}$
. By the inductive hypothesis,
![]() $y\not \vDash _{0}\psi _{1}$
. If
$y\not \vDash _{0}\psi _{1}$
. If
![]() $x=y$
, then
$x=y$
, then
![]() $x\not \vDash _{0}\psi _{1}$
, hence
$x\not \vDash _{0}\psi _{1}$
, hence
![]() $x\not \vDash _{0}\square \psi _{1}$
. If
$x\not \vDash _{0}\square \psi _{1}$
. If
![]() $x\neq y$
, then as
$x\neq y$
, then as
![]() $xR_{1}y$
, we have
$xR_{1}y$
, we have
![]() and
and
![]() $x\vDash _{0}\square \gamma $
implies
$x\vDash _{0}\square \gamma $
implies
![]() $y\vDash _{0}\square \gamma $
for all
$y\vDash _{0}\square \gamma $
for all
![]() $\square \gamma \in \mathsf {Sub}(\varphi )$
. Since
$\square \gamma \in \mathsf {Sub}(\varphi )$
. Since
![]() $y\not \vDash _{0}\psi _{1}$
, we have
$y\not \vDash _{0}\psi _{1}$
, we have
![]() $y\not \vDash _{0}\square \psi _{1}$
. Thus,
$y\not \vDash _{0}\square \psi _{1}$
. Thus,
![]() $x\not \vDash _{0}\square \psi _{1}$
.⊣
$x\not \vDash _{0}\square \psi _{1}$
.⊣
6.2 Step 2: Ensuring all clusters are finite
In this step we use the standard filtration technique to construct
![]() $\mathfrak F_2$
from
$\mathfrak F_2$
from
![]() $\mathfrak F_1$
by ‘collapsing’
$\mathfrak F_1$
by ‘collapsing’
![]() $E_{1}$
-clusters into finitely many classes. Thus, each cluster in
$E_{1}$
-clusters into finitely many classes. Thus, each cluster in
![]() $\mathfrak F_2$
will be finite.
$\mathfrak F_2$
will be finite.
Define an equivalence relation
![]() $\sim $
on
$\sim $
on
![]() $W_{1}$
by
$W_{1}$
by
We construct
![]() $\mathfrak {F}_{2}=(W_{2},R_{2},E_{2})$
as follows:
$\mathfrak {F}_{2}=(W_{2},R_{2},E_{2})$
as follows:
-
•
 $W_{2}= W_{1}/{\sim }=\{[x] \mid x\in W_{1}\}$
where
$W_{2}= W_{1}/{\sim }=\{[x] \mid x\in W_{1}\}$
where
 $[x]$
is the
$[x]$
is the
 $\sim $
-equivalence class of x.
$\sim $
-equivalence class of x. -
• For
 $[x],[y]\in W_{2}$
,
$[x],[y]\in W_{2}$
,
 $[x]R_{2}[y]\Leftrightarrow [x]=[y]$
or
$[x]R_{2}[y]\Leftrightarrow [x]=[y]$
or
 $xR_{1}y$
.
$xR_{1}y$
. -
• For
 $[x],[y]\in W_{2}$
,
$[x],[y]\in W_{2}$
,
 $[x]E_{2}[y]\Leftrightarrow xE_{1}y$
.
$[x]E_{2}[y]\Leftrightarrow xE_{1}y$
. -
•
 $\nu _{2}(p)=\{[x] \mid x\in \nu _{1}(p)\}$
for all
$\nu _{2}(p)=\{[x] \mid x\in \nu _{1}(p)\}$
for all
 $p\in \mathsf {Sub}(\varphi )$
, and
$p\in \mathsf {Sub}(\varphi )$
, and
 $\nu _{2}(q)=\varnothing $
for all other propositional variables q.
$\nu _{2}(q)=\varnothing $
for all other propositional variables q.
Lemma 6.4. The relations
![]() $E_2$
and
$E_2$
and
![]() $R_2$
are well defined, and so is the valuation
$R_2$
are well defined, and so is the valuation
![]() $\nu_2$
.
$\nu_2$
.
Proof. It is easy to see that
![]() $E_2$
and
$E_2$
and
![]() $\nu_2$
are well defined. We show that
$\nu_2$
are well defined. We show that
![]() $R_2$
is well defined. Let
$R_2$
is well defined. Let
![]() $x, y, x', y' \in W_1$
with
$x, y, x', y' \in W_1$
with
![]() $x\sim x'$
,
$x\sim x'$
,
![]() $y\sim y'$
, and
$y\sim y'$
, and
![]() $[x]R_{2}[y]$
. Then
$[x]R_{2}[y]$
. Then
![]() $[x]=[y]$
or
$[x]=[y]$
or
![]() $xR_{1}y$
. If
$xR_{1}y$
. If
![]() $[x]=[y]$
, we have
$[x]=[y]$
, we have
![]() $[x']=[x]=[y]=[y']$
, and so
$[x']=[x]=[y]=[y']$
, and so
![]() $[x']R_{2}[y']$
. If
$[x']R_{2}[y']$
. If
![]() $xR_{1}y$
, then
$xR_{1}y$
, then
![]() $x=y$
or
$x=y$
or
![]() and
and
![]() $x\vDash _{0}\square \gamma $
implies
$x\vDash _{0}\square \gamma $
implies
![]() $y\vDash _{0}\square \gamma $
for all
$y\vDash _{0}\square \gamma $
for all
![]() $\square \gamma \in \mathsf {Sub}(\varphi )$
. The former case implies
$\square \gamma \in \mathsf {Sub}(\varphi )$
. The former case implies
![]() $[x]=[y]$
which we have already considered. In the latter case, from
$[x]=[y]$
which we have already considered. In the latter case, from
![]() it follows that
it follows that
![]() $xQ_{0}y$
and
$xQ_{0}y$
and
![]() $x E{\kern-2pt}\!\!\!\!\ /_0 y$
by Lemma 6.2(3). Note that
$x E{\kern-2pt}\!\!\!\!\ /_0 y$
by Lemma 6.2(3). Note that
![]() $x' \sim x$
implies
$x' \sim x$
implies
![]() $x' E_1 x$
and so
$x' E_1 x$
and so
![]() $x ' E_0 x$
. Similarly,
$x ' E_0 x$
. Similarly,
![]() $y ' E_0 y$
. By transitivity of
$y ' E_0 y$
. By transitivity of
![]() $Q_0$
we thus have
$Q_0$
we thus have
![]() $x' Q_0 y'$
. Moreover,
$x' Q_0 y'$
. Moreover,
![]() $x ' E_0 x$
,
$x ' E_0 x$
,
![]() $y ' E_0 y$
, and
$y ' E_0 y$
, and
![]() $x E{\kern-2pt}\!\!\!\!\ /_0 y$
imply that
$x E{\kern-2pt}\!\!\!\!\ /_0 y$
imply that
![]() $x' E{\kern-2pt}\!\!\!\!\ /_0 y'$
. Thus,
$x' E{\kern-2pt}\!\!\!\!\ /_0 y'$
. Thus,
![]() by Lemma 6.2(3). If
by Lemma 6.2(3). If
![]() $\Box \gamma \in \mathsf {Sub}(\varphi )$
and
$\Box \gamma \in \mathsf {Sub}(\varphi )$
and
![]() $x'\vDash _{0}\square \gamma $
, then
$x'\vDash _{0}\square \gamma $
, then
![]() $x\vDash _{0}\square \gamma $
since
$x\vDash _{0}\square \gamma $
since
![]() $x' \sim x$
. So
$x' \sim x$
. So
![]() $y\vDash _{0}\square \gamma $
by assumption. But then
$y\vDash _{0}\square \gamma $
by assumption. But then
![]() $y' \vDash _{0}\square \gamma $
since
$y' \vDash _{0}\square \gamma $
since
![]() $y' \sim y$
. This shows that
$y' \sim y$
. This shows that
![]() $x' R_1 y'$
, so
$x' R_1 y'$
, so
![]() $[x'] R_2 [y']$
.⊣
$[x'] R_2 [y']$
.⊣
In the following lemma we highlight some properties of
![]() $\mathfrak {F}_{2}$
.
$\mathfrak {F}_{2}$
.
Lemma 6.5.
-
1.
 $R_{2}$
is a partial order.
$R_{2}$
is a partial order. -
2.
 $E_{2}$
is an equivalence relation.
$E_{2}$
is an equivalence relation. -
3.
 $R_{2}$
and
$R_{2}$
and
 $E_{2}$
satisfy commutativity.
$E_{2}$
satisfy commutativity. -
4.
 $\mathfrak {F}_{2}$
has clean clusters.
$\mathfrak {F}_{2}$
has clean clusters. -
5. For
 $[x]\in W_{2}$
,
$[x]\in W_{2}$
,
 $|E_{2}([x])|\leq 2^n$
, where
$|E_{2}([x])|\leq 2^n$
, where
 $n=|\mathsf {Sub}(\varphi ) |$
.
$n=|\mathsf {Sub}(\varphi ) |$
. -
6. For
 $[x]\in W_{2}$
and
$[x]\in W_{2}$
and
 $\square \gamma \in \mathsf {Sub}(\varphi )$
, if
$\square \gamma \in \mathsf {Sub}(\varphi )$
, if
 $x\not \vDash _{1}\square \gamma $
, then there is
$x\not \vDash _{1}\square \gamma $
, then there is
 $[y]\in W_{2}$
such that
$[y]\in W_{2}$
such that
 $[x]R_{2}[y]$
and
$[x]R_{2}[y]$
and
 $y\not \vDash _{1}\square \gamma\ R_{1}$
-maximally.
$y\not \vDash _{1}\square \gamma\ R_{1}$
-maximally.
Proof. (1) Reflexivity of
![]() $R_{2}$
is immediate from the definition, and transitivity and antisymmetry follow from transitivity and antisymmetry of
$R_{2}$
is immediate from the definition, and transitivity and antisymmetry follow from transitivity and antisymmetry of
![]() $R_1$
.
$R_1$
.
(2) This follows from
![]() $E_1$
being an equivalence relation.
$E_1$
being an equivalence relation.
(3) This follows from
![]() $R_{1}$
and
$R_{1}$
and
![]() $E_{1}$
satisfying commutativity.
$E_{1}$
satisfying commutativity.
(4) Suppose there are
![]() $[x]\neq [y]$
in
$[x]\neq [y]$
in
![]() $W_2$
with
$W_2$
with
![]() $[x]R_{2}[y]$
and
$[x]R_{2}[y]$
and
![]() $[x]E_{2}[y]$
. Then
$[x]E_{2}[y]$
. Then
![]() $x \neq y$
, so by the definition of
$x \neq y$
, so by the definition of
![]() $R_{2}$
and
$R_{2}$
and
![]() $E_{2}$
, we have
$E_{2}$
, we have
![]() $xR_{1}y$
and
$xR_{1}y$
and
![]() $xE_{1}y$
which yields a dirty cluster in
$xE_{1}y$
which yields a dirty cluster in
![]() $\mathfrak F_1$
, contradicting Lemma 6.2(8).
$\mathfrak F_1$
, contradicting Lemma 6.2(8).
(5) This follows from the fact that there are at most
![]() $2^n \sim $
-equivalence classes in each cluster (see, e.g., [Reference Chagrov and Zakharyaschev12, Proposition 5.24]).
$2^n \sim $
-equivalence classes in each cluster (see, e.g., [Reference Chagrov and Zakharyaschev12, Proposition 5.24]).
(6) Suppose
![]() $x\not \vDash _{1}\square \gamma $
. By Lemma 6.3,
$x\not \vDash _{1}\square \gamma $
. By Lemma 6.3,
![]() $x\not \vDash _{0}\square \gamma $
, so by Lemma 6.2(9), there is
$x\not \vDash _{0}\square \gamma $
, so by Lemma 6.2(9), there is
![]() $y\in W_{1}$
such that
$y\in W_{1}$
such that
![]() $xR_{1}y$
,
$xR_{1}y$
,
![]() $y\in A\cap \max _{R_0}E_{0}(A)$
, and
$y\in A\cap \max _{R_0}E_{0}(A)$
, and
![]() $y\not \vDash _{0}\square \gamma\ R_{0}$
-maximally, where
$y\not \vDash _{0}\square \gamma\ R_{0}$
-maximally, where
Then
![]() $[x]R_{2}[y]$
and by Lemma 6.3,
$[x]R_{2}[y]$
and by Lemma 6.3,
![]() $y\not \vDash _{1}\square \gamma $
. We show that y is
$y\not \vDash _{1}\square \gamma $
. We show that y is
![]() $R_{1}$
-maximal with respect to
$R_{1}$
-maximal with respect to
![]() $\square \gamma $
. Suppose
$\square \gamma $
. Suppose
![]() $yR_{1}z$
and
$yR_{1}z$
and
![]() $z\not \vDash _{1}\square \gamma $
. By Lemma 6.3,
$z\not \vDash _{1}\square \gamma $
. By Lemma 6.3,
![]() $z\not \vDash _{0}\square \gamma $
, and from
$z\not \vDash _{0}\square \gamma $
, and from
![]() $yR_{1}z$
it follows that
$yR_{1}z$
it follows that
![]() $y=z$
or
$y=z$
or
![]() and
and
![]() $y\vDash _{0}\square \psi $
implies
$y\vDash _{0}\square \psi $
implies
![]() $z\vDash _{0}\square \psi $
for all
$z\vDash _{0}\square \psi $
for all
![]() $\square \psi \in \mathsf {Sub}(\varphi )$
. Suppose the latter. Since
$\square \psi \in \mathsf {Sub}(\varphi )$
. Suppose the latter. Since
![]() $z\not \vDash _{0}\square \gamma $
, we have
$z\not \vDash _{0}\square \gamma $
, we have
![]() $z\in \nu _{0}(\neg \square \gamma )$
. If
$z\in \nu _{0}(\neg \square \gamma )$
. If
![]() $x\vDash _{0}\square \psi $
for
$x\vDash _{0}\square \psi $
for
![]() $\square \psi \in \mathsf {Sub}(\varphi )$
, then
$\square \psi \in \mathsf {Sub}(\varphi )$
, then
![]() $y\in A$
implies
$y\in A$
implies
![]() $y\vDash _{0}\square \psi $
. So
$y\vDash _{0}\square \psi $
. So
![]() $yR_{1}z$
then gives
$yR_{1}z$
then gives
![]() $z\vDash _{0}\square \psi $
. Therefore,
$z\vDash _{0}\square \psi $
. Therefore,
![]() $z\in \bigcap \{\nu _{0}(\square \psi ) \mid \square \psi \in \mathsf {Sub}(\varphi ) \mbox { and } x\vDash _{0}\square \psi \}$
, and hence
$z\in \bigcap \{\nu _{0}(\square \psi ) \mid \square \psi \in \mathsf {Sub}(\varphi ) \mbox { and } x\vDash _{0}\square \psi \}$
, and hence
![]() $z\in A$
. As
$z\in A$
. As
![]() , there is
, there is
![]() $w\in W_{0}$
such that
$w\in W_{0}$
such that
![]() $y\neq w$
,
$y\neq w$
,
![]() $yR_{0}w$
, and
$yR_{0}w$
, and
![]() $wE_{0}z$
. Then
$wE_{0}z$
. Then
![]() $w\in E_{0}(A)$
, and maximality of y in
$w\in E_{0}(A)$
, and maximality of y in
![]() $E_{0}(A)$
yields
$E_{0}(A)$
yields
![]() $y=w$
, contradicting
$y=w$
, contradicting
![]() $y\neq w$
. Thus,
$y\neq w$
. Thus,
![]() $y=z$
, and so y is
$y=z$
, and so y is
![]() $R_{1}$
-maximal with respect to
$R_{1}$
-maximal with respect to
![]() $\square \gamma $
.⊣
$\square \gamma $
.⊣
We conclude Step 2 by showing the truth lemma for
![]() $\mathfrak {F}_{2}$
.
$\mathfrak {F}_{2}$
.
Lemma 6.6 (Truth Lemma)
For all
![]() $x\in W_{1}$
and
$x\in W_{1}$
and
![]() $\psi \in \mathsf {Sub}(\varphi )$
,
$\psi \in \mathsf {Sub}(\varphi )$
,
Proof. The proof is by induction on the complexity of
![]() $\psi $
. The base case
$\psi $
. The base case
![]() $\psi =p$
follows from the definition of
$\psi =p$
follows from the definition of
![]() $\nu _{2}$
. The cases of
$\nu _{2}$
. The cases of
![]() $\psi =\psi _{1}\vee \psi _{2}$
and
$\psi =\psi _{1}\vee \psi _{2}$
and
![]() $\psi =\neg \psi _{1}$
are straightforward, and the
$\psi =\neg \psi _{1}$
are straightforward, and the
![]() $\forall $
-case follows from the definition of
$\forall $
-case follows from the definition of
![]() $E_2$
. Suppose that
$E_2$
. Suppose that
![]() $\psi = \Box \psi _1$
. If
$\psi = \Box \psi _1$
. If
![]() $x\not \vDash _{1}\square \psi _{1}$
, then there is
$x\not \vDash _{1}\square \psi _{1}$
, then there is
![]() $y\in W_1$
with
$y\in W_1$
with
![]() $xR_{1}y$
and
$xR_{1}y$
and
![]() $y\not \vDash _{1}\psi _{1}$
. Therefore,
$y\not \vDash _{1}\psi _{1}$
. Therefore,
![]() $[x]R_{2}[y]$
and
$[x]R_{2}[y]$
and
![]() $[y]\not \vDash _{2}\psi _{1}$
by the inductive hypothesis. Thus,
$[y]\not \vDash _{2}\psi _{1}$
by the inductive hypothesis. Thus,
![]() $[x]\not \vDash _{2}\square \psi _{1}$
. Conversely, if
$[x]\not \vDash _{2}\square \psi _{1}$
. Conversely, if
![]() $[x]\not \vDash _{2}\square \psi _{1}$
, then there is
$[x]\not \vDash _{2}\square \psi _{1}$
, then there is
![]() $y\in W_1$
with
$y\in W_1$
with
![]() $[x] R_2 [y]$
and
$[x] R_2 [y]$
and
![]() $[y]\not \vDash _{2}\psi _{1}$
. By the inductive hypothesis,
$[y]\not \vDash _{2}\psi _{1}$
. By the inductive hypothesis,
![]() $y \not \vDash _{1} \psi _{1}$
. If
$y \not \vDash _{1} \psi _{1}$
. If
![]() $[x] = [y]$
, then
$[x] = [y]$
, then
![]() $x \not \vDash _{1} \square \psi _{1}$
by definition of
$x \not \vDash _{1} \square \psi _{1}$
by definition of
![]() $\sim $
. If
$\sim $
. If
![]() $[x] \neq [y]$
, then
$[x] \neq [y]$
, then
![]() $x R_1 y$
and again
$x R_1 y$
and again
![]() $x \not \vDash _{1} \square \psi _{1}$
.⊣
$x \not \vDash _{1} \square \psi _{1}$
.⊣
6.3 Step 3: Ensuring a finite frame
We are ready for our final step, in which we construct
![]() $\mathfrak {F}_{3}=(W_{3},R_{3},E_{3})$
by selective filtration from
$\mathfrak {F}_{3}=(W_{3},R_{3},E_{3})$
by selective filtration from
![]() $\mathfrak {F}_{2}$
. This is done by constructing a sequence of finite partially ordered
$\mathfrak {F}_{2}$
. This is done by constructing a sequence of finite partially ordered
![]() $\mathsf {MS4}$
-frames with clean clusters
$\mathsf {MS4}$
-frames with clean clusters
![]() $\mathfrak {F}_{3.h}=(W_{3.h},R_{3.h},E_{3.h})$
such that
$\mathfrak {F}_{3.h}=(W_{3.h},R_{3.h},E_{3.h})$
such that
![]() $\mathfrak {F}_{3.h}\subseteq \mathfrak {F}_{3.h+1}$
for all
$\mathfrak {F}_{3.h}\subseteq \mathfrak {F}_{3.h+1}$
for all
![]() $h<\omega $
. We then show that this construction eventually terminates.
$h<\omega $
. We then show that this construction eventually terminates.
Similar to the construction for
![]() $\mathsf {M^{+}IPC}$
, for each point
$\mathsf {M^{+}IPC}$
, for each point
![]() $[x]\in W_{2}$
that we select, we create a copy of the point, give it a new name, say t, and let
$[x]\in W_{2}$
that we select, we create a copy of the point, give it a new name, say t, and let
![]() $\widehat {t}=[x]$
denote the original point in
$\widehat {t}=[x]$
denote the original point in
![]() $W_{2}$
that t represents and will behave similar to. However, we take a bit more care with the copies in this construction than in the construction for
$W_{2}$
that t represents and will behave similar to. However, we take a bit more care with the copies in this construction than in the construction for
![]() $\mathsf {M^{+}IPC}$
. In particular, we will never create two copies of the same original point within one cluster. This will ensure that the cluster size in
$\mathsf {M^{+}IPC}$
. In particular, we will never create two copies of the same original point within one cluster. This will ensure that the cluster size in
![]() $\mathfrak {F}_{3}$
has the same bound as the cluster size in
$\mathfrak {F}_{3}$
has the same bound as the cluster size in
![]() $\mathfrak {F}_{2}$
.
$\mathfrak {F}_{2}$
.
Before we begin the construction, we highlight an important property we will need for selecting our points.
Lemma 6.7. For
![]() $[x]\in W_{2}$
and
$[x]\in W_{2}$
and
![]() $\square \gamma \in \mathsf {Sub}(\varphi )$
, if
$\square \gamma \in \mathsf {Sub}(\varphi )$
, if
![]() $[x]\not \vDash _{2}\square \gamma $
, then there is
$[x]\not \vDash _{2}\square \gamma $
, then there is
![]() $[y]\in W_{2}$
such that
$[y]\in W_{2}$
such that
![]() $[x]R_{2}[y]$
and
$[x]R_{2}[y]$
and
![]() $[y]\not \vDash _{2}\square \gamma\ R_{2}$
-maximally.
$[y]\not \vDash _{2}\square \gamma\ R_{2}$
-maximally.
Proof. Suppose
![]() $[x]\not \vDash _{2}\square \gamma $
. By Lemma 6.6,
$[x]\not \vDash _{2}\square \gamma $
. By Lemma 6.6,
![]() $x\not \vDash _{1}\square \gamma $
, and by Lemma 6.5(6), there is
$x\not \vDash _{1}\square \gamma $
, and by Lemma 6.5(6), there is
![]() $[y]\in W_{2}$
such that
$[y]\in W_{2}$
such that
![]() $[x]R_{2}[y]$
and
$[x]R_{2}[y]$
and
![]() $y\not \vDash _{1}\square \gamma\ R_{1}$
-maximally. Applying Lemma 6.6 again yields
$y\not \vDash _{1}\square \gamma\ R_{1}$
-maximally. Applying Lemma 6.6 again yields
![]() $[y]\not \vDash _{2}\square \gamma $
. To see that
$[y]\not \vDash _{2}\square \gamma $
. To see that
![]() $[y]$
is
$[y]$
is
![]() $R_{2}$
-maximal with respect to
$R_{2}$
-maximal with respect to
![]() $\square \gamma $
, suppose
$\square \gamma $
, suppose
![]() $[y]R_{2}[z]$
and
$[y]R_{2}[z]$
and
![]() $[z]\not \vDash _{2}\square \gamma $
. By definition of
$[z]\not \vDash _{2}\square \gamma $
. By definition of
![]() $R_{2}$
, either
$R_{2}$
, either
![]() $[y]=[z]$
or
$[y]=[z]$
or
![]() $yR_{1}z$
. If
$yR_{1}z$
. If
![]() $yR_{1}z$
, then by
$yR_{1}z$
, then by
![]() $R_{1}$
-maximality of y, we have
$R_{1}$
-maximality of y, we have
![]() $y=z$
, so
$y=z$
, so
![]() $[y]=[z]$
, and hence
$[y]=[z]$
, and hence
![]() $[y]$
must be
$[y]$
must be
![]() $R_{2}$
-maximal with respect to
$R_{2}$
-maximal with respect to
![]() $\square \gamma $
. ⊣
$\square \gamma $
. ⊣
Throughout the construction, for each
![]() $t\in W_{3.h}$
, we associate the following sets of formulas:
$t\in W_{3.h}$
, we associate the following sets of formulas:
 $$\begin{align*}\Sigma^{\forall}(t) &= \{\forall\delta\in\mathsf{Sub}(\varphi)\mid\widehat {t}\ \not\vDash_{2}\forall\delta\text\},\\ \Sigma^{\square}(t) &= \{\square\gamma\in\mathsf{Sub}(\varphi)\mid\widehat {t}\ \not\vDash_{2}\square\gamma, \widehat{t}\ \vDash_{2}\gamma\}. \end{align*}$$
$$\begin{align*}\Sigma^{\forall}(t) &= \{\forall\delta\in\mathsf{Sub}(\varphi)\mid\widehat {t}\ \not\vDash_{2}\forall\delta\text\},\\ \Sigma^{\square}(t) &= \{\square\gamma\in\mathsf{Sub}(\varphi)\mid\widehat {t}\ \not\vDash_{2}\square\gamma, \widehat{t}\ \vDash_{2}\gamma\}. \end{align*}$$
We start with
![]() $\mathfrak {F}_{3.0}=(W_{3.0},R_{3.0},E_{3.0})$
where
$\mathfrak {F}_{3.0}=(W_{3.0},R_{3.0},E_{3.0})$
where
and
![]() $\widehat {t_{0}}=[x_0]\in W_{2}$
is a point with
$\widehat {t_{0}}=[x_0]\in W_{2}$
is a point with
![]() $[x_0]\not \vDash _{2}\varphi $
. This will be a root of our frame and has
$[x_0]\not \vDash _{2}\varphi $
. This will be a root of our frame and has
![]() $Q_{3}$
-depth
$Q_{3}$
-depth
![]() $1$
. Let
$1$
. Let
![]() $W_{3.-1}=R_{3.-1}= E_{3.-1}= \varnothing $
. Suppose
$W_{3.-1}=R_{3.-1}= E_{3.-1}= \varnothing $
. Suppose
![]() $\mathfrak {F}_{3.h-1}=(W_{3.h-1},R_{3.h-1},E_{3.h-1})$
has already been constructed and is a partially ordered
$\mathfrak {F}_{3.h-1}=(W_{3.h-1},R_{3.h-1},E_{3.h-1})$
has already been constructed and is a partially ordered
![]() $\mathsf {MS4}$
-frame with clean clusters. We construct
$\mathsf {MS4}$
-frame with clean clusters. We construct
![]() $\mathfrak {F}_{3.h}$
by the following steps.
$\mathfrak {F}_{3.h}$
by the following steps.
![]() $\forall$
-step (Horizontal): Let
$\forall$
-step (Horizontal): Let
![]() $W_{3.h}^{\forall }=W_{3.h-1}$
,
$W_{3.h}^{\forall }=W_{3.h-1}$
,
![]() $R_{3.h}^{\forall }=R_{3.h-1}$
, and
$R_{3.h}^{\forall }=R_{3.h-1}$
, and
![]() $E_{3.h}^{\forall }=E_{3.h-1}$
. For each cluster
$E_{3.h}^{\forall }=E_{3.h-1}$
. For each cluster
![]() $E_{3.h}(t)\subseteq W_{3.h-1}\backslash W_{3.h-1}^{\forall }$
, consider
$E_{3.h}(t)\subseteq W_{3.h-1}\backslash W_{3.h-1}^{\forall }$
, consider
![]() $\forall \delta \in \Sigma ^{\forall }(t)$
. If there is no
$\forall \delta \in \Sigma ^{\forall }(t)$
. If there is no
![]() $s\in W_{3.h}^{\forall }$
already such that
$s\in W_{3.h}^{\forall }$
already such that
![]() $tE_{3.h}^{\forall }s$
and
$tE_{3.h}^{\forall }s$
and
![]() $\widehat {s}\ \not \vDash _{2}\delta $
, we add a witness to our new frame as follows. Since
$\widehat {s}\ \not \vDash _{2}\delta $
, we add a witness to our new frame as follows. Since
![]() $\widehat {t}\ \not \vDash _{2}\forall \delta $
, there exists
$\widehat {t}\ \not \vDash _{2}\forall \delta $
, there exists
![]() $[x]\in W_{2}$
such that
$[x]\in W_{2}$
such that
![]() $\widehat {t}E_{2}[x]$
and
$\widehat {t}E_{2}[x]$
and
![]() $[x]\not \vDash _{2}\delta $
. We add the point s to
$[x]\not \vDash _{2}\delta $
. We add the point s to
![]() $W_{3.h}^{\forall }$
where
$W_{3.h}^{\forall }$
where
![]() $\widehat {s}=[x]$
(s is a distinct new copy of
$\widehat {s}=[x]$
(s is a distinct new copy of
![]() $[x]$
), the relations
$[x]$
), the relations
![]() $(s,s)$
to
$(s,s)$
to
![]() $R_{3.h}^{\forall }$
, the relations
$R_{3.h}^{\forall }$
, the relations
![]() $(t,s)$
to
$(t,s)$
to
![]() $E_{3.h}^{\forall }$
and generate the least equivalence relation.
$E_{3.h}^{\forall }$
and generate the least equivalence relation.
![]() $\square$
-step (Vertical): Let
$\square$
-step (Vertical): Let
![]() $W_{3.h}^{\square }=W_{3.h}^{\forall }$
,
$W_{3.h}^{\square }=W_{3.h}^{\forall }$
,
![]() $R_{3.h}^{\square }=R_{3.h}^{\forall }$
, and
$R_{3.h}^{\square }=R_{3.h}^{\forall }$
, and
![]() $E_{3.h}^{\square }=E_{3.h}^{\forall }$
. For
$E_{3.h}^{\square }=E_{3.h}^{\forall }$
. For
![]() $t\in W_{3.h}^{\forall }\backslash W_{3.h-1}^{\forall }$
(hence including any points added in the horizontal step), consider
$t\in W_{3.h}^{\forall }\backslash W_{3.h-1}^{\forall }$
(hence including any points added in the horizontal step), consider
![]() $\square \gamma \in \Sigma ^{\square }(t)$
where
$\square \gamma \in \Sigma ^{\square }(t)$
where
![]() $\widehat {t}\ \not \vDash _{2}\square \gamma $
, but
$\widehat {t}\ \not \vDash _{2}\square \gamma $
, but
![]() $\widehat {t}\ \vDash _{2}\gamma $
(thus, t isn’t witnessing the formula
$\widehat {t}\ \vDash _{2}\gamma $
(thus, t isn’t witnessing the formula
![]() $\square \gamma $
itself), and there is no
$\square \gamma $
itself), and there is no
![]() $s\in W_{3.h}^{\square }$
already such that
$s\in W_{3.h}^{\square }$
already such that
![]() $tR_{3.h}^{\square }s$
and
$tR_{3.h}^{\square }s$
and
![]() $\widehat {s}\ \not \vDash _{2}\square \gamma\ R_{2}$
-maximally. For each such
$\widehat {s}\ \not \vDash _{2}\square \gamma\ R_{2}$
-maximally. For each such
![]() $\square \gamma $
, since
$\square \gamma $
, since
![]() $\widehat {t}\ \not \vDash _{2}\square \gamma $
and
$\widehat {t}\ \not \vDash _{2}\square \gamma $
and
![]() $\widehat {t}=[w]$
for some
$\widehat {t}=[w]$
for some
![]() $[w]\in W_{2}$
, we have
$[w]\in W_{2}$
, we have
![]() $[w]\not \vDash _{2}\square \gamma $
. By Lemma 6.7, there is
$[w]\not \vDash _{2}\square \gamma $
. By Lemma 6.7, there is
![]() $[x]\in W_{2}$
such that
$[x]\in W_{2}$
such that
![]() $[w]R_{2}[x]$
and
$[w]R_{2}[x]$
and
![]() $[x]$
is
$[x]$
is
![]() $R_{2}$
-maximal with respect to
$R_{2}$
-maximal with respect to
![]() $\square \gamma $
. We add the point s to
$\square \gamma $
. We add the point s to
![]() $W_{3.h}^{\square }$
where
$W_{3.h}^{\square }$
where
![]() $\widehat {s}=[x]$
,
$\widehat {s}=[x]$
,
![]() $(t,s)$
and
$(t,s)$
and
![]() $(s,s)$
to
$(s,s)$
to
![]() $R_{3.h}^{\square }$
and close under transitivity, and add
$R_{3.h}^{\square }$
and close under transitivity, and add
![]() $(s,s)$
to
$(s,s)$
to
![]() $E_{3.h}^{\square }$
. To make sure commutativity is satisfied, for each
$E_{3.h}^{\square }$
. To make sure commutativity is satisfied, for each
![]() $w\in E_{3.h}^{\square }(t)$
, if there is already
$w\in E_{3.h}^{\square }(t)$
, if there is already
![]() $s_{w}\in E_{3.h}^{\square }(s)$
such that
$s_{w}\in E_{3.h}^{\square }(s)$
such that
![]() $\widehat {w}R_{2}\widehat {s_{w}}$
, we simply add the relation
$\widehat {w}R_{2}\widehat {s_{w}}$
, we simply add the relation
![]() $(w, s_{w})$
to
$(w, s_{w})$
to
![]() $R_{3.h}^{\square }$
. If there is no such
$R_{3.h}^{\square }$
. If there is no such
![]() $s_{w}$
, then by commutativity in
$s_{w}$
, then by commutativity in
![]() $W_{2}$
, there is
$W_{2}$
, there is
![]() $[x_{w}]\in W_2$
such that
$[x_{w}]\in W_2$
such that
![]() $\widehat {w}R_{2}[x_{w}]$
and
$\widehat {w}R_{2}[x_{w}]$
and
![]() $[x_{w}]E_{2}[x]$
, so we add
$[x_{w}]E_{2}[x]$
, so we add
![]() $s_{w}$
to
$s_{w}$
to
![]() $W_{3.h}^{\square }$
, where
$W_{3.h}^{\square }$
, where
![]() $\widehat {s_{w}}=[x_{w}]$
. We then add
$\widehat {s_{w}}=[x_{w}]$
. We then add
![]() $(w,s_{w})$
to
$(w,s_{w})$
to
![]() $R_{3.h}^{\square }$
and close it under reflexivity and transitivity, and add
$R_{3.h}^{\square }$
and close it under reflexivity and transitivity, and add
![]() $(s_{w},s)$
to
$(s_{w},s)$
to
![]() $E_{3.h}^{\square }$
and generate the smallest equivalence relation.
$E_{3.h}^{\square }$
and generate the smallest equivalence relation.
To end this stage of the construction, we let
![]() $\mathfrak {F}_{3.h}=(W_{3.h},R_{3.h},E_{3.h})$
where
$\mathfrak {F}_{3.h}=(W_{3.h},R_{3.h},E_{3.h})$
where
Lemma 6.8.
![]() $\mathfrak {F}_{3.h}$
is a finite partially ordered
$\mathfrak {F}_{3.h}$
is a finite partially ordered
![]() $\mathsf {MS4}$
-frame with clean clusters.
$\mathsf {MS4}$
-frame with clean clusters.
Proof. That
![]() $\mathfrak {F}_{3.h}$
is finite follows from the construction. Since in the
$\mathfrak {F}_{3.h}$
is finite follows from the construction. Since in the
![]() $\forall $
-step we only added reflexive arrows to
$\forall $
-step we only added reflexive arrows to
![]() $R_{3.h}^{\forall }$
, we have that
$R_{3.h}^{\forall }$
, we have that
![]() $R_{3.h}^{\forall }$
is a partial order. In the
$R_{3.h}^{\forall }$
is a partial order. In the
![]() $\Box $
-step we close
$\Box $
-step we close
![]() $R_{3.h}^{\Box }$
under reflexivity and transitivity each time we add a new arrow, so
$R_{3.h}^{\Box }$
under reflexivity and transitivity each time we add a new arrow, so
![]() $R_{3.h}^{\Box }$
is reflexive and transitive. Moreover, we only add
$R_{3.h}^{\Box }$
is reflexive and transitive. Moreover, we only add
![]() $R_{3.h}^{\Box }$
arrows from points that were already present in
$R_{3.h}^{\Box }$
arrows from points that were already present in
![]() $W_{3.h}^{\forall }$
into points that are freshly added in the
$W_{3.h}^{\forall }$
into points that are freshly added in the
![]() $\Box $
-step of round h. Thus,
$\Box $
-step of round h. Thus,
![]() $R_{3.h}^{\Box }$
is antisymmetric. That
$R_{3.h}^{\Box }$
is antisymmetric. That
![]() $E_{3.h}$
is an equivalence relation and that
$E_{3.h}$
is an equivalence relation and that
![]() $\mathfrak {F}_{3.h}$
satisfies commutativity follow from the construction. Finally, to see that
$\mathfrak {F}_{3.h}$
satisfies commutativity follow from the construction. Finally, to see that
![]() $\mathfrak {F}_{3.h}$
has only clean clusters, note that in the
$\mathfrak {F}_{3.h}$
has only clean clusters, note that in the
![]() $\forall $
-step all freshly introduced
$\forall $
-step all freshly introduced
![]() $E_h$
-relations are of the shape
$E_h$
-relations are of the shape
![]() $(s, t)$
where s or
$(s, t)$
where s or
![]() $t \in W^{\forall }_{3.h} \setminus W_{3.h-1}$
. Since no non-reflexive
$t \in W^{\forall }_{3.h} \setminus W_{3.h-1}$
. Since no non-reflexive
![]() $R_h$
-arrows are introduced in this step, no dirty cluster could have been built. We have already discussed the shape of the
$R_h$
-arrows are introduced in this step, no dirty cluster could have been built. We have already discussed the shape of the
![]() $R_{h}$
arrows introduced in the
$R_{h}$
arrows introduced in the
![]() $\square $
-step. This guarantees that no cluster in
$\square $
-step. This guarantees that no cluster in
![]() $W^{\forall }_{3.h}$
is made dirty. The freshly introduced
$W^{\forall }_{3.h}$
is made dirty. The freshly introduced
![]() $E_h$
-relations in these steps are of the shape
$E_h$
-relations in these steps are of the shape
![]() $(s, t)$
where
$(s, t)$
where
![]() $s, t \in W^{\square }_{3.h} \setminus W^{\forall }_{3.h}$
. Since no non-reflexive
$s, t \in W^{\square }_{3.h} \setminus W^{\forall }_{3.h}$
. Since no non-reflexive
![]() $R_h$
-relations exist between these points, we infer that all clusters are clean.⊣
$R_h$
-relations exist between these points, we infer that all clusters are clean.⊣
The following lemma summarizes some useful properties of
![]() $\mathfrak {F}_{3}$
. In the following let
$\mathfrak {F}_{3}$
. In the following let
Lemma 6.9. Let
![]() $t,u\in W_{3.h}$
.
$t,u\in W_{3.h}$
.
-
1. If
 $tE_{3.h}u$
, then
$tE_{3.h}u$
, then
 $\widehat {t}E_{2}\widehat {u}$
.
$\widehat {t}E_{2}\widehat {u}$
. -
2. If
 $t E_{3.h} u$
, then
$t E_{3.h} u$
, then
 $\Sigma ^{\forall }(t) =\Sigma ^{\forall }(u)$
.
$\Sigma ^{\forall }(t) =\Sigma ^{\forall }(u)$
.
 $($
This ensures that we only need to perform the
$($
This ensures that we only need to perform the
 $\forall $
-step once per cluster
$\forall $
-step once per cluster
 $)$
.
$)$
. -
3. If
 $t E_{3.h}u$
and
$t E_{3.h}u$
and
 $t\neq u$
, then
$t\neq u$
, then
 $\widehat {t}\neq \widehat {u}$
.
$\widehat {t}\neq \widehat {u}$
.
 $($
This ensures that one cluster does not contain two different copies of the same point, so our cluster size remains bounded
$($
This ensures that one cluster does not contain two different copies of the same point, so our cluster size remains bounded
 $)$
.
$)$
. -
4. If
 , then
, then
 .
. -
5. If
 $tR_{3.h}u$
, then
$tR_{3.h}u$
, then
 $\widehat {t}R_{2}\widehat {u}$
.
$\widehat {t}R_{2}\widehat {u}$
. -
6. If
 , then
, then
 . Thus, if
. Thus, if
 , then
, then
 $\widehat {t}\neq \widehat {u}$
.
$\widehat {t}\neq \widehat {u}$
. -
7. A formula
 $\square \gamma \in \mathsf {Sub}(\varphi )$
can be witnessed at most
$\square \gamma \in \mathsf {Sub}(\varphi )$
can be witnessed at most
 $2^n$
times in clusters along an
$2^n$
times in clusters along an
 $R_{3.h}$
-chain.
$R_{3.h}$
-chain.
 $($
This shows that
$($
This shows that
 $\square \gamma $
can be witnessed at most
$\square \gamma $
can be witnessed at most
 $2^n$
times per
$2^n$
times per
 $Q_{3.h}$
-chain.
$Q_{3.h}$
-chain.
 $)$
$)$
Proof. (1) This follows from the construction.
(2) By (1),
![]() $t E_{3.h}u$
implies
$t E_{3.h}u$
implies
![]() $\widehat {t} E_{2} \widehat {u}$
, so
$\widehat {t} E_{2} \widehat {u}$
, so
![]() $\widehat {t}\ \vDash _{2} \forall \gamma $
iff
$\widehat {t}\ \vDash _{2} \forall \gamma $
iff
![]() $\widehat {u}\ \vDash _{2}\forall \gamma $
.
$\widehat {u}\ \vDash _{2}\forall \gamma $
.
(3) Suppose
![]() $t E_{3.h}u$
,
$t E_{3.h}u$
,
![]() $t\neq u$
, and
$t\neq u$
, and
![]() $\widehat {t}=\widehat {u}$
. Without loss of generality assume that t was added to the cluster before u, so either u is added to witness some formula
$\widehat {t}=\widehat {u}$
. Without loss of generality assume that t was added to the cluster before u, so either u is added to witness some formula
![]() $\forall \delta _{i}$
where
$\forall \delta _{i}$
where
![]() $\widehat {u}\ \not \vDash _{2}\delta _{i}$
, or u is added as a commutativity witness for some point from the cluster immediately below. However, by construction, u would not have been added to witness a formula
$\widehat {u}\ \not \vDash _{2}\delta _{i}$
, or u is added as a commutativity witness for some point from the cluster immediately below. However, by construction, u would not have been added to witness a formula
![]() $\forall \delta _{i}$
, because if
$\forall \delta _{i}$
, because if
![]() $\ \widehat {u}\ \not \vDash _{2}\delta _{i}$
, then
$\ \widehat {u}\ \not \vDash _{2}\delta _{i}$
, then
![]() $\widehat {t}=\widehat {u}$
implies that
$\widehat {t}=\widehat {u}$
implies that
![]() $\widehat {t}\ \not \vDash _{2}\delta _{i}$
, so t is already a viable witness in the cluster for any such formula, contradicting the
$\widehat {t}\ \not \vDash _{2}\delta _{i}$
, so t is already a viable witness in the cluster for any such formula, contradicting the
![]() $\forall $
-step of the construction. Furthermore, u would not be added as a commutativity witness for some point
$\forall $
-step of the construction. Furthermore, u would not be added as a commutativity witness for some point
![]() $w$
in the cluster immediately below, because then in
$w$
in the cluster immediately below, because then in
![]() $W_{2}$
we would have
$W_{2}$
we would have
![]() $\widehat {w}R_{2}\widehat {u}$
, so
$\widehat {w}R_{2}\widehat {u}$
, so
![]() $\widehat {w}R_{2}\widehat {t}$
, and a new
$\widehat {w}R_{2}\widehat {t}$
, and a new
![]() $R_{3.h}$
-relation would have been added from
$R_{3.h}$
-relation would have been added from
![]() $w$
to t instead, contradicting the
$w$
to t instead, contradicting the
![]() $\square $
-step of the construction. Thus, we must have
$\square $
-step of the construction. Thus, we must have
![]() $\widehat {t}\neq \widehat {u}$
.
$\widehat {t}\neq \widehat {u}$
.
(4) Suppose
![]() . Then there is
. Then there is
![]() $[w]\in W_{2}$
with
$[w]\in W_{2}$
with
![]() $[t]\neq [w]$
,
$[t]\neq [w]$
,
![]() $[t]R_{2}[w]$
, and
$[t]R_{2}[w]$
, and
![]() $[w]E_{2}[u]$
. From the definitions of
$[w]E_{2}[u]$
. From the definitions of
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
,
$E_{2}$
,
![]() $[w]E_{2}[u]$
implies
$[w]E_{2}[u]$
implies
![]() $wE_{0}u$
. By definition of
$wE_{0}u$
. By definition of
![]() $R_{2}$
,
$R_{2}$
,
![]() $[t]R_{2}[w]$
and
$[t]R_{2}[w]$
and
![]() $[t]\neq [w]$
imply
$[t]\neq [w]$
imply
![]() $tR_{1}w$
. Since
$tR_{1}w$
. Since
![]() $[t]\neq [w]$
, we have
$[t]\neq [w]$
, we have
![]() $t\neq w$
, so
$t\neq w$
, so
![]() by the definition of
by the definition of
![]() $R_{1}$
. Then there is
$R_{1}$
. Then there is
![]() $v\in W_{1}$
with
$v\in W_{1}$
with
![]() $t\neq v$
,
$t\neq v$
,
![]() $tR_{0}v$
, and
$tR_{0}v$
, and
![]() $vE_{0}w$
. Since
$vE_{0}w$
. Since
![]() $vE_{0}w$
, we have
$vE_{0}w$
, we have
![]() $vE_{0}u$
. Thus,
$vE_{0}u$
. Thus,
![]() $t\neq v$
,
$t\neq v$
,
![]() $tR_{0}v$
, and
$tR_{0}v$
, and
![]() $vE_{0}u$
, and hence
$vE_{0}u$
, and hence
![]() .
.
(5) This follows from the construction.
(6) If
![]() , then there is
, then there is
![]() $w$
such that
$w$
such that
![]() $t\neq w$
,
$t\neq w$
,
![]() $tR_{3.h}w$
, and
$tR_{3.h}w$
, and
![]() $wE_{3.h}u$
. By (5),
$wE_{3.h}u$
. By (5),
![]() $\widehat {t}R_{2}\widehat {w}$
and
$\widehat {t}R_{2}\widehat {w}$
and
![]() $\widehat {w}$
must come from a different cluster in
$\widehat {w}$
must come from a different cluster in
![]() $W_{2}$
than
$W_{2}$
than
![]() $\widehat {t}$
, so
$\widehat {t}$
, so
![]() $\widehat {t}\neq \widehat {w}$
. We also have
$\widehat {t}\neq \widehat {w}$
. We also have
![]() $\widehat {w}E_{2}\widehat {u}$
by (1), so
$\widehat {w}E_{2}\widehat {u}$
by (1), so
![]() . Because
. Because
![]() $\mathfrak {F}_{2}$
has clean clusters, we must have
$\mathfrak {F}_{2}$
has clean clusters, we must have
![]() $\widehat {t}\neq \widehat {u}$
.
$\widehat {t}\neq \widehat {u}$
.
(7) Suppose that
![]() $x_1,\ldots ,x_{2^{n}+1}$
are all in different
$x_1,\ldots ,x_{2^{n}+1}$
are all in different
![]() $E_{3.h}$
-clusters along an
$E_{3.h}$
-clusters along an
![]() $R_{3.h}$
-chain (where
$R_{3.h}$
-chain (where
![]() $\widehat {x}_1=[w_{1}],\ldots ,\widehat {x}_{2^{n}+1}=[w_{2^{n}+1}]$
), so
$\widehat {x}_1=[w_{1}],\ldots ,\widehat {x}_{2^{n}+1}=[w_{2^{n}+1}]$
), so
![]() , and all have been added to witness a formula
, and all have been added to witness a formula
![]() $\square \gamma \in \mathsf {Sub}(\varphi )$
. Thus,
$\square \gamma \in \mathsf {Sub}(\varphi )$
. Thus,
![]() $\widehat {x_{i}}\ \not \vDash _{2}\square \gamma\ R_2$
-maximally for
$\widehat {x_{i}}\ \not \vDash _{2}\square \gamma\ R_2$
-maximally for
![]() $i=1,\ldots ,2^{n}+1$
. Because there are only
$i=1,\ldots ,2^{n}+1$
. Because there are only
![]() $2^{n}$
subsets of
$2^{n}$
subsets of
![]() $\mathsf {Sub}(\varphi )$
(where
$\mathsf {Sub}(\varphi )$
(where
![]() $n=\lvert \mathsf {Sub}(\varphi )\rvert $
), the pigeonhole principle implies that there are some i and j with
$n=\lvert \mathsf {Sub}(\varphi )\rvert $
), the pigeonhole principle implies that there are some i and j with
![]() $i\neq j$
(assume
$i\neq j$
(assume
![]() $i<j$
) where
$i<j$
) where
![]() $\widehat {x_i}$
and
$\widehat {x_i}$
and
![]() $\widehat {x_j}$
satisfy the same subformulas of
$\widehat {x_j}$
satisfy the same subformulas of
![]() $\varphi $
. By (6),
$\varphi $
. By (6),
![]() and
and
![]() $\widehat {x_{i}}\neq \widehat {x_{j}}$
. If
$\widehat {x_{i}}\neq \widehat {x_{j}}$
. If
![]() $\ \widehat {x_{i}}R_{2}\widehat {x_{j}}$
, then
$\ \widehat {x_{i}}R_{2}\widehat {x_{j}}$
, then
![]() $R_{2}$
-maximality of
$R_{2}$
-maximality of
![]() $\widehat {x_{i}}$
with respect to
$\widehat {x_{i}}$
with respect to
![]() $\square \gamma $
implies
$\square \gamma $
implies
![]() $\widehat {x_{i}}=\widehat {x_{j}}$
, contradicting
$\widehat {x_{i}}=\widehat {x_{j}}$
, contradicting
![]() $\widehat {x_{i}}\neq \widehat {x_{j}}$
, so we must have
$\widehat {x_{i}}\neq \widehat {x_{j}}$
, so we must have
![]() $\widehat {x_{i}}R{\kern-2pt}\!\!\!\!\ /_{2}\widehat {x_{j}}$
and hence
$\widehat {x_{i}}R{\kern-2pt}\!\!\!\!\ /_{2}\widehat {x_{j}}$
and hence
![]() $[w_{i}]R{\kern-2pt}\!\!\!\!\ /_{2}[w_{j}]$
. Since
$[w_{i}]R{\kern-2pt}\!\!\!\!\ /_{2}[w_{j}]$
. Since
![]() we have
we have
![]() . By (4), we then have
. By (4), we then have
![]() . Since
. Since
![]() $[w_i]$
and
$[w_i]$
and
![]() $[w_j]$
satisfy the same formulas in
$[w_j]$
satisfy the same formulas in
![]() $\mathsf {Sub}(\varphi )$
, we have
$\mathsf {Sub}(\varphi )$
, we have
![]() $[w_i]\vDash _{2}\square \beta \Leftrightarrow [w_j]\vDash _{2}\square \beta $
for
$[w_i]\vDash _{2}\square \beta \Leftrightarrow [w_j]\vDash _{2}\square \beta $
for
![]() $\square \beta \in \mathsf {Sub}(\varphi )$
. By Lemmas 6.6 and 6.3,
$\square \beta \in \mathsf {Sub}(\varphi )$
. By Lemmas 6.6 and 6.3,
![]() $w_{i}\vDash _{0}\square \beta \Leftrightarrow w_{j}\vDash _{0}\square \beta $
. Thus,
$w_{i}\vDash _{0}\square \beta \Leftrightarrow w_{j}\vDash _{0}\square \beta $
. Thus,
![]() $w_{i}R_{1}w_{j}$
and hence
$w_{i}R_{1}w_{j}$
and hence
![]() $[w_i]R_{2}[w_j]$
, a contradiction.⊣
$[w_i]R_{2}[w_j]$
, a contradiction.⊣
We now prove that the end result of our construction is a finite frame, using the definitions of bounded cluster size, bounded R-branching, and bounded R-depth given in Definition 5.10.
Lemma 6.10. For all
![]() $h<\omega $
, the cluster size of
$h<\omega $
, the cluster size of
![]() $\mathfrak {F}_{3.h}=(W_{3.h},R_{3.h},E_{3.h})$
is bounded by
$\mathfrak {F}_{3.h}=(W_{3.h},R_{3.h},E_{3.h})$
is bounded by
![]() $2^{n}$
.
$2^{n}$
.
Proof. By Lemma 6.5(5), the cluster size in
![]() $\mathfrak F_2$
is bounded by
$\mathfrak F_2$
is bounded by
![]() $2^{n}$
, and by Lemma 6.9(3), we do not add copies of the same points to a cluster in
$2^{n}$
, and by Lemma 6.9(3), we do not add copies of the same points to a cluster in
![]() $\mathfrak {F}_{3.h}$
. Thus, cluster size in
$\mathfrak {F}_{3.h}$
. Thus, cluster size in
![]() $\mathfrak F_{3.h}$
is bounded by
$\mathfrak F_{3.h}$
is bounded by
![]() $2^{n}$
.⊣
$2^{n}$
.⊣
Lemma 6.11. For all
![]() $h<\omega $
, the
$h<\omega $
, the
![]() $R_{3.h}$
-branching of
$R_{3.h}$
-branching of
![]() $\mathfrak {F}_{3.h}=(W_{3.h},R_{3.h},E_{3.h})$
is bounded by
$\mathfrak {F}_{3.h}=(W_{3.h},R_{3.h},E_{3.h})$
is bounded by
![]() $2^{n}\cdot m$
.
$2^{n}\cdot m$
.
Proof. It is sufficient to show that each
![]() $t\in W_{3.j-1}$
, for
$t\in W_{3.j-1}$
, for
![]() $j\leq h$
, has at most
$j\leq h$
, has at most
![]() $2^{n}\cdot m$
immediate
$2^{n}\cdot m$
immediate
![]() $R_{3.j}$
-successors. By construction, we add at most m-many immediate
$R_{3.j}$
-successors. By construction, we add at most m-many immediate
![]() $R_{3.j}$
-successors to t for formulas of the form
$R_{3.j}$
-successors to t for formulas of the form
![]() $\square \psi \in \mathsf {Sub}(\varphi )$
. Each
$\square \psi \in \mathsf {Sub}(\varphi )$
. Each
![]() $y\in E_{3.j}(t)$
also needs at most m-many immediate
$y\in E_{3.j}(t)$
also needs at most m-many immediate
![]() $R_{3.j}$
-successors to witness
$R_{3.j}$
-successors to witness
![]() $\square $
-formulas. Since there are at most
$\square $
-formulas. Since there are at most
![]() $2^{n}$
-many such y (including t itself), we must add at most
$2^{n}$
-many such y (including t itself), we must add at most
![]() $2^{n}\cdot m$
immediate
$2^{n}\cdot m$
immediate
![]() $R_{3.j}$
successors to t (see the diagram below):
$R_{3.j}$
successors to t (see the diagram below):

⊣
Lemma 6.12. For all
![]() $h<\omega $
, the
$h<\omega $
, the
![]() $R_{3.h}$
-depth of
$R_{3.h}$
-depth of
![]() $\mathfrak {F}_{3.h}=(W_{3.h},R_{3.h},E_{3.h})$
is bounded by
$\mathfrak {F}_{3.h}=(W_{3.h},R_{3.h},E_{3.h})$
is bounded by
![]() $2^{n}\cdot m +1$
.
$2^{n}\cdot m +1$
.
Proof. By construction, to make an immediate vertical move from some cluster
![]() $E_{3.h}(t)$
to another cluster
$E_{3.h}(t)$
to another cluster
![]() $E_{3.h}(u)$
(with
$E_{3.h}(u)$
(with
![]() $t\neq u$
), there must be some point
$t\neq u$
), there must be some point
![]() $x\in E_{3.h}(t)$
and formula
$x\in E_{3.h}(t)$
and formula
![]() $\square \psi \in \Sigma ^{\square }(x)$
requiring a witness y, where
$\square \psi \in \Sigma ^{\square }(x)$
requiring a witness y, where
![]() $y\in E_{3.h}(u)$
,
$y\in E_{3.h}(u)$
,
![]() $xR_{3.h}y$
, and y is added in the
$xR_{3.h}y$
, and y is added in the
![]() $\square $
-step of the construction. Starting from the bottom cluster
$\square $
-step of the construction. Starting from the bottom cluster
![]() $E_{3.h}(t_{0})$
, by Lemma 6.9(7), each of our m-many
$E_{3.h}(t_{0})$
, by Lemma 6.9(7), each of our m-many
![]() $\square $
-formulas can be witnessed at most
$\square $
-formulas can be witnessed at most
![]() $2^{n}$
times in clusters along an
$2^{n}$
times in clusters along an
![]() $R_{3.h}$
-chain. Thus, we add at most
$R_{3.h}$
-chain. Thus, we add at most
![]() $2^n \cdot m$
elements to an
$2^n \cdot m$
elements to an
![]() $R_{3.h}$
chain originating from this cluster, with the total length of the chain (including the starting point) being at most
$R_{3.h}$
chain originating from this cluster, with the total length of the chain (including the starting point) being at most
![]() $2^{n}\cdot m +1$
(see the diagram below):
$2^{n}\cdot m +1$
(see the diagram below):

Lemma 6.13. There is
![]() $h \in \omega $
such that
$h \in \omega $
such that
![]() $\mathfrak F_{3.h'} = \mathfrak F_{3.h}$
for all
$\mathfrak F_{3.h'} = \mathfrak F_{3.h}$
for all
![]() $h' \geq h$
.
$h' \geq h$
.
Proof. As in the proof of Lemma 5.15, we observe that in stage k of the construction, all
![]() $R_{3.h}$
-chains are bounded by k. Since, by Lemma 6.12, the
$R_{3.h}$
-chains are bounded by k. Since, by Lemma 6.12, the
![]() $R_{3.h}$
-depth of
$R_{3.h}$
-depth of
![]() $\mathfrak F_{3.h}$
is bounded by
$\mathfrak F_{3.h}$
is bounded by
![]() $2^{n}\cdot m +1$
, we have
$2^{n}\cdot m +1$
, we have
![]() $\mathfrak F_{3.h'} = \mathfrak F_{2^{n}\cdot m +1}$
for all
$\mathfrak F_{3.h'} = \mathfrak F_{2^{n}\cdot m +1}$
for all
![]() $h' \geq 2^{n}\cdot m +1$
.⊣
$h' \geq 2^{n}\cdot m +1$
.⊣
Set
![]() $\mathfrak {F}_3=(W_3,R_3,E_3)$
where
$\mathfrak {F}_3=(W_3,R_3,E_3)$
where
and h is as in Lemma 6.13. As an immediate consequence of Lemma 6.8, we obtain:
Lemma 6.14.
![]() $\mathfrak {F}_{3}=(W_{3},R_{3},E_{3})$
is a finite
$\mathfrak {F}_{3}=(W_{3},R_{3},E_{3})$
is a finite
![]() $\mathsf {M^{+}Grz}$
-frame.
$\mathsf {M^{+}Grz}$
-frame.
Finally, we verify that our frame validates precisely the formulas we want it to validate. Define a valuation
![]() $\nu _{3}$
on
$\nu _{3}$
on
![]() $W_{3}$
by
$W_{3}$
by
![]() $\nu _{3}(p)=\{t\in W_{3} \mid \widehat {t}\in \nu _{2}(p)\}$
for
$\nu _{3}(p)=\{t\in W_{3} \mid \widehat {t}\in \nu _{2}(p)\}$
for
![]() $p\in \mathsf {Sub}(\varphi )$
and
$p\in \mathsf {Sub}(\varphi )$
and
![]() $\nu _{3}(q)=\varnothing $
for variables q not occurring in
$\nu _{3}(q)=\varnothing $
for variables q not occurring in
![]() $\varphi $
.
$\varphi $
.
Lemma 6.15 (Truth Lemma)
For all
![]() $x\in W_{3}$
and
$x\in W_{3}$
and
![]() $\psi \in \mathsf {Sub}(\varphi )$
,
$\psi \in \mathsf {Sub}(\varphi )$
,
Proof. The proof is by induction on the complexity of
![]() $\psi $
and again we only consider the cases where
$\psi $
and again we only consider the cases where
![]() $\psi =\forall \psi _{1}$
or
$\psi =\forall \psi _{1}$
or
![]() $\psi =\square \psi _{1}$
.
$\psi =\square \psi _{1}$
.
Suppose
![]() $\psi =\forall \psi _{1}$
. If
$\psi =\forall \psi _{1}$
. If
![]() $\ \widehat {x}\ \not \vDash _{2}\forall \psi _{1}$
, then
$\ \widehat {x}\ \not \vDash _{2}\forall \psi _{1}$
, then
![]() $\forall \psi _{1}\in \Sigma ^{\forall }(x)$
, so at some point in the construction of
$\forall \psi _{1}\in \Sigma ^{\forall }(x)$
, so at some point in the construction of
![]() $\mathfrak {F}_{3}$
we add s to
$\mathfrak {F}_{3}$
we add s to
![]() $W_{3}$
and
$W_{3}$
and
![]() $(x,s)$
to
$(x,s)$
to
![]() $E_{3}$
where
$E_{3}$
where
![]() $\widehat {s}\ \not \vDash _{2}\psi _{1}$
. By the inductive hypothesis,
$\widehat {s}\ \not \vDash _{2}\psi _{1}$
. By the inductive hypothesis,
![]() $s\not \vDash _{3}\psi _{1}$
, hence
$s\not \vDash _{3}\psi _{1}$
, hence
![]() $x\not \vDash _{3}\forall \psi _{1}$
. Conversely, if
$x\not \vDash _{3}\forall \psi _{1}$
. Conversely, if
![]() $x\not \vDash _{3}\forall \psi _{1}$
, then there is
$x\not \vDash _{3}\forall \psi _{1}$
, then there is
![]() $w\in W_{3}$
with
$w\in W_{3}$
with
![]() $xE_{3}w$
and
$xE_{3}w$
and
![]() $w\not \vDash _{3}\psi _{1}$
. By the inductive hypothesis,
$w\not \vDash _{3}\psi _{1}$
. By the inductive hypothesis,
![]() $\widehat {w}\ \not \vDash _{2}\psi _{1}$
, and by Lemma 6.9(1),
$\widehat {w}\ \not \vDash _{2}\psi _{1}$
, and by Lemma 6.9(1),
![]() $xE_{3}w$
implies
$xE_{3}w$
implies
![]() $\widehat {x}E_{2}\widehat {w}$
, so
$\widehat {x}E_{2}\widehat {w}$
, so
![]() $\widehat {x}\ \not \vDash _{2}\forall \psi _{1}$
.
$\widehat {x}\ \not \vDash _{2}\forall \psi _{1}$
.
Suppose
![]() $\psi =\square \psi _{1}$
. If
$\psi =\square \psi _{1}$
. If
![]() $\ \widehat {x}\ \not \vDash _{2}\square \psi _{1}$
, then either
$\ \widehat {x}\ \not \vDash _{2}\square \psi _{1}$
, then either
![]() $\widehat {x}\ \not \vDash _{2}\psi _{1}$
or
$\widehat {x}\ \not \vDash _{2}\psi _{1}$
or
![]() $\widehat {x}\ \vDash _{2}\psi _{1}$
. If
$\widehat {x}\ \vDash _{2}\psi _{1}$
. If
![]() $\ \widehat {x}\ \not \vDash _{2}\psi _{1}$
, then by the inductive hypothesis we have
$\ \widehat {x}\ \not \vDash _{2}\psi _{1}$
, then by the inductive hypothesis we have
![]() $x\not \vDash _{3}\psi _{1}$
, hence
$x\not \vDash _{3}\psi _{1}$
, hence
![]() $x\not \vDash _{3}\square \psi _{1}$
. If
$x\not \vDash _{3}\square \psi _{1}$
. If
![]() $\ \widehat {x}\ \vDash _{2}\psi _{1}$
, then
$\ \widehat {x}\ \vDash _{2}\psi _{1}$
, then
![]() $\square \psi _{1}\in \Sigma ^{\square }(x)$
, so at some point in the construction of
$\square \psi _{1}\in \Sigma ^{\square }(x)$
, so at some point in the construction of
![]() $\mathfrak {F}_{3}$
we add s to
$\mathfrak {F}_{3}$
we add s to
![]() $W_{3}$
and
$W_{3}$
and
![]() $(x,s)$
to
$(x,s)$
to
![]() $R_{3}$
where
$R_{3}$
where
![]() $\widehat {s}\ \not \vDash _{2}\psi _{1}$
. By the inductive hypothesis,
$\widehat {s}\ \not \vDash _{2}\psi _{1}$
. By the inductive hypothesis,
![]() $s\not \vDash _{3}\psi _{1}$
, hence
$s\not \vDash _{3}\psi _{1}$
, hence
![]() $x\not \vDash _{3}\square \psi _{1}$
. Conversely, if
$x\not \vDash _{3}\square \psi _{1}$
. Conversely, if
![]() $x\not \vDash _{3}\square \psi _{1}$
, then there is
$x\not \vDash _{3}\square \psi _{1}$
, then there is
![]() $w\in W_{3}$
with
$w\in W_{3}$
with
![]() $xR_{3}w$
and
$xR_{3}w$
and
![]() $w\not \vDash _{3}\psi _{1}$
. By the inductive hypothesis,
$w\not \vDash _{3}\psi _{1}$
. By the inductive hypothesis,
![]() $\widehat {w}\ \not \vDash _{2}\psi _{1}$
, and by Lemma 6.9(5),
$\widehat {w}\ \not \vDash _{2}\psi _{1}$
, and by Lemma 6.9(5),
![]() $xR_{3}w$
implies
$xR_{3}w$
implies
![]() $\widehat {x}R_{2}\widehat {w}$
, so
$\widehat {x}R_{2}\widehat {w}$
, so
![]() $\widehat {x}\ \not \vDash _{2}\square \psi _{1}$
.⊣
$\widehat {x}\ \not \vDash _{2}\square \psi _{1}$
.⊣
We thus arrive at our desired result:
Theorem 6.16.
![]() $\mathsf {M^{+}Grz}$
has the finite model property.
$\mathsf {M^{+}Grz}$
has the finite model property.
As an immediate corollary to Theorem 6.16, we have:
Corollary 6.17.
![]() $\mathsf {M^{+}Grz}$
is decidable.
$\mathsf {M^{+}Grz}$
is decidable.