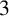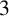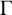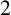1 Introduction
Graphs considered in this paper are finite, undirected, loopless, but allowed to have multiple edges. Let
![]() $\Gamma $
be a graph. As usual, we use
$\Gamma $
be a graph. As usual, we use
![]() $V(\Gamma )$
and
$V(\Gamma )$
and
![]() $E(\Gamma )$
to denote the vertex set and edge set of
$E(\Gamma )$
to denote the vertex set and edge set of
![]() $\Gamma $
, respectively. An orientation
$\Gamma $
, respectively. An orientation
![]() $\mathcal {D}$
of
$\mathcal {D}$
of
![]() $\Gamma $
is an assignment of one of the two possible orientations for every
$\Gamma $
is an assignment of one of the two possible orientations for every
![]() $e\in E(\Gamma )$
. Let
$e\in E(\Gamma )$
. Let
![]() $\varphi $
be a mapping from
$\varphi $
be a mapping from
![]() $E(\Gamma )$
to the set of integers and k a positive integer. For every
$E(\Gamma )$
to the set of integers and k a positive integer. For every
![]() $v\in V(G)$
, we use
$v\in V(G)$
, we use
![]() $\varphi ^{+}(v)$
to denote the sum of values
$\varphi ^{+}(v)$
to denote the sum of values
![]() $\varphi (e)$
of edges e with orientation originating from v and
$\varphi (e)$
of edges e with orientation originating from v and
![]() $\varphi ^{-}(v)$
the sum of values
$\varphi ^{-}(v)$
the sum of values
![]() $\varphi (e)$
of edges e with orientation pointing to v. If
$\varphi (e)$
of edges e with orientation pointing to v. If
![]() $-k<\varphi (e)<k$
for every
$-k<\varphi (e)<k$
for every
![]() $e\in E(\Gamma )$
and
$e\in E(\Gamma )$
and
![]() $\varphi ^{+}(v)=\varphi ^{-}(v)$
for every
$\varphi ^{+}(v)=\varphi ^{-}(v)$
for every
![]() $v\in V(\Gamma )$
, then we call the ordered pair
$v\in V(\Gamma )$
, then we call the ordered pair
![]() $(\mathcal {D}, \varphi )$
a k-flow of
$(\mathcal {D}, \varphi )$
a k-flow of
![]() $\Gamma $
. If further
$\Gamma $
. If further
![]() $\varphi (e)\neq 0$
for every
$\varphi (e)\neq 0$
for every
![]() $e\in E(\Gamma )$
, then we call
$e\in E(\Gamma )$
, then we call
![]() $(\mathcal {D}, \varphi )$
a nowhere-zero k-flow of
$(\mathcal {D}, \varphi )$
a nowhere-zero k-flow of
![]() $\Gamma $
. For convenience, we use
$\Gamma $
. For convenience, we use
![]() $\mathcal {NZ}_k$
to denote the family of graphs which admit a nowhere-zero k-flow.
$\mathcal {NZ}_k$
to denote the family of graphs which admit a nowhere-zero k-flow.
Tutte proposed three conjectures in the middle of the last century on integer flows which are still unsolved, namely the
![]() $5$
-flow,
$5$
-flow,
![]() $4$
-flow and
$4$
-flow and
![]() $3$
-flow conjectures. The
$3$
-flow conjectures. The
![]() $3$
-flow conjecture (see, for example, [Reference Zhang16, Conjecture 1.1.8]) is stated as follows: every
$3$
-flow conjecture (see, for example, [Reference Zhang16, Conjecture 1.1.8]) is stated as follows: every
![]() $4$
-edge-connected graph is contained in
$4$
-edge-connected graph is contained in
![]() $\mathcal {NZ}_3$
. By the equivalent version of the
$\mathcal {NZ}_3$
. By the equivalent version of the
![]() $3$
-flow conjecture given by Kochol [Reference Kochol6], it suffices to prove this conjecture for
$3$
-flow conjecture given by Kochol [Reference Kochol6], it suffices to prove this conjecture for
![]() $5$
-edge-connected graphs. However, it was conjectured by Jaeger [Reference Jaeger5] that every k-edge-connected graph is contained in
$5$
-edge-connected graphs. However, it was conjectured by Jaeger [Reference Jaeger5] that every k-edge-connected graph is contained in
![]() $\mathcal {NZ}_3$
for some given positive integer k. This so called weak
$\mathcal {NZ}_3$
for some given positive integer k. This so called weak
![]() $3$
-flow conjecture was solved by Thomassen [Reference Thomassen14] who proved that the statement holds for an
$3$
-flow conjecture was solved by Thomassen [Reference Thomassen14] who proved that the statement holds for an
![]() $8$
-edge-connected graph. Lovász et al. [Reference Lovász, Thomassen, Wu and Zhang8] improved this breakthrough by proving that the statement of the weak
$8$
-edge-connected graph. Lovász et al. [Reference Lovász, Thomassen, Wu and Zhang8] improved this breakthrough by proving that the statement of the weak
![]() $3$
-flow conjecture is true when
$3$
-flow conjecture is true when
![]() $k=6$
. However, the
$k=6$
. However, the
![]() $3$
-flow conjecture remains wide open for
$3$
-flow conjecture remains wide open for
![]() $5$
-edge-connected graphs. In this situation, it is natural to attempt to verify the conjecture for interesting families of graphs, for example, vertex-transitive graphs.
$5$
-edge-connected graphs. In this situation, it is natural to attempt to verify the conjecture for interesting families of graphs, for example, vertex-transitive graphs.
A graph
![]() $\Gamma $
is vertex-transitive if its automorphism group
$\Gamma $
is vertex-transitive if its automorphism group
![]() $\mathrm {Aut}(\Gamma )$
acts transitively on
$\mathrm {Aut}(\Gamma )$
acts transitively on
![]() $V(\Gamma )$
. A subgroup G of
$V(\Gamma )$
. A subgroup G of
![]() $\mathrm {Aut}(\Gamma )$
is said to be minimally vertex-transitive if G is transitive on
$\mathrm {Aut}(\Gamma )$
is said to be minimally vertex-transitive if G is transitive on
![]() $V(\Gamma )$
, but any proper subgroup of G is intransitive on
$V(\Gamma )$
, but any proper subgroup of G is intransitive on
![]() $V(\Gamma )$
. In particular, if G acts regularly (transitively and every nontrivial element fixes no vertex) on
$V(\Gamma )$
. In particular, if G acts regularly (transitively and every nontrivial element fixes no vertex) on
![]() $V(\Gamma )$
, then
$V(\Gamma )$
, then
![]() $\Gamma $
is called a Cayley graph on G. A graph is said to be k-regular (or regular for short) if each of its vertices has valency k where k is a positive integer. It is obvious that every vertex-transitive graph is regular. In [Reference Mader9], it was proved that the edge connectivity of a connected vertex-transitive simple graph is equal to its valency. Thus, the
$\Gamma $
is called a Cayley graph on G. A graph is said to be k-regular (or regular for short) if each of its vertices has valency k where k is a positive integer. It is obvious that every vertex-transitive graph is regular. In [Reference Mader9], it was proved that the edge connectivity of a connected vertex-transitive simple graph is equal to its valency. Thus, the
![]() $3$
-flow conjecture for vertex-transitive graphs asserts that every vertex-transitive simple graph of valency at least four is contained in
$3$
-flow conjecture for vertex-transitive graphs asserts that every vertex-transitive simple graph of valency at least four is contained in
![]() $\mathcal {NZ}_3$
. In this direction, the
$\mathcal {NZ}_3$
. In this direction, the
![]() $3$
-flow conjecture was verified for Cayley graphs on abelian groups [Reference Potočnik, Škoviera and Škrekovski11], nilpotent groups [Reference Nánásiová and Škoviera10], dihedral groups [Reference Yang and Li15], generalised dihedral groups [Reference Li and Li7], generalised quaternion groups [Reference Li and Li7], generalised dicyclic groups [Reference Ahanjideh and Iranmanesh1], groups of order
$3$
-flow conjecture was verified for Cayley graphs on abelian groups [Reference Potočnik, Škoviera and Škrekovski11], nilpotent groups [Reference Nánásiová and Škoviera10], dihedral groups [Reference Yang and Li15], generalised dihedral groups [Reference Li and Li7], generalised quaternion groups [Reference Li and Li7], generalised dicyclic groups [Reference Ahanjideh and Iranmanesh1], groups of order
![]() $pq^2$
(p and q are two primes) (J. Zhang and Z. Zhang, ‘Nowhere-zero 3-flows in Cayley graphs of order
$pq^2$
(p and q are two primes) (J. Zhang and Z. Zhang, ‘Nowhere-zero 3-flows in Cayley graphs of order
![]() $pq^2$
’, submitted for publication) and two families of supersolvable groups [Reference Zhang and Zhou17]. Very recently, the first author and Zhou [Reference Zhang and Zhou18] proved that a graph of valency at least four is contained in
$pq^2$
’, submitted for publication) and two families of supersolvable groups [Reference Zhang and Zhou17]. Very recently, the first author and Zhou [Reference Zhang and Zhou18] proved that a graph of valency at least four is contained in
![]() $\mathcal {NZ}_3$
if its automorphism group has a vertex-transitive nilpotent subgroup.
$\mathcal {NZ}_3$
if its automorphism group has a vertex-transitive nilpotent subgroup.
In [Reference Nánásiová and Škoviera10], to study nowhere-zero
![]() $3$
-flows in Cayley graphs, Nánásiová and Škoviera introduced the method of decomposing a graph into a union of closed ladders. They proved that a Cayley graph of valency at least four on a group G is contained in
$3$
-flows in Cayley graphs, Nánásiová and Škoviera introduced the method of decomposing a graph into a union of closed ladders. They proved that a Cayley graph of valency at least four on a group G is contained in
![]() $\mathcal {NZ}_3$
if its connected set contains a central involution of G. They also proved that every Cayley graph of valency at least four on a group which is a direct product of a
$\mathcal {NZ}_3$
if its connected set contains a central involution of G. They also proved that every Cayley graph of valency at least four on a group which is a direct product of a
![]() $2$
-subgroup and a subgroup of odd order is contained in
$2$
-subgroup and a subgroup of odd order is contained in
![]() $\mathcal {NZ}_3$
. In this paper, we attempt to generalise the above two results to vertex-transitive graphs. We obtain the following two theorems.
$\mathcal {NZ}_3$
. In this paper, we attempt to generalise the above two results to vertex-transitive graphs. We obtain the following two theorems.
Theorem 1.1. Let
![]() $\Gamma $
be a vertex-transitive graph of order twice an odd number and valency at least
$\Gamma $
be a vertex-transitive graph of order twice an odd number and valency at least
![]() $4$
. Let G be a minimally vertex-transitive subgroup of the automorphism group of
$4$
. Let G be a minimally vertex-transitive subgroup of the automorphism group of
![]() $\Gamma $
. If G contains a central involution, then
$\Gamma $
. If G contains a central involution, then
![]() $\Gamma \in \mathcal {NZ}_3$
.
$\Gamma \in \mathcal {NZ}_3$
.
Theorem 1.2. Let
![]() $\Gamma $
be a graph of valency at least four. If there exists a subgroup of
$\Gamma $
be a graph of valency at least four. If there exists a subgroup of
![]() $\mathrm {Aut}(\Gamma )$
which acts transitively on
$\mathrm {Aut}(\Gamma )$
which acts transitively on
![]() $V(\Gamma )$
and is a direct product of a
$V(\Gamma )$
and is a direct product of a
![]() $2$
-subgroup and a subgroup of odd order, then
$2$
-subgroup and a subgroup of odd order, then
![]() $\Gamma \in \mathcal {NZ}_3$
.
$\Gamma \in \mathcal {NZ}_3$
.
The proof of Theorem 1.2 relies on Theorem 1.1 and the main result of [Reference Zhang and Zhou18].
2 Preparations
Let
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
be two graphs. The Cartesian product
$\Gamma _2$
be two graphs. The Cartesian product
![]() $\Gamma :=\Gamma _1\square \Gamma _2$
of
$\Gamma :=\Gamma _1\square \Gamma _2$
of
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
is the graph defined as follows:
$\Gamma _2$
is the graph defined as follows:
-
•
 $V(\Gamma )=V(\Gamma _1)\times V(\Gamma _2)$
;
$V(\Gamma )=V(\Gamma _1)\times V(\Gamma _2)$
; -
•
 $E(\Gamma )=V(\Gamma _1)\times E(\Gamma _2)\cup E(\Gamma _1)\times V(\Gamma _2)$
;
$E(\Gamma )=V(\Gamma _1)\times E(\Gamma _2)\cup E(\Gamma _1)\times V(\Gamma _2)$
; -
• each
 $(u_{1},e_2)\in V(\Gamma _1)\times E(\Gamma _2)$
is an edge with ends
$(u_{1},e_2)\in V(\Gamma _1)\times E(\Gamma _2)$
is an edge with ends
 $(u_{1},u_2)$
and
$(u_{1},u_2)$
and
 $(u_{1},v_2)$
, where
$(u_{1},v_2)$
, where
 $e_2$
is an edge in
$e_2$
is an edge in
 $E(\Gamma _2)$
with ends
$E(\Gamma _2)$
with ends
 $u_2$
and
$u_2$
and
 $v_2$
;
$v_2$
; -
• each
 $(e_{1},u_2)\in E(\Gamma _1)\times V(\Gamma _2)$
is an edge with ends
$(e_{1},u_2)\in E(\Gamma _1)\times V(\Gamma _2)$
is an edge with ends
 $(u_{1},u_2)$
and
$(u_{1},u_2)$
and
 $(v_{1},u_2)$
, where
$(v_{1},u_2)$
, where
 $e_1$
is an edge in
$e_1$
is an edge in
 $E(\Gamma _1)$
with ends
$E(\Gamma _1)$
with ends
 $u_1$
and
$u_1$
and
 $v_1$
.
$v_1$
.
Let
![]() $C_n$
be the cycle of length n which has vertex set
$C_n$
be the cycle of length n which has vertex set
![]() $\{1,\ldots ,n\}$
and edge set
$\{1,\ldots ,n\}$
and edge set
![]() $\{\{1,2\},\ldots ,\{n-1,n\},\{n,1\}\}$
. Let
$\{\{1,2\},\ldots ,\{n-1,n\},\{n,1\}\}$
. Let
![]() $K_2$
be the complete graph of order two with vertex set
$K_2$
be the complete graph of order two with vertex set
![]() $\{0,1\}$
. The graph
$\{0,1\}$
. The graph
![]() $CL_n:=C_n \Box K_2$
is called a circular ladder. The Möbius ladder
$CL_n:=C_n \Box K_2$
is called a circular ladder. The Möbius ladder
![]() $M_n$
is a graph obtained from
$M_n$
is a graph obtained from
![]() $CL_n$
by replacing the edges
$CL_n$
by replacing the edges
![]() $\{(1,0),(n,0)\}$
and
$\{(1,0),(n,0)\}$
and
![]() $\{(1,1),(n,1)\}$
with
$\{(1,1),(n,1)\}$
with
![]() $\{(1,0),(n,1)\}$
and
$\{(1,0),(n,1)\}$
and
![]() $\{(1,1),(n,0)\}$
, respectively (see Figure 1). A graph is called a closed ladder if it is a circular ladder or a Möbius ladder. In a closed ladder
$\{(1,1),(n,0)\}$
, respectively (see Figure 1). A graph is called a closed ladder if it is a circular ladder or a Möbius ladder. In a closed ladder
![]() $\Gamma $
, every edge of the form
$\Gamma $
, every edge of the form
![]() $\{(i,0),(i,1)\}$
is called a rung of
$\{(i,0),(i,1)\}$
is called a rung of
![]() $\Gamma $
. We use
$\Gamma $
. We use
![]() $R(\Gamma )$
to denote the set of all rungs of
$R(\Gamma )$
to denote the set of all rungs of
![]() $\Gamma $
.
$\Gamma $
.

Figure 1
![]() $CL_n$
and
$CL_n$
and
![]() $M_n$
.
$M_n$
.
In [Reference Nánásiová and Škoviera10], the method of decomposing a graph into a union of closed ladders was introduced to study nowhere-zero
![]() $3$
-flows in Cayley graphs. The following lemma, given in [Reference Li and Li7], is derived from the proof of [Reference Nánásiová and Škoviera10, Theorem 3.3].
$3$
-flows in Cayley graphs. The following lemma, given in [Reference Li and Li7], is derived from the proof of [Reference Nánásiová and Škoviera10, Theorem 3.3].
Lemma 2.1. Let
![]() $\Gamma :=\bigcup _{i=1}^{s}\Theta _i$
be a connected graph where every subgraph
$\Gamma :=\bigcup _{i=1}^{s}\Theta _i$
be a connected graph where every subgraph
![]() $\Theta _i$
is a closed ladder. If
$\Theta _i$
is a closed ladder. If
![]() $E(\Theta _i)\cap E(\Theta _j)=R(\Theta _i)\cap R(\Theta _j)$
for any pair of distinct
$E(\Theta _i)\cap E(\Theta _j)=R(\Theta _i)\cap R(\Theta _j)$
for any pair of distinct
![]() $i,j\in \{1,\ldots ,s\}$
and each edge of
$i,j\in \{1,\ldots ,s\}$
and each edge of
![]() $\bigcup _{i=1}^{s}R(\Theta _i)$
is contained in at least two closed ladders in
$\bigcup _{i=1}^{s}R(\Theta _i)$
is contained in at least two closed ladders in
![]() $\{\Theta _1,\ldots ,\Theta _s\}$
, then
$\{\Theta _1,\ldots ,\Theta _s\}$
, then
![]() $\Gamma $
is contained in
$\Gamma $
is contained in
![]() $\mathcal {NZ}_3$
.
$\mathcal {NZ}_3$
.
A graph is said to be even if each of its vertices is of even valency. It is well known [Reference Bondy and Murty2, Theorem 21.4] that every even graph is contained in
![]() $\mathcal {NZ}_k$
for all integers
$\mathcal {NZ}_k$
for all integers
![]() $k\geq 2$
. Let
$k\geq 2$
. Let
![]() $\Gamma $
be a graph and E a subset of
$\Gamma $
be a graph and E a subset of
![]() $E(\Gamma )$
. We use
$E(\Gamma )$
. We use
![]() $\Gamma -E$
to denote the subgraph of
$\Gamma -E$
to denote the subgraph of
![]() $\Gamma $
with vertex set
$\Gamma $
with vertex set
![]() $V(\Gamma )$
and edge set
$V(\Gamma )$
and edge set
![]() $E(\Gamma )-E$
. A subgraph
$E(\Gamma )-E$
. A subgraph
![]() $\Gamma '$
of
$\Gamma '$
of
![]() $\Gamma $
is called a parity subgraph of
$\Gamma $
is called a parity subgraph of
![]() $\Gamma $
if
$\Gamma $
if
![]() $\Gamma -E(\Gamma ')$
is even. It is also well known [Reference Bondy and Murty2, Theorem 21.5] that a cubic bipartite graph is contained in
$\Gamma -E(\Gamma ')$
is even. It is also well known [Reference Bondy and Murty2, Theorem 21.5] that a cubic bipartite graph is contained in
![]() $\mathcal {NZ}_3$
. All that leads to the following obvious lemma.
$\mathcal {NZ}_3$
. All that leads to the following obvious lemma.
Lemma 2.2. Let
![]() $\Gamma $
be a graph and
$\Gamma $
be a graph and
![]() $\Gamma '$
a parity subgraph of
$\Gamma '$
a parity subgraph of
![]() $\Gamma $
. If
$\Gamma $
. If
![]() $\Gamma '\in \mathcal {NZ}_3$
, then
$\Gamma '\in \mathcal {NZ}_3$
, then
![]() $\Gamma \in \mathcal {NZ}_3$
. In particular, if every vertex of
$\Gamma \in \mathcal {NZ}_3$
. In particular, if every vertex of
![]() $\Gamma $
is of odd valency and
$\Gamma $
is of odd valency and
![]() $\Gamma '$
is a spanning cubic bipartite subgraph of
$\Gamma '$
is a spanning cubic bipartite subgraph of
![]() $\Gamma $
, then
$\Gamma $
, then
![]() $\Gamma \in \mathcal {NZ}_3$
.
$\Gamma \in \mathcal {NZ}_3$
.
In [Reference Imrich and Škrekovski4], it was proved that the Cartesian product of two nontrivial connected bipartite graphs is contained in
![]() $\mathcal {NZ}_3$
. This result was generalised in [Reference Shu and Zhang13] by proving that the Cartesian product of every pair of graphs is contained in
$\mathcal {NZ}_3$
. This result was generalised in [Reference Shu and Zhang13] by proving that the Cartesian product of every pair of graphs is contained in
![]() $\mathcal {NZ}_3$
except when one factor has a cut edge and every block of another factor is a circuit of odd length. By using Lemma 2.1, we prove the following lemma.
$\mathcal {NZ}_3$
except when one factor has a cut edge and every block of another factor is a circuit of odd length. By using Lemma 2.1, we prove the following lemma.
Lemma 2.3. Let
![]() $\Gamma _1$
be an even graph with minimum valency at least four and
$\Gamma _1$
be an even graph with minimum valency at least four and
![]() $\Gamma _2$
be an arbitrary graph. Then
$\Gamma _2$
be an arbitrary graph. Then
![]() $\Gamma _1\square \Gamma _2$
is contained in
$\Gamma _1\square \Gamma _2$
is contained in
![]() $\mathcal {NZ}_3$
.
$\mathcal {NZ}_3$
.
Proof. Let
![]() $\Gamma _{11},\ldots ,\Gamma _{1m}$
be all the connected components of
$\Gamma _{11},\ldots ,\Gamma _{1m}$
be all the connected components of
![]() $\Gamma _{1}$
. Then
$\Gamma _{1}$
. Then
![]() $\Gamma _1\square \Gamma _2$
is an edge-disjoint union of
$\Gamma _1\square \Gamma _2$
is an edge-disjoint union of
![]() $\Gamma _{11}\square \Gamma _2,\ldots ,\Gamma _{1m}\square \Gamma _2$
. Therefore,
$\Gamma _{11}\square \Gamma _2,\ldots ,\Gamma _{1m}\square \Gamma _2$
. Therefore,
![]() $\Gamma _1\square \Gamma _2\in \mathcal {NZ}_3$
if and only if
$\Gamma _1\square \Gamma _2\in \mathcal {NZ}_3$
if and only if
![]() $\Gamma _{1i}\square \Gamma _2\in \mathcal {NZ}_3$
for every
$\Gamma _{1i}\square \Gamma _2\in \mathcal {NZ}_3$
for every
![]() $1\leq i\leq m$
. Since
$1\leq i\leq m$
. Since
![]() $\Gamma _{1}$
is an even graph with minimum valency at least four,
$\Gamma _{1}$
is an even graph with minimum valency at least four,
![]() $\Gamma _{1i}$
is an even graph with minimum valency at least four for every
$\Gamma _{1i}$
is an even graph with minimum valency at least four for every
![]() $1\leq i\leq m$
. Therefore, we assume that
$1\leq i\leq m$
. Therefore, we assume that
![]() $\Gamma _1$
is connected (for otherwise, we consider its components). By Veblen’s theorem [Reference Bondy and Murty2, Theorem 2.7], every even graph is an edge disjoint union of cycles. Therefore, there is a family
$\Gamma _1$
is connected (for otherwise, we consider its components). By Veblen’s theorem [Reference Bondy and Murty2, Theorem 2.7], every even graph is an edge disjoint union of cycles. Therefore, there is a family
![]() $\mathcal {F}_1$
of edge disjoint cycles of
$\mathcal {F}_1$
of edge disjoint cycles of
![]() $\Gamma _1$
such that
$\Gamma _1$
such that
![]() $\bigcup _{\Sigma \in \mathcal {F}_1}\Sigma =\Gamma _1$
. Let
$\bigcup _{\Sigma \in \mathcal {F}_1}\Sigma =\Gamma _1$
. Let
![]() $\mathcal {F}_2$
be the decomposition of
$\mathcal {F}_2$
be the decomposition of
![]() $\Gamma _2$
such that every member of
$\Gamma _2$
such that every member of
![]() $\mathcal {F}_2$
is either a complete graph of order two or a trivial graph with just one isolated vertex in
$\mathcal {F}_2$
is either a complete graph of order two or a trivial graph with just one isolated vertex in
![]() $\Gamma _2$
(note that every graph has such a decomposition).
$\Gamma _2$
(note that every graph has such a decomposition).
Consider an arbitrary member
![]() $\Lambda \in \mathcal {F}_2$
. If
$\Lambda \in \mathcal {F}_2$
. If
![]() $\Lambda $
is a trivial graph, then
$\Lambda $
is a trivial graph, then
![]() $\Gamma _1\square \Lambda $
is isomorphic to
$\Gamma _1\square \Lambda $
is isomorphic to
![]() $\Gamma _1$
and therefore an even graph. Since every even graph is contained in
$\Gamma _1$
and therefore an even graph. Since every even graph is contained in
![]() $\mathcal {NZ}_3$
, we have
$\mathcal {NZ}_3$
, we have
![]() $\Gamma _1\square \Lambda \in \mathcal {NZ}_3$
. Now consider the case that
$\Gamma _1\square \Lambda \in \mathcal {NZ}_3$
. Now consider the case that
![]() $\Lambda $
is the complete graph of order two. Set
$\Lambda $
is the complete graph of order two. Set
![]() $\mathcal {F}_1=\{\Sigma _{1},\ldots ,\Sigma _{s}\}$
and
$\mathcal {F}_1=\{\Sigma _{1},\ldots ,\Sigma _{s}\}$
and
![]() $\Theta _i=\Sigma _{i}\square \Lambda $
for every
$\Theta _i=\Sigma _{i}\square \Lambda $
for every
![]() $\Sigma _{i}\in \mathcal {F}_1$
. Then
$\Sigma _{i}\in \mathcal {F}_1$
. Then
![]() $\mathcal {F}:=\{\Theta _{1},\ldots ,\Theta _{s}\}$
is a family of circular ladders. It is obvious that
$\mathcal {F}:=\{\Theta _{1},\ldots ,\Theta _{s}\}$
is a family of circular ladders. It is obvious that
![]() $\Gamma _1\square \Lambda =\bigcup _{i=1}^{s}\Theta _i$
. Moreover,
$\Gamma _1\square \Lambda =\bigcup _{i=1}^{s}\Theta _i$
. Moreover,
![]() $\Gamma _1\square \Lambda $
is connected as both
$\Gamma _1\square \Lambda $
is connected as both
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Lambda $
are connected. Let
$\Lambda $
are connected. Let
![]() $1\leq i<j\leq s$
. Since
$1\leq i<j\leq s$
. Since
![]() $\Sigma _{i}$
and
$\Sigma _{i}$
and
![]() $\Sigma _{j}$
have no common edge,
$\Sigma _{j}$
have no common edge,
![]() $E(\Theta _i)\cap E(\Theta _j)=R(\Theta _i)\cap R(\Theta _j)$
. Since the minimum valency of
$E(\Theta _i)\cap E(\Theta _j)=R(\Theta _i)\cap R(\Theta _j)$
. Since the minimum valency of
![]() $\Gamma _1$
is at least four, every vertex of
$\Gamma _1$
is at least four, every vertex of
![]() $\Gamma _1$
is contained in at least two cycles in
$\Gamma _1$
is contained in at least two cycles in
![]() $\mathcal {F}_1$
. It follows that each edge of
$\mathcal {F}_1$
. It follows that each edge of
![]() $\bigcup _{i=1}^{s}R(\Theta _i)$
is contained in at least two members of
$\bigcup _{i=1}^{s}R(\Theta _i)$
is contained in at least two members of
![]() $\mathcal {F}$
. By Lemma 2.1,
$\mathcal {F}$
. By Lemma 2.1,
![]() $\Gamma _1\square \Lambda \in \mathcal {NZ}_3$
.
$\Gamma _1\square \Lambda \in \mathcal {NZ}_3$
.
Set
![]() $\mathcal {F}_2=\{\Lambda _1,\ldots ,\Lambda _{t}\}$
. By the above discussion,
$\mathcal {F}_2=\{\Lambda _1,\ldots ,\Lambda _{t}\}$
. By the above discussion,
![]() $\Gamma _1\square \Lambda _{i}\in \mathcal {NZ}_3$
for every
$\Gamma _1\square \Lambda _{i}\in \mathcal {NZ}_3$
for every
![]() $\Lambda _{i}\in \mathcal {F}_2$
. Since
$\Lambda _{i}\in \mathcal {F}_2$
. Since
![]() $\Gamma _{1}\square \Gamma _2$
is the edge disjoint union of
$\Gamma _{1}\square \Gamma _2$
is the edge disjoint union of
![]() $\Gamma _1\square \Lambda _{1},\ldots ,\Gamma _1\square \Lambda _{t}$
, we have
$\Gamma _1\square \Lambda _{1},\ldots ,\Gamma _1\square \Lambda _{t}$
, we have
![]() $\Gamma _{1}\square \Gamma _2\in \mathcal {NZ}_3$
.
$\Gamma _{1}\square \Gamma _2\in \mathcal {NZ}_3$
.
The following lemma is extracted from [Reference Zhang and Zhou18, Lemma 4.8].
Lemma 2.4. Let
![]() $\Gamma $
be a graph of valency five whose automorphism group contains a vertex-transitive subgroup G having a central involution z. Suppose that
$\Gamma $
be a graph of valency five whose automorphism group contains a vertex-transitive subgroup G having a central involution z. Suppose that
![]() $\Gamma $
has a perfect matching M of which every edge is of the form
$\Gamma $
has a perfect matching M of which every edge is of the form
![]() $\{v,z(v)\}$
,
$\{v,z(v)\}$
,
![]() $v\in V(\Gamma )$
. If
$v\in V(\Gamma )$
. If
![]() $\Gamma $
is an edge-disjoint union of M,
$\Gamma $
is an edge-disjoint union of M,
![]() $\Gamma _{1}$
and
$\Gamma _{1}$
and
![]() $\Gamma _{2}$
, where
$\Gamma _{2}$
, where
![]() $\Gamma _{1}$
and
$\Gamma _{1}$
and
![]() $\Gamma _{2}$
are both spanning
$\Gamma _{2}$
are both spanning
![]() $2$
-regular subgraphs of
$2$
-regular subgraphs of
![]() $\Gamma $
preserved by G, then
$\Gamma $
preserved by G, then
![]() $\Gamma \in \mathcal {NZ}_3$
.
$\Gamma \in \mathcal {NZ}_3$
.
3 Proof of Theorems 1.1 and 1.2
Proof of Theorem 1.1
Let
![]() $\Gamma $
be a graph of order
$\Gamma $
be a graph of order
![]() $2n$
, where n is an odd number. We assume that
$2n$
, where n is an odd number. We assume that
![]() $\Gamma $
is of odd valency as
$\Gamma $
is of odd valency as
![]() $\Gamma \in \mathcal {NZ}_3$
if
$\Gamma \in \mathcal {NZ}_3$
if
![]() $\Gamma $
is even. Let G be a minimally vertex-transitive subgroup of the automorphism group of
$\Gamma $
is even. Let G be a minimally vertex-transitive subgroup of the automorphism group of
![]() $\Gamma $
and z a central involution of G.
$\Gamma $
and z a central involution of G.
We first prove that z does not fix any vertex of
![]() $\Gamma $
. Otherwise, if
$\Gamma $
. Otherwise, if
![]() $z(v)=v$
for some
$z(v)=v$
for some
![]() $v\in V(\Gamma )$
, then
$v\in V(\Gamma )$
, then
![]() $z(g(v))=zg(v)=gz(v)=g(v)$
for all
$z(g(v))=zg(v)=gz(v)=g(v)$
for all
![]() $g\in G$
. Since G acts transitively on
$g\in G$
. Since G acts transitively on
![]() $V(\Gamma )$
, it follows that z fixes all vertices of
$V(\Gamma )$
, it follows that z fixes all vertices of
![]() $\Gamma $
. This contradicts the fact that z is not the identity automorphism of
$\Gamma $
. This contradicts the fact that z is not the identity automorphism of
![]() $\Gamma $
.
$\Gamma $
.
Since z does not fix any vertex of
![]() $\Gamma $
and
$\Gamma $
and
![]() $\vert V(\Gamma )\vert =2n$
, we conclude that z is a permutation factorising into n disjoint transpositions. Therefore, z is an odd permutation on
$\vert V(\Gamma )\vert =2n$
, we conclude that z is a permutation factorising into n disjoint transpositions. Therefore, z is an odd permutation on
![]() $V(\Gamma )$
as n is an odd number. Let H be a subset of G consisting of all even permutations of G. Then
$V(\Gamma )$
as n is an odd number. Let H be a subset of G consisting of all even permutations of G. Then
![]() $z\notin H$
and H is a normal subgroup of G of index
$z\notin H$
and H is a normal subgroup of G of index
![]() $2$
. Since both
$2$
. Since both
![]() $\langle z\rangle $
and H are normal in G and
$\langle z\rangle $
and H are normal in G and
![]() $\langle z\rangle \cap H={1}$
, we get
$\langle z\rangle \cap H={1}$
, we get
![]() $G=\langle z\rangle \times H$
.
$G=\langle z\rangle \times H$
.
Since G is minimally transitive on
![]() $V(\Gamma )$
, we deduce that H is intransitive on
$V(\Gamma )$
, we deduce that H is intransitive on
![]() $V(\Gamma )$
. Let u be an arbitrary vertex of
$V(\Gamma )$
. Let u be an arbitrary vertex of
![]() $\Gamma $
. Then
$\Gamma $
. Then
![]() $\vert G:G_u\vert =|V(\Gamma )|=2n$
and
$\vert G:G_u\vert =|V(\Gamma )|=2n$
and
![]() $|H:H_u|$
is a nontrivial divisor of
$|H:H_u|$
is a nontrivial divisor of
![]() $2n$
. Since
$2n$
. Since
![]() $|H:H_u|=(1/2)|G:H_u|\geq (1/2)|G:G_u|=n$
, it follows that
$|H:H_u|=(1/2)|G:H_u|\geq (1/2)|G:G_u|=n$
, it follows that
![]() $|H:H_u|=n$
. Therefore, the action of H on
$|H:H_u|=n$
. Therefore, the action of H on
![]() $V(\Gamma )$
has two orbits. Let U be the orbit of u under the action of H on
$V(\Gamma )$
has two orbits. Let U be the orbit of u under the action of H on
![]() $V(\Gamma )$
. Then
$V(\Gamma )$
. Then
![]() $z(U)$
is the orbit of
$z(U)$
is the orbit of
![]() $z(u)$
under the action of H on
$z(u)$
under the action of H on
![]() $V(\Gamma )$
as
$V(\Gamma )$
as
![]() $zh=hz$
for all
$zh=hz$
for all
![]() $h\in H$
. Since
$h\in H$
. Since
![]() $G=\langle z\rangle \times H$
acts transitively on
$G=\langle z\rangle \times H$
acts transitively on
![]() $V(\Gamma )$
, we have
$V(\Gamma )$
, we have
![]() $U\cap z(U)=\emptyset $
and
$U\cap z(U)=\emptyset $
and
![]() $U\cup z(U)=V(\Gamma )$
. Let
$U\cup z(U)=V(\Gamma )$
. Let
![]() $\Gamma [U]$
and
$\Gamma [U]$
and
![]() $\Gamma [z(U)]$
be the subgraphs of
$\Gamma [z(U)]$
be the subgraphs of
![]() $\Gamma $
induced by U and
$\Gamma $
induced by U and
![]() $z(U)$
, respectively. Then
$z(U)$
, respectively. Then
![]() $\Gamma [U]$
and
$\Gamma [U]$
and
![]() $\Gamma [z(U)]$
are isomorphic and have no common edges. Since U is the orbit of u under the action of H and H preserves
$\Gamma [z(U)]$
are isomorphic and have no common edges. Since U is the orbit of u under the action of H and H preserves
![]() $\Gamma [U]$
, we conclude that
$\Gamma [U]$
, we conclude that
![]() $\Gamma [U]$
is a regular graph. Assume that
$\Gamma [U]$
is a regular graph. Assume that
![]() $\Gamma [U]$
is of valency s. Since
$\Gamma [U]$
is of valency s. Since
![]() $\Gamma [U]$
and
$\Gamma [U]$
and
![]() $\Gamma [z(U)]$
are isomorphic and have no common edges,
$\Gamma [z(U)]$
are isomorphic and have no common edges,
![]() $\Gamma [U]\cup \Gamma [z(U)]$
is an s-regular graph. Let
$\Gamma [U]\cup \Gamma [z(U)]$
is an s-regular graph. Let
![]() $\Gamma '$
be the graph obtained from
$\Gamma '$
be the graph obtained from
![]() $\Gamma $
by removing all the edges of
$\Gamma $
by removing all the edges of
![]() $\Gamma [U]\cup \Gamma [z(U)]$
. Then
$\Gamma [U]\cup \Gamma [z(U)]$
. Then
![]() $\Gamma '$
is a regular bipartite graph with bipartition
$\Gamma '$
is a regular bipartite graph with bipartition
![]() $\{U,z(U)\}$
. Assume that
$\{U,z(U)\}$
. Assume that
![]() $\Gamma '$
is of valency t. Then
$\Gamma '$
is of valency t. Then
![]() $\Gamma $
is of valency
$\Gamma $
is of valency
![]() $s+t$
. In particular,
$s+t$
. In particular,
![]() $s+t$
is an odd number at least five. Since
$s+t$
is an odd number at least five. Since
![]() $\Gamma [U]$
is an s-regular graph of odd order, s is an even number and therefore t is an odd number.
$\Gamma [U]$
is an s-regular graph of odd order, s is an even number and therefore t is an odd number.
By [Reference Bondy and Murty2, Corollary 16.5], every regular bipartite graph has a perfect matching. Therefore,
![]() $\Gamma '$
has a perfect matching. If
$\Gamma '$
has a perfect matching. If
![]() $t\geq 3$
, then, by removing a number of perfect matchings, one can get a spanning cubic bipartite subgraph
$t\geq 3$
, then, by removing a number of perfect matchings, one can get a spanning cubic bipartite subgraph
![]() $\Gamma ''$
of
$\Gamma ''$
of
![]() $\Gamma '$
which is also a spanning cubic bipartite subgraph of
$\Gamma '$
which is also a spanning cubic bipartite subgraph of
![]() $\Gamma $
. By Lemma 2.2,
$\Gamma $
. By Lemma 2.2,
![]() $\Gamma \in \mathcal {NZ}_3$
.
$\Gamma \in \mathcal {NZ}_3$
.
From now on, we assume that
![]() $t=1$
. Then there exists a permutation
$t=1$
. Then there exists a permutation
![]() $\mu $
on U such that
$\mu $
on U such that
![]() $z\mu (v)$
is the unique vertex in
$z\mu (v)$
is the unique vertex in
![]() $z(U)$
adjacent to v for all
$z(U)$
adjacent to v for all
![]() $v\in U$
. Since
$v\in U$
. Since
![]() $z\in \mathrm {Aut}(\Gamma )$
, we see that
$z\in \mathrm {Aut}(\Gamma )$
, we see that
![]() $z(v)$
is the unique vertex in
$z(v)$
is the unique vertex in
![]() $z(U)$
adjacent to
$z(U)$
adjacent to
![]() $\mu (v)$
. Therefore,
$\mu (v)$
. Therefore,
![]() $\mu ^2(v)=v$
. It follows that
$\mu ^2(v)=v$
. It follows that
![]() $\mu $
fixes at least one vertex in U as the number n of vertices of U is odd. Without loss of generality, assume
$\mu $
fixes at least one vertex in U as the number n of vertices of U is odd. Without loss of generality, assume
![]() $\mu (u)=u$
. Then u is adjacent to
$\mu (u)=u$
. Then u is adjacent to
![]() $z(u)$
. Since H is transitive on U and
$z(u)$
. Since H is transitive on U and
![]() $zh=hz$
for all
$zh=hz$
for all
![]() $h\in H$
, we conclude that v is adjacent to
$h\in H$
, we conclude that v is adjacent to
![]() $z(v)$
for all
$z(v)$
for all
![]() $v\in U$
. In other words,
$v\in U$
. In other words,
![]() $\mu $
is the identity permutation. Note that
$\mu $
is the identity permutation. Note that
![]() $\Gamma [U]$
is an even regular graph of valency at least four. Let
$\Gamma [U]$
is an even regular graph of valency at least four. Let
![]() $\Sigma =\Gamma [U]\square K_2$
be the Cartesian product of
$\Sigma =\Gamma [U]\square K_2$
be the Cartesian product of
![]() $\Gamma [U]$
and
$\Gamma [U]$
and
![]() $K_2$
, where
$K_2$
, where
![]() $K_2$
is the complete graph of order two with vertex set
$K_2$
is the complete graph of order two with vertex set
![]() $\{0,1\}$
. By Lemma 2.3,
$\{0,1\}$
. By Lemma 2.3,
![]() $\Sigma \in \mathcal {NZ}_3$
. Define a mapping
$\Sigma \in \mathcal {NZ}_3$
. Define a mapping
![]() $\psi $
from
$\psi $
from
![]() $V(\Gamma )$
to
$V(\Gamma )$
to
![]() $V(\Sigma )$
as follows:
$V(\Sigma )$
as follows:
 $$ \begin{align*} \psi(v)= \begin{cases} (v,0) & \mbox{if}~v\in U, \\ (z(v),1) & \mbox{if}~v\in z(U). \\ \end{cases} \end{align*} $$
$$ \begin{align*} \psi(v)= \begin{cases} (v,0) & \mbox{if}~v\in U, \\ (z(v),1) & \mbox{if}~v\in z(U). \\ \end{cases} \end{align*} $$
It is straightforward to check that
![]() $\psi $
is a well-defined bijection from
$\psi $
is a well-defined bijection from
![]() $V(\Gamma )$
to
$V(\Gamma )$
to
![]() $V(\Sigma )$
. We further prove that
$V(\Sigma )$
. We further prove that
![]() $\psi $
is an isomorphism.
$\psi $
is an isomorphism.
Let
![]() $v_1$
and
$v_1$
and
![]() $v_2$
be two vertices of
$v_2$
be two vertices of
![]() $\Gamma $
. Since
$\Gamma $
. Since
![]() $\Gamma [U]$
is an induced subgraph of
$\Gamma [U]$
is an induced subgraph of
![]() $\Gamma $
, every edge in
$\Gamma $
, every edge in
![]() $\Gamma $
joining two vertices in U is contained in
$\Gamma $
joining two vertices in U is contained in
![]() $\Gamma [U]$
. Therefore, if
$\Gamma [U]$
. Therefore, if
![]() $v_1,v_2\in U$
, then by the definition of a Cartesian product, the number of edges in
$v_1,v_2\in U$
, then by the definition of a Cartesian product, the number of edges in
![]() $\Gamma $
joining
$\Gamma $
joining
![]() $v_1$
and
$v_1$
and
![]() $v_2$
is equal to the number of edges in
$v_2$
is equal to the number of edges in
![]() $\Sigma $
joining
$\Sigma $
joining
![]() $(v_1,0)$
and
$(v_1,0)$
and
![]() $(v_2,0)$
. If
$(v_2,0)$
. If
![]() $v_1,v_2\in z(U)$
, then
$v_1,v_2\in z(U)$
, then
![]() $z(v_1),z(v_2)\in U$
. Since
$z(v_1),z(v_2)\in U$
. Since
![]() $z\in \mathrm {Aut}(\Gamma )$
, the number of edges in
$z\in \mathrm {Aut}(\Gamma )$
, the number of edges in
![]() $\Gamma $
joining
$\Gamma $
joining
![]() $v_1$
and
$v_1$
and
![]() $v_2$
is equal to the number joining
$v_2$
is equal to the number joining
![]() $z(v_1)$
and
$z(v_1)$
and
![]() $z(v_2)$
. It follows that the number of edges in
$z(v_2)$
. It follows that the number of edges in
![]() $\Gamma $
joining
$\Gamma $
joining
![]() $v_1$
and
$v_1$
and
![]() $v_2$
is equal to the number of edges in
$v_2$
is equal to the number of edges in
![]() $\Sigma $
joining
$\Sigma $
joining
![]() $(z(v_1),1)$
and
$(z(v_1),1)$
and
![]() $(z(v_2),1)$
. Now consider the case that one of the two vertices
$(z(v_2),1)$
. Now consider the case that one of the two vertices
![]() $v_1$
and
$v_1$
and
![]() $v_2$
is contained in U and another is contained in
$v_2$
is contained in U and another is contained in
![]() $z(U)$
. Without loss of generality, assume that
$z(U)$
. Without loss of generality, assume that
![]() $v_1\in U$
and
$v_1\in U$
and
![]() $v_2\in z(U)$
. Then
$v_2\in z(U)$
. Then
 $$ \begin{align*} v_1~\mbox{is adjacent to}~v_2~\mbox{in}~\Gamma & \Longleftrightarrow v_2=z(v_1)\\ & \Longleftrightarrow v_1=z(v_2)\\ & \Longleftrightarrow (v_1,0)~\mbox{is adjacent to}~(z(v_2),1)~\mbox{in}~\Sigma. \end{align*} $$
$$ \begin{align*} v_1~\mbox{is adjacent to}~v_2~\mbox{in}~\Gamma & \Longleftrightarrow v_2=z(v_1)\\ & \Longleftrightarrow v_1=z(v_2)\\ & \Longleftrightarrow (v_1,0)~\mbox{is adjacent to}~(z(v_2),1)~\mbox{in}~\Sigma. \end{align*} $$
The discussion above implies that the number of edges joining
![]() $v_1$
and
$v_1$
and
![]() $v_2$
in
$v_2$
in
![]() $\Gamma $
is equal to the number of edges in
$\Gamma $
is equal to the number of edges in
![]() $\Sigma $
joining
$\Sigma $
joining
![]() $\psi (v_1)$
and
$\psi (v_1)$
and
![]() $\psi (v_2)$
. Therefore,
$\psi (v_2)$
. Therefore,
![]() $\psi $
is an isomorphism from
$\psi $
is an isomorphism from
![]() $\Gamma $
to
$\Gamma $
to
![]() $\Sigma $
. Since
$\Sigma $
. Since
![]() $\Sigma \in \mathcal {NZ}_3$
, we have
$\Sigma \in \mathcal {NZ}_3$
, we have
![]() $\Gamma \in \mathcal {NZ}_3$
.
$\Gamma \in \mathcal {NZ}_3$
.
Proof of Theorem 1.2
Let
![]() $\Gamma $
be a graph of valency at least four and G a subgroup of
$\Gamma $
be a graph of valency at least four and G a subgroup of
![]() $\mathrm {Aut}(\Gamma )$
acting transitively on
$\mathrm {Aut}(\Gamma )$
acting transitively on
![]() $V(\Gamma )$
and being a direct product of a
$V(\Gamma )$
and being a direct product of a
![]() $2$
-subgroup Q and a subgroup H of odd order. We assume that
$2$
-subgroup Q and a subgroup H of odd order. We assume that
![]() $\Gamma $
is of odd valency as
$\Gamma $
is of odd valency as
![]() $\Gamma \in \mathcal {NZ}_3$
whenever the valency of
$\Gamma \in \mathcal {NZ}_3$
whenever the valency of
![]() $\Gamma $
is even. Then
$\Gamma $
is even. Then
![]() $\Gamma $
is of even order and it follows that Q is nontrivial.
$\Gamma $
is of even order and it follows that Q is nontrivial.
We proceed by induction on the order
![]() $\vert Q\vert $
of Q. By Theorem 1.1,
$\vert Q\vert $
of Q. By Theorem 1.1,
![]() $\Gamma \in \mathcal {NZ}_3$
if
$\Gamma \in \mathcal {NZ}_3$
if
![]() $\vert Q\vert =2$
. Now assume
$\vert Q\vert =2$
. Now assume
![]() $\vert Q\vert>2$
. Suppose that the theorem is true for all graphs whose automorphism groups have a vertex-transitive subgroup which is a direct product of a
$\vert Q\vert>2$
. Suppose that the theorem is true for all graphs whose automorphism groups have a vertex-transitive subgroup which is a direct product of a
![]() $2$
-subgroup of order less that
$2$
-subgroup of order less that
![]() $\vert Q\vert $
and a subgroup of odd order.
$\vert Q\vert $
and a subgroup of odd order.
It is well known [Reference Rotman12, Theorem 4.2] that every
![]() $2$
-group has a nontrivial centre. Let z be an involution contained in the centre of Q. Since
$2$
-group has a nontrivial centre. Let z be an involution contained in the centre of Q. Since
![]() $G=Q\times H$
, we see that z is also contained in the centre of G. Therefore,
$G=Q\times H$
, we see that z is also contained in the centre of G. Therefore,
![]() $\langle z\rangle $
is a normal subgroup of G and z does not fix any vertex of
$\langle z\rangle $
is a normal subgroup of G and z does not fix any vertex of
![]() $\Gamma $
. Set
$\Gamma $
. Set
![]() $\tilde {v}:=\{v,z(v)\}$
for every
$\tilde {v}:=\{v,z(v)\}$
for every
![]() $v\in V(\Gamma )$
and
$v\in V(\Gamma )$
and
![]() $\tilde {V}:=\{\tilde {v}\mid v\in V(\Gamma )\}$
. Let
$\tilde {V}:=\{\tilde {v}\mid v\in V(\Gamma )\}$
. Let
![]() $\Gamma [\tilde {v}]$
be the subgraph of
$\Gamma [\tilde {v}]$
be the subgraph of
![]() $\Gamma $
induced by
$\Gamma $
induced by
![]() $\tilde {v}$
. Since G acts transitively on
$\tilde {v}$
. Since G acts transitively on
![]() $V(\Gamma )$
, it follows that
$V(\Gamma )$
, it follows that
![]() $\Gamma [\tilde {u}]$
and
$\Gamma [\tilde {u}]$
and
![]() $\Gamma [\tilde {v}]$
are isomorphic for every pair of vertices
$\Gamma [\tilde {v}]$
are isomorphic for every pair of vertices
![]() $u,v\in V(\Gamma )$
. Set
$u,v\in V(\Gamma )$
. Set
![]() $\Gamma '=\bigcup _{\tilde {v}\in \tilde {V}}\Gamma [\tilde {v}]$
and
$\Gamma '=\bigcup _{\tilde {v}\in \tilde {V}}\Gamma [\tilde {v}]$
and
![]() $\Gamma ''=\Gamma -E(\Gamma ')$
. Then both
$\Gamma ''=\Gamma -E(\Gamma ')$
. Then both
![]() $\Gamma '$
and
$\Gamma '$
and
![]() $\Gamma ''$
are spanning subgraphs of
$\Gamma ''$
are spanning subgraphs of
![]() $\Gamma $
preserved by G. Therefore,
$\Gamma $
preserved by G. Therefore,
![]() $\Gamma '$
and
$\Gamma '$
and
![]() $\Gamma ''$
are both vertex-transitive. Assume that the valency of
$\Gamma ''$
are both vertex-transitive. Assume that the valency of
![]() $\Gamma '$
and
$\Gamma '$
and
![]() $\Gamma ''$
are s and t, respectively. Then
$\Gamma ''$
are s and t, respectively. Then
![]() $\Gamma $
is of valency
$\Gamma $
is of valency
![]() $s+t$
. In particular,
$s+t$
. In particular,
![]() $s+t$
is odd.
$s+t$
is odd.
Case 1:
![]() $s\geq 2$
. Note that every connected component of
$s\geq 2$
. Note that every connected component of
![]() $\Gamma '$
is a graph with two vertices joined by s edges. Therefore,
$\Gamma '$
is a graph with two vertices joined by s edges. Therefore,
![]() $\Gamma '$
is a bipartite graph. If
$\Gamma '$
is a bipartite graph. If
![]() $s\geq 3$
, then
$s\geq 3$
, then
![]() $\Gamma '$
has a spanning cubic bipartite graph which is also a spanning cubic bipartite graph of
$\Gamma '$
has a spanning cubic bipartite graph which is also a spanning cubic bipartite graph of
![]() $\Gamma $
. It follows from Lemma 2.2 that
$\Gamma $
. It follows from Lemma 2.2 that
![]() $\Gamma \in \mathcal {NZ}_3$
. If
$\Gamma \in \mathcal {NZ}_3$
. If
![]() $s=2$
, then t is odd. By [Reference Godsil and Royle3, Theorem 3.51], every vertex-transitive graph of odd valency has a perfect matching. Therefore,
$s=2$
, then t is odd. By [Reference Godsil and Royle3, Theorem 3.51], every vertex-transitive graph of odd valency has a perfect matching. Therefore,
![]() $\Gamma ''$
has a perfect matching M. Since every connected component of
$\Gamma ''$
has a perfect matching M. Since every connected component of
![]() $\Gamma '$
is a graph with two vertices joined by two edges, every connected component of
$\Gamma '$
is a graph with two vertices joined by two edges, every connected component of
![]() $\Gamma '\cup M$
is a graph obtained from an even length cycle by adding a parallel edge to each edge of one of the two perfect matchings of this cycle. Therefore,
$\Gamma '\cup M$
is a graph obtained from an even length cycle by adding a parallel edge to each edge of one of the two perfect matchings of this cycle. Therefore,
![]() $\Gamma '\cup M$
is a spanning cubic bipartite graph of
$\Gamma '\cup M$
is a spanning cubic bipartite graph of
![]() $\Gamma $
and it follows from Lemma 2.2 that
$\Gamma $
and it follows from Lemma 2.2 that
![]() $\Gamma \in \mathcal {NZ}_3$
.
$\Gamma \in \mathcal {NZ}_3$
.
Case 2:
![]() $s=0$
. In this case,
$s=0$
. In this case,
![]() $\tilde {v}$
is an independent set of
$\tilde {v}$
is an independent set of
![]() $\Gamma $
for every
$\Gamma $
for every
![]() $\tilde {v}\in \tilde {V}$
. Use
$\tilde {v}\in \tilde {V}$
. Use
![]() $\tilde {\Gamma }$
to denote the graph with vertex set
$\tilde {\Gamma }$
to denote the graph with vertex set
![]() $\tilde {V}$
and every pair of vertices
$\tilde {V}$
and every pair of vertices
![]() $\tilde {u}$
and
$\tilde {u}$
and
![]() $\tilde {v}$
being joined by
$\tilde {v}$
being joined by
![]() $\ell $
edges if and only if the subgraph
$\ell $
edges if and only if the subgraph
![]() $\Gamma [\tilde {u}\cup \tilde {v}]$
of
$\Gamma [\tilde {u}\cup \tilde {v}]$
of
![]() $\Gamma $
induced by
$\Gamma $
induced by
![]() $\tilde {u}\cup \tilde {v}$
is
$\tilde {u}\cup \tilde {v}$
is
![]() $\ell $
-regular (we treat an independent set as a
$\ell $
-regular (we treat an independent set as a
![]() $0$
-regular graph). Then
$0$
-regular graph). Then
![]() $\tilde {\Gamma }$
is a graph of odd valency at least five and
$\tilde {\Gamma }$
is a graph of odd valency at least five and
![]() $\Gamma $
is a cover (see [Reference Potočnik, Škoviera and Škrekovski11]) of
$\Gamma $
is a cover (see [Reference Potočnik, Škoviera and Škrekovski11]) of
![]() $\tilde {\Gamma }$
. Furthermore,
$\tilde {\Gamma }$
. Furthermore,
![]() $\mathrm {Aut}(\tilde {\Gamma })$
contains
$\mathrm {Aut}(\tilde {\Gamma })$
contains
![]() $G/\langle z\rangle $
as a subgroup acting transitively on the vertex set
$G/\langle z\rangle $
as a subgroup acting transitively on the vertex set
![]() $\tilde {V}$
of
$\tilde {V}$
of
![]() $\tilde {\Gamma }$
. Note that
$\tilde {\Gamma }$
. Note that
![]() $G/\langle z\rangle =Q/\langle z\rangle \times H\langle z\rangle /\langle z\rangle $
and
$G/\langle z\rangle =Q/\langle z\rangle \times H\langle z\rangle /\langle z\rangle $
and
![]() $Q/\langle z\rangle $
is of order less than Q. By the induction hypothesis,
$Q/\langle z\rangle $
is of order less than Q. By the induction hypothesis,
![]() $\tilde {\Gamma }\in \mathcal {NZ}_3$
. It is known [Reference Potočnik, Škoviera and Škrekovski11, Proposition 2.3] that if a graph admits a nowhere-zero
$\tilde {\Gamma }\in \mathcal {NZ}_3$
. It is known [Reference Potočnik, Škoviera and Škrekovski11, Proposition 2.3] that if a graph admits a nowhere-zero
![]() $3$
-flow, then each of its covers does too. Therefore,
$3$
-flow, then each of its covers does too. Therefore,
![]() $\Gamma \in \mathcal {NZ}_3$
.
$\Gamma \in \mathcal {NZ}_3$
.
Case 3:
![]() $s=1$
. In this case,
$s=1$
. In this case,
![]() $\Gamma '$
is a perfect matching of
$\Gamma '$
is a perfect matching of
![]() $\Gamma $
. Since every group of odd order is solvable, H is a solvable group. Let
$\Gamma $
. Since every group of odd order is solvable, H is a solvable group. Let
![]() $H'$
be the derived subgroup of H. Then
$H'$
be the derived subgroup of H. Then
![]() $H'$
is a proper subgroup of H and normal in G. If H is abelian, then G (
$H'$
is a proper subgroup of H and normal in G. If H is abelian, then G (
![]() $=Q\times H$
) is nilpotent. By [Reference Zhang and Zhou18, Theorem 1.1],
$=Q\times H$
) is nilpotent. By [Reference Zhang and Zhou18, Theorem 1.1],
![]() $\Gamma \in \mathcal {NZ}_3$
. Now assume that H is nonabelian. Then
$\Gamma \in \mathcal {NZ}_3$
. Now assume that H is nonabelian. Then
![]() $H'$
is nontrivial and
$H'$
is nontrivial and
![]() $G/H'=QH'/H'\times H/H'$
is nilpotent. Use
$G/H'=QH'/H'\times H/H'$
is nilpotent. Use
![]() $\bar {v}$
to denote the orbit of v under the action of
$\bar {v}$
to denote the orbit of v under the action of
![]() $H'$
and
$H'$
and
![]() $\Gamma [\bar {v}]$
the subgraph of
$\Gamma [\bar {v}]$
the subgraph of
![]() $\Gamma $
induced by
$\Gamma $
induced by
![]() $\bar {v}$
. Then
$\bar {v}$
. Then
![]() $\Gamma [\bar {v}]$
is a vertex-transitive graph of odd order as
$\Gamma [\bar {v}]$
is a vertex-transitive graph of odd order as
![]() $H'$
acts transitively on
$H'$
acts transitively on
![]() $\bar {v}$
. Therefore,
$\bar {v}$
. Therefore,
![]() $\Gamma [\bar {v}]$
is a regular graph of even valency, say r. Set
$\Gamma [\bar {v}]$
is a regular graph of even valency, say r. Set
![]() $\Sigma =\bigcup _{v\in V(\Gamma )}\Gamma [\bar {v}]$
. Then
$\Sigma =\bigcup _{v\in V(\Gamma )}\Gamma [\bar {v}]$
. Then
![]() $\Gamma '\cup \Sigma $
is of valency
$\Gamma '\cup \Sigma $
is of valency
![]() $r+1$
and the automorphism group of every connected component of
$r+1$
and the automorphism group of every connected component of
![]() $\Gamma '\cup \Sigma $
contains
$\Gamma '\cup \Sigma $
contains
![]() $\langle z\rangle \times H'$
as a subgroup acting transitively on the vertex set. If
$\langle z\rangle \times H'$
as a subgroup acting transitively on the vertex set. If
![]() $r\geq 4$
, then by Theorem 1.1, every connected component of
$r\geq 4$
, then by Theorem 1.1, every connected component of
![]() $\Gamma '\cup \Sigma $
is contained in
$\Gamma '\cup \Sigma $
is contained in
![]() $\mathcal {NZ}_3$
and therefore,
$\mathcal {NZ}_3$
and therefore,
![]() $\Gamma '\cup \Sigma \in \mathcal {NZ}_3$
. Since
$\Gamma '\cup \Sigma \in \mathcal {NZ}_3$
. Since
![]() $\Gamma '\cup \Sigma $
is a parity subgraph of
$\Gamma '\cup \Sigma $
is a parity subgraph of
![]() $\Gamma $
, it follows from Lemma 2.2 that
$\Gamma $
, it follows from Lemma 2.2 that
![]() $\Gamma \in \mathcal {NZ}_3$
. If
$\Gamma \in \mathcal {NZ}_3$
. If
![]() $t-r\geq 4$
, then the subgraph
$t-r\geq 4$
, then the subgraph
![]() $\Gamma ^{*}:=\Gamma -E(\Sigma )$
of
$\Gamma ^{*}:=\Gamma -E(\Sigma )$
of
![]() $\Gamma $
is of odd valency at least five. Let
$\Gamma $
is of odd valency at least five. Let
![]() $\overline {\Gamma ^{*}}$
be the graph with vertex set
$\overline {\Gamma ^{*}}$
be the graph with vertex set
![]() $\{\bar {v}\mid v\in V\}$
and every pair of vertices
$\{\bar {v}\mid v\in V\}$
and every pair of vertices
![]() $\bar {u}$
and
$\bar {u}$
and
![]() $\bar {v}$
being joined by
$\bar {v}$
being joined by
![]() $\ell $
-edges if and only if
$\ell $
-edges if and only if
![]() $\bar {u}\cup \bar {v}$
induces a
$\bar {u}\cup \bar {v}$
induces a
![]() $\ell $
-regular subgraph of
$\ell $
-regular subgraph of
![]() $\Gamma ^{*}$
. Then
$\Gamma ^{*}$
. Then
![]() $\Gamma ^{*}$
is a cover of
$\Gamma ^{*}$
is a cover of
![]() $\overline {\Gamma ^{*}}$
. Note that
$\overline {\Gamma ^{*}}$
. Note that
![]() $\mathrm {Aut}(\overline {\Gamma ^{*}})$
contains
$\mathrm {Aut}(\overline {\Gamma ^{*}})$
contains
![]() $QH'/H'\times H/H'$
as a subgroup acting transitively on the vertex set. Since
$QH'/H'\times H/H'$
as a subgroup acting transitively on the vertex set. Since
![]() $QH'/H'\times H/H'$
is nilpotent, it follows from [Reference Zhang and Zhou18] that
$QH'/H'\times H/H'$
is nilpotent, it follows from [Reference Zhang and Zhou18] that
![]() $\overline {\Gamma ^{*}}\in \mathcal {NZ}_3$
. By [Reference Potočnik, Škoviera and Škrekovski11, Proposition 2.3],
$\overline {\Gamma ^{*}}\in \mathcal {NZ}_3$
. By [Reference Potočnik, Škoviera and Škrekovski11, Proposition 2.3],
![]() $\Gamma ^{*}\in \mathcal {NZ}_3$
. Since
$\Gamma ^{*}\in \mathcal {NZ}_3$
. Since
![]() $\Gamma ^{*}$
is a parity subgraph of
$\Gamma ^{*}$
is a parity subgraph of
![]() $\Gamma $
, by Lemma 2.2, we have
$\Gamma $
, by Lemma 2.2, we have
![]() $\Gamma \in \mathcal {NZ}_3$
. Now we assume that both r and
$\Gamma \in \mathcal {NZ}_3$
. Now we assume that both r and
![]() $t-r$
are less than four. Since
$t-r$
are less than four. Since
![]() $t\geq 4$
and r is even, we have
$t\geq 4$
and r is even, we have
![]() $r=t-r=2$
. Then
$r=t-r=2$
. Then
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Gamma ''-E(\Sigma )$
are both spanning
$\Gamma ''-E(\Sigma )$
are both spanning
![]() $2$
-regular subgraphs of
$2$
-regular subgraphs of
![]() $\Gamma $
preserved by G. Note that
$\Gamma $
preserved by G. Note that
![]() $\Gamma '$
is a perfect matching of which every edge is of the form
$\Gamma '$
is a perfect matching of which every edge is of the form
![]() $\{v,z(v)\}$
. Note also that
$\{v,z(v)\}$
. Note also that
![]() $\Gamma $
is an edge-disjoint union of
$\Gamma $
is an edge-disjoint union of
![]() $\Gamma '$
,
$\Gamma '$
,
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Gamma ''-E(\Sigma )$
. By Lemma 2.4,
$\Gamma ''-E(\Sigma )$
. By Lemma 2.4,
![]() $\Gamma \in \mathcal {NZ}_3$
.
$\Gamma \in \mathcal {NZ}_3$
.