Let  $a$,
$a$, 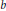 $b$, and
$b$, and  $c$ be primitive Pythagorean numbers such that
$c$ be primitive Pythagorean numbers such that 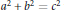 ${{a}^{2}}\,+\,{{b}^{2}}\,=\,{{c}^{2}}$ with
${{a}^{2}}\,+\,{{b}^{2}}\,=\,{{c}^{2}}$ with 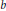 $b$ even. In this paper, we show that if
$b$ even. In this paper, we show that if  ${{b}_{0}}\,\equiv \,\in \,\,\,\left( \bmod \,a \right)$ with
${{b}_{0}}\,\equiv \,\in \,\,\,\left( \bmod \,a \right)$ with 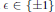 $\text{ }\!\!\varepsilon\!\!\text{ }\,\in \,\left\{ \pm 1 \right\}$ for certain positive divisors
$\text{ }\!\!\varepsilon\!\!\text{ }\,\in \,\left\{ \pm 1 \right\}$ for certain positive divisors 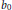 ${{b}_{0}}$ of
${{b}_{0}}$ of 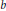 $b$, then the Diophantine equation
$b$, then the Diophantine equation 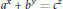 ${{a}^{x}}\,+\,{{b}^{y}}\,=\,{{c}^{z}}$ has only the positive solution
${{a}^{x}}\,+\,{{b}^{y}}\,=\,{{c}^{z}}$ has only the positive solution 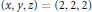 $\left( x,\,y,\,z \right)\,=\,\left( 2,\,2,\,2 \right)$.
$\left( x,\,y,\,z \right)\,=\,\left( 2,\,2,\,2 \right)$.
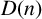 $D(n)$
$D(n)$
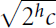 $\sqrt{{{2}^{h}}c}$
$\sqrt{{{2}^{h}}c}$