We solve several multi-parameter families of binomial Thue equations of arbitrary degree; for example, we solve the equation
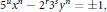 $${{5}^{u}}{{x}^{n}}-{{2}^{r}}{{3}^{5}}{{y}^{n}}=\pm 1,$$
$${{5}^{u}}{{x}^{n}}-{{2}^{r}}{{3}^{5}}{{y}^{n}}=\pm 1,$$
in non-zero integers 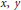 $x,y$ and positive integers
$x,y$ and positive integers 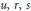 $u,r,s$ and
$u,r,s$ and 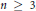 $n\ge 3$. Our approach uses several Frey curves simultaneously, Galois representations and level-lowering, new lower bounds for linear forms in 3 logarithms due to Mignotte and a famous theorem of Bennett on binomial Thue equations.
$n\ge 3$. Our approach uses several Frey curves simultaneously, Galois representations and level-lowering, new lower bounds for linear forms in 3 logarithms due to Mignotte and a famous theorem of Bennett on binomial Thue equations.