Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T16:10:03.037Z Has data issue: false hasContentIssue false
  • English
  • Français

A Multi-Frey Approach to Some Multi-Parameter Families of Diophantine Equations

Published online by Cambridge University Press:  20 November 2018

Yann Bugeaud ,
Maurice Mignotte  and
Samir Siksek
Yann Bugeaud
Affiliation:
Université Louis Pasteur, U.F.R. de mathématiques, 7, rue René Descartes, 67084 Strasbourg Cedex, France e-mail:, bugeaud@math.u-strasbg.fre-mail:, mignotte@math.u-strasbg.fr
Maurice Mignotte
Affiliation:
Institute of Mathematics, University of Warwick, Coventry, CV4 7AL, U.K. e-mail:, siksek@maths.warwick.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We solve several multi-parameter families of binomial Thue equations of arbitrary degree; for example, we solve the equation

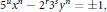$${{5}^{u}}{{x}^{n}}-{{2}^{r}}{{3}^{5}}{{y}^{n}}=\pm 1,$$

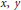in non-zero integers $x,y$ and positive integers 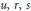$u,r,s$ and 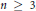$n\ge 3$. Our approach uses several Frey curves simultaneously, Galois representations and level-lowering, new lower bounds for linear forms in 3 logarithms due to Mignotte and a famous theorem of Bennett on binomial Thue equations.

Keywords

11F8011D6111D5911J8611Y50Diophantine equationsFrey curveslevel-loweringlinear forms in logarithmsThue equations
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 3 , 01 June 2008 , pp. 491 - 519
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Batut, C., Belabas, K., Bernardi, D., Cohen, H., and Olivier, M., User's guide to PARI-GP, version 2.1.1. (See also http://pari.math.u-bordeaux.fr/).Google Scholar
[2] Bennett, M. A., Rational approximation to algebraic numbers of small height: The Diophantine equation |axn − byn| = 1. J. Reine Angew.Math. 535(2001), 1–49.Google Scholar
[3] Bennett, M. A., Products of consecutive integers, Bull. London Math. Soc. 36(2004), no. 5, 683–694.Google Scholar
[4] Bennett, M. A. and Skinner, C. M., Ternary Diophantine equations via Galois representations and modular forms, Canad. J. Math. 56(2004), no. 1, 23–54.Google Scholar
[5] Bennett, M. A., V. Vatsal, and S. Yazdani, Ternary Diophantine equations of signature (p, p, 3) , Compos. Math. 140(2004), no. 6, 1399–1416.Google Scholar
[6] Bilu, Yu. and Hanrot, G., Solving Thue equations of high degree. J. Number Theory 60(1996), 373–392.Google Scholar
[7] Bosma, W., Cannon, J., and Playoust, C., The Magma algebra system I: The user language. J. Symbolic. Comput. 24(1997), no. 3-4, 235–265. (Also http://www.maths.usyd.edu.au:8000/u/magma/.)Google Scholar
[8] Breuil, C., Conrad, B., Diamond, F., and Taylor, R., On the modularity of elliptic curves over Q: wild 3-adic exercises. J. Amer.Math. Soc. 14(2001), no. 4, 843–939.Google Scholar
[9] Bugeaud, Y.,Mignotte, M., and Siksek, S., Classical and modular approaches to exponential Diophantine equations I. Fibonacci and Lucas perfect powers., Ann. of Math. 163(2006), 969–1018.Google Scholar
[10] Bugeaud, Y.,Mignotte, M., and Siksek, S., Classical and modular approaches to exponential Diophantine equations II. The Lebesgue–Nagell Equation. Compos. Math. 142(2006), no. 1, 31–62.Google Scholar
[11] Conrad, B., Diamond, F., amd Taylor, R., Modularity of certain potentially Barsotti-Tate Galois representations. J. Amer.Math. Soc. 12(1999), no. 2, 521–567.Google Scholar
[12] Cremona, J. E., Algorithms for modular elliptic curves. Second edition, Cambridge University Press, Cambridge, 1997.Google Scholar
[13] Cremona, J. E., Elliptic curve data. http://www.warwick.ac.uk/staff/J.E.Cremona/ Google Scholar
[14] Darmon, H. and Merel, L., Winding quotients and some variants of Fermat's Last theorem. J. Reine Angew.Math. 490(1997), 81–100.Google Scholar
[15] Diamond, F., On deformation rings and Hecke rings. Ann. of Math. 144(1996), no. 1, 137–166.Google Scholar
[16] Frey, G., Links between stable elliptic curves and certain Diophantine equations. Ann. Univ. Sarav. Ser. Math. 1(1986), no. 1.Google Scholar
[17] Frey, G., Links between solutions of A − B = C and elliptic curves. In: Number Theory, Lecture Notes in Math. 1380, Springer, New York, 1989, pp. 31–62.Google Scholar
[18] Heuberger, C., On general families of parametrized Thue equations. In: Algebraic Number Theory and Diophantine Analysis, de Gruyter, Berlin, 2000, pp. 215–238.Google Scholar
[19] Kraus, A., Majorations effectives pour l’équation de Fermat généralisée, Canad. J. Math. 49(1997), no. 6, 1139–1161.Google Scholar
[20] Kraus, A., Sur l’équation a3 + b3 = cp. Experiment. Math. 7(1998), no. 1, 1–13.Google Scholar
[21] Kraus, A. and J. Oesterlé, Sur une question de B. Mazur. Math. Ann. 293(1992), no. 2, 259–275.Google Scholar
[22] Matveev, E. M., An explicit lower bound for a homogeneous rational linear form in logarithms of algebraic numbers. II. Izv. Ross. Akad. Nauk Ser.Mat. 64(2000), 125–180; English transl. in Izv. Math. 64(2000), 1217–1269.Google Scholar
[23] Mazur, B., Rational isogenies of prime degree. Invent.Math. 44(1978), no. 2, 129–162.Google Scholar
[24] Mignotte, M., A kit on linear forms in 3 logarithms, to appear.www-irma.u-strasbg.fr/˜ bugeaud/travaux/kit.pdf [25] K. Ribet, On modular representations of Gal arising from modular forms. Invent.Math. 100(1990), no. 2, 431–476.Google Scholar
[26] Mignotte, M., On the equation ap + 2α bp + cp = 0, Acta Arith. 79(1997), no. 1, 7–15.Google Scholar
[27] Serre, J.-P., Abelian l-adic representations and elliptic curves. W. A. Benjamin, New York, 1968.Google Scholar
[28] Serre, J.-P., Sur les représentations modulaires de degré 2 de Gal. Duke Math. J. 54 (1987), no. 1, 179–230.Google Scholar
[29] Siksek, S., The modular approach to Diophantine equations. In: Number Theory, Vol. II. Chapter 5. Graduate Texts in Mathematics 240, Springer-Verlag, Berlin, 2007.Google Scholar
[30] Stein, W. A., An introduction to computing modular forms using modular symbols, In: Modular Forms: A Computational Approach. Graduate Studies in Mathematics 79, American Mathematical Society, Providence, RI, 2007.Google Scholar
[31] Taylor, R. L. and A.Wiles, Ring theoretic properties of certain Hecke algebras. Ann. of Math. 141(1995), no. 3, 553–572.Google Scholar
[32] Thomas, E., Complete solutions to a family of cubic Diophantine equations. J. Number Theory 34(1990), no. 2, 235–250.Google Scholar
[33] Wiles, A., Modular elliptic curves and Fermat's last theorem. Ann. of Math. 141(1995), no. 3, 443–551.Google Scholar