It is well known that the diffeomorphism type of the Milnor fibration of a (Newton) nondegenerate polynomial function f is uniquely determined by the Newton boundary of f. In the present paper, we generalize this result to certain degenerate functions, namely we show that the diffeomorphism type of the Milnor fibration of a (possibly degenerate) polynomial function of the form $f=f^1\cdots f^{k_0}$ is uniquely determined by the Newton boundaries of $f^1,\ldots , f^{k_0}$ if $\{f^{k_1}=\cdots =f^{k_m}=0\}$ is a nondegenerate complete intersection variety for any $k_1,\ldots ,k_m\in \{1,\ldots , k_0\}$ .

The symbolic analytic spread of an ideal $I$ is defined in terms of the rate of growth of the minimal number of generators of its symbolic powers. In this article, we find upper bounds for the symbolic analytic spread under certain conditions in terms of other invariants of $I$. Our methods also work for more general systems of ideals. As applications, we provide bounds for the (local) Kodaira dimension of divisors, the arithmetic rank, and the Frobenius complexity. We also show sufficient conditions for an ideal to be a set-theoretic complete intersection.

We obtain, via the formalism of tensor actions, a complete classification of the localizing subcategories of the stable derived category of any affine scheme that has hypersurface singularities or is a complete intersection in a regular scheme; in particular, this classifies the thick subcategories of the singularity categories of such rings. The analogous result is also proved for certain locally complete intersection schemes. It is also shown that from each of these classifications one can deduce the (relative) telescope conjecture.

In this paper we examine different problems regarding complete intersection varieties of high multidegree in a smooth complex projective variety. First we prove an existence theorem for jet differential equations that generalizes a theorem of Diverio. Then we show how one can deduce hyperbolicity for generic complete intersections of high multidegree and high codimension from the known results on hypersurfaces. Finally, motivated by a conjecture of Debarre, we focus on the positivity of the cotangent bundle of complete intersections, and prove some results towards this conjecture; among other things, we prove that a generic complete intersection surface of high multidegree in a projective space of dimension at least four has an ample cotangent bundle.

We generalize Gaeta’s theorem to the family of determinantal schemes. In other words, we show that the schemes defined by minors of a fixed size of a matrix with polynomial entries belong to the same G-biliaison class of a complete intersection whenever they have maximal possible codimension, given the size of the matrix and of the minors that define them.

The classical Schubert cells on a flag manifold $G/P$ give a cell decomposition for $G/P$ whose Kronecker duals (known as Schubert classes) form an additive base for the integral cohomology $H^{\ast}(G/P)$. We present a formula that expresses Steenrod mod-$p$ operations on Schubert classes in $G/P$ in terms of Cartan numbers of $G$.

The aim of this article is to provide methods for constructing smooth projective complex varieties with ample cotangent bundle. We prove that the intersection of at least n/2 sufficiently ample general hypersurfaces in a complex abelian variety of dimension n has ample cotangent bundle. We also discuss analogous questions for complete intersections in the projective space. Finally, we present an unpublished result of Bogomolov which states that a general linear section of small dimension of a product of sufficiently many smooth projective varieties with big cotangent bundle has ample cotangent bundle.

In this paper, we find configurations of points in $n$-dimensional projective space $\left( {{\mathbb{P}}^{n}} \right)$ which simultaneously generalize both $k$-configurations and reduced 0-dimensional complete intersections. Recall that $k$-configurations in ${{\mathbb{P}}^{2}}$ are disjoint unions of distinct points on lines and in ${{\mathbb{P}}^{n}}$ are inductively disjoint unions of $k$-configurations on hyperplanes, subject to certain conditions. Furthermore, the Hilbert function of a $k$-configuration is determined from those of the smaller $k$-configurations. We call our generalized constructions ${{k}_{D}}$-configurations, where $D\,=\,\left\{ {{d}_{1}},\ldots ,{{d}_{r}} \right\}$ (a set of $r$ positive integers with repetition allowed) is the type of a given complete intersection in ${{\mathbb{P}}^{n}}$. We show that the Hilbert function of any ${{k}_{D}}$-configuration can be obtained from those of smaller ${{k}_{D}}$-configurations. We then provide applications of this result in two different directions, both of which are motivated by corresponding results about $k$-configurations.

Let 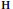$\mathbf{H}$ be the Hilbert function of some set of distinct points in 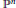${{\mathbb{P}}^{n}}$ and let 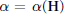$\alpha \,=\,\alpha (\mathbf{H})$ be the least degree of a hypersurface of 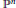${{\mathbb{P}}^{n}}$ containing these points. Write 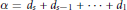$\alpha ={{d}_{s}}+{{d}_{s-1}}+\cdot \cdot \cdot +{{d}_{1}}$ (where 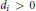${{d}_{i}}>0$ ). 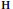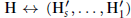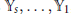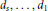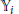We canonically decompose $\mathbf{H}$ into $s$ other Hilbert functions $\text{H}\leftrightarrow \text{(}{{\text{H}'}_{s}}\text{,}...\text{,}{{\text{H}'}_{1}}\text{)}$ and show how to find sets of distinct points ${{\mathbb{Y}}_{s}},...,{{\mathbb{Y}}_{1}}$ , lying on reduced hypersurfaces of degrees ${{d}_{s}},...,{{d}_{1}}$ (respectively) such that the Hilbert function of ${{\mathbb{Y}}_{i}}$ is 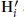${{\text{H'}}_{i}}$ and the Hilbert function of $\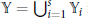mathbb{Y}=\bigcup _{i=1}^{s}\,{{\mathbb{Y}}_{i}}$ is 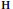$\mathbf{H}$. Some extremal properties of this canonical decomposition are also explored.

Let A be the coordinate ring of a set of s points in pn(k). After examining what the Hilbert function of A tells us about the conductor of A, we then determine the possible conductors for those coordinate rings which have the Hilbert function of a complete intersection in P2(k).

We give a criterion in order that an affine variety defined over any field has a complete intersection (ci.) embedding into some affine space. Moreover we give an example of a smooth real curve C all of whose embeddings into affine spaces are c.i.; nevertheless it has an embedding into ℝ3 which cannot be realized as a c.i. by polynomials.