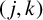 $(\,j,k)$-ENTRY
$(\,j,k)$-ENTRY 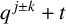 $q^{\,j\pm k}+t$
$q^{\,j\pm k}+t$
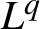 $L^{q}$
-spectra of measures on planar non-conformal attractors
$L^{q}$
-spectra of measures on planar non-conformal attractors