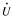If A is an elementary abelian group, let 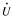 (A) denote the group of units, modulo torsion, of the group ring Z[A]. We study
(A) denote the group of units, modulo torsion, of the group ring Z[A]. We study 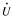 (A) by means of the composite
(A) by means of the composite
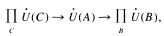
where C and B run over all cyclic subgroups and factor-groups, respectively. This map, γ, is known to be injective; its index, too, is known. In this paper, we determine the rank of γ tensored (over Z);with various fields. Our main result depends only on the functoriality of