Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hoechsmann, Klaus
1987.
Units and class-groups in integral elementary abelian group rings.
Journal of Pure and Applied Algebra,
Vol. 47,
Issue. 3,
p.
253.
Hoechsmann, Klaus
1992.
Exotic units in group rings of rankp 2.
Archiv der Mathematik,
Vol. 58,
Issue. 3,
p.
239.
Sehgal, S.K.
2003.
Vol. 3,
Issue. ,
p.
455.

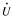 (A)
(A)