Ryabukhin showed that there is a correspondence between elementary radical classes of rings and certain filters of ideals of the free ring on one generator, analogous to the Gabriel correspondence between torsion classes of left unital modules and certain filters of left ideals of the coefficient ring. This correspondence is further explored here. All possibilities for the intersection of the ideals in a filter are catalogued, and the connections between filters and other ways of describing elementary radical classes are investigated. Some generalisations to nonassociative rings and groups are also presented.

In this paper it is shown how nonpointed exactness provides a framework which allows a simple categorical treatment of the basics of Kurosh–Amitsur radical theory in the nonpointed case. This is made possible by a new approach to semi-exactness, in the sense of the first author, using adjoint functors. This framework also reveals how categorical closure operators arise as radical theories.

Lattices of radicals have been extensively studied, for example in the class of associative rings, leading to some interesting results. In this paper we investigate the lattice L of all radicals in the class of all finite groups. We also consider some of its important sublattices. In particular, we prove that the lattice L is closed to being modular, the lattice Lh of all hereditary radicals is a Boolean algebra, and there exists a natural, useful projection of the lattice L onto Lh.

Let ρ be a supernilpotent radical. Let ρ* be the class of all rings A such that either A is a simple ring in ρ or the factor ring A/I is in ρ for every nonzero ideal I of A and every minimal ideal M of A is in ρ. Let be the lower radical determined by ρ* and let ρφ denote the upper radical determined by the class of all subdirectly irreducible rings with ρ-semisimple hearts. Le Roux and Heyman proved that is a supernilpotent radical with and they asked whether if ρ is replaced by β, ℒ , 𝒩 or 𝒥 , where β, ℒ , 𝒩 and 𝒥 denote the Baer, the Levitzki, the Koethe and the Jacobson radical, respectively. In the present paper we will give a negative answer to this question by showing that if ρ is a supernilpotent radical whose semisimple class contains a nonzero nonsimple * -ring without minimal ideals, then is a nonspecial radical and consequently . We recall that a prime ring A is a * -ring if A/I is in β for every .

An ideal 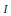$I$ of a ring 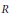$R$ is called a radical ideal if 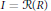$I\,=\,\mathcal{R}(R)$ where 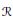$\mathcal{R}$ is a radical in the sense of Kurosh–Amitsur. The main theorem of this paper asserts that if 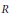$R$ is a valuation domain, then a proper ideal 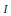$I$ of 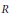$R$ is a radical ideal if and only if 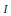$I$ is a distinguished ideal of 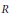$R$ (the latter property means that if 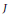$J$ and 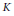$K$ are ideals of 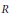$R$ such that 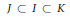$J\,\subset \,I\,\subset \,K$ then we cannot have 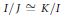$I/J\,\cong \,K/I$ as rings) and that such an ideal is necessarily prime. Examples are exhibited which show that, unlike prime ideals, distinguished ideals are not characterizable in terms of a property of the underlying value group of the valuation domain.

We prove that the lower radical, determined by a set of rings, is strong if and only if it is the lower radical determined by a ring with zero multiplication.

We prove that polynomial rings in one indeterminate over nil rings are antiregular radical and uniformly strongly prime radical. These give some approximations of Köthe's problem. We also study the uniformly strongly prime and superprime radicals of polynomial rings in non-commuting indeterminates. Moreover, we show that the semi-uniformly strongly prime radical coincides with the uniformly strongly prime radical and that the class of semi-superprime rings is closed under taking finite subdirect sums.

A characterization of all special atoms in the from of the upper radical generated by the class of all prime rings outside the smallest special class containing some prime ring is provided and prime rings for which the above mentioned upper radical coincides with the prime radical are investigated.

Some properties of the singular ideal are established. In particular its behaviour when passing to one-sided ideals is studied. Obtained results are applied to study some radicals related to the singular ideal. In particular a radical S such that for every ring R, S(R) and R/S(R) are close to being a singular ring and a non-singular ring, respectively, is constructed.

Let R be a ring and P(R) the sum of all periodic ideals of R. We prove that P(R) is the intersection of all prime ideals Pα such that contains no nontrivial periodic ideals. We also prove that P(R) = 0 if and only if Rs is a subdirect product of prime rings Rα with P(Rα) = 0.