The uniserial $p$-adic space groups of coclass $r$ play a central role in the classification of the finite $p$-groups of coclass $r$. A practical algorithm to determine up to isomorphism the uniserial $p$-adic space groups of coclass $r$, where $p$ is an odd prime, is described. As an application, these groups are constructed or counted for some values on $p$ and $r$. For example, it is observed that there are 137 299 953 383 uniserial 3-adic space groups of coclass 4.
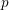 $p$-ADIC COHOMOLOGY
$p$-ADIC COHOMOLOGY