We find an upper bound for the number of groups of order n up to isomorphism in the variety ${\mathfrak {S}}={\mathfrak {A}_p}{\mathfrak {A}_q}{\mathfrak {A}_r}$, where p, q and r are distinct primes. We also find a bound on the orders and on the number of conjugacy classes of subgroups that are maximal amongst the subgroups of the general linear group that are also in the variety $\mathfrak {A}_q\mathfrak {A}_r$.

Dolfi, Guralnick, Praeger and Spiga asked whether there exist infinitely many primitive groups of twisted wreath type with non-trivial coprime subdegrees. Here, we settle this question in the affirmative. We construct infinite families of primitive twisted wreath permutation groups with non-trivial coprime subdegrees. In particular, we define a primitive twisted wreath group G(m, q) constructed from the non-abelian simple group PSL(2, q) and a primitive permutation group of diagonal type with socle PSL(2, q)m, and determine many subdegrees for this group. A consequence is that we determine all values of m and q for which G(m, q) has non-trivial coprime subdegrees. In the case where m = 2 and 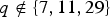$q\notin \{7,11,29\}$, we obtain a full classification of all pairs of non-trivial coprime subdegrees.

We present a classification of the nilpotent primitive subgroups of $\mathrm{GL}(n,q)$, up to conjugacy in $\mathrm{GL}(n,q)$. Groups in the classification are specified explicitly by generating sets of matrices, where each generating set has size at most 2. Additionally we give an algorithm designed to provide electronic access to the classification for any $n$ and $q$.